Abstract
Active suspensions, of which a bath of swimming microorganisms is a paradigmatic example, denote large collections of individual particles or macromolecules capable of converting fuel into mechanical work and microstructural stresses. Such systems, which have excited much research in the last decade, exhibit complex dynamical behaviors such as large-scale correlated motions and pattern formation due to hydrodynamic interactions. In this chapter, we summarize efforts to model these systems using particle simulations and continuum kinetic theories. After reviewing results from experiments and simulations, we present a general kinetic model for a suspension of self-propelled rodlike particles and discuss its stability and nonlinear dynamics. We then address extensions of this model that capture the effect of steric interactions in concentrated systems, the impact of confinement and interactions with boundaries, and the effect of the suspending medium rheology. Finally, we discuss new active systems such as those that involve the interactions of biopolymers with immersed motor proteins and surface-bound suspensions of chemically powered particles.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Background
Examples of soft active systems: (a) collective motion in a suspension of swimming Bacillus subtilis, where arrows show the velocity field [1]; (b) dynamic clusters in swarms of bacteria, where arrows show the direction of motion of the particles [2]; (c) spontaneous motion in a suspension of microtubules and kinesin motors confined at a two-dimensional interface [3]; (d) large-scale swirling motion in a suspension of actin filaments transported by wall-tethered myosin molecular motors [4]; (e) swarming of self-propelling liquid droplets in a Hele-Shaw cell [5]; (f) long-range order of vibrated polar disks on a two-dimensional substrate [6]. (Reproduced with permission)
The emerging field of soft active matter has excited much research in the last decade in areas as diverse as biophysics, colloidal science, fluid mechanics, and statistical physics [7–9]. Broadly speaking, an active matter system consists of a large collection of individual agents, such as particles or macromolecules, that convert some form of energy (typically chemical) into mechanical work. This work, in turn, leads to microstructural changes in the system, either via direct contact interactions or through long-ranged nonlocal interactions mediated by a suspending medium. Dramatic manifestations of these interactions include spontaneous unsteady flows on mesoscopic length scales, the formation of complex spatiotemporal patterns, and the emergence of directed collective motion. A wide variety of biological and physical systems fall into this broad definition, including (see Fig. 9.1): suspensions of self-propelled microorganisms such as motile bacteria and microscopic algae [10–12], the cell cytoskeleton and cytoplasm [13–15], solutions of motor proteins and biological filaments such as actin [4] and microtubules [3, 16, 17], reactive and driven colloidal suspensions [18–22], reactive emulsions [5], and shaken granular materials [23, 24]. A central question in all of these systems is the relation between the mechanics and interactions on the scale of individual particles and the ensuing self-organization and collective dynamics on the system scale [25].
Of particular interest to us here are so-called wet active systems, or active suspensions, in which the active particles are suspended in a viscous fluid and long-ranged hydrodynamic interactions are important. Numerous experiments have focused on the dynamics in suspensions of swimming bacteria. Some of the observations that have been made on this system include: the emergence of complex chaotic flows on length scales much greater than the particle dimensions and characterized by unsteady whirls and jets [10–12, 26, 27], enhanced particle velocities [10], a transition to collective motion when the bacterial density exceeds a certain threshold [11], local polar ordering [11], complex patterns and density fluctuations [28], enhanced swimmer and passive tracer diffusion [29–32], efficient fluid mixing [28, 33, 34], and bizarre rheologies created by particle activity [35–38].
The key ingredient to understanding how hydrodynamic interactions can yield such phenomena is the fluid flow set up by an isolated swimming particle. Because of their small sizes and the highly viscous environments in which they live, biological swimmers such as bacteria and microphytes move in the realm of low Reynolds numbers, where inertial forces are negligible and viscous stresses dominate [39]. In this regime, typical macroscopic mechanisms for locomotion are inefficient (or even inoperative) and novel strategies have evolved that are based on so-called non-reciprocal shape deformations [40]. Common locomotion mechanisms are based on the beating or rotation of flagellar appendages or the propagation of metachronal waves on the surface of ciliated cells [39, 41]. In the case of flagellar propulsion, which is the typical mode of locomotion in motile bacteria such as Bacillus subtilis and Escherichia coli as well as certain types of microalgae including Chlamydomonas reinhardtii, the cyclic nonreciprocal deformation of the flagella imparts a net propulsive thrust F p on the surrounding fluid in the direction opposite the net swimming motion, which we henceforth characterize in terms of a unit vector p. As microorganisms are typically neutrally buoyant, or nearly so, the net force on a particle must vanish in the limit of zero Reynolds number unless an external field is applied, and therefore an equal and opposite viscous drag force \(\mathbf{F}_{d} = -\mathbf{F}_{p}\) is also exerted on the fluid by the other parts of the organism (typically the cell body). This simple description of the forces on a microorganism suggests that their net effect on the suspending fluid is a force dipole, which drives a long-ranged flow with slow 1∕r 2 spatial decay in three dimensions, where r is the distance from the particle center. In the far field, the fluid velocity at relative position r from the particle can be expressed as
in terms of the fundamental solution \(\mathbf{J}(\mathbf{r}) = (1/8\pi \eta )(\mathbf{I} +\hat{ \mathbf{r}}\hat{\mathbf{r}})/r\) of the Stokes equations or response to a localized point force [44]. In Eq. (9.1), η denotes the viscosity of the fluid, and the second-order tensor S, called the stresslet, is the symmetric first moment of the stresses exerted by the particle on the fluid and can be obtained as S(p) = σ 0 pp. Its magnitude is given by σ 0 = ± | F p | ℓ, where ℓ is the distance between the points of application of the thrust and drag forces and scales with the particle length. The sign of σ 0 depends on the position of the thrust and drag forces relative to the swimming direction: σ 0 < 0 for a pusher particle that exerts a thrust with its tail (such as B. subtilis and E. coli), whereas σ 0 > 0 for a head-actuated puller particle (such as C. reinhardtii). A simple force balance on the cell body and based on Stokes drag also shows that the stresslet is linearly related to the swimming speed V s of the particle as \(\sigma _{0} \propto V _{s}\eta \ell^{2}\). Schematic diagrams of pusher and puller particles and their flows are shown in Figs. 9.2a–b. It is interesting to note that the notion of pushers and pullers is not limited to self-propelled particles. One can indeed envisage a particle that exerts a force dipole on the fluid (σ 0 ≠ 0) but does not swim (V s = 0), and so-called shakers, which can be either pushers or pullers, have been proposed as a very basic model for the dynamics of suspensions of microtubule bundles that extend in length due to motor-protein activity [3]. Immotile force dipoles could also be produced by elaborations of the synthesis process that produces the motile chemically-powered motors discussed in Sect. 4.2.
(a)–(b) Schematic diagrams of pusher and puller particles, of which E. coli and C. reinhardtii are paradigmatic examples. The swimming direction is indicated by p, and the red arrows show the direction of the induced fluid flow. (c) Experimental measurement of the flow field near an individual E. coli, showing good agreement with an extensile dipole flow [42]. (d) Experimental measurement of the time-averaged flow field near an individual C. reinhardtii, showing a complex flow in the near field and good agreement with a contractile dipole flow in the far field [43]. (Parts (c) and (d) reproduced with permission)
The elementary description of a swimming particle in terms of a force dipole has been tested experimentally with relative success. As illustrated in Fig. 9.2c, Drescher et al. [42] used particle-image velocimetry to measure the flow field around isolated E. coli cells and found good agreement with the flow field predicted by Eq. (9.1) with a negative stresslet, although strong noisy fluctuations were reported in the far field where the velocity field is the weakest. Similarly, Guasto et al. [43] and Drescher et al. [45] observed the flow field driven by C. reinhardtii: they uncovered a complex near-field flow structure that is best captured by a set of three off-centered point forces (corresponding to the cell body and two anterior flagella), but confirmed that the far-field flow can again be modeled as a dipole flow with a net positive stresslet. Guasto et al. [43] also noted that the flow around C. reinhardtii is time-periodic, with period equal to the duration of a swimming stroke, and in fact even reverses direction over the course of one stroke: we will not consider such time-dependence in the following discussion and only focus on the effect of the net time-averaged flow. Recent theoretical models, however, have suggested that such unsteady dynamics can lead to synchronization and novel instabilities as a result of hydrodynamic interactions [46, 47].
Knowledge of the velocity field driven by an isolated particle forms the basis for the modeling and study of hydrodynamic interactions between swimmers. While this description has been used to consider pair interactions [48–50], it can also be deployed to model large-scale suspensions. Hernández-Ortiz et al. [51] developed a minimal swimmer model in which a self-propelled microorganism is represented as a rigid bead-rod dumbbell. Propulsion arises as a result of a “phantom flagellum” exerting a force on the fluid at an off-centered point along the swimmer axis, causing the translation of the dumbbell at a velocity \(V _{s} = \vert \mathbf{F}_{p}\vert /2\zeta\), where ζ = 6π η a is the drag coefficient of each bead of radius a, and where hydrodynamic interactions between the two beads have been neglected. Because the propulsive force exerted by the flagellum is exactly balanced by the total drag on the dumbbell , the leading effect on the fluid is again that of a force dipole. This model was applied to simulate confined suspensions of many swimmers [51, 52], where it was shown to capture many qualitative features observed in experiments on bacterial suspensions, including enhanced diffusivities and large-scale correlated flows. More elaborate simulation models have also been developed over the years, though at the cost of increased computational complexity. This includes Pedley and coworkers’ Stokesian dynamics simulations of spherical squirmers [53], which propel as a result of a prescribed surface slip velocity and are an appropriate model for ciliated microorganisms. These simulations also showed enhanced motile particle and tracer diffusion [54, 55], as well as the development of large-scale coherent structures[56–58].
Numerical simulation of a semi-dilute suspension of self-propelled slender-rods above the onset of collective motion [59]: (a) snapshot of the particle distribution, showing coherent dynamic clusters with local orientational order; (b) hydrodynamic velocity field in a plane. (Adapted with permission)
In recent work, we also developed detailed simulations of active suspensions based on a slender-body model for hydrodynamically interacting rodlike particles [59, 60]. In this model, the particles propel themselves by exerting a prescribed tangential stress on some part of their surfaces, and both pusher and puller particles can be modeled by an appropriate choice of the stress distribution. In semi-dilute suspensions of pushers, large-scale chaotic flows taking place near the system size were observed (Fig. 9.3), together with increased swimming speeds and strong particle diffusion; no such dynamics were found in suspensions of pullers, which always remained uniform and isotropic.
Such particle simulations are useful for testing models and for detailed comparison with experiments, but are often too costly to simulate systems of realistic sizes and only yield limited analytical insight into the physical mechanisms involved. Another approach, which circumvents these limitations, consists in modeling the suspension as a continuum. Several continuum models have been developed for active suspensions, using a variety of approaches. In a seminal paper, Simha and Ramaswamy [61] extended phenomenological models for passive polar liquid crystals to account for activity. They wrote down an evolution equation for the polarization field n(r, t), which will be defined more precisely in Sect. 2.1, in which terms accounting for self-propulsion, diffusion, and rotation by the mean-field flow were included. This evolution equation was coupled to the Navier-Stokes equations for the fluid motion, forced by an active stress term capturing the effect of the force dipoles on the fluid. Based on this model, they predicted in the Stokesian limit a long-wave instability of globally aligned suspensions. Other phenomenological models have been proposed to account for additional effects such as steric interactions , which are included via ad hoc terms constructed based on symmetries [8, 12, 62–65].
In another related approach, which is the focus of this chapter, kinetic equations are self-consistently derived from a first-principles mean-field description of interactions between particles using coarse-graining. Such a model was introduced in our previous work [66, 67] and is based on a Smoluchowski equation for the conservation of the particle probability distribution function, in which the fluxes describe the linear and angular motions of the particles in the mean-field hydrodynamic flow driven by self-propulsion. This flow is obtained by solution of the Stokes equations forced by a coarse-grained active stress tensor similar to that used in the model of Simha and Ramaswamy [61]. This coupled system of partial differential equations can then be analyzed theoretically in the vicinity of theoretically relevant base states, or integrated numerically to investigate dynamics in the nonlinear regime. Extensions to include more complex effects such as an external flow [68], chemotaxis in a chemical field [69, 70], or steric interactions at high concentrations [71] have also been described.
In this chapter, we review our recent theoretical work on the continuum modeling of active suspensions. We begin in Sect. 2 by deriving a basic kinetic model for a suspension of slender swimmers interacting via force-dipole hydrodynamic interactions, where we show that the dynamics can be captured by a Smoluchowski equation for the particle distribution function, coupled to the Stokes equations for the fluid velocity in which the effect of the force dipoles on the flow is shown to amount to an effective active stress. After discussing theoretical and computational results on this model, a number of extensions are presented in Sects. 3 and 4, and we conclude in Sect. 5.
2 A Simple Kinetic Model
2.1 Smoluchowski Equation
In this section, we present the basic kinetic model introduced in our previous work [66, 67], which shares similarities with classic models for suspensions of passive rodlike particles [72, 73]. A very similar theory for active suspensions was independently proposed by Subramanian and Koch [74].
In the present model, we describe the configuration of the suspension at time t in terms of the probability distribution function Ψ(r, p, t) of finding a particle with center-of-mass position r and orientation p (with | p | 2 = 1). It is normalized as
where V is the volume of the system, Ω is the unit sphere of orientations, and \(n = N/V\) is the mean number density in a suspension of N particles. Conservation of particle number requires that Ψ(r, p, t) satisfy the Smoluchowski equation [72]
where \(\nabla _{p} = (\mathbf{I} -\mathbf{pp}) \cdot (\partial /\partial \mathbf{p})\) denotes the gradient operator on the unit sphere. The flux velocities \(\dot{\mathbf{r}}\) and \(\dot{\mathbf{p}}\) describe the linear and angular motions of the particles in the suspension. The linear velocity of a particle is expressed as the sum of the single-particle swimming velocity V s p (assumed to be unaffected by interactions) and the local background fluid velocity u(r, t) and also includes a contribution from translational diffusion with diffusivity D (assumed to be isotropic):
The rotational velocity of a swimmer is modeled as
The first term on the right-hand side captures rotation of an anisotropic particle in the local flow according to Jeffery’s equation [75], where \(\mathbf{E} = (\nabla \mathbf{u} + \nabla \mathbf{u}^{T})/2\) and \(\mathbf{W} = (\nabla \mathbf{u} -\nabla \mathbf{u}^{T})/2\) denote the rate-of-strain and vorticity tensors, respectively. The parameter β characterizes the shape of the particle, with \(\beta = (a^{2} - 1)/(a^{2} + 1)\) for a spheroid of aspect ratio a and β ≈ 1 for a slender particle [76]. Rotational diffusion is also included with diffusivity d.
Equations (9.4)–(9.5), and in particular the contributions from the mean-field flow u(r, t), are strictly valid for a linear flow field and provide an accurate estimate of the velocities if the characteristic length scale of the flow is much greater than the particle size, a good approximation in a sufficiently dilute suspension. If velocity variations on the scale of a particle are significant, these can be captured using the more accurate Faxén laws for a slender body [77] or a spheroidal particle [44].
The physical origin of the diffusive terms in Eqs. (9.4)–(9.5) deserves some discussion. While Brownian diffusion due to thermal fluctuations can be significant in colloidal systems [19, 21], it is generally negligible in suspensions of biological swimmers. As demonstrated in experiments [42, 78], diffusion still occurs in biological systems owing to shape imperfections or noise in the swimming actuation. In a dilute suspension, these effects can be described in terms of constant diffusion coefficients D 0 and d 0. We note, however, that rotational diffusion alone leads to a random walk in space owing to its coupling with the swimming motion, resulting in enhanced spatial diffusion at long times by a mechanism similar to generalized Taylor dispersion [79, 80], with a net translational diffusivity given by \(D = D_{0} + V _{s}^{2}/6d\) in three dimensions [60, 81]. In addition to diffusion due to noise, fluid-mediated hydrodynamic interactions between particles can also result in hydrodynamic diffusion in semi-dilute and concentrated systems. At fairly low concentrations (n ℓ 3 ≲ 1), a simple argument based on pair interactions suggests that d ∝ n ℓ 3, from which D ∝ (n ℓ 3)−1 [74, 82], and such scalings have indeed been verified in particle simulations [60].
While the distribution function Ψ(r, p, t) fully characterizes the configuration of the particles in the suspension, it is often useful to consider its orientational moments, which have easy physical interpretations. Of particular interest are the zeroth, first, and second moments, which correspond respectively to the concentration field c(r, t), polar order parameter n(r, t), and nematic order parameter Q(r, t). These are defined as
where \(\langle \cdot \rangle\) denotes the orientational average:
Evolution equations for c, n, and Q can be obtained by taking moments of the Smoluchowski equation (9.3):
where \(\mathcal{D}_{t} \equiv \partial _{t} + \mathbf{u} \cdot \nabla \) is the material derivative. Unsurprisingly perhaps, these equations involve the third and fourth moments \(\langle \mathbf{ppp}\rangle\) and \(\langle \mathbf{pppp}\rangle\) of the distribution function and can therefore only be used together with a closure model, unlike the more general and self-contained description in terms of Ψ(r, p, t). Several closure models have been proposed in the past, usually based on various approximations such as weak or strong flow or near isotropy (see references in Saintillan and Shelley [9]) or by interpolating between such states [83].
2.2 Mean-Field Flow and Active Stress Tensor
Evolution of the Smoluchowski equation requires knowledge of the mean-field hydrodynamic velocity in the suspension. While this velocity could include a contribution from an external flow [68], we are primarily interested in the flow driven by the suspended particles themselves as they propel through the fluid. In a dilute suspension, the velocity u(r, t) can then be obtained as the superposition of all the point dipole flows induced by individual particles. For a given distribution Ψ(r, p, t), the velocity at point r is therefore expressed as a convolution:
where \(\mathbf{u}^{d}(\mathbf{r}\vert \mathbf{p})\) is the single-particle dipolar flow given in Eq. (9.1). This single-particle flow can be shown to satisfy the Stokes equations forced by a dipole singularity as
where δ(r) is the three-dimensional Dirac delta function and q d denotes the pressure. By combining Eqs. (9.11) and (9.12), it is straightforward to show that the mean-field velocity u(r, t) and its associated pressure field q(r, t) satisfy
together with the incompressibility condition \(\nabla \cdot \mathbf{u}(\mathbf{r},t) = 0\). After manipulations, this can be rewritten
The second-order tensor inside the divergence on the right-hand side is the local configurational average of the particle stresslet: \(\langle \sigma _{0}\mathbf{pp}\rangle =\langle \mathbf{S}(\mathbf{p})\rangle\). Following classic theories for the stress in particle suspensions [84, 85], it can be interpreted as an extra stress induced by the particles, which we term active stress and define more precisely as
We have made the tensor traceless by removing an isotropic tensor that only modifies the pressure but has no effect on the flow. It can be seen that the active stress is related to the nematic order parameter as: \(\boldsymbol{\varSigma }^{a}(\mathbf{r},t) =\sigma _{0}c(\mathbf{r},t)\mathbf{Q}(\mathbf{r},t)\), implying that active stresses vanish in the isotropic state and are caused by the nematic alignment of the swimmers. We also note that the active stress has the same tensorial form as the Brownian stress \(\boldsymbol{\varSigma }^{b}(\mathbf{r},t) =\langle 3kT(\mathbf{pp} -\mathbf{I}/3)\rangle\) in suspensions of passive rodlike polymers [72]. One significant difference, however, lies in the sign of the stresslet strength σ 0, which is negative for pusher particles. Note also that the expression for the active stress tensor (9.15), which we derived here for a distribution of point dipoles, is in fact more general and can be used for a suspension of finite-sized axisymmetric particles such as swimming rods [9], though these more detailed derivations yield additional contributions of higher order in volume concentration [71, 86].
In the following, we find it useful to nondimensionalize lengths by the characteristic scale \(l_{c} =\ell /\nu\), where \(\nu = N\ell^{3}/V = n\ell^{3}\) is an effective volume fraction, and time by \(t_{c} = V _{s}/l_{c}\). The distribution function Ψ is also scaled by the mean number density n. Upon these scalings, the dipole strength σ 0 appearing in the active stress tensor is replaced by a dimensionless signed coefficient \(\alpha =\sigma _{0}/V _{s}\eta \ell^{2}\). After non-dimensionalization, the basic kinetic system is given by
whose nondimensional coefficients, aside from the shape factor β, are the signed O(1) parameter α and the rescaled diffusion coefficients D and d.
This model is very similar structurally to those developed by Doi and coworkers to describe the dynamics of passive rod suspensions [72, 87]. The primary differences are the additional contribution (i.e., p) to Eq. (9.17) for \(\dot{\mathbf{r}}\) coming from locomotion and that α > 0 for the dipolar extra stress in passive rod suspensions. That said, the origins of the dipolar stress are very different in the two cases. For active suspensions it arises from the swimming of pushers or pullers, while in the passive case it arises from rotational thermodynamic fluctuations which we have neglected here. For both passive and active systems, the existence of global “entropy solutions” has recently been proved by Chen and Liu [88].
2.3 The Conformational Entropy
Much insight can be gained into the differences between pusher and puller suspensions by consideration of the system’s conformational entropy [67], which we define in terms of the distribution function as
where \(\varPsi _{\,0} = 1/4\pi\) denotes the constant value of Ψ for a uniform isotropic suspension. It is straightforward to show that the entropy is a positive quantity and that it reaches its minimum of zero only for Ψ ≡ Ψ 0. The entropy \(\mathcal{S}(t)\) therefore provides a global measure of the level of fluctuations in the system, both orientational and spatial. When linearized about the uniform isotropic state Ψ 0, it reduces to the squared \(\mathcal{L}_{2}\) norm in r and p. Using the kinetic equations above, one can derive an expression for its rate of change:
The last term in Eq. (9.21), which is always negative, arises due to diffusive processes which tend to homogenize the suspension and decrease the entropy. However, the first term on the right-hand side, which arises from active stresses in the fluid, can be either positive or negative depending on the sign of α. In a suspension of pullers (α > 0), this term is negative definite and drives the system towards equilibrium. In the case of pushers (α < 0), however, the active stress term becomes positive and can increase fluctuations in the system by driving \(\mathcal{S}\) away from zero. This suggests that pusher suspensions may be subject to the spontaneous growth of fluctuations whereas pullers are not, and this fundamental difference between the role of active stresses in pusher and puller suspensions is further examined by a more detailed stability analysis as described next.
2.4 Stability of the Uniform Isotropic State
The uniform isotropic state \(\varPsi \equiv \varPsi _{0} = 1/4\pi\) is an exact steady solution of the above continuum model, whose stability can be investigated. Perturbing Ψ 0 by a plane wave of the form \(\tilde{\varPsi }(\mathbf{p},\mathbf{k})\exp (\mathrm{i}\mathbf{k} \cdot \mathbf{r} +\lambda t)\) and linearizing the governing equations yields an eigenvalue problem for the growth rate λ and eigenmode \(\tilde{\varPsi }\) that can be solved numerically [66, 67]. In agreement with the analysis on the configurational entropy in Sect. 2.3, solutions of the eigenvalue problem reveal fundamentally different dynamics in suspensions of rear- and front-actuated swimmers. In puller suspensions, the real growth rate Re(λ) is found to be negative at all wavenumbers, indicating that the uniform isotropic state is stable to infinitesimal perturbations. This is indeed borne out by particle simulations in the dilute and semi-dilute regimes [59], which never show the emergence of collective motion. On the other hand, the solution of the eigenvalue problem for a suspension of pushers, which is shown in Fig. 9.4a, shows a positive growth rate at low wavenumbers, suggesting that long-wavelength fluctuations can amplify as a result of hydrodynamic interactions. Moreover, Fig. 9.4a shows that the fastest growing linear modes occur near k = 0, implying that the linear analysis does not yield a dominant length scale independent of system size.
(a) Real and imaginary parts of the complex growth rate λ for a plane-wave perturbation with respect to the uniform isotropic state as function of wavenumber k in the absence of diffusion. (b) Evolution of the concentration field c(r, t) in a three-dimensional periodic simulation of a suspension of pushers, starting near the state of uniform isotropy
Consideration of the eigenmodes demonstrates that this linear instability is not associated with the growth of concentration fluctuations (\(\tilde{c} = 0\)), but rather with the local nematic alignment of the particles. More precisely, the nematic order tensor parameter for the unstable eigenfunctions can be shown to be of the form
where \(\hat{\mathbf{k}}\) denotes the wave direction and \(\hat{\mathbf{k}}_{\perp }\) is any direction orthogonal to \(\hat{\mathbf{k}}\). In the language of liquid crystals , such spatial fluctuations of the nematic order parameter correspond to “bend” modes, as also predicted in other studies based on moment equations [89], and such bend modes are indeed visible in particle simulations such as that of Fig. 9.3a.
An important result also shown in Fig. 9.4a is the decay of the growth rate with increasing wavenumber, which even results in stabilization at high k. As discussed by Hohenegger and Shelley [90], this indicates that there exists a critical system size above which pusher suspensions become unstable. In dimensional variables, this criterion is written more specifically in terms of the linear system size \(L = V ^{1/3}\) as
where k c is the dimensionless wavenumber for which λ(k c ) = 0 and is a function of α and of the diffusion coefficients. The condition (9.23) states that instability occurs either in dense systems (large ν) or in large systems (large L∕ℓ), and this criterion was systematically tested and confirmed in our previous particle simulations [59], where good agreement was found for the value of k c .
Another interesting interpretation for this instability involves the active power input generated by the swimming particles in the fluid. The global power input \(\mathcal{P}(t)\) was introduced in our previous work [67], where we also used an energy balance on the momentum equation (9.19) to show that it equates the rate of viscous dissipation in the fluid:
Assuming a cubic periodic domain of unit length L, a simple application of Parseval’s identity allows one to rewrite \(\mathcal{P}(t)\) in terms of the Fourier coefficients \(\tilde{\mathbf{E}}(\mathbf{k},t)\) of the rate-of-strain tensor, which themselves can be related to the Fourier coefficients \(\tilde{\mathbf{Q}}(\mathbf{k},t)\) of the nematic order tensor parameter:
Time evolution of the active power input per particle in direct numerical simulations of pushers and pullers in a cubic periodic box of size L = 10ℓ at various volume fractions ν. (Adapted with permission from Saintillan and Shelley [59])
where the last term was obtained assuming that \(c(\mathbf{r},t) \approx 1\), a valid approximation in the linear regime. From the form of the right-hand side, it is clear that only Fourier modes of the form of (9.22) will contribute to the power input, which can be interpreted as the total energy of the unstable bend modes in the system. The growth of \(\mathcal{P}(t)\) therefore provides a direct measure of instability. Its evolution in particle simulations was considered in our previous work [59] and is shown in Fig. 9.5 for suspensions of pushers and pullers at various concentrations. In agreement with the theoretical prediction, the power only grows in sufficiently concentrated suspensions of pushers. In suspensions of pullers, it decreases below the dilute value corresponding to isolated swimmers, suggesting that particles in fact reorganize in a subtle way so as to suppress bend modes in the system.
After the initial transient growth, a statistical steady state is reached as a result of diffusive processes, which counteract the instability as expected from Eq. (9.21). No steady solution is observed in simulations, which instead show unsteady chaotic dynamics with the formation of dense and nematically aligned particle clusters that quasi-periodically form and break up over time as shown in Fig. 9.4b. As we argued above, the growth of concentration fluctuations is not predicted by the linear analysis, but it can be explained as a result of nonlinearities. Equation (9.8) for the concentration field, which is written in dimensionless variables as
shows that concentration fluctuations can only grow through the source term on the right-hand side, which arises from self-propulsion. The mechanism can be understood as follows [67]: (i) the linear instability for the nematic order parameter first causes local alignment of the particles, which is primarily nematic but also generally involves some weak polarity due to random fluctuations in the initial condition; (ii) this net polarity then leads to concentration of particles as a result of self-propulsion in regions where \(\nabla \cdot (c\mathbf{n}) < 0\). Interestingly, this also suggests that no concentration fluctuations would arise in a suspension of either apolar or non-self-propelled active particles (so-called shakers) , for which the source term on the right-hand side of Eq. (9.26) is strictly zero.
As a side note, the case of nonmotile shakers is particularly revealing as to the linear structure of an active suspension. As discussed in Sect. 1, a shaker suspension is simply an ensemble of immotile force dipoles that are moved by whatever velocity field they produce by their collective flows (i.e., set V s = 0 in Eq. (9.4) while retaining the active stress in the momentum equation). This simple model again satisfies the entropy equality (9.21). Betterton et al. [91] further showed that in this case the linearized model simplifies remarkably by introducing a vector stream function \(\boldsymbol{\varPhi }\) and the vorticity \(\boldsymbol{\omega }\). Then we have
where Betterton et al. showed that h satisfies the simple dynamics
For plane-wave perturbations, this equation has the simple growth-rate relation \(\lambda (k) = -(\alpha /5 + 6d) - Dk^{2}\) and hence can show instability only if particle extensile flows are sufficiently strong to overcome rotational diffusion, that is, when α < −30d. More to the point though, Eq. (9.28) shows that an active suspension has a very elementary underlying linear structure of a simple exponential growth, driven by activity and damped by rotational diffusion and regularized by spatial diffusion. Note that unlike the motile case [90], there is no loss of solutions, at a finite k, to the plane-wave eigenvalue problem when d = 0.
3 Extensions and Applications
3.1 Concentrated Suspensions
The kinetic model described above is based on a dilute assumption and only includes mean-field hydrodynamic interactions between particles. While this approximation is valid at sufficiently low volume fractions [59], it is likely to break down in concentrated systems in which particle-particle contact interactions become significant. Including such interactions is important to accurately capture dynamics in bacterial suspensions, as the onset of collective motion in experiments is typically observed at high densities [11]; in fact, it has sometimes even been suggested that contacts may be the dominant effect leading to collective dynamics. While accounting for contacts in particle simulations is feasible [60, 92], albeit at a high computational cost, it is not as straightforward within the context of our kinetic theory as such interactions are discrete and pairwise. Aranson et al. [62] proposed a continuum model to account for steric interactions based on a collision operator having the effect of aligning contacting particles, in qualitative agreement with experimental observations. To correctly account for collisions, however, their model requires knowledge of the pair distribution function in the suspension, which was approximated as the product of two singlet distributions. Similarly, Baskaran and Marchetti [93] developed a kinetic theory for self-propelled hard rods in two dimensions accounting for pairwise collisions. They were able to show that the leading effect of collisions is to modify the orientational flux by addition of an aligning torque of the same form as the classic Onsager potential for excluded-volume interactions in passive rodlike polymer suspensions [94].
Based on this observation, Ezhilan et al. [71] adapted the kinetic model discussed in Sect. 2 to account for contact interactions in a mean-field framework similar to that used in classic theories for passive rods. Specifically, following the work of [87], we account for contacts by including an effective steric torque derived from a potential U:
where the interaction kernel is taken to be the phenomenological Maier-Saupe kernel: \(K(\mathbf{p},\mathbf{p}') = -U_{0}(\mathbf{p} \cdot \mathbf{p}')^{2}\) with strength constant U 0 [95]. Inserting the expression for K into Eq. (9.29) and taking the orientational gradient yield a new expression for the rotational velocity:
where it can be seen that the new term causes alignment of p along the principal axes of the nematic order tensor parameter Q associated with positive eigenvalues, i.e., along the local preferred directions of nematic alignment.
The first effect of this additional torque is to allow for non-isotropic nematic base states as volume concentration increases. As shown by Ezhilan et al. [71], the transition from isotropy to nematic alignment, which is the same as that occurring in liquid crystalline systems, is governed by the dimensionless group \(\xi = 2U_{0}\nu /d\) representing the ratio of the steric alignment torque to rotational diffusion. All spatially uniform base states can be shown to be axisymmetric and of the Boltzmann form
where θ denotes the angle between p and the direction of nematic alignment, which must be specified. Here, the parameter δ governs the shape of the orientation distribution and is a zero of the function
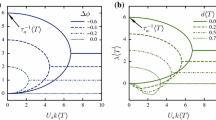
(a) Isotropic-to-nematic transition in a concentrated suspension as the parameter \(\xi = 2U_{0}\nu /d\) is increased. Branch 1 is isotropic, whereas branches 2 and 3 are nematic. (b)–(c) Stability diagrams for pusher and puller suspensions, showing the stability of the three branches in each case. (Adapted with permission from Ezhilan et al. [71])
It is easy to see that δ = 0 is a solution, which corresponds to the isotropic base state. However, when ξ ≥ ξ c ≈ 13. 46, there exist two other zeroes corresponding to nematic orientation distributions, as illustrated in Fig. 9.6a showing the three branches of the function δ(ξ). Positive values of δ are achieved on branch 2, which corresponds to the strongest nematic alignment; negative values are also possible along branch 3 and indicate a preferential alignment in the plane normal to the axis of symmetry. A simple consideration of the total steric interaction energy on each branch suggests that above ξ c the energy is minimized on branch 2, which is consistent with the concept of an isotropic-to-nematic transition as concentration increases.
This energy argument, however, does not imply that such base states are hydrodynamically stable. To investigate the stability of these branches, the kinetic model of Sect. 2 must also be modified to account for additional stresses that arise at finite concentrations: first, passive viscous stresses due to the interactions of the particles with the local flow [83] have to be included and lead to an effective increase in the viscosity of the suspension, unlike active stresses that tend to decrease it in suspensions of pushers [37]. Second, steric interactions also lead to an additional stress contribution which was previously calculated for slender particles [71, 72]. Using this model, Ezhilan et al. [71] numerically studied the stability of the various base states, and results are summarized in Figs. 9.6b–c for both pusher and puller particles. In the case of pushers, the isotropic base state (branch 1) becomes unstable with increasing concentration before the isotropic-to-nematic transition occurs: this instability is of hydrodynamic origin and simply corresponds to the basic instability described in Sect. 2.4. The case of pullers, however, is more interesting. It is found that the isotropic base state loses stability at ξ = 15 when branch 1 intersects branch 3 as a result of steric interactions only. Branch 3, however, is always unstable. Branch 2, which has the lowest steric interaction energy, is stable at first but eventually also loses stability when ξ increases as result of hydrodynamic modes. This high-concentration instability of puller suspensions is quite surprising and is corroborated by numerical simulations. To our knowledge it has never been observed in experiments, perhaps because biological pullers are scarce and the few species that exist, including Chlamydomonas, have nearly spherical bodies and are therefore unlikely to undergo the isotropic-to-nematic transition.
While the model described above provides a qualitative understanding of the effect of collisions on the dynamics, it is based on a number of strong approximations and on a phenomenological mean-field description of steric interactions in terms of the Maier-Saupe potential. First, the validity of this description can be questioned and should ideally be tested using particle simulations. These are quite expensive in the concentrated regime even for passive rods [96] and have yet to be developed for self-propelled particles in three dimensions. Second, the description of the stresses typically used in the kinetic models such as those discussed herein is based on a dilute assumption, resulting in stresses that depend linearly or quadratically on density; a more accurate description of these stresses should account for multiple reflections between particles as well as multi-body interactions, though models of this type have been limited to passive rod suspensions [97]. Finally, the kinetic theory outlined above used a single velocity field u to describe the transport of the fluid and particle phases. This is a good approximation in the dilute limit but is likely to break down at high volume concentrations, where a two-fluid approach would be more appropriate [63, 98].
3.2 Confinement
Experimental evidence suggests that interactions with rigid boundaries in confined environments can be highly complex and play an important role in the dynamics and transport properties. Some examples of the complex effects that have been reported under confinement include: accumulation of particles at boundaries [38, 99, 100], upstream swimming in channel flows [101], unexpected scattering dynamics [102, 103], modified diffusivities [104], circular swimming trajectories [105], and spontaneous flow transitions [106, 107]. Modeling efforts on the role of boundaries and the effects of confinement, however, have been relatively scarce. Analytical models and numerical simulations indeed predict concentration at boundaries [51, 52, 108, 109], both as a result of hydrodynamic interactions [110] and because of particle self-propulsion, though models for collision rules are often chosen in an ad hoc manner.
The modeling of wall interactions in continuum theories has also been relatively limited. In phenomenological theories for active liquid crystals, boundary conditions are often formulated in terms of anchoring conditions for the nematic order parameter [111–113], which are borrowed from classic liquid crystal theories but do not account for the unique nature of wall interactions due to self-propulsion. Within the context of the kinetic model of Sect. 2, a natural boundary condition to enforce at impenetrable walls consists in prescribing zero net translational flux in the wall-normal direction (with unit normal N): \(\mathbf{N} \cdot \dot{\mathbf{r}} = 0\). Inserting Eq. (9.17) for the flux velocity, this translates into a Robin boundary condition
which expresses the balance between the swimming flux towards the wall and the diffusive flux away from it, and this simple boundary condition has been shown to capture many features observed in experiments. Note that Eq. (9.33) neglects the finite size of the particles, which forbids configurations near the boundaries leading to overlap of the particles with the wall and is expected to result in a thin depletion layer as seen in experiments [114]; more complex boundary conditions that account for excluded-volume interactions have also been formulated, both in the context of passive suspensions [115] and also recently for active particles [116].
As a simple example of application of Eq. (9.33), Ezhilan and Saintillan [116] analyzed the case of a suspension confined between two parallel flat plates separated by a gap 2H in the limit of infinite dilution where hydrodynamic interactions can be entirely neglected. Assuming the Taylor dispersion relation \(D = V _{s}^{2}/6d\) for the translational diffusivity, the dimensionless Smoluchowski equation (9.16) reduces at steady state to a simple partial differential equation expressing the balance of self-propulsion and translational and rotational diffusion:
Here, z ∈ [−1, 1] is the wall-normal coordinate, \(\theta =\cos ^{-1}(\mathbf{p} \cdot \mathbf{N})\) is the polar angle measured with respect to the wall-normal direction, and we have introduced a swimming Péclet number comparing the relative magnitude of self-propulsion to rotational diffusion: \(\mathrm{Pe}_{s} = V _{s}/2Hd\). Equation (9.34) should be solved subject to the boundary condition (9.33), which simplifies to
A numerical solution of Eqs. (9.34)–(9.35) was obtained by Ezhilan and Saintillan [116] and is shown in Fig. 9.7, where both the concentration c(z) and wall-normal polarization m z (z) = c(z)n z (z) are plotted. A net accumulation of particles is observed near both boundaries, in agreement with experiments [99] and simulations [51, 109]. This accumulation is accompanied by a net polarization towards the boundaries, and both effects are found to become stronger as Pe s decreases, which corresponds to an effective decrease in translational diffusivity owing to the Taylor dispersion scaling. This accumulation and corresponding polarization are easily understood physically: any particle inside the channel will tend to swim to the wall towards which it points and accumulate there until rotational diffusion causes it to reverse polarity. Note that this accumulation is not a result of hydrodynamic interactions with the boundaries, though it has been suggested that hydrodynamic interactions can reinforce migration in pusher suspensions due to the reflection of the dipolar flow driven by the swimmers [99]. One interesting consequence of this net polarization occurs when a pressure-driven flow is applied between the two plates: particles near the walls rotate under the flow in such a way that they preferentially point upstream, causing them to swim against the flow. This curious prediction is consistent with experimental observations using bacteria in microfluidic devices [101, 117, 118] and has also been observed in simulations [109, 119].
The effect of confinement has also been studied theoretically in closed domains. Woodhouse and Goldstein [106] posited that a suspension of shakers could serve as a basic model for the dynamics of biopolymers moved by immersed motor proteins. To simplify the model, they assumed a uniform particle concentration (which is an allowable state of the system) and employed a classical moment closure scheme of Hinch and Leal [83] to find an approximate dynamical equation for the nematic order parameter Q. Evolving this equation in a circular two-dimensional domain, they assumed a no-slip boundary condition on the background velocity and the boundary condition \(\partial \mathbf{Q}/\partial \mathbf{N} = \mathbf{0}\) for the nematic tensor, which is consistent with Eq. (9.33) after setting V s = 0. Using numerical simulations, they identified the existence of a bifurcation, with increasing active stress strength α, from an isotropic state with no flow to a unipolar vortical flow driven by suspension activity, as shown in Fig. 9.8. Higher levels of active stress can lead to successive bifurcations with yet more complex vortical flows, sometimes oscillatory, and with nematic orientation singularities. Such vortical flows are indeed observed in experiments on confined drops of cytoskeletal extracts [15], as well as in drops of confined suspensions [107]. Jhang and Shelley [120] found consistent results using the full unapproximated suspension model of Sect. 2, again using the no-slip condition and the no-flux boundary condition \(\partial \varPsi /\partial \mathbf{N} = 0\) on the boundary of a circular domain.
Numerical simulation by Woodhouse and Goldstein [106] of the spontaneous flow in a two-dimensional shaker suspension confined in a circular domain and modeled using a closure approximation: (a) shows Schlieren patterns of the nematic order director, whereas (b) shows flow streamlines, with darker streamlines indicating faster flow. (Adapted with permission)
Not only does confinement affect particle distributions in the dilute regime, but it also modifies the way particles interact hydrodynamically. This is particularly apparent in the case of strong confinement where the size of the particles is on the order of the geometric dimensions of the domain, say the gap width in a Hele-Shaw geometry. This situation was analyzed theoretically by Brotto et al. [121] using a similar continuum kinetic theory as in Sect. 2 in the case of a two-dimensional monolayer of particles confined between two flat plates. As explained in their study, the leading effects of confinement are twofold. Firstly, as is well known from studies on passive suspensions [122, 123], momentum screening by the rigid boundaries leads to the rapid decay as 1∕r 3 of the flow driven by the force dipole due to self-propulsion. On the other hand, the motion of the finite-sized swimmers relative to the fluid results in a mass dipole which now decays as 1∕r 2 in confinement, as opposed to 1∕r 3 in bulk systems. On large length scales, the disturbance flow due to this mass dipole is expected to dominate interactions and is now expressed in two dimensions as
The dipole strength is proportional to the relative velocity between the swimmer and the suspending fluid: \(\boldsymbol{\chi }=\chi _{0}[\dot{\mathbf{r}} -\mathbf{u}(\mathbf{r})]\), where the prefactor χ 0 scales as the particle surface area in the plane of the flow and is independent of the propulsion mechanism. Secondly, Brotto et al also argued that confinement can modify the way particles respond to a given flow field: in particular, fore-aft asymmetric particles (such as much flagellated swimmers) are expected to align not only with the velocity gradient as in Jeffery’s equation (9.18) but also with the velocity itself as a result of the lubricated friction with the neighboring walls. To capture this effect, they derived a modified equation for the rotational flux velocity to read
Here, the parameter β′ depends on particle shape: it is zero for a fore-aft symmetric particle, positive for a “large-tail” swimmer that aligns with the flow, and negative for a “large-head” swimmer that aligns against the flow. Based on these effects, they derived a kinetic model similar to that of Sect. 2 and analyzed the stability of the uniform isotropic base state. They uncovered a long-wave instability in suspensions of large-head swimmers (for which β′ < 0), which pertains to splay components of the nematic tensor above a certain level of activity. Their analysis was subsequently refined by Lefauve and Saintillan [124], who also performed direct numerical simulations of point particles in two-dimensional geometries. Above the threshold of instability, complex dynamics illustrated in Fig. 9.9 were observed that differed significantly from those observed in unconfined suspensions: when β′ < 0, particles were found to arrange in longitudinal polarized waves with a net curvature indicative of splay, whereas for β′ > 0 they converged into active lanes circulating around large-scale vortices. Recent numerical work on the same system by Tsang and Kanso [125] also predicted the formation of stable clusters when β′ < 0 and proposed an interpretation of β′ in terms of flagellar activity.
Particle simulations of two-dimensional swimmer suspensions in a Hele-Shaw geometry, based on the model of Brotto et al. [121]: (a) large-head swimmers (β′ < 0) form polarized density waves with splay, whereas (b) large-tail swimmers (β′ > 0) organize into active lanes circulating around large-scale vortices. (Adapted with permission from Lefauve and Saintillan [124])
3.3 Chemotaxis
The ability of swimming microorganisms to detect and respond to external stimuli such as chemical fields is critical to biological functions such as nutrient and oxygen uptake, toxin avoidance, colony growth, and cell-cell communication for gene regulation or aggregation. The method used by many bacteria to perform chemotaxis (or directed migration along a chemical gradient) is a modulated run-and-tumble dynamics [126]. Here, “runs” of directed bacterial swimming are interspersed with random reorientations, or “tumbles,” resulting from the unbundling and rebundling of their flagella. These arbitrary changes in swimming direction lead to a random walk in space [81], which can be biased towards a particular direction by modulating the frequency λ of tumbles. More specifically, a bacterium that tumbles less frequently when it swims in the direction of increasing chemical concentration will on average drift towards regions of higher concentration. Run-and-tumble dynamics can be easily incorporated into the kinetic framework discussed here. In particular, the Smoluchowski equation is modified to
Here λ is the tumbling frequency away from orientation p and depends upon \(\tilde{\mathcal{D}}_{t}C = \partial _{t}C + (\mathbf{u} + V _{s}\mathbf{p}) \cdot \nabla C\), which is the rate of change of the chemical concentration C along the swimming path. The function K(p, p′) is called the “turning kernel” and captures correlations between pre- and post-tumbling orientations. One expects K to be independent of frame orientation and so depend only upon p ⋅ p′. Subramanian et al. [127] proposed the form \(K(\mathbf{p},\mathbf{p}') = B\exp (B\,\mathbf{p} \cdot \mathbf{p'})/4\pi \sinh B\), which yields small changes in orientation for large values of B, and an uncorrelated, uniform post-tumble orientation as B → 0. The fluxes and stresses are taken to be unchanged from Sect. 2.
Motivated by experiments [28], recent studies have considered chemotaxis in an externally imposed gradient of a chemoattractant, say oxygen. Koch and coworkers [127–129] focused on linear stability analyses in the case where the oxygen field is prescribed and unaffected by the flow. Subramanian et al. [127] considered an infinite suspension of run-and-tumble bacteria in a uniform oxygen gradient, using a model very similar to the one described here. They showed that run-and-tumble dynamics yields an anisotropic orientation distribution, with a net polarization in the direction of the gradient. Performing a linear stability analysis, they found that chemotaxis has a destabilizing effect and tends to reduce the critical bacterial concentration for instability that they had previously derived in the absence of the tumbling bias [74]. Kasyap and Koch [128, 129] analyzed the stability of a confined suspension of run-and-tumble bacteria when the chemoattractant gradient lies in the direction of confinement, as in the experiments of Sokolov et al. [28]. In this geometry they showed that the base state is one of inhomogeneous bacterial concentration and stress, both increasing exponentially across the channel. These inhomogeneous base states allow new couplings within the linearized dynamics. Kasyap and Koch [128] performed a long-wavelength analysis and showed a quadratic increase of the perturbation growth rate with wavenumber, and that active stresses drive flows that tend to reinforce density fluctuations in the plane of the film. Kasyap and Koch [129] later presented a more complete analysis and showed the existence of a linear mode of maximal growth, providing quite good quantitative agreement with the transition to instability observed in the experiments of Sokolov et al. [28].
The effects of oxygen transport were also modeled in numerical simulations by Ezhilan et al. [69]. They considered the dynamics of aerotactic bacteria confined to liquid films suspended in an oxygen-rich environment and swimming towards sources of oxygen while simultaneously consuming it. The dynamics they observed were quite similar to the experiments of Sokolov et al. [28] and are illustrated in Fig. 9.10(a): first, bacteria and oxygen concentration approached steady profiles in thin films, but above a critical film thickness, three-dimensional chaotic dynamics were observed with dense plumes of bacteria penetrating the bulk. In very thick films, a dense bacterial layer was also observed near the film centerline and was explained by the nearly uniform oxygen concentration in that region, where chemotaxis ceases. The onset of instability in these nonlinear simulations compared favorably to the prediction of the linear stability analysis of Kasyap and Koch [128].
(a) Dynamics in films of aerotactic bacteria in the continuum simulations of Ezhilan et al. [69]: in thin films (top row), both bacterial and oxygen concentrations reach steady profiles; as the film thickness is increased (bottom row), a transition to unsteady dynamics is observed, with the formation of bacterial plumes and enhanced oxygen transport. (b) Structure and dynamics of swimmer concentration in autochemotactic suspensions in simulations by Lushi et al. [70]. Lower figures show the corresponding flow streamlines and polar order parameter. (Adapted with permission)
A very different situation arises when the chemoattractant is secreted by the swimming bacteria themselves, as was recently modeled by Lushi et al. [70] who were inspired by studies showing bacterial self-concentration as a result of chemotactic focusing [130], as well as communication processes in bacterial colonies via quorum sensing [131, 132]. This situation has been studied using the celebrated Keller–Segel model [133] and its many variants, though all neglected the effect of the fluid flow generated by the swimmers. Lushi et al. [70] coupled the run-and-tumble chemotaxis model to a transport equation for the chemoattractant concentration that modeled chemoattractant production, depletion, and diffusion. One steady state for this system is uniform isotropy for the swimmers, with a balance of production and degradation in the chemoattractant concentration. Linearizing around this state for a simplified version of the model, Lushi et al. [70] found two uncoupled stability problems for chemotactically driven aggregation and alignment-driven large-scale flows. As a function of tumbling frequency, they identified different regimes where instabilities to aggregation, or alignment, or both, are dominating. Their nonlinear simulations showed, for pushers, that chemotactically driven aggregation was halted by the eruption of local hydrodynamic instabilities, while for pullers the competition of aggregation and active stresses yielded steady-state spots of finite size.
3.4 Fluid Viscoelasticity
The effect of non-Newtonian fluid response upon microorganism locomotion has been studied intensely over the past few years; see, for example, Vélez-Cordero and Lauga [134] and the references therein, as well as the chapter by Guy and Thomases in this volume. The main issue considered has generally been the effect of fluid viscoelasticity upon single swimmer speeds and efficiencies, while comparatively little has as yet been understood on non-Newtonian effects upon collective behavior. In a first effort, Bozorgi and Underhill [135, 136] have extended the kinetic model of Sect. 2 by adding a non-Newtonian stress tensor to the momentum equation (9.19):
where the stress tensor \(\boldsymbol{\varSigma }^{e}\) arises from various viscoelastic constitutive laws and where β captures the nondimensional strength of polymer stress coupling to the momentum balance. Bozorgi and Underhill analyzed the linear stability of various viscoelastic fluid models near the state of isotropy and homogeneity.
One model they studied closely is the Oldroyd-B model [137], which is built upon the assumption that polymer coils respond as Hookean springs to distension by the flow. In this case, the polymer stress obeys the upper-convected evolution equation
where Wi is the Weissenberg number relating the strength of flow forcing to polymer relaxation. For Oldroyd-B, they use the analytic reduction developed by Hohenegger and Shelley [86] and study the linearized dynamics when projected to the first azimuthal mode on the unit sphere of orientations. By expanding in associated Legendre polynomials, this yields an infinite-dimensional, but essentially tridiagonal, eigenfunction/eigenvalue problem for the growth rates. From this, they showed that rotational diffusion, in confluence with viscoelasticity, fundamentally alters the nature of collective instabilities, yielding growing oscillations at long wavelengths, and a biased suppression of growth as a function of k that shifts the maximal growth rate from k = 0 to intermediate values. One possible weakness of their approach is that viscoelasticity is only felt by the swimmers through the large-scale stresses that produce the background velocity field against which the swimmers move. In particular, viscoelasticity is not introduced in determining the single-particle fluxes of Eqs. (9.17)–(9.18), which assume a Newtonian flow on the scale of the particles.
4 Other Active Fluids
While we have focused on suspensions of micro-swimmers, there are other examples of active fluids where the active stresses devolve from other sources of activity and microstructural displacement. We discuss two here: suspensions of microtubules and bound translocating motor proteins and surface-bound populations of particles whose chemical activity creates Marangoni stresses.
4.1 Microtubules and Motor Proteins
Microtubules (MTs; stiff biological polymers composed of tubulin protein subunits) and motor proteins are the building blocks of self-organized biological structures such as the mitotic spindle and the centrosomal MT array [138]. They are also the ingredients in liquid-crystalline active fluids powered by ATP and driven out of equilibrium by motor-protein activity to display complex flows and persistent defect dynamics. MTs are polar polymers, typically polymerizing and depolymerizing from their “plus-end.” The interactions of a motor protein with an MT are also typically polar, with its active motion along the MT being towards either plus- or minus-ends, depending on the motor type.
Active stresses or forces can be created in such systems by the interaction of MTs with immersed motor proteins, often bound to cellular organelles or vesicles, or by motor proteins mechanically coupling together MTs, with their activity inducing their relative displacement. A possible example of the first is the process of nuclear migration in early development, where the “pronuclear complex” containing male and female genetic material is transported to the center of an embryonic cell as shown in Fig. 9.11a. This transport is associated with two dynamic MT arrays emanating from “centrioles,” and ends with the nuclear complex rotating so that the centrioles are aligned with the cell’s anterior-posterior axis. This is the so-called proper position of the complex so that cell division may proceed smoothly.
(a) MT-based dynamics in a live single-celled Caenorhabditis elegans embryo: migration of the male and female pronuclei, pronuclear meeting, centration, and spindle reorientation. (b) Numerical simulation of MT-based pronuclear translation, showing transport of a passive scalar (top) and flow streamlines (bottom). (Adapted with permission from Shinar et al. [14])
While various models of pronuclear migration have been put forward, including interactions of the MT array with the cell cortex, one possible contributing mechanism is the active transport of organelles along MTs towards the centrosomes by dynein motor proteins–minus-end-directed motor proteins–bound to organelle surfaces. Inspired by previous modeling work by Kimura and Onami [139], Shinar et al. [14] investigated this nuclear positioning model as a fluid-structure interaction problem where active agents within the cytoplasm (the cellular fluidic medium) exert minus-end-directed pulling forces upon immersed MTs. To achieve proper force balance–motor proteins can exert no mean force upon the system—these pulling forces upon MTs are balanced by oppositely directed forces acting upon the cytoplasm. Shinar et al. [14] simulated this model using a computational method related to the immersed boundary method [140], and Fig. 9.11b shows the migration and cytoplasmic flows as a model nuclear complex is pulled into the cell center by immersed motor proteins and is then rotated into proper position. We note that the observed cytoplasmic flows along MTs are also observed in vivo and that experiments of Kimura and Kimura [141] showed that positioning and cytoplasmic flows were much slowed by blocking the binding of dynein to organelles. Finally, in unpublished work using a reduced model, Fang and Shelley have shown that the rotation can be explained by a stability calculation that shows that “proper position” is the only mechanically stable orientation for the centriole axis.
Motor proteins can also mediate interactions between MTs by providing a direct and active mechanical coupling of MTs by motor complexes of two or more end-directed motors connected by a molecular tether. Here, the nature of this interaction will depend strongly on whether an MT pair is polar-aligned or anti-aligned. In the latter case, the complex’s motors walk in opposite directions on each MT, inducing a relative sliding of the MTs. This process is called “polarity sorting.”
The physics of filament sliding and polarity sorting by two-headed molecular motors has been studied experimentally [4, 16, 143]. In early experiments, biofilaments were driven into static self-organized patterns such as vortices and asters, reminiscent of structures observed in vivo. Very recently, in experiments of Sanchez et al. [3], active networks were formed of MTs and synthetic tetrameric kinesin-1 motor complexes with the aid of a depletant. In the presence of ATP, motor complexes can bind pairs of MTs and walk along MTs towards their plus-ends. When suspended in bulk, depletion interactions drove the formation of extended, highly ordered MT bundles characterized by bundle extension and fracture and correlated with spontaneous large-scale fluid flows. When MT bundles were adsorbed onto an oil-water interface, they formed a dense, nematically ordered 2D state and exhibited an active nematic phase characterized by the spontaneous generation and annihilation of disclination defect pairs.
Gao et al. [142] have developed a multiscale model that identifies the possible sources of destabilizing active stresses. They first performed detailed Brownian dynamics-Monte Carlo (BDMC) simulations which incorporate excluded-volume interactions between model MTs, thermal fluctuations, explicit translocating motors with binding/unbinding kinetics that satisfy detailed balance, and a force-velocity relation. These simulations show the generation of activity-driven extensile stresses from polarity sorting of anti-aligned MTs and from “cross-link relaxation” of polar-aligned MTs. It also provides coefficients for polarity-specific active stresses for a kinetic theory that incorporates polarity sorting and long-range hydrodynamic interactions, using a similar approach to that described in Sect. 2. Roughly, the center-of-mass flux in Eq. (9.17) is replaced by
where, again, n is the polar order parameter defined in Eq. (9.6). This new term captures the sliding of an MT (at orientation p) relative to a background of MTs of mixed polarity and can be derived by considering a cluster of polar-aligned and anti-aligned MTs coupled together by translocating cross-links. The active stress is replaced by
where α aa and α pa are dimensionless stresslet strengths associated with anti-aligned and polar-aligned interactions, respectively. The BDMC simulations estimate these as being negative, and hence corresponding to destabilizing dipolar stresses, with α aa being the larger. The anti-aligned stresses arise from extensional flows, similar to those for pusher particles, induced by polarity sorting and biases in motor-protein binding and unbinding. The polar-aligned stresses are also extensile but arise from a more subtle statistical mechanical effect associated with temporal relaxation of the motor-protein tether.
(a) Experiment by Sanchez et al. [3] showing the active nematic state of a suspension of MTs and kinesin clusters confined at an interface between two fluids, showing the generation and annihilation of disclination defect pairs. (b)–(c) Two-dimensional continuum simulation by Gao et al. [142] of a suspensions of MTs and kinesin clusters: (b) velocity field overlaying the vorticity, and (c) nematic director field and scalar order parameter. (Adapted with permission)
Simulations of this polar active nematic model are shown in Fig. 9.12b–c. Simulating in regions of flow instability, Gao et al. [142] find persistently unsteady flows that are correlated with the continual genesis, propagation, and annihilation of ± 1∕2 order disclination defect pairs. To wit, Fig. 9.12b shows the background velocity field u = (u, v) overlaying the vorticity ω. The dynamics are complex and turbulent, and qualitatively very similar to those reported by Sanchez et al. [3]. Also very similar are the MT orientation dynamics. Fig. 9.12c shows the nematic director field and scalar order parameter from the tensor order parameter Q. The local orientation is highly correlated with the flow structures seen in (b). We see also that the plane is littered with ± 1∕2 order defects which propagate freely about the system. These defects exist in regions of small nematic order and are born as opposing pairs in elongated low-order regions. These regions are themselves associated with fluid jets, locally decreasing nematic order, and increasing curvature of director field lines. The \(+1/2\) order defects propagate away along their central axis and at a much higher velocity than those of \(-1/2\) order. The relatively higher velocity in the neighborhood of a \(+1/2\) order defect appears as a localized jet, in the direction of defect motion, between two oppositely signed vortices.
Gao et al. [142] also identified the characteristic length scales of this model as those associated with linearized plane-wave models of maximal growth rate, and posited experimental tests of their model. Related to this work are studies based upon Q-tensor field theories similar in flavor to that of Woodhouse and Goldstein [106]; see for instance Giomi et al. [144] and Thampi et al. [145]. In these general models, the precise origins of the active stress driving the system are unidentified, though they do reproduce elements of the experiments such as defect genesis, motion, and annihilation.
4.2 Chemically Active Particles
(a) Typical trajectories of self-propelled rods on a surface, showing the circular trajectories caused by shape asymmetry [21]. (b) Self-propelled rods moving on a surface are found to orbit around sedimented spherical colloids [114]. (c) Continuum simulations of the model of Masoud and Shelley [146] for chemotactic collapse of active colloids at an interface, showing both the velocity field and chemical concentration field in the bulk of the liquid. (Adapted with permission)
Recent technological advances have enabled the fabrication of synthetic microswimmers that convert chemical energy into directional motion [20, 147]. One widely studied system consists of micron-scale bimetallic gold-platinum rods. When immersed in a hydrogen peroxide solution, the rods show directed motion along their axes [18]. Theoretical studies have proposed that these rods move through a chemically powered electrophoretic mechanism which generates a slip flow along the rod surface from the gold to the platinum portions [148]. Experimental studies show that such particles interact with surfaces by flipping and sliding along walls and being captured into orbits around sedimented colloids as shown in Fig. 9.13a and b. Little if any work has, as yet, studied hydrodynamically mediated collective dynamics. One inhibiting feature of this system is that oxygen is an end product of the chemical reactions driving the rods, and when the rods are at high concentration the dissolved oxygen comes out of solution, forming large bubbles that disrupt the experiment. Work on collective behavior in these systems has tended to focus instead on the role of the fuel concentration field, which diffuses and is consumed by the active particles, and its relations to chemokinetic behaviors [149, 150].
Chemically active particles were recently considered in a very different setting. Masoud and Shelley [146] studied the dynamics of chemically active immotile particles that are embedded in a gas-fluid interface. The particles’ chemical activity does not produce any phoretic flows, but does create a spatially diffusing chemical concentration field C. On the surface, this chemical field changes the local surface tension, and any consequent surface tension gradients will produce “active” Marangoni shear stresses driving fluid flows that move the particles [151].
Masoud and Shelley [146] considered the case of a flat interface over a incompressible Stokesian fluid of depth H and viscosity η, assuming that diffusion of the chemical species was fast compared with advection and that surface tension depended linearly upon the surface chemical concentration. The surface concentration Ψ of active particles obeys the advection-diffusion equation
where Pe p is a Péclet number comparing the particle diffusion time scale to advection arising from Marangoni stresses, \(\nabla _{2} = (\partial _{x},\partial _{y})\) is the 2D surface gradient operator, \(\Delta _{2} = \nabla _{2}^{2}\), and U is the 2D surface velocity found by solving the 3D Stokes equations driven by a surface Marangoni stress induced by chemical gradients. Of particular interest is the case where particle activity raises the surface tension.
Both the 3D quasi-static diffusion equation for chemical concentration and the 3D Stokes equations for the fluid flow can be solved via Fourier transform in (x, y), and Masoud and Shelley [146] show that the surface velocity’s Fourier transform satisfies the relation
where \(\mathbf{k} = (k_{x},k_{y})\) is the 2D wave vector, k = | k | , and \(\delta = H/L\) is the dimensionless layer depth where L is a horizontal system length scale. Equation (9.44) can be interpreted as a nonlocal surface integral operator acting upon the density Ψ. Here Ω(λ) is an explicit monotonically increasing function for which \(\varOmega = 1/4 + O(\lambda ^{2})\) for small λ (shallow layers) and Ω → 1∕2 exponentially fast as \(\lambda \rightarrow \infty \) (deep layers).
Particularly interesting are the limits of shallow and deep layers where Eq. (9.44) reduces to \(\tilde{\mathbf{U}} =\nu i\mathbf{k}/k^{2}\tilde{\varPsi }\) with \(\nu = 1/4\) (shallow) or 1∕2 (deep) or \(\mathbf{U} = -\nu \Delta _{2}^{-1}\nabla _{2}\varPsi\). Hence, in real space we have
and this equation is spatially nonlocal due to the inverse Laplacian.
Very surprisingly, upon rescaling, this PDE recovers the iconic 2D parabolic-elliptic Keller–Segel (KS) model of autotactic aggregation:
which was originally conceived as a model for the aggregation of slime molds [133]. Here ϕ is the concentration field of microorganisms that produces a rapidly diffusing chemoattractant of concentration ρ. Read as a kinetic equation for species number conservation, Eq. (9.46) states that microorganisms move along gradients of the self-generated chemoattractant with speed χ∇ρ. The KS model has been the focus of decades of study in PDE analysis (see Horstmann [153] for a comprehensive review), and a great deal is understood about its dynamics. Especially interesting is the 2D case, as is relevant here. For instance, given a sufficient mass of organisms in the plane, the 2D Keller–Segel model suffers chemotactic collapse in finite time, with a finite mass of organisms concentrating at a point. The collapse is approximately self-similar, with \(\phi \approx \zeta (t)^{-2}\varPhi \left (\mathbf{x}/\zeta (t)\right )\) for some scaling function Φ and a scale ζ whose dominant algebraic behavior is \(\sqrt{t_{c } - t}\) where t c is the collapse time.
Chemotactic collapse describes very well the aggregation dynamics observed for chemically active particles. Masoud and Shelley [146] simulated Eqs.(9.43)–(9.44) for mean values of Ψ that are large enough to induce two-dimensional instabilities. Figure 9.13c shows the result by plotting the 3D structure of the chemical concentration field and the fluid velocity field. On the surface there has been a rapid accumulation of active particles to the centers and corners of the domain, where the initial particle concentration was peaked. Descriptively, the initial higher concentration of particles yielded a peak in the chemical surface concentration and hence higher surface tensions there. The associated Marangoni stresses created inward flows which concentrated yet more active particles there, leading to yet greater surface tension and stronger flows. Like the KS model, an aggregative finite-time collapse is observed, and Fig. 9.13c is a snapshot right before the collapse time. The particle density field Ψ has a similar structure to that of the surface field of C, but is yet sharper as C is one derivative smoother. In a marked difference from the KS model, here the surface fluid flows towards the aggregation points are associated with 3D flow structures, and Fig. 9.13c shows the formation of a downward jet and encircling vortex ring within the bulk fluid.
The model by Masoud and Shelley [146] is in search of an experiment and originally arose from casual observations of chemically powered motile rods moving on a free surface. However, if such a scenario could be realized, then this dynamics of particle aggregation and 3D flows might prove useful in self-assembly processes and in droplet locomotion.
5 Outlook
There is tremendous ongoing activity in the field of active matter, of which active suspensions are a particular subset. One area which we did not discuss here, because it is yet substantially unformed, is that of flocking or schooling of organisms flying or swimming at high Reynolds number. A complicating factor is that a flocking organism is likely responding to both unsteady fluid forces and sensory information of multiple modalities (and of course, these are not even well separated). There has been great progress in understanding how perception and response may influence ordering and collective behavior, via Vicsek-type models [25, 152]. However, a particular aspect of high Reynolds flows is that the “storage” of shed vorticity into the flow yields a history dependence to body-body interactions that is difficult to capture in a phenomenological model.
Another large area of increasing inquiry is the activity-induced robustness and self-assembly of cellular structures such as the mitotic spindle and the cellular cytoskeleton. Here, theoretical approaches from soft-condensed matter physics, such as generalized hydrodynamics, elasticity, liquid crystals, and polymer dynamics, have proven very useful. Most of the activity in these areas has been carried out by theoretical biophysicists and relatively little by applied mathematicians and engineers. Consequently, tools such as high-performance computing and sophisticated methods from computational fluid dynamics have not as yet made a substantial impact.
Finally, we have heard it remarked that there are many more theoretical models in the field of active matter than there are definitive experiments. This seems patently true and is partly a reflection of the relative ease of coming up with a model with some interesting dynamics (usually agent-based) versus the difficulty of performing experiments using real organisms or synthesizing active materials. Firmly connecting mathematical models to experiments through principled modeling and thorough exploration is difficult and seems best pursued through both many-particle simulations and continuum models.
References
I. Aranson, Physics 6, 61 (2013)
H.P. Zhang, A. Be’er, E.L. Florin, H.L. Swinney, Proc. Natl. Acad. Sci. USA 107, 13626 (2010)
T. Sanchez, D. Chen, S. DeCamp, M. Heymann, Z. Dogic, Nature 491, 431 (2012)
V. Schaller, C. Weber, C. Semmrich, E. Frey, A.R. Bausch, Nature 467, 73 (2010)
S. Thutupalli, R. Seeman, S. Herminghaus, New J. Phys. 13, 073021 (2011)
C.A. Weber, T. Hanke, J. Deseigne, S. Léonard, O. Dauchot, E. Frey, H. Chaté, Phys. Rev. Lett. 110, 208001 (2013)
S. Ramaswamy, Annu. Rev. Condens. Matt. 1, 323 (2010)
M.C. Marchetti, J.F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, R. Aditi Simha. Rev. Mod. Phys. 85, 1143 (2013)
D. Saintillan, M.J. Shelley, C.R. Physique 14, 497 (2013)
C. Dombrowski, L. Cisneros, S. Chatkaew, R.E. Goldstein, J.O. Kessler, Phys. Rev. Lett. 93, 098103 (2004)
L.H. Cisneros, J.O. Kessler, S. Ganguly, R.E. Goldstein, Phys. Rev. E 83, 061907 (2011)
J. Dunkel, S. Heidenreich, K. Drescher, H.H. Wensink, M. Bar, R.E. Goldstein, Phys. Rev. Lett. 110, 228102 (2013)
S. Köhler, V. Schaller, A.R. Bausch, PLoS ONE 6, e23798 (2011)
T. Shinar, M. Mana, F. Piano, M. Shelley, Proc. Natl. Acad. Sci. 108, 10508 (2011)
F. Woodhouse, R.E. Goldstein, Proc. Natl. Acad. Sci. USA 110, 14132 (2013)
F. Nedelec, T. Surrey, A.C. Maggs, S. Leibler, Nature 389, 305 (1997)
Y. Sumino, K.H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté, K. Oiwa, Nature 483, 448 (2012)
W.F. Paxton, K.C. Kistler, C.C. Olmeda, A. Sen, S.K.S. Angelo, Y. Cao, T.E. Mallouk, P.E. Lammert, V.H. Crespi, J. Am. Chem. Soc. 126, 13424 (2004)
J.R. Howse, R.A.L. Jones, A.J. Ryan, T. Gough, R. Vafabakhsh, R. Golestanian, Phys. Rev. Lett. 99, 048102 (2007)
S.J. Ebbens, J.R. Howse, Soft Matter 6, 726 (2010)
D. Takagi, A. Braunschweig, J. Zhang, M. Shelley, Phys. Rev. Lett. 110, 038301 (2013)
A. Bricard, J.B. Caussin, N. Desreumaux, O. Dauchot, D. Bartolo, Nature 503, 95 (2013)
A. Kudrolli, G. Lumay, D. Volfson, L.S. Tsimring, Phys. Rev. Lett. 100, 058001 (2008)
J. Deseigne, O. Dauchot, H. Chaté, Phys. Rev. Lett. 105, 098001 (2010)
T. Vicsek, A. Zafeiris, Phys. Rep. 517, 71 (2012)
N.H. Mendelson, A. Bourque, K. Wilkening, K.R. Anderson, J.C. Watkins, J. Bacteriol. 181, 600 (1999)
I. Tuval, L. Cisneros, C. Dombrowski, C.W. Wolgemuth, J.O. Kessler, R.E. Goldstein, Proc. Natl. Acad. Sci. USA 102, 2277 (2005)
A. Sokolov, R.E. Goldstein, F.I. Feldchtein, I.S. Aranson, Phys. Rev. E 80, 031903 (2009)
X.L. Wu, A. Libchaber, Phys. Rev. Lett. 84, 3017 (2000)
K.C. Leptos, J.S. Guasto, J.P. Gollub, A.I. Pesci, R.E. Goldstein, Phys. Rev. Lett. 103, 198103 (2009)
G.L. Miño, J. Dunstan, A. Rousselet, E. Clément, R. Soto, J. Fluid Mech. 729, 423 (2013)
J. Orozco, B. Jurado-Sánchez, G. Wagner, W. Gao, R. Vazquez-Duhalt, S. Sattayasamitsathit, M. Galarnyk, A. Cortés, D. Saintillan, J. Wang, Langmuir 30, 5082 (2014)
M.J. Kim, K.S. Breuer, Anal. Chem. 79, 955 (2007)
H. Kurtuldu, J.S. Guasto, K.A. Johnson, J.P. Gollub, Phys. Rev. Lett. 108, 10391 (2011)
A. Sokolov, I.S. Aranson, Phys. Rev. Lett. 103, 148101 (2009)
L. Giomi, T.B. Liverpool, M.C. Marchetti, Phys. Rev. E 81, 051908 (2010)
D. Saintillan, Exp. Mech. 50, 1275 (2010)
J. Gachelin, G. Miño, H. Berthet, A. Lindner, A. Rousselet, E. Clément, Phys. Rev. Lett. 110, 268103 (2013)
E. Lauga, T.R. Powers, Rep. Prog. Phys. 72, 096601 (2009)
E.M. Purcell, Am. J. Phys. 45, 3 (1977)
C. Brennen, H. Winet, Annu. Rev. Fluid Mech. 9, 339 (1977)
K. Drescher, J. Dunkel, L.H. Cisneros, S. Ganguly, R.E. Goldstein, Proc. Natl. Acad. Sci. USA 108, 10940 (2011)
J.S. Guasto, K.A. Johnson, J.P. Gollub, Phys. Rev. Lett. 105, 168102 (2010)
S. Kim, S.J. Karrila, Microhydrodynamics: Principles and Selected Applications (Dover, NewYork, 2005)
K. Drescher, R.E. Goldstein, N. Michel, M. Polin, I. Tuval, Phys. Rev. Lett. 105, 168101 (2010)
S. Fürthauer, S. Ramaswamy, Phys. Rev. Lett. 111, 238102 (2013)
M. Leoni, T.B. Liverpool, Phys. Rev. Lett. 112, 148104 (2014)
T. Ishikawa, M.P. Simmonds, T.J. Pedley, J. Fluid Mech. 568, 119 (2006)
Q. Liao, G. Subramanian, M.P. DeLisa, D.L. Koch, M. Wu, Phys. Fluids 19, 061701 (2007)
V. Gyrya, I.S. Aranson, L.V. Berlyand, D. Karpeev, Bull. Math. Bio. 72, 148 (2010)
J.P. Hernández-Ortiz, C.G. Stoltz, M.D. Graham, Phys. Rev. Lett. 95, 204501 (2005)
J.P. Hernández-Ortiz, P.T. Underhill, M.D. Graham, J. Phys.: Condens. Matter 21, 204107 (2009)
J.R. Blake, J. Fluid Mech. 46, 199 (1971)
T. Ishikawa, T.J. Pedley, J. Fluid Mech. 588, 437 (2007)
T. Ishikawa, J.T. Locsei, T.J. Pedley, Phys. Rev. E 82, 021408 (2010)
T. Ishikawa, T.J. Pedley, Phys. Rev. Lett. 100, 088103 (2008)
T. Ishikawa, J.T. Locsei, T.J. Pedley, J. Fluid Mech. 615, 401 (2008)
A.A. Evans, T. Ishikawa, T. Yamaguchi, E. Lauga, Phys. Fluids 23, 111702 (2011)
D. Saintillan, M. Shelley, J.R. Soc. Interface 9, 571 (2012)
D. Saintillan, M. Shelley, Phys. Rev. Lett. 99, 058102 (2007)
R.A. Simha, S. Ramaswamy, Phys. Rev. Lett. 89, 058101 (2002)
I.S. Aranson, A. Sokolov, J.O. Kessler, R.E. Goldstein, Phys. Rev. E 75, 040901 (2007)
C. Wolgemuth, J. Biophys.95, 1564 (2008)
S. Mishra, A. Baskaran, M.C. Marchetti, Phys. Rev. E 81, 061916 (2010)
J. Dunkel, S. Heidenreich, M. Bär, R.E. Goldstein, New J. Phys. 15, 045016 (2013)
D. Saintillan, M. Shelley, Phys. Rev. Lett. 100, 178103 (2008)
D. Saintillan, M. Shelley, Phys. Fluids 20, 123304 (2008)
A. Alizadeh Pahlavan, D. Saintillan, Phys. Fluids 23, 011901 (2011)
B. Ezhilan, A. Alizadeh Pahlavan, D. Saintillan, Phys. Fluids 24, 091701 (2012)
E. Lushi, R.E. Goldstein, M.J. Shelley, Phys. Rev. E 86, 040902 (2012)
B. Ezhilan, M.J. Shelley, D. Saintillan, Phys. Fluids 25, 070607 (2013)
M. Doi, S.F. Edwards, The Theory of Polymer Dynamics (Oxford University Press, Oxford, 1986)
D.L. Koch, E.S.G. Shaqfeh, J. Fluid Mech. 209, 521 (1989)
G. Subramanian, D.L. Koch, J. Fluid Mech. 632, 359 (2009)
G.B. Jeffery, Proc. R. Soc. Lond. A 102, 161 (1922)
F.P. Bretherton, J. Fluid Mech. 14, 284 (1962)
G.K. Batchelor, J. Fluid Mech. 44, 419 (1970)
M. Garcia, S. Berti, P. Peyla, S. Rafaï, Phys. Rev. E 83, 035301 (2011)
H. Brenner, J. Colloid Interface Sci. 71, 189 (1979)
H. Brenner, PhysicoChem. Hydrodyn. 1, 91 (1980)
H.C. Berg, Random Walks in Biology (Princeton University Press, Princeton, 1983)
P. Underhill, J. Hernández-Ortiz, M. Graham, Phys. Rev. Lett. 100, 248101 (2008)
E.J. Hinch, L.G. Leal, J. Fluid Mech. 76, 187 (1976)
J.H. Irving, J.G. Kirkwood, J. Chem. Phys. 18, 817 (1950)
G.K. Batchelor, J. Fluid Mech. 41, 545 (1970)
C. Hohenegger, M. Shelley, in New Trends in the Physics and Mechanics of Biological Systems, ed. by M. Ben-Amar, A. Goriely, M. Muller, L. Cugliandolo (Oxford University Press, Oxford, 2011)
M. Doi, S.F. Edwards, J. Chem. Soc. Faraday Trans. II 74, 560 (1978)
X. Chen, J.G. Liu, J. Differ. Equat. 254, 2764 (2013)
A. Baskaran, M.C. Marchetti, Proc. Natl. Acad. Sci. USA 106, 15567 (2009)
C. Hohenegger, M. Shelley, Phys. Rev. E 81, 046311 (2010)
M. Betterton, A.S. Jhang, M. Shelley, In preparation (2014)
J.E. Butler, E.S.G. Shaqfeh, J. Fluid Mech. 468, 205 (2002)
A. Baskaran, M.C. Marchetti, J. Stat. Mech.: Theor. Exp. 2010, 04019 (2010)
L. Onsager, Ann. N. Y. Acad. Sci. 51, 627 (1949)
W. Maier, A. Saupe, Z. Naturforsch. 13, 564 (1958)
P.D. Cobb, J.E. Butler, J. Chem. Phys. 123, 054908 (2005)
E.S.G. Shaqfeh, G.H. Fredrickson, Phys. Fluids A 2, 7 (1990)
P.R. Nott, E. Guazzelli, O. Pouliquen, Phys. Fluids 23, 043304 (2011)
A.P. Berke, L. Turner, H.C. Berg, E. Lauga, Phys. Rev. Lett. 101, 038102 (2008)
G. Li, J.X. Tang, Phys. Rev. Lett. 103, 078101 (2009)
J. Hill, O. Kalkanci, J.L. McMurry, H. Koser, Phys. Rev. Lett. 98, 068101 (2007)
V. Kantsler, J. Dunkel, M. Polin, R.E. Goldstein, Proc. Natl. Acad. Sci. USA 110, 1187 (2013)
E. Altshuler, G. Miño, C. Perez-Penichet, L. del Rio, A. Lindner, A. Rousselet, E. Clément, Soft Matter 9, 1864 (2013)
G. Miño, T.E. Mallouk, T. Darnige, M. Hoyos, J. Dauchet, J. Dunstan, R. Soto, Y. Wang, A. Rousselet, E. Clément, Phys. Rev. Lett. 106, 048102 (2011)
E. Lauga, W.R. DiLuzio, G.M. Whitesides, H.A. Stone, J. Biophys. 90, 400 (2006)
F.G. Woodhouse, R.E. Goldstein, Phys. Rev. Lett. 109, 168105 (2012)
H. Wioland, F.G. Woodhouse, J. Dunkel, J.O. Kessler, R.E. Goldstein, Phys. Rev. Lett. 110, 268102 (2013)
A. Costanzo, R. Di Leonardo, G. Ruocco, L. Angelani, J. Phys.: Condens. Matter 24, 065101 (2012)
S. Chilukuri, C.H. Collins, P.T. Underhill, J. Phys.: Condens. Matter 26, 115101 (2014)
S.E. Spagnolie, E. Lauga, J. Fluid Mech. 700, 105 (2012)
R. Voituriez, J.F. Joanny, J. Prost, Europhys. Lett. 70, 404 (2005)
S.A. Edwards, J.M. Yeomans, Europhys. Lett. 85, 18008 (2009)
M. Ravnik, J.M. Yeomans, Phys. Rev. Lett. 110, 026001 (2013)
D. Takagi, J. Palacci, A. Braunschweig, M. Shelley, J. Zhang, Soft Matter 10, 1784 (2014)
R.L. Schiek, E.S.G. Shaqfeh, J. Fluid Mech. 296, 271 (1995)
B. Ezhilan, D. Saintillan, Submitted (2014)
T. Kaya, H. Koser, Biophys. J. 102, 1514 (2012)
Y. Shen, A. Siryapon, S. Lecuyer, Z. Gitai, H.A. Stone, Biophys. J. 103, 146 (2012)
R.W. Nash, R. Adhikari, J. Tailleur, M.E. Cates, Phys. Rev. Lett. 104, 258101 (2010)
A. Jhang, M. Shelley, In preparation (2014)
T. Brotto, J.B. Caussin, E. Lauga, D. Bartolo, Phys. Rev. Lett. 110, 038101 (2013)
N. Liron, S. Mochon, J. Eng. Math. 10, 287 (1976)
S. Bhattacharya, J. Bławzdziewicz, E. Wajnryb, J. Comp. Phys. 212, 718 (2006)
A. Lefauve, D. Saintillan, Phys. Rev. E 89, 021002 (2014)
A.C.H. Tsang, E. Kanso, Flagella-induced transitions in the collective behavior of confined microswimmers. Phys. Rev. E 90, 021001(R) (2014)
H.C. Berg, D.A. Brown, Nature 239, 500 (1972)
G. Subramanian, D.L. Koch, S.R. Fitzgibbon, Phys. Fluids 23, 041901 (2011)
T. Kasyap, D. Koch, Phys. Rev. Lett. 108, 038101 (2012)
T. Kasyap, D. Koch, J. Fluid Mech. 741, 619 (2014)
E.O. Budrene, H.C. Berg, Nature 349, 630 (1991)
B.L. Bassler, Cell 109, 421 (2002)
S. Park, P.M. Wolanin, E.A. Yuzbashyan, P. Silberzan, J.B. Stock, R.H. Austin, Science 301, 188 (2003)
E.F. Keller, L.A. Segel, J. Theor. Biol. 30, 225 (1971)
J.R. Vélez-Cordero, E. Lauga, J Non-Newtonian Fluid Mech 199, 37 (2013)
Y. Bozorgi, P. Underhill, Phys. Rev. E 84, 061901 (2011)
Y. Bozorgi, P. Underhill, J. Rheo. 57, 511 (2013)
R.B. Bird, R.C. Armstrong, O. Hassager, Dynamics of Polymeric Liquids (Wiley-Interscience, 1987)
K.J. Helmke, R. Heald, J.D. Wilbur, Int Rev Cell Mol Biol 306, 83 (2013)
A. Kimura, S. Onami, Dev Cell 8, 765 (2005)
C.S. Peskin, Acta numerica 11, 479 (2002)
K. Kimura, A. Kimura, Proc. Natl. Acad. Sci. USA 108, 137 (2011)
T. Gao, R. Blackwell, M. Glaser, M. Betterton, M. Shelley, Submitted (2014)
T. Surrey, F. Nédélec, S. Leibler, E. Karsenti, Science 292, 1167 (2001)
L. Giomi, M. Bowick, X. Ma, M. Marchetti, Phys. Rev. Lett. 110, 228101 (2013)
S. Thampi, R. Golestanian, J. Yeomans, Phys. Rev. Lett. 111, 118101 (2013)
H. Masoud, M. Shelley, Phys. Rev. Lett. 112, 128304 (2014)
J. Wang, Nanomachines: Fundamentals and Applications (Wiley, NewYork, 2013)
J.L. Moran, P.M. Wheat, J.D. Posner, Phys. Rev. E 81, 065302 (2010)
Y. Hong, N.M. Blackman, N.D. Kopp, A. Sen, D. Velegol, Phys. Rev. Lett. 99, 178103 (2007)
Y. Hong, D. Velegol, N. Chaturvedi, A. Sen, Phys. Chem. Chem. Phys. 12, 1423 (2010)
H. Masoud, H.A. Stone, J. Fluid Mech. 741, R4 (2014)
T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, O. Shochet, Phys. Rev. Lett. 74, 1226 (1995)
D. Horstmann, From 1970 until present: The Keller-Segel model in chemotaxis and its consequences. Jahresber. Deutsch. Math.-Verein. 105, 103–165 (2003)
Acknowledgment
We thank our many students and postdocs that have worked with us on the topic of active suspensions and materials. We also much appreciate the editorial patience extended to us during the preparation of this chapter. DS acknowledges the support of NSF grants DMS-0920931 and CBET-1150590 (CAREER). MJS acknowledges the support of NSF grants DMR-0820341 (NYU MRSEC), DMS-0920930, DOE grant DE-FG02-88ER25053, and NIH grant R01 GM104976-03.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media New York
About this chapter
Cite this chapter
Saintillan, D., Shelley, M.J. (2015). Theory of Active Suspensions. In: Spagnolie, S. (eds) Complex Fluids in Biological Systems. Biological and Medical Physics, Biomedical Engineering. Springer, New York, NY. https://doi.org/10.1007/978-1-4939-2065-5_9
Download citation
DOI: https://doi.org/10.1007/978-1-4939-2065-5_9
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4939-2064-8
Online ISBN: 978-1-4939-2065-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)