Numerical Solutions of the 1D Convection–Diffusion–Reaction and the Burgers Equation Using Implicit Multi-stage and Finite Element Methods

Abstract

In this work we apply the semi-discrete formulation, where the time variable is discretized using an implicit multi-stage method and the space variable is discretized using the finite element method, to obtain numerical solutions for the 1D convection–diffusion–reaction and the Burgers equation, whose analytical solutions are known. More specifically, we use the implicit multi-stage method of second and fourth-order for time discretization. For space discretization, we use three finite elements methods, least square (LSFEM), Galerkin (GFEM) and streamline-upwind Petrov-Galerkin (SUPG). We present an error analysis, comparing the numerical with analytical solutions. We verify that the implicit multi-stage second-order method when combined with the LSFEM, GFEM and SUPG, increased the region of convergence of the numerical solutions. LSFEM presented the better performance when compared to GFEM and SUPG.

15.1 Introduction

In the last decades, developments in computational mechanics motivated extensive research on numerical solutions that had an important impact on society [OdEtAl03]. In particular, we are interested in procedures that can be adapted to problems involving convective, diffusive, and reactive processes. These problems have a vast applicability (see [GoCoCa00], [TaShDe07], [KuEsDa04]), such as the simulation of pollution effects in rivers; modeling of the evolution of oil and natural gas reserves in the underground; modeling of heat transfer problems, dispersion of pollutants; modeling of cosmological scenarios, analysis in seismology; phenomenology of turbulence; the theory of shock waves; and in many other applications.

Usually, the studies employ implicit multi-stage methods combined with the finite element method to increase the convergence region of the obtained results (see [DoRoHu00], [Ve04], [RoSa07], [TiYu11]). In this discussion, we consider the implicit multi-stage method of second-order R ₁₁ and fourth-order R ₂₂, for the discretization of the temporal domain and we use three formulations of the finite element method type for the discretization of the spatial domain, i.e., least squares (LSFEM), Galerkin (GFEM), and streamline-upwind Petrov–Galerkin (SUPG) to solve the 1D convection–diffusion–reaction and the Burgers equation.

15.2 Statement of the Problems

15.2.1 1D Convection–Diffusion–Reaction Equation

We consider the 1D convection–diffusion–reaction problem, consisting in finding $u(x,t): \Omega \rightarrow \mathbb{R}$ such that

$$\displaystyle{ u_{t}(x,t) + vu_{x}(x,t) - Du_{xx}(x,t) +\sigma u(x,t) = f(x,t),\quad \mbox{ in $\Omega $}, }$$

(15.1)

$$\displaystyle{ u(0,t) = u(l,t) = 0\quad \mbox{ on $\Gamma $}, }$$

(15.2)

$$\displaystyle{ u(x,0) = u_{0}(x)\quad \forall x \in \Omega, }$$

(15.3)

where $\Omega \subset \mathbb{R}$ is an open bounded domain with boundary Γ =  ∂ Ω. The coefficients of (15.1) are $v: \Omega \rightarrow \mathbb{R}$, the velocity field; D ≥ 0, the diffusion coefficient; $\sigma: \Omega \rightarrow \mathbb{R}$, the linear reaction coefficient; $f: \Omega \rightarrow \mathbb{R}$, the source term and (15.2) a Dirichlet boundary, and (15.3) the initial condition. We can rewrite (15.1) as $u_{t} + \mathcal{L}(u) = f$, where the spatial differential operator is defined as

$$\displaystyle{ \mathcal{L}(u) = vu_{x} - Du_{xx} +\sigma u }$$

(15.4)

and $\mathcal{L} = \mathcal{L}_{conv} + \mathcal{L}_{dif} + \mathcal{L}_{reac}$ represents the sum of the linear convective, diffusive, and reactive operators, respectively.

15.2.2 Burgers Equation

Here, we consider the Burgers equation problem

$$\displaystyle{ u_{t}(x,t) + u(x,t)u_{x}(x,t) -\epsilon u_{xx}(x,t) = f(x,t)\quad \mbox{ in $\Omega $}, }$$

(15.5)

$$\displaystyle{ u(0,t) = u(l,t) = 0\quad \mbox{ on $\Gamma $}, }$$

(15.6)

$$\displaystyle{ u(x,0) = u_{0}(x)\quad \forall x \in \Omega \;. }$$

(15.7)

The coefficients of (15.5) are given by $\epsilon = 1/Re$, the coefficient of viscosity of the fluid, R e the Reynolds number. Further, u(x, t) is the x-component of the fluid velocity field, $f: \Omega \rightarrow \mathbb{R}$, the source term and (15.6) a Dirichlet boundary condition, and (15.7) the initial condition, where u ₀ is a known function. We can rewrite (15.5) as

$$\displaystyle{ u_{t} + \mathcal{L}(u) = f, }$$

where the spatial operator is defined as

$$\displaystyle{ \mathcal{L}(u) = uu_{x} -\epsilon u_{xx}\;, }$$

(15.8)

and $\mathcal{L} = \mathcal{L}_{conv} + \mathcal{L}_{dif}$ represents the sum of the nonlinear and linear convective and diffusive operators.

15.3 Numerical Methods

15.3.1 Time Discretization

We consider the time parts of (15.1) and (15.5). The time variable is discretized using the implicit multi-stage methods of second order R ₁₁ and fourth order R ₂₂ [HuRoDo02]. The implicit multi-stage method is given in incremental form by

$$\displaystyle{ \frac{\Delta u} {\Delta t} -\mathbf{W}\bigtriangleup u_{t} = \mathbf{w}u_{t}^{n}, }$$

(15.9)

where the unknown $\Delta u \in {\mathbb{R}}^{n}$ is a vector with dimension n. The vector Δ u _t is the partial derivative of Δ u with respect to time. The time derivatives in (15.9) are replaced by spatial derivatives using the differential equations (15.4). The coefficients in $\mathcal{L}$ are assumed smooth for the accuracy analysis.

$$\displaystyle{ \frac{\Delta u} {\Delta t} + \mathbf{W}\mathcal{L}(\Delta u) = \mathbf{w}[{f}^{n} -\mathcal{L}({u}^{n})] + \mathbf{W}\Delta f. }$$

Here, Δ u is defined in (15.9), where W, Δ f and w depends on each particular method. We will linearize the convective term of (15.8), which will become a pointwise linear operator. For illustration we show the compact form for the methods R ₁₁ and R ₂₂.

R ₁₁ (Crank–Nicolson):

$$\displaystyle\begin{array}{rcl} & & \Delta u = {u}^{n+1} - {u}^{n};\quad \Delta f = {f}^{n+1} - {f}^{n}; {}\\ & & \qquad \qquad \mathbf{W} = 1/2;\quad \mathbf{w} = 1. {}\\ \end{array}$$

R ₂₂:

$$\begin{array}{lll}\displaystyle \Delta u = \left \{\begin{array}{llll} {u}^{n+1/2} - {u}^{n} \\ {u}^{n+1} - {u}^{n+1/2} \end{array} \right \}; \\ \Delta f = \left \{\begin{array}{llll} {f}^{n+1/2} - {f}^{n} \\ {f}^{n+1} - {f}^{n+1/2} \end{array} \right \};\\ \mathbf{W} = \frac{1} {24}\left [\begin{array}{lll} 7 & - 1\\ 13 & 5 \end{array} \right ];\quad \mathbf{w} = \frac{1} {2}\left \{\begin{array}{llll} 1\\ 1 \end{array} \right \}.\end{array} $$

15.3.2 Spatial Discretization

We shall now construct a finite-dimensional subspace V _h of $V = H_{0}^{1}(0,l)$ formed by piecewise linear functions of the set of m elements of V denoted by $V _{h} = [\varphi _{0},\ldots,\varphi _{m}]$. The basis functions $\varphi _{j}$ are from the finite element method considering a partition $x_{0} < x_{1} < x_{2}\ldots < x_{m-1} < x_{m}.$

15.3.3 Finite Element Method via Least Squares

Using the implicit multi-stage method defined above for the time discretization of (15.1), the least squares method is applied at each t _n + 1 in (15.9) $n = 0,1,2,\ldots,N$, u ⁿ, which are assumed to be known. Let the set of test solutions V = H ₀ ¹(0, L) and the functional

$$\displaystyle{ \mathcal{F}: V \rightarrow \mathbb{R},\quad {u}^{n+1} \rightarrow \mathcal{F}({u}^{n+1}). }$$

To minimize the functional $\mathcal{F}$ with respect to u ^n + 1 for $n = 0,1,2,\ldots,N$, we use the Gâteaux derivative [BeNa08]. Thus, we can solve the variational problem where u ^n + 1 ∈ V is to be found such that

$$\displaystyle{ a_{M}({u}^{n+1},w) = F_{ M}(w)\quad \forall w \in V. }$$

The problem (15.1)–(15.3) is the solved using LSFEM and considering the subspace $V _{h} \subset V$, for $n = 0,1,2,\ldots,N$. The problem consists then in finding an approximate solution $u_{h}^{n+1} \in V _{h}$ such that

$$\displaystyle{ a_{M}(u_{h}^{n+1},w_{ h}) = F_{M}(w_{h})\quad \forall w_{h} \in V. }$$

15.3.4 Finite Element Method via Galerkin Procedure

Using the implicit multi-stage method defined above for the time discretization of (15.1), the Galerkin method is applied at each t _n + 1 in (15.9) $n = 0,1,2,\ldots,N$, u ⁿ and are assumed to be known. Let the set $V = H_{0}^{1}(0,L)$, then the weak formulation of the problem is to find u ^n + 1 ∈ V such that $a_{G}({u}^{n+1},w) = F_{G}(w)$, $\forall w \in V$. To solve the problem (15.1)–(15.3) using GFEM, we consider the subspace $V _{h} \subset V$, for $n = 0,1,2,\ldots,N$. Thus, the problem consists in finding an approximate solution $u_{h}^{n+1} \in V _{h}$ such that

$$\displaystyle{ a_{G}(u_{h}^{n+1},w_{ h}) = F_{G}(w_{h})\;,\ \ \ \forall w_{h} \in V _{h}\;. }$$

(15.10)

15.3.5 Finite Element Method via Streamline-Upwind Petrov–Galerkin Procedure

The SUPG stabilization for (15.1) is attained by finding $u_{h} \in V _{h}$ such that

$$\displaystyle{ a_{G}(u_{h},w_{h}) + E_{\text{SUPG}}(u_{h},w_{h}) = F_{G}(w_{h})\quad \forall w_{h} \in V _{h}, }$$

where $E_{\text{SUPG}}(u_{h},w_{h})$ indicates the terms of perturbation that are added to the standard variational formulation (15.10). These terms assure that consistency and numerical stability is given by the expression

$$\displaystyle{ E_{\text{SUPG}}(u_{h},w_{h}) =\sum _{e_{j}}(\mathcal{P}(w_{h}),\tau \mathcal{R}(u_{h}))_{{\Omega }^{j}}, }$$

where $\mathcal{P}(w)$ is a certain operator applied to the test function, τ is the stabilization parameter, and $\mathcal{R}$ is the residual of the differential equation defined by [DoRpHu03]

$$\displaystyle\begin{array}{rcl} & & \qquad \qquad \quad \qquad \mathcal{P}(w) = v\frac{\partial w_{h}} {\partial x}, {}\\ & & \qquad \qquad \mathcal{R} = v\frac{\partial u_{h}} {\partial x} - D\frac{{\partial }^{2}u_{h}} {\partial {x}^{2}} +\sigma u_{h} - f, {}\\ & & \tau ={ \left (\frac{2v} {h} + \frac{4D} {{h}^{2}} +\sigma \right )}^{-1} = \frac{h} {2v}{\left (1 + \frac{1} {Pe} + \frac{h\sigma } {2v}\right )}^{-1}. {}\\ \end{array}$$

Here, h is the size of the grid, P e is the Péclet number and v, D and σ are the coefficients defined in equation (15.1). To solve the problem (15.1)–(15.3) using SUPG, one considers the subspace $V _{h} \subset V$ for $n = 0,1,2,\ldots,N$ and determines an approximate solution $u_{h}^{n+1} \in V _{h}$ such that

$$\displaystyle{ a_{G}(u_{h}^{n+1},w_{ h}) + E_{\text{SUPG}}(u_{h}^{n+1},w_{ h}) = F_{G}(w_{h})\quad \forall w_{h} \in V _{h}. }$$

Next, we linearize the convective term in (15.5), which changes the size of the element in each stage using the information from the previous step [KuEsDa04] that casts the Burgers equation into a linear local problem.

15.3.6 Linearization of the Convective Term

Upon multiplying both sides of (15.5) by a test function w ∈ V and integrating out the x-degree of freedom yields

$$\displaystyle{ \int _{0}^{l}(u_{ t} + uu_{x} -\epsilon u_{xx} - f)w\,dx = 0. }$$

(15.11)

A numerical solution to problem (15.5)–(15.7) is constructed in the region 0 ≤ x ≤ l with boundary conditions specified at x = 0 and x = l. To this end, we consider the finite dimensional subspace V _h , where the basis functions $\varphi _{j}$ are from the finite element method considering a partition $x_{0} < x_{1} < x_{2}\ldots < x_{m-1} < x_{m}$ of size

$$\displaystyle{ h_{j} = x_{j} - x_{j-1}. }$$

We now construct a test function u _h , and the parameters that are to describe the function u _h are the values $u_{0},u_{1},u_{2}\ldots,u_{m}$ at the nodes x _j . Therefore, we can write the approximate equation (15.11)

$$\displaystyle\begin{array}{rcl} & & \sum _{j=0}^{m}\int _{ 0}^{l}\bigg(\frac{\partial u_{j}} {\partial t} \,\varphi _{i}(x) +\eta \frac{\partial \varphi _{j}(x)} {\partial x} \,\varphi _{i}(x)u_{j} {}\\ & & \qquad \qquad \qquad \qquad \qquad -\epsilon \frac{{\partial }^{2}\varphi _{j}(x)} {\partial {x}^{2}} \,\varphi _{i}(x)u_{j} - f\varphi _{i}u_{j}\bigg)\,dx = 0\quad \forall \varphi _{i},\,\varphi _{j} \in V _{h}, {}\\ \end{array}$$

where $\eta = u_{0}\Delta t/h_{j}$ and Δ t is the time step, and $w_{h} =\varphi _{i}(x)$, i = 0, 1, 2, …, m. Thus, the Burgers equation becomes a 1D linear local problem.

Now, we consider the development for the 1D convection–diffusion–reaction equation in this case σ = 0, D = ε, and v = η. For the Burgers equation, the value of the stabilization parameter τ, which is used by SUPG [DoRpHu03], is

$$\displaystyle{ \tau ={({\left (2u/h\right )}^{2} + 9{\left (4\epsilon /({h}^{2})\right )}^{2})}^{-1/2}, }$$

where h is the size of the grid and $\epsilon = 1/Re$, with R e and u defined in (15.5).

15.4 Numerical Results

15.4.1 1D Convection–Diffusion–Reaction Equation

Consider the 1D convection–diffusion–reaction problem (15.1)–(15.3) with the function f(x, t) = 0 and the initial condition given by a Gaussian distribution

$$\displaystyle{ u(x,0) =\exp \left \{-{\left (\frac{x - x_{0}} {\ell} \right )}^{2}\right \}. }$$

For a linear decay term, − σ u, the analytical solution on − ∞ < x < ∞ is [DoRpHu03]

$$\displaystyle{ u(x,t) = \frac{\exp (-\sigma t)} {\gamma (t)} \exp \left \{-{\left (\frac{x - x_{0} - vt} {\ell\gamma (t)} \right )}^{2}\right \}, }$$

(15.12)

where

$$\displaystyle{ \gamma (t) = \sqrt{1 +{ \frac{4Dt} {\ell}^{2}}}. }$$

For this example we consider 0 ≤ x ≤ l, l = 2 the domain of the 1D problem. For illustration, we present some results with 100 linear elements and

$$\displaystyle{ x_{0} = 1/4,\quad \ell = 1/25,\quad v = 1,\quad \sigma = 0.1,\quad C = 1,\quad Pe = 100, }$$

where v and σ are the coefficients of (15.1) and C and P e are the Courant and Péclet numbers, respectively.

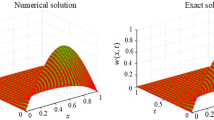
In Fig. 15.1 we present comparisons between the Padé approximants of R ₁₁ and R ₂₂ modified by the formulations GFEM, LSFEM, and SUPG, with $\Delta t = \Delta x = 0.02$. The analysis of stability and convergence are shown for the time limit t = 1 and compared with the analytical solution (15.12). One observes in Fig. 15.1 that the implicit multi-stage method of fourth-order R ₂₂ modified by the formulations GFEM, LSFEM, and SUPG smoothed out the numerical oscillations. We present the errors between the methods evaluated for function grid refinement ($h = 1/50$, $h = 1/680$ and $h = 1/1000$) in Fig. 15.2 and for function time step refinement (Δ t = 0. 5, Δ t = 0. 05 and Δ t = 0. 01) in Fig. 15.3 using the L ²-norm.

Fig. 15.1

Comparisons of the Padé approximants R ₁₁ and R ₂₂ together with the formulations (a) GFEM, (b) LSFEM, and (c) SUPG

Fig. 15.2

Convergence of the numerical results with the grid refinement for the example 1D convection-diffusion-reaction problem

Fig. 15.3

Convergence of the numerical results with the time step refinement for the example 1D convection-diffusion-reaction problem

15.4.2 The Burgers Equation

We consider an analytical solution for the Burgers equation (15.5) and (15.6) given by [KuEsDa04]

$$\displaystyle{ u(x,t) = \frac{2\epsilon \pi \exp {(\pi }^{2}\epsilon t)\sin (\pi x)} {a +\exp ({-\pi }^{2}\epsilon t)\cos (\pi x)},\quad a > 1, }$$

with initial condition

$$\displaystyle{ u(x,0) = \frac{2\epsilon \pi \sin (\pi x)} {a +\cos (\pi x)},\quad a > 1, }$$

where $\epsilon = 1/Re$ is the coefficient of viscosity of the fluid and R e represents the Reynolds number. Let 0 ≤ x ≤ 1 be the domain with the boundary conditions $u(0,t) = u(1,t) = 0.$ To illustrate some results we used 50 linear elements and R e = 10000.

Figure 15.4 presents comparisons between the Padé approximants of R ₁₁ and R ₂₂ modified by the formulations GFEM, LSFEM, and SUPG, respectively, with $\Delta t = \Delta x = 0.02$ and as an analysis of stability and convergence we present the results of the formulations for the upper time limit t = 1 and compare these findings with the analytical solution (15.12). One observes in Fig. 15.5, that the implicit multi-stage method of fourth-order R ₂₂, modified by the formulations GFEM, LSFEM and SUPG smoothed out numerical oscillations. We present the errors between the methods, evaluated for function grid refinement ($h = 2/50$, $h = 2/100$, and $h\,=\,2/500$), in Fig. 15.5 and for function time step refinement (Δ t = 0. 03, Δ t = 0. 02 and Δ t = 0. 01) in Fig. 15.6 using the L ² norm.

Fig. 15.4

Comparisons between the Padé approximants R ₁₁ and R ₂₂ modified by the formulations (a) GFEM, (b) LSFEM and (c) SUPG

Fig. 15.5

Convergence of the numerical results with grid refinement for the example the Burgers equation

Fig. 15.6

Convergence of the numerical results with time step refinement for the example the Burgers equation

15.5 Conclusions

We conclude that the implicit multi-stage method of fourth-order R ₂₂, when complemented by the finite element methods studied here, proved efficient since the Padé approximant R ₂₂ increased the convergence region of the numerical solutions. We also note that the LSFEM eliminated the oscillations of numerical solutions more efficiently than the methods GFEM and SUPG.