An efficient spectral-Galerkin method for solving two-dimensional nonlinear system of advection–diffusion–reaction equations

Abstract

The spectral Legendre–Galerkin method for solving a two-dimensional nonlinear system of advection–diffusion–reaction equations on a rectangular domain is presented and compared with analytical solution. The proposed method is based on the Legendre–Galerkin formulation for the linear terms and computation of the nonlinear terms in the Chebyshev–Gauss–Lobatto points. The main difference of the spectral Legendre–Galerkin method presented in the current paper with the classic Legendre–Galerkin method is in treating the nonlinear terms and imposing boundary conditions. Indeed, in the spectral Legendre–Galerkin method the nonlinear terms are efficiently handled using the Chebyshev–Gauss–Lobatto points and also the boundary conditions are imposed strongly as collocation methods. Combination of the proposed method with a semi-implicit time integration method such as the Leapfrog–Crank–Nicolson scheme leads to reducing the complexity of computations and obtaining a linear algebraic system of equations. Efficiency and spectral accuracy of the proposed method are demonstrated numerically by some examples.

1 Introduction

In this paper, we consider the following coupled system of advection–diffusion–reaction equations:

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {L}}\mathbf{u }={\mathcal {F}}(t,\mathbf{x },\mathbf{u }), &{} ~~\text {in} ~~\Omega \times (0,T],\\ {\mathcal {B}}\mathbf{u }=\mathbf{g }, &{} ~~\text {on} ~~\partial \Omega \times (0,T],\\ \mathbf{u }(\mathbf{x },0)=\mathbf{u }_0(\mathbf{x }),&{} ~~ \text {in}~~ \Omega \times \{0\},\\ \end{array} \right. \end{aligned}$$

(1.1)

where $\Omega$ is a bounded domain in ${\mathbb {R}}^2$ with a smooth or piecewise smooth boundary, $\mathbf{u }=(u_1,u_2,\ldots ,u_m)$ is vector of concentration of the physical or biological species, ${\mathcal {F}}=(F_1,F_2,\ldots ,F_m)$ is a vector including reaction terms in form of

$$\begin{aligned} F_i(t,\mathbf{x },\mathbf{u })=-R_i(u_1,u_2,\ldots ,u_m)-f_i(\mathbf{x },t),\quad i=1,2\ldots ,m, \end{aligned}$$

in which

$$\begin{aligned} R_i(u_1,u_2,\ldots ,u_m)=\sum _{k,j=1}^m b_{i,kj} u_ku_j+\sum _{j=1}^m c_{i,j}u_j, \end{aligned}$$

(1.2)

and $b_{i,kj}$, $c_{i,j}$ are kinetic coefficients. Also in (1.1), ${\mathcal {B}}=(B_1,B_2,\ldots ,B_m)$ is vector of boundary operators and $\mathbf{g }$, $\mathbf{u }_0(\mathbf{x })$ are vectors of boundary and initial conditions, respectively. Further, ${\mathcal {L}}=({\mathcal {L}}_1,{\mathcal {L}}_2,\ldots ,{\mathcal {L}}_m)$ is a m-dimensional vector with components of ${\mathcal {L}}_k=\frac{\partial }{\partial t}-L_k$ in which $L_k$ is defined as follows

$$\begin{aligned} L_k=-\mathbf{v } \cdot \nabla u_k+d_k\Delta u_k, \end{aligned}$$

where $\mathbf{v }\in {\mathbb {R}}^2$ is velocity vector in the advection term and $d_i, (i=1,2,\ldots ,m)$ are positive parameters of diffusion.

Since $R_i$ in (1.2) involves the product of concentrations, (1.1) is a nonlinear system of differential equations.

Many phenomena in various fields of science such as physics, biology, ecology and biochemistry are modeled by a system of advection–diffusion–reaction. Transport of air pollutants [33, 34, 74, 75], the influences of the unidirectional flow on spatial patterns of community composition and species replacement in the river ecosystems [39], formation of complex spatial structures in systems of interacting chemical species [50, 51], groundwater and surface water [76], ash-fall from volcano [45], transport of water vapour in the Earth’s atmosphere [63, 84, 85], computer graphics [13] and many other biological patterns are some events which arise through the processes of advection–diffusion–reaction.

The nonlinear system of advection–diffusion–reaction is composed of three distinct terms: advection terms which describe transport of each component due to velocity field $\mathbf{v }$, diffusion (turbulent) terms which are related to random motion of each component due to the turbulent nature of the flow field and reaction terms which describe interaction of the involved species [13]. If $\mathbf{v }=0$ in (1.1), then we are concerned with a nonlinear system of diffusion–reaction equations which has many applications, particularly, in population dynamics of interacting species like as diffusive Lotka–Volterra system [37].

There are a lot of works in relation to the theoretical and numerical aspects of such systems like (1.1). As mentioned in [61], the system of advection–diffusion–reaction equations (1.1) admits a rich class of solutions ranging from a relatively simple linear advection to nonlinear reaction–diffusion waves leading to the formation of complex, spatially nonhomogeneous patterns. Unique solvability of quasi-linear parabolic system is analyzed in [32]. An optimal control problem for the Lotka–Volterra system with diffusion is considered in [28] and also it has been proved that this system has a unique positive solution with some bounded properties. Existence of the bistable traveling wave solution of reaction–diffusion equations that model the interaction of n mutualist species is proved in [29] and also uniqueness of their bistable traveling wave solution is shown by homotopy approach incorporated with the Liapunov–Schmidt method. Furthermore, [39] gives some analytical discussion on advection–diffusion–reaction equations, coupled by Lotka–Volterra interaction terms, about the effects of dispersal patterns on competing species. Spatial structures and front propagation of the reaction–diffusion systems are considered in [6]. An advection–diffusion–reaction model for the pattern formulation is proposed in [48]. Also behavior of the model, especially the effects of the advection term on a simple reaction–diffusion system is studied by numerical calculation.

Numerical solution of nonlinear advection–diffusion–reaction systems also has been an interesting subject for many researchers and, therefore, some numerical methods such as finite difference, spectral methods, finite elements and finite volume are applied for solving them. Finite difference methods due to their simplicity are applied for system of advection–diffusion–reaction equations in different papers [7, 20, 25, 36, 47, 52–56, 80, 81]. In [82] high-order compact finite difference is proposed for (1.1) and Richardson extrapolation is also used for obtaining fourth-order accuracy in time. A compact finite difference method is presented in [36] using Crank–Nicolson technique in time discretization and fourth-order Padé approximation to space derivative. Asymptotic behavior of the finite difference solutions of nonlinear integro-differential reaction–diffusion equations is considered in [83]. Nonstandard finite difference schemes for one-space dimension single nonlinear reaction–diffusion partial differential equation with linear advection are extended in [46]. [86] is devoted to generalize quasilinearization method for solving nonlinear advection–diffusion–reaction systems. A finite volume algorithm which first approximates convection and diffusive fluxes and then solves the resulting ODE system is proposed in [61] for the solution of the advection–diffusion–reaction equations on the sphere. A fully discrete $H^1$-Galerkin method with quadrature is proposed in [15] for nonlinear single parabolic advection–diffusion–reaction equation. Also in [24] high-order finite volume scheme is derived for nonlinear system of advection–diffusion–reaction with stiff algebraic source terms. The system (1.1) is introduced in [37] and a finite element method together with its error analysis is considered for it. A Legendre spectral element method is proposed in [8] for one-dimensional predator–prey system on a large spatial domain. An efficient pseudo-spectral Legendre Galerkin method for solving a nonlinear partial integro-differential equation arising in population dynamics is introduced in [12]. An implicit–explicit Runge–Kutta–Chebyshev (RKC) method which treats diffusion and advection terms explicitly and the highly stiff reaction terms implicitly is proposed in [79]. In [4] a second-order exponential integrator for semidiscretized advection–diffusion–reaction equations is obtained that is five times faster than a classical second-order implicit solver. An operator splitting algorithm which splits homogeneous equations into advection, diffusion and reactions and then solves them by backward method of characteristic, finite element method and an explicit Runge–Kutta, respectively, is presented in [31] for a system of one-dimensional advection–diffusion–reaction equations. Also in [13] a numerical operator splitting for time integration of three-dimensional advection–diffusion–reaction system is implemented and three different methods of second-order accuracy are derived for solving, separately, each term that appeared in the model. Finite element solution of reaction–diffusion equations with advection and nonconforming finite element methods with subgrid viscosity for solving single advection–diffusion–reaction equation are considered in [38] and [11], respectively. Discontinuous hp-finite element methods for second-order elliptic and parabolic advection–reaction equations are considered in [26]. Performance of three different time integration methods, i.e. Euler backward, second-order Rosenbrock and implicit–explicit Runge–kutta–Chebyshev is examined in [78]. More details about time integration of (1.1) are presented in [30]. A multiscale variational method is proposed in [27] to solve the advection–diffusion equation. A couple implicit integration factor (IIF) method and its higher dimensional analog compact IIF with weighted essentially non-oscillatory (WENO) methods using the operator splitting approach is presented in [88] to solve advection–diffusion–reaction equations. In [57] numerical method using establishing a difference scheme based on singular perturbed theory and Green’s function is investigated for the system of reaction–diffusion equations in one-dimension and some estimates of the derivatives of the solution are obtained.

Depending on various applications, Eq. (1.1) can be imposed with different boundary conditions. In this paper we apply spectral Legendre–Galerkin method for nonlinear system (1.1) on a rectangular domain $\Omega$ with homogeneous Dirichlet boundary conditions. Nonhomogeneous essential boundary conditions can be achieved by lifting an arbitrary function satisfying the boundary conditions and modifying the right-hand side of the equation.

Galerkin methods [2, 5, 16, 22, 77] are one of the most important weighted residual methods which are able to solve many kinds of operator equations and have been applied by many authors in various fields of science and engineering, see, e.g., [3, 17, 18, 21, 23, 44, 69–72, 87].

The key property of the Galerkin approach is selecting a finite dimensional subspace of the Hilbert space (trial function space) for approximation of solution and imposing orthogonality relation of the obtained error to a finite dimensional space (test function space) which is the same to the trial space. If the trial and test spaces in the Galerkin method are different, the obtained method is called Petrov–Galerkin [2]. The main deficiency of the Galerkin methods is that their implementation for the nonlinear problems is rather difficult. However, using orthogonal polynomials as a basis for the approximation (trial) space makes these methods easier to be implemented by no need to compute the integral terms arising in inner product for the linear terms. Chebyshev–Galerkin methods due to the non-uniform weight function for the Chebyshev polynomials give rise to a complex and non-symmetric system of equations [66]. Therefore, in this paper we use the Legendre polynomials as the basis of the approximation space in the Galerkin method. These polynomials with the unit weight function are very efficient in the computations. For approximating the nonlinear terms in the Galerkin method, a nice approach based on pseudo-spectral methods was proposed in [66]. However, the idea of using Chebyshev nodes in the Legendre collocation method was first introduced by Don et. al [9] for the parabolic and hyperbolic equations, but implementation of these methods in [66] and [9] is different. For using this approach three essential steps must be performed in the Legendre–Galerkin method. The first step is computing the nonlinear terms at the Chebyshev–Gauss–Lobatto points; the second step is using the fast Fourier transform (FFT) between the physical and spectral Chebyshev spaces and the third step is applying a proper algorithm for finding the coefficients of the Legendre expansion from Chebyshev one [66].

The Legendre–Gauss–Lobatto points are not available in an explicit form, so there is not any fast Legendre transform between function values at the Legendre–Gauss–Lobatto points (physical space) and the Legendre expansion coefficients (spectral space) and also computational complexity of this process is ${O}(N^2)$ [1, 66, 67]. On the other hand, the Chebyshev–Gauss–Lobatto points are given in the explicit form and the fast Chebyshev transform or the fast Fourier transform (FFT) between their physical and spectral spaces can be efficiently performed in ${O}(N\text {log}_2N)$ operations. Therefore, weakness of the Legendre–Galerkin method for approximating the nonlinear terms is treated using the Chebyshev–Gauss–Lobatto points. Indeed, the Chebyshev pseudo-spectral Legendre–Galerkin method which encompasses advantages of the both Chebyshev–Galerkin and Legendre–Galerkin methods is used in this paper. The contribution of paper is generalization of the Chebyshev–Legendre–Galerkin method to a two-dimensional nonlinear system of equations. In the proposed method, the linear parts of the problem are approximated by the Legendre–Galerkin method and the nonlinear parts are computed by the interpolation operator at the Chebyshev–Gauss–Lobatto nodes. Therefore, easy computation of nonlinear terms is combined with the good stability properties of the Legendre–Galerkin methods. Combination of the Chebyshev pseudo-spectral Legendre–Galerkin method with a classic semi-implicit time integration scheme such as Leapfrog–Crank–Nicolson which treats the linear parts implicitly and the nonlinear parts explicitly yields a matrix equation that can be converted to a linear algebraic system of equations at each time step . Also in some cases of (1.1), including pure reaction–diffusion system (i.e. $\mathbf{v }=0$) or non-diffusive case of it (i.e. $d_1=0$, $d_2=0$), the resulting matrix equation, due to symmetry of the coefficient matrix, can be solved efficiently by the Schur matrix decomposition or generalized eigenvalue problem methods.

The Chebyshev–Legendre–Galerkin or Petrov–Galerkin methods for solving many kinds of problems have been applied by some authors. In [66] Shen introduced this kind of Chebyshev–Legendre–Galerkin method and applied it for the elliptic problems. Also he proposed an efficient algorithm for transforming between coefficients of the Chebyshev expansion and of the Legendre expansion. The class of spectral Galerkin methods based on Legendre and Chebyshev polynomials for direct solution of the second- and fourth-order equations are proposed in [67, 68], respectively. The Chebyshev pseudo-spectral Legendre–Petrov–Galerkin method is considered for the modified Kawahara equation in [65] and fourth-order differential equations in [73]. Also in [43] the Legendre–Petrov–Galerkin method is applied for the Korteweg-de Vries equation and in [42] this method is proposed for the third-order differential equations. A Legendre Galerkin–Chebyshev collocation method is developed for Burgers-like equations in [35]. Second-order equations are solved by the Chebyshev–Petrov–Galerkin method in [10]. Chebyshev–Legendre spectral method is presented for the nonlinear conservative laws in [40, 41].

The remainder of the paper is organized as follows: In the next section we propose the Chebyshev pseudo-spectral Legendre–Galerkin method for solving nonlinear system (1.1) on a rectangular domain $\Omega$. Some numerical results are presented in Sect. 3 which demonstrate the spectral accuracy and efficiency of the proposed method. Finally Sect. 4 includes some concluding remarks.

2 Chebyshev–Legendre Galerkin method

In this section the Chebyshev–Legendre Galerkin method is proposed for a two-dimensional nonlinear system (1.1) on a rectangular domain $\Omega$ with homogeneous boundary condition as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {L}}\mathbf{u }={\mathcal {F}}(t,\mathbf{x },\mathbf{u }), &{} ~~\text {in} ~~\Omega \times (0,T],\\ \mathbf{u }=0, &{} ~~\text {on} ~~\partial \Omega \times (0,T],\\ \mathbf{u }(\mathbf{x },0)=\mathbf{u }_0(\mathbf{x }),&{} ~~ \text {in}~~ \Omega \times \{0\},\\ \end{array} \right. \end{aligned}$$

(2.1)

where without loss of generality we suppose that $\Omega =I^2$, where $I=(-1,1)$ and operators of ${\mathcal {L}}$, and ${\mathcal {F}}$ are defined similar to the previous.

In the case of nonhomogeneous boundary conditions in Eq. (1.1), we can decompose the exact solution into a known lifted function $\mathbf{u }^d$ which satisfies at the boundary conditions and an unknown function $\mathbf{u }^h$ which is zero on the boundaries. By setting $\mathbf{u }=\mathbf{u }^h+\mathbf{u }^d$ such that ${\mathcal {B}}\mathbf{u }^d=\mathbf{g }$ and ${\mathcal {B}}\mathbf{u }^h=0$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {L}}\mathbf{u }^h={\mathcal {F}}^*(t,\mathbf{x },\mathbf{u }^h), &{} ~~\text {in} ~~\Omega \times (0,T],\\ {\mathcal {B}}\mathbf{u }^h=0, &{} ~~\text {on} ~~\partial \Omega \times (0,T],\\ \mathbf{u }^h(\mathbf{x },0)=\mathbf{u }_0(\mathbf{x })-\mathbf{u }^d(\mathbf{x },0),&{} ~~ \text {in}~~ \Omega \times \{0\},\\ \end{array} \right. \end{aligned}$$

(2.2)

in which ${\mathcal {F}}^*(t,\mathbf{x },\mathbf{u }^h)={\mathcal {F}}(t,\mathbf{x },\mathbf{u }^h+\mathbf{u }^d)- {\mathcal {L}}\mathbf{u }^d$.

2.1 Preliminaries

If $L_n(x)$ denotes the nth Legendre polynomial which has orthogonal property with respect to $L^2$ inner product on the interval $[-1,1]$ with the unit weight function, then the Legendre-Gauss quadrature formula is as follows:

$$\begin{aligned} \int _{-1}^1 f(y) dy \approx \sum _{j=0}^{N}f(y_j)w_j, \end{aligned}$$

where distinct nodes $y_0<y_1< \cdots <y_N$ are $N+1$ roots of $L_{N+1}(x)$ in $(-1,1)$ and $\{w_j\}_{j=0}^N$ are the corresponding weights. While, explicit formulae for the quadrature nodes are not known, the quadrature weights can be expressed by the following relation:

$$\begin{aligned} w_j=\frac{2}{(1-y_j^2)[ L_{N+1}^\prime (y_j)]^2},\quad j=0,1,\ldots ,N. \end{aligned}$$

In the rest of the current paper we need to introduce the Sobolev space. Let $\Omega$ be an open subset in ${\mathbb {R}}^n$ and $w(\mathbf{x })$ be a positive weight function on $\Omega$. For any non-negative integer m, $H_w^m(\Omega )$ is the weighted Sobolev space with norm $\Vert .\Vert _{\Omega ,m,w}$ that is defined as

$$\begin{aligned} H_w^m(\Omega )=\{u\in L^2_w(\Omega );~D^\alpha u\in L^2_w(\Omega ),~\forall |\alpha |\le m\}, \end{aligned}$$

where for a given multi-index $\alpha =(\alpha _1,\ldots ,\alpha _n)\in {\mathbb {Z}}_+^n$, we have

$$\begin{aligned} D^\alpha u=\frac{\partial ^{|\alpha |}u}{\partial x_1^{\alpha _1},\ldots ,\partial x_n^{\alpha _n}},\quad |\alpha |=\sum _{i=1}^n \alpha _i. \end{aligned}$$

In particular, the norm and inner product of $L^2_w(\Omega )~(=H^0_w(\Omega ))$ are denoted by $\Vert .\Vert _{\Omega ,w}$, and $\langle , \rangle _{\Omega ,w}$, respectively. We will drop the subscript w in all notations, whenever $w\equiv 1$.

2.2 Implementation

We suppose $V_N^0={\mathbb {P}}_N(\Omega )\cap H_0^1(\Omega )$ is the trial (test) function space, in which ${\mathbb {P}}_N(\Omega )$ is the space of all algebraic two variables polynomials of degree at most N with respect to each variable and

$$\begin{aligned} H_0^1(\Omega )=\{v\in H^1(\Omega ); v|_{\partial {\Omega }}=0\}. \end{aligned}$$

From computational aspects and for the sake of efficiency it is essential to use the combinations of orthogonal polynomials (with respect to the inner product $\langle ,\rangle _\Omega$) as the basis of $V_N^0$. With this choice, the inner products arisen in the linear terms of the weak form are computed easily using orthogonality properties of basis and without any integration. For the nonlinear terms, as mentioned earlier, we use the Chebyshev–Gauss–Lobatto points which enable us to approximate these terms by the Legendre polynomials expansion in the case of the Legendre–Galerkin method [66]. The natural choice for basis of $V_N^0$ is the tensor product of basis functions in the one dimensional case. Indeed, it can be trivially proved that

$$\begin{aligned} V_N^0=span\{\psi _{m,n}(x,y);~0\le m,n\le N-2\}, \end{aligned}$$

in which $\psi _{m,n}(x,y)=\phi _m(x)\phi _n(y)$ and

$$\begin{aligned} \phi _n(x)=\frac{1}{\sqrt{4n+6}}(L_n(x)-L_{n+2}(x)). \end{aligned}$$

Multiplying both sides of ith equation of (2.1) by $w\in H_0^1(\Omega )$ and integration by parts over $\Omega$, we have the following weak form of (2.1):

$$\begin{aligned} \left\{ \begin{array}{ll} \langle \frac{\partial u_i}{\partial t},w\rangle _\Omega +\mathbf{v }\cdot \langle \nabla u_i,w\rangle _\Omega +d_i\langle \nabla u_i,\nabla w\rangle _\Omega +\langle R_i(\mathbf{u }),w\rangle _\Omega +\langle f_i,w\rangle _\Omega =0, &{} ~~t\in (0,T],\\ \langle u_i(0),w\rangle _\Omega =\langle {u_0}_i,w\rangle _\Omega , \end{array} \right. \end{aligned}$$

where $u_i(t)\in H_0^1(\Omega )$ and $1\le i \le m$.

Also the semi-discrete Chebyshev–Legendre–Galerkin method for problem (2.1) is to find $U_i^N(t)\in V_N^0$ such that for any $w\in V_N^0$

$$\begin{aligned} \left\{ \begin{array}{ll} \langle \frac{\partial U_i^N}{\partial t},w\rangle _\Omega +\mathbf{v }\cdot \langle \nabla U_i^N,w\rangle _\Omega +d_i\langle \nabla U_i^N,\nabla w\rangle _\Omega \\ +\langle I_N^C R_i(\mathbf{U }^N(t)),w\rangle _\Omega +\langle I_N^C f_i(t),w\rangle _\Omega =0, &{}~~ t\in (0,T],~~i=1,2,\ldots ,m,\\ \langle U_i^N(0),w\rangle _\Omega =\langle I_N^C{u_0}_i,w\rangle _\Omega , \end{array} \right. \end{aligned}$$

(2.3)

in which $I_N^C$ is the interpolation operator at $\{(\theta _i,\theta _j)\}_{i,j=0}^{N-2}$ on $\Omega =I^2$ where $\theta _i=\text {cos}(\frac{i\pi }{N-2})$ are the Chebyshev–Gauss–Lobatto nodes on I. Also $\mathbf{U }^N(t)$ is the vector of approximate solutions including $U_i^N(t)$, i.e.

$$\begin{aligned} \mathbf{U }^N(t)=\left( \begin{array}{c} U_1^N(t) \\ U_2^N(t) \\ \vdots \\ U_m^N(t)\\ \end{array} \right) \approx \left( \begin{array}{c} u_1(t) \\ u_2(t) \\ \vdots \\ u_m(t)\\ \end{array} \right) . \end{aligned}$$

For linearization of the aforementioned weak form in (2.3), we use the semi-implicit second-order Leapfrog–Crank–Nicolson time integration method which treats the linear part of equation implicitly and the nonlinear part explicitly. Also this semi-implicit method has larger stability region than explicit ones and has been used extensively in the computational applied sciences. Therefore, for a given time step $\delta t$, the fully discrete Chebyshev–Legendre–Galerkin method for problem (2.1) is to find $U_i^N(t_k)\in V_N^0$ such that for any $w\in V_N^0$

$$\begin{aligned} \left\{ \begin{array}{ll} \langle U_i^N({\hat{t}}_k),w\rangle _\Omega +\mathbf{v }\cdot \langle \nabla U_i^N({\tilde{t}}_k),w\rangle _\Omega +d_i\langle \nabla U_i^N({\tilde{t}}_k),\nabla w\rangle _\Omega \\ +\langle I_N^C R_i(\mathbf{U }^N(t_k)),w\rangle _\Omega +\langle I_N^C f_i({\tilde{t}}_k),w\rangle _\Omega =0, &{} ~~t\in (0,T],~~i=1,2,\ldots ,m,\\ \langle U_i^N(t_1),w\rangle _\Omega =\langle I_N^C({u_0}_i+\delta t\frac{\partial u_i}{\partial t}|_{t=0}),w\rangle _\Omega ,\\ \langle U_i^N(0),w\rangle _\Omega =\langle I_N^C{u_0}_i,w\rangle _\Omega ,\\ \end{array} \right. \end{aligned}$$

(2.4)

in which ${\hat{t}}_k$, and ${\tilde{t}}_k$ stand for the following definition:

$$\begin{aligned} h({\hat{t}}_k)=\frac{h(t_{k+1})-h(t_{k-1})}{2\delta t},\quad h({\tilde{t}}_k)=\frac{h(t_{k+1})+h(t_{k-1})}{2}. \end{aligned}$$

Now for each $1\le i\le m$, the terms on the right-hand side of (2.4) which include the interpolation operator $I_N^C$ must be approximated by the Legendre expansion. This work is done by employing the nice and efficient algorithm proposed in [66]. This algorithm for $R_i(\mathbf{U }^N(t_k))$ is as follows:

For finding coefficients of the Legendre expansion of $f_i({\tilde{t}}_k)$, and ${u_0}_i+\delta t\frac{\partial u_i}{\partial t}|_{t=0}$, for each i, a similar algorithm can be used.

As mentioned in step 3 of the presented algorithm, we must apply a suitable algorithm to find coefficients of the Legendre expansion from coefficients of the Chebyshev one. Alpert and Rohklin [1] introduced an ${O}(N)$ algorithm which is efficient for large N and is based on the fast multipole method [19]. But Shen [66] proposed a similar algorithm whose complexity is almost $\text {min}\{\frac{1}{2}N^2,CN\}$ in one-dimensional space where C is a large constant. Hence, for moderate values of N, Shen’s algorithm is more efficient than the algorithm introduced in [1]. In one-dimensional case, the second and third steps of Algorithm 1 can be done in about $(\frac{5}{2}N\text {log}_2N+4N)+\text {min}\Big \{\frac{1}{2}N^2,CN\Big \}\sim {O}(N\text {log}_2N)$ as computed in [66]. Since multi-dimensional transform in the tensor product form is performed through a sequence of one-dimensional transforms, the two-dimensional version of Algorithm 1 can be done in ${O}(N^2\text {log}_2N)$ operations for $N>m$.

In the following, we describe extension of the Shen’s algorithm [66] to the two-dimensional case which can be applied in step 3 of the presented algorithm for finding the Legendre expansion coefficients from the coefficients of Chebyshev expansion.

If ${\tilde{b}}_{i,j}=\langle L_i,T_j\rangle _\Omega$, then the recurrence relation for computing ${\tilde{b}}_{i,j}$ is proposed in [66] as follows:

$$\begin{aligned} {\tilde{b}}_{i,j+1}=\frac{2i+2}{2i+1}{\tilde{b}}_{i+1,j}+\frac{2i}{2i+1}{\tilde{b}}_{i-1,j}-{\tilde{b}}_{i,j-1}, \end{aligned}$$

(2.5)

and with defining $b_{i,j}=(i+\frac{1}{2}){\tilde{b}}_{i,j}$, the vector of coefficients of Legendre expansion, $\mathbf{g^* }$, is obtained as follows:

$$\begin{aligned} \mathbf{g^* }=B\mathbf{f }, \end{aligned}$$

where $B=(b_{i,j})$, and $\mathbf{f }$ is vector of coefficients of Chebyshev expansion.

Now suppose

$$\begin{aligned} \sum _{i,j=0}^{N-2} h_{i,j}T_i(x)T_j(y)=\sum _{k,l=0}^{N-2}m_{k,l}L_k(x)L_l(y), \end{aligned}$$

and $H=(h_{i,j})$, $M=(m_{k,l})$. Multiplying both sides of the above relation in $L_p(x)L_q(y)$ and then integrating on $\Omega$ with respect to the Legendre weight, we obtain

$$\begin{aligned} \sum _{i,j=0}^{N-2}h_{i,j}\langle T_iT_j,L_pL_q\rangle _\Omega =\sum _{k,l=0}^{N-2} m_{k,l}\langle L_kL_l, L_pL_q\rangle _{\Omega }, \end{aligned}$$

or in an equivalent form we can write

$$\begin{aligned} \sum _{i,j=0}^{N-2} h_{i,j}\langle T_i,L_p\rangle _{I}\langle T_j,L_q\rangle _{I}=\sum _{k,l=0}^{N-2} m_{k,l}\langle L_k,L_p\rangle _{I}\langle L_l,L_q\rangle _{I}. \end{aligned}$$

(2.6)

If $c_{i,j}=\langle L_i,L_j\rangle _{I}$, then the matrix form of (2.6) is as follows:

$$\begin{aligned} {\tilde{B}}H{\tilde{B}}^t=CMC, \end{aligned}$$

in which $C=(c_{i,j})$, ${\tilde{B}}=({\tilde{b}}_{i,j})$ where ${\tilde{b}}_{i,j}$ will be obtained by the recurrence relation presented in (2.5) and ${\tilde{B}}^t$ is transpose of ${\tilde{B}}$. Also, due to the orthogonality property of the Legendre polynomials, C is a diagonal matrix and its inverse will be easily computed. Therefore, the Legendre expansion coefficients can be found from Chebyshev expansion coefficients by

$$\begin{aligned} M=C^{-1}{\tilde{B}}H{\tilde{B}}^tC^{-1}. \end{aligned}$$

(2.7)

By expanding

$$\begin{aligned} U_i^{N}(x,y,t)=\sum _{k,j=0}^{N-2}{\hat{u}}_{i,k,j}^{\small {N}}(t)\psi _{k,j}(x,y),\quad i=1,2\ldots ,m, \end{aligned}$$

and take $w=\psi _{l,m}$ in (2.4); then we have

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{'\small {N}}(t)\langle \psi _{k,j},\psi _{l,m}\rangle _\Omega + \mathbf{v }\cdot \left( \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(t)\langle \nabla \psi _{k,j},\psi _{l,m}\rangle _\Omega \right) +d_i\displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(t)\langle \nabla \psi _{k,j},\nabla \psi _{l,m}\rangle _\Omega \\ +\displaystyle \sum _{k,j=0}^{N-2}{\mathscr {R}}_{i,k,j}^{*}(t)\langle L_kL_j,\psi _{l,m}\rangle _\Omega + \displaystyle \sum _{k,j=0}^{N-2}{\mathscr {F}}_{i,k,j}^{*}(t)\langle L_kL_j,\psi _{l,m}\rangle _\Omega =0, \\ \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(t_1)\langle \psi _{k,j},\psi _{l,m}\rangle _\Omega =\displaystyle \sum _{k,j=0}^{N-2}{\mathscr {K}}_{i,k,j}^{*}\langle L_kL_j,\psi _{l,m}\rangle _\Omega ,~~~~~~~~~~~~~~~\qquad i=1,2,\ldots ,m,\\ \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(0)\langle \psi _{k,j},\psi _{l,m}\rangle _\Omega =\displaystyle \sum _{k,j=0}^{N-2}{\mathscr {I}}_{i,k,j}^{*}\langle L_kL_j,\psi _{l,m}\rangle _\Omega , \end{array} \right. \end{aligned}$$

or in an equivalent form

$$\begin{aligned} \left\{ \begin{array}{lllll} \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{'\small {N}}(t)\langle \phi _{k},\phi _{l}\rangle _I \langle \phi _{j},\phi _{m}\rangle _I +v_1\displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(t)\langle \phi '_{k},\phi _{l}\rangle _I\langle \phi _{j},\phi _{m}\rangle _I +v_2\displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(t)\langle \phi _{k},\phi _{l}\rangle _I\langle \phi '_{j},\phi _{m}\rangle _I \\ +d_i\left( \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(t)\langle \phi '_{k},\phi '_{l}\rangle _I\langle \phi _{j},\phi _{m}\rangle _I +\displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(t)\langle \phi _{k},\phi _{l}\rangle _I\langle \phi '_{j},\phi '_{m}\rangle _I\right) \\ +\displaystyle \sum _{k,j=0}^{N-2}{\mathscr {R}}_{i,k,j}^{*}(t)\langle L_k,\phi _l\rangle _I\langle L_j,\phi _{m}\rangle _I + \displaystyle \sum _{k,j=0}^{N-2}{\mathscr {F}}_{i,k,j}^{*}(t)\langle L_k,\phi _l\rangle _I\langle L_j,\phi _{m}\rangle _I=0,\quad i=1,2,\ldots ,m, \\ \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{'\small {N}}(t_1)\langle \phi _{k},\phi _{l}\rangle _I \langle \phi _{j},\phi _{m}\rangle _I=\displaystyle \sum _{k,j=0}^{N-2}{\mathscr {K}}_{i,k,j}^{*}\langle L_k,\phi _l\rangle _I\langle L_j,\phi _{m}\rangle _I,\\ \displaystyle \sum _{k,j=0}^{N-2}{{\hat{u}}}_{i,k,j}^{\small {N}}(0)\langle \phi _{k},\phi _{l}\rangle _I \langle \phi _{j},\phi _{m}\rangle _I=\displaystyle \sum _{k,j=0}^{N-2}{\mathscr {I}}_{i,k,j}^{*}\langle L_k,\phi _l\rangle _I\langle L_j,\phi _{m}\rangle _I, \end{array} \right. \end{aligned}$$

where matrices ${\mathscr {R}}_{i}^{*}(t)$ and ${\mathscr {F}}_i^{*}(t)$ are Legendre expansion coefficients of $R_i(\mathbf{U }^N(t))$ and $f_i(t)$, respectively, at time t and ${\mathscr {K}}_i^{*}$ is matrix of Legendre expansion coefficients of ${u_0}_i+\delta t\frac{\partial u_i}{\partial t}|_{t=0}$, and ${\mathscr {I}}_i^{*}$ is matrix of ${u_0}_i$ that all will be obtained by (2.7).

Let us denote $\alpha _{m,n}=\langle \phi _n,\phi _m\rangle _\Omega$, $\beta _{m,n}=\langle \nabla \phi _n,\nabla \phi _m\rangle _\Omega$, $\eta _{m,n}=\langle \nabla \phi _n,\phi _m\rangle _\Omega$, and $\gamma _{m,n}=\langle L_n,\phi _m\rangle _\Omega$; then for $0\le m,n\le N-2$, we get

$$\begin{aligned} \alpha _{m,n}= & {} \left\{ \begin{array}{ll} c_nc_m(\frac{2}{2n+1}+\frac{2}{2n+5}), &{} n=m, \\ -\frac{2c_nc_m}{2m+5}, &{} n=m+2, \\ -\frac{2c_nc_m}{2n+5}, &{} n=m-2, \\ 0, &{} \text {otherwise}, \end{array} \right. \\ \beta _{m,n}= & {} \left\{ \begin{array}{ll} 1, &{} n=m, \\ 0, &{} \text {otherwise}, \end{array} \right. \\ \eta _{m,n}= & {} \left\{ \begin{array}{ll} -2c_mc_n, &{} n=m-1, \\ 2c_mc_n, &{} n=m+1, \\ 0, &{} \text {otherwise}, \end{array} \right. \\ \gamma _{m,n}= & {} \left\{ \begin{array}{ll} \frac{2c_m}{2n+1}, &{} n=m, \\ -\frac{2c_n}{2m+5}, &{} n=m+2, \\ 0, &{} \text {otherwise}, \end{array} \right. \end{aligned}$$

where $c_n=\frac{1}{\sqrt{4n+6}}$.

Therefore, with defining $V_i^N(t)=({{\hat{u}}}_{i,k,j}^{\small {N}}(t))_{k,j}$, which encompasses coefficients in approximation of $u_i$ as a matrix, and supposing $X_i^k=V_i^N(t_{k+1})$, and $Y_i^k=V_i^N(t_{k-1})$, at each time step in (2.4) we must solve m matrix equations as follows:

$$\begin{aligned} AX_i^kA+\tau _1DX_i^kA+\tau _2AX_i^kD^t+\sigma _i(X_i^kA+AX_i^k)=W_i,\quad i=1,2\ldots ,m, \end{aligned}$$

(2.8)

in which

$$\begin{aligned} W_i=AY_i^kA-\tau _1DY_i^kA-\tau _2AY_i^kD^t-\sigma _i(Y_i^kA+AY_i^k)-\delta tC(2{\mathscr {R}}_{i}^{*}(t_k)+{\mathscr {F}}_i^{*}(t_{k-1})+{\mathscr {F}}_i^{*}(t_{k+1}))C^t, \end{aligned}$$

is known for each i, at time step $t_{k+1}$ and $\tau _1=v_1\delta t$, $\tau _2=v_2\delta t$, $\sigma _i=d_i\delta t$. Also matrices $A=(\alpha _{m,n})$, $D=(\eta _{m,n})$, $C=(\gamma _{m,n})$ are defined in the previous. In other words, at any time step and for each i we are dealing with a matrix equation in the form

$$\begin{aligned} AXA+\tau _1DXA+\tau _2AXD^t+\sigma (XA+AX)=W, \end{aligned}$$

(2.9)

where W is a known matrix. We can also rewrite the above matrix equation as a standard linear system using the tensor product notation as follows:

$$\begin{aligned} (A\otimes A+\tau _1D\otimes A+\tau _2A\otimes D+\sigma I\otimes A+\sigma A\otimes I){\mathbf {x}}=\mathbf {w} , \end{aligned}$$

where $\mathbf {x}$, and $\mathbf {w}$ are vectorization of unknown coefficients matrix X and known matrix W, respectively. Indeed, we have $\mathbf {x} =vec(X)$, $\mathbf {w} =vec(W)$. Also $\otimes$ denotes the tensor product of matrices, i.e. $A\otimes D=(\alpha _{i,j}D)_{i,j=0,1,\ldots ,\small {N-2}}$.

Remark

If we are concerned with a diffusion–reaction system, i.e. the velocity vector is equal to zero ($\mathbf{v }=0$) in (1.1), then (2.8) can be solved efficiently by the matrix decomposition methods. Considering that A is symmetric and using the real version of the Schur decomposition, there exists an orthogonal matrix Q such that

$$\begin{aligned} Q^tAQ=T, \end{aligned}$$

in which T is a diagonal matrix formed from the eigenvalues of A. Therefore, with defining $X=ZQ^t$ and multiplying both sides of (2.9) by Q and also using orthogonal property of Q, we obtain

$$\begin{aligned} AZT+\sigma (ZT+AZ)=WQ. \end{aligned}$$

(2.10)

The pth column of Eq. (2.10) can be written as

$$\begin{aligned} \lambda _pAZ_p+\sigma (\lambda _pZ_p+AZ_p)=(WQ)_p, \end{aligned}$$

(2.11)

where the index p indicates the pth column of the matrix and $\lambda _p$ is the pth eigenvalue of A. Finally (2.9) will be equivalent to solving $N-1$ systems of linear algebraic equations in the form of (2.11), simultaneously. We must note that the matrix A in (2.9) is fixed and at each time step remains unchanged; hence it is enough to decompose A only once to compute matrices Q, and T for using at each time step.

Therefore, the proposed scheme is as simple as finite difference method but with higher order accuracy (exponential convergence) in spatial coordinates and second-order convergence in time that are confirmed by the numerical results. Also, unlike the most paper which are concerned with nonlinear system (1.1), there is no iteration in this method.

3 Numerical experiments

In this section we implement Chebyshev–Legendre–Galerkin method for some examples of nonlinear system of advection–diffusion–reaction equations. Computations are performed for various advection vector $\mathbf{v }$, diffusion and kinetic coefficients, $d_i$, $b_{i,j,k}$ and $c_{i,j}$. The right-hand sides ($f_i$’s) are obtained by applying the differential operator to the exact solutions. The numerical experiments confirm the second-order convergence in time and the spectral accuracy in space.

In each example, graphs of relative errors in two norms $L_{\infty }$, and $L_2$ are plotted at $t=1$ with different time steps and different values of the spectral discretization parameter N. Errors are defined at the uniform grid $x_{i,j}=(x_i,x_j)$ in $[-1,1]^2$ and time t as follows:

$$\begin{aligned} \Vert e_i(t)\Vert _{\infty }=\frac{\Vert U_i^N(.,t)-u_i(.,t)\Vert _{\infty }}{\Vert u_i(.,t)\Vert _{\infty }},\quad \Vert e_i(t)\Vert _{2}=\frac{\Vert U_i^N(.,t)-u_i(.,t)\Vert _{2}}{\Vert u_i(.,t)\Vert _{2}},\quad i=1,2,\ldots ,m \end{aligned}$$

where

$$\begin{aligned} x_j=-1+\frac{2j}{\ell },\quad 0\le j\le \ell ,~~\ell =1000, \end{aligned}$$

and $U_i^N(x,t)$, and $u_i(x,t)$ are the ith numerical and exact solutions, respectively.

Example 1 (advection–diffusion–reaction system) This example is devoted to solve system of advection–diffusion–reaction (1.1) for $m=3$, velocity vector $\mathbf{v }=(1,1)$, and $d_i=i$, $(i=1,2,3)$. Indeed, we consider the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u_1}{\partial t}+\frac{\partial u_1}{\partial x}+\frac{\partial u_1}{\partial y}-\Delta u_1+R_1(u_1,u_2,u_3)+f_1(\mathbf{x },t)=0, \\ \frac{\partial u_2}{\partial t}+\frac{\partial u_2}{\partial x}+\frac{\partial u_2}{\partial y}-2\Delta u_2+R_2(u_1,u_2,u_3)+f_2(\mathbf{x },t)=0, \\ \frac{\partial u_3}{\partial t}+\frac{\partial u_3}{\partial x}+\frac{\partial u_3}{\partial y}-3\Delta u_3+R_3(u_1,u_2,u_3)+f_3(\mathbf{x },t)=0, \end{array} \right. \end{aligned}$$

(3.1)

in which $R_1=u_1u_2+u_1u_3$, $R_2=u_1+u_2+u_3$, and $R_3=u_2u_3$ and the exact solutions are supposed to be

$$\begin{aligned} \left\{ \begin{array}{ll} u_1(x,y,t)=(1-x^2)(1-y^2)\text {cos}(t), \\ u_2(x,y,t)=(1+e^{-t})\text {sin}(\pi x)\text {sin}(\pi y),\\ u_3(x,y,t)=(1-x^6)(1-y^6)\text {sinh}(x+y-t^2). \end{array} \right. \end{aligned}$$

Also $f_1$, $f_2$ and $f_3$ are smooth source functions which are chosen corresponding to the exact solutions.

For different definitions of reaction terms $R_i$, such systems like (3.1) have many applications in various fields of science. In [48] the modeling of synchronous oscillation in the plasmodium is stated by the above system and the quantities $u_1$, $u_2$, and $u_3$ are interpreted by concentrations of chemical substance in the free compartment of ectoplasm, non-free compartment of ectoplasm and endoplasmic compartment, respectively. Also in [6] a mathematical framework for the main qualitative features of plankton patchiness is presented in which $u_1$ is maximum phytoplankton content supported by a parcel of water in the absence of grazing, $u_2$ is distribution of phytoplankton and $u_3$ is mortality.

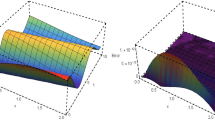
In Fig. 1 the numerical solutions of (3.1) for $N=30$ and $\delta t=10^{-5}$ are plotted at $t=1$. Also The behavior of $L_{\infty }$, and $L_2$ errors at $t=1$ versus N are plotted in Fig. 2 for different time steps. Furthermore, the error values are shown in Tables 1, 2 confirming that the order of convergence (rate) in time is two and in space is spectral (exponential).

In all tabular results, we use the abbreviation notation x(n) instead of $x\times 10^n$.

Fig. 1

Numerical solutions of (3.1) for $N=30$, $\delta t=10^{-5}$ at $t=1$

Table 1 The $L_\infty$, $L_2$ errors of (3.1) at $t=1$ for $\delta t=10^{-5}$

Table 2 The $L_\infty$, $L_2$ errors of (3.1) at $t=1$ for $N=30$

Example 2 (predator–prey system) In this example, generalized predator–prey system with many applications in populations dynamics and ecology is considered as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u_1}{\partial t}=D\Delta u_1+ru_1(1-\frac{u_1}{v_0})-cu_2g(u_1)-f_1(\mathbf{x },t), \\ \frac{\partial u_2}{\partial t}=D\Delta u_2-bu_2+au_2g(u_1)-f_2(\mathbf{x },t), \\ \end{array} \right. \end{aligned}$$

(3.2)

where r, c, a, b, $v_0$ are positive parameters and D is the diffusivity. Also $u_2$, and $u_1$ are concentrations of predators and preys, respectively. As mentioned in [6], the function $g(\cdot )$ represents the prey consumption rate per predator as a function of the maximal consumption rate, c. Parameters a and r denote maximal per capita predator and prey birth rates; for predators, that is the birth rate when the prey density is very high, while for prey, it is the birth rate at very low prey density. The per capita predator death rate is denoted by b, and $v_0$ is the prey carrying capacity.

We suppose

$$\begin{aligned} \left\{ \begin{array}{ll} u_1(x,y,t)=\frac{({e}^{x^2-1}-1)({e}^{y^2-1}-1)}{1+t^2}, \\ u_2(x,y,t)=(e^{\text {sin}(\pi x)}-1)(e^{\text {cos}(\frac{\pi }{2} y)}-1)(1+t^4), \\ \end{array} \right. \end{aligned}$$

are the exact solutions of (3.2) with taking $g(u)=u+u^3$, and the parameters $D=1.5$, $c=r=v_0=0.5$, $a=b=1$. Also $f_1$ and $f_2$ are defined according to the exact solutions.

Fig. 2

Diagram of error $\Vert e(i)\Vert _{\infty }$, and $\Vert e(i)\Vert _{2}$, ($i=1,2,3$), versus N for (3.1)

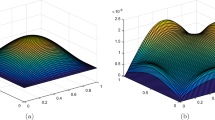
For $N=30$ and $\delta t=10^{-5}$ the numerical solutions at $t=1$ are drawn in Fig. 3. In Tables 3 and 4, error values for different spectral discretization parameter, N, and different time steps are listed, respectively. As can be predicted, the rate of convergence in time is approximately two. The behavior of $L_{\infty }$, and $L_2$ errors at $t=1$ versus N are depicted in Fig. 4 for different time steps.

Fig. 3

Numerical solutions of (3.2) for $N=30$, $\delta t=10^{-5}$ at $t=1$

Table 3 The $L_\infty$, $L_2$ errors of (3.2) at $t=1$ for $\delta t=10^{-5}$

Table 4 The $L_\infty$, $L_2$ errors of (3.2) at $t=1$ for $N=30$

Fig. 4

Diagram of error $\Vert e(i)\Vert _{\infty }$, and $\Vert e(i)\Vert _{2}$, (i = 1, 2), versus N for (3.2)

Example 3 (Fitzhugh–Nagumo system) As the last example, we investigate Fitzhugh–Nagumo system that originally has been introduced as a mathematical model for the neural activity [14, 49]. This model is presented as

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u_1}{\partial t}-D\Delta u_1-u_1(u_1-1)(a-u_1)+u_2+f_1(\mathbf{x },t)=0, \\ \frac{\partial u_2}{\partial t}-bu_1+\gamma u_2+f_2(\mathbf{x },t)=0, \\ \end{array} \right. \end{aligned}$$

(3.3)

where $u_1$ is the activator, $u_2$ is the inhibitor, and a, b, $\gamma$ are positive parameters.

We take the exact solutions as

$$\begin{aligned} \left\{ \begin{array}{ll} u_1(x,y,t)=\frac{(1-x^4)(1-y^4)}{(1+t^2+y^2)(1+t^2+x^2)}, \\ u_2(x,y,t)=\frac{\text {sin}(\pi x)\text {sin}(\pi y)}{\text {e}^{tx}+\text {e}^{-ty}}, \\ \end{array} \right. \end{aligned}$$

and define the source functions $f_1$ and $f_2$ accordingly.

The numerical solutions at $t=1$ for $N=30$ and $\delta t=10^{-5}$ are plotted in Fig. 5. Error values for different spectral discretization parameter, N, are presented in Table 5 and also in Table 6 they are listed for different time steps. The behavior of $L_{\infty }$, and $L_2$ errors at $t=1$ versus N are drawn in Fig. 6 for different time steps.

Fig. 5

Diagram of error $\Vert e(i)\Vert _{\infty }$, and $\Vert e(i)\Vert _{2}$, ($i=1,2$), versus N for (3.3)

Table 5 The $L_\infty$, $L_2$ errors of (3.3) at $t=1$ for $\delta t=10^{-5}$

Table 6 The $L_\infty$, $L_2$ errors of (3.3) at $t=1$ for $N =30$

Fig. 6

Numerical solutions of (3.3) for $N=30$, $\delta t=10^{-5}$ at $t=1$

The numerical results presented in all examples confirm the second-order convergence in time and the spectral accuracy in space, but as can be seen in each example, there exists a certain value of N such $N_0$ whose increasing spectral discretization parameter, N, greater than $N_0$, has no significant effect on decreasing error and rate of convergence will be almost equal to zero. This fact is due to the time discretization error, because according to the error bound of the proposed method which is approximately in form of $\kappa ((\delta t)^2+ N^{-m+1})$, only increasing spectral discretization parameter, N, or decreasing time step $\delta t$ solely, will not reduce the obtained error and for this purpose we must increase N, and decrease $\delta t$, simultaneously.

4 Conclusion

In this paper we used the Legendre–Galerkin method combined with the Chebyshev-collocation technique for spatial discretization and Leapfrog–Crank–Nicolson scheme for time advancing to solve a two-dimensional nonlinear advection–diffusion–reaction system. As can be seen, the advantage of this method over the classic Galerkin methods is its efficiency in solving nonlinear equations by converting the equation to solve a linear system of algebraic equations or a matrix equation that can be solved by decomposition methods in some cases. Numerical examples demonstrate the efficiency and spectral accuracy of the proposed method. Also the results presented in each example indicate that only increasing spectral discretization parameter N or decreasing time step $\delta t$ will not reduce the obtained error and, therefore, we must increase N and decrease $\delta t$, simultaneously.