Diagnosis and Control of Nonlinear Oscillations of a Fluttering Plate

Abstract

This chapter focuses on both diagnosing and controlling the nonlinear dynamic responses of a fluttering plate excited by a high-velocity air flow. Six modes of the motion are considered for obtaining the numerical solutions of the system, and the modes are used to investigate the nonlinear dynamic responses of the fluttering. Due to the different characteristics of the diagnosing methods for nonlinear systems, Lyapunov Exponent method is employed to detect the system motion of each mode, while the Periodicity Ratio method is utilized to detect the behavior of entire system motion subjected to non-periodic excitations generated by the air flow. A newly developed control strategy, modified FSMC method, is applied to control the nonlinear oscillatory responses of the system. The approaches presented in this chapter have research and engineering application significances in the fields of aerodynamics, nonlinear dynamics, aircraft design, and design of space vehicles.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

Flutter behavior of plates exposed to air flow has been a subject of major interest and wide research attention because of its exceptional importance in the areas of aerodynamics, aircraft design, and design of space vehicles. The life expectancy and survivability of fluttering panels on high supersonic aircraft, for example, depend substantially on their resistance to the nonlinear fluttering oscillations of the panels subjected to excitations generated by high-speed air flow.

Von Karman’s large deflection theory [1] has been employed by most researchers in the field. The Galerkin method [2, 3] was utilized by Dowell [4, 5] and the latter studies [6–8]. By the integration over the panel surface, these allow the numerical integration to a system of nonlinear ordinary differential equations. The dynamic behaviors, including deflection, stress, and frequency, under 2D and 3D, were analyzed with respect to various parameters. In a survey reported by Garrick and Reed [9], an overview of an aircraft flutter in historical retrospective is presented by the authors. The influence of maneuvering on the nonlinear response of a fluttering buckled plate on an aircraft has been studied by Sipcic [10], which suggests amplitude modulation as a possible new mode of transition to chaos. The flutter phenomenon in aeroelasticity and the mathematical analysis are given by Shubov [11]. Models of fluid–structure interaction with precise mathematical formulations available are selected and analytical results are obtained to explain flutter and its treatments. Due to the high velocity of fluid, thermal effects caused by friction have to be taken into consideration, which actually makes the problem more complicated. Enormous work could be found in this area such as [12–16]. Due to the existence of the effects of the aerodynamic, inertial, and elastic forces, the dynamic behaviors of the fluttering plate become extremely complicated especially when the speed of external fluid flow increases. One would expect that it would be of fundamental importance to know the role of the system parameters related to the different responses of the system.

Numerous research and great contributions have been made in investigating the characteristics of fluttering plates by researchers and engineers as mentioned above. The criteria for distinguishing the characteristics of the systems are crucial. Techniques providing high efficiency and accuracy in diagnosing and quantifying different characteristics such as chaos, periodicity, quasiperiodicity, and other nonlinear characteristics are always demanded. There are several methods available in the literature for determining the onset of chaotic oscillations and some predictive and diagnostic criteria for chaos are also reported [17–21]. Power spectral density is one of such methods that can be used to distinguish chaos from regular behavior of deterministic systems or generic stationary stochastic behavior [22]. Fractal Dimensions approach is able to identify the chaotic attractors’ dimension [23–27]. Among all the diagnosing approaches, Lyapunov Exponent approach is probably the most popular approach [28, 29] due to its efficiency and simplicity. It measures the sensitivity of a system to initial conditions and therefore classifies the system’s responses as either convergent or divergent and it is suitable for describing whether a response of the plate is convergent or divergent. However, Lyapunov Exponents cannot be used to distinguish quasiperiodicity and non-periodicity of a system. Periodicity Ratio method is developed Dai and Singh [30]. This approach and can be used to identify almost all the nonlinear characteristics and to be employed to plot the periodic–quasiperiodic–chaotic diagram efficiently for nonlinear dynamical systems.

In most applications of engineering, the nonlinear or irregular responses of the beams are desired to be controlled. Numerous control techniques and theories are available in the field. In 1992, a control theory, namely the theory of sliding modes control (SMC), was proposed and it has been pointed out that this control theory is of high efficiency in the control of multidimensional systems operating under conditions of uncertainties [31]. A decade later, an improved control strategy, which was developed on the basis of SMC, was developed with implementation of fuzzy logic theories and named as fuzzy sliding mode control (FSMC). Many researchers used the strategy and demonstrated the effectiveness of this control strategy in suppressing the nonlinear response of the system [32–34]. The FSMC strategy was also used in controlling the chaotic response of a micro mechanical resonator under electrostatic forces applied at both sides of the resonator, modeled as a beam [35]. In their study, the FSMC strategy demonstrated high efficiency in stabilizing the vibrations of the targeted system. It should be noticed the existing FSMC strategy is merely suitable to be applied in the system derived by first-order discretization. However, for the cases of second or higher order discretization and more reliable and accurate solutions, the existing FSMC strategy is not applicable. Therefore, a modified FSMC strategy [36] is developed.

This research is firstly to diagnose the characteristics of a plate subjected to non-periodic excitations of high-velocity flow with both Lyapunov Exponent (LE) and Periodicity Ratio (PR) methods. The responses of the fluttering plate are to be analyzed with considerations of various varying systems parameters. Furthermore, it would be interesting to apply the control theory to the nonlinear response of the system to reduce the harm. As figured out by Dowell [4] corresponding to the parameters selected in the study, 4–6 modes, rather than two modes, should be employed for quantitative accuracy. Hence, in this section the modified FSMC will be applied to control and stabilized the chaotic oscillation of the fluttering 2D plate, which has been described in terms of six modes as mentioned in the previous section. The main purpose of the present work focuses on the nonlinear influence of the system and applying control theory such as FSMC to reduce the system vibrations, where a chaotic case is used as the control example. The knowledge of detecting and controlling the flutter behavior of a vibrating plate is useful.

Governing Equation for the Motion of a 2D Plate

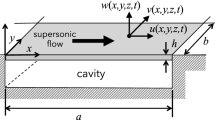
Same as Dowell’s research, the fluttering plate considered in this research has simply supported boundaries, is a flat thin plate with infinite length in the y-direction and length L in the x-direction. The thickness is negligible in comparing with the other geometric dimensions of the plate. The panel is subjected to a supersonic flow over the outside surface with constant velocity ${U_{\infty }}$. Gravity is perpendicular to the plate. The plate is induced to vibrate along the z-direction due to the loading generated by the interaction between the high-velocity flow and the plate, which is dominating and thus of great importance.

To obtain the governing equations of the motion of a 2D fluttering plate, some assumptions adopted are presented first as follows:

• The von Karman’s large deflection plate theory is employed;

• The effects of in-plane load and static pressure differential are taken into consideration;

• The plate is undergoing cylindrical bending but no span-wise bending.

Based on the assumptions above, the governing equation reads [9]:

$$ D\frac{{{\partial^4}w}}{{\partial {x^4}}}-\left( {{N_x}+N_x^{(a) }} \right)\frac{{{\partial^2}w}}{{\partial {x^2}}}+{\rho_m}h\frac{{{\partial^2}w}}{{\partial {t^2}}}+\left( {p-{p_{\infty }}} \right)=\varDelta p $$

(3.1)

where

$$ {N_x}=\alpha Eh/2L\int\nolimits_0^L {{{{\left( {\partial w/\partial x} \right)}}^2}dx} $$

$$\begin{array}{lll} {N_x}& = &\alpha Eh/2L\int\nolimits_0^L {{{{\left( {\partial w/\partial x} \right)}}^2}dx} \nonumber\\ \alpha & = & KL/(KL+Eh) \end{array}$$

(3.2)

Following quasi-steady, supersonic theory, we have

$$ p-{p_{\infty }}=\frac{2q }{\beta}\left[ {\frac{{\partial w}}{{\partial x}}+\left( {\frac{{{M^2}-2}}{{{M^2}-1}}} \right)\frac{1}{U}\frac{{\partial w}}{{\partial t}}} \right] $$

(3.3)

Applying the nondimensionalization as follows:

$$ \xi =x/a $$

$$ \tau =t{{\left( {D/{\rho_m}h{a^4}} \right)}^{1/2 }} $$

$$ W=w/h $$

$$ \lambda =2q{a^3}/\beta D $$

$$ \mu =\rho a/{\rho_m}h $$

$$ P=\varDelta p{a^4}/Dh $$

(3.4)

Substituting Eqs. (3.2)–(3.4) into (3.1), the non-dimensionalized governing equation can be expressed as

$$ \begin{array} {lll} & W^{\prime \prime \prime \prime}-\alpha 6(1-{\nu^2})\left[ {\int\nolimits_0^1 {{{{\left( {W^{\prime}} \right)}}^2}d\xi } } \right]W^{\prime \prime}-{R_x}W^{\prime \prime}+\frac{{{\partial^2}W}}{{\partial {\tau^2}}}\hfill\\ & \quad +\lambda \left\{ {W^{\prime}+\left( {\frac{{{M^2}-2}}{{{M^2}-1}}} \right){{{\left( {\frac{\mu }{{\beta \lambda }}} \right)}}^{{\frac{1}{2}}}}\frac{{\partial W}}{{\partial \tau }}} \right\}=P \end{array} $$

(3.5)

For large Mach number, $M\gg 1$, the simplified relationship can be applied

$$ {{\left[ {\frac{{{M^2}-2}}{{{M^2}-1}}} \right]}^2}\frac{\mu }{\beta}\to \frac{\mu }{M} $$

(3.6)

Following the Galerkin Method [37], for simply supported plate, the nondimensional displacement $W(\xi, \tau )$ can be expressed as:

$$ W(\xi, \tau )=\sum\limits_{m=1}^{\infty } {{a_m}(\tau )} \cdot \sin m\pi \xi $$

(3.7)

Substituting Eqs. (3.6) and (3.7) into Eq. (3.5), Eq. (3.5) can be rewritten as:

$$ \begin{array}{lll}&\sum {{a_m}{{{(m\pi )}}^4}\sin m\pi \xi } +\alpha 6(1-{\nu^2})\times \left[ {\sum\limits_r {a_r^2\frac{{{{{\left( {r\pi } \right)}}^2}}}{2}} } \right]\sum\limits_m {{a_m}{{{\left( {m\pi } \right)}}^2}\sin m\pi \xi }\hfill\\ & \quad +{R_x}\sum\limits_m {{a_m}{{{\left( {m\pi } \right)}}^2}\sin m\pi \xi } +\sum\limits_m {\frac{{{d^2}{a_m}}}{{d{\tau^2}}}\sin m\pi \xi }\hfill\\ & \quad +\lambda \left[ {\sum\limits_m {{a_m}\left( {m\pi } \right)\cos m\pi \xi } +{{{\left( {\frac{\mu }{{M\lambda }}} \right)}}^{{\frac{1}{2}}}}\sum\limits_m {\frac{{d{a_m}}}{{d\tau }}\sin m\pi \xi } } \right]=P \\[-2pc] \end{array} $$

(3.8)

By multiplying Eq. (3.8) by $\sin m\pi \xi$ and integrating over the length of the panel, Eq. (3.8) can be reduced into a set of ordinary differential equations.

$$ \begin{array}{lll}&{a_s}\frac{{{{{\left( {s\pi } \right)}}^4}}}{2}+\alpha 6\left( {1-{\nu^2}} \right)\left[ {\sum\limits_r {a_r^2\frac{{{{{\left( {r\pi } \right)}}^2}}}{2}} } \right]{a_s}\frac{{{{{\left( {s\pi } \right)}}^2}}}{2}+{R_x}{a_s}\frac{{{{{\left( {s\pi } \right)}}^2}}}{2}+\frac{{{d^2}{a_m}}}{{d{\tau^2}}}\frac{1}{2}\hfill\\ & \quad +\lambda \left\{\sum\limits_m {\frac{sm }{{{s^2}-{m^2}}}\times } \left[ {1-{(-1)^{s+m }}} \right]{a_m}+\frac{1}{2}{{\left( {\frac{\mu }{{M\lambda }}} \right)}^{{\frac{1}{2}}}}\frac{{d{a_s}}}{{d\tau }}\right\}\hfill\\ & \quad =P\frac{{\left[ {1-{(-1)^2}} \right]}}{{s\pi }},s=1,\cdots, \infty \end{array} $$

(3.9)

Equation (3.9) is comprised of a coupled set of ordinary, nonlinear differential equations with respect to time. The equations will be numerically solved. It has been reported by Garrick and Reed [9] that to obtain accurate solutions, at least four modes must be used. When the in-plane or static pressure loading produces larger tension in the plate, more modes would be taken into consideration. In this chapter, under the range of parameters applied, all the calculations are performed using six modes.

Periodicity Ratio Method

It is widely acknowledged that the corresponding Poincare map for a steady state periodic motion of a dynamic system consists of a finite number of visible points [30, 38]. The visible points in the Poincare map are then the points overlapping many points periodically appeared. On the other hand, the points in the Poincare map of a chaotic case must distribute in an unpredictable manner. This implies that the overlapping points in the Poincare map of a chaotic response are extremely minimal. Quasiperiodic response is another type of phenomenon in nonlinear dynamic systems. A quasiperiodic case may also contain negligibly small number of overlapping points, though some regularity of the system responses can be identified. Based on these findings, Dai and Singh [30, 39, 40] proposed an index named Periodicity Ratio (PR) which counts the ratio of periodic points among all the points in the Poincare map. The methodology of Periodicity Ratio approach is based on the measure of periodicity of a response of a nonlinear system. The more periodic a dynamic system is, the closer the corresponding PR value is to a unit. When the PR approaches zero, the corresponding system has no periodicity at all and therefore represents either chaotic or quasiperiodic response of the system. The most significant advantage of the Periodicity Ratio method is that the PR value can be used as a single value index in diagnosing the periodicity therefore the behavior of a dynamic system. Moreover, Periodicity Ratio method reveals the fact that there are infinite number of fashions of motion in between chaos and periodic responses for a nonlinear dynamic system.

The Periodicity Ratio is defined as [30]:

$$ \gamma =\mathop{\lim}\limits_{{n\to \infty }}\frac{NPP }{n} $$

(3.10)

where NPP is the number of periodically overlapping points and n is designated as the total number of all the points in the Poincare map. NPP in Eq. (3.10) can be calculated by

$$ NPP=\phi (1)+\sum\limits_{m=2}^n {(\phi (m).P(\prod\limits_{j=1}^{m-1 } {Q(\phi (j))} ))} $$

(3.11)

where

$$ \phi (l)=\sum\limits_{i=m+q+1}^n {P(\prod\limits_{h=0}^{q-l } {Q({X_{i+h }}-{X_{m+l+h }})} )(\prod\limits_{k=1}^l {Q({X_{i-k }}-{X_{m+l-k }})} )} $$

(3.12)

which represents the number of points periodically overlapping the lth point in the Poincare map. In the above two equations, q, m, i, and l are all positive integers. Note that q value in the above equation can be different from one group of points to another group of points.

In the above equations, two step functions $Q(y),P(z)$ are introduced. The two step functions are expressible in the form

$$ Q(y)=\left\{ \begin{gathered} 1,\ \mathrm{if}\ y=0 \hfill \\ 0,\ \mathrm{if}\ y\ne 0 \hfill \\ \end{gathered} \right.,P(z)=\left\{ \begin{gathered} 0,\ \mathrm{if}\ \mathrm{z}=0 \hfill \\ 1,\ \mathrm{if}\ \mathrm{z}\ne 0 \hfill \\ \end{gathered} \right. $$

(3.13)

In order to describe the visible and overlapping points in a Poincare map, introduce ${X_i}=\left\{ \begin{aligned} {x_i} \hfill \\ {{\dot{x}}_i} \end{aligned} \right\}$ and denote it as a vector of both displacement and velocity. With this designation, the determination of whether or not a point in the Poincare map is an overlapping point is based on the judgment described by the following equations.

$$ \begin{gathered} {X_{ki }}={x_k}-{x_i} \hfill \\ {{\dot{X}}_{ki }}={{\dot{x}}_k}-{{\dot{x}}_i} \hfill \\ \end{gathered} $$

(3.14)

where k is an integer in the range of 1 ≤ k ≤ j and j represents the finite number of points (known as visible points) appearing in the Poincare map corresponding to a dynamic system, and $\dot{X}$ is the time derivative of $X$. Points under consideration are overlapping points if and only if the following conditions are satisfied.

$$ \begin{gathered} {X_{ki }}=0 \hfill \\ {{\dot{X}}_{ki }}=0 \hfill \\ \end{gathered} $$

(3.15)

In this case, the way to obtain the points in the Poincare map is to get several points with same displacements since the fixed time step of the irregular excitation system is hardly to be captured [20]. Specifically, the peak and bottom value in every period of the wave form will be collected. If the system finally leads to a periodic solution, after a long enough period of time, all the points of the Poincare map will converge to a finite number of individual points which must have the form $\{{X_m},{X_{m+1 }},\ldots,{X_{m+q }}\}$.

Thus, any overlapping point ${X_p}$ in a Poincare map would be a periodic point, if and only if the following condition is satisfied:

$$ P(\sum\limits_{i=0}^q {\{ {P(\prod\limits_{h=0}^{q-l } {Q({X_{i+h }}-{X_{m+l+h }})} )(\prod\limits_{k=1}^l {Q({X_{i-k }}-{X_{m+l-k }})} )} \})=1} $$

(3.16)

Once the periodic points are determined completely, the Periodicity Ratio can be determined accurately.

If the behavior of a system in a steady state is periodic, the points in the corresponding Poincare map must all be overlapping points. Accordingly, the value of the Periodicity Ratio, $\gamma$, should simply be unity. For a chaotic response of a system, on the other hand, the number of periodic points overlapped should be zero or insignificant in comparing with n. This is to say, $\gamma$ approaches zero for chaos.

With the definition of the Periodicity Ratio, $\gamma$ is clearly a quantified description of periodicity for a dynamic system. This is to state that $\gamma$ indicates quantitatively how close the response of a dynamic system is to a perfect periodic motion. For example, a motion with $\gamma$ equals to 0.9 is more close to a periodic motion in comparing with a motion to which $\gamma$ equals to 0.8. Contrastively, a motion with $\gamma$ approaching zero will show no periodic behavior, and therefore is a perfectly nonperiodic motion. When $\gamma$ takes a value such that $0<\gamma <1$, it implies that some points in the Poincare map are periodically overlapping points while the others are not. Nonperiodic cases in between chaos and periodic motions may include the intermittent chaos in which chaotic motions occur between periods of regular motion.

It should be noted, however, the expression shown in Eq. (3.10) is theoretical, as it requires an infinitely large number of n for a perfect measurement of $\gamma$ and the time range considered must be $t\in [0,\infty )$ such that $t$ will be sufficient for a perfect $\gamma$. This implies that the Periodicity Ratio $\gamma$ can be precisely calculated only in the cases for which the analytical solutions corresponding to the dynamical systems are available. For most nonlinear dynamic systems, however, the calculation for the Periodicity Ratio has been done on a numerical basis with the aid of a computer, as analytical solutions for these systems are not available. As $Q(y),$ $P(z)$ in the equations are step functions, the numerical calculation for γ can be conveniently carried out. In numerically determining for $\gamma$, therefore, a sufficiently large n should be used in performing the actual numerical calculation for $\gamma$ in the practice of numerical calculation. In computing the Periodicity Ratio, errors caused by numerical calculation and by the mathematical models of numerical purpose should also be considered. Furthermore, in numerically calculating for $\gamma$, all of the n points must be compared to see whether they are overlapping points or not. Once a point is counted as an overlapping point, it should not be counted again in the numerical calculations.

For nonlinear dynamic systems, a motion with Periodicity Ratio equals to zero may not necessarily be a chaotic motion. By the definition of Periodicity Ratio, a perfect quasiperiodic motion also has a Periodicity Ratio of zero. In this case, another technique, Lyapunov Exponent approach can be employed.

Lyapunov Exponent Spectrum

The definition of Lyapunov Exponent is associated with a measure of the average rates of expansion and contraction of trajectories surrounding a given trajectory. They are asymptotic quantities, defined locally in state space, and describe the exponential rate at which a perturbation to a trajectory of a system grows or decays with time at a certain location in the state space. They are useful in characterizing the asymptotic state of an evolution. The spectrum of Lyapunov Exponent has proven to be one of the practically sound techniques for diagnosing chaotic systems. It is probably the most widely used index in characterizing the behaviors of nonlinear dynamic systems. The approach is based on the important characteristic that chaos of a nonlinear dynamic system is sensitivity to initial conditions, which counts the average exponential rates of divergence or convergence of close orbits of a vibrating object in the phase space of a dynamic system. Wolf et al. [29] gave a powerful and efficient method for determining Lyapunov Exponents from time series. Rong et al. [41] investigated the principal resonance of a stochastic Mathieu oscillator to random parametric excitation and gave the conclusion that the instability of the stochastic Mathieu system depends on the sign of the maximum Lyapunov Exponent. Lyapunov Exponent was also used to analyze the numerical characteristic [42]. It is usually determined by experiments or computer simulations. Nayfeh has clearly described the definition of Lyapunov Exponent as followings [20].

Let $X(t)$ such that $X(t=0)={X_0}$ represent a trajectory of the system governed by the following n-dimensional autonomous system:

$$ \dot{\mathbf{x}} =\mathrm{F}(\mathbf{x};\mathrm{M}) $$

(3.17)

where the vector $\mathbf{x}$ is made up of n state variables, the vector function $\mathrm{F}$ describes the nonlinear evolution of the system, and $\mathrm{M}$ represents a vector of control parameters. Denoting the perturbation provided to $X(t)$ by $y(t)$ and assuming it to be small, an equation after linearization in the disturbance terms can be obtained. The perturbation is governed by

$$ \frac{dy(t) }{dt }=Jy(t) $$

(3.18)

where, in general, $J={D_x}\mathrm{F}(\mathbf{x}(t);\mathrm{M})$ is a $n\times n$ matrix with time dependent coefficients. If we consider an initial deviation $y(0)$, its evolution is described by

$$ y(t)=\varPhi (t)y(0) $$

(3.19)

where $\varPhi (t)$ is the fundamental (transition) matrix solution of Eq. (3.18) associated with the trajectory $X(t)$.

For an appropriately chosen $y(0)$ in Eq. (3.19), the rate of the exponential expansion or contraction in the direction of $y(0)$ on the trajectory passing through ${X_0}$ is given by

$$ {{\bar{\lambda}}_i}=\mathop{\lim}\limits_{{t\to \infty }}\frac{1}{t}\ln (\frac{{\left\| {y(t)} \right\|}}{{\left\| {y(0)} \right\|}}) $$

(3.20)

where the symbol $\left\| {} \right\|$ denotes a vector norm. The asymptotic quantity ${{\bar{\lambda}}_i}$ is then defined as the Lyapunov Exponent. There are several different methods to calculate the Lyapunov Exponent, such as the whole Lyapunov Exponent, global and local Lyapunov Exponent, and Lyapunov Spectrum. The method of whole Lyapunov Exponent also known as the Maximum Lyapunov Exponent is suitable for the discrete differential system, whereas the Lyapunov Spectrum is more suitable for continuous differential systems [20]. The global Lyapunov exponent, on the other hand, gives a measure for the total predictability of a system; whereas the Local Lyapunov Exponent estimates the local predictability around a given point ${X_0}$ in phase space.

Specifically, to obtain the Lyapunov spectrum for a continuous dynamical system, a set of n linearly independent vectors ${y_1},{y_2},\ldots,{y_n}$ may form the basis for the n-dimensional state space. Choosing an initial deviation along each of these n factors, n Lyapunov Exponent ${{\bar{\lambda}}_i}({y_i})$ can be determined. The set of n numbers ${{\bar{\lambda}}_i}({y_i})$ is defined as the Lyapunov spectrum. For system (3.17), n orthonormal initial vectors ${y_i}$ such that ${y_1}=(1,0,0,\ldots ),{y_2}=(0,1,0,\ldots ),\ldots,{y_n}=(0,0,0,\ldots,1)$ can be assigned. For each of these initial vectors, Eqs. (3.17) and (3.18) can be integrated for a finite time ${T_f}$ and a set of vectors ${y_1}({T_f}),{y_2}({T_f}),\ldots,{y_n}({T_f})$ can then be obtained. The new set of vectors is orthonormalized using the Gram-Schmidt procedure to produce

$$ {{\hat{y}}_1}=\frac{{{y_1}({T_f})}}{{\left\| {{y_1}({T_f})} \right\|}} $$

$$ {{\hat{y}}_n}=\frac{{{y_n}({T_f})-\sum\nolimits_{i=1}^{n-1 } {[{y_n}({T_f}).{{\hat{y}}_i}]{{\hat{y}}_i}} }}{{\left\| {{y_n}({T_f})-\sum\nolimits_{i=1}^{n-1 } {[{y_n}({T_f}).{{\hat{y}}_i}]{{\hat{y}}_i}} } \right\|}} $$

(3.21)

Subsequently, using $X(t={T_f})$ as an initial condition for Eq. (3.18) and using each of the ${{\hat{y}}_i}$ as an initial condition for Eq. (3.19), Eqs. (3.18) and (3.19) can be integrated again for a finite time and carry out the Gram-Schmidt procedure to obtain a new set of orthonormal vectors. The norm in the denominator can be denoted by $N_j^k$. Thus, after repeating the integrations and the processes of Gram-Schmidt orthonormalization r times, the Lyapunov Exponent can be obtained from

$$ {{\hat{\lambda}}_i}=\frac{1}{{r{T_f}}}\sum\limits_{k=1}^r {\ln N_j^k} $$

(3.22)

The Lyapunov spectrum can thus be determined.

Utilizing Lyapunov Exponent and Periodicity Ratio Methods to Detect the System Motions

From the above description about Lyapunov Exponents, the Jacobi matrix which is directly related to the expressions of the system equations is required for calculation in every step. However, the system displacement in Eq. (3.7) cannot be obtained by this way because the Jacobi matrix would vary with different mode whose governing equation is stated in Eq. (3.9). And the Jacobi matrix for the whole system displacement cannot be combined by the individual matrix under each mode. Therefore, Lyapunov Exponents could only measure the system behavior at each mode other than the whole trend, which can disclose certain system properties while still not enough to diagnose the real system behavior, since the involved modes are only introduced by the mathematical transformation that in the real model the behavior under single mode cannot be distinguished from each other. So it is not that typical to use the behavior under each mode to represent the whole system. In the meantime, the Periodicity Ratio Method does not have the difficulty to determine the varied Jacobi matrix since it merely depends on the system solutions, which is forward straight to be obtained once the system solutions are numerically solved in this case.

Based on Eq. (3.9), the Jacobi matrix for calculating the Lyapunov Exponents at each mode (s = 1, 2, 3, 4, 5, 6) is specifically formulized as

$$ J=\left[ \begin{aligned} \begin{array}{*{20}{c}} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & {-{{{\left( {s\pi } \right)}}^4}-\alpha 6\left( {1-{\nu^2}} \right)\left[ {\sum\limits_r {a_r^2\frac{{{{{\left( {r\pi } \right)}}^2}}}{2}} } \right]{{{\left( {s\pi } \right)}}^2}-{R_x}{{{\left( {s\pi } \right)}}^2}} & {-\frac{1}{2}{{{\left( {\frac{{\mu \lambda }}{M}} \right)}}^{{\frac{1}{2}}}}} \\ \end{array} \end{aligned} \right] $$

(3.23)

Several typical motions and their corresponding PR values and LE values are demonstrated as the following, with figures and descriptions. It should be notice that the wave form and phase diagram figures for Lyapunov Exponent approach are corresponding to each and every modes of the six modes of oscillatory responses of the panel, as needed in determining for all the Lyapunov Exponents. Moreover, the Lyapunov Exponents of each of the modes are different, i.e., can be positive representing divergent responses of the panel or negative representing convergent response of the panel. The PR approach considers the behavior of the plate system as a whole. In the calculations of the PR approach, the motion in the first 15 s is discarded to waive the initial effect.

Fig. 3.1

Wave form and phase diagram of a buckled motion. $Rx=-3{\pi^2},$ $\lambda =60$

Fig. 3.2

Wave form and phase diagram of a buckled motion at mode 1. $Rx=-3{\pi^2},$ $\lambda =60,$ $LE=(-0.0803,-0.1510,-2.8592)$

A buckled motion is exhibited in the series figures of Figs. 3.1, 3.2, 3.3, and 3.4. In this case the plate is a stabilized at a position other than at the equilibrium. Figure 3.1 illustrates the whole system motion in wave form and phase diagram. The wave forms and phase diagrams for the first three modes are shown in the Figs. 3.2, 3.3, and 3.4. These three modes contribute most to the whole system responses including displacements and velocities.

Fig. 3.3

Wave form and phase diagram of a buckled motion at mode 2. $Rx=-3{\pi^2},$ $\lambda =60$, $LE=(-0.0301,-0.0472,-0.0473)$

Fig. 3.4

Wave form and phase diagram of a buckled motion at mode 3. $Rx=-3{\pi^2},$ $\lambda =60,$ $LE=(-0.0023,-0.0256-0.0677)$

The series of figures in Figs. 3.5, 3.6, and 3.7 are showing the sectioning points for calculating the PR index. The diamonds in Fig. 3.5 are the peak displacements and the stars in Fig. 3.5 are the bottom displacements. They are both used to calculate the PR values. Figure 3.6 shows the velocities of corresponding points, from which it can be seen the velocities of all the collected peak and bottom points are close to zero. The deviation from the theoretical zero value is due to the numerical calculation errors. It seems a bit suspicious in Fig. 3.5 that the peak points and bottom points are always a cluster without clear distinguishment. To test the way to collect the peak and bottom points of the whole displacement, the displacements of peak and bottom are collected within mode 1 and mode 2 in Figs. 3.6 and 3.7 and verification explains the cluster of peak and bottom points is caused by the supposition of the motion at different modes.

Fig. 3.5

Maximum and minimum points sectioning of a buckled motion. $Rx=-3{\pi^2},$ $\lambda =60,$ $PR = 0.9798$

Fig. 3.6

Maximum and minimum points sectioning of a buckled motion at mode 1. $Rx=-3{\pi^2},$ $\lambda =60$

Fig. 3.7

Maximum and minimum points sectioning of a buckled motion at mode 2. $Rx=-3{\pi^2},$ $\lambda =60$

Figures 3.8, 3.9, 3.10, and 3.11 is about a chaotic case. Figure 3.8 is the whole system motion in wave form and phase diagram. Figures 3.9, 3.10, and 3.11 are respectively the wave forms and phase diagrams for the first three modes which contribute most to the whole system displacement. The corresponding Lyapunov Exponents are calculated under each mode other than the system whole motion.

Fig. 3.8

Wave form and phase diagram of a chaotic motion.$Rx=-4.5{\pi^2},$ $\lambda =117$

Fig. 3.9

Wave form and phase diagram of a chaotic motion at mode 1 $Rx=-4.5{\pi^2},$ $\lambda =117,$ $LE=(0.1366,-0.0172,-0.2994)$

Fig. 3.10

Wave form and phase diagram of a chaotic motion at mode 2. $Rx=-4.5{\pi^2},$ $\lambda =117,$ $LE=(0.1317,-0.0172,-0.2994)$

Fig. 3.11

Wave form and phase diagram of a chaotic motion at mode 3. $Rx=-4.5{\pi^2},$ $\lambda =117,$ $LE=(0.0812,-0.0848,-0.4265)$

Similar as before, in Fig. 3.12, peak points and bottom points are collected for each period to calculate the PR index of the system whole motion. The diamonds are the peak displacements and the stars are the bottom displacements.

Fig. 3.12

Maximum and minimum points sectioning of a chaotic motion. $Rx=-4.5{\pi^2},$ $\lambda =117,$ $PR = 0$

Figure 3.13 is the whole system motion of a periodic case in wave form and phase diagram. Different from the buckled and chaotic case which just include the motion of first three modes, Figs. 3.14, 3.15, 3.16, 3.17, 3.18, and 3.19 are the wave forms and phase diagrams of each mode of all the six modes. This is because none of six modes can be neglected for considering the system motion since all of the displacement is not small. Another reason is to show some incompatible cases of the results diagnosed by Lyaponov Exponents and Periodicity Ratio. Again, sectioning points are collected in Fig. 3.20 which includes the diamonds and the stars representing the peak displacements and the bottom displacements respectively.

Fig. 3.13

Wave form and phase diagram of a periodic motion. $Rx=-4{\pi^2},$ $\lambda =375$

Fig. 3.14

Wave form and phase diagram of a chaotic motion at mode 1. $Rx=-4{\pi^2},$ $\lambda =375,$ $LE=(-0.094,-0.1617,-0.8203)$

Fig. 3.15

Wave form and phase diagram of a chaotic motion at mode 2. $Rx=-4{\pi^2},$ $\lambda =375,$ $LE=(-0.0044,-0.2296,-0.2647)$

Fig. 3.16

Wave form and phase diagram of a chaotic motion at mode 3. $Rx=-4{\pi^2},$ $\lambda =375,$ $LE=(0.0022,-0.3437,-0.3726)$

Fig. 3.17

Wave form and phase diagram of a chaotic motion at mode 4. $Rx=-4{\pi^2},$ $\lambda =375,$ $LE=(0.0033,-0.2817,-0.3414)$

Fig. 3.18

Wave form and phase diagram of a chaotic motion at mode 5. $Rx=-4{\pi^2},$ $\lambda =375,$ $LE=(0.0038,-0.0689,-0.7586)$

Fig. 3.19

Wave form and phase diagram of a chaotic motion at mode 6. $Rx=-4{\pi^2},$ $\lambda =375,$ $LE=(0.0024,-0.3903,-0.4275)$

Fig. 3.20

Maximum and minimum points sectioning of a periodic motion. $Rx=-4{\pi^2},$ $\lambda =375,$ $PR=0.9775$

The last case is a stabilized motion case. Figure 3.21 is the whole system motion in wave form and phase diagram. Same as the buckled and chaotic case which just includes the motion of first three modes, Figs. 3.22, 3.23, and 3.24 are the wave forms and phase diagrams of each mode of first three modes of the system motion. And Fig. 3.25 is about the peak and bottom points in a 2 s time span, the reason for considering such a small time span is to show the fluctuation of the curve in a very limited displacement variation range.

Fig. 3.21

Wave form and phase diagram of a flat motion at $Rx=-0.8,$ $\lambda =210$

Fig. 3.22

Wave form and phase diagram of a flat motion at mode 1. $Rx=-0.8,$ $\lambda =210,$ $LE=(-0.0501,-0.9997,-1.0003)$

Fig. 3.23

Wave form and phase diagram of a flat motion at mode 2. $Rx=-0.8,$ $\lambda =210,$ $LE=(-0.0533,-0.2574,-0.2286)$

Fig. 3.24

Wave form and phase diagram of a flat motion at mode 3. $Rx=-0.8,$ $\lambda =210,$ $LE=(-0.0624,-0.4869,-0.5131)$

Fig. 3.25

Wave form and phase diagram of a flat motion. $Rx=-0.8,$ $\lambda =210,$ $PR = 0.9997$

From the above illustration of the different motions, several characters of the behavior of the fluttering plate can be categorized

• The diagnosed behavior of the system by LE and PR method most time reach the compatible conclusions. By PR method, the buckled and flat motions all have the PR value of 1. Their motions at most separated modes have negative or zero Lyapunov Exponent which indicates convergence. And chaotic motion has the expected zero values for the whole system displacement and positive Lyapunov Exponent which indicates divergence. Both methods are powerful to distinguish the system behavior, while PR method is much easier to calculate since the calculation procedure is not affected by the forms of the system.

• For the most stabilized static case like buckled and flat case, the displacement at first three modes are much larger than the other modes that they are the main contributors to the whole system displacement. Comparing Figs. 3.5, 3.6, and 3.7 with 3.21, 3.22, 3.23 and 3.24, though both stabilized at last, the flat motion convergences more quickly than the buckled motion to the equilibrium position. Therefore, the last three modes can be neglected. For the dynamic system like periodic and chaotic case, all the six modes need to be included to consider the system motion.

• For the periodic case in Figs. 3.13, 3.14, 3.15, 3.16, 3.17, 3.18, and 3.19, although each motion at mode 3 to mode 5 is more like divergent as the maximum Lyapunov Exponent is a little bit larger than zero; the whole system motion is diagnosed as periodicity. This is because the supposition effect of the system motion at several modes may have canceling effect with others. This case exhibits the advantage of PR method to LE method when the individual diagnosis of the motion of each mode is not consistent with each other.

Control of Nonlinear Oscillations with Modified Fuzzy Sliding Mode Control Strategy

Equation (3.9) can be expressed as

$$ \begin{array}{lll}&\frac{{{d^2}{a_s}}}{{d{\tau^2}}}=-{a_s}{{\left( {s\pi } \right)}^4}-\alpha 12\left( {1-{\upsilon^2}} \right)\left[ {\sum\limits_r {a_r^2\frac{{{{{\left( {r\pi } \right)}}^2}}}{2}} } \right]{a_s}\frac{{{{{\left( {s\pi } \right)}}^2}}}{2}-{R_x}{a_s}{{\left( {s\pi } \right)}^2}\hfill\\ & \quad -\lambda 2\left\{ {\sum\limits_m {\frac{sm }{{{s^2}-{m^2}}}} \times \left[ {1-{{{\left( {-1} \right)}}^{s+m }}} \right]{a_m}+\frac{1}{2}{{{\left( {\frac{\mu }{{M\lambda }}} \right)}}^{{\frac{1}{2}}}}\frac{{d{a_s}}}{{d\tau }}} \right\}+P2\frac{{\left[ {1-{{{\left( {-1} \right)}}^s}} \right]}}{{s\pi }} \end{array} $$

(3.24)

where $s=1,\ldots,\infty$.

Thus, based on the modified FSMC [36], the control strategy of the 2D fluttering plate can be derived as

$$ \left\{ {\begin{array}{*{20}{c}} \displaystyle{\frac{{d{a_{s1 }}}}{{d\tau }}={a_{s2 }}} \\ \displaystyle{\frac{{d{a_{s2 }}}}{{d\tau }}={f_s}\left( {\mathrm{a},\tau } \right)+{d_s}\left( {\mathrm{a},\tau } \right)+{u_s}} \\ \end{array}} \right. $$

$$ \left\{ {\begin{array}{*{20}{c}} \displaystyle{\frac{{d{x_{s1 }}}}{{d\tau }}={x_{s2 }}} \\ \displaystyle{\frac{{d{x_{s2 }}}}{{d\tau }}={g_s}\left( {\mathrm{x},\tau } \right)} \\ \end{array}} \right. $$

(3.25)

where $s=1,\ldots,\infty$, ${d_s}\left( {\mathrm{a},\tau } \right)$ denotes the uncertain external disturbance corresponding to the $s\mathrm{th}$ mode, ${u_s}\in R$ denotes the control input corresponding to the $s\mathrm{th}$ mode, $\mathrm{a}$ is the column vector of the velocity and acceleration of the $s$ modes and is given as $\mathrm{a}={{\left[ {{a_{11 }}{\,}{\,}{a_{12 }}{\,}{\,}{a_{21 }}{\,}{\,}{a_{22 }}{\,}{} \cdot s {\,}{\,}{a_{s1 }}{\,}{\,}{a_{s2 }}} \right]}^T}$, ${x_{s1 }}$ denotes the reference signal corresponding to the $s\mathrm{th}$ mode, ${g_s}\left( {\mathrm{x},\tau } \right)$ denotes the specific expression of $\frac{{d{x_{s2 }}}}{{d\tau }}$, $\mathrm{x}$ is the column vector of the velocity and acceleration of the control input corresponding to the $s$ modes and is given as $\mathrm{x}={{\left[ {{x_{11 }}{\,}{\,}{x_{12 }}{\,}{\,}{x_{21 }}{\,}{\,}{x_{22 }}{\,}{} \cdot s {\,}{\,}{x_{s1 }}{\,}{\,}{x_{s2 }}} \right]}^T}$, and ${f_s}\left( {\mathrm{a},\tau } \right)$ denotes the specific expression of $\frac{{{d^2}{a_s}}}{{d{\tau^2}}}$ and is given below:

$$ {f_s}\left( {\mathrm{a},\tau } \right)=-{a_s}{{\left( {s\pi } \right)}^4}-\alpha 12\left( {1-{\upsilon^2}} \right)\left[ {\sum\limits_r {a_r^2\frac{{{{{\left( {r\pi } \right)}}^2}}}{2}} } \right]{a_s}\frac{{{{{\left( {s\pi } \right)}}^2}}}{2}-{R_x}{a_s}{{\left( {s\pi } \right)}^2} $$

$$ -\lambda 2\left\{ {\sum\limits_m {\frac{sm }{{{s^2}-{m^2}}}} \times \left[ {1-{{{\left( {-1} \right)}}^{s+m }}} \right]{a_m}+\frac{1}{2}{{{\left( {\frac{\mu }{{M\lambda }}} \right)}}^{{\frac{1}{2}}}}\frac{{d{a_s}}}{{d\tau }}} \right\}+P2\frac{{\left[ {1-{{{\left( {-1} \right)}}^s}} \right]}}{{s\pi }} $$

(3.26)

Based on the FSMC ([32, 33]), the control input ${u_s}$ is given as

$$ {u_s}=ue{q_s}-k{f_s}*u{f_s} $$

(3.27)

where $ue{q_s}$ is the equivalent control input corresponding to the $s\mathrm{th}$ mode and is given as

$$ ue{q_s}=-\left[ {\left( {{a_{s2 }}-{x_{s2 }}} \right)+{\eta_s}*\left( {{a_{s1 }}-{x_{s1 }}} \right)} \right] $$

(3.28)

and ${\eta_s}\in {R^{+}}$; $k{f_s}>\left| {{a_{s1 }}} \right|$ is the normalization factor of $\mathrm{a}$ corresponding to the $s\mathrm{th}$ mode, and $u{f_s}$ is determined by the fuzzy control rule shown in the Table 3.1.

Table 3.1 The fuzzy rule of $u{f_s}$

In this section, the modified FSMC will be applied in controlling and stabilizing the chaotic motion of the 2D fluttering plate, which has been identified with LE and PR methods and shown in Figs. 3.8, 3.9, 3.10, and 3.11.

The initial condition is given below:

$$ {a_{11 }}=0.01,\,{a_{21 }}=0.01,\,{a_{31 }}=0.01,\,{a_{41 }}=0.01,\,{a_{51 }}=0.01,\,{a_{61 }}=0.01 $$

$$ {a_{12 }}=0,\,{a_{22 }}=0,\,{a_{32 }}=0,\,{a_{42 }}=0.,\,{a_{52 }}=0,\,{a_{62 }}=0 $$

The uncertain external disturbance is given below:

$$ {d_1}\left( {\mathrm{a},\tau } \right)=-0.01\sin \left( {{a_{11 }}} \right), $$

$$ {d_2}\left( {\mathrm{a},\tau } \right)=-0.005\sin \left( {{a_{21 }}} \right), $$

$$ {d_3}\left( {\mathrm{a},\tau } \right)=-0.001\sin \left( {{a_{31 }}} \right), $$

$$ {d_4}\left( {\mathrm{a},\tau } \right)=-0.0001\sin \left( {{a_{41 }}} \right), $$

$$ {d_5}\left( {\mathrm{a},\tau } \right)=-0.00002\sin \left( {{a_{51 }}} \right), $$

$$ {d_6}\left( {\mathrm{a},\tau } \right)=-0.00001\sin \left( {{a_{61 }}} \right) $$

The reference signals are given below:

$$ {x_{11 }}=0.8\sin \left( {\pi \tau } \right),\,{x_{21 }}=0.3\sin \left( {\pi \tau } \right),\,{x_{31 }}=0.03\sin \left( {\pi \tau } \right) $$

$$ {x_{41 }}=0.005\sin \left( {\pi \tau } \right),\,{x_{51 }}=0.001\sin \left( {\pi \tau } \right),\,{x_{61 }}=0.0005\sin \left( {\pi \tau } \right) $$

${\eta_s}$ and $k{f_s}$ are given below:

$$ {\eta_1}={\eta_2}={\eta_3}={\eta_4}={\eta_5}={\eta_6}=1500 $$

$$ k{f_1}=k{f_2}=k{f_3}=k{f_4}=k{f_5}=k{f_6}=50 $$

The responses corresponding to the six modes are presented in Figs. 3.32, 3.33, 3.34, 3.35, 3.36, and 3.37. It can be discovered: once the modified FSMC is applied, the motion of the six modes will be synchronized to the corresponding reference signals and gradually stabilized.

The control inputs corresponding to the six modes are presented in Figs. 3.32, 3.33, 3.34, 3.35, 3.36, and 3.37 from which it can be learned the control inputs corresponding to the six modes would vary periodically. Besides, from Figs. 3.26, 3.27, 3.28, 3.29, 3.30, 3.31 and Figs. 3.32, 3.33, 3.34, 3.35, 3.36, 3.37, it can be found the higher the number of the mode is, the lower the amplitude of the vibration of the mode will be, and the smaller the control input corresponding to the mode will be required.

The response of the specific point, which is located at 75% length of the beam, is presented in Fig. 3.38. It can be discovered once the modified FSMC is applied, the motion of the six modes will be synchronized and gradually stabilized, and thus the response of the selected point of the fluttering 2D plate will be stabilized from the chaotic motion into a periodic motion, amplitude of which will be reduced as well.

Fig. 3.26

Wave form and phase diagram of the motion at mode 1 after the modified FSMC applied. ${R_x}=-4{\pi^2}$, $\lambda =117$

Fig. 3.27

Wave form and phase diagram of the motion at mode 2 after the modified FSMC applied. ${R_x}=-4{\pi^2}$, $\lambda =117$

Fig. 3.28

Wave form and phase diagram of the motion at mode 3 after the modified FSMC applied. ${R_x}=-4{\pi^2}$, $\lambda =117$

Fig. 3.29

Wave form and phase diagram of the motion at mode 4 after the modified FSMC applied. ${R_x}=-4{\pi^2}$, $\lambda =117$

Fig. 3.30

Wave form and phase diagram of the motion at mode 5 after the modified FSMC applied. ${R_x}=-4{\pi^2}$, $\lambda =117$

Fig. 3.31

Wave form and phase diagram of the motion at mode 6 after the modified FSMC applied. ${R_x}=-4{\pi^2}$, $\lambda =117$

Fig. 3.32

Control input at mode 1

Fig. 3.33

Control input at mode 2

Fig. 3.34

Control input at mode 3

Fig. 3.35

Control input at mode 4

Fig. 3.36

Control input at mode 5

Fig. 3.37

Control input at mode 6

Fig. 3.38

Wave form and phase diagram of the selected point located at the 75% length of the beam after the application of the modified FSMC

Key Symbols

$D$

Plate stiffness

$E$

Modulus of elasticity

$h$

Plate thickness

$K$

Spring constant

$L$

Panel length

M

Mach number

$m$

Mode number

${N_x}$

In-plane force

$N_x^{(a) }$

Applied in-plane force

$p-{p_{\infty }}$

Aerodynamic pressure

$\varDelta p$

Static pressure differential across the panel

$P$

${{{\varDelta p{l^4}}} \left/ {Dh } \right.}$

${R_x}$

${{{N_x^{(a) }{L^2}}} \left/ {D} \right.}$

$r$

Mode number

$s$

Mode number

$t$

Time

${U_{\infty }}$

Flow velocity

$W$

${w \left/ {h} \right.}$

$w$

Plate deflection

$\alpha$

Spring stiffness parameter

$\beta$

${{({M^2}-1)}^{{{1 \left/ {2} \right.}}}}$

$\lambda$

${{{2q{a^3}}} \left/ {{\beta D}} \right.}$

$\mu$

${{{\rho L}} \left/ {{{\rho_m}h}} \right.}$

$\nu$

Poisson’s ratio

$\rho$

Air density

${\rho_m}$

Plate density

$\tau$

$t{{({D / {{{\rho_m}h{l^4}}} })}^{{{1 \left/ {2} \right.}}}}$

${a_{s1 }}$

The displacement corresponding to the $s\mathrm{th}$ mode

${a_{s2 }}$

The velocity corresponding to the $s\mathrm{th}$ mode

${x_{s1 }}$

The displacement of the reference signal of the $s\mathrm{th}$ mode

${x_{s2 }}$

The velocity of the reference signal corresponding to the $s\mathrm{th}$ mode

$\mathrm{a}$

The column vector of the velocity and acceleration of the $s$ modes

${f_s}\left( {\mathrm{a},\tau } \right)$

The expression of the acceleration corresponding to the $s\mathrm{th}$ modes

${g_s}\left( {\mathrm{a},\tau } \right)$

The expression of the reference signal acceleration of the $s\mathrm{th}$ mode

${d_s}\left( {\mathrm{a},\tau } \right)$

The uncertain external disturbance corresponding to the $s\mathrm{th}$ mode

${u_s}$

The control input corresponding to the $s\mathrm{th}$ mode

$R$

Real number

$ue{q_s}$

The equivalent control input corresponding to the $s\mathrm{th}$ mode

${\eta_s}$

A positive real number

$k{f_s}$

The normalization factor of $\mathrm{a}$ corresponding to the $s\mathrm{th}$ mode

$n$

The number of points in Poincare map

$NPP$

The number of periodically overlapped points in Poincare map

$Q(.),P(.)$

The step functions

$\gamma$

The periodicity ratio

${f_s}(\mathrm{a},\tau )$

The expression of the acceleration corresponding to the $s\mathrm{th}$ modes

$J$

The Jacobian matrix

$LE(\hat{\lambda})$

Lyapunov Exponents