Chaos analysis of a single-bay flutter panel

Abstract

A dynamical system can often be described in terms of partial differential equations (EDP) or ordinary differential equations (ODE) equations. Moreover, if the long-term dynamic behavior represented in a phase space converges in a disordered way to an attractor, this response is called chaotic. In many cases, it is considered deterministic chaos, i.e., the response follows a unique evolution, which is sensitive to initial conditions, making the behavior difficult or impossible to predict. Such phenomenon can be found in aeroelastic panels, subject to aerodynamic loads and temperature variation, which is the subject of study in this paper. This work address the dynamic analysis of a flat rectangular plate under flutter panel conditions. The system was modeled using Rayleigh-Ritz approximation and the temporal response is obtained using numerical integration by New-Mark method. The dynamic analysis of the system is performed by obtaining the Poincaré plane by Hénon algorithm. Furthermore, using the brute-force search, or exhaustive search, and the Poincaré plane, the bifurcation diagrams were plotted for different pressure and temperature factors. In addition, the 0-1 test for chaos by time series was used to detect the occurrence of non-regular stationary responses. Finally, in the cases of chaos, the Lyapunov exponents were computed using the Sato algorithm. The results showed that the current approach was able to assess the presence or not of deterministic chaos. Furthermore, the results showed how the dynamic pressure and temperature factor affect the dynamic responses.

1 Introduction

Aerospace vehicles are designed to fly at supersonic velocities, what subjects their structures, especially their outer skin, to unsteady aerodynamic and thermal loading, which usually can lead to aerothermoelastic instability. Such behavior is a complex and nonlinear mathematical problem, showing periodic and aperiodic responses. In many cases, determinist chaos can be observed for a certain range of values for a given parameter of control of the panels.

Starting in the 1960s, some works were performed to better investigate the dynamic instability of plates and shells under supersonic regimes. Dowell [1] investigated the flutter of multibay panels at high supersonic speeds. Later on, Dugundj [2] worked on panels with a high number of Mach in the supersonic regime, emphasizing the role of damping, establishing the relationship between standing waves and non-stationary waves in the panel flutter and their border effects. A tool that is widely used in panel analysis is the finite element method that was employed by Olson [3], where an application of this method was made for a two-dimensional supersonic problem.

In 1970, Dowell [4] made a comparison between theoretical data and experimental data obtained in a wind tunnel, in order to review concepts about aeroelastic stability of panels. In 1973, Sander et al. [5] used the finite element method representing non-stationary aerodynamic force in order to generalize unknown displacements in a supersonic problem. In 1977, Mei [6] used the finite element method in order to determine the characteristics of a two-dimensional nonlinear aeroelastic panel based on aerodynamic forces from quasi-static aerodynamic theory. In 1976, again using the finite element method, Yang and Han [7] analyzed buckling on a panel with high deflection due to aerodynamic heating.

Beginning in 1980, McIntosh Jr. et al. [8] incorporated linear and nonlinear stiffness to a panel and compared the mathematical results of the nonlinear theory with the experimental results, also performing the linear stability analysis of the system. In 1983, Han and Yang [9] used a high-order triangular finite element method on a supersonic nonlinear aeroelastic panel, discretizing it in 54 nodes, and performed the dynamic analysis of this physical system. In 1985, Lottatti [10] studied the effect of non-conservative forces connected with damping, and published his work performed on a supersonic aeroelastic panel.

In the 1990s, Xue and Mei published a work [11] using a nonlinear aeroelastic panel as a model analyzing the effect of temperature. In this paper, they presented the graph of dynamic pressure versus temperature, in which it is defined the regions of stability, cycle-limit, buckling, and where there might be chaos. Another significant work in the same decade was the one of Mei et al. [12], where they reviewed some experimental methods and presented the following analytical methods: Garlerkin integration, harmonic balance, and finite element method, which was used in the frequency domain.

In 2002, Gordnier and Visbal [13] worked on a three-dimensional case of a nonlinear aeroelastic panel with a bias more focused on computational fluid dynamics, where they solved the complete Navier-Stokes equation for Von Kármán panel equations in the subsonic and supersonic regimes using finite differences. A year later, Pourtakdoust and Fazelzadeh [14] performed a chaotic analysis of a viscoelastic panel flutter under supersonic regime. Through the nonlinear differential equation, the Garlerkin equation is applied and the numerical integration is performed by the fourth-order Runge-Kutta method, where the static divergence and the Hopf bifurcation of the contour are present.

Composite materials in the 2000s began to be extensively investigated. The work of Kouchakzadeh et al. [15] examined the panel flutter of a general laminated composite plate using the classical plate theory along with the von Kármán nonlinear strain and piston theory. Moreover, Guimarães et al. [16] have recently studied the prediction of the multibay composite panel flutter in the supersonic regime for a finite element and a Rayleigh-Ritz models.

Regarding chaos analysis in panel flutter, some works have been published in recent years. Alder [17] investigated the nonlinear dynamics of prestressed panels in low supersonic turbulent flow by three different aerodynamic models. Mathematical tools was also used to evaluate the chaos analysis, such as bifurcation diagrams and Poincaŕe maps. Westin et al. [18] have recently used the 0-1 test for chaos in panel flutter and compared experimental data with theoretical data. Shishaeva et al. investigated the aeroelastic instability of a plate in an airflow by direct time-domain numerical simulation, accounting for the nonlinear development of growing oscillations in case of several linearly growing eigenmodes [19]. Later on, Shishaeva et al. [20] studied the development of nonlinear panel flutter oscillations, i.e., the sequence of bifurcations of limit cycles when the flow speed is continuously increasing or decreasing. In addition, Xie et al. [21] presented an analysis of a supersonic flow on a rectangular plate using mathematical tools to obtain the Poincaré plane and Lyapunov exponents by varying the pressure and temperature parameters. Next, Xie et al. [22] did the same analysis for the same physical system, but in this paper the authors used the Proper Orthogonal Decomposition (POD) method, a method of reducing equations and variables to a system of ordinary differential equations (ODE). More recently, and following the same methodology, Xie et al. [23] evaluated and compared the effects of different levels of wear on the same physical systems. What this current work differs from the last three works cited is that to obtain the Poincaré plane, the three works use the time series method, while this work uses the Hénon algorithm [24]. In the calculation of the Lyapunov exponent, the three works use a method of numerical time integration [25], while the current work uses an experimental method with time series by Sato algorithm [26, 27]. Furthermore, the current work presents a broader analysis of deterministic chaos using the 0-1 test for chaos.

Along those lines, this work aims to present a chaos analysis in a nonlinear panel flutter using mathematical tools, such as Poincaré map [24]. Through the Poincaré map methodology, the brute-force method [28] is used, along with the 0-1 test for chaos [29], which is a quantitative method for chaos analysis. Then, the Sato algorithm [26, 27] is used to estimate the largest Lyapunov exponent of the system, in order to evaluate the occurrence of deterministic chaos in the system.

2 Model description

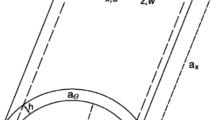
The model consists of a plate of dimensions $a\times b$ on a cavity where air flows on supersonic regime (Figure 1). The edges of the plate are simply supported. The plate itself can rotate, but it is not able to make translation. It is assumed the plane stress state, with displacements (u, v, w) in the (x, y, z)-direction, respectively. The Kirchhoff hypothesis is considered to assume that transverse and shear strains are zero, being the transverse displacement (w) independent of the transverse coordinate (z).

Fig. 1

Illustration of a rectangular plate model used in the supersonic flutter analysis, from [30]

Hence, the following equations are obtained:

$$\begin{aligned}&u(x,y,z,t)=u_0(x,y,t)-z\frac{\partial w_0(x,y,t)}{\partial x} \end{aligned}$$

(1)

$$\begin{aligned}&v(x,y,z,t)=v_0(x,y,t)-z\frac{\partial w_0(x,y,t)}{\partial y} \end{aligned}$$

(2)

$$\begin{aligned}&w(x,y,z,t)=w_0(x,y,t) \end{aligned}$$

(3)

where the $u_0$, $v_0$ and $w_0$ are the displacements in the mid-plane. Next, for the solution of the model, stress and displacement based on von Kármán’s nonlinear relations with small strain and large rotations [31] are considered. Thus, the following matrix equation is obtained:

$$\begin{aligned} \begin{bmatrix} {\mathbf {Q}}\\ {\mathbf {M}} \end{bmatrix}= \begin{bmatrix} {\mathbf {A}} &{} 0\\ 0 &{} {\mathbf {D}} \end{bmatrix}\begin{bmatrix} \mathbf {E^{L}}+\mathbf {E^{NL}}\\ \mathbf {\kappa } \end{bmatrix} \end{aligned}$$

(4)

where ${\mathbf {M}}$ is the vector of moments and ${\mathbf {Q}}$ the vector of forces. The matrices ${\mathbf {A}}$ and ${\mathbf {D}}$ represent the membrane and bending terms, which are given by:

$$\begin{aligned} {\mathbf {A}}=\frac{Eh}{1-\nu ^{2}}\begin{bmatrix} 1 &{} \nu &{} 0\\ \nu &{} 1 &{} 0\\ 0 &{} 0 &{} \frac{1}{2}(1-\nu ) \end{bmatrix} \end{aligned}$$

(5)

and

$$\begin{aligned} {\mathbf {D}}=\frac{Eh^{3}}{12(1-\nu ^{2})}\begin{bmatrix} 1 &{} \nu &{} 0\\ \nu &{} 1 &{} 0\\ 0 &{} 0 &{} \frac{1}{2}(1-\nu ) \end{bmatrix} \end{aligned}$$

(6)

where E is the Young’s modulus, $\nu$ the Poisson’s ratio, and h the thickness of the panel.

The next steps are to obtain the kinetic and potential energies of the plate considering the thermal effects and the effects of the aerodynamic pressure on the panel. The thermal effects depend on the temperature factor $\varDelta T$ and the effects of the dynamic pressure depend on the dynamic pressure itself ($q_{dyn}$) and the Mach number (M).

The thermal effects are incorporated in the model throughout in-plane normal and shear loads ($N_{xx}$, $N_{yy}$, $N_{xy}$) defined as:

$$\begin{aligned} {\mathbf {N}}_{\varDelta T} = \left[ {N_{xx} \quad N_{yy} \quad N_{xy}}\right] ^T = {\mathbf {A}} {\varDelta T} \left[ {\alpha _{x} \quad \alpha _{y} \quad \alpha _{xy}}\right] ^T \end{aligned}$$

(7)

where $\left[ {\alpha _{x} \quad \alpha _{y} \quad \alpha _{xy}}\right] ^T$ are the thermal expansion coefficients and ${\varDelta T}$ is represents the temperature variation.

The external loading due to the unsteady aerodynamic pressure distribution in supersonic flight regime is included to the model using the first-order piston theory approach [32, 33]. The method considers that the supersonic flow over the panel creates a low unsteady pressure distribution over the panel’s upper surface, where the pressure difference distribution is given by:

$$\begin{aligned} \varDelta P \left( w(x,y,t)\right) = -\frac{2 q_{\mathrm{dyn}}}{\sqrt{M^2-1}} \left[ \left( \frac{\partial w}{\partial x} + \frac{M^2-2}{M^2-1} \frac{1}{U_{\infty }} \frac{\partial w}{\partial t}\right) \right] \ \ , \end{aligned}$$

(8)

where $q_{dyn}$ is the free-stream dynamic pressure, M the Mach number, and $U_{\infty }$ is the airspeed aligned with the x direction.

The approximations for the displacements $u_0$, $v_0$ and $w_0$ of the plate are made using the Rayleigh-Ritz approximation, obtaining the following matrix system:

$$\begin{aligned} \begin{Bmatrix} u_0(x,y,t)\\ v_0(x,y,t)\\ w_0(x,y,t) \end{Bmatrix}= \begin{bmatrix} \mathbf {S_u^T} &{}{\mathbf {0}} &{}{\mathbf {0}} \\ {\mathbf {0}}&{} \mathbf {S_v^T} &{}{\mathbf {0}} \\ {\mathbf {0}}&{} {\mathbf {0}}&{} \mathbf {S_w^T} \end{bmatrix}\begin{Bmatrix} \mathbf {q_u}\\ \mathbf {q_v}\\ \mathbf {q_w} \end{Bmatrix}= {\mathbf {S}}{(u,v,w)}\mathbf {q_{sp}} \end{aligned}$$

(9)

knowing that $\mathbf {q_u}$, $\mathbf {q_v}$ and $\mathbf {q_w}$ are vectors containing $M_{(i)} \times N_{(i)}$ for $i = [u, w, v]$ independent generalized coordinates, as well as $\mathbf {S_u}$, $\mathbf {S_v}$ and $\mathbf {S_w}$ are form functions assumed along the directions x, y and z, respectively.

The system’s aeroelastic equation is obtained by applying the Lagrange formulation, which for this system becomes:

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial E_{kin}}{\partial {\dot{q}}}\right) -\left( \frac{\partial E_{kin}}{\partial q}\right) +\left( \frac{\partial U}{\partial q}\right) = \frac{\partial (\delta W)}{\partial (\delta q)} \end{aligned}$$

(10)

where $E_{kin}$ is the kinetic energy and U the potential energy. The aeroelastic equation is finally given by:

$$\begin{aligned}&{\mathbf {M}}{\ddot{\mathbf {q}}}(t)+g{\mathbf {C}}{\dot{\mathbf {q}}}(t)+[{\lambda }\mathbf {K_{a}}\nonumber \\&\quad +{\varDelta }T\mathbf {K_{G}}+{\mathbf {K}}+\mathbf {K_{pi}}+\mathbf {K_{NL_{1}}}(u,v,w)+\mathbf {K_{NL_{2}}}(w)]{\mathbf {q}}(t)={\mathbf {0}} \end{aligned}$$

(11)

where, ${\mathbf {M}}$ and ${\mathbf {K}}$ are the mass and stiffness matrix; $g {\mathbf {C}}$ and $\mathbf {K_a}$ contain the aerodynamic effects in the structural dynamics, while $\mathbf {K_G}$ considers the stiffness variation due to thermal effects. The matrix $\mathbf {K_{pi}}$, $\mathbf {K_{NL_1}}$ and $\mathbf {K_{NL_2}}$ are the nonlinear matrix in the in-plane and out-of-plane displacements, respectively.

The dynamic representation of the system in Eq. (11) in the state space is done by considering the state vector ${\mathbf {Q}}(t)=[{\mathbf {q}}(t),{\dot{\mathbf {q}}}(t)]$. The following dynamic system is then obtained:

$$\begin{aligned} \dot{{\mathbf {Q}}}(t)= {\mathbf {A}}(u,v,w) \, {\mathbf {Q}}(t) \end{aligned}$$

(12)

where

$$\begin{aligned} {\mathbf {A}}(u,v,w)=\begin{pmatrix} {\mathbf {0}} &{} {\mathbf {I}}\\ -\mathbf {M^{-1}} \mathbf {K_{nl}}(u,v,w) &{} -\mathbf {M^{-1}} g{\mathbf {G}} \end{pmatrix} \end{aligned}$$

with $\mathbf {K_{nl}}(u,v,w) = {\lambda }\mathbf {K_{a}}+{\varDelta }T\mathbf {K_{G}}+{\mathbf {K}}+\mathbf {K_{pi}}+\mathbf {K_{NL_{1}}}(u,v,w)+\mathbf {K_{NL_{2}}}(w)$.

Guimarães et al. [30] state that supersonic single bay panel under thermal load might induce several dynamic behaviors, depending on the aerodynamic and thermal conditions. The dynamic response can be an oscillating damped response, periodic (limit cycle oscillations), quasi-period and chaotic responses. Concerning the engineering point of view, one might be able to predict the behavior and/or the amplitudes obtained for each of these types of responses.

The current work details a methodology for treating nonlinear dynamic systems for mapping the type and amplitudes of oscillations for each combination of aerodynamic and thermal effects.

3 Methodology for the nonlinear aeroelastic response

A detailed procedure to evaluate the dynamic response of the nonlinear aeroelastic plate under thermal loads is described in this section. The proposed procedure is firstly being able to evaluate the Poincaré map based on the modified Hénon algorithm. This map allows to obtain the bifurcation diagrams of the aeroelastic system for different thermal or aerodynamic conditions. Depending on the characteristics of the response obtained in the bifurcation diagrams at certain operational condition, it is possible to guess the occurrence of non-regular response which might be related to a chaotic one.

The evidence of the non-regular response is performed later by observing the Poincaré plane. The 0-1 test for chaos can be used to verify the existence of deterministic chaos in the dynamic response based on time series. The 0-1 test corresponds to a qualitative analysis and any quantification about the severity of the chaos is estimated by the Lyapunov exponents.

3.1 Poincaré plane with modified Hénon algorithm

The Poincaré plane can be used to characterize the attractor of the dynamic system. Periodic attractor is defined by finite points disposed separately on the Poincaré plane. Quasi-periodic response is defined by finite points disposed in a closed orbits on the Poincaré plane. Chaotic attractor is defined by infinite scattered points on the Poincaré plane [24].

Consider the aeroelastic equation of the simply supported panel described in Eq. (12). In order to solve the system of partial differential equations, the Rayleigh-Ritz method was used to obtain a system of ordinary differential equations (Eq. (9)) with 45 equations and 45 variables, where the first 15 variables refer to position, the next 15 equations refer to velocity and the last 15 refer to acceleration.

In order to plot the Poincaré plane, it is necessary to define a specific plane. For the current study, the Poincaré plane chosen was the following:

$$\begin{aligned} {Q}_3(t) = 0 \end{aligned}$$

(13)

where $Q_3$ corresponds to the third variable of the state vector ${\mathbf {Q}}(t)$.

Thus, to obtain the Poincaré plane using the Hénon algorithm [24], the system must be in the state-space. Integrating this system over time, you only get position and velocity, unlike the New-Mark method which also provides acceleration. Consequently, using this method, only the first 30 variables of the differential system are obtained as an output response. Furthermore, having the point in the Poincaré plane, one continues to integrate the system by the New-Mark method to then obtain the trajectory of the phase subspace. This is done iteratively until this trajectory intersects the Poincaré plane again.

Therefore, considering the vector field of the dynamic system in Eq. (12) is defined by the vector function ${\mathbf {f}}(Q,Q,Q)$, the intersection points of the trajectories of the phase subspace with the Poincaré plane (see Eq. (13)) can be precisely determined by rewriting the dynamic system of Eq. (12) in the following form:

$$\begin{aligned} \begin{aligned} \frac{dQ_{1}}{dQ_{3}}&=\frac{f_{1}}{f_{3}} \\ \frac{dQ_{2}}{dQ_{3}}&=\frac{f_{2}}{f_{3}} \\ \frac{dt}{dQ_{3}}&=\frac{1}{f_{3}} \\ \frac{dQ_{4}}{dQ_{3}}&=\frac{f_{4}}{f_{3}} \\ \vdots&= \vdots \\ \frac{dQ_{30}}{dQ_{3}}&=\frac{f_{30}}{f_{3}} \end{aligned} \end{aligned}$$

(14)

or generally defined by:

$$\begin{aligned} {\mathbf {P}}' = {\mathbf {g}}({\mathbf {P}},{\mathbf {P}},{\mathbf {P}}) \end{aligned}$$

(15)

with ( )’ = $\frac{\partial }{\partial Q_3}( )$ and the vector ${\mathbf {P}}$ being defined by ${\mathbf {P}}= \left[ Q_1, Q_2, t, Q_4, \dots , Q_{30} \right] ^T$.

Using the methodology presented by Palaniyandi [24], the following steps describe the procedures done to obtain the plane of Poincaré:

• Step 1 Integrate Eq. (11) with a given time step using the Newmark’s Time Integration method.

• Step 2 Once the trajectory intersects tge Poincaré plane accordingly to a certain direction with respect to its normal, one can determine the error ${\varDelta }Q_{3_{N}}$, which corresponds to the distance along $Q_3$ axis between the Poincaré plane and the nearest point of the trajectory after intersecting it.

• Step 3 Integrate Eq. (15) with a step of ${\varDelta }q_{3_{N}}$ using the MATLAB ODE45 function in order to precisely determine the intersection point at the Poincaré plane.

• Step 4 Compute the values of W(t) e ${\dot{W}}(t)$ using the values from the previous step by making $W(t)=\mathbf {{S_{u}}^{T}}\mathbf {q(t)}$ and ${\dot{W}}(t)=\mathbf {{S_{v}}^{T}}\mathbf {{\dot{q}}(t)}$.

• Step 5 Continue the numerical integration of Eq. (11) until step 2 is verified and then repeat the steps 3–6.

3.2 0-1 test for chaos

The 0-1 test is applied for the temporal series obtained for W(t) in order to determine qualitatively the characteristic of the signal, i.e., periodic or chaotic. The temporal series chosen for the analysis are based on the observation done with the Poincaré plane. The occurrence of dispersed points in the Poincaré plane might indicate a chaotic behavior.

Based on the methodology used by Gottwald and Melbourne [29], the following mathematical formulation for the nonlinear aeroelastic panel problem is presented.

Consider q(t) obtained from Eq. (12) through Newmark’s time integration. The displacement W(t) of the plate is defined as follows:

$$\begin{aligned} W(t)=\mathbf {{S_{u}}^{T}}\mathbf {q(t)} \end{aligned}$$

(16)

For the case of continuous time, one way of obtaining the two time series p and q is to take the points that were obtained in the Poincaré plane, in their respective order over time. Equation (17) shows how the time series can be obtained:

$$\begin{aligned} \begin{aligned}&{\varvec{\Phi }}(i)=\mathbf {W(i)} \\&\mathbf {p(i)}=\mathbf {p(i-1)}+{\varvec{\Phi (i)}}\cos (ci)\\&\mathbf {q(i)}=\mathbf {q(i-1)}+{\varvec{\Phi (i)}}\sin (ci)\\&{\varvec{\Phi }}\mathbf {(i+1)}=\mathbf {W(i+1)} \end{aligned} \end{aligned}$$

(17)

where c is a constant defined between $\left[ 0,2\pi \right]$.

Having the time series p and q, the quadratic displacement is then calculated, which is defined as:

$$\begin{aligned} \mathbf {M_c(j)}=\frac{1}{N}\left( \sum _{i=1}^{N}\left( \left( \mathbf {p(i+j)} -\mathbf {p(i)}\right) ^2+\left( \mathbf {q(i+j)}-\mathbf {q(i)}\right) ^2\right) \right) \end{aligned}$$

(18)

In the current work, a time of 105 seconds is used to obtain a Poincaré map, where the number of points obtained varies in each case. The value of the variable n is 1/6 of the total points obtained in the Poincaré plane, which is the maximum value of j in Eq. (18). After computing Eq. (18), the following formula is calculated:

$$\begin{aligned} \mathbf {V_{osc}(c,j)}=(E\varPhi )^2\frac{1-\cos (jc)}{1-\cos (c)} \end{aligned}$$

(19)

where $j=(1,2,...,n)$ and $E\varPhi$ is given by:

$$\begin{aligned} E\varPhi =\frac{1}{N}\sum _{i=1}^{N}{\varvec{\Phi (i)}} \end{aligned}$$

(20)

Then, subtracting $\mathbf {V_{osc}}$ from $\mathbf {M_c}$, $\mathbf {D_c}$ is obtained:

$$\begin{aligned} \mathbf {D_{c}(j)}=\mathbf {M_c(j)}-\mathbf {V_{osc}(c,j)} \end{aligned}$$

(21)

The correlation method is then used to calculate K, which indicates whether the temporal series of the system is chaotic or not.

3.2.1 Correlation method

First of all, the covariance and variance of the magnitudes $\epsilon =(1,2,3,\ldots ,n)$ and ${\varvec{\varDelta }}=(D_c(1),D_c(2),D_c(3),\ldots ,D_c(n))$ are calculated:

$$\begin{aligned} \begin{aligned} \mathbf {cov}({\epsilon },\varvec{\Delta })= \frac{1}{n}\sum _{j=1}^{n}\left( \left( \epsilon {\mathbf {(j)}} -{\bar{\epsilon }}\right) \left( {\varvec{\Delta }}\mathbf {(j)}-{\bar{\varDelta }}\right) \right) \\ {\bar{\epsilon }}=\frac{1}{n}\sum _{j=1}^{n}\epsilon {\mathbf {(j)}}, {\bar{\varDelta }}=\frac{1}{n}\sum _{j=1}^{n}{\varvec{\Delta }}\mathbf {(j)}\\ \mathbf {var}({\epsilon })=\mathbf {cov}(\epsilon ,\epsilon ), \quad \mathbf {var}({\varvec{\Delta }})=\mathbf {cov}({\varvec{\Delta }},{\varvec{\Delta }}) \end{aligned} \end{aligned}$$

(22)

Finally, to calculate the value of K, it is used the following equation for the correlation:

$$\begin{aligned} {K}=\mathbf {corr}(\epsilon ,{\varvec{\Delta }}) =\dfrac{\mathbf {cov}({\epsilon },\varvec{\Delta })}{\sqrt{\mathbf {var}(\epsilon ){\mathbf {var}}({\varvec{\Delta }}))}} \end{aligned}$$

(23)

The value of K is contained in the range of $-1$ to 1. In this case, if the system is chaotic, it will be close to 1, and if it is periodic, it will be approximately zero.

Finally, care must be taken with the variable c of Eq. (19), as the time series p and q from the previous step are disturbed by a harmonic excitation. For certain values of c, these excitations may resonate with the time series, distorting the 0-1 test result for chaos. This is shown in detail in Sect. 4, which comprises the results and discussion section.

3.3 Sato algorithm

According to Parlitz [27] and Rosenstein et al. [26], in the beginning of the methodology, the attractor of the simply supported panel is defined once again with the first W(t) coordinate given by Eq. (16). Considering $\delta t$ as the time delay of the arbitrarily chosen attractor at the beginning, the following expression is obtained:

$$\begin{aligned} \mathbf {X_1}=\left( W(t),W(t+\delta t),W(t+2\delta t),\ldots ,W(t+(n-1)\delta t)\right) \end{aligned}$$

(24)

To determine the delay that should be used in the method, the correlation function should be calculated in relation to the time domain and the new delay will be chosen as the first time the function touches the time axis only. Consider the following expression:

$$\begin{aligned} \varPsi (t)=\dfrac{n^{-1}\sum \nolimits _{i=1}^{n}\left[ W(t_i)-{\bar{W}}\right] \left[ W(t_i+t) -{\bar{W}}\right] }{n^{-1}\sum \nolimits _{i=1}^{n}\left[ W(t_i)-{\bar{W}}\right] ^2} \end{aligned}$$

(25)

After having the new delay of the attractor, its $N-1$ neighbors are determined as follows:

$$\begin{aligned}&\mathbf {X_2}=\left( W(t+\delta t),W(t+2\delta t),W(t+3\delta t),\ldots ,W(t+n\delta t)\right) \nonumber \\&\mathbf {X_3}=\left( W(t+2\delta t),W(t+3\delta t),W(t+4\delta t),\ldots ,W(t+(n+1)\delta t)\right) \nonumber \\&\mathbf {X_4}=\left( W(t+3\delta t),W(t+4\delta t),W(t+5\delta t),\ldots ,W(t+(n+2)\delta t)\right) \nonumber \\&\vdots \nonumber \\&\mathbf {X_N}=\left( W(t+(N-1)\delta t),W(t+N\delta t),W(t+(N+1)\delta t),\ldots ,W(t+(N+n-2)\delta t)\right) \end{aligned}$$

(26)

Let $N_d$ be the number of points for each time series, so the relationship $N=N_d-(n-1)\delta t$ is valid.

Consider that $d_j(t)$ is the set of the smallest distances according to a tolerance of the N attractors to a neighbor among the $N-1$ neighbors in time t. Let $t = 0$ be the initial time condition and $\varDelta {t}$ the time discretization interval. Thus, the following is obtained according to Sato:

$$\begin{aligned} \varLambda _i(t,k)=\frac{1}{k\varDelta {t}}.\frac{1}{N-k}\sum _{j=1}^{N-k}\ln \dfrac{d_{j}(k\varDelta {t})}{d_j(0)} \end{aligned}$$

(27)

In Eq. (27), $t=k\varDelta {t}$, $\varLambda _i$ is the exponential divergence given by the j-th nearest neighbor to the vector $X_i$ in time t.

When calculating the greatest exponent of Lyapunov, the following relationship is valid:

$$\begin{aligned} d_{j}(t)=C_je^{\varLambda _1(k\varDelta {t})} \end{aligned}$$

(28)

where $C_j=d_j(0)$.

In Eq. (28), when the natural logarithm of both sides of the equation is applied, it is obtained:

$$\begin{aligned} \ln (d_j(t))=\ln (C_j)+\varLambda _1(k\varDelta {t}) \end{aligned}$$

(29)

The greatest Lyapunov exponent is then obtained as follows:

$$\begin{aligned} y(t)=\frac{1}{\varDelta {t}}<\ln {d_j(t)}> \end{aligned}$$

(30)

It should be noted that $<>$ denotes the average of the nearest j neighbors.

The formulation that goes from Eq. (27) to (30) is the basis of the work of Sato [34]. One can use a generalization of the Sato algorithm rewriting Eq. (27) as follows:

$$\begin{aligned} \varLambda _i(t,k)=\frac{1}{k\varDelta {t}}<\ln \left( \frac{d_j(k\varDelta {t})}{d_j(0)}\right) > \end{aligned}$$

(31)

By Eq. (31), it is possible to plot the graph of $\varLambda (t, k)$ as a function of t. Then, if enough time is used, one can notice a linear region in the beginning of the plot, which is followed by a curve tending to a constant value, as $\varLambda (t, k)$ increases. However, this graph will present undesirable noises. It is possible to eliminate most of them by following a procedure in which Eq. (31) is first rewritten as:

$$\begin{aligned} \begin{aligned} \varLambda _i(t,k)=\frac{1}{k\varDelta {t}}\left(<\ln (d_j(k\varDelta {t}))>-<\ln (d_j(0))>\right) \\ \varLambda _i(t,k)=\frac{1}{k}\left[ y(t)-y(0)\right] \end{aligned} \end{aligned}$$

(32)

At this point, it comes to differentiate y(t) so that Eq. (33) is obtained:

$$\begin{aligned} y'(i'\varDelta {t})=\sum _{i=0}^{i'}\varLambda (i\varDelta {t},k)=\frac{1}{k}\left( \sum _{i=0}^{i'}y((i+k)\varDelta {t}\right) -\sum _{i=0}^{i'}y(i\varDelta {t})) \end{aligned}$$

(33)

By manipulating Eq. (33), it is possible to prove that:

$$\begin{aligned} y'(i'\varDelta {t})=\sum _{i=i'+1}^{i'+k}y(i\varDelta {t})+cte \end{aligned}$$

(34)

Equation (34) proves that $y'(i'\varDelta {t})$ is equal to $y(i\varDelta {t})$ smoothed by a moving average filter with k points.

The greatest exponent of Lyapunov is found by obtaining the slope of $y'(i'\varDelta {t})$ as a function of the number of points i of the linear part of the graph, and, for that, it is done a least squares regression.

The number of points $i'$ in Eqs. (33) and (34) must be half the number of points in which the linear part of the graph is noisy.

4 Results and discussion

4.1 Bifurcation diagram for $\lambda$=199.9

The bifurcation diagram for $\lambda = 199.9$ (Fig. 2) was obtained using the brute-force method [28] along with the Hénon algorithm applied to the aeroelastic equation of the panel, using as Poincaré plane the third mode which is equal to zero.

Fig. 2

Bifurcation diagram in function of T for $\lambda =199.9$

The phase spaces graphs of the time series q and p of 0-1 test for chaos are depicted in Fig. 3.

Fig. 3

Phase spaces of time series q and p of 0-1 test for $\lambda =199.9$

Furthermore, Fig. 4 depicts the graphs of the values of the parameter K from 0-1 test for chaos in function of c.

Fig. 4

Values of parameter K from test 0-1 test for chaos in function of c for $\lambda =199.9$

The analysis of Figs. 2, 3 and 4 shows that for the first two values of T there are two periodic systems. In the phase spaces there are two closed figures and in the $K \times c$ graphs we have oscillations around the value of $c = 0$, and in both cases we have resonance peaks that happen in the values of $c = 0$ and $c = 2\pi$; however, the first positive determination of the angle $2 \pi$ rad is equal to 0, being the same resonance peak that gives a distorted value for K equal to 1. Nonetheless, analyzing the entire graph, in both cases there is a regular movement. In the case of $T = 2.4$, the system is chaotic due to the fact that the phase space presents a disordered figure. In addition, the value of K is always around 1, which indicates this characteristic.

Moving forward, Fig. 5 depicts the phase space of the coordinate w of the plate:

Fig. 5

Phase space of the coordinate w of the plate for $\lambda =199.9$

Looking at Fig. 5, one can say that in the first two graphs of the phase space, i.e., for $T = 2.02$ and $T = 2.15$, the paths are well defined; in the third graph, i.e., for $T = 2.4$, we notice several lines making different contours so that they do not form the same trajectory throughout their cycles. According to Nayfeh et al. [35], the characteristic attractor that indicates chaos does not have a well-defined path, and there may be irregular folds. Thus, based on this concept and based on the bifurcation diagram and on the 0-1 test for chaos, it can be said that in the first two cases the system is periodic, while in the third it has a characteristic behavior of deterministic chaos.

Next, Fig. 6 depicts the Poincaré planes for three values of T. These planes are delimited for mode 3 of the aeroelastic equation of the panel being equal to zero. Also, Fig. 7 presents the time responses of the panel.

Fig. 6

Poincaré planes for $T=2.02$, 2.15, and 2.4 with $\lambda =199.9$

Fig. 7

Time response of the panel for $T=2.02$, 2.15, and 2.4 with $\lambda =199.9$

Checking the graphs for $T = 2.02$ in Figs. 6 and 7, we have the values of $w^\prime /h$ and w/h at one point only in the Poincaré plane. Although in Fig. 6 a horizontal line appears, the variation of $w^\prime /h$ is very small, so that if it were seen on a larger scale, it would be visible as a single point. Still looking at Figs.  6 and 7, but for the value of $T = 2.15$, the Poincaré plane has more than one point, which means that the system can be periodic or quasi-periodic. However, a Poincaré plane for a quasi-periodic system has a closed and dense trajectory, being a torus in a view of a 3D phase subspace, which is not the case. Therefore, it is possible to say that the system for the second value analyzed ($T = 2.15$) is periodic. Finally, for $T = 2.4$, there are many points scattered in the Poincaré plane, which means that if we simulated the system for this case for a time t tending to infinity we would have infinite points in the Poincaré plane, characterizing a chaotic system.

For one more verification and analysis, the Lyapunov exponent was calculated for the cases in which the system is chaotic by the Sato algorithm. As previously presented, the only case found is that corresponding to the value of $T = 2.4$ with $\lambda = 199.9$. The results of the analysis of the Lyapunov exponent are depicted in Fig. 8.

Fig. 8

Chaotic system analysis by Sato’s algorithm, for $T = 2.4$ with $\lambda = 199.9$

As shown in Fig. 8, the Lyapunov exponent for this case is $\varLambda = 0.51$, which is the slope of the straight line obtained by the least squares method.

4.2 Bifurcation diagram for $\lambda$=219.9

Similarly to the one presented above, i.e., using the same procedures and methods described in the previous section, here are presented the analysis and results for the bifurcation diagram in function of T for the value of $\lambda = 219.9$, which is depicted in Fig. 9.

Fig. 9

Bifurcation diagram in function of T for $\lambda =219.9$

Nevertheless, the graphs of the time series q and p of 0-1 test for chaos are shown in Fig. 10.

Fig. 10

Phase spaces of time series q and p of 0-1 test for $\lambda =219.9$

Next, Fig. 11 show the plots of $K \times c$ for five different values of T ($T=2.02$, 2.15, 2.4, 2.7, and 2.9) from the bifurcation diagram for $\lambda =219.9$:

Fig. 11

Values of parameter K from 0-1 test for chaos in function of c for $\lambda =219.9$

The results from Figs. 10 and 11 show that for the values of T equal to 2.02, 2.15 and 2.4, the system presents a regular dynamic, which includes closed trajectories in the phase spaces (Fig. 10 ). In the $K \times c$ charts (Fig. 11), the values of K oscillate around $k = 0$, showing a peak of resonance in the first chart ($T =2.02$), while in the second graph ($T = 2.15$), the system diverges to $K = -1$ in the value $c = 0$ and $2\pi$. In addition, it has a resonance peak at $c = \pi$. In the case of $T = 2.4$, there are three resonance peaks tending to the highest possible value on the $K \times c$ graph (Fig. 11). For the values of $T = 2.7$ and 2.9, the system behaves in a chaotic manner with values of K around 1 and disordered figures in the phase spaces (Fig. 10).

Moreover, Fig. 12 depicts the phase space of the coordinate w of the plate.

Fig. 12

Phase space of the coordinate w of the plate for $\lambda =219.9$

The results presented in the phase spaces in Fig. 12 corroborate the conclusions presented from the results of 0-1 test for chaos. The first three cases $T = 2.02$, $T = 2.15$ and $T = 2.4$ have well-defined trajectories, which characterizes regular periodic movement. For the values of $T = 2.7$ and $T = 2.9$, the trajectory in the phase space is disordered, which characterizes deterministic chaos.

Moreover, Fig. 13 depicts the Poincaré planes for five values of T.

Fig. 13

Poincaré planes for $T=2.02$, 2.15, 2.4, 2.7, and 2.9 with $\lambda =219.9$

The Poincaré planes also confirm what was stated earlier. As discussed in the results for $\lambda =199.9$, the first three graphs show typical Poincaré planes where the systems are periodic, and the last two graphs show typical behavior of deterministic chaos.

The following graphs depicted in Fig. 14 illustrate the time responses of the panel. Also, Fig. 15 presents the results for the computation of the Lyapunov exponent by Sato algorithm for five values of T: 2.02, 2.15, 2.4, 2.7, and 2.9.

Fig. 14

Time response of the panel for $T=2.02$, 2.15, 2.4, 2.7, and 2.9 with $\lambda =219.9$

Fig. 15

Chaotic system analysis by Sato’s algorithm, for $T = 2.7$ and 2.9 with $\lambda = 219.9$

For the cases of $T = 2.7$ and $T = 2.9$, where there was chaotic behavior of the panel, the values of Lyapunov exponents are 0.43 and 0.56, respectively.

4.3 Bifurcation diagram for $\lambda$=230

Likewise what was performed previously, in Fig. 16 is the bifurcation diagram varying T with a fixed value of $\lambda = 230$.

Fig. 16

Bifurcation diagram in function of T for $\lambda =230$

The phase spaces graphs of the time series q and p of 0–1 test for chaos are depicted in Fig. 17. Furthermore, the graphs of $K \times c$ for five T values from the bifurcation diagram for $\lambda = 230$ are illustrated in Fig. 18.

Fig. 17

Phase spaces of time series q and p of 0-1 test for $\lambda =230$

Fig. 18

Values of parameter K from 0-1 test for chaos in function of c for $\lambda =230$

As shown in Figs. 17 and 18, in the last case, where $T=2.9$, the post-flutter panel system presents chaotic behavior with the phase space of the time series q and p disordered and the values of K in the test for chaos show all values close to 1, which indicates deterministic chaos. In the other four cases, the systems have periodic characteristics, with figures in the $q \times p$ phase space closed and K values oscillating around 0 for most of the c values. In addition, there is a resonance peak in the case of $T = 2.02$, with a value of K tending to the maximum possible value. For $T=2.15$ and $T=2.4$, the graphs show two resonance peaks in both cases, and for $T = 2.7$ there are seven resonance peaks.

Moving forward, Fig. 19 depicts the phase space of the coordinate w of the plate:

Fig. 19

Phase space of the coordinate w of the plate for $\lambda =230$

Analyzing the phase spaces, Fig. 19 confirms the conclusions presented from Figs. 17 and 18. The behavior of the trajectories of the phase spaces shows that, in the first four cases ($T = 2.02$, 2.15, 2.4, 2.7, and 2.9), the movement is periodic, while in the last case ($T = 2.9$) the behavior is chaotic. This can also be seen in the Poincaré planes depicted in Fig. 20.

Fig. 20

Poincaré planes for $T=2.02$, 2.15, 2.4, 2.7, and 2.9 with $\lambda =230$

Next, the following Figs. 21 and 22 depict, respectively, the time responses of the panel and the Sato’s algorithm used to find the value of the Lyapunov exponent.

Fig. 21

Time response of the panel for $T=2.02$, 2.15, 2.4, 2.7, and 2.9 with $\lambda =230$

Fig. 22

Chaotic system analysis by Sato’s algorithm, for $T = 2.9$ with $\lambda = 230$

In the case of $T = 2.9$, in which the system presents deterministic chaos, the value of Lyapunov’s exponent, as shown in the regression graph, is 0.49.

4.4 Bifurcation diagram for T=2.7

In the previous section, the bifurcation diagram was obtained fixing a value of $\lambda$ and varying the values of T. But here, it is performed the opposite, i.e., the number of T is fixed and the value of $\lambda$ varies accordingly. Thus, Fig. 23 depicts the bifurcation diagram for $T=2.7$.

Fig. 23

Bifurcation diagram in function of $\lambda$ T for $T=2.7$

The following graphs (Fig. 24) illustrate the phase space of the time series of 0-1 test for deterministic chaos with the following values of $\lambda$: 215, 240, 260, and 280.

Fig. 24

Phase spaces of time series q and p of 0-1 test for $T=2.7$

The $K \times c$ graphs for four values of $\lambda$ from the bifurcation diagram with $T = 2.7$ are depicted in Fig. 25.

Fig. 25

Values of parameter K from 0-1 test for chaos in function of c for $T=2.7$

Analyzing Figs. 24 and 25, one can say that for $\lambda =215$ the system is chaotic because the phase space presents a disordered figure and the value of k in function of c is always around 1. The last three images show regular dynamic systems, and their phase spaces show closed figures. In the graphs of the test 0 or 1 varying c, and for the value of $\lambda =240$, most of the values of K are around 0 and $-0.5$. In the case of $\lambda =260$ and $lambda=280$, there are values of k equal to zero with seven resonance peaks in the first graph and 4 resonance peaks in the second.

Moving forward, Fig. 26 depicts the phase space of the coordinate w of the plate:

Fig. 26

Phase space of the coordinate w of the plate for $T=2.7$

Therefore, from all that has been presented, it is evident that there is a chaotic behavior for $\lambda =215$ and movements with periodic oscillations for the last three charts. So, in Fig. 27 below, it is presented the Poincaré planes for four values of $\lambda$.

Fig. 27

Poincaré planes for $\lambda =215$, $\lambda =240$, $\lambda =260$, and $\lambda =280$ with $T=2.7$

The Poincaré planes (Fig. 27) show a chaotic behavior for $\lambda =215$, while for the values of $\lambda$ equal to 240, 260 and 280, the behavior is periodic.

Next, Fig. 28 illustrates the time responses of the panel and Fig. 29 represents the Sato’s algorithm, which is used to find the value of Lyapunov’s exponent in the chaotic case with a value of $\lambda =215$. As shown in Fig. 29, the coefficient is equal to 0.54.

Fig. 28

Time response of the panel for $\lambda =215$, $\lambda =240$, $\lambda =260$, and $\lambda =280$ with $T=2.7$

Fig. 29

Chaotic system analysis by Sato’s algorithm, for $\lambda = 215$ with $T = 2.7$

4.5 Bifurcation diagram for T=2.9

The last bifurcation diagram is presented with $T=2.9$ and $\lambda$ ranging from 200 to 30, as shown in Fig. 30.

Fig. 30

Bifurcation diagram in function of $\lambda$ T for $T=2.9$

In Fig. 31 below are the graphs for the time series p and q in their phase spaces for the same values of $\lambda$ used in the case of $T=2.7$, i.e., $\lambda =215$, 240, 260, and 280.

Fig. 31

Phase spaces of time series q and p of 0-1 test for $T=2.9$

The graphs $K \times c$ for $T=2.9$ and four different values of $\lambda$ from bifurcation diagram (Fig. 30) are displayed in Fig. 32.

Fig. 32

Values of parameter K from test 0-1 test for chaos in function of c for $T=2.9$

Analyzing the phase spaces (Fig. 31) and the graphs of K in function of c (Fig. 32), one can say that for $\lambda = 215$ and $\lambda = 240$ the behavior of the system is chaotic, since its phase spaces do not present closed figures. In addition, these figures are decentralized and the value of K is always close to 1 for the entire range of c values. In the case of $\lambda = 260$, its phase space presents a different figure, i.e., it does not present a behavior similar to that of a chaotic system or a periodic system. However, on the $K \times c$ graph, the K values vary widely between low and high values. Then, the analysis of the Poincaré map shows that the system is quasi-periodic. In the latter case, i.e., $\lambda = 280$, the phase space presents a closed figure, whereas in the $K \times c$ graph the values of K are null in much of the c value range, reaching values equal to 1 in the four resonance peaks. It is worth mentioning that due to these resonances, some values of K are distorted for 0-1 test for chaos.

Moreover, Fig. 33 presents the graphs for the phase space of the movement of the plate. In the first two figures ($\lambda =215$ and 240), the trajectories are disordered, which characterizes chaos. In the third figure ($\lambda =260$), there is not a single trajectory, but the trajectories follow a pattern, which makes it possible to say that there is no chaos in this case, the movement can be periodic or quasi-periodic. In the latter case ($\lambda =280$), there is a well-defined trajectory, which characterizes periodic movement.

Fig. 33

Phase space of the coordinate w of the plate for $T=2.9$

Next, Fig. 34 shows the Poincaré planes for four different values of $\lambda$.

Fig. 34

Poincaré planes for $\lambda =215$, $\lambda =240$, $\lambda =260$, and $\lambda =280$ with $T=2.9$

In the Poincaré planes for $\lambda$ equal to 215 and 240, it is possible to observe chaos in the system. For $\lambda = 280$, it is clear that the panel’s behavior is periodic. All of this is corroborated by the previous conclusions from Fig. 33. The case that is interesting and can raise questions is the case for $\lambda = 260$. In this figure, there is a torus that forms in the Poincaré plane some closed figures. This can characterize both a periodic and a quasi-periodic movement. According to [36], in the case of a system being quasi-periodic, the figure in the closed format has its contours densely filled, occupying the entire contour of the figure. On the other hand, if the movement is periodic, the closed image contains spaces between the points that form the figure, because once the movement is periodic, the trajectory passes repeatedly through these points. Also, in the case of $\lambda = 260$, there are closed geometric figures filled in densely, which characterizes a quasi-periodic system.

Furthermore, Fig. 35 presents the time responses of the panel.

Fig. 35

Time response of the panel for $\lambda =215$, $\lambda =240$, $\lambda =260$, and $\lambda =280$ with $T=2.9$

Finally, the Lyapunov exponent was calculated for the cases in which the system is chaotic by the Sato’s algorithm. The results are depicted in Fig. 36.

Fig. 36

Chaotic system analysis by Sato’s algorithm, for $\lambda = 215$ and 240 with $T = 2.9$

Thus, for $\lambda =215$, Lypunov’s exponent has a value of 0.42, while for $\lambda =240$ it has a value of 0.63. Note that in all regression plots the square root of the correlation factor $R^2$ was shown.

5 Concluding remarks

In this work, a dynamic analysis of flutter of a rectangular panel was proposed, seeking to verify the chaotic regions, varying the dynamic pressure and the temperature factor, and how the dynamic responses are affected by those parameters. Previous works [21,22,23] presented the dynamic pressure diagram versus the temperature factor, where four different regions are found: stable, limit cycle, buckling, and periodic non-harmonic. Based on those works, it was possible to determine in which region there could be chaos and, from that, plot the bifurcation diagrams as a function of both dynamic pressure and temperature factor. Having the bifurcation diagrams obtained from Poincaré plane and 0-1 test for chaos, it is possible to state in which situations there is deterministic chaos.

The first tool presented was the Poincaré plane, and the bifurcation diagram is obtained from it. Both are not new in the literature on panel flutter; however, this is the first work to use that tool applying the Tucker method and the Hénon algorithm. Analyzing the Poincaré planes and the phase spaces, one can say that the method presented results with great precision.

The 0-1 test for chaos was carried out in order to determine whether the system has chaos or not. It was done using the time series obtained through the points of the Poincaré plane. The parameter c was varied from 0 to $2\pi$ in order to know which value of the parameter K is predominant to then determine the dynamic characteristics of the system, where the value 0 represents a regular system and the value 1 represents a deterministic chaos. Thus, it was possible to verify in what distorted values of c there are peaks of K. This analysis had not yet been done in panel flutter, since in the work of Westin [18], in which this methodology was presented, only an analysis with experimental data was performed comparing the theoretical value for a single value of the parameter c. Moreover, analyzing the characteristics of $p\times q$ phase space, it is observed that when the system presents a regular or periodic behavior, there is a well-defined geometric figure; the same is not true when the system is chaotic.

Lyapunov exponents were successfully estimated using the Sato algorithm, which is estimated by the use of time series through linear regression. The use of time series to calculate the Lyapunov exponent is a method that can be used with great confidence when there are positive Lyapunov exponents in the system under study. This approach is an experimental method that until then had not been used in panel flutter, which becomes a significant contribution of this paper. The results obtained show that the linear regressions presented a coefficient $R^2$ close to 1, which means an accurate linear regression; in other words, the slope represents more precisely the Lyapunov exponent for temporal responses with deterministic chaos.

Overall, this work managed to present pertinent analyzes regarding the nonlinear dynamics of panels in situations of aeroelastic instability (flutter). In addition, this work presents new methods for performing dynamic analysis, including tools that are little or not yet used. Nevertheless, the work presents a complete methodology for the analysis of dynamic systems that can be used in different applications, serving for several future works.