Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Analysis of fluid flow and heat transfer in porous medium or in partly porous configurations between two parallel plates has been a subject of fundamental importance. It is relevant to a lot of industrial applications such as heat exchangers, electronic cooling, heat pipes and many important thermal engineering applications. In many of such aforesaid applications Darcy’s model (see, e.g.,  [23, 33]) is used to represent the fluid flow in porous media. This model equation describes the relation between the rate of flow and pressure gradient through porous medium. But, it has been observed that the Darcy model is not compatible with the existence of wall-bounded porous medium (Beavers et al. [4], Beavers et al. [5]). It has been also observed that proportionality between pressure gradient and fluid velocity does not hold for high-velocity fluid flow in porous media [13]. This phenomenon has been the subject of many theoretical and experimental investigations. Thus, in order to describe more complex situation, for example, to incorporate inertial effects and high-velocity flow, Darcy’s law has been generalized for many such behaviors (see the exhaustive list of early works in [23]). Many earlier and recent investigations are mainly divided into two parts: firstly, to establish an upper bound (according to most of experiment critical value of Reynolds numbers Re in the range 1 to 15) for the range of validity of Darcy’s equation and to provide relationship which predicts the nonlinear flow behavior [10]; secondly, to provide a physical basis for the generalized equation of motion and to identify mechanism which is responsible for the nonlinear flow behavior.

Opinions on the mechanism responsible for the onset of non-linearity at high flow velocities are diverse. Early descriptions of high-velocity flow attributing to the nonlinearity are due to the occurrence of turbulence. However, experiments have indicated that the onset of turbulence occurs at much higher velocity, i.e., \(\mathrm{Re} \approx 300\) (Dybbs and Edwards [10]). Thus deviations from Darcy’s law are not solely due to turbulence. They may be due to microscopic inertial forces. This concept has been widely accepted [7]. The rise of nonlinear terms are also due to increase of microscopic drag forces on the pore walls. The Forchheimer type of equations presented here support this point of view. In the most commonly used Forchheimer model inertia appears as a drag proportional to the square of the velocity [16]. In [4, 5] the authors have shown experimentally that for high velocity a quadratic term in the Darcy law is required for a fluid flow through porous medium bounded by wall and hence a modified form of Darcy’s equation has been used. Joseph et al. [16] later presented Forchheimer modification of the Darcy law. Darcy–Forchheimer model in the context of forced convection partly filled with porous configurations has been studied by Kuznetsov [18, 19].

Considerable attention has also been given to the fluid flow in parallel-plate configuration, where fluid flow is induced by the motion of the plates. Sekharan et al. [29] have studied the unsteady flow between two oscillating plates and further it has been studied by Hayat [14] in the context of dipolar fluid. Debnath et al. [8] explained the flow between two oscillating plates in connection with hydromagnetic flow of a dusty fluid. Bujurke et al. [6] have included second-order fluid in a single domain (combining the terms for porous and fluid domain). Transport phenomena in a composite domain consisting of a porous layer exchanging momentum, heat, and/or constituents with an adjacent fluid layer are encountered in a wide range of industrial applications like thermal insulation, filtration processes, dendritic solidification, storage of nuclear waste, and spreading on porous substrate. Applications are extended to environmental problems like geothermal system, benthic boundary layers, and ground water pollution. Recently a brief overview on natural convection in partially porous media (saturated) has been reported by Gobin and Goyeau [12]. Their discussion mostly includes clear fluid region described by the Stokes equation and momentum equation in the homogeneous porous layer by the Darcy law. The analytical solutions of the fluid flow and heat transfer of the viscous fluid in a partly porous configuration bounded by two oscillating plates have been recently reported by Sharma et al. [30]. Darcy’s model is employed in their work to study the fluid velocity within the plates and the rate of heat transfer on the plates. Drag effects on the flow and heat transfer in such fluid and solid configuration have not been considered and therefore corresponding Darcy one-dimensional linear model is solved analytically. There is a lot of discussion [22] regarding inclusion of viscous dissipation term in energy equation. Hassanizadeh and Gray [13] pointed out that macroscopic intrafluid stress terms are not important in porous media flow and that in the case of very coarse soil with low value of specific surface of the solid phase and near the medium boundaries intrafluid stress terms are comparable to drag forces. Effects of viscous dissipation term have been studied by Murty and Singh [21] and they found that effect of viscous dissipation increases as the flow region changes from non-Darcy regime to Darcy regime. Aydin and Kaya [2] published a paper in which viscous dissipation term was included in energy equation. They observed that viscous dissipation enhances heat transfer for wall cooling case and reduces heat transfer for wall heating case. All such discussions were made in non-Darcian flow regime in a porous medium. After this paper was published Rees and Magyari [28] published a comment by stating that in the free stream region the viscous dissipation term \((\nu /{c}_{p}){\left (\partial u/\partial y\right )}^{2}\) will be zero in the presence of \((\nu /K{c}_{p}){u}^{2}\). Here ν is the kinematic viscosity and the definition of the symbols \(K,{c}_{p},u\), and y is given in Eqs. 3–3. According to them in case of thermal equilibrium between porous medium and wall the first term will behave like a heat generation source and create heating effect like the adiabatic heating observed for a clear fluid. In a reply to Rees and Magyari’s comment Aydin and Kaya [3] opined that viscous dissipation term would be included with Forchheimer term in the boundary layer region.

Rajagopal [27], while studying hierarchies of approximate models, proposed several models for flow of fluids in porous medium. One such model that can result under some assumptions is the Darcy–Forchheimer model. Some of the important assumptions considered in his study are:

  • Only interacting forces that come into play are due to frictional forces, which the fluid encounters at the boundary of the pore. This is a drag-like force proportional to the difference in velocity between two constituents and the drag coefficient is a constant quantity.

  • Frictional effects within the fluid due to viscosity are neglected.

  • Due to slowness of fluid inertial nonlinearity can be ignored.

The assumption that the effects of viscosity can be neglected does not mean that fluid has no viscosity. First and second assumptions together imply that the viscosity of fluid and roughness of solid surface lead to greater frictional resistance(dissipation) at the porous boundaries of solid than the frictional resistance in the fluid. Forchheimer pointed out that deviation from Darcy’s law was largely due to kinetic effect of fluid. Accordingly kinetic energy term \((\rho {C}_{F}/\sqrt{K}){u}^{2}\) is included in Darcy’s law. The definition of symbols ρ and C F is defined in Eq. 3.

This presentation deals more specifically with problems of fluid flow and heat transfer in a channel involving clear fluid domain and porous domain. The flow within the porous domain is described by Darcy–Forchheimer model and the flow in clear fluid domain is formulated by Navier–Stokes equations. The heat convection and Forchheimer drag effects are studied particularly at low Reynolds number. The transition from clear fluid domain to porous domain is defined by the spatial variation of the thermophysical properties. In Sect. 2 governing equations for fluid flow in clear fluid domain and porous domain are formulated. Section 3 is devoted to solution procedure. Results, discussion and physical interpretations are given in Sect. 4 and finally conclusions are embedded in Sect. 5. The analytical results for the simplified Darcy one-dimensional linear equations of motion for velocity are given in the Appendix.

2 Equations

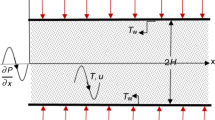
A typical flow scenario is illustrated in Fig. 1: it shows the flow of a fully developed laminar flow in a region partially filled with porous medium of finite thickness of size h bounded by two parallel plates in the presence of oscillating wall temperature. The region between two plates is filled with fluid and initially both the fluid and plates are at rest. Flow is then induced by the motion of the plate in its own plane. Entire fluid region is divided equally into two regions, one is clear fluid region bounded by an upper wall and an interface and the other is the porous fluid region bounded by an interface and the bottom wall. The bottom and upper plates lie at \({y}^{{_\ast}} = -h\) and \({y}^{{_\ast}} = h\), respectively. The interface of the two regions lies at \({y}^{{_\ast}} = 0\). The horizontal coordinate \({x}^{{_\ast}}\) is taken along the interface with \({y}^{{_\ast}}\) perpendicular to it. The fluid is assumed incompressible and Newtonian and the porous medium is isotropic and homogeneous. Let us consider two domain approaches in which the plates are long, impermeable and oscillating with uniform velocity u 0 and frequency w  ∗ . The length of the channel is larger than the height. So buoyancy effect is safely neglected here.

Fig. 1
figure 1

Sketch of flow geometry

Full size image

The set of governing equations for the flow in the clear fluid region neglecting oscillatory body force can be presented as

$$\begin{array}{rcl} \rho \,\frac{\partial {u}_{1}^{{_\ast}}} {\partial {t}^{{_\ast}}} = {\mu }_{1}\,\frac{{\partial }^{2}{u}_{1}^{{_\ast}}} {\partial {y}^{{_\ast}2}} ,\quad 0 < {y}^{{_\ast}} < h& &\end{array}$$
(1)
$$\begin{array}{rcl} \rho \,{c}_{p}\left (\frac{\partial {T}_{1}^{{_\ast}}} {\partial {t}^{{_\ast}}} + {u}_{1}^{{_\ast}}\frac{\partial {T}_{1}^{{_\ast}}} {\partial {y}^{{_\ast}}} \right ) = {k}_{1}\,\frac{{\partial }^{2}{T}_{1}^{{_\ast}}} {\partial {y}^{{_\ast}2}} + {\mu }_{1}\,{\left (\frac{\partial {u}_{1}^{{_\ast}}} {\partial {y}^{{_\ast}}} \right )}^{2},\quad 0 < {y}^{{_\ast}} < h,& &\end{array}$$
(2)

in which t  ∗  is time, ρ is the density of the fluid, and c p is the specific heat at constant pressure. Here, \({u}_{1}^{{_\ast}}\), \({T}_{1}^{{_\ast}}\), \({\mu }_{1}\), and k 1 are the fluid velocity, temperature, coefficient of viscosity and thermal conductivity, respectively. Equation 1 is a thermal energy equation in clear fluid domain. The derivation of energy equation can be found, for example, in [1]. The index ‘1’ is chosen here to specify the notations of the clear fluid domain. The index ‘2’ will be used later for the porous domain. In the above equations the asterisk(*) implies dimensional variables.

The governing equations in the porous domain are the momentum equation which is due to the Darcy–Forchheimer equation and the temperature equation and can be given as

$$\begin{array}{rcl} \rho \,\frac{\partial {u}_{2}^{{_\ast}}} {\partial {t}^{{_\ast}}} = {\mu }_{2}\,\frac{{\partial }^{2}{u}_{2}^{{_\ast}}} {\partial {y}^{{_\ast}2}} - \frac{{\mu }_{1}} {{K}^{{_\ast}}}\,{u}_{2}^{{_\ast}}- \rho \, \frac{{C}_{F}} {\sqrt{{K}^{{_\ast}}}}{u}_{2}^{{_\ast}2},\quad - h < {y}^{{_\ast}} < 0& &\end{array}$$
(3)
$$\begin{array}{rcl} \rho \ {c}_{p}\left (\frac{\partial {T}_{2}^{{_\ast}}} {\partial {t}^{{_\ast}}} + {u}_{2}^{{_\ast}}\frac{\partial {T}_{2}^{{_\ast}}} {\partial {y}^{{_\ast}}} \right ) = {k}_{2}\,\frac{{\partial }^{2}{T}_{2}^{{_\ast}}} {\partial {y}^{{_\ast}2}} + \frac{{\mu }_{1}} {{K}^{{_\ast}}}\,{u}_{2}^{{_\ast}2} + \rho \, \frac{{C}_{F}} {\sqrt{{K}^{{_\ast}}}}\,{u}_{2}^{{_\ast}3},\quad - h < {y}^{{_\ast}} < 0,& &\end{array}$$
(4)

where K  ∗  is the permeability of the isotropic porous medium, k 2 is the effective thermal conductivity, and \({\mu }_{2}\) is the effective viscosity for the porous region. Here the symbol C F (nondimensional) stands for the Forchheimer coefficient (see, e.g., [32]), which is used in expressing the inertial term in Eq. 3. An empirically based correlation for this coefficient can be found in [31]. The fluid viscosity \({\mu }_{1}\) is different from effective viscosity \({\mu }_{2}\) of porous region (Martys et al. [20] and Givler et al. [11]). The formulation is an extension of the problem presented by Sharma et al. [30].

In the energy Eq. 3 the last two terms represent dissipation effect. The first term is the viscous dissipation in Darcy’s limit (\({K}^{{_\ast}}\rightarrow 0\))(see, e.g., Ingham et al. [15]), while the second term is the Forchheimer–Darcy dissipation term. The viscous dissipation term is neglected in Darcy–Forchheimer approximation (see, e.g., [27]). For the discussions and derivations of Eqs. 3–3, we refer the reader to Joseph et al. [16], Nield [22], Payne et al. [26], and Kaviany [17].

The corresponding boundary conditions for the velocity field and temperature at the upper plate are

$$\mbox{ At}\;{y}^{{_\ast}} = h :\; {u}_{ 1}^{{_\ast}} = {u}_{ 0}\,\cos ({w}^{{_\ast}}{t}^{{_\ast}}),\quad {T}_{ 1}^{{_\ast}} = {T}_{ 0}(1 +\cos ({w}^{{_\ast}}{t}^{{_\ast}})),$$
(5)

where u 0 and T 0 are the mean velocity and mean temperature of the plate, respectively, and \({w}^{{_\ast}}\) is the frequency of oscillation of the plate. The interface boundary conditions are due to the continuity of the velocity, temperature, and the balance of heat flux and the stress jump.

$$\begin{array}{rcl} \mbox{ At}\;{y}^{{_\ast}} = 0 : {u}_{ 1}^{{_\ast}} = {u}_{ 2}^{{_\ast}},\;{T}_{ 1}^{{_\ast}} = {T}_{ 2}^{{_\ast}},\;{k}_{ 1}\,\frac{\partial {T}_{1}^{{_\ast}}} {\partial {y}^{{_\ast}}} = {k}_{2}\,\frac{\partial {T}_{2}^{{_\ast}}} {\partial {y}^{{_\ast}}} ,\;{\mu }_{2}\,\frac{\partial {u}_{2}^{{_\ast}}} {\partial {y}^{{_\ast}}} - {\mu }_{1}\,\frac{\partial {u}_{1}^{{_\ast}}} {\partial {y}^{{_\ast}}} = \beta \frac{{\mu }_{1}} {\sqrt{{K}^{{_\ast}}}}{u}_{1}^{{_\ast}}.& &\end{array}$$
(6)

Here β is the adjustable parameter in the stress jump boundary condition. Such an imposition was justified and used previously by [19],[24] and [25].

Analogously, the boundary conditions at the bottom plate are

$$\mbox{ At}\;{y}^{{_\ast}} = -h : {u}_{ 2}^{{_\ast}} = {u}_{ 0}\,cos({w}^{{_\ast}}{t}^{{_\ast}}),\quad {T}_{ 2}^{{_\ast}} = {T}_{ 0}(1 + cos({w}^{{_\ast}}{t}^{{_\ast}})).$$
(7)

Equations 1–7 constitute the mathematical formulation of the problem under consideration. Nondimensionalizing the governing equations 1–3 using dimensionless (without asterisks) variables given by

$$\begin{array}{rcl} {y}^{{_\ast}} = hy,\quad {t}^{{_\ast}} = \frac{h} {{u}_{0}}t,\quad {w}^{{_\ast}} = \frac{{u}_{0}} {h} w& & \\ {u}_{k}^{{_\ast}} = {u}_{ 0}{u}_{k},\quad {T}_{k}^{{_\ast}} = {T}_{ 0}{T}_{k} + {T}_{0}\quad for\;k = 1,2& & \\ m = \frac{{\mu }_{1}} {{\mu }_{2}},\quad n = \frac{{k}_{1}} {{k}_{2}},\quad {K}^{{_\ast}} = {h}^{2}K.& &\end{array}$$
(8)

The equations are obtained as

$$\begin{array}{rcl} \frac{\partial {u}_{1}} {\partial t} = \frac{1} {\mathrm{Re}} \frac{{\partial }^{2}{u}_{1}} {\partial {y}^{2}} ,\quad 0 < y < 1& &\end{array}$$
(9)
$$\begin{array}{rcl} \frac{\partial {T}_{1}} {\partial t} + {u}_{1}\frac{\partial {T}_{1}} {\partial y} = \frac{1} {\mathrm{Pr}\,\mathrm{Re}} \frac{{\partial }^{2}{T}_{1}} {\partial {y}^{2}} + \frac{\mathrm{Ec}} {\mathrm{Re}}\,{\left (\frac{\partial {u}_{1}} {\partial y} \right )}^{2},\quad 0 < y < 1& &\end{array}$$
(10)

and

$$\begin{array}{rcl} \frac{\partial {u}_{2}} {\partial t} = \frac{1} {m\mathrm{Re}} \frac{{\partial }^{2}{u}_{2}} {\partial {y}^{2}} - \frac{1} {\mathrm{Re}\,K}\,{u}_{2} - \frac{{C}_{F}} {\sqrt{K}}\,\,{u}_{2}^{2},\quad - 1 < y < 0& &\end{array}$$
(11)
$$\begin{array}{rcl} \frac{\partial {T}_{2}} {\partial t} + {u}_{2}\frac{\partial {T}_{2}} {\partial y} = \frac{1} {n\,\mathrm{Pr}\mathrm{Re}} \frac{{\partial }^{2}{T}_{2}} {\partial {y}^{2}} + \frac{\mathrm{Ec}} {K\,\mathrm{Re}}\,{u}_{2}^{2} +\mathrm{ Ec} \frac{{C}_{F}} {\sqrt{K}}\,{u}_{2}^{3},\quad - 1 < y < 0& &\end{array}$$
(12)

where \(\mathrm{Re} = \rho {u}_{0}h/{\mu }_{1}\) is the dimensionless Reynolds number that characterizes the relation between inertial and viscous forces, \(\mathrm{Pr} = {\mu }_{1}{c}_{p}/{k}_{1}\) is the dimensionless Prandtl number which expresses the ratio of kinematic viscosity to thermal diffusivity, and \(\mathrm{Ec} = {u}_{0}^{2}/{c}_{p}{T}_{0}\) is the Eckert number that approximates the ratio of the kinematic energy and thermal energy. Here the viscosity ratio(m) and the thermal conductivity ratio(n) are defined in terms of the clear fluid with respect to the fluid in the porous domain.

Using Eq. 8, the boundary condition equations 5–7 can be written as

$$\begin{array}{rcl} \mbox{ At}\;y = 1 :\; {u}_{1} =\cos (wt),\quad {T}_{1} =\cos (wt),& &\end{array}$$
(13)
$$\begin{array}{rcl} \mbox{ At}\;y = 0 : {u}_{1} = {u}_{2},\quad {T}_{1} = {T}_{2},\quad n\,\frac{\partial {T}_{1}} {\partial y} = \frac{\partial {T}_{2}} {\partial y} ,\quad \frac{\partial {u}_{2}} {\partial y} - m\,\frac{\partial {u}_{1}} {\partial y} = \frac{\beta m} {\sqrt{K}}{u}_{1},& &\end{array}$$
(14)
$$\begin{array}{rcl} \mbox{ At}\;y = -1 :\; {u}_{2} =\cos (wt),\quad {T}_{2} =\cos (wt).& &\end{array}$$
(15)

3 Procedure

In order to explain the given physical problem the model is reduced to suitable form. Since the flow of the fluid under consideration is due to the oscillations of the plates, the solution of the equations is presented in the following form:

$$\begin{array}{rcl}{ u}_{j} = {f}_{j}{e}^{iwt},\qquad \mathit{for}\quad j = 1,2& &\end{array}$$
(16)
$$\begin{array}{rcl}{ T}_{j} = {F}_{j}{e}^{iwt},\qquad \mathit{for}\quad j = 1,2& &\end{array}$$
(17)

where only the real part of the complex quantities has physical meaning. Here f j and F j are the complex amplitudes of the oscillation and they do not depend upon time t but depend only on space variable y and that w is a constant. The symbol i stands for the complex imaginary number. To obtain an expression for f j and \({F}_{j}\), simply substitute Eqs. 16 and 17 in Eqs. 9–15. After simple calculation we find that the functions \({f}_{1},{f}_{2},{F}_{1}\), and F 2 must satisfy the following:

$$\begin{array}{rcl} & {f}_{1}^{ \prime \prime } - i\,w\,\mathrm{Re}\,{f}_{1} = 0&\end{array}$$
(18)
$$\begin{array}{rcl} & {F}_{1}^{ \prime \prime } -\mathrm{ Pr}\,\mathrm{Re}\,{e}^{iwt}\,{f}_{1}\,{F}_{1}^{ \prime } - i\,w\,\mathrm{Pr}\,\mathrm{Re}\,{F}_{1} +\mathrm{ Pr}\,\mathrm{Ec}\,{e}^{iwt}\,{f}_{1}^{ \prime 2} = 0&\end{array}$$
(19)
$$\begin{array}{rcl} & {f}_{2}^{ \prime \prime } -\left (\dfrac{m} {K} + i\,w\,m\,\mathrm{Re}\right ){f}_{2} -\mathrm{ Re}\,m\,{e}^{iwt} \dfrac{{C}_{F}} {\sqrt{K}}{f}_{2}^{2} = 0&\end{array}$$
(20)
$$\begin{array}{rcl} & {F}_{2}^{ \prime \prime } - n\mathrm{Re}\mathrm{Pr}\left ({e}^{iwt}{f}_{2}{F}_{2}^{ \prime } + iw{F}_{2}\right ) + n\mathrm{Ec}\mathrm{Pr}{e}^{iwt}\left ( \dfrac{1} {K}{f}_{2}^{2}\right ) + \dfrac{n\mathrm{Pr}\mathrm{Re}\mathrm{Ec}{C}_{F}} {\sqrt{K}} {e}^{2iwt}{f}_{2}^{3} = 0&\end{array}$$
(21)

subject to the boundary and interface conditions:

$$\begin{array}{rcl}{ f}_{1}(1) = 1,\;{F}_{1}(1) = 1,\;{f}_{2}(-1) = 1,\;{F}_{2}(-1) = 1& &\end{array}$$
(22)
$$\begin{array}{rcl}{ f}_{1}(0) = {f}_{2}(0),\;{F}_{1}(0) = {F}_{2}(0),\;n{F}_{1}^{ \prime }(0) = {F}_{ 2}^{ \prime }(0),{f}_{ 2}^{ \prime }(0) - m{f}_{ 1}^{ \prime }(0) = \frac{{\boldsymbol \beta} m} {\sqrt{\boldsymbol K}}{f}_{1}(0),& &\end{array}$$
(23)

where the prime stands for the derivative with respect to y.

The solution of the model equations 18–22 neglecting Forchheimer drag term reduces to Darcy flow and is a special case of the present problem. Eqs. 18–21 together with the boundary condition equations 22–22 are solved numerically to study the effect of \({C}_{F}\). First of all, velocity field in a complete domain is solved and subsequently temperature field is evaluated. For a numerical integration, the following procedure has been used which is similar to the one used by Deng et al. [9]:

  • The constant \({f}_{1}^{ \prime }(1) = {f}_{0}\) is first introduced. Now trial value for \({f}_{0}\) is assumed, and then Eq. 18 can be treated as initial value problem and may be solved by Runge–Kutta fourth-order method over the domain \(0 \leq y \leq 1.\)

  • Next at y = 0 the interface conditions are evaluated using Eqs. 22 for a prescribed value of m.

  • Equation 20 is now treated as initial value problem and integrated over the domain \(-1 \leq y \leq 0\) using the Runge–Kutta method of order four, the same one that we used in the first step. The boundary conditions \({f}_{2}(0) = {f}_{1}(0)\) and \({f}_{2}^{ \prime }(0) = m{f}_{1}^{ \prime }(0) + \beta m{f}_{1}(0)/\sqrt{K}\) are used for the solution of Eq. 20.

  • The solution with trial value of f 0 is computed with boundary condition at \(y = -1\). Newton’s Raphson method, a root finding procedure, is used to update the value of f 0 until the boundary condition at \(y = -1\), i.e., \({f}_{2}(-1) = 1\) is satisfied with a tolerance of \(1 \times 1{0}^{-6}\).

The temperature equations are solved by the similar procedure.

4 Discussion

4.1 Validation

To demonstrate the successful implementation of the numerical algorithm the numerical results are compared with those obtained from the analytical solutions for the Darcy flow velocity (\({C}_{F} = 0\), β = 0).

Fig. 2
figure 2

Velocity profiles at two different phases for different values of permeability parameter K with w = 8, m = 0. 4, Re = 1, C F  = 0, and β = 0

Full size image

The algorithm is implemented in scientific computing program MATLAB. The details of analytical expression for the velocity field are given in Appendix. The numerical simulation for Eq. 16 is obtained by solving system of Eqs. 18 and 20 with corresponding boundary conditions using 201 grid points for each fluid domain. The simulation results for velocity profiles at two different phases for different values of permeability parameters are shown in Fig. 2 and the flow parameters are reported in the figure caption. Comparison of results shows that numerical and analytical solutions are in close agreement and thereby validating numerical approach. It can be also observed that the fluid velocity increases with an increase in the permeability parameter due to the overall reduction in damping resistance offered by porous matrix. At the initial phase wt = 0, fluid attains maximum velocity on the plate and then decreases exponentially as the fluid moves towards interface. But when phase increases, for example, \(wt = \pi /2\), the maximum velocity is observed in the middle of the domain.

4.2 and Velocity Distribution

The Fluid moving through a porous medium, it experiences a drag force which is due to frictional drag and form drag. Let us discuss quadratic drag effect on the flow pattern. The distribution of velocity is shown at different phases for different values of Forchheimer coefficient (Figs. 3–6).

Fig. 3
figure 3

Velocity profile at phase wt = 0

Full size image
Fig. 6
figure 6

Velocity profile at phase wt = π

Full size image

The model parameters m = 0. 4, Re = 1, K = 0. 5, w = 8, and β = 0. 1 are considered for the simulation. Clearly the fluid flow is parabolic in nature (Figs. 3 and 4) inside the channel. But, the presence of solid matrix inside the porous medium reduces the velocity field. Maximum velocity of the fluid flow is seen in the clear fluid region near to the axis. However, at the interface and inside the porous medium, the flow is obstructed due to frictional drag.

Fig. 4
figure 4

Velocity profile at phase \(wt = \pi /4\)

Full size image

Again comparing various curves in either of the plot, it is concluded that the higher the convective current, the greater is the drag effect, so also the thickness of the boundary layer decreases. It is interesting to note that oscillating plate for different phases wt produces reversal in the flow (Figs. 5 and 6).

Fig. 5
figure 5

Velocity profile at phase \(wt = \pi /2\)

Full size image

Reynolds number frequently arise when performing dimensional analysis in the viscous flow equations. Figure 7 depicts the effect of Reynolds number in the clear fluid domain as well as porous fluid domain. Velocity field is higher in clear fluid domain than in porous fluid domain at a constant Reynolds number. Low Reynolds number indicate laminar flow, which is characterized by smooth constant flow. When Reynolds number increases gradually, in this context, viscous effect decreases and flow pattern is dominated by oscillating plate (for Re = 2 in Figure 7). It can be further seen that with the increase of Reynolds number the interface velocity decreases faster due to drag effects.

Fig. 7
figure 7

Variation of velocity profiles with increase Reynolds numbers Re with \(wt = \pi /2\), w = 8, m = 0. 4, K = 0. 5, C F  = 0. 1, and β = 0. 1

Full size image

To conclude the discussion on velocity in two different domains we consider the effect of adjustable parameter β in the stress jump boundary condition (Fig. 8). The model parameters w = 8, m = 0. 4, K = 0. 5, C F  = 0. 1, and Re = 1 are considered for the simulation at phase \(wt = \pi /2\). As evident, when β = 0, the transition of fluid flow from clear fluid domain to porous domain is not smooth. Slight increase of β from 0 to 0.39 makes the velocity gradient same in both regions causing a smooth transition of fluid from one region to another. In case of β = 1, the velocity gradients of two regions are unequal and there is a misalignment. Physically there is a distortion for β = 0 and β = 1. However, at β = 0. 39, the transition of the flow is smooth at the interface.

Fig. 8
figure 8

Variation of velocity profiles for different values of stress jump parameter β

Full size image

4.2.1 Friction

The dimensionless skin friction at the upper and lower plates is given by \(\big{(}\frac{\partial {u}_{1}} {\partial y}{ \big{)}}_{y=1}\) and \(\big{(}\frac{\partial {u}_{2}} {\partial y}{ \big{)}}_{y=-1}\), respectively.

The computed values at two different phases wt = 0 and \(wt = \pi /2\) for nondimensional parameters Re = 1, w = 8, m = 0. 4, and β = 0. 1 are visualized against the permeability parameter (K) in Figs. 9 and 10. As evident skin friction is independent of permeability parameter in clear fluid region (see skin friction in the upper plate (UP) in Figs. 9 and 10). But this effect on lower plate is clearly visible. The skin friction almost attains constant values for K > 0. 4 (Fig. 9) and it increases with the decrease of permeability parameter K. It is also interesting to analyze the differences between the profiles of the skin friction at lower plate(LP) with and without drag effects. As seen from Fig. 9 this difference is quite significant (see skin friction in the lower plate (LP) in Figs. 9 and 10). This is interesting because drag effect has no contribution in clear fluid region. The skin friction is greater in case of non-Darcian fluid(C F  = 1) as compared to Darcian case (C F  = 0). Negative skin friction is observed in the clear fluid region at phase wt = 0 which may be attributed to the fact that there is a flow reversal at the boundary layer near the plate. With the advancement of phase wt from 0 to π ∕ 2 the reverse effect is observed in Fig. 10.

Fig. 9
figure 9

Skin friction at the upper plate (UP) and lower plate (LP) at phase wt = 0

Full size image
Fig. 10
figure 10

Skin friction at the upper plate (UP) and lower plate (LP) at phase \(wt = \pi /2\)

Full size image

4.2.2 Distribution

In the following the simulated temperature distributions in the respective domains are analyzed. Figure 11 illustrates the profiles of temperature distribution at phase wt = 0 for various values of thermal conductivity ratios (n) for fixed m = 0. 4, \(\mathrm{Re} = 1\), C F  = 1, β = 0. 1, Pr = 0. 5, and Ec = 0. 1.

Fig. 11
figure 11

Temperature profile for different conductivity ratios with \(\mathrm{Pr} = 0.5\) and Ec = 0. 1

Full size image

This temperature distributions correspond to the velocity distribution that is depicted in Fig. 12. It can be observed that the conductivity ratio substantially influences the temperature distribution in both the domains. The smaller the conductivity ratio implies the higher thermal conductivity of the porous domain. Since the porous medium is in direct contact with the heated wall heat is transferred by conduction through solid boundaries. So temperature of porous medium is higher than in the clear fluid domain close to the interface and for small n. It is further noticed that lower value of thermal conductivity ratio indicates a sharp jump of thermal boundary layer at the interface of two regions.

Fig. 12
figure 12

Corresponding velocity profile for the computation of temperature distribution (Fig. 11) at phase wt = 0 with m = 0. 4, Re = 1, C F  = 1, and β = 0. 1

Full size image

The effect of Eckert number (Ec) on the temperature distribution is described in Fig. 13. It is observed that the temperature increases in the clear fluid region with the increasing value of Ec. This effect is only visible at near to the interface in porous domain. Eckert number that measures the kinetic energy transformed into heat by viscous dissipation. In high Eckert number flow, frictional heating dominates the boundary-layer fluid temperature and consequently rate of heat transfer to the fluid through the wall is higher.

Fig. 13
figure 13

Variation of temperature profiles with increasing Eckert numbers (Ec) for the velocity profile given in Fig. 12 with n = 0. 8 and Pr = 0. 5

Full size image

Another physical quantity of interest in this problem, the local convective heat transfer rate at the surface characterized by the Nusselt number, is easily computed. The dimensionless Nusselt number at the respective plates are given by

$$\begin{array}{rcl} \mathit{At}\ \mathit{the}\ \mathit{upper}\ \mathit{plate :}\quad N{u}_{1}& =& -\Bigg{(}\frac{\partial {T}_{1}} {\partial y}{ \Bigg{)}}_{y=1}. \\ \mathit{At}\ \mathit{the}\ \mathit{lower}\ \mathit{plate :}\quad N{u}_{2}& =& -\Bigg{(}\frac{\partial {T}_{2}} {\partial y}{ \Bigg{)}}_{y=-1}.\end{array}$$

The dependence of Nusselt number on the permeability parameter for different values of the Forchheimer coefficient is described in Figs. 14 and 15. This figures are computed for w = 8, m = 0. 4, n = 0. 8, Re = 1, Pr = 0. 5, Ec = 0. 1, and β = 0. 1 at phase wt = 0. Moreover the effect of heat convection on the Nusselt number is analyzed. The results depicted in Fig. 14 correspond to the Nusselt number at the lower plate. The simulation result shows that the convection reduces the Nusselt number for all permeability parameter K. The reason is obvious that near the lower plate conduction dominates the flow and Nusselt number decreases. It is also evident that the higher the drag effect the lesser is the Nusselt number for both convection and without convection. It can be seen further that the increase in permeability results in the increase of rate of wall heat transfer as more heat is transferred away from the wall by convection. The wall effect due to solid wall is effective in a length scale of K = 0. 5. In the clear fluid region convection dominates the flow. Decrease in Nusselt number is observed (Fig. 15) with convection than without convection because convection causes the motion to be turbulence. It is also observed that Nusselt number is all most independent of permeability parameter. Since drag effect has no role to play in the clear fluid region, therefore heat transfer rate is independent of drag coefficient.

Fig. 14
figure 14

Nusselt number at lower plate

Full size image
Fig. 15
figure 15

Nusselt number at upper plate

Full size image

5 Conclusion

Non-Darcian effects on the viscous fluid in partly porous configurations have been investigated numerically. The Navier–Stokes and Darcy–Forchheimer equations are employed in clear fluid and porous medium, respectively. Conclusion of this study is summarized below:

  • Fluid flow is almost parabolic in nature between two oscillating plates. Clearly velocity field in the clear fluid region is larger than porous region and minimum value of thermal boundary layer shifts towards interface.

  • Drag effect reduces the flow field. There exist three flow resistances, the bulk damping resistance due to porous structure, the viscous resistance due to boundary and the resistance due to inertial forces.

  • In between the two oscillating plates clear fluid domain and porous fluid domain coexist. At the interface the transition of fluid is not smooth. This depends upon adjustable parameter, i.e., the stress jump boundary condition. Proper choice of adjustable parameter may give rise to smooth transition.

  • The heat conductivity ratio also plays important role in temperature distribution. In the clear fluid region the thermal boundary layer attains minimum value near the axis y = 0 and minimum value of thermal boundary layer shifts towards interface, while in the porous domain the thermal boundary layer attains minimum value at the interface and gradually increases to unity at the plate.

  • In case of lower plate flow is dominated by conductive heat transfer. The evolution of the flow with increasing permeability results from the competition between two opposing effects. Higher permeability results in a better penetration in porous layer by the flow and consequently the diffusive effect of the imposed temperature is lower. The flow is then accelerated resulting higher heat transfer. In case of upper plate heat transfer is independent of permeability parameter.

The present investigation of the study of non-Darcian effects on the viscous flow in partly porous configuration between two oscillating plates can be utilized as the basis for many scientific and engineering applications and for studying more complex problems.

6 Appendix

The analytical solutions for the Darcian velocity fields u 1 and u 2 are obtained by first solving Eqs. 18 and 20 with corresponding boundary conditions(with C F  = 0 and β = 0) and then the real part of Eq. 16 yields the following expression. These analytical results are compared with numerical simulations in Fig. 2, showing a good agreement.

$$\begin{array}{rcl}{ u}_{1}(y,t) = {S}_{11}\,\cos (w\,t) - {S}_{12}\,\sin (w\,t),& \quad \mathit{for}\;\;\;0 \leq y \leq 1\qquad & \\ {u}_{2}(y,t) = {S}_{21}\,\cos (w\,t) - {S}_{22}\,\sin (w\,t),& \quad \mathit{for}\; - 1 \leq y \leq 0\qquad & \\ \end{array}$$

where

$$\begin{array}{rcl} {S}_{11} = \frac{({a}_{8}\,{m}_{7} + {b}_{8}\,{n}_{7})} {{m}_{7}^{2} + {n}_{7}^{2}} ,\quad {S}_{12} = \frac{({b}_{8}\,{m}_{7} - {a}_{8}\,{n}_{7})} {{m}_{7}^{2} + {n}_{7}^{2}} & & \\ {S}_{21} = \frac{({p}_{5}\,{m}_{7} + {q}_{5}\,{n}_{7})} {{m}_{7}^{2} + {n}_{7}^{2}} ,\quad {S}_{22} = \frac{({q}_{5}\,{m}_{7} - {p}_{5}\,{m}_{7})} {{m}_{7}^{2} + {n}_{7}^{2}} & & \\ \end{array}$$

with

$$\begin{array}{rcl} {m}_{7} = {m}_{3} + {m}_{6},\quad & {n}_{7} = {n}_{3} + {n}_{6} & \\ {m}_{3} = {m}_{2}\,{c}_{1} - {n}_{2}\,{d}_{1},\quad & {n}_{3} = {m}_{2}\,{d}_{1} + {n}_{2}\,{c}_{1} & \\ {m}_{6} = {m}_{5}\,{c}_{2} + {n}_{5}\,{d}_{2},\quad & {n}_{6} = {n}_{5}\,{c}_{2} - {m}_{5}\,{d}_{2} & \\ {m}_{2} = {x}_{2}\,{m}_{1} + {y}_{2}\,{n}_{1},\quad & {n}_{2} = {x}_{2}\,{n}_{1} - {y}_{2}\,{m}_{1} & \\ {c}_{2} =\sin ({x}_{22})\cosh ({y}_{22}),\quad & {d}_{2} =\cos ({x}_{22})\sinh ({y}_{22}) & \\ {c}_{1} =\cos ({x}_{22})\cosh ({y}_{22}),\quad & {d}_{1} =\sin ({x}_{22})\sinh ({y}_{22}) & \\ {m}_{1} = -1 + {\alpha }_{3}\,\cos (2{y}_{1}),\quad & {n}_{1} = {\alpha }_{3}\,\sin (2{y}_{1}) & \\ {m}_{5} = m\,\sqrt{k}\,({y}_{1}\,{m}_{4} - {y}_{1}\,{n}_{4}),\quad & {n}_{5} = m\,\sqrt{k}\,({y}_{1}\,{m}_{4} + {y}_{1}\,{n}_{4}) & \\ {m}_{4} = 1 + {\alpha }_{3}\,\cos (2{y}_{1}),\quad & {n}_{4} = {\alpha }_{3}\,\sin (2{y}_{1}) & \\ {x}_{22} = \frac{{x}_{2}} {\sqrt{k}},\quad & {y}_{22} = \frac{{y}_{2}} {\sqrt{k}} & \\ {x}_{2} = \frac{1} {\sqrt{2}}\sqrt{\sqrt{{m}^{2 } + {(m\,w\,k\,\mathrm{Re })}^{2 }} - m},\quad & {y}_{2} = \frac{1} {\sqrt{2}}\sqrt{\sqrt{{m}^{2 } + {(m\,w\,k\,\mathrm{Re })}^{2 }} + m}& \\ {y}_{1} = \sqrt{\frac{w\,\mathrm{Re }} {2}} ,\quad & {\alpha }_{3} = exp(2{y}_{1}) & \\ {a}_{8} = {a}_{11} + {a}_{4} + {a}_{7},\quad & {b}_{8} = {b}_{11} + {b}_{4} + {b}_{7} & \\ {a}_{7} = {a}_{6}\,{c}_{2} + {b}_{6}\,{d}_{2},\quad & {b}_{7} = {b}_{6}\,{c}_{2} - {a}_{6}\,{d}_{2} & \\ {a}_{6} = m\,\sqrt{k}\,({y}_{1}\,{a}_{5} - {y}_{1}\,{b}_{5}),\quad & {b}_{6} = m\,\sqrt{k}({y}_{1}\,{a}_{5} + {y}_{1}\,{b}_{5}) & \\ {a}_{5} = {\beta }_{2}\,\cos ({y}_{1}\,(1 - y)) + {\alpha }_{2}\,\cos ({y}_{1}\,(1 + y)),\quad & {b}_{5} = {\beta }_{2}\,\sin ({y}_{1}\,(1 - y)) + {\alpha }_{2}\,\sin ({y}_{1}\,(1 + y))& \\ {\alpha }_{2} = exp({y}_{1}\,(1 + y)),\quad & {\beta }_{2} = exp({y}_{1}\,(1 - y)) & \\ {a}_{4} = {a}_{3}\,{c}_{1} - {b}_{3}\,{d}_{1},\quad & {b}_{4} = {a}_{3}\,{d}_{1} + {b}_{3}\,{c}_{1} & \\ {a}_{3} = {x}_{2}\,{a}_{2} + {y}_{2}\,{b}_{2},\quad & {b}_{3} = {x}_{2}\,{b}_{2} - {a}_{2}\,{y}_{2} & \\ {a}_{2} = {\alpha }_{2}\,\cos ({y}_{1}\,(1 + y)) - {\beta }_{2}\,\cos ({y}_{1}\,(1 - y)),\quad & {b}_{2} = {\alpha }_{2}\,\sin ({y}_{1}\,(1 + y)) - {\beta }_{2}\,\sin ({y}_{1}\,(1 - y))& \\ {a}_{11} = {x}_{2}\,{a}_{1} + {y}_{2}\,{b}_{1},\quad & {b}_{11} = {x}_{2}\,{b}_{1} - {y}_{2}\,{a}_{1} & \\ {a}_{1} = {\alpha }_{1}\,\cos ({y}_{1}\,(2 - y)) - {\beta }_{1}\,\cos ({y}_{1}\,y),\quad & {b}_{1} = {\alpha }_{1}\,\sin ({y}_{1}\,(2 - y)) - {\beta }_{1}\,\sin ({y}_{1}\,y) & \\ {\alpha }_{1} = exp({y}_{1}\,(2 - y)),\quad & {\beta }_{1} = exp({y}_{1}\,y) & \\ {p}_{5} = {p}_{1} - {p}_{2} + {p}_{4},\quad & {q}_{5} = {q}_{1} - {q}_{2} + {q}_{4} & \\ {p}_{4} = {p}_{3}\,{c}_{5} + {q}_{3}\,{d}_{5},\quad & {q}_{4} = {q}_{3}\,{c}_{5} - {p}_{3}\,{d}_{5} & \\ {p}_{3} = 2\,m\,\sqrt{k}\,({\alpha }_{4}\,{y}_{1}\,\cos ({y}_{1}) - {\alpha }_{4}\,{y}_{1}\,\sin ({y}_{1}),\quad & {q}_{3} = 2\,m\,\sqrt{k}\,({\alpha }_{4}\,{y}_{1}\,\cos ({y}_{1}) + {\alpha }_{4}\,{y}_{1}\,\sin ({y}_{1}) & \\ {\alpha }_{4} = exp({y}_{1})\quad & & \\ {c}_{5} =\sin ({x}_{44})\cosh ({y}_{44}),\quad & {d}_{5} =\cos ({x}_{44})\sinh ({y}_{44}) & \\ {x}_{44} = {x}_{22}\,(1 + y),\quad & {y}_{44} = {y}_{22}\,(1 + y) & \\ {p}_{2} = {m}_{5}\,{c}_{4} + {n}_{5}\,{d}_{4},\quad & {q}_{2} = {n}_{5}\,{c}_{4} - {m}_{5}\,{d}_{4} & \\ {c}_{4} =\sin ({x}_{33})\cosh ({y}_{33}),\quad & {d}_{4} =\cos ({x}_{33})\sinh ({y}_{33}) & \\ {x}_{33} = y\,{x}_{22},\quad & {y}_{33} = y\,{y}_{22} & \\ {p}_{1} = {m}_{2}\,{c}_{3} - {n}_{2}\,{d}_{3},\quad & {q}_{1} = {m}_{2}\,{d}_{3} + {n}_{2}\,{c}_{3} & \\ {c}_{3} =\cos ({x}_{33})\cosh ({y}_{33}),\quad & {d}_{3} =\sin ({x}_{33})\sinh ({y}_{33}) & \\ \end{array}$$