Acoustic Bubbles, Acoustic Streaming, and Cavitation Microstreaming

Abstract

The phenomena of acoustic streaming and cavitation microstreaming can seem very complex, but underpinning them are fundamental concepts of fluid dynamics that are common to many similar systems. In this chapter, key aspects of fluid dynamics leading to bubble acoustics, acoustic streaming, and microstreaming are outlined. Basic concepts of sound are introduced, focusing on the special case of the sound waves produced by a bubble and how a bubble creates sound and responds to sound. The difference between linear and nonlinear theory for the time-dependent radius of an oscillating bubble is outlined. The concept of mean streaming is then introduced; this is when a purely oscillatory flow causes a net fluid motion. The origin of mean streaming is emphasized: the nonlinear term in Euler’s momentum equation. It is explained that there are two classes of mean streaming: acoustic streaming, created when the ultrasonic power is high and has some gradient with distance, and microstreaming, created when the gradient is high on a small scale. Applications of acoustic streaming and microstreaming in biomedicine and engineering and the latest research are reviewed.

Fluid Dynamics

Introduction

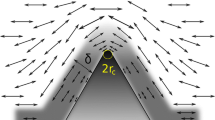
Scientists and engineers who first encounter bubble physics are confronted by a bewildering variety of phenomena that can occur when a bubble’s volume oscillates. In Fig. 1, a microstreaming flow can be seen around a bubble that is also undergoing oscillations in shape. The flow is three-dimensional and represents an interplay of forces controlled by three physical properties: compressibility, surface tension, and viscosity. Bubble oscillations account for observations as mundane as the splashing sound of running water and as exotic as the emission of light by a tiny bubble. Bubble oscillations – and the flows they drive – are used in technologies commonplace as the ultrasonic cleaning of jewelry and as specialized as the removal of gas from photographic coatings. Bubble acoustics has been applied to predict the severity of erupting volcanoes and the energy lost by breaking ocean waves. Bubble oscillations and microstreaming flows help to destroy kidney stones and tumors but also erode metal ship’s propellers. Cavitation physics is used by shrimp to capture their prey. Bubble-acoustic microstreaming is thought to speed the dissolution of blood clots in the brain and to transport foreign genes into a cell for therapy. Some examples of this great variety of situations can be found in Manasseh and Ooi [32].

Fig. 1

Acoustic microstreaming field created around a bubble of approximate radius 200 μm driven at 12.94 kHz (From Tho et al. [54]. Reprinted under a CSIRO Licence to Publish)

However, all these phenomena have a common explanation. Before delving into the specifics of bubble acoustics, cavitation, acoustic streaming, and microstreaming, it is important to understand that this “zoo” of diverse phenomena is really composed of members of the same family: the physics of fluids. Moreover, the origin of this behavior can be understood from just four fundamental equations, expressing the laws of conservation of mass, momentum, and energy and of the constitution of matter.

Basic Definitions

We first need to define a fluid. Colloquially, we could say “a fluid is a substance that can flow,” but there is a more precise, scientific definition: a fluid is a substance that can deform indefinitely when a shear stress is applied. Both gases and liquids are fluids, and cavitation physics has been put to practical use in liquids as diverse as water, blood, mercury, molten lava, and the sap of trees. This attribute of indefinite deformation under shear stress is vital, because when we introduce the form of Newton’s second law appropriate to a fluid, terms appear that are unique to fluids. These terms mean that fluids can not only transmit and respond to ultrasound, but also they can flow in response to ultrasound.

In contrast with fluids, when a shear stress is applied to a solid, it will deform to a certain extent that depends on its stiffness, then stop deforming. If the stress is increased sufficiently, the solid will fail – colloquially, we can say it has broken.

In the context of bubble acoustics and cavitation, there is a key difference between gases and liquids: gases are much more compressible than liquids. This means that we will be able to capture the essential physics of bubble acoustics by initially assuming the gas in the bubble is compressible while the liquid surrounding it is incompressible – an important simplification.

The Constitutive Law Relating Pressure and Density

The extent to which any substance (a solid, liquid, or a gas) can be compressed is given by that substance’s bulk modulus, K, where

$$ K=\rho \frac{\partial p}{\partial \rho }, $$

(1)

where ρ is the density of the substance and p is the pressure applied to it. This is a fundamental relation between the density of a substance (for a given mass, a relation with the volume of a substance) and the pressure applied to it. This is an example of a constitutive law of matter. We will return to (1) when we consider sound propagation in liquids. However, for a gas, (1) can be simplified to the ideal gas law,

$$ {p}_1{V}_1^{\kappa }={p}_0{V}_0^{\kappa }, $$

(2)

where p is the pressure in the gas, V is the volume of the gas (the volume of the bubble), and κ is the polytropic index, which depends on the way with which the gas is compressed under the applied pressure. (If the pressure is less than ambient, the resulting negative compression is called rarefaction). The subscript 0 refers to the initial state of the gas, and the subscript 1 refers to the altered state of the gas after the compression; the subscript 0 often signifies the rest or equilibrium state when the bubble is not oscillating. In bubble acoustics, two extreme approximations for κ are sometimes used: either the compression is adiabatic, which means no heat is gained or lost by the gas in the bubble, or it is isothermal, which means the temperature of the gas in the bubble is a constant. In the adiabatic limit, $\kappa =\gamma \equiv Cp/C\upsilon,$ the ratio of specific heats of the gas, which is a fundamental property of the gas, depends only on the number of degrees of freedom of movement of the atoms that make up the gas molecule. For diatomic molecules like nitrogen and oxygen (which make up most of the atmospheric air), 7 = 7/5. In the isothermal limit, κ = 1, and the ideal gas law is further simplified to Boyle’s law,

$$ {p}_1{V}_1={p}_0{V}_0, $$

(3)

first published by Robert Boyle in 1662. The adiabatic limit is often used for large bubbles undergoing small volumetric vibrations, while the isothermal limit is often used for small bubbles undergoing small volumetric vibrations. Cavitation bubbles may be small, but they often undergo large vibrations. Thus, a value of κ somewhere in between unity and 7 may need to be used.

Conservation of Mass

The law of conservation of mass for a continuum (a solid, liquid, or gas) is a mathematical statement of the fact that mass is neither created nor destroyed, under the assumptions of continuum mechanics. Only if we consider nuclear reactions, (or, at the very small scale, quantum effects), can mass be changed into energy (or appear and disappear). A fluid flow transports mass into and out of a volume. Because the fluid flow may be three-dimensional, the velocity is a vector, u. By considering an infinitesimal element of fluid volume, it is easy to show that

$$ \frac{\partial \rho }{\partial t}=-\mathbf{\nabla}.\left(\rho \boldsymbol{u}\right), $$

(4)

i.e., that the rate of change of density with time is equal to the divergence of the mass flux.

Conservation of Momentum

The law of conservation of momentum was first understood by Isaac Newton in 1687, who formulated it as Newton’s second law,

$$ \boldsymbol{F}=m\boldsymbol{a}, $$

where F is the vector force applied to a mass m and a is the vector acceleration due to the application of the force. While Newton’s second law applies to all matter, when written out for a fluid flow, the acceleration a in Newton’s second law takes a more complex form that was derived by Leonhard Euler in 1757. The essential difference when a fluid accelerates, as opposed to a rigid solid, is that fluid acceleration appears even if the velocity field does not change with time, when velocity changes with space. This vital difference understood by Euler is what makes acoustic streaming and microstreaming possible. The conservation of momentum is expressed in Euler’s equation as

$$ \frac{\mathrm{D}\left(\rho \boldsymbol{u}\right)}{\mathrm{D}t}=\nabla p+\rho \mathbf{g}, $$

(5)

where g is the acceleration due to gravity. By expanding the left-hand side of Euler’s equation, (5), we can see how this unique property of a fluid is manifested,

$$ \frac{\mathrm{D}\left(\rho \boldsymbol{u}\right)}{\mathrm{D}t}=\frac{\partial \left(\rho \boldsymbol{u}\right)}{\partial t}+\boldsymbol{u}\cdot \mathbf{\nabla}\left(\rho \boldsymbol{u}\right). $$

(6)

The term $\partial \left(\rho \boldsymbol{u}\right)/\partial t$ is exactly the same for a fluid as for a solid. However, the term $\boldsymbol{u}\cdot \mathbf{\nabla}\left(\rho u\right)$ is the nonlinear term in Euler’s equation that represents a fluid’s ability to change its velocity by changing its position in space. It is sometimes called the advective term.

Finally, by the early nineteenth century, the work of Claude-Louis Navier and George Gabriel Stokes leads to the inclusion of stresses due to viscosity, giving the Navier-Stokes momentum equation

$$ \frac{\mathrm{D}\left(\rho \boldsymbol{u}\right)}{\mathrm{D}t}=\nabla \cdotp \boldsymbol{\tau} +\rho \mathrm{g}, $$

(7)

where τ is the stress tensor, a quantity that conveniently includes both the pressure and the viscous shear stresses applied to the fluid.

Significance of the Nonlinearity in the Momentum Equation

Acoustic streaming and microstreaming phenomena are only possible because of the nonlinear term in Euler’s equation. In fact, as we will see in section “The Rectification of Oscillation by the Nonlinear Term,” acoustic streaming and microstreaming phenomena are only some examples of very many other streaming phenomena that can occur when waves are the primary flow. Let us see the significance of this nonlinear term by looking at only the radial equation out of the three equations for the three dimensions of the vector Euler’s equation (5). For simplicity but not necessity, assume the density is a constant and that forces due to gravity are in balance, giving

$$ \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}=-\frac{1}{\rho}\frac{\partial p}{\partial r}, $$

(8)

where r is the radial direction in a spherical coordinate system (r, ϕ, θ). We need only to examine the nonlinear term,

$$ u\frac{\partial u}{\partial r}, $$

in (8) to understand what is possible. The vital feature of this nonlinear term is that it is a velocity multiplied by a velocity gradient. This means that for this term to exist, there must be a gradient in the velocity. It is also quadratic in the velocity.

Jumping ahead of ourselves somewhat, let us imagine we have solved (4) and (7) – or, at least, simplified versions of them – and have found a solution such that

$$ u=U\left(r,\phi, \theta \right) \cos \left(\omega t\right). $$

(9)

In other words, a fluid flow that oscillates sinusoidally with time has radian frequency u and has any sort of field in space, U(t, ϕ, θ). To arrive at such a solution, we would probably have had to ignore the nonlinear term, by assuming it is negligibly small (linearize the equation). Now, however, an interesting consequence of the nonlinear term can be seen. Substituting (9) back into (8) and averaging over time, we can immediately see that the time average of the term $\partial u/\partial t$ is zero, because the average of a sine or a cosine is zero. However, the time average of the term u $\partial u/\partial r$ is not zero, because it varies with time as cos²(ωt), and average with time of a cosine squared is not zero.

Thus, any time we linearize the equations of fluid dynamics and arrive at a wave solution, the true nonlinear equations will generate a term that does not average to zero over time. Provided there is a gradient (i.e., $\partial u/\partial r$ is not zero), there will inevitably be a driver for net motion – a small but steady flow that continues over time, added to the much larger, primary oscillatory motion that cancels out over time. Small it may be, but it persists, and it is this persistence that has many interesting consequences to be outlined in sections “Acoustic Streaming” and “Acoustic Microstreaming.”

The notion that there is a “second-order” nonlinear behavior superimposed on the “first-order” linear behavior proceeds directly from the mathematical approach of perturbation theory, in which the nonlinearity is assumed to be weak, so that it is only a modification to the primarily oscillatory linear behavior. Before mathematically deriving the first-order solutions such as (9), we should physically explain this nonlinear “rectification” of oscillatory motion.

The Rectification of Oscillation by the Nonlinear Term

As just noted, it is a fundamental feature of all fluid flows that admit waves that a primarily oscillatory motion can have a small net “drift” superimposed on it [47]. This holds true for waves in the ocean as well as for ultrasonic waves, and indeed for other classes of fluid wave motion, such as the large-scale waves in the atmosphere that affect our weather and climate. As a wave crest passes, it causes the fluid (and anything suspended in it) to move in one direction, and as a wave trough passes, the fluid is made to retrace its motion to its point of origin, as shown by the simple orbit on the left-hand side of Fig. 2. After the passage of each wave, there is no net displacement, at least according to the linear theory. This linear model of waves is, however, only exact if the amplitude of the waves is infinitesimally small.

Fig. 2

Rectification of oscillatory motion by the nonlinear term in the fluid dynamics equation of motion, giving a net “drift” or “streaming” motion. The equation is (8), where, for simplicity, only one dimension of Euler’s three-dimensional momentum (Eq. 5) is shown and the fluid is assumed to be of constant density and with gravitational forces in balance (Image by R. Manasseh)

In reality, the fluid does not return precisely to its starting point after the passage of each wave, as shown by the “incomplete” orbits on the right-hand side of Fig. 2. There is a rectification of the oscillatory motion due to the nonlinear term. Although the discrepancy in position of the fluid after each cycle is tiny compared with the motion it undergoes during each cycle, unlike the orbital motion, the discrepancy does not cancel out, and the discrepancies persist – and accumulate. Over many waves, the effect can be significant, and with ultrasonics, a million waves can pass in a second. The result is a net drift of the fluid – a streaming motion.

It is because of this fundamental physics that rip currents are created at ocean beaches, sand and flotsam are transported in the ocean, acoustic currents are created, and colloidal particles and biological cells are transported in ultrasonics.

As noted in section “Conservation of Momentum,” the nonlinearity in the momentum equations of fluid dynamics creating this net motion is quadratic. This means that all streaming motions will be proportional to the wave amplitude squared and thus proportional to the wave power. Thus, the higher the power, the greater the net fluid motions, increasing in general linearly with power. The net motions are second-order effects. This means that although they vary with the square of the wave amplitude, their velocity is much weaker than the velocity with which the fluid oscillates as the waves pass.

Furthermore, the quadratic nonlinearity is actually a velocity multiplied by the gradient in velocity with distance. Thus, in order for the net motion to be possible, there should be a gradient in the wave velocity with distance. The larger the gradient, the larger is the local net motion.

The ocean rip current is induced by the dissipation as waves shoal onto a beach, leading to a gradient in the ocean wave power with distance. Analogously, acoustic streaming is induced by the dissipation due to viscous and scattering effects, leading to a gradient in the sound wave power with distance. Figure 3 shows a simple illustration of acoustic streaming over several tens of centimeters. Acoustic streaming will be further detailed in section “Large-Scale Acoustic Streaming.”

Fig. 3

Acoustic streaming in a water tank. Drops of dye released at the surface fall owing to their slightly greater density and are caught up in the acoustic streaming “jet” of speed roughly 0.02 m s⁻¹ created by a 2.25 MHz transducer (at image left) driven by a continuous wave signal. Since the tank is of finite length, the flow created by the jet must recirculate, and evidence of the recirculation can be seen in the curvature of the dye lines above the jet. The bolts visible at the tank bottom are about 55 mm apart (Image courtesy of P. Lai; further details of this experiment are in Lai [21])

Acoustics

Conservation of Mass and Momentum for the Sound Wave Case

Sound is a phenomenon in which a continuum (a solid, liquid, or a gas) is alternately compressed and expanded (or “rarefied”) by waves propagating through it. Although the compressions and rarefactions are not obvious to the casual observer, scientists deduced that this was occurring by careful studies and experiments in the eighteenth and early nineteenth centuries. The compressions and rarefactions are small, so that they would normally be neglected relative to other factors, such as advection and friction due to large flows or deformations. However, if the other factors are absent, only the compressions and rarefactions are left. Indeed, far away from active zones (such as near cavitating bubbles) where flows or deformations are large, sound is the only variation left, transmitting information about what happened in those zones throughout the continuum.

In both (4) and (7), the density is allowed to vary in space and time. This is necessary, since the propagation of sound inherently relies on the compressibility of a continuum. Compression (or “dilatation”) changes the density of the continuum.

In general (4) and (7) are difficult to solve, particularly owing to the nonlinearity in (7). Fortunately, we know that for most sound waves the changes in density are small relative to the average density, ρ0, and that the velocities are small. Hence, as anticipated in section “Significance of the Nonlinearity in the Momentum Equation,” we can neglect terms in which small variables are multiplied together (linearize the equations). The mass conservation equation (4) becomes

$$ \frac{\partial \rho }{dt}=-{\rho}_0\mathbf{\nabla}\cdot \boldsymbol{u}. $$

(10)

The momentum equation is likewise linearized, throwing away for the time being the interesting nonlinear term that we noted in section “Significance of the Nonlinearity in the Momentum Equation” which was the origin of acoustic streaming and microstreaming. Furthermore, assuming that friction is small eliminates the shear stresses from τ, leaving only the normal stress due to pressure, p; viscosity can be considered in a more detailed analysis. The gravity force can be neglected for now by assuming horizontal motion, but using a more detailed analysis, it is possible to show that gravity is completely negligible no matter which way the sound propagates. Equation (7) then becomes

$$ {\rho}_0\frac{\partial \boldsymbol{u}}{\partial t}=-\mathbf{\nabla}p. $$

(11)

We have two vector equations involving three variables, ρ and p and the vector u. We can eliminate one of the variables by combining the mass and momentum conservation equations. Differentiating (10) with respect to time and taking the divergence of (11) gives

$$ \frac{\partial^2\rho }{\partial {t}^2}=-{\rho}_0\mathbf{\nabla}\cdot \frac{\partial \boldsymbol{u}}{\partial t}, $$

(12)

$$ {\rho}_0\mathbf{\nabla}\cdot \frac{\partial \boldsymbol{u}}{\partial t}=-{\mathbf{\nabla}}^2p, $$

(13)

and substituting (12) into (13) gives

$$ \frac{\partial^2\rho }{\partial {t}^2}-{\mathbf{\nabla}}^2p=0. $$

(14)

We now find the resulting momentum equation is unclosed: there is an additional variable, ρ. What is needed is the relation between normal stress (pressure) and volumetric strain (which is related to the density). We need a constitutive law relating stress and strain. This is the bulk modulus, K, that was given in (1). Integrating (1) with respect to ρ,

$$ K \ln \rho =p+\mathrm{const}., $$

(15)

and using our initial condition that when p = p ₀, ρ = ρ ₀ gives the constant as $K \ln {\rho}_0-{p}_0.$ Inserting this constant and rearranging gives

$$ K \ln\;\left(\frac{\rho }{\rho_0}\right)=p-{p}_0. $$

(16)

The natural log in (16) makes it a nonlinear relation. However, (14) was derived assuming the density only varies slightly from ρ ₀, so it is consistent for us to make the same assumption regarding (16). Thus, we will apply the Taylor series expansion for the natural log function to (16). In this operation we will define the small variation in density as ${\rho}^{\prime }=\rho -{\rho}_0,$ so that

$$ \ln \left(\frac{\rho }{\rho_0}\right)= \ln \left(1+\frac{\rho^{\prime }}{\rho_0}\right), $$

(17)

and remembering the Taylor series expansion for natural log for any small variation α about 1,

$$ \begin{array}{l} \ln \left(1+\alpha \right)= \ln (1)+\frac{1}{1+\alpha}\alpha -\frac{1}{\left(1+{\alpha}^2\right)}{\alpha}^2+\dots, \\ {} \simeq 0+\alpha -{\alpha}^2+\dots, \end{array} $$

where $\alpha ={\rho}^{\prime }/{\rho}_0,$ to first order (16) becomes

$$ \begin{array}{l}K\left(\frac{\rho -{\rho}_0}{\rho_0}\right)=p-{p}_0,\\ {}\Rightarrow \rho =\frac{\rho_0}{K}\left(p-{p}_0\right)+{p}_0.\end{array} $$

(18)

Now that we have ρ as a function of p, we have our second equation. We need only to differentiate (18) twice with respect to time, and substituting into (14), we get

$$ \frac{\partial^2p}{\partial {t}^2}-{c}^2{\mathbf{\nabla}}^2p=0, $$

(19)

where $c=\sqrt{\left(K/{\rho}_0\right)}.$

Equation 19 is the linear one-dimensional wave equation. All small one-dimensional waves, whether they are electromagnetic waves, ripples on water, or sound waves as in our case, obey this equation. The constant c is the speed of sound. It is worth noting that the bulk modulus K can be related to the total pressure (including the atmospheric pressure) P ₀ by K = γP ₀ where γ is the adiabatic index. Hence another expression for c is

$$ c=\sqrt{\left(\gamma {P}_0/{\rho}_0\right)}. $$

(20)

Solution of the Wave Equation

To solve the wave equation, we can use one of two methods: the method of separation of variables or d’Alembert’s method. Here, separation of variables will be used. This assumes that the pressure p can be split into two functions, one only of time and one only of space,

$$ p=T(t)X(x). $$

(21)

For simplicity assume there is only one dimension in space, x. (The calculation below applies to three dimensions just as well.) Then, substituting into the one-dimensional version of (19) gives

$$ \frac{\partial^2T}{\partial {t}^2}X={c}^2T\frac{\partial^2X}{\partial {x}^2}, $$

(22)

and dividing both sides by XT gives

$$ \frac{1}{T}\frac{\partial^2T}{\partial {t}^2}={c}^2\frac{1}{X}\frac{\partial^2X}{\partial {x}^2}. $$

(23)

Now, the left-hand side of (23) is a function of t only, while the right-hand side is a function of x only. The only possibility is that both sides are equal to a constant, which we shall call −ω ², giving

$$ \frac{\partial^2T}{\partial {t}^2}=-{\omega}^2T, $$

(24)

$$ \Rightarrow T={A}_1 \cos \left(\omega t\right)+{A}_2 \sin \left(\omega t\right). $$

(25)

Since both a sin and a cos are solutions of (24), we need to include both possibilities. (If we had assumed the constant was simply C say, a slightly longer but more general way to the answer is to say the solution is of the form ${\mathrm{e}}^{\varOmega t}\pm {\mathrm{e}}^{-\varOmega t}$ where $\varOmega =\sqrt{C}$ is a complex number.) Likewise,

$$ \frac{\partial^2X}{\partial {t}^2}=-\frac{\omega^2}{c^2}X, $$

(26)

with solution

$$ X={A}_3 \cos (kx)+{A}_4 \sin (kx), $$

(27)

where $k=\omega /c,$ giving the general solution

$$ p=\left({A}_1 \cos \left(\omega t\right)+{A}_2 \sin \left(\omega t\right)\right)\left({A}_3 \cos (kx)+{A}_4 \sin (kx)\right). $$

(28)

In general, we need to introduce boundary and initial conditions to get the four constants A ₁, A ₂, A ₃, and A ₄. Nonetheless, it is already clear that a solution to (19) consists of waves in both space and time. A further interesting property of the solution becomes apparent on applying some trigonometric identities (e.g., $\cos \left(\alpha +\beta \right)= \cos \alpha \cos \beta - \sin\;\alpha \sin \beta$ and so on) to (28). After some algebra we get

$$ p={B}_1 \cos \left(k\left(x-ct\right)\right)+{B}_2 \sin \left(k\left(x-ct\right)\right) $$

(29)

$$ +{B}_3 \cos \left(k\left(x+ct\right)\right)+{B}_4 \sin \left(k\left(x+ct\right)\right), $$

(30)

where B ₁, B ₂, B ₃ and B ₄ are constants made up of A ₁, A ₂, A ₃ and A ₄. The key property is that x − ct and x + ct are the arguments of the wave functions. This means that time and space are interchangeable – we can always find a time t for a given point x where the waves look the same as at another point. And we can always find a point for a given time where the waves look the same at another time. All linear waves, be they electromagnetic waves, ocean waves, or sound waves, have this property.

The fact that we have both x − ct and x+ ct means that a disturbance to the pressure field in a fluid propagates with the speed of sound both right and left from the source of the disturbance.

The frequency of the waves in radians per second is ω; the frequency in s⁻¹ (Hertz) is given by $f=\omega /\left(2\pi \right),$ which is usually of more practical relevance since oscillations are usually measured in cycles per second. Similarly, the constant k in (30) is called the wavenumber and is related to the more physical wavelength, λ, by $\lambda =\left(2\pi \right)/k;$ the wavelength is the distance in meters from one pressure maximum to the next. As for any waves, then, the speed of sound is related to the physical quantities of frequency and wavelength by

$$ c=f\lambda . $$

(31)

Acoustic Impedance

Now that we have found the pressure in a sound wave, let us see what the velocity of the fluid u is. Remember, this is the velocity with which the fluid particles are set into motion by the passage of the wave. It is completely different to (and in the case of sound waves, much smaller than) the speed c with which the waves propagate. Let us go back to (11) and again assume one-dimensional motion for simplicity, so that (11) becomes

$$ {\rho}_0\frac{\partial u}{\partial t}=-\frac{\partial p}{\partial x}. $$

(32)

Now, substituting our solution in the general form of (30) into (32) and imagining the constants are chosen so that waves are propagating in one direction (say +x) gives

$$ u=\frac{1}{\rho_0c}p. $$

(33)

(Imagining the constants are chosen so the wave propagates with a negative speed, in the –x direction, gives the same relation.) Note that the quantity ρ ₀ c called the acoustic impedance is a property of the fluid only. The relation (33), written as $p={\rho}_0cu,$ makes it clear that we have an analogy with electromagnetic theory; with u the analog of electric current and p the analog of voltage, the acoustic impedance represents the resistance of the medium to the propagation of an alternating velocity field, just as electric impedance represents the resistance of a wire to the propagation of alternating current.

The Rayleigh-Plesset-Noltingk-Neppiras-Poritsky Equation

Rayleigh’s Derivation of the Collapse of a Spherical Cavity

Rayleigh [45] considered the fluid dynamics of the collapse of a spherical cavity of liquid, motivated by problems of cavitation damage to ships’ propellers. He considered the bubble to be at the center of a spherically symmetric coordinate system, which means that the only motions possible are radial. The conservation of mass (4) for a spherically symmetric system is given by

$$ \frac{1}{r^2}\frac{\partial \left({r}^2\rho u\right)}{\partial r}=-\frac{\partial \rho }{\partial t}, $$

(34)

where u is the outward velocity of the liquid induced by the pulsating bubble.

Now we will make a surprising assumption – that the liquid is incompressible. This is surprising because in section “Conservation of Mass and Momentum for the Sound Wave Case” we noted that sound waves certainly require compressibility to exist; we will later be using the frequency of the pulsating bubble for the frequency of the sound waves in the liquid. However, whether the liquid is compressible or incompressible has only a tiny influence on the pulsation of the bubble, which is dominated by the much greater compressibility of the gas. The right-hand side of (34) is thus zero. Integrating (34) with respect to r and noting that when $\mathrm{r}=R(t),$ where R(t) is the time-varying radius of the bubble, $u=\mathrm{d}R/\mathrm{d}t\equiv \dot{R}(t)$ gives

$$ u=\frac{R{(t)}^2}{r^2}\dot{R}(t). $$

(35)

The equation of radial momentum balance is Euler’s equation, (8), assuming incompressibility and spherical symmetry, and applied to the liquid only, and ignoring dissipation for simplicity. Substituting (35) into the derivatives in (8) gives

$$ \frac{\partial u}{\partial t}=\frac{2R{\dot{R}}^2}{r^2}+\frac{R^2}{r^2}\ddot{R}, \mathrm{and} \frac{\partial u}{\partial r}=-2\frac{R^2}{r^3}\dot{R}, $$

(36)

and substituting these into (8) gives

$$ \frac{2R}{r^2}{\dot{R}}^2+\frac{R^2}{r^2}\ddot{R}-2\frac{R^4}{r^5}{\dot{R}}^2=-\frac{1}{\rho}\frac{\partial p}{\partial r}. $$

(37)

Now, we want to eliminate the spatial (r) dependence of (37), so integrate (37) from r = R to some arbitrary radius r = D giving

$$ {\left[-\frac{2R}{r}{\dot{R}}^2-\frac{R^2}{r}\ddot{R}+\frac{1}{2}\frac{R^4}{r^4}{\dot{R}}^2\right]}_R^D=-\frac{1}{\rho}\left(p(D)-p(R)\right). $$

(38)

Now send D → ∞ and assume that at infinity p = P ₀, giving

$$ 2{\dot{R}}^2+R\ddot{R}-\frac{1}{2}{\dot{R}}^2=-\frac{1}{\rho}\left({P}_0-p(R)\right). $$

(39)

Now p(R) is the absolute pressure in the liquid just outside the bubble, and neglecting surface tension makes this the same as the pressure inside the bubble. Thus, using the ideal gas law (2),

$$ p(R)V{(R)}^{\kappa }={P}_0V{\left({R}_0\right)}^{\kappa }, $$

so that p(R) is given by

$$ p(R)={P}_0{\left({R}_0/R\right)}^{3\kappa }, $$

and thus (39) becomes

$$ R\ddot{R}+\frac{3}{2}{\dot{R}}^2=-\frac{1}{\rho}\left({P}_0-{P}_0{\left({R}_0/R\right)}^{3\kappa}\right). $$

(40)

Like the Euler momentum equation from which it was derived, (40) is a nonlinear equation: it has the quadratic nonlinearity due to fluid advection on its left-hand side, worsened by an additional nonlinearity that is due to the geometric spreading from a point source. Moreover, the bubble radius R(t) appears on the denominator on the right-hand side, raised to a power that is, in general, a non-integer. If the bubble radius was to suddenly become small, very complex behavior would ensue, and indeed it does, as amply documented in the extensive literature on nonlinear microbubble dynamics (e.g., Lauterborn [24] and Leighton [25]). Rayleigh [45] stopped at the equivalent of (40), since he was concerned about the pressure created during the nonlinear collapse process rather than the natural frequency of the bubble.

Linearization Giving the Bubble Natural Frequency: The Minnaert Equation

To determine the natural frequency of the bubble, linearize (40) with the assumption $R(t)={R}_0+\delta (t)$ where $\delta \ll {R}_0,$ and R ₀ is the equilibrium radius of the bubble. Thus, δ is a perturbation in the bubble’s radius that is positive outward from the bubble. The left-hand side of (40) becomes simply ${R}_0\ddot{\delta},$ while a Taylor series expansion gives

$$ {P}_0{\left({R}_0/R\right)}^{3\kappa}\simeq {P}_0\left(1-\left(3\kappa /{R}_0\right)\delta \right), $$

(41)

and substituting this into (40) gives

$$ {R}_0\ddot{\delta}=-\frac{1}{\rho }{P}_0\left(3\kappa /{R}_o\right)\delta, $$

(42)

giving the equation for simple harmonic motion

$$ \ddot{\delta}=-{\omega}_0^2\delta . $$

(43)

The radian frequency is now

$$ {\omega}_0=\sqrt{\frac{3\kappa {P}_0}{\rho }}\frac{1}{R_0}, $$

(44)

and the frequency in Hertz is

$$ {f}_0=\frac{1}{2\pi}\sqrt{\frac{3\kappa {P}_0}{\rho }}\frac{1}{R_0}. $$

(45)

It is worth noting that Minnaert (1933) derived (45) by heuristically assuming simple harmonic motion at the outset and balancing the kinetic and potential energies at each extreme of the motion. This obscures some of the assumptions, in particular the assumptions of an incompressible liquid, no dissipation of any kind, and small-amplitude behavior, giving linearity. Nonetheless, it was Minnaert who first quantified the relation between bubble size and its natural frequency, and hence (45) is called Minnaert’s equation. The simple harmonic relation (43) expresses the essential physics of bubble acoustics: it can be thought of as a mass bouncing on a spring. The spring is a spherical spring consisting of the compressible gas, while the mass is the liquid surrounding the gas.

For bubbles of air (or nitrogen, oxygen, or indeed any diatomic gas) oscillating in water at approximately atmospheric pressure and room temperature, (45) can be approximated as

$$ {f}_0\simeq \frac{3.29}{R_0}, $$

(46)

so that, for example, the millimeter-sized bubbles one sees when pouring water into a glass naturally make sounds in the kilohertz range that we can hear: a 1 mm radius bubble makes a sound of about 3.3 kHz. This explains why humans can hear the sound of splashing and running water and of ocean waves breaking. Meanwhile, a 1 μm radius bubble, which is smaller than a blood cell, would have a natural frequency in the megahertz range, explaining why microbubbles are used as medical ultrasound contrast agents. (Bubbles this small have a frequency modified by other effects, as noted in section “Full Rayleigh-Plesset-Noltingk-Neppiras-Poritsky Equation.”)

The linear approximation (41) shows that the perturbation in liquid pressure just outside a bubble, p′, is given by

$$ {p}^{\prime }=-{P}_0\left(3\kappa /{R}_0\right)\delta . $$

(47)

This makes sense; if δ is positive, the bubble is expanded, so the liquid pressure is below P ₀ and hence p′ is negative. Equivalently, using (42) gives

$$ {p}^{\prime }=\rho {R}_0\ddot{\delta}, $$

(48)

and the acceleration of the liquid, $a\equiv \ddot{\delta},$ is given by

$$ a=\frac{1}{\rho {R}_0}{p}^{\prime }. $$

(49)

Full Rayleigh-Plesset-Noltingk-Neppiras-Poritsky Equation

During the twentieth century, successive modifications and improvements were made to the derivation in section “Rayleigh’s Derivation of the Collapse of a Spherical Cavity,” and as a consequence the resulting equation is sometimes given all the names of the key workers contributing to its derivation, so that is it called the Rayleigh-Plesset-Noltingk-Neppiras-Poritsky (RPNNP) equation. An account of its derivation was given by Neppiras [36], and the background to each addition to Rayleigh’s original work is covered by Leighton [25].

Surface tension and vapor pressure are included by modifications to the pressure term, giving

$$ R\ddot{R}+\frac{3}{2}{\dot{R}}^2=-\frac{1}{\rho}\left(\left({P}_0+\frac{2\sigma }{R}-{p}_{\upsilon}\right)-\left({P}_0+\frac{2\sigma }{R}-{p}_{\upsilon}\right){\left({R}_0/R\right)}^{3\kappa}\right), $$

(50)

where σ is the surface tension constant of the interface between the gas in the bubble and the surrounding liquid, and p _υ is the vapor pressure due to those liquid molecules that have evaporated into the bubble. These are further constitutive properties of fluids, in addition to the constant κ from the ideal gas law, that are now considered. Including viscous damping means that the incompressible Navier-Stokes equation, (7), rather than Euler’s equation, is now the form of the momentum equation being used. This gives

$$ R\ddot{R}+\frac{3}{2}{\dot{R}}^2=-\frac{1}{\rho}\left[\left({P}_0+\frac{2\sigma }{R}-{p}_{\upsilon}\right)-\left({P}_0+\frac{2\sigma }{R}-{p}_{\upsilon}\right){\left({R}_0/R\right)}^{3\kappa }+\frac{4\mu }{R}\dot{R}\right], $$

(51)

where μ is the dynamic viscosity of the liquid. Linearizing as in section “Linearization Giving the Bubble Natural Frequency: The Minnaert Equation,” the natural frequency of the bubble including these effects [25] is now

$$ {f}_0=\frac{1}{2\pi}\sqrt{\frac{1}{\rho}\left[3\kappa \left({P}_0+\frac{2\sigma }{R}-{p}_{\upsilon}\right)-\left(\frac{2\sigma }{R}-{p}_{\upsilon }+\frac{4{\mu}^2}{\rho {R}_0^2}\right)\right]}\frac{1}{R_0}. $$

(52)

However, it is only for micron-sized bubbles that the frequency predicted by (52) differs notably from the Minnaert frequency (45). It is important to note that viscous dissipation is not the only source of energy loss from the bubble. Energy is also lost to sound radiation (here we finally acknowledge the compressibility of the liquid) and to heat loss; the latter may be accommodated by appropriately modifying κ [25].

During some cavitation conditions, the speed with which the bubble expands and contracts can be so large that it becomes a substantial fraction of the speed of sound. In this case, continuing to assume the liquid is incompressible is doubly inappropriate: not only does liquid compressibility radiate away energy, modifying the bubble’s natural frequency, it alters the nonlinear terms in the momentum equation that can no longer be ignored. The only recourse to solution is then numerical. Researchers including Herring, Trilling, and Gilmore modified the RPNNP equation to include the effects of a finite speed of sound [36]. Presently, the equation most often used to represent all the effects noted above is the Keller-Miksis equation. The Keller-Miksis equation has been further modified to include the dynamics of a thin flexible shell encapsulating the bubble, modeling an ultrasound contrast agent, and to include the effects of multiple bubbles interacting [10]. Since the focus of this chapter is on acoustic streaming and microstreaming rather than the extremes of cavitation collapse, we will not further detail the fascinating but complex literature on highly nonlinear bubble oscillations. Acoustic streaming and microstreaming may be described as weakly nonlinear phenomena, which can be modeled by the perturbation theory concept described in general terms in section “Significance of the Nonlinearity in the Momentum Equation.”

Bubble Trapped in a Narrow Tube

There have been several microfluidic applications in which an acoustically driven bubble trapped in a tube or microchannel has been proposed and tested as a flow actuator [6, 7, 56], and sonochemical reactions have been generated in such a system [52].

By following the same approach as in section “Rayleigh’s Derivation of the Collapse of a Spherical Cavity,” the linear natural frequency, ignoring surface tension and viscosity and assuming both the bubble and the liquid slug are long compared with the tube radius, is given by

$$ {f}_0=\left(\frac{1}{2\pi}\sqrt{\frac{\kappa {P}_0}{\rho }}\right)\frac{1}{\sqrt{L_0S}}, $$

(53)

where L ₀ is the equilibrium bubble length and S is the length of the liquid slug in the tube. In this simplistic example, the basic physics is even clearer than in the classical spherical bubble considered by Rayleigh and Minnaert: a mass of liquid contained in a tube is bouncing on the long “spring” formed by the bubble in the tube.

It is interesting to note that at a vastly greater scale than microfluidics, the same fundamental physics has been analyzed to predict the size of gas bubbles in Strombolian volcanoes, given measurements of the rumbling frequency. A bubble of gas is trapped in a tube, and above it is a mass of molten magma [58]. The size of the bubble may indicate the hazard presented by the impending eruption.

Two-Dimensional Planar Bubble

A two-dimensional or planar bubble could also occur in microfluidic contexts, for example, Liu et al. [30]. An equivalent would be a cylindrical bubble only capable of radial expansion and contraction. This system differs fundamentally from the three-dimensional bubble: the two-dimensional equivalent of the three-dimensional integration that leads from (38) to (39) is unbounded as D → ∞, so that the domain size D is always a variable in the natural frequency. Thus, the two-dimensional bubble has a linear resonant frequency given by

$$ {f}_0=\left(\frac{1}{2\pi}\sqrt{\frac{2\kappa {P}_0}{\rho }}\right)\frac{1}{R_0\sqrt{ \ln \left(D/{R}_0\right)}}, $$

(54)

whereas before R ₀ is the equilibrium bubble radius and D is the radius of the liquid domain enclosing it.

Acoustic Streaming

Large-Scale Acoustic Streaming

Rayleigh [46] analyzed the acoustic streaming induced by sound waves propagating between parallel plates. This is usually called Rayleigh streaming. It was at this time that he applied the mathematical technique of perturbation theory to deal with the non-zero time-averaged flow created by the nonlinear term in Euler’s equation, as described in section “Significance of the Nonlinearity in the Momentum Equation.”

Large-scale streaming due to ultrasound was originally called the “quartz wind” [11] owing to the quartz crystals used to produce ultrasound; it is also called Eckart streaming. Streak photographs of Eckart streaming extending a few centimeters from an ultrasonic transducer are shown in Fig. 4. Recall from section “The Rectification of Oscillation by the Nonlinear Term” that the only requirement for the nonlinear term to exist, and thus for streaming to occur, is that a gradient should exist in the first-order sound field. Any ultrasonic transducer will create a near-field effect (see, e.g., Kinsler and Frey [19]): owing to the finite size of the transducer, the field will change rapidly with distance away from it, gradually becoming more uniform at distances much greater than the transducer size. As distance from the transducer increases further, the field will eventually fall off simply, owing to geometric spreading. Thus one might expect some streaming even in the theoretical absence of dissipation.

Fig. 4

Acoustic streaming field (Eckart streaming) created by a transducer 4 mm in diameter (seen at image top center) emitting 32 MHz pulses of 0.5 μs duration at 31 kHz pulse repetition rate into a 64 × 64 × 90 mm rectangular box. Streaming speeds reach a maximum of about 15 mm s⁻¹ (Reprinted from Nowicki et al. [39]. Copyright (1998), with permission from Elsevier)

Where the ultrasonic intensity is high enough to cause cavitation, as is usually the case when commercial sonotrodes or ultrasonic horns are used in chemical or biochemical preparations, acoustic streaming occurs together with cavitation. These systems can be extremely complex, with linear and nonlinear interactions between the cavitation bubbles and with the microstreaming associated with the microbubbles (see section “Basic Observations of Microstreaming”) occurring at the small scale, as well as the large-scale streaming occurring. Significant power is lost from the sound waves in generating the cavitation bubbles, which locally absorb and scatter the sound waves. Thus, the effect of cavitation is to enhance the overall dissipation of energy from the sound waves, increasing the negative gradient in the acoustic field and reducing the distance from the source that the sound can penetrate. This may enhance the acoustic streaming closer to the source of the ultrasound, while limiting the extent to which the streaming penetrates.

Applications of Acoustic Streaming

It was suggested by Betheras [1] that the acoustic streaming created by a medical ultrasound scanner could be useful in medical diagnosis of cysts. A cyst is a lesion in the body that is often, though not always, filled with fluid. Ovarian cysts and related lesions in the body such as endometriomas could be benign or malignant, but the only true test is invasive biopsy or surgery [12]. If such cysts, which may be a few centimeters in size, contain fluid only, they are less likely to be malignant, but if they contain solid or more viscous matter, the risk of malignancy may be higher [12].

Medical scanners include a Doppler feature that permits them to measure the speed of blood flow. Normally, acoustic streaming caused by a medical ultrasound scanner is slower than blood flow, but in a cyst, there is no background flow at all, so the acoustic streaming can become visible. It is a complicated phenomenon because the scanner creates the streaming flow it is measuring. The velocity is a function of cyst size, location, shape, and the rheology of the fluid in the cyst. In addition to cysts of the female reproductive system, acoustic streaming has also been used in diagnoses of cysts in breast tissue [37].

Acoustic streaming flows in model cysts were studied by Zauhar et al. [62]. The velocity fields in an elastic spheroidal cavity were measured by Sznitman and Rösgen [51] using particle image velocimetry (PIV). A variety of acoustically transparent model cysts and rectilinear chambers were mounted at various locations in a much larger tank fitted with an ultrasonic transducer, and velocity fields were measured by PIV (Lai [21], as reported by Lai et al. [22]). It was found that the size and shape of the cavity in which the streaming occurred had a significant effect on the flow pattern. Furthermore, the streaming velocity profile depended on the location of the chamber relative to the transducer’s focus point, as illustrated in Fig. 5.

Fig. 5

Effect of chamber location on profiles of acoustic streaming. Velocity component along the transducer axis is shown. The rectilinear chamber is 50 mm long and is immersed in a large tank driven by a 2.25 MHz transducer. Lines from top to bottom are, respectively, velocity along the central line of maximum cross-sectional velocity and averages over the central 12.5 %, 25 %, and 50 % of the chamber cross-section, with shading around the line indicating 95 % statistical confidence intervals. Note a different vertical scale on right-hand panel since velocities are lower farther from the transducer (From Lai [21]. Courtesy of P. Lai)

High-power ultrasound has also been applied to molten metals, generating acoustic streaming (e.g., Kang et al. [17]) in an effort to improve the stirring and crystallization of the metal.

While acoustic streaming has these beneficial applications, when ultrasound is used to separate particles from liquid (see section “Motion of Particles Relative to Fluid” below), the acoustic streaming may disrupt the desired separation effect [27]. Hence, optimum power levels below which acoustic streaming is not detrimental need to be established.

Motion of Particles Relative to Fluid

The collection of fine rigid particles at the nodes of a standing wave sound field was clearly observed in the nineteenth century in the Kundt’s tube, invented by Kundt in 1866. As just noted, Rayleigh [46] dealt with the nonlinearity in the governing equations using a perturbation approach. In Rayleigh’s approach, the linear sound wave problem would be solved first, and the nonlinear streaming flow solved assuming that the linear solution, substituted into the nonlinear terms and time averaged, drove the streaming.

As will be outlined in section “Basic Observations of Microstreaming,” it is the presence of a boundary layer and hence a non-zero gradient near the particle that makes a net motion possible. King [18] showed that particles could be made to drift in either traveling or standing waves. An appropriate second-order analysis leads to the derivation of an “acoustic radiation force” acting on particles with a different density or compressibility to their surrounds. King [18] calculated the radiation force on a rigid sphere much smaller than the sound wavelength. It was found that the radiation force would be an order of magnitude greater if the particle were in a standing wave field rather than a traveling wave field. If a standing wave field is created, particles will rapidly be attracted to the nodes or antinodes in the standing wave field depending on their density and compressibility relative to the carrier fluid. This phenomenon leads to the possibility of using ultrasound for separation.

Applications of ultrasonic separation to the food industry were outlined by Vilkhu et al. [59], and recent advances in ultrasonic separation were reviewed by Leong et al. [28].

Acoustic Microstreaming

Basic Observations of Microstreaming

Acoustic microstreaming is most usually called cavitation microstreaming in the literature. That is because it is most often created by a microbubble, and microbubbles are often created by cavitation. Acoustic microstreaming need not rely at all on the presence of microbubbles, but owing to the powerful effect microbubbles have on locally concentrating the sound field and thus creating large local gradients, acoustic microstreaming is most prominent when microbubbles are involved. Recall from section “Significance of the Nonlinearity in the Momentum Equation” that a gradient in the sound field is a prerequisite for any streaming.

While several types of acoustic streaming flow had been analyzed theoretically in the nineteenth and early twentieth centuries, the streaming flow around a sphere in a sound field – a typical particle in a Kundt’s tube – was analyzed by Lane [23] using the approach of Rayleigh [46]. Significantly, Lane [23] recognized that there would be inner vortices (primary vortices) in the boundary layer (or Stokes layer) around a spherical particle in a sound field. These primary vortices would drive outer vortices (secondary vortices) over scales similar to several radii of the sphere (Fig. 6). Flow speeds in the primary vortices would be expected to be much higher than in the secondary vortices. Lane attempted an experiment with millimeter-sized spheres at audio frequencies, but had difficulty making observations and found the vortex size was overpredicted by theory.

Fig. 6

Lane’s original drawing of the primary microstreaming vortices around both a cylinder and a spherical particle. The innermost streamline of each secondary vortex is also shown, extending outwards at the top of the figure and at either side at the bottom. Note that the structure of the vortices is slightly different for the cylinder and the sphere (Reproduced with permission from Lane [23]. Copyright 1955, Acoustical Society of America)

Lane’s identification of the primary and secondary vortices around a spherical particle was a first in acoustics, but is not unique in fluid dynamics. There are several other analogous flows at macroscopic scales, for example, when a circular cylinder is oscillated normal to its axis, primary vortices appear that are smaller than the cylinder, which in turn drive secondary vortices much larger than the cylinder (e.g., the experiment by Masakazu Tatsuno, published in van Dyke [57]). Engineers study such flows which might occur, for example, as ocean waves pass the leg of a platform in the sea. In a more recent example, centimeter-sized spheres were oscillated through amplitudes in the order of the sphere diameter and at frequencies in the order of a tenth of a cycle per second [42]. Both primary and secondary vortices were easily measured since the scales are in centimeters.

The Stokes layer thickness scales with (2 μ/(ρω))^1/2, where ω is the applied frequency, and since for water μ/ρ ≃ 10⁻⁶, in the very low frequency experiment of Otto et al. [42], the Stokes layer thickness would be on the order of millimeters. However, an ultrasonic frequency, say 200 kHz, would result in a Stokes layer thickness around a micron – only a couple of wavelengths of light. Thus, since the boundary layer around ultrasonically driven microbubbles is so thin, it is only the secondary vortices that are usually observed in microstreaming around microbubbles – in cavitation microstreaming.

Cavitation microstreaming was first studied by Kolb and Nyborg [20], who allowed cavitation bubbles to form under the influence of various frequencies in the audible range, mostly 11.4 kHz and below. Kolb and Nyborg noted that streaming is most pronounced when the bubble is oscillating in its volumetric mode. This is consistent with the note above on the “concentrating” effect of bubbles: volumetric oscillations remove energy from the applied sound field, which at the scale of the bubble is in the form of plane waves, and reradiate sound as spherical waves that have a large local gradient. Kolb and Nyborg [20] also noted that microstreaming was pronounced when the bubble is on a solid boundary. The presence of a solid boundary can be modeled by a bubble interacting with its mirror image which is just touching it [32, 50], a situation that again would lead to a locally large gradient.

Research into cavitation microstreaming continued in the 1950s with the work of Elder [13], who used a precision hypodermic needle to inject bubbles of a controlled size of about 30 μm radius. The frequency was 10 kHz, and driving pressure amplitudes were varied in a range from about 0.2 to 0.9 kPa. Streaming velocities were visually estimated to be less than 0.0005 ms⁻¹ – about half a millimeter per second. Elder [13] classified microstreaming into different regimes that were observed for different liquid viscosities and different sound amplitudes and frequencies. Although the boundary layers near the bubble surface were too thin to be observed, their importance was recognized by both Kolb and Nyborg [20] and Elder [13] by analogy with other acoustic streaming phenomena. Elder [13] also noted the earlier theory of Nyborg [40] that predicted the speed of the jet of liquid created between vortices.

Theoretical Analyses of Microstreaming

A key theoretical work was undertaken by Davidson and Riley [5]. They studied the streaming field around a drop or bubble that was oscillating in translation along an axis, but not oscillating volumetrically. An important feature of their analysis was that they considered only the second-order problem for the streaming, assuming the oscillatory motion due to the bubble and the incident sound field was prescribed. This approach follows logically from the mathematics of perturbation theory. Moreover, the streaming flow was assumed to be incompressible, which was consistent with the approach of Nyborg [40] and again dates back to Rayleigh [46].

The work of Davidson and Riley [5] was subsequently extended by Wu and Du [61] who made the same fundamental assumption as Davidson and Riley [5]: the streaming flow was incompressible and was driven by a prescribed bubble motion. Wu and Du [61] identified two modes of streaming. If the bubble is purely translating, the result is a microstreaming pattern of four vortices (a “quadrupole” pattern). However, if the bubble is undergoing volumetric pulsations, the result is a pattern of two vortices (a “dipole” pattern). They found that the streaming due to volumetric pulsation is stronger than that due to translation, which was consistent with the observation of Elder [13] that microstreaming was most pronounced near the bubble’s resonance frequency. It is important to note that Wu and Du’s calculations were just outside the Stokes layer and hence were calculations of the secondary vortices.

Longuet-Higgins [31] continued the approach of using perturbation theory with the same assumption of incompressible streaming driven by a prescribed velocity field. Although Longuet-Higgins did not explicitly say the calculations were outside the boundary layer, his boundary condition required the gradient of tangential velocity to become zero at the “bubble radius,” effectively placing an artificial boundary at the streamline separating the primary and secondary vortices. Like Wu and Du [61], Longuet-Higgins found a quadrupole pattern when the bubble was translating and a dipole pattern when it was undergoing volumetric pulsations. He combined the two modes of oscillation; recalling that microstreaming results from nonlinear physics, this is not simply a matter of superposition. Indeed, Longuet-Higgins calculated that the microstreaming velocities are proportional to the product of the amplitudes of the two modes of oscillation and that the presence of volumetric pulsations enhanced the translation mode.

It is worth noting that, owing to the incompressibility assumption in all the works of Nyborg [40], Davidson and Riley [5], Wu and Du [61], and Longuet-Higgins [31], the streaming flow field was no different to what might be produced if, for example, a spherical toy balloon were pulsating in volume in a bathtub, in various combinations with and without to and from oscillations of the sphere, with no sound waves present. This assumption probably remains valid while the magnitude of the streaming velocity is small compared with the speed of sound.

The work of Wu and Du [61] was reevaluated by Doinikov and Bouakaz [8], who determined that Wu and Du’s neglect of viscous effects outside the boundary layer caused a severe underestimation of the acoustic streaming velocity. Doinikov and Bouakaz [8] recalculated the radial and tangential components of the streaming velocity immediately outside the boundary layer for a case considered by Wu and Du [61]. Doinikov and Bouakaz [8] found that the true velocities were over an order of magnitude higher, reaching 0.03 ms⁻¹ for a bubble of radius 33 μm driven at 100 kHz and about 55 kPa. This speed, at the boundary between the primary and secondary vortices, reached centimeters per second, contrasting with earlier predictions of fractions of a millimeter per second – and experimental measurements of secondary vortex speeds also in fractions of a millimeter per second.

It is important to recall that all these theories [5, 8, 31, 40, 61] were all predicated upon the perturbation method originally proposed by Rayleigh [46] for acoustic streaming: the linear first-order solution, once found (or simply prescribed), drives the second order where the streaming is manifested, and so on. This mathematical approach means that the analyses, while they have produced successful phenomenological comparisons with experiment, have an inherent disconnection between the acoustic behavior and the streaming behavior – a disconnect that is fundamentally due to the mathematical principle of perturbation theory. We might expect this approach to cause problems when the acoustic amplitude in the immediate vicinity of the microbubble is no longer predictable by linear theory; for example, when there is cavitation collapse or any other circumstance in which the amplitude with which the bubble radius is pulsating is large compared with its equilibrium radius. The assumption of incompressibility in the second-order streaming flows could also lose validity under the extremely nonlinear conditions commonly produced in sonochemical systems.

Even if the bubble dynamics is linear, the presence of many bubbles nearby could alter the local acoustic field owing to bubble-acoustic interactions (e.g., Nikolovska et al. [38]). The microstreaming field around a pair of microbubbles was calculated analytically by Wang and Chen [60], who found that radial streaming velocities were suppressed in favor of the tangential velocities.

Experimental Quantifications of Microstreaming

As noted earlier, the experiments of Kolb and Nyborg [20] and Elder [13] had already observed the secondary vortices around microbubbles, and Elder [13] had estimated streaming speeds. However they had not observed the primary vortices. Gormley and Wu [15] observed streaming around a 55 μm commercial contrast agent microbubble. The flow was revealed by fine particles forming streaks. Since the frequency was 160 kHz, the Stokes layer thickness and hence the primary vortices would have been too small to see, just as in the earlier studies. The work of Gormley and Wu [15] was significant in that the microstreaming flow was photographed; the literature in the 1950s had presented sketches based on observations. Furthermore, Gormley and Wu’s observations were around microbubbles that were not simple gas-in-liquid bubbles; they had a “shell” composed of a partially denatured protein, albumin.

Tho et al. [55] conducted micro-particle image velocimetry (micro-PIV) experiments on the microstreaming flows around microbubbles that were large enough, typically greater than 200 μm in radius, for detailed velocity fields to be quantified for the first time. The bubbles were sessile or pendant within a microchamber and thus had a contact circle with the chamber wall. The sound was applied by a piezoceramic disk that caused the chamber wall to flex. Applied frequencies were 2–13 kHz, and the pressure amplitudes were around 0.1–0.5 kPa.

Tho et al. [54] then studied cases where the bubble not only translated and pulsated but also underwent simultaneous translations around two orthogonal axes. Thus, the bubble center was made to trace out a circle, an ellipse or a line along a single axis, with or without volumetric pulsations, each selected by a particular frequency of insonation and bubble location in the microdevice. The path the bubble center traced out was also measured.

As theoretically predicted earlier [31, 61], translations along one axis corresponded to a quadrupole microstreaming pattern (Fig. 7), while volumetric pulsations corresponded to a dipole (Fig. 8). However, circular or elliptical paths created circular or elliptical vortices surrounding the bubble; as the minor axis of the bubble-translation-path ellipse tended to zero, the quadrupole pattern was recovered. As in previous studies, only the secondary vortices could be observed, with microstreaming speeds of up to 0.00045 ms⁻¹ – less than half a millimeter per second. Although Tho et al.’s bubbles were about six times larger than those studied by Elder [13], frequencies and applied pressure amplitudes were similar, as were magnitudes of the measured velocities.

Fig. 7

Quadrupole microstreaming pattern for a bubble oscillating in translation only, showing the secondary vortex pattern. (a) Theoretical prediction for a bubble in an infinite domain (Reprinted from Longuet-Higgins [31] by courtesy of The Royal Society); (b) Experimental streak image around a bubble of radius 242 ± 10 μm attached to a microchamber wall and driven at 2.422 kHz, such that the bubble oscillated in translation only (From Tho et al. [54]. Reprinted under a CSIRO Licence to Publish)

Fig. 8

Dipole microstreaming pattern for a bubble oscillating volumetrically only, showing the secondary vortex pattern. (a) Theoretical prediction for a bubble in an infinite domain (Reproduced with permission from Wu and Du [61]. Copyright 1997, Acoustical Society of America. Longuet-Higgins [31] only plotted results for volumetric plus translational oscillation); (b) Experimental streak image around a bubble of radius 271 ± 4 μm attached to a microchamber wall and driven at 8.658 kHz, such that the bubble oscillated volumetrically only (From Tho et al. [54]. Reprinted under a CSIRO Licence to Publish)

Microstreaming flows around multiple bubbles were also measured by Tho et al. [54], with up to four nearby bubbles studied. Flows around pairs of bubbles could be quadrupole (Fig. 9), dipole, or elliptical depending on the mode of oscillation, whereas Wang and Chen [60] later predicted predominantly tangential flows around a bubble pair.

Fig. 9

Quadrupole microstreaming around a pair of bubbles. Left-hand bubble radius 212 μm, right-hand 208 μm, driven at 2.267 kHz. (a) Experimental streak image; (b) PIV data (From Tho [53], reprinted courtesy of P. Tho)

In 2010, Collis et al. claimed to be the first to simultaneously observe and measure the primary vortices as well as the secondary vortices in an acoustically driven microbubble (Fig. 10). The primary vortex visualization was achieved by observing tracer particles adsorbed onto the bubble surface. For a 135 μm bubble driven at 28 kHz and 12 kPa (a pressure amplitude later calibrated by Leong et al. [26]), they estimated that the primary vortex speed 0.013 ± 0.002 ms⁻¹ was two orders of magnitude higher than the secondary vortex speed. Although parameters were different from those studied at about the same time by Doinikov and Bouakaz [8], it is interesting that the primary vortex speed was also in the centimeters per second range predicted by Doinikov and Bouakaz [8].

Fig. 10

Putative identification of the primary microstreaming vortices at a microbubble surface. A 135 μm radius bubble excited at 28 kHz was imaged with varying exposure times to estimate the velocity of primary vortices, giving 0:013 ± 0:002 ms⁻¹. Line approximately indicates the bubble surface. In the regime applied, vortices were irregular. Exposure times were (a) 5884 μs; (b) 8322 μs; (c) 11,767 μs (From Collis et al. [4]. Reprinted with the authors’ permission)

Effects of Bubble Surface Properties on Microstreaming

As noted above, microstreaming is still observed when there is no gas-liquid interface of the bubble, rather a flexible “shell” material [15]. This can be expected, since all that is required for microstreaming is an acoustic boundary layer in which there is a large gradient in velocity. Thus, altering the properties of the surface might be expected to alter the velocity gradient in the boundary and thus the microstreaming. The effect of surfactants on microstreaming around a microbubble was studied by Leong et al. [26]. They carefully introduced different surfactant molecules such that the surface tension was maintained fixed while the molecular headgroup – the part of the molecule in the water – was altered in size. Microstreaming velocities were measured by micro-PIV. It was found that the surfactant molecule dodecyltrimethylammonium chloride (DTAC) caused significantly higher streaming velocities than other surfactants such as sodium dodecyl sulfate (SDS) or in plain water.

Bioeffects of Microstreaming

Cavitation microstreaming was noted to have a detrimental effect on cells in the 1950s, when “sonic destruction” of Paramecium cells was observed to be caused specifically by microstreaming flows [13]. This effect is distinct from the simple destruction of cells owing to the violence of cavitation collapse, which is utilized in commercial laboratory “cell disruptor” sonotrodes. Microstreaming from a microbubble was observed to disrupt an artificial vesicle – a model biological cell – by Marmottant and Hilgenfeldt [34].

Over the past decade, the relevance of microstreaming to beneficial ends has been proposed, particularly to the phenomena of sonoporation and sonothrombolysis (e.g., Manasseh et al. [33]).

It is important to understand the biological significance of the steady stresses due to microstreaming, compared to the transient stresses due to the first-order microbubble volumetric pulsation. The stresses due to the first-order linear or nonlinear bubble oscillation, which have been studied theoretically (e.g., Doinikov and Bouakaz [9]) in the sonoporation context, reverse every cycle. The primary oscillation cycles due to first-order ultrasound occur millions of times per second, whereas cell biological processes such as protein expression occur over timescales of minutes. Thus, the first-order ultrasound appears to be far too rapid to directly influence biological processes, unless, of course, the oscillatory stresses are high enough to cause permanent or semipermanent damage to the cell membrane. In contrast, the steady or quasi-steady stresses due to microstreaming are closer in timescale to the mechanical stresses known to influence cell processes [49].

The speed of flow in the primary vortices may have particular significance for the bioeffects of microstreaming. Collis et al. [3] proposed that the concept of surface divergence was relevant to sonoporation, sonothrombolysis, and kindred phenomena. The surface divergence metric, which can be extracted from micro-PIV measurements of microstreaming flows, could represent the extent to which a cell surface is being stretched or compressed by microstreaming flows. Such steady or at least quasi-steady stresses on cell membranes are known to cause, for example, stem cells to proliferate more rapidly and even differentiate into more specialized cell types [49].

Microstreaming in Micromixing and Microseparation

Mixing at microscale is a notorious problem. True mixing of two bodies of fluid containing different molecules is ultimately achieved by molecular diffusion. However, diffusion acts over short distances, thus taking a very long time in quiescent fluids to completely intermingle the two types of molecules. Fluid motion can stretch and fold the interface between the two fluids, thus allowing diffusion to do its work over a short distance. This stretching and folding is efficiently accomplished by turbulence, in which chaotic vortices at many scales create ever-longer boundaries between the two fluids and thus ever-shorter distances. Unfortunately, the absence of turbulence at microscale means that microscale stirring is necessary.

Microstreaming around a microbubble was demonstrated as a mechanism of micromixing in a microdevice by Liu et al. [30]. It was suggested by Manasseh et al. [33] that the micromixing due to microbubble-induced microstreaming could be responsible for the therapeutic benefits of ultrasound contrast agents, particularly in sonothrombolysis. Meanwhile, noting that what was needed for microstreaming was a large gradient in the sound field, which did not necessarily require a microbubble, Petkovic-Duran et al. [43] demonstrated effective micromixing within a drop with a small radius; by alternating “vortex” and “dipole” patterns of microstreaming, they also achieved a more efficient, “chaotic” micromixing. Subsequently, the micromixing due to drop-based microstreaming was able to improve the yield of RNA from a single cell by 100-fold [2]. The frequencies applied were so low, around 140–350 Hz, that they may have caused shape-mode resonances of the entire drop. However, similarly low frequencies were also shown to create microstreaming in a completely enclosed microchannel [41].

Microstreaming flows could also do the opposite of mixing; by creating a vortex, they can be used to trap particles [29, 44, 48].

Microstreamers in Cavitating Systems

It was noted by Blake in 1949 (as reported in Neppiras [36]) that cavitation microbubbles can form “streamers” in which the microbubbles appear to be mutually attracted into long, twisting ribbons or streams. Since microstreamers are composed of a large number of microbubbles, the scales of this motion are larger than the microstreaming around individual bubbles described in sections “Basic Observations of Microstreaming,” “Theoretical Analyses of Microstreaming,” “Experimental Quantifications of Microstreaming,” “Effects of Bubble Surface Properties on Microstreaming,” “Bioeffects of Microstreaming,” and “Microstreaming in Micromixing and Microseparation.” The streamer is thought to be formed by an attractive radiation force between bubbles, called the secondary Bjerknes force (e.g., Mettin et al. [16] and Jiao et al. [35]). However, we may speculate that microstreaming could contribute to maintaining the structure of the streamer. Highly ordered microstreamers can also be generated when microbubbles are created from ultrasonically excited pits [14].

Conclusions and Future Directions

The laws of fluid dynamics were introduced and applied to bubble acoustics, acoustic streaming, and cavitation microstreaming. The laws of conservation of mass and momentum and a constitutive law for the gas in the bubble, neglecting liquid compressibility, viscosity, surface tension, and vapor pressure, are sufficient to predict that a bubble will oscillate in volume with a natural frequency, called the Minnaert frequency. This natural frequency of bubble volumetric oscillation is inversely proportional to its size, and bubbles microns to tens of microns in size oscillate at ultrasonic frequencies. The full form of the Rayleigh-Plesset-Noltingk-Neppiras-Poritsky equation for bubble acoustics also requires knowledge of the fluid constitutive properties of viscosity, surface tension, and vapor pressure, but these significantly alter the Minnaert frequency only for bubbles microns in size. For bubbles undergoing cavitation collapse, as well as for an accurate estimation of losses due to sound radiation, liquid compressibility must be considered, leading to the Keller-Miksis equation. The final modifications attempt to include the dynamics of a thin shell encapsulating the bubble, modeling medical ultrasound contrast agents.

The momentum equation for fluid dynamics in the absence of viscosity and liquid compressibility, Euler’s equation, reveals the origin of acoustic streaming and microstreaming. These were shown to be due to the nonlinear term in Euler’s equation. This nonlinearity represents the attribute that distinguishes a fluid from a solid: its ability to accelerate purely by moving into a region where the fluid velocity is different. The nonlinear term is the fluid velocity multiplied by the gradient with distance of the fluid velocity. If the fluid velocity is primarily oscillatory, which is the case with all fluid waves, including sound waves, the primary oscillation averages to zero. However, the nonlinear term does not average to zero over time. Thus there is a driver for a net streaming motion that, unlike the primary oscillation, does not average to zero.

Because the nonlinear term is a velocity multiplied by a velocity gradient, there are two ways in which the nonlinear term could be significant. The velocity could be high, in other words the ultrasonic power could be high, and this leads to acoustic streaming. However, even if the power is not particularly high, if the velocity gradient is high, as would occur in the immediate vicinity of an oscillating bubble, the nonlinear term could again be significant. This leads to cavitation microstreaming.

Future research should consider the effect of microstreaming on the relative motion of multiple bubbles or particles and the effects of interfacial chemistry on microstreaming. Furthermore, the ability of microstreaming to create stresses on biological surfaces needs further exploration.