Shear Transformation Zones in Amorphous Polymers: Geometrical and Micromechanical Properties

Abstract

Glassy polymers are extensively used as high impact resistant, low density, and clear materials in industries. Due to the lack of the long-range order in the microstructures of glassy solids, plastic deformation is different from that in crystalline solids. Shear transformation zones (STZs) are believed to be the plasticity carriers in amorphous solids and defined as the localized atomic or molecular deformation patches induced by shear. Despite a great effort in characterizing these local disturbance regions in metallic glasses (MGs), there are still many unknowns relating to the microstructural and micromechanical characteristics of STZs in glassy polymers. This chapter is aimed at investigating the flow phenomenon in polycarbonate (PC) and poly(methyl methacrylate) (PMMA) as glassy polymers and obtaining the mechanical and geometrical characteristics of their STZs. To achieve this goal, the nanoindentation experiments are performed on samples with two different thermal histories: as-cast and annealed, and temperature and strain rate dependency of the yield stress of PC and PMMA are studied. Based on the experimental results, it is showed that the flow in PC and PMMA is a homogeneous phenomenon at tested temperatures and strain rates. The homogeneous flow theory is then applied to analyze the STZs quantitatively. The achieved results are discussed for their possible uniqueness or applicability to all glassy polymers in the context of amorphous plasticity.

Introduction

Over the past several years, many researches have been conducted on investigating the mechanical behavior of polymers, due to the extensive use of them for design and development of a variety of components and structures. In general, polymers are divided in two different categories: semicrystalline and amorphous (glassy) polymers. Amorphous polymers are composed of entangled and disordered long molecular chains, and there is no significant chain alignment in their intra- and intermolecular structures. Since the molecular structure of the polymeric glasses (PGs) is totally different from that of the crystalline solids, the plastic deformation process does not obey the crystal plasticity rules. Moreover, in contrast to many crystalline solids, the postyield behavior begins with a softening at the onset of the yielding in the stress-strain characteristic behavior of PGs, and then continues by a hardening which starts at the specific strain and ends up at the break point (Boyce et al. 1988; Stoclet et al. 2010). There is a large body of literature dealing with the process of yielding and characterizing the mechanism of nonlinear elastoplastic deformation in glassy polymers, which resulted in different physical and phenomenological models (Ree and Eyring 1955; Robertson 1966; Argon 1973; Boyce et al. 1988; Arruda et al. 1995; Anand and Gurtin 2003; Mulliken and Boyce 2006; Chen and Schweizer 2011; Voyiadjis and Samadi-Dooki 2016).

In the context of crystal plasticity, crystal dislocations are the principal carriers of plasticity, and their slips result in plastic deformation (Argon 2008). But, since there is no long-range coherence in atomic or molecular structure of glassy solids, there are no analogous mobile defects. Consequently, the flow and the mechanism of plastic response in the microstructural level are different from the crystalline solids. The ongoing widely recognized mechanism for the plastic response of all types of disordered solids, including metallic glasses, glassy polymers, and covalent glasses, is the cooperative localized rearrangement of molecular or atomic patches in small distinct regions which are called shear transformation zones (STZs) (Spaepen 1977; Falk 2007; Schuh et al. 2007; Pauly et al. 2010; Argon 2013). Especially, the presence of seperate plastic deformation units has been experimentally recognized in glassy polymers and attributed to the formation of STZs (Oleinik et al. 2007).

The STZs are isolated irreversible stress relaxation events which form around free volume sites with the thermal fluctuations assistance under the action of an applied shear stress (Argon 1979; Falk et al. 2005; Argon 2013). The absence of long-range coherence in glassy materials results in the sessile transformations which, once formed, do not expand by translational movements of their interfaces. Therefore, the plasticity mediated by the shear transformations is nucleation controlled (Argon 1993; Spathis and Kontou 2001). Since PGs are considered as homogeneous and isotropic materials, a localized disturbance in their bulk can be considered as an Eshelby inclusion problem (Eshelby 1957). The Eshelby leading-edge homogenization method, which has been extensively applied for solving a broad area of problems in inhomogeneous media (Tandon and Weng 1984; Shodja et al. 2003; Malekmotiei et al. 2013), is based on the strain compatibility of a medium containing no-elastic strains (Mura 1987). Using this method for amorphous solids, the STZ’s nucleation energy, which is necessary to relate the shear flow stress to the shear flow strain rate through an Arrhenius function, can be obtained (Argon 2013). Based on the Eshelby solution, the microgeometrical and micromechanical properties of the embedded STZ, i.e., size, shape, and transformation shear strain, are determining parameters for evaluating the STZ’s nucleation energy in glassy solids. Therefore, these characteristics have been extensively studied, especially for metallic glasses (Yang et al. 2007; Pan et al. 2008; Pan et al. 2009; Ju et al. 2011). It has been found that a single STZ in MGs possesses an avearge volume of less than 10 nm³ including ≤500 atoms (Pan et al. 2008), with the average nucleation energy of about 1.5 eV (Yu et al. 2010) and transformation shear strain of 0.07 (Argon 2013).

In contrast, the number of studies devoted to evaluate the STZs quantitatively in glassy polymers is limited. The plastic deformation units pertaining parameters of some glassy polymers have been obtaind by Argon and Bessonov (1977) based on double kink theory (Argon 1973). Later, in a molecular dynamics simulations, Mott et al. (1993) scrutinized the plastic deformation kinematics in amorphous atactic polypropylene, and found the transformation shear strain of about 0.015 in the spherical plastic flow units with the average 10 nm diameter. Moreover, Ho et al. (2003) also inquired the correlation between the STZ size scale and entanglement density by performing different compressive tests on mixable polystyrene-poly(2,6-dimethyl-1,4-phenylene oxide) (PS-PPO) blends at different mix ratios.

In this chapter, the nanoindentation technique is used to probe the flow nature of poly(methyl methacrylate) (PMMA) and polycarbonate (PC) as glassy polymers, and, consequently, their STZs’ micromechanical and geometrical characteristics are obtained. This chapter is organized as follows: in the first section, the experimental procedure is explained in two parts: sample preparation and the nanoindentation technique. In the second section, it is first shown that at tested temperatures and strain rates, the flow is homogeneous in these polymers. The homogeneous flow theory is then elaborated based on the Eshelby solution for nonelastic strain in an embedded inclusion in the representative volume element (RVE) and the Arrhenius function relating the shear flow stress to the shear flow strain rate. In the third section, the obtained results from the nanoindentation experiments on samples with two different thermal histories, as-cast and annealed, are presented. The characteristic properties of STZs including the nucleation energy barrier, size and shape of an STZ, and the shear activation volume are then obtained by utilizing the flow theory. Furthermore, the observed jump in the activation energy of the STZ is ascribed to the β-transition, and the energy barrier for this transition is found to be about 10% of the STZ nucleation energy. At the end, the concluding remarks are summarized in the last section.

Experimental Procedure

Sample Preparation

Commercially available 2.0- and 5.0-mm-thick sheets of amorphous poly (methyl methacrylate) (PMMA) and polycarbonate (PC), Goodfellow® catalogue #ME303020 and #L5433027, Cambridge, UK, are selected for this study, respectively. There is no preexisting molecular chain orientation in the sheets since they have been produced through the traditional method of cell cast. All the sheets are cut into 20 × 20 mm² samples small enough for handling the nanoindentation experiments. The residues of the protective film covering the sheets are then removed by washing them with 30% isopropyl alcohol (IPA), and thoroughly rinsing by distilled water. To eliminate any moisture caused by the washing process, all the specimens are stored in a desiccator for at least 10 days before any experiment. The glass transition temperature (T_g) of the samples are measured by means of a TA Instruments 2920 differential scanning calorimetry (DSC) device, which is operating under the nitrogen flow and by using standard aluminum pans. The DSC cycles are conducted at 10 °C min⁻¹ from ambient temperature to 200 and 250 °C for PMMA and PC, respectively. The calorimetric measurements reveal that the glass transition temperature of the PMMA and PC specimens are about 110 and 148 °C, respectively.

Half of the samples, prepared as described above, are subjected to the following thermal treatment to study the effect of thermal history on their STZs’ micromechanical and microstructural characteristics. Initially, they are annealed at 120 °C for 4 h in a vacuum oven. They are then cooled down at 10 °C h⁻¹ to room temperature. This thermal process is done in a vacuum oven to prevent the specimens’ surfaces oxidation (Hirata et al. 1985). An Agilent 5500 atomic force microscope (AFM) and a Wyko Optical Profiler are used to measure the surface roughness of the samples, which markedly has effects on the nanoindentation experiment results (Kim et al. 2007; Nagy et al. 2013). The average surface roughness (R_a) of the PMMA and PC samples are measured to be 0.372 ± 0.013 and 0.305 ± 0.021 nm, respectively. Accordingly, since the samples’ surfaces can be assumed as almost flat (Kim et al. 2007), no modification is needed for the obtained experimental results. Figure 1 represents a sample AFM scanning of the specimen surface. To indent the samples, they are mounted on aluminum stubs applying thermoresistant epoxy putty (Drummond™ Nu-Doh Epoxy Repair Compound Titanium Reinforced) for indentations at high temperature on hot-stage apparatus and super glue for indentations at ambient temperature.

Fig. 1

Sample of AFM scanning of the PMMA sample surface (Reprinted from Malekmotiei et al. 2015)

Nanoindentation Technique

The nanoindentation technique has been utilized to measure the mechanical properties of the materials including the elastic modulus, E, and the hardness, H. The indentation load-hold-unload cycles have been performed using an MTS Nanoindenter® XP equipped with a three-sided pyramidal Berkovich diamond tip. The analysis of the applied load-indentation depth curves is mainly based on the original formalism developed by Oliver and Pharr (1992, 2004) as described in the following.

The hardness is described as the mean contact pressure under the indenter as follows:

$$ H=\frac{P_{\mathrm{max}}}{A_c} $$

(1)

in which P _max is the peak indentation load and A _c is the projected area of the tip-sample contact at the maximum load. According to Eq. 1, one needs an accurate measurement of the projected contact area under the load to evaluate the hardness from indentation load-displacement data. For a perfectly sharp Berkovich indenter, the contact area which is a function of the contact depth, h _c, can be calculated as

$$ {A}_c=24.56{h_c}^2 $$

(2)

For a practical indenter, which is not ideally sharp, the contact area function is required to be obtained by tip calibration with introducing additional terms to the aforementioned second-order relation as follows:

$$ {A}_c=24.56{h_c}^2+{C}_1{h_c}^1+{C}_2{h_c}^{1/2}+{C}_3{h_c}^{1/4}+\dots +{C}_8{h_c}^{1/128} $$

(3)

where C ₁ through C ₈ are constant coefficients which account for deviations from ideal geometry due to the blunting of the tip, and determined by using the indentation results on a standard fused silica sample and curve fitting performed on the Analyst® software. To obtain the exact contact area, an accurate determination of the depth over which the test material makes contact with the indenter, h _c, is required. The contact depth is generally different from the total penetration depth, and is estimated using

$$ {h}_c=h-\varepsilon \frac{P}{S} $$

(4)

in which S is the measured elastic contact stiffness and ε is a constant which depends on the indenter geometry (for a Berkovich indenter ε = 0.75) (Oliver and Pharr 1992).

The elastic modulus of the sample, E, is calculated from Eq. 5 as follows:

$$ \frac{1}{E_r}=\frac{1-{\nu}^2}{E}+\frac{1-{\nu_i}^2}{E_i} $$

(5)

In this equation, E _i and v _i are the indenter elastic modulus and Poisson’s ratio, respectively, ν is the sample Poisson’s ratio, and E _r is the reduced elastic modulus. The reduced modulus which accounts for elastic deformation in both the indenter and the sample can be obtained from the following relation developed by Sneddon (1965)

$$ {E}_r=\frac{S}{2\beta}\sqrt{\frac{\uppi}{A_c}} $$

(6)

where β is a constant that depends on the indenter geometry and equals to 1.034 for the Berkovich tip.

Room-Temperature CSM Nanoindentation

The room temperature nanoindentation experiments are conducted by employing the continuous stiffness measurement (CSM) technique. The CSM method makes the continuous measurement of the mechanical properties of materials possible during the indentation loading segment from zero to the maximum indentation depth during a single test; this includes the measurement of the elastic contact stiffness at any point along the loading curve, and not just at the point of initial unload as in the basic mode (Pethica and Oliver 1988; Lucas et al. 1998; Li and Bhushan 2002; Hay et al. 2010). In this technique, a small sinusoidally varying load is superimposed on top of the primary loading signal that drives the motion of the indenter, and the resulting response of the system is analyzed by means of a frequency-specific amplifier. The displacement amplitude and the frequency of the superimposed oscillating force are set as 2 nm and 45 Hz, respectively, which are optimum values for the MTS nanoindentation® XP.

Utilizing the so-called CSM technique, the indentation load-hold-unload cycles are performed by keeping the loading rate divided by the load ratio $\left(\dot{P}/P\right)$ constant during the loading segment over the course of a single indentation test. In a deep indentation test, where the indentation size effect (ISE) is negligible (i.e., the hardness value is almost constant), the loading path follows a Hertzian contact relation as P=αh ^β, where P represents the indentation load, h is the indentation depth, α is a material dependent parameter, and β is a curve fitting parameter close to 2 for the Berkovich tip (Johnson 1987; Zhang et al. 2005). Accordingly, for a pyramidal indenter, the indentation strain rate $\dot{\varepsilon}_i$, which is defined as the descent rate of the indenter divided by its instantaneous depth, can be obtained by

$$ {\dot{\varepsilon}}_i=\frac{\dot{h}}{h}=\frac{1}{\beta}\frac{\dot{P}}{P} $$

(7)

Therefore, since the $\dot{P}/P$ ratio is remained constant during the CSM test, at deep enough indentations, the indentation strain rate approaches a constant value equal to $\frac{1}{2}\frac{\dot{P}}{P}$ (Lucas and Oliver 1999; Voyiadjis and Malekmotiei 2016). Moreover, the effective shear strain rate induced by the indentation is then related to the indentation strain rate as follows:

$$ \dot{\gamma}=\sqrt{3}C{\dot{\varepsilon}}_i=\frac{\sqrt{3}C}{\beta}\frac{\dot{P}}{P} $$

(8)

where C is a constant equal to 0.09 (Poisl et al. 1995; Schuh and Nieh 2003; Schuh et al. 2004).

After samples preparation and calibration of the indenter tip function, the tests are carried out by typical loading-hold-unloading sequences as follows: prior to any measurement, the tip is held on the top of the sample surface until its drift rate is stabilized at a rate below 0.05 nms⁻¹. The tip then starts to travel downward until it reaches the surface. Once the indenter tip comes into the contact with the sample surface, the loading segment begins with the constant value of $\dot{P}/P$ until a predefined maximum depth of about 10 μm; the load is then held at the maximum value for 10 s to account for the material creep behavior of the polymer surface; and finally, the unloading stage is carried out with the constant unloading rate until 10% of the maximum load is attained. Since one of the main purposes of this study is investigation of the strain rate dependency of the flow in PMMA and PC, a series of experiments are conducted at room temperature with the values of $\dot{P}/P$ varying from 0.001–0.2 and 0.002–0.4 s⁻¹ on annealed and as-cast PMMA and PC samples, respectively. A total of 25 indents are performed for each $\dot{P}/P$ value with a minimum distance of 150 μm between neighboring indents to prevent from interaction.

High-Temperature Nanoindentation Procedure

The MTS Nanoindenter® XP is equipped with temperature control system for elevated temperature nanoindentation tests. The system includes a hot stage, a coolant apparatus to transfer the extra heat to the outside of the instrument, and a heat shield to keep the indenter transducer apart from the heat source. The load control experiments are performed by using the basic method which is employed for high-temperature indentations. To make sure that there is no indentation size effect, and making the obtained date comparable to those of the CSM tests as well, the experiments are carried out with a maximum load of 300 mN. Loading rates of 4, 10, 50, 100, and 300 mNs⁻¹ for PMMA and 10, 100, and 300 mNs⁻¹ for PC, which are constant during the tests, are applied for temperatures varying from room temperature to 100 and 140 °C (slightly lower than the samples glass transition temperature) for PMMA and PC, respectively.

While the loading rate $\dot{P}$ is kept constant during the loading and unloading segments of the basic mode, evaluating the $\dot{P}/P$ ratio shows that it changes with 1/h ^β during the test since the load-depth (P-h) curve follows a Hertzian relation according to the statements in the preceding section. Therefore, the indentation strain rate ${\dot{\varepsilon}}_i$ varies as 1/h ^β during a test as well. Using Eqs. 7 and 8 to calculate the effective shear strain rate, an average value of $\dot{P}/P$ over the deep part of the indentation (5 μm in this study) is considered in each test. Accordingly, the corresponding effective shear strain rates for the load rates given above are 0.0014, 0.0035, 0.0175, 0.035, and 0.105 s⁻¹ for PMMA and 0.0035, 0.035, and 0.105 s⁻¹ for PC, respectively.

Applying a thermoresistant epoxy putty (Drummond™ Nu-Doh Epoxy Repair Compound Titanium Reinforced), the samples are mounted on the hot stage. Since polymer samples and the adhering thermoresistant have low thermal conductivity, the temperature of the sample surface can be considerably different from the set temperature. For precise evaluation, at the end of the tests, an Omega® SA1-K-SRTC thermocouple is attached to a sample surface to measure its temperature. The temperature is recorded by means of an Omega® HH74K handheld monitoring device coupled with the thermocouple. The discrepancy between the measured and set temperatures is significant for high temperatures. The number of indentation points for each set temperature and loading rate is reduced to 12 for the elevated temperature tests to minimize the risk of the contamination of the tip by the softened polymer at high temperatures; the minimum distance of the adjacent indents is also increased to 200 μm. Prior to performing the loading cycle, each sample is heated to the set temperature inside the indenter; and then it is left to equilibrate for 2 –3 h. On the onset of the test cycle, the tip is held at the distance of about 1 μm from the sample surface for about 10 min to adjust allowable thermal drift. This delayed contact is believed to help the tip to reach a thermal equilibrium with the sample.

Theory of Homogeneous Flow for Glassy Polymers

The inhomogeneous flow in amorphous solids is mediated by the formation of shear bands, whereas their homogeneous flow is triggered by the nucleation of STZs (Spaepen 1977). There are some important differences between inhomogeneous and homogenous flows of glassy solids. While the inhomogeneous flow is strain rate independent in a way that the flow stress does not change significantly with the strain rate, in a homogenous flow, the higher strain rate applied to the sample results in a considerable higher flow stress (Schuh and Nieh 2003; Schuh et al. 2007; Yang et al. 2007). Another significant distinction is the generation of multiple pop-ins in the load-displacement curves during the inhomogeneous flow which appears only in the nanoindentation experiments (Golovin et al. 2001; Zhang et al. 2005; Yang et al. 2007).

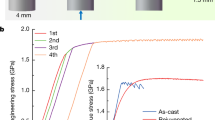
It has been shown that the flow behavior of metallic glasses is temperature dependent in a sense that there exists a transition from inhomogeneous to homogeneous flow at a certain temperature. The temperature at which the transition happens is also strain rate sensitive: the higher the applied strain rate, the higher the transition temperature (Yang et al. 2007). To investigate the flow nature in PMMA and PC as glassy polymers, the nanoindentation tests are performed on both as-cast and annealed samples. Figures 2 and 3 represent the variation of the hardness with temperature for as-cast and annealed PMMA and PC samples at different loading rates, respectively. Considering the direct relation between the hardness H and the flow stress σ _y as H=κσ _y with κ is Tabor’s factor, these figures show that the hardness (or flow stress) is greatly strain rate sensitive in a way that a higher hardness is obtained at a higher strain rate (loading rate) at a given temperature. This observed rate-dependent softening, which is attributed to the thermally activated nature of the flow, indicates that the flow of PMMA and PC at tested temperatures, which are below their glass transition temperatures T_g, is homogeneous. In addition, Figs. 4 and 5 show the load-displacement (P-h) curves of the samples at the loading rates of 10 and 300 mNs⁻¹ and different temperatures. All the curves are represented with the origin offset of 2 μm except the first one at room temperature. Since the curves are smooth with no pop-in events, Figs. 4 and 5 further confirm the homogenous nature of the flow in PMMA and PC at tested temperatures and strain rates.

Fig. 2

Variation of the PMMA hardness with temperature at different loading rates for (a) as-cast and (b) annealed samples. The data points at the load rate of 4 mNs⁻¹ and 361 K are not shown due to their high standard deviation values (Reprinted from Malekmotiei et al. 2015)

Fig. 3

Variation of the PC hardness with temperature at different loading rates for (a) as-cast and (b) annealed samples (Reprinted from Samadi-Dooki et al. 2016)

Fig. 4

Load-indentation depth curves for as-cast and annealed PMMA samples at different temperatures and the loading rates of (a) 10 mNs⁻¹, and (b) 300 mNs⁻¹ (Reprinted from Malekmotiei et al. 2015)

Fig. 5

The load-indentation depth curves for as-cast (solid line) and annealed (dashed line) PC samples at different temperatures and loading rates of (a) 10 mNs⁻¹ and (b) 300 mNs⁻¹ (Reprinted from Samadi-Dooki et al. 2016)

The flow in glassy solids is mediated by the irreversible local disturbances which form rearranged atomic (in MGs) or molecular (in PGs) clusters. These cooperative rearrangements result in isolated unit increments of shear, and are known as shear transformation zones (STZs). While in the homogeneous flow regime each volume element has contribution to the total plastic strain, the strain is localized in distinct shear bands in the inhomogeneous flow regime (Spaepen 1977). The thermally activated homogeneous flow in glassy polymers can be described based on the flow mechanism developed by Spaepen (1977) and Argon (1979). For the STZs-mediated homogeneous flow in glassy solids, the kinetics relation for the shear strain rate $\dot{\gamma}$ due to the applied shear stress τ is well expressed by an Arrhenius relation as follows (Spaepen 1977; Argon 1979):

$$ \dot{\gamma}={\dot{\gamma}}_0\exp \left(-\frac{\Delta {F}_0}{k_BT}\right)\sinh \left(\frac{\gamma^T\varOmega \tau}{2{k}_BT}\right) $$

(9)

where ${\dot{\gamma}}_0$ is the pre-exponential factor proportional to the attempt frequency, k _B is the Boltzmann constant, T is the absolute temperature, and ∆F ₀ is the nucleation energy of an STZ with the shear strain y ^T occurring in a region of volume Ω. The factor 2 in the denominator of the argument of the hyperbolic function is due to the reverse transformation probability (Spaepen 1977). To evaluate the nucleation energy of an STZ, this locally transformed region has been treated as an embedded volume with nonelastic strain the micromechanical field of which can be obtained by using the Eshelby inclusion model (Eshelby 1957). For the RVE shown in Fig.6, the free energy of the nucleation of a single STZ is given as follows:

$$ \Delta {F}_0=\left[\Xi \left(\nu \right)+\Psi \left(\nu \right){\beta}^2\right]\mu {\left({\gamma}^T\right)}^2\Omega $$

(10)

in which μ is the shear modulus, Ξ(ν) and Ψ(ν) are functions of the Poisson’s ratio ν, and pertain to the shear and dilatational components of the transformation strain tensor, respectively. The coefficient β is the dilatancy parameter and can be obtained from the pressure sensitivity of the flow. While $\Psi \left(\nu \right)=\frac{2\left(1+\nu \right)}{9\left(1-\nu \right)}$ is independent of the aspect ratio of the ellipsoid, Ξ(ν) is shape dependent (Mura 1987). The STZ’s characteristics in Eq. 9, such as shear strain, size, and activation energy, have been experimentally obtained for different metallic glasses (see Chap. 7 of Argon (2013) for details), but their numerical evaluation for PGs have been limited to some theoretical modeling and simulations (Mott et al. 1993; Argon 2013), and a few experimental studies (Argon and Bessonov 1977; Ho et al. 2003).

Fig. 6

Representative volume element (RVE) of polymer matrix containing a single shear transformation zone (STZ) (Reprinted from Malekmotiei et al. 2015)

Since γ ^T Ωτ ≫ 2k _B T for conventional PGs at temperatures below their glass transition, Eq. 9 can be rearranged as:

$$ \ln \dot{\gamma}=\frac{\gamma^T\Omega }{2{k}_BT}\tau +{C}_1 $$

(11)

where ${C}_1=\ln \frac{{\dot{\gamma}}_0}{2}-\frac{\Delta {F}_0}{k_BT}$ represents a temperature-dependent parameter. In Eq. 11, the material constant γ ^T Ω, which is proportional to the important characteristic parameter of glassy polymers known as shear activation volume V^* (Ward 1971), can be determined from the derivative of the natural logarithm of the strain rate $\left(\ln \dot{\gamma}\right)$ with respect to the shear flow stress (τ). Accordingly, considering the effect of hydrostatic pressure on the shear yield stress of polymers, the modified shear activation volume is obtained from Eq. 12 as follows (Ward 1971; Ho et al. 2003):

$$ {V}^{\ast }=\left(1-\alpha\beta \right){\gamma}^T\Omega =2{k}_BT\left(1-\alpha \beta \right)\frac{\partial\ \mathit{ln}\ \dot{\gamma}}{\partial \tau } $$

(12)

where β is the yield stress sensitivity to the pressure as defined before, and α is the loading condition constant which is between 0.6 and 0.7 for different compressive loading conditions (Ward 1971; Tervoort 1996). In fact, one can conclude from Eq.12 that the shear activation volume is a modified STZ volume with considering the dilatation effect. Furthermore, since γ ^T is assumed to be a universal constant for all glassy polymers and equals about 0.02 (Mott et al. 1993; Ho et al. 2003), the size of the single shear transformation zone Ω can be obtained. Rearranging Eq. 9 for a constant strain rate, the shear flow stress can be expressed as a linear function of temperature as follows:

$$ \tau =\Theta {C}_2+\frac{2\Delta {F}_0}{\gamma^T\Omega } $$

(13)

where ${C}_2=\frac{2{k}_B}{\gamma^T\Omega}\left(\ln \dot{\gamma}-\ln \frac{{\dot{\gamma}}_0}{2}\right)$ is representing a strain rate-dependent constant. As a result, the activation energy of an individual STZ, ∆F ₀, can be calculated from the linear interpolation of the variation of the flow shear stress with temperature by incorporating the obtained γ ^T Ω values. Knowing all the STZ’s parameters in Eq.10, one can obtain the numerical value of Ξ(ν) and, consequently, an approximation of the STZ’s shape in glassy polymers.

Results and Discussion

Calibrating the Nanoindentation Results

The instrumented-indentation testing (IIT) can be employed for the purpose of probing the mechanical properties including hardness and elastic modulus of very small volumes of materials including polymers, which both of them depend on the applied load on the sample surface and the contact area. In the nanoindentation experiments, the load is recorded with an nN scale precision while the contact area is calculated as a function of the tip geometry and contact depth. Since the tip in a practical indenter is not ideally sharp, the contact area function is required to be obtained by calibrating the tip with introducing a polynomial approximation (Oliver and Pharr 1992; Voyiadjis and Zhang 2015). Using the results of the indentation on standard fused silica sample, the tip areal function is calibrated to obtain reliable results.

It is also worth noting that the material pile-up around the penetrating tip can significantly alter the contact area and affect the measured mechanical properties of the material especially at shallow depths of the indentation. Using the optical profiler, the pile-up values are precisely measured for the indentation on PMMA and PC samples. As can be seen in Fig. 7, which shows a sample of pile-up measurement on PC specimen, the pile-up is highly unsymmetrical with the maximum values around the pyramidal tip faces. The maximum pile-up is measured to be about 400 nm, which in comparison with the maximum indentation depth of 10 μm is very small. For that reason, the pile-up effect is neglected in the nanoindentation measurements.

Fig. 7

A sample of the indentation pile-up measurement on PC specimen using Wyko Optical Profiler (Reprinted from Samadi-Dooki et al. 2016)

Another important observation during the nanoindentation experiments is the increment of the hardness values at shallow indentation depths which is known as indentation size effect (ISE) (Briscoe et al. 1998; Voyiadjis and Zhang 2015). To prevent the ISE in the current study, the CSM indentation results are first evaluated to find the indentation depth beyond which the obtained hardness reaches the stable value. The variation of hardness versus the indentation depth for both annealed and as-cast PMMA and PC samples are presented in Figs. 8 and 9, respectively. As these figures show, the profound ISE is completely eliminated for the indentation depth beyond 2 and 4 μm for PMMA and PC samples, respectively. Accordingly, the hardness values are averaged over the indentation depth beyond 5 μm where the indentation size effect is absent. The elevated temperature tests are performed by using the basic mode in which the hardness value is only reported at the maximum indentation depth. While the maximum indentation depth is the input for the CSM technique, the maximum load is the input in the basic mode. As mentioned before, to avoid the indentation size effect, and also make the obtained date comparable to those of the CSM tests, the high temperature experiments are carried out with a maximum load of 300 mN, which corresponds to the maximum indentation depth of about 10 μm. Furthermore, since the ISE reduces at elevated temperatures (Voyiadjis et al. 2011), it is assured that the obtained hardness results are within the stable region.

Fig. 8

Variation of the hardness versus the indentation depth for three different $\dot{P}/P$ values for (a) as-cast and (b) annealed PMMA samples. The legend numbers represent the $\dot{P}/P$ values (Reprinted from Malekmotiei et al. 2015)

Fig. 9

Variation of the hardness versus the indentation depth for three different $\dot{P}/P$ values for (a) as-cast and (b) annealed PC samples. The legend numbers represent the $\dot{P}/P$ values (Reprinted from Samadi-Dooki et al. 2016)

Shear Activation Volume

In addition to the hardness, the elastic modulus is another mechanical property of the material which is continuously recorded during the loading segment of the CSM nanoindentation as a function of displacement. Figures 10 and 11 represent the variation of the material elastic modulus versus the indentation depth for some selected $\dot{P}/P$ values for PMMA and PC samples, respectively. In comparison to the hardness, the elastic modulus is almost constant for the indentation depth beyond about 100 and 150 nm for both as-cast and annealed PMMA and PC samples, respectively. More importantly, while the hardness values significantly change with the strain rate (see Figs. 8 and 9), the elastic modulus does not show any significant strain rate sensitivity.

Fig. 10

Variation of the elastic modulus versus the indentation depth for three different $\dot{P}/P$ values for (a) as-cast and (b) annealed PMMA samples. The legend numbers represent the $\dot{P}/P$ values (Reprinted from Malekmotiei et al. 2015)

Fig. 11

Variation of the elastic modulus versus the indentation depth for three different $\dot{P}/P$ values for (a) as-cast and (b) annealed PC samples. The legend numbers represent the $\dot{P}/P$ values (Reprinted from Samadi-Dooki et al. 2016)

Using the Tabor’s factor, the hardness values H obtained from the nanoindentation experiments can be converted to the yield stress σ _y of the material as follows:

$$ H={\kappa \sigma}_y $$

(14)

in which κ is Tabor’s factor which is approximately 3.3 for amorphous polymers at high indentation strains (Prasad et al. 2009). Additionally, since the shear flow stress is about half of the yield stress in plane stress condition for monotonic loading (Yang et al. 2007), the ratio of the hardness to the shear flow stress is about 6.6. Figures 12 and 13 illustrate the shear flow stress-shear strain rate data points for the as-cast and annealed PMMA and PC samples measured by CSM method at room temperature, respectively. The obtained results for PC are in good agreement with the ones obtained by Bauwens-Crowet et al. (1969) at 21.5 °C. As it is expected, the annealed samples have slightly bigger shear flow stresses compared to the as-cast ones at the same shear strain rate (Jancar et al. 2013). The outstanding feature of Fig. 12 is the existence of a significant transition at a certain value of the strain rate beyond which the strain rate sensitivity of the shear flow stress increases. This phenomenon is believed to be a result of strain rate shift of the β-relaxation process in the storage modulus of the PMMA, which is related to the restriction of the ester side group rotations at high strain rates, besides the intermolecular and local back bone motion restrictions (Calleja et al. 1994; Mulliken and Boyce 2006; Argon 2013). As obviously shown in Fig. 12, the transition shear strain rate is approximately 0.005 s⁻¹ for both as-cast and annealed PMMA samples. Following the descriptions presented in Mulliken and Boyce (2006), the flow stress regimes below and above the transition shear strain rate might be referred to as α and β regimes, respectively. However, it is noteworthy to mention that since the room temperature β-transition strain rate of PC has been previously detected to be about 10² s⁻¹ (Mulliken and Boyce 2006), which is beyond the strain rates that can be applied in nanoindentation experiments, no considerable jump is observed in Fig. 13 for the range of strain rates in this study.

Fig. 12

Variation of the shear flow stress with the shear strain rate for both as-cast and annealed PMMA samples (Reprinted from Malekmotiei et al. 2015)

Fig. 13

Variation of the shear flow stress with the shear strain rate for both as-cast and annealed PC samples (Reprinted from Samadi-Dooki et al. 2016)

Based on Eqs. 11 and 12, the shear activation volume V ^* for an amorphous polymer can be obtained by linear interpolation of the $\tau -\ln \dot{\gamma}$ curve. In these figures, the slopes of the semilogarithmic stress-strain rate plots are almost the same for samples with different thermal history, which suggest that the shear activation volume and, therefore, the size of a single STZ are almost independent of the thermal history of the samples. Incorporating Eq. 11 and the data represented on Figs. 12 and 13, the factor γ ^T Ω for as-cast and annealed samples is obtained about 3.66 and 3.69 nm³ for PMMA, and 8.94 and 9.14 nm³ for PC, respectively. Accordingly, by assuming α = 0.65, β = 0.204 for PMMA (Ward 1971) and 0.27 for PC (Rittel and Dorogoy 2008), V ^* is found to be 3.17 and 3.20 nm³ in α regime for PMMA, and 7.37 and 7.54 nm³ for PC, for as-cast and annealed samples, respectively. The obtained values of shear activation volume are in consonance with the molecular dynamics simulation results (Argon 2013). As results show, the shear activation volume for samples with different thermal histories is almost the same, and this small discrepancy might be due to the short time of annealing in this study (4 h). Since it has been shown that the flow stress of glassy polymers increases logarithmically with the annealing time at temperatures below their glass transitions (Hutchinson et al. 1999), a more profound difference might be expected between the shear flow stress results of the as-cast and annealed samples in Figs. 12 and 13 for longer annealing time. However, the increased difference may or may not result in a considerable difference in the shear activation volume since it depends on the slope of the $\tau -\ln \dot{\gamma}$ plots and not the shear flow stress solely.

STZ’s Activation Energy

In light of Eq. 13, linear interpolation of the flow stress as a function of the temperature τ−T can be used to obtain the STZ’s activation energy. Figures 14 and 15 represent the variance of the shear flow stress of PMMA and PC with temperature, respectively, for different strain rates which is well interpolated with linear functions at each loading rate. Assuming the parameter γ ^T Ω does not vary with temperature, the STZ’s activation energy for both as-cast and annealed samples can be calculated at different shear strain rates as shown in Fig. 16 for PMMA. One of the most important features of this figure is the existence of jump in the activation energy at the strain rate range of 0.0035–0.0175 s⁻¹ which is consistent with the β-transition strain rate obtained from room-temperature CSM nanoindentation. Therefore, this jump might be referred to as the β-transition activation energy. Although the discrepancy in the activation energy for the annealed and as-cast samples is small for strain rates above the β-transition strain rate, the difference is profound for strain rates below this transition. Since the annealed PMMA sample is expected to have more ordered chains in comparison to the as-cast one, the slip and rotation of these chains are more restricted in this sample; consequently, the STZ’s activation energy increases. In contrast, beyond the β-transition strain rate, the rapid loading does not allow the chains to rotate or slip smoothly which puts the annealed and as-cast samples in the same deformation condition, and as a result, the activation energy of STZs for high strain rates is approximately identical for samples with different thermal histories.

Fig. 14

Variation of the shear flow stress with temperature at different loading rates for (a) as-cast and (b) annealed PMMA samples (Reprinted from Malekmotiei et al. 2015)

Fig. 15

Variation of the shear flow stress with temperature at different loading rates for (a) as-cast and (b) annealed PC samples (Reprinted from Samadi-Dooki et al. 2016)

Fig. 16

STZ’s activation energy for both as-cast and annealed PMMA samples at different shear strain rates (Reprinted from Malekmotiei et al. 2015)

Another important feature of Fig. 16 is that the β-transition activation energy is much bigger for the as-cast PMMA than the annealed one (almost threetimes). Furthermore, the β-transition energy is about one order of magnitude smaller than the thermal activation energy of an STZ for PMMA, which is in agreement with the findings of Barral et al. (1994) who found almost the same ratio for a system containing a diglycidyl ether of bisphenol A (DGEBA) and 1,3-bisaminomethylcyclohexane (1,3-BAC). In comparison, the β-transition activation energy has been obtained to be almost equal to the STZ’s activation energy in the metallic glasses (Yu et al. 2010).

As defined in Eq. 10, the Helmholtz free energy also depends on the shear modulus μ of the material which itself is temperature dependent. Since the shear modulus of the PMMA does not change considerably for temperatures below about 100 K (Gall and McCrum 1961), Eq. 13 is still valid, and ∆F ₀ might be referred to as activation energy at 0–100 K. Using the elastic modulus data for different temperatures, obtained by basic method nanoindentation, and the relation between the elastic modulus and shear modulus as: $\mu =\frac{E}{2\left(1+\nu \right)}$, the variation of the shear modulus with temperature for both as-cast and annealed PMMA samples at two different strain rates are represented in Fig. 17. Assuming the variation to remain linear for temperatures down to 100 K, and constant for temperatures below 100 K which is a valid assumption based on the experiments of Gall and McCrum (1961), the variation of the STZ’s activation energy with temperature can be obtained as shown in Fig. 18. It is also noticeable that the STZ’s activation energy is around 0.6 eV at room temperature which is about one-third of that for metallic glasses (Yu et al. 2010).

Fig. 17

Variation of the shear modulus with temperature for as-cast and annealed PMMA samples at two different loading rates (Reprinted from Malekmotiei et al. 2015)

Fig. 18

Variation of the STZ’s activation energy with temperature for as-cast and annealed PMMA samples at two different loading rates (Reprinted from Malekmotiei et al. 2015)

Doing the same calculations on the obtained results for PC samples, the activation energy of a single STZ is presented in Table 1. As expected, the activation energy is slightly bigger for the annealed samples, and is almost strain rate insensitive which is in agreement with continuum mechanics principles. Since the obtained activation energies are calculated using the extrapolation of the τ−T values to the 0 K, they should be referred to as the zero Kelvin STZ’s activation energies, and are shown by ∆F ₀ hereafter. It should be mentioned that since the room temperature β-transition strain rate of PC is beyond the strain rates in this study, the β-transition activation energy barrier cannot be captured for PC samples.

Table 1 Characteristic properties of the STZs in PC for samples with different thermal histories (Reprinted from Samadi-Dooki et al. 2016)

STZ’s Geometry

Incorporating Eqs. 10 and 13, the intercept of τ−T linear interpolation with τ axis is equal to $\frac{2\Delta {F}_0}{\gamma^T\Omega }=2\left[\Xi \left(\nu \right)+\Psi \left(\nu \right){\beta}^2\right]{\mu \gamma}^T$. As it is mentioned before, $\Psi \left(\nu \right)=\frac{2\left(1+\nu \right)}{9\left(1-\nu \right)}$ does not vary with the STZ shape, and is about 0.5 and 0.48 for PMMA and PC, respectively (considering the Poisson’s ratio of 0.38 for PMMA and 0.37 for PC). However, Ξ(ν) is determined by the shape of the STZ which varies between $\frac{7-5\nu }{30\left(1-\nu \right)}=0.27$ and 0.5 pertaining to the spherical and flat ellipsoidal shape of STZ, respectively (Mura 1987). Taking μ ₀ = 3.1 GPa from Fig. 17 and β = 0.204, the value of γ ^T varies between 0.03 and 0.05 for PMMA, with the lower and upper bonds pertaining to the flat ellipsoidal and spherical transformation zones, respectively. Based on the molecular dynamics simulation (Mott et al. 1993), the shear strain (γ^T) of 0.05 is a large value for polymeric glasses; therefore, the shape of the transformation zone is more likely to be a flat ellipsoid for PMMA instead of a sphere. Using the previously obtained factor γ ^T Ω and assuming γ ^T = 0.03, the volume of an individual plastic deformation unit Ω, which is almost the same for as-cast and annealed PMMA samples, is obtained about 123 nm³ which is at least one order of magnitude bigger than that of the metallic glasses (Pan et al. 2008; Yu et al. 2010). Assuming the PMMA monomers as cylinders with the length of 1.55 Å and radius of 2.85 Å (Argon and Bessonov 1977), the single STZ is found to contain about 3000 monomers.

In a same way, using μ ₀ = 2.4 GPa (Argon 2013) and β = 0.27 (Rittel and Dorogoy 2008), γ ^T is obtained equal to 0.035 for the spherical and about 0.02 for the flat ellipsoidal shapes of the STZ for both as-cast and annealed PC samples. Due to the aforementioned reason, it can be inferred that the STZs in PC are regions with the shapes close to flat ellipsoids rather than spheres. In addition, the volume of an STZ, Ω, is calculated to be about 470 and 488 nm³ which has in average 5,600 and 5,800 idealized cylindrical shape monomers with 2.8 Å length and 3.09 Å radius (Argon and Bessonov 1977) for the as-cast and annealed PC samples, respectively. All the obtained characteristic properties of a single STZ in PC samples are presented in Table 1.

Concluding Remarks

In summary, nanoindentation experiments conducted on as-cast and annealed specimens are studied to explore the temperature and strain rate sensitivity of the flow in poly(methyl methacrylate) (PMMA) and polycarbonate (PC) as amorphous polymers. Showing that the flow is homogeneous in these polymers at temperatures below their glass transitions and incorporating a homogeneous flow theory, geometrical and micromechanical characteristics of the shear transformation zones (STZs), as main carriers of plasticity in amorphous polymers, have been investigated in the molecular level. Since the experimental studies on the STZs in glassy polymers is less addressed in the literature in comparison to the metallic glasses, the nanoindentation technique is employed as an accurate, repeatable, and nondestructive method to answer some of the current open questions in this area. The findings suggest that the STZs are flat ellipsoidal regions with the volume of about 123 and 480 nm³ and the transformation shear strain of about 0.03 and 0.02 in PMMA and PC samples, respectively. In addition, the nucleation energy of the shear transportation zones for both samples as well as the β-transition energy barrier for PMMA samples has been obtained. The procedure used for obtaining the β-transition energy based on the nanoindentation technique is an innovative approach which can be used for other glassy solids. The experimentally evaluated parameters produce unequivocal values as inputs for further theoretical and numerical investigations of yielding and plasticity in polymeric glasses.

In light of the obtained results for PMMA and PC, the following remarks are made:

• 1. The STZ’s nucleation energy in amorphous polymers is about 1 eV which is not considerably smaller than that of the metallic glasses. Since the nucleation energy of an STZ directly depends on the material shear modulus, this energy is expected to be much higher for MGs due to their considerably bigger shear modulus. However, the nucleation energy also depends on the STZ size. Therefore, the bigger size of the STZs in PGs compared to MGs compensates for their shear modulus discrepancy, and levels the activation energy in two materials.

• 2. The transformation shear strain γ ^T is slightly bigger than what is believed to be the universal value for PGs. The transformation shear strain has been considered to be about 0.015 in all types of glassy polymers (Argon 2013); however, the current study suggests that this parameter is unique to a particular polymer, and is about 0.02 in PC and 0.03 in PMMA.

• 3. While this work suggests that the shear transformation zones are formed in the regions with the shape close to the flat ellipsoid in PMMA and PC, the STZ shape is assumed to be spherical in all types of glassy solids (Ho et al. 2003; Argon 2013; Li et al. 2013).

• 4. Since all experiments are performed at temperatures beyond 0.6 Tg, the observed homogeneous flow is in accordance with the amorphous flow theory at elevated temperatures (Argon 1979, 2013). With the current nanoindentation technology, it seems impossible to perform experiments at temperatures below 0.6 Tg for available PGs (−43 and −20 °C for PMMA and PC, respectively). Undoubtedly, experiments at temperatures below 0.6 Tg would result in a better understanding of the flow nature in glassy polymers at a wider temperature range.

• 5. The obtained results for the STZs shape are based on the acceptable values of transformation shear strain in polymers which is considerably smaller than that in metallic glasses. A precise evaluation requires the STZs direct observation, which is not possible and convenient since STZs are local transition events rather than being actual defects like dislocations, or their indirect observation via localized stress field monitoring, which to the best of the authors’ knowledge has not been reported yet. The only indirect experimental measurement of the STZ’s size scale is one by Liu et al. (2011) in which the 2.5 nm size of the viscoelastic heterogeneities observed by transmission electron microscopy (TEM) has been related to the size of the STZ in a metallic glass.