Size Effects and Material Length Scales in Nanoindentation for Metals

Abstract

In nanoindentation experiments at submicron indentation depths, the hardness decreases with the increasing indentation depth. This phenomenon is termed as the indentation size effect. In order to predict the indentation size effect, the classical continuum needs to be enhanced with the strain gradient plasticity theory. The strain gradient plasticity theory provides a nonlocal term in addition to the classical theory. A material length scale parameter is required to be incorporated into the constitutive expression in order to characterize the size effects in different materials. By comparing the model of hardness as a function of the indentation depth with the nanoindentation experimental results, the length scale can be determined. Recent nanoindentation experiments on polycrystalline metals have shown an additional hardening segment in the hardness curves instead of the solely decreasing hardness as a function of the indentation depth. It is believed that the accumulation of dislocations near the grain boundaries during nanoindentation causes the additional increase in hardness. In order to isolate the influence of the grain boundary, bicrystal metals are tested near the grain boundary at different distances. The results show that the hardness increases with the decreasing distance between the indenter and the grain boundary, providing a new type of size effect. The length scales at different distances are determined using the modified model of hardness and the nanoindentation experimental results on bicrystal metals.

Introduction

It has been found in experiments at the microscopic scale that the mechanical response increases as the size of the specimen decreases. The phenomenon is termed as the size effect. Size effects have been reported in tests of metals in small scales such as microbending, microtorsion, and bulge tests (Fleck and Hutchinson 1997; Stolken and Evans 1998; Chen et al. 2007; Xiang and Vlassak 2005). It is believed that the size effects are attributed to nonuniform deformation in the small scale during the tests (Nye 1953). Geometrically necessary dislocations (GNDs) are generated in order to accommodate the deformation. The GNDs act as barriers of the generation of the statistically stored dislocations (SSDs), resulting in the increase of the mechanical response (De Guzman et al. 1993; Stelmashenko et al. 1993; Fleck et al. 1994; Ma and Clarke 1995). The classical continuum theory is only able to predict the macroscopic and therefore not capable in capturing the changes of mechanical responses. A nonlocal term is required in addition to the classical theory. In the study of the plastic deformation, the strain gradient plasticity theory is applied by adding a strain gradient term into the classical expression (Aifantis 1992; Zbib and Aifantis 1998). In order to characterize the influence of the strain gradient, a length scale parameter is required to be incorporated into the expression of the strain gradient plasticity theory. The length scale is an intrinsic parameter and each material has its unique length scale. Therefore, it becomes of great importance to determine the material intrinsic length scale. With the length scale determined, the strain gradient plasticity theory is able to predict the mechanical behaviors in both microscopic and macroscopic scales, bridging the gap between large and small scales.

When using the strain gradient plasticity theory to derive the expression of the length scales, material parameters are needed in order to represent the behavior for different materials. In order to determine the length scale for a specific material, the materials need to be determined from experimental results. Nanoindentation experiments are believed to be the most effective technique to determine the material length scales (Begley and Hutchinson 1998). In nanoindentation at small depth, the hardness increases with the decreasing indentation depth (McElhaney et al. 1998). The size effect encountered in nanoindentation is referred to the indentation size effect. With the use of the conical or Berkovich indenter, the indentation is said to be self-similar. The GND density can be calculated for a self-similar indent from the geometry of the indenter (Nix and Gao 1998). The hardness can be mapped from the stress-strain relation using Tabor’s factor in macroscopic scale (Tabor 1951). In microscopic scales, the hardness is related to the dislocation density according to Taylor’s hardening law. The hardness expression needs to incorporate the expression of the length scale in order to predict the indentation size effect. By comparing the experiments and the expression of hardness, the material parameters in the expression of the length scale can be determined.

More recent nanoindentation experiments in polycrystalline materials have shown that instead of the solely decreasing hardness with the increasing indentation depth, there is a hardening-softening phenomenon observed (Yang and Vehoff 2007; Voyiadjis and Peters 2010). The additional increase in hardness is believed to be due to the interaction between the dislocations generated by the penetration of the indenter and the grain boundaries . As there is difficulty for dislocations to transfer across the grain boundary, the dislocations accumulate near the grain boundaries. The local dislocation density increases due to the accumulation of dislocations, resulting in the additional increase in hardness. Once the dislocations start to move across the grain boundary at certain point, the dislocation density starts to decrease, which explains the softening effect following the hardening. In order to characterize the grain boundary effect as well the temperature and strain rate dependency of the length scale, a model considering the temperature and strain rate dependency of indentation size effect (TRISE) is developed (Voyiadjis et al. 2011). The length scale is written as a function of the temperature, plastic strain rate, and the grain size. By comparing the TRISE model with nanoindentation experiments at different temperatures, plastic strain rates, and grain sizes, the length scales can be determined.

In order to confirm the contribution of grain boundaries to the hardening-softening phenomenon, the investigation of the grain boundary is isolated through bicrystalline materials, where there is only one grain boundary. Nanoindentation experiments are conducted near the grain boundary at different distances between the indenter and the grain boundary (Voyiadjis and Zhang 2015; Zhang and Voyiadjis 2016). Single crystal behavior is observed for indents made with large distances to the grain boundary, without showing the additional hardening. Only the indents in close proximity of the grain boundary show the hardening-softening effect and there is a stronger hardening effect when the distance is smaller, providing a new type of size effect. The influence of the grain boundary on the hardness during nanoindentation is thus confirmed by experiments. The TRISE model is rewritten by replacing the grain size with the distance between the grain boundary and the indenter. The length scales of bicrystalline materials can be determined through the comparisons between the developed TRISE model and the nanoindentation experiments in order to characterize the size effect regarding the grain boundary.

In this chapter, the dependencies of temperature, plastic strain rate, grain size, and the distance between the indents and the grain boundary are addressed during nanoindentation experiments on single crystal, polycrystalline, and bicrystalline materials. The TRISE model is developed and applied in order to predict the hardness as a function of the indentation depth. The equivalent plastic strain as a function of the indentation depth during nanoindentation is determined through the finite element method. ABAQUS/Explicit software is used in order to simulate the indentation problem. The materials tested are body-centered cubic (BCC) and face-centered cubic (FCC) materials. In order to show the distinct behaviors between FCC and BCC materials during the simulation, user material subroutines VUMAT are incorporated for BCC and FCC metals, respectively. The length scales are determined through the comparison between the nanoindentation experiments and the developed TRISE models.

Nonlocal Theory

According to the nonlocal theory , the material properties at a given material point are not only dependent on their local counterparts but also depend on the state of the neighboring space. While the classical continuum theory only provides the predictions of the local point, the nonlocal theory enhances the classical theory by giving a nonlocal gradient term. The nonlocal term is taken as the characterization of the interactions from the neighboring space. The nonlocal expression was incorporated through an integral form for the elastic models of materials (Kroner 1967; Eringen and Edelen 1972). In the integral format, the nonlocal measure $\overline{A}$ at a given material point x is expressed through the weighted average of its local counterpart A over the surrounding volume V within a small distance d from the point x as follows:

$$ \overline{A}=\frac{1}{V}\underset{V}{\int}w(d)A\left(x+d\right)dV $$

(1)

where 𝒘(d) is a weight function that decays gradually with the distance d. It should be noted that there is a limit of the distance d, which is the internal characteristic length that shows the range of the influence of the nonlocal term.

The integration can be solved analytically for the elasticity problems. However, it is not practical to solve the integration for more complicated plasticity problems. Therefore, the integral expression needs to be simplified. The local counterpart 𝑨 in the integral can be approximated using the Taylor’s series expansion at d = 0 as follows (Muhlhaus and Aifantis 1991; Vardoulakis and Aifantis 1991):

$$ A\left(x+d\right)=A(x)+\nabla A\left(x\right)d+\frac{1}{2!}{\nabla}^2A(x){d}^2+\frac{1}{3!}{\nabla}^3A(x){d}^3+\dots $$

(2)

where ∇ⁱ denotes the ith order of the gradient operator. The expression can be further simplified considering only the isotropic behaviors. Therefore, the odd terms vanish in Eq. 2 and the nonlocal expression can be rewritten as follows:

$$ \overline{A}=\frac{1}{V}\underset{V}{\int }w(d)A(x)dV+\frac{1}{2!V}\underset{V}{\int }w(d){\nabla}^2A(x){d}^2dV $$

(3)

Rewriting Eq. 3 as a partial differential equation yields the following expression:

$$ \overline{A}=A+\left(\frac{1}{2!V}\underset{V}{\int }w(d){d}^2\mathrm{dV}\right){\nabla}^2p $$

(4)

with

$$ \frac{1}{V}\underset{V}{\int }w(d)\mathrm{dV}=1 $$

(5)

Therefore, the simplified nonlocal expression can be eventually expressed as follows:

$$ \overline{A}=A+{l}^2{\nabla}^2A $$

(6)

In Eq. 6, the second-order gradient term is incorporated in addition to the original local counterpart. A length scale parameter 𝑙 is used in order to weigh the gradient term, reflecting the characteristic length of the influence of the gradient.

Considering the nonuniform deformation of materials in micro- and nanoscales, the strain is usually used in order to characterize the material behaviors. By writing the nonlocal expression using the expression of strain and strain gradient, the strain gradient plasticity (SGP) theory can be written in the format of Eq. 6 as follows:

$$ \overline{p}=p+{l}^2{\eta}^2 $$

(7a)

where $\overline{p}$ is the total accumulated plastic strain with its local counterpart 𝑝 and the gradient term 𝜂, and 𝑙 is the material length scale that characterizes the influence of the strain gradient.

Another approach was developed through a phenomenological theory of strain gradient plasticity based on gradients of rotation, which fits the framework of the couple stress theory (Fleck and Hutchinson 1993). By assuming that the strain energy density is only dependent on the second von Mises invariant of strain, the strain gradient plasticity theory can be expressed based on that the strain energy density is only dependent on the overall effective strain as follows:

$$ \overline{p}=\sqrt{p^2+{l}^2{\eta}^2} $$

(7b)

A more general expression (Voyiadjis and Abu Al-Rub 2005) for the strain gradient plasticity theory considering the expressions in Eqs. 6, 7a, and 7b was later proposed as follows:

$$ \overline{p}={\left[{p}^{\boldsymbol{\gamma}}+{\left( l\eta \right)}^{\boldsymbol{\gamma}}\right]}^{1/\boldsymbol{\gamma}} $$

(8)

where 𝛾 is a fitting parameter.

Physically Based Material Length Scale

As shown in Eq. 8, the total accumulated plastic strain can be determined through its local counterpart and the strain gradient term. It becomes of great importance in the determination of the material length scale parameter, as it captures the intrinsic gradient effects for different materials. From the continuum theory, the flow stress can be written through the plastic strain given in Eq. 8 as follows:

$$ \sigma =k{\left[{p}^{\boldsymbol{\gamma}}+{\left( l\eta \right)}^{\boldsymbol{\gamma}}\right]}^{1/\mathrm{m}\upgamma} $$

(9)

where 𝑚 and 𝑘 are material constants. Equation 8 is capable to predict the constitutive relations in both macroscopic scale through the local counterpart and microscopic scale through the coupling between the local and gradient terms. Therefore, by determining the length scale parameter, the strain gradient enhanced classical continuum theory is able to bridge the gap between large and small scales.

In Eq. 9, the local term p is related to the SSDs as it represents the uniform deformation at macroscopic scales. The plastic shear strain 𝛾^𝑝 can be defined as a function of SSD density ρ_S as follows (Bammann and Aifantis 1982):

$$ {\gamma}^p={b}_S{L}_S{\rho}_S $$

(10)

where 𝑏_𝑆 is the magnitude of Burgers vector of SSDs and 𝐿_𝑆 is the mean space between SSDs. The local plastic strain ${\varepsilon}_{\mathrm{ij}}^p$ can then be determined from 𝛾^𝑝 using Schmid orientation tensor 𝑀_𝑖𝑗 as follows:

$$ {\varepsilon}_{\mathrm{ij}}^p={\gamma}^p{M}_{\mathrm{ij}} $$

(11)

where

$$ p=\sqrt{2{\varepsilon}_{\mathrm{ij}}^p{\varepsilon}_{\mathrm{ij}}^p/3} $$

(12)

When relating the plastic strain between macroscopic and microscopic scales, the Schmid orientation factor which is an average form of the Schmid tensor is always used (Bammann and Aifantis 1987; Dorgan and Voyiadjis 2003). With that being said, the local plastic strain can be expresses as follows:

$$ p={b}_S{L}_S{\rho}_SM $$

(13)

where 𝑀 is the Schmid factor which is usually taken to be 0.5 (Bammann and Aifantis 1982).

The gradient term in Eq. 9 is related to the GNDs as it represents the nonuniform deformation that occurred in small scales. The gradient 𝜂 can be expressed through GND density 𝜌_𝐺 and the Nye factor as follows (Arsenlis and Parks 1999):

$$ \eta =\frac{{\boldsymbol{\rho}}_G{b}_G}{\overline{r}} $$

(14)

where 𝑏_𝐺 is the magnitude of the Burgers factor of GNDs and $\overline{r}$ is the Nye factor.

In microscopic scales, the flow stress can be related to the dislocation densities generated by the plastic deformation through Taylor’s hardening law as follows:

$$ {\tau}_S={\alpha}_S{\mathrm{Gb}}_s\sqrt{\rho_S} $$

(15)

$$ {\tau}_G={\alpha}_G{\mathrm{Gb}}_G\sqrt{\rho_G} $$

(16)

where 𝜏_𝑆 and 𝜏_𝐺 are the shear flow stress corresponding to SSD density and GND density, respectively; 𝑏_𝑆 and 𝑏_𝐺 are the magnitudes of the Burgers vectors for SSDs and GNDs, respectively; 𝐺 is the shear modulus; and α_𝑆 and α_𝐺 are statistical coefficients which account for the deviation from regular spatial arrangements of SSDs and GNDs populations, respectively. The total shear flow stress, 𝜏_𝑓, which is required to initiate a significant plastic deformation, can be obtained by coupling the flow stresses given by Eqs. 15 and 16 as follows:

$$ {\tau}_f={\left[{\tau}_S^{\beta }+{\tau}_G^{\beta}\right]}^{1/\beta } $$

(17)

where 𝛽 is a constant fitting parameter.

A more general expression for the total shear flow stress can be written in terms of the total dislocation density from the combination of Eqs. 15, 16, and 17 as follows:

$$ \tau ={\alpha}_S{\mathrm{Gb}}_S\sqrt{\rho_T} $$

(18)

with

$$ {\rho}_T={\left[{\rho}_S^{\beta /2}+{\left({\alpha}_G^2{b}_G^2{\rho}_G/{\alpha}_S^2{b}_S^2\right)}^{\beta /2}\right]}^{2/\beta } $$

(19)

The plastic flow stress is related to the shear flow stress through a constant 𝑍 as follows:

$$ \sigma =\mathrm{ZT}={\alpha}_S{\mathrm{ZGb}}_S\sqrt{\rho_T} $$

(20)

Comparing Eqs. 9 and 20 and considering Eqs. 13, 14, and 19, the following expressions can be determined:

$$ \gamma =\beta /2 $$

(21)

$$ m=2 $$

(22)

$$ k={\alpha}_G\mathrm{GZ}\sqrt{b_S/{L}_SM} $$

(23)

$$ l={\left({\alpha}_G/{\alpha}_S\right)}^2\left({b}_G/{b}_S\right){L}_SM\overline{r} $$

(24)

At the beginning, the length scales were determined as a constant value. However, it has been reported that 𝐿_𝑆 is not a constant but it is equal to the grain size initially and saturates toward values in the order of micrometer in large strains (Gracio 1994). 𝐿_𝑆 can be written as a function of the grain size and the plastic strain as follows:

$$ {L}_S=\frac{\mathrm{Dd}}{D+{\mathrm{dp}}^{1/m}} $$

(25)

where d is the average grain size, D is the macroscopic characteristic size of the specimen, 𝑝 is the equivalent plastic strain, and 𝑚 is the hardening exponent. It can be seen from Eq. 24 that the length scale is proportional to 𝐿_𝑆. Therefore, the length scales of crystalline materials are not constant during the deformation. This has also been experimentally and theoretically verified in the work of Voyiadjis and Abu Al-Rub (2005).

Due to the fact that the GND density during deformation is strain rate and temperature dependent, the Nye factor in Eq. 24 can be expressed as a function of the strain rate and temperature as follows (Voyiadjis and Almasri 2009):

$$ \overline{r}=\frac{{\mathrm{Ae}}^{\left(-{E}_r/\mathrm{RT}\right)}}{1+{\mathrm{C}\dot{\mathrm{p}}}^q} $$

(26)

where the temperature factor is incorporated through the Arrhenius equation; $\dot{p}$ is the equivalent plastic strain rate; and 𝐴, 𝐶, and 𝑞 are constants. Substituting Eqs. 25 and 26 into Eq. 24 yields a variable length scale that varies with the grain size, temperature, strain rate, and equivalent plastic strain as follows (Voyiadjis et al. 2011):

$$ l={\left({\alpha}_G/{\alpha}_S\right)}^2\left({b}_G/{b}_S\right)M\left(\frac{\delta_1{\mathrm{de}}^{\left({E}_r/ RT\right)}}{\left(1+{\delta}_2{\mathrm{dp}}^{\left(1/m\right)}\right)\left(1+{\delta}_3{\left(\dot{p}\right)}^q\right)}\right) $$

(27)

where 𝛿₁, 𝛿₂, and 𝛿₃ are material parameters that need to be determined through experimental results. For single crystal materials, there is no effect of the grain size during the deformation. Therefore, the length scale for single crystal materials can be expressed without grain size d as follows:

$$ l={\left({\alpha}_G/{\alpha}_S\right)}^2\left({b}_G/{b}_S\right)M\left(\frac{\delta_1{e}^{\left(-{E}_r/\mathrm{RT}\right)}}{\left(1+{\delta}_2{\mathrm{p}}^{\left(1/m\right)}\right)\left(1+{\delta}_3{\left(\dot{p}\right)}^q\right)}\right) $$

(28)

Determination of the Length Scales

Nanoindentation experiments are believed to be the most effective technique to determine the length scales. The indentations made using a conical or a Berkovich indenter have self-similar shapes, which means once the indent is initially formed, the size of the indent grows and the shape keeps similar. The GND and SSD densities can be calculated during the indentation process. The material hardness is related to the flow stress according to Tabor’s factor. Therefore, the hardness can be written as a function of the dislocation densities through Eqs. 18, 19, and 20 as follows:

$$ H=\kappa {\sigma}_f=Z{\kappa \alpha}_S{\mathit{Gb}}_S{\left[{\rho_S}^{\beta /2}+{\left({\alpha}_G{b}_G/{\alpha}_S{b}_S\right)}^{\beta }{\rho_G}^{\beta /2}\right]}^{1/\beta } $$

(29)

where 𝜅 is Tabor’s factor relating the hardness and the flow stress. As shown in Eq. 29, the hardness is a function of both GND density and SSD density, which represents the deformation in the micro- and nanoscales where GNDs and SSDs interact with each other. However, in the case of large deformation, the effect of GNDs vanishes and the deformation is mainly attributed to the SSDs. The hardness in macroscopic scales, 𝐻₀, is thus only related to the SSD density as follows:

$$ {H}_0=Z{\kappa \tau}_S=Z{\kappa \alpha}_S{\mathrm{Gb}}_S\sqrt{\rho_S} $$

(30)

Using Eqs. 29 and 30 and assuming that 𝛼_G=𝛼_S and b_G=b_S, the ratio (H/H₀)^β can be derived as follows:

$$ {\left(\frac{H}{H_0}\right)}^{\beta }=1+{\left(\frac{\rho_G}{\rho_S}\right)}^{\beta /2} $$

(31)

The nanoindentation experiments provide the material hardness as a function of the indentation depth. If the dislocation densities can be calculated as through the indentation depth, the hardness from the model can be compared with the hardness determined by the experiments.

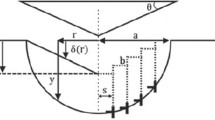
The GND density during nanoindentation can be calculated through the geometry of the indenter. The cross-sectional profile of the indentation process using a conical indenter is shown in Fig. 1. The profile of a Berkovich indenter can be represented by the conical indenter if the surface angle 𝜃 is taken to be 0.358 (Radian), since the cross-sectional areas and the volumes are identical between the conical and pyramidal Berkovich indenters.

Fig. 1

Sample being indented by a conical indenter (Reprinted from Voyiadjis and Zhang (2015))

The dislocation loops are generated by the penetration of the indenter and therefore the plastic deformation volume can be assumed as a semisphere. The GND density can be determined as the total length of dislocations divided by the volume of the semisphere, where the dislocation length can be calculated based on the geometry of the indenter. Without considering the influence of the grain boundaries , the GND density can be written as follows (Nix and Gao 1998):

$$ {\rho}_G=\frac{3{\mathrm{tan}}^2\theta }{2{b}_Gh} $$

(32)

It can be seen from Eq. 32 that the GND density decreases with the increasing indentation depth, proving that the nonuniform deformation decays with the increase of deformation and the nonlocal gradient becomes less significant.

In order to capture the hardening-softening phenomenon, grain boundaries were incorporated into the profile as shown in Fig. 2. When the plastic zone expands and reaches the grain boundaries, the diameter of the semisphere is equal to the average grain size.

Fig. 2

Nanoindentation cross-sectional profile of a polycrystalline sample (Reprinted from Voyiadjis et al. (2011))

However, a more accurate calculation can be approached by removing the volume occupied by the indenter from the semisphere (Yang and Vehoff 2007). The GND density can be written as follows (Voyiadjis and Peters 2010)

$$ {\rho}_G=\frac{\frac{\pi }{b_G}\frac{h^2}{\operatorname{tan}\theta }}{\frac{\pi }{12}{d}^3-8.19{h}^3} $$

(33)

where d represents the average grain size in polycrystalline materials.

The SSD density can be derived from the Tabor’s mapping of hardness-indentation depth from flow stress-plastic strain (Voyiadjis and Peters 2010). The SSD density 𝜌_𝑆 can be written as follows:

$$ {\rho}_S=\frac{c\overline{r}{\alpha}_G^2{b}_G\operatorname{tan}\theta }{{\mathrm{lb}}_S^2{\alpha}_S^2} $$

(34)

where c is a material constant of order 1 from Tabor’s mapping.

Combining Eqs. 31, 32, and 34 and assuming that 𝛼_G=𝛼_S and b_G=b_S, the hardness of single crystal materials can be derived as a function of the indentation depth as follows:

$$ H={H}_0{\left\{1+{\left[\frac{3M\operatorname{tan}\theta }{2\mathit{ch}}\times \frac{\delta_1{e}^{-{E}_r/\mathit{RT}}}{\left(1+{\delta}_2{p}^{1/m}\right)\left(1+{\delta}_3{\dot{p}}^q\right)}\right]}^{\beta /2}\right\}}^{1/\beta } $$

(35)

For polycrystalline materials, similar derivation can be made through Eqs. 31, 33, and 34 as follows:

$$ H={H}_0{\left\{1+{\left[\frac{M\pi {\left(h-{h}_1\right)}^2}{\left(\frac{\pi }{12}{d}^3-8.19{h}^3\right)c{\mathrm{tan}}^2\theta}\times \frac{\delta_1{\mathrm{de}}^{-{E}_r/ RT}}{\left(1+{\delta}_2{dp}^{1/m}\right)\left(1+{\delta}_3{\dot{p}}^q\right)}\right]}^{\beta /2}\right\}}^{1/\beta } $$

(36)

In order to isolate the influence of the grain boundary, bicrystalline materials are used and nanoindentations are made close to the single grain boundary near the grain boundary. The grain size in bicrystalline materials is not a parameter as it is in the size of the macroscopic scale. The distance 𝑟 between the grain boundary and the indenter tip is used to represent the size of the plastic zone. When the plastic zone reaches the grain boundary, the radius of the semisphere is equal to the distance 𝑟 as shown in Fig. 3.

Fig. 3

Nanoindentation cross-sectional profile of a bicrystalline sample (Reprinted with permission from Voyiadjis and Zhang (2015)).

By using the distance 𝑟 instead of the grain size d, the GND density during nanoindentation of bicrystalline materials can be written as follows:

$$ {\rho}_G=\frac{\frac{\pi }{b_G}\frac{h^2}{\operatorname{tan}\theta }}{\frac{2}{3}\pi {r}^3-8.19{h}^3} $$

(37)

Therefore, the hardness expression of a bicrystalline material during nanoindentation can be written as follows:

$$ H={H}_0{\left\{1+{\left[\frac{M\pi {\left(h-{h}_1\right)}^2}{\left(\frac{2\pi }{3}{r}^3+8.19{h}^3\right)c{\mathrm{tan}}^2\theta}\times \frac{\delta_1{\mathrm{re}}^{-{E}_r/\mathrm{RT}}}{\left(1+{\delta}_2{\mathrm{rp}}^{1/m}\right)\left(1+{\delta}_3{\dot{p}}^q\right)}\right]}^{\beta /2}\right\}}^{1/\beta } $$

(38)

The length scale expression given by Eqs. 27 and 28 are incorporated into Eqs. 35, 36, and 38. The material parameters 𝛿₁, 𝛿₂, and 𝛿₃ can be determined by comparing Eqs.35, 36, and 38 with nanoindentation experimental results for single crystal, polycrystalline materials, and bicrystalline materials, respectively. Therefore, the length scale parameters can be determined for materials with different microstructures, respectively.

Furthermore, a better approach of the hardness expression can be applied through a cyclic plasticity model (Voyiadjis and Abu Al-Rub 2003) as follows:

$$ {H}_{\mathit{new}}={H}_{\mathit{old}}+C(h){H}_{\mathit{old}} $$

(39)

with

$$ C(h)=\sqrt{\frac{1}{h}} $$

(40)

where 𝐻_𝑜𝑙d is the hardness given by Eqs. 35, 36, and 38 and 𝐻_𝑛𝑒𝑤 is the corrected value using the cyclic model.

In order to write the hardness 𝐻 as a function of the indentation depth h in Eqs. 35, 36, and 38, the equivalent plastic strain 𝑝 is also required to be as a function of h. It is difficult to determine 𝑝 as a function of h experimentally as the plastic deformation during nanoindentation is complicated. Therefore, finite element simulation is needed to capture this relationship (Voyiadjis and Peters 2010). Commercial finite element analysis software ABAQUS is used throughout an indentation problem. The testing sample is represented by a cube with dimension of 50 μm. The Berkovich indenter is modeled on top of the cubic sample as a blunt three-side pyramid as shown in Fig. 4. The tip of the indenter is set to be an equilateral triangle with 20 nm sides. The ABAQUS interaction module is used in order to simulate the contact between the indenter and the sample. A specific velocity field is assigned in order to drive the indenter to penetrate to the desired indentation depths according to the experiments. In order to show the different behaviors between FCC and BCC materials, a user material subroutine VUMAT is used during the simulation (Voyiadjis et al. 2011). After the indentation process is completed, the equivalent plastic strain 𝑝 under the indenter can be viewed as shown in Fig. 5. The value of 𝑝 at each time step can be determined through the contour plots as well as the indentation depth at each step. Therefore, the equivalent plastic strain as a function of the indentation depth can be determined by taking values of 𝑝 and $\hbar$ at each step.

Fig. 4

Indentation model before the simulation (Reprinted from Voyiadjis and Zhang (2015))

Fig. 5

Contour plot of equivalent plastic strain at the maximum indentation depth (Reprinted from Voyiadjis and Zhang (2015))

Applications on Single Crystal, Polycrystalline, and Bicrystalline Metals

Nanoindentation experiments are performed on metals with different microstructures in order to validate the prediction of the computational models and to determine the material parameters of the expressions of the length scales. Based on the temperature and strain rate indentation size effect (TRISE), nanoindentation experiments are conducted on single crystal and polycrystalline samples at different temperatures and strain rates. On bicrystalline samples, the experiments are carried out near the grain boundary at different distances in order to characterize the influence of the grain boundary on the material hardness. Nanoindentations at different strain rates are also performed at the same distance between the grain boundary and the indenter in order to confirm the rate dependency during nanoindentation on bicrystalline materials. The experimental results are compared with the prediction of hardness of the TRISE model. The length scales of materials with different microstructures are determined through the determinations of the material parameters from the comparisons. All testing samples are polished to acquire the accurate and consistent experimental results.

Sample Preparations

In nanoindentation , the hardness is not a direct measurement from the test. It is determined from the direct measurement of load and displacement through a tip area function (Oliver and Pharr 1992). The tip area function is determined through a model assuming that the indenter penetrates perpendicularly into a flat sample surface. Therefore, in order to obtain accurate experimental results, the surface of the sample needs to be polished in order to approach the flat condition as assumed by the theory. It is required by the nanoindentaion technique that the surface roughness must be smaller than one tenth of the maximum indentation depth. Therefore, if the hardness information at smaller indentation depths is needed, the surface roughness needs to be controlled to be lower.

Several polishing procedures are applied in order to improve the surface roughness. Mechanical polishing is usually applied firstly in order to level the entire surface to be horizontal. Silica carbide polishing papers with polishing particles of different sizes are used depending on the initial surface condition: the rougher the surface, the greater the size of polishing particles. After the use of each polishing paper, the surface is examined using a light microscope to make sure that the scratches on the surface are in the same size. Chemical-mechanical polishing is applied following the mechanical polishing when the polishing paper with the minimum size of polishing particles is used. In the chemical-mechanical polishing process, 50 nm colloidal silica or alumina polishing particles are used depending on the type of materials to be polished. By adjusting the PH values of the polishing slurries, chemical reactions between the polishing particles and the polishing sample can be initiated so that the surface roughness is lowered more effectively compared to the mechanical polishing process. The improvement of the surface quality of an iron sample is shown in Fig. 6. It shows that the surface roughness is improved and the defects such as voids and scratches are also improved.

Fig. 6

SEM images of surfaces of testing sample in different polishing conditions: (a) without polishing, (b) after mechanical polishing, and (c) after chemical-mechanical polishing

In addition to the surface roughness, the plastic deformation layer on top of the surface is another concern for nanoindentation experiments. Due to the mechanical abrasion between the polishing particles and the sample, plastic deformation layer is induced no matter how small the polishing particles are used. The hardness varies if there is a plastic deformation that occurred in the indenter area, especially for tests in bicrystalline materials when the indentation depth is as small as a few tens of nanometers where the hardening-softening phenomenon is observed. Electro-polishing is widely used in order to remove the plastic deformation layer. Chemical reactions occur in the electrolyte solution and the peak material on the surface is removed by the electrical current during the electro-polishing process. As no mechanical abrasion is induced, there is no plastic deformation created in the electro-polishing process. Although electro-polishing process is very effective in removing the plastic deformation, it has its disadvantages that the electrical current must be controlled carefully at a constant value; otherwise damages are induced on the surface. Vibratory polishing is another process that can remove the plastic deformation layer. In a vibratory polisher, a vertical vibration is added in addition to the rotation of the polishing pad. The down force pressure during polishing is thus minimized by the vibration so that only the peak material on the surface is removed in a very gentle manner. Due to the minimal down force pressure, the mechanical abrasion between the particles (usually alumina or colloidal silica) and the sample does induce significant plastic deformation. After the vibratory polishing process for bicrystalline samples, the grain boundary is observed under the light microscope as shown in Fig. 7. The pen mark is made on the surface of the bicrystal where the single grain boundary is formed during the growth of the bicrystal.

Fig. 7

Visualization of the grain boundary after vibratory on a bicrystalline aluminum (Reprinted from Voyiadjis and Zhang (2015))

Temperature and Strain Rate Dependency on Single Crystal and Polycrystalline Metals

The TRISE model incorporates the temperature and strain rate parameters into the expression of the length scale. As the expression of hardness is written using the length scale, the hardness is predicted to be dependent on the temperature and the strain rate. In order to verify the prediction of the TRISE model and material parameters needed for the length scales, nanoindentation experiments are conducted on various metals with single crystal and polycrystalline microstructures at different temperatures and strain rates. The material parameters are determined by comparing the TRISE model and the experiments. The length scales are eventually determined for single crystal and polycrystalline materials at different strain rates and temperatures.

In aluminum and copper single crystals, nanoindentation experiments are performed on a polished surface at different strain rates of 0.05 s⁻¹ , 0.08 s⁻¹ , and 0.10 s⁻¹. It shows from the experimental results in Fig. 8 that the hardness increases with the increasing strain rate for both metals. The TRISE model for single crystal given by Eq. 35 is applied by giving different values for the parameter equivalent plastic strain rate $\dot{p}$. It shows a good agreement between the experimental results and the predictions from the hardness expression. This proves that the TRISE model is able to predict the influence given by the strain rates. Moreover, there is no hardening-softening phenomenon observed which validates the assumption that no dislocation is accumulated with the absence of grain boundaries .

Fig. 8

Comparisons between TRISE models and nanoindentation experiments: (a) copper single crystal and (b) aluminum single crystal (Reprinted from Voyiadjis et al. (2011))

The material parameters shown in Table 1 are obtained through the comparisons and the length scales of copper and aluminum single crystals as shown in Fig. 9.

Table 1 Materials parameters used in Eq. 35 for single crystals (Reprinted from Voyiadjis et al. 2011)

Fig. 9

Material length scales of single crystals: (a) copper and (b) aluminum (Reprinted from Voyiadjis et al. (2011))

Although no hardening-softening phenomenon is observed due to the absence of the grain boundaries, the experimental results and the TRISE model both show that the hardness decreases with increasing indentation depth. This is due to the generation of GNDs at small depth where nonuniform deformation is significant during the initial formation of the indent. The GNDs also interact with the SSDs as obstacles of the movement of SSDs, giving rise to the increase of hardness at smaller depths. The material length scales for both single crystals show the length scale decrease with the increase of the equivalent plastic strain, which means the strain gradient is greater when deformation is smaller. The determination of the length scale verifies the strain gradient plasticity theory that the stress mechanical responses are greater when the strain gradients are higher. It also shows in the length scales that a variable length scale expression needs to be used instead of the constant length scale determined in the previous research, which proves that a variable length scale is more realistic and the expression can be applied to different problems.

Nanoindentation experiments are conducted on polycrystalline copper and aluminum in order to capture the hardening-softening phenomenon as well as the strain rate dependency. TRISE model given by Eq. 36 is applied to compare with the experimental results. As shown in Fig. 10, the hardness initially decreases with indentation depth at very small depth less than 50 nm. The hardening-softening phenomenon is observed following the decreasing hardness segment. The experimental results show that at very small indentation depth where the plastic deformation does not reach the grain boundaries, the polycrystalline materials behave similarly with respect to single crystal materials. However, due to the presence of the grain boundaries , the expansion of the plastic zone is constrained and dislocations start to accumulate near the grain boundary. The local increase of the dislocation density gives rise to the increase of the material hardness, causing the hardening-softening phenomenon. Nanoindentation experiments are also performed at different strain rates. It shows in both experiments and TRISE model that the hardness increases with the increasing strain rate, verifying the strain rate dependency on polycrystalline materials.

Fig. 10

Nanoindentation experiments and TRISE model of polycrystalline materials: (a) copper and (b) aluminum at different strain rates (Reprinted from Voyiadjis et al. (2011))

The length scales for polycrystalline copper and aluminum can be determined by comparing the experimental results and TRISE model in determining the material parameters. Using the parameters given in Table 2, the length scales of both materials are obtained as a function of the equivalent plastic strain as shown in Fig.11.

Table 2 Materials parameters used in Eq. 36 for polycrystalline materials (Reprinted from Voyiadjis et al. 2011)

Fig. 11

Length scales as a function of the equivalent plastic strain for polycrystalline materials: (a) copper and (b) aluminum at different strain rates (Reprinted from Voyiadjis et al. 2011)

As shown in Fig. 11, the length scale decreases with the increasing strain rate. When the strain rate is increased, the deformation occurs faster and the dislocations do not have the sufficient time to generate and are trapped by the local nonuniform deformation. This causes the additional increase of the strain gradient, resulting in the increase of the material hardness.

Nanoindentation experiments are performed on iron (Bahr et al. 1999) and gold (Volinsky et al. 2004) at different temperatures in order to study the temperature dependency. Different temperatures are given to the TRISE model and the comparisons between the experiments and models are presented in Fig. 12 Voyiadjis and Faghihi (2012). It shows that the hardness decreases with the increase of the temperature. The higher mobility of the dislocations causes the decrease of the dislocation density and thus the hardness decreases.

Fig. 12

Nanoindentation experiments at different temperatures on (a) iron single crystal and (b) gold polycrystalline film (Reprinted from Voyiadjis and Faghihi (2012))

The length scales of iron and gold are obtained through the comparison and it shows in Fig.13 that the length scales increase with the increasing temperature, causing the decrease in the material hardness. As iron is a BCC metal and gold is an FCC metal, it shows that the TRISE model works for both BCC and FCC metals in predicting the indentation size effect and determining the length scales.

Fig. 13

Length scales at different temperatures: (a) iron and (b) gold (Reprinted from Voyiadjis and Faghihi (2012))

Influence of the Grain Boundaries on Bicrystal Metals

As discussed in the previous section, the distance between the indenter and the grain boundary during nanoindentation has an impact on the hardness behavior of materials with grain boundaries. In the case of polycrystalline materials, the grain size d characterizes the interactions between the dislocations and the grain boundaries. The distance between the indenter and the grain boundary becomes greater when the grain size increases. Nanoindentation experiments are performed on Nickel samples with different grain sizes (Yang and Vehoff 2007). The TRISE model given by Eq. 36 is applied by assigning different values to the grain size 𝑑 (Voyiadjis and Faghihi 2012).The comparison between the experiments and the prediction of TRISE model is shown in Fig. 14. It shows in the experiments that as the grain size increases, the hardness during the hardening-softening segment decreases. As the dislocations only accumulate when they move to the grain boundaries, the greater grain size allows the dislocations to move in a greater space comparing to the condition of smaller grain size. The dislocation density thus decreases, resulting in the decrease in hardness. The experimental results show a good agreement with the predictions given by the TRISE model at different grain sizes as shown in Fig. 14.

Fig. 14

Comparison between the experiments and the TRISE model at different strain rates (Reprinted from Voyiadjis and Faghihi (2012))

The size of the plastic zone increases with the increasing indentation depth. When the grain size is smaller, the plastic zone reaches the grain boundary at lower depth. As the grain size increases, the plastic zone reaches the grain boundary at greater depth. When the grain size is as much as 80 μm, the size of the plastic zone is smaller than the grain size. There is no accumulation of the grain boundary and no hardening-softening phenomenon is observed. The length scales at different grain sizes are obtained from the comparison. It shows in Fig. 15 that the length scale decreases as the grain size decreases. The grain boundaries act as constrains that block the influence of the strain gradient, which causes the smaller characteristic length scale when the grain size is smaller.

Fig. 15

Length scales as a function of the equivalent plastic strain at different grain sizes (Reprinted from Voyiadjis and Faghihi (2012))

In order to isolate the investigation on the influence of the grain boundary, bicrystalline materials are tested near the single grain boundary at different distances. After the Aluminum sample is polished, the single grain boundary is observed as shown in Fig. 7. However, it is only visible using a 10× microscope in the Nanoindenter. The distance between the indenter and the grain boundary can be only measured using a 40× microscope. In order to identify the position of the grain boundary, the two indents are made on two points on the grain boundary under a 10× microscope. The grain boundary can thus be represented by the straight line connecting the two marking indents under the 40× microscope. A straight line of nanoindentations are performed near the grain boundary with the angle between the line of indents and the grain boundary to be 20° as shown in Fig. 16a (Voyiadjis and Zhang 2015).

Fig. 16

Nanoindentations near the grain boundary at different distances: (a) image under the 40× microscope and (b) the magnified image of (a) (Reprinted from Voyiadjis and Zhang (2015))

It is noted that the depths of the indentations are 500 nm and the spacing is 5 μm. In order to make sure that there is no interaction between the close indents, experiments are made on other locations and the results show that there is no significant interaction observed. The difference in the microstructures from two grains is not considered here. Therefore, the five indents on one side of the grain boundary are selected for the investigation. The distances between the center of the indents and the grain boundary are measured using the scale in the image as shown in Fig. 16b. The experimental results of the five indents are presented in Fig. 17. It shows that for the two indents that are far from the grain boundary, there is no hardening-softening phenomenon observed. The grain boundary does not have the impact on the accumulation of dislocations when the distance is large, showing the single crystal behavior. It also shows in Fig. 17 that hardening-softening phenomenon is observed for the rest three indents and as the distance becomes smaller, there is a greater hardening effect. This observation verifies the assumption of the influence of the grain boundary that more dislocations are accumulated between the indenter and the grain boundary when the distance is smaller. The higher dislocation density at smaller distances causes the increase in hardness.

Fig. 17

Hardness versus indentation depth curves for five indents with different distances between the indenter and the grain boundary. The two solid curves represent the indents without hardening-softening phenomenon. The three dashed lines show the influence of the grain boundary on material hardness (Reprinted from Voyiadjis and Zhang (2015))

The developed TRISE model for bicrystalline materials given by Eq. 38 is applied by assigning different values of the distance 𝑟 measured from the experiments. The comparison between the TRISE model and the experimental results of the three indents with the grain boundary effect is given in Fig. 18. The developed TRISE model shows its capability to predict the hardness with the presence of the single grain boundary. It also reflects the prediction that there is a higher hardening effect as the indents are made closer to the grain boundary. The material parameters in Eq. 38 are determined by the comparison between the TRISE model and the experimental results. The material length scales are obtained as shown in Fig. 19 through the determination of material parameters given in Table 3.

Fig. 18

Comparison of TRISE model with experimental results for the three indents with hardening-softening effect. The solid lines are obtained from the TRISE model and the dashed lines are the experimental results (Reprinted from Voyiadjis and Zhang (2015))

Fig. 19

Length scales as a function of the equivalent plastic strain at different values of r (Reprinted from Voyiadjis and Zhang (2015))

Table 3 Material parameters for bicrystalline Aluminum (Reprinted from Voyiadjis and Zhang 2015)

The length scale decreases as the distance between the indenter and the grain boundary decreases. The grain boundary and the indenter both act as obstacles of the influence of the strain field. Therefore, the impact range of the strain gradient is shorter when the distance becomes smaller, resulting in a smaller characteristic length scale. The decrease in the length scale, in return, causes the increase of the strain gradient and thus causes the additional increase on material hardness.

Similar nanoindentation experiments are performed on a bicrystalline copper which is also an FCC metal. The grain boundary is also represented by a straight line connecting the two marking indents made on two points of the straight grain boundary. A line of indents are made across the grain boundary with the angle between indentation line and the grain boundary to be 5° as shown in Fig. 20a (Zhang and Voyiadjis 2016). The image in Fig. 20a is zoomed in order to show the details of the distance between the indent and the grain boundary as shown in Fig. 20b. The distances are measured using the scale considering the magnification. Artificial effect is added to Fig. 20b in order to show the clear contrast between the indents and the sample surface.

Fig. 20

Nanoindentation experiments with different distances from the grain boundary: (a) image under the 40× microscope and (b) a zoomed view of (a) (Reprinted from Zhang and Voyiadjis (2016))

The experimental results of the three indents shown in Fig. 20b on the same side of the grain boundary as well as the indent made right on the grain boundary are presented in Fig. 21. The indent on the grain boundary solely decreases with the increasing indentation depth. When the indent is made on the grain boundary, the dislocations start to generate into the two grains on both sides of the grain boundary. There is no additional obstacle of the generation of dislocations and therefore no hardening-softening phenomenon is observed. This proves the assumption of the influence of the grain boundary on the other side. Hardening-softening effect is observed for the three indents within a close distance to the grain boundary. It also shows in Fig. 21 that as the distance becomes smaller, there is a greater hardening effect, similarly to the observation made from the experiments of Aluminum bicrystal. The experiments on Copper bicrystal confirm the influence of the grain boundary on the material hardness on FCC metal.

Fig. 21

Hardness versus indentation depth curves from nanoindentation experiments at different distances to the grain boundary and right on the grain boundary (Reprinted from Zhang and Voyiadjis (2016))

Due to the tip rounding of the indenter, strain hardening may be induced during nanoindentation at very small indentation depths. In order to confirm that the hardening is solely attributed to the accumulation of dislocations, the elastic moduli of the three indents at different distances are presented in Fig. 22. It shows that after the depth of 20 nm, the elastic moduli from the three indents are constants on the average. This means that after the depth of 20 nm where the hardening effect is captured, there is no strain hardening effect induced as the elastic modulus is not dependent on the indentation size effect but only dependent on the strain hardening. The information of elastic moduli confirms that the hardening effect observed for the Copper bicrystal is only attributed to the accumulation of dislocations between the indenter and the grain boundary.

Fig. 22

Elastic modulus as a function of the indentation depth for three indents near the grain boundary (Reprinted from Zhang and Voyiadjis (2016))

The developed TRISE model given by Eq. 38 is applied for the copper bicrystal with different values of distances. The comparison between the TRISE model and experimental results is presented in Fig. 23. The length scales at different distances for the Copper bicrystal are determined as shown in Fig. 24 using the material parameters determined from the comparison as shown in Table 4.

Fig. 23

Comparison between the TRISE model and nanoindentation experiments at different distances between the indenter and the grain boundary (Reprinted from Zhang and Voyiadjis (2016))

Fig. 24

Material length scales as a function of the equivalent plastic strain for Copper bicrystal at different distances between the indenter and the grain boundary (Reprinted from Zhang and Voyiadjis (2016))

Table 4 Material parameters of Copper bicrystal (Reprinted with permission from Zhang and Voyiadjis 2016)

The comparison shows the capability of the developed TRISE model on Copper bicrystal. As shown in Fig. 24, the length scale decreases as the distance 𝑟 becomes smaller, which confirms the influence of the grain boundary on the material behavior of FCC metals.

Moreover, the strain rate dependency is studied for Copper bicrystal. Nanoindentation experiments are performed at the same distance from the grain boundary at different strain rates of 0.05s⁽⁻¹⁾ , 0.08s⁻¹ , and 0.10s⁻¹. As shown in Fig. 25, the hardness increases with the increasing strain rates. It is worth noting that this increase is not only for the hardening-softening segment but for the entire depth. This is because the strain rate has the influence on material behaviors in both micro- and macroscales.

Fig. 25

Hardness vs. indentation depth for nanoindentation experiments at different strain rates with the same distance r (Reprinted from Zhang and Voyiadjis (2016))

The TRISE model given by Eq. 38 is applied with different values of strain rates. The material length scales are determined using different values of strain rates and the material parameters given by Table 4. It shows in Fig. 26 that the length scale decreases with the increase of the strain rate. The strain rate dependency for Copper bicrystal is similar with the observation made from the polycrystalline copper.

Fig. 26

Length scales as a function of the equivalent plastic strain at different strain rates for Copper bicrystal (Reprinted from Zhang and Voyiadjis (2016))

Summary and Conclusion

The size effect during nanoindentation is addressed in this chapter. The classical continuum theory is not capable in predicting the indentation size effect as it does not incorporate the length scale in the constitutive expression. Strain gradient plasticity theory is applied in order to capture the size effect. The expression of a physically based length scale is determined from the strain gradient plasticity theory. In order to determine the material length scales, nanoindentation experiments are performed on single crystals, polycrystalline materials and bicrystalline materials. The constitutive equation is mapped into hardness versus indentation depth and the material parameters are determined from the expression of hardness and the experimental results.

The material length scale is dependent on the temperature, equivalent plastic strain rate, and grain size in polycrystalline materials. A TRISE model is applied in order to capture the dependencies of temperature, strain rate, and grain size. Nanoindentation experiments are performed on single crystal and polycrystalline materials. From the comparison between the TRISE model and experimental results, the length scales at different temperatures, strain rates, and grain sizes are determined.

The results of nanoindentation experiments on single crystal Copper and Aluminum show that the hardness solely decreases with the increase of the indentation depth. The TRISE model for single crystal is able to predict the hardness obtained from experiments of single crystal materials. The nanoindentation experiments on polycrystalline Copper and Aluminum show the hardening-softening effect due to the presence of grain boundaries. The TRISE model is capable in predicting the hardening-softening phenomenon. The temperature dependency is addressed by the TRISE model at different temperatures and nanoindentation experiments on iron and gold. Both TRISE model and experiments show that the hardness decreases with the increasing temperatures. Nanoindentation experiments are performed at different strain rates on both polycrystalline and single copper and aluminum. It is shown by the TRISE model and experimental results that hardness increases as the strain rate increases. The material length scales are determined by the comparison between the TRISE model and the experiments. The dependencies of length scales on the temperature, strain rate, and grain size verify the theory that higher strain gradient causes greater material hardness.

In order to isolate the influence of the grain boundary, bicrystalline copper and aluminum are used and nanoindentation experiments are performed near the grain boundary at different distances. The TRISE model is developed based on the structure of bicrystals. The length scales are determined by comparing the developed TRISE model and the experimental results on bicrystalline materials.

The experimental results on bicrystalline copper and aluminum show that the material behaves like a single crystal when the indents are made with large distances from the grain boundary. The hardening-softening phenomenon is only observed for the indents made in close proximity to the grain boundary. The experimental observation validates that the increase of hardness is attributed to the presence of the grain boundary. The accumulation of dislocations near the grain boundary causes the increase of dislocation density, resulting in the additional hardening effect. The influence of the grain boundary is further investigated through nanoindentation experiments near the grain boundary at different distances. The TRISE model is developed for bicrystalline materials by replacing the grain size 𝑑 in polycrystalline models with the distance 𝑟 between the indents and the grain boundary. The developed TRISE model shows its capability to predict the fact that there is a stronger hardening effect when the distance 𝑟 becomes smaller as shown by nanoindentation experiments, providing a new type of size effect with respect to the distance 𝑟. The length scales of bicrystalline copper and aluminum show that as the indents are made closer to the grain boundary, the length scales decrease. The grain boundary and the indenter act as obstacles that prevent the strain gradient from influencing the space outside the volume constrained by the obstacles. Therefore, the characteristic length scale at smaller distance is lower and in return causes the increase in the strain gradient and dislocation density. The increase of dislocation density causes the additional hardening effect during nanoindentation. The rate dependency is also investigated on bicrystalline copper through nanoindentation experiments at different strain rates with a fixed distance from the grain boundary. Both experimental results and the TRISE model show an increase of hardness with the increasing strain rate, similarly to the rate dependency in single crystal and polycrystalline materials.

For all the length scales determined in this chapter, it shows that the length scale decreases with the increasing equivalent plastic strain and approaches to zero when the deformation is large. This behavior of the length scale proves the strain gradient plasticity theory in addressing the size effect during nanoindentation. When the indentation depth is small, the shape of the indent is initially formed. GNDs are required to accommodate the nonuniform deformation in the formation of the indent. As the indenter penetrates deeper, the indent grows to a greater size with a similar shape because of the use of the self-similar Berkovich indenter. The amount of uniform deformation increases and SSDs are required to generate the uniform deformation. Therefore, the GND density decreases gradually with the increase of the indentation depth and the strain gradient becomes smaller. The influence of the decreasing strain gradient causes the decrease of the characteristic length. When the deformation becomes larger in the macroscopic scale, uniform deformation dominates and there is no influence of the strain gradient, resulting in a zero value of the length scale in large deformations.