Keywords

Introduction

The interest of many researchers has been recently directed to study the mechanical properties of polymers in small size scales due to their extensive use in nano- and microscale elements over the past decades. A large series of constitutive models and experimental methods by which the properties of this class of materials can be thoroughly captured in millimeter or larger size scales has been presented (Hasan et al. 1993; Hoy and Robbins 2006; Van Breemen et al. 2012; Mulliken and Boyce 2006; Anand and Gurtin 2003; Voyiadjis and Samadi-Dooki 2016); however, there are still many questions about the behavior and deformation mechanism of polymers in submicron size scales. To acquire the precise and reliable results for mechanical properties, including elastic modulus and hardness, of very small volumes of materials, instrumented-indentation testing (IIT) can be employed (Al-Haik et al. 2004; Boersma et al. 2004; Lee et al. 2004; Zeng et al. 2012). In this technique, an indenter induces a localized deformation by applying a specified load on the material surface. Basically, there are two different indentation methods: (1) basic mode in which, with monotonic loading and unloading, the mechanical properties are only measured at the predefined maximum load from the unloading curve, and (2) continuous stiffness measurement (CSM) mode in which a small oscillation force is superimposed on the primary loading signal, and the resulting response of the system is analyzed through a frequency-specific amplifier. Employing the second procedure, the material mechanical properties can be continuously measured from zero to the maximum indentation depth during the loading segment. In addition, while in the former, the contact stiffness is measured just at the initial point of the unloading, the measurement of the contact stiffness at any point along the loading segment is possible in the latter with a smaller time constant (Li and Bhushan 2002; Hay et al. 2010; Pethica and Oliver 1988). Therefore, the small time constant of the CSM method makes it more useful for measuring the properties of materials especially those which are strongly time dependent like polymers. The loading (or strain) rate is controlled in a different way in these two modes; during the basic mode, the load is applied with a constant rate on the sample surface by the indenter until it reaches a determined maximum value; however, in the CSM mode, the indenter travels up to a predefined maximum depth and the load is controlled so that the loading rate divided by the load (\( \dot{P}/P \)) remains constant over the course of a single indentation.

The loading and strain rates are adjustable parameters in nanoindentation experiments, and their variations have shown profound effects on the mechanical response of time-dependent materials like polymers (Odegard et al. 2005; Mazeran et al. 2012; Samadi-Dooki et al. 2016; Malekmotiei et al. 2015; Kraft et al. 2001; White et al. 2005; Zhang et al. 2009; Shen et al. 2004). That being the case, a closer look at the strain (loading) rate variation during the indentation is required since the generated strain and stress fields in the material due to the loading by a self-similar tip is inhomogeneous. In the basic mode nanoindentation , although the test is conducted with a constant loading rate\( \dot{P} \), the strain rate is considerably decreasing at shallow depths, and it eventually approaches almost stable value after a long distance travel of the tip into the material. For this reason, an average value of the strain rate over the deep part of the indentation can be considered as the representative strain rate of the test (Schuh and Nieh 2003). On the other hand, in the CSM nanoindentation experiments, the \( \dot{P}/P \) ratio is set as a constant value at the beginning of the test. It has been shown that the indentation strain rate can also be assumed to remain constant during the constant \( \dot{P}/P \) experiment where the material hardness has the steady-state value, i.e., \( \dot{H}=0 \) (Lucas and Oliver 1999). However, the indentation size effect (ISE), which is the increment of hardness as the indentation depth decreases, has been observed during the nanoindentation experiments on many materials including crystalline and amorphous solids (Briscoe et al. 1998; Voyiadjis and Zhang 2015). In a study on Al-based foams, it has been observed that the strain rate varies about three orders of magnitude during the first 200 nm of the indentation before reaching a steady-state value (Kraft et al. 2001). As a result, in the case of the CSM mode, the indentation strain rate can be considered constant in that part of the test where the ISE is negligible.

Conducting the CSM nanoindentation experiments on PMMA and PC as polymeric glasses, the variation of the strain rate during the course of a single test is investigated as a main goal in this chapter. Examining the variation of the \( \dot{P}/P \) ratio during the test shows that although the \( \dot{P}/P \) ratio is set to remain invariant during the loading segment, it takes a considerable tip travel distance until it stabilizes and reaches the set value. Furthermore, the indentation strain rate, which has been incorrectly considered as the \( \dot{P}/P \) ratio in some studies (Shen et al. 2004, 2006; Vachhani et al. 2013), is also found to change at shallow depths of indentation. The obtained results show a good correlation between the instantaneous indentation strain rate, which is evaluated directly from the indentation depth-time data recorded during the loading segment, and the strain rate relation proposed by Lucas and Oliver (1999) based on the variation of the load and hardness. As another purpose, the possible relation between the variation of the strain rate during the nanoindentation and the observed ISE in polymers is also scrutinized in this chapter. While the high values of strain rate in shallow depths can cause the increment of material hardness, it is discussed here that it cannot be the reason for the observed ISE since the obtained high values of hardness could be the result of the indentation strain rates which are orders of magnitude higher than the actual recorded strain rate values.

Materials and Methods

Sample Preparation

The commercially manufactured (Goodfellow, Cambridge, UK) polymeric glasses including PMMA and PC , 2.0 and 5.0 mm-thick sheets, respectively, are considered for this investigation. The sheets are first cut into 20 × 20 mm squares, and then washed with 30% isopropyl alcohol (IPA) to eliminate the remainders of the protective film, and at the end rinsed with distilled water. Using a TA Instruments 2920 differential scanning calorimetry (DSC) machine, the glass transition temperature (Tg) of the specimens is measured to be about 110 °C and 148 °C for PMMA and PC, respectively. The samples are annealed at 120 °C for 4 h to remove any thermal history, and then cooled down to ambient temperature with the rate of 10 °C/h in a vacuum oven. The roughness of sample surface is one of the factors which affects the nanoindentation results since high values of roughness can make inaccuracy in the hardness of material measurements; therefore, to capture the surface topography of the samples, an Agilent 5500 atomic force microscope (AFM) is utilized. Since the average surface roughness, Ra, of the PC and PMMA specimens are 0.411 ± 0.033 and 0.372 ± 0.013 nm, respectively, one can assume the flat surface for samples (Kim et al.2007), and there is no need to modify the obtained results for materials’ hardness (Voyiadjis and Malekmotiei 2016).

Nanoindentation Analysis

To address the goal of this chapter which is scrutinizing the strain rate variation during the course of a single nanoindentation experiment and its effect on the observed ISE, an MTS Nanoindenter® XP equipped with a three-sided pyramidal Berkovich diamond tip is employed (Voyiadjis and Malekmotiei 2016). The mechanical properties of the specimens are measured through the CSM mode indentation in which the load-hold-unload sequences are carried out with the constant \( \dot{P}/P \) during the loading stage. According to the formulations developed by Oliver and Pharr (2004), the material hardness is defined as the mean contact pressure under the indenter as follows:

$$ H=\frac{P}{A_c} $$
(1)

where P is the applied load on the sample surface and Ac is the projected contact area of the hardness impression at that load. Based on this discerption, a precise measurement of the contact area between the sample surface and the indenter tip is required to calculate the hardness. The contact area is a function of the contact depth, hc, and equal to Ac = 24.56hc2 for a perfect Berkovich indenter tip. The one used for these experiments is not ideally sharp; so, the contact area function is obtained through calibrating the tip which improves the accuracy of the contact area measurements by accounting for the tip imperfections and leads to introducing some additional terms to the above relation as:

$$ {A}_c=24.56{h_c}^2+{C}_1{h_c}^1+{C}_2{h_c}^{1/2}+{C}_3{h_c}^{1/4}+\dots +{C}_8{h_c}^{1/128} $$
(2)

in which C1 through C8 are constant coefficients which are obtained based on the results of the nanoindentation on fused silica as a standard sample. Another important parameter that needs to be accurately determined is the depth over which the material is in contact with the tip (hc). The contact depth is estimated using

$$ {h}_c=h-\varepsilon \frac{P}{S}. $$
(3)

where h is the total penetration depth, S is the elastic contact stiffness, and ε is a constant that depends on the indenter geometry (for a Berkovich indenter ε = 0.75 (Oliver and Pharr 1992)). As already stated, the CSM technique makes the continuous measurement of the contact stiffness as a function of depth possible during the loading segment of the indentation. Considering the imposed driving force as P = P0 eiωt and the indenter displacement response as h(ω) = h0 e(iωt + α), the elastic contact stiffness is calculated as follows:

$$ S={\left[\frac{1}{\frac{P_0}{h\left(\omega \right)}\cos\left(\alpha \right)-\left({K}_s-m{\omega}^2\right)}-\frac{1}{K_f}\right]}^{-1} $$
(4)

in which P0 is the force oscillation magnitude, ω is the oscillation frequency, h0 is the resulting displacement oscillation magnitude, and α is the phase angle between the displacement and force signals. The other contributing parameters are the leaf spring constant, Ks, that supports the indenter, the indenter mass, m, and the indenter frame stiffness, Kf (Li and Bhushan 2002).

Another mechanical property measured in the nanoindentation experiments is the elastic modulus of the sample, E, which is calculated by the following relation:

$$ \frac{1}{E_r}=\frac{1-{\nu}^2}{E}+\frac{1-{\nu_i}^2}{E_i}. $$
(5)

where Eris the reduced elastic modulus which attributes to the elastic deformation in both the sample and indenter, ν is the sample Poisson’s ratio, and Ei and vi are the indenter elastic modulus and Poisson’s ratio, respectively. Sneddon (1965) has developed a relation for the reduced elastic modulus as follows:

$$ {E}_r=\frac{S}{2\beta}\sqrt{\frac{\uppi}{A_c}}. $$
(6)

where β as a constant depends on the indenter geometry and is about 1.034 for the Berkovich tip. Subsequently, as a main feature of the CSM method, the material hardness and elastic modulus are measured as continuous functions of depth with the course of an individual loading-unloading cycle.

The Indentation Strain Rate

Basically in the nanoindentation experiments, the strain rate affects the material in a direction perpendicular to the sample surface and is correlated with the displacement/loading rate of the indentation. For a pyramidal indenter, the indentation strain rate is defined as the penetration rate of the indenter into the material divided by its instantaneous depth as follows (Mayo and Nix 1988):

$$ {\dot{\epsilon}}_i=\left(\frac{1}{h}\right)\left(\frac{dh}{dt}\right). $$
(7)

where t is time. In a study, Lucas and Oliver (1999) investigated that by keeping the loading rate divided by the load (\( \dot{P}/P \)) constant during the CSM nanoindentation, the indentation strain rate can also remain constant. It has been shown that incorporating the loading and hardness data, the indentation strain rate can be obtained as (Lucas and Oliver 1999):

$$ {\dot{\epsilon}}_i=\frac{\dot{h}}{h}=\frac{1}{2}\left(\frac{\dot{P}}{P}-\frac{\dot{H}}{H}\right). $$
(8)

in which \( \dot{H} \) is the hardness variation rate and other parameters are defined before. According to Eq. 8, the indentation strain rate reaches a constant value \( \left(\frac{1}{2}\frac{\dot{P}}{P}\right) \)at large indentation depths where the material hardness is almost unvaried, i.e., \( \dot{H}=0 \).

It is noteworthy to mention that two main simplifying assumptions have made to get this relation: (a) the projected contact area relation is considered as A = 24.56h2 which is used for an ideal Berkovich indenter tip, and (b) instead of the contact or plastic depth, the total depth is used in the contact area function.

Experimental Procedure

As mentioned in preceding sections, as a first step, the specimens should be thoroughly prepared and the tip should be carefully calibrated; the tests then are triggered by running the loading-hold-unloading cycles as follows: before any measurement, the tip drift should be controlled at a rate below 0.05 nms−1, so it is held on the top of the sample surface until it gains the stabilized rate. The tip then moves downward to reach the material surface. As soon as the tip touches the sample surface, the loading stage begins with a constant \( \dot{P}/P \) ratio and it continues until a specified maximum depth of 10 μm. To account for the creep behavior of the polymer, the load is then held at this stage for 10 s, and eventually, the unloading part is carried out with a constant unloading rate until 10% of the maximum load. Since the goals are investigating the variation of \( \dot{P}/P \) ratio during the whole nanoindentation experiment from zero to the maximum depth, and also its contribution on the indentation strain rate, a series of tests are performed on annealed PMMA and PC samples with three different set values of \( \dot{P}/P \) (0.005, 0.05, and 0.11 s−1). For each \( \dot{P}/P \) ratio, 25 indents are accomplished to get the accurate results and to prevent from interaction of the indents, 150 μm distance is considered between them.

Results and Discussion

Variation of the \( \dot{P}/P \) in the Course of an Indentation

The applied load on the sample and the tip travel distance are recorded as unbroken curves in the CSM nanoindentation experiments with nN and sub-nm exactness, respectively. Since the loading rate divided by the load is constant during the loading stage, i.e., \( \dot{P}/P=\eta \), the load is expected to be an exponential function of time as follows:

$$ P=\beta {e}^{\eta t}. $$
(9)

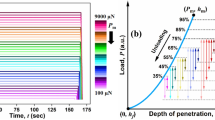
where β is the constant obtained by solving the ordinary differential equation (ODE). The load variation with time during the loading section of the nanoindentation on PC sample is presented in Fig. 1 (Voyiadjis and Malekmotiei 2016); the figure shows the results for three different set \( \dot{P}/P \) ratios and their exponential interpolations (lines) for comparison. The result curves depart from the exponential behavior at shallow indentation depths while they behave in accordance with the exponential variation within the long tip travel distance, especially for higher \( \dot{P}/P \) values. This discrepancy at the early stages of loading is due to the fact that based on Eq. 9, the initial loading condition is P(0) = β; however, the set initial condition for the experiment process is P(0) = 0. Thus, the indenter \( \dot{P}/P \) ratio can be adjusted to the set \( \dot{P}/P \) value after several nanometers of indentation displacement (or several seconds).

Fig. 1
figure 1

Variation of load versus time response of the indenter for PC sample measured on the loading segment of the nanoindentation experiment at three different set \( \dot{P}/P \) values. The lines represent the exponential interpolations (Reprinted from Voyiadjis and Malekmotiei 2016)

Full size image

The actual variation of \( \dot{P}/P \) ratio as a function of the indentation depth is presented in Fig. 2 for PC and PMMA (Voyiadjis and Malekmotiei 2016) at three different set values of this ratio which are shown as horizontal dashed lines. As mentioned before, the actual \( \dot{P}/P \) values do not approach their set values right after the indenter tip comes into the contact with the sample surface. Furthermore, the depth at which the \( \dot{P}/P \) ratio stabilizes does not depend on the material; however, it is extremely dependent on the set \( \dot{P}/P \) value. As depicted in Fig. 2 (Voyiadjis and Malekmotiei 2016), the depth beyond which the actual \( \dot{P}/P \) approaches the set value and stabilizes is smaller for the bigger set value of \( \dot{P}/P \): it is almost 1000 nm for the set \( \dot{P}/P \) value of 0.005 s−1 and reduces to 200 and 100 nm for the set \( \dot{P}/P \) values of 0.05 and 0.11 s−1, respectively. Interestingly, the starting point of actual value of \( \dot{P}/P \) is not dependent on the material and set \( \dot{P}/P \) ratio, and it approximately equals 0.3 s−1 for all experiments.

Fig. 2
figure 2

Variation of the actual \( \dot{P}/P \) values with indentation depth at three different set \( \dot{P}/P \) values for (a) PC and (b) PMMA (Reprinted from Voyiadjis and Malekmotiei (2016))

Full size image

Variation of the Strain Rate in the Course of an Indentation

In the CSM nanoindentation method, since the tip displacement is recorded continuously with time, the indentation strain rate can be directly calculated by using Eq. 7 and simple numerical differentiation as a continuous function of the indentation depth. In addition, indirect evaluation of the indentation strain rate during the loading segment of the test is possible by incorporating Eq. 7 and using the recorded load on the sample and the measured material hardness as functions of the depth. Since to employ Eq. 8 the variation of the instantaneous hardness rate divided by hardness (\( \dot{H}/H \)) is required, this parameter is represented in Fig. 3 (Voyiadjis and Malekmotiei 2016) at three different set \( \dot{P}/P \) ratios for PC and PMMA . As depicted in Fig. 5, the material hardness is higher at shallower indentation depths (indentation size effect) and then reaches a plateau at the certain depth which is the representative of the macroscopic hardness. Therefore, this trend results in the negative values of the \( \dot{H}/H \) ratio at the initial stages of the loading section and finally zero values of \( \dot{H}/H \) at deep part of the indentation (see Fig. 3). As another result obtained from Fig. 3, the depth beyond which \( \dot{H} \) can be assumed zero depends on the material and the set \( \dot{P}/P \) value.

Fig. 3
figure 3

Variation of the instantaneous hardness rate divided by hardness \( \left(\frac{\dot{H}}{H}\right) \) with indentation depth for PC and PMMA at set \( \dot{P}/P \) equal to (a) 0.005, (b) 0.05, and (c) 0.11 s−1 (Reprinted from Voyiadjis and Malekmotiei (2016))

Full size image

Figure 4 (Voyiadjis and Malekmotiei 2016) displays the variation of the indentation strain rate with the indentation depth calculated based on the two different approaches. Since both methods show almost the same results, it reveals the validity of the assumptions made by Lucas and Oliver (1999) to obtain Eq. 8 not only for deep but also shallow indentations of polymeric glasses. The most important result is that the indentation strain rate is not constant during the loading segment of the CSM nanoindentation of glassy polymers, and its variation is material and rate dependent. However, it can be assumed to be constant and equal to \( \frac{1}{2}\frac{\dot{P}}{P} \)for deep enough indentation experiments.

Fig. 4
figure 4

Variation of the indentation strain rate based on Eq. 7 (△) and Eq. 8 (○) versus indentation depth for experiments on PC (a–c) and PMMA (d–f) at three different set \( \dot{P}/P \) values. The dashed lines represent the expected values of strain rate \( \left(\frac{1}{2}\frac{\dot{P}}{P}\right) \) (Reprinted from Voyiadjis and Malekmotiei (2016))

Full size image

Indentation Size Effect

In rate-dependent materials including polymers, the flow stress extremely depends on the applied loading (strain) rate: the higher the experiment strain rate, the higher the yield stress (Voyiadjis and Samadi-Dooki 2016; Samadi-Dooki et al. 2016; Malekmotiei et al. 2015; Richeton et al. 2006; Rottler and Robbins 2003). Therefore, since there is a relation between the flow stress and hardness of the material through Tabor’s relation (Prasad et al. 2009), the higher value of hardness is expected from nanoindentation with the higher strain rate. The variation of hardness versus the tip displacement is presented in Fig. 5 (Voyiadjis and Malekmotiei 2016) for experiments on PC and PMMA samples at three different set \( \dot{P}/P \) values. It is observed that the obtained hardness values are higher as the strain rate increases; especially, the macroscopic hardness which is the hardness at the deep part of the nanoindentation and is the plateau for each curve depends on both material and strain rate. It is clear in these figures that the strain rate dependency of PMMA is more considerable which is, physically, demonstrated as smaller shear activation volumes in this material (Malekmotiei et al. 2015). Another observation in Fig. 5 is the profound increment of the hardness as the depth decreases during each indentation which is known as the ISE at nanoscales (Shen et al. 2006; Lam and Chong 1999; Zhang and Xu 2002). Due to the above-mentioned reason, the increased values of the material hardness at shallow indentation depths might be correlated with the higher values of the strain rate at these depths. However, an exact quantitative analysis is needed to understand and evaluate this possible relationship.

Fig. 5
figure 5

Variation of the hardness versus indentation depth during the loading segment of the experiments on (a) PC and (b) PMMA at three different set \( \dot{P}/P \) values (Reprinted from Voyiadjis and Malekmotiei (2016))

Full size image

Many studies show that there is a linear relationship between the flow stress (or hardness) of the polymeric glasses and the logarithm of the strain rate. The explicit relationships have been previously obtained for PC and PMMA by nanoindentation evaluations (Samadi-Dooki et al.2016; Malekmotiei et al.2015). Using the obtained formulations and the strain rate variation during indentation, the fictitious hardness can be calculated for each test. It should be mentioned that to calculate the fictitious hardness, it is assumed that the hardness variation is just the result of the strain rate variation during the loading stage. Figure 6 shows the actual measured hardness as well as the calculated hardness versus the indentation depth for PC and PMMA at three different set \( \dot{P}/P \) values for comparison. The curves of PC sample show that the calculated hardness is almost constant and there is no considerable change during a test; however, its variation during each indentation on PMMA sample is notably large in amount and follows almost the same hardening pattern at shallow depths as the actual hardness variation trend. In addition, for PMMA, the calculated hardness is the same (about 336 MPa) for all \( \dot{P}/P \) values when the loading stage is triggered, which is acceptable for the reason that the strain rate at the beginning of the indentation is also the same for different \( \dot{P}/P \) ratios (Fig. 4), while the actual hardness at this point (maximum hardness in each curve) is different for different \( \dot{P}/P \) values in both PC and PMMA. More importantly, as Fig. 4 represents the strain rate variation in the course of an indentation is approximately material independent, however, PMMA reveals a more intense strain rate dependency of hardness response than PC (Fig. 5); therefore, a more profound indentation size effect is expected to be observed in the nanoindentation of PMMA. Nevertheless, the real situation is different since the hardness variation at shallow depths is more noticeable for PC in comparison with PMMA (see Figs. 5 and 6) (Voyiadjis and Malekmotiei 2016). The main result from these observations is that although the strain rate variation during the loading segment of the CSM nanoindentation on PC and PMMA is notable, it cannot be the major cause of the observed ISE in amorphous polymers. As a matter of fact, the indentation strain rate variation during the loading has no contribution to the observed ISE of PC and its contribution to the ISE phenomenon in PMMA is negligible. Additionally, assuming the constant strain rate during the CSM nanoindentation of polymeric glasses for the size effect studies seems to be reasonable and there should exist other mechanisms behind this phenomenon which are correlated to the localization and or free surface effects (Alisafaei and Han 2015; Han et al. 2016).

Fig. 6
figure 6

Variation of the calculated (△) and actual (○) hardness versus indentation depth during the loading segment of the experiments on PC (a–c) and PMMA (d–f) at three different set \( \dot{P}/P \) values (Reprinted from Voyiadjis and Malekmotiei (2016))

Full size image

It is noteworthy to mention that another important factor which can affect the contact area and, subsequently, the measured hardness, especially at shallow depths of the indentation, is the material pile-up around the indenter tip. In Fig. 6, since the calculated hardness is obtained from the direct measurement of the indentation strain rate (\( \dot{h}/h\Big) \) (Samadi-Dooki et al. 2016; Malekmotiei et al. 2015), it is not affected by the material pile-up, while the actual measured hardness in this figure could be affected by the pile-up. For this reason, the material pile-up around the tip could be another factor that causes the difference between the calculated hardness of material and the actual one.

Fig. 7
figure 7

Variation of the elastic modulus versus indentation depth during the loading segment of the experiments on (a) PC , and (b) PMMA at three different set \( \dot{P}/P \) values (Reprinted from Voyiadjis and Malekmotiei (2016))

Full size image

Another important phenomenon which is usually observed during the CSM nanoindentation experiments is a small size effect on the recorded elastic modulus of the material. As shown in Fig. 7 (Voyiadjis and Malekmotiei 2016), it is an increased Young’s modulus at shallower indentation depths. This phenomenon is in contrast to the earlier observations from particle embedment experiments (Teichroeb and Forrest 2003; Karim and McKenna 2011, 2012, 2013; Hutcheson and McKenna 2007). As discussed comprehensively in the literature (Parry and Tabor 1973, 1974) the applied hydrostatic pressure on the polymer samples can hamper the chain movements which are required for relaxation processes and can subsequently result in a considerable increment of the glass transition temperatures of the material. Based on that, it has been proposed that, in nanoindentation experiments, the contact loading at the indenter tip-polymer interface induces hydrostatic pressure under the tip which increases the glass transition temperature of the sample near the surface, and correspondingly, the increased stiffness of the material at low indentation depths has been related to the increment of Tg (Gacoin et al. 2006; Tweedie et al. 2007). Therefore, the observed considerable material stiffening at shallow indentation depths (for depths of <50 nm in Fig. 7) (Voyiadjis and Malekmotiei 2016) could also attribute to the elevated values of Tg at the surface layer within this tip travel distance compared to the bulk. Moreover, incorporating the shear transformation theory, Voyiadjis and Samadi-Dooki (2016) have proposed a model for yielding and plasticity of amorphous polymers which shows the relationship between the yield stress (which is proportional to hardness through Tabor’s relation) and an activation energy which itself is a function of the elastic modulus of the material. Thus, as another confirmation, there exists a possibility that the increased hardness observed at the shallow indentation depths to be interrelated to the increased elastic modulus at these depths. This hypothesis, however, should be viewed as a qualitative observation and treated cautiously since there is a noticeable difference between the length scales during which the elastic modulus and hardness increments are observed (see Figs. 5 and 7).

Conclusions

The mechanical behavior of viscoelastic-viscoplastic materials, including polymers, strongly depends on the rate at which they are loaded. In the case of the nanoindentation, where these behaviors are evaluated at nanoscales, there are different methods in which the loading rate can be controlled in a way that the strain rate changes or remains constant during the experiment. For many reasons, for example, to study the effect of the temperature, thermal history, composition of alloys, etc., it is desirable to conduct a test during which the strain rate remains constant. The continuous stiffness measurement (CSM) nanoindentation is a technique which offers testing at constant loading rate to load ratio (\( \dot{P}/P \)) ratios; this has been manifested as constant strain rates during the test. In this chapter, the assumption of the constant strain rate during this nanoindentation technique is studied for glassy polymers. Investigating the instantaneous variations of \( \dot{P}/P \) and strain rate during the CSM nanoindentation on poly(methyl methacrylate) (PMMA) and polycarbonate (PC) samples showed that this assumption is not valid during the whole test and the strain rate changes in the early stages of the indentation before acceptable stabilization; the depth beyond that this parameter stabilizes depends on the material and the set \( \dot{P}/P \) value. It has been shown that although by assuming the constant value of \( \dot{P}/P \), an exponential load-time response of the indenter is expected, the load-time curves do not obey the exponential variation in early stages of the loading. The reason is the incompatibility of the actual initial load with the initial condition of the exponential loading which is required to assure a constant \( \dot{P}/P \). To overcome this problem, one can apply a very small load prior to the main loading segment of the experiment; this adjusts the aforementioned incompatibility of the initial condition. By this adjustment, it is expected that the \( \dot{P}/P \) value during the whole test remains constant and equals the initial set value. However, it may not lead to a constant strain rate since the hardness variation rate also contributes to the strain rate variation as proposed by Lucas and Oliver (1999). The strain rate can be assumed constant only at deep enough indentations where the load-displacement curve obeys the Hertzian relation (Malekmotiei et al. 2015). In this chapter, the possible effect of the variation of the strain rate during the indentation on the observed indentation size effect (ISE) in amorphous polymers has also been discussed (Voyiadjis and Malekmotiei 2016). While it is concluded that the increased strain rate within the shallow indentation depths cannot be the sole reason for the observed profound ISE, contribution of the other factors, such as material pile-up around the tip and stiffening due to the glass transition temperature (Tg) shift induced by the hydrostatic component of the stress, have been qualitatively discussed.