Developing Virtual Microstructures and Statistically Equivalent Representative Volume Elements for Polycrystalline Materials

Abstract

This chapter introduces computational methods for generating virtual material microstructures of engineering materials with heterogeneities. Microstructures of polycrystalline materials containing localized features such as annealing twins, particulates or precipitates, and subgrain phases are the focus of this discussion. The methods use data from characterization methods to provide 3D statistical distribution and correlation functions that serve as inputs to the virtual microstructure generation process. Computational methods infer 3D statistical descriptors from 2D surface data and use stereology or other optimization-based projection techniques for 2D to 3D development. The chapter reviews the DREAM.3D software package and discusses newly developed methods to incorporate twins, particles, and subgrain-scale phases. Finally, the microstructure-based SERVE is introduced in the realm of establishing microstructure-property relations.

1 Introduction

The recent years have seen an increasing trend in the use of microstructure-based mechanistic models for predicting material deformation and extreme behavior like fracture and fatigue response. A primal need in the development of image-based micromechanical models is the creation of representative 3D virtual models of the microstructures. An obvious path is by direct image reconstruction from 3D experimental data on sample volumes of the microstructure. Such experimental data may be extracted from electron backscatter diffraction (EBSD) or scanning electron microscopy (SEM) images of serial-sectioning samples (Groeber et al. 2006) or from various computed tomography techniques (Turner et al. 2017). Deterministic models of the microstructure, representing the exact data from experiments (Bhandari et al. 2007), however, are not necessarily best suited for micromechanical simulations, since the microstructure itself may have significant spatial variations.

A less direct but effective approach is to represent structure through the use of tools that generate statistical distribution functions equivalent to desired sets obtained from experimental observations. These “statistically equivalent” virtual microstructures must capture the statistics of characteristic variables, such as grain shape and size, crystallographic orientations, and misorientations and their correlations (Groeber et al. 2008a,b). The approach generally entails quantification of experimental data followed by microstructure generation that statistically match material measurements to a predetermined degree of accuracy. It is capable of limiting the need for abundant data collection, as well as supplementing information when direct 3D data is unavailable. Furthermore it enables the incorporation of microstructural statistics in higher length-scale constitutive relations for microstructure-property relations. Finally, the ability to generate virtual microstructural instantiations allows for virtual design or sampling of the potential microstructural space, driving toward tailoring materials structure.

Creating statistically “accurate” material instantiations for many engineering materials is still in its infancy with many gaps and opportunities. Recent efforts, centered around integrated computational materials engineering (ICME) and the materials genome initiative (MGI) , assume at their core that both the material structure and functionality of materials can be captured in a digital environment. It is imperative to the success of these initiatives that the materials community develop methodologies for creating digital analogues to real materials. In practice, it is common to generate performance models with limited amount of microstructural information. Typically, simple geometric shapes or tessellations are used to represent microstructures with consideration of lower moments such as average values. The use of such lower moments is often inadequate for accurate prediction of many properties of interest, such as fatigue, fracture, creep, etc. Higher statistical moments of the microstructural distributions, depicting extreme values, are needed for these predictions. While 3D data collection plays a critical role, especially when extreme properties are of interest, 3D experimental methods alone are often not adequate for this framework. Many microstructural arrangements must be interrogated for probabilistic understanding of the relation between microstructure and these properties. To facilitate this, experimental data should be coupled with characterization methods to provide 3D statistical distribution and correlation functions that serve as the inputs to the synthetic microstructure generation process. An additional incentive in this development is to infer 3D statistical descriptors from 2D observations and surface data through the use of stereology or other projection techniques. This is particularly relevant due to the fact that 3D experimental techniques remain unavailable or prohibitively expensive to a large portion of the materials community.

Various methods have been proposed in the literature for generating polycrystalline or polyphase microstructures, e.g., in Sundararaghavan and Zabaras (2005), Kumar et al. (2016), Rollett et al. (2007), Saylor et al. (2004), Guo et al. (2014), Jiao et al. (2007, 2013) and Hasanabadi et al. (2016). In Sundararaghavan and Zabaras (2005), reconstruction of 3D microstructures is solved as a pattern recognition problem, where a microstructure database is used with limited statistical information available from planar images. Microstructures are represented in the form of undirected probabilistic graphs or Markov random fields for computing probability distribution of statistically similar microstructures in Kumar et al. (2016). In Rollett et al. (2007), a 3D grain-structure generation method is based on statistical data gathered from sections on different planes with assigned orientations. Statistically representative polycrystalline microstructures are computationally simulated in Saylor et al. (2004) from geometric and crystallographic observations from orthogonal sections. Maps on the orthogonal planes characterize the sizes, shapes, and orientations of grains, and a voxel-based tessellation technique is subsequently used to generate the microstructure. A dilation-erosion method is developed in Guo et al. (2014) for stochastic reconstruction of 3D duplex stainless steel microstructure containing percolating filamentary ferrite phase from 2D optical micrographs. In Jiao et al. (2007), the authors have concluded that the two-point correlation function space of a statistically homogeneous material can be expressed through a map, constructed on a selected set of bases of the function space. A procedure to model and predict microstructure evolution of lead-tin alloys has been developed using the two-point correlation function associated with different phases in Jiao et al. (2013). A method for 3D microstructure reconstruction from two-point correlation functions of 2D cross sections using conditional probability theorems and a phase-recovery algorithm is developed in Hasanabadi et al. (2016). The n-point correlation functions have been further used in Tewari et al. (2004) and Niezgoda et al. (2010) to reconstruct the microstructure and obtain homogenized properties. Recent work by the author’s group combines optimization tools like Genetic Algorithms (Goldberg 1989) with stereology-based projection techniques to develop 3D microstructures from 2D data (Pinz et al. 2018; Tu et al. 2019).

Direct numerical simulations (DNS) of large microstructural regions can be computationally prohibitive. To negotiate this, representative computational domains must be optimally defined for evaluating effective properties without having to solve large microstructural regions. This has led to the concept of a representative volume element (RVE) , which is foundational to computational estimates of structure-property relations. Originally introduced in Hill (1963) as a microstructural subdomain that is representative of the entire microstructure in an average sense, the RVE definition has undergone variations (Ostoja-Starzewski 2006; Torquato 2002; Pyrz 2006). For microstructures with nonuniformly dispersed heterogeneities, the statistically equivalent RVE or SERVE has been defined in Swaminathan et al. (2006), Swaminathan and Ghosh (2006) and McDowell et al. (2011) as the smallest microstructural domain, for which statistical distribution functions of morphological parameters, as well as material properties, converge to those for the entire microstructure. Based on the convergence property in focus, the SERVE can be classified into two categories, viz., (i) the microstructure-based SERVE or M-SERVE, in which morphological and crystallographic characteristics of the microstructure are the sole determinants of the representative volume, and (ii) the property-based SERVE or P-SERVE that are determined from convergence of selected material properties.

This chapter is aimed at discussing methods of generating 3D statistically equivalent virtual microstructures and M-SERVEs of structural materials that are characterized by polycrystalline and/or polyphase microstructures. It begins with a description of the open-source software package DREAM.3D, which is a popular, user-friendly standardized code for generating synthetic material instantiations. Subsequently some recent developments in modeling polyphase materials and polycrystalline materials, containing heterogeneities such as micro-twins and particulates, are discussed.

2 Creating Statistically Equivalent Virtual Polycrystalline Microstructures Using DREAM.3D

DREAM.3D is an open-source software package focused on creating a high-level programming environment to process, segment, quantify, represent, and manipulate digital microstructure data. A central goal of DREAM.3D is to enable the translation of microstructure quantification to a digital basis with easy-to-use software tools. The DREAM.3D environment is constructed to allow independently developed filters and plug-ins to interface with one another, enabling small research groups, government laboratories, start-up companies, and major industrial corporations to collaborate and leverage each other’s work. While DREAM.3D is a general suite of microstructure processing tools, one of the most common uses of the software is generating virtual material volumes for input into simulations of various types. This can readily be seen by viewing the references to the original publication introducing DREAM.3D (Groeber and Jackson 2014). The latest release of DREAM.3D can be downloaded from the website given in Jackson (2018).

Synthetic builders generally consist of two major processes, viz., generating features and spatial arrangements within a computational volume. Features may be generated by sampling the size, shape, and morphological and crystallographic orientation distributions observed by some experimental technique. Next, the features are placed in the volume with specific focus on the local neighborhoods of features. The sampling procedure, as well as the constraints used to place the features in the volume, is briefly described here. More detailed descriptions of the synthetic generation procedure can be found in Groeber et al. (2008a,b).

2.1 Representative Feature Generation

Idealized geometric objects have distributions of size, shape, and morphological orientation equivalent to those observed in the experimental volume, representing grains. In this representation, each feature is modeled as a geometric object (i.e., ellipsoid, super-ellipsoid, cube-octahedron, etc.) with a volume (V), a set of aspect ratios (b/a, c/a), and a morphological orientation (ϕ₁, Φ, ϕ₂) corresponding to the orientation of the major principal axes (a,b,c) relative to the global axes. First the experimental feature volume distribution is sampled, which is represented by the cumulative distribution function (CDF) fit to the experimental data. Many investigations have shown the feature volume distribution to be well represented within 1 → 2 standard deviations of the mean, by a log-normal distribution (Zhang et al. 2004; Groeber et al. 2008b). It has been shown in Donegan et al. (2013) that grain size distributions tend to deviate from log-normal near the tails of the distribution. This can be accounted for by sampling from a piecewise distribution using a different form near the tails. Features are sampled until the total volume of all features generated is slightly larger than the volume of the synthetic microstructural model (typically around 10% larger). Additional volume is needed because some features may lie partially outside the domain or overlap other features. If the volume being generated is to have periodic boundaries, then additional volume is not needed because the portion of the features that fall outside of the domain will be placed on the opposite side. Subsequent to the volume assignment, feature shapes are assigned in conformity with CDFs of the aspect ratios (b/a, c/a). The corresponding CDFs are represented in terms of a beta distribution, due to its bounds of [0,1]. Additionally, the shape distributions are treated as a function of grain size by assigning unique shape distribution functions to discretely binned volume ranges of grain size. The morphological orientation of each feature is defined by a set of rotations (ϕ₁, Φ, ϕ₂) needed to transform the global coordinates (X,Y,Z) onto the principal axes of the feature (X’, Y’, Z’). The orientation space is discretized into cubic bins, and the density in each bin represents the fraction of grains with that morphological orientation. Ellipsoidal orientations are created and assigned based on sampling this probability density function (PDF), similar to the size and shape distributions. The output of this process is a set of geometric objects, representative of the features having statistically equivalent volume, aspect ratio, and morphological orientations as the experimental reference data.

2.2 Feature Placement

Spatial arrangement of features in a microstructure and their subsequent interactions drive local material response that can manifest in macroscopic heterogeneity. After generating a set of geometric objects, it is important that the placement of the features captures the local microstructural discontinuities. There are multiple issues to consider when packing the features. The density of the objects, represented by the features, is one of the largest factors in developing the packing algorithm. For example, features representing particles of a low volume fraction phase will certainly be placed differently than features representing grains in a fully dense polycrystalline material. In the fully dense grain, for example, care must be taken to pack the volume as densely as possible, but minimize overlap between features in order to retain each feature’s prescribed shape. In both cases, the local neighborhood of the feature (i.e., neighboring features) must also be addressed during placement. The low volume fraction particles should be spaced equivalently to the experimental/reference data, and the densely packed grains should neighbor grains of sizes, shapes, and orientations similar to those seen in the experimental/reference data.

Alternative viable options for feature packing have been discussed in Groeber et al. (2008a) and Saylor et al. (2004). The approach used in DREAM.3D is a hybrid of methods in these references. The set of voxelized features are initially randomly placed in the volume. The features are then moved and swapped while enforcing constraints such as overlap or gap limits, number of neighboring features, size distributions of neighboring features etc. This approach generally yields near-optimal space filling through the overlap/gap limits and produces realistic neighborhoods by requiring local grain arrangements to match experimentally obtained metrics. The number of constraints affects the feasibility of finding a globally optimum arrangement. All clusters of unassigned voxels, corresponding to morphological incompatibility of features, are filled by a pseudo-grain coarsening process. A constrained Voronoi tessellation method discussed in Groeber et al. (2008b) is implemented to replace the voxelized representation of the grain aggregates by a solid-body surface representation of the grain boundaries.

A final step in the generation procedure is the assignment of crystallographic orientations to the placed features. The process of assigning crystallographic orientations is similar to the morphological orientation assignment process previously described, though they do not affect the grain morphology. Rotations transform the global coordinate axes to the crystal coordinate system, rather than the principal axes of the grain. Orientations are swapped and replaced while optimizing comparison to the experimental orientation and misorientation distributions .

2.3 Generating Statistically Equivalent 3D Virtual Microstructures

An example, demonstrating the use of the DREAM.3D software for microstructural characterization and 3D virtual microstructure reconstruction of a titanium alloy Ti-7Al, is shown in Fig. 1. This material has a predominantly hcp crystallographic structure (Pilchak 2013). A surface scan of the electron backscattered diffraction (EBSD) maps of the Ti-7Al alloy is shown in Fig. 1a. The morphological and crystallographic orientation, misorientation, and micro-texture distribution data from EBSD scans are input into the DREAM.3D software. The simulated statistically equivalent microstructure of dimensions 300 × 300 × 300 μm containing 515 grains is shown in Fig. 1b with colors representing the < c > -axis misorientation with neighboring grains. The simulated pole figures are compared with those from EBSD data in Fig. 1c. Furthermore the probability density functions of misorientation and grain size are compared with those from EBSD maps in Fig. 1d, e respectively. Good agreement is generally seen between the simulated and experimental probability density functions.

Fig. 1

(a) EBSD scan of Ti-7AL; (b) statistically equivalent 300 × 300 × 300 μm virtual microstructure containing 515 grains and showing the color plot of < c > -axis misorientation; comparison of (c) orientation distribution, (d) misorientation distribution, and (e) grain size distribution of the simulated microstructure with those from the EBSD data

3 Beyond DREAM.3D: Creating Statistically Equivalent RVEs of Polycrystalline and Polyphase Microstructures

While the DREAM.3D software is capable of generating virtual polycrystalline microstructures and SERVEs for various metals and alloys, incorporation of more complex microstructural features is still in nascent stages. Such features include those contained in polyphase and polycrystalline microstructures, e.g., annealing twins or particles and precipitates inside grains. This section will summarize a suite of algorithms that have been developed for creating M-SERVEs of complex polycrystalline and polyphase microstructures belonging to three distinct categories. These are:

• 1. Polycrystalline microstructures with localized features like annealing Σ3 twin boundaries, shown in Fig. 2a;

• 2. Multiphase microstructures like subgrain γ − γ′ microstructure of Ni-based superalloys, shown in Fig. 7a;

• 3. Polycrystalline microstructures with dispersed precipitates and particles, e.g., for Al 7075-T6, shown in Fig. 10a.

Fig. 2

(a) Serial sectioned EBSD images, (b) computer-assembled sections of EBSD images manifesting polycrystalline microstructure including twins, and (c) polycrystalline microstructure of parent grains only after removing twins, for the Ni-based superalloy Ren$\acute {e}$88-DT

3.1 Polycrystalline Microstructures with Annealing Twin Boundaries

Figure 2a shows EBSD images of a set of parallel sections of the superalloy Ren$\acute {e}$-88 DT microstructure, obtained by wire electrical discharge machining (EDM) of a 10 × 5 × 1 mm sample (Lenthe 2017). The 3D assembly and microstructure reconstruction are performed in the DREAM.3D software using (i) slice registration and alignment, (ii) voxel level cleanup, (iii) feature segmentation, and (iv) artifact removal as detailed in Bagri et al. (2018). Twin-related domains are grouped with a 5^∘ tolerance on both the disorientation axis and the disorientation angle. The resulting stacked and assembled 3D polycrystalline microstructure containing annealing twins is shown in Fig. 2b, where the grains are segmented with a 2^∘ tolerance. The ensemble contains 440 twins in 300 parent grains for a total of 740 twins and grains. The polycrystalline microstructure is dominated by large aspect ratio, annealing Σ3 twins that have a 60^∘ misorientation angle about the < 111 > crystal lattice axis. Details on the reconstruction of M-SERVEs are given in Bagri et al. (2018).

The following steps are executed in sequence to generate statistically equivalent volumes of twinned polycrystalline microstructures from scanned EBSD images.

• 1. Process the EBSD section data and construct the digitally assembled polycrystalline ensemble including twins;

• 2. Identify and remove twins from the digitally assembled microstructure to manifest the parent grains shown in Fig. 2c;

• 3. Extract the statistics of parent grains from the EBSD data;

• 4. Create statistically equivalent virtual parent grain microstructures from the 3D EBSD data;

• 5. Extract correlation statistics of twins with respect to parent grains from the EBSD data in the digitally assembled microstructure;

• 6. Insert twins in the parent microstructure to match statistical correlations.

The DREAM.3D software (Groeber and Jackson 2014) is employed in steps 1–4 to create the digital polycrystalline ensembles from EBSD data in Fig. 2d: remove twins in Fig. 2c and subsequently extract statistics of the parent grains. The statistics of characteristic features in the twin-free parent grains in Fig. 2c, including probability distributions of grain size, orientation, and misorientation angle, are acquired following (Groeber et al. 2008a,b). The probability density distribution of grain size is shown in Fig. 3b. For instances where only 2D EBSD are available, methods of estimating 3D grain sizes from 2D surface data, e.g., through the stereology relation d_3D ∼ 4∕πd_2D (Groeber et al. 2008a), may be used.

Fig. 3

(a) Schematic of twins and parent grain and (b) statistics of grain size distribution after removing twins

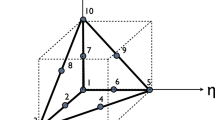
In step 5, sample statistics are extracted from the EBSD data to generate probability distribution and correlation functions of twins with respect to parent grains. These are subsequently used to insert twins in the parent microstructure. A schematic representing the relation of a twin with the parent grain is shown in Fig. 3a. Statistical analysis shows the parent grain size d, number of twins in parent grain n, minimum distance x of the twin from the parent grain centroid, and the twin thickness t are strongly correlated. The joint probability distribution of the correlation between twins and parent grains is expressed through a function P₀(d, n, t, x). The correlation statistics and joint probability distributions are shown in Fig. 4.

Fig. 4

Correlation statistics from the EBSD data: (a) joint probability density distribution of the parent grain size and number of twins and (b) conditional probability density distribution of twin thickness

The algorithm to insert twins in the parent grain microstructure consists of the following steps.

• 1. Use the joint probability distribution of parent grain size and number of twins $P_1(d,n)=\int \int P_0(d,n,t,x)~ dt ~ dx$ and the conditional probability distributions of both twin distance from parent centroid P₂(x|d = D, n = N) and twin thickness P₃(t|d = D, n = N) for twin insertion.

• 2. Determine the number of twins, twin thickness, and the twin distance from parent centroid using a Monte Carlo-based acceptance-rejection scheme.

• 3. Locate the (111) plane at a distance x from the parent centroid.

• 4. Identify voxels that are at a distance $\frac {t}{2}$ from the mid-thickness (111) plane.

• 5. Calculate the rotation matrix from the rotation matrices of the parent grain and the twin with respect to parent, i.e., R = R_parentR_twin

• 6. Determine Euler angles of the twin, and reassign them to voxels of the twin.

The four-dimensional probability distribution P₀(d, n, t, x) requires a very large number of grains. Hence, a marginal probability function is used, when a smaller set of statistical information is available. In step 1, the joint probability density distribution, e.g., in Fig. 4a, is used for parent grain and number of twins per parent, while the conditional probability distributions are used for the twin thickness (Fig. 4b) and twin distance from the parent centroid. With this assumption, the four-dimensional distribution space is approximated as:

$$\displaystyle \begin{aligned} P_0(d,n,t,x)\approx P_1(d,n) P_2(x | d=D, n=N) P_3(t | d=D, n=N) \end{aligned} $$

(1)

This approximation is valid for any parent grain size and associated twins, where the twin size and distance from the parent centroid are uncorrelated. When inserting the coherent twins, they must be placed with the proper orientation relationship to the parent. The twin boundary plane orientation in the specimen frame m_s is first determined using the crystallographic orientation vector of the parent grain as m_s = R_parentm_p, where R_parent and m_p = (111) are the parent grain rotation matrix and grain boundary plane orientation vector in the crystal coordinates, respectively. Subsequently, the plane is located at a previously selected distance x from the parent centroid. The grain boundary plane will pass through the point ${\mathbf {x}}_p={\mathbf {x}}_c+x \frac {{\mathbf {m}}_s}{\|{\mathbf {m}}_s\|}$. Here, x_p is the position vector of a point in the grain boundary, x_c is the position vector of the parent grain centroid, and ∥m_s∥ is the norm of the grain boundary normal. The rotation matrix of the twin in the specimen frame R is obtained from the rotation matrix of parent grain R_parent and the rotation matrix of the twin with respect to parent grain R_twin as R = R_ParentR_twin. Using the components of R, the Euler angles of twins are expressed as:

$$\displaystyle \begin{aligned} \phi_1=tan^{-1}(-\frac{R_{13}}{R_{23}}), ~~~ \varPhi=cos^{-1}(R_{33}), ~~~ \phi_2=tan^{-1}(\frac{R_{31}}{R_{32}}) \end{aligned} $$

(2)

Repeating steps 1–6, the set of twins are inserted into the parent grain microstructure.

3.1.1 An Example of Validated M-SERVE Generation

The algorithm is used with EBSD data in Alam et al. (2016) for validating the virtual microstructure generation process. The statistics shown, e.g., in Fig. 4 are used to insert twins in the parent grain microstructure. A 250 × 250 × 250 μm 3D-SEVPM consisting a total of 1700 parent and twins is shown in Fig. 5a. The cumulative distribution function of the twin distance d from parent centroid for this 3D-SEVPM is compared with that from the EBSD scan in Fig. 5b.

Fig. 5

(a) Simulated 3D statistically equivalent polycrystalline microstructure (3D-SEVPM) with twins inserted in the parent grains and (b) comparison of the cumulative distribution function of twin distance d from parent centroid in the EBSD scan and 3D-SEVPM of size 250 μm

Studies in Bagri et al. (2018) have shown that the 3D-SEVPM converges to the M-SERVE at 150 μm, which corresponds to approximately 400 grains and twins. Comparison of the M-SERVE statistics with the EBSD data is made through a few probability distributions. The distribution of the global misorientation and twin thickness is compared in Fig. 6. The prominent peak in misorientation angle distribution at 60^∘ indicates the presence of twins in the microstructure. A good agreement is obtained for all the distribution plots. This is a step in validating the virtual microstructure generation method. In both the EBSD data and M-SERVE, about 40% of the parent grains are seen to remain untwinned .

Fig. 6

Probability distribution of (a, b) misorientation angle and (c, d) twin thickness from the EBSD data and the M-SERVE, respectively

3.2 Two-Phase Microstructures Underlying Polycrystalline Grains

Polycrystalline nickel-based superalloys like Ren$\acute {e}$-88 DT have an underlying subgrain-scale two-phase microstructure consisting of a dispersion of γ and γ′ precipitates, as shown in Fig. 7a. Subgrain-scale morphological characteristics like volume fraction, mean size, and channel-width or spacing of γ′ precipitates have a major effect on their mechanical properties (Unocic et al. 2011). Modeling their mechanical and physical behavior requires robust representation of these morphological features in the M-SERVE. Many approaches have been employed to include precipitate structure in performance simulations, e.g., Pollock and Argon (1992), Nouailhas and Cailletaud (1996), Busso et al. (2000), Fromm et al. (2012), Parthasarathy et al. (2004) and Keshavarz and Ghosh (2015).

Fig. 7

(a) Scanning electron microscope image of a microstructural section of Ren$\acute {e}$-88 DT acquired by FIB serial sectioning, (b) segmented SEM image after thresholding and despeckling, and (c) spurious connectivity from serial sectioning after segmentation

This section discusses a methodology developed in Pinz et al. (2018) for generating M-SERVEs of two-phase γ − γ′ microstructures from 2D microstructural scans of 3D data, using the following steps.

• 1. FIB-SEM serial sectioning: Acquisition of high-fidelity 3D γ − γ′ microstructural data necessitates a high-throughput automated serial-sectioning process coupled with high-resolution SEM data extraction.

• 2. Image processing and data cleanup: Cleanup and subsequent segmentation of γ and γ′ phases generate a reference 3D voxelization of the microstructure.

• 3. Feature extraction and statistical characterization: Parametrization and statistical characterization of the γ′ precipitate morphology and designation of the relative precipitate positions are needed for establishing spatial distributions.

• 4. Statistically equivalent microstructural reconstruction: Optimally minimum microstructures are generated with morphological and spatial statistics equivalent to those of the large-imaged microstructures .

3.2.1 Data Extraction with 3D FIB Serial Sectioning and SEM-Based Imaging

Recent advances in tomographic methods, e.g., in Uchic et al. (2006), and Echlin et al. (2014) and image processing tools have greatly increased the accessibility of 3D data sets for a variety of materials. Microstructural data used for the generation of the polyphase M-SERVE is obtained from Lenthe (2017), where a FIB is used to expose parallel layers of the material that are imaged with a SEM. A sample section is shown in Fig. 7a. The in-plane resolution is 2.5 nm per pixel with 20 nm between the slices. The sections are aligned via a convolution method to reduce the effects of instrumental drift. The contrast difference between the γ and γ′ phases is not large enough to allow for robust automatic segmentation of the SEM images (Pollock and Tin 2006) and can require extensive cleanup.

3.2.2 Image Segmentation

The FIB-SEM technique in Lenthe (2017) is used to collect 180 gray-scale images, each with a size of 1996 × 1596 pixels. The resultant image stack yields a 3 × 4 × 5 μm volume. An automated image segmentation process begins with local noise reduction followed by image sharpening to enhance the contrast between the phases. The sharpened image stack is segmented with a minimum entropy threshold (Li and Lee 1993) as shown in Fig. 7b. Sections are interpolated between extracted images in all three directions. The interaction volume of the SEM causes spurious connectivity between the precipitates as shown in Fig. 7c. A watershed segmentation procedure (Meyer 1994) is used to separate the conjoined precipitates using a gradient field given as:

$$\displaystyle \begin{aligned} \mathcal{G}(i,j,k) = \mathcal{B}_{\mathrm{int}}(i,j,k) \frac{\sum_{\bar{i}=0}^{N_{x}} \sum_{\bar{j}=0}^{N_{y}} \sum_{\bar{k}=0}^{N_{z}}{\mathcal{D}_{\mathrm{int}}(\bar{i},\bar{j},\bar{k})}e^{-\left [ \left ( \frac{(\bar{i}-i)^2}{2\sigma^2} \right )+\left ( \frac{(\bar{j}-j)^2}{2\sigma^2} \right )+\left ( \frac{(\bar{k}-k)^2}{2\sigma^2} \right )\right ]}}{\sum_{\bar{i}=0}^{N_{x}} \sum_{\bar{j}=0}^{N_{y}} \sum_{\bar{k}=0}^{N_{z}}e^{-\left [ \left ( \frac{(\bar{i}-i)^2}{2\sigma^2} \right )+\left ( \frac{(\bar{j}-j)^2}{2\sigma^2} \right )+\left ( \frac{(\bar{k}-k)^2}{2\sigma^2} \right )\right ]}} \end{aligned} $$

(3)

where $\bar {i},\bar {j},\bar {k}$ are dummy indices, N_x, N_y, and N_z are the number of voxels in the x, y, z directions, respectively, and N_slice is the total number of slices after interpolation. $\mathcal {D}_{\mathrm {int}}$ is a map from each voxel to the value of its distance to the nearest boundary in the plane, and $\mathcal {B}_{\mathrm {int}}$ is a binarized map relative to $\mathcal {D}_{\mathrm {int}}$. The latter is an indicator function of whether a voxel (i, j, k) is in a precipitate or not. The standard deviation σ of the Gaussian blur is set to $\frac {1}{10}$th of the mean particle radius. This gradient field is chosen to reduce disconnected over-segmentation by the watershed algorithm. The purpose of the 3D Gaussian blur is to mitigate effects from the voxelization of the precipitate edges. After application to the initially connected inclusions, the watershed segmentation algorithm produces a final binary voxelized map $\mathcal {B}_{\mathrm {final}}$ that contains approximately 6000 contiguous precipitates.

3.2.3 Mapping Precipitate Domain to a 3D Parametric Function Model

Homogenized constitutive models require the precipitate morphology to be described by a parametrized function with a finite number of parameters and coefficients. These parameters may be calibrated from the actual surface profiles by optimization. The chosen parametric function for surface representation represents a generalized super-ellipsoid (GSE) , delineated as:

$$\displaystyle \begin{aligned} \left( \frac{\bar{x}}{a} \right )^{N1} + \left ( \frac{\bar{y}}{b} \right )^{N2} + \left ( \frac{\bar{z}}{c} \right )^{N3} = 1 {} \end{aligned} $$

(4)

The position vector $\bar {\mathbf {x}}(=\bar {x},\bar {y},\bar {z})$ corresponds to the location of a GSE surface point x_p(= x_p, y_p, z_p) relative to its centroid x₀(= x₀, y₀, z₀) in its principal coordinate system represented by the Euler angles (ϕ₁, Φ, ϕ₂). The relative coordinates are expressed as $\left \{ {\bar {\mathbf {x}}} \right \}= \left [\mathbf {R} \right ] \left \{ {\mathbf {x}}_p-{\mathbf {x}}_0 \right \}$, where $\left [ \mathbf {R} \right ]$ is the rotation matrix for the precipitate coordinate system. In Eq. (4) a, b, c correspond to the principal axis lengths of the super-ellipsoid, and N1, N2, N3 are exponents representing the shape. The parametrized function in Eq. (4) entails evaluation of the parameter set $Y_{\mathrm {par}} \in \left \{x_0,y_0,z_0,N1,N2,N3,a,b,c,\phi _1,\varPhi ,\phi _2 \right \}$. The parameters are calibrated by solving an optimization problem that minimizes the orthogonal distance between m surface points of a precipitate and the parametrized surface as:

$$\displaystyle \begin{aligned} &\underset{Y_{\mathrm{par}}}{\text{Minimize}} ~ \sum_{i=1}^{m} D^2_i=\sum_{i=1}^{m} \|{\mathbf{x}}_i-({\mathbf{x}}_p)_i\|{}^2= \sum_{i=1}^{m} \left\{ x_i - (x_p)_i \right \}^2 \\&\quad +\left \{ y_i - (y_p)_i \right \}^2 + \left \{ z_i - (z_p)_i \right \}^2 {} \end{aligned} $$

(5)

$$\displaystyle \begin{aligned} &\text{subject to the constraint that each point }i\text{ belongs to the GSE surface} \\ &\left( \frac{\bar{x}_i}{a} \right )^{N1} + \left ( \frac{\bar{y}_i}{b} \right )^{N2} + \left ( \frac{\bar{z}_i}{c} \right )^{N3} = 1 ~~\forall~ i \in [1,m] {} \end{aligned} $$

(5b)

The variable D_i corresponds to the absolute Euclidean distance between a surface point on the precipitate at coordinates (x_i = (x_i, y_i, z_i)) for a point i and its conjugate surface point (x_p)_i = (x_p)_i, (y_p)_i, (z_p)_i on the parametrized GSE in the current iterate.

3.2.4 Validation of Precipitate Mapping and Reconstruction

Distributions of morphological parameters of the precipitates generated are used to validate the effectiveness of the parametrization.

I. Dice Index: The Dice index (DI) is used as a goodness-of-fit metric to compare the orthogonal distance minimization (ODM) algorithm with an alternate moment-based algorithm proposed in MacSleyne et al. (2009). DI is defined as the volume of overlap between two objects (the actual precipitate and the GSE) divided by the composite volume of the union of the two objects as: $DI=\frac {V_{FIB}\cap V_{GSE}}{V_{FIB}\cup V_{GSE} }$. It ranges from 0 corresponding to no overlap to 1 for perfect intersection. In Fig. 8a, the distribution of DI is compared for GSE’s generated by alternate methods. “FULL” corresponds to N1 ≠ N2 ≠ N3, while “REDUCED” has N = N1 = N2 = N3.

Fig. 8

Probability distribution of (a) the DI for equivalent ellipsoids generated by alternative methods and (b) shape parameters in the ODM algorithm and MLE shifted log-normal distribution

II. Size, Shape, and Orientation Distributions: The distributions of the major, minor, and intermediate axes a, c, and b, respectively, represent the size and aspect ratio of the precipitate. Figure 8b compares the distribution of the shape parameter N obtained in the ODM algorithm to a log-normal distribution representation of the same by the maximum likelihood estimation (MLE). Orientations of the GSEs by the ODM algorithm with reduced shape parameters are used to generate equivalent orientation distribution functions using spherical harmonics for crystallographic texture.

3.2.5 Statistically Equivalent Microstructure by Dispersing Precipitates

A set of precipitates with representative morphological parameters are generated to yield a desired volume fraction. A placement algorithm that involves random allocation with local perturbation to avoid precipitate overlap, as well as microstructural shuffling through an energy minimization scheme for positional stability, is implemented. This method is iteratively continued with precipitate size scaling until the experimental volume fraction is attained.

An optimization schedule is executed to minimize the difference in the two-point correlation function S₂ for the experimental microstructure and the 3D statistically equivalent virtual microstructures (3D-SEVMs) . The two-point correlation function S₂ is a statistically convergent measure of the microstructural heterogeneity in Tewari et al. (2004) and Jiao et al. (2007). For isotropic distributions, it can be approximated by a closed-form solution as:

$$\displaystyle \begin{aligned} S_2(r) = {V_f}^{2} + {V_f}(1-{V_f})e^{\frac{-r}{r_0}} \frac{\mathrm{sin}\left ( \frac{2 \pi r}{a_0} \right )}{\frac{2 \pi r}{a_0}} {} \end{aligned} $$

(6)

where V_f represents the volume fraction of precipitates and a₀ and r₀ are calibrated parameters. A genetic algorithms (GA)-based optimization (Goldberg 1989) is used to minimize the difference in the S₂ function. The fitness function is expressed as:

$$\displaystyle \begin{aligned} FF_{S_2} = \left (\frac{a_o-a_o^{\mathrm{target}}}{a_o^{\mathrm{target}}} \right )^2 + \left (\frac{r_o-r_o^{\mathrm{target}}}{r_o^{\mathrm{target}}} \right )^2 {} \end{aligned} $$

(7)

Figure 9a shows examples of the reconstructed 3D-SEVMs for N_p = 10, 50, 100, and 200 precipitates. Validation tests of 3D-SEVMs are conducted by comparing morphological metrics that are not optimized during the reconstruction process. One relevant metric for plastic deformation is the distance to precipitate surface (DPS) distribution. Figure 9b shows a cumulative distribution function of DPS for experimental and 3D-SEVM volumes, exhibiting good agreement. Figure 9c plots the Kolmogorov-Smirnov (KS) test (Massey 1951) statistic between the 3D-SEVM with N_p= 10, 50, 100, and 200 precipitates and the FIB-SEM microstructural data. Both the median and an upper bound of the sampling error with frequency of 0.96 are plotted in this figure. The 3D-SEVM with 200 precipitates is sufficient for convergence, and hence this is the designated M-SERVE as detailed in Pinz et al. (2018).

Fig. 9

(a) Reconstructed 3D-SEVMs with 10, 50, 100, and 200 precipitates; (b) cumulative distribution function of distance to precipitate surface, generated from experimental data and 3D-SEVM; and (c) median and 96th percentile expected KS test statistic with 10, 50, 100, and 200 precipitates

3.3 Polycrystalline Microstructures with Dispersed Precipitates

Many engineering alloys have precipitates or particles dispersed in their polycrystalline microstructure. For example, the 7000-series aluminum alloys, e.g., Al 7075-T6, contain iron-rich or magnesium-rich precipitates in the aluminum matrix, as shown in Fig. 10a. Various models have been proposed for microstructure generation of porous materials and particle-reinforced metals, e.g., in Baniassadi et al. (2011), Rollett et al. (2006) and Guo et al. (2014). Following developments in the previous sections, this section discusses a method for constructing 3D virtual microstructures from 2D micrographs, accounting for grain and particle shape distributions, spatial arrangements of precipitates, as well as precipitate-grain spatial correlations. Stereological concepts are numerically implemented into a genetic algorithm (GA)-based optimization framework as detailed in Tu et al. (2019).

Fig. 10

Inverse pole figure maps of EBSD data and SEM images of TD/ND plane of the Al7075-T651 sample containing particles in polycrystalline microstructure; (b) DREAM.3D reconstructed 392-grain virtual microstructure; comparing statistical distributions of the virtual grain morphology with EBSD data for (c) grain size, (d) aspect ratio c/b

3.3.1 Stereological Reconstruction of the Grain Microstructure

Figure 10a shows a representative EBSD scan of a cross section from an aluminum alloy (7075-T6). Crystallographic orientation and misorientation distributions, as well as morphological distributions, e.g., grain size, aspect ratio distributions, are extracted from these scans. Stereological estimations of 3D size and aspect ratio distributions are made from 2D surface data following (Underwood 1972), and the 3D microstructure is constructed by DREAM.3D using these distributions. Figures 10 and 11 compare the morphological and crystallographic statistics of a 392-grain virtual microstructure with those from EBSD data.

Fig. 11

Comparing crystallographic distributions of the virtual grain with EBSD data for (a) orientation distribution (pole figures) and (b) misorientation distribution

3.3.2 Mapping Distributions of Precipitates to Parametrized GSEs

SEM images of precipitates are mapped to distributions of 3D generalized super-ellipsoids (GSEs) , similar to Sect. 3.3. Image processing of the SEM images includes contrast enhancement (adaptive histogram equalization), binarization (gray level thresholding), and noise removal (Wiener filtering). The SEM particle contours on the 2D surface are fitted to generalized super-ellipse using the 2D version of Eq. (5). The microstructures show precipitate clustering along the rolling direction (RD) (Rollett et al. 2007). The isotropic two-point correlation function or radial distribution function in Jiao et al. (2007) and Wang et al. (2016) is unable to characterize this directional clustering. The two-point correlation analysis of precipitates in the RD/ND plane in Fig. 12a shows a clear trend of directional clustering along the RD direction. Furthermore, the precipitate-grain spatial correlation is represented by the conditional probability distribution of the minimum distance to grain boundaries for a given precipitate size. Fracture toughness of aluminum alloys is sensitive to the closeness of precipitates to grain boundaries (Cai et al. 2007), which is obtained by overlaying the EBSD and SEM 2D data sets. Figure 12b manifests the clustering of precipitates of various sizes near grain boundaries.

Fig. 12

(a) Anisotropic two-point correlation function for precipitates and (b) conditional probability distribution of the distance to grain boundaries and precipitate size in the RD/ND plane

3.3.3 GA-Based Stereological Mapping from 2D to 3D Microstructures

A genetic algorithm (GA)-based optimization method (Goldberg 1989) is used to search for parameters of the 3D precipitate distributions, by minimizing the difference in cumulative distribution functions (CDFs) of 2D statistics of the virtual and experimental microstructures, using the equation:

$$\displaystyle \begin{aligned} \underset{X_k}{\text{Minimize}}\frac{1}{N_{\mathrm{descriptor}}}\sum_{k=1}^{N_{\mathrm{descriptor}}}\frac{1}{N_{\mathrm{bin}}^{(k)}}\sum_{i=1}^{N_{\mathrm{bin}}^{(k)}}\left|CDF_i^{\mathrm{experimental}} - CDF_i^{\mathrm{virtual}}\right| {} \end{aligned} $$

(8)

where N_descriptor corresponds to the number of descriptors, e.g., precipitate size, aspect ratio, shape parameter, and principal axes orientation. X_k stores the 3D shape distribution parameters for the k-th descriptor, and $N_{\mathrm {bin}}^{(k)}$ is the number of bins allocated to represent the cumulative distribution of descriptor k. Candidate sets of 3D super-ellipsoid semiaxis length (a, b, c), shape parameter (n), and principal axes orientation (α, β, γ) distribution parameters are stored in the array X. For every candidate set, representative 2D orthogonal sections are derived statistically from 3D virtual microstructures and compared with the EBSD surface image data. Subsequently, the parameters of the sectioned super-ellipses are solved with the method of undetermined coefficients. With known statistics of the virtually sectioned super-ellipses and experimental surface data, individual fitnesses are calculated from the minimization problem involving crossover and mutation operations.

3.3.4 Planting Precipitates in the DREAM.3D-Generated Grain Microstructure

The 3D super-ellipsoidal precipitates are now spatially dispersed in the 3D parent polycrystalline matrix. The dispersion of precipitate centroids is optimized by the GA methodology such that the anisotropic S₂ function and precipitate-grain spatial correlations of the sections match the experimental distributions. The fitness function of the optimization process is written as:

$$\displaystyle \begin{aligned} \begin{aligned} \underset{\mathbf{C}}{\mathrm{Minimize}} ~ &\frac{1}{N_{\mathrm{descriptor}}}\sum_{k=1}^{N_{\mathrm{descriptor}}}\\ &\left\{ \frac{1}{N_{\mathrm{section}}}\sum_{m=1}^{N_{\mathrm{section}}} \frac{1}{N_{\mathrm{bin}}^{(k)}*M_{\mathrm{bin}}^{(k)}}\sum_j^{N_{\mathrm{bin}}^{(k)}}\sum_i^{M_{\mathrm{bin}}^{(k)}}\left|CDF_{ij}^{\mathrm{virtual}} - CDF_{ij}^{\mathrm{experimental}}\right|\right\} \end{aligned} {} \end{aligned} $$

(9)

where C is the centroidal coordinates of precipitates, N_descriptor is the number of descriptors, N_section is the number of sections, and $N_{\mathrm {bin}}^{(k)}$ and $M_{\mathrm {bin}}^{(k)}$ are the number of bins used for the cumulative distribution function of a descriptor k.

The resulting two-phase reconstructed microstructure is shown in Fig. 13b. Figure 13b shows that the precipitates cluster along the RD (x-axis) in good agreement with the experimentally obtained microstructural distribution. Quantitative comparison of virtual and experimental microstructures in Fig. 14 shows good match of the 2D precipitate-precipitate and precipitate-grain boundary correlations.

Fig. 13

Representation of the of reconstructed two-phase microstructure with (a) precipitates only and (b) precipitates embedded in Al polycrystalline microstructure with grain boundaries

Fig. 14

Convergence of 2D statistics of particle descriptors to the experimental data: (a) particle-particle near neighbor distance with respect to the RDND plane data, (b) particle minimum distance to GB in (RDND)

3.3.5 Convergence of the M-SERVE

The convergence of various microstructural descriptors is studied for assessing the M-SERVE size. The descriptors include grain morphology, grain crystallography, particle morphology, and particle-grain spatial correlation. The errors in these distributions are estimated by the Kolmogorov-Smirnov test. From the M-SERVE convergence characteristics in Fig. 15 for two-point and precipitate-grain correlations, it is found that the M-SERVE size is controlled by precipitate-grain correlations. It converges for approximately 450 grains with 4500 precipitates .

Fig. 15

Convergence of M-SERVE with respect to (a) 3D particle two-point correlation function and (b) 3D distance to grain boundary-precipitate size joint distribution

4 Conclusions

This chapter discusses the development of computational methods for simulating statistically equivalent virtual microstructures of materials with complex heterogeneities. The methods consider polycrystalline materials containing localized features such as annealing twins, particulates or precipitates, and subgrain-scale precipitates in their polycrystalline structure. Data from image analysis and characterization are used to construct 3D statistical distribution and correlation functions. This serves as input to the virtual microstructure generation process. 3D experimental data extraction techniques are sometimes unavailable or prohibitively expensive to generate. Consequently, the methods accommodate computational approaches that infer 3D statistical descriptors and functions from 2D observations and surface data, from stereology and other optimization-based projection techniques. The chapter introduces the open-source software package DREAM.3D that is now widely used for generating virtual microstructures of polycrystalline materials. It then goes beyond DREAM.3D into more newly developed methods for incorporating twins, particles, and subgrain-scale phases in polycrystalline microstructures. Finally the concept of the microstructure-based SERVE or M-SERVE, in which morphological and crystallographic characteristics of the microstructure are determinants of the statistically equivalent representative volume element, is introduced.