Abstract
This chapter deals with the fundamental mathematical tools and the associated computational aspects for constructing the stochastic models of random matrices that appear in the nonparametric method of uncertainties and in the random constitutive equations for multiscale stochastic modeling of heterogeneous materials. The explicit construction of ensembles of random matrices but also the presentation of numerical tools for constructing general ensembles of random matrices are presented and can be used for high stochastic dimension. The developments presented are illustrated for the nonparametric method for multiscale stochastic modeling of heterogeneous linear elastic materials and for the nonparametric stochastic models of uncertainties in computational structural dynamics.
Access provided by CONRICYT-eBooks. Download reference work entry PDF
Similar content being viewed by others
Keywords
- Random matrix
- Symmetric random matrix
- Positive-definite random matrix
- Nonparametric uncertainty
- Nonparametric method for uncertainty quantification
- Random vector
- Maximum entropy principle
- Non-Gaussian
- Generator
- Random elastic medium
- Uncertainty quantification in linear structural dynamics
- Uncertainty quantification in nonlinear structural dynamics
- Parametric-nonparametric uncertainties
- Identification
- Inverse problem
- Statistical inverse problem
1 Introduction
It is well known that the parametric method for uncertainty quantification consists in constructing stochastic models of the uncertain physical parameters of a computational model that results from the discretization of a boundary value problem. The parametric method is efficient for taking into account the variabilities of physical parameters, but has not the capability to take into account the model uncertainties induced by modeling errors that are introduced during the construction of the computational model. The nonparametric method for the uncertainty quantification is a way for constructing a stochastic model of the model uncertainties induced by the modeling errors. It is also an approach for constructing stochastic models of constitutive equations of materials involving some non-Gaussian tensor-valued random fields, such as in the framework of elasticity, thermoelasticity, electromagnetism, etc. The random matrix theory is a fundamental tool that is really efficient for performing stochastic modeling of matrices that appear in the nonparametric method of uncertainties and in the random constitutive equations for multiscale stochastic modeling of heterogeneous materials. The applications of the nonparametric stochastic modeling of uncertainties and of the random matrix theory presented in this chapter have been developed and validated for many fields of computational sciences and engineering, in particular for dynamical systems encountered in aeronautics and aerospace engineering [7, 20, 78, 88, 91, 94], in biomechanics [30, 31], in environment [32], in nuclear engineering [9, 12, 13, 29], in soil-structure interaction and for the wave propagations in soils [4, 5, 26, 27], in rotor dynamics [79, 80, 82] and vibration of turbomachines [18, 19, 22, 70], in vibroacoustics of automotive vehicles [3, 38–40, 61], but also, in continuum mechanics for multiscale stochastic modeling of heterogeneous materials [48, 49, 51–53], for the heat transfer in complex composites and for their nonlinear thermomechanic analyses [97, 98].
The chapter is organized as follows:
-
Notions on random matrices and on the nonparametric method for uncertainty quantification: What is a random matrix and what is the nonparametric method for uncertainty quantification?
-
Brief history concerning the random matrix theory and the nonparametric method for UQ and its connection with the random matrix theory.
-
Overview and mathematical notations used in the chapter.
-
Maximum entropy principle (MaxEnt) for constructing random matrices.
-
Fundamental ensemble for the symmetric real random matrices with a unit mean value.
-
Fundamental ensembles for positive-definite symmetric real random matrices.
-
Ensembles of random matrices for the nonparametric method in uncertainty quantification.
-
The MaxEnt as a numerical tool for constructing ensembles of random matrices.
-
The MaxEnt for constructing the pdf of a random vector.
-
Nonparametric stochastic model for constitutive equation in linear elasticity.
-
Nonparametric stochastic model of uncertainties in computational linear structural dynamics.
-
Parametric-nonparametric uncertainties in computational nonlinear structural dynamics.
-
Some key research findings and applications.
2 Notions on Random Matrices and on the Nonparametric Method for Uncertainty Quantification
2.1 What Is a Random Matrix?
A real (or complex) matrix is a rectangular or a square array of real (or complex) numbers, arranged in rows and columns. The individual items in a matrix are called its elements or its entries.
A real (or complex) random matrix is a matrix-valued random variable, which means that its entries are real (or complex) random variables. The random matrix theory is related to the fundamental mathematical methods required for constructing the probability distribution of such a random matrix, for constructing a generator of independent realizations, for analyzing some algebraic properties and some spectral properties, etc.
Let us give an example for illustrating the types of problems related to the random matrix theory. Let us consider a random matrix [A], defined on a probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in a set \(\mathbb{S}_{n}\) of matrices, which is a subset of the set \(\mathbb{M}_{n}^{S}(\mathbb{R})\) of all the symmetric (n × n) real matrices. Thus, for θ in Θ, the realization [A(θ)] is a deterministic matrix in \(\mathbb{S}_{n} \subset \mathbb{M}_{n}^{S}(\mathbb{R})\). Fundamental questions are related to the definition and to the construction of the probability distribution P [A] of such a random matrix [A]. If this probability distribution is defined by a probability density function (pdf) with respect a volume element d S A, which is a mapping [A] ↦ p [A]([A]) from \(\mathbb{M}_{n}^{S}(\mathbb{R})\) into \(\mathbb{R}^{+} = [0,+\infty [\), for which its support is \(\mathbb{S}_{n}\) (which implies that p [A]([A]) = 0 if \([A]\notin \mathbb{S}_{n}\)), then how must the volume element d S A be defined, how is the integration over \(\mathbb{M}_{n}^{S}(\mathbb{R})\) defined, and what are the methods and tools for constructing pdf p [A] and its generator of independent realizations? For instance, such a pdf cannot simply be defined in giving the pdf of every entry [A] jk for many reasons among the following ones. As random matrix [A] is symmetric, all the entries are not algebraically independent, and therefore, only the n(n + 1)∕2 random variables {[A]1 ≤ j ≤ k ≤ n } must be considered. In addition, if \(\mathbb{S}_{n}\) is the subset \(\mathbb{M}_{n}^{+}(\mathbb{R})\) of all the positive-definite symmetric (n × n) real matrices, then there is an algebraic constraint that relates the random variables {[A]1 ≤ j ≤ k ≤ n } in order that [A] be with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\), and such an algebraic constraint implies that all the random variables {[A]1 ≤ j ≤ k ≤ n } are statistically dependent .
2.2 What Is the Nonparametric Method for Uncertainty Quantification?
The parametric method for uncertainty quantification consists in constructing stochastic models of the uncertain physical parameters (geometry, boundary conditions, material properties, etc) of a computational model that results from the discretization of a boundary value problem. The parametric method, which introduces prior and posterior stochastic models of the uncertain physical parameters of the computational model, has not the capability to take into account model uncertainties induced by modeling errors that are introduced during the construction of the computational model.
The nonparametric method for uncertainty quantification consists in constructing a stochastic model of both the uncertain physical parameters and the model uncertainties induced by the modeling errors, without separating the effects of the two types of uncertainties. Such an approach consists in directly constructing stochastic models of matrices representing operators of the problem considered and not in using the parametric method for the uncertain physical parameters whose matrices depend. Initially developed for uncertainty quantification in computational structural dynamics, the use of the nonparametric method has been extended for constructing stochastic models of matrices of computational models, such as the nonparametric stochastic model for constitutive equation in linear elasticity.
The parametric-nonparametric method for uncertainty quantification consists in using simultaneously in a computational model, the parametric method for constructing stochastic models of certain of its uncertain physical parameters, and the nonparametric method for constructing a stochastic model of both, the other uncertain physical parameters and the model uncertainties induced by the modeling errors, in separating the effects of the two types of uncertainties.
Consequently, the nonparametric method for uncertainty quantification uses the random matrix theory.
3 A Brief History
3.1 Random Matrix Theory (RMT)
The random matrix theory (RMT) were introduced and developed in mathematical statistics by Wishart and others in the 1930s and was intensively studied by physicists and mathematicians in the context of nuclear physics. These works began with Wigner [125] in the 1950s and received an important effort in the 1960s by Dyson, Mehta, Wigner [36, 37, 126], and others. In 1965, Poter [92] published a volume of important papers in this field, followed, in 1967, by the first edition of the Mehta book [72] whose second edition [73] published in 1991 gives a synthesis of the random matrix theory. For applications in physics, an important ensemble of the random matrix theory is the Gaussian orthogonal ensemble (GOE) for which the elements are constituted of real symmetric random matrices with statistically independent entries and which are invariant under orthogonal linear transformations (this ensemble can be viewed as a generalization of a Gaussian real-valued random variable to a symmetric real square random matrix).
For an introduction to multivariate statistical analysis, we refer the reader to [2], for an overview on explicit probability distributions of ensembles of random matrices and their properties, to [55] and, for analytical mathematical methods devoted to the random matrix theory, to [74].
RMT has been used in other domains than nuclear physics. In 1984 and 1986, Bohigas et al. [14, 15] found that the level fluctuations of the quantum Sinai’s billard were able to predict with the GOE of random matrices. In 1989, Weaver [124] showed that the higher frequencies of an elastodynamic structure constituted of a small aluminum block had the behavior of the eigenvalues of a matrix belonging to the GOE. Then, Bohigas, Legrand, Schmidt, and Sornette [16, 65, 66, 99] studied the high-frequency spectral statistics with the GOE for elastodynamics and vibration problems in the high-frequency range. Langley [64] showed that, in the high-frequency range, the system of natural frequencies of linear uncertain dynamic systems is a non-Poisson point process. These results have been validated for the high-frequency range in elastodynamics. A synthesis of theses aspects related to quantum chaos and random matrix theory, devoted to linear acoustics and vibration, can be found in the book edited by Wright and Weaver [127].
3.2 Nonparametric Method for UQ and Its Connection with the RMT
The nonparametric method was initially be introduced by Soize [106, 107] in 1999–2000 for uncertainty quantification in computational linear structural dynamics in order to take into account the model uncertainties induced by the modeling errors that could not be addressed by the parametric method. The concept of the nonparametric method then consisted in modeling the generalized matrices of the reduced-order model of the computational model by random matrices. It should be noted that the terminology “nonparametric” is not at all connected to the “nonparametric statistics” but was introduced to show the differences between the well-known parametric method consisting in constructing a stochastic model of uncertain physical parameters of the computational model, and the new proposed nonparametric method that consisted in modeling the generalized matrices of the reduced-order model by random matrices, related to the operators of the problem. Later, the parametric-nonparametric method has been introduced [113].
Early in the development of the concept of the nonparametric method, a problem has occurred in the choice of ensembles of random matrices. Indeed the ensembles of random matrices coming from the RMT were not adapted to stochastic modeling required by the nonparametric method. For instance, the GOE of random matrices could not be used for the generalized mass matrix, which must be positive definite, what is not the case for a random matrix belonging to GOE. Consequently, new ensembles of random matrices have had to be developed [76, 107, 108, 110, 115], using the maximum entropy (MaxEnt) principle, for implementing the concept of the nonparametric method for various computational models in mechanics, for which the matrices must verify various algebraic properties. In addition, parameterizations of the new ensembles of random matrices have been introduced in the different constructions in order to be in capability to quantify simply the level of uncertainties. These ensembles of random matrices have been constructed with a parameterization exhibiting a small number of hyperparameters, what allows for identifying the hyperparameters in using experimental data, solving a statistical inverse problems for random matrices that are, in general, in very high dimension. In these constructions, for certain types of available information, an explicit solution of the MaxEnt principle has been obtained, giving an explicit description of the ensembles of random matrices and of the corresponding generator s of realizations. Nevertheless, for other cases of available information coming from computational models, there is no explicit solution of the MaxEnt, and therefore, a numerical tool adapted to the high dimension has had to be developed [112].
Finally, during these last 15 years the nonparametric method has extensively been used and extended, with experimental validations, to many problems in linear and nonlinear structural dynamics, in fluid-structure interaction and in vibroacoustics, in unsteady aeroelasticity, in soil-structure interaction, in continuum mechanics of solids for the nonparametric stochastic modeling of the constitutive equations in linear and nonlinear elasticity, in thermoelasticity, etc. A brief overview on all the experimental validations and applications in different fields is given in the last Sect. 15.
4 Overview
This chapter is constituted of two main parts:
-
The first one is devoted to the presentation of ensembles of random matrices that are explicitly described and also deals with an efficient numerical tool for constructing ensembles of random matrices when an explicit construction cannot be obtained. The presentation is focused to the fundamental results and to the fundamental tools related to ensembles of random matrices that are useful for constructing nonparametric stochastic models for uncertainty quantification in computational mechanics and in computational science and engineering, in such a framework, for the construction of nonparametric stochastic models of the random tensors or the tensor-valued random fields and also for the nonparametric stochastic models of uncertainties in linear and nonlinear structural dynamics.
All the ensembles of random matrices, which have been developed for the nonparametric method of uncertainties in computational sciences and engineering, are given hereinafter using a unified presentation based on the use of the MaxEnt principle, what allow us, not only to learn about the useful ensembles of random matrices for which the probability distributions and the associated generators of independent realizations are explicitly known but also to present a general tool for constructing any ensemble of random matrices, possibly using computation in high dimension.
-
The second part deals with the nonparametric method for uncertainty quantification, which uses the new ensembles of random matrices that have been constructed in the context of the development of the nonparametric method and that are detailed in the first part. The presentation is limited to the nonparametric stochastic model for constitutive equation in linear elasticity, to the nonparametric stochastic model of uncertainties in computational linear structural dynamics for damped elastic structures but also for viscoelastic structures, and to the parametric-nonparametric uncertainties in computational nonlinear structural dynamics. In the last Sect. 15 brief bibliographical analysis is given concerning the propagation of uncertainties using nonparametric or parametric-nonparametric stochastic models of uncertainties, some additional ingredients useful for the nonparametric stochastic modeling of uncertainties, some experimental validations of the nonparametric method of uncertainties, and finally some applications of the nonparametric stochastic modeling of uncertainties in different fields of computational sciences and engineering.
5 Notations
The following algebraic notations are used through all the developments devoted to this chapter.
5.1 Euclidean and Hermitian Spaces
Let x = (x 1, …, x n ) be a vector in \(\mathbb{K}^{n}\) with \(\mathbb{K} = \mathbb{R}\) (the set of all the real numbers) or \(\mathbb{K} = \mathbb{C}\) (the set of all the complex numbers). The Euclidean space \(\mathbb{R}^{n}\) (or the Hermitian space \(\mathbb{C}^{n}\)) is equipped with the usual inner product \(< \mathbf{x},\mathbf{y} >=\sum\nolimits_{ j=1}^{n}x_{j}\overline{y}_{j}\) and the associated norm ∥x∥ = <x, x>1∕2 in which \(\overline{y}_{j}\) is the complex conjugate of the complex number y j and where \(\overline{y}_{j} = y_{j}\) when y j is a real number.
5.2 Sets of Matrices
-
\(\mathbb{M}_{n,m}(\mathbb{R})\) be the set of all the (n × m) real matrices.
-
\(\mathbb{M}_{n}(\mathbb{R}) = \mathbb{M}_{n,n}(\mathbb{R})\) the square matrices.
-
\(\mathbb{M}_{n}(\mathbb{C})\) be the set of all the (n × m) complex matrices.
-
\(\mathbb{M}_{n}^{S}(\mathbb{R})\) be the set of all the symmetric (n × n) real matrices.
-
\(\mathbb{M}_{n}^{+0}(\mathbb{R})\) be the set of all the semipositive-definite symmetric (n × n) real matrices.
-
\(\mathbb{M}_{n}^{+}(\mathbb{R})\) be the set of all the positive-definite symmetric (n × n) real matrices.
The ensembles of real matrices are such that
5.3 Kronecker Symbol, Unit Matrix, and Indicator Function
The Kronecker symbol is denoted as δ
jk
and is such that δ
jk
= 0 if j ≠ k and δ
jj
= 1. The unit (or identity) matrix in \(\mathbb{M}_{n}(\mathbb{R})\) is denoted as [I
n
] and is such that [I
n
]
jk
= δ
jk
. Let \(\mathbb{S}\) be any subset of any set \(\mathbb{M}\), possibly with \(\mathbb{S} = \mathbb{M}\). The indicator function  defined on set \(\mathbb{M}\) is such that
defined on set \(\mathbb{M}\) is such that  if \(M \in \mathbb{S} \subset \mathbb{M}\) and
if \(M \in \mathbb{S} \subset \mathbb{M}\) and  if \(M\not\in \mathbb{S}\).
if \(M\not\in \mathbb{S}\).
5.4 Norms and Usual Operators
-
(i)
The determinant of a matrix [G] in \(\mathbb{M}_{n}(\mathbb{R})\) is denoted as det[G], and its trace is denoted as tr[G] = ∑ n j = 1 G jj .
-
(ii)
The transpose of a matrix [G] in \(\mathbb{M}_{n,m}(\mathbb{R})\) is denoted as [G]T, which is in \(\mathbb{M}_{m,n}(\mathbb{R})\).
-
(iii)
The operator norm of a matrix [G] in \(\mathbb{M}_{n,m}(\mathbb{R})\) is denoted as ∥G∥ = sup∥x∥ ≤ 1∥[G] x∥ for all x in \(\mathbb{R}^{m}\), which is such that ∥[G] x∥ ≤ ∥G∥∥x∥ for all x in \(\mathbb{R}^{m}\).
-
(iv)
For [G] and [H] in \(\mathbb{M}_{n,m}(\mathbb{R})\), we denote ≪[G], [H]≫ = tr{[G]T[H]} and the Frobenius norm (or Hilbert-Schmidt norm) ∥G∥ F of [G] is such that ∥G∥ 2 F = ≪[G], [G]≫ = tr{[G]T[G]} = ∑ n j = 1 ∑ m k = 1 G 2 jk , which is such that \(\Vert G\Vert \leq \Vert G\Vert _{F} \leq \sqrt{n} \Vert G\Vert\).
5.5 Order Relation in the Set of All the Positive-Definite Real Matrices
Let [G] and [H] be two matrices in \(\mathbb{M}_{n}^{+}(\mathbb{R})\). The notation [G] > [H] means that the matrix [G] − [H] belongs to \(\mathbb{M}_{n}^{+}(\mathbb{R})\).
5.6 Probability Space, Mathematical Expectation, and Space of Second-Order Random Vectors
The mathematical expectation relative to a probability space \((\varTheta,\mathcal{T},P)\) is denoted as E. The space of all the second-order random variables, defined on \((\varTheta,\mathcal{T},P)\), with values in \(\mathbb{R}^{n}\), equipped with the inner product ((X, Y)) = E{< X, Y >} and with the associated norm |||X||| = ((X, X))1∕2, is a Hilbert space denoted as \(\mathcal{L}_{n}^{2}\).
6 The MaxEnt for Constructing Random Matrices
The measure of uncertainties using the entropy of information has been introduced by Shannon [103] in the framework of the development of information theory. The maximum entropy (MaxEnt) principle (that is to say, the maximization of the level of uncertainties) has been introduced by Jaynes [58] and allows a prior probability model of any random variables to be constructed, under the constraints defined by the available information. This principle appears as a major tool to construct the prior probability models. All the ensembles of random matrices presented hereinafter (including the well-known Gaussian Orthogonal Ensemble) are constructed in the framework of a unified presentation using the MaxEnt. This means that the probability distributions of the random matrices belonging to these ensembles are constructed using the MaxEnt.
6.1 Volume Element and Probability Density Function (PDF)
This section deals with the definition of a probability density function (pdf) of a random matrix [G] with values in the Euclidean space \(\mathbb{M}_{n}^{S}(\mathbb{R})\) (set of all the symmetric (n × n) real matrices, equipped with the inner product ≪[G], [H]≫ = tr{[G]T[H]}). In order to correctly defined the integration on Euclidean space \(\mathbb{M}_{n}^{S}(\mathbb{R})\), it is necessary to define the volume element on this space.
6.1.1 Volume Element on the Euclidean Space of Symmetric Real Matrices
In order to well understand the principle of the construction of the volume element on Euclidean space \(\mathbb{M}_{n}^{S}(\mathbb{R})\), the construction of the volume element on Euclidean spaces \(\mathbb{R}^{n}\) and \(\mathbb{M}_{n}(\mathbb{R})\) is first introduced.
-
(i) Volume element on Euclidean space \(\mathbb{R}^{n}\). Let {e 1, …, e n } be the orthonormal basis of \(\mathbb{R}^{n}\) such that e j = (0, …, 1, …, 0) is the null vector with 1 in position j. Consequently, <e j , e k > = δ jk . Any vector x = (x 1, …, x n ) in \(\mathbb{R}^{n}\) can then be written as x = ∑ n j = 1 x j e j . This Euclidean structure on \(\mathbb{R}^{n}\) defines the volume element d x on \(\mathbb{R}^{n}\) such that d x = ∏ n j = 1 dx j .
-
(ii) Volume element on Euclidean space \(\mathbb{M}_{n}(\mathbb{R})\). Similarly, let {[b jk ]} jk be the orthonormal basis of \(\mathbb{M}_{n}(\mathbb{R})\) such that [b jk ] = e j e T k . Consequently, we have ≪[b jk ], [b j′k′] = δ jj′ δ kk′. Any matrix [G] in \(\mathbb{M}_{n}(\mathbb{R})\) can be written as [G] = ∑ n j, k = 1 G jk [b jk ] in which G jk = [G] jk . This Euclidean structure on \(\mathbb{M}_{n}(\mathbb{R})\) defines the volume element dG on \(\mathbb{M}_{n}(\mathbb{R})\) such that dG = ∏ n j, k = 1 dG jk .
-
(iii) Volume element on Euclidean space \(\mathbb{M}_{n}^{S}(\mathbb{R})\). Let {[b S jk ], 1 ≤ j ≤ k ≤ n} be the orthonormal basis of \(\mathbb{M}_{n}^{S}(\mathbb{R})\) such that [b S jj ] = e j e j T and \([b_{jk}^{S}] = (\mathbf{e}_{j}\,\mathbf{e}_{k}^{T} + \mathbf{e}_{k}\,\mathbf{e}_{j}^{T})/\sqrt{2}\) if j < k. We have ≪[b S jk ], [b S j′k′ ]≫ = δ jj′ δ kk′ for j ≤ k and j′ ≤ k′. Any symmetric matrix [G] in \(\mathbb{M}_{n}^{S}(\mathbb{R})\) can be written as [G] = ∑ 1 ≤ j ≤ k ≤ n G S jk [b S jk ] in which G jj S = G jj and \(G_{jk}^{S} = \sqrt{2}\,G_{jk}\) if j < k. This Euclidean structure on \(\mathbb{M}_{n}^{S}(\mathbb{R})\) defines the volume element d S G on \(\mathbb{M}_{n}^{S}(\mathbb{R})\) such that d S G = ∏ 1 ≤ j ≤ k ≤ n dG S jk . The volume element is then defined by
$$\displaystyle{ d^{S}G = 2^{n(n-1)/4}\,\prod _{ 1\leq j\leq k\leq n}\,dG_{jk}. }$$(8.1)
6.1.2 Probability Density Function of a Symmetric Real Random Matrix
Let [G] be a random matrix, defined on a probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in \(\mathbb{M}_{n}^{S}(\mathbb{R})\) whose probability distribution P [G] = p [G]([G]) d S G is defined by a pdf [G] ↦ p [G]([G]) from \(\mathbb{M}_{n}^{S}(\mathbb{R})\) into \(\mathbb{R}^{+} = [0,+\infty [\) with respect to the volume element d S G on \(\mathbb{M}_{n}^{S}(\mathbb{R})\). This pdf verifies the normalization condition,
in which the volume element d S G is defined by Eq. (8.1).
6.1.3 Support of the Probability Density Function
The support of pdf p [G], denoted as supp p [G], is any subset \(\mathbb{S}_{n}\) of \(\mathbb{M}_{n}^{S}(\mathbb{R})\), possibly with \(\mathbb{S}_{n} = \mathbb{M}_{n}^{S}(\mathbb{R})\). For instance, we can have \(\mathbb{S}_{n} = \mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\), which means that [G] is a random matrix with values in the positive-definite symmetric (n × n) real matrices. Thus, p [G]([G]) = 0 for [G] not in \(\mathbb{S}_{n}\), and Eq. (8.2) can be rewritten as
It should be noted that, in the context of the construction of the unknown pdf p [G], it is assumed that support \(\mathbb{S}_{n}\) is a given (known) set.
6.2 The Shannon Entropy as a Measure of Uncertainties
The Shannon measure [103] of uncertainties of random matrix [G] is defined by the entropy of information (Shannon’s entropy), \(\mathcal{E}(p_{[\mathbf{G}}])\), of pdf p [G] whose support is \(\mathbb{S}_{n} \subset \mathbb{M}_{n}^{S}(\mathbb{R})\), such that
which can be rewritten as \(\mathcal{E}(p_{[\mathbf{G}]}) = -E\{\log {\bigl (p_{[\mathbf{G}]}([\mathbf{G}])\bigr )}\). For any pdf p [G] defined on \(\mathbb{M}_{n}^{S}(\mathbb{R})\) and with support \(\mathbb{S}_{n}\), entropy \(\mathcal{E}(p_{[\mathbf{G}]})\) is a real number. The uncertainty increases when the Shannon entropy increases. More the Shannon entropy is small and more the level of uncertainties is small. If \(\mathcal{E}(p_{[\mathbf{G}]})\) goes to −∞, then the level of uncertainties goes to zero, and random matrix [G] goes to a deterministic matrix for the convergence in probability distribution (in probability law).
6.3 The MaxEnt Principle
As explained before, the use of the MaxEnt principle requires to correctly defined the available information related to random matrix [G] for which pdf p [G] (that is unknown with a given support \(\mathbb{S}_{n}\)) has to be constructed.
6.3.1 Available Information
It is assumed that the available information related to random matrix [G] is represented by the following equation on \(\mathbb{R}^{\mu }\), where μ is a finite positive integer,
in which p [G] ↦ h(p [G]) = (h 1(p [G]), …, h μ (p [G])) is a given functional of p [G], with values in \(\mathbb{R}^{\mu }\). For instance, if the mean value E{[G]} = [G] of [G] is a given matrix in \(\mathbb{S}_{n}\), and if this mean value [G] corresponds to the only available information, then \(h_{\alpha }(p_{[\mathbf{G}]}) =\int _{\mathbb{S}_{n}}G_{jk}\,p_{[\mathbf{G}]}([G])\,\,d^{S}G -\underline{G}_{jk}\), in which α = 1, …, μ is associated with the couple of indices (j, k) such as 1 ≤ j ≤ k ≤ n and where μ = n(n + 1)∕2.
6.3.2 The Admissible Sets for the pdf
The following admissible sets \(\mathcal{C}_{\mathrm{ free}}\) and \(\mathcal{C}_{\mathrm{ ad}}\) are introduced for defining the optimization problem resulting from the use of the MaxEnt principle in order to construct the pdf of random matrix [G]. The set \(\mathcal{C}_{\mathrm{ free}}\) is made up of all the pdf p: [G] ↦ p([G]), defined on \(\mathbb{M}_{n}^{S}(\mathbb{R})\), with support \(\mathbb{S}_{n} \subset \mathbb{M}_{n}^{S}(\mathbb{R})\),
The set \(\mathcal{C}_{\mathrm{ ad}}\) is the subset of \(\mathcal{C}_{\mathrm{ free}}\) for which all the pdf p in \(\mathcal{C}_{\mathrm{ free}}\) satisfy the constraint defined by
6.3.3 Optimization Problem for Constructing the pdf
The use of the MaxEnt principle for constructing the pdf p [G] of random matrix [G] yields the following optimization problem:
The optimization problem defined by Eq. (8.8) on set \(\mathcal{C}_{\mathrm{ ad}}\) is transformed in an optimization problem on \(\mathcal{C}_{\mathrm{ free}}\) in introducing the Lagrange multipliers associated with the constraints defined by Eqs. (8.5) [58, 60, 107]. This type of construction and the analysis of the existence and the uniqueness of a solution of the optimization problem defined by Eq. (8.8) are detailed in Sect. 10.
7 A Fundamental Ensemble for the Symmetric Real Random Matrices with a Unit Mean Value
A fundamental ensemble for the symmetric real random matrices is the Gaussian orthogonal ensemble (GOE) that is an ensemble of random matrices [G], defined on a probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in \(\mathbb{M}_{n}^{S}(\mathbb{R})\), defined by a pdf p [G] on \(\mathbb{M}_{n}^{S}(\mathbb{R})\) with respect to the volume element d S G, for which the support \(\mathbb{S}_{n}\) of p G is \(\mathbb{M}_{n}^{S}(\mathbb{R})\), and satisfying the additional properties defined hereinafter.
7.1 Classical Definition [74]
The additional properties of a random matrix [G] belonging to GOE are (i) invariance under any real orthogonal transformation, that is to say, for any orthogonal (n × n) real matrix [R] such that [R]T[R] = [R] [R]T = [I n ], the pdf (with respect to d S G) of the random matrix [R]T[G] [R] is equal to pdf p G of random matrix [G], and (ii) statistical independence of all the real random variables {G jk , 1 ≤ j ≤ k ≤ n}.
7.2 Definition by the MaxEnt and Calculation of the pdf
Alternatively to the properties introduced in the classical definition, the additional properties of a random matrix [G] belonging to GOE are the following. For all 1 ≤ j ≤ k ≤ n,
in which δ > 0 is a given positive-valued hyperparameter whose interpretation is given after. The GOE is then defined using the MaxEnt principle for the available information given by Eq. (8.9), which defines mapping h (see Eq. (8.5)). The corresponding ensemble is written as GOE δ . In Eq. (8.9), the first equation means that the symmetric random matrix [G] is centered, and the second one means that its fourth-order covariance tensor is diagonal. Using the MaxEnt principle for random matrix [G] yields the following unique explicit expression for the pdf p G with respect to the volume element d S G:
in which c G is the constant of normalization such that Eq. (8.2) is verified. It can then be deduced that {G jk , 1 ≤ j ≤ k ≤ n} are Gaussian independent real random variables such that Eq. (8.9) is verified. Consequently, for all 1 ≤ j ≤ k ≤ n, the pdf (with respect to dg on \(\mathbb{R}\)) of the Gaussian real random variable G jk is \(p_{\mathbf{G}_{jk}}(g) = (\sqrt{2\pi }\sigma _{jk})^{-1}\exp \{ - g^{2}/(2\sigma _{jk}^{2})\}\) in which the variance of random variable G jk is σ 2 jk = (1 + δ jk ) δ 2∕(n + 1).
7.3 Decentering and Interpretation of Hyperparameter δ
Let [G GOE] be the random matrix with values in \(\mathbb{M}_{n}^{S}(\mathbb{R})\) such that [G GOE] = [I n ] + [G] in which [G] is a random matrix belonging to the GOE δ defined before. Therefore [G GOE] is not centered and its mean value is E{[G GOE]} = [I n ]. The coefficient of variation of the random matrix [G GOE] is defined [109] by
and δ GOE = δ. The parameter \(2\delta /\sqrt{n + 1}\) can be used to specify a scale.
7.4 Generator of Realizations
For θ ∈ Θ, any realization [G GOE(θ)] is given by [G GOE(θ)] = [I n ] + [G(θ)] with, for 1 ≤ j ≤ k ≤ n, G kj (θ) = G jk (θ) and G jk (θ) = σ jk U jk (θ), in which {U jk (θ)}1 ≤ j ≤ k ≤ n is the realization of n(n + 1)∕2 independent copies of a normalized (centered and unit variance) Gaussian real random variable.
7.5 Use of the GOE Ensemble in Uncertainty Quantification
The GOE can then be viewed as a generalization of the Gaussian real random variables to the Gaussian symmetric real random matrices. It can be seen that [G GOE] is with values in \(\mathbb{M}_{n}^{S}(\mathbb{R})\) but is not positive. In addition, for all fixed n,
-
(i)
It has been proved by Weaver [124] and others (see [127] and included references) that the GOE is well adapted for describing universal fluctuations of the eigenfrequencies for generic elastodynamical, acoustical, and elastoacoustical systems, in the high-frequency range corresponding to the asymptotic behavior of the largest eigenfrequencies.
-
(ii)
On the other hand, random matrix [G GOE] cannot be used for stochastic modeling of a symmetric real matrix for which a positiveness property and an integrability of its inverse are required. Such a situation is similar to the following one that is well known for the scalar case. Let us consider the scalar equation in u: ( G + G) u = v in which v is a given real number, G is a given positive number, and G is a positive parameter. This equation has a unique solution u = ( G + G)−1 v. Let us assume that G is uncertain and is modeled by a centered random variable G. We then obtain the random equation in U: ( G + G)U = v. If the random solution U must have finite statistical fluctuations, that is to say, U must be a second-order random variable (this is generally required due to physical considerations), then G cannot be chosen as a Gaussian second-order centered real random variable, because with such a Gaussian stochastic modeling, the solution U = (G + G)−1 v is not a second-order random variable, because E{U 2} = +∞ due to the non integrability of the function G ↦ (G + G)−2 at point G = −G.
8 Fundamental Ensembles for Positive-Definite Symmetric Real Random Matrices
In this section, we present fundamental ensembles of positive-definite symmetric real random matrices, SG +0 , SG + ɛ , SG + b , and SG + λ , which have been developed and analyzed for constructing other ensembles of random matrices used for the nonparametric stochastic modeling of matrices encountered in uncertainty quantification.
-
The ensemble SG +0 is a subset of all the positive-definite symmetric real (n × n) random matrices for which the mean value is the unit matrix and for which the lower bound is the zero matrix. This ensemble has been introduced and analyzed in [107, 108] in the context of the development of the nonparametric method of model uncertainties induced my modeling errors in computational dynamics. This ensemble has later been used for constructing other ensembles of random matrices encountered in the nonparametric stochastic modeling of uncertainties [110].
-
The ensemble SG + ɛ is a subset of all the positive-definite symmetric real (n × n) random matrices for which the mean value is the unit matrix and for which there is an arbitrary lower bound that is a positive-definite matrix controlled by an arbitrary positive number ɛ that can be chosen as small as is desired [114]. In such an ensemble, the lower bound does not correspond to a given matrix that results from a physical model, but allows for assuring a uniform ellipticity for the stochastic modeling of elliptic operators encountered in uncertainty quantification of boundary value problems. The construction of this ensemble is directly derived from ensemble SG +0 ,
-
The ensemble SG + b is a subset of all the positive-definite random matrices for which the mean value is either not given or is equal to the unit matrix [28, 50] and for which a lower bound and an upper bound are given positive-definite matrices. In this ensemble, the lower bound and the upper bound are not arbitrary positive-definite matrices, but are given matrices that result from a physical model. The ensemble is interesting for the nonparametric stochastic modeling of tensors and tensor-valued random fields for describing uncertain physical properties in elasticity, poroelasticity, thermics, etc.
-
The ensemble SG + λ , introduced in [76], is a subset of all the positive-definite random matrices for which the mean value is the unit matrix, for which the lower bound is the zero matrix, and for which the second-order moments of diagonal entries are imposed. In the context of the nonparametric stochastic modeling of uncertainties, this ensemble allows for imposing the variances of certain random eigenvalues of stochastic generalized eigenvalue problems, such as the eigenfrequency problem in structural dynamics.
8.1 Ensemble SG0 + of Positive-Definite Random Matrices With a Unit Mean Value
8.1.1 Definition of SG0 + Using the MaxEnt and Expression of the pdf
The ensemble SG +0 of random matrices [G 0], defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in the set \(\mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\), is constructed using the MaxEnt with the following available information, which defines mapping h (see Eq. (8.5)):
The support of the pdf is the subset \(\mathbb{S}_{n} = \mathbb{M}_{n}^{+}(\mathbb{R})\) of \(\mathbb{M}_{n}^{S}(\mathbb{R})\). This pdf \(p_{[\mathbf{G}_{0}]}\) (with respect to the volume element d S G on the set \(\mathbb{M}_{n}^{S}(\mathbb{R})\)) verifies the normalization condition and is written as

The positive parameter δ is a such that 0 < δ < (n + 1)1∕2(n + 5)−1∕2, which allows the level of statistical fluctuations of random matrix [G 0] to be controlled and which is defined by
The normalization positive constant \(c_{G_{0}}\) is such that
where, for all z > 0, Γ(z) = ∫ +∞0 t z−1 e −t dt. Note that {[G 0] jk , 1 ≤ j ≤ k ≤ n} are dependent random variables. If (n + 1)∕δ 2 is an integer, then this pdf coincides with the Wishart probability distribution [2, 107]. If (n + 1)∕δ 2 is not an integer, then this probability density function can be viewed as a particular case of the Wishart distribution, in infinite dimension, for stochastic processes [104].
8.1.2 Second-Order Moments
Random matrix [G 0] is such that E{∥G 0∥2} ≤ E{∥G 0∥ 2 F } < +∞, which proves that [G 0] is a second-order random variable. The mean value of random matrix [G 0] is unit matrix [I n ]. The covariance C jk, j′k′ = E{[G 0] jk − [I n ] jk ) ([G 0] j′k′ − [I n ] j′k′)} of the real-valued random variables [G 0] jk and [G 0] j′k′ is \(C_{jk,j'k'} = \delta ^{2}(n + 1)^{-1}{\bigl \{\delta _{j'k}\,\delta _{jk'} +\delta _{jj'}\,\delta _{kk'}\bigr \}}\). The variance of real-valued random variable [G 0] jk is σ 2 jk = C jk, jk = δ 2(n + 1)−1(1 + δ jk ).
8.1.3 Invariance of Ensemble SG0 + Under Real Orthogonal Transformations
Ensemble SG +0 is invariant under real orthogonal transformations. This means that the pdf (with respect to d S G) of the random matrix [R]T[G 0] [R] is equal to the pdf (with respect to d S G) of random matrix [G 0] for any real orthogonal matrix [R] belonging to \(\mathbb{M}_{n}(\mathbb{R})\).
8.1.4 Invertibility and Convergence Property When Dimension Goes to Infinity
Since [G 0] is a positive-definite random matrix, [G 0] is invertible almost surely, which means that for \(\mathcal{P}\)-almost θ in Θ, the inverse [G 0(θ)]−1 of the matrix [G 0(θ)] exists. This last property does not guarantee that [G 0]−1 is a second-order random variable, that is to say, that \(E\{\Vert [\mathbf{G}_{0}]^{-1}\Vert _{F}^{2}\} =\int _{\varTheta }\Vert [\mathbf{G}_{0}(\theta )]^{-1}\Vert _{F}^{2}\,d\mathcal{P}(\theta )\) is finite. However, it is proved [108] that
and that the following fundamental property holds:
in which C δ is a positive finite constant that is independent of n but that depends on δ. This means that n ↦ E{∥[G 0]−1∥2} is a bounded function from {n ≥ 2} into \(\mathbb{R}^{+}\).
It should be noted that the invertibility property defined by Eqs. (8.17) and (8.18) is due to the constraint \(E\{\log (\det [\mathbf{G}_{0}])\} =\nu _{G_{0}}\) with \(\vert \nu _{G_{0}}\vert < +\infty \). This is the reason why the truncated Gaussian distribution restricted to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) does not satisfy this invertibility condition that is required for stochastic modeling in many cases.
8.1.5 Probability Density Function of the Random Eigenvalues
Let \(\boldsymbol{\Lambda } = (\varLambda _{1},\ldots,\varLambda _{n})\) be the positive-valued random eigenvalues of the random matrix [G 0] belonging to ensemble SG +0 , such that \([\mathbf{G}_{0}]\,\boldsymbol{\Phi }^{j} =\varLambda _{j}\,\boldsymbol{\Phi }^{j}\) in which \(\boldsymbol{\Phi }^{j}\) is the random eigenvector associated with the random eigenvalue Λ j . The joint probability density function \(p_{\boldsymbol{\Lambda }}(\boldsymbol{\lambda }) = p_{\varLambda _{1},\ldots,\varLambda _{n}}(\lambda _{1},\ldots,\lambda _{n})\) with respect to \(d\boldsymbol{\lambda } = d\lambda _{1}\ldots d\lambda _{n}\) of \(\boldsymbol{\Lambda } = (\varLambda _{1},\ldots,\varLambda _{n})\) is written [107] as

in which c Λ is a constant of normalization defined by the equation ∫ +∞0 …∫ +∞0 \(p_{\boldsymbol{\Lambda }}(\boldsymbol{\lambda })\,d\boldsymbol{\lambda } = 1\). All the random eigenvalues Λ j of random matrix [G 0] in SG +0 are positive almost surely, while this assertion is not true for the random eigenvalues Λ j GOE of the random matrix [G GOE] = [I n ] + [G] in which [G] is a random matrix belonging to the GOE δ ensemble.
8.1.6 Algebraic Representation and Generator of Realizations
The generator of realizations of random matrix [G 0] whose pdf is defined by Eq. (8.14) is directly deduced from the following algebraic representation of [G 0] in SG +0 . Random matrix [G 0] is written as [G 0] = [L]T [L] in which [L] is an upper triangular real (n × n) random matrix such that:
-
(i)
The random variables {[L] jk , j ≤ k} are independent;
-
(ii)
For j < k, the real-valued random variable [L] jk is written as [L] jk = σ n U jk in which σ n = δ(n + 1)−1∕2 and where U jk is a real-valued Gaussian random variable with zero mean and variance equal to 1;
-
(iii)
For j = k, the positive-valued random variable [L] jj is written as \([\mathbf{L}]_{jj} =\sigma _{n}\sqrt{2V _{j}}\) in which σ n is defined before and where V j is a positive-valued gamma random variable whose pdf is
 in which \(a_{j} = \frac{n+1} {2\delta ^{2}} + \frac{1-j} {2}\).
in which \(a_{j} = \frac{n+1} {2\delta ^{2}} + \frac{1-j} {2}\).
It should be noted that the set { {U jk }1 ≤ j < k ≤ n , {V j }1 ≤ j ≤ n } of random variables are statistically independent, and the pdf of each diagonal element [L] jj of random matrix [L] depends on the rank j of the entry.
For θ ∈ Θ, any realization [G 0(θ)] is then deduced from the algebraic representation given before, using the realization {U jk (θ)}1 ≤ j < k ≤ n of n(n − 1)∕2 independent copies of a normalized (zero mean and unit variance) Gaussian real random variable and using the realization {V j (θ)}1 ≤ j ≤ n of the n independent positive-valued gamma random variable V j with parameter a j .
8.2 Ensemble SG ɛ + of Positive-Definite Random Matrices with a Unit Mean Value and an Arbitrary Positive-Definite Lower Bound
The ensemble SG + ɛ is a subset of all the positive-definite random matrices for which the mean value is the unit matrix and for which there is an arbitrary lower bound that is a positive-definite matrix controlled by an arbitrary positive number ɛ that can be chosen as small as is desired. In this ensemble, the lower bound does not correspond to a given matrix that results from a physical model.
Ensemble SG + ɛ is the set of the random matrices [G] with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\), which are written as
in which [G 0] is a random matrix in SG +0 , with mean value E{[G 0]} = [I n ], and for which the level of statistical fluctuations is controlled by the hyperparameter δ defined by Eq. (8.15) and where ɛ is any positive number (note that for ɛ = 0, SG + ɛ = SG +0 and then [G] = [G 0]). This definition shows that, almost surely,
in which the lower bound is the positive-definite matrix [G ℓ ] = c ɛ [I n ] with c ɛ = ɛ∕(1 + ɛ). For all ɛ > 0, we have
with \(\nu _{G_{\varepsilon }} =\nu _{G_{0}} - n\log (1+\varepsilon )\). The coefficient of variation δ G of random matrix [G], defined by
is such that
where δ is the hyperparameter defined by Eq. (8.15).
8.2.1 Generator of Realizations
For θ ∈ Θ, any realization [G(θ)] of [G] is given by \([\mathbf{G}(\theta )] = \frac{1} {1+\varepsilon }\{[\mathbf{G}_{0}(\theta )] +\varepsilon \, [I_{n}]\}\) in which [G 0(θ)] is a realization of random matrix [G 0] constructed as explained before.
8.2.2 Lower Bound and Invertibility
For all ɛ > 0, the bilinear form b(X, Y) = (([G] X, Y)) on \(\mathcal{L}_{n}^{2} \times \mathcal{L}_{n}^{2}\) is such that
Random matrix [G] is invertible almost surely and its inverse [G]−1 is a second-order random variable, E{∥[G]−1∥ 2 F } < +∞.
8.3 Ensemble SG b + of Positive-Definite Random Matrices with Given Lower and Upper Bounds and with or without Given Mean Value
The ensemble SG + b is a subset of all the positive-definite random matrices for which the mean value is either the unit matrix or is not given and for which a lower bound and an upper bound are given positive-definite matrices. In this ensemble, the lower bound and the upper bound are not arbitrary positive-definite matrices, but are given matrices that result from a physical model.
The ensemble SG + b is constituted of random matrices [G b ], defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in the set \(\mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\), such that
in which the lower bound [G ℓ ] and the upper bound [G u ] are given matrices in \(\mathbb{M}_{n}^{+}(\mathbb{R})\) such that [G ℓ ] < [G u ]. The support of the pdf \(p_{[\mathbf{G}_{b}]}\) (with respect to the volume element d S G on \(\mathbb{M}_{n}^{S}(\mathbb{R})\)) of random matrix [G b ] is the subset \(\mathbb{S}_{n}\) of \(\mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\) such that
The available information associated with the presence of the lower and upper bounds is defined by
in which ν ℓ and ν u are two constants such that | ν ℓ | < +∞ and | ν u | < +∞. The mean value [G b ] = E{[G b ]} is given by
The positive parameter δ b , which allows the level of statistical fluctuations of random matrix [G b ] to be controlled, is defined by
8.3.1 Definition of SG b + for a Non-given Mean Value Using the MaxEnt
The mean value [G b ] of random matrix [G b ] is not given and therefore does not constitute an available information. In this case, the ensemble SG + b is constructed using the MaxEnt with the available information given by Eq. (8.28) (that defines mapping h introduced in Eq. (8.5) and rewritten for \(p_{[\mathbf{G}_{b}]}\)). The pdf \(p_{[\mathbf{G}_{b}]}\) is the generalized matrix-variate beta-type I pdf [55]:

in which \(c_{G_{b}}\) is the normalization constant and where α > (n − 1)∕2 and β > (n − 1)∕2 are two real parameters that are unknown and that depend on the two unknown constants ν ℓ and ν u . The mean value [G b ] must be calculated using Eqs. (8.29) and (8.31), and the hyperparameter δ b , which characterizes the level of statistical fluctuations, must be calculated using Eqs. (8.30) and (8.31). Consequently, [G b ] and δ b depend on α and β. It can be seen that, for n ≥ 2, the two scalar parameters α and β are not sufficient for identifying the mean value [G b ] that is in \(\mathbb{S}_{n}\) and the hyperparameter δ b . An efficient algorithm for generating realizations of [G b ] can be found in [28].
8.3.2 Definition of SG b + for a Given Mean Value Using the MaxEnt
The mean value [G b ] of random matrix [G b ] is given such that [G ℓ ] < [G b ] < [G u ]. In this case, the ensemble SG + b is constructed using the MaxEnt with the available information given by Eqs. (8.28) and (8.29) that defines mapping h introduced in Eq. (8.5). Following the construction proposed in [50], the following change of variable is introduced:
This equation shows that the random matrix [A 0] is with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\). Introducing the mean value [A 0] = E{[A 0]} that belongs to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and is Cholesky factorization [A 0] = [L 0]T [L 0] in which [L 0] is an upper triangular real (n × n) matrix, random matrix [A 0] can be written as [A 0] = [L 0]T [G 0] [L 0] with [G 0] that belongs to ensemble SG +0 depending on the hyperparameter δ defined by Eq. (8.15). The inversion of Eq. (8.32) yields
It can then be seen that for any arbitrary small ɛ 0 > 0 (for instance, ɛ 0 = 10−6), we have
For δ and [L 0] fixed, for θ in Θ, the realization [G 0(θ)] of random matrix [G 0] in SG +0 is constructed using the generator of [G 0], which has been detailed before. The mean value E{[G b ]} and the hyperparameter δ b defined by Eq. (8.30) are estimated with the corresponding realization \([\mathbf{G}_{b}(\theta )] = [G_{\ell}] + \left ([\underline{L}_{0}]^{T}\,[\mathbf{G}_{0}(\theta )]\,[\underline{L}_{0}] + [G_{\ell u}]^{-1}\right )^{-1}\) of random matrix [G b ]. Let \(\mathcal{U}_{L}\) be the set of all the upper triangular real (n × n) matrices [L 0] with positive diagonal entries. For a fixed value of δ, and for a given target value of [G b ], the value [L opt0 ] of [L 0] is calculated in solving the optimization problem
in which the cost function \(\mathcal{F}\) is deduced from Eq. (8.34) and is written as
8.4 Ensemble SG λ + of Positive-Definite Random Matrices with a Unit Mean Value and Imposed Second-Order Moments
The ensemble SG + λ is a subset of all the positive-definite random matrices for which the mean value is the unit matrix, for which the lower bound is the zero matrix, and for which the second-order moments of diagonal entries are imposed. In the context of nonparametric stochastic modeling of uncertainties, this ensemble allows for imposing the variances of certain random eigenvalues of stochastic generalized eigenvalue problems.
8.4.1 Definition of SG λ + Using the MaxEnt and Expression of the pdf
The ensemble SG + λ of random matrices [G λ ], defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in the set \(\mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\), is constructed using the MaxEnt with the following available information, which defines mapping h (see Eq. (8.5)):
in which \(\vert \nu _{G_{\lambda }}\vert < +\infty \), with m < n, and where s 21 , …, s 2 m are m given positive constants. The pdf \(p_{[\mathbf{G}_{\lambda }]}\) (with respect to the volume element d S G on the set \(\mathbb{M}_{n}^{S}(\mathbb{R})\) has a support that is \(\mathbb{S}_{n} = \mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\) of \(\mathbb{M}_{n}^{S}(\mathbb{R})\). The pdf verifies the normalization condition and is written [76] as

in which \(C_{G_{\lambda }}\) is the normalization constant and α is a parameter such that n + 2α − 1 > 0, where [μ] is a diagonal real (n × n) matrix such that μ jj = (n + 2α − 1)∕2 for j > m and where μ 11, …, μ mm and τ 1, …, τ m are 2m positive parameters, which are expressed as a function of α and s 21 , …, s 2 m . The level of statistical fluctuations of random matrix [G λ ] is controlled by the positive hyperparameter δ that is defined by
and where δ is such that
8.4.2 Generator of Realizations
For given m < n, δ, and s 21 , …, s 2 m , the explicit generator of realizations of random matrix [G λ ] whose pdf is defined by Eq. (8.38) is detailed in [76].
9 Ensembles of Random Matrices for the Nonparametric Method in Uncertainty Quantification
In this section, we present the ensembles SE +0 , SE + ɛ , SE+0, SErect, and SEHT of random matrices which result from some transformations of the fundamental ensembles introduced before. These ensembles of random matrices are useful for performing the nonparametric stochastic modeling of matrices encountered in uncertainty quantification of computational models in structural dynamics, acoustics, vibroacoustics, fluid-structure interaction, unsteady aeroelasticity, soil-structure interaction, etc., but also in solid mechanics (elasticity tensors of random elastic continuous media, matrix-valued random fields for heterogeneous microstructures of materials), thermic (thermal conductivity tensor), electromagnetism (dielectric tensor), etc.
The ensembles of random matrices, devoted to the construction of nonparametric stochastic models of matrices encountered in uncertainty quantification, are briefly summarized below and then are mathematically detailed:
-
The ensemble SE +0 is a subset of all the positive-definite random matrices for which the mean values are given and differ from the unit matrix (unlike to ensemble SG +0 ) and for which the lower bound is the zero matrix. This ensemble is constructed as a transformation of ensemble SG +0 in keeping all the mathematical properties of ensemble SG +0 such as the positiveness.
-
The ensemble SE + ɛ is a subset of all the positive-definite random matrices for which the mean value is a given positive-definite matrix and for which there is an arbitrary lower bound that is a positive-definite matrix controlled by an arbitrary positive number ɛ that can be chosen as small as is desired. In this ensemble, the lower bound does not correspond to a given matrix that results from a physical model. This ensemble is constructed as a transformation of ensemble SG + ɛ and has the same area of use than ensemble SE +0 for stochastic modeling in uncertainty quantification but for which a lower bound is required in the stochastic modeling for mathematical reasons.
-
The ensemble SE+0 is similar to ensemble SG +0 but is constituted of semipositive-definite (m × m) real random matrices for which the mean value is a given semipositive-definite matrix. This ensemble is constructed as a transformation of positive-definite (n × n) real random matrices belonging to ensemble SG +0 , with n < m, in which the dimension of the null space is m − n. Such an ensemble is useful for the nonparametric stochastic modeling of uncertainties such as those encountered in structural dynamics in presence of rigid body displacements.
-
The ensemble SErect is an ensemble of rectangular random matrices for which the mean value is a given rectangular matrix and which is constructed using ensemble SE + ɛ . This ensemble is useful for the nonparametric stochastic modeling of some uncertain coupling operators encountered, for instance, in fluid-structure interaction and in vibroacoustics.
-
The ensemble SEHT is a set of random functions with values in the set of the complex matrices such that the real part and the imaginary part are positive-definite random matrices that are constrained by an underlying Hilbert transform induced by a causality property. This ensemble allows for a nonparametric stochastic modeling in uncertainty quantification encountered, for instance, in linear viscoelasticity.
9.1 Ensemble SE0 + of Positive-Definite Random Matrices with a Given Mean Value
The ensemble SE +0 is a subset of all the positive-definite random matrices for which the mean values are given and differ from the unit matrix (unlike to ensemble SG +0 ). This ensemble is constructed as a transformation of ensemble SG +0 in keeping all the mathematical properties of ensemble SG +0 such as the positiveness [107].
9.1.1 Definition of Ensemble SE0 +
Any random matrix [A 0] in ensemble SE +0 is defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), is with values in \(\mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\), and is such that
in which the mean value [A] is a given matrix in \(\mathbb{M}_{n}^{+}(\mathbb{R})\).
9.1.2 Expression of [A0] as a Transformation of [G0] and Generator of Realizations
Positive-definite mean matrix [A] is factorized (Cholesky) as
in which [L A ] is an upper triangular matrix in \(\mathbb{M}_{n}(\mathbb{R})\). Taking into account Eq. (8.41) and the definition of ensemble SG +0 , any random matrix [A 0] in ensemble SE +0 is written as
in which the random matrix [G 0] belongs to ensemble SG +0 , with mean value E{[G 0]} = [I n ], and for which the level of statistical fluctuations is controlled by the hyperparameter δ defined by Eq. (8.15).
Generator of realizations. For all θ in Θ, the realization [G 0(θ)] of [G 0] is constructed as explained before. The realization [A 0(θ)] of random matrix [A 0] is calculated by [A 0(θ)] = [L A ]T[G 0(θ)] [L A ].
Remark 1.
It should be noted that the mean matrix [A] could also been written as [A] = [A]1∕2 [A]1∕2 in which [A]1∕2 is the square root of [A] in \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and the random matrix [A 0] could then be written as [A 0] = [A]1∕2 [G 0] [A]1∕2.
9.1.3 Properties of Random Matrix [A0]
Any random matrix [A 0] in ensemble SE +0 is a second-order random variable,
and its inverse [A 0]−1 exists almost surely and is a second-order random variable,
9.1.4 Covariance Tensor and Coefficient of Variation of Random Matrix [A0]
The covariance C jk, j′k′ = E{([A 0] jk − A jk )([A 0] j′k′ − A j′k′)} of random variables [A 0] jk and [A 0] j′k′ is written as
and the variance σ 2 jk = C jk, jk of random variable [A 0] jk is
The coefficient of variation \(\delta _{A_{0}}\) of random matrix [A 0] is defined by
Since E{∥A 0 − A∥ 2 F } = ∑ n j = 1 ∑ n k = 1 σ 2 jk , we have
9.2 Ensemble SE ɛ + of Positive-Definite Random Matrices with a Given Mean Value and an Arbitrary Positive-Definite Lower Bound
The ensemble SE + ɛ is a set of positive-definite random matrices for which the mean value is a given positive-definite matrix and for which there is an arbitrary lower bound that is a positive-definite matrix controlled by an arbitrary positive number ɛ that can be chosen as small as is desired. In this ensemble, the lower bound does not correspond to a given matrix that results from a physical model. This ensemble is then constructed as a transformation of ensemble SG + ɛ and has the same area of use than ensemble SE +0 for stochastic modeling in uncertainty quantification, but for which a lower bound is required in the stochastic modeling for mathematical reasons.
9.2.1 Definition of Ensemble SE ɛ +
For a fixed positive value of parameter ɛ (generally chosen very small, as 10−6), any random matrix [A] in ensemble SE + ɛ is defined on probability space \((\varTheta,\mathcal{T},\mathcal{P})\), is with values in \(\mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\), and is such that
in which [L A ] is the upper triangular matrix in \(\mathbb{M}_{n}(\mathbb{R})\) corresponding by the Cholesky factorization [L A ]T [L A ] = [A] of the positive-definite mean matrix [A] = E{[A]} of random matrix [A], and where the random matrix [G] belongs to ensemble SG + ɛ , with mean value E{[G]} = [I n ] and for which the coefficient of variation δ G is defined by Eq. (8.24) as a function of the hyperparameter δ defined by Eq. (8.15), which allows the level of statistical fluctuations to be controlled. It should be noted that for ɛ = 0, [G] = [G 0] that yields [A] = [A 0], and consequently, the ensemble SE + ɛ coincides with SE +0 (if ɛ = 0).
Generator of realizations. For all θ in Θ, the realization [G(θ)] of [G] is constructed as explained before. The realization [A(θ)] of random matrix [A] is calculated by [A(θ)] = [L A ]T[G(θ)] [L A ].
9.2.2 Properties of Random Matrix [A]
Almost surely, we have
in which [A 0] is defined by Eq. (8.43) and where the lower bound is the positive-definite matrix [A ℓ ] = c ɛ [A] with c ɛ = ɛ∕(1 + ɛ), and we have the following properties:
with \(\nu _{A} =\nu _{A_{0}} - n\log (1+\varepsilon )\). For all ɛ > 0, random matrix [A] in ensemble SE + ɛ is a second-order random variable,
and the bilinear form b A (X, Y) = (([A] X, Y)) on \(\mathcal{L}_{n}^{2} \times \mathcal{L}_{n}^{2}\) is such that
Random matrix [A] is invertible almost surely and its inverse [A]−1 is a second-order random variable,
The coefficient of variation δ A of random matrix [A], defined by
is such that
in which \(\delta _{A_{0}}\) is defined by Eq. (8.49).
9.3 Ensemble SE+0 of Semipositive-Definite Random Matrices with a Given Semipositive-Definite Mean Value
The ensemble SE+0 is similar to ensemble SG +0 but is constituted of semipositive-definite (m × m) real random matrices [A] for which the mean value is a given semipositive-definite matrix. This ensemble is constructed [110] as a transformation of positive-definite (n × n) real random matrices [G 0] belonging to ensemble SG +0 , with n < m.
9.3.1 Algebraic Structure of the Random Matrices in SE+0
The ensemble SE+0 is constituted of random matrix [A] with values in the set \(\mathbb{M}_{m}^{+0}(\mathbb{R})\) such that the null space of [A], denoted as null([A]), is deterministic and is a subspace of \(\mathbb{R}^{m}\) with a fixed dimension μ null < m. This deterministic null space is defined as the null space of the mean value [A] = E{[A]} that is given in \(\mathbb{M}_{m}^{+0}(\mathbb{R})\). We then have
There is a rectangular matrix [R A ] in \(\mathbb{M}_{n,m}(\mathbb{R})\), with n = m −μ null, such that
Such a factorization is performed using classical algorithms [47].
9.3.2 Definition and Construction of Ensemble SE+0
The ensemble SE+0 is then defined as the subset of all the second-order random matrices [A], defined on probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in the set \(\mathbb{M}_{m}^{+0}(\mathbb{R})\), which are written as
in which [G] is a positive-definite symmetric (n × n) real random matrix belonging to ensemble SE + ɛ , with mean value E{[G]} = [I n ] and for which the coefficient of variation δ G is defined by Eq. (8.24) as a function of the hyperparameter δ defined by Eq. (8.15), which allows the level of statistical fluctuations to be controlled.
Generator of realizations. For all θ in Θ, the realization [G(θ)] of [G] is constructed as explained before. The realization [A(θ)] of random matrix [A] is calculated by [A(θ)] = [R A ]T[G(θ)] [R A ].
9.4 Ensemble SErect of Rectangular Random Matrices with a Given Mean Value
The ensemble SErect is an ensemble of rectangular random matrices for which the mean value is a given rectangular matrix and which is constructed with the MaxEnt. Such an ensemble depends on the available information and consequently, is not unique. We present hereinafter the construction proposed in [110], which is based on the use of a fundamental algebraic property for rectangular real matrices, which allows ensemble SE + ɛ to be used.
9.4.1 Decomposition of a Rectangular Matrix
Let [A] be a rectangular real matrix in \(\mathbb{M}_{m,n}(\mathbb{R})\) for which its null space is reduced to {0} ([A] x = 0 yields x = 0). Such a rectangular matrix [A] can be written as
in which the square matrix [T] and the rectangular matrix [U] are such that
The construction of the decomposition defined by Eq. (8.61) can be performed, for instance, by using the singular value decomposition of [A].
9.4.2 Definition of Ensemble SErect
Let [A] be a given rectangular real matrix in \(\mathbb{M}_{m,n}(\mathbb{R})\) with a null space reduced to {0} and whose decomposition is given by Eqs. (8.61) and (8.62). Since symmetric real matrix [T] is positive definite, there is an upper triangular matrix [L T ] in \(\mathbb{M}_{n}(\mathbb{R})\) such that [T] = [L T ]T [L T ] that corresponds to the Cholesky factorization of matrix [T].
A random rectangular matrix [A] belonging to ensemble SErect is a second-order random matrix defined on probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in \(\mathbb{M}_{m,n}(\mathbb{R})\), whose mean value is the rectangular matrix [A] = E{[A]}, and which is written as
in which the random (n × n) matrix [T] belongs to ensemble SE + ɛ and is then written as
The random matrix [G] belongs to ensemble SG + ɛ in which [G] is a positive-definite symmetric (n × n) real random matrix belonging to ensemble SE + ɛ , with mean value E{[G]} = [I n ] and for which the coefficient of variation δ G is defined by Eq. (8.24) as a function of hyperparameter δ defined by Eq. (8.15), which allows the level of statistical fluctuations to be controlled.
Generator of realizations. For all θ in Θ, the realization [G(θ)] of [G] is constructed as explained before. The realization [A(θ)] of random matrix [A] is calculated by [A(θ)] = [U][L T ]T[G(θ)] [L T ].
9.5 Ensemble SEHT of a Pair of Positive-Definite Matrix-Valued Random Functions Related by a Hilbert Transform
The ensemble SEHT is a set of random functions ω ↦ [Z(ω)] = [K(ω)] + iω [D(ω)] indexed by \(\mathbb{R}\) with values in a subset of all the (n × n) complex matrices such that [K(ω)] and [D(ω)] are positive-definite random matrices that are constrained by an underlying Hilbert transform induced by a causality property [115].
9.5.1 Defining the Deterministic Matrix Problem
We consider a family of complex (n × n) matrices [Z(ω)] depending on a parameter ω in \(\mathbb{R}\), such that [Z(ω)] = iω [D(ω)] + [K(ω)] where i is the pure imaginary complex number (\(i = \sqrt{-1}\)) and where, for all ω in \(\mathbb{R}\),
-
(i)
[D(ω)] and [K(ω)] belong to \(\mathbb{M}_{n}^{+}(\mathbb{R})\).
-
(ii)
[D(−ω)] = [D(ω)] and [K(−ω)] = [K(ω)].
-
(iii)
Matrices [D(ω)] and [K(ω)] are such that
$$\displaystyle{ \omega \,[D(\omega )] = [\widehat{N}^{I}(\omega )],\quad [K(\omega )] = [K_{ 0}] + [\widehat{N}^{R}(\omega )]. }$$(8.65)The real matrices \([\widehat{N}^{R}(\omega )]\) and \([\widehat{N}^{I}(\omega )]\) are the real part and the imaginary part of the (n × n) complex matrix \([\widehat{N}(\omega )] =\int _{\mathbb{R}}e^{-i\omega t}[N(t)]\,dt\) that is the Fourier transform of an integrable function t ↦ [N(t)] from \(\mathbb{R}\) into \(\mathbb{M}_{n}(\mathbb{R})\) such that [N(t)] = [0] for t < 0 (causal function). Consequently, \(\omega \mapsto [\widehat{N}^{R}(\omega )]\) and \(\omega \mapsto [\widehat{N}^{I}(\omega )]\) are continuous functions on \(\mathbb{R}\), which goes to [0] as | ω | → +∞ and which are related by the Hilbert transform [90],
$$\displaystyle{ [\widehat{N}^{R}(\omega )] = \frac{1} {\pi } \mathrm{ p.v}\int _{-\infty }^{+\infty }\frac{1} {\omega -\omega '}\,[\widehat{N}^{I}(\omega ')]\,d\omega ', }$$(8.66)in which p.v. denotes the Cauchy principal value. The real matrix [K 0] belongs to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and can be written as
$$\displaystyle{ [K_{0}] = [K(0)] + \frac{2} {\pi } \int _{0}^{+\infty }[D(\omega )]\,d\omega =\lim _{\vert \omega \vert \rightarrow +\infty }[K(\omega )], }$$(8.67)and consequently, we have the following equation:
$$\displaystyle{ [K(\omega )] = [K(0)] + \frac{\omega } {\pi }\,\mathrm{ p.v}\int _{-\infty }^{+\infty }\frac{1} {\omega -\omega '}\,[D(\omega ')]\,d\omega '. }$$(8.68)
9.5.2 Construction of a Nonparametric Stochastic Model
The construction of a nonparametric stochastic model then consists in modeling, for all real ω, the positive-definite symmetric (n × n) real matrices [D(ω)] and [K(ω)] by random matrices [D(ω)] and [K(ω)] such that
For ω ≥ 0, the construction of the stochastic model of the family of random matrices [D(ω)] and [K(ω)] is carried out as follows:
-
(i)
Constructing the family [D(ω)] of random matrices such that, for fixed ω, [D(ω)] = [L D (ω)]T [G D ] [L D (ω)], where [L D (ω)] is the upper triangular real (n × n) matrix resulting from the Cholesky decomposition of the positive-definite symmetric real matrix [D(ω)] = [L D (ω)]T [L D (ω)] and where [G D ] is a (n × n) random matrix that belongs to ensemble SG + ɛ , for which the hyperparameter δ is rewritten as δ D . Hyperparameter δ D allows the level of uncertainties to be controlled for random matrix [D(ω)].
-
(ii)
Constructing the random matrix [K(0)] = [L K(0)]T [G K(0)] [L K(0)] in which [L K(0)] is the upper triangular real (n × n) matrix resulting from the Cholesky decomposition of the positive-definite symmetric real matrix [K(0)] = [L K(0)]T [L K(0)] and where [G K(0)] is a (n × n) random matrix that belongs to ensemble SG + ɛ , for which the hyperparameter δ is rewritten as δ K . Hyperparameter δ K allows the level of uncertainties to be controlled for random matrix [K(0)].
-
(iii)
For fixed ω ≥ 0, constructing the random matrix [K(ω)] using the equation,
$$\displaystyle{ [\mathbf{K}(\omega )] = [\mathbf{K}(0)] + \frac{\omega } {\pi }\,\mathrm{ p.v}\int _{-\infty }^{+\infty }\frac{1} {\omega -\omega '}\,[\mathbf{D}(\omega ')]\,d\omega ', }$$(8.71)or equivalently,
$$\displaystyle{ [\mathbf{K}(\omega )] = [\mathbf{K}(0)] + \frac{2\,\omega ^{2}} {\pi } \,\mathrm{ p.v}\int _{0}^{+\infty } \frac{1} {\omega ^{2} -\omega '^{2}}\,[\mathbf{D}(\omega ')]\,d\omega '. }$$(8.72)The last equation can also be rewritten as the following equation recommended for computation (because the singularity in u = 1 is independent of ω):
$$\displaystyle\begin{array}{rcl} [\mathbf{K}(\omega )]& =& [\mathbf{K}(0)] + \frac{2\,\omega } {\pi } \,\mathrm{ p.v}\int _{0}^{+\infty }\, \frac{1} {1 - u^{2}}\,[\mathbf{D}(\omega u)]\,du, \\ & =& [\mathbf{K}(0)] + \frac{2\,\omega } {\pi } \,\,\lim _{\eta \rightarrow 0}\left \{\int _{0}^{1-\eta } +\int _{ 1+\eta }^{+\infty }\right \}.\end{array}$$(8.73) -
(iv)
For fixed ω < 0, [K(ω)] is calculated using the even property, [K(ω)] = [K(−ω)]. With such a construction, it can be verified that, for all ω ≥ 0, [K(ω)] is a positive-definite random matrix. The following sufficient condition is proved in [115]. If for all real vector y = (y 1, …, y n ), and if almost surely the random function ω ↦ <[D(ω)] y, y> is decreasing in ω for ω ≥ 0, then, for all ω ≥ 0, [K(ω)] is a positive-definite random matrix.
10 MaxEnt as a Numerical Tool for Constructing Ensembles of Random Matrices
In the previous sections, we have presented fundamental ensembles of random matrices constructed with the MaxEnt principle. For these fundamental ensembles the optimization problem defined by Eq. (8.8) has been solved exactly, what has allowed us to explicitly construct the fundamental ensembles of random matrices and also to explicitly describe the generators of realizations. This was possible thanks to the type of the available information that was used to define the admissible set (see Eq. (8.7)). In many cases, the available information does not allow the Lagrange multipliers to be explicitly calculated and, thus, does not allow for solving explicitly the optimization problem defined by Eq. (8.8).
In this framework of the nonexistence of an explicit solution for constructing the pdf of random matrices using the MaxEnt principle under the constraints defined by the available information, the first difficulty consists of the computation of the Lagrange multipliers with an adapted algorithm that must be robust for the high dimension. In addition, the computation of the Lagrange multipliers requires the calculation of integrals in high dimension, which can be estimated only by the Monte Carlo method. Therefore a generator of realizations of the pdf, which is parameterized by the unknown Lagrange multipliers that are currently being calculated, must be constructed. This problem is particularly difficult for the high dimension. An advanced and efficient methodology is presented hereinafter for the case of the high dimension [112] (thus allows also for treating the cases of the small dimension and then for any dimension).
10.1 Available Information and Parameterization
Let [A] be a random matrix defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in any subset \(\mathbb{S}_{n}\) of \(\mathbb{M}_{n}^{S}(\mathbb{R})\), possibly with \(\mathbb{S}_{n} = \mathbb{M}_{n}^{S}(\mathbb{R})\). For instance, \(\mathbb{S}_{n}\) can be \(\mathbb{M}_{n}^{+}(\mathbb{R})\). Let p [A] be the pdf of [A] with respect to the volume element d S A on \(\mathbb{M}_{n}^{S}(\mathbb{R})\) (see Eq. (8.1). The support, denoted as supp p [A] of pdf [A], is \(\mathbb{S}_{n}\). Thus, p [A]([A]) = 0 for [A] not in \(\mathbb{S}_{n}\), and the normalization condition is written as
The available information is defined by the following equation on \(\mathbb{R}^{\mu }\):
in which f = (f 1, …, f μ ) is a given vector in \(\mathbb{R}^{\mu }\) with μ ≥ 1, where \([A]\mapsto \boldsymbol{\mathcal{G}}([A]) = (\mathcal{G}_{1}([A]),\ldots,\mathcal{G}_{\mu }([A]))\) is a given mapping from \(\mathbb{S}_{n}\) into \(\mathbb{R}^{\mu }\), and where E is the mathematical expectation. For instance, mapping \(\boldsymbol{\mathcal{G}}\) can be defined by the mean value E[A] = [A] in which [A] is a given matrix in \(\mathbb{S}_{n}\) and by the condition E{log(det[A])} = c A in which | c A | < +∞. A parameterization of ensemble \(\mathbb{S}_{n}\) is introduced such that any matrix [A] in \(\mathbb{S}_{n}\) is written as
in which y = (y 1, …, y N ) is a vector in \(\mathbb{R}^{N}\) and where \(\mathbf{y}\mapsto [\mathcal{A}(\mathbf{y})]\) is a given mapping from \(\mathbb{R}^{N}\) into \(\mathbb{S}_{n}\). Let y ↦ g(y) = (g 1(y), …, g μ (y)) be the mapping from \(\mathbb{R}^{N}\) into \(\mathbb{R}^{\mu }\) such that
Let Y = (Y 1, …, Y N ) be a \(\mathbb{R}^{N}\)-valued second-order random variable for which the probability distribution on \(\mathbb{R}^{N}\) is represented by the pdf y ↦ p Y (y) from \(\mathbb{R}^{N}\) into \(\mathbb{R}^{+} = [0,+\infty [\) with respect to d y = dy 1 …dy N . The support of function p Y is \(\mathbb{R}^{N}\). Function p Y satisfies the normalization condition:
For random vector Y, the available information is deduced from Eqs. (8.75) to (8.77) and is written as
10.1.1 Example of Parameterization
If \(\,\mathbb{S}_{n} = \mathbb{M}_{n}^{+}(\mathbb{R})\), then the parameterization, \([A] = [\mathcal{A}(\mathbf{y})]\), of [A] can be constructed in several ways. In order to obtain good properties for the random matrix \([\mathbf{A}] = [\mathcal{A}(\mathbf{Y})]\) in which Y is a \(\mathbb{R}^{N}\)-valued second-order random variable, deterministic matrix [A] is written as
with ɛ > 0, where [A 0] belongs to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and where [L A ] is the upper triangular (n × n) real matrix corresponding to the Cholesky factorization [L A ]T [L A ] = [A] of the mean matrix [A] = E{[A]} that is given in \(\mathbb{M}_{n}^{+}(\mathbb{R})\). Positive-definite matrix [A 0] can be written in two different forms (inducing different properties for random matrix [A]):
-
(i)
Exponential-type representation [54, 86]. Matrix [A 0] is written as \([A_{0}] =\exp\nolimits_{\mathbb{M}}([G])\) in which the matrix [G] belongs to \(\mathbb{M}_{n}^{S}(\mathbb{R})\) and where \(\exp\nolimits_{\mathbb{M}}\) denotes the exponential of the symmetric real matrices.
-
(ii)
Square-type representation [86, 111]. Matrix [A 0] is written as [A 0] = [L]T [L] in which [L] belongs to the set \(\mathcal{U}_{L}\) of all the upper triangular (n × n) real matrices with positive diagonal entries and where \([L] = \mathcal{L}([G])\) in which \(\mathcal{L}\) is a given mapping from \(\mathbb{M}_{n}^{S}(\mathbb{R})\) into \(\mathcal{U}_{L}\).
For this two representations, the parameterization is constructed in taking for y, the N = n(n + 1)∕2 independent entries {[G] jk , 1 ≤ j ≤ k ≤ n} of symmetric real matrix [G]. Then for all y in \(\mathbb{R}^{N}\), \([A] = [\mathcal{A}(\mathbf{y})]\) is in \(\mathbb{S}_{n}\), that is to say, is a positive-definite matrix.
10.2 Construction of the pdf of Random Vector Y Using the MaxEnt
The unknown pdf p Y with support \(\mathbb{R}^{N}\), whose normalization condition is given by Eq. (8.78), is constructed using the MaxEnt principle for which the available information is defined by Eq. (8.79). This construction is detailed in the next Sect. 11.
11 MaxEnt for Constructing the pdf of a Random Vector
Let Y = (Y 1, …, Y N ) be a \(\mathbb{R}^{N}\)-valued second-order random variable for which the probability distribution P Y (d y) on \(\mathbb{R}^{N}\) is represented by the pdf y ↦ p Y (y) from \(\mathbb{R}^{N}\) into \(\mathbb{R}^{+} = [0,+\infty [\) with respect to d y = dy 1 …dy N . The support of function p Y is \(\mathbb{R}^{N}\). Function p Y satisfies the normalization condition
The unknown pdf p Y is constructed using the MaxEnt principle for which the available information is
in which y ↦ g(y) = (g 1(y), …, g μ (y)) is a given mapping from \(\mathbb{R}^{N}\) into \(\mathbb{R}^{\mu }\). Equation (8.81) is rewritten as
Let \(\mathcal{C}_{p}\) be the set of all the integrable positive-valued functions y ↦ p(y) on \(\mathbb{R}^{N}\), whose support is \(\mathbb{R}^{N}\). Let \(\mathcal{C}\) be the set of all the functions p belonging to \(\mathcal{C}_{p}\) and satisfying the constraints defined by Eqs. (8.80) and (8.82),
The maximum entropy principle [58] consists in constructing p Y in \(\mathcal{C}\) such that
in which the Shannon entropy \(\mathcal{E}(p)\) of p is defined [103] by
where log is the Neperian logarithm. In order to solve the optimization problem defined by Eq. (8.84), a Lagrange multiplier \(\lambda _{0} \in \mathbb{R}^{+}\) (associated with the constraint defined by Eq. (8.80)) and a Lagrange multiplier \(\boldsymbol{\lambda } \in \mathcal{C}_{\boldsymbol{\lambda }}\subset \mathbb{R}^{\mu }\) (associated with the constraint defined by Eq. (8.82)) are introduced, in which the admissible set \(\mathcal{C}_{\boldsymbol{\lambda }}\) is defined by
The solution of Eq. (8.84) can be written (see the proof in the next section) as
in which the normalization constant c sol0 is written as c sol0 = exp(−λ sol0 ) and where the method for calculating \((\lambda _{0}^{\mathrm{ sol}},\boldsymbol{\lambda }^{\mathrm{ sol}}) \in \mathbb{R}^{+} \times \mathcal{C}_{\boldsymbol{\lambda }}\) is presented in the next two sections.
11.1 Existence and Uniqueness of a Solution to the MaxEnt
The introduction of the Lagrange multipliers λ 0 and \(\boldsymbol{\lambda }\) and the analysis of existence and uniqueness of the solution of the MaxEnt corresponding to the solution of the optimization problem defined by Eq. (8.84) are presented hereafter [53].
-
The first step of the proof consists in assuming that there exists a unique solution (denoted as p Y ) to the optimization problem defined by Eq. (8.84). The functionals
$$\displaystyle{ p\mapsto \int _{\mathbb{R}^{N}}\,p(\mathbf{y})\,d\mathbf{y} - 1\quad \mathrm{ and}\quad p\mapsto \int _{\mathbb{R}^{N}}\mathbf{g}(\mathbf{y})\,p(\mathbf{y})\,d\mathbf{y} -\mathbf{f}, }$$(8.88)are continuously differentiable on \(\mathcal{C}_{p}\) and are assumed to be such that p Y is a regular point (see p. 187 of [68]). The constraints appearing in set \(\mathcal{C}\) are taken into account by using the Lagrange multiplier method. Using the Lagrange multipliers \(\lambda _{0} \in \mathbb{R}^{+}\) and \(\boldsymbol{\lambda } \in \mathcal{C}_{\boldsymbol{\lambda }}\) defined by Eq. (8.86), the Lagrangian \(\mathcal{L}\) can be written, for all p in \(\mathcal{C}_{p}\), as
$$\displaystyle\begin{array}{rcl} \mathcal{L}(p;\lambda _{0},\boldsymbol{\lambda })\,=\,\mathcal{E}(p)\,-\,(\lambda _{0}\,-\,1)\left (\int _{\mathbb{R}^{N}}p(\mathbf{y})\,d\mathbf{y} - 1 \right )- < \boldsymbol{\lambda }, \int _{\mathbb{R}^{N}}\mathbf{g}(\mathbf{y})p(\mathbf{y})\,d\mathbf{y}\,-\,\mathbf{f} >.\end{array}$$(8.89)From Theorem 2, p. 188, of [68], it can be deduced that there exists \((\lambda _{0}^{\mathrm{ sol}},\boldsymbol{\lambda }^{\mathrm{ sol}})\) such that the functional \((p,\lambda _{0},\boldsymbol{\lambda })\mapsto \mathcal{L}(p;\lambda _{0},\boldsymbol{\lambda })\) is stationary at p Y (given by Eq. (8.87)) for λ 0 = λ sol0 and \(\boldsymbol{\lambda } = \boldsymbol{\lambda }^{\mathrm{ sol}}\).
-
The second step deals with the explicit construction of a family \(\mathcal{F}_{p}\) of pdf indexed by \((\lambda _{0},\boldsymbol{\lambda })\), which renders \(p\mapsto \mathcal{L}(p;\lambda _{0},\boldsymbol{\lambda })\) extremum. It is further proved that this extremum is unique and turns out to be a maximum. For any \((\lambda _{0},\boldsymbol{\lambda })\) fixed in \(\mathbb{R}^{+} \times \mathcal{C}_{\boldsymbol{\lambda }}\), it can first be deduced from the calculus of variations (Theorem 3.11.16, p. 341, in [101]) that the aforementioned extremum, denoted by \(p_{\lambda _{0},\boldsymbol{\lambda }}\), is written as
$$\displaystyle{ p_{\lambda _{0},\boldsymbol{\lambda }}(\mathbf{y}) =\exp (-\lambda _{0}- < \boldsymbol{\lambda },\mathbf{g}(\mathbf{y}) >),\quad \forall \mathbf{y} \in \mathbb{R}^{N}. }$$(8.90)For any fixed value of λ 0 in \(\mathbb{R}^{+}\) and \(\boldsymbol{\lambda }\) in \(\mathcal{C}_{\boldsymbol{\lambda }}\), the uniqueness of this extremum directly follows from the uniqueness of the solution for the Euler equation that is derived from the calculus of variations. Upon calculating the second-order derivative with respect to p, at point \(p_{\lambda _{0},\boldsymbol{\lambda }}\), of the Lagrangian, it can be shown that this extremum is, indeed, a maximum.
-
In a third step, using Eq. (8.90), it is proved that if there exists \((\lambda _{0}^{\mathrm{ sol}},\boldsymbol{\lambda }^{\mathrm{ sol}})\) in \(\mathbb{R}^{+} \times \mathcal{C}_{\boldsymbol{\lambda }}\) such that the solution of the constraint equations \(\int _{\mathbb{R}^{N}}p_{\lambda _{0},\boldsymbol{\lambda }}(\mathbf{y})\,d\mathbf{y} = 1\) and \(\int _{\mathbb{R}^{N}}\mathbf{g}(\mathbf{y})\,p_{\lambda _{0},\boldsymbol{\lambda }}(\mathbf{y})\,d\mathbf{y} = \mathbf{f}\), in \((\lambda _{0},\boldsymbol{\lambda })\) and then \((\lambda _{0}^{\mathrm{ sol}},\boldsymbol{\lambda }^{\mathrm{ sol}})\) is unique. These constraints are rewritten as
$$\displaystyle\begin{array}{rcl} \int _{\mathbb{R}^{N}}\exp (-\lambda _{0}- < \boldsymbol{\lambda },\mathbf{g}(\mathbf{y}) >)\,d\mathbf{y} = 1.\end{array}$$(8.91)$$\displaystyle\begin{array}{rcl} \int _{\mathbb{R}^{N}}\mathbf{g}(\mathbf{y})\,\exp (-\lambda _{0}- < \boldsymbol{\lambda },\mathbf{g}(\mathbf{y}) >)\,d\mathbf{y} = \mathbf{f}.\end{array}$$(8.92)Introducing the notations,
these constraint equations are written as
It is assumed that the optimization problem stated by Eq. (8.84) is well posed in the sense that the constraints are algebraically independent, that is to say, that there exists a bounded subset \(\mathcal{S}\) of \(\mathbb{R}^{N}\), with \(\int _{\mathcal{S}}d\mathbf{y} > 0\), such that for any nonzero vector v in \(\mathbb{R}^{1+\mu }\),
Let \(\boldsymbol{\Lambda }\mapsto H(\boldsymbol{\Lambda })\) be the function defined by
The gradient \(\boldsymbol{\nabla }H(\boldsymbol{\Lambda })\) of \(H(\boldsymbol{\Lambda })\) with respect to \(\boldsymbol{\Lambda }\) is written as
so that any solution of \(\boldsymbol{\nabla }H(\boldsymbol{\Lambda }) = \mathbf{0}\) satisfies Eq. (8.93) (and conversely). It is assumed that H admits at least one critical point. The Hessian matrix \([H''(\boldsymbol{\Lambda })]\) is written as
Since \(\mathcal{S}\subset \mathbb{R}^{N}\), it turns out that, for any nonzero vector v in \(\mathbb{R}^{1+\mu }\),
Therefore, function \(\boldsymbol{\Lambda }\mapsto H(\boldsymbol{\Lambda })\) is strictly convex that ensures the uniqueness of the critical point of H (should it exist). Under the aforementioned assumption of algebraic independence for the constraints, it follows that if \(\boldsymbol{\Lambda }^{\mathrm{ sol}}\) (such that the constraint defined by Eq. (8.93) is fulfilled) exists, then \(\boldsymbol{\Lambda }^{\mathrm{ sol}}\) is unique and corresponds to the solution of the following optimization problem:
where H is the strictly convex function defined by Eq. (8.95). The unique solution p Y of the optimization problem defined by Eq. (8.84) is the given by Eq. (8.87) with \((\lambda _{0}^{\mathrm{ sol}},\boldsymbol{\lambda }^{\mathrm{ sol}}) = \boldsymbol{\Lambda }^{\mathrm{ sol}}\).
11.2 Numerical Calculation of the Lagrange Multipliers
When there is no explicit solution \((\lambda _{0}^{\mathrm{ sol}},\boldsymbol{\lambda }^{\mathrm{ sol}}) = \boldsymbol{\Lambda }^{\mathrm{ sol}}\) of Eq. (8.93) in \(\boldsymbol{\Lambda }\), \(\boldsymbol{\Lambda }^{\mathrm{ sol}}\) must be numerically calculated and the numerical method used must be robust for the high dimension. The numerical method could be based on the optimization problem defined by Eq. (8.99). Unfortunately, with such a formulation, the constant of normalization, c 0 = exp(−λ 0), is directly involved in the numerical calculations, what is not robust in high dimension. The numerical method proposed hereinafter [11] is based on the minimization of the convex objective function introduced in [1]. Using Eqs. (8.80) and (8.87), pdf p Y can be rewritten as
in which \(c_{0}(\boldsymbol{\lambda })\) is defined by
Since exp(−λ 0) = c 0(λ 0), and taking into account Eq. (8.101), the constraint equation defined by Eq. (8.92) can be rewritten as
The optimization problem defined by Eq. (8.99), which allows for calculating \((\lambda _{0}^{\mathrm{ sol}},\boldsymbol{\lambda }^{\mathrm{ sol}}) = \boldsymbol{\Lambda }^{\mathrm{ sol}}\), is replaced by the more convenient optimization problem that allows \(\boldsymbol{\lambda }^{\mathrm{ sol}}\) to be computed,
in which the objective function Γ is defined by
Once \(\boldsymbol{\lambda }^{\mathrm{ sol}}\) is calculated, c sol0 is given by \(c_{0}^{\mathrm{ sol}} = c_{0}(\boldsymbol{\lambda }^{\mathrm{ sol}})\). Let \(\{\mathbf{Y}_{\boldsymbol{\lambda }},\boldsymbol{\lambda } \in \mathcal{C}_{\boldsymbol{\lambda }}\}\) be the family of random variables with values in \(\mathbb{R}^{N}\), for which pdf \(p_{\mathbf{Y}_{\boldsymbol{\lambda }}}\) is defined, for all \(\boldsymbol{\lambda }\) in \(\mathcal{C}_{\boldsymbol{\lambda }}\), by
The gradient vector \(\boldsymbol{\nabla }\varGamma (\boldsymbol{\lambda })\) and the Hessian matrix \([\varGamma ''(\boldsymbol{\lambda })]\) of function \(\lambda \mapsto \varGamma (\boldsymbol{\lambda })\) can be written as
Matrix \([\varGamma ''(\boldsymbol{\lambda })]\) is thus the covariance matrix of the random vector \(\mathbf{g}(\mathbf{Y}_{\boldsymbol{\lambda }})\) and is positive definite (the constraints have been assumed to be algebraically independent). Consequently, function \(\boldsymbol{\lambda }\mapsto \varGamma (\boldsymbol{\lambda })\) is strictly convex and reaches its minimum for \(\boldsymbol{\lambda }^{\text{sol}}\) which is such that \(\boldsymbol{\nabla }\varGamma (\boldsymbol{\lambda }^{\mathrm{ sol}}) = \mathbf{0}\). The optimization problem defined by Eq. (8.103) can be solved using any minimization algorithm. Since function Γ is strictly convex, the Newton iterative method can be applied to the increasing function \(\boldsymbol{\lambda }\mapsto \boldsymbol{\nabla }\varGamma (\boldsymbol{\lambda })\) for searching \(\boldsymbol{\lambda }^{\mathrm{ sol}}\) such that \(\boldsymbol{\nabla }\varGamma (\boldsymbol{\lambda }^{\mathrm{ sol}}) = \mathbf{0}\). This iterative method is not unconditionally convergent. Consequently, an under-relaxation is introduced and the iterative algorithm is written as
in which α belongs to [0, 1] in order to ensure the convergence. At each iteration ℓ, the error is calculated by
in order to control the convergence. The performance of the algorithm depends on the choice of the initial condition that can be found in [11]. For high dimension problem, the mathematical expectations appearing in Eqs. (8.106), (8.107), and (8.109) are calculated using a Markov chain Monte Carlo (MCMC) method that does not require the calculation of the normalization constant \(c_{0}(\boldsymbol{\lambda })\) in the pdf defined by Eq. (8.105).
11.3 Generator for Random Vector \( \mathrm{Y}_{\lambda}\) and Estimation of the Mathematical Expectations in High Dimension
For \(\boldsymbol{\lambda }\) fixed in \(\mathcal{C}_{\boldsymbol{\lambda }}\subset \mathbb{R}^{\mu }\), the pdf \(p_{\mathbf{Y}_{\boldsymbol{\lambda }}}\) on \(\mathbb{R}^{N}\) of the \(\mathbb{R}^{N}\)-valued random variable \(\mathbf{Y}_{\boldsymbol{\lambda }}\) is defined by Eq. (8.105). Let w be a given mapping from \(\mathbb{R}^{N}\) into an Euclidean space such that \(E\{w(\mathbf{Y}_{\boldsymbol{\lambda }})\} =\int _{\mathbb{R}^{N}}w(\mathbf{y})\,p_{\mathbf{Y}_{\boldsymbol{\lambda }}}\,d\mathbf{y}\) is finite. For instance, w can be such that \(w(\mathbf{Y}_{\boldsymbol{\lambda }}) = \mathbf{g}(\mathbf{Y}_{\boldsymbol{\lambda }})\) or \(w(\mathbf{Y}_{\boldsymbol{\lambda }}) = \mathbf{g}(\mathbf{Y}_{\boldsymbol{\lambda }})\,\mathbf{g}(\mathbf{Y}_{\boldsymbol{\lambda }})^{T}\). These two choices allow for calculating the mathematical expectation in high dimension, \(E\{\mathbf{g}(\mathbf{Y}_{\boldsymbol{\lambda }})\}\) and \(E\{\mathbf{g}(\mathbf{Y}_{\boldsymbol{\lambda }})\,\mathbf{g}(\mathbf{Y}_{\boldsymbol{\lambda }})^{T}\}\), which are required for computing the gradient and the Hessian defined by Eqs. (8.106) and (8.107).
The estimation of \(E\{w(\mathbf{Y}_{\boldsymbol{\lambda }})\}\) requires a generator of realizations of random vector \(\mathbf{Y}_{\boldsymbol{\lambda }}\), which is constructed using the Markov chain Monte Carlo method (MCMC) [59, 95, 117]. With the MCMC method, the transition kernel of the homogeneous Markov chain can be constructed using the Metropolis-Hastings algorithm [57, 75] (that requires the definition of a good proposal distribution), the Gibbs sampling [42] (that requires the knowledge of the conditional distribution), or the slice sampling [83] (that can exhibit difficulties related to the general shape of the probability distribution, in particular for multimodal distributions). In general, these algorithms are efficient, but can also be not efficient if there exist attraction regions which do not correspond to the invariant measure under consideration and tricky even in high dimension. These cases cannot easily be detected and are time consuming.
We refer the reader to the references given hereinbefore for the usual MCMC methods, and we present after a more advanced method that is very robust in high dimension, which have been introduced in [112] and used, for instance, in [11, 51]. The method presented looks like to the Gibbs approach but corresponds to a more direct construction of a random generator of realizations for random variable \(\mathbf{Y}_{\boldsymbol{\lambda }}\) whose probability distribution is \(p_{\mathbf{Y}_{\boldsymbol{\lambda }}}\,d\mathbf{y}\). The difference between the Gibbs algorithm and the proposed algorithm is that the convergence in the proposed method can be studied with all the mathematical results concerning the existence and uniqueness of Itô stochastic differential equation (ISDE). In addition, a parameter is introduced which allows the transient part of the response to be killed in order to get more rapidly the stationary solution corresponding to the invariant measure. Thus, the construction of the transition kernel by using the detailed balance equation is replaced by the construction of an ISDE, which admits \(p_{\mathbf{Y}_{\boldsymbol{\lambda }}}\,d\mathbf{y}\) (defined by Eq. (8.105)) as a unique invariant measure. The ergodic method or the Monte Carlo method is used for estimating \(E\{w(\mathbf{Y}_{\boldsymbol{\lambda }})\}\).
11.3.1 Random Generator and Estimation of Mathematical Expectations
It is assumed that \(\boldsymbol{\lambda }\) is fixed in \(\mathcal{C}_{\boldsymbol{\lambda }}\subset \mathbb{R}^{\mu }\), and for simplifying the notation, \(\boldsymbol{\lambda }\) is omitted. Let u ↦ Φ(u) be the function from \(\mathbb{R}^{N}\) into \(\mathbb{R}\) defined by
Let \(\{(\mathbf{U}(r),\mathbf{V}(r)),r \in \mathbb{R}^{+}\}\) be the Markov stochastic process defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), indexed by \(\mathbb{R}^{+} = [0,+\infty [\), with values in \(\mathbb{R}^{N} \times \mathbb{R}^{N}\), satisfying, for all r > 0, the following ISDE with initial conditions:
in which u 0 and v 0 are given vectors in \(\mathbb{R}^{N}\) (that will be taken as zero in the application presented later) and where W = (W 1, …, W N ) is the normalized Wiener process defined on \((\varTheta,\mathcal{T},\mathcal{P})\) indexed by \(\mathbb{R}^{+}\) with values in \(\mathbb{R}^{N}\). The matrix-valued autocorrelation function [R W (r, r′)] = E{W(r) W(r′)T} of W is then written as [R W (r, r′)] = min(r, r′) [I n ]. In Eq. (8.112), the free parameter f 0 > 0 allows a dissipation term to be introduced in the nonlinear second-order dynamical system (formulated in the Hamiltonian form with an additional dissipative term) in order to kill the transient part of the response and consequently to get more rapidly the stationary solution corresponding to the invariant measure. It is assumed that function g is such that function u ↦ Φ(u) (i) is continuous on \(\mathbb{R}^{N}\), (ii) is such that \(\mathbf{u}\mapsto \Vert \boldsymbol{\nabla }_{\mathbf{u}}\varPhi (\mathbf{u})\Vert\) is a locally bounded function on \(\mathbb{R}^{N}\) (i.e., is bounded on all compact set in \(\mathbb{R}^{N}\)), and (iii) is such that
Under hypotheses (i) to (iii), and using Theorems 4 to 7 in pages 211 to 216 of Ref. [105], in which the Hamiltonian is taken as \(\mathbb{H}(\mathbf{u},\mathbf{v}) =\Vert \mathbf{v}\Vert ^{2}/2 +\varPhi (\mathbf{u})\), and using [33, 62] for the ergodic property, it can be deduced that the problem defined by Eqs. (8.111), (8.112), and (8.113) admits a unique solution. This solution is a second-order diffusion stochastic process {(U(r), V(r)), \(r \in \mathbb{R}^{+}\}\), which converges to a stationary and ergodic diffusion stochastic process {(U st(r st), V st(r st)), r st ≥ 0}, when r goes to infinity, associated with the invariant probability measure P st(d u, d v) = ρ st(u, v) d u d v. The probability density function (u, v) ↦ ρ st(u, v) on \(\mathbb{R}^{N} \times \mathbb{R}^{N}\) is the unique solution of the steady-state Fokker-Planck equation associated with Eqs. (8.111)– (8.112) and is written (see pp. 120 to 123 in [105]), as
in which c N is the constant of normalization. Equations (8.105), (8.110), and (8.117) yield
Random variable \(\mathbf{Y}_{\boldsymbol{\lambda }}\) (for which the pdf \(p_{\mathbf{Y}_{\boldsymbol{\lambda }}}\) is defined by Eq. (8.105)) can then be written, for all fixed positive value of r st, as
The free parameter f 0 > 0 introduced in Eq. (8.112) allows a dissipation term to be introduced in the nonlinear dynamical system for obtaining more rapidly the asymptotic behavior corresponding to the stationary and ergodic solution associated with the invariant measure. Using Eq. (8.119) and the ergodic property of stationary stochastic process U st yield
in which, for θ ∈ Θ, U(⋅ , θ) is any realization of U.
11.3.2 Discretization Scheme and Estimating the Mathematical Expectations
A discretization scheme must be used for numerically solving Eqs. (8.111), (8.112), and (8.113). For general surveys on discretization schemes for ISDE, we refer the reader to [63, 118, 119] (among others). The present case, related to a Hamiltonian dynamical system, has also been analyzed using an implicit Euler scheme in [120]. Hereinafter, we present the Störmer-Verlet scheme, which is an efficient scheme that preserves energy for nondissipative Hamiltonian dynamical systems (see [56] for reviews about this scheme in the deterministic case, and see [17] and the references therein for the stochastic case).
Let M ≥ 1 be an integer. The ISDE defined by Eqs. (8.111), (8.112), and (8.113) is solved on the finite interval \(\mathcal{R} = [0,(M - 1)\,\varDelta r]\), in which Δr is the sampling step of the continuous index parameter r. The integration scheme is based on the use of the M sampling points r k such that r k = (k − 1) Δr for k = 1, …, M. The following notations are introduced: U k = U(r k ), V k = V(r k ), and W k = W(r k )), for k = 1, …, M, with U 1 = u 0, V 1 = v 0, and W 1 = 0. Let {Δ W k+1 = W k+1−W k, k = 1, …, M − 1} be the family of the independent Gaussian second-order centered \(\mathbb{R}^{N}\)-valued random variables such that E{Δ W k+1 (Δ W k+1)T} = Δr [I n ]. For k = 1, …, M − 1, the Störmer-Verlet scheme yields
with the initial condition defined by (8.113), where b = f 0 Δr ∕4 and where \(\mathbf{L}^{k+\frac{1} {2} }\) is the \(\mathbb{R}^{N}\)-valued random variable such that \(\mathbf{L}^{k+\frac{1} {2} } = -\{\boldsymbol{\nabla }_{\mathbf{u}}\varPhi (\mathbf{u})\}_{\mathbf{ u} =\mathbf{U}^{k+ \frac{1} {2} }}\).
For a given realization θ in Θ, the sequence {U k(θ), k = 1, …, M} is constructed using Eqs. (8.121), (8.122), and (8.123). The discretization of Eq. (8.120) yields the following estimation of the mathematical expectation:
in which, for f 0 fixed, the integer M 0 > 1 is chosen to remove the transient part of the response induced by the initial condition.
For details concerning the optimal choice of the numerical parameters, such as M 0, M, f 0, Δ r , u 0, and v 0, we refer the reader to [11, 51, 54, 112].
12 Nonparametric Stochastic Model For Constitutive Equation in Linear Elasticity
This section deals with a nonparametric stochastic model for random elasticity matrices in the framework of the three-dimensional linear elasticity in continuum mechanics, using the methodologies and some of the results that have been given in the two previous sections: “Fundamental Ensembles for Positive-Definite Symmetric Real Random Matrices” and “MaxEnt as a Numerical Tool for Constructing Ensemble of Random Matrices.” The developments given hereinafter correspond to a synthesis of works detailed in [51, 53, 54].
From a continuum mechanics point of view, the framework is the 3D linear elasticity of a homogeneous random medium (material) at a given scale. Let \([\widetilde{\mathbf{C}}]\) be the random elasticity matrix for which the nonparametric stochastic model has to be derived. Random matrix \([\widetilde{\mathbf{C}}]\) is defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\) and is with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\) with n = 6. This matrix corresponds to the so-called Kelvin’s matrix representation of the fourth-order symmetric elasticity tensor in 3D linear elasticity [71]. The symmetry classes for a linear elastic material, that is to say, the linear elastic symmetries, are [23] isotropic, cubic, transversely isotropic, trigonal, tetragonal, orthotropic, monoclinic, and anisotropic. From a stochastic modeling point of view, the random elasticity matrix \([\widetilde{\mathbf{C}}]\) satisfies the following properties:
-
(i)
Random matrix \([\widetilde{\mathbf{C}}]\) is assumed to have a mean value that belongs to \(\mathbb{M}_{n}^{+}(\mathbb{R})\), but is, in mean, close to a given symmetry class induced by a material symmetry, denoted as \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) and which is a subset of \(\mathbb{M}_{n}^{+}(\mathbb{R})\),
$$\displaystyle{ [\widetilde{\underline{C}}] = E\{[\widetilde{\mathbf{C}}]\} \in \mathbb{M}_{n}^{+}(\mathbb{R}). }$$(8.125) -
(ii)
Random matrix \([\widetilde{\mathbf{C}}]\) admits a positive-definite lower bound [C ℓ ] belonging to \(\mathbb{M}_{n}^{+}(\mathbb{R})\)
$$\displaystyle{ [\widetilde{\mathbf{C}}] - [C_{\ell}] > 0\quad a.s. }$$(8.126) -
(iii)
The statistical fluctuations of random elasticity matrix \([\widetilde{\mathbf{C}}]\) belong mainly to the symmetry class, but can be more or less anisotropic with respect to the above symmetry. The level of statistical fluctuations in the symmetry class must be controlled independently of the level of statistical anisotropic fluctuations.
12.1 Positive-Definite Matrices Having a Symmetry Class
For the positive-definite symmetric (n × n) real matrices, a given symmetry class is defined by a subset \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R}) \subset \mathbb{M}_{n}^{+}(\mathbb{R})\) such that any matrix [M] exhibiting the above symmetry then belongs to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) and can be written as
in which {[E sym j ], j = 1, …, N} is the matrix algebraic basis of \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) (Walpole’s tensor basis [122]) and where the admissible subset \(\mathcal{C}_{\mathbf{m}}\) of \(\mathbb{R}^{N}\) is such that
It should be noted that the basis matrices [E sym j ] are symmetric matrices belonging to \(\mathbb{M}_{n}^{S}(\mathbb{R})\), but are not positive definite, that is to say, do not belong to \(\mathbb{M}_{n}^{+}(\mathbb{R})\). The dimension N for all material symmetry classes is 2 for isotropic, 3 for cubic, 5 for transversely isotropic, 6 or 7 for trigonal, 6 or 7 for tetragonal, 9 for orthotropic, 13 for monoclinic, and 21 for anisotropic. The following properties are proved (see [54, 122]):
-
(i)
If [M] and [M′] belong to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\), then
$$\displaystyle\begin{array}{rcl} [M]\,[M'] \in \mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R}),\quad [M]^{-1} \in \mathbb{M}_{ n}^{\mathrm{ sym}}(\mathbb{R}),\quad [M]^{1/2} \in \mathbb{M}_{ n}^{\mathrm{ sym}}(\mathbb{R}).\end{array}$$(8.129) -
(ii)
Any matrix [N] belonging to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) can be written as
$$\displaystyle{ [N] =\exp\nolimits_{\mathbb{M}}([\mathcal{N}]),\quad [\mathcal{N}] =\sum _{ j=1}^{N}y_{ j}\,[E_{j}^{\mathrm{ sym}}],\quad \mathbf{y} = (y_{ 1},\ldots,y_{N}) \in \mathbb{R}^{N}, }$$(8.130)in which \(\exp\nolimits_{\mathbb{M}}\) is the exponential of symmetric real matrices. It should be noted that matrix \([\mathcal{N}]\) is a symmetric real matrix but does not belong to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) (because y is in \(\mathbb{R}^{N}\) and therefore \([\mathcal{N}]\) is not a positive-definite matrix).
12.2 Representation Introducing a Positive-Definite Lower Bound
Using Eq. (8.126), the representation of random elasticity matrix \([\widetilde{\mathbf{C}}]\) is written as
in which the lower bound is the deterministic matrix [C ℓ ] belonging to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and where \([\mathbf{C}] = [\widetilde{\mathbf{C}}] - [C_{\ell}]\) is a random matrix with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\). The mean value [C] = E{[C]} of [C] is written as
in which \([\widetilde{\underline{C}}]\) is defined by Eq. (8.125). Such a lower bound can be defined in two ways:
-
(1)
If some microstructural information is available, [C ℓ ] may be computed, either by using some well-known micromechanics-based bounds (such as the Reuss bound, for heterogeneous materials made up with ordered phases with deterministic properties) or by using a numerical approximation based on the realizations of the stochastic lower bound obtained from computational homogenization and invoking the Huet partition theorem (see the discussion in [49]).
-
(2)
In the absence of such information, a simple a priori expression for [C ℓ ] can be obtained as \([C_{\ell}] =\epsilon [\widetilde{\underline{C}}]\) with 0 ≤ ε < 1, from which it can be deduced that \([\underline{C}] = (1-\epsilon )[\widetilde{\underline{C}}] > 0\).
12.3 Introducing Deterministic Matrices [A] and [S]
Let [A] be the deterministic matrix in \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) defined by
in which \([\underline{C}] \in \mathbb{M}_{n}^{+}(\mathbb{R})\) is defined by Eq. (8.132) and where P sym is the projection operator from \(\mathbb{M}_{n}^{+}(\mathbb{R})\) on \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\).
-
(i)
For a given symmetry class with N < 21, if there is no anisotropic statistical fluctuations, then the mean matrix [C] belongs to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) and consequently [A] is equal to [C].
-
(ii)
If the class of symmetry is anisotropic (thus N = 21), then \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) coincides with \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and again [A] is equal to the mean matrix [C] that belongs to \(\mathbb{M}_{n}^{+}(\mathbb{R})\).
-
(iii)
In general, for a given symmetry class with N < 21, and due to the presence of anisotropic statistical fluctuations, the mean matrix [C] of random matrix [C] belongs to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) but does not belong to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\). For this case, an invertible deterministic (n × n) real matrix [S] is introduced such that
$$\displaystyle{ [\underline{C}] = [\underline{S}]^{T}\,[\underline{A}]\,[\underline{S}]. }$$(8.134)The construction of [S] is performed as follows. Let [L C ] and [L A ] be the upper triangular real matrices with positive diagonal entries resulting from the Cholesky factorization of matrices [C] and [A],
$$\displaystyle{ [\underline{C}] = [L_{\underline{C}}]^{T}\,[L_{\underline{ C}}],\quad [\underline{A}] = [L_{\underline{A}}]^{T}\,[L_{\underline{ A}}]. }$$(8.135)Therefore, the matrix [S] is written as
$$\displaystyle{ [\underline{S}] = [L_{\underline{A}}]^{-1}\,[L_{\underline{ C}}]. }$$(8.136)It should be noted that for cases (i) and (ii), Eq. (8.136) shows that [S] = [I n ].
12.4 Nonparametric Stochastic Model for [C]
In order that the statistical fluctuations of random matrix [C] belong mainly to the symmetry class \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) and exhibit more or less some anisotropic fluctuations around this symmetry class, and in order that the level of statistical fluctuations in the symmetry class is controlled independently of the level of statistical anisotropic fluctuation, the use of the nonparametric method leads us to introduce the following representation:
in which:
-
(1)
The deterministic (n × n) real matrix [S] is defined by Eq. (8.136).
-
(2)
[G 0] belongs to ensemble SG +0 of random matrices and models the anisotropic statistical fluctuations. The mean value of random matrix [G 0] is matrix [I n ] (see Eq. (8.13)). The level of the statistical fluctuations of [G 0] is controlled by the hyperparameter δ defined by Eq. (8.15).
-
(3)
The random matrix [A]1∕2 is the square root of a random matrix [A] with values in \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R}) \subset \mathbb{M}_{n}^{+}(\mathbb{R})\), which models the statistical fluctuations in the given symmetry class and which is statistically independent of random matrix [G 0]. The mean value of random matrix [A] is the matrix [A] defined by Eq. (8.133),
$$\displaystyle{ E\{[\mathbf{A}]\} = [\underline{A}]\,\, \in \,\, \mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R}) \subset \mathbb{M}_{ n}^{+}(\mathbb{R}). }$$(8.138)The level of the statistical fluctuations of [A] is controlled by the coefficient of variation δ A defined by
$$\displaystyle{ \delta _{A} = \left \{\frac{E\{\Vert \mathbf{A} -\underline{ A}\Vert _{F}^{2}\}} {\Vert \underline{A}\Vert _{F}^{2}} \right \}^{1/2}. }$$(8.139)Taking into account the statistical independence of A and G 0 and taking the mathematical expectation of the two members of Eq. (8.137) yield Eq. (8.134).
12.4.1 Remarks Concerning the Control of the Statistical Fluctuations and the Limit Cases
-
(1)
For a given symmetry class with N < 21, if the level of anisotropic statistical fluctuations goes to zero, that is to say, if δ → 0 what implies that [G 0] goes to [I n ] (in probability distribution) and implies that [A] goes to [C] and thus [S] goes to [I n ], then Eq. (8.137) shows that [C] goes to [A] (in probability distribution), which is a random matrix with values in \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\).
-
(2)
If the given symmetry class is anisotropic (N = 21) and δ A → 0, then [A] goes to the mean matrix [C], [S] goes to [I n ], and [A] goes to [A] that goes to [C] (in probability distribution). Then [C] goes to [C]1∕2 [G 0] [C]1∕2, which is the full anisotropic nonparametric stochastic modeling of [C].
12.5 Construction of [A] Using the MaxEnt Principle
In this section, random matrix [A] that allows for describing the statistical fluctuations in the class of symmetry \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) with N < 21 is constructed using the MaxEnt principle and, in particular, using all the results and notations introduced in Sect. 10.
12.5.1 Defining the Available Information
Let p [A] be the unknown pdf of random matrix [A], with respect to volume element d S A on \(\mathbb{M}_{n}^{S}(\mathbb{R})\) (see Eq. (8.1)), with values in the given symmetry class \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R}) \subset \mathbb{M}_{n}^{+}(\mathbb{R}) \subset \mathbb{M}_{n}^{S}(\mathbb{R})\) with N < 21. The support, supp p [A], is the subset \(\mathbb{S}_{n} = \mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\), and the normalization condition is given by Eq. (8.74). The available information is defined by
in which [A] is the matrix in \(\mathbb{S}_{n}\), defined by Eq. (8.133), and where the second available information is introduced in order that pdf [A] ↦ p [A]([A]) decreases toward zero when ∥A∥ F goes to zero. The constant c A that has no physical meaning is re-expressed as a function of the hyperparameter δ A defined by Eq. (8.139). This available information defines the vector f = (f 1, …, f μ ) in \(\mathbb{R}^{\mu }\) with μ = n(n + 1)∕2 + 1 and defines the mapping \([A]\mapsto \boldsymbol{\mathcal{G}}([A]) = (\mathcal{G}_{1}([A]),\ldots,\mathcal{G}_{\mu }([A]))\) from \(\mathbb{S}_{n}\) into \(\mathbb{R}^{\mu }\), such that (see Eq. (8.75))
12.5.2 Defining the Parameterization
The objective is to construct the parameterization of ensemble \(\mathbb{S}_{n} = \mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\), such that any matrix [A] in \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) is written (see Eq. (8.76)) as
in which y = (y 1, …, y N ) is a vector in \(\mathbb{R}^{N}\) and where \(\mathbf{y}\mapsto [\mathcal{A}(\mathbf{y})]\) is a given mapping from \(\mathbb{R}^{N}\) into \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\). Let [A]1∕2 be the square root of matrix \([\underline{A}] \in \mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R}) \subset \mathbb{M}_{n}^{+}(\mathbb{R})\) that is defined by Eq. (8.133). Due to Eq. (8.129), [A]1∕2 belongs to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\). Any matrix [A] in \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) can then be written as
in which, due to Eq. (8.129) and due to the invertibility of [A]1∕2, [N] is a unique matrix belonging to \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\). Using Eq. (8.130), matrix [N] has the following representation:
Consequently, Eqs. (8.143) and (8.144) define the parameterization \([A] = [\mathcal{A}(\mathbf{y})]\).
12.5.3 Construction of [A] Using the Parameterization and Generator of Realizations
The random matrix [A] with values in \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\) is then written
in which [N] is the random matrix with values in \(\mathbb{M}_{n}^{\mathrm{ sym}}(\mathbb{R})\), which is written as
in which Y = (Y 1, …, Y N ) is the random vector with values in \(\mathbb{R}^{N}\) whose pdf p Y on \(\mathbb{R}^{N}\) and the generator of realizations have been detailed in Sect. 10. Since [N] can be written as [N] = [A]−1∕2 [A] [A]−1∕2, and since E[A] = [A] (see Eq. (8.140)), it can be deduced that
13 Nonparametric Stochastic Model of Uncertainties in Computational Linear Structural Dynamics
The nonparametric method for stochastic modeling of uncertainties has been introduced in [106, 107] to take into account both the model-parameter uncertainties and the model uncertainties induced by modeling errors in computational linear structural dynamics, without separating the contribution of each one of these two types of uncertainties.
The nonparametric method is presented hereinafter for linear vibrations of fixed linear structures (no rigid body displacement, but only deformation), formulated in the frequency domain, and for which two cases are considered:
-
The case of damped linear elastic structures for which the damping and the stiffness matrices of the computational model are independent of the frequency.
-
The case of linear viscoelastic structures for which the damping and the stiffness matrices of the computational model depend on the frequency.
13.1 Methodology
The methodology of the nonparametric method consists in introducing:
-
(i)
A mean computational model for the linear dynamics of the structure,
-
(ii)
A reduced-order model (ROM) of the mean computational model,
-
(iii)
The nonparametric stochastic modeling of both the model-parameter uncertainties and the model uncertainties induced by modeling errors, consisting in modeling the mass, damping, and stiffness matrices of the ROM by random matrices,
-
(iv)
A prior probability model of the random matrices based on the use of the fundamental ensembles of random matrices introduced previously,
-
(v)
An estimation of the hyperparameters of the prior probability model of uncertainties if some experimental data are available.
The extension to the case of vibrations of free linear structures (presence of rigid body displacements and of elastic deformations) is straightforward, because it is sufficient to construct the ROM (which is then devoted only to the prediction of the structural deformations) in projecting the response on the elastic structural modes (without including the rigid body modes) [89].
13.2 Mean Computational Model in Linear Structural Dynamics
The dynamical system is a damped fixed elastic structure for which the vibrations are studied around a static equilibrium configuration considered as a natural state without prestresses and which is subjected to an external load. For given nominal values of the parameters of the dynamical system, the finite element model [128] is called the mean computational model, which is written, in the time domain, as

in which  is the vector of the m degrees of freedom (DOF) (displacements and/or rotations);
is the vector of the m degrees of freedom (DOF) (displacements and/or rotations);  and
and  are the velocity and acceleration vectors;
are the velocity and acceleration vectors;  is the external load vector of the m inputs (forces and/or moments); and \([\mathbb{M}]\), \([\mathbb{D}]\), and \([\mathbb{K}]\) are the mass, damping, and stiffness matrices of the mean computational model, respectively, which belong to \(\mathbb{M}_{m}^{+}(\mathbb{R})\).
is the external load vector of the m inputs (forces and/or moments); and \([\mathbb{M}]\), \([\mathbb{D}]\), and \([\mathbb{K}]\) are the mass, damping, and stiffness matrices of the mean computational model, respectively, which belong to \(\mathbb{M}_{m}^{+}(\mathbb{R})\).
-
The solution
 of the time evolution problem is constructed in solving Eq. (8.148) for t > 0 with the initial conditions
of the time evolution problem is constructed in solving Eq. (8.148) for t > 0 with the initial conditions  and
and  .
. -
The forced response
 is such that, for all t fixed in \(\mathbb{R}\),
is such that, for all t fixed in \(\mathbb{R}\),  verifies Eq. (8.148), and its Fourier transform
verifies Eq. (8.148), and its Fourier transform  is such that, for all ω in \(\mathbb{R}\),
is such that, for all ω in \(\mathbb{R}\), (8.149)
(8.149)in which
 is the Fourier transform of
is the Fourier transform of  . As \([\mathbb{M}]\), \([\mathbb{D}]\), and \([\mathbb{K}]\) are positive-definite matrices, the \(\mathbb{M}_{m}(\mathbb{C})\)-valued frequency response function
. As \([\mathbb{M}]\), \([\mathbb{D}]\), and \([\mathbb{K}]\) are positive-definite matrices, the \(\mathbb{M}_{m}(\mathbb{C})\)-valued frequency response function 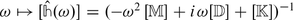 is a bounded function on \(\mathbb{R}\). From a point of view of the nonparametric stochastic modeling of uncertainties, it is equivalent of presenting the time evolution problem or the forced response problem expressed in the frequency domain. Nevertheless, for such a linear system, the analysis is mainly carried out in the frequency domain. In order to limit the developments, the forced response problem expressed in the frequency domain is presented.
is a bounded function on \(\mathbb{R}\). From a point of view of the nonparametric stochastic modeling of uncertainties, it is equivalent of presenting the time evolution problem or the forced response problem expressed in the frequency domain. Nevertheless, for such a linear system, the analysis is mainly carried out in the frequency domain. In order to limit the developments, the forced response problem expressed in the frequency domain is presented.
13.3 Reduced-Order Model (ROM) of the Mean Computational Model
The ROM of the mean computational model is constructed for analyzing the response of the structure over a frequency band \(\mathcal{B}\) (bounded symmetric interval of pulsations in rad/s) such that
and is obtained in using the method of modal superposition (or modal analysis) [8, 87]. The generalized eigenvalue problem associated with the mass and stiffness matrices of the mean computational model is written as
for which the eigenvalues 0 < λ 1 ≤ λ 2 ≤ … ≤ λ m and the associated elastic structural modes \(\{\boldsymbol{\phi }_{1},\boldsymbol{\phi }_{2},\ldots,\boldsymbol{\phi }_{m}\}\) are such that
in which \(\omega _{\alpha } = \sqrt{\lambda _{\alpha }}\) is the eigenfrequency of elastic structural mode \(\boldsymbol{\phi }_{\alpha }\) whose normalization is defined by the generalized mass μ
α
. Let \(\mathbb{H}_{n}\) be the subspace of \(\mathbb{R}^{m}\) spanned by \(\{\boldsymbol{\phi }_{1},\ldots,\boldsymbol{\phi }_{n}\}\) with n ≪ m and let \(\mathbb{H}_{n}^{c}\) be its complexified (i.e., \(\mathbb{H}_{n}^{c} = \mathbb{H}_{n} + i\,\mathbb{H}_{n}\)). Let [Φ] be the (m × n) real matrix whose columns are vectors \(\{\boldsymbol{\phi }_{1},\ldots,\boldsymbol{\phi }_{n}\}\). The ROM of the mean computational model is obtained as the projection x
n(ω) of  on \(\mathbb{H}_{n}^{c}\), which is written as x
n(ω) = [Φ] q(ω) in which q(ω) is the vector in \(\mathbb{C}^{n}\) of the generalized coordinates and is written, for all ω in \(\mathcal{B}\), as
on \(\mathbb{H}_{n}^{c}\), which is written as x
n(ω) = [Φ] q(ω) in which q(ω) is the vector in \(\mathbb{C}^{n}\) of the generalized coordinates and is written, for all ω in \(\mathcal{B}\), as
in which [M], [D], and [K] (generalized mass, damping, and stiffness matrices) belong to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and are such that
In general, [D] is a full matrix. The generalized force f(ω) is a \(\mathbb{C}^{n}\)-vector such that  in which
in which  is the Fourier transform of
is the Fourier transform of  , which is assumed to be a bounded function on \(\mathbb{R}\).
, which is assumed to be a bounded function on \(\mathbb{R}\).
13.3.1 Convergence of the ROM with Respect to n Over Frequency Band of Analysis \(\mathcal{B}\)
For the given frequency band of analysis \(\mathcal{B}\), and for a fixed value of the relative error ɛ 0 with 0 < ɛ 0 ≪ 1, let n 0 (depending on ɛ 0) be the smallest value of n such that 1 ≤ n 0 < m, for which, for all ω in \(\mathcal{B}\), the convergence of the ROM (with respect to dimension n) is reached with relative error ɛ 0 (if n 0 was equal to m, then ɛ would be equal to 0). The value of n 0 is such that

in which  . In practice, for large computational model, Eq. (8.157) is replaced by a convergence analysis of x
n to x on \(\mathcal{B}\) for a given subset of generalized forces f.
. In practice, for large computational model, Eq. (8.157) is replaced by a convergence analysis of x
n to x on \(\mathcal{B}\) for a given subset of generalized forces f.
13.4 Nonparametric Stochastic Model of Both the Model-Parameter Uncertainties and the Model Uncertainties (Modeling Errors)
For the given frequency band of analysis \(\mathcal{B}\), and for n fixed to the value n 0 such that Eq. (8.157) is verified, the nonparametric stochastic model of uncertainties consists in replacing in Eq. (8.155) the deterministic matrices [M], [D], and [K] by random matrices [M], [D], and [K] defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\). The deterministic ROM defined by Eqs. (8.154) and (8.155) is then replaced by the following stochastic ROM:
in which, for all ω in \(\mathcal{B}\), X n(ω) and Q(ω) are \(\mathbb{C}^{m}\)- and \(\mathbb{C}^{n}\)-valued random vectors defined on probability space \((\varTheta,\mathcal{T},\mathcal{P})\).
13.4.1 Available Information for Constructing a Prior Probability Model of [M], [D], and [K]
The available information for constructing the prior probability model of random matrices [M], [D], and [K] using the MaxEnt principle are the following:
-
(i)
Random matrices [M], [D], and [K] are with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\).
-
(ii)
The mean values of these random matrices are chosen as the corresponding matrices in the ROM of the mean computational model,
$$\displaystyle{ E\{[\mathbf{M}]\} = [M],\,\,E\{[\mathbf{D}]\} = [D],\,\,E\{[\mathbf{K}]\} = [K]. }$$(8.160) -
(iii)
The prior probability model of these random matrices must be chosen such that, for all ω in \(\mathcal{B}\), the solution Q(ω) of Eq. (8.159) is a second-order \(\mathbb{C}^{n}\)-valued random variable, that is to say, such that
$$\displaystyle{ E\{\Vert (-\omega ^{2}[\mathbf{M}] + i\omega [\mathbf{D}] + [\mathbf{K}])^{-1}\Vert _{ F}^{2}\} < +\infty,\quad \forall \omega \in \mathcal{B}. }$$(8.161)
13.4.2 Prior Probability Model of [M], [D], and [K], Hyperparameters and Generator of Realizations
The joint pdf of random matrices [M], [D], and [K] is constructed using the MaxEnt principle under the constraints defined by the available information described before. Taking into account such an available information, it is proved [107] that these three random matrices are statistically independent. Taking into account Eqs. (8.52), (8.55), (8.160), and (8.161), each random matrix [M], [D], and [K] is then chosen in ensemble SE + ɛ of the positive-definite random matrices with a given mean value and an arbitrary positive-definite lower bound. The level of uncertainties, for each type of forces (mass, damping, and stiffness), is controlled by the three hyperparameters δ M , δ D , and δ K of the pdf of random matrices [M], [D], and [K], which are defined by Eq. (8.56). The generator of realizations for ensemble SE + ɛ has explicitly been described.
13.5 Case of Linear Viscoelastic Structures
The dynamical system is a fixed viscoelastic structure for which the vibrations are studied around a static equilibrium configuration considered as a natural state without prestresses and which is subjected to an external load. Consequently, in the frequency domain, the damping and stiffness matrices depend on frequency ω, instead of to be independent of the frequency as in the previous analyzed case. Consequently, two aspects must be addressed. The first one is relative to the choice of the basis for constructing the ROM, and the second one is the nonparametric stochastic modeling of the frequency dependent damping and stiffness matrices which are related by a Hilbert transform; we then use for such a nonparametric stochastic modeling ensemble SEHT of a pair of positive-definite matrix-valued random functions related to a Hilbert transform.
13.5.1 Mean Computational Model, ROM, and Convergence
In such a case, the mean computational model defined by Eq. (8.149) is replaced by the following:

For constructing the ROM, the projection basis is chosen as previously in taking the stiffness matrix at zero frequency. The generalized eigenvalue problem, defined by Eq. (8.151), is then rewritten as \([\mathbb{K}(0)]\,\boldsymbol{\phi } =\lambda \, [\mathbb{M}]\,\boldsymbol{\phi }\). With such a choice of a basis, Eqs. (8.154) to (8.156) that defined the ROM for all ω belonging to the frequency band of analysis \(\mathcal{B}\) are replaced by
in which [M], [D(ω)], and [K(ω)] belong to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and are such that
The matrices [D(ω)] and [K(ω)] are full matrices belonging to \(\mathbb{M}_{n}^{+}(\mathbb{R})\), which verify (see [89]) all the mathematical properties introduced in the construction of ensemble SEHT and, in particular, verify Eqs. (8.65) to (8.68). For ɛ 0 fixed, the value n 0 of the dimension n of the ROM is such that Eq. (8.157) holds (equation in which the frequency dependence of the damping and stiffness matrices is introduced). In practice, for large computational model, this criterion is replaced by a convergence analysis of x n to x on \(\mathcal{B}\) for a given subset of generalized forces f.
13.5.2 Nonparametric Stochastic Model of Both the Model-Parameter Uncertainties and the Model Uncertainties (Modeling Errors)
For the given frequency band of analysis \(\mathcal{B}\), and for n fixed to the value n 0, the nonparametric stochastic model of uncertainties consists in replacing in Eq. (8.164) the deterministic matrices [M], [D(ω)], and [K(ω)] by random matrices [M], [D(ω)], and [K(ω)] defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\). The deterministic ROM defined by Eqs. (8.163) and (8.164) is then replaced by the following stochastic ROM:
in which, for all ω in \(\mathcal{B}\), X n(ω) and Q(ω) are \(\mathbb{C}^{m}\)- and \(\mathbb{C}^{n}\)-valued random vectors defined on probability space \((\varTheta,\mathcal{T},\mathcal{P})\).
13.5.3 Available Information for Constructing a Prior Probability Model of [M], [D(ω)], and [K(ω)]
The available information for constructing the prior probability model of random matrices [M], [D(ω)], and [K(ω)] using the MaxEnt principle are, for all ω in \(\mathcal{B}\):
-
(i)
Random matrices [M], [D(ω)], and [K(ω)] are with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\).
-
(ii)
The mean values of these random matrices are chosen as the corresponding matrices in the ROM of the mean computational model,
$$\displaystyle{ E\{[\mathbf{M}]\} = [M],\,\,E\{[\mathbf{D}(\omega )]\} = [D(\omega )],\,\,E\{[\mathbf{K}(\omega )]\} = [K(\omega )]. }$$(8.168) -
(iii)
The random matrices [D(ω)] and [K(ω)] are such that
$$\displaystyle{ [\mathbf{D}(-\omega )] = [\mathbf{D}(\omega )],\,\,[\mathbf{K}(-\omega )] = [\mathbf{K}(\omega )]. }$$(8.169) -
(iv)
The prior probability model of these random matrices must be chosen for that, for all ω in \(\mathcal{B}\), the solution Q(ω) of Eq. (8.167) is a second-order \(\mathbb{C}^{n}\)-valued random variable, that is to say, for that
$$\displaystyle{ E\{\Vert (-\omega ^{2}[\mathbf{M}] + i\omega [\mathbf{D}(\omega )] + [\mathbf{K}(\omega )])^{-1}\Vert _{ F}^{2}\} < +\infty,\quad \forall \omega \in \mathcal{B}. }$$(8.170) -
(v)
The algebraic dependence between [D(ω)] and [K(ω)] induced by the causality must be preserved, which means that random matrix [K(ω)] is given by Eq. (8.72) as a function of random matrix [K(0)] and the family of random matrices {[D(ω)], ω ≥ 0},
$$\displaystyle{ [\mathbf{K}(\omega )] = [\mathbf{K}(0)] + \frac{2\,\omega ^{2}} {\pi } \,\mathrm{ p.v}\int \nolimits_{0}^{+\infty } \frac{1} {\omega ^{2} -\omega '^{2}}\,[\mathbf{D}(\omega ')]\,d\omega ',\quad \forall \,\omega \geq 0. }$$(8.171)
13.5.4 Prior Probability Model of [M], [D(ω)], and [K(0)], Hyperparameters, and Generator of Realizations
Taking into account the available information, the use of the MaxEnt principle yields that random matrices [M], {[D(ω)], ω ≥ 0}, and [K(0)] are statistically independent.
-
As previously, random matrix [M] is chosen in ensemble SE + ɛ of the positive-definite random matrices with a given mean value and an arbitrary positive-definite lower bound. The pdf is explicitly defined and depends on the hyperparameter δ M defined by Eq. (8.56). The generator of realizations is the generator of the ensemble SE + ɛ , which was explicitly defined.
-
For all fixed ω, random matrices [D(ω)] and [K(0)] that are statistically independent are constructed as explained in the section devoted to ensemble SEHT. The levels of uncertainties of random matrices [D(ω)] and [K(0)] are controlled by the two frequency-independent hyperparameters δ D and δ K introduced in paragraphs (i) and (ii) located after Eq. (8.70). The generator of realizations is directly deduced from the generator of realizations of fundamental ensemble SG + ɛ , which was explicitly defined.
-
With such a nonparametric stochastic modeling, the level of uncertainties is controlled by hyperparameters δ M , δ D , and δ K , and the generators of realizations of random matrices [M], [D(ω)], and [K(0)] are explicitly described .
13.6 Estimation of the Hyperparameters of the Nonparametric Stochastic Model of Uncertainties
For the nonparametric stochastic model of uncertainties in computational linear structural dynamics, dimension n of the ROM is fixed to the value n 0 for which the response of the ROM of the mean computational model is converged with respect to n. The prior probability model of uncertainties then depends on the vector-valued hyperparameter \(\boldsymbol{\delta }_{\mathrm{ npar}} = (\delta _{M},\delta _{D},\delta _{K})\) belonging to an admissible set \(\mathcal{C}_{\mathrm{ npar}}\).
-
If no experimental data are available, then \(\boldsymbol{\delta }_{\mathrm{ npar}}\) must be considered as a vector-valued parameter for performing a sensitivity analysis of the stochastic solution with respect to the level of uncertainties. Such a nonparametric stochastic model of both the model-parameter uncertainties and the model uncertainties then allows the robustness of the solution to be analyzed as a function of the level of uncertainties which is controlled by \(\boldsymbol{\delta }_{\mathrm{ npar}}\).
-
If experimental data are available, an estimation of \(\boldsymbol{\delta }_{\mathrm{ npar}}\) can be carried out, for instance, using a least square method or the maximum likelihood method [102, 117, 123]. Let W be the random real vector which is observed, which is independent of ω, but which depends on \(\{\mathbf{X}^{n}(\omega ),\omega \in \mathcal{B}\}\) where X n(ω) is the second-order random complex vector given by Eq. (8.158) or (8.166). For all \(\boldsymbol{\delta }_{\mathrm{ npar}}\) in \(\mathcal{C}_{\mathrm{ npar}}\), the probability density function of W is denoted as \(\mathbf{w}\mapsto p_{\mathbf{W}}(\mathbf{w};\boldsymbol{\delta }_{\mathrm{ npar}})\). Using the maximum likelihood method, the optimal value \(\boldsymbol{\delta }_{\mathrm{ npar}}^{\mathrm{ opt}}\) of \(\boldsymbol{\delta }_{\mathrm{ npar}}\) is estimated by maximizing the logarithm of the likelihood function,
$$\displaystyle{ \boldsymbol{\delta }_{\mathrm{ npar}}^{\mathrm{ opt}} =\arg \max _{\boldsymbol{\delta }_{\mathrm{ npar}}\in \mathcal{C}_{\mathrm{ npar}}}\sum _{\ell=1}^{\nu _{\mathrm{ exp}}}\log \,p_{\mathbf{ W}}(\mathbf{w}_{\ell}^{\mathrm{ exp}};\boldsymbol{\delta }_{\mathrm{ npar}}). }$$(8.172)in which \(\mathbf{w}_{1}^{\mathrm{ exp}},\ldots,\mathbf{w}_{\nu _{\mathrm{ exp}}}^{\mathrm{ exp}}\) are ν exp independent experimental data corresponding to W.
14 Parametric-Nonparametric Uncertainties in Computational Nonlinear Structural Dynamics
The last two presented sections have been devoted to the nonparametric stochastic model of both the model-parameter uncertainties and the model uncertainties induced by the modeling errors, without separating the contribution of each one of these two types of uncertainties. Sometimes, there is an interest of separating the uncertainties for a small number of model parameters that exhibit an important sensitivity on the responses, from uncertainties induced by the model uncertainties and the uncertainties on other model parameters.
Such an objective requires to use a parametric-nonparametric stochastic model of uncertainties, also called the generalized probabilistic approach of uncertainties in computational structural dynamics, which has been introduced in [113].
As the nonparametric stochastic model of uncertainties has been presented in the previous sections for linear dynamical systems formulated in the frequency domain, in the present section, the parametric-nonparametric stochastic model of uncertainties is presented in computational nonlinear structural dynamics formulated in the time domain.
14.1 Mean Nonlinear Computational Model in Structural Dynamics
The dynamical system is a damped fixed structure for which the nonlinear vibrations are studied in the time domain around a static equilibrium configuration considered as a natural state without prestresses and subjected to an external load. For given nominal values of the model parameters of the dynamical system, the basic finite element model is called the mean nonlinear computational model. In addition, it is assumed that a set of model parameters has been identified as sensitive parameters that are uncertain. These uncertain model parameters are the components of a vector \(\tilde{\mathbf{y}}\) belonging to an admissible set \(\mathcal{C}_{\mathrm{ par}}\) which is a subset of \(\mathbb{R}^{N}\). It is assumed that a parameterization is constructed such that \(\tilde{\mathbf{y}} =\boldsymbol{ \mathcal{Y}}(\mathbf{y})\) in which \(\mathbf{y}\mapsto \boldsymbol{\mathcal{Y}}(\mathbf{y})\) is a given and known function from \(\mathcal{C}_{\mathrm{ par}}\) into \(\mathbb{R}^{N}\). For instance, if the component \(\tilde{y}_{j}\) of \(\tilde{\mathbf{y}}\) must belong to [0, +∞[, then \(\tilde{y}_{j}\) could be defined as exp(y j ) with \(y_{j} \in \mathbb{R}\), which yields \(\mathcal{Y}_{j}(\mathbf{y}) =\exp (y_{j})\). Hereinafter, it is then assumed that the uncertain model parameters are represented by vector y = (y 1, …, y N ) belonging to \(\mathbb{R}^{N}\). The nonlinear mean computational model, depending on uncertain model parameter y, is written as

in which  is the unknown time response vector of the m degrees of freedom (DOF) (displacements and/or rotations);
is the unknown time response vector of the m degrees of freedom (DOF) (displacements and/or rotations);  and
and  are the velocity and acceleration vectors respectively;
are the velocity and acceleration vectors respectively;  is the known external load vector of the m inputs (forces and/or moments); \([\mathbb{M}(\mathbf{y})]\), \([\mathbb{D}(\mathbf{y})]\), and \([\mathbb{K}(\mathbf{y})]\) are the mass, damping, and stiffness matrices of the linear part of the mean nonlinear computational model, respectively, which belong to \(\mathbb{M}_{m}^{+}(\mathbb{R})\); and
is the known external load vector of the m inputs (forces and/or moments); \([\mathbb{M}(\mathbf{y})]\), \([\mathbb{D}(\mathbf{y})]\), and \([\mathbb{K}(\mathbf{y})]\) are the mass, damping, and stiffness matrices of the linear part of the mean nonlinear computational model, respectively, which belong to \(\mathbb{M}_{m}^{+}(\mathbb{R})\); and  is the nonlinear mapping that models the local nonlinear forces (such as nonlinear elastic barriers).
is the nonlinear mapping that models the local nonlinear forces (such as nonlinear elastic barriers).
We are interested in the time evolution problem defined by Eq. (8.173) for t > 0 with the initial conditions  and
and  .
.
14.2 Reduced-Order Model (ROM) of the Mean Nonlinear Computational Model
For all y fixed in \(\mathbb{R}^{N}\), let \(\{\boldsymbol{\phi }_{1}(\mathbf{y}),\ldots,\boldsymbol{\phi }_{m}(\mathbf{y})\}\) be an algebraic basis of \(\mathbb{R}^{m}\) constructed, for instance, either using the elastic structural modes of the linearized system, using the elastic structural modes of the underlying linear system, or using the POD (proper orthogonal decomposition) modes of the nonlinear system). Hereinafter, it is assumed that the elastic structural modes of the underlying linear system are used for constructing the ROM of the mean nonlinear computational model (such a choice is not intrusive with respect to a black-box software, but in counterpart requires a large parallel computation induced by all the sampling values of y, which are considered by the stochastic solver).
For each value of y given in \(\mathbb{R}^{N}\), the generalized eigenvalue problem associated with the mean mass and stiffness matrices is written as
for which the eigenvalues 0 < λ 1(y) ≤ λ 2(y) ≤ … ≤ λ m (y) and the associated elastic structural modes \(\{\boldsymbol{\phi }_{1}(\mathbf{y}),\boldsymbol{\phi }_{2}(\mathbf{y}),\ldots,\boldsymbol{\phi }_{m}(\mathbf{y})\}\) are such that
in which \(\omega _{\alpha }(\mathbf{y}) = \sqrt{\lambda _{\alpha }(\mathbf{y} )}\) is the eigenfrequency of elastic structural mode \(\boldsymbol{\phi }_{\alpha }(\mathbf{y})\) whose normalization is defined by the generalized mass μ
α
(y). Let [ϕ(y)] be the (m × n) real matrix whose columns are vectors \(\{\boldsymbol{\phi }_{1}(\mathbf{y}),\ldots,\boldsymbol{\phi }_{n}(\mathbf{y})\}\). For y fixed in \(\mathbb{R}^{N}\) and for all fixed t > 0, the ROM is obtained as the projection x
n(t) of  on the subspace of \(\mathbb{R}^{m}\) spanned by \(\{\boldsymbol{\phi }_{1}(\mathbf{y}),\ldots,\boldsymbol{\phi }_{n}(\mathbf{y})\}\) with n ≪ m, which is written as x
n(t) = [ϕ(y)] q(t) in which q(t) is the vector in \(\mathbb{R}^{n}\) of the generalized coordinates and is written, for all t > 0, as
on the subspace of \(\mathbb{R}^{m}\) spanned by \(\{\boldsymbol{\phi }_{1}(\mathbf{y}),\ldots,\boldsymbol{\phi }_{n}(\mathbf{y})\}\) with n ≪ m, which is written as x
n(t) = [ϕ(y)] q(t) in which q(t) is the vector in \(\mathbb{R}^{n}\) of the generalized coordinates and is written, for all t > 0, as
in which [M(y)], [D(y)], and [K(y)] (generalized mass, damping, and stiffness matrices) belong to \(\mathbb{M}_{n}^{+}(\mathbb{R})\) and are such that
In general, [D(y)] is a full matrix. The generalized force f(t; y) is a \(\mathbb{R}^{n}\)-vector such that  . The generalized nonlinear force is such that
. The generalized nonlinear force is such that  .
.
Convergence of the ROM with respect to
n. Let n
0 be the value of n, for which, for a given accuracy and for all y in \(\mathbb{R}^{N}\), the response x
n is converged to  for all n > n
0.
for all n > n
0.
14.3 Parametric-Nonparametric Stochastic Modeling of Uncertainties
In all this section, the value of n is fixed to the value n 0 defined hereinbefore.
14.3.1 Methodology
-
The parametric stochastic modeling of uncertainties consists in modeling uncertain model parameter y by a second-order random variable Y = (Y 1, …, Y N ), defined on the probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in \(\mathbb{R}^{N}\). Consequently, deterministic matrices [M(y)], [D(y)], and [K(y)] defined by Eqs. (8.179)– (8.180) become the second-order random matrices, [M(Y)], [D(Y)], and [K(Y)], defined on probability space \((\varTheta,\mathcal{T},\mathcal{P})\), with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\). The mean values of these random matrices are the matrices in \(\mathbb{M}_{n}^{+}(\mathbb{R})\) such that
$$\displaystyle{ [\underline{M}] = E\{[M(\mathbf{Y})]\},\quad [\underline{D}] = E\{[D(\mathbf{Y})]\},\quad [\underline{K}] = E\{[K(\mathbf{Y})]\}, }$$(8.181) -
The nonparametric stochastic modeling of uncertainties consists, for all y fixed in \(\mathbb{R}^{N}\), in modeling matrices [M(y)], [D(y)], and [K(y)] defined by Eqs. (8.179)– (8.180), by the second-order random matrices [M(y)] = { θ′ ↦ [M(θ′; y)]}, [D(y)] = { θ′ ↦ [D(θ′; y)]}, and [K(y)] = { θ′ ↦ [K(θ′; x)]}, defined on another probability space \((\varTheta ',\mathcal{T}',\mathcal{P}')\) (and thus independent of Y), with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\).
-
The parametric-nonparametric stochastic modeling of uncertainties consists, in Eq. (8.178)):
-
(i)
In modeling [M(y)], [D(y)], and [K(y)] by random matrices [M(y)], [D(y)], and [K(y)],
-
(ii)
In modeling uncertain model parameter y by the \(\mathbb{R}^{N}\)-valued random variable Y.
Consequently, the statistically dependent random matrices [M(Y)] = {(θ, θ′) ↦ [M(θ′; Y(θ))]}, [D(Y)] = {(θ, θ′) ↦ [D(θ′; Y(θ))]} and [K(Y)] = {(θ, θ′) ↦ [K(θ′; Y(θ))]} are measurable mappings from Θ ×Θ′ into \(\mathbb{M}_{n}^{+}(\mathbb{R})\). The deterministic ROM defined by Eqs. (8.177)– (8.178) is then replaced by the following stochastic ROM:
$$\displaystyle\begin{array}{rcl} \mathbf{X}^{n}(t) = [\phi (\mathbf{Y})]\,\mathbf{Q}(t),& & {}\end{array}$$(8.182)$$\displaystyle\begin{array}{rcl} [\mathbf{M}(\mathbf{Y})]\,\ddot{\mathbf{Q}}(t) + [\mathbf{D}(\mathbf{Y})]\,\dot{\mathbf{Q}}(t) + [\mathbf{K}(\mathbf{Y})]\,\mathbf{Q}(t) + \mathbf{F}_{\mathrm{ NL}}(\mathbf{Q}(t),\dot{\mathbf{Q}}(t);\mathbf{Y}) = \mathbf{f}(t;\mathbf{Y}),& & {}\end{array}$$(8.183)in which for all fixed t, X n(t) = {(θ, θ′) ↦ X n(θ, θ′; t)} and Q(t) = {(θ, θ′) ↦ Q(θ, θ′; t)} are \(\mathbb{R}^{m}\)- and \(\mathbb{R}^{n}\)-valued random vectors defined for (θ, θ′) in Θ ×Θ′.
-
(i)
14.3.2 Prior Probability Model of Y, Hyperparameters, and Generator of Realizations
The prior pdf p Y on \(\mathbb{R}^{N}\) of random vector Y is constructed using the MaxEnt principle under the constraints defined by the available information given by Eq. (8.81), as explained in Sect. 11, in which a generator of realizations {Y(θ), θ ∈ Θ} has been detailed. Such a generator depends on the hyperparameters related to the available information. In general, the hyperparameters are the mean vector y = E{Y} belonging to \(\mathbb{R}^{N}\) and a vector-valued hyperparameter \(\boldsymbol{\delta }_{\mathrm{ par}}\) that belongs to an admissible set \(\mathcal{C}_{\mathrm{ par}}\), which allows the level of parametric uncertainties to be controlled.
14.3.3 Prior Probability Model of [M(y)], [D(y)], and [K(y)], Hyperparameters, and Generator of Realizations
Similarly to the construction given in section entitled “Nonparametric Stochastic Model of Uncertainties in Computational Linear Structural Dynamics”, for all y fixed in \(\mathbb{R}^{N}\), random matrices [M(y)], [D(y)], and [K(y)], are statistically independent and written as
in which, for all y in \(\mathbb{R}^{N}\), [L M (y)], [L D (y)], and [L K (y)] are the upper triangular matrices such that (Cholesky factorization) [M(y)] = [L M (y)]T [L M (y)], [D(y)] = [L D (y)]T [L D (y)], and [K(y)] = [L K (y)]T [L K (y)]. In Eqs. (8.184) to (8.186), [G M ], [G D ], and [G K ] are independent random matrices defined on probability space \((\varTheta ',\mathcal{T}',\mathcal{P}')\), with values in \(\mathbb{M}_{n}^{+}(\mathbb{R})\), independent of y, and belonging to fundamental ensemble SG + ɛ of random matrices. The level of nonparametric uncertainties is controlled by the coefficients of variation \(\delta _{G_{M}}\), \(\delta _{G_{D}}\), and \(\delta _{G_{K}}\) defined by Eq. (8.24) and the vector-valued parameter \(\boldsymbol{\delta }_{\mathrm{ npar}}\) is defined as \(\boldsymbol{\delta }_{\mathrm{ npar}} = (\delta _{M},\delta _{D},\delta _{K})\) that belongs to an admissible set \(\mathcal{C}_{\mathrm{ npar}}\). The generator of realizations {[G M (θ′)], [G D (θ′)], [G K (θ′)] for θ′ in Θ′ is explicitly described in the section devoted to the construction of ensembles SG + ɛ and SG +0 .
14.3.4 Mean Values of Random Matrices [M(Y)], [D(Y)], [K(Z)] and Hyperparameters of the Parametric-Nonparametric Stochastic Model of Uncertainties
Taking into account the construction presented hereinbefore, we have
in which the matrices [M], [D], and [K] are the deterministic matrices defined by Eq. (8.181). The hyperparameters of the parametric-nonparametric stochastic model of uncertainties are
14.4 Estimation of the Hyperparameters of the Parametric-Nonparametric Stochastic Model of Uncertainties
The value of n is fixed to the value n 0 that has been defined. The parametric-nonparametric stochastic model of uncertainties is controlled by the hyperparameters defined by Eq. (8.188).
-
If no experimental data are available, then y can be fixed to a nominal value y 0, and \(\boldsymbol{\delta }_{\mathrm{ par}}\) and \(\boldsymbol{\delta }_{\mathrm{ npar}}\) must be considered as parameters to perform a sensitivity analysis of the stochastic solution. Such a parametric-nonparametric stochastic model of uncertainties allows the robustness of the solution to be analyzed as a function of the level of uncertainties controlled by \(\boldsymbol{\delta }_{\mathrm{ par}}\) and \(\boldsymbol{\delta }_{\mathrm{ npar}}\).
-
If experimental data are available, an estimation of y, \(\boldsymbol{\delta }_{\mathrm{ par}}\), and \(\boldsymbol{\delta }_{\mathrm{ npar}}\) can be carried out, for instance, using a least square method or the maximum likelihood method [102, 117, 123]. Let W be the random real vector which is observed, which is independent of t, but which depends on {X n(t), t ≥ 0} where X n(t) is the second-order stochastic solution of Eq. (8.182)– (8.183) for t > 0 with initial conditions for t = 0. Let \(\mathbf{r} = (\underline{\mathbf{y}},\boldsymbol{\delta }_{\mathrm{ par}},\boldsymbol{\delta }_{\mathrm{ npar}})\) be the vector-valued hyperparameter belonging to the admissible set \(\mathcal{C}_{\mathbf{r}} = \mathbb{R}^{N}\, \times \mathcal{C}_{\mathrm{ par}}\, \times \mathcal{C}_{\mathrm{ npar}}\). For all r in \(\mathcal{C}_{\mathbf{r}}\), the probability density function of W is denoted as w ↦ p W (w; r). Using the maximum likelihood method, the optimal values r opt of r are estimated by maximizing the logarithm of the likelihood function,
$$\displaystyle{ \mathbf{r}^{\mathrm{ opt}} =\arg \,\max _{\mathbf{r}\in \mathcal{C}_{\mathbf{r}}}\sum _{\ell=1}^{\nu _{\mathrm{ exp}}}\log \,p_{\mathbf{ W}}(\mathbf{w}_{\ell}^{\mathrm{ exp}};\mathbf{r}). }$$(8.189)in which \(\mathbf{w}_{1}^{\mathrm{ exp}},\ldots,\mathbf{w}_{\nu _{\mathrm{ exp}}}^{\mathrm{ exp}}\) are ν exp independent experimental data corresponding to W.
15 Key Research Findings and Applications
15.1 Propagation of Uncertainties Using Nonparametric or Parametric-Nonparametric Stochastic Models of Uncertainties
The stochastic modeling introduces some random vectors and some random matrices in the stochastic computational models. Consequently, a stochastic solver is required. Two distinct classes of techniques can be used:
-
The first one is constituted of the stochastic spectral methods, pioneered by Roger Ghanem in 1990–1991 [43, 44], consisting in performing a projection of the Galerkin type (see [45, 46, 67, 69, 84, 121]), and of separated representations methods [34, 85]. This class of techniques allows for obtaining a great precision for the approximated solution that is constructed.
-
The second class is composed of methods based on a direct simulation of which the most popular is the Monte Carlo numerical simulation method (see, for instance, [41, 96]). With such a method, the convergence can be controlled during the computation, and its speed of convergence is independent of the stochastic dimension and can be improved using either advanced Monte Carlo simulation procedures [100], or a technique of subset simulation [6], or finally a method of local simulation domain [93]. The Monte Carlo simulation method is a stochastic solver that is particularly well adapted to the high stochastic dimension induced by the random matrices introduced by the nonparametric method of uncertainties.
15.2 Experimental Validations of the Nonparametric Method of Uncertainties
The nonparametric stochastic modeling of uncertainties has been experimentally validated through applications in different domains of computational sciences and engineering, in particular:
-
In linear dynamics, for the dynamics of complex structures in the low-frequency domain [7, 12, 13]; for the dynamics of structures with nonhomogeneous uncertainties, in the low-frequency domain [24] and in transient dynamics [35]; and finally for the dynamics of composite sandwich panels in low- and medium-frequency domains [25];
-
In nonlinear dynamics, for nonlinear structural dynamics of fuel assemblies [9], for nonlinear post-buckling static and dynamical analyses of uncertain cylindrical shells [21], and for some nonlinear reduced-order models [81];
-
In linear structural acoustics, for the vibroacoustic of complex structures in low- and medium-frequency domains [38], with sound-insulation layers [39], and for the wave propagation in multilayer live tissues in the ultrasonic domain [30];
-
In continuum mechanics of solids, for the nonlinear thermomechanical analysis [97] and the heat transfer in complex composite panels [98] and for linear elasticity of composited reinforced with fibers at mesoscale [48].
15.3 Additional Ingredients for the Nonparametric Stochastic Modeling of Uncertainties
Some important ingredients have been developed for having the tools required for performing the nonparametric stochastic modeling of uncertainties in linear and nonlinear dynamics of mechanical systems, in particular:
-
The dynamic substructuring with uncertain substructures which allows for the nonparametric modeling of nonhomogeneous uncertainties in different parts of a structure [116];
-
The nonparametric stochastic modeling of uncertain structures with uncertain boundary conditions/coupling between substructures [78];
-
The nonparametric stochastic modeling of matrices that depend on the frequency and that are related by a Hilbert transform due to the existence of causality properties, such as those encountered in the linear viscoelasticity theory [89, 115];
-
The multi-body dynamics for which there are uncertain bodies (mass, center of mass, inertia tensor), for which the uncertainties in the bodies come from a lack of knowledge of the distribution of the mass inside the bodies (for instance, the spatial distribution of the passengers inside a high-speed train) [10];
-
The nonparametric stochastic modeling in vibroacoustics of complex systems for low- and medium-frequency domains, including the stochastic modeling of the coupling matrices between the structure and the acoustic cavities [38, 89, 110];
-
The formulation of the nonparametric stochastic modeling of the nonlinear operators occurring in the static and the dynamics of uncertain geometrically nonlinear structures [21, 77, 81].
15.4 Applications of the Nonparametric Stochastic Modeling of Uncertainties in Different Fields of Computational Sciencesand Engineering
16 Conclusions
In this chapter, fundamental mathematical tools have been presented concerning the random matrix theory, which are useful for many problems encountered in uncertainty quantification, in particular for the nonparametric method of the multiscale stochastic modeling of heterogeneous elastic materials, and for the nonparametric stochastic models of uncertainties in computational structural dynamics. The explicit construction of ensembles of random matrices but also the presentation of numerical tools for constructing general ensembles of random matrices are presented and can be used in high dimension. Many applications and validations have already been performed in many fields of computational sciences and engineering, but the methodologies and tools presented can be used and developed for many other problems for which uncertainties must be quantified.
References
Agmon, N., Alhassid, Y., Levine, R.D.: An algorithm for finding the distribution of maximal entropy. J. Comput. Phys. 30, 250–258 (1979)
Anderson, T.W.: An Introduction to Multivariate Statistical Analysis, 3rd edn. John Wiley & Sons, New York (2003)
Arnoux, A., Batou, A., Soize, C., Gagliardini, L.: Stochastic reduced order computational model of structures having numerous local elastic modes in low frequency dynamics. J. Sound Vib. 332(16), 3667–3680 (2013)
Arnst, M., Clouteau, D., Chebli, H., Othman, R., Degrande, G.: A non-parametric probabilistic model for ground-borne vibrations in buildings. Probab. Eng. Mech. 21(1), 18–34 (2006)
Arnst, M., Clouteau, D., Bonnet, M.: Inversion of probabilistic structural models using measured transfer functions. Comput. Methods Appl. Mech. Eng. 197(6–8), 589–608 (2008)
Au, S.K., Beck, J.L.: Subset simulation and its application to seismic risk based on dynamic analysis. J. Eng. Mech. – ASCE 129(8), 901–917 (2003)
Avalos, J., Swenson, E.D., Mignolet, M.P., Lindsley, N.J.: Stochastic modeling of structural uncertainty/variability from ground vibration modal test data. J. Aircr. 49(3), 870–884 (2012)
Bathe, K.J., Wilson, E.L.: Numerical Methods in Finite Element Analysis. Prentice-Hall, New York (1976)
Batou, A., Soize, C.: Experimental identification of turbulent fluid forces applied to fuel assemblies using an uncertain model and fretting-wear estimation. Mech. Syst. Signal Pr. 23(7), 2141–2153 (2009)
Batou, A., Soize, C.: Rigid multibody system dynamics with uncertain rigid bodies. Multibody Syst. Dyn. 27(3), 285–319 (2012)
Batou, A., Soize, C.: Calculation of Lagrange multipliers in the construction of maximum entropydistributions in high stochastic dimension. SIAM/ASA J. Uncertain. Quantif. 1(1), 431–451 (2013)
Batou, A., Soize, C., Audebert, S.: Model identification in computational stochastic dynamics using experimental modal data. Mech. Syst. Signal Pr. 50–51, 307–322 (2014)
Batou, A., Soize, C., Corus, M.: Experimental identification of an uncertain computational dynamical model representing a family of structures. Comput. Struct. 89(13–14), 1440–1448 (2011)
Bohigas, O., Giannoni, M.J., Schmit, C.: Characterization of chaotic quantum spectra and universality of level fluctuation laws. Phys. Rev. Lett. 52(1), 1–4 (1984)
Bohigas, O., Giannoni, M.J., Schmit, C.: Spectral fluctuations of classically chaotic quantum systems. In: Seligman, T.H., Nishioka, H. (eds.) Quantum Chaos and Statistical Nuclear Physics, pp. 18–40. Springer, New York (1986)
Bohigas, O., Legrand, O., Schmit, C., Sornette, D.: Comment on spectral statistics in elastodynamics. J. Acoust. Soc. Am. 89(3), 1456–1458 (1991)
Burrage, K., Lenane, I., Lythe, G.: Numerical methods for second-order stochastic differential equations. SIAM J. Sci. Comput. 29, 245–264 (2007)
Capiez-Lernout, E., Soize, C.: Nonparametric modeling of random uncertainties for dynamic response of mistuned bladed disks. ASME J. Eng. Gas Turbines Power 126(3), 600–618 (2004)
Capiez-Lernout, E., Soize, C., Lombard, J.P., Dupont, C., Seinturier, E.: Blade manufacturing tolerances definition for a mistuned industrial bladed disk. ASME J. Eng. Gas Turbines Power 127(3), 621–628 (2005)
Capiez-Lernout, E., Pellissetti, M., Pradlwarter, H., Schueller, G.I., Soize, C.: Data and model uncertainties in complex aerospace engineering systems. J. Sound Vib. 295(3–5), 923–938 (2006)
Capiez-Lernout, E., Soize, C., Mignolet, M.: Post-buckling nonlinear static and dynamical analyses of uncertain cylindrical shells and experimental validation. Comput. Methods Appl. Mech. Eng. 271(1), 210–230 (2014)
Capiez-Lernout, E., Soize, C., Mbaye, M.: Mistuning analysis and uncertainty quantification of an industrial bladed disk with geometrical nonlinearity. J. Sound Vib. 356, 124–143 (2015)
Chadwick, P., Vianello, M., Cowin, S.C.: A new proof that the number of linear elastic symmetries is eight. J. Mech. Phys. Solids 49, 2471–2492 (2001)
Chebli, H., Soize, C.: Experimental validation of a nonparametric probabilistic model of non homogeneous uncertainties for dynamical systems. J. Acoust. Soc. Am. 115(2), 697–705 (2004)
Chen, C., Duhamel, D., Soize, C.: Probabilistic approach for model and data uncertainties and its experimental identification in structural dynamics: case of composite sandwich panels. J. Sound Vib. 294(1–2), 64–81 (2006)
Cottereau, R., Clouteau, D., Soize, C.: Construction of a probabilistic model for impedance matrices. Comput. Methods Appl. Mech. Eng. 196(17–20), 2252–2268 (2007)
Cottereau, R., Clouteau, D., Soize, C.: Probabilistic impedance of foundation, impact of the seismic design on uncertain soils. Earthq. Eng. Struct. D. 37(6), 899–918 (2008)
Das, S., Ghanem, R.: A bounded random matrix approach for stochastic upscaling. Multiscale Model. Simul. 8(1), 296–325 (2009)
Desceliers, C., Soize, C., Cambier, S.: Non-parametric – parametric model for random uncertainties in nonlinear structural dynamics – application to earthquake engineering. Earthq. Eng. Struct. Dyn. 33(3), 315–327 (2004)
Desceliers, C., Soize, C., Grimal, Q., Talmant, M., Naili, S.: Determination of the random anisotropic elasticity layer using transient wave propagation in a fluid-solid multilayer: model and experiments. J. Acoust. Soc. Am. 125(4), 2027–2034 (2009)
Desceliers, C., Soize, C., Naili, S., Haiat, G.: Probabilistic model of the human cortical bone with mechanical alterations in ultrasonic range. Mech. Syst. Signal Pr. 32, 170–177 (2012)
Desceliers, C., Soize, C., Yanez-Godoy, H., Houdu, E., Poupard, O.: Robustness analysis of an uncertain computational model to predict well integrity for geologic CO2 sequestration. Comput. Mech. 17(2), 307–323 (2013)
Doob, J.L.: Stochastic Processes. John Wiley & Sons, New York (1990)
Doostan, A., Iaccarino, G.: A least-squares approximation of partial differential equations with high dimensional random inputs. J. Comput. Phys. 228(12), 4332–4345 (2009)
Duchereau, J., Soize, C.: Transient dynamics in structures with nonhomogeneous uncertainties induced by complex joints. Mech. Syst. Signal Pr. 20(4), 854–867 (2006)
Dyson, F.J.: Statistical theory of the energy levels of complex systems. Parts I, II, III. J. Math. Phys. 3, 140–175 (1962)
Dyson, F.J., Mehta, M.L.: Statistical theory of the energy levels of complex systems. Parts IV, V. J. Math. Phys. 4, 701–719 (1963)
Durand, J.F., Soize, C., Gagliardini, L.: Structural-acoustic modeling of automotive vehicles in presence of uncertainties and experimental identification and validation. J. Acoust. Soc. Am. 124(3), 1513–1525 (2008)
Fernandez, C., Soize, C., Gagliardini, L.: Fuzzy structure theory modeling of sound-insulation layers in complex vibroacoustic uncertain systems – theory and experimental validation. J. Acoust. Soc. Am. 125(1), 138–153 (2009)
Fernandez, C., Soize, C., Gagliardini, L.: Sound-insulation layer modelling in car computational vibroacoustics in the medium-frequency range. Acta Acust. United Ac. 96(3), 437–444 (2010)
Fishman, G.S.: Monte Carlo: Concepts, Algorithms, and Applications. Springer, New York (1996)
Geman, S., Geman, D.: Stochastic relaxation, Gibbs distribution and the Bayesian distribution of images. IEEE Trans. Pattern Anal. Mach. Intell. PAM I-6, 721–741 (1984)
Ghanem, R., Spanos, P.D.: Polynomial chaos in stochastic finite elements. J. Appl. Mech. Trans. ASME 57(1), 197–202 (1990)
Ghanem, R., Spanos, P.D.: Stochastic Finite Elements: A Spectral Approach. Springer, New York (1991)
Ghanem, R., Spanos, P.D.: Stochastic Finite Elements: A spectral Approach (rev. edn.). Dover Publications, New York (2003)
Ghosh, D., Ghanem, R.: Stochastic convergence acceleration through basis enrichment of polynomial chaos expansions. Int. J. Numer. Methods Eng. 73(2), 162–184 (2008)
Golub, G.H., Van Loan, C.F.: Matrix Computations, Fourth, The Johns Hopkins University Press, Baltimore (2013)
Guilleminot, J., Soize, C., Kondo, D.: Mesoscale probabilistic models for the elasticity tensor of fiber reinforced composites: experimental identification and numerical aspects. Mech. Mater. 41(12), 1309–1322 (2009)
Guilleminot, J., Noshadravan, A., Soize, C., Ghanem, R.G.: A probabilistic model for bounded elasticity tensor random fields with application to polycrystalline microstructures. Comput. Methods Appl. Mech. Eng. 200, 1637–1648 (2011)
Guilleminot, J., Soize, C.: Probabilistic modeling of apparent tensors in elastostatics: a MaxEnt approach under material symmetry and stochastic boundedness constraints. Probab. Eng. Mech. 28(SI), 118–124 (2012)
Guilleminot, J., Soize, C.: Generalized stochastic approach for constitutive equation in linear elasticity: a random matrix model. Int. J. Numer. Methods Eng. 90(5), 613–635 (2012)
Guilleminot, J., Soize, C., Ghanem, R.: Stochastic representation for anisotropic permeability tensor random fields. Int. J. Numer. Anal. Met. Geom. 36(13), 1592–1608 (2012)
Guilleminot, J., Soize, C.: On the statistical dependence for the components of random elasticity tensors exhibiting material symmetry properties. J. Elast. 111(2), 109–130 (2013)
Guilleminot, J., Soize, C.: Stochastic model and generator for random fields with symmetry properties: application to the mesoscopic modeling of elastic random media. Multiscale Model. Simul. (A SIAM Interdiscip. J.) 11(3), 840–870 (2013)
Gupta, A.K., Nagar, D.K.: Matrix Variate Distributions. Chapman & Hall/CRC, Boca Raton (2000)
Hairer, E., Lubich, C., G. Wanner, G.: Geometric Numerical Integration. Structure-Preserving Algorithms for Ordinary Differential Equations. Springer, Heidelberg (2002)
Hastings, W.K.: Monte Carlo sampling methods using Markov chains and their applications. Biometrika 109, 57–97 (1970)
Jaynes, E.T.: Information theory and statistical mechanics. Phys. Rev. 106(4), 620–630 and 108(2), 171–190 (1957)
Kaipio, J., Somersalo, E.: Statistical and Computational Inverse Problems. Springer, New York (2005)
Kapur, J.N., Kesavan, H.K.: Entropy Optimization Principles with Applications. Academic, San Diego (1992)
Kassem, M., Soize, C., Gagliardini, L.: Structural partitioning of complex structures in the medium-frequency range. An application to an automotive vehicle. J. Sound Vib. 330(5), 937–946 (2011)
Khasminskii, R.:Stochastic Stability of Differential Equations, 2nd edn. Springer, Heidelberg (2012)
Kloeden, P.E., Platen, E.: Numerical Solution of Stochastic Differentials Equations. Springer, Heidelberg (1992)
Langley, R.S.: A non-Poisson model for the vibration analysis of uncertain dynamic systems. Proc. R. Soc. Ser. A 455, 3325–3349 (1999)
Legrand, O., Sornette, D.: Coarse-grained properties of the chaotic trajectories in the stadium. Physica D 44, 229–235 (1990)
Legrand, O., Schmit, C., Sornette, D.: Quantum chaos methods applied to high-frequency plate vibrations. Europhys. Lett. 18(2), 101–106 (1992)
Le Maître, O.P., Knio, O.M.: Spectral Methods for Uncertainty Quantification with Applications to Computational Fluid Dynamics. Springer, Heidelberg (2010)
Luenberger, D.G.: Optimization by Vector Space Methods. John Wiley & Sons, New York (2009)
Matthies, H.G., Keese, A.: Galerkin methods for linear and nonlinear elliptic stochastic partial differential equations. Comput. Methods Appl. Mech. Eng. 194(12–16), 1295–1331 (2005)
Mbaye, M., Soize, C., Ousty, J.P., Capiez-Lernout, E.: Robust analysis of design in vibration of turbomachines. J. Turbomach. 135(2), 021008-1–021008-8 (2013)
Mehrabadi, M.M., Cowin, S.C.: Eigentensors of linear anisotropic elastic materials. Q. J. Mech. Appl. Math. 43:15–41 (1990)
Mehta, M.L.: Random Matrices and the Statistical Theory of Energy Levels. Academic, New York (1967)
Mehta, M.L.: Random Matrices, Revised and Enlarged, 2nd edn. Academic Press, San Diego (1991)
Mehta, M.L.: Random Matrices, 3rd edn. Elsevier, San Diego (2014)
Metropolis, N., Ulam, S.: The Monte Carlo method. J. Am. Stat. Assoc. 49, 335–341 (1949)
Mignolet, M.P., Soize, C.: Nonparametric stochastic modeling of linear systems with prescribed variance of several natural frequencies. Probab. Eng. Mech. 23(2–3), 267–278 (2008)
Mignolet, M.P., Soize, C.: Stochastic reduced order models for uncertain nonlinear dynamical systems. Comput. Methods Appl. Mech. Eng. 197(45–48), 3951–3963 (2008)
Mignolet, M.P., Soize, C., Avalos, J.: Nonparametric stochastic modeling of structures with uncertain boundary conditions/coupling between substructures. AIAA J. 51(6), 1296–1308 (2013)
Murthy, R., Mignolet, M.P., El-Shafei, A.: Nonparametric stochastic modeling of uncertainty in rotordynamics-Part I: Formulation. J. Eng. Gas Turb. Power 132, 092501-1–092501-7 (2009)
Murthy, R., Mignolet, M.P., El-Shafei, A.: Nonparametric stochastic modeling of uncertainty in rotordynamics-Part II: applications. J. Eng. Gas Turb. Power 132, 092502-1–092502-11 (2010)
Murthy, R., Wang, X.Q., Perez, R., Mignolet, M.P., Richter, L.A.: Uncertainty-based experimental validation of nonlinear reduced order models. J. Sound Vib. 331, 1097–1114 (2012)
Murthy, R., Tomei, J.C., Wang, X.Q., Mignolet, M.P., El-Shafei, A.: Nonparametric stochastic modeling of structural uncertainty in rotordynamics: Unbalance and balancing aspects. J. Eng. Gas Turb. Power 136, 62506-1–62506-11 (2014)
Neal, R.M.: Slice sampling. Ann. Stat. 31, 705–767 (2003)
Nouy, A.: Recent developments in spectral stochastic methods for the numerical solution of stochastic partial differential equations. Arch. Comput. Methods Eng. 16(3), 251–285 (2009)
Nouy, A.: Proper Generalized Decomposition and separated representations for the numerical solution of high dimensional stochastic problems. Arch. Comput. Methods Eng. 16(3), 403–434 (2010)
Nouy, A., Soize, C.: Random fields representations for stochastic elliptic boundary value problems and statistical inverse problems. Eur. J. Appl. Math. 25(3), 339–373 (2014)
Ohayon, R., Soize, C.: Structural Acoustics and Vibration. Academic, San Diego (1998)
Ohayon, R., Soize, C.: Advanced computational dissipative structural acoustics and fluid-structure interaction in low- and medium-frequency domains. Reduced-order models and uncertainty quantification. Int. J. Aeronaut. Space Sci. 13(2), 127–153 (2012)
Ohayon, R., Soize, C.: Advanced Computational Vibroacoustics. Reduced-Order Models and Uncertainty Quantification. Cambridge University Press, New York (2014)
Papoulis, A.: Signal Analysis. McGraw-Hill, New York (1977)
Pellissetti, M., Capiez-Lernout, E., Pradlwarter, H., Soize, C., Schueller, G.I.: Reliability analysis of a satellite structure with a parametric and a non-parametric probabilistic model. Comput. Methods Appl. Mech. Eng. 198(2), 344–357 (2008)
Poter, C.E.: Statistical Theories of Spectra: Fluctuations. Academic, New York (1965)
Pradlwarter, H.J., Schueller, G.I.: Local domain Monte Carlo simulation. Struct. Saf. 32(5), 275–280 (2010)
Ritto, T.G., Soize, C., Rochinha, F.A., Sampaio, R.: Dynamic stability of a pipe conveying fluid with an uncertain computational model. J. Fluid Struct. 49, 412–426 (2014)
Robert, C.P., Casella, G.: Monte Carlo Statistical Methods. Springer, New York (2005)
Rubinstein, R.Y., Kroese, D.P.: Simulation and the Monte Carlo Method, 2nd edn. John Wiley & Sons, New York (2008)
Sakji, S., Soize, C., Heck, J.V.: Probabilistic uncertainties modeling for thermomechanical analysis of plasterboard submitted to fire load. J. Struct. Eng. – ASCE 134(10), 1611–1618 (2008)
Sakji, S., Soize, C., Heck, J.V.: Computational stochastic heat transfer with model uncertainties in a plasterboard submitted to fire load and experimental validation. Fire Mater. 33(3), 109–127 (2009)
Schmit, C.: Quantum and classical properties of some billiards on the hyperbolic plane. In: Giannoni, M.J., Voros, A., Zinn-Justin, J. (eds.) Chaos and Quantum Physics, pp. 333–369. North-Holland, Amsterdam (1991)
Schueller, G.I.: Efficient Monte Carlo simulation procedures in structural uncertainty and reliability analysis – recent advances. Struct. Eng. Mech. 32(1), 1–20 (2009)
Schwartz, L.: Analyse II Calcul Différentiel et Equations Différentielles. Hermann, Paris (1997)
Serfling, R.J.: Approximation Theorems of Mathematical Statistics. John Wiley & Sons, New York (1980)
Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423, 623–659 (1948)
Soize, C.: Oscillators submitted to squared Gaussian processes. J. Math. Phys. 21(10), 2500–2507 (1980)
Soize, C.: The Fokker-Planck Equation for Stochastic Dynamical Systems and its Explicit Steady State Solutions. World Scientific Publishing Co Pte Ltd, Singapore (1994)
Soize, C.: A nonparametric model of random uncertainties in linear structural dynamics. In: Bouc R., Soize, C. (eds.) Progress in Stochastic Structural Dynamics, pp. 109–138. Publications LMA-CNRS, Marseille (1999). ISBN 2-909669-16-5
Soize, C.: A nonparametric model of random uncertainties for reduced matrix models in structural dynamics. Probab. Eng. Mech. 15(3), 277–294 (2000)
Soize, C.: Maximum entropy approach for modeling random uncertainties in transient elastodynamics. J. Acoust. Soc. Am. 109(5), 1979–1996 (2001)
Soize, C.: Random matrix theory and non-parametric model of random uncertainties. J. Sound Vib. 263(4), 893–916 (2003)
Soize, C.: Random matrix theory for modeling random uncertainties in computational mechanics. Comput. Methods Appl. Mech. Eng. 194(12–16), 1333–1366 (2005)
Soize, C.: Non Gaussian positive-definite matrix-valued random fields for elliptic stochastic partial differential operators. Comput. Methods Appl. Mech. Eng. 195(1–3), 26–64 (2006)
Soize, C.: Construction of probability distributions in high dimension using the maximum entropy principle. Applications to stochastic processes, random fields and random matrices. Int. J. Numer. Methods Eng. 76(10), 1583–1611 (2008)
Soize, C.: Generalized Probabilistic approach of uncertainties in computational dynamics using random matrices and polynomial chaos decompositions. Int. J. Numer. Methods Eng. 81(8), 939–970 (2010)
Soize, C.: Stochastic Models of Uncertainties in Computational Mechanics. American Society of Civil Engineers (ASCE), Reston (2012)
Soize, C., Poloskov, I.E.: Time-domain formulation in computational dynamics for linear viscoelastic media with model uncertainties and stochastic excitation. Comput. Math. Appl. 64(11), 3594–3612 (2012)
Soize, C., Chebli, H.: Random uncertainties model in dynamic substructuring using a nonparametric probabilistic model. J. Eng. Mech.-ASCE 129(4), 449–457 (2003)
Spall, J.C.: Introduction to Stochastic Search and Optimization. John Wiley & Sons, Hoboken (2003)
Talay, D., Tubaro, L.: Expansion of the global error for numerical schemes solving stochastic differential equation. Stoch. Anal. Appl. 8(4), 94–120 (1990)
Talay, D.: Simulation and numerical analysis of stochastic differential systems. In: Kree, P., Wedig, W. (eds.) Probabilistic Methods in Applied Physics. Lecture Notes in Physics, vol. 451, pp. 54–96. Springer, Heidelberg (1995)
Talay, D.: Stochastic Hamiltonian system: exponential convergence to the invariant measure and discretization by the implicit Euler scheme. Markov Process. Relat. Fields 8, 163–198 (2002)
Tipireddy, R., Ghanem, R.: Basis adaptation in homogeneous chaos spaces. J. Comput. Phys. 259, 304–317 (2014)
Walpole, L.J.: Elastic behavior of composite materials: theoretical foundations. Adv. Appl. Mech. 21, 169–242 (1981)
Walter, E., Pronzato, L.: Identification of Parametric Models from Experimental Data. Springer, Berlin (1997)
Weaver, R.L.: Spectral statistics in elastodynamics. J. Acoust. Soc. Am. 85(3), 1005–1013 (1989)
Wigner, E.P.: On the statistical distribution of the widths and spacings of nuclear resonance levels. Proc. Camb. Philos. Soc. 47, 790–798 (1951)
Wigner, E.P.: Distribution laws for the roots of a random Hermitian matrix In: Poter, C.E. (ed.) Statistical Theories of Spectra: Fluctuations, pp. 446–461. Academic, New York (1965)
Wright, M., Weaver, R.: New Directions in Linear Acoustics and Vibration. Quantum Chaos, Random Matrix Theory, and Complexity. Cambridge University Press, New York (2010)
Zienkiewicz, O.C., Taylor, R.L.: The Finite Element Method For Solid and Structural Mechanics, Sixth edition. Elsevier, Butterworth-Heinemann, Amsterdam (2005)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing Switzerland
About this entry
Cite this entry
Soize, C. (2017). Random Matrix Models and Nonparametric Method for Uncertainty Quantification. In: Ghanem, R., Higdon, D., Owhadi, H. (eds) Handbook of Uncertainty Quantification. Springer, Cham. https://doi.org/10.1007/978-3-319-12385-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-12385-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-12384-4
Online ISBN: 978-3-319-12385-1
eBook Packages: Mathematics and StatisticsReference Module Computer Science and Engineering




 in which
in which  of the time evolution problem is constructed in solving Eq. (
of the time evolution problem is constructed in solving Eq. ( and
and  .
. is such that, for all t fixed in
is such that, for all t fixed in  verifies Eq. (
verifies Eq. ( is such that, for all ω in
is such that, for all ω in 
 is the Fourier transform of
is the Fourier transform of  . As
. As 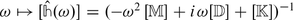 is a bounded function on
is a bounded function on