Stability, Pointing, and Orientation

Abstract

This chapter gives an overview of the attitude determination and control system (ADCS) of spacecraft, focusing on small satellites. The ADCS is an important subsystem to insure satellite orientation stability and accuracy of pointing various payloads at specific targets. The introductory section will give an overview of the active ADCS feedback loop and lists some requirements and typical control methods utilized. The next section presents some background theory in attitude dynamics, kinematics, and the significant external disturbance torques in low earth orbit (LEO). Then some techniques used for angular rate and attitude determination are presented, followed by the control laws for magnetic detumbling and reaction wheel attitude control. A complete section is dedicated to a practical example of the calculations to determine the pointing accuracy and stability of a high-resolution (Hi-Res) imaging payload on a minisatellite. Finally the chapter concludes with examples and specifications of typical ADCS sensor and actuator hardware that are commercially available.

1 Introduction

The use of active attitude control and determination on small satellites is growing, but still less than 60% of all orbiting nanosatellites are 3-axis stabilized. According to an ADCS survey in 2017 by the Chinese Academy of Sciences (Xia et al. 2017) of nanosatellites (mass between 1 and 10 kg), 483 were launched successfully since 2003 until 2016. The ADCS information of 357 nanosatellites were available for statistical analysis. Of the 357 nanosatellites, only 5% had no ADCS, 17% used passive magnetic control, 2% used gravity gradient stabilization, 6% used other passive methods of stabilization (e.g., aerodynamic), 2% were spin stabilized, 11% used active magnetic control, 3% were momentum wheel stabilized, and 54% were reaction wheel 3-axis stabilized. In a 2014 review (Janse van Vuuren 2015) of 42 small satellites (excluding CubeSats) from 6.5 to 94 kg launch mass over the past 25 years, 5% had no control, 19% only passive control, and 76% some form of active control. The list of ADCS sensors was magnetometers (90%), sun sensors (80%), Earth sensors (10%), GPS (33%), rate sensors (40%), and star trackers (35%). The list of ADCS actuators was permanent magnets (20%), magnetic torquers (80%), momentum wheels (8%), reaction wheels (40%), propulsion systems (18%), gravity-gradient booms (15%), and control moment gyros (3%).

2 Attitude Determination and Control Subsystem (ADCS) Overview

The attitude determination and control system (ADCS) detumbles, stabilizes, points, and rotates a satellite into a desired orientation (attitude) despite any external or internal disturbances torques acting on it. A satellite’s payload requires a specific pointing direction whether the payload is a camera, a science instrument, or an antenna. Satellites also require a specific orientation for thermal control or power control, i.e., to acquire the sun for their solar panels. The ADCS system uses sensors in order to determine a satellite’s attitude or angular rates and actuators to maneuver the vehicle to a required orientation. The ADCS needs to achieve the various mission and payload objectives such as pointing accuracy, stability, rotation rate (slew), and sensing with many physical constraints such as mass, power, volume, computer power/storage, the space environment, robustness/lifetime, and cost. The ADCS is a synthesis of two subsystems the attitude determination system (ADS) and the attitude control system (ACS) which controls the attitude/angular rate of a satellite as depicted below in Fig. 1.

Fig. 1

ADCS block diagram

An example of ADCS sensor and actuator hardware for a small 3-axis stabilized satellite is shown in Fig. 2. In this example all the ADCS sensors, actuators, and processors communicate via a distributed dual ADCS CAN (Controller Area Network) bus. The ADCS processor is dedicated to the attitude control system, although the OBC (onboard computer) can serve as a backup ADCS processor. The text in brackets indicates the type of processor used. The ADCS interface samples the coarse sun sensors (CSS1,2,3) and magnetometers and commands the magnetic torquer rods. The reaction wheel units (RW unit-1,2,3,4) are mounted in a tetrahedral configuration for redundancy and interface the fiber-optic gyros (FOG-1,2,3,4) for accurate angular rate measurements. A global position receiver (GPS RX) is used to accurately measure the satellite’s orbit position, velocity, and time. A propulsion controller is implemented to control a cold gas propulsion system to do small orbit corrections and maintenance. The accurate absolute attitude sensors are the star trackers (A, B), sun sensors (1,2,3), and earth horizon sensors (EHS-1,2).

Fig. 2

Example ADCS hardware for a small satellite

3 ADCS Requirements and Control Methods

In this section only active attitude control methods will be considered as most small satellites currently no longer use exclusively passive methods, e.g., permanent magnets to track the local magnetic field direction, gravity gradient torque to align the satellite’s long axis with the nadir/zenith direction, and drag-induced aerodynamic torques to align the center-of-pressure (CoP) to center-of-mass (CoM) vector toward the orbit velocity vector. Although these passive methods can damp oscillations of the relevant body axis direction with libration/nutation dampers (typically viscous fluid tubes or rings), the rotations around this stabilized body axis cannot be controlled. For this reason these passive methods will mostly be combined with an active attitude or angular rate controller.

The need for active attitude control is determined by the small satellite mission and its attitude requirements. As mentioned in the introduction, most small satellite missions have specific attitude pointing and stabilization requirements, and thus an ADCS with some capability is needed. Active attitude control also comes in different flavors. Simple tumbling control modes can be implemented with the minimum of hardware and power requirements. Stabilized attitude (roll, pitch, and yaw angles controlled to a constant attitude) can be achieved using a momentum wheel, while full 3-axis control has the ability to perform commanded slew maneuvers which places the most demanding requirements on volume, mass, and power resources. A list of requirements that are usually considered for satellite ADCS are summarized in Table 1 below.

Table 1 General ADCS requirements

The methods for active attitude stabilization and control are briefly discussed in the following paragraphs:

3.1 Gravity Gradient Assist

It exploits Newton’s law of general gravitation and through the use of gravitational forces can always keep a specific spacecraft axis nadir pointing. This is achieved by using a boom extending a small distinct mass (usually a magnetometer in order to minimize magnetic interference) from the spacecraft (which becomes the second distinct mass) by some distance. These two masses which are connected by a thin and light boom can then be used to exploit the difference in gravitational pull on the main satellite platform and on the additional mass (magnetometer) due to the difference in their distance from Earth. This small difference can be sufficient to enable the satellite/additional mass system to be aligned with the radius vector at all times as an orbiting pendulum. The gravity gradient stabilization scheme can be beneficial for coarse pointing (~5 deg) around the nadir axis, while the other two axes still will need to be stabilized. The oscillations of the nadir-pointing axis are called librations and can be damped with an active magnetic controller. The rotation around the nadir direction can also be controlled by an active magnetic controller or a moment exchange actuator, e.g., a reaction or momentum wheel for higher accuracy.

3.2 Magnetic

By approximating the Earth’s magnetic field in low earth orbit (LEO) as a dipole, it is possible to have a satellite fitted with a magnetometer to measure the Earth’s magnetic field vector and use magnetic coils or rods (magnetorquers) to generate torques to control the satellite’s attitude and angular rates. Due to a constraint in the direction of these magnetic torques, i.e., they are zero in the direction of the local magnetic field vector, these control torques cannot perfectly compensate for external disturbance torques on the satellite’s attitude. This means for accurate attitude pointing the magnetic torques must be combined with passive control torques, e.g., gravity gradient or passively stable aerodynamic torques. The active magnetic torques can also be used to manage the angular momentum buildup on momentum exchange actuators, e.g., to ensure zero bias speeds on reaction wheels or offset reference speeds on momentum wheels.

3.3 Spinners

Spinning a satellite body generates an angular momentum vector which gives inertial stiffness to the satellite’s attitude by keeping the spin axis fixed in inertial space. The angular momentum generated provides gyroscopic stiffness to the spinning satellite, making it less prone to external disturbances and more stable for propulsion thruster firings. Spinning the satellite after detumbling into a Y-Thomson attitude (Thomson 1962), where the satellite will align its maximum moment-of-inertia (MoI) axis normal to the orbit plane. This scheme will ensure a low-energy control method using a known spinning attitude with predictable antenna gain for ground communications or solar panel placement for a predictable power input.

3.4 Bias Momentum 3-Axis

For a 3-axis stable attitude, a momentum bias with a single momentum wheel aligned to the pitch axis normal to the orbit plane. Gyroscopic stiffness is used in order to control the vehicle by keeping the momentum wheel spinning at a biased reference speed. Small variations in the wheel speed allow for the control of the pitch axis. Yaw-roll coupling for nadir-pointing applications can be used to control the other two axes. Combined with magnetic controllers, the yaw-roll oscillations (nutations) can effectively be damped and the momentum wheel speed maintained at the biased reference speed. Although the satellite will be 3-axis stable, only the pitch axis can be controlled easily and accurately to a reference attitude. The roll and yaw axes will be controlled to zero angles.

3.5 Zero Momentum 3-Axis

In these systems, reaction wheels are used for each spacecraft axis in order to compensate for external disturbances and to implement various commanded attitude maneuvers. This is the most versatile and accurate attitude control system as pointing and slewing of any satellite axis are possible towards various earth and inertial targets, e.g., ground stations, earth imaging ground targets, sun, moon, stars, etc. A measured or estimated pointing error is used to torque the reaction wheels to ensure angular momentum exchange between the wheel discs and the satellite body to reduce the pointing error to zero. External torque disturbances can lead to wheel angular momentum buildup and eventual saturation. The increase in angular momentum to saturation levels requires a desaturation strategy which is called “momentum dumping” or unloading. This is achieved by using magnetorquers and to a much lesser extend thrusters (typically for larger satellites), thus enabling the wheels to operate around zero speed values. This strategy will also ensure the lowest reaction wheel power consumption as wheel power increase significantly with wheel speed.

3.6 Small Satellite ADCS Accuracies

The typical attitude control accuracies and constraints that can be obtained using the active control methods of the previous sections are summarized in Table 2. The accuracies listed depends also on the satellite’s orbit (external disturbance torques) and satellite size. Smaller satellites are normally less accurate due to a higher sensitivity to external disturbance torques and less accurate attitude and angular rate sensors.

Table 2 ADCS accuracies and constraints

4 ADCS Background Theory

4.1 Coordinate Frame Definitions

A satellite’s attitude is normally controlled with respect to the orbit referenced coordinates (ORC), where the Z_O axis points toward nadir, the X_O axis points toward the velocity vector for a near circular orbit, and the Y_O axis along the orbit plane anti-normal direction. The aerodynamic N_Aero and gravity gradient N_GG disturbance torque vectors are also conveniently modelled in ORC. The satellite body coordinates (SBC) as defined in the body frame will nominally be aligned with the ORC frame at zero pitch, roll and yaw attitude. See Fig. 3 for a representation of these coordinate frames. Since the sun and satellite orbits are propagated in the J2000 earth-centered inertial coordinate frame (ECI), we require a transformation matrix from ECI to ORC coordinates. This can easily be calculated from the satellite position ${\overline{\mathbf{u}}}_I$ and velocity ${\overline{\mathbf{v}}}_I$ unit vectors (obtained using the position and velocity outputs of the satellite orbit propagator):

$$ {\mathbf{A}}_{I/O}=\left[\begin{array}{c}{\left({\overline{\mathbf{u}}}_I\times \left({\overline{\mathbf{v}}}_I\times {\overline{\mathbf{u}}}_I\right)\right)}^T\\ {}{\left({\overline{\mathbf{v}}}_I\times {\overline{\mathbf{u}}}_I\right)}^T\\ {}-{\overline{\mathbf{u}}}_I^T\end{array}\right] $$

(1)

Fig. 3

Orbit (ORC), inertial (ECI), and spacecraft body (SBC) coordinate frames

4.2 Attitude Kinematics

The attitude of an earth orbiting satellite can be expressed as a quaternion vector q to avoid any singularities to determine the orientation with respect to the ORC frame. The ORC reference body rates, ${\omega}_B^O={\left[{\omega}_{xo},{\omega}_{yo},{\omega}_{zo}\right]}^T$, must be used to propagate the quaternion kinematics as:

$$ \left[\begin{array}{c}{\dot{q}}_1\\ {}{\dot{q}}_2\\ {}{\dot{q}}_3\\ {}{\dot{q}}_4\end{array}\right]=0.5\;\left[\begin{array}{cccc}0& {\omega}_{zo}& -{\omega}_{yo}& {\omega}_{xo}\\ {}-{\omega}_{zo}& 0& {\omega}_{xo}& {\omega}_{yo}\\ {}{\omega}_{yo}& -{\omega}_{xo}& 0& {\omega}_{zo}\\ {}-{\omega}_{xo}& -{\omega}_{yo}& -{\omega}_{zo}& 0\end{array}\right]\;\left[\begin{array}{c}{q}_1\\ {}{q}_2\\ {}{q}_3\\ {}{q}_4\end{array}\right] $$

(2)

The attitude matrix to describe the transformation from ORC to SBC can be expressed in terms of quaternions as:

$$ {\mathbf{A}}_{O/B}=\left[\begin{array}{ccc}{q}_1^2-{q}_2^2-{q}_3^2+{q}_4^2& 2\left({q}_1{q}_2+{q}_3{q}_4\right)& 2\left({q}_1{q}_3-{q}_2{q}_4\right)\\ {}2\left({q}_1{q}_2-{q}_3{q}_4\right)& -{q}_1^2+{q}_2^2-{q}_3^2+{q}_4^2& 2\left({q}_2{q}_3+{q}_1{q}_4\right)\\ {}2\left({q}_1{q}_3+{q}_2{q}_4\right)& 2\left({q}_2{q}_3-{q}_1{q}_4\right)& -{q}_1^2-{q}_2^2+{q}_3^2+{q}_4^2\end{array}\right]\, $$

(3)

Note: In Eqs. (1) and (2), a quaternion definition is used where the first three elements of the quaternion form the vector part and the last element the scalar part of the quaternion. Another definition where the scalar part of the quaternion is in the first element is also commonly used. The former quaternion definition will be used throughout this chapter.

The attitude is normally presented as pitch θ, roll φ, and yaw ψ angles, defined as successive rotations, starting with the first rotation from the ORC axes and ending after the final rotation in the SBC axis. If a Euler 213 sequence (first θ around Y_O, then φ around X, and finally ψ around Z_B) is used, then the attitude matrix and Euler angles can be computed as:

$$ {\displaystyle \begin{array}{l}{\mathbf{A}}_{O/B}=\left[\begin{array}{ccc} C\psi C\theta + S\psi S\varphi\;S\theta \, & S\psi C\varphi\;& - C\psi\;S\theta + S\psi S\varphi\;C\theta\;\\ {}- S\psi C\theta + C\psi S\varphi\;S\theta\;& C\psi C\varphi\;& S\psi S\theta + C\psi S\varphi\;C\theta\;\\ {} C\varphi\;S\theta\;& - S\varphi\;& C\varphi\;C\theta \end{array}\right]\\ {}\mathrm{with},\\ {}\, \mathrm{C}=\mathrm{cosine}\, \mathrm{function},\, \mathrm{S}=\mathrm{sine}\, \mathrm{function}\end{array}} $$

(4)

and

$$ {\displaystyle \begin{array}{l}\theta =\arctan 4\;\left({A}_{31},{A}_{33}\right)\\ {}\varphi =-\arcsin\;\left({A}_{32}\right)\\ {}\psi =\arctan 4\;\left({A}_{12},{A}_{22}\right)\end{array}} $$

(5)

This Euler angle representation will allow unlimited rotations in pitch and yaw, but only maximum ±90° rotations in roll.

4.3 Attitude Dynamics

The attitude dynamics of an earth orbiting satellite can be derived using the Euler equation:

$$ \mathbf{I}{\dot{\boldsymbol{\upomega}}}_B^I={\mathbf{N}}_{GG}+{\mathbf{N}}_D+{\mathbf{N}}_W+{\mathbf{N}}_{MT}-{\boldsymbol{\upomega}}_B^I\times \left(\mathbf{I}{\boldsymbol{\upomega}}_B^I+{\mathbf{h}}_W\right) $$

(6)

with ${\boldsymbol{\upomega}}_B^I={\boldsymbol{\upomega}}_B^O+{\mathbf{A}}_{O/B}{\left[0\, -{\omega}_o\, 0\right]}^T$ the inertially referenced body rate vector, ${\mathbf{N}}_{GG}=3{\omega}_o^2\left({\mathbf{z}}_o^B\times \mathbf{I}\;{\mathbf{z}}_o^B\right)$ the gravity gradient disturbance torque vector, with ${\mathbf{z}}_o^B={\mathbf{A}}_{O/B}{\left[0,0,1\right]}^T$the orbit nadir unit vector in body coordinates, N_D is the external disturbance torques (e.g., from aerodynamic and solar pressure forces), ${\mathbf{N}}_W=-{\dot{\mathbf{h}}}_W$ is the reaction or momentum wheel torque vector, with h_W the wheel angular momentum vector, N_MT is the magnetic control torque, ω_o the orbit angular rate (a constant for a circular orbit and a time variable for an eccentric orbit), and I is the inertia matrix of the satellite.

4.4 External Disturbance Torques

For satellites in low earth orbit, the typical unmodelled disturbance torques are from aerodynamic and solar pressure forces and from magnetic moments. The unmodelled magnetic moments are mostly caused by poor harness layout where current loops can form when supplying power to the spacecraft subsystems. Another source of magnetic moment disturbances, especially significant on nanosatellites, is from currents flowing in solar panels due to the solar cell connections. The latter has caused many CubeSats to spun up when left uncontrolled for long periods of time, and in some cases, they became unrecoverable when eventually reaching a very high spin rate.

4.4.1 Aerodynamic

The dominant external disturbance torque on a satellite at low altitude, as is the case for many small satellite missions, will be aerodynamic torque disturbances caused by the atmospheric drag pressure force on the external surfaces and deployables of a satellite. These torques can be calculated by using the panel method of partial accommodation theory. The external surface of the satellite is divided into several flat segments and the torque disturbance of each segment calculated and summed for the total disturbance torque (Steyn and Lappas 2011):

$$ {\mathbf{N}}_{Aero}={\sum}_{i=1}^n\left\{\rho\;\left({\mathbf{u}}_I,t\right)\;{\left\Vert {\mathbf{v}}_A^B\right\Vert}^2{A}_i\mathit{\cos}\left({\alpha}_i\right)\left[{\sigma}_t\left({\mathbf{r}}_i\times {\overline{\mathbf{v}}}_A^B\right)+\left\{{\sigma}_nS+\left(2-{\sigma}_n-{\sigma}_t\right)\cos \left({\alpha}_i\right)\right\}\;\left({\mathbf{r}}_i\times {\overline{\mathbf{n}}}_i\right)\right]\right\} $$

(7)

$$ {\mathbf{v}}_A^B={\mathbf{A}}_{O/B}{\mathbf{A}}_{I/O}\left[{\mathbf{u}}_I\times \left[\begin{array}{c}0\\ {}0\\ {}-{\omega}_E\end{array}\right]-{\mathbf{v}}_I\right] $$

(8)

with ${\mathbf{v}}_A^B$ the atmospheric velocity in SBC and ρ(u_I, t) the atmospheric density at orbit position and local time, see Fig. 4, ω_E= earth’s rotation rate = 7.29212 × 10⁻⁵ rad/s, A_i the surface area of segment i, $\cos \left({\alpha}_i\right)={\overline{\mathbf{v}}}_A^B\bullet {\overline{\mathbf{n}}}_i$ the cosine of angle between unit atmospheric velocity vector and ${\overline{\mathbf{n}}}_i$ the normal unit vector of segment i, r_i the satellite CoM to segment i’s CoP vector, $S={v}_b/\left\Vert {\mathbf{v}}_A^B\right\Vert$ the ratio of molecular exit velocity v_b to atmospheric velocity ≈ 0.05 (for a 700 km altitude), σ_n the normal accommodation coefficient ≈ 0.8 (for a 700 km altitude), and σ_t the tangential accommodation coefficient ≈ 0.8 (for a 700 km altitude).

Fig. 4

An example of atmospheric density variation

4.4.2 Solar

The solar radiation pressure force and related torque depend on the absorption, specular and diffuse reflection coefficients of the external satellite surfaces, and deployables. The disturbance torques caused by the solar force are normally about two orders of magnitude less than the aerodynamic disturbances in low earth orbit, and its influence can normally be ignored. Where this force becomes significant is when a large area, highly reflective solar sail is deployed; see (Steyn and Lappas 2011) for a typical solar sail example.

4.4.3 Magnetic Moment

Internal magnetic moments due to currents flowing in an enclosed loop or residual magnetic dipoles from permanent magnets in electric motors, electromagnetic valves, or ferromagnetic material can cause time-varying magnetic moments that are difficult to accurately model or estimate. The sun’s rays on solar panel surfaces will also cause magnetic moments normal to the surface and proportional to the sun vector component normal to the surface; the magnetic disturbance torque from a solar panel i can then be calculated as:

$$ {\mathbf{N}}_{M\_ SPi}={M}_{SPi}H\cos \left({\alpha}_i\right){\overline{\mathbf{n}}}_{SPi}\times {\mathbf{B}}_B $$

(9)

with $\cos \left({\alpha}_i\right)={\overline{\mathbf{s}}}_B\bullet {\overline{\mathbf{n}}}_{SPi}$ the cosine of angle between the unit sun direction vector ${\overline{\mathbf{s}}}_B$ in SBC and the ${\overline{\mathbf{n}}}_{SPi}$the normal unit vector to the solar panel i surface, M_SPi the maximum magnetic moment of solar panel i when the sun is normal to the panel, H = {0, 1}, i.e., 0 when the cosine of angle is negative (sun behind the solar panel) and 1 (sun on solar panel) when positive and B_B the local B-field vector in SBC.

5 Attitude and Angular Rate Determination

To implement the attitude and angular rate controllers of the next section and to calculate the desired control torques, measurements or estimates of the orbit referenced angular rate vector and attitude quaternion must be known at each sampling instance of the onboard ADCS computer. A quaternion error can be calculated if the reference attitude quaternion and an estimated quaternion representing the current satellite attitude are available. The current satellite quaternion can be determined every sampling period using a TRIAD algorithm (Shuster and Oh 1981) from measured ${\overline{\mathbf{v}}}_B$ (in SBC) and modelled ${\overline{\mathbf{v}}}_O$ (in ORC) unit direction vectors from two different attitude sensor types, e.g., magnetometer/sun or sun-earth (nadir) combination of sensors. A more elaborate method QUEST (Shuster and Oh 1981) is optimally combining more than two vector pairs for attitude determination, e.g., from matched star tracker measurements.

As an example, a digital sun sensor can be used to measure the sun direction unit vector ${\overline{\mathbf{s}}}_B$ in SBC, and an IR earth sensor can measure the nadir unit vector ${\overline{\mathbf{n}}}_B$ in SBC. If the sun and satellite orbits are modelled, the sun to satellite unit vector in ORC, ${\overline{\mathbf{s}}}_O$ can also easily be calculated onboard in Eq. (10), and the nadir unit vector in ORC ${\overline{\mathbf{n}}}_O$ will simply be ${\left[0,0,1\right]}^T$, the direction of the ORC Z_O-axis.

The modelled (ORC) sun to satellite unit vector can be calculated from simple analytical sun and satellite (e.g., SGP4) orbit models in ECI coordinates. The ECI referenced unit vector can then be transformed to ORC coordinates using the known current satellite Keplerian angles:

$$ {\overline{\mathbf{s}}}_O={\mathbf{A}}_{I/O}\;{\overline{\mathbf{s}}}_I $$

(10)

with ${\overline{\mathbf{s}}}_I$ = ECI sun to satellite unit vector from sun and satellite orbit models.

5.1 TRIAD Method for Deterministic Attitude Determination

Two orthonormal triads are formed from the measured (observed) and modelled (referenced) vector pairs as presented above:

$$ {\displaystyle \begin{array}{l}{\overline{\mathbf{o}}}_1={\overline{\mathbf{n}}}_B,\, {\overline{\mathbf{o}}}_2={\overline{\mathbf{n}}}_B\times {\overline{\mathbf{s}}}_B,\, {\overline{\mathbf{o}}}_3={\overline{\mathbf{o}}}_1\times {\overline{\mathbf{o}}}_2\\ {}{\overline{\mathbf{r}}}_1={\overline{\mathbf{n}}}_O,\, {\overline{\mathbf{r}}}_2={\overline{\mathbf{n}}}_O\times {\overline{\mathbf{s}}}_O,\, {\overline{\mathbf{r}}}_3={\overline{\mathbf{r}}}_1\times {\overline{\mathbf{r}}}_2\end{array}} $$

(11)

The estimated ORC to SBC transformation matrix can then be calculated as:

$$ {\mathbf{A}}_{O/B}\left(\hat{\mathbf{q}}\right)=\left[{\overline{\mathbf{o}}}_1\, {\overline{\mathbf{o}}}_2\, {\overline{\mathbf{o}}}_3\right]{\left[\begin{array}{ccc}{\overline{\mathbf{r}}}_1\, & {\overline{\mathbf{r}}}_2\, & {\overline{\mathbf{r}}}_3\end{array}\right]}^T $$

(12)

and

$$ {\displaystyle \begin{array}{l}{\hat{q}}_4=\sqrt{1+{A}_{11}+{A}_{22}+{A}_{33}}/2\quad {\hat{q}}_1=\pm \sqrt{1+{A}_{11}-{A}_{22}-{A}_{33}}/2\, \\ {}{\hat{q}}_1=\left[{A}_{23}-{A}_{32}\right]/\left(4{\hat{q}}_4\right)\quad \mathrm{or}\quad {\hat{q}}_2=\left[{A}_{12}+{A}_{21}\right]/\left(4{\hat{q}}_1\right)\ \\ {}{\hat{q}}_2=\left[{A}_{31}-{A}_{13}\right]/\left(4{\hat{q}}_4\right)\quad\quad\quad {\hat{q}}_3=\left[{A}_{13}+{A}_{31}\right]/\left(4{\hat{q}}_1\right)\, \\ {}{\hat{q}}_3=\left[{A}_{12}-{A}_{21}\right]/\left(4{\hat{q}}_4\right)\quad\quad\quad {\hat{q}}_4=\left[{A}_{23}-{A}_{32}\right]/\left(4{\hat{q}}_1\right)\, \end{array}} $$

(13)

5.2 Kalman Rate Estimator

To accurately measure low angular rates as experienced during 3-axis stabilization, a high-performance IMU will be required; this will neither fit in a small satellite nor be cost-effective. Low-cost MEMS rate sensors currently are still noisy and also experience high bias drift or temperature sensitivity. A modified implementation of a Kalman rate estimator can be used for the gyroless estimation of the nanosatellite body rates. This estimator was successfully used in many small satellite missions, such as the SNAP-1 nanosatellite mission (Steyn and Hashida 2001). It used magnetic field vector measurements that are continuously available, and the body measured rate of change of the geomagnetic field vector direction can be used as a measurement input for this rate estimator. However, this vector is not inertially fixed as it rotates twice per polar orbit. The estimated inertial referenced body rates will therefore have errors contributed by the magnetic field vector rotation rate. A more accurate estimated rate vector can be determined by measuring the sun vector, which only rotates inertially once per year. As the sun vector measurements are only available during the sunlit part of each orbit, when the sun is within the field of view (FOV) of a sun sensor, the Kalman rate estimator will propagate the angular rates when no measurements are available. A nadir-pointing small satellite is nominally rotating once per orbit within the ORC (around the body -Y_B axis), and full observability, using the sun vector measurement, is typically ensured. The only exception is when the satellite body rate vector is always aligned with the sun vector direction, else the angular rate vector with respect to an almost inertially fixed sun direction can be estimated as ${\overset{\frown }{\omega}}_B^I={\left[{\hat{\omega}}_{xi},{\hat{\omega}}_{yi},{\hat{\omega}}_{zi}\right]}^T$. The expected measurement error will therefore include the sun sensor measurement noise and a negligibly small satellite-to-sun inertial rotation.

5.2.1 System Model

The discrete Kalman filter state vector x(k) is defined as the inertially referenced body rate vector ${\boldsymbol{\upomega}}_B^I(k)$. From the Euler dynamic model of Eq. (6) without wheel actuators, the continuous time model becomes:

$$ {\displaystyle \begin{array}{l}{\dot{\boldsymbol{\upomega}}}_B^I(t)={\mathbf{I}}^{-1}\left({\mathbf{N}}_{MT}(t)+{\mathbf{N}}_{GG}(t)-{\boldsymbol{\upomega}}_B^I(t)\times \mathbf{I}{\boldsymbol{\upomega}}_B^I(t)\right)\\ {}\dot{\mathbf{x}}(t)=\mathbf{F}\;\mathbf{x}(t)+\mathbf{G}\;\mathbf{u}(t)+\mathbf{s}(t)\end{array}} $$

(14)

with

$$ {\displaystyle \begin{array}{l}\mathbf{F}=\left[\mathbf{0}\right],\, \mathbf{G}={\mathbf{I}}^{-1},\, \mathbf{u}(t)={\mathbf{N}}_{MT}(t)=\, \mathrm{Control}\ \mathrm{input}\ \mathrm{vector}\\ {}\mathbf{s}(t)={\mathbf{I}}^{-1}\left({\mathbf{N}}_{GG}(t)-{\boldsymbol{\upomega}}_B^I(t)\times \mathbf{I}{\boldsymbol{\upomega}}_B^I(t)\right)=\, \mathrm{System}\ \mathrm{noise}\ \mathrm{vector}\end{array}} $$

The discrete system model will then be

$$ \mathbf{x}\left(k+1\right)=\Phi\;\mathbf{x}(k)+\Gamma\;\mathbf{u}(k)+\mathbf{s}(k) $$

(15)

with

$$ {\displaystyle \begin{array}{l}\Phi =\left[{\mathbf{1}}_{3x3}\right],\, \Gamma ={\mathbf{I}}^{-1}{T}_s\\ {}{T}_s=\, \mathrm{Kalman}\ \mathrm{filter}\ \mathrm{sampling}\ \mathrm{period}\\ {}\mathbf{s}(k)=N\left\{\mathbf{0},\mathbf{Q}(k)\right\}\, =\, \mathrm{Zero}\ \mathrm{mean}\ \mathrm{system}\ \mathrm{noise}\ \mathrm{vector}\ \mathrm{with}\ \mathrm{covariance}\ \mathrm{matrix}\ \mathbf{Q}\end{array}} $$

5.2.2 Measurement Model

If we assume the satellite-to-sun vector as “inertially fixed” due to the large distance from the earth to sun compared to the earth to satellite and the slow rotation of the earth around the sun, the rate of change of the sun sensor measured unit vector can be used to accurately estimate the inertial referenced body angular rates. The magnetometer unit vector, as an orbit rotating vector, can also be used for continuous measurement updates but with expected rate estimation errors of approximately twice the orbit rate ω_o. For the rest of this discussion and the derivation of the measurement model, we assume the sun vector measurements will be used when they are available to update the Kalman rate estimator. Successive sun vector measurements will result in a small-angle discrete approximation of the vector rotation matrix:

$$ \overline{\mathbf{s}}(k)=\Delta \mathbf{A}(k)\;\mathbf{s}\left(k-1\right) $$

(16)

with

$$ {\displaystyle \begin{array}{l}\Delta \mathbf{A}(k)\approx \left[\begin{array}{ccc}1& {\omega}_{zi}(k){T}_s& -{\omega}_{yi}(k){T}_s\\ {}-{\omega}_{zi}(k){T}_s& 1& {\omega}_{xi}(k){T}_s\\ {}{\omega}_{yi}(k){T}_s& -{\omega}_{xi}(k){T}_s& 1\end{array}\right]\\ {}\quad \approx \left[{\mathbf{1}}_{3x3}\right]+\Lambda \left\{{\boldsymbol{\upomega}}_B^I(k)\right\}\end{array}} $$

(17)

The Kalman filter measurement model then becomes,

$$ {\displaystyle \begin{array}{l}\Delta \mathbf{s}(k)=\overline{\mathbf{s}}(k)-\overline{\mathbf{s}}\left(k-1\right)=\Lambda \left\{{\boldsymbol{\upomega}}_B^I(k)\right\}\, \overline{\mathbf{s}}\left(k-1\right)\\ {}\mathbf{y}(k)=\Delta \mathbf{s}(k)=\mathbf{H}(k)\;\mathbf{x}(k)+\mathbf{m}(k)\end{array}} $$

(18)

with

$$ \mathbf{H}(k)=\left[\begin{array}{ccc}0& -{s}_z\left(k-1\right){T}_s& {s}_y\left(k-1\right){T}_s\\ {}{s}_z\left(k-1\right){T}_s& 0& -{s}_x\left(k-1\right){T}_s\\ {}-{s}_y\left(k-1\right){T}_s& {s}_x\left(k-1\right){T}_s& 0\end{array}\right] $$

(19)

and m(k) = N{0, R(k)} as zero measurement noise, with covariance R.

5.2.3 Kalman Filter Algorithm

Define ${\mathbf{P}}_k\equiv E\left\{{\mathbf{x}}_k.{\mathbf{x}}_k^T\right\}$ as the state covariance matrix, and then the following steps are executed every sampling period T_s, between measurements (at time step k):

• 1. Numerically integrate the nonlinear dynamic model of Eq. (14):

  $$ {\hat{\mathbf{x}}}_{k+1/k}={\hat{\mathbf{x}}}_{k/k}+0.5{T}_s\left(3\Delta {\mathbf{x}}_k-\Delta {\mathbf{x}}_{k-1}\right)\operatorname{}\left\{\mathrm{Modified}\ \mathrm{Euler}\ \mathrm{Integration}\right\} $$

  (20)

  with

  $$ \Delta {\mathbf{x}}_k={\mathbf{I}}^{-1}\left({\mathbf{N}}_{MT}(k)-{\hat{\boldsymbol{\upomega}}}_B^I(k)\times \mathbf{I}{\hat{\boldsymbol{\upomega}}}_B^I(k)\right) $$

  (21)

• 2. Propagate the state covariance matrix:

  $$ {\mathbf{P}}_{k+1/k}=\Phi\;{\mathbf{P}}_{k/k}\;{\Phi}^T+\mathbf{Q}={\mathbf{P}}_{k/k}+\mathbf{Q} $$

  (22)

  Across measurements (at time step k + 1 and only in sunlit part of orbit):

• 3. Gain update, compute H_k+1 from Eq. (19) using previous vector measurements $\overline{\mathbf{s}}(k)$:

  $$ {\mathbf{K}}_{k+1}={\mathbf{P}}_{k+1/k}{\mathbf{H}}_{k+1}^T{\left[{\mathbf{H}}_{k+1}{\mathbf{P}}_{k+1/k}{\mathbf{H}}_{k+1}^T+\mathbf{R}\right]}^T $$

  (23)

• 4. Update the system state:

  $$ {\hat{\mathbf{x}}}_{k+1/k+1}={\hat{\mathbf{x}}}_{k+1/k}+{\mathbf{K}}_{k+1}\left({\mathbf{y}}_{k+1}-{\mathbf{H}}_{k+1}{\hat{\mathbf{x}}}_{k+1/k}\right) $$

  (24)

  with

  $$ {\mathbf{y}}_{k+1}=\overline{\mathbf{s}}\left(k+1\right)-\overline{\mathbf{s}}(k) $$

• 5. Update the state covariance matrix:

  $$ {\mathbf{P}}_{k+1/k+1}=\left[{\mathbf{1}}_{3x3}+{\mathbf{K}}_{k+1}{\mathbf{H}}_{k+1}\right]\;{\mathbf{P}}_{k+1/k} $$

  (25)

Finally the estimated ORC angular rate vector can be calculated from the Kalman filtered estimated ECI rate vector, using the TRIAD result of Eq. (12):

$$ {\hat{\boldsymbol{\upomega}}}_B^O(k)={\hat{\boldsymbol{\upomega}}}_B^I(k)-{\mathbf{A}}_{O/B}\left(\hat{\mathbf{q}}(k)\right)\;{\left[0\, -{\omega}_o\, 0\right]}^T $$

(26)

Figure 5 shows the simulation Kalman rate estimation results of a satellite with a hemispherical FOV digital sun sensor. The satellite is in an approximate 500 km polar orbit with 05h45 LTAN, giving a short eclipse period. The initial ECI referenced body rate vector values are [0.5, 0.0, 1.0] °/s. The estimated rate values track and propagate the true ECI rates accurately. The estimated rates are smooth when they are propagated, e.g., during the eclipse period from approximately 3600 to 4600 seconds. The digital sun sensor has a RMS angular error of 0.1°, and the Kalman rate estimation RMS error is 0.02 °/s.

Fig. 5

Simulated sun sensor-based Kalman rate filter results

Figure 6 presents actual Kalman rate estimation results obtained as real-time telemetry data points during the commissioning of a small microsatellite, when using only magnetometer measurements.

Fig. 6

Onboard magnetometer-based Kalman rate filter telemetry results

5.3 Extended Kalman Filter Estimators

Before any of the wheel control modes can be applied to a satellite, more accurate and continuous angular rate and attitude knowledge will be required. An extended Kalman filter (EKF) can be used to estimate the full attitude state of the satellite from all attitude sensor SBC measurements (e.g., from magnetometer, sun, nadir, and star sensors) and the corresponding ORC modelled vectors; see (Steyn 1995) for a detailed derivation. The seven-element discrete state vector to be estimated is defined as:

$$ \hat{\mathbf{x}}(k)=\left[\begin{array}{c}{\hat{\boldsymbol{\upomega}}}_B^I(k)\\ {}\hat{\mathbf{q}}(k)\end{array}\right] $$

(27)

A disadvantage of the full state EKF is that the estimation accuracy will depend not only on the sensor measurement noise but also on the size of the modelling errors in the Euler dynamic model in Eq. (6), i.e., the uncertainty of the spacecraft’s moments and products of inertia, the unknown external disturbance torques, and the actual actuator output torques. If the satellite’s inertially referenced body rate vector ${\boldsymbol{\upomega}}_B^I(k)$ can be accurately measured with inertial rate sensors (gyroscopes), the EKF does not have to model the spacecraft’s uncertain dynamics, and a six-element discrete state vector can be defined as:

$$ \hat{\mathbf{x}}(k)=\left[\begin{array}{c}\hat{\mathbf{b}}(k)\\ {}\hat{\mathbf{q}}(k)\end{array}\right] $$

(28)

with $\hat{\mathbf{b}}(k)$ the estimated bias vector of the 3-axis angular rate sensor and inertial rate sensor model:

$$ {\hat{\boldsymbol{\upomega}}}_B^I(k)={\boldsymbol{\upomega}}_{GYRO}(k)-\mathbf{b}(k)+\mathbf{m}(k) $$

where ω_GYRO(k) is the 3-axis angular rate sensor measurement vector, b(k) is the rate sensor bias vector, and m(k) the measurement noise vector. See (Lefferts et al. 1982) for a detailed derivation of the rate sensor-based EKF.

Only extremely expensive and high-performance rate sensors, e.g., fiber-optic and ring-laser gyroscopes, will be able to measure the 3-axis inertially referenced angular rates of satellites with the required accuracy. The angular rate sensor bias can be significant in most sensors, e.g., a MEMS type and when it is required for the attitude to be propagated by integration of the rate sensor measurements, the estimation of the sensor bias becomes mandatory.

The innovation used in the EKF is the vector cross product of a measured body reference unit vector and a modelled orbit reference unit vector, transformed to the body coordinates by the estimated attitude transformation matrix $\mathbf{A}\left[\hat{\mathbf{q}}(k)\right]$:

$$ \mathbf{e}(k)={\overline{\mathbf{v}}}_B(k)\times \mathbf{A}\left[\hat{\mathbf{q}}(k)\right]\, {\overline{\mathbf{v}}}_O(k) $$

(29)

with ${\displaystyle \begin{array}{l}{\overline{\mathbf{v}}}_B(k)={\mathbf{B}}_{magm}(k)/\left\Vert {\mathbf{B}}_{magm}(k)\right\Vert \, \mathrm{or}\, {\mathbf{S}}_{sun}(k)/\left\Vert {\mathbf{S}}_{sun}(k)\right\Vert \\ {}{\overline{\mathbf{v}}}_O(k)={\mathbf{B}}_{igrf}(k)/\left\Vert {\mathbf{B}}_{igrf}(k)\right\Vert \, \mathrm{or}\, {\mathbf{S}}_{orbit}(k)/\left\Vert {\mathbf{S}}_{orbit}(k)\right\Vert \end{array}}$, e.g., for magnetic and sun vector pairs

The onboard magnetometer measurements must first be offline calibrated by comparing the measured B-field magnitude to the International Geomagnetic Reference Field (IGRF) model’s magnitude. This is can be done by sampling at least a full orbit’s raw or pre-launch calibrated magnetometer vector measurements and the corresponding IGRF modelled magnetic vectors. These data samples can then be further ground processed by using an attitude independent 3-axis magnetometer calibration method (Crassidis et al. 2005) to estimate the gain (scaling and orthogonality) matrix G_cal and offset (bias) vector O_cal.

Thereafter calibrated magnetometer measurements can be determined for use in the EKF:

$$ {\mathbf{B}}_{magm}(k)={\mathbf{G}}_{cal}{\mathbf{B}}_{raw}(k)-{\mathbf{O}}_{cal} $$

(30)

Figure 7 shows typical pre- and post-calibration comparison results of a magnetometer when the onboard magnetic magnitude is compared to an IGRF model output for a CubeSat in a 400 km International Space Station orbit.

Fig. 7

Magnetometer pre-calibration (1σ = 2.848 μT) and post-calibration (1σ = 0.365 μT)

6 Attitude and Angular Rate Controllers

6.1 Detumbling Magnetic Controllers

After release from the launcher stage, the small satellite will first be detumbled using minimum ADCS resources and power, to bring it to a controlled spin rate and/or spinning attitude, typically a Y-Thomson spin (Thomson 1962). A Y-Thomson spin will ensure that the satellite will align its body Y_B axis normal to the orbit plane, i.e., with the satellite rotating within the orbit plane. This not only results in a controlled spin rate but also in a known spin attitude, without the need to estimate onboard the satellite’s attitude. The only requirement for a stable Y-Thomson spin will be that the body Y_B axis must have the largest moment of inertia (I_yy MOI parameter) and small (< 3% MOI) products of inertia parameters. A simple B-dot (Stickler and Alfriend 1974) magnetic controller will quickly dump any X_B and Z_B axes angular rates and align the Y_B axis to the orbit plane normal vector. Using measurements from a single MEMS rate sensor, the Y_B spin rate can then be magnetically controlled to an inertially referenced spin rate of typically −2 °/s (the reference rate depends on the magnitude of the external disturbance torques and must be high enough to ensure a sufficient gyroscopic stiffness). The magnetic detumbling controllers require only the measured magnetic field vector components (from a 3-axis magnetometer) and the inertially referenced Y_B body rate (from the Kalman rate estimator on Sect. 1.5.2 or a rate sensor measurement) and can be applied continuously. The magnetic-only controllers used during detumbling can be:

$$ {\displaystyle \begin{array}{l}{M}_y={K}_d\raisebox{1ex}{$ d\beta $}\!\left/ \!\raisebox{-1ex}{$ d t$}\right.\quad \mathrm{for}\, \beta =\operatorname{arccos}\, \left(\raisebox{1ex}{${B}_{my}$}\!\left/ \!\raisebox{-1ex}{$\left\Vert {\mathbf{B}}_{meas}\right\Vert $}\right.\right)\quad \left\{\mathrm{Bdot}\ \mathrm{controller}\right\}\\ {}{M}_x={K}_s\left({\omega}_{yi}-{\omega}_{yref}\right) \operatorname {sgn}\left({B}_{mz}\right)\quad \mathrm{for}\quad \left|{B}_{mz}\right|>\left|{B}_{mx}\right|\, \left\{\mathrm{Y}\ \mathrm{spin}\ \mathrm{controller}\right\}\\ {}{M}_z=-{K}_s\left({\omega}_{yi}-{\omega}_{yref}\right) \operatorname {sgn}\left({B}_{mx}\right)\, \mathrm{for}\quad \left|{B}_{mx}\right|>\left|{B}_{mz}\right|\, \left\{\mathrm{Y}\ \mathrm{spin}\ \mathrm{controller}\right\}\end{array}} $$

(31)

with β the angle between the body Y_B axis and the local B-field vector, K_d and K_s are the detumbling and spin controller gains, and ω_yrefthe reference Y_B body spin rate. M_x,y,z are the magnetic torquer moments in Am² units that can be scaled to pulse width modulated (PWM) outputs M_{PMW_x,y,z}, as most magnetorquers on satellites are current controlled via discrete switching amplifiers. As the magnetorquer magnetic moments can disturb the local magnetic field measurements, we typically limit the magnetorquer on time to 80% of the discrete magnetic controller period T_s to leave a window for undisturbed magnetometer sampling.

The pulse outputs of the magnetorquers are therefore saturated to 80% of the controller period T_s,

$$ sat\left\{\;{M}_{PWM\_i}\right\}=\operatorname{sgn}\left({M}_{PWM\_i}\right)\, \min \left\{\;\left|\;{M}_{PWM\_i}\right|,0.8{T}_s\right\}\, \mathrm{for}\, i=x,y,z $$

(32)

The average magnetic moment and torque vector during a controller period can then be calculated as:

$$ {\mathbf{M}}_{avg}=\frac{M_{\mathrm{max}}}{T_s} sat\left\{{\mathbf{M}}_{PWM}\right\}\, {\mathrm{Am}}^2 $$

(33)

$$ {\mathbf{N}}_{MT}={\mathbf{M}}_{avg}\times {\mathbf{B}}_B $$

(34)

with M_max the maximum “on” magnetic moment of the magnetorquer and B_B the true magnetic field vector SBC.

Figures 8 and 9 show a typical detumbling performance from an initial angular rate of ${\omega}_B^I(0)={\left[4,0,2\right]}^T$°/sec. During the first 1000 seconds, no control was done, and then the detumbling and Y-spin controller of Eq. (31) were enabled. Within less than an orbit, the satellite was controlled to a − 1°/sec Y-Thomson spin, using only the magnetorquers. The body angular rates were estimated by the Kalman rate filter as presented above utilizing only the raw magnetometer vector measurements.

Fig. 8

Attitude angles during magnetic detumbling to a Y-Thomson spin

Fig. 9

Angular rates during magnetic detumbling to a Y-Thomson spin

6.2 Y-Momentum Wheel Controller

From the Y-Thomson body spin of the previous section, a momentum wheel aligned to the Y_B body axis can be used to absorb the Y-body momentum and control the pitch angle with small roll and yaw angles, e.g., to maintain a nadir-pointing attitude for earth imaging payloads and directional antennae for ground station communications. The Y-momentum wheel controller can be implemented with attitude and rate estimations from an EKF, as

$$ {N}_{wy}(k)={K}_{py}\;\arcsin\;\left({\hat{q}}_2(k) \operatorname {sgn}\left({\hat{q}}_4(k)\right)\right)+{K}_{dy}\;{\hat{\omega}}_{yo}(k) $$

(35)

with K_py and K_dy the proportional and derivative gains.

To maintain the Y-wheel momentum at a certain reference level (corresponding to the initial Y_B body momentum during the Y-spin mode) and to damp anybody nutation rates in the X_B and Z_B axes, a magnetic cross-product control law can be utilized (Steyn and Hashida 2001):

$$ \mathbf{M}(k)=\frac{\mathbf{e}(k)\times \mathbf{B}(k)}{\left\Vert \mathbf{B}(k)\right\Vert } $$

(36)

with

$$ \mathbf{e}(k)=\left[\begin{array}{c}{K}_n\, {\hat{\omega}}_{xo}(k)\\ {}{K}_h\, \left({h}_{wy}(k)-{h}_{wy- ref}\right)\\ {}{K}_n\, {\hat{\omega}}_{zo}(k)\end{array}\right] $$

(37)

where K_n is the nutation damping gain, K_h is the Y-wheel momentum control gain, and h_wy − ref is the Y-wheel reference angular momentum.

The cross-product controller of Eq. (36) is applied continuously. During initial commissioning, the Y-momentum control mode can be used to calibrate and determine the alignment of all the accurate attitude sensors, i.e., sun and earth horizon (nadir) sensors and star tracker. After the in-orbit calibration and alignment parameters have been determined, the measurements from these sensors can then be included in an EKF to improve the attitude and rate estimation accuracy. Next, the nanosatellite will be ready for a 3-axis reaction wheel control mode, when required for full 3-axis pointing capability.

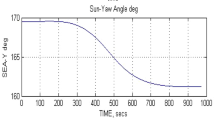
Figures 10 and 11 present the detumbling results where an offset Y-wheel speed (momentum) can assist to detumble a satellite into a stable Y-Thomson spin for cases where the Y_B axis MOI is not the largest. The detumbling is done during the first orbit until time 5700 seconds with the Y-Wheel speed at −1000 rpm. Then the Y-Wheel speed is ramped to −3700 rpm to absorb the Y-body spin, and at 6000 seconds, the Y-Wheel controller of Eq. (35) is enabled to control the pitch attitude to zero, and the magnetic cross-product controller of Eq. (36) is enabled to damp the roll/yaw nutation and maintain the Y-Wheel angular momentum at a wheel speed of approximately −3700 rpm. At 7000 seconds a pitch reference of +30° and 250 seconds later of −30° is commanded, before returning back to nadir pointing at 7500 seconds.

Fig. 10

Attitude angles from Y-Thomson detumbling to Y-Momentum wheel control

Fig. 11

Y-Momentum wheel speed during Y-Thomson detumbling and Y-Momentum control

6.3 3-Axis Reaction Wheel Controllers

From the Y-momentum wheel mode, the X_B and Z_B reaction wheels can be activated and a 3-axis reaction wheel controller implemented using the estimated attitude and angular rates using the EKF of Sect. 1.5.3. The globally stable quaternion feedback controller of (Wie et al. 1989) can be modified to become an orbit referenced pointing control law. The quaternion and rate reference vectors can be generated from a sun orbit model for a sun-pointing attitude (to maximize solar energy generation on deployed solar panels), or it can be a zero vector for a nadir-pointing attitude or any specified constant attitude reference for a specific roll, pitch, or yaw requirement (see Fig. 12). The 3-axis reaction wheel control law (wheel torque vector) to be used for all these cases is:

$$ {\mathbf{N}}_w(k)={K}_{P1}\mathbf{I}{\overset{\rightharpoonup }{\mathbf{q}}}_{err}(k)+{K}_{D1}\mathbf{I}{\hat{\boldsymbol{\upomega}}}_B^O(k)-{\hat{\boldsymbol{\upomega}}}_B^I(k)\times \left(\mathbf{I}{\hat{\boldsymbol{\upomega}}}_B^I(k)+{\mathbf{h}}_w(k)\right) $$

(38)

with ${K}_{P1}=2{\omega}_n^2,\, {K}_{D1}=2{\zeta \omega}_n$the pointing gains for a required controller closed-loop bandwidth and damping factor. I is the satellite moment of inertia matrix, h_w(k) is the measured angular momentum of the reaction wheels: ${\hat{\omega}}_B^O(k)={\left[{\hat{\omega}}_{xo}(k),{\hat{\omega}}_{yo}(k),{\hat{\omega}}_{zo}(k)\right]}^T$is the body orbit reference angular rate estimate, ${\overset{\rightharpoonup }{\mathbf{q}}}_{err}(k)={\left[{q}_{1e}(k),{q}_{2e}(k),{q}_{3e}(k)\right]}^T$is the vector part of the error quaternion q_err, where

$$ {\displaystyle \begin{array}{l}{\mathbf{q}}_{err}(k)={\mathbf{q}}_{com}(k)\oplus \, \hat{\mathbf{q}}(k)\\ {}\left[\begin{array}{c}{q}_{1e}\\ {}{q}_{2e}\\ {}{q}_{3e}\\ {}{q}_{4e}\end{array}\right]=\left[\begin{array}{cccc}{q}_{4c}& {q}_{3c}& -{q}_{2c}& -{q}_{1c}\\ {}-{q}_{3c}& {q}_{4c}& {q}_{1c}& -{q}_{2c}\\ {}{q}_{2c}& -{q}_{1c}& {q}_{4c}& -{q}_{3c}\\ {}{q}_{1c}& {q}_{2c}& {q}_{3c}& {q}_{4c}\end{array}\right]\left[\begin{array}{c}{\hat{q}}_1\\ {}{\hat{q}}_2\\ {}{\hat{q}}_3\\ {}{\hat{q}}_4\end{array}\right]\end{array}} $$

(39)

with q_com(k) the commanded reference quaternion, e.g., a sun direction quaternion and ⊕ for quaternion division.

Fig. 12

Target tracking geometry

A nominal reaction wheel control mode can be, for example, do sun-pointing in the sunlit part of the orbit and nadir pointing, i.e., ${\mathbf{q}}_{com}(k)={\left[0,0,0,1\right]}^T$, in eclipse. The nadir-pointing attitude will ensure optimal antenna coverage for ground communication during eclipse and thermal stability to the imager telescope. Continuous momentum management of the reaction wheels can be done using a simple cross-product magnetic controller (Steyn 1995):

$$ \mathbf{M}(k)={K}_m\frac{{\mathbf{h}}_w(k)\times \mathbf{B}(k)}{\left\Vert \mathbf{B}(k)\right\Vert } $$

(40)

with K_mthe momentum dumping gain.

The tracking of ground targets can also be accurately done by uploading the earth target’s coordinates a-priory. A target tracking generator is then used onboard to calculate the commanded quaternion q_com(k) and angular rate vectors for the reaction wheel controllers as derived in (Chen et al. 2000). The geometry during target tracking to calculate the satellite to target vector in ORC is shown in Fig. 12. The 3-axis reaction wheel control law is similar to the quaternion feedback controller of Eqs. (38) and (39), but an integral term of the quaternion error ${\overset{\rightharpoonup }{\mathbf{q}}}_{ierr}$is added for improved tracking accuracy, where:

$$ {\overset{\rightharpoonup }{\mathbf{q}}}_{i\; err}(k)\cong {\overset{\rightharpoonup }{\mathbf{q}}}_{i\; err}\left(k-1\right)+{\overset{\rightharpoonup }{\mathbf{q}}}_{err}(k)\;{T}_s $$

(41)

The ground target tracking control law then becomes

$$ {\displaystyle \begin{array}{l}{\mathbf{N}}_w(k)={K}_{P2}\mathbf{I}{\overset{\rightharpoonup }{\mathbf{q}}}_{err}(k)+{K}_{I2}\mathbf{I}{\overset{\rightharpoonup }{\mathbf{q}}}_{i\; err}(k)+{K}_{D2}\mathbf{I}\left[{\hat{\boldsymbol{\upomega}}}_B^O(k)-{\boldsymbol{\upomega}}_{com}^O(k)\right]\\ {}\quad -{\hat{\boldsymbol{\upomega}}}_B^I(k)\times \left[\mathbf{I}{\hat{\boldsymbol{\upomega}}}_B^I(k)+{\mathbf{h}}_w(k)\right]\end{array}} $$

(42)

with ${K}_{P2}=2\left({\omega}_n^2+2{\zeta \omega}_n/\Delta T\right),\, {K}_{D2}=2{\zeta \omega}_n+1/\Delta T,\, {K}_{I2}=2{\omega}_n^2/\Delta T,$ ω_n, ζ the dominant second-order closed-loop specifications, ΔT = 10/ζω_n the time constant for integral control, and ${\boldsymbol{\upomega}}_{com}^O(k)$ the ORC target tracking angular rate commanded vector.

Figures 13 and 14 show the typical performance over an orbit of the 3-axis reaction wheel controllers of a LEO small satellite. Initially the attitude is controlled to nadir pointing (zero RPY). Between 600 and 1600 seconds, a ground target close to the sub-satellite ground track is tracked, with roll angle varying between +2° and − 4°, i.e., for an almost overhead pass. At 2000 seconds a sun-tracking control law is enabled to point the solar panels mounted on the zenith pointing satellite facet toward the sun. During eclipse (from 3099 to 5262 seconds) the sun tracking control law automatically revert back to nadir pointing to ensure improved antennae pointing for ground station communication.

Fig. 13

Attitude angles during target tracking, sun tracking, and nadir-pointing control

Fig. 14

Reaction wheel speeds during target tracking, sun tracking, and nadir-pointing control

7 Pointing Accuracy and Stability

The ADCS requirements for an earth observation (EO) satellite are mostly driven by the imager, the “main payload.” These are determined by the Hi-Res camera as it will present the highest performance requirements for pointing accuracy, pointing stability, and platform agility. This section uses a hypothetical Hi-Res camera and satellite as an example to satisfy the following user requirements:

• Hi-Res ground sampling distance (GSD) of 1 m/pixel resolution on 7 μm square pixel dimensions

• Hi-Res swath of 12 km (assuming 12,000 active pixels per line)

• Agility of 30° roll and pitch rotations in 20 seconds

• Pointing control error of 200 m (1σ) at center of target

• Pointing knowledge error of 20 m (1σ) at center of target

• Pointing stability less than 0.1 pixel smear during time delay integration (TDI) imaging

• Pointing range in pitch and roll at ±30°

• 128 TDI stages (pixel rows) at the maximum integration setting

• 500 km near circular sun-synchronous orbit with 09 h30 am/pm local time at equatorial crossings

• 450 kg minisatellite with principle moments of inertia (MOI) I_XX = I_YY = 270 kgm² and I_ZZ = 63 kgm²

7.1 Selected ADCS Hardware

7.1.1 Reaction Wheels

Four wheels in a tetrahedral configuration (see Fig. 15) with reaction wheel specifications:

• Maximum torque: N_max = 0.2 Nm

• Maximum angular momentum: h_max = 10 Nms (± 5000 rpm)

• Speed control accuracy: Δω < 0.6 rpm RMS

• Static unbalance <4.5 g.cm

• Dynamic unbalance <14.4 g.cm²

Fig. 15

Tetrahedral reaction wheel configuration

7.1.2 Star Tracker

A star tracker with dual optical heads with 60° separation between boresight directions to prevent sun blinding at certain attitude pointing angles. The star tracker specifications are:

• Accuracy: 4 arcsec 1σ in boresight direction and 20 arcsec 1σ boresight rotation for 10 stars at 5 Hz.

• Exclusion angles: 30° sun and Earth

• Max tracking rate: 5 °/sec.

7.1.3 Angular Rate Sensor

A fiber-optic gyroscope (FOG) is selected to measure the angular rates per satellite axis. The FOG specifications are:

• Random walk <0.08 °/√hr → measurement noise = 4 milli-deg/sec (1σ)

• Bias drift <1.5 °/hr. = 1.5 arcsec/sec

• Bias stability <0.05 °/hr. = 0.05 arcsec/sec

• Update rate 10 Hz

7.1.4 Space GPS Receiver

The orbit position is measured accurately with a GPS receiver with the following relevant specifications:

• 3D position accuracy <10 m (1σ)

• Update rate 1 Hz

7.2 Jitter Analysis (Platform Stability)

7.2.1 Stability Requirement

Assume a maximum 10% pixel smear over the 128 TDI stages. For a 500 km orbit, V_sat = 7.613 km/sec and V_ground = 7.06 km/sec. Assume an imaging quality factor Q = 1, i.e., pixel ground size = GSD.

The exposure time for a 128 stage TDI sensor is therefore t_exp = 128.GSD/V_ground = 18.1 milli-sec.

The GSD pixel angle: θ_pixel (500 km) = tan⁻¹(GSD/500e3) = 0.4125 arcsec.

The stability requirement for roll and pitch pointing is then ω_stability(pitch/roll) = 0.1 θ_pixel/t_exp = 2.28 arcsec/sec.

For yaw rotations the end pixels will be 6000 pixels from the 12,000 pixel line center; therefore a 0.1 pixel rotation at the end of a line will be ψ_pixel = tan⁻¹(0.1/6000) = 3.44 arcsec and ω_stability(yaw) = ψ_pixel/t_exp = 189.9 arcsec/sec.

The worst-case stability requirement is then for roll/pitch stability = 2.28 arcsec/sec.

The factors determining the platform stability during TDI integration will be discussed next.

7.2.2 Reaction Wheel Unbalance

Assume a four-wheel tetrahedral reaction wheel configuration with a wheel speed bias of ω_wbias = 1000 rpm = 104.7 rad/sec = 16.7 Hz.

7.2.2.1 Static Unbalance

Assume for the tetrahedral configuration the static unbalance mr = 4.5 g.cm = 4.5e-5 kg.m and the worst-case unbalanced wheel disc CoM at 0.3 m from the satellite CoM.

The static unbalance forces in the X_BZ_B and Y_BZ_B plane for pitch and roll disturbance:

$$ {F}_{su}= mr{\omega}^2=4.5\mathrm{e}\hbox{-} 5{(104.7)}^2\mathit{\sin}(104.7t)\mathrm{N} $$

The static unbalance angular accelerations will be:

$$ {\dot{\omega}}_{x/y}=\frac{0.3{F}_{su}}{I_{XX/ YY}}=5.5\mathrm{e}\hbox{-} 4\mathit{\sin}(104.7t)\mathrm{rad}/{\sec}^2 $$

The angular rate disturbance amplitude due to static unbalance will then be:

$$ \left|{\omega}_{x/y\ static}\right|=\frac{\left|{\dot{\omega}}_{x/y}\right|}{\omega_{wbias}}=\underline {1.08 \operatorname {arcsec}/\sec}\, \left(@16.7\ \mathrm{Hz}\right) $$

7.2.2.2 Dynamic Unbalance

Assume for the tetrahedral configuration the dynamic unbalance mrd = 14.4 g.cm² = 1.44e-6 kg.m². The dynamic unbalance torque amplitude around the body axes causing attitude disturbances will be

$$ \left|{N}_{du}\right|= mrd{\omega}^2=1.44\mathrm{e}\hbox{-} 6{(104.7)}^2=1.58\mathrm{e}\hbox{-} 2\mathrm{Nm} $$

The dynamic unbalance torque around the roll and pitch axes will be

$$ \left|{\dot{\omega}}_{x/y}\right|=\frac{\left|{N}_{du}\right|}{I_{XX/ YY}}=1.58\mathrm{e}\hbox{-} 2/270=5.9\mathrm{e}\hbox{-} 5\ \mathrm{rad}/{\sec}^2 $$

The angular rate disturbance amplitude will then be

$$ \left|{\omega}_{x/y\ dynamic}\right|=\frac{\left|{\dot{\omega}}_{x/y}\right|}{\omega_{wbias}}=\underline {0.12 \operatorname {arcsec}/\sec}\, \left(@16.7\ \mathrm{Hz}\right) $$

Therefore the worst-case jitter will be due to static unbalance; this can be reduced by placing the RWs closer to the CoM of the satellite or by reducing the RW bias wheel speed.

7.2.3 Reaction Wheel Control Torque Disturbances

The brushless DC motor (BDCM) control of the reaction wheel speed will induce the following disturbance torques to the satellite body.

7.2.3.1 Nonlinear Friction

Stiction when crossing zero speeds. A typical stiction torque for a similar sized tetrahedral reaction wheel configuration is 4 milli-Nm. The wheel acceleration in a controller settling time of 10T_s = 1 sec due to stiction, when the wheel stop and start, is (T_s = reaction wheel controller sampling time)

$$ \frac{\Delta \omega }{\Delta t}=\frac{N_{stiction}}{I_{XX/ YY}}=\frac{4e-3}{235}=3.1 \operatorname {arcsec}/{\sec}^2 $$

$$ \Delta {\omega}_{stiction}=\underline {3.1 \operatorname {arcsec}/\sec}\operatorname{}\left(\mathrm{assuming}\ \mathrm{a}\ 1\ \sec\ \mathrm{RW}\ \mathrm{controller}\ \mathrm{settling}\ \mathrm{time}\right) $$

This angular disturbance clearly exceeds the stability requirement during imaging; therefore the RW speeds must be prevented from zero speed crossings, i.e., biased reaction wheels will be required in the tetrahedral configuration.

7.2.4 BDCM Torque Ripple

Assume 25% of the nominal torque (20 milli-Nm) during imaging as the torque ripple at the motor’s commutation rate multiplied by the reaction wheel bias speed ω_wbias. The ripple torque will then be:

$$ {N}_{ripple}=5\ \mathrm{milli}\hbox{-} \mathrm{Nm}@100\ \mathrm{Hz}\operatorname{}\left\{6\ \mathrm{poles}\ \mathrm{x}\ 16.7\ \mathrm{Hz}@1000\ \mathrm{rpm}\right\} $$

The ripple torque angular rate disturbance amplitude will then be:

$$ \left|{\omega}_{ripple}\right|=\left({N}_{ripple}/{I}_{XX/ YY}\right)/628.2\ \mathrm{rad}/\mathrm{s}=\underline {0.006 \operatorname {arcsec}/\sec}\, \left(@100\ \mathrm{Hz}\right) $$

7.2.4.1 Reaction Wheel Control Torque

Assume a 1% of maximum tetrahedral torque increment every reaction wheel controller sampling time T_s:

$$ \varDelta {N}_{wheel}=0.01{N}_{wmax}=2.0\ \mathrm{milli}\hbox{-} \mathrm{Nm}\ \mathrm{in}\;{T}_s=0.1\ \sec $$

The ripple torque angular rate disturbance amplitude will then be:

$$ {\omega}_{control}=\left(\varDelta {N}_{wheel}/{I}_{XX/ YY}\right).{T}_s=\underline {0.15 \operatorname {arcsec}/\sec } $$

7.2.4.2 Reaction Wheel Speed Discretization

Assuming a speed control discretization step amplitude of Δω_wheel = 0.6 rpm = 3.6^°/sec and reaction wheel moment of inertia I_wheel = 1.91e-2 kgm², then the wheel speed discretization will cause a body angular rate disturbance of

$$ \varDelta {\omega}_{x/y}=\varDelta {\omega}_{wheel}{I}_{wheel}/{I}_{XX/ YY}=1.1 \operatorname {arcsec}/\sec $$

This value is close to the roll/pitch stability requirement of 2.28 arcsec/sec for a 128 stage TDI image sensor. Neither the star tracker or FOG rate sensors can measure down to this low resolution. With only the reaction wheels controlled to an accuracy not worse than 0.6 rpm (1σ), the satellite platform stability requirement will be met.

7.3 Pointing Error Budget

The different contributions to a ground target’s pointing error from a 500 km altitude are:

• Attitude knowledge error from the dual star tracker measurements

  Accuracy <4 arcsec (1σ) = 9.7 meter

• GPS position error projected to the ground

  Accuracy of satellite’s in-orbit position <10 m (1σ) = 9.3 meter

• Timing accuracy (image timestamp correlation)

  2 milli-sec (1σ) worst case assumed due to software latency = 14.1 meter @V_ground = 7.06 km/sec.

Therefore the combined (1σ) geolocation measurement accuracy = 19.5 meter (satisfies requirement)

• The attitude control accuracy <0.02° (1σ) = 174.5 meter

Therefore, the total (1σ) pointing control error = 194.0 meter (satisfies requirement).

Other possible errors to consider:

• Maximum structural alignment variation (thermal) between main telescope and star tracker boresights <10 arcsec, thus <24.2 meter pointing error that can possibly be compensated for with a thermal model

• Atmospheric optical distortion for off-nadir angles and ionospheric errors for GPS signals

7.4 Satellite Platform Agility

Assume a four-wheel tetrahedral configuration with maximum total torque and angular momentum placed in the Y_B axis direction:

$$ {\mathbf{N}}_{THmax}=\left[\begin{array}{c}1.89\\ {}2.0\\ {}1.63\end{array}\right]{\mathbf{N}}_{Wmax}\, \mathrm{and}\, {\mathbf{h}}_{THmax}=\left[\begin{array}{c}1.89\\ {}2.0\\ {}1.63\end{array}\right]{\mathbf{h}}_{Wmax} $$

Then,

$$ {N}_{TH max}\left({Y}_B\right)=400\ \mathrm{milli}\hbox{-} \mathrm{Nm},\, {h}_{TH\mathit{\max}}\left({Y}_B\right)=20\ \mathrm{Nms} $$

$$ {\omega}_{ymax}=0.7{h}_{THmax}/{I}_{YY}=0.0519\ \mathrm{rad}/\sec \approx {3.0}^{{}^{\circ}}/\sec $$

$$ {\dot{\omega}}_{ymax}={N}_{THmax}/{I}_{YY}=\mathrm{Acc}=0.00148\ \mathrm{rad}/{\sec}^2={0.85}^{{}^{\circ}}{/\sec}^2 $$

For a bang-off-bang minimum-time rotation around Y_B, we assume 70% of reaction wheel angular momentum is still available to do the maneuver (20% of each reaction wheel’s angular momentum is used to bias the tetrahedral configuration, and 10% is available to compensate for external disturbances). The bang-off-bang minimum-time angular rate rotation profile is shown in Fig. 16. The time to accelerate at maximum torque to ω_ymax is t_a = 3.0/0.85 = 3.5 seconds, and the pitch rotation angle to t_a is θ_a = 0.5ω_ymaxt_a = 5.25^°. The deceleration phase of the rotation profile will take similar time and angle as the acceleration phase; thus the coasting phase for a 30° pitch rotation will take t_c = (30^° – 2θ_a)/ω_ymax = 6.5 seconds. Therefore, the minimum final time for a 30° pitch rotation will be ${t}_f=2{t}_a+{t}_c=7+6.5=\underline {13.5\ \mathrm{seconds}}$. Similar calculations for a 30° roll rotation (X_B axis), where the ω_xmax ≈ 2.8^°/ sec , t_a = 3.3 seconds, ϕ_a = 4.6°, and t_c = 7.4 seconds, give a minimum final time t_f = 14 seconds. Both these rotation times are less than the requirement of 20 seconds specified in the beginning of this section.

Fig. 16

Pitch angular rate profile during a minimum-time slew maneuver

8 ADCS Sensor and Actuator Hardware

The ADCS sensors typically used on small satellites are limited by mass, volume, and power constraints. Over the last couple of years, the available technology has improved and became more compact and lower power due to an increase in the density of semiconductor integrated circuits and advances in MEMS technology and nanomechanics. Therefore, most ADCS sensor and actuator types flying on larger satellites can now be found in miniaturized form for small satellite use. Although their performance in some aspects are still not the same as their larger and more power hungry bigger brothers, the gap is slowly closing, i.e., where the laws of physics do allow it. The next section will present some examples of these small satellite ADCS components that are available commercially and successfully used in various small satellite missions.

8.1 3-Axis Magnetometers

Fluxgate 3-axis magnetometers give the best noise performance, and their sensitivity and bias errors with temperature are better compared to MEMS type magnetoresistive and magneto-inductive sensors typically used in nanosatellites. The MEMS types with build-in bias and temperature correction circuitry and calibration equations have been used successfully on nanosatellites. For most magnetic control ADCS systems where accuracy is not a hard requirement, the MEMS type magnetometers are ideally suited with their inherent small size and low-power specifications. Table 3 compares the performance parameters of magnetometer types typically used on small satellites.

Table 3 Performance parameters of some 3-axis magnetometer types

To reduce the influence of magnetic disturbances from the spacecraft bus, it is advisable to mount magnetometers on the external facets of the satellite and sometimes have them deployable; see Fig. 17 for a 3-axis microsatellite fluxgate magnetometer and a nanosatellite deployable 3-axis MEMS magnetometer.

Fig. 17

Magnetometers: Left, fluxgate (Bartington), and right, CubeSat deployable MEMS (CubeSpace)

8.2 Sun Sensors

The sun as a bright inertial object in the celestial sky is perfectly suited for accurate attitude vector measurements using a relative low cost, mass, and power-type sensing device. Sun sensors vary from planar photodiodes or solar cells where the short circuit current is measured to get a value proportional to the cosine of the sun angle to the surface normal. Six of these sensors mounted with unobstructed hemispherical view each on the facets of a box-type satellite will always give the components of the sun direction vector from up to three sensors facing the sun. Due to earth albedo absorption and a non-ideal cosine response (due to reflections at low angles from the sensor surface), the sun vector accuracy from these coarse sensors is at best about ±5°, but mass and power are negligible. Higher accuracy sensors often make use of MEMS position-sensitive detectors (PSD) and optical windowing to give a sun direction vector measurement from the sun azimuth and elevation measurement angles. Table 4 gives some performance parameters of commercially available sun sensors and Fig. 18 show images of these sensors.

Fig. 18

Digital 2-axis sun sensors: Left, NFSS-411 (NewSpace), and right, SSOC-D60 (Solar MEMS)

Table 4 Performance parameters of high accuracy sun sensors for small satellites

8.3 Star Trackers

The most accurate attitude sensors used on small satellites are star trackers. They are sensors with very sensitive light detectors, typically charge-coupled devices (CCD); in some case these sensors are also cooled to reduce the thermal noise for an increased signal-to-noise ratio. The FOV of these sensors depends on the visual magnitude (M_v) stars that can be detected, e.g., for a CCD detector sensitive enough to see a 6.5 M_v star, a FOV of 15° will ensure at least three stars to be visible for more than 99% of the celestial sphere. The stars detected in the FOV will be slightly defocused to enable the star centroid to be accurately determined using a center of gravity method. The separation distances (angles) between all the measured stars are then matched to reference stars in an onboard star catalogue. For example, a unique match will be detected when a matching triangle can be found of three measured and reference stars. All other visible star separation angles will then be matched to generate the maximum number of measured stars in the SBC frame and reference stars in the ECI frame for star tracking.

After the initial processing intensive “lost-in-space” matching process, successive measurements will only be used to track their matched reference stars by searching in a small region around their previous position, assuming a slow rotating satellite. The tracking process is processing less intensive than star matching, and this enables most star trackers to generate vector pair solutions typically between 1 and 10 Hz for further attitude and rate determination use in an EKF estimator. Star trackers on larger satellites have typical RMS accuracies of less than 5 arcseconds in the boresight direction and 15 arcsec in boresight rotation. This performance is made possible by high-quality low distortion optics and very sensitive star detection. For nanosatellites the high CCD power requirement and large optics with sun and earth blocking baffles are inhibiting factors. However, a few nano-sized star trackers have already been developed and some also successfully flight qualified. See Table 5 for typical performance specifications of these small satellite star trackers; Fig. 19 shows images of these accurate sensors.

Table 5 Performance parameters of typical star trackers for small satellites

Fig. 19

Star Trackers: Left, Auriga (Sodern), and right, MAI-SS (Adcole Maryland)

8.4 Angular Rate Sensors

Accurate measurement of the inertially referenced low angular rates of small satellites, during 3-axis stabilization, is possible using low measurement noise and low bias drift fiber-optic gyroscopes (FOG). The development of MEMS rate sensors is continuously improving, almost matching the performance of lower cost FOGs. To measure the initial high tumbling rates of nanosatellites, MEMS rate sensors can be utilized effectively. Table 6 gives a performance comparison between a tactical grade FOG sensor, high-performance 3-axis MEMS angular rate sensor, and an integrated circuit packaged MEMS rate sensor; it is clear that the performance gap is reducing. Fig. 20 show images of these angular rate sensors.

Fig. 20

Single axis angular rate sensors: Left, μFORS-3 U (Northrop Grumman), and right, STIM300 (Sensonor)

Table 6 Performance parameters of typical angular rate sensors for small satellites

8.5 Magnetorquers

Actuators to generate magnetic moments for interaction with the geomagnetic field can easily be scaled for small satellite use. Magnetic torquer rods are preferred due to their smaller volume, power, and mass compared to torquer coils, but sometimes due to layout problems, air-core coils will be used. Torquer rods make use of a low remanence ferromagnetic core, e.g., MuMetal or Supra-50 alloys are suitable. Torquer rods will give a magnetic moment amplification of 80 to 120 compared to an air-core coil; therefore they use less current and power and a smaller enclosed area for a similar magnetic moment. The physical placing of the torquer rods are critical as they can influence each other, and the direction of the generated magnetic moment can rotate, especially if they are separated by distances less than a rod length (except for a symmetric T-configuration, see Fig. 21). By pulse width modulation of the X_B, Y_B, and Z_B magnetorquer currents, a magnetic moment vector in any desired direction and size can be produced. Table 7 show typical performance parameters for these small satellite magnetorquers.

Fig. 21

Magnetorquers: Left, NMTR-X (NewSpace), and right, CubeTorquer (CubeSpace)

Table 7 Performance parameters of typical magnetorquers for small satellites

8.6 Reaction/Momentum Wheels

Reaction/momentum wheels are actuators that operate using the principal of preservation of angular momentum, to exchange the controlled angular momentum in the wheel disc’s rotation speed to the body of the satellite. A reaction wheel assembly normally consists of a brushless DC motor (BDCM) with a shaft-mounted disc acting as a flywheel. The flywheel’s speed is accurately measured with a shaft encoder to enable a feedback speed control system for accurate angular momentum control. The flywheel’s size is chosen according to the momentum storage requirements of a satellite in a specific orbit. The BDCM torque is selected to meet the agility requirements during rotation maneuvers, i.e., how fast the satellite body must rotate during these maneuvers. Precise speed control with optimized low-power requirements and small volume and mass are the driving factors for the wheel choice on small satellites.

The difference between reaction wheels and momentum wheels lies only in the application of the wheel’s angular momentum to control the satellite’s attitude. A reaction wheel operates in a near-zero momentum bias configuration, i.e., to limit the gyroscopic torques caused by an angular momentum vector during 3-axis attitude rotations. A momentum wheel operates around an offset speed to give an angular momentum bias to the satellite’s body for gyroscopic stiffness. This means a momentum wheel will control the satellite’s attitude actively in the wheel spin axis direction through momentum exchange (by varying the wheel speed) and passively through gyroscopic stiffness by keeping the attitude in the other two axes.

For a full 3-axis rotation capability, a minimum of three reaction wheels will be required, and the wheel speeds will be controlled around zero average speed. For redundancy reasons and to enable offset wheel speeds (to avoid the wheel torque disturbances at zero speed crossings), more than three reaction wheels can be used while still ensuring a zero average momentum vector applied to the satellite body. For example, four reaction wheels can be used in a forth skewed wheel, tetrahedral, or pyramid configuration (see Fig. 15 for a tetrahedral cluster).

Commercially available small satellite wheels are high-performance micromechanical devices, e.g., they are balanced to low static and dynamic specifications to limit wheel vibrations affecting the payload performance, they use special vacuum-rated bearings to ensure a long life in space, and they have to survive the launcher forces and vibrations. The typical performance specifications of these small satellite wheels vary according to their momentum storage capability; see Table 8 and Fig. 22.

Table 8 Performance parameters of typical reaction/momentum wheels for small satellites

Fig. 22

Reaction/momentum wheels: Left, VRW-1 (Vectronic), and right, CubeWheels (CubeSpace)

8.7 Integrated ADCS Modules for NanoSats

A few complete ADCS solutions are commercially available for nanosatellite missions:

• (A) The MAI-500 unit from Adcole Maryland Aerospace is a 0.6 U CubeSat-sized ADCS featuring two star trackers. It has a total mass of 1049 g and size of 100 × 100 × 62.3 mm. The average power consumption during nadir pointing is 2130 mW and specifies a pointing accuracy of 0.1°. See Fig. 23 for a photo of the MAI-500 unit.

• (B) The Y-Momentum CubeADCS (CubeSpace) was originally developed for the QB50 mission. A 3-axis reaction wheel integrated ADCS bundle was since developed for higher accuracy pointing capability. These integrated ADCS units are currently flying successfully on several 2 U, 3 U, and 6 U CubeSat missions. An integrated 3-axis CubeADCS flight unit is shown in Fig. 24. It has a total mass of 554 g and size of 96 × 96 × 62 mm to fit into a 0.6 U CubeSat volume. The average power consumption is 571 mW. It is a 3-axis reaction wheel unit with nadir, sun, moon, and ground target pointing capability. It uses Y_B and Z_B magnetic torquer rods plus a X_B torquer coil, 3-axis MEMS rate sensors, coarse sun sensors, and deployable 3-axis magnetometer during low-power angular rate detumbling and safe mode control. For higher pointing (< 0.1° 3-σ) and tracking performance, a CubeSense fine sun and nadir sensor and CubeStar star tracker with stellar gyro capability can be added. A space GPS receiver can also be seamlessly integrated to these units. Various state estimators including a full state and gyro-based extended Kalman filter are implemented to enable the quaternion feedback reaction wheel controllers to do autonomous attitude control.

• (C) The iADCS100 (Hyperion) was initially developed to be the most compact high-performance ADCS for 1 U to 3 U CubeSats. The launching customer was the AALTO-1 satellite, launched in June 2017. The unit’s layout is shown in Fig. 25. It has a total mass of 400 g, depending on the wheel momentum storage. The size of 95 × 90 × 32 mm will fit into a 0.3 U CubeSat volume. The nominal power consumption is 1400 mW. It is a three-reaction wheel unit with 3-axis target, nadir, and sun-pointing capability. It uses three magnetorquers and a built-in magnetometer for attitude detumbling and safe mode control. For ADCS sensors a ST200 star tracker, 3-axis MEMS rate sensors and plug-in sun sensors are used.

Fig. 23

MAI-500 ADCS unit for CubeSats (Adcole Maryland)

Fig. 24

CubeADCS 3-axis unit for 2 U to 6 U CubeSats (CubeSpace)

Fig. 25

iADCS100 integrated ADCS unit for 1 U to 3 U CubeSats (Hyperion)

9 Future Directions

The ADCS of small satellites is constantly improving as nanotechnology and onboard processing capability enable the miniaturization of hardware and the implementation of more advanced software algorithms. As mentioned in the introduction, most nanosatellites are now launched with full 3-axis attitude control capability. The pointing accuracy and stability of small satellites are approaching the performance previously possible only on large satellites. With the improvements in ADCS, more challenging applications, e.g., as found in space astronomy, can now be implemented on small satellites only limited by the payload mass, volume, and power requirements.

Research and improvements in small satellite propulsion systems (e.g., pulse plasma thrusters – PPTs) and accurate, agile actuators (e.g., control moment gyros – CMGs) are still required to further expand their future ADCS capability. However, missions requiring formation flying and large constellations of small satellites are becoming a current reality due to the lowering of costs and the increase in ADCS performance now possible.

10 Cross-References

• Flight Software and Software-Driven Approaches to Small Satellite Networks

• High Altitude Platform Systems (HAPS) and Unmanned Aerial Vehicles (UAV) as an Alternative to Small Satellites

• Hosted Payload Packages as a Form of Small Satellite System

• Network Control Systems for Large-Scale Constellations

• Overview of Small Satellite Technology and Systems Design

• Power Systems for Small Satellites

• RF and optical Communications for Small Satellites

• Small Satellite Antennas

• Small Satellite Constellations and End-of-Life Deorbit Considerations

• Small Satellite Radio Link Fundamentals

• Small Satellites and Structural Design

• Spectrum Frequency Allocation Issues and Concerns for Small Satellites