Investigations of masonry churches seismic performance with numerical models: application to a case study

Abstract

Recovering and preserving ancient churches is necessary to ensure the transmission of this cultural heritage to the future generations. To this scope, it is necessary to evaluate their performance in seismic prone areas, to design interventions capable of reducing their vulnerability ensuring also their safety use for the faithful. In this paper, investigations on seismic performance of masonry churches are illustrated by applying two different numerical methods on a case study, an existing brick masonry church. The seismic assessment is conducted by applying two simplified methods proposed by the current Italian Directive containing the Guidelines for assessment and reduction of cultural heritage seismic risk. Moreover, linear kinematic analysis is used also for investigating the influence of main parameters governing to the main façade simple overturning and narthex longitudinal response. The investigations performed highlight that the activation multiplier of macro-element response mechanism may significantly vary according to the assumptions made and that also, as narthex longitudinal response, a minimization procedure of the activation multiplier is required.

1 Introduction

Nowadays the scientific community shows a growing attention for the protection of cultural heritage, especially in seismic areas, to avoid damage and/or collapse of buildings having a great cultural importance, with consequent loss of priceless heritages and human lives. In particular, the development of risk assessment procedures and management plans aimed at conservation of cultural heritage involve experts with different backgrounds. According to this, several documents were published by many scientific and cultural organizations, such as UNESCO [1], International Council on Monuments and Sites [2], the International Centre for the Study of the Preservation and Restoration of Cultural Property [3], the risk identification atlas developed by Mexican Centre for Disaster Prevention [4], and the development of territorial information systems for the knowledge of the damage risks of the tangible cultural heritage [5].

To date, in the published literature, several methodologies have been proposed to assess seismic performance of existing structures having historical value, such as for ancient churches, with a different refinement level.

Among the others, as presented in [6] and [7], a preliminary structural assessment of historical buildings may be carried out through a knowledge-based approach, validated on four case studies, and capable of identifying any local mechanism and vulnerability element. A specific methodology aimed at recognizing the collapse mechanisms of church architectural elements is proposed in [8]. In this study, the systematic observation of the structural damage discussed in [9] after the Italian Friuli earthquake is considered for demonstrating that the seismic response of these elements is almost autonomous from the whole building. In [10] a two-steps procedure is proposed by considering several case studies and comparing the numerical predictions with the observed seismic damage after the 2009 L'Aquila earthquake. Whereas, in [11] a limit state analysis of an ancient buildings stock is performed, to identify the weaknesses and vulnerabilities of these existing buildings by proposing, as well, fragility curves useful for seismic risk analysis. Comparison among numerical results obtained with simplified and refined approach is discussed in [12], where also the importance of implementing finite element models is discussed for designing required interventions. Refined numerical investigations are presented also in [13] to analyze the failure mechanisms with the damage amplification to design retrofitting intervention. Similar approaches may be found in [14] and [15], where the nonlinear dynamic behavior of towers is predicted and discussed. The importance of non-destructive tests results in implementing numerical models is discussed, for instance, in [16] and in [17] where models are chosen taking into account the detected damage for programming the required interventions.

Recently, in the Italian Directive [18] a multi-level approach is proposed, consisting of three levels of evaluation and permitting to assess churches seismic vulnerability with an increasing refinement level. A comparison among the results obtained by applying these levels of evaluation is discussed in [19] and [20], where two samples of case studies are chosen to assess the seismic response of ancient masonry churches located in Matera. The same procedure may be also implemented in different structures, as reported in [21], where the seismic performance of a multi-span masonry arch bridge is evaluated through numerical analyses having different refinement level.

In this framework, the present work deals with the seismic vulnerability assessment of an existing brick masonry church according to the multi-level approach proposed by the Italian Directive [18]. The case study chosen is the San Rocco Church, located in Pisticci, Italy, built in 1930s. Firstly, the Level of Valuation 1 (indicated as LV1 method) is used for the church and more accurately for the bell tower considered independent on the church. Then, a more refined assessment is performed through the Level of Valuation 2 (indicated as LV2 method) using the macro-element approach, as it will be later discussed. In particular, main façade simple overturning and narthex longitudinal response are investigated in detail with the linear kinematic analysis to study the influence of the main parameters governing the mechanism activation.

2 Seismic assessment methods

The Italian Directive [18] contains Guidelines for evaluation and reduction of seismic risk of cultural heritage. It has been issued with the intent to guide designers in a knowledge path, to assess seismic performance and to design interventions of a cultural heritage. In accordance with this document, three distinct evaluations levels are indicated, requiring an increasing information level and refinement (in terms of geometrical and construction details, and materials characterization), and indicated briefly as LV1, LV2 and LV3. Basically, they are developed starting from the fact that, as observed from the systematic analysis of damages suffered by ancient churches during the last Italian seismic events, structural damage is redundant arising only in some architectural portions called macro-elements. It was observed that seismic response of the macro-elements (such as façade, aula, apse, bell tower, dome, triumphal arch) was substantially autonomous from the church as a whole, and that damage was lumped only in the most vulnerable response mechanisms of these macro-elements. In [22], a correlation between macro-seismic intensity and damage is carried out through an inspection related to several Italian churches aimed to the identification of macro-elements and their damage level. After this survey, in [23], the specific vulnerability of each possible collapse mechanism is evaluated. The macro-element approach, developed for Italian churches, has been also recently extended to Mexican churches, where additional macro-elements with respect to the Italian churches have been also identified [24].

The LV1 method permits a qualitative analysis for evaluating a global seismic performance of a certain manufact, and is particularly useful for territorial evaluations. The strategy of proposing a unique index measuring the church seismic vulnerability is largely applied within the scientific literature. For instance, in [25], three simplified indexes are proposed and combined each other to study the seismic assessment of masonry buildings through a fast screening and to prioritize deeper investigations. These three safety indexes are applied on two databases including several churches in [26], providing results highly influenced by the buildings geometry and construction details. Also, in [27], the buildings architectural features are of great importance to investigate the seismic vulnerability and risk and to program interventions following a priority scale. Instead, in [28], the seismic vulnerability on large scale of masonry building aggregates is evaluated through a speedy procedure supported by the finite element method. In [29], two case studies severely damaged by the 2012 Emilia earthquake are analyzed and a comparison between the numerical results and the damage observed is provided. A more complete statistical procedure is applied in [30] to assess the seismic risk of a sample of unreinforced masonry churches and the vulnerability modifiers influencing the observed collapse mechanisms.

Whereas, the LV2 method is devoted to more punctual analyses evaluating the local response of a certain portion of a structure, based on the macro-elements approach allowing of designing required interventions. A crucial point is represented by the macro-element identification, that is strictly depending on structural details such as existing cracking patterns, connections among elements, techniques and construction sequences. Several studies have been published, focused on different aspects influencing the seismic behavior of structure portions. For instance, the overturning mechanism and its interaction with orthogonal walls are investigated in [31] and [32]. More in detail, in [31], the façade overturning due either to a vertical crack at the connection or a diagonal crack on the transversal wall is examined. While, in [32], a simple analytical model is developed to calculate load factors related to various collapse mechanisms involving wall assemblies. The compressive strength influence in a two-blocks mechanism out-of-plane overturning is studied in [33].

Finally, the LV3 method implies implementation of refined numerical models and represents the most refined model for predicting the seismic response of a church. The application of this method is out of the aim of the present work.

2.1 LV1 method

The LV1 method provides the church vulnerability index i_v from which the ground acceleration corresponding to the achievement of damage limit state (DLS) and life-safety limit state (LSLS) may be estimated. This method is particularly useful for evaluations at a territorial scale since, using qualitative and not quantitative data collected after a survey, provides the ground acceleration through empirical relationships established from the observed damage on Italian churches due to the earthquakes occurred in the past. Therefore, this method estimates a global performance of a church, that is correlated to a vulnerability index. Finally, with this method it is not possible of designing any structural intervention.

As for the vulnerability index i_v, it may range between 0 and 1, and is defined with the expression:

$${i}_{v}=\frac{1}{6}\frac{\sum_{k=1}^{28}{\rho }_{k}\left({v}_{ki}-{v}_{kp}\right)}{\sum_{k=1}^{28}{\rho }_{k}}+\frac{1}{2}.$$

(1)

The Eq. (1) represents a weighted average among the vulnerabilities extended to all 28 damage mechanisms of the macro-elements. If some macro-element is not present, then, the summation of the Eq. (1) is extended only to the macro-element damage mechanisms that may activate. ρ_k is the weight assigned to each collapse mechanism, corresponding to: 0 if a mechanism is not present or not active, or between 0.5 and 1 in the other cases. The weight ρ_k = 1 is assigned to the main damage mechanisms of macro-elements (façade overturning, aula transverse response, triumphal arch response), while for other damage mechanisms (such as prothyrum—narthex response, transept, chapels mechanisms, etc.) a weight comprised between 0.5 and 1 may be assigned case by case in relation with the macro-element importance within the church examined. v_ki and v_kp are, respectively, the scores assigned to the vulnerability and to any seismic-resistant device (if present) of the k-th considered mechanism.

Then, through Eqs. (2) and (3) the seismic capacity in terms of ground acceleration for DLS and LSLS may be calculated [18]:

$${a}_{DLS}S=0.025\bullet {1.8}^{2.75-3.44{i}_{v}}, (g)$$

(2)

$${a}_{LSLS}S=0.025\bullet {1.8}^{5.1-3.44{i}_{v}}, (g)$$

(3)

where S is the stratigraphic amplification depending on the foundation soil.

Usually, the seismic capacity previously estimated may be compared with the expected demand. To this scope, a verification ratio is introduced, that may be expressed directly in terms of acceleration, depending on the limit state (LS) considered (DLS or LSLS). This ratio, indicated as acceleration factor f_a,LS, is given by the ground acceleration corresponding to the achievement of the LS (a_LS) over the expected one (a_g,LS) having a reference return period (T_R,LS), both referred to rigid soil:

$${f}_{a,LS}=\frac{{a}_{LS}}{{a}_{g,LS}}.$$

(4)

Alternatively, the verification ratio may be calculated in terms of return period related to the seismic capacity and to the expected seismic action. This ratio defined as safety index I_S,LS may be calculated as follows:

$${I}_{S,LS}=\frac{{T}_{LS}}{{T}_{R,LS}},$$

(5)

where T_LS is the return period associated to the ground acceleration associated to the seismic capacity a_LS (for LSLS or DLS), and T_R,LS is the return period of the expected seismic action (a_g,LS). By knowing a_LS, the related T_LS may be calculated with the following expression:

$${T}_{LS}={T}_{R1}\bullet {10}^{log\left({T}_{R2}/{T}_{R1}\right)\bullet log\left({a}_{LS}S/CF{a}_{1}{S}_{1}\right)/log\left({a}_{2}{S}_{2}/{a}_{1}{S}_{1}\right)},$$

(6)

where a₁S₁ and a₂S₂ are the ground accelerations (from the seismic hazard map) multiplied to the stratigraphic amplification S in which a_LS is included; T_R1 and T_R2 are the related return periods; CF is the Confidence Factor defined as function of the structure knowledge level [18]. Whereas, T_R,LS may be calculated with the Eq. (7), where V_R is the reference period, and P_VR the probability of exceedance associated to the limit state, corresponding to 61% and 10% for damage limit state and life-safety limit state, respectively.

$${T}_{R,LS}=-\frac{{V}_{R}}{\mathrm{ln}\left(1-{P}_{{V}_{R}}\right)}.$$

(7)

For both verification ratios, if the required seismic protection level is satisfied for a certain LS both the safety index I_S,LS and the acceleration factor f_a,LS result greater than the unity.

2.2 LV2 method

The LV2 method is applied when seismic assessment and interventions design are conducted by referring to architectural elements structurally independent on the entire construction (named macro-elements) that may have different failure mechanisms under seismic lateral loads. With this method it is necessary to consider the construction history and any cracking pattern so that each singular macro-element may be correctly identified. Contrarily to the LV1 method, this method has the advantage of locally evaluating the seismic response of all the macro-elements response mechanisms, defining among them the most vulnerable one. Consequently, this method permits to evaluate more accurately the seismic performance of a church, allowing also of designing the required local interventions. A crucial point in the application of the LV2 method is represented by the macro-elements choice, whose seismic response may be considerably influenced by the boundary conditions. However, for simplicity, very frequently a conservative approach is followed so that the boundary conditions are defined by neglecting all the secondary contributions that would increase the activation multipliers.

This method implies the linear kinematic analysis application, where the macro-element failure mode may be schematized as a rigid blocks chain, externally and internally connected by flexural hinges supposed to be placed where the most likely crack formation may occur, by assuming that [34]: the masonry has infinite strength in compression, no strength in tension, and any sliding among the rigid blocks is excluded. A lateral force system, proportional to the masses, is increased until the structural instability arises for an inadmissible thrust line.

According to this method for a certain lateral response mechanism, the activation multiplier α₀ may be found by means of the Theorem of Virtual Works [18], and then the related spectral acceleration a₀^* is calculated by referring to an equivalent non-linear single degree of freedom system (SDOF) through the standard modal analysis principles:

$${a}_{0}^{*}=\frac{{\alpha }_{0}\sum_{i=1}^{n+m}{P}_{i}}{{M}^{*}CF}=\frac{{\alpha }_{0}g}{{e}^{*}CF},$$

(8)

where g is the gravity acceleration; $\sum_{i=1}^{n+m}{P}_{i}$ is the dead weights sum whose masses produce horizontal inertial forces under seismic action, involved into the kinematic chain; CF is the Confidence Factor [18].

The seismic spectral acceleration a₀^* represents the capacity of the mechanism considered that should be compared with the related demand. Note that, according to Eurocode 8 [35], the failure mechanism beginning is associated to the DLS.

According to the Italian Design Code [36], safety verifications for DLS and LSLS have to be conducted by referring to the a₀^*. In particular for DLS and macro-elements directly connected at ground level it should be verified that:

$${a}_{0}^{*}>{a}_{g}\left({P}_{VR}\right)\bullet S,$$

(9)

where ${a}_{g}\left({P}_{VR}\right)\bullet S$ is the earthquake spectrum demand corresponding to the expected Peak Ground Acceleration depending on the site seismic hazard. ${a}_{g}\left({P}_{VR}\right)$ is related to the exceedance probability within the reference life (V_R), and S is the stratigraphic amplification associated to the foundation soil. When the macro-element is not directly connected to the ground floor (such as, for instance, the gable overturning), the dynamic amplification of the response should be taken into account. Considering that the mechanism is placed at a certain height z with respect to the ground, the verification may be conducted as follows:

$${a}_{0}^{*}>{S}_{e}\left({T}_{1}\right)\bullet \psi \left(z\right)\bullet \gamma ,$$

(10)

where ${S}_{e}\left({T}_{1}\right)$ is the spectral ordinate related to the assumed seismic protection level (through P_VR considered into V_R) for T₁ (the vibration period of the entire structure along the considered direction); $\psi \left(z\right)$ is the first vibration mode normalized at the structure top. In absence of more accurate evaluation, it may be assumed that $\psi \left(z\right)=z/H$, where H is the structure height respect to the foundation floor; z is the height of the constraints barycenter of rigid blocks involved into the mechanism; γ is the corresponding modal participating coefficient that, in absence of more accurate evaluations, may be assumed equal to $\gamma =3N/\left(2N+1\right)$ where N is the number of structure stories. For the churches typology, it is suggested the following relationship for the fundamental period T₁ [37]:

$${\mathrm{T}}_{1}=0.07{H}^\frac{3}{4},$$

(11)

where H is the height of the structure up to the eave line.

Whereas, in the case of LSLS, the safety verifications have to be performed by considering the behavior factor q. In accordance with this method, if the rigid blocks are ground-connected it must be verified that

$${a}_{0}^{*}>\frac{{a}_{g}\left({P}_{VR}\right)\bullet S}{q},$$

(12)

where the symbols are the same of the Eq. (9), and q is the behavior factor measuring the dissipative capacity of the considered mechanism, that may be assumed equal to 2 according to [36] and [38].

In the case of macro-element placed at a certain height and not directly ground-connected, in addition to the Eq. (12), it has also to verify for the LSLS that:

$${a}_{0}^{*}>\frac{{S}_{e}\left({T}_{1}\right)\bullet \psi \left(Z\right)\bullet \gamma }{q},$$

(13)

where symbols are described for the Eq. (10).

3 Case study: San Rocco Church in Pisticci

San Rocco Church is located in Pisticci, in province of Matera (Italy). In the past, where actually we can find the church there was a previous Purgatory Church, built between 1742 and 1747, that was demolished together with the adjacent house for constructing the current church studied in this paper.

San Rocco Church was designed by the architect Ernesto Lapadula with engineer Nunzio Di Tursi, and constructed between 1930 and 1933. Unfortunately, just after 20 years, the church suffered structural damages, due to subsoil settlements originated by an alleged underground spring water passing exactly under the church. In the ‘70 s, several interventions were done to repair these structural damages that, however, appeared again so that since 2011 the church was definitively closed to public worship. To date, long and deep cracks affect the main nave wall behind the altar and the right lateral wall (for who has the main façade at the back) [39].

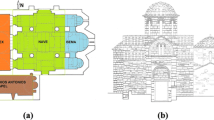
Current images of San Rocco Church are reported in Fig. 1. In particular, Fig. 1a shows an external view of the church, where it is possible to note the important narthex connected to the main façade. Whereas, Fig. 1b–c illustrates two internal views of the main nave: Fig. 1b was taken looking at the main façade (the altar was on the right), while Fig. 1c reports an important diagonal crack running on the wall behind the altar. Finally, Fig. 1d shows another external view, in particular a side view looking at the bell tower.

Fig. 1

a Frontal view of San Rocco Church, b internal view looking at the main façade, c diagonal crack interesting the wall behind the altar, and d bell tower

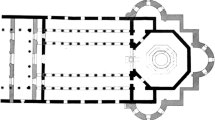
The church has in plan a central nave with two lateral naves (Fig. 2a), having the particularity that the plan tripartition does not coincide with the main façade tripartition: in fact, the three narthex arches do not correspond to the three internal naves, but they entirely fall within the central nave.

Fig. 2

San Rocco Church: a plan, b transverse section and c longitudinal section

The main nave, 7.86 m width and 9.53 m height, is separated from the lateral naves by masonry columns having section of 0.58 m × 0.43 m with a different height: 5.23 m in the lateral naves and 7.43 m in the presbyterial area (Fig. 2b), supporting barrel vaults covering the lateral naves mounted on IPE 200 steel beams (Fig. 2c). Finally, base floor consists of the following layers: marble tiles of 20 cm × 20 cm; compacted concrete of 8 cm thickness; compacted soil with cement-based pozzolana of 15 cm thickness; crawl space filled with dry stone contacting the ground.

In summary, the characteristics of the considered church may be summarized as follows:

• Plan configuration: basilica plan configuration inscribed in a rectangle of 20.76 m × 13.04 m.

• Roof structures: main nave is covered by horizontal concrete floor with hollow lightening clay blocks having 44 cm of thickness reaching the height of 10.75 m. On this floor there are masonry pillars and IPE 160 beams above them supporting the gable roof, consisting of wooden beams and clay roof tiles, reaching the height of 12.26 m. The lateral naves are covered by brick masonry vaulted structures up to a height of 9.96 m.

• Bell tower: a brick masonry bell tower incorporated in the church plan. It has a base of 2.85 m × 2.72 m, a total height of 18.50 with walls up to a thickness of 55 cm, and reaching the maximum height of 19.55 m. It is characterized by a belfry 2.97 m height with single lancet window surmounted by a four-pitched roof.

• Foundations: continuous foundations made of solid bricks, without internal core, at variable heights according to the ground slope, along the entire church perimeter and also present, for transverse connection, below the naves columns.

• Structural interventions: there is no structural intervention with the aim of reducing the seismic vulnerability.

Vertical walls are made with mortar and bricks units without any internal core. Mortar joints have 1 cm thickness, while solid bricks have dimensions of 6 cm × 13 cm × 26 cm and arranged in multiple-leaves up to 55 cm of thickness. By analyzing a single masonry panel of a surface of 1 m × 1 m (Fig. 3) it can be deduced that the texture is of good quality since: 77% of bricks and 23% of mortar are present (Fig. 3a-b); mortar joints are horizontal (Fig. 3c) with no vertical alignment (Fig. 3d).

Fig. 3

Masonry texture: a picture of masonry panel from the south-west façade, b schematization of the masonry panel, c horizontal mortar joints and d vertical mortar joints

3.1 Seismic action definition

In this study, the seismic action is defined through a response spectrum for the two limit states considered, that are the damage limit state (DLS) and the life-safety limit state. (LSLS).

To define the seismic action, a nominal life V_N equal to 50 years is assumed by supposing, due to the structure importance, a coefficient of use of C_U = 1.5. Therefore, the observation time (reference period) for the seismic action has been assumed equal to V_R = 75 yrs.

As for the seismic hazard, Matera falls within a moderate seismic prone area, since in the past only moderate seismic events occurred. According to the Italian Seismic Code [40] a return period of T_R = 75 yrs and of T_R = 712 yrs has to be considered for DLS and LSLS, respectively. The response spectra of the horizontal component are reported in Fig. 4a, by considering, as indicated in [41] a damping ratio equal to 10% for masonry structures. Further, the design spectrum refers to the LSLS by assuming, as indicated in the Italian Instructions for the application of the Ministerial Decree M.D. (2008 and 2018), a behavior factor q = 2.

Fig. 4

a Elastic and design spectra of the seismic action horizontal component for DLS and LSLS, b expected Peak Ground Acceleration a_g versus return period T_R (in semi-logarithmic scale)

In Fig. 4b, the ground acceleration on rock soil a_g is reported in logarithmic scale of return period T_R. In the same figure, the values of a_g for all LS considered by the Italian Design Code [40] are reported. In particular, for DLS a_g,DLS = 0.054 g, while for LSLS a_g,LSLS = 0.111 g.

3.2 Application of the LV1 method

3.2.1 Church seismic assessment

To assess the seismic performance of San Rocco Church, in this study a Confidence Factor CF equal to 1 and a stratigraphic factor S equal to 1.2 are assumed. Seismic performance is evaluated for LSLS (having a probability of exceedance P_VR = 10% in V_R) and for DLS (P_VR = 63% in V_R).

According to this method, Table 1 reports, for each possible damage mechanism that may occur within the church, the related weight ρ_k, and the resulting score for v_ki (vulnerability indicator) and v_kp (seismic-resistant device). Finally, for completeness, also n_i and n_p (number of vulnerability indicators and of seismic-resistant devices) are indicated [18].

Table 1 Evaluation of ρ_k, v_ki and v_kp for each possible damage mechanism of San Rocco Church

Therefore, by applying the Eq. (1) the vulnerability index results i_v = 0.538, leading to the ground acceleration [Eqs. (2) and (3)] a_DLS and a_LSLS summarized in the Table 2. They represent the church seismic capacity DLS and LSLS considered in terms of ground acceleration. These values have to be compared with the corresponding seismic demand a_g, related to the seismic hazard site and previously reported in the Fig. 4b.

Table 2 Ground acceleration corresponding to the achievement of the two limit states considered

In addition, the Table 2 reports as well:

• the factor f_a,DLS (f_a,LSLS) expressing the ratio capacity a_DLSS (a_LSLSS) over demand a_g,DLSS (a_g,LSLSS) in terms of ground acceleration calculated as defined in the Eq. (4);

• the seismic safety index I_S,DLS (I_S,LSLS) given by the ratio between the return period T_DLS (T_LSLS) corresponding to the seismic action a_DLS (a_LSLS) and the reference one T_R,DLS (T_R,LSLS). As for the T_DLS (T_LSLS), the Eq. (5) is applied where a logarithmic interpolation is used within the points defining the site seismic hazard. Note that since to a_DLS = 0.0353 g should correspond to a return period less than 30 years, a T_DLS as indicated by [40] equal to 30 years has to be assumed.

Note that, as summarized in the Table 2, the ratios calculated are greater than 1 only in the case of LSLS. This means that, according to the LV1 method, safety verification is satisfied only for LSLS, while in the case of DLS interventions should designed.

3.2.2 Bell tower seismic assessment

In this study, the bell tower is accurately evaluated also by considering this element independent on the entire church. According to the LV1 method proposed by the Italian Directive [18], a simplified seismic assessment may be carried out by assuming the bell tower as a cantilever subjected to a vertical load (due to its self-weight) and to a set of horizontal forces generated by seismic action. The tower is schematized as a sequence of blocks, where each of them has uniformity of characteristics (of materials and of section geometry). The seismic capacity is assessed by assuming a capacity model where the masonry is partialized resisting only in compression.

Several configurations may be assumed depending on the possible interaction of the bell tower with the surrounding elements, that may reduce its deflection length under seismic action. In particular, in this study two different configurations are assumed, referred to the:

• total height (indicated as Configuration 1), considering the tower as a cantilever free of oscillating in all directions, from the base up to the top having a total length of 18.50 m, neglecting any possible lateral restrain along the height;

• reduced height (indicated as Configuration 2), where it is assumed that the only tower part above the height of 6.84 m is free of oscillating due to the presence of lateral sacristy.

For both the configurations, indicated in the Fig. 5a, four sections are considered (Fig. 5b–e) since along the tower height four different resisting sections may be individuated due to the different configurations provoked by the adjacent structures interaction, that are: Section 1, corresponding to the base section; Section 2, individuated by the interaction with the sacristy on the right; Section 3, at the intersection between the bell tower and the main nave roof; Section 4, representing the belfry base.

Fig. 5

a Bell tower in the two configurations considered (view from south-west side), b Section 1 (base section), c Section 2 at height of 6.84 m, d Section 3 at height of 9.05 m and e Section 4 at height of 14.94 m (belfry base) (dimensions are in meter)

The lateral seismic force applied at each block barycenter F_i, by assuming a linear distribution, may be obtained as follows:

$${F}_{i}=\frac{{W}_{i}{z}_{i}}{\sum_{k=1}^{n}{W}_{k}{z}_{k}}{F}_{h}.$$

(14)

F_h is the base shear calculated as ${F}_{h}=0.85{S}_{e}\left({T}_{1}\right)W/qg$; ${S}_{e}\left({T}_{1}\right)$ is the elastic response spectrum ordinate; T₁ is the fundamental period that may be calculated with the expression $T=0.0187\bullet H$; H represents the tower deflection height, depending on the configuration assumed in the seismic assessment; $W=\sum {W}_{i}$ is the overall weight; W_i and z_i are, respectively, the block weight and barycenter height, the last measured with respect to the ground level assumed; q is the behavior factor that, in this study is assumed, as indicated in Italian Directive [18], equal to 3; g is the gravity acceleration.

Figure 6 shows the forces applied at each block barycenter, obtained through Eq. (14) for the two configurations considered.

Fig. 6

a Configuration 1 and b Configuration 2 assumed with the forces F_i and the shear diagrams

By imposing that in the i-th section the ultimate moment M_u,i is reached, the elastic response spectrum ordinate S_e,LSLS,i corresponding to the LSLS and the related ground acceleration a_LSLS may be calculated as follows [18]:

$${S}_{e,LSLS,i}\left({T}_{1}\right)=\frac{qg{M}_{u,i}\sum_{k=1}^{n}{z}_{k}{W}_{k}}{0.85W\left(\sum_{k=i}^{n}{z}_{k}^{2}{W}_{k}-{z}_{i}^{*}\sum_{k=i}^{n}{z}_{k}{W}_{k}\right)CF},$$

(15)

$${a}_{LSLS}=\frac{{S}_{e,LSLS}}{S{F}_{0}} { T}_{B}\le {T}_{1}<{T}_{C}$$

(16)

$${a}_{LSLS}=\frac{{S}_{e,LSLS}}{S{F}_{0}}\frac{{T}_{1}}{{T}_{C}} {T}_{C}\le {T}_{1}<{T}_{D}$$

(17)

where T_B, T_C and T_D are the response spectrum characteristic periods; $S={S}_{S}{S}_{T}$ is the coefficient taking into account the subsoil category and topographic conditions. In the case analyzed, the Eq. (16) is applied.

As regards ultimate moment M_u,i, it may be calculated as follows, by considering the tower with a hollow rectangular section. By assuming that the acting normal stress is not greater than $0.85{f}_{d}{a}_{i}{s}_{i}$, the ultimate moment M_u,i may be calculated as:

$${M}_{u,i}=\frac{{\sigma }_{0i}{A}_{i}}{2}\left({b}_{i}-\frac{{\sigma }_{0i}{A}_{i}}{0.85{a}_{i}{f}_{d}}\right),$$

(18)

where a_i is the i-th section side, excluding openings, perpendicular to the seismic action direction; b_i is the i-th section side parallel to the seismic action direction; A_i is the i-th section total area excluding any opening; σ_0i is the average normal stress in the analysis section equal to $W/{A}_{i}$, where W is the structure weight above the i-th section; f_d is the masonry design compressive strength: in accordance with the [38] a compressive strength value equal to 3.45 N/mm² is assumed.

In summary, Fig. 7 and Table 3 show the results of the seismic assessment according to the method applied, for the four sections considered in the two configurations assumed. In particular, in the Table 3, the ultimate moment M_u,i, the elastic response spectrum ordinate S_e,LSLS(T₁), the corresponding ground acceleration a_LSLS, the returning period T_LSLS, the safety index I_S,LSLS and the acceleration factor f_a,LSLS are reported. The seismic assessment is conducted separately for both directions x and y, considered acting positive and negative (Fig. 5b-e). The same results are reported in a histogram form in the Fig. 7.

Fig. 7

Configuration 1 and Configuration 2: a and b elastic response spectrum ordinate S_e,LSLS(T₁), c and d ground acceleration a_LSLS, e and f safety index I_S,LSLS, g and h acceleration factor f_a,LSLS

Table 3 Seismic assessment results for each section studied in the two configurations considered

It should be noted that, as it was easy to expect, the Configuration 1 is more conservative with respect to the Configuration 2, since the Configuration 1 resulting values of S_e,LSLS(T₁), a_LSLS, I_S,LSLS, and f_a,LSLS are lower than the ones of the Configuration 2. Moreover, the lowest seismic vulnerability is found along the y direction, and equal for both versus to a_LSLSS = 0.139 g with a return period T_LSLS = 848 years. Anyway, these values yield to an acceleration factor f_a,LSLS and safety index I_S,LSLS greater than the unity. Therefore, the tower would be verified in accordance with the method considered. Note that, due to the low site seismic hazard, in several cases the ground acceleration a_LSLS results greater than the highest one provided by the national seismic hazard map. Therefore, in these cases, as indicated in the Italian Design Code [40], a return period T_LSLS equal to 2475 years is assumed.

3.3 Application of the LV2 method

In applying the LV2 method, some potential failure mechanisms are considered in this study according to the characteristics of the church examined. The linear kinematic analysis is used by assuming, due to the good quality of the masonry investigated, that all masonry portions are composed by rigid monolithic blocks, punctually connected among them and with the ground floor.

In particular, as shown in Fig. 8, the following response mechanisms are investigated through the linear kinematic analysis:

• Main façade simple overturning (Fig. 8a), by neglecting the restraining action due to orthogonal walls. This macro-element is subjected only to the self-weight since no other vertical load due to the main aula roof is present.

• Main façade composed overturning, where a diagonal wedge of the lateral walls is considered (Fig. 8b). In this case, a full connection among the façade and lateral walls is taken into account, differently from the simple overturning mechanism previously considered. Moreover, the vertical load portion acting on the lateral walls involved into the mechanism assumed is considered for calculating the activation multiplier. For this mechanism an inclination of 30° for diagonal wedge is conservatively assumed provided that the higher the inclination the higher the activation multiplier. However, as it will be discussed later, as for the main façade simple overturning the capacity model considered assumes a vertical stair step crack between the façade and the orthogonal wall.

• Narthex longitudinal response, calculated by neglecting the connection with the lateral walls and considering a distributed vertical load at the colonnade top due to the narthex roof (Fig. 8c).

• Colonnade longitudinal response. This mechanism is calculated by considering this macro-element completely independent on the main façade, applying at the colonnade top as well a distributed load representing the main aula roof loads (Fig. 8d).

• South-west façade local (Fig. 8e) and global simple overturning (Fig. 8f). This lateral façade is free of overturning since no interaction with the adjacent building is present. In the case of south-west façade local overturning, only the self-weight of the macro-element is considered. While, in the case of south-west façade global overturning, the vertical load due to the main aula roof is considered. For both the macro-elements, no interaction with orthogonal walls is considered.

Fig. 8

The potential failure mechanisms considered in the case of San Rocco Church: a main façade simple overturning, b main façade composed overturning, c) narthex longitudinal response, d colonnade longitudinal response, e south-west façade local simple overturning and f south-west façade global simple overturning

Further, in this study, the main façade simple overturning and the narthex longitudinal response are investigated in detail as it will be shown in the next paragraphs. As for the former, also walls restraining action is considered, as indicated in the [38]. Whereas, as for the latter the research of the minimum multiplier by varying the relative position of the hinges is illustrated. Discussions about these mechanisms are illustrated in the next paragraphs, while in this section only the minimum values are reported.

Table 4 summarizes the activation multipliers α₀ obtained. In this case, the main façade simple overturning results the most vulnerable mechanism with α₀ = 0.045, while the composed overturning involving lateral walls has an activation multiplier much higher and equal to α₀ = 0.334. It should be remarked that the simple overturning activation multiplier is calculated with a conservative approach where the orthogonal walls restraining action is completely neglecting.

Table 4 Activation multiplier α₀ related to the activation of the considered macro-elements mechanisms

As far as the in-plane response of narthex and colonnade are concerned, activation multiplier equal to 0.047 and to 0.051 are found. They are calculated by varying the relative positions of the internal hinges for minimizing the lateral loads multiplier.

Finally, for the south-west façade, both overturning mechanisms provide quite similar values for the activation multiplier. The minimum value, found in the case of global overturning mechanism, results equal to α₀ = 0.059.

Instead, in Fig. 9a–b the ground accelerations a_DLSS (a_LSLSS) determining the achievement of DLS (LSLS) for each kinematic mechanism considered are represented [Eqs. (9) and (12)]. In this case we found that the minimum a_DLSS (a_LSLSS) is equal to 0.046 g (0.092 g) corresponding to the main façade simple overturning. By comparing these values with the ones obtained with the LV1 method we note that: in the case of LSLS the LV1 method provides values of a_LSLSS equal to 0.168 g for the church and 0.139 g for bell tower. Therefore, for this LS the LV1 method overestimates the seismic response with respect to the LV2 one here discussed, providing a_LSLSS = 0.092 g as the lowest value. On the contrary, as for the DLS, the LV1 and LV2 methods provide a_DLSS values in agreement among them: 0.0424 g in the case of LV1 method, and 0.046 g in the case of the LV2 method. Therefore, this demonstrates that in the case analyzed it is impossible to correlate among them the results obtained with the two methods considered.

Fig. 9

Peak ground accelerations a a_DLSS and b a_LSLSS related to the activation of the considered macro-elements mechanisms respect to the expected accelerations for each Limit State

In the same histogram, it is also reported the seismic demand in terms of ground acceleration, corresponding in the case under consideration to a_g,DLSS = 0.0648 g (a_g,LSLSS = 0.133 g), where S is assumed equal to 1.2. One may note that, with exception of main façade composed overturning and colonnade longitudinal response, in both Limit States considered, and south-west façade local simple overturning in DLS, all the potential failure mechanisms should be activated. Again, the most vulnerable one results the main façade simple overturning.

In the following, the results obtained for calculating the activation multiplier of the main façade simple overturning and narthex longitudinal response are illustrated in detail. As previously stated, in the case of the main façade simple overturning also the activation multiplier variation depending on the restraining wall action is considered. While for the narthex longitudinal response a minimization procedure is applied for researching the minimum activation multiplier.

3.3.1 Main façade simple overturning including orthogonal walls restraining action

In the previous application of the LV2 method, where some potential failure mechanisms are considered, it has been assumed that the façade overturning occurs in the simplest way, that is by neglecting any restraining action due to the presence of the orthogonal walls. Under this simple assumption the main façade monolithically rotates with respect to the base.

However, recently in the [38], a more refined model is proposed, where additional resistant contributions are considered occurring along a hypothetic vertical stair step crack (Fig. 10a) due to the restraining orthogonal walls (F₁) and to an eventual vertical load (F₂).

Fig. 10

a Schematization of vertical stair step crack due to the restraining orthogonal walls (F₁) and to an eventual vertical load (F₂), b deformed configurations at varying z and c activation multiplier α_i

Precisely, the resisting contribution of the lateral walls may be considered unless the construction details permit of concluding that no interaction with transverse walls is present, or else there is an evident detachment from the main façade. The contribution of each lateral wall F₁, that is a stabilizing contribution, may be calculated with a friction model providing, along the crack, a linear horizontal stress distribution, whose resultant may be considered applied at 2/3 h, where h is the wall height, given by the expression:

$$F_{1} = 0.4n\left( {n + 1} \right)\phi \mu l^{2} t_{s} w,$$

(19)

where n is the brick rows number interested by the vertical crack ($n=h/{h}_{b}$, where h_b is the medium height of the masonry elements); l is the single friction joint length, overlap between the bricks of two consecutive rows; ɸ is the damping coefficient, defined as $\phi = h_{b} /l$; µ is the friction coefficient; t_S is the transverse wall thickness; w is the masonry specific weight.

In addition, the resisting contribution F₂ due to the vertical load applied at a certain wall height may be calculated by assuming, again, a friction resistance having a uniform distribution along the height into the horizontal mortar beds involved in the stair step crack. F₂, applied at h/2, may be calculated as:

$${F}_{2}=\mu \bullet \sigma \bullet n\bullet {t}_{s}\bullet l,$$

(20)

where σ is the tension on the transverse wall, given by $\sigma =q/{t}_{s}$ where q is the load applied at the top due, for instance, to a load floor, parapets, etc., and the other symbols are the same of the Eq. (19).

By applying the Principle of Virtual Works, the following expression for the activation multiplier may be derived:

$${\alpha }_{tot}=\frac{{x}_{G}}{{y}_{G}}+\frac{2}{3}\frac{{F}_{1}h}{W{y}_{G}}+\frac{{F}_{2}h}{W{y}_{G}}={\alpha }_{0}+{\alpha }_{1}+{\alpha }_{2},$$

(21)

where W is the main façade self-weight, x_G and y_G are the barycenter coordinates where the W is applied, and the other symbols are indicated in Fig. 10a. Therefore, α₀, α₁, and α₂ may be intended as:

• α₀ is the mechanism activation multiplier in the case of simple overturning considering acting only the wall self-weight;

• α₁ is the increment in terms of activation multiplier due to the stabilizing contribution of the friction resistances of the orthogonal walls;

• α₂ is the increment in terms of activation multiplier due to the stabilizing contribution of the vertical load at top.

By referring to the main façade of the case study considered, for different height z of the hinge (Fig. 10b) the multipliers α₀, α₁, α₂ and α_tot are plotted in Fig. 10c. In this way the possibility that only a façade portion overturning is considered, with a flexural hinge placed at a certain height z. It should be noted that α_tot has a non-linear trend with the height, reaching a minimum value at 9 m. This is due to the fact that, while α₀ increases as the hinge height increases, α₁ and α₂ have, on the contrary, an opposite trend (i.e. they reduce as the height increases). It is important to remark that the obtained results are independent on the dynamic amplification since they refer to the activation multiplier and not to the related ground acceleration.

In the following, starting from the activation multiplier α_tot calculated, the corresponding ground accelerations for the two Limit States a_DLS and a_LSLS are derived. They are calculated starting from the seismic spectral acceleration a_tot,0^* [Eq. (8)], using the Eqs. (9) and (12) for ground-connected (i.e. no dynamic amplification is taken into account) mechanisms, and using the Eqs. (10) and (13) for not ground-connected (i.e. taking into account dynamic amplification). Table 5 summarizes the equations implemented for obtaining the seismic capacity curves reported in the Fig. 11 according to the [36] and [38] formulations. In these equations the following simplified assumptions are made: q is the behavior factor equal to 2; ${S}_{e}\left({T}_{1}\right)$ is the spectral ordinate for the Limit State considered, assumed for simplicity equal to ${a}_{g}S\bullet {F}_{o}\bullet \eta$, where F_o is equal to 2.5, and η is the factor altering the elastic spectrum depending on the viscous damping ($\eta =1/q$); ɣ is the modal participation coefficient, by assumed equal to 1.1; $\psi \left(z\right)$ is the first vibration mode normalized at the top of the structure assumed equal to $\psi \left(z\right)=z/h$, where h is the total height of the façade and z is the height of the constraints barycenter of rigid blocks involved into the mechanism.

Table 5 Equations implemented for calculating the ground acceleration corresponding to the seismic capacity related to both DLS and LSLS

Fig. 11

a Ground acceleration a_DLSS corresponding to the achievement of DLS, b ground acceleration a_LSLSS corresponding to the achievement of LSLS, c ratios of a_totS/a₀S and a_totS/(a₀ + a₁)S for DLS and LSLS

Figure 11 reports the resulting ground accelerations a_DLSS (Fig. 11a) and a_LSLSS (Fig. 11b) found in the case analyzed. These graphs illustrate, for each Limit State and by varying the hinge height at the base, the following ground accelerations values: a₀S derived from α₀ corresponding to the simple overturning (no resistance contributions of orthogonal walls); (a₀ + a₁)S derived from α₀ + α₁ (i.e. including F₁), and a_totS = (a₀ + a₁ + a₂)S derived from α_tot (including both resistance contributions F₁ and F₂). Figure 11a–b also show, for DLS and LSLS, with a marked line the minimum values (between ground-connected and not ground-connected formulations of the Table 5) of a₀S and a_totS. Also, for comparison, the a₀S value calculated for the entire main façade with the hinge at the base is reported (with a vertical dashed line). Firstly, it should be noted that for DLS (LSLS) up to a certain height z the ground-connected assumption for the mechanism considered provides lower values of a_DLSS (a_LSLSS). Moreover, a_totS minimum value reduces as the height hinge increases in both Limit States (Fig. 11a–b). However, as it was easy to expect, a_totS results always higher than a₀S, calculated by neglecting any friction contribution and, therefore, with the most conservative approach. At the base a₀S corresponds to the values reported in the histogram of the Fig. 9 discussed in the previous section.

To better quantify how the considered resistance contributions (F₁ and F₂) influence the resulting seismic capacity of the main façade overturning, Fig. 11c illustrates two different ratios, that are a_totS/a₀S and a_totS/(a₀ + a₁)S, where the ground accelerations considered are the minimum values between ground-connected and not ground-connected formulations of the Table 5. Note that ratios are equal for both Limit States since they are independent on the behavior factor q assumed. As it is clear to observe, at the base a ratio a_totS/a₀S higher than 25 is obtained. While, in the case of a_totS/(a₀ + a₁)S the ratio considerably reduces down to 1.11 at the façade base (the dashed vertical line represents ratios equal to 1). This means that the friction resistance activated by the restraining orthogonal walls (F₁) is dominant within the formulation considered by [36], representing the most important contribution for determining the seismic capacity of the mechanism considered. On the contrary the contribution due to the vertical load applied at a certain wall height (F₂) is not relevant since the ratio a_totS/(a₀ + a₁)S is very close to the dashed vertical line representing ratios equal to 1. Finally, the resistant contribution F₁ permits of significantly increasing the seismic capacity with respect to the conservative assumption of simple overturning without any resistance contribution.

3.3.2 Narthex longitudinal response

This paragraph describes in detail the seismic capacity evaluation of the narthex longitudinal response, numerically reported in the histograms of Fig. 9.

As previously discussed, the seismic capacity is assessed through a minimization process, by calculating the activation multiplier minimum value of several configurations by applying the linear kinematic analysis, where the narthex colonnade is considered as a series of rigid blocks connected among them with flexural hinges. In this study, it is assumed that all columns are hinged at base, while the hinges position on arches may vary. More in detail, Fig. 12a represents a possible narthex kinematic, due to a virtual unitary rotation θ₁ imposed with respect to the hinge A, assumed positive if clockwise. Moreover, Fig. 12b shows the mechanism schematization for a generic configuration where the following forces are considered acting on each block: the self-weight G_i, seismic force αG_i, the floor load P_i and the relative seismic force αP_i, where α is the unknown activation multiplier.

Fig. 12

Narthex longitudinal response schematization: a possible mechanism configuration and b acting forces (dimensions are in meters)

A parametric analysis is conducted by varying the arches hinges position by assuming in the schematization adopted that the narthex is a free architectural part not connected with the main façade and not considering, for simplicity, the gable roof at the narthex top.

By considering that each arch has a known shape, the position of a hinge is uniquely determined by knowing its abscissa. Therefore, in this study the variables assumed are the first and second hinge belonging to each arch, that are: Δx_AB and Δx_AC for the first arch; Δx_DE and Δx_DF for the second arch; Δx_GH and Δx_GI for the third arch.

For simplicity, it is assumed in any possible configuration that the relative position of the first hinge in each arch is equal, and expressed through the parameter λ, defined as follows:

$$\lambda =\Delta {\mathrm{x}}_{\mathrm{AB}}/{\mathrm{L}}_{1}=\Delta {\mathrm{x}}_{\mathrm{DE}}/{\mathrm{L}}_{2}=\Delta {\mathrm{x}}_{\mathrm{GH}}/{\mathrm{L}}_{3},$$

(22)

where L₁, L₂ and L₃ are the lengths, respectively, of the first, second and third arch.

Keeping λ fixed, the position of the second hinge is varied, expressed through the parameter μ, defined as:

$$\mu =\Delta {\mathrm{x}}_{\mathrm{AC}}/{\mathrm{L}}_{1}=\Delta {\mathrm{x}}_{\mathrm{DF}}/{\mathrm{L}}_{2}=\Delta {\mathrm{x}}_{\mathrm{GI}}/{\mathrm{L}}_{3},$$

(23)

that, similarly to λ, is assumed equal in each arch.

For each of the configuration assumed, virtual rotations θ₂, θ₃, …, θ₇ of all blocks are determined by means of kinematic compatibility equations. Then, the activation multiplier α₀ and the spectral acceleration a₀^* are evaluated, from which the corresponding ground acceleration a_DLSS (a_LSLSS) corresponding to the achievement of DLS (LSLS) are calculated [Eqs. (9) and (12)]. In this case the distributed vertical load p_i equal to 4.74 kN/ml is considered at the top of the narthex. This distributed load is calculated for influence area by considering the loads (included the self-weight) acting on the narthex roof.

Precisely, Fig. 13 shows virtual rotations obtained by imposing θ₁ = 1. In particular, Fig. 13a–d refers to four values of λ: 0 (Fig. 13a), 0.25 (Fig. 13b), 0.5 (Fig. 13c), and 0.75 (Fig. 13d). In this schematization it is assumed, as existence conditions necessary for the mechanism activation, that when θ₁ = 1 other virtual rotations (θ₂,…, θ₇) are alternatively positive and negative. Therefore, in the graphs, only values respecting this existence condition are plotted.

Fig. 13

Virtual rotations θ_i by varying λ. a λ = 0, b λ = 0.25, c λ = 0.5 and d λ = 0.75

Once virtual rotations are known for each configuration considered, the activation multiplier α₀ (Fig. 14a), the related participating mass fraction e^* (Fig. 14b) and the spectral acceleration a₀^* (Fig. 14c) are calculated. These graphs are plotted for several values of λ (first arch hinge position) and by varying μ (second hinge position). As it is possible to note, for a certain value of λ the activation multiplier α₀ tends to reduce by increasing μ (Fig. 14a), while the participating mass fraction e^* increases (Fig. 14b). Finally, the spectral acceleration a₀^* reduces as μ increases for any λ curve. In this case we found that the minimum of a₀^* is equal to 0.059 g for λ = 0.25 and μ = 1. From this value the ground accelerations for DLS and LSLS reported in the histogram of Fig. 9 are calculated.

Fig. 14

a Activation multiplier α₀, b participating mass fraction e^*and c spectral acceleration a₀* for the narthex longitudinal response (p_i = 4.74 kN/ml)

To highlight that the arches hinges position may not be aprioristically fixed and that their position where the minimum a₀^* verifies may change case by case, Fig. 15 reports the a₀^* curves by varying the distributed vertical load p_i. In particular, the Fig. 15 compares a₀^* curves obtained by considering: p_i = 0 kN/ml (Fig. 15a), p_i = 4.74 kN/ml (Fig. 15b) that is the reference value considered in this study whose a₀^* curves are reported in Fig. 14c, and p_i = 47.4 kN/ml, i.e. the reference value increased of 10 times (Fig. 15c). By comparing the a₀^* curves it is possible to note that:

• for p_i = 0 kN/ml it is found that the minimum a₀^* is equal to a₀^* = 0.062 g, for λ = 0.2 and μ = 1;

• for p_i = 4.74 kN/ml the minimum a₀^* is equal to a₀^* = 0.059 g, for λ = 0.25 and μ = 1;

• for p_i = 47.4 kN/ml the minimum a₀^* is equal to a₀^* = 0.04 g, for λ = 0.4 and μ = 1;

Fig. 15

Spectral acceleration a₀^* with a distributed load p_i equal to a 0 kN/ml, b 4.74 kN/ml and c 47.4 kN/ml

As it was easy to expect, the higher the distributed vertical load p_i, the lower the spectral acceleration a₀^*; moreover, the hinges position corresponding to the minimum a₀^* is different among the three load conditions: in fact, the ratio λ increases as p_i increases, while μ remains unchanged.

Finally, a parametric analysis is conducted also considering a steel tie-rod of 40 mm diameter and a 390 N/mm² yield design strength placed at 8 m height. The obtained results are reported in Fig. 16, in terms of: activation multiplier α₀ (Fig. 16a), participating mass fraction e^* (Fig. 16b), and spectral acceleration a₀^* (Fig. 16c). It should be noted that, again, for a given value of λ, α₀ and a₀^* reduce as μ increases, even if in this case the obtained values are significantly higher than the ones found not considering the steel tie-rod (Fig. 14). Note that in this case the minimum a₀^* results equal to 0.305 g with λ = 0 and μ = 1, considerably higher than the case without tie-rod (a₀^* = 0.059 g indicated with a dashed line in the Fig. 16c). Moreover, the steel tie-rod also modifies, under the assumption made, the arches hinges positions since in this case the minimum a₀* is given placing the arches hinges at the beginning and end of each arch. This again demonstrates that according to the linear kinematic analysis (LV2 method) the block dimensions involved into the mechanism may not be independently fixed but for a correct seismic assessment evaluation a minimization process of the activation multiplier is necessary by iteratively modifying the hinges positions.

Fig. 16

Narthex with a longitudinal steel tie-rod. a Activation multiplier α₀, b participating mass fraction e^* and c spectral acceleration a₀^*

3.3.3 Bell tower local collapse mechanisms

For completeness, in this study also two local mechanisms of the bell tower are studied.

First, the out-of-plane overturning of a corner is analyzed, as schematized in the Fig. 17. In particular, Fig. 17a simulates the possible out-of-plane overturning of the bell tower portion, while Fig. 17b depicts forces acting on each rigid block. In this mechanism three hinges are assumed in the points A, B and C (Fig. 17) corresponding to the Section 3 the Section 4 and the belfry top, respectively. Then, the activation multiplier α₀ and the spectral acceleration a₀^* are obtained through the application of the linear kinematic analysis, considering a Confidence Factor CF = 1. For this mechanism it is found α₀ = 0.033 and a₀^* = 0.04 g corresponding to the following seismic capacity: a_DLSS = 0.04 g and a_LSLSS = 0.08 g. Note that, in accordance with the LV1 method previously described, by assessing the global seismic capacity of the tower, a spectral acceleration a_LSLSS = 0.139 g has been obtained. Therefore, the local mechanism has a seismic vulnerability significantly higher than the global one.

Fig. 17

Out-of-plane overturning of the bell tower corner: a possible mechanism configuration and b acting forces (dimensions are in meters)

It should be noted that, for the out-of-plane overturning of corner, both a_DLSS and a_LSLSS are lower than the seismic demand a_g,DLSS = 0.0648 g and a_g,LSLSS = 0.133 g. Therefore, a steel tie-rod may be inserted to improve the mechanism strength. By considering, for instance, a steel tie-rod of 33 mm diameter and a 224 N/mm² yield design strength (the corresponding force is indicated with T in Fig. 17b) we obtain α₀ = 0.237 and a₀^* = 0.282 g, corresponding to a_DLSS = 0.282 g and a_LSLSS = 0.564 g. With these interventions, the seismic capacity results higher than the demand a_g,DLSS and a_g,LSLSS.

The second local mechanism considered is the belfry longitudinal response, where four hinges at the columns edges are assumed (Fig. 18a). The activation multiplier α₀ and the spectral acceleration a₀^* obtained through the schematization of Fig. 18b, considering a CF = 1, are equal respectively to α₀ = 0.547 and a₀^* = 0.614 g, with a seismic capacity of a_DLSS = 0.614 g and a_LSLSS = 1.228 g. These values are considerably higher than the corresponding seismic demand a_g,DLSS and a_g,LSLSS.

Fig. 18

Belfry longitudinal response: a possible mechanism configuration and b acting forces (dimensions are in meters)

4 Conclusions

In this paper, numerical investigations on seismic performance of masonry churches have been illustrated, by considering two simplified methods proposed by the current Italian Directive containing the Guidelines for assessment and reduction of cultural heritage seismic risk. To this scope a case study has been considered, an existing brick masonry church, having in plan a basilica configuration with also a bell tower.

As for the main façade overturning, it is important to remark that in the capacity model adopted the dominant contribution is given by the friction resistance (indicated as F₁) due to the restraining orthogonal walls. In the case analyzed the capacity model adopted provides a spectral acceleration resulting 25 times higher than the one calculated by considering a simple overturning without any restraining action due to the orthogonal walls.

The parametric analysis conducted on the longitudinal response of the narthex has highlighted that the spectral acceleration a₀^* depends on the hinges relative position and on the acting loads. As shown by the obtained results, an a-priori assumption of the hinges position may lead to an underestimation, within the method considered, of the macro-element seismic capacity.

Finally, as far as the bell tower mechanism is considered, the local mechanism consisting on the out-of-plane overturning of the bell tower corner has a ground acceleration lower than the one evaluated by considering a global response of the tower.

In particular, the work carried out has involved the use of the linear kinematic analysis implying simplified numerical models well-known in the published literature. They have allowed to define the seismic capacity in terms of activation threshold of each mechanisms considered. This approach, as known, is strongly conditioned by the boundary conditions that may vary case by case due to construction details and/or existing cracks, which may suggest the assumption of the most suitable numerical model. However, a prerequisite for using the methods applied in this study has been the monolithic walls assumption, with consequently the exclusion of any local disintegration of the masonry texture. In the case study analyzed the good quality of the masonry has permitted of ignoring this very vulnerable response mechanism.

Moreover, it should be noted that it is not possible to define a direct correlation between the results obtained with the LV1 and the LV2 method. Therefore, certainly the LV1 method allows a fast and global analysis for seismic assessment of a church, useful for evaluations at a territorial scale. However, more detailed analyses must be performed for local mechanisms, considering the related boundary conditions contributing to the seismic local response.