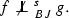Abstract
We study the relation of mutual strong Birkhoff–James orthogonality in two classical \(C^*\)-algebras: the \(C^*\)-algebra \({\mathbb {B}}(H)\) of all bounded linear operators on a complex Hilbert space H and the commutative, possibly nonunital, \(C^*\)-algebra. With the help of the induced graph it is shown that this relation alone can characterize right invertible elements. Moreover, in the case of commutative unital \(C^*\)-algebras, it can detect the existence of a point with a countable local basis in the corresponding compact Hausdorff space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An efficient way to study some binary relation on a certain set is by using the relation graph. The graph generated by a mutual orthogonality relation for the elements of an associative ring is introduced in [6] and studied in [13]. In this paper we investigate the orthogonality graph on certain \(C^*\)-algebras defined by the mutual strong Birkhoff–James orthogonality.
The concept of strong Birkhoff–James orthogonality first appeared in [2] in the context of Hilbert \(C^*\)-modules which are a generalization of Hilbert spaces in a way that instead of the usual inner product with values in a field \({\mathbb {F}}\in \{{\mathbb {R}},{\mathbb {C}}\}\) we have an inner product with values in a \(C^*\)-algebra (see e.g. [22]). Hilbert \(C^*\)-modules are Banach spaces with the norm defined by the \(C^*\)-algebra norm: the norm of an element of a module is the positive square root of the norm of its inner square. Besides Hilbert spaces, one of the most important examples of Hilbert \(C^*\)-modules are \(C^*\)-algebras. If \(\mathcal {A}\) is a \(C^*\)-algebra, then we can regard it as a Hilbert \(C^*\)-module over itself with the algebra multiplication as a (right) module action and an inner product defined as \(\langle a,b\rangle =a^*b\).
Recall that in a normed linear space X we say that \(x\in X\) is Birkhoff–James orthogonal to \(y\in X\), and write \(x\perp _{BJ}y,\) if
that is, if the distance from x to the one-dimensional subspace of X spanned by y is equal to the norm of x. This type of orthogonality was first introduced by Birkhoff in [9] and then studied by James [15,16,17]. There are many papers about Birkhoff–James orthogonality in general \(C^*\)-algebras and, in particular, in the \(C^*\)-algebra \({\mathbb {B}}(H)\) of bounded linear operators on a Hilbert space H with respect to the operator norm. Some basic results in the special case when one of the operators is the identity operator were obtained by Stampfli [25] in the study on derivations. Later Magajna [21] in his study on the distance to finite-dimensional subspaces in operator algebras observed that Stampfli’s results hold in general. Also, several other authors studied the topic, including Bhatia and Šemrl [7]. Having characterizations of the Birkhoff–James orthogonality in \({\mathbb {B}}(H)\) the natural further steps were to obtain characterizations in general \(C^*\)-algebras and Hilbert \(C^*\)-modules [1, 8]. The study of Birkhoff–James orthogonality is still very extensive and it goes in various directions, for example, studying approximate Birkhoff–James orthogonality and orthogonality with respect to some norm other than the operator norm (see e.g. [12, 19, 24, 27]).
The strong Birkhoff–James orthogonality is introduced as a version of the standard Birkhoff–James orthogonality which takes into account not only the linear but also the modular structure of Hilbert \(C^*\)-modules. If X is a (right) Hilbert \(C^*\)-module over a \(C^*\)-algebra \(\mathcal {A},\) then we say that \(x\in X\) is strongly Birkhoff–James orthogonal to \(y\in X\), and write \(x\perp _{BJ}^sy\), if
that is, if the distance from x to the right submodule of X generated by y equals the norm of x. First characterizations and properties of the strong Birkhoff–James orthogonality in Hilbert \(C^*\)-modules were obtained by proving the equivalence of the strong Birkhoff–James orthogonality of x and y and the classical Birkhoff–James orthogonality of certain elements defined by x and y [2]. Some further results on the (strong) Birkhoff–James orthogonality in \(C^*\)-algebras and Hilbert \(C^*\)-modules were discussed in [1, 3, 5, 23] and many other papers.
In particular, in a \(C^*\)-algebra \(\mathcal {A}\), regarded as a right Hilbert \(C^*\)-module over itself, \(a\in \mathcal {A}\) is strongly Birkhoff–James orthogonal to \(b\in \mathcal {A}\) if
It is easy to check that for a, b in an arbitrary \(C^*\)-algebra \(\mathcal {A}\) it holds
but the reverse implications do not hold unless \(\mathcal {A}\) is isomorphic to \({\mathbb {C}}\) (see [2, p. 112] and [3]). The strong Birkhoff–James orthogonality is not symmetric, that is, in general \(a\perp _{BJ}^sb\) does not imply \(b\perp _{BJ}^sa\) (again, the only \(C^*\)-algebra in which \(\perp _{BJ}^s\) is symmetric is the \(C^*\)-algebra of complex numbers, see [5, Corollary 2.7]). For example, if \(\mathcal {A}\) is the \(C^*\)-algebra of all bounded linear operators on some Hilbert space H of the dimension at least 2, \(P\in {\mathbb {B}}(H)\) any rank-one projection, then it is easy to see that \(I\perp _{BJ}^sP\) but \(P\not \perp _{BJ}^sI\).
However, as we shall see in the sequel, it can happen that both \(a\perp _{BJ}^sb\) and \(b\perp _{BJ}^sa\) hold for nonzero elements \(a,b\in \mathcal {A}\) (not just in the obvious case when \(a^*b=0\)), and this is the relation we discuss in this paper.
Definition 1.1
We say that elements \(a,b\in \mathcal {A}\) are mutually strongly Birkhoff–James orthogonal, and we write  , if \(a\perp _{BJ}^sb\) and \(b\perp _{BJ}^sa.\)
, if \(a\perp _{BJ}^sb\) and \(b\perp _{BJ}^sa.\)
We shall study the graph, called orthograph, related to  relation. Let \(\varGamma (\mathcal {A})\) be the graph with the vertex set
relation. Let \(\varGamma (\mathcal {A})\) be the graph with the vertex set
and with vertices \([a],[b]\in V(\varGamma (\mathcal {A}))\)adjacent if  . We identify vertices with their representatives, that is, we write a instead of [a].
. We identify vertices with their representatives, that is, we write a instead of [a].
Let us recall some basic definitions from the graph theory that we shall use in this paper. A graph is said to be connected if there exists a path from any vertex to any other vertex of the graph. A connected component of a graph is a maximal (in the sense of inclusion) connected subgraph. The distance between two distinct vertices is the length of the shortest path between them. If there is no path between some vertices, then their distance is \(\infty \); the distance from a vertex to itself is understood to be 0. The diameter \(\text{ diam } (\varGamma )\) of a graph \(\varGamma \) is the maximum of distances between vertices for all pairs of vertices in the graph; in the same way we define the diameter of a connected component of a graph. A vertex in a graph is isolated if there is no path between this vertex and any other vertex in the graph.
We shall discuss two classes of \(C^*\)-algebras:
-
the \(C^*\)-algebra \({\mathbb {B}}(H)\) of all bounded linear operators on a complex Hilbert space \((H, (\cdot |\cdot ))\) with the operator norm, and
-
the commutative \(C^*\)-algebras, that is, the \(C^*\)-algebra C(K) of all continuous functions on a compact Hausdorff space K with the maximum norm, and the \(C^*\)-algebra \(C_0(\varOmega )\) of all continuous functions on a locally compact Hausdorff space \(\varOmega \) vanishing at infinity.
Let us begin with a simple observation that applies to a general unital \(C^*\)-algebra.
Lemma 1.2
If b is a right invertible element in a unital \(C^*\)-algebra \(\mathcal {A}\), then \(a\perp _{BJ}^sb\) implies \(a=0\). In particular, right invertible elements of a unital \(C^*\)-algebra are isolated vertices in \(\varGamma (\mathcal {A})\).
Proof
Let \(a\in \mathcal {A}\) be such that \(a\perp _{BJ}^sb\). Then, putting \(c:=-b^{-1}_r a\) in (2), where \(b^{-1}_r\) is a right inverse of b, we get \(\Vert a\Vert \le \Vert a-bb^{-1}_r a\Vert =0,\) so \(a=0\). \(\square \)
The rest of the paper is organized as follows.
We consider first the case \({\mathbb {B}}(H)\) with \(dim \,H<\infty .\) By Lemma 1.2, invertible operators are isolated vertices. We show that any two noninvertible operators on a Hilbert space of dimension at least 4 can be connected by a path of length at most 3 (Theorem 2.9). Also, for a three-dimensional space H paths between noninvertible operators always exist, but it can happen that we sometimes need a path of length 4, while in the two-dimensional case there are no paths between some pairs of noninvertible operators.
In the third section we assume that H is infinite-dimensional. We show that the set of all \(A\in {\mathbb {B}}(H)\) which have no right inverse is a connected component of diameter 3 (Theorem 3.7).
The last two sections are devoted to commutative \(C^*\)-algebras. It is well known that every unital commutative \(C^*\)-algebra is \(*\)-isomorphic to the \(C^*\)-algebra C(K) of all complex continuous functions on a compact Hausdorff space K, while a nonunital commutative \(C^*\)-algebra is \(*\)-isomorphic to the \(C^*\)-algebra \(C_0(\varOmega )\) of all complex continuous functions on a locally compact Hausdorff space \(\varOmega \) vanishing at infinity. We show that the mutual strong Birkhoff–James orthogonality relation on C(K) alone distinguishes among compacts which possess a point with a countable local basis and those in which no point has a countable local basis—in the first case the set of all noninvertible elements (that is, nonisolated vertices) is a connected component of diameter 3, while in the latter case the diameter of this connected component is 2 (Theorem 4.5). Similar results are obtained in the nonunital case (Theorem 5.4).
2 \(C^*\)-algebra \({\mathbb {B}}(H)\) with a finite-dimensional Hilbert space H
We shall make use of the following characterization of the strong Birkhoff–James orthogonality ( [2, Proposition 2.8]).
Theorem 2.1
Let H be a complex Hilbert space and \(A,B\in {\mathbb {B}}(H)\). The following statements hold.
-
(1)
\(A\perp _{BJ}^sB\) if and only if there is a sequence of unit vectors \((x_n)\) in H such that \(\lim _{n\rightarrow \infty }\Vert A x_n\Vert =\Vert A\Vert \) and \(\lim _{n\rightarrow \infty }B^*Ax_n=0\).
-
(2)
If \(dim \,H<\infty ,\) then \(A\perp _{BJ}^sB\) if and only if there is a unit vector \(x\in H\) such that \(\Vert A x\Vert =\Vert A\Vert \) and \(B^*Ax=0\).
In the sequel, the image and the kernel of \(A\in {\mathbb {B}}(H)\) will be denoted by \(Im \,A\) and \(Ker \,A\), respectively. The closure of the linear span of a subset V of H will be denoted by \(\overline{span \,V}\).
Since on finite-dimensional spaces an operator \(A\in {\mathbb {B}}(H)\) is invertible if and only if it is right invertible, by Lemma 1.2 it remains to consider existence and length of paths between noninvertible elements in \({\mathbb {B}}(H)\). Observe that a noninvertible element is never an isolated vertex: if A is noninvertible then there is a nonzero \(x\perp Im \,A\), so for the orthogonal projection P onto \(span \,\{x\}\) we have \(P^*A=0,\) giving 
We begin with the case when H is two-dimensional. The following lemma is a direct consequence of (2) of Theorem 2.1: if A is a rank-one operator and \(A\perp _{BJ}^sB\), then \(A^*B=0\).
Lemma 2.2
Let H be a complex Hilbert space, \(dim \,H=2\). Let \(A,B\in {\mathbb {B}}(H)\) be nonzero noninvertible operators. Then:

Proposition 2.3
Let H be a complex Hilbert space, \(dim \,H=2\). Suppose that for nonzero noninvertible \(A,B\in {\mathbb {B}}(H)\) there exist \(n\in {\mathbb {N}}\) and nonzero operators \(C_1,\ldots ,C_n\) in \({\mathbb {B}}(H)\) such that  . Then \(A^*B=0\) or \(Im \,A=Im \,B\).
. Then \(A^*B=0\) or \(Im \,A=Im \,B\).
Proof
By Lemma 1.2, if such a sequence exists, then all the operators \(C_i\) must be noninvertible.
Suppose there is a nonzero \(C_1\in {\mathbb {B}}(H)\) such that  . Then by Lemma 2.2 we have \(Im \,A\perp Im \,C_1\) and \(Im \,C_1\perp Im \,B\), so \(Im \,A=Im \,B.\) The same conclusion holds for every path of even length.
. Then by Lemma 2.2 we have \(Im \,A\perp Im \,C_1\) and \(Im \,C_1\perp Im \,B\), so \(Im \,A=Im \,B.\) The same conclusion holds for every path of even length.
Suppose nonzero \(C_1,C_2\in {\mathbb {B}}(H)\) are such that  . As above, \(Im \,A=Im \,C_2\perp Im \,B\) and therefore \(A^*B=0\). We conclude the same for other paths of odd length. \(\square \)
. As above, \(Im \,A=Im \,C_2\perp Im \,B\) and therefore \(A^*B=0\). We conclude the same for other paths of odd length. \(\square \)
Proposition 2.4
Let H be a complex Hilbert space, \(dim \,H=2\). The connected components of the orthograph \(\varGamma ({\mathbb {B}}(H))\) are either isolated vertices or the sets of the form
where \(x\in H\) is nonzero. The diameter of each \(\mathcal {S}_x\) is 2.
Proof
Let \(A,B\in \mathcal {S}_x\) for some nonzero \(x\in H\). Then either \(Im \, A\perp Im \,B\) or \(Im \, A= Im \,B\). In the first case we have  . In the second case, let P be the rank-one orthogonal projection onto \((Im \, A)^\perp \). Then \(P\in \mathcal {S}_x\) and
. In the second case, let P be the rank-one orthogonal projection onto \((Im \, A)^\perp \). Then \(P\in \mathcal {S}_x\) and  . Therefore, \(\mathcal {S}_x\) is connected and its diameter is 2.
. Therefore, \(\mathcal {S}_x\) is connected and its diameter is 2.
Let us show that all connected components with more than one element are of this form. Let \(\mathcal {S}'\) be such a connected component and choose any nonzero A in it. Since A is not isolated, A is noninvertible, so there is a nonzero \(x\in H\) such that \(Im \,A=span \,\{x\}\). Let us show that \(\mathcal {S}'=\mathcal {S}_x\). If \(B\in \mathcal {S}'\) then, by Proposition 2.3, \(Im \,A=Im \,B\) or \(Im \,A\perp Im \,B,\) which implies that \(B\in \mathcal {S}_x,\) so \(\mathcal {S}'\subseteq \mathcal {S}_x\). For the other inclusion, suppose \(B\in \mathcal {S}_x\). Then B is connected to A by the first part of the proof, so \(B\in \mathcal {S}'\). \(\square \)
The situation is different if \(dim \,H\ge 3\).
Proposition 2.5
Let H be a complex Hilbert space, \(3\le dim \,H<\infty \). Let \(A,B\in {\mathbb {B}}(H)\) be nonzero noninvertible operators. Then there are nonzero operators \(C_1,C_2,C_3\in {\mathbb {B}}(H)\) such that  .
.
Proof
Since A and B are noninvertible, there are nonzero vectors \(v_A\in Ker \,A^*\) and \(v_B\in Ker \,B^*\). Take a nonzero vector \(v\in span \,\{v_A,v_B\}^\perp \). Let \(C_1,C_2,C_3\in {\mathbb {B}}(H)\) be orthogonal projections onto \(span \,\{v_A\},\)\(span \,\{v\},\) and \(span \,\{v_B\},\) respectively. Then \(A^*C_1=C_1^*C_2=C_2^*C_3=C_3^*B=0\) and the statement follows. \(\square \)
The following example shows that, whenever \(dim \,H\ge 3\), there are noninvertible \(A,B\in {\mathbb {B}}(H)\) which cannot be connected by a path of length 2.
Example 2.6
Let H be a complex (finite or infinite-dimensional) Hilbert space, \(dim \,H\ge 3,\) and \(e_1,e_2\in H\) mutually orthogonal unit vectors. Let \(A\in {\mathbb {B}}(H)\) be the orthogonal projection onto \(span \,\{e_1\}\). Let \(B\in {\mathbb {B}}(H)\) be such that \(Be_1=Be_2=\frac{1}{2}(e_1+e_2)\), and \(Bx=\frac{1}{2}x\) for \(x\in span \{e_1,e_2\}^\perp \). Note that A and B are self-adjoint and noninvertible, \(Ker \,A^*=span \,\{e_1\}^\perp \) and \(Ker \,B^*=span \,\{e_1-e_2\}.\) Since \(A^*B\ne 0\), it follows from
[4, Proposition 2.3] that  .
.
Suppose \(C\in {\mathbb {B}}(H)\) is such that  . Again by
[4, Proposition 2.3],
. Again by
[4, Proposition 2.3],  implies \(C^*A=0,\) that is, \(Im \,C\perp span \,\{e_1\}\). By Theorem 2.1, since
implies \(C^*A=0,\) that is, \(Im \,C\perp span \,\{e_1\}\). By Theorem 2.1, since  , there is a sequence of unit vectors \(x_n\in H\) such that \(\lim _{n\rightarrow \infty }\Vert Cx_n\Vert =\Vert C\Vert \) and \(\lim _{n\rightarrow \infty }B^*Cx_n=0\). Since \(Cx_n\perp e_1\) for all n, we have \(Cx_n=\lambda _n e_2+y_n\) for some \(\lambda _n\in {\mathbb {C}}\) and \(y_n\in span \{e_1,e_2\}^\perp \). From \(\lim _{n\rightarrow \infty }B^*Cx_n=\lim _{n\rightarrow \infty }(\frac{1}{2}\lambda _n(e_1+e_2)+\frac{1}{2}y_n)=0\) we get \(\lim _{n\rightarrow \infty }\lambda _n=0\) and \(\lim _{n\rightarrow \infty }y_n=0\). Then we have \(\lim _{n\rightarrow \infty }Cx_n=0\), so \(\Vert C\Vert =0,\) that is, \(C=0\).
, there is a sequence of unit vectors \(x_n\in H\) such that \(\lim _{n\rightarrow \infty }\Vert Cx_n\Vert =\Vert C\Vert \) and \(\lim _{n\rightarrow \infty }B^*Cx_n=0\). Since \(Cx_n\perp e_1\) for all n, we have \(Cx_n=\lambda _n e_2+y_n\) for some \(\lambda _n\in {\mathbb {C}}\) and \(y_n\in span \{e_1,e_2\}^\perp \). From \(\lim _{n\rightarrow \infty }B^*Cx_n=\lim _{n\rightarrow \infty }(\frac{1}{2}\lambda _n(e_1+e_2)+\frac{1}{2}y_n)=0\) we get \(\lim _{n\rightarrow \infty }\lambda _n=0\) and \(\lim _{n\rightarrow \infty }y_n=0\). Then we have \(\lim _{n\rightarrow \infty }Cx_n=0\), so \(\Vert C\Vert =0,\) that is, \(C=0\).
If \(dim \,H\ge 4\) then the path from Proposition 2.5 can be shortened.
Proposition 2.7
Let H be a complex Hilbert space, \(4\le dim \,H<\infty \). Let \(A,B\in {\mathbb {B}}(H)\) be nonzero noninvertible operators. Then there are nonzero operators \(C_1,C_2\in {\mathbb {B}}(H)\) such that  .
.
Proof
Let \(x,y\in H\) be unit vectors such that \(\Vert Ax\Vert =\Vert A\Vert \) and \(\Vert By\Vert =\Vert B\Vert \). Since A and B are noninvertible, there are unit vectors \(v_A\in Ker \,A^*\) and \(v_B\in Ker \,B^*\). If their inner product satisfies \((v_A|v_B)=0,\) we define \(v:=v_A\) and \(w:=v_B.\)
If \((v_A|v_B) \ne 0,\) we take a unit vector \(v\in span \,\{Ax,v_B\}^\perp ,\) and then a unit vector \(w\in span \,\{By, v_A, v\}^\perp \). Define \(C_1,C_2\in {\mathbb {B}}(H)\) as
Note that \(\Vert C_1v_A\Vert =\Vert C_1v\Vert =\Vert C_1\Vert \) and \(\Vert C_2w\Vert =\Vert C_2v_B\Vert =\Vert C_2\Vert \). Since \(Ax\perp Im \,C_1,\) we have \(C_1^*Ax=0\). It also holds \(A^*C_1v_A=0\). Therefore, by Theorem 2.1,  . Note that \(w\perp Im \,C_1\) implies \(C_1^*C_2w=C_1^*w=0,\) while \(v\perp Im \,C_2\) implies \(C_2^*C_1v=C_2^*v=0\). This proves that
. Note that \(w\perp Im \,C_1\) implies \(C_1^*C_2w=C_1^*w=0,\) while \(v\perp Im \,C_2\) implies \(C_2^*C_1v=C_2^*v=0\). This proves that  . Since \(By\perp Im \,C_2,\) we have \(C_2^*By=0\). It also holds \(B^*C_2v_B=B^*v_B=0,\) and therefore
. Since \(By\perp Im \,C_2,\) we have \(C_2^*By=0\). It also holds \(B^*C_2v_B=B^*v_B=0,\) and therefore  . \(\square \)
. \(\square \)
It remains to find operators at a distance four when \(dim \,H=3\).
Example 2.8
Let H be a complex Hilbert space, \(dim \,H=3\). Let \(\{e_1,e_2,e_3\}\) be an orthonormal basis of H, and \(A,B\in {\mathbb {B}}(H)\) defined as
We shall show that:
-
(i)
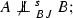
-
(ii)
if
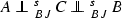 then \(C=0\);
then \(C=0\); -
(iii)
if
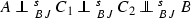 , then \(C_1=0\) or \(C_2=0\).
, then \(C_1=0\) or \(C_2=0\).
It can be easily checked that \(A^*=A,\)\(B^*=B,\)\(\Vert A\Vert =\Vert B\Vert =1,\) and \(Ker \,A^{*}=span \,\{e_1-e_2\},\)\(Ker \,B^{*}=span \,\{e_2-e_3\}\). Note that \(A(e_1+e_2)=e_1+e_2\) and \(B(e_2+e_3)=e_2+e_3\). An easy computation shows that \(\Vert Ax\Vert =\Vert A\Vert \Vert x\Vert \) if and only if \(x\in span \,\{e_1+e_2\}\), while \(\Vert By\Vert =\Vert B\Vert \Vert y\Vert \) if and only if \(y\in span \,\{e_2+e_3\}.\)
First, suppose  . Then there is a unit vector \(x\in H\) such that \(\Vert Ax\Vert =\Vert A\Vert \) and \(B^{*}Ax=0\). Then \(x\in span \,\{e_1+e_2\},\) and therefore \(x=Ax\in Ker \,B^{*}=span \,\{e_2-e_3\},\) a contradiction. Hence
. Then there is a unit vector \(x\in H\) such that \(\Vert Ax\Vert =\Vert A\Vert \) and \(B^{*}Ax=0\). Then \(x\in span \,\{e_1+e_2\},\) and therefore \(x=Ax\in Ker \,B^{*}=span \,\{e_2-e_3\},\) a contradiction. Hence  .
.
Suppose now there is a nonzero \(C\in {\mathbb {B}}(H)\) such that  . Since \(C\perp _{BJ}^sA,\) there is a unit vector \(u\in H\) such that \(A^{*}Cu=0\) and \(\Vert Cu\Vert =\Vert C\Vert \). Thus, \(Cu\in Ker \,A^*,\) so \(Cu=\lambda (e_1-e_2)\) for some \(\lambda \in {\mathbb {C}}{\setminus }\{0\},\) and therefore \(e_1-e_2\in Im \,C\). Since \(B\perp _{BJ}^sC\) and \(\Vert By\Vert =\Vert B\Vert \Vert y\Vert \) if and only if \(y\in span \,\{e_2+e_3\}\), we have \(C^*B(e_2+e_3)=0,\) i.e., \(C^*(e_2+e_3)=0\). Thus, \(e_2+e_3\in Ker \,C^*\) which implies that \((e_2+e_3|e_1-e_2)=0\), since \(e_1-e_2\in Im \,C\). This is impossible, so (ii) holds.
. Since \(C\perp _{BJ}^sA,\) there is a unit vector \(u\in H\) such that \(A^{*}Cu=0\) and \(\Vert Cu\Vert =\Vert C\Vert \). Thus, \(Cu\in Ker \,A^*,\) so \(Cu=\lambda (e_1-e_2)\) for some \(\lambda \in {\mathbb {C}}{\setminus }\{0\},\) and therefore \(e_1-e_2\in Im \,C\). Since \(B\perp _{BJ}^sC\) and \(\Vert By\Vert =\Vert B\Vert \Vert y\Vert \) if and only if \(y\in span \,\{e_2+e_3\}\), we have \(C^*B(e_2+e_3)=0,\) i.e., \(C^*(e_2+e_3)=0\). Thus, \(e_2+e_3\in Ker \,C^*\) which implies that \((e_2+e_3|e_1-e_2)=0\), since \(e_1-e_2\in Im \,C\). This is impossible, so (ii) holds.
Finally, suppose there are nonzero \(C_1,C_2\in {\mathbb {B}}(H)\) such that

Since \(A\perp _{BJ}^sC_1\) and \(\Vert Ax\Vert =\Vert A\Vert \Vert x\Vert \) if and only if \(x\in span \,\{e_1+e_2\},\) we get \(C_1^*A(e_1+e_2)=0\) which implies \(C_1^*(e_1+e_2)=0,\) i.e., \(e_1+e_2\in Ker \,C_1^*\). Since \(C_1\perp _{BJ}^sA,\) there is a unit vector \(u_1\in H\) such that \(\Vert C_1u_1\Vert =\Vert C_1\Vert \) and \(A^*C_1u_1=0\). Thus, \(C_1u_1\in Ker \,A^*,\) so \(C_1u_1=\lambda (e_1-e_2)\) for some \(\lambda \in {\mathbb {C}}{\setminus }\{0\},\) and therefore \(e_1-e_2\in Im \,C_1\). Since  there are unit vectors \(u_2,u_3\in H\) such that \(\Vert C_1u_2\Vert =\Vert C_1\Vert ,\)\(\Vert C_2u_3\Vert =\Vert C_2\Vert ,\)\(C_2^*C_1u_2=0\) and \(C_1^*C_2u_3=0,\) so \(C_1u_2\in Ker \,C_2^*\) and \(C_2u_3\in Ker \,C_1^*\). Since \(B\perp _{BJ}^sC_2\) and \(\Vert By\Vert =\Vert B\Vert \Vert y\Vert \) if and only if \(y\in span \,\{e_2+e_3\}\), we have \(C_2^*B(e_2+e_3)=0\) which implies \(C_2^*(e_2+e_3)=0,\) i.e., \(e_2+e_3\in Ker \,C_2^*\). Since \(C_2\perp _{BJ}^sB,\) there is a unit vector \(u_4\in H\) such that \(\Vert C_2u_4\Vert =\Vert C_2\Vert \) and \(B^*C_2u_4=0\). Thus, \(C_2u_4\in Ker \,B^*,\) so \(C_2u_4=\mu (e_2-e_3)\) for some \(\mu \in {\mathbb {C}}{\setminus }\{0\},\) and therefore \(e_2-e_3\in Im \,C_2\). We have obtained that
there are unit vectors \(u_2,u_3\in H\) such that \(\Vert C_1u_2\Vert =\Vert C_1\Vert ,\)\(\Vert C_2u_3\Vert =\Vert C_2\Vert ,\)\(C_2^*C_1u_2=0\) and \(C_1^*C_2u_3=0,\) so \(C_1u_2\in Ker \,C_2^*\) and \(C_2u_3\in Ker \,C_1^*\). Since \(B\perp _{BJ}^sC_2\) and \(\Vert By\Vert =\Vert B\Vert \Vert y\Vert \) if and only if \(y\in span \,\{e_2+e_3\}\), we have \(C_2^*B(e_2+e_3)=0\) which implies \(C_2^*(e_2+e_3)=0,\) i.e., \(e_2+e_3\in Ker \,C_2^*\). Since \(C_2\perp _{BJ}^sB,\) there is a unit vector \(u_4\in H\) such that \(\Vert C_2u_4\Vert =\Vert C_2\Vert \) and \(B^*C_2u_4=0\). Thus, \(C_2u_4\in Ker \,B^*,\) so \(C_2u_4=\mu (e_2-e_3)\) for some \(\mu \in {\mathbb {C}}{\setminus }\{0\},\) and therefore \(e_2-e_3\in Im \,C_2\). We have obtained that
Suppose that \(dim \,Ker \,C_1^*=1\). Then \(C_2u_3=\nu (e_1+e_2)\) for some \(\nu \in {\mathbb {C}}{\setminus }\{0\}\). However, this cannot be true, since \(e_2+e_3\in Ker \,C_2^*\), and therefore \((C_2u_3 |e_2+e_3)=0\). We conclude that \(dim \,Ker \,C_1^*\ge 2\). Since \(C_1\ne 0\) and \(dim \,H=3,\) it follows that \(dim \,Ker \,C_1^*= 2\) and \(dim \,Im \,C_1=1\). Then \(C_1u_2=\kappa (e_1-e_2)\) for some \(\kappa \in {\mathbb {C}}{\setminus }\{0\}\). However, this contradicts the fact that \((C_1u_2|e_2-e_3) =0\), since \(e_2-e_3\in Im \,C_2\) and \(C_1u_2\in Ker \,C_2^*\). This proves our statement.
Let us summarize the obtained results.
Theorem 2.9
Let \(\mathcal {S}\) be the set of all nonzero noninvertible operators acting on a finite-dimensional complex Hilbert space H.
-
(1)
\(A\in {\mathbb {B}}(H)\) is an isolated vertex of the orthograph \(\varGamma ({\mathbb {B}}(H))\) if and only if A is invertible.
-
(2)
If \(dim \,H=2,\) then \(\mathcal {S}\) is not connected. The connected components of the orthograph \(\varGamma ({\mathbb {B}}(H))\) are either isolated vertices or the sets of the form
$$\begin{aligned} \mathcal {S}_x=\{A\in {\mathbb {B}}(H):Im \, A=span \,\{x\} \text{ or } Im \, A=span \,\{x\}^\perp \} \end{aligned}$$where \(x\in H\) is nonzero. The diameter of each \(\mathcal {S}_x\) is 2.
-
(3)
If \(dim \,H =3,\) then \(\mathcal {S}\) is a connected component whose diameter is 4.
-
(4)
If \(dim \,H\ge 4,\) then \(\mathcal {S}\) is a connected component whose diameter is 3.
3 \(C^*\)-algebra \({\mathbb {B}}(H)\) with an infinite-dimensional Hilbert space H
In this section we consider the orthograph of \({\mathbb {B}}(H)\) for an infinite-dimensional complex Hilbert space H. Observe first that Example 2.6 provides existence of noninvertible operators in \({\mathbb {B}}(H)\) whose distance is at least 3 for both finite-dimensional and infinite-dimensional space H.
Recall that a sequence \((x_n)\) of unit vectors in H converges weakly to \(x\in H\) if \(\lim _{n\rightarrow \infty }(x_n|y)=(x|y)\) for every \(y\in H\). We write \(x_n \overset{w}{\rightarrow } x\).
We start with several technical lemmas.
Lemma 3.1
Let H be an infinite-dimensional complex Hilbert space, and suppose \(A\in {\mathbb {B}}(H)\) does not attain its norm. If \((x_n)\) is a sequence of unit vectors in H such that \(\lim _{n\rightarrow \infty }\Vert Ax_n\Vert =\Vert A\Vert \), then there exists a subsequence \((x_{n_k})_k\) of \((x_n)\) such that \(Ax_{n_k} \overset{w}{\rightarrow } 0\).
Proof
First note that
Since \((x_n)\) is a bounded sequence, there are \(x \in H\) and a subsequence \((x_{n_k})_k\) of \((x_n)\) such that \(x_{n_k} \overset{w}{\rightarrow } x\). Then we get
so (3) implies that \((A^*A-\Vert A\Vert ^2 I)x=0,\) that is, \(\Vert Ax\Vert =\Vert A\Vert \Vert x\Vert \). By our assumption, it follows that \(x = 0\). Thus, \(x_{n_k} \overset{w}{\rightarrow } 0\), and therefore \(Ax_{n_k} \overset{w}{\rightarrow } 0\). \(\square \)
Lemma 3.2
Let H be an infinite-dimensional complex Hilbert space, and \(A\in {\mathbb {B}}(H)\). Suppose that A is not right invertible and \(\mathop {\mathrm {Ker}}A^* = \{ 0 \}\). Then there exists a sequence of unit vectors \((y_n)\) in H such that \(y_n \overset{w}{\rightarrow } 0\) and \(\lim _{n\rightarrow \infty } A^*y_n = 0\).
Proof
Assume that there exists \(c > 0\) such that \(\Vert A^*x\Vert \ge c \Vert x\Vert \) for all \(x \in H\). Then \(\mathop {\mathrm {Im}}A^*\) is closed in H and \(A^*:H \rightarrow \mathop {\mathrm {Im}}A^*\) is a topological isomorphism. Hence \(A^*\) is left invertible, so A is right invertible, a contradiction. Thus there exists a sequence of unit vectors \((x_n)\) in H such that \(\lim _{n\rightarrow \infty } A^*x_n = 0\).
Since \((x_n)\) is a bounded sequence, there are \(x \in H\) and a subsequence \((x_{n_k})_k\) of \((x_n)\) such that \(x_{n_k} \overset{w}{\rightarrow } x\). Then \(A^*x_{n_k} \overset{w}{\rightarrow } A^*x\), so \(A^*x = 0\). Since \(\mathop {\mathrm {Ker}}A^* = \{0\}\), we have \(x = 0\), so \(x_{n_k} \overset{w}{\rightarrow } 0\). Then \((y_k)=(x_{n_k})\) is a required sequence. \(\square \)
The following lemma states that every sequence of unit vectors weakly converging to zero contains a subsequence which is close to an orthonormal sequence (see [14, p. 300]).
Lemma 3.3
Let H be an infinite-dimensional complex Hilbert space. Let \((x_n)\) be a sequence of unit vectors in H such that \(x_n \overset{w}{\rightarrow } 0\). Then there exist a subsequence \((x_{n_k})_k\) of \((x_n)\) and an orthonormal sequence \((e_k)\) in H such that \(e_1=x_{n_1}=x_1\) and \(\lim _{k \rightarrow \infty } \Vert x_{n_k}-e_k\Vert = 0\).
Lemma 3.4
Let \((e_n)\) and \((f_n)\) be two orthonormal sequences in H. Then there exist subsequences \((e_{k_l})_l\) of \((e_k)\) and \((f_{k_j})_j\) of \((f_k)\) such that
where \(P_{V_f}\) is the orthogonal projection onto \(V_f = \overline{span \,\{ f_{k_j} : j \in {\mathbb {N}} \}}\).
Proof
Note that we can always achieve \(e_{k_1} = e_1\) and \(f_{k_1} = f_1\) by adding \(e_1\) and \(f_1\) to the beginning of the subsequences obtained, since \(\lim _{n \rightarrow \infty } (e_n| f_1) = 0\). Hence it is sufficient to find \((e_{k_l})_l\) and \((f_{k_j})_j\) such that \(\lim _{l \rightarrow \infty } P_{V_f}(e_{k_l}) = 0\).
For each \(n \in {\mathbb {N}}\) we now construct two sequences \((e^{(n)}_k)_{k}\) and \((f^{(n)}_k)_k\), the subspace \(V_n \subseteq H\) and \(a_n \in {\mathbb {R}}\) which satisfy the following properties:
-
(a)
\(V_n = \overline{span \,\{ f^{(n)}_k:k\in {\mathbb {N}}\}}\);
-
(b)
\((e^{(1)}_k)_k\) is a subsequence of \((e_k)_k\), and \((f^{(1)}_k)_k = (f_k)_k\);
-
(c)
\((e_k^{(n+1)})_k\) is a subsequence of \((e_k^{(n)})_k\), and \((f_k^{(n+1)})_k\) is a subsequence of \((f_k^{(n)})_k\), so \(V_{n + 1} \subseteq V_n\);
-
(d)
\(\lim _{k \rightarrow \infty } \Vert P_{V_n}(e^{(n)}_k) \Vert < a_n + \frac{1}{\left( \sqrt{2}\right) ^{n-1}}\);
-
(e)
\(\lim _{n \rightarrow \infty } a_n = 0\).
We define \((e^{(n)}_k)\), \((f^{(n)}_k)\), \(V_n\) and \(a_n\) with the properties (a)-(d) recursively as follows.
If \(n = 1\) we put \((f^{(1)}_k)_k = (f_k)_k\), \(V_1 = \overline{span \,\{ f^{(1)}_k \}}\) and \(a_1 = {\underline{\mathrm{lim}}} _{k \rightarrow \infty } \Vert P_{V_1}(e_k) \Vert \) (here \({\underline{\mathrm{lim}}}\) denotes the limit inferior) and then choose \((e^{(1)}_k)_k\) to be a subsequence of \((e_k)_k\) such that \(\lim _{k \rightarrow \infty } \Vert P_{V_1}(e^{(1)}_k) \Vert < a_1 + 1\).
Suppose \(a_n\), \(V_n\), \((e^{(n)}_k)_k\) and \((f^{(n)}_k)_k\) with the properties (a)–(d) are constructed for some \(n \in {\mathbb {N}}\). Consider two subsequences of \((f^{(n)}_k)_k\), namely, \((g^{(1)}_k)_k = (f^{(n)}_{2k -1})_k\) and \((g^{(2)}_k)_k= (f^{(n)}_{2k})_k\). For \(j=1,2\) let \(V^{(j)}_g = \overline{span \,\{ g^{(j)}_k \}}\) and
Let \(m\in \{1,2\}\) be such that \(b^{(m)}=\min \{b^{(1)}, b^{(2)}\}\). We set \((f^{(n+1)}_k) _k= (g^{(m)}_k)_k\), \(a_{n+1} = b^{(m)}\), \(V_{n+1} = V^{(m)}_g\) and \((e^{(n+1)}_k)_k\) a subsequence of \((e^{(n)}_k)_k\) such that \(\lim _{k \rightarrow \infty } \Vert P_{V_{n+1}}(e^{(n+1)}_k) \Vert < a_{n+1} + \frac{1}{\left( \sqrt{2}\right) ^n}\), so (a)–(d) are satisfied.
Also, observe that \(V^{(1)}_g \perp V^{(2)}_g\) and \(V_n = V^{(1)}_g \oplus V^{(2)}_g\), so it follows from (d) that \((b^{(1)})^2 + (b^{(2)})^2 < \left( a_n + \frac{1}{\left( \sqrt{2}\right) ^{n-1}}\right) ^2\). By the choice of \(a_{n+1}\) we get from here that \(a_{n+1} < \frac{a_n}{\sqrt{2}} + \frac{1}{\left( \sqrt{2}\right) ^n}.\) Since this holds for each \(n \in {\mathbb {N}}\), we inductively get
so \(\lim _{n \rightarrow \infty } a_n = 0\) which proves (e).
Consider \((e_{k_l})_l = (e^{(l)}_l)_l\), \((f_{k_j})_j = (f^{(j)}_j)_j\), and \(V_f = \overline{span \,\{ f_{k_j} : j \in {\mathbb {N}} \}}\). We need to show that
Let \(\varepsilon > 0\). We can find \(N \in {\mathbb {N}}\) such that \(a_{N+1} + \frac{1}{\left( \sqrt{2}\right) ^N} < \frac{\varepsilon }{2}\). For such N we define subspaces
Then \(V_{\le N} \perp V_{>N}\), \(V_f = V_{\le N} \oplus V_{>N}\) and \(V_{>N} \subseteq V_{N+1}.\)
Since \((e_{k_l})_l \overset{w}{\rightarrow } 0\) and \(V_{\le N}\) is finite-dimensional, there exists \(M_1 \in {\mathbb {N}}\) such that
Moreover, \((e_{k_l})_{l \ge N + 1}\) is a subsequence of \((e^{(N+1)}_k)_k\), so by (d) there exists \(M_2 \in {\mathbb {N}}\) such that
Then for all \(l> {\max }\{M_1, M_2\}\) it follows from (4) and (5) that
\(\square \)
Finally, we are in a position to prove that right noninvertible elements are not isolated vertices. However, the following proposition says even more.
Proposition 3.5
Let H be an infinite-dimensional complex Hilbert space and \(A \in {\mathbb {B}}(H)\) not right invertible. Then there exists an orthonormal sequence \((f_j)\) which satisfies the following property: if \((f_{j_m})_m\) is an arbitrary subsequence of \((f_j)\) such that \(f_{j_1} = f_1\) then for the orthogonal projection P onto \( \overline{span \,\{ f_{j_m} : m \in {\mathbb {N}} \}}\) we have  .
.
Proof
Assume without loss of generality that \(\Vert A\Vert = 1\). Consider two cases, depending on whether or not A attains its norm.
-
(1)
Suppose there is a unit vector \(x_A \in H\) such that \(\Vert Ax_A\Vert = \Vert A\Vert \). Then let \((e_k)\) be an arbitrary orthonormal system such that \(e_1 = Ax_A\).
-
(2)
Otherwise, it follows from Lemma 3.1 that there exists a sequence of unit vectors \((x_n)\) in H such that \(\lim _{n\rightarrow \infty } \Vert Ax_n\Vert = \Vert A\Vert \) and \(Ax_n \overset{w}{\rightarrow } 0\). We may assume that \(\Vert Ax_n\Vert \ne 0\) for all \(n \in {\mathbb {N}}\). Then, by Lemma 3.3, there exist a subsequence \((x_{n_k})_k\) and an orthonormal sequence \((e_k)\) such that \(\lim _{k \rightarrow \infty } \left( \frac{Ax_{n_k}}{\Vert Ax_{n_k}\Vert } - e_k \right) = 0\). We now consider the sequence \(({\tilde{x}}_k) = (x_{n_k})_k\), so \(\lim _{k \rightarrow \infty } \Vert A {\tilde{x}}_k\Vert = \Vert A\Vert \) and
$$\begin{aligned} \lim _{k \rightarrow \infty } (A {\tilde{x}}_k - e_k) = \lim _{k \rightarrow \infty } \left( \frac{A {\tilde{x}}_k}{\Vert A {\tilde{x}}_k\Vert } - e_k \right) = 0. \end{aligned}$$
As for \(\mathop {\mathrm {Ker}}A^*\), there are also two cases possible.
-
(a)
If \(\mathop {\mathrm {Ker}}A^* \ne \{0\}\) then there exists \(y_A \in H\) such that \(\Vert y_A\Vert = 1\) and \(A^*y_A = 0\). Clearly, if \(x_A\) exists then \(Ax_A \perp y_A\). Let \((f_k)\) be an arbitrary orthonormal system such that \(f_1 = y_A\) and, in the case when \(x_A\) exists, we require that \(Ax_A \perp f_k\) for all \(k \in {\mathbb {N}}\).
-
(b)
Otherwise, Lemma 3.2 implies that there exists a sequence of unit vectors \((y_n)\) in H such that \(\lim _{n\rightarrow \infty } A^*y_n = 0\) and \(y_n \overset{w}{\rightarrow } 0\). Then, by Lemma 3.3, there exist a subsequence \((y_{n_k})_k\) and an orthonormal sequence \((f_k)\) such that \(\lim _{k \rightarrow \infty } (y_{n_k} - f_k) = 0\). Hence \(\lim _{k \rightarrow \infty } A^*f_k = 0\) and \(f_k \overset{w}{\rightarrow } 0\). Note that if \(x_A\) exists then we can choose \((f_k)\) to be orthogonal to \(Ax_A\) (we can set \(y_0 = Ax_A\), use Lemma 3.3 for \((y_n)_{n \in {\mathbb {N}}_0}\), and then remove \(f_0 = Ax_A\)).
Now we have constructed two orthonormal sequences \((e_n)\) and \((f_n)\) in H and we are ready to apply Lemma 3.4. So, there exist two subsequences \((e_{k_l})_l\) and \((f_{k_j})_j\) of \((e_n)\) and \((f_n),\) respectively, such that
where \(V_f = \overline{span \,\{f_{k_j} : j \in {\mathbb {N}} \}}\) and \(P_{V_f}\) is the orthogonal projection onto \(V_f\). We now show that \((f_{k_j})_j\) is the desired sequence. Note that it is sufficient to prove that  , since we can pass to any subsequence of \((f_{k_j})_j\) which contains its first element without losing conditions from (6). We denote \(P = P_{V_f}\).
, since we can pass to any subsequence of \((f_{k_j})_j\) which contains its first element without losing conditions from (6). We denote \(P = P_{V_f}\).
Let us show that \(A \perp _{BJ}^sP\).
-
(1)
If A attains its norm at \(x_A\) then \(Ax_A \perp V_f\), so \(P^* A x_A = P A x_A = 0\).
-
(2)
Otherwise, \(\lim _{l \rightarrow \infty } P^* A {\tilde{x}}_{k_l} = \lim _{l \rightarrow \infty } P A {\tilde{x}}_{k_l} = \lim _{l \rightarrow \infty } P e_{k_l} = 0\).
Further, we show that \(P \perp _{BJ}^sA\).
-
(a)
If \(\mathop {\mathrm {Ker}}A^*\ne \{0\}\), then \(y_A \in V_f\), so \(\Vert Py_A\Vert =\Vert P\Vert \) and \(A^* P y_A = A^* y_A = 0\).
-
(b)
Otherwise, \(P f_{k_j} = f_{k_j}\) for all \(j \in {\mathbb {N}}\), so \(\lim _{j \rightarrow \infty } \Vert P f_{k_j}\Vert = \Vert P \Vert \) and
$$\begin{aligned} \lim _{j \rightarrow \infty } A^* P f_{k_j} = \lim _{j \rightarrow \infty } A^* f_{k_j} = 0. \end{aligned}$$
Hence we have  . \(\square \)
. \(\square \)
Remark 3.6
If \(\mathop {\mathrm {Ker}}A^* \ne \{ 0 \}\) then \(f_1 \in \mathop {\mathrm {Ker}}A^*\) and the condition \(f_{j_1} = f_1\) is essential for \((f_{j_m})_m\) to satisfy  . Otherwise, it can easily be omitted which is clear from the proof.
. Otherwise, it can easily be omitted which is clear from the proof.
We are finally ready for the main theorem of this section.
Theorem 3.7
Let H be an infinite-dimensional complex Hilbert space and
The following statements hold.
-
(1)
An operator \(A\in {\mathbb {B}}(H)\) is an isolated vertex of the orthograph \(\varGamma ({\mathbb {B}}(H))\) if and only if A is right invertible.
-
(2)
The set \(\mathcal {S}\) is a connected component of the orthograph \(\varGamma ({\mathbb {B}}(H))\) whose diameter is 3.
Proof
- (1)
-
(2)
Assume \(A,B \in \mathcal {S}\). We shall prove that there are nonzero operators \(C_A, C_B \in {\mathbb {B}}(H)\) such that
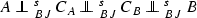 .
.
Let \((f_j^A)\) and \((f_j^B)\) be the sequences from Proposition 3.5 for A and B, respectively, \(V_A = \overline{span \,\{ f_j^A : j \in {\mathbb {N}} \}}\) and \(V_B = \overline{span \,\{ f_j^B : j \in {\mathbb {N}} \}}\). By Lemma 3.4, we may replace \((f_j^A)\) and \((f_j^B)\) with their subsequences such that first elements are preserved and \(\lim _{j \rightarrow \infty } P_{V_A} (f_j^B) = 0\). Then we may use Lemma 3.4 again and obtain \(\lim _{j \rightarrow \infty } P_{V_B} (f_j^A) = 0\). Note that for the subsequences the condition \(\lim _{j \rightarrow \infty } P_{V_A} (f_j^B) = 0\) also holds.
We now take \(C_A = P_{V_A}\) and \(C_B = P_{V_B}\). By Proposition 3.5, we have  and
and  . Moreover, \(f_j^A=C_Af_j^A\), so \(\Vert C_Af_j^A\Vert =\Vert C_A\Vert \) and \(\lim _{j \rightarrow \infty } P_{V_B} (f_j^A) = 0\) imply \(C_A \perp _{BJ}^sC_B\). In the same manner, \(f_j^B=C_Bf_j^B\), so \(\Vert C_Bf_j^B\Vert =\Vert C_B\Vert \) and \(\lim _{j \rightarrow \infty } P_{V_A} (f_j^B) = 0\) imply \(C_B \perp _{BJ}^sC_A\). Hence
. Moreover, \(f_j^A=C_Af_j^A\), so \(\Vert C_Af_j^A\Vert =\Vert C_A\Vert \) and \(\lim _{j \rightarrow \infty } P_{V_B} (f_j^A) = 0\) imply \(C_A \perp _{BJ}^sC_B\). In the same manner, \(f_j^B=C_Bf_j^B\), so \(\Vert C_Bf_j^B\Vert =\Vert C_B\Vert \) and \(\lim _{j \rightarrow \infty } P_{V_A} (f_j^B) = 0\) imply \(C_B \perp _{BJ}^sC_A\). Hence  .
.
This, together with Example 2.6, completes the proof. \(\square \)
4 Commutative unital \(C^*\)-algebras
Let K be a compact Hausdorff space and C(K) the \(C^*\)-algebra of all continuous complex valued functions on K with the norm \(\Vert f\Vert = \max \{|f(t)|:t\in K\}\). Then C(K) is a unital commutative \(C^*\)-algebra and every unital commutative \(C^*\)-algebra is isomorphic to a \(C^*\)-algebra of this type for some compact Hausdorff space ( [10, II.2.2.4 and II.1.1.3.(2)]).
The following result is Corollary 2.1 from [18].
Theorem 4.1
Let K be a compact Hausdorff space, \(f,g\in C(K)\) and
Then \(f\perp _{BJ}g\) if and only if the set \(\{\overline{f(t)}g(t):t\in E_f\}\) is not contained in an open half plane (in \({\mathbb {C}}\)) with boundary that contains the origin.
Using this result we easily get a characterization of the strong Birkhoff–James orthogonality in C(K).
Proposition 4.2
Let K be a compact Hausdorff space, \(f,g\in C(K), f\ne 0\). Then \(f\perp _{BJ}^sg\) if and only if there is \(t_0\in K\) such that \(|f(t_0)|=\Vert f\Vert \) and \(g(t_0)=0\).
Proof
By [2, Theorem 2.5], we know that \(f\perp _{BJ}^sg\) if and only if \(f\perp _{BJ}g{\overline{g}}f\). (Here we regard the \(C^*\)-algebra C(K) as a Hilbert \(C^*\)-module over itself with the inner product of a and b defined as \(a^*b\).) By Theorem 4.1, \(f\perp _{BJ}g{\overline{g}}f\) if and only if the set
is not contained in an open half plane in \({\mathbb {C}}\) with boundary that contains the origin. Obviously, this happens if and only if there is \(t_0\in E_f\) such that \(g(t_0)=0\). \(\square \)
If \(|K| \ge 3\) then the diameter of \(\varGamma (C(K))\) can be equal to either two or three. To distinguish these cases, we will need the following technical result.
Lemma 4.3
Let K be a compact Hausdorff space and \(t_0\in K.\) Then there is \(f\in C(K)\) whose only zero is \(t_0\) if and only if \(t_0\) has a countable local basis in K.
Proof
Suppose \(t_0\in K\) has a countable local basis \((U_n)_n\) in K. Then the sets \(K{\setminus } U_n,n\in {\mathbb {N}},\) are closed and do not intersect the closed set \(A=\{t_0\}\). By Urysohn’s lemma we construct a sequence of continuous functions \(f_n:K \rightarrow [0,1]\) which vanish at \(t_0\) and equal 1 on \(K{\setminus } U_n\) ( [20, Theorem 4.2]). Define \(f := \sum _{n=1}^\infty \frac{1}{2^n} f_n\). By Weierstraß M-test, the sum converges uniformly, so f is continuous and \(f(t_0)=0\). If \(t \ne t_0\), then by the Hausdorff property t does not belong to some neighborhood of \(t_0\), and since \((U_n)_n\) is a local basis, there exists n such that \(t\notin U_n\). Then \(t\in K{\setminus } U_n\), so \(f(t) > 0\). Therefore, the weighted sum f is a continuous function on K with only one zero.
Conversely, suppose there is a function \(f\in C(K)\) with a unique zero \(t_0\in K\). Without loss of generality we may assume that \(f\ge 0,\) that is, \(f:K\rightarrow [0,\infty )\). For each \(n\in {\mathbb {N}}\) we denote \(U_n=f^{-1}\left( \left[ 0,\frac{1}{n}\right) \right) \). Then \(U_n\) are open sets in K containing \(t_0\). Let U be an arbitrary open neighborhood of \(t_0\). Then \(K{\setminus } U\) is compact, as a closed subset of a compact set, so f attains its minimum \(\alpha \) on \(K{\setminus } U\). Since \(f(t)>0\) for \(t\in K{\setminus } U\), we have \(\alpha >0\). Let \(m\in {\mathbb {N}}\) be such that \(\frac{1}{m}<\alpha \). If \(t\in U_m\) then \(f(t)<\frac{1}{m}<\alpha \), so \(t\notin K{\setminus } U\), that is, \(t\in U\). Therefore, \(U_m\subseteq U\). This shows that \((U_n)_n\) is a countable local basis of \(t_0\). \(\square \)
The next lemma provides a lower bound for the diameter of \(\varGamma (C(K))\) in the case when some point in K has a countable local basis.
Lemma 4.4
Let K be a compact Hausdorff space, \(|K|\ge 3\). Suppose there is a point in K with a countable local basis. Then there are nonzero functions \(f,g\in C(K)\), both having at least one zero, such that  and the only \(h\in C(K)\) which satisfies
and the only \(h\in C(K)\) which satisfies  is \(h=0.\)
is \(h=0.\)
Proof
Suppose \(t_1\in K\) has a countable local basis. By Lemma 4.3 there is \(f\in C(K)\) such that \(t_1\) is its only zero. Replacing f with \({\overline{f}}f\) we may assume that f is nonnegative. Let f attain its norm in \(t''.\)
We additionally may assume that there is \(t'\in K,t'\ne t_1,\) such that \(f(t')<\Vert f\Vert \). Namely, if \(f(t)=\Vert f\Vert \) for all \(t\in K{\setminus }\{t_1\}\), then take \(t'\in K{\setminus }\{t_1,t''\}\), construct a continuous function \(\alpha :K\rightarrow [0,1]\) such that \(\alpha (t_1)=\alpha (t')=0\) and \(\alpha (t'')=1\) and replace f with \(f+\alpha \). So, we now have that \(0<f(t')<\Vert f\Vert \), \(t_1\) is the only zero of f, and f attains its norm in \(t''.\)
Further, we may assume that \(f(t')>\frac{1}{2}\Vert f\Vert \): if not, then construct a continuous function \(\beta :K\rightarrow [0,1]\) such that \(\beta (t_1)=0\) and \(\beta (t')=\beta (t'')=1\) and replace f with \(f+\Vert f\Vert \beta \).
Let us define g as
Then \(g\in C(K)\) is nonzero, \(g(t')=0\), and \(t_1\) is the unique point at which g attains its norm (since \(\Vert g\Vert =f(t')\)). Observe that \(f\not \perp _{BJ}^sg,\) because \(g(t)=0\) if and only if \(f(t)=f(t')\) and then \(|f(t)|=|f(t')|\ne \Vert f\Vert .\) Therefore  .
.
Suppose \(h\in C(K)\) is such that  . From \(h\perp _{BJ}^sf\) it follows that \(|h(t_1)|= \Vert h\Vert \), since \(t_1\) is the only zero for f. On the other hand, \(g\perp _{BJ}^sh\) implies \(h(t_1)=0\), since \(t_1\) is the only point in K at which g attains its norm. Therefore, \(h=0\). \(\square \)
. From \(h\perp _{BJ}^sf\) it follows that \(|h(t_1)|= \Vert h\Vert \), since \(t_1\) is the only zero for f. On the other hand, \(g\perp _{BJ}^sh\) implies \(h(t_1)=0\), since \(t_1\) is the only point in K at which g attains its norm. Therefore, \(h=0\). \(\square \)
We now prove the main theorem of this section.
Theorem 4.5
Suppose K is a compact Hausdorff space with \(|K|\ge 3\). Let
The following statements hold.
-
(1)
Isolated points in \(\varGamma (C(K))\) are exactly invertible elements of C(K), that is, nonzero elements of \(C(K){\setminus } \mathcal {S}_K.\)
-
(2)
The set \(\mathcal {S}_K\) is a connected component of the orthograph \(\varGamma (C(K))\). Its diameter is 3 if at least one point of K has a countable local basis, otherwise its diameter is 2.
Remark 4.6
An example of a compact Hausdorff space where no point has a countable local basis is \(I^I\), the set of all functions from \(I=[0,1]\) into itself, equipped with a product topology (which on each factor I coincides with a standard topology on I).
Proof
(1) Suppose \(f\in \mathcal {S}_K\) and let \(t_1,t_2\in K\) be such that \(f(t_1)=0\) and \(|f(t_2)|=\Vert f\Vert \). Then there exists \(h\in C(K)\) such that \(|h(t_1)|=\Vert h\Vert \ne 0\) and \(h(t_2)=0\) and, by Proposition 4.2, it holds  , so f is not isolated in \(\varGamma (C(K))\).
, so f is not isolated in \(\varGamma (C(K))\).
For the converse we apply Lemma 1.2.
(2) Let us first show that the diameter of \(\varGamma (\mathcal {S}_K)\) is at least two. Take a nonnegative nonzero function \(f\in S_K\) such that for some \(t_1,t',t''\in K\) it holds
(such a function can be constructed in a similar way as in the proof of the previous lemma). Then \(f^2\) and f do not belong to the same vertex of the orthograph and, by Proposition 4.2, 
To prove the upper bounds, take any two functions \(f,g\in \mathcal {S}_K \) such that  . Suppose \(|K|\ge 4\) and let \(t_1,s_1,t_2,s_2\in K\) be such that
. Suppose \(|K|\ge 4\) and let \(t_1,s_1,t_2,s_2\in K\) be such that
If \(t_1,t_2,s_1,s_2\) are four different points, then we take \(h\in C(K)\) such that
and hence  . Suppose that some points among \(t_1,t_2,s_1,s_2\) are the same. Of course, \(t_1\ne t_2\) and \(s_1\ne s_2\).
. Suppose that some points among \(t_1,t_2,s_1,s_2\) are the same. Of course, \(t_1\ne t_2\) and \(s_1\ne s_2\).
(a) If \(t_1=s_1\) or \(t_2=s_2\) then \(t_2\ne s_1\) and \(s_2\ne t_1\), so h as in (8) is still a well-defined nonzero function such that  .
.
(b) If \(t_1=s_2\) and \(t_2=s_1\), then  which contradicts our assumption.
which contradicts our assumption.
(c) It remains to consider the case \(t_1=s_2\) and \(t_2\ne s_1\) (the case \(t_1\ne s_2\) and \(t_2= s_1\) is analogous). Observe that then \(t_1, t_2, s_1\) are three different points. We split into two subcases.
First, suppose that f has two distinct zeros: \(t_1\) and \(t_1'\). Observe that \(t_1'\ne t_2.\) We can also assume \(t_1'\ne s_1\), otherwise we can repeat arguments from (a) with \(t_1'\) replaced by \(t_1\). Hence, \(t_1',t_1,t_2,s_1\) are four different points. Let \(h\in C(K)\) be a nonzero function such that
Then  .
.
Suppose, still under case (c), that \(t_1\) is the only zero of f. Construct nonzero functions \(h_1,h_2\in C(K)\) such that
Then 
By Lemma 4.3, if no point of K has a countable local basis, then each noninvertible function on K has at least two zeros, so for all \(f,g\in \mathcal {S}_K\) there is a nonzero \(h\in \mathcal {S}_K\) such that  Therefore, in this case the diameter is 2. Further, if some point of K has a countable local basis, then there is a noninvertible function with only one zero. From the above proof and Lemma 4.4 we conclude that in this case the diameter of \(\varGamma (\mathcal {S}_K)\) is 3.
Therefore, in this case the diameter is 2. Further, if some point of K has a countable local basis, then there is a noninvertible function with only one zero. From the above proof and Lemma 4.4 we conclude that in this case the diameter of \(\varGamma (\mathcal {S}_K)\) is 3.
Let us now verify the case \(|K|=3\) (that is, \({\mathbb {C}}^3\) with the maximum norm). As above, find \(t_1,s_1,t_2,s_2\in K\) with the properties as in (7). Since \(|K|=3,\) some points among \(t_1,t_2,s_1,s_2\) are the same and the discussion is as before. Of course, an ordered triple in \({\mathbb {C}}^3\) with only one zero coordinate exists. Therefore, the diameter in this case is 3. \(\square \)
Remark 4.7
If \(|K|=2\) then C(K) coincides with \({\mathbb {C}}^2\) with the maximum norm. If \(\mathcal {S}_K\) is defined as in Theorem 4.5 then \(\mathcal {S}_K=\{\lambda (0,1),\mu (1,0):\lambda ,\mu \in {\mathbb {C}}{\setminus }\{0\}\}\) and, obviously,  .
.
5 Commutative nonunital \(C^*\)-algebras
Let us now consider the case of a nonunital commutative \(C^*\)-algebra. For each such a \(C^*\)-algebra \(\mathcal {A}\) there is a noncompact locally compact Hausdorff space \(\varOmega \) such that \(\mathcal {A}\) is isomorphic to \(C_0(\varOmega )\), the \(C^*\)-algebra of all continuous complex functions on \(\varOmega \) vanishing at infinity. Let \(K=\varOmega \cup \{s_0\}\) be the one-point compactification of \(\varOmega .\) Then we can identify \(C_0(\varOmega )\) with the \(C^*\)-subalgebra \(\{f\in C(K): f(s_0)=0\}\) of C(K).
We first need to extend Proposition 4.2.
Proposition 5.1
Let \(K=\varOmega \cup \{s_0\}\) be the one-point compactification of a noncompact locally compact Hausdorff space \(\varOmega \), \(f,g\in C_0(\varOmega ), f\ne 0\). Then \(f\perp _{BJ}^sg\) if and only if there is \(t_0\in \varOmega \) such that \(|f(t_0)|=\Vert f\Vert \) and \(g(t_0)=0\).
Proof
Let \(f,g\in C_0(\varOmega )\) be such that \(f\perp _{BJ}^sg\) in \(C_0(\varOmega ).\) This means that
On the other hand, if we regard the same f and g as elements of C(K), then \(f\perp _{BJ}^sg\) in C(K) means that
Although (10) seems stronger than (9), they are actually equivalent. Namely, by [2, Theorem 2.5], for two elements a and b in any \(C^*\)-algebra \(\mathcal {A}\) it holds that \(a\perp _{BJ}^sb\) (in \(\mathcal {A}\)) if and only \(a\perp _{BJ}bb^*a\), that is \(\Vert a+\lambda bb^*a\Vert \ge \Vert a\Vert \) for all \(\lambda \in {\mathbb {C}}.\) Therefore, since the norm on C(K) extends the norm on \(C_0(\varOmega ),\) both (9) and (10) are equivalent to \(f\perp _{BJ} g{\overline{g}}f,\) which does not depend on the ambient \(C^*\)-algebra (it is only important that f and g are in \(C_0(\varOmega )\subseteq C(K)\)).
So, if \(f,g\in C_0(\varOmega )\) are nonzero functions such that \(f\perp _{BJ}^sg\) (in \(C_0(\varOmega )\) and then also in C(K)), then by Proposition 4.2 there is \(t_0\in K\) such that \(|f(t_0)|=\Vert f\Vert \) and \(g(t_0)=0.\) Since \(f\ne 0\), it has to be \(t_0\ne s_0\), so \(t_0\in \varOmega .\) The converse is obvious. \(\square \)
The following lemma is based on Lemma 4.3.
Lemma 5.2
Let \(K=\varOmega \cup \{s_0\}\) be the one-point compactification of a noncompact locally compact Hausdorff space \(\varOmega \). Then there is \(f\in C_0(\varOmega )\) which, besides \(s_0\), has exactly one zero \(t_0\in \varOmega \) if and only if \(s_0\) and \(t_0\) both have countable local bases in K.
Proof
Suppose \(s_0,t_0\in K\) have countable local bases in K. By Lemma 4.3, there are \(f_0,g_0\in C(K)\) such that \(s_0\) is the only zero for \(f_0\), and \(t_0\) is the only zero for \(g_0.\) Then \(f=f_0g_0\) belongs to \(C_0(\varOmega )\) and its only zeros are \(s_0\) and \(t_0.\)
Suppose now that there is a function \(f\in C_0(\varOmega )\) with only two zeros, \(s_0\) and \(t_0.\) Without loss of generality we may assume that \(f:K\rightarrow [0,\infty ).\) By Urysohn’s lemma we construct a continuous function \(g:K\rightarrow [0,1]\) such that \(g(s_0)=0\) and \(g(t_0)=1.\) Then \(s_0\in K\) is the only zero of \(h=f+g\in C(K)\), so by Lemma 4.3 we conclude that \(s_0\) has a countable local basis in K. Similarly, we can conclude that \(t_0\) has a countable local basis in K. \(\square \)
Similar to the unital case (see Lemma 4.4), functions in \(C_0(\varOmega )\) with only one zero in \(\varOmega \) will produce pairs of functions for which paths of length less than three are not possible.
Lemma 5.3
Let \(K=\varOmega \cup \{s_0\}\) be the one-point compactification of a noncompact locally compact Hausdorff space \(\varOmega \). Suppose there is \(t_1\in \varOmega \) such that \(s_0\) and \(t_1\) have countable local bases in K. Then there are nonzero functions \(f,g\in C_0(\varOmega )\), both having zeros in \(\varOmega \), such that  and the only \(h\in C_0(\varOmega )\) which satisfies
and the only \(h\in C_0(\varOmega )\) which satisfies  is \(h=0.\)
is \(h=0.\)
Proof
By Lemma 5.2 there is \(f\in C_0(\varOmega )\) such that \(t_1\) and \(s_0\) are the only zeros of f. Replacing f with \({\overline{f}}f\) we may assume that f is nonnegative. As in the proof of Lemma 4.4 we may assume that there is \(t'\ne s_0,t_1\) such that \(f(t')\ne \Vert f\Vert .\)
Let \(g_1\in C(K)\) be a nonnegative function such that \(t_1\) is the unique point at which \(g_1\) attains its maximum. (Such \(g_1\) exists: since \(t_1\) has a countable local basis, there is \(\alpha \in C(K)\) such that \(t_1\) is its only zero. Then we can take \(g_1(t)=\Vert \alpha \Vert -|\alpha (t)|\).) We may also assume that \(g_1(t')=g_1(s_0)\). Namely, if \(g_1(t')\ne g_1(s_0)\), for example, \(g_1(t')> g_1(s_0),\) construct a continuous function \(\beta :K\rightarrow [0,1]\) such that \(\beta (s_0)=\beta (t_1)=1\) and \(\beta (t')=0\) and replace \(g_1\) with \(g_1+(g_1(t')-g_1(s_0))\beta \).
We shall modify \(g_1\) to the function g in \(C_0(\varOmega )\) which also attains its maximum only at \(t_1\), which has a zero in \(\varOmega \) and such that  .
.
The set
is closed and \(t',s_0\notin K_1.\) Let \(\gamma :K\rightarrow [0,1]\) be a continuous function such that \(\gamma (s_0)=\gamma (t')=0\) and \(\gamma (t)=1\) for \(t\in K_1.\) Define
Then we have the following.
-
(1)
It holds \(g(s_0)=g(t')=0,\) so \(g\in C_0(\varOmega )\) and it has a zero in \(\varOmega .\)
-
(2)
If f attains its norm at t, then \(t\in K_1{\setminus }\{t_1\}\) and therefore \(g(t)=g_1(t)+2\Vert g_1\Vert \ne 0.\) This proves that
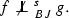
-
(3)
Obviously, \(g(t_1)=3\Vert g_1\Vert \). Further, it is easy to check that
$$\begin{aligned} -\Vert g_1\Vert <-g_1(s_0)\le g(t)\le g_1(t)+2\Vert g_1\Vert \gamma (t)\le 3\Vert g_1\Vert \quad \forall t\in K, \end{aligned}$$so \(\Vert g\Vert =3\Vert g_1\Vert .\) Now we know that g attains its maximum at \(t_1,\) but let us show that \(t_1\) is the unique point with that property. Suppose \(|g(t)|=3\Vert g_1\Vert \) for some \(t\in K\). Since \(g(t)\ge -g_1(s_0)\), it is impossible that \(g(t)=-3\Vert g_1\Vert \). Since g is a real valued function, it remains to consider the case when \(g(t)=3\Vert g_1\Vert .\) A simple computation shows that then
$$\begin{aligned} (\Vert g_1\Vert -g_1(t))+(2\Vert g_1\Vert +g_1(s_0))(1-\gamma (t))=0. \end{aligned}$$Since both summands on the left hand side of this equality are nonnegative, they sum up to 0 if and only if both of them are equal to zero, that is \(g_1(t)=\Vert g_1\Vert \) and \(\gamma (t)=1.\) The only t which satisfies these conditions is \(t_1.\) Therefore, \(t_1\) is the only point at which g attains its maximum.
Finally, suppose \(h\in C_0(\varOmega )\) is such that  . By Proposition 5.1, from \(h\perp _{BJ}^sf\) it follows that \(|h(t_1)|= \Vert h\Vert \), since \(t_1\) is the only zero of f in \(\varOmega .\) On the other hand, \(g\perp _{BJ}^sh\) implies \(h(t_1)=0\), since \(t_1\) is the only point in \(\varOmega \) at which g attains its norm. Therefore, \(h=0\). \(\square \)
. By Proposition 5.1, from \(h\perp _{BJ}^sf\) it follows that \(|h(t_1)|= \Vert h\Vert \), since \(t_1\) is the only zero of f in \(\varOmega .\) On the other hand, \(g\perp _{BJ}^sh\) implies \(h(t_1)=0\), since \(t_1\) is the only point in \(\varOmega \) at which g attains its norm. Therefore, \(h=0\). \(\square \)
We are now ready to describe the diameter of components in the orthograph \(\varGamma (C_0(\varOmega )).\)
Theorem 5.4
Let \(\varOmega \) be a noncompact locally compact Hausdorff space, \(K=\varOmega \cup \{s_0\}\) the one-point compactification of \(\varOmega \). Let
The following statements hold.
-
(1)
Isolated vertices in \(\varGamma (C_0(\varOmega ))\) exist if and only if \(s_0\) has a countable local basis in K; in this case the set of all isolated vertices equals the set of nonzero elements of \(C_0(\varOmega ){\setminus } \mathcal {S}_\varOmega .\)
-
(2)
The set \(\mathcal {S}_\varOmega \) is a connected component of the orthograph \(\varGamma (C_0(\varOmega ))\). Its diameter is 3 if there is \(t_1\in \varOmega \) such that \(s_0\) and \(t_1\) have countable local bases in K, otherwise its diameter is 2.
Proof
(1) Suppose \(s_0\in K\) has a countable local basis in K. By Lemma 4.3, there is a function \(f\in C(K)\) such that \(s_0\) is its only zero, that is, \(f\in C_0(\varOmega )\) and f does not have zeros in \(\varOmega .\) Then, by Proposition 5.1, there is no nonzero \(g\in C_0(\varOmega )\) such that \(g\perp _{BJ}^sf.\) Therefore, all such f are isolated vertices in \(\varGamma (C_0(\varOmega )).\)
Suppose \(s_0\in K\) does not have a countable local basis in K. Then each \(f\in C_0(\varOmega )\) has another zero, say \(t_1\in \varOmega \). Let \(t_2\in K\) be such that \(|f(t_2)|=\Vert f\Vert .\) Construct nonzero \(g\in C(K)\) such that \(g(s_0)=g(t_2)=0\) and \(|g(t_1)|=\Vert g\Vert .\) Then \(g\in C_0(\varOmega )\) and  so f is not an isolated vertex in \(\varGamma (C_0(\varOmega ))\).
so f is not an isolated vertex in \(\varGamma (C_0(\varOmega ))\).
(2) The proof is analogous to the proof of Theorem 4.5. The only difference is that the functions constructed there have to be in \(C_0(\varOmega )\), that is, we additionally require that \(s_0\) is their zero. Since all the points \(t_1,t_2,s_1,s_2,t',t''\), that appear in the construction of these functions, differ from \(s_0\), this additional condition does not collide with other required conditions. Also, we use Lemmas 5.2 and 5.3 to get the diameter of \(\varGamma (\mathcal {S}_\varOmega )\). \(\square \)
6 Concluding remarks
We conclude the paper with some final thoughts.
(1) As we have mentioned in the introductory section, the notion of the strong Birkhoff–James orthogonality was first introduced in the setting of Hilbert \(C^*\)-modules as a modular version of the classical Birkhoff–James orthogonality. We assumed that Hilbert \(C^*\)-modules were right modules, but the same can be done for left Hilbert \(C^*\)-modules. It is well known that every right Hilbert \(C^*\)-module is also a left Hilbert \(C^*\)-module (in general, over some other \(C^*\)-algebra, see [10, II.7.6.5]).
When regarding a \(C^*\)-algebra \(\mathcal {A}\) as a left Hilbert \(C^*\)-module over itself, then a (left) module action is an algebra multiplication from the left, and the inner product of a and b is defined as \(ab^*\). Then, instead of (2) we have the following relation:
Of course, in the case of commutative \(C^*\)-algebras this is the same as (2). In general, since the involution is an antilinear isometric antiautomorphism of \(\mathcal {A}\), this is equivalent to
that is, (11) is equivalent to \(a^*\perp _{BJ}^sb^*.\) Therefore, description of the orthograph with respect to the “left” mutual strong Birkhoff–James orthogonality follows from the results obtained for the (right) mutual strong Birkhoff–James orthogonality.
(2) By Lemma 1.2 from the introduction, each right-invertible element in a unital \(C^*\)-algebra is an isolated vertex in the discussed orthograph. In the cases of \({\mathbb {B}}(H)\) and C(K) the converses also hold: right invertible elements are the only isolated vertices. It is an open question whether the converse of Lemma 1.2 holds: if \(\mathcal {A}\) is an arbitrary unital \(C^*\)-algebra and \(a\in \mathcal {A}\) an isolated vertex in \(\varGamma (\mathcal {A})\), is a necessarily right-invertible?
(3) In the previous section we consider a nonunital commutative \(C^*\)-algebra, so all its elements are right-noninvertible when regarded as elements of the unitization C(K) of the \(C^*\)-algebra \(C_0(\varOmega )\) (and therefore nonisolated in \(\varGamma (C(K))\)). However, some elements of \(C_0(\varOmega )\) may still be isolated vertices in \(\varGamma (C_0(\varOmega )).\) Also, it would be interesting to consider the case \({\mathbb {K}}(H)\) of all compact operators on an infinite-dimensional Hilbert space.
(4) Linear preserver problems concern the characterization of linear maps of an algebra \(\mathcal {A}\) into itself which preserve certain properties of some elements of \(\mathcal {A}\) or relations between them. For example, automorphisms and antiautomorphisms of algebras preserve many relations and properties, so in various preserver problems they appear not just as examples, but the only examples of such mappings. Describing orthogonality preservers is an interesting topic studied by many authors; for the preservers of the (strong) Birkhoff–James orthogonality see e.g. [4, 11, 26]. Knowing orthographs one can describe (linear) mappings which preserve the relation defining the orthograph. In our subsequent paper we shall discuss maps that preserve the mutual strong Birkhoff–James orthogonality in certain \(C^*\)-algebras.
References
Arambašić, Lj., Rajić, R.: The Birkhoff–James orthogonality in Hilbert \(C^*\)-modules. Linear Algebra Appl. 437(7), 1913–1929 (2012)
Arambašić, Lj., Rajić, R.: A strong version of the Birkhoff–James orthogonality in Hilbert \(C^*\)-modules. Ann. Funct. Anal. 5(1), 109–120 (2014)
Arambašić, Lj., Rajić, R.: On three concepts of orthogonality in Hilbert \(C^*\)-modules. Linear Multilinear A. 63(7), 1485–1500 (2015)
Arambašić, Lj., Rajić, R.: Operators preserving the strong Birkhoff–James orthogonality on \(\mathbb{B}(H)\). Linear Algebra Appl. 471, 394–404 (2015)
Arambašić, Lj., Rajić, R.: On symmetry of the (strong) Birkhoff–James orthogonality in Hilbert \(C^*\)-modules. Ann. Funct. Anal. 7(1), 17–23 (2016)
Bakhadly, B.R., Guterman, A.E., Markova, O.V.: Graphs defined by orthogonality. J. Math. Sci. 207, 698–717 (2015)
Bhatia, R., Šemrl, P.: Orthogonality of matrices and some distance problems. Linear Algebra Appl. 287(1–3), 77–85 (1999)
Bhattacharyya, T., Grover, P.: Characterization of Birkhoff–James orthogonality. J. Math. Anal. Appl. 407(2), 350–358 (2013)
Birkhoff, G.: Orthogonality in linear metric spaces. Duke Math. J. 1, 169–172 (1935)
Blackadar, B.: Operator Algebras. Theory of \(C^*\)-algebras and von Neumann Algebras. Encyclopaedia of Mathematical Sciences, vol. 122. Springer, Berlin (2006)
Blanco, A., Turnšek, A.: On maps that preserve orthogonality in normed spaces. Proc. R. Soc. Edinb. Sect. A 136, 709–716 (2006)
Chmieliński, J., Wójcik, P.: Approximate symmetry of Birkhoff orthogonality. J. Math. Anal. Appl. 461(1), 625–640 (2018)
Guterman, A.E., Markova, O.V.: Orthogonality graphs of matrices over skew fields. Zap. Nauchn. Sem. POMI, 463, 81–93 (2017); English translation: J. Math. Sci. (N. Y.) 232(6), 797–804 (2018)
Halmos, P.R.: Limsups of lats. Indiana Univ. Math. J. 29, 293–311 (1980)
James, R.C.: Orthogonality in normed linear spaces. Duke Math. J. 12, 291–302 (1945)
James, R.C.: Inner products in normed linear spaces. Bull. Am. Math. Soc. 53, 559–566 (1947)
James, R.C.: Orthogonality and linear functionals in normed linear spaces. Trans. Am. Math. Soc. 61, 265–292 (1947)
Kečkić, D.: Orthogonality and smooth points in \(C(K)\) and \(C_b(\Omega )\). Eurasian Math. J. 3(4), 44–52 (2012)
Komuro, N., Saito, K.S., Tanaka, R.: On symmetry of Birkhoff orthogonality in the positive cones of \(C^*\)-algebras with applications. J. Math. Anal. Appl. 474(2), 1488–1497 (2019)
Lang, S.: Real and Functional Analysis. Graduate Texts in Mathematics, 3rd edn. Springer, New York (1993)
Magajna, B.: On the distance to finite-dimensional subspaces in operator algebras. J. Lond. Math. Soc. 47(2), 516–532 (1993)
Manuilov, V.M., Troïtsky, E.V.: Hilbert \(C^*\)-Modules. Translations of Mathematical Monographs, vol. 22. American Mathematical Society, Providence (2005)
Moslehian, M.S., Zamani, A.: Characterizations of operator Birkhoff–James orthogonality. Can. Math. Bull. 60(4), 816–829 (2017)
Paul, K., Sain, D., Mal, A., Mandal, K.: Orthogonality of bounded linear operators on complex Banach spaces. Adv. Oper. Theory 3(3), 699–709 (2018)
Stampfli, J.G.: The norm of a derivation. Pac. J. Math. 33, 737–747 (1970)
Turnšek, A.: On operators preserving James’ orthogonality. Linear Algebra Appl. 407, 189–195 (2005)
Zamani, A., Wójcik, P.: Numerical radius orthogonality in \(C^*\)-algebras. Ann. Funct. Anal. (2020). https://doi.org/10.1007/s43034-020-00071-z
Acknowledgements
The authors thank the anonymous referees for useful comments and suggestions that helped improve the presentation from the original manuscript. Ljiljana Arambašić and Rajna Rajić were fully supported by the Croatian Science Foundation under the project IP-2016-06-1046. Alexander Guterman and Svetlana Zhilina were fully supported by RSF grant 17-11-01124. Bojan Kuzma acknowledges the financial support from the Slovenian Research Agency, ARRS (research core funding No. P1-0222 and No. P1-0285).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Michael Frank.
Rights and permissions
About this article
Cite this article
Arambašić, L., Guterman, A., Kuzma, B. et al. Orthograph related to mutual strong Birkhoff–James orthogonality in \(C^*\)-algebras. Banach J. Math. Anal. 14, 1751–1772 (2020). https://doi.org/10.1007/s43037-020-00074-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s43037-020-00074-x




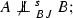
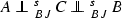 then
then 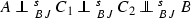 , then
, then 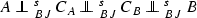 .
.