Pointwise conditions for perturbed Hammerstein integral equations with monotone nonlinear, nonlocal elements

Abstract

We consider perturbed Hammerstein integral equations of the form

$$\begin{aligned} y(t)= & {} \gamma _1(t)F_1(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1} (y))+\gamma _2(t)F_2(\psi _1(y),\psi _2(y),\dots ,\psi _{n_2}(y))\\&+\,\lambda \int _0^1G(t,s)f(s,y(s))\ ds, \end{aligned}$$

where the $\varphi _i$’s and $\psi _i$’s are linear functionals realized as Stieltjes integrals with associated signed Stieltjes measures. Positive solutions of the integral equation can be related to positive solutions of boundary value problems, and we demonstrate that such problems have solutions under relatively mild hypotheses on the functions $F_1$, $F_2$, and f. We provide examples to illustrate the applicability of the results and their relationship to existing results in the literature, and we mention applications to radially symmetric solutions of PDEs as well as beam deflection modeling. Our results are achieved by using a nonstandard order cone together with an associated nonstandard open set.

1 Introduction

In this paper we consider perturbed Hammerstein integral equations of the form

$$\begin{aligned} \begin{aligned} y(t)&=\gamma _1(t)F_1(\varphi _1(y),\varphi _2(y),\dots , \varphi _{n_1}(y))+\gamma _2(t)F_2(\psi _1(y),\psi _2(y),\dots ,\psi _{n_2}(y))\\&\quad +\,\lambda \int _0^1G(t,s)f(s,y(s))\ ds, \end{aligned} \end{aligned}$$

(1.1)

where $0\le t\le 1$. In (1.1) the functions $\varvec{\xi }\mapsto F_i(\varvec{\xi })$, for $i=1,2$, are assumed to be continuous, nondecreasing scalar-valued maps on ${\mathbb {R}}^{n_i}$, and the collection of functionals $\{\varphi _i\}_{i=1}^{n_1}$ and $\{\psi _j\}_{j=1}^{n_2}$, where $n_1$, $n_2\in {\mathbb {N}}$, are assumed to be linear functionals realized as

$$\begin{aligned} \varphi _i(y)=\int _{[0,1]}y(s)\ d\alpha _i(s) \end{aligned}$$

and

$$\begin{aligned} \psi _j(y)=\int _{[0,1]}y(s)\ d\beta _j(s), \end{aligned}$$

where the measures associated to these Stieltjes integrals are allowed to be signed. In addition, the maps $t\mapsto \gamma _i(t)$, $(t,s)\mapsto G(t,s)$, and $(t,y)\mapsto f(t,y)$ are continuous on [0, 1], $[0,1]\times [0,1]$, and $[0,1]\times [0,+\infty )$, respectively; the precise hypotheses utilized are given in Sect. 2. Notice that solutions of integral equation (1.1) can be associated to solutions of various nonlocal boundary value problems (BVPs) with multiple nonlocal elements. BVPs with one or more nonlocal elements can be used in modeling temperature regulation, beam deformation and displacement, and chemical reactor theory among other applications—see Infante and Pietramala [16, 18] and Cabada, Infante, and Tojo [4] for additional details.

We would like to mention a few immediate applications of our results. Since we study the very general integral equation (1.1) a couple of specific applications are as follows:

• radially symmetric solutions of the elliptic PDE

  $$\begin{aligned} -(\Delta u)(\varvec{x})=a(t)g(|u(\varvec{x})|)\text {, }0<R_1\le |\varvec{x}|\le R_2<+\infty \text {, }\varvec{x}\in {\mathbb {R}}^{n} \end{aligned}$$

  (1.2)

  equipped with (radially symmetric) nonlocal boundary conditions.

• solutions to ODEs of the form

  $$\begin{aligned} u^{(4)}(t)=f(t,u(t))\text {, }t\in (0,1) \end{aligned}$$

  (1.3)

  subject to nonlocal boundary conditions.

In the case of problem (1.2) it is known (see, for example, Goodrich [13], Infante and Pietramala [19], Lan [25], and Lan and Webb [26]) that one can transform PDE (1.2) into an ODE. Then, in the case of nonlocal boundary conditions, we can study existence of solution of (1.2) by studying the corresponding problem for (1.1).

In the case of problem (1.3) this type of ODE can model the deflections of an elastic beam—see, for example, either Anderson and Hoffacker [1] or Infante and Pietramala [17]. In this case, if we equip (1.3) with nonlocal boundary conditions, then this can represent controllers on the beam that affect, for example, the displacement of the beam or the shearing force at a point. So, if (1.3) is equipped with the nonlocal boundary condition

$$\begin{aligned} u''(1)-\varphi (u)=0, \end{aligned}$$

where $\varphi (u)$ is a nonlocal element, then this could model a controller located along the bar that affects the bending moment at the right endpoint ($t=1$) of the bar.

Our primary contribution is to show that we can obtain the existence of a positive solution to problem (1.1), for example, by assuming relatively mild hypotheses on the functions and functionals appearing in the perturbed Hammerstein equation. In particular, in past works on problems involving nonlinear, nonlocal elements it has been common to assume that the functions $F_1$ and $F_2$ satisfy either asymptotic or uniform growth conditions. Here, by contrast, in some cases the only condition we need impose on either $F_1$ or $F_2$ is a pointwise condition—see Theorem 2.5. In addition, we demonstrate in Remark 2.10 that in some cases our methodology is more broadly and easily applicable than competing methodologies.

More specifically, in previous papers by the author [9, 10] relatively general nonlocal conditions were considered. However, in those works it was required that such nonlocal elements be “asymptotically related” to a linear nonlocal element—an idea borrowed, essentially, from regularity theory (cf., Chipot and Evans [6] or Foss and Goodrich [8], for example). This resulted in somewhat technical conditions that had to be checked in order to the apply the results—see, for example, [9, Conditions (H1)–(H7), (H1b), (H2b), (H4b)] and [10, (H1)–(H6)].

In addition, recent papers by the author, namely [11,12,13,14], have considered rather general nonlocal, nonlinear elements. However, the methods utilized in [11,12,13,14] do not permit multiple nonlocal elements as in (1.1). By contrast, they only permit a single nonlocal element. The admission of two or more nonlocal elements requires a slightly different approach. The reason for this is that, as explained later in this section, our methods rely on controlling the size of the nonlocal elements—i.e., we want to have as precise information as possible regarding the value of $\varphi _i(y)$ and $\psi _j(y)$ for each i and j. This, however, turns out to be a somewhat delicate problem. Essentially, this is a topological problem since for sets $\{E_j\}_{j=1}^{n}$ it is generally not the case that $\partial \left( \bigcap _{j=1}^{n}E_j\right) =\bigcap _{j=1}^{n}\partial E_j$. As a consequence of this topological fact, while we have good control over the size of any one nonlocal element, it turns out to be difficult to control simultaneously the size of all $n_1+n_2$ elements appearing in (1.1)—this is due to the construction of the sets ${\widehat{V}}_{\rho ,\varphi _i}$ and ${\widehat{V}}_{\rho ,\psi _i}$ in (1.5). Therefore, for these reasons we must proceed somewhat more cautiously when dealing now with multiple nonlocal elements as opposed to a single element, and this is reflected in the fact that we consider here only the case in which the functions $F_1$ and $F_2$ are nondecreasing.

Furthermore, we would like to mention that in a recent paper of Cianciaruso, Infante, and Pietramala [7] the authors treat very general nonlocal elements, somewhat akin to the formulation in (1.1). However, the authors’ methodology requires one to find linear functionals that act as upper and lower bounds on the nonlocal element. Moreover, their results apply to nonlocal elements with positive Stieltjes measures only. By contrast our methodology applies to signed measures and, in addition, our conditions on $F_1$ and $F_2$ can be pointwise in character, which, in particular, means that we do not have to search for linear functionals to act as appropriate upper and lower bounds on our nonlocal elements. In fact, we show by means of Example 2.9 and Remark 2.10 that in some cases our methodology is more straightforward, easier to apply, and more widely applicable than other methodologies, including the one introduced in [7]. In addition, since the recent paper by Cabada, Infante, and Tojo [5] makes use of the same basic hypotheses on the nonlocal elements as in [7], albeit in a more general overall problem, the same comments apply to the methodology utilized in [5].

In order to deduce our main results we utilize the nonstandard cone ${\mathcal {K}}$ defined by

$$\begin{aligned} {\mathcal {K}}:= & {} \left\{ y\in {\mathscr {C}}([0,1])\ : \ y(t)\ge 0,\varphi _i(y)\ge \left( \inf _{s\in S_0}\frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s) \ d\alpha _i(t)\right) \Vert y\Vert \text {,}\right. \nonumber \\ \quad \psi _j(y)\ge & {} \left. \left( \inf _{s\in S_0}\frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s)\ d\beta _j(t)\right) \Vert y\Vert \text {, }\min _{t\in [a,b]}y(t)\ge \eta _0\Vert y\Vert \right\} , \end{aligned}$$

(1.4)

where $\eta _0\in (0,1]$, $(a,b)\Subset (0,1)$, and $S_0\subseteq [0,1]$ is some set of full measure on which, for each $i\in {\mathbb {N}}_1^{n_1}:=\{1,2,\dots ,n_1\}$ and $j\in {\mathbb {N}}_1^{n_2}:=\{1,2,\dots ,n_2\}$, the quantities

$$\begin{aligned} \inf _{s\in S_0}\frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s)\ d\alpha _i(t)\quad \text {and}\quad \inf _{s\in S_0}\frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s)\ d\beta _j(t) \end{aligned}$$

in (1.4) are positive real numbers; here and throughout we define the map $s\mapsto {\mathscr {G}}(s)$ by ${\mathscr {G}}(s):=\sup _{t\in [0,1]}G(t,s)$. Hence, in our analysis of problem (1.1) we reduce the collection of possible solution functions to those that result in the coercivity of the functionals $\varphi _i$ and $\psi _j$. The cone ${\mathcal {K}}$ was first introduced by the author in some recent papers [11,12,13,14], none of which, as already mentioned, addressed the general formulation suggested by (1.1). Strictly speaking, our methodology does not require the Harnack-like inequality $\min _{t\in [a,b]}y(t)\ge \eta _0\Vert y\Vert$ in ${\mathcal {K}}$, but its inclusion can improve the existence results for problem (1.1).

As a consequence of our focus on the coercivity of the functionals, we also utilize a nonstandard open set that proves useful in improving the existence theorems one can provide in special cases. In particular, here we make use of the sets, which are relatively open in ${\mathcal {K}}$,

$$\begin{aligned} {\widehat{V}}_{\rho ,\varphi _i}:=\{y\in {\mathcal {K}}\ : \ \varphi _i(y)<\rho \}\quad \text {and}\quad {\widehat{V}}_{\rho ,\psi _i}:=\{y\in {\mathcal {K}}\ : \ \psi _i(y)<\rho \}. \end{aligned}$$

(1.5)

These types of sets were used by the author in [11] in the context of fractional-order differential equations. By using these sets together with the classical Leray–Schauder index, we demonstrate that we can improve the existence results that can be achieved. The use of (1.5) is only feasible since we have in hand the coercivity conditions in ${\mathcal {K}}$. Thus, this is an upshot of restricting the elements of ${\mathcal {K}}$ to those that cause the linear functionals to be coercive. In any case, we describe ${\widehat{V}}_{\rho ,\varphi _i}$ and ${\widehat{V}}_{\rho ,\psi _i}$ in greater detail in Sect. 2.

To conclude this section we briefly mention some of the literature related to our study of problem (1.1) that has not already been mentioned. The papers by Picone [27] and Whyburn [30], while classical, are of historical value for those interested in the origins of boundary value problems with nonlocal-type boundary conditions. More recently, numerous papers have appeared in the last several years on various problems (e.g., perturbed Hammerstein integral equations, ordinary differential equations, elliptic partial differential equations) with nonlocal elements. For example, Webb and Infante [28, 29] provided an elegant and general framework for addressing nonlocal boundary value problems. Cabada, Cid, and Infante [3], Infante [16], Infante, Minhós, and Pietramala [20], Jankowski [21], Karakostas and Tsamatos [22, 23], Karakostas [24], and Yang [31, 32] similarly considered boundary value problems with nonlocal boundary conditions. In addition, Anderson [2] specifically considered nonlinear boundary conditions in a relatively general context. Finally, the monographs by Guo and Lakshmikantham [15] and by Zeidler [33] are good references for the topological fixed point theory used in our proofs in Sect. 2.

But as alluded to earlier in this section, among the preceding papers that treat nonlinear, nonlocal boundary conditions, none of them utilizes pointwise-type conditions in the context of multiple nonlocal elements, owing to the fact that each of these works uses more classical cones and associated open sets. Here, by contrast, we demonstrate explicitly that the use of the ${\widehat{V}}$-type sets in certain circumstances can yield some advantages over more traditional approaches even when arbitrarily many nonlocal elements are treated simultaneously.

2 Preliminaries, main result, and discussion

We begin by stating the various conditions that we impose on integral equation (1.1). These are listed as (H1)–(H5) below. Note that conditions (H1), (H3), and (H4) impose various regularity and structural conditions on the functionals $\varphi _i$ and $\psi _j$ as well as the kernel G. Condition (H2) imposes regularity and growth conditions on the functions $\gamma _i$ and $F_i$. Finally, condition (H5) ensures that $\gamma _1$, $\gamma _2\in {\mathcal {K}}$. Note that throughout this paper we denote by $\Vert \cdot \Vert$ the usual maximum norm on the space ${\mathscr {C}}([0,1])$.

H1::

For each $i\in {\mathbb {N}}_1^{n_1}$ and $j\in {\mathbb {N}}_{1}^{n_2}$ the functionals $\varphi _i(y)$ and $\psi _j(y)$ have the form

$$\begin{aligned} \varphi _i(y):=\int _{[0,1]}y(t)\ d\alpha _i(t)\text {, }\psi _j(y):=\int _{[0,1]}y(t)\ d\beta _j(t), \end{aligned}$$

where $\alpha _i$, $\beta _j\ : \ [0,1]\rightarrow {\mathbb {R}}$ are of bounded variation on [0, 1]. Moreover, we denote by $C_1^i$, $D_1^j>0$ finite constants such that

$$\begin{aligned} |\varphi _i(y)|\le C_1^i\Vert y\Vert \quad \text {and}\quad |\psi _j(y)|\le D_1^j\Vert y\Vert , \end{aligned}$$

for each $y\in {\mathscr {C}}([0,1])$.

H2::

(1):

The functions $\gamma _1$, $\gamma _2\ : \ [0,1]\rightarrow [0,+\infty )$ and $f\ : \ [0,1]\times [0,+\infty )\rightarrow [0,+\infty )$ are continuous.

(2):

There exists at least one index $i_0\in \{1,2\}$ such that $\Vert \gamma _{i_0}\Vert >0$.

(3):

For each $i=1,2$ the function $F_i\ : \ {\mathbb {R}}^{n_i}\rightarrow {\mathbb {R}}$ is monotone increasing in the sense that if $\varvec{x}\le \varvec{y}$, then $F_i(\varvec{x})\le F_i(\varvec{y})$; note that we follow the convention that given $\varvec{x}:=(x_1,x_2,\dots ,x_n)$, $\varvec{y}:=(y_1,y_2,\dots ,y_n)\in {\mathbb {R}}^{n}$, then $\varvec{x}\le \varvec{y}$ if and only if $x_i\le y_i$ for each $i\in {\mathbb {N}}_1^{n}$.

H3::

The map $G\ : \ [0,1]\times [0,1]\rightarrow [0,+\infty )$ satisfies:

(1):

$G\in L^1([0,1]\times [0,1])$;

(2):

for a.e. $s\in [0,1]$ it follows that

$$\begin{aligned} \lim _{t\rightarrow \tau }|G(t,s)-G(\tau ,s)|=0 \end{aligned}$$

for each $\tau \in [0,1]$;

(3):

${\mathscr {G}}(s)=\sup _{t\in [0,1]}G(t,s)<+\infty$ for each $s\in [0,1]$; and

(4):

there exists an interval $(a,b)\Subset (0,1)$ and a constant $\eta _0:=\eta _0(a,b)\in (0,1]$ such that

$$\begin{aligned} \min _{t\in [a,b]}G(t,s)\ge \eta _0{\mathscr {G}}(s), \end{aligned}$$

for each $s\in [0,1]$.

H4::

Assume that for each $i\in {\mathbb {N}}_1^{n_1}$ and $j\in {\mathbb {N}}_1^{n_2}$ the maps

$$\begin{aligned} s\mapsto \frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s)\ d\alpha _i(t)\quad \text {and}\quad s\mapsto \frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s)\ d\beta _j(t) \end{aligned}$$

are defined for each $s\in S_0$, where $S_0\subseteq [0,1]$ has full measure (i.e., $\left| S_0\right| =1$), and that the constants defined by

$$\begin{aligned} C_0^i:=\inf _{s\in S_0}\frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s)\ d\alpha _i(t) \end{aligned}$$

and

$$\begin{aligned} D_0^j:=\inf _{s\in S_0}\frac{1}{{\mathscr {G}}(s)}\int _0^1G(t,s)\ d\beta _j(t) \end{aligned}$$

satisfy

$$\begin{aligned} C_0^i\text {, }D_0^j\in (0,+\infty ), \end{aligned}$$

for each $i\in {\mathbb {N}}_1^{n_1}$ and $j\in {\mathbb {N}}_1^{n_2}$.

H5::

For $k=1,2$ we have that

$$\begin{aligned} \varphi _i\left( \gamma _k\right) \ge C_0^i\Vert \gamma _k\Vert \text { and }\psi _j\left( \gamma _k\right) \ge D_0^j\Vert \gamma _k\Vert , \end{aligned}$$

for each $i\in {\mathbb {N}}_1^{n_1}$ and $j\in {\mathbb {N}}_1^{n_2}$, and also that

$$\begin{aligned} \min _{t\in [a,b]}\gamma _k(t)\ge \eta _0\Vert \gamma _k\Vert \end{aligned}$$

for each $k=1,2$, where $\eta _0$, a, and b are the same numbers as in condition (H3.4) above.

Remark 2.1

Note that by condition (H5) it follows that ${\mathcal {K}}\ne \varnothing$.

Next we provide some properties of the sets ${\widehat{V}}_{\rho ,\varphi _i}$ and ${\widehat{V}}_{\rho ,\psi _j}$, which are important for the results that follow. The proofs of these results can be isolated from [11], and so, we do not repeat the proofs here. Note that in Lemma 2.2 and the sequel we denote by $\Omega _{\rho }$, for $\rho >0$, the set

$$\begin{aligned} \Omega _{\rho }:=\{y\in {\mathcal {K}}\ : \ \Vert y\Vert <\rho \}. \end{aligned}$$

Lemma 2.2

For each fixed $\rho >0$, $i\in {\mathbb {N}}_1^{n_1}$, and $j\in {\mathbb {N}}_1^{n_2}$, it holds that

$$\begin{aligned} \Omega _{\frac{\rho }{C_1^i}}\subseteq {\widehat{V}}_{\rho ,\varphi _i}\subseteq \Omega _{\frac{\rho }{C_0^i}}. \end{aligned}$$

and that

$$\begin{aligned} \Omega _{\frac{\rho }{D_1^j}}\subseteq {\widehat{V}}_{\rho ,\psi _j}\subseteq \Omega _{\frac{\rho }{D_0^j}}. \end{aligned}$$

Lemma 2.3

For each fixed $\rho >0$, $i\in {\mathbb {N}}_1^{n_1}$, and $j\in {\mathbb {N}}_1^{n_2}$, each of the sets ${\widehat{V}}_{\rho ,\varphi _i}$ and ${\widehat{V}}_{\rho ,\psi _j}$ defined in (1.5) is a (relatively) open set in ${\mathcal {K}}$ and, furthermore, is bounded.

We next introduce some notation that we use in this section.

Remark 2.4

For compact sets $X\subset [0,1]$ and $Y\subseteq [0,+\infty )$ we denote by $f_{X\times Y}^{m}$ the set

$$\begin{aligned} f_{X\times Y}^{m}:=\min _{(t,y)\in X\times Y}f(t,y) \end{aligned}$$

and by $f_{X\times Y}^{M}$ the set

$$\begin{aligned} f_{X\times Y}^{m}:=\max _{(t,y)\in X\times Y}f(t,y). \end{aligned}$$

Now we state and prove the first main existence result for problem (1.1), which considers the case in which $F_1(\varvec{\xi })\not \equiv 0$ and $F_2(\varvec{\xi })\equiv 0$. Note that in what follows we define the operator $T\ : \ {\mathcal {K}}\rightarrow {\mathscr {C}}([0,1])$ by

$$\begin{aligned} (Ty)(t):= & {} \gamma _1(t)F_1(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1}(y))+\gamma _2(t)F_2(\psi _1(y),\psi _2(y),\dots ,\psi _{n_2}(y))\\&+\,\lambda \int _0^1G(t,s)f(s,y(s))\ ds. \end{aligned}$$

Then, in the usual way, a fixed point of T will correspond to the solution of integral equation (1.1).

Theorem 2.5

Assume that conditions (H1)–(H5) are satisfied with $\Vert \gamma _1\Vert >0$, $F_1(\varvec{\xi })\not \equiv 0$, and $F_2(\varvec{\xi })\equiv 0$. In addition, assume that there exist numbers $\rho _1$, $\rho _2>0$, with $\rho _1\ne \rho _2$, such that each of the following is true.

• (1) For the number $\rho _1$ it holds that

  $$\begin{aligned} \begin{aligned}&F_1(\varvec{0})\left( \min _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\&\quad \quad +\lambda \left( f_{[a,b]\times \left[ \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}\right] }^m\right) \min _{1\le j\le n_1}\int _a^b\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds>\rho _1, \end{aligned} \end{aligned}$$

  for the numbers a, $b\in {\mathbb {R}}$ in condition (H3.4).

• (2) For the number $\rho _2$ it holds that

  $$\begin{aligned} \begin{aligned}&F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\&\quad +\lambda \left( f_{[0,1]\times \left[ 0,\min _{1\le j\le n_1}\frac{\rho _2}{C_0^j}\right] }^{M}\right) \max _{1\le j\le n_1}\int _0^1\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds<\rho _2. \end{aligned} \end{aligned}$$

Then problem (1.1) has at least one positive solution.

Proof

It is clear that the operator T is completely continuous due to the regularity conditions imposed by conditions (H1)–(H5). At the same time by repeating arguments given in [11] one can show that $T({\mathcal {K}})\subseteq {\mathcal {K}}$. So, we do not show that here.

Instead we will now show that $\mu y\ne Ty$ for all $\mu \ge 1$ and $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right)$. To this end, suppose for contradiction that there exists a number $\mu \ge 1$ and a function $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right)$ such that $\mu y=Ty$. Now, since

$$\begin{aligned} y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) , \end{aligned}$$

we know that

$$\begin{aligned} \varphi _j(y)\le \rho _2, \end{aligned}$$

(2.1)

for each $1\le j\le n_1$. Furthermore, because y is in the boundary of $\bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}$, there must exist an index $j_0\in {\mathbb {N}}_{1}^{n_1}$ such that

$$\begin{aligned} \varphi _{j_0}(y)=\rho _2. \end{aligned}$$

Consequently, applying $\varphi _{j_0}$ to both sides of the operator equation $\mu y=Ty$ we obtain

$$\begin{aligned} \begin{aligned} \rho _2&\le \mu \varphi _{j_0}(y)\\&=\varphi _{j_0}\left( \gamma _1\right) F_1(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1}(y))+\lambda \int _0^1\int _0^1 G(t,s)f(s,y(s))\ d\alpha _{j_0}(t)\ ds. \end{aligned} \end{aligned}$$

Moreover, since $\varvec{\xi }\mapsto F_1(\varvec{\xi })$ is a monotone map it follows that

$$\begin{aligned} F_1(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1}(y))\le F_1(\rho _2,\rho _2,\dots ,\rho _2), \end{aligned}$$

where we have utilized inequality (2.1). Thus, we conclude that

$$\begin{aligned} \begin{aligned} \rho _2&\le \mu \varphi _{j_0}(y)\\&=\varphi _{j_0}\left( \gamma _1\right) F_1(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1}(y)){+}\lambda \int _0^1\int _0^1 G(t,s)f(s,y(s))\ d\alpha _{j_0}(t)\ ds\\&\le \varphi _{j_0}\left( \gamma _1\right) F_1(\rho _2,\rho _2,\dots ,\rho _2)+\lambda \int _0^1\int _0^1 G(t,s)f(s,y(s))\ d\alpha _{j_0}(t)\ ds\\&\le F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\&\quad +\,\max _{1\le j\le n_1}\lambda \int _0^1\int _0^1 G(t,s)f(s,y(s))\ d\alpha _{j}(t)\ ds. \end{aligned} \end{aligned}$$

(2.2)

Now, as mentioned above we have that $\varphi _j(y)\le \rho _2$ for each $j\in {\mathbb {N}}_1^{n_1}$. Consequently, by the coercivity of the functions $\varphi _j$, it follows that

$$\begin{aligned} C_0^j\Vert y\Vert \le \varphi _j(y)\le \rho _2, \end{aligned}$$

for each $j\in {\mathbb {N}}_1^{n_1}$. Therefore, we conclude that

$$\begin{aligned} \Vert y\Vert \le \frac{\rho _2}{C_0^j}, \end{aligned}$$

for each $j\in {\mathbb {N}}_1^{n_1}$. In particular, this means that

$$\begin{aligned} \Vert y\Vert \le \min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} . \end{aligned}$$

In addition, we notice that

$$\begin{aligned} \begin{aligned}&\int _0^1\int _0^1G(t,s)f(s,y(s))\ d\alpha _j(t)\ ds\\&\quad =\int _0^1\underbrace{\left[ \int _0^1G(t,s)\ d\alpha _j(t)\right] }_{\ge 0\text {, a.e. }s\in [0,1]}f(s,y(s))\ ds\\&\quad \ge \int _0^1\int _0^1G(t,s)\left( f_{[0,1]\times \left[ 0,\min _{1\le j\le n_1}\frac{\rho _2}{C_0^j}\right] }^{M}\right) \ d\alpha _j(t)\ ds. \end{aligned} \end{aligned}$$

Thus, from the preceding inequality, estimate (2.2), and condition (2) in the statement of the theorem we estimate

$$\begin{aligned} \begin{aligned} \rho _2&\le F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\ {}&\qquad +\max _{1\le j\le n_1}\lambda \int _0^1\int _0^1 G(t,s)f(s,y(s))\ d\alpha _{j}(t)\ ds\\ {}&\le F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _{}\left( \gamma _1\right) \right) \\ {}&\qquad +\lambda \left( f_{[0,1]\times \left[ 0,\min _{1\le j\le n_1}\frac{\rho _2}{C_0^j}\right] }^{M}\right) \max _{1\le j\le n_1}\int _0^1\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds\\ {}&<\rho _2, \end{aligned} \end{aligned}$$

which is a contradiction. Consequently, we conclude that

$$\begin{aligned} i_{{\mathcal {K}}}\left( T,\bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) =1. \end{aligned}$$

On the other hand, let $e(t):=\gamma _1(t)$; recall that $\Vert \gamma _1\Vert \ne 0$ and that $\gamma _1\in {\mathcal {K}}$. We claim that for each $\mu \ge 0$ and $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right)$ that $y\ne Ty+\mu e$. So, suppose for contradiction that there does exist $\mu \ge 0$ and $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right)$ such that $y=Ty+\mu e$.

Now, since $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right)$ it follows that

$$\begin{aligned} 0\le \varphi _j(y)\le \rho _1, \end{aligned}$$

for all $1\le j\le n_1$. As in the preceding part of the proof, there must exist an index $j_0\in {\mathbb {N}}_1^{n_1}$ such that $\varphi _{j_0}(y)=\rho _1$. Applying this functional to both sides of the equation $y=Ty+\mu e$ we obtain the estimate

$$\begin{aligned} \rho _1{\ge }\varphi _{j_0}\left( \gamma _1\right) F_1(\varphi _1(y),\varphi _2(y),{\dots },\varphi _{n_1}(y)){+}\lambda \int _0^1\int _0^1G(t,s)f(s,y(s))\ d\alpha _{j_0}(t)\ ds. \end{aligned}$$

Moreover, together with the monotonicity of the map $\varvec{\xi }\mapsto F_1(\varvec{\xi })$, it follows that

$$\begin{aligned} F(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1}(y))\ge F_1(0,0,\dots ,0)=:F_1(\varvec{0}). \end{aligned}$$

Consequently, we deduce that

$$\begin{aligned} \begin{aligned} \rho _1&{\ge }\varphi _{j_0}\left( \gamma _1\right) F_1(\varphi _1(y),\varphi _2(y),{\dots },\varphi _{n_1}(y)){+}\lambda \int _0^1\int _0^1G(t,s)f(s,y(s))\ d\alpha _{j_0}(t)\ ds\\&\ge \varphi _{j_0}\left( \gamma _1\right) F_1(\varvec{0})+\lambda \int _0^1\int _0^1G(t,s)f(s,y(s))\ d\alpha _{j_0}(t)\ ds. \end{aligned} \end{aligned}$$

(2.3)

At the same time, since $\varphi _{j_0}(y)=\rho _1$ we know that

$$\begin{aligned} C_1^{j_0}\Vert y\Vert \ge \varphi _{j_0}(y)=\rho _1, \end{aligned}$$

whence

$$\begin{aligned} \Vert y\Vert \ge \frac{\rho _1}{C_1^{j_0}}\ge \frac{\rho _1}{\max _{1\le j\le n_1}C_1^j}. \end{aligned}$$

Similarly, since $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right)$, it follows that

$$\begin{aligned} C_0^j\Vert y\Vert \le \varphi _j(y)\le \rho _1, \end{aligned}$$

for each $j\in {\mathbb {N}}_1^{n_1}$, from which it follows that

$$\begin{aligned} y(t)\le \Vert y\Vert \le \frac{\rho _1}{C_0^j}\le \frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}, \end{aligned}$$

for each $t\in [0,1]$. Likewise it follows that

$$\begin{aligned} y(s)\ge \min _{t\in [a,b]}y(t)\ge \eta _0\Vert y\Vert \ge \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j}, \end{aligned}$$

for each $s\in [a,b]$. All in all, then, we conclude that

$$\begin{aligned} \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j}\le y(t)\le \frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}, \end{aligned}$$

for each $t\in [a,b]$. Consequently, we deduce that for $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right)$ we must have that

$$\begin{aligned} f(t,y)\ge f_{[a,b]\times \left[ \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}\right] }^m, \end{aligned}$$

for each $t\in [a,b]$. It thus follows from the above estimates together with inequality (2.3) that

$$\begin{aligned} \begin{aligned} \rho _1&\ge \varphi _{j_0}\left( \gamma _1\right) F_1(\mathbf {0})+\lambda \int _0^1\int _0^1G(t,s)f(s,y(s))\ d\alpha _{j_0}(t)\ ds\\ {}&\ge \varphi _{j_0}\left( \gamma _1\right) F_1(\mathbf {0})\\ {}&\qquad +\lambda \left( f_{[a,b]\times \left[ \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}\right] }^m\right) \int _a^b\int _0^1 G(t,s)\ d\alpha _{j_0}(t)\ ds\\ {}&\ge F_1(\mathbf {0})\left( \min _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\ {}&\qquad +\lambda \left( f_{[a,b]\times \left[ \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}\right] }^m\right) \min _{1\le j\le n_1}\int _a^b\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds\\ {}&>\rho _1,\end{aligned} \end{aligned}$$

(2.4)

which is a contradiction; note that to obtain inequality (2.4) we have used that

$$\begin{aligned} \int _0^1G(t,s)\ d\alpha _{j_0}(t)\ge 0, \end{aligned}$$

a.e. $s\in [0,1]$. Therefore, we conclude that

$$\begin{aligned} i_{{\mathcal {K}}}\left( T,\bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right) =0. \end{aligned}$$

In summary, we conclude that there exists a function $y_0$ satisfying

$$\begin{aligned} y_0\in \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) \setminus \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right) , \end{aligned}$$

if $\rho _2>\rho _1>0$, or satisfying

$$\begin{aligned} y_0\in \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right) \setminus \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) , \end{aligned}$$

if $\rho _1>\rho _2>0$, such that $Ty_0=y_0$. Note that if $y\in \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}$, then $\varphi _j(y)<\rho _1$ for each $1\le j\le n_1$. At the same time, if $y\in \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}$, then $\varphi _j(y)<\rho _2$ for each $1\le j\le n_1$. Therefore, if $\rho _2>\rho _1>0$, then it follows that if $y\in \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}$, then

$$\begin{aligned} \varphi _j(y)<\rho _1<\rho _2, \end{aligned}$$

for each $1\le j\le n_1$, whence $y\in \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}$. Consequently, we conclude that

$$\begin{aligned} \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\subseteq \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}, \end{aligned}$$

and this inclusion is strict provided that $\rho _1\ne \rho _2$. Similarly, if $\rho _1>\rho _2>0$, then

$$\begin{aligned} \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\subseteq \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}, \end{aligned}$$

with strict inclusion. In other words, we may safely conclude that

$$\begin{aligned} \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) \setminus \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right) \ne \varnothing \end{aligned}$$

in case $\rho _2>\rho _1>0$, and similarly that

$$\begin{aligned} \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right) \setminus \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) \ne \varnothing \end{aligned}$$

in case $\rho _1>\rho _2>0$, thus ensuring that $y_0$ does not belong to the empty set. Finally, since the function $y_0$ is a positive solution of problem (1.1), the proof is thus complete. $\square$

We next present a variation of Theorem 2.5 that allows for slightly more flexibility in some circumstances.

Corollary 2.6

Assume that conditions (H1)–(H5) are satisfied with $\Vert \gamma _1\Vert >0$, $F_1(\varvec{\xi })\not \equiv 0$, and $F_2(\varvec{\xi })\equiv 0$. In addition, assume that there exist numbers $\rho _1$, $\rho _2>0$, with $\rho _1\ne \rho _2$, such that each of the following is true.

• (1) For the number $\rho _1$ it holds that

  $$\begin{aligned} \begin{aligned}&F_1\left( \frac{\rho _1C_0^1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1C_0^2}{\max _{1\le j\le n_1}C_1^j},\dots ,\frac{\rho _1C_0^{n_1}}{\max _{1\le j\le n_1}C_1^j}\right) \left( \min _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\&\quad \quad +\lambda \left( f_{[a,b]\times \left[ \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}\right] }^m\right) \min _{1\le j\le n_1}\int _a^b\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds>\rho _1, \end{aligned} \end{aligned}$$

  for the numbers a, $b\in {\mathbb {R}}$ in condition (H3.4).

• (2) For the number $\rho _2$ it holds that

  $$\begin{aligned} \begin{aligned}&F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\&\quad +\lambda \left( f_{[0,1]\times \left[ 0,\min _{1\le j\le n_1}\frac{\rho _2}{C_0^j}\right] }^{M}\right) \max _{1\le j\le n_1}\int _0^1\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds<\rho _2. \end{aligned} \end{aligned}$$

Then problem (1.1) has at least one positive solution.

Proof

The proof is essentially the same as that of Theorem 2.5 with one exception. Instead of using the monotonicity of $F_1$ to write

$$\begin{aligned} F_1(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1}(y))\ge F_1(\varvec{0}), \end{aligned}$$

we instead recall that

$$\begin{aligned} \varphi _j(y)\ge C_0^j\Vert y\Vert , \end{aligned}$$

for each $j\in {\mathbb {N}}_1^{n_1}$. Then noticing that

$$\begin{aligned} \Vert y\Vert \ge \frac{\rho _1}{\max _{1\le j\le n_1}C_1^j}, \end{aligned}$$

for each $j\in {\mathbb {N}}_1^{n_1}$, it follows upon combining these two preceding estimates that

$$\begin{aligned} \begin{aligned}&F_1(\varphi _1(y),\varphi _2(y),\dots ,\varphi _{n_1}(y))\\&\quad \ge F_1\left( \frac{\rho _1C_0^1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1C_0^2}{\max _{1\le j\le n_1}C_1^j},\dots ,\frac{\rho _1C_0^{n_1}}{\max _{1\le j\le n_1}C_1^j}\right) , \end{aligned} \end{aligned}$$

from which the desired conclusion follows. $\square$

Remark 2.7

Evidently numerous variations of the argument in condition (1) of Corollary 2.6 can be written.

Numerous other variations of Theorem 2.5 may be provided if one desires. For example, instead of applying $\varphi _{j_0}$ to both sides of the operator equation $\mu y=Ty$ in the first part of the proof of Theorem 2.5, we could instead apply $\psi _{j_0}$. Nonetheless, for the sake of brevity we provide only one such corollary. This corollary demonstrates that if both $F_1(\varvec{\xi })\not \equiv 0$ and $F_2(\varvec{\xi })\not \equiv 0$, then a modified version of Theorem 2.5 may be written.

Corollary 2.8

Assume that conditions (H1)–(H5) are satisfied. In addition, assume that there exist numbers $\rho _1$, $\rho _2>0$, with $\rho _1\ne \rho _2$, such that each of the following is true.

• (1) For the number $\rho _1$ it holds that

  $$\begin{aligned} \begin{aligned}&F_1(\varvec{0})\left( \min _{1\le j\le n_1}\varphi _{j}\left( \gamma _1\right) \right) \\&\quad \quad +\lambda \left( f_{[a,b]\times \left[ \frac{\eta _0\rho _1}{\max _{1\le j\le n_1}C_1^j},\frac{\rho _1}{\min _{1\le j\le n_1}C_0^j}\right] }^m\right) \min _{1\le j\le n_1}\int _a^b\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds>\rho _1. \end{aligned} \end{aligned}$$

• (2) For the number $\rho _2$ it holds that

  $$\begin{aligned} \begin{aligned}&F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _1\right) \right) \\&\quad +F_2\left( D_1^1\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} ,\dots ,D_1^{n_2}\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} \right) \left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _2\right) \right) \\&\quad +\lambda \left( f_{[0,1]\times \left[ 0,\min _{1\le j\le n_1}\frac{\rho _2}{C_0^j}\right] }^{M}\right) \max _{1\le j\le n_1}\int _0^1\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds\\&<\rho _2. \end{aligned} \end{aligned}$$

Then problem (1.1) has at least one positive solution.

Proof

Since $(t,\varvec{\xi })\mapsto \gamma _2(t)F_2(\varvec{\xi })$ is a nonnegative map, it follows that repeating exactly the same steps as in the proof of Theorem 2.5 we obtain that

$$\begin{aligned} i_{{\mathcal {K}}}\left( T,\bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _1,\varphi _j}\right) =0. \end{aligned}$$

So, we will not repeat that part of the proof.

On the other hand, the proof that

$$\begin{aligned} i_{{\mathcal {K}}}\left( T,\bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) =1 \end{aligned}$$

changes slightly. As before, assume for contradiction the existence of $\mu \ge 1$ and $y\in \partial \left( \bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right)$ such that $\mu y=Ty$. Then $\varphi _j(y)<\rho _2$ for each $1\le j\le n_1$ and there exists $j_0\in {\mathbb {N}}_1^{n_1}$ such that $\varphi _{j_0}(y)=\rho _2$. Just as in the proof of Theorem 2.5 we find that

$$\begin{aligned} \begin{aligned} \rho _2&\le F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _1\right) \right) \\&\quad +F_2(\psi _1(y),\psi _2(y),\dots ,\psi _{n_2}(y))\left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _2\right) \right) \\&\quad +\max _{1\le j\le n_1}\lambda \int _0^1\int _0^1G(t,s)f(s,y(s))\ d\alpha _j(t)\ ds. \end{aligned} \end{aligned}$$

Now, as calculated in the proof of Theorem 2.5 we notice that

$$\begin{aligned} \Vert y\Vert \le \min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} . \end{aligned}$$

This means that

$$\begin{aligned} \psi _j(y)\le D_1^j\Vert y\Vert \le D_1^j\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} , \end{aligned}$$

for each $j\in {\mathbb {N}}_1^{n_1}$. Since the map $\varvec{\xi }\mapsto F_2(\varvec{\xi })$ is increasing, it follows that

$$\begin{aligned} \begin{aligned}&F_2(\psi _1(y),\psi _2(y),\dots ,\psi _{n_2}(y))\\&\quad \le F_2\left( D_1^1\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} ,D_1^2\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} ,\dots ,D_1^{n_2}\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} \right) . \end{aligned} \end{aligned}$$

And from the preceding estimates we conclude that

$$\begin{aligned} \rho _2&\le F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _1\right) \right) \\ {}&\qquad +F_2(\psi _1(y),\psi _2(y),\dots ,\psi _{n_2}(y))\left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _2\right) \right) \\ {}&\qquad +\max _{1\le j\le n_1}\lambda \int _0^1\int _0^1G(t,s)f(s,y(s))\ d\alpha _j(t)\ ds\\ {}&\le F_1(\rho _2,\rho _2,\dots ,\rho _2)\left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _1\right) \right) \\ {}&\qquad +F_2\left( D_1^1\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} ,\dots ,D_1^{n_2}\min _{1\le j\le n_1}\left\{ \frac{\rho _2}{C_0^j}\right\} \right) \left( \max _{1\le j\le n_1}\varphi _j\left( \gamma _2\right) \right) \\ {}&\qquad +\lambda \left( f_{[0,1]\times \left[ 0,\min _{1\le j\le n_1}\frac{\rho _2}{C_0^j}\right] }^{M}\right) \max _{1\le j\le n_1}\int _0^1\int _0^1 G(t,s)\ d\alpha _{j}(t)\ ds. \end{aligned}$$

Consequently, condition (2) in the statement of the corollary yields the contradiction $\rho _2<\rho _2$, and so, we conclude that

$$\begin{aligned} i_{{\mathcal {K}}}\left( T,\bigcap _{j=1}^{n_1}{\widehat{V}}_{\rho _2,\varphi _j}\right) =1. \end{aligned}$$

Thus, in the end we are able to arrive at the same conclusion as in the proof of Theorem 2.5. And this completes the proof. $\square$

We conclude with a couple examples to illustrate the application of the result and, moreover, to compare its application to other related results in the literature. We will specialize our example to the case in which $n_1=2$ and $F_2(\varvec{\xi })\equiv 0$ in order to keep the example clearer and more manageable. More complicated situations can be treated, of course.

In addition, while this example illustrates the application of the results to the case of a second-order ODE with nonlocal BCs, as was mentioned in Sect. 1 it is easy to see that the same calculations lead to applications to radially symmetric solutions of elliptic PDEs as well as beam deflection models with nonlocal controllers. Since these extensions are straightforward, we give the example in the situation of a second-order ODE to focus more clearly on the application of the results rather than various applications.

Example 2.9

Consider the boundary value problem given by

$$\begin{aligned} \begin{aligned} -y''&=\lambda f(t,y(t))\text {, }t\in (0,1)\\ y(0)&=\left( y\left( \frac{1}{2}\right) \right) ^2+\sqrt{y\left( \frac{3}{4}\right) }\\ y(1)&=0. \end{aligned} \end{aligned}$$

(2.5)

Observe that in this case we define $F_1$, $F_2\ : \ [0,+\infty )\times [0,+\infty )\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} \begin{aligned} F_1(\varvec{x})&:=x_1^2+\sqrt{x_2}\\ F_2(\varvec{x})&\equiv 0. \end{aligned} \end{aligned}$$

If we put $\gamma _1(t):=1-t$ and $\gamma _2(t)\equiv 0$ as well as

$$\begin{aligned} \varphi _1(y):=y\left( \frac{1}{2}\right) \text {, }\varphi _2(y):=y\left( \frac{3}{4}\right) \text {, and }G(t,s):={\left\{ \begin{array}{ll} t(1-s)\text {, }&{}\quad 0\le t\le s\le 1\\ s(1-t)\text {, }&{}\quad 0\le s\le t\le 1\end{array}\right. } \end{aligned}$$

in integral equation (1.1), then solutions of the integral equation correspond to solutions of boundary value problem (2.5). Notice, importantly, that the map $\varvec{x}\mapsto F_1(\varvec{x})$ is increasing in each argument in the sense that if $\varvec{x}\le \varvec{y}$, then $F_1(\varvec{x})\le F_1(\varvec{y})$.

We now perform some preliminary calculations. Notice that

$$\begin{aligned} \varphi _1\left( \gamma _1\right) =\frac{1}{2}\quad \text {and}\quad \varphi _2\left( \gamma _1\right) =\frac{1}{4}. \end{aligned}$$

(2.6)

In addition, we calculate the following; note that we have elected to put $[a,b]:=\left[ \frac{1}{4},\frac{3}{4}\right]$ in this example.

$$\begin{aligned} \begin{aligned} \int _{\frac{1}{4}}^{\frac{3}{4}}\int _0^1G(t,s)\ d\alpha _1(t)\ ds&=\frac{1}{16}\\ \int _{\frac{1}{4}}^{\frac{3}{4}}\int _0^1G(t,s)\ d\alpha _2(t)\ ds&=\frac{3}{16}\\ \int _0^1\int _0^1G(t,s)\ d\alpha _1(t)\ ds&=\frac{1}{8}\\ \int _0^1\int _0^1G(t,s)\ d\alpha _2(t)\ ds&=\frac{3}{32}\\ C_0^1=\inf _{s\in (0,1)}\frac{1}{s(1-s)}G\left( \frac{1}{2},s\right)&=\frac{1}{2}\\ C_0^2=\inf _{s\in (0,1)}\frac{1}{s(1-s)}G\left( \frac{3}{4},s\right)&=\frac{1}{4}\\ C_1^1&=1\\ C_1^2&=1 \end{aligned} \end{aligned}$$

(2.7)

So,

$$\begin{aligned} \min \{C_0^1,C_0^2\}=\frac{1}{4}\quad \text {and}\quad \max \{C_1^1,C_1^2\}=1. \end{aligned}$$

Note also that $\eta _0:=\frac{1}{4}$ here and that each of the following is true.

$$\begin{aligned} \begin{aligned} \varphi _1(\gamma _1)&=\frac{1}{2}\ge C_0^1\Vert \gamma _1\Vert \\ \varphi _2(\gamma _1)&=\frac{1}{4}\ge C_0^2\Vert \gamma _1\Vert \\ \min _{t\in \left[ \frac{1}{4},\frac{3}{4}\right] }\gamma _1(t)&=\frac{1}{4}\ge \eta _0\Vert \gamma _1\Vert \end{aligned} \end{aligned}$$

Then using (2.6)–(2.7) we see that condition (1) in Theorem 2.5 reduces to

$$\begin{aligned} 16\rho _1<\lambda f_{\left[ \frac{1}{4},\frac{3}{4}\right] \times \left[ \frac{1}{4}\rho _1,4\rho _1\right] }^{m}, \end{aligned}$$

whereas condition (2) reduces to

$$\begin{aligned} \frac{1}{2}\left( \rho _2+\frac{1}{\sqrt{\rho _2}}\right) +\frac{1}{8\rho _2}\lambda f_{[0,1]\times \left[ 0,2\rho _2\right] }^{M}<1. \end{aligned}$$

We note that in order for condition (2) to be satisfied we must have that

$$\begin{aligned} \frac{1}{2}\left( \rho _2+\frac{1}{\sqrt{\rho _2}}\right) <1, \end{aligned}$$

and this inequality is satisfied only if $\rho _2\in (0.382,1)$ to three decimal places of accuracy; thus, it is not a vacuous condition. For example, if we select $\rho _1:=4$ and $\rho _2:=\frac{2}{5}$, then both conditions are satisfied provided that

$$\begin{aligned} \lambda >32\left( f_{\left[ \frac{1}{4},\frac{3}{4}\right] \times [1,16]}^{m}\right) ^{-1} \end{aligned}$$

and

$$\begin{aligned} \frac{1}{2}\left( \frac{2}{5}+\sqrt{\frac{5}{2}}\right) +\frac{5}{16}\lambda f_{[0,1]\times \left[ 0,\frac{4}{5}\right] }^{M}<1. \end{aligned}$$

In other words, problem (1.1) will have at least one positive solution, $y_0$, satisfying the localization $y_0\in \overline{{\widehat{V}}_{4}}\setminus {\widehat{V}}_{0.4}$ provided that

$$\begin{aligned} \lambda \in \left( 32\left( f_{\left[ \frac{1}{4},\frac{3}{4}\right] \times [1,16]}^{m}\right) ^{-1},\frac{16}{5}\left( f_{[0,1]\times \left[ 0,\frac{4}{5}\right] }^{M}\right) ^{-1}\left[ 1-\frac{1}{2}\left( \frac{2}{5}+\sqrt{\frac{5}{2}}\right) \right] \right) , \end{aligned}$$

assuming that this set is nonempty, which requires that

$$\begin{aligned} \left( f_{[0,1]\times \left[ 0,\frac{4}{5}\right] }^{M}\right) \left( f_{\left[ \frac{1}{4},\frac{3}{4}\right] \times [1,16]}^{m}\right) ^{-1}<\frac{1}{10}\left[ 1-\frac{1}{2}\left( \frac{2}{5}+\sqrt{\frac{5}{2}}\right) \right] \approx 0.159. \end{aligned}$$

Alternatively, if we set $\lambda =1$, then problem (2.5) becomes

$$\begin{aligned} \begin{aligned} -y''&=f(t,y(t))\text {, }t\in (0,1)\\ y(0)&=\left( y\left( \frac{1}{2}\right) \right) ^2+\sqrt{y\left( \frac{3}{4}\right) }\\ y(1)&=0. \end{aligned} \end{aligned}$$

(2.8)

It then follows from Theorem 2.5 that problem (2.8) will have at least one positive solution provided that f satisfies (to three decimal places of accuracy)

$$\begin{aligned} \begin{aligned} f_{\left[ \frac{1}{4},\frac{3}{4}\right] \times [1,16]}^{m}&>32\\ f_{[0,1]\times \left[ 0,\frac{4}{5}\right] }^{M}&<0.0302. \end{aligned} \end{aligned}$$

Remark 2.10

It is worth considering the result of Example 2.9 in the context of the recent results by Cianciaruso, Infante, and Pietramala [7]. In particular, we will show that while the methodology developed in our paper applies easily to problem (2.5) as demonstrated by Example 2.9, the methodology developed in [7] does not apply so easily the same problem.

Utilizing the methodology developed in [7] and applying it to problem (2.5) we would need to find, among other things, a linear functional $\alpha ^{\rho }$ such that

$$\begin{aligned} \left( y\left( \frac{1}{2}\right) \right) ^2+\sqrt{y\left( \frac{3}{4}\right) }<\alpha ^{\rho }(y), \end{aligned}$$

for each $y\in \partial \Omega _{\rho }:=\{y\in {\mathscr {C}}([0,1])\ : \ \Vert y\Vert =\rho \}$, for some number $\rho >0$. Importantly, $\alpha ^{\rho }$ must satisfy the auxiliary condition

$$\begin{aligned} \alpha ^{\rho }\left( \gamma _1\right) <1. \end{aligned}$$

(2.9)

Suppose that we choose

$$\begin{aligned} \alpha ^{\rho }(y):=Ay\left( \frac{1}{2}\right) , \end{aligned}$$

for some constant $A>0$ to be determined. Condition (2.9) requires that

$$\begin{aligned} \frac{1}{2}A<1 \end{aligned}$$

so that $A<2$. Since

$$\begin{aligned} \left( y\left( \frac{1}{2}\right) \right) ^2+\sqrt{y\left( \frac{3}{4}\right) }<\Vert y\Vert ^2+\sqrt{\Vert y\Vert } \end{aligned}$$

and

$$\begin{aligned} Ay\left( \frac{1}{2}\right) >\frac{1}{4}A\Vert y\Vert , \end{aligned}$$

if we employ the same Harnack inequality as before (as the authors of [7] do as well), namely $\min _{\frac{1}{4}\le t\le \frac{3}{4}}y(t)\ge \frac{1}{4}\Vert y\Vert$, then it follows that if

$$\begin{aligned} \Vert y\Vert ^2+\sqrt{\Vert y\Vert }<\frac{1}{4}A\Vert y\Vert , \end{aligned}$$

(2.10)

then $\left( y\left( \frac{1}{2}\right) \right) ^2+\sqrt{y\left( \frac{3}{4}\right) }<\alpha ^{\rho }(y)$ will hold as desired. As A increases, the range of values of $\Vert y\Vert$ such that (2.10) is satisfied increases. Recalling from above that $A<2$ must hold, if we put $A=2$, then (2.10) becomes

$$\begin{aligned} \Vert y\Vert ^2+\sqrt{\Vert y\Vert }<\frac{1}{2}\Vert y\Vert , \end{aligned}$$

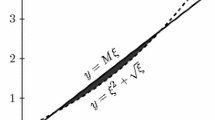
which has no real-valued solutions in $\Vert y\Vert$. In other words, a straightforward analysis of $\alpha ^{\rho }$ does not show it to be an admissible “upper bound functional” in the methodology of [7]. Similar comments apply to the choice $\alpha ^{\rho }(y):=Ay\left( \frac{3}{4}\right)$. The drawing below shows the configuration of the graph of the maps $\xi \mapsto \xi ^2+\sqrt{\xi }$ and $\xi \mapsto \frac{1}{2}\xi$.

Notice that the dashed curve, which is the graph of $y=\xi ^2+\sqrt{\xi }$ lies above the solid curve, which is the graph of $y=\frac{1}{2}\xi$.

On the other hand, if we try

$$\begin{aligned} {\widehat{\alpha }}^{\rho }(y):=Ay\left( \frac{1}{2}\right) +By\left( \frac{3}{4}\right) , \end{aligned}$$

for constants A, $B>0$ to be determined, then since we again need that ${\widehat{\alpha }}\left( \gamma _1\right) <1$ it follows that the constants A and B must satisfy

$$\begin{aligned} \frac{1}{2}A+\frac{1}{4}B<1. \end{aligned}$$

(2.11)

At the same time using the Harnack inequality $\min _{\frac{1}{4}\le t\le \frac{3}{4}}y(t)\ge \frac{1}{4}\Vert y\Vert$ we may estimate ${\widehat{\alpha }}^{\rho }$ from below by

$$\begin{aligned} {\widehat{\alpha }}^{\rho }(y)\ge \frac{1}{4}A\Vert y\Vert +\frac{1}{4}B\Vert y\Vert =\frac{1}{4}(A+B)\Vert y\Vert . \end{aligned}$$

Thus, if

$$\begin{aligned} \left( y\left( \frac{1}{2}\right) \right) ^2+\sqrt{y\left( \frac{3}{4}\right) }<\Vert y\Vert ^2+\sqrt{\Vert y\Vert }\le \frac{1}{4}(A+B)\Vert y\Vert \le {\widehat{\alpha }}^{\rho }(y) \end{aligned}$$

(2.12)

is satisfied for each $y\in \partial \Omega _{\rho }$, for some $\rho >0$, then the functional ${\widehat{\alpha }}^{\rho }$ will serve as a suitable upper bound, provided that inequality (2.11) holds. But conditions (2.11)–(2.12) are not compatible since there exist no values of A, B, $\rho >0$ such that $\Vert y\Vert =\rho$ implies (2.11)–(2.12).

All in all, as regards problem (2.5) we see that the methodology we have presented in this paper may be more easily applicable since it does not rely on discovering a functional $\alpha ^{\rho }$ and then demonstrating that it acts as a suitable upper bound on the nonlocal element. Rather by means of ${\mathcal {K}}$ and the ${\widehat{V}}$-type sets we can restrict our analysis to “pointwise values”. So, in some cases the methodology introduced here may be easier and more flexible to apply than competing methodologies.

Remark 2.11

We remark that while we have compared our methodology here with competing methodologies in the case of nonlinear, nonlocal boundary conditions, it is, nonetheless, the case that Theorem 2.5 can apply to the case of linear nonlocal boundary conditions.