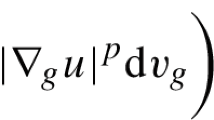Abstract
We initiate a low-order regularity theory for vectorial minimizers of the functional

where \(\varvec{\textit{w}}:\mathcal {M}\rightarrow \mathcal {N}\) and \(\mathcal {M}\) and \(\mathcal {N}\) are orientable Riemannian manifolds, in the case where G is only asymptotically convex. In particular, we prove three interrelated regularity results. The first result establishes partial Morrey regularity estimates, and Hölder continuity, for minimizers. For the second result by utilizing the obtained partial Hölder continuity, we prove a partial Caccioppoli-type inequality for minimizers. Finally, this result then allows us to deduce a higher integrability result for the gradient of minimizers of this functional. Since we work in the asymptotically convex setting, our results apply to far more general integrands than previously available in the literature for this type of problem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With \(m\ge 2\), let \((\mathcal {M},\varvec{\mathsf {g}})\) be a bounded, connected, smooth, and positively oriented m-dimensional Riemannian manifold with metric tensor \(\varvec{\mathsf {g}}\in \mathscr {C}^{\infty }(\mathcal {M}; T^*\mathcal {M}\odot T^*\mathcal {M})\) (In Sect. 2, we summarize the notation used). Let \(\,\mathrm {d}\mu _{\varvec{\mathsf {g}}}\) represent the volume form for \(\mathcal {M}\). In this paper, we investigate the regularity of minimizers of the functional

among weakly differentiable mappings \(\varvec{\textit{w}}: \mathcal {M}\rightarrow \mathcal {N}\), where \(\mathcal {N}\) is a (not necessarily bounded) smooth orientable n-dimensional Riemannian manifold isometrically embedded in \(\mathbb {R}^\ell \). Throughout this work, we assume that \(\partial \mathcal {N}=\emptyset \)—i.e., \(\mathcal {N}\) has empty boundary. Our assumptions on the integrand \(G{:}\;\mathcal {M}\times \mathcal {N}\times (\mathbb {R}^\ell \otimes T^*\mathcal {M})\rightarrow \mathbb {R}\) appearing in (1.1) are quite flexible. For each \(\varvec{\textit{z}}\in \mathcal {M}\) and \(\varvec{\xi }\in \mathbb {R}^\ell \otimes T^*\mathcal {M}\), put

where \(\left\{ \frac{\partial }{\partial z^i}\right\} _{i=1}^m\) is an orthonormal basis for the tangent space  . Let \(\varvec{\mathsf {A}}:\mathcal {M}\times \mathcal {N}\rightarrow (\mathbb {R}^\ell \odot \mathbb {R}^\ell )\otimes (T^*\mathcal {M}\odot T^*\mathcal {M})\) be uniformly positive definite, in the sense that there is a \(\Lambda >0\) such that
. Let \(\varvec{\mathsf {A}}:\mathcal {M}\times \mathcal {N}\rightarrow (\mathbb {R}^\ell \odot \mathbb {R}^\ell )\otimes (T^*\mathcal {M}\odot T^*\mathcal {M})\) be uniformly positive definite, in the sense that there is a \(\Lambda >0\) such that

for all \((\varvec{\textit{z}},\varvec{\textit{w}})\in \mathcal {M}\times \mathcal {N}\) and each \(\varvec{\xi }\in \mathbb {R}^\ell \otimes T^*\mathcal {M}\). The primary assumption, roughly speaking, is that for each \(\varvec{\textit{z}}\in \mathcal {M}\) the function \(\varvec{\xi }\mapsto G(\varvec{\textit{z}},\varvec{\textit{w}},\varvec{\xi })\) behaves like \(\left[ \varvec{\mathsf {A}}(\varvec{\textit{z}},\varvec{\textit{w}})(\varvec{\xi }\otimes \varvec{\xi })\right] ^\frac{p}{2}\), for some \(p\ge 2\), whenever  is sufficiently large in magnitude. To be more precise, we assume the following: there is a \(\gamma >0\) such that for each \(\varepsilon >0\), there is a \(\sigma _\varepsilon \in L^{p,\gamma }(\mathcal {M})\) so that
is sufficiently large in magnitude. To be more precise, we assume the following: there is a \(\gamma >0\) such that for each \(\varepsilon >0\), there is a \(\sigma _\varepsilon \in L^{p,\gamma }(\mathcal {M})\) so that

whenever  . Here \(L^{p,\gamma }(\mathcal {M})\) refers to a Morrey space on \(\mathcal {M}\) as defined in Sect. 2. The other main assumption is the following natural growth condition: there is a \(\Lambda >0\) and \(\overline{\sigma }\in L^{p,\gamma }(\mathcal {M})\) such that
. Here \(L^{p,\gamma }(\mathcal {M})\) refers to a Morrey space on \(\mathcal {M}\) as defined in Sect. 2. The other main assumption is the following natural growth condition: there is a \(\Lambda >0\) and \(\overline{\sigma }\in L^{p,\gamma }(\mathcal {M})\) such that

for each \((\varvec{\textit{z}},\varvec{\textit{w}},\varvec{\xi })\in \mathcal {M}\times \mathcal {N}\times (\mathbb {R}^\ell \otimes T^*\mathcal {M})\). If the admissible mappings were not required to satisfy a manifold constraint and, in addition, the asymptotic relatedness was with respect to the map \(\varvec{\xi }\mapsto \left( \varvec{\xi }\otimes \varvec{\xi }\right) ^{\frac{p}{2}}\) only, then these conditions would be essentially sufficient to establish everywhere Hölder continuity of a minimizer—see, for example, [22, 23]. In this paper, however, we consider mappings into the target manifold \(\mathcal {N}\), and it is well known that one can only expect partial regularity results in this case—that is, regularity within an open set of full measure.
The purpose of this work is to initiate a low-order regularity theory for integral functionals, whose integrands are only asymptotically convex, in the Riemannian manifold setting. As mentioned in the previous paragraph, we achieve this in the context where G may retain dependence on \(\varvec{\textit{w}}\) even as \(|\varvec{\xi }|\rightarrow +\infty \), an allowance, which, as we describe in the sequel, is relatively rare even in the much simpler Euclidean setting.
More specifically, our investigation produces three interconnected results. Suppose that \(\varvec{\textit{u}}:\mathcal {M}\rightarrow \mathcal {N}\) is a minimizer for (1.1). Let \(\mathcal {M}_{\rho }(\varvec{\textit{z}}_0)\subseteq \mathcal {M}\) be the relatively open geodesic ball of radius \(\rho \) centered at \(\varvec{\textit{z}}_0\). Our first result establishes partial Morrey regularity for the minimizer. More specifically, we show that whenever \(\varvec{\textit{z}}_0\in \mathcal {M}\) is such that

is sufficiently small, then this quantity remains small (in fact it decays) as the geodesic radius of the domain of integration decreases. Using the fact that the quantity in (*) can be made as small as we wish throughout sufficiently small neighborhoods of each Lebesgue point of \(\varvec{\mathsf {d}}\varvec{\textit{u}}\), we obtain the partial Morrey regularity for \(\varvec{\mathsf {d}}\varvec{\textit{u}}\). A by-product of this result is that \(\varvec{\textit{u}}\) is partially Hölder continuous with a closed singular set that has Hausdorff dimension of at most \(m-p\). Our second result shows that the differential of the minimizer \(\varvec{\textit{u}}\) also satisfies a partial Caccioppoli inequality. As with the Morrey regularity result, we show that whenever the quantity in (*) is sufficiently small, the Caccioppoli inequality holds. Now, the Morrey regularity result ensures that (*) remains small as the radius of the domain of integration decreases. It follows that the Caccioppoli inequality holds throughout an open neighborhood of the set of Lebesgue points of \(\varvec{\mathsf {d}}\varvec{\textit{u}}\). As with the Morrey regularity result, we can say that the set on which the Caccioppoli inequality fails to hold is closed and has Hausdorff dimension of at most \(m-p\). Our final result invokes a well-known argument utilizing Gehring’s lemma to obtain partial higher integrability of \(\varvec{\mathsf {d}}\varvec{\textit{u}}\) from the Caccioppoli inequality.
Let us also mention at this juncture the basic strategy used to obtain our results. Essentially, we follow a blow-up strategy to deduce our primary results. In particular, Lemmata 3.1 and 3.2 constitute some of the central, novel contributions of this work, and to deduce these results, we analyze the behavior of an appropriate blow-up sequence, namely
see (3.1) in the sequel. In the definition of the collection \(\left\{ \varvec{\textit{v}}_i\right\} _{i=1}^{\infty }\) we have that \(\varvec{\varphi }_0\) is an element of a local coordinate chart, whereas \(\varvec{\textit{u}}\) is a minimizer of (1.1). The blow-up technique in regularity theory is by now classical in the sense that it has been used for some time—see, for example, either Evans and Gariepy [15] or Fusco and Hutchinson [29] for clearly written and typical examples of the blow-up technique in regularity theory. Nonetheless, our utilization of the technique in this work is significantly complicated by the fact that both the domain and codomain of \(\varvec{\textit{u}}\) are Riemannian manifolds.
In particular, Lemma 3.1 establishes that, under appropriate hypotheses, which are detailed in Sect. 3, the blow-up sequence \(\left\{ \varvec{\textit{v}}_i\right\} _{i=1}^{\infty }\) has the property that its weak limit, say \(\varvec{\textit{v}}\), is a \((\varvec{\mathsf {B}},p)\)-harmonic function—see (2.4). This leads to \(\varvec{\textit{v}}\) possessing good regularity properties, which are then utilized in the proof of the partial Hölder continuity result of Sect. 4. The difficulty in proving Lemma 3.1 is the care that is required in constructing an arbitrary comparison map. In particular, a careful sequence of steps is required to construct this comparison map and then, at last, to demonstrate the minimality of \(\varvec{\textit{v}}\).
On the other hand, Lemma 3.2 demonstrates that if we consider the same blow-up sequence \(\left\{ \varvec{\textit{v}}_i\right\} _{i=1}^{\infty }\) as in the proof of Lemma 3.1, then under appropriate hypotheses, it holds that \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) strongly in \(W_{\mathrm {loc}}^{1,p}\left( \mathcal {B}_1^m;\mathbb {R}^{\ell }\right) \). This lemma is then used to produce the partial Caccioppoli inequality, which then, finally, produces a higher integrability result.
Another difficulty that occurs in our arguments is that great care is required in switching from the manifold to the local Euclidean space and back again; of course, this issue is moot if one works solely with the Euclidean problem. The particular problem is that when we make this switch, the radius of, say, a geodesic ball in the manifold does not remain invariant when transforming this ball, via a local homeomorphism, to a coordinate ball in the Euclidean space. Then when, inevitably, we wish to pass back to the manifold, the radii again vary. Moreover, we can only assert a range within which the altered radii must live. In any case, keeping track of these changing radii requires careful arguments and bookkeeping to ensure that the many inequalities which arise in the arguments are carefully justified. This especially requires great care in the proof of the partial Caccioppoli result, alluded to above, wherein we must switch between the manifold and a suitable local coordinate chart and yet back again, all the while keeping very careful track of the change of the associated radii of the balls in the integral estimates.
Having described the general thrust of our results together with the associated techniques we utilize to obtain them, we now contextualize our results by discussing the existing literature on the type of problem investigated in this paper. Let us first mention the problem of partial regularity in the Euclidean setting. In particular, it has been known since De Giorgi’s [8] fundamental work in the late 1960s that vectorial minimizers to variational problems need not be everywhere continuous. Instead, it is typically shown that there exists an open set \(\varOmega _0\) of full measure on which the minimizer possesses some degree of regularity and outside of which the minimizer may be singular; depending upon the structure conditions imposed on the problem, everywhere regularity may also be achievable at times. For example, in addition to the now-classical works by Giaquinta and Giusti [31, 32] and Giaquinta and Modica [33–35], these sorts of problems have been studied in the context of VMO structure conditions [3–5, 7, 43, 53–57], boundary regularity [2], irregular growth [18], parabolic-type problems [48], singular set estimation [46], elliptic systems [21], asymptotic convexity [19, 23], and obstacle problems [10, 11]. The monographs by Giaquinta [30] and Giusti [38] provide excellent overviews of the whole of regularity theory. Furthermore, Mingione [50, 51] has produced two very readable survey papers regarding regularity theory for minimizers of functionals as well as weak solutions of elliptic PDEs.
A typical assumption to make when studying the regularity of minimizers of the functional
is that the map \((\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\mapsto f(\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\) is convex in \(\varvec{\xi }\). It is thus of interest to investigate regularity in the setting where f fails to satisfy a convexity assumption. Along these lines, the notion of asymptotic relatedness, which implies a sort of convexity “at infinity”, has proved to be the source of a most fruitful idea in regularity theory. Essentially, and as made precise in Definition 2.10, we assume that as \(|\varvec{\xi }|\rightarrow +\infty \) the map \((\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\mapsto f(\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\) “looks like” a more regular map, say \((\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\mapsto G(\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\), and in this way, we are able to move most of the typical hypotheses one would make about f onto the map G; in fact, the notion of asymptotic relatedness has even proved to be useful in the somewhat disparate area of boundary value problems for ordinary differential equations—see [39–42]. As concerns its use in the context of regularity theory, the concept of asymptotic relatedness was first introduced by Chipot and Evans [6]. Raymond [58] later investigated the regularity properties of minimizers of the functional
where f is asymptotically related to the p-energy map \(\varvec{\xi }\mapsto |\varvec{\xi }|^p\) and g is a Carathéodory function; it is worth noting that Raymond treated the superquadratic setting—i.e., where \(p>2\). In fact, the subquadratic setting was treated later by Pasarelli di Napoli and Verde [52]. More recent results in the context of asymptotic relatedness assumptions may be found in the works of Scheven and Schmidt [60, 61].
We should also like to mention that in the Euclidean setting, i.e., where \(\mathcal {M}:=\mathbb {R}^{n}\) and \(\mathcal {N}:=\mathbb {R}^{N}\), Foss and Goodrich have recently proved in [20] that for the functional (1.3) partial Hölder regularity is enjoyed by a minimizing map \(\varvec{\textit{u}}\ : \ \varOmega \subseteq \mathbb {R}^{n}\rightarrow \mathbb {R}^N\) under very weak structure hypotheses—namely, that the map \((\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\mapsto f(\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\) is asymptotically related to the functional \(a(\varvec{\textit{x}},\varvec{\textit{u}})F(\varvec{\xi })\), where F has p-Uhlenbeck structure and the map \((\varvec{\textit{x}},\varvec{\textit{u}})\mapsto a(\varvec{\textit{x}},\varvec{\textit{u}})\) is continuous and uniformly bounded on \(\varOmega \times \mathbb {R}^{N}\). Due to the recent investigations of Scheven and Schmidt [60] as well as Dolzmann et al. [9], the partial regularity results produced by Foss and Goodrich are sharp in the setting studied in [20]. Moreover, the results of [20] are also of interest since they allow f to maintain dependence on \(\varvec{\textit{u}}\) even as \(|\varvec{\xi }|\rightarrow +\infty \).
In contrast to the richness of existing results in the Euclidean setting, when it comes to the regularity properties of minimizers of the very general functional given in (1.1), wherein the minimizer maps between Riemannian manifolds, the existing results are much more scarce and, in particular, restricted in nature. In part, we direct the reader to Simon’s monograph [65] for some general results on p-energies and properties of harmonic maps, each of which we briefly discuss next.
In particular, we begin by recalling that a series of classic papers by both Uhlenbeck [68] and by Schoen and Uhlenbeck [62–64] provide, among other results, regularity theorems for minimizers of the functional
where it is assumed that \(\varvec{\textit{u}}\ {:}\; \ \varOmega \subseteq \mathcal {M}\rightarrow \mathcal {N}\); here \(\mathcal {M}\) and \(\mathcal {N}\) are Riemannian manifolds. The treatment of (1.4) is quite broad since, in fact, the integrand may be replaced by \(F(|\varvec{\mathsf {d}}\varvec{\textit{u}}|)\) for some sufficiently regular map \(\varvec{\xi }\mapsto F(\varvec{\xi })\), and, in addition, systems of PDEs associated to (1.4) are considered in [62–64, 68]. For instance, in [62] they obtain, under suitable hypotheses, a smoothness result concerning a harmonic minimizer \(\varvec{\textit{u}}\); they also address the Hausdorff dimension of the singular set. In [63] boundary regularity is addressed, whereas, finally, in [64] they extend their previous studies to the case in which the target manifold, \(\mathcal {N}\), is either a sphere or a closed hemisphere. These early works by Schoen and Uhlenbeck are fundamental, but, naturally, they only concern a restricted class of functionals, and so, more complicated functionals as well as functionals whose integrands are less regular are not considered. It should also be mentioned that Evans [14] considered (1.4) and demonstrated that if the target manifold—i.e., \(\mathcal {N}\)—is the \(m-1\) sphere, \(\mathcal {S}^{m-1}\), then one finds that a weakly harmonic mapping \(\varvec{\textit{u}}\) is of class \(\mathscr {C}^{\infty }\left( V;\mathcal {S}^{m-1}\right) \), where \(V\subseteq \varOmega \subseteq \mathbb {R}^n\) is open and satisfies the Hausdorff measure estimate \(\mathscr {H}^{n-2}(\varOmega {\setminus } V)=0\). A similar energy, namely
where \(\varvec{\textit{u}}\ {:}\; \ \mathbb {R}^m\rightarrow (\mathcal {N},\mathscr {F})\), where \((\mathcal {N},\mathscr {F})\) is a Finsler manifold with \(\mathscr {F}\) a Finsler structure, was considered by Tachikawa [66], who proved partial Hölder continuity of minimizers together with an associated Hausdorff estimate on the singular set; a similar problem is treated by Tachikawa in [67], wherein boundary regularity is treated. Although we shall not be interested in Finsler manifolds in this paper, we observe that [66, 67] treat functionals, whose integrands have a very special, though admittedly important, form.
Later, in a series of papers by Fuchs [24–27], the problem of regularity of minimizers of the p-energy functional
as well as the regularity of minimizers of the so-called splitting functional
were treated, where again it is assumed that \(\varvec{\textit{u}}\ {:}\;\ \mathcal {M}\rightarrow \mathcal {N}\), in which \(\mathcal {M}\) and \(\mathcal {N}\) are Riemannian manifolds. One of the keys to Fuchs’ analysis is the construction and proof of a suitable Caccioppoli-type inequality, the conclusion of which is realized as

In addition, Fuchs [28], utilizing a result of Evans [14], also demonstrated a.e. \(\mathscr {C}^{1}\) regularity of p-harmonic maps, whose codomain is the sphere \(\mathcal {S}^{k-1}\). In any case, once again and as with the earlier work of Schoen and Uhlenbeck, Fuchs’ work only permits one to treat a restricted class of functionals.
Another article worth mentioning is a contribution by Duzaar and Mingione [12]. In this paper, the authors consider minimizers of the p-energy (1.5) for maps of the form \(\varvec{\textit{u}}\ {:}\; \ \varOmega \rightarrow \mathcal {M}\), where \(\varOmega \) is an open subset of \(\mathbb {R}^n\), \(n\ge 2\), and \(\mathcal {M}\) is a compact, smooth Riemannian manifold of dimension at least two. In particular, they deduce an appropriate p-harmonic approximation lemma. They then present some regularity results for such maps. A related article by Rivière and Strzelecki [59] addresses certain properties of p-harmonic maps in the manifold setting.
Similarly, Fardoun and Regbaoui [16] have recently considered the regularity of minimizers of the p-energy
where \(u\ : \mathcal {M}\rightarrow \mathcal {N}\) is a map between compact Riemannian manifolds \(\mathcal {M}\) and \(\mathcal {N}\). The authors, in particular, argue the \(\mathscr {C}^{1,\alpha }(\varOmega ;\mathcal {N})\) regularity of a minimizer \(\varvec{\textit{u}}\) for some \(0<\alpha <1\), with \(\varOmega \subseteq \mathcal {M}\) open, provided that the range of \(\varvec{\textit{u}}\) is contained in a small geodesic ball about some point of \(\mathcal {N}\).
Finally, we mention the well-known paper of Luckhaus [49]. In fact, Luckhaus’ work will be most helpful to us here, for, as is mentioned in Sect. 3, we use certain of the ideas developed in [49] as a starting point for constructing and proving the main results of this paper; in particular, the so-called Luckhaus Lemma [49, Lemma 1] is central for our purposes here. In any case, Luckhaus considered the general functional
where \(\varvec{\textit{u}}\) maps between Riemannian manifolds \(\mathcal {M}\) and \(\mathcal {N}\). Essentially, it is assumed that G satisfies standard p-growth and a blow-up condition with respect to its third argument. Moreover, and crucially different from our work in this paper, it is also assumed that the map \((\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\mapsto G(\varvec{\textit{x}},\varvec{\textit{u}},\varvec{\xi })\) is convex in \(\varvec{\xi }\) for all pairs \((\varvec{\textit{x}},\varvec{\textit{u}})\in \varOmega \times \mathcal {N}\).
In consideration of the preceding paragraphs, we note a substantial difference between the manifold and Euclidean settings. Indeed, although it is surely the case that the regularity theory for asymptotically convex functionals is incomplete in the Euclidean setting, there nonetheless exists a rich and deep existing literature on these problems, and many substantial results have been established. By contrast, the corresponding theory in the Riemannian manifold setting is essentially void, existing results instead relying on the underlying functional possessing special forms, such as the p-energy in (1.5) or the splitting functional in (1.6). Even in the case of Luckhaus’ study, it is nonetheless assumed that the partial map \(\varvec{\xi }\mapsto G(\cdot ,\cdot ,\varvec{\xi })\) is convex. In summary, then, the results of this paper are the first to treat the asymptotically convex problem in the Riemannian manifold setting. Moreover, in addition to the regularity results we provide, the partial Caccioppoli and reverse Hölder inequalities that we provide are of independent interest in and of themselves, given their centrality in the study of the regularity of minimizing maps.
To conclude this section, we briefly mention the outline of the remainder of this paper. In Sect. 2 we collect several preliminary lemmata, definitions, and notations that will be used throughout the remainder of the paper. In Sect. 3 we prove two key lemmata that form the basis for the proofs of the partial Caccioppoli and reverse Hölder inequalities as well as the partial regularity results in Sects. 4 and 5. The proofs of these lemmata begin with Luckhaus’ ideas in [49], but eventually require considerable and careful modification of the ideas in [49]. Finally, in Sects. 4 and 5 we use the two lemmata of Sect. 3 to prove very generally applicable partial Caccioppoli and reverse Hölder inequalities as well as the partial Hölder continuity result.
2 Preliminaries
In this section, we collect some notations and preliminary definitions that will be used throughout this paper. We also provide some fundamental lemmata, such as the well-known Luckhaus lemma, which also are utilized at several points in the sequel. All manifolds are assumed to be smooth and oriented. The Riemannian manifolds \((\mathcal {M},\varvec{\mathsf {g}})\) and \(\mathcal {N}\), as described in the introduction, are fixed for the remainder of the paper. As indicated before, we take advantage of the Nash-Moser embedding theorem and assume that \(\mathcal {N}\) is isometrically embedded in \(\mathbb {R}^\ell \). The texts by Jost [45] and Lee [47] are excellent references for the material that we briefly review in this section.
2.1 Euclidean sets
Given \(k\ge m\), we use \(\mathcal {B}_{\rho }^m(\varvec{\textit{x}})\subset \mathbb {R}^k\) to denote an m-ball of radius \(\rho \) centered at \(\varvec{\textit{x}}\in \mathbb {R}^k\) that is open with respect to the relative topology of each m-dimensional hyperplane in \(\mathbb {R}^k\). An m-sphere, i.e., the boundary of an \((m+1)\)-ball, of radius \(\rho \) centered at \(\varvec{\textit{x}}\) is represented by \(\mathcal {S}_{\rho }^m(\varvec{\textit{x}})\). When a statement is independent of the center \(\varvec{\textit{x}}\) or the center can be easily determined from the context, then we will typically just use \(\mathcal {B}^m_\rho \) and \(\mathcal {S}^m_\rho \). For similar reasons, we may also suppress the dimension of the ball or sphere. We will use \(\mathcal {B}(\varvec{\textit{x}})\) and \(\mathcal {S}(\varvec{\textit{x}})\) for a unit ball and a unit sphere, respectively, centered at \(\varvec{\textit{x}}\).
For a Euclidean space \(\mathbb {R}^j\), we use \(|\cdot |\) for the standard Euclidean, or Frobenius, norm and \(\langle \cdot ,\cdot \rangle \) for the standard inner product. Given \(\mathcal {A}\subseteq \mathbb {R}^j\) and \(\varvec{\textit{x}}_0\in \mathbb {R}^j\), we define the minimum distance from \(\varvec{\textit{x}}_0\) to \(\mathcal {A}\) by

If \(\mathcal {A}\) is Lebesgue measurable, then we denote its Lebesgue measure by \(|\mathcal {A}|\). Finally, given a linear subspace \(\mathcal {Y}\subseteq \mathbb {R}^j\), we set
2.2 Manifolds and mappings
Given two vector spaces \(\mathcal {A}\) and \(\mathcal {B}\), we use \(\mathcal {A}\otimes \mathcal {B}\) to denote the space of tensor products of members from \(\mathcal {A}\) with members from \(\mathcal {B}\). We use \(\mathcal {A}\odot \mathcal {B}\subseteq \mathcal {A}\otimes \mathcal {B}\) for the symmetric products of elements of \(\mathcal {A}\) with elements of \(\mathcal {B}\) and \(\mathcal {A}\wedge \mathcal {A}\subseteq \mathcal {A}\otimes \mathcal {B}\) for the antisymmetric products. For brevity, we write \(\otimes ^2\mathcal {A}\) for \(\mathcal {A}\otimes \mathcal {A}\), and given an element \(\varvec{\mathsf {a}}\in \mathcal {A}\), we may use \(\otimes ^2\varvec{\mathsf {a}}\) for \(\varvec{\mathsf {a}}\otimes \varvec{\mathsf {a}}\). A similar convention will be used for \(\mathcal {A}\odot \mathcal {A}\).
Suppose that \(\mathcal {Q}\) is an m-dimensional Riemannian manifold with metric \(\varvec{\mathsf {r}}\). We use  for the tangent space to \(\mathcal {Q}\) at \(\varvec{\textit{q}}\in \mathcal {Q}\) and
for the tangent space to \(\mathcal {Q}\) at \(\varvec{\textit{q}}\in \mathcal {Q}\) and  for the cotangent (dual) space. The tangent bundle for \(\mathcal {Q}\) is denoted by \(T\mathcal {Q}\); the cotangent bundle is represented by \(T^*\mathcal {Q}\). At each \(\varvec{\textit{q}}\in \mathcal {Q}\), the metric \(\varvec{\mathsf {r}}\in \mathscr {C}^{\infty }(\mathcal {Q};\odot ^2 T^*\mathcal {Q})\) is a positive definite symmetric bilinear form defined on
for the cotangent (dual) space. The tangent bundle for \(\mathcal {Q}\) is denoted by \(T\mathcal {Q}\); the cotangent bundle is represented by \(T^*\mathcal {Q}\). At each \(\varvec{\textit{q}}\in \mathcal {Q}\), the metric \(\varvec{\mathsf {r}}\in \mathscr {C}^{\infty }(\mathcal {Q};\odot ^2 T^*\mathcal {Q})\) is a positive definite symmetric bilinear form defined on  . For each \(\varvec{\textit{q}}\in \mathcal {Q}\), the metric induces an inner product
. For each \(\varvec{\textit{q}}\in \mathcal {Q}\), the metric induces an inner product  defined by
defined by

The associated norm is denoted by  . Let \(\mathrm{dist}\,_\mathcal {Q}(\varvec{\textit{q}}_1,\varvec{\textit{q}}_2)\) denote the geodesic distance between \(\varvec{\textit{q}}_1,\varvec{\textit{q}}_2\in \mathcal {Q}\). We define the geodesic ball of radius \(\rho >0\) centered at \(\varvec{\textit{q}}_0\in \mathcal {Q}\) by
. Let \(\mathrm{dist}\,_\mathcal {Q}(\varvec{\textit{q}}_1,\varvec{\textit{q}}_2)\) denote the geodesic distance between \(\varvec{\textit{q}}_1,\varvec{\textit{q}}_2\in \mathcal {Q}\). We define the geodesic ball of radius \(\rho >0\) centered at \(\varvec{\textit{q}}_0\in \mathcal {Q}\) by
When convenient, we will instead use \(\mathcal {B}_\rho (\varvec{\textit{q}}_0)\), and as with the Euclidean ball, when appropriate we may suppress the center \(\varvec{\textit{q}}_0\) and just use \(\mathcal {B}_\rho \). The topology on \(\mathcal {Q}\) that we use is the smallest one in which the geodesic balls are open. An open submanifold of \(\mathcal {Q}\) is a submanifold \(\mathcal {Q}'\subseteq \mathcal {Q}\) that is open in the topology on \(\mathcal {Q}\). Given \(\mathcal {A}\subseteq \mathcal {Q}\), we use \(\overline{\mathcal {A}}\) to denote its closure in \(\mathcal {Q}\) and \(\mathrm{int}\,(\mathcal {A})\) for its interior. The boundary of \(\mathcal {A}\) is denoted by \(\partial \mathcal {A}\). If \(\mathcal {Q}'\) is an open submanifold of \(\mathcal {Q}\) such that \(\overline{\mathcal {Q}'}\) is compact with respect to the topology on \(\mathcal {Q}\), we say that \(\mathcal {Q}'\) is compactly contained in \(\mathcal {Q}\) and write \(\mathcal {Q}'\Subset \mathcal {Q}\).
We use \(\,\mathrm {d}\mu _{\varvec{\mathsf {r}}}\) to denote the volume form and \(\mu _{\varvec{\mathsf {r}}}\) for the associated Riemannian measure on \((\mathcal {Q},\varvec{\mathsf {r}})\). Whenever we refer to a measure on \(\mathcal {Q}\), we mean \(\mu _{\varvec{\mathsf {r}}}\). For a measurable set \(E\subseteq \mathcal {Q}\), we have
A set \(\mathcal {Q}_0\subseteq \mathcal {Q}\) is said to have full measure in \(\mathcal {Q}\) if \(\mu _{\varvec{\mathsf {r}}}(\mathcal {Q}\setminus \mathcal {Q}_0)=0\). Given a mapping \(\varvec{\textit{w}}\in L^1(\mathcal {Q};\mathbb {R}^\ell )\) and a measurable set \(E\subseteq \mathcal {Q}\), with \(\mu _{\varvec{\mathsf {r}}}(E)>0\), we define the mean value of \(\varvec{\textit{w}}\) over E by

For convenience, if \(E=\mathcal {B}^\mathcal {Q}_\rho (\varvec{\textit{q}}_0)\) for some \(\varvec{\textit{q}}_0\in \mathcal {Q}\) and \(\rho >0\), then we might use \(\left( \varvec{\textit{w}}\right) _{\varvec{\textit{q}}_0,\rho }\), or just \(\left( \varvec{\textit{w}}\right) _\rho \), for \(\left( \varvec{\textit{w}}\right) _{\mathcal {B}^\mathcal {Q}_{\rho }(\varvec{\textit{q}}_0)}\). Similar notation will be used for averages of balls in an Euclidean space.
Let \(k\in \mathbb {N}\) and \(\mathcal {R}\), an n-dimensional Riemannian manifold, be given. If \(\varvec{\textit{u}}\in \mathscr {C}^{k}(\mathcal {Q};\mathcal {R})\), then the differential map \(\varvec{\mathsf {d}}\varvec{\textit{u}}\in \mathscr {C}^{k-1}(\mathcal {Q};T\mathcal {R}\otimes T^*\mathcal {Q})\) is the unique map that satisfies
for each \(\varvec{\textit{q}}_0\in \mathcal {Q}\), \(\varvec{\xi }\in T_{\varvec{\textit{q}}_0}\mathcal {Q}\), and \(f\in \mathscr {C}^{1}(\mathcal {R};\mathbb {R})\). We extend this notation to also represent a weak differential. If \(\mathcal {R}\) is identified with an isometric embedding in \(\mathbb {R}^\ell \), then as indicated in the Introduction, we define the Hilbert–Schmidt norm of \(\varvec{\mathsf {d}}\varvec{\textit{u}}\) at \(\varvec{\textit{q}}_0\) by
Here \(\left\{ \frac{\partial }{\partial q^i}\right\} _{i=1}^m\) is an orthonormal basis for \(T_{\varvec{\textit{q}}_0}\mathcal {Q}\). Let \((\mathcal {V},\varvec{\varphi })\) be a local coordinate chart on \(\mathcal {Q}\), with \(\varvec{\textit{q}}_0\in \mathcal {V}\), and let \(\left\{ \frac{\partial }{\partial x^i}\right\} _{i=1}^m\) be an orthonormal basis for \(T_{\varvec{\varphi }(\varvec{\textit{q}})}\mathbb {R}^m\) for each \(\varvec{\textit{q}}\in \mathcal {V}\). We denote the local coordinates in \(\mathcal {V}\) by \(\varvec{\varphi }(\varvec{\textit{q}})=(x^1(\varvec{\textit{q}}),\dots ,x^m(\varvec{\textit{q}}))\). With \(\varvec{\textit{x}}=\varvec{\varphi }(\varvec{\textit{q}})\), the metric \(\varvec{\mathsf {r}}\) is represented in local coordinates by a matrix \(\varvec{\textit{r}}\) with components
for \(1\le i_1,i_2\le m\). The inverse \(\varvec{\textit{r}}^{-1}\) of this matrix has components \(r^{i_1,i_2}\). In these local coordinates, the norm of \(\varvec{\mathsf {d}}\varvec{\textit{u}}(\varvec{\textit{q}}_0)=\varvec{\mathsf {d}}\varvec{\textit{u}}(\varvec{\varphi }^{-1}(\varvec{\textit{x}}_0))\) defined above is given by
Suppose that \(\mathcal {Q}\) is identified with an embedding into \(\mathbb {R}^j\). We define \(\varPi _\mathcal {Q}:\mathbb {R}^j\rightarrow 2^\mathcal {Q}\) by
In general, this projection onto \(\mathcal {Q}\) is multi-valued. There are, however, open sets \(U\subseteq \mathbb {R}^j\) such that \(\mathcal {Q}\subset U\) and \(\varPi _\mathcal {Q}\) is uni-valued on U. Set \(\varOmega _{\mathcal {Q}}\subseteq \mathbb {R}^\ell \) to be the union of all such sets. We will also use \(\varPi _\mathcal {Q}\) to denote the corresponding uni-valued nearest-point projection map \(\varPi _\mathcal {Q}:\varOmega _{\mathcal {Q}}\rightarrow \mathcal {Q}\). It can be verified that \(\varPi _\mathcal {Q}\) is differentiable and Lipschitz on \(\varOmega _{\mathcal {Q}}\) (see e.g., [1]). Now suppose that \(\mathcal {P}\Subset \mathcal {Q}\). Then, according to [17], there is a \(\delta >0\) such that for each \(\varvec{\textit{q}}\in \partial \varOmega _{\mathcal {Q}}\setminus \overline{\mathcal {Q}}\), we have \(\mathrm{dist}\,(\varvec{\textit{q}},\mathcal {P})>\delta \). Moreover, the following limits hold:
and
Here we have identified \(T_{\varvec{\textit{p}}}\mathcal {Q}\) with an m-dimensional linear subspace of \(\mathbb {R}^j\) for each \(\varvec{\textit{p}}\in \mathcal {P}\).
2.3 Function spaces
Definition 2.1
Given an open bounded set \(U\subseteq \mathbb {R}^m\), for each \(p\in [1,+\infty )\) and \(\gamma \in [0,m]\), we define the Morrey space
For each \(\gamma \in [0,\infty )\), we also define the Campanato space
We write \(\varvec{\textit{w}}\in L_{\mathrm{loc}\,}^{p,\gamma }(U;\mathbb {R}^j)\) if \(\varvec{\textit{w}}\in L^{p,\gamma }(V;\mathbb {R}^j)\) for each \(V\Subset U\). The local version of \(\mathscr {L}^{p,\gamma }(U;\mathbb {R}^j)\) is analogously defined.
The extension of the Morrey and Campanato spaces to compact Riemannian manifolds was developed in [37]. For the remainder of this section, let \((\mathcal {Q},\varvec{\mathsf {r}})\) be a compact m-dimensional Riemannian manifold.
Definition 2.2
For each \(p\in [1,\infty )\) and \(\gamma \in [0,m]\), set
and for \(\gamma \in [0,\infty )\), put
Using the geodesic distance, we define Hölder continuity on \(\mathcal {Q}\).
Definition 2.3
For each \(\alpha \in (0,1]\), we define
In [37] it is shown that Definition 2.3 is essentially equivalent to Hölder continuity in local coordinates.
Proposition 2.4
Suppose that \(\varvec{\textit{w}}\in \mathscr {C}^{0,\alpha }(\mathcal {Q};\mathbb {R}^j)\) for some \(\alpha \in (0,1]\). For each \(\varvec{\textit{q}}_0\in \mathcal {Q}\), there is a local coordinate chart \((\mathcal {V},\varvec{\varphi })\) on \(\mathcal {Q}\) such that \(\varvec{\textit{q}}_0\in \mathcal {V}\) and \(\varvec{\textit{w}}\circ \varvec{\varphi }^{-1}\in \mathscr {C}^{0,\alpha }(\varvec{\varphi }(\mathcal {V});\mathbb {R}^j)\).
We next introduce a couple of Sobolev-type spaces that we need.
Definition 2.5
For each \(p\in [1,+\infty )\), set
Since  is isomorphic to \(\mathbb {R}^m\) for each \(\varvec{\textit{q}}\in \mathcal {Q}\), we may identify
is isomorphic to \(\mathbb {R}^m\) for each \(\varvec{\textit{q}}\in \mathcal {Q}\), we may identify  with \(\mathbb {R}^{j\times m}\) and make the following
with \(\mathbb {R}^{j\times m}\) and make the following
Definition 2.6
For each \(p\in [1,\infty )\) and \(\gamma \in [0,m]\), we define the following Sobolev–Morrey space:
The compactness of \(\mathcal {Q}\) and the Poincaré inequality in Euclidean spaces yields the following
Theorem 2.7
Let \(p\in [1,\infty )\) be given. There is an \(\overline{R}(\mathcal {Q})>0\) and \(\overline{K}(\mathcal {Q},j,p)<\infty \) such that for each \(\varvec{\textit{w}}\in W^{1,p}(\mathcal {Q};\mathbb {R}^j)\) and \(0<r<\overline{R}\) the following scale-invariant Poincaré inequality holds for each \(\varvec{\textit{q}}_0\in \mathcal {Q}\):

Finally, we collect several embedding results.
Proposition 2.8
Let \(p\in [1,\infty )\) be given.
-
(i)
For each \(\gamma \in [0,m]\), the space \(W^{1,(p,\gamma )}(\mathcal {Q};\mathbb {R}^j)\) is continuously embedded into the space \(\mathscr {L}^{p,p+\gamma }(\mathcal {Q};\mathbb {R}^j)\).
-
(ii)
For each \(\gamma \in (m,m+p)\) the space \(\mathscr {L}^{p,\gamma }(\mathcal {Q};\mathbb {R}^j)\) is isomorphic to \(\mathscr {C}^{0,\frac{\gamma -m}{p}}(\mathcal {Q};\mathbb {R}^j)\).
Remark 2.9
Combining the above embeddings, it follows that \(W^{1,(p,\gamma )}(\mathcal {Q};\mathbb {R}^j)\) is continuously embedded into \(\mathscr {C}^{0,\frac{\gamma +p-m}{p}}(\mathcal {Q};\mathbb {R}^j)\), for each \(\gamma \in (m-p,m)\) (or for each \(\gamma \in (0,m)\) if \(p>m\)).
2.4 General assumptions
Next we define asymptotical relatedness.
Definition 2.10
Let \(F,G:\mathcal {M}\times \mathcal {N}\times (\mathbb {R}^\ell \otimes T^*\mathcal {M})\rightarrow \mathbb {R}\) and \(\gamma \in [0,n]\) be given. We say that F and G are \((p,\gamma )\)-asymptotically related if the following is satisfied: there is a family \(\{\sigma _\varepsilon \}_{\varepsilon >0}\subset L^{p,\gamma }(\mathcal {M})\) such that for each \(\varepsilon >0\) and each \(\varvec{\textit{z}}\in \mathcal {M}\) it holds that

whenever  .
.
Remark 2.11
Note that because the function \(\sigma _{\varepsilon }\) in the above definition is only required to belong to the Morrey space \(L^{p,\gamma }\), it is possible that \(\sigma _\varepsilon \) is essentially unbounded at some points in \(\mathcal {M}\). Thus at some \(\varvec{\textit{z}}\in \mathcal {M}\), the condition in Definition 2.10 may, in fact, impose no asymptotic restriction on F and G whatsoever.
Remark 2.12
Using the triangle inequality, the condition for \((p,\gamma )\)-asymptotic relatedness is an equivalence relation.
We now discuss the structural conditions that we assume the integrand G satisfies.

Remark 2.13
If \(p>m\), then we only require \(\gamma \in [0,m)\). The restriction on \(\gamma \) ensures \(p-m+\gamma >0\).
For the rest of the paper, the function \(\omega \) and the family \(\{\sigma _\varepsilon \}_{\varepsilon >0}\) provided by Definition 2.10 are fixed.
Define the functional \(I:W^{1,p}(\mathcal {M};\mathcal {N})\rightarrow \mathbb {R}\) by
for all \(\varvec{\textit{w}}\in W^{1,p}(\mathcal {M};\mathcal {N})\). Throughout the sequel, we assume that \(\varvec{\textit{u}}\in W^{1,p}(\mathcal {M};\mathcal {N})\) is a local minimizer for I. By this, we mean that
for each \(\varvec{\textit{w}}\in W^{1,p}(\mathcal {M};\mathcal {N})\) satisfying \(\mathrm{supp}\,(\varvec{\textit{u}}-\varvec{\textit{w}})\Subset \mathcal {M}\). Of course, if \(\mathcal {M}\) is a compact manifold, then \(\mathrm{supp}\,(\varvec{\textit{u}}-\varvec{\textit{w}})\) is a compact subset of \(\mathcal {M}\) for all \(\varvec{\textit{w}}\in W^{1,p}(\mathcal {M};\mathcal {N})\). For each \(\varvec{\mathsf {B}}\in \left( \odot ^2\mathbb {R}^n\right) \otimes \left( \odot ^2\mathbb {R}^m\right) \), we also define the functional \(J[\cdot ;\varvec{\mathsf {B}}]:W^{1,p}\left( \mathcal {B}^m_1;\mathbb {R}^n\right) \rightarrow \mathbb {R}\) by
We will refer to minimizers of \(J[\cdot ;\varvec{\mathsf {B}}]\) as \((\varvec{\mathsf {B}},p)\)-harmonic.
2.5 Preliminary lemmata
In the following lemma, we introduce \(\alpha \mapsto \lfloor \alpha \rfloor \) for the floor function and \(\mathscr {H}^{m-1}\) for the \((m-1)\)-dimensional Hausdorff measure. This lemma provides a transition map between two functions specified on the boundary of an annulus. The key result is that this can be done with some control on the \(L^p\) norm of the differential of the transition map as well as some control on how far the values of the transition map deviate from its boundary values.
Lemma 2.14
(Luckhaus Lemma) [49, Lemma 1] Let \(\varvec{\textit{v}},\varvec{\textit{w}}\in W^{1,p}\left( \mathcal {S}^{m-1}_1;\mathbb {R}^j\right) \), \(\lambda \in \left( 0,\frac{1}{2}\right] \), \(\beta \in \left( \frac{\lfloor p-1\rfloor }{p},1\right) \), and \(\eta \in (0,1)\) be given. Define the constant K by
Then there are constants \(c_1:=c_1(j,m,p)\) and \(c_2:=c_2(j,m,p,\beta )\), and a map \(\varvec{\psi }\in W^{1,p}\left( \mathcal {B}^m_1\setminus \mathcal {B}^m_{1-\lambda };\mathbb {R}^j\right) \) satisfying
-
(i)
$$\begin{aligned} \varvec{\psi }(\varvec{\textit{x}})=\left\{ \begin{array}{ll} \varvec{\textit{v}}\left( \frac{\varvec{\textit{x}}}{1-\lambda }\right) , &{}\quad \varvec{\textit{x}}\in \mathcal {S}^{m-1}_{1-\lambda }\\ \varvec{\textit{w}}(\varvec{\textit{x}}), &{}\quad \varvec{\textit{x}}\in \mathcal {S}^{m-1}_1 \end{array}\right. \end{aligned}$$
-
(ii)
$$\begin{aligned} \int \limits _{\mathcal {B}^m_1\setminus \mathcal {B}^m_{1-\lambda }}|\varvec{\mathsf {d}}\varvec{\psi }|^p\,\mathrm {d}\varvec{\textit{x}}\le c_1 K^p\left( 1+\frac{\eta ^p}{\lambda ^p}\right) \lambda \end{aligned}$$
-
(iii)
and
$$\begin{aligned} \varvec{\psi }(\mathcal {B}_1\setminus \mathcal {B}_{1-\lambda }) \subseteq \varvec{\textit{v}}(\mathcal {S}_1)\cup \varvec{\textit{w}}(\mathcal {S}_1)\cup \left\{ \varvec{\textit{y}}\in \mathbb {R}^j: \mathrm{dist}\,(\varvec{\textit{y}},\varvec{\textit{v}}(\mathcal {S}_1))+\mathrm{dist}\,(\varvec{\textit{y}},\varvec{\textit{w}}(\mathcal {S}_1))< R_0\right\} , \end{aligned}$$where \( R_0= c_2 K\eta ^{1-\beta }\lambda ^{\frac{\lfloor p-1\rfloor -(m-1)}{p}}\).
The next lemma provides a Morrey regularity estimate for \((\varvec{\mathsf {B}},p)\)-harmonic maps from a unit ball into a Euclidean space.
Lemma 2.15
Let a positive definite \(\varvec{\mathsf {B}}\in (\odot ^2\mathbb {R}^n)\otimes (\odot ^2\mathbb {R}^m)\) be given. Suppose that \(\varvec{\textit{v}}\in W^{1,p}(\mathcal {B}^m_1;\mathbb {R}^n)\) is a local minimizer for the functional \(J[\cdot ;\varvec{\mathsf {B}}]\). Then for each \(\alpha \in [0,1)\) (or \(\alpha \in [\frac{p-m}{p},1)\) if \(p>m\)) there is a constant \(c_3 =c_3 (n,m,p,\alpha ,\varvec{\mathsf {B}})\) such that
for all \(\rho \in (0,1)\); i.e., \(\varvec{\textit{v}}\in W^{1,(p,m-(1-\alpha )p)}_{\mathrm{loc}\,}(\mathcal {B}^m_1;\mathbb {R}^n)\).
Remark 2.16
Lemma 2.15 is an application of Lemma 2 from [49] using the following estimate for the minimizer \(\varvec{\textit{v}}\):
This estimate is obtained via a minor modification of Uhlenbeck’s regularity argument, in [68], for solutions to elliptic systems (see also [36] and [44]).
The final lemma for this section establishes the coercivity for the integrand G. Recall that we are working under the assumptions (A1)–(A4).
Lemma 2.17
There is a constant \(c_4 >0\) such that the function G satisfies the following coercivity condition: for each \((\varvec{\textit{z}},\varvec{\textit{w}},\varvec{\xi })\in \mathcal {M}\times \mathcal {N}\times (\mathbb {R}^\ell \otimes T^*\mathcal {M})\) we find that
Proof
Omitted—see, for example, [20, Lemma 2.7]. \(\square \)
Notation 2.18
In the sequel, the number \(C\ge 1\) shall represent a constant that may change from line to line. In general, we shall not indicate the dependence of C on the other constants in a given argument. However, we make the declaration that C shall depend neither on the functions involved in the argument, e.g., \(\varvec{\textit{w}}\) and \(\varvec{\textit{u}}\), nor on the radius of the balls utilized in the arguments. Any other specific dependence that is important in the argument shall be noted. In particular, constants of which we especially wish to keep track shall be denoted by \(c_1\), \(c_2\), and so forth, and in this latter case the dependence shall be explicitly noted—e.g., \(c_1:=c_1(m)\).
3 Main lemmata
In this section, we prove two key lemmata. These will provide the principal ingredients for proving the main results of this paper in Sects. 4 and 5.
3.1 Statement and Proof of Lemma 3.1
Our first lemma shows that the weak limit of the blow-up sequence, based on the minimizer \(\varvec{\textit{u}}\), is a minimizer for the functional \(J[\cdot ;\varvec{\mathsf {A}}_0]\). The map \(\varvec{\mathsf {A}}_0\) is defined by \(\varvec{\mathsf {A}}\) frozen at an appropriate point. This will be used to prove an appropriate decay estimate in Sect. 4 that subsequently yields the partial Hölder continuity result.
Lemma 3.1
Let \(\mathcal {M}'\Subset \mathcal {M}\) and \(\{\delta _i,\rho _i\}_{i=1}^\infty \subset (0,1)\), such that \(\delta _i,\rho _i\rightarrow 0^+\), be given. Also let \(\{\varvec{\textit{z}}_i\}_{i=1}^\infty \subset \mathcal {M}'\), with a single local coordinate chart \((\mathcal {V}_0,\varvec{\varphi }_0)\) on \(\mathcal {M}\) such that \(\varvec{\textit{z}}_i\in \mathcal {V}_0\) and \(\mathcal {B}^m_{\rho _i}(\varvec{\varphi }_0(\varvec{\textit{z}}_i))\Subset \varvec{\varphi }_0(\mathcal {V}_0)\), be given. For each \(i\in \mathbb {N}\):
-
(a)
We assume that \(\left( \varvec{\textit{u}}\right) _{\varvec{\textit{z}}_i,\rho _i}\in \varOmega _{\mathcal {N}}\), and define \(\varvec{\textit{a}}_i\in \mathcal {N}\) by \(\varvec{\textit{a}}_i:=\varPi _{\mathcal {N}}\left( \left( \varvec{\textit{u}}\right) _{\varvec{\textit{z}}_i,\rho _i}\right) \).
-
(b)
Let \(\varvec{\textit{v}}_i\in W^{1,p}(\mathcal {B}^m_1;\mathbb {R}^\ell )\) be defined by
$$\begin{aligned} \varvec{\textit{v}}_i(\varvec{\textit{x}}):=\frac{\varvec{\textit{u}}(\varvec{\varphi }_0^{-1}(\varvec{\varphi }_0(\varvec{\textit{z}}_i)+\rho _i\varvec{\textit{x}}))-\varvec{\textit{a}}_i}{\delta _i}. \end{aligned}$$(3.1)
Assume:
-
(c)
We have \(\lim _{i\rightarrow \infty }\rho _i^{p-m+\gamma }/\delta _i^p=0\). (Recall that \(\gamma \) was fixed so that \(p-m+\gamma >0\).)
-
(d)
There is a \(\varvec{\textit{z}}_0\in \mathcal {M}\) such that \(\lim _{i\rightarrow \infty }\mathrm{dist}\,_{\mathcal {M}}(\varvec{\textit{z}}_i,\varvec{\textit{z}}_0)=0\).
-
(e)
There is an \(\varvec{\textit{a}}_0\in \mathcal {N}\) such that \(\varvec{\textit{a}}_i\rightarrow \varvec{\textit{a}}_0\) in \(\mathbb {R}^\ell \).
-
(f)
There is a \(\varvec{\textit{v}}\in W^{1,p}(\mathcal {B}^m_1;T_{\varvec{\textit{a}}_0}\mathcal {N})\) such that \(\varvec{\textit{v}}_i\rightharpoonup \varvec{\textit{v}}\) in \(W^{1,p}(\mathcal {B}^m_1;\mathbb {R}^\ell )\), upon identifying \(T_{\varvec{\textit{a}}_0}\mathcal {N}\) with an n-dimensional subspace of \(\mathbb {R}^\ell \).
Let \(\varvec{\mathsf {A}}_0\in \left( \odot ^2\mathbb {R}^n\right) \otimes \left( \odot ^2\mathbb {R}^m\right) \) be the local coordinate representation, with respect to \((\mathcal {V}_0,\varvec{\varphi }_0)\), of \(\varvec{\mathsf {A}}(\varvec{\textit{z}}_0,\varvec{\textit{a}}_0)\). Then, upon identifying \(T_{\varvec{\textit{a}}_0}\mathcal {N}\) with \(\mathbb {R}^n\), the mapping \(\varvec{\textit{v}}\) is a local minimizer of \(J[\cdot ;\varvec{\mathsf {A}}_0]\).
Proof
Our proof is an adaptation of an argument used in [49]. The main issues to be addressed are that \(\mathcal {M}\) is not assumed to be a Euclidean set and the generality of the asymptotic relatedness condition that G satisfies. Because the proof is lengthy, we break it into several constituent parts.
3.1.1 Nearest-point projection map
Define the sequence \(\{\varvec{\textit{x}}_i\}_{i=1}^\infty \subset \varvec{\varphi }_0(\mathcal {V}_0)\) by \(\varvec{\textit{x}}_i:=\varvec{\varphi }_0(\varvec{\textit{z}}_i)\). From assumption (d), we conclude that there is an \(\varvec{\textit{x}}_0\in \varvec{\varphi }_0(\mathcal {V}_0)\) such that \(\varvec{\textit{x}}_i\rightarrow \varvec{\textit{x}}_0\) in \(\mathbb {R}^m\). Assumption (e) implies \(\{\varvec{\textit{a}}_i\}_{i=1}^\infty \) is a bounded sequence. Hence, there is an \(\mathcal {N}'\Subset \mathcal {N}\) such that \(\{\varvec{\textit{a}}_i\}_{i=1}^\infty \subset \mathcal {N}'\). We may select a sequence \(\{L_i\}_{i=1}^\infty \) so that \(\lim _{i\rightarrow \infty }L_i=\infty \) and yet still have \(\lim _{i\rightarrow \infty }\delta _i L_i=0\) and, from (2.1) and (2.2),
and
In Sect. 2.2, we defined \(\varOmega _{\mathcal {N}}\) to be the domain of \(\varPi _{\mathcal {N}}\). Since we are ultimately only interested in the limit as \(i\rightarrow \infty \) and since \(\mathcal {N}'\) is compact, without loss, for each \(i\in \mathbb {N}\) we may assume that \(\mathcal {B}^\ell _{3\delta _i L_i}(\varvec{\textit{a}}_i)\subset \varOmega _{\mathcal {N}}\). Since \(\varPi _{\mathcal {N}}\) is uniformly Lipschitz on \(\bigcup _{i=1}^\infty \mathcal {B}_{3\delta _i L_i}(\varvec{\textit{a}}_i)\), there is a constant \(C_\varPi \ge 1\) such that
for each \(\varvec{\textit{y}}_1,\varvec{\textit{y}}_2\in \bigcup _{i=1}^\infty \mathcal {B}_{3\delta _i L_i}(\varvec{\textit{a}}_i)\).
3.1.2 Mappings
\(\varvec{\textit{w}}\): The comparison map for \(\varvec{\textit{v}}\)
Let \(\varvec{\textit{w}}\in W^{1,p}(\mathcal {B}^m_1;T_{\varvec{\textit{a}}_0}\mathcal {N})\) such that \(\mathrm{supp}\,(\varvec{\textit{v}}-\varvec{\textit{w}})\Subset \mathcal {B}_1\) be given and fixed. Select \(\widehat{\rho }\in (0,1)\) so that \(\mathrm{supp}\,(\varvec{\textit{v}}-\varvec{\textit{w}})\subset \mathcal {B}_{\widehat{\rho }}\). Thus, \(\varvec{\textit{v}}(\varvec{\textit{x}})=\varvec{\textit{w}}(\varvec{\textit{x}})\) for a.e. \(\varvec{\textit{x}}\in \mathcal {B}_1\setminus \mathcal {B}_{\widehat{\rho }}\). Since \(\varvec{\textit{v}}_i\rightharpoonup \varvec{\textit{v}}\) in \(W^{1,p}\) (assumption (f)), it follows that \(\{\varvec{\textit{v}}_i\}_{i=1}^\infty \) is bounded in \(W^{1,p}\). By the Rellich-Kondrachov theorem, there is an unrelabeled subsequence so that \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(L^p(\mathcal {B}_1^m;\mathbb {R}^\ell )\). We may now pick \(\overline{\rho }\in (\widehat{\rho },1)\) so that both of the following hold:
and
To show that \(\varvec{\textit{v}}\) is a minimizer, we need to take advantage of the assumption that each \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{v}}_i\) is a local minimizer for the functional I, where we recall that I is defined in (2.3). The map \(\varvec{\textit{w}}\), however, does not satisfy the constraint that \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}\) maps into \(\mathcal {N}\). Therefore \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}\) cannot be used directly as a comparison map. To overcome this requires transforming \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}\) into a sequence of maps that are comparable to \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{v}}_i\). Moreover, this needs to be done in such a way that, as \(i\in \mathbb {N}\) gets large, this transformation approaches an identity, in some sense. At each stage of the transformation, we will establish the convergence, in \(W^{1,p}(\mathcal {B}^m_{\overline{\rho }};\mathbb {R}^\ell )\), of the new sequence of maps to the original \(\varvec{\textit{w}}\).
\(\widetilde{\varvec{\textit{w}}}_i\): The rotated truncations of \(\varvec{\textit{w}}\)
Definition of \(\widetilde{\varvec{\textit{w}}}_i\): The first component of this transformation involves mapping the image of \(\varvec{\textit{w}}\) from \(T_{\varvec{\textit{a}}_0}\mathcal {N}\) to \(T_{\varvec{\textit{a}}_i}\mathcal {N}\) and then truncating to ensure the projection map can be used. By viewing, for each \(\varvec{\textit{y}}\in \mathcal {N}\), the tangent space \(T_{\varvec{\textit{y}}}\mathcal {N}\) as an n-dimensional linear subspace of \(\mathbb {R}^\ell \), this can be accomplished through a rotation. Define \(\varvec{\mathsf {Q}}_{\varvec{\textit{y}}}\in \mathbb {R}^\ell \otimes \mathbb {R}^\ell \) as the rotation—i.e., orientation preserving isometry—operator that maps \(T_{\varvec{\textit{a}}_0}\mathcal {N}\) onto \(T_{\varvec{\textit{y}}}\mathcal {N}\). Since \(\varvec{\textit{a}}_i\rightarrow \varvec{\textit{a}}_0\) in \(\mathbb {R}^\ell \), the smoothness of \(\mathcal {N}\) implies
Define the sequence of truncated rotated maps \(\{\widetilde{\varvec{\textit{w}}}_i\}_{i=1}^\infty \subset W^{1,p}(\mathcal {B}_1;T_{\varvec{\textit{a}}_i}\mathcal {N})\cap L^\infty (\mathcal {B}_1;T_{\varvec{\textit{a}}_i}\mathcal {N})\) by
so \(\Vert \widetilde{\varvec{\textit{w}}}_i\Vert _{L^\infty (\mathcal {B}_1)}\le L_i/C^2_\varPi \), for each \(i\in \mathbb {N}\), and \(\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\widetilde{\varvec{\textit{w}}}_i(\varvec{\textit{x}}))\) is well defined for each \(\varvec{\textit{x}}\in \mathcal {B}^m_1\).
Convergence of \(\widetilde{\varvec{\textit{w}}}_i\): We now verify that \(\widetilde{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}\). Denote the identity map by \(\varvec{\mathsf {I}}\). From (3.7), we see that
and
Thus, \(\lim _{i\rightarrow \infty }\left| \big \{\varvec{\textit{x}}\in \mathcal {B}_1:\varvec{\textit{w}}(\varvec{\textit{x}})\ne \varvec{\mathsf {Q}}_{\varvec{\textit{a}}_i}^{-1}\widetilde{\varvec{\textit{w}}}_i(\varvec{\textit{x}})\text { or }\varvec{\mathsf {d}}\varvec{\textit{w}}(\varvec{\textit{x}})\ne \varvec{\mathsf {d}}[\varvec{\mathsf {Q}}_{\varvec{\textit{a}}_i}^{-1}\widetilde{\varvec{\textit{w}}}_i(\varvec{\textit{x}})]\big \}\right| =0\) and
Also
Hence \(\varvec{\mathsf {Q}}_{\varvec{\textit{a}}_i}^{-1}\widetilde{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_1;T_{\varvec{\textit{a}}_0}\mathcal {N})\). Combining this with (3.6) implies \(\widetilde{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\).
\(\overline{\varvec{\textit{w}}}_i\): The oscillations in \(\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\widetilde{\varvec{\textit{w}}}_i)\)
Definition of \(\overline{\varvec{\textit{w}}}_i\): The next step is to project each \(\varvec{\textit{a}}_i+\delta _i\widetilde{\varvec{\textit{w}}}_i\) onto \(\mathcal {N}\). As was mentioned before, this projection is well defined, so we may define \(\{\overline{\varvec{\textit{w}}}_i\}_{i=1}^\infty \subset W^{1,p}\left( \mathcal {B}_1^m;\mathbb {R}^\ell \right) \) by
We note that the Lipschitz continuity of \(\varPi _{\mathcal {N}}\) implies \(\Vert \overline{\varvec{\textit{w}}}_i\Vert _{L^\infty (\mathcal {B}_1)}\le L_i/C_\varPi \) for each \(i\in \mathbb {N}\).
Convergence of \(\overline{\varvec{\textit{w}}}_i\): To facilitate the production of a transition map between \(\overline{\varvec{\textit{w}}}_i\) and \(\varvec{\textit{v}}_i\), we will show both \(\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_1^m;\mathbb {R}^\ell )\) and \(\overline{\varvec{\textit{w}}}_i-\varvec{\textit{v}}_i\rightarrow \varvec{\textit{0}}\) in \(L^p(\mathcal {S}^{m-1}_{\overline{\rho }};\mathbb {R}^\ell )\). Based on the convergence of \(\widetilde{\varvec{\textit{w}}}\) already established, we have
Since \(\varvec{\textit{a}}_i+\delta _i\widetilde{\varvec{\textit{w}}}_i(\varvec{\textit{x}})\in \mathcal {B}^\ell _{3\delta _i L_i}\cap [\varvec{\textit{a}}_i+ T_{\varvec{\textit{a}}_i}\mathcal {N}]\) for each \(\varvec{\textit{x}}\in \mathcal {B}_1\), the limit (3.2) implies \(\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(L^p(\mathcal {B}_1;\mathbb {R}^\ell )\). Next we again use the convergence of \(\widetilde{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}\) to conclude that
Now, \(\varvec{\mathsf {d}}\widetilde{\varvec{\textit{w}}}_i(\varvec{\textit{x}})\in T_{\varvec{\textit{a}}_i}\mathcal {N}\) for each \(\varvec{\textit{x}}\in \mathcal {B}_1\), so it follows from (3.3) that \(\varvec{\mathsf {d}}\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\mathsf {d}}\varvec{\textit{w}}\) in \(L^p(\mathcal {B}_1;\mathbb {R}^{\ell \times m})\). Thus, \(\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\).
We now argue that \(\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{v}}_i\) in \(L^p(\mathcal {S}^{m-1}_{\overline{\rho }};\mathbb {R}^\ell )\). From (3.4), we write
We again deduce from (3.2) that the first limit (on the right-hand side) vanishes. Recalling (3.6) yields
\(\varvec{\textit{w}}^*_i\): The transition map between \(\overline{\varvec{\textit{w}}}_i\) and \(\varvec{\textit{v}}_i\)
Definition of \(\varvec{\textit{w}}^*_i\): We are now in position to produce a map that provides a transition from \(\overline{\varvec{\textit{w}}}_i\) to \(\varvec{\textit{v}}_i\) on an annular region within \(\mathcal {B}_1^m\). Define \(\{\eta _i\}_{i=1}^\infty \) by
From the convergence \(\overline{\varvec{\textit{w}}}_i-\varvec{\textit{v}}_i\rightarrow \varvec{\textit{0}}\) in \(L^p(\mathcal {S}^{m-1}_{\overline{\rho }};\mathbb {R}^\ell )\) just established, we have \(\lim _{i\rightarrow \infty }\eta _i=0\). Let the sequence \(\{\lambda _i\}_{i=1}^\infty \subset (0,1)\) be defined by
so that
For the transition map, we use the Luckhaus Lemma. Fix \(\beta \in \left( \frac{\lfloor p-1\rfloor }{p},1\right) \). Define the sequence \(\left\{ K_i\right\} _{i=1}^{\infty }\subset \mathbb {R}\) so that
Invoking Lemma 2.14 yields transition maps \(\{\varvec{\psi }_i\}_{i=1}^\infty \in W^{1,p}(\mathcal {B}^m_1\setminus \mathcal {B}^m_{1-\lambda _i};\mathbb {R}^\ell )\) satisfying
and
Here
where \(\beta \) was fixed above. We now let \(\varvec{\textit{w}}^*_i\in W^{1,p}(\mathcal {B}_1^m;\mathbb {R}^\ell )\) be given by the following definition.
Note that for \(\varvec{\textit{x}}\in \mathcal {S}^m_{\overline{\rho }(1-\lambda _i)}\), we find that \(\varvec{\psi }_i(\frac{\varvec{\textit{x}}}{\overline{\rho }})=\overline{\varvec{\textit{w}}}_i(\frac{\varvec{\textit{x}}}{1-\lambda _i})\); and for \(\varvec{\textit{x}}\in \mathcal {S}^m_{\overline{\rho }}\), we have \(\varvec{\psi }_i(\frac{\varvec{\textit{x}}}{\overline{\rho }})=\varvec{\textit{v}}_i(\varvec{\textit{x}})\). Also since \(1-\beta >0\), we conclude that
Moreover, \(\sup _{i\in \mathbb {N}}K_i<\infty \). It follows that \(\lim _{i\rightarrow \infty }R_i=0\). Again, as we are interested in the limit as \(i\rightarrow \infty \), we may assume without loss of generality that \(R_i<1\le L_i/C_\varPi \) for each \(i\in \mathbb {N}\). Recall that \(\Vert \overline{\varvec{\textit{w}}}_i\Vert _{L^\infty }\le L_i/C_\varPi \). The bound on the range of \(\varvec{\psi }_i\) in (3.14) implies that for each \(x\in \mathcal {B}_{\overline{\rho }}\setminus \mathcal {B}_{\overline{\rho }(1-\lambda _i)}\)
As each of \(\varvec{\textit{a}}_i+\delta _i\overline{\varvec{\textit{w}}}_i\) and \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{v}}_i\) has range in \(\mathcal {N}\), we conclude that \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i(\mathcal {B}_1^m)\subset \varOmega _{\mathcal {N}}\). The map we ultimately use to compare with each \(\varvec{\textit{v}}_i\) is \(\delta _i^{-1}[\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i)-\varvec{\textit{a}}_i]\).
Convergence of \(\varvec{\textit{w}}^*_i\): First we argue that \(\varvec{\textit{w}}^*_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_{\overline{\rho }}^m;\mathbb {R}^\ell )\). Let us check the convergence of \(\varvec{\textit{w}}^*_i\rightarrow \varvec{\textit{w}}\) in \(L^p\). Based on the definition in (3.15) and the convergence of \(\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\), we write
Clearly, we have that \(\left[ \overline{\varvec{\textit{w}}}_i(\frac{\varvec{\textit{x}}}{1-\lambda _i})-\overline{\varvec{\textit{w}}}_i(\varvec{\textit{x}})\right] \rightarrow 0\) for a.e. \(\varvec{\textit{x}}\in \mathcal {B}_{\overline{\rho }}\). We also see that \(\left| \overline{\varvec{\textit{w}}}_i(\frac{\varvec{\textit{x}}}{1-\lambda _i})-\overline{\varvec{\textit{w}}}_i(\varvec{\textit{x}})\right| ^p\le C\left\{ |\varvec{\textit{w}}(\varvec{\textit{x}})|^p+|\varvec{\textit{w}}(\frac{\varvec{\textit{x}}}{1-\lambda _i})|^p\right\} \). The Lebesgue dominated convergence theorem implies \(\lim _{i\rightarrow \infty }I_{1,i}=0\).
We now examine \(\lim _{i\rightarrow \infty }I_{2,i}\). The bound on the range of \(\varvec{\psi }_i\) in (3.14) implies that
for each \(\varvec{\textit{x}}\in \mathcal {B}_{\overline{\rho }}\setminus \mathcal {B}_{\overline{\rho }(1-\lambda _i)}\). Since \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\in L^p(\mathcal {B}_1^m;\mathbb {R}^\ell )\), \(\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\in L^p(\mathcal {B}_1^m;\mathbb {R}^\ell )\), and \(\lim _{i\rightarrow \infty }|\mathcal {B}_{\overline{\rho }}\setminus \mathcal {B}_{\overline{\rho }(1-\lambda _i)}|=0\), we have
From this limit and (3.16), we may estimate
Thus, \(\varvec{\textit{w}}^*_i\rightarrow \varvec{\textit{w}}\) in \(L^p(\mathcal {B}_\rho ^m;\mathbb {R}^\ell )\).
Now we turn to the convergence of \(\varvec{\mathsf {d}}\varvec{\textit{w}}_i^*\rightarrow \varvec{\mathsf {d}}\varvec{\textit{w}}\) in \(L^p\). As before, the convergence of \(\overline{\varvec{\textit{w}}}_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}\) and the definition of \(\varvec{\textit{w}}_i\) yields
As was done with \(I_{1,i}\) above, the Lebesgue dominated convergence theorem may be used to argue that \(\lim _{i\rightarrow \infty }I_{3,i}=0\). For the limit of \(I_{4,i}\), we recall that \(\sup _{i\in \mathbb {N}}K_i<\infty \), so (3.11) and the inequality in (3.13) imply
since \(\varvec{\textit{w}}\in W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\) and \(\lim _{i\rightarrow \infty }|\mathcal {B}_{\overline{\rho }}\setminus \mathcal {B}_{\overline{\rho }(1-\lambda _i)}|=0\). This completes the argument that \(\varvec{\textit{w}}^*_i\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_{\overline{\rho }};\mathbb {R}^\ell )\).
\(\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i)\): The comparison map for \(\varvec{\textit{v}}_i\)
Finally, we demonstrate the convergence \(\delta _i^{-1}[\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i)-\varvec{\textit{a}}_i]\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_{\overline{\rho }};\mathbb {R}^\ell )\). For each \(i\in \mathbb {N}\) and each \(\varvec{\textit{x}}\in \mathcal {B}_{\overline{\rho }(1-\lambda _i)}\), we find that \(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i(\varvec{\textit{x}})\) is already in \(\mathcal {N}\), so \(\delta _i^{-1}[\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i(\varvec{\textit{x}}))-\varvec{\textit{a}}_i]=\varvec{\textit{w}}^*_i(\varvec{\textit{x}})\). From the convergence of \(\varvec{\textit{w}}^*_i\) that was just established, we conclude that
It remains to show the convergence on \(\mathcal {B}_{\overline{\rho }}\setminus \mathcal {B}_{\overline{\rho }(1-\lambda _i)}\), for which we again use the fact that the measure of this set vanishes in the limit. Since \(\varPi _{\mathcal {N}}\) is Lipschitz, for \(\varvec{\textit{x}}\in \mathcal {B}_{\overline{\rho }}\setminus \mathcal {B}_{\overline{\rho }(1-\lambda _i)}\) we have the estimate
Now \(\varvec{\textit{w}}^*_i\rightarrow \varvec{\textit{w}}\) in \(L^p(\mathcal {B}_{\overline{\rho }};\mathbb {R}^\ell )\) implies
Hence,
This verifies that \(\delta _i^{-1}[\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i)-\varvec{\textit{a}}_i]\rightarrow \varvec{\textit{w}}\) in \(L^p(\mathcal {B}_{\overline{\rho }};\mathbb {R}^\ell )\). To finish the argument, we again use the fact that \(\varPi _{\mathcal {N}}\) is Lipschitz to estimate
Using the same argument that showed \(\lim _{i\rightarrow \infty }I_{4,i}=0\), we see that the above limit vanishes as well. This establishes the convergence \(\delta _i^{-1}[\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}^*_i)-\varvec{\textit{a}}_i]\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_{\overline{\rho }};\mathbb {R}^\ell )\). With this in hand, we now are ready to begin comparing \(J[\varvec{\textit{v}};\varvec{\mathsf {A}}_0]\) to \(J[\varvec{\textit{w}};\varvec{\mathsf {A}}_0]\).
Comparison between \(J[\varvec{\textit{v}};\varvec{\mathsf {A}}_0]\) and \(J[\varvec{\textit{w}};\varvec{\mathsf {A}}_0]\)
3.1.3 Definitions
Before proceeding to compare \(J[\varvec{\textit{v}};\varvec{\mathsf {A}}_0]\) to \(J[\varvec{\textit{w}};\varvec{\mathsf {A}}_0]\), we need to make a few more definitions. Given \(\varvec{\textit{z}}\in \mathcal {V}_0\) and \(\varvec{\textit{w}}\in \mathbb {R}^\ell \), we will require a representation of \(\varvec{\mathsf {A}}(\varvec{\textit{z}},\varvec{\textit{w}})\) and \(\varvec{\mathsf {g}}(\varvec{\textit{z}})\) in local coordinates. With \(\{\frac{\partial }{\partial x^j}\}_{j=1}^m\) an orthonormal basis for \(T_{\varvec{\textit{x}}}\mathbb {R}^m\) for each \(\varvec{\textit{x}}\in \varvec{\varphi }_0(\mathcal {V}_0)\), and \(\{\,\mathrm {d}w^\alpha \}_{\alpha =1}^\ell \) an orthonormal basis for \(T^*_{\varvec{\textit{w}}}\mathbb {R}^\ell \) for each \(\varvec{\textit{w}}\in \mathbb {R}^\ell \), we define the components of the tensor-valued maps \(\varvec{\textit{A}}\in \mathscr {C}^{}\left( \varvec{\varphi }_0\left( \mathcal {V}_0\right) \times \mathbb {R}^\ell ;\left( \odot ^2\mathbb {R}^\ell \right) \otimes \left( \odot ^2\mathbb {R}^m\right) \right) \) and \(\varvec{\textit{g}}\in \mathscr {C}^{\infty }\left( \varvec{\varphi }_0\left( \mathcal {V}_0\right) ;\odot ^2\mathbb {R}^m\right) \) by
and
The components of the inverse matrix \(\varvec{\textit{g}}^{-1}\) are denoted by \(g^{j_1,j_2}\) for \(1\le j_1,j_2\le m\). We put \(\varvec{\textit{A}}_0:=\varvec{\textit{A}}(\varvec{\textit{x}}_0,\varvec{\textit{a}}_0)\) and \(\varvec{\textit{g}}_0:=\varvec{\textit{g}}(\varvec{\textit{x}}_0)\). For convenience let \(\varvec{\zeta }_i\in \mathscr {C}^{\infty }\left( \mathbb {R}^m;\mathbb {R}^m\right) \) be given by
for each \(i\in \mathbb {N}\). Also define \(\{\varvec{\textit{A}}_i\}_{i=1}^\infty \subset \mathscr {C}^{}\left( \mathcal {B}_1^m\times \mathbb {R}^\ell ;\left( \odot ^2\mathbb {R}^\ell \right) \otimes \left( \odot ^2\mathbb {R}^m\right) \right) \) and \(\{\varvec{\textit{g}}_i\}_{i=1}^\infty \subset \mathscr {C}^{\infty }(\mathcal {B}_1^m;\odot ^2\mathbb {R}^m)\) by
Let \(\varvec{\textit{g}}_i^{-1}\) denote the inverse of \(\varvec{\textit{g}}_i\). The uniform continuity of \(\varvec{\textit{g}}\) on \(\varvec{\varphi }_0(\mathcal {V})\) implies
Assumption (A2) implies that for each \(r>0\)
Recalling that \(\varvec{\textit{x}}_i\rightarrow \varvec{\textit{x}}_0\) in \(\mathbb {R}^m\) and that by hypothesis \(\varvec{\varphi }_0^{-1}\in \mathscr {C}^{\infty }\left( \varvec{\varphi }_0(\mathcal {V}_0);\mathcal {N}\right) \) and \(\varvec{\textit{a}}_i\rightarrow \varvec{\textit{a}}_0\) in \(\mathbb {R}^\ell \), we deduce that for each \(r>0\)
Assumption (A1) implies \(\varvec{\textit{A}}_0\) is positive definite.
For each \(i\in \mathbb {N}\), define \(\varvec{\textit{u}}_i\in W^{1,p}(\varvec{\varphi }_0^{-1}(\mathcal {B}_{\rho _i}^m(\varvec{\textit{x}}_i));\mathcal {N})\) by
For each \(\varepsilon >0\), also define the sequence of measurable sets \(\{E_{\varepsilon ,i}\}_{i=1}^\infty \) by
For each \(\varvec{\textit{x}}\in \mathcal {B}_1^m\) we compute
For each \(i\in \mathbb {N}\), define \(\varvec{\xi }_i\in L^p(\mathcal {B}_1^m;\mathbb {R}^\ell \otimes \mathbb {R}^m)\) by
so
Since \(\delta _i^{-1}[\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{w}}_i)-\varvec{\textit{a}}_i]\rightarrow \varvec{\textit{w}}\) in \(W^{1,p}(\mathcal {B}_{\overline{\rho }}^m;\mathbb {R}^\ell )\), we deduce that
We note that the representation of \(\varvec{\varphi }_0\) in local coordinates is \(\varvec{\textit{x}}\) and moreover that the map \(\varvec{\mathsf {d}}\varvec{\varphi }_0\in \mathscr {C}^{\infty }(\varvec{\varphi }_0^{-1}(\mathcal {B}_{\rho _i}^m(\varvec{\textit{x}}_i));\mathbb {R}^m\otimes T^*\mathcal {M})\) is the identity matrix \(\varvec{\textit{I}}\in \mathbb {R}^m\otimes \mathbb {R}^m\) in local coordinates.
3.1.4 Main estimates
Let \(\varepsilon >0\) be given. We write
Using the convergence in (3.21) and the uniform convergence of \(\sqrt{\det \varvec{\textit{g}}_i}\rightarrow \sqrt{\det \varvec{\textit{g}}_0}\) and of \(\varvec{\textit{A}}_i\) to \(\varvec{\textit{A}}_0\), in (3.18) and (3.19), we conclude that
We also have from (3.21) that \(\frac{\rho _i}{\delta _i}\varvec{\xi }_i\rightarrow \varvec{\textit{w}}\) in \(L^p(\mathcal {B}_{\overline{\rho }}^m;\mathbb {R}^\ell \otimes \mathbb {R}^m)\). Thus,
Recall that \(\varvec{\mathsf {d}}\varvec{\varphi }_0\) is \(\varvec{\textit{I}}\) in local coordinates. Turning to \(II_{2,i}\), we change variables to get
For each \(i\in \mathbb {N}\), put
The asymptotic convexity assumption in (A4) implies
for every \(\varvec{\textit{z}}\in \varvec{\varphi }_i^{-1}(E_{\varepsilon ,i})\). Hence,
Rewriting definition (3.1), for each \(\varvec{\textit{z}}\in \varvec{\varphi }_i^{-1}(\mathcal {B}_{\overline{\rho }})\) we get
Thus,
Since \(\varvec{\textit{u}}\) is a local minimizer for I, and \(\varvec{\textit{u}}_i=\varvec{\textit{u}}\) on \(\mathcal {B}_{1}\setminus \mathcal {B}_{\overline{\rho }}\), for each \(i\in \mathbb {N}\), we must have that
Therefore,
We now work to estimate \(II_{3,i}\) from below in terms of \(J[\varvec{\textit{v}},\varvec{\mathsf {B}}_0]\). For each \(i\in \mathbb {N}\), set
Assumption (A4) yields
for each \(\varvec{\textit{z}}\in \varvec{\varphi }_i^{-1}(F_i)\). It follows that
The identification of \(\varvec{\varphi }_0\) with \(\varvec{\textit{x}}\) in local coordinates implies the identity element \(\varvec{\mathsf {I}}\in T^*\mathcal {M}\otimes T^*\mathcal {M}\) is represented by \(\varvec{\mathsf {d}}\varvec{\varphi }_0^{-1}\in \mathscr {C}^{\infty }(\mathcal {B}_{\rho _i}(\varvec{\textit{x}}_i); T^*\mathcal {M}\otimes \mathbb {R}^m)\). Upon changing variables again we obtain
3.1.5 Final comparison
Collecting the above estimate along with the estimates (3.22), (3.23), and (3.24) gives us
We observe that
Thus,
for each \(\varvec{\textit{x}}\in \mathcal {B}_{\overline{\rho }}\). The uniform convergence in each of (3.18) and (3.19) along with the strong convergence of \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(L^p\) implies
Since \(\varvec{\textit{A}}_0\) is positive definite, this integral is weakly lower semicontinuous in \(L^p\). It follows from the weak convergence \(\varvec{\textit{v}}_i\rightharpoonup \varvec{\textit{v}}\) in \(L^p\), provided by assumption (f), that
The growth condition in (A3) allows us to estimate
Here we used the inequality \(\left| \varvec{\mathsf {d}}\varvec{\textit{u}}_i(\varvec{\textit{z}})\right| _{\mathbb {R}^\ell \otimes T^*_{\varvec{\textit{z}}}\mathcal {M}}\le \sigma _\varepsilon (\varvec{\textit{z}})\), which holds for each \(\varvec{\textit{z}}\in \varvec{\varphi }_i^{-1}(\mathcal {B}_{\overline{\rho }}\setminus E_i)\) by the definition of \(E_{\varepsilon ,i}\) in (3.20); we have also used the fact that from the definitions of \(\varvec{\varphi }_0\), \(\varvec{\varphi }_i\), and \(\varvec{\zeta }_i\) we notice that
Since \(\varvec{\varphi }_0^{-1}(\mathcal {B}_{\rho _i}(\varvec{\textit{x}}_i))\subset \mathcal {V}_0\subseteq \mathcal {M}'\) and \(\mathcal {M}'\) is compactly contained in \(\mathcal {M}\), there must be a constant \(C'<\infty \) such that \(\varvec{\varphi }_0^{-1}(\mathcal {B}_{\rho _i}(\varvec{\textit{x}}_i))\subseteq \mathcal {B}^{\mathcal {M}}_{C'\rho _i}(\varvec{\textit{z}}_i)\) for each \(i\in \mathbb {N}\). By hypothesis \(\overline{\sigma },|\sigma _{\varepsilon }|^p\in L^{1,\gamma }(\mathcal {M})\) and \(\lim _{i\rightarrow \infty }\rho _i^{p-m+\gamma }/\delta _i^p=0\). Hence,
Completely analogous arguments yield
Next we see that
Using the local coordinate representation produces:
Continuing with a change of variables using \(\varvec{\zeta }_i=\varvec{\textit{x}}_i+\rho _i\varvec{\textit{x}}\) yields
Thus,
The analysis of \(\limsup _{i\rightarrow \infty }\rho _i^{p-m}II_{9,i}\) is similar. We obtain
Using the above estimates in (3.26) yields
Put \(\varvec{\mathsf {A}}_0:=\varvec{\mathsf {A}}(\varvec{\textit{z}}_0,\varvec{\textit{a}}_0)\). Thus, \(\varvec{\mathsf {A}}_0\) is just the restriction of \(\varvec{\textit{A}}_0\) to \((\odot ^2 T_{\varvec{\textit{a}}_0}\mathcal {N})\otimes (\odot ^2\mathbb {R}^m)\), and so \(\varvec{\mathsf {A}}_0\left( \otimes ^2\varvec{\mathsf {d}}\varvec{\textit{v}}\right) =\varvec{\textit{A}}_0\left( \otimes ^2\varvec{\mathsf {d}}\varvec{\textit{v}}\right) \) and \(\varvec{\mathsf {A}}_0\left( \otimes ^2\varvec{\mathsf {d}}\varvec{\textit{w}}\right) =\varvec{\textit{A}}_0\left( \otimes ^2\varvec{\mathsf {d}}\varvec{\textit{w}}\right) \). The last estimate is valid for each \(\varepsilon >0\) and \(\sup _{i\in \mathbb {N}}\Vert \varvec{\mathsf {d}}\varvec{\textit{v}}_i\Vert _{L^p(\mathcal {B}_1^m;\mathbb {R}^\ell )}<\infty \). We may therefore take the limit as \(\varepsilon \rightarrow 0^+\) to get
As this demonstrates the desired minimality of \(\varvec{\textit{v}}\), the proof is thus complete. \(\square \)
3.2 Statement and Proof of Lemma 3.2
The second lemma shows that if the blow-up sequence converges weakly to some map, then it actually converges strongly. This second lemma is, in part, used in establishing the partial Caccioppoli inequality.
Lemma 3.2
Let \(\mathcal {M}'\Subset \mathcal {M}\) and \(\{\delta _i,\rho _i\}_{i=1}^\infty \subset (0,1)\), such that \(\delta _i,\rho _i\rightarrow 0^+\), be given. Also let \(\{\varvec{\textit{z}}_i\}_{i=1}^\infty \subset \mathcal {M}'\), with a single local coordinate chart \((\mathcal {V}_0,\varvec{\varphi }_0)\) on \(\mathcal {M}\) such that \(\varvec{\textit{z}}_i\in \mathcal {V}_0\) and \(\mathcal {B}^m_{\rho _i}(\varvec{\varphi }_0(\varvec{\textit{z}}_i))\Subset \varvec{\varphi }_0(\mathcal {V}_0)\), be given. For each \(i\in \mathbb {N}\): let \(\{\varvec{\textit{a}}_0\}\cup \{\varvec{\textit{a}}_i\}_{i=1}^\infty \subset \mathcal {N}\), \(\varvec{\textit{z}}_0\in \mathcal {M}\) and \(\{\varvec{\textit{v}}_i\}_{i=1}^\infty \subset W^{1,p}(\mathcal {B}_1^m;\mathbb {R}^\ell )\) along with assumptions (a)–(f) be as described in Lemma 3.1. Then we have the strong convergence \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(W^{1,p}_{\mathrm{loc}\,}(\mathcal {B}_1^m;\mathbb {R}^\ell )\).
Proof
Several elements of the setup that we need are the same as were used in the proof of Lemma 3.1. We will therefore take advantage of some of the definitions already made in that proof. As with the proof of Lemma 3.1 we have broken the proof into several steps.
First we observe that the Rellich-Kondrachov theorem yields \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(L^p(\mathcal {B}_1^m;\mathbb {R}^\ell )\). It only remains to verify that \(\varvec{\mathsf {d}}\varvec{\textit{v}}_i\rightarrow \varvec{\mathsf {d}}\varvec{\textit{v}}\) in \(L^p(\mathcal {B}_{\widehat{\rho }}^m;\mathbb {R}^\ell \otimes \mathbb {R}^m)\) for each \(\widehat{\rho }\in (0,1)\).
3.2.1 Definitions
Select \(\widehat{\rho }\in (0,1)\), which is henceforth fixed but otherwise arbitrary. It is enough to show \(\varvec{\mathsf {d}}\varvec{\textit{v}}_i\rightarrow \varvec{\mathsf {d}}\varvec{\textit{v}}\) in \(L^p(\mathcal {B}_{\overline{\rho }}^m;\mathbb {R}^\ell \otimes \mathbb {R}^m)\) for some \(\overline{\rho }\in (\widehat{\rho },1)\). Since \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(L^p\), we may find a number \(\overline{\rho }\in (\widehat{\rho },1)\) such that
and
For Lemma 3.1, we modified a given \(\varvec{\textit{w}}\in W^{1,p}(\mathcal {B}_1^m;T_{\varvec{\textit{a}}_0}\mathcal {N})\) into a sequence \(\{\varvec{\textit{w}}_i^*\}_{i=1}^\infty \) via a series of transformations. Since \(\varvec{\textit{v}}\) is a choice for a map in \(W^{1,p}(\mathcal {B}_1^m;T_{\varvec{\textit{a}}_0}\mathcal {N})\), we use the exact same transformations to produce a sequence \(\{\varvec{\textit{v}}^*_i\}_{i=1}^\infty \subset W^{1,p}(\mathcal {B}_1^m;\mathbb {R}^\ell )\) with the following properties: for each \(i\in \mathbb {N}\), it holds that
-
(i)
\(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{v}}^*_i(\varvec{\textit{x}})\in \varOmega _{\mathcal {N}}\) for all \(\varvec{\textit{x}}\in \mathcal {B}_1\);
-
(ii)
\(\varvec{\textit{v}}^*_i(\varvec{\textit{x}})=\varvec{\textit{v}}_i(\varvec{\textit{x}})\) for all \(\varvec{\textit{x}}\in \mathcal {B}_1\setminus \overline{\mathcal {B}}_{\overline{\rho }}\);
-
(iii)
\(\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{v}}_i^*(\varvec{\textit{x}}))\) is well defined for each \(\varvec{\textit{x}}\in \mathcal {B}_{\overline{\rho }}\);
-
(iv)
\(\lim _{i\rightarrow \infty }\Vert \varvec{\textit{v}}_i^*-\varvec{\textit{v}}\Vert _{W^{1,p}(\mathcal {B}_{\overline{\rho }}^m;\mathbb {R}^\ell )}=0\); and
-
(v)
\(\lim _{i\rightarrow \infty } \left\| \frac{\varPi _{\mathcal {N}}(\varvec{\textit{a}}_i+\delta _i\varvec{\textit{v}}_i^*)-\varvec{\textit{a}}_i}{\delta _i}-\varvec{\textit{v}}\right\| _{W^{1,p}(\mathcal {B}_{\overline{\rho }};\mathbb {R}^\ell )}=0\).
Before estimating \(\Vert \varvec{\mathsf {d}}\varvec{\textit{v}}_i-\varvec{\mathsf {d}}\varvec{\textit{v}}\Vert ^p_{L^p(\mathbb {R}^\ell \otimes \mathbb {R}^m)}\), we recall a few more definitions that were used in the proof of Lemma 3.1. The sequences \(\{\varvec{\zeta }_i\}_{i=1}^\infty \subset \mathscr {C}^{\infty }(\mathbb {R}^m;\mathbb {R}^m)\) and \(\{\varvec{\varphi }_i\}_{i=1}^\infty \subset \mathscr {C}^{\infty }(\mathcal {V}_0;\mathbb {R}^m)\) are given by
For each \(i\in \mathbb {N}\), define the map \(\varvec{\textit{w}}_i\in W^{1,p}\left( \varvec{\varphi }_i^{-1}(\mathcal {B}_{1}^m(\varvec{\textit{x}}_i));\mathcal {N}\right) \) by
Note that \(\varvec{\textit{w}}_i\) is well defined by property (iii) for \(\varvec{\textit{v}}^*_i\).
Let \(\{\varvec{\textit{A}}_i\}_{i=1}^\infty \subset \mathscr {C}^{}\left( \mathcal {B}_1^m\times \mathbb {R}^\ell ;\left( \odot ^2\mathbb {R}^\ell \right) \otimes \left( \odot ^2\mathbb {R}^m\right) \right) \) and \(\{\varvec{\textit{g}}_i\}_{i=1}^\infty \subset \mathscr {C}^{\infty }\left( \mathcal {B}_1^m;\odot ^2\mathbb {R}^m\right) \) be defined as in (3.17). Thus the convergences in (3.18) and (3.19) are both valid. These in combination with the strong convergence \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(L^p(\mathcal {B}_1;\mathbb {R}^\ell )\) imply
Let \(\varvec{\textit{A}}_0\in (\odot ^2\mathbb {R}^\ell )\otimes (\odot ^2\mathbb {R}^m)\) be the local coordinate representation, with respect to \((\mathcal {V}_0,\varvec{\varphi }_0)\), of \(\varvec{\mathsf {A}}(\varvec{\textit{z}}_0,\varvec{\textit{a}}_0)\).
3.2.2 Upper bound for \(\lim _{i\rightarrow \infty }\int \limits _{\mathcal {B}_{\overline{\rho }}}\left| \varvec{\mathsf {d}}\varvec{\textit{v}}_i-\varvec{\mathsf {d}}\varvec{\textit{v}}\right| \,\mathrm {d}\varvec{\textit{x}}\)
The positive definiteness of \(\varvec{\mathsf {A}}\), and hence \(\varvec{\textit{A}}_i\), allows us to write
The convergence in (3.28) and the boundedness assumption in (A1) imply both that
and that
Now the weak convergence \(\varvec{\mathsf {d}}\varvec{\textit{v}}_i\rightharpoonup \varvec{\mathsf {d}}\varvec{\textit{v}}\) in \(L^p\) implies the last integral above vanishes as \(i\rightarrow \infty \). Recalling the uniform convergence in (3.18) gives
By definition
Changing variables in \(I_{1,i}\) gives us
Let \(\varepsilon >0\) be given. Define the sequences \(\{E_i,F_i\}_{i=1}^\infty \subseteq \mathcal {B}^m_{\overline{\rho }}\) by
and
Using the growth condition in (A1) and the asymptotic property in (A4) we may write

Property (ii) implies \(\varvec{\textit{w}}_i(\varvec{\textit{z}})=\varvec{\textit{u}}(\varvec{\textit{z}})\) for each \(\varvec{\textit{z}}\in \varvec{\varphi }_i^{-1}(\mathcal {B}_1\setminus \overline{\mathcal {B}}_{\overline{\rho }})\). Since \(\varvec{\textit{u}}\) is a minimizer for the functional I, we have the bound

Assumptions (A3) and (A4) yield

We now provide an estimate of the middle integral appearing in the upper bound for \(I_{2,i}\) above. First of all, observe that from the definition of \(\varvec{\textit{w}}_i\) in (3.27), we have
Second of all, we introduce a change of variables into the middle integral appearing on the right-hand side of the upper bound for \(I_{2,i}\) by means of the substitution \(\varvec{\textit{x}}=\varvec{\varphi }_i(\varvec{\textit{z}})\). Observe that it then holds that
which corresponds to the volume correction factor from the substitution and in which we use the notation \(\left| \varvec{\mathsf {d}}\varvec{\varphi }_0\left( \varvec{\varphi }_i^{-1}(\varvec{\textit{x}})\right) \right| ^{-1}:=\left[ \textsf {det}\left( \varvec{\mathsf {d}}\varvec{\varphi }_0\left( \varvec{\varphi }_i^{-1}(\varvec{\textit{x}})\right) \right) \right] ^{-1}\). We then obtain that
where we have used the fact that in local coordinates \(\varvec{\varphi }_0\) is the identity map, and, hence, \(\varvec{\mathsf {d}}\varvec{\varphi }_0\) is represented by the identity matrix in \(\mathbb {R}^m\otimes \mathbb {R}^m\), as was mentioned earlier in the proof of Lemma 3.1. In summary, we obtain

Let us also notice at this juncture that
which since
in \(L^p\left( \mathcal {B}_{\overline{\rho }}\right) \) implies that
a fact that shall be used momentarily.
3.2.3 The convergence \(\varvec{\mathsf {d}}\varvec{\textit{v}}_i\rightarrow \varvec{\mathsf {d}}\varvec{\textit{v}}\) in \(L^p_{\mathrm{loc}\,}(\mathcal {B}_1;\mathbb {R}^\ell \otimes \mathbb {R}^m)\)
Using the last estimate for (3.30) and inserting the result into (3.29) yields
Essentially the same argument that showed that \(\limsup _{i\rightarrow \infty }\frac{\rho _i^{p-m}}{\delta _i^p}II_{4,i}=0\) in the proof of Lemma 3.1 also shows that \(\limsup _{i\rightarrow \infty }\frac{\rho _i^{p-m}}{\delta _i^p}I_{5,i}=0\) here. The analysis of \(I_{4,i}\) is analogous to what was used for \(II_{5,i}\) and \(II_{9,i}\) for proof of Lemma 3.1. We get
Turning to \(I_{3,i}\), property (v) and the uniform convergence both in (3.18) and (3.19) together with the previous demonstration that \(\frac{\rho _i}{\delta _i}\varvec{\mathsf {d}}\varvec{\textit{w}}_i\circ \varvec{\varphi }_i^{-1}\rightarrow \varvec{\mathsf {d}}\varvec{\textit{v}}\) in \(L^p\left( \mathcal {B}_{\overline{\rho }}\right) \) jointly imply
Hence,
Since \(\sup _{i\in \mathbb {N}}\Vert \varvec{\mathsf {d}}\varvec{\textit{v}}_i\Vert _{L^p(\mathcal {B}_1;\mathbb {R}^\ell \otimes \mathbb {R}^m)}<\infty \), by taking the limit \(\varepsilon \rightarrow 0^+\) we conclude that
Thus, \(\lim _{i\rightarrow \infty }\Vert \varvec{\mathsf {d}}\varvec{\textit{v}}_i-\varvec{\mathsf {d}}\varvec{\textit{v}}\Vert _{L^p(\mathcal {B}{\widehat{\rho }};\mathbb {R}^\ell \otimes \mathbb {R}^m)}=0\), and since \(\widehat{\rho }\in (0,1)\) was arbitrary, the lemma is proved. \(\square \)
4 Partial Hölder continuity
In this section, we prove partial Hölder continuity for a minimizer \(\varvec{\textit{u}}\in W^{1,p}(\mathcal {M};\mathcal {N})\) for I. Having proved Lemmata 3.1 and 3.2 in Sect. 3, we are now in possession of the principal ingredients needed to deduce the Hölder continuity. We must first establish a decay estimate, which we label Lemma 4.1; we then demonstrate in the proof of Theorem 4.2 that the decay estimate can be iterated to obtain the desired Morrey estimate. Finally, with the Morrey regularity of \(\varvec{\mathsf {d}}\varvec{\textit{u}}\) shown, we are then at last able to deduce the partial Hölder continuity of \(\varvec{\textit{u}}\) in the standard way.
4.1 Decay lemma
We begin by stating and proving the relevant decay lemma.
Lemma 4.1
Let \(\alpha \in \left( 0,\frac{p-m+\gamma }{p}\right) \), \(\kappa >0\), and \(\mathcal {M}'\Subset \mathcal {M}\) be given. Suppose that \(\varvec{\textit{u}}\) is a minimizer of (1.1). Then there exist constants \(r_0,\delta _0>0\), and \(c_5 >1\), with the following property: if \(r<r_0\) and \(\mathcal {B}_r(\varvec{\textit{z}}_0)\subset \mathcal {M}'\), then
-
(a)
$$\begin{aligned} |\left( \varvec{\textit{u}}\right) _{\varvec{\textit{z}}_0,r_0}|<\kappa \end{aligned}$$
and
-
(b)
$$\begin{aligned} r^{\alpha p}+ r^{p-m}\int \limits _{\mathcal {B}^{\mathcal {M}}_{r}(\varvec{\textit{z}}_0)} |\varvec{\mathsf {d}}\varvec{\textit{u}}(\varvec{\textit{z}})|^p_{\mathbb {R}^\ell \otimes T^*_{\varvec{\textit{z}}}\mathcal {M}}\,\mathrm {d}\mu _{\varvec{\mathsf {g}}} <\delta _0, \end{aligned}$$
together imply that
Proof
The proof of this decay lemma is inspired by the proof of [49, Proposition 1]. In particular, as in the proof of [49, Proposition 1], we prove the decay lemma by contradiction. Furthermore, much of the divergence from Luckhaus’ argument in [49] has been isolated in Lemma 3.1. For convenience in the sequel, we introduce statement (S), which is the desired implication of this lemma:

We need to translate this statement into suitable local coordinates. Let \(\left\{ (\mathcal {V}_{\widehat{\varvec{\textit{z}}}},\varvec{\varphi }_{\widehat{\varvec{\textit{z}}}})\right\} _{{\widehat{\varvec{\textit{z}}}}\in \mathcal {M}}\) be a smooth atlas of geodesic orthonormal (Riemannian normal) coordinate charts (see, e.g. [45] or [47]). For each \({\widehat{\varvec{\textit{z}}}}\in \mathcal {M}\), let \(\varvec{\textit{g}}_{{\widehat{\varvec{\textit{z}}}}}\in \mathscr {C}^{\infty }(\varvec{\varphi }_{{\widehat{\varvec{\textit{z}}}}}(\mathcal {V}_{{\widehat{\varvec{\textit{z}}}}});\odot ^2\mathbb {R}^m)\) be the representation of the metric \(\varvec{\mathsf {g}}\) with respect to the local coordinate chart \((\mathcal {V}_{{\widehat{\varvec{\textit{z}}}}},\varvec{\varphi }_{\widehat{\varvec{\textit{z}}}})\). Without loss of generality, we may assume that \(\mathcal {V}_{{\widehat{\varvec{\textit{z}}}}}\) has been selected so that
for each \(\varvec{\textit{x}}\in \varvec{\varphi }_{{\widehat{\varvec{\textit{z}}}}}(\mathcal {V}_{\widehat{\varvec{\textit{z}}}})\) and all \(\varvec{\textit{y}}\in \mathbb {R}^m\). Thus, in particular,
whenever \(\mathcal {B}^{\mathcal {M}}_{2r}(\varvec{\textit{z}})\subseteq \mathcal {V}_{\widehat{\varvec{\textit{z}}}}\). Since \(\mathcal {M}'\) is compactly contained in \(\mathcal {M}\), we may extract a finite family \(\left\{ (\mathcal {V}_j,\varvec{\varphi }_{j})\right\} _{j=1}^{\overline{j}}\) from \(\left\{ (\mathcal {V}_{{\widehat{\varvec{\textit{z}}}}},\varvec{\varphi }_{{\widehat{\varvec{\textit{z}}}}})\right\} _{{\widehat{\varvec{\textit{z}}}}\in \mathcal {M}}\) such that \(\overline{\mathcal {M}'}\subseteq \bigcup _{j=1}^{\overline{j}}\mathcal {V}_j\). Moreover, we may select an \(r_0>0\) such that for each \(\varvec{\textit{z}}_0\in \overline{\mathcal {M}'}\) we find that \(\mathcal {B}^{\mathcal {M}}_{r_0}(\varvec{\textit{z}}_0)\subset \mathcal {V}_{j_0}\) for some \(j_0\in \{1,\dots ,\overline{j}\}\). We use (4.1) and (4.2) to deduce that (S) will follow from a verification of the following statement:

Let us suppose that (S’) is not true. Then the following alternative must hold:

where the sequence \(\left\{ \rho _i'\right\} _{i=1}^{\infty }\) is defined by
The constant \(c_5 '>4\) will be determined later in the proof. We assume (Alt) holds and will reach a contradiction.
Since \(\mathcal {M}'\) is compactly contained in \(\mathcal {M}\), there is a \(\varvec{\textit{z}}_0\in \overline{\mathcal {M}'}\) such that
It is, therefore, no loss of generality to assume that there is a single coordinate chart \((\mathcal {V},\varvec{\varphi })\), among \(\{(\mathcal {V}_j,\varvec{\varphi }_j)\}_{j=1}^{\overline{j}}\), and an \(r_0>0\) such that \(\mathcal {B}_{r_0}^{\mathcal {M}}(\varvec{\textit{z}}_0)\subset \mathcal {V}\). In addition, we may assume that \(\bigcup _{i=1}^\infty \mathcal {B}_{2\rho _i}^{\mathcal {M}}(\varvec{\textit{z}}_i)\subset \mathcal {B}_{r_0}^{\mathcal {M}}(\varvec{\textit{z}}_0)\). Let us define the sequence \(\{\varvec{\textit{x}}_i\}_{i=1}^\infty \in \mathbb {R}^m\) by \(\varvec{\textit{x}}_i:=\varvec{\varphi }(\varvec{\textit{z}}_i)\). Then \(\lim _{i\rightarrow \infty }\varvec{\textit{x}}_i=\varvec{\textit{x}}_0=:\varvec{\varphi }(\varvec{\textit{z}}_0)\). We immediately observe that (4.4) implies

for each \(i\in \mathbb {N}\), and where the constant C appearing in (4.6) depends only on m. Observe in particular that, since \(p\alpha <p-m+\gamma \), we must have
We now argue that \(\left( \varvec{\textit{u}}\circ \varvec{\varphi }^{-1}\right) _{\varvec{\textit{x}}_i,\rho _i}\in \varOmega _{\mathcal {N}}\) for i large enough. For each \(\varvec{\textit{x}}\in \mathcal {B}_{\rho _i}(\varvec{\textit{x}}_i)\), we estimate
Hence,

and Theorem 2.7 and (4.6) imply that

It follows that \(\lim _{i\rightarrow \infty }\mathrm{dist}\,\left( \left( \varvec{\textit{u}}\circ \varvec{\varphi }^{-1}\right) _{\varvec{\textit{x}}_i,\frac{\rho _i}{2}},\mathcal {N}\right) =0\), so there is no loss in assuming that \(\left\{ \left( \varvec{\textit{u}}\circ \varvec{\varphi }^{-1}\right) _{\varvec{\textit{x}}_i,\frac{\rho _i}{2}}\right\} _{i=1}^\infty \subset \varOmega _{\mathcal {N}}\). For each \(i\in \mathbb {N}\), we may therefore define
Moreover, the continuity of \(\varPi _{\mathcal {N}}\) and the uniform bound in (4.3) allows us to further assume that there is an \(\varvec{\textit{a}}_0\in \mathcal {N}\) such that \(\lim _{i\rightarrow \infty }|\varvec{\textit{a}}_i-\varvec{\textit{a}}_0|=0\).
Define \(\{\varvec{\zeta }_i\}_{i=1}^\infty \subset \mathscr {C}^{\infty }(\mathbb {R}^m;\mathbb {R}^m)\) and \(\{\varvec{\varphi }_i\}_{i=1}^\infty \subset \mathscr {C}^{\infty }(\mathcal {V};\mathbb {R}^m)\) by
We define the blow-up sequence \(\{\varvec{\textit{v}}_i\}_{i=1}^\infty \subset W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\) by
Let us verify that there is a \(\varvec{\textit{v}}\in W^{1,p}(\mathcal {B}_1^m; T_{\varvec{\textit{a}}_0}\mathcal {N})\) such that \(\varvec{\textit{v}}_i\rightharpoonup \varvec{\textit{v}}\) in \(W^{1,p}(\mathcal {B}_1^m;\mathbb {R}^\ell )\). Let \(\varvec{\textit{g}}\in \mathscr {C}^{\infty }(\varvec{\varphi }(\mathcal {V});\odot ^2\mathbb {R}^m)\) be the local representation of \(\varvec{\mathsf {g}}\), so \(\varvec{\textit{g}}\) is uniformly bounded and positive definite by (4.1). By definition and a change of variables
Recall that \(\varPi _{\mathcal {N}}\) is Lipschitz continuous. Theorem 2.7 and (4.6) imply

We also deduce from (4.6) that

Hence, \(\{\varvec{\textit{v}}_i\}_{i=1}^\infty \) is uniformly bounded in \(W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\). Therefore, there is a subsequence, which we do not relabel, and a map \(\varvec{\textit{v}}\in W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\) such that \(\varvec{\textit{v}}_i\rightharpoonup \varvec{\textit{v}}\) in \(W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\).
We now argue that the range of \(\varvec{\textit{v}}\) is actually contained a.e. in \(T_{\varvec{\textit{a}}_0}\mathcal {N}\). As in Lemma 3.1, for each \(\varvec{\textit{y}}\in \mathcal {N}\) we define  as the rotation operator that maps \(T_{\varvec{\textit{a}}_0}\mathcal {N}\) onto \(T_{\varvec{\textit{y}}}\mathcal {N}\). From (4.7), we deduce that
as the rotation operator that maps \(T_{\varvec{\textit{a}}_0}\mathcal {N}\) onto \(T_{\varvec{\textit{y}}}\mathcal {N}\). From (4.7), we deduce that
Since \(\mathcal {N}\) is smooth, we find that \(\varvec{\textit{y}}\mapsto \varvec{\mathsf {Q}}^{-1}_{\varvec{\textit{y}}}\in \mathscr {C}^{\infty }(\mathcal {N};\mathbb {R}^\ell \otimes \mathbb {R}^\ell )\). It follows that \(\varvec{\textit{x}}\mapsto \varvec{\mathsf {Q}}^{-1}_{\varvec{\textit{u}}(\varvec{\varphi }_i^{-1}(\varvec{\textit{x}}))}\in L^\infty (\mathcal {B}_1^m;\mathbb {R}^\ell \otimes \mathbb {R}^\ell )\) and that for a.e. \(\varvec{\textit{x}}\in \mathcal {B}_1^m\) we have
For each \(i\in \mathbb {N}\) define \(\varvec{\textit{q}}_i\in L^p(\mathcal {B}_1;T_{\varvec{\textit{a}}_0}\mathcal {N})\) by
Now we use \(\varvec{\textit{q}}_i\) to provide an estimate in \(L^p\) as to how far the range of \(\varvec{\textit{v}}_i\) is from \(T_{\varvec{\textit{a}}_0}\mathcal {N}\). Since \(\varvec{\textit{v}}_i(0)=0\) for each \(i\in \mathbb {N}\), we have
Thus,
and we conclude that \(\varvec{\textit{v}}\in W^{1,p}(\mathcal {B}_1^m;T_{\varvec{\textit{a}}_0}\mathcal {N})\).
The sequences \(\{\rho _i,\delta _i,\varvec{\textit{a}}_i,\varvec{\textit{z}}_i,\varvec{\textit{v}}_i\}_{i=1}^\infty \) and the coordinate chart \((\mathcal {V},\varvec{\varphi })\) satisfy all the hypotheses in both Lemma 3.1 and Lemma 3.2. We therefore conclude that \(\varvec{\textit{v}}\) is a local minimizer for the functional \(J[\cdot ;\varvec{\mathsf {A}}_0]\), with \(\varvec{\mathsf {A}}_0:=\varvec{\mathsf {A}}(\varvec{\textit{z}}_0,\varvec{\textit{a}}_0)\), and moreover that we have the strong convergence \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(W_{\mathrm{loc}\,}^{1,p}(\mathcal {B}_1^m;\mathbb {R}^\ell )\).
Finally, we work toward determining a value for \(c_5 '\) that produces a contradiction. Recall that
with \(c_5 '>4\) yet to be determined. From (4.4) and (4.5) and the definition of \(\varvec{\textit{v}}_i\), we have
Recalling the definitions of \(\varvec{\varphi }_i\) and \(\varvec{\zeta }_i\), we find that
Thus, upon changing variables and using the strong convergence \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) in \(W^{1,p}_{\mathrm{loc}\,}(\mathcal {B}_1^m;\mathbb {R}^\ell )\), we obtain
Select \(\overline{\alpha }\in (\alpha ,1)\). By Lemma 2.15, there is a constant \(c_3 \) such that
from which it follows that
where C and \(c_3 \) are constants that are independent of \(c_5 '\). Since \(\overline{\alpha }-\alpha >0\), it follows that \(c_5 '>4\) may be selected large enough to yield a contradiction. Consequently, we deduce that statement (S) is true, and since this implies that the conclusion of Lemma 4.1 holds, it follows that the proof is complete. \(\square \)
4.2 Partial regularity result
Our next result, which we label Theorem 4.2, proves that any minimizer \(\varvec{\textit{u}}\) of (1.1) must be Hölder continuous at a.e. \(\varvec{\textit{z}}\in \mathcal {M}\); the precise statement of the result specifies not only the degree of Hölder continuity that can be expected but also describes the points at which this regularity fails. To prove this result, we follow the well-known technique of demonstrating that we can inductively iterate Lemma 4.1. This implies that, essentially, at any Lebesgue point for the gradient \(\varvec{\mathsf {d}}\varvec{\textit{u}}\) such that the quantity \(\limsup _{\rho \rightarrow 0^+}\left| (\varvec{\textit{u}})_{\varvec{\textit{z}}_0,\rho }\right| \) remains bounded, we may conclude that \(\varvec{\mathsf {d}}\varvec{\textit{u}}\) satisfies a Morrey regularity estimate on a small ball about the Lebesgue point. This will then allow us to conclude the partial Hölder continuity of \(\varvec{\textit{u}}\).
Theorem 4.2
Let \(\alpha \in \left( 0,\frac{p-m+\gamma }{p}\right) \). Suppose that \(\varvec{\textit{u}}\) is a minimizer of (1.1). Define the set \(\mathcal {M}_0^*\subseteq \mathcal {M}\) by

Then there exists an open submanifold \(\mathcal {M}_0\) of \(\mathcal {M}\) such that \(\mathcal {M}_0^*\subseteq \mathcal {M}_0\) and for each number \(\beta \in \left( 0,\min \{m-p,\alpha p\}\right) \) we find that
In addition, it holds that
Proof
We first need to show that we can inductively iterate the estimate provided by Lemma 4.1. To carry out this program, we proceed in a manner similar to [29, Lemma 6.1], though certain of the details here are more complicated. In order to accomplish this, we shall appeal to Lemma 4.1.
To this end, recall from Lemma 4.1 that for each \(\varvec{\textit{z}}_0\in \mathcal {M}'\Subset \mathcal {M}\), there exist numbers \(\kappa \) and \(\delta _0\) such that whenever
-
(a)
$$\begin{aligned} \left| \left( \varvec{\textit{u}}\right) _{\varvec{\textit{z}}_0,r}\right| <\kappa \end{aligned}$$
and
-
(b)

collectively hold, then there is \(r_0\) such that for each \(r\in \left( 0,r_0\right) \) the decay estimate
thus follows; this we called statement (S) in the proof of Lemma 4.1. With this in mind, henceforth let \(\varvec{\textit{z}}_0\in \mathcal {M}\) be a fixed but arbitrary point such that (a)–(b) above hold; the choice of \(\delta _0\) will be specified later in the proof—see, specifically, inequality (4.15) in the sequel. Now, fix a number \(\rho _0\) satisfying \(0<\rho _0<r_0\). Then by means of Lemma 4.1 we conclude that the estimate

holds. We shall inductively iterate estimate (4.8).
So, for this purpose let us define
Note that \(c_5 >1\) so that \(\rho _i<\rho _{i-1}\) and \(\lim _{i\rightarrow \infty }\rho _i=0\). In order to complete the inductive iteration, we first need to check that the smallness condition on the quantity \(\left| \left( \varvec{\textit{u}}\right) _{\varvec{\textit{z}}_0,\rho _i}\right| \) remains controllable at each step of the iteration. This is essential if we are inductively reapply Lemma 4.1. Therefore, assume Lemma 4.1 applies on the finite sequence of radii \(\left\{ \rho _i\right\} _{i=0}^{i_0}\) and, moreover, that \(\left| \left( \varvec{\textit{u}}\right) _{\varvec{\textit{z}}_0,\rho _0}\right| \le \kappa \)—i.e., the average is initially small. Then we first estimate
where to obtain estimate (4.9) we have used Hölder’s inequality, Poincaré’s inequality, as well as the fact that it can be shown that

By reapplying statement (S) from Lemma 4.1 a total of \((j-1)\)-times, we next obtain the upper bound
Now, using the fact that \(\rho _{j-k}=c_5 ^{k-j}\rho _0\) and putting this into the preceding estimate we deduce that, for \(j\ge 2\),
where we have invoked the initial smallness estimate in the second-to-last inequality. Thus, putting estimates (4.10)–(4.11) into (4.9) we deduce
Now, recalling that \(0<c_5 ^{-1}<1\) and appealing to Fubini’s theorem, observe that we may write
where we have used the fact that \((j-1)^{\frac{1}{p}}\le j-1\). Thus, the series converges, and so, we conclude that
Recalling that \(c_5 \) has no dependence on \(\delta _0\), without loss we may assume that \(\delta _0\) was initially so small that, say,
whence
This proves inductively that if on the first \(i_0-1\) balls the average of \(\varvec{\textit{u}}\) remains sufficiently small, then it continues to remain small on the \(i_0\)-th ball. In particular, if we initially put \(\delta _0:=\delta _0(2\kappa )\) rather than \(\delta _0:=\delta _0(\kappa )\) in the statement of Lemma 4.1, then (4.9)–(4.16) imply that we will be able to reapply Lemma 4.1 at the \(i_0\)-th step of the iteration.
In fact, inequality (4.16) now allows us to apply Lemma 4.1 but with \(\delta _0(2\kappa )\) replacing \(\delta _0(\kappa )\) and \(\rho _{i_0}\) replacing \(\rho _0\). So, for notational convenience in this final part of the proof, put
and define the function \(\varphi \ : \ [0,+\infty )\rightarrow [0,+\infty )\) by

Then recalling again Lemma 4.1 we have the following preliminary estimate
from which we may write
In observation of the estimates of the preceding paragraphs, we may repeatedly apply Lemma 4.1 to obtain by induction the estimate
for any \(k\in \mathbb {N}\). Indeed, to prove (4.17) we merely notice that it trivially holds in case \(k=1\) since this follows from Lemma 4.1, as above, whereas if we assume that (4.17) holds for some arbitrary but fixed \(k\in \mathbb {N}\), then we may compute
where in (4.18) the first inequality follows from an initial reapplication of Lemma 4.1, which is allowable due to the fact that we have already shown that \(\left| \left( \varvec{\textit{u}}\right) _{\varvec{\textit{z}}_0,\rho _i}\right| \) remains small throughout the iteration. Furthermore, the second inequality in (4.18) follows from an application of the induction hypothesis itself. Thus, (4.18) proves that the inductive iteration (4.17) holds.
Suppose now that we are given a number \(\rho ^*>0\) sufficiently small. Then we may find \(k\in \mathbb {N}\) such that \(\tau ^{k+1}\rho _0\le \rho ^*<\tau ^k\rho _0\). Moreover, let \(\beta \) be a fixed but otherwise arbitrary number satisfying \(\beta \in (0,m-p)\) and also \(\alpha p-\beta >0\). From these and the preceding estimates it follows that

whence

In the preceding estimate, it is evident that
On the other hand, since \(\beta >0\) holds, an application of L’Hôpital’s rule implies that
And from these observations, it follows that upon taking the supremum of both sides of the above estimate we deduce that

Now, by the continuity of the map \(\rho \mapsto \varphi (\rho )\) we infer that the above estimate holds on an open neighborhood of \(\varvec{\textit{z}}_0\), say \(\mathscr {U}_{\varvec{\textit{z}}_0}\). Define the set \(\mathcal {M}_0\subseteq \mathcal {M}\) by
where the union is taken over all \(\varvec{\textit{z}}_0\in \mathcal {M}\) such that (a)–(b) hold and, hence, the Morrey-type estimate of the previous paragraph holds. Evidently \(\mathcal {M}_0\) is open. In addition, the inclusion
obviously holds. Consider an arbitrary but fixed \(\mathcal {M}'\) such that \(\mathcal {M}'\Subset \mathcal {M}_0\). Then by the compactness of \(\overline{\mathcal {M}'}\) it follows that there is a subcollection \(\mathscr {G}:=\left\{ \mathscr {U}_{\varvec{\textit{z}}_i}\right\} _{i=1}^{n}\) such that \(\mathscr {G}\) forms an open cover for \(\overline{\mathcal {M}'}\). But then we may assert that \(\varvec{\mathsf {d}}\varvec{\textit{u}}\in L^{p,\alpha p+m-p-\beta }\left( \mathcal {M}'\right) \).
Finally, utilizing the arbitrariness of \(\mathcal {M}'\) the above argument implies that
At last from (4.19) we conclude that \(\varvec{\textit{u}}\) satisfies
But combining this fact together with an application of Proposition 2.8 implies that
which completes the partial regularity argument. Note that the embedding result of Proposition 2.8 may be invoked since we earlier required that \(\alpha p-\beta >0\), which implies that \(\alpha p+m-p-\beta >m-p\). Furthermore, due to the structure of the set \(\mathcal {M}_0^*\), standard arguments, which we omit (see, for example, [30, Theorem 2.2, §4.2]), imply the Hausdorff measure estimate
But since \(\mathcal {M}_0\supseteq \mathcal {M}_0^*\), this final estimate implies that
And this completes the proof. \(\square \)
Remark 4.3
Notice that by the restrictions imposed on \(\gamma \), it follows that
Remark 4.4
Notice that by the restrictions imposed on the various parameters in the statement of Theorem 4.2, especially that \(\alpha <\frac{p-m+\gamma }{p}\), we may estimate
as \(\beta \rightarrow 0^+\). Similarly, since the embedding theorem utilized at the end of the proof of Theorem 4.2 only applies in case \(\alpha p-\beta >0\), it follows that we may also estimate
All in all, then, combining (4.20) together with Remark 4.3, we see that by suitably modulating the Morrey exponent \(\gamma \), which recall controls the strength of the Morrey regularity satisfied by the map \(\varvec{\textit{z}}\mapsto \sigma _{\varepsilon }(\varvec{\textit{z}})\), the degree of partial Hölder continuity obtained in Theorem 4.2 can be phrased as \(\varvec{\textit{u}}\in \mathscr {C}_{\mathrm {loc}}^{0,\vartheta (\gamma )}\left( \mathcal {M}_0\right) \), where \(\vartheta (\gamma )\rightarrow 1^-\) as \(\gamma \rightarrow m^-\). In particular, it holds that
Remark 4.5
In light of Remark 4.4, we see that the degree of partial Hölder continuity enjoyed by a minimizer \(\varvec{\textit{u}}\) and the dependence of this regularity on the regularity of \(\sigma _{\varepsilon }\) is precisely analogous to the Euclidean setting—cf., [20, 43] and the references therein.
5 Partial Caccioppoli and reverse Hölder inequalities
Having obtained in Sect. 4 partial Hölder continuity of minimizers of the functional

in the present section, we deduce a partial Caccioppoli-type inequality for minimizers of this same functional and from this estimate deduce partial higher integrability for a minimizer \(\varvec{\textit{u}}\) of (1.1). We point out that this result is only a “partial” Caccioppoli inequality since it only is guaranteed to hold at those points \(\varvec{\textit{z}}_0\) such that \(\varvec{\textit{z}}_0\in \mathcal {M}_0\)—i.e., at \(\varvec{\textit{z}}_0\in \mathcal {M}\) such that, essentially, the smallness conditions provided in (a) and (b) in the statement of Lemma 4.1 hold. In any case, since most of the technical estimates have already been dispatched in the previous sections of this paper, the arguments required to deduce these final two results are relatively brief and uncomplicated.
5.1 Partial Caccioppoli inequality
In order to prove the partial Caccioppoli inequality, Theorem 5.2, we first state and prove a proposition, which will be required in the proof of Theorem 5.2; the content of this proposition is similar in spirit to that of [13, Lemma 6]. This proposition essentially allows us to transition from an integral on the manifold \(\mathcal {M}\) to an integral on a local coordinate chart by suitably rescaling the radius of the ball \(\mathcal {B}^{\mathcal {M}}_{R}\), while at the same time transferring the average value of \(\varvec{\textit{u}}\) from a geodesic ball on \(\mathcal {M}\) to a coordinate ball, this latter point being the key contribution of the proposition.
Proposition 5.1
Let \(\varvec{\textit{u}}\) be a minimizer of problem (1.1) and let \(\mathcal {M}'\Subset \mathcal {M}\) be arbitrary but fixed. Then there exists a constant \( c_6 := c_6 (p)\) such that for any \(R>0\) and \(\varvec{\textit{z}}_0\in \mathcal {M}\) satisfying \(\mathcal {B}^{\mathcal {M}}_{R}\left( \varvec{\textit{z}}_0\right) \subseteq \mathcal {M}'\), it holds that

where \(\varvec{\textit{x}}_0=\varvec{\varphi }\left( \varvec{\textit{z}}_0\right) \) for \((\mathcal {V},\varvec{\varphi })\) a local coordinate chart with \(\varvec{\textit{z}}_0\in \mathcal {V}\).
Proof
Let \(\varvec{\textit{u}}\) be as in the statement of the proposition. For the point \(\varvec{\textit{z}}_0\in \mathcal {M}\) given in the statement of the proposition, put \(\varvec{\textit{x}}_0:=\varvec{\varphi }\left( \varvec{\textit{z}}_0\right) \), where \(\varvec{\varphi }\) is a homeomorphism from a suitable local coordinate chart \((\mathcal {V},\varvec{\varphi })\); as in the previous results in this paper, since this proposition really need only hold for \(R>0\) small, there is no loss in assuming that R is sufficiently small such that \(\mathcal {B}^{\mathcal {M}}_{R}\left( \varvec{\textit{z}}_0\right) \subseteq \mathcal {V}\). Let \(M_{p}^{\mathcal {M}}\in \mathcal {N}\) represent the unique minimizer for the map

Now let \(\varvec{\alpha }_0\in \mathbb {R}^{\ell }\) be given. Then the minimality of \(M_{p}^{\mathcal {M}}\) implies at once that

At the same time, we observe that an application of both the triangle inequality and of Jensen’s inequality implies the estimate

whence

Now, put \(\varvec{\alpha }_0:=(\varvec{\textit{u}})_{R}^{\mathcal {M}}\in \mathbb {R}^{\ell }\). Then invoking both inequality (5.1) and inequality (5.2), together with (4.1)–(4.2) from earlier in the proof of Lemma 4.1, we thus obtain

as claimed. And this completes the proof. \(\square \)
Theorem 5.2
Let \(\varvec{\textit{u}}\in W^{1,p}(\varOmega )\) be a minimizer for (1.1). Then the set \(\mathcal {M}_0\subseteq \mathcal {M}\), defined in the statement of Theorem 4.2, is an open submanifold of \(\mathcal {M}\), and for each \(\mathcal {M}'\Subset \mathcal {M}_0\) it holds that for each \(\varvec{\textit{z}}\in \mathcal {M}'\) there is a constant \(C<+\infty \) and \(R_0>0\) such that

for each \(R\le R_0\).
Proof
From Theorem 4.2, for each \(\beta \in (0,\min \{\alpha p,m-p\})\) we have that
In particular, since \(\alpha p-\beta >0\), there is an \(\varepsilon _0>0\) such that \(\varvec{\mathsf {d}}\varvec{\textit{u}}\in L^{p,m-p+\varepsilon _0}(\mathcal {M}')\). Hence, for each \(\varvec{\textit{z}}_0\in \mathcal {M}'\), we find that

Suppose for the sake of contradiction that the statement in the lemma is false. Then we have the following alternative: There is a sequence \(\left\{ R_i\right\} _{i=1}^{\infty }\subseteq (0,+\infty )\) such that \(R_i\rightarrow 0^+\) and \(\left\{ \varvec{\textit{z}}_i\right\} _{\i =1}^{\infty }\subseteq \mathcal {M}'\) such that

where the constant \(C<+\infty \) will be identified at the end of the proof. Since \(\mathcal {M}'\) is compact, upon taking a subsequence if necessary, we may assume that \(\varvec{\textit{z}}_i\rightarrow \varvec{\textit{z}}_0\) for some \(\varvec{\textit{z}}_0\in \mathcal {M}'\). Moreover there is a sequence \(\left\{ \widetilde{\delta }_i\right\} _{i=1}^{\infty }\subseteq (0,+\infty )\) such that \(\widetilde{\delta }_i\rightarrow 0^+\) and

where (5.4) follows, in part, from the initial estimate in this proof.
Just as in the proof of Lemma 4.1, we will convert (5.3)–(5.4) to local coordinates. Furthermore, just as in the proof of Lemma 4.1 we may assume the existence of a single coordinate chart \((\mathcal {V},\varvec{\varphi })\) such that
With this in mind, we shall put \(\varvec{\textit{x}}_i:=\varvec{\varphi }\left( \varvec{\textit{z}}_i\right) \) in the sequel. In particular, by observing that (4.1)–(4.2) may be again assumed, it follows that (5.3)–(5.4) may be phrased in local coordinates by assuming that
but that

Observe that to obtain inequality (5.6), we apply Proposition 5.1 to obtain the estimate

Similar to the previous proofs, for each \(i\in \mathbb {N}\) define \(\varvec{\varphi }_i\) and \(\varvec{\zeta }_i\) by
and then define the blow-up sequence \(\left\{ \varvec{\textit{v}}_i\right\} _{i=1}^{\infty }\subset W^{1,p}(\mathcal {B}_1;\mathbb {R}^\ell )\) by
where, but for the change in radius, as in the proof of Lemma 4.1 we put
Observe that the collection \(\left\{ \varvec{\textit{v}}_i\right\} _{i=1}^{\infty }\) is defined essentially as in the proof of Lemma 4.1. In fact, due to the definition of \(\delta _i\) in (5.5) we deduce that

which is exactly (4.6) from earlier, modulo the change of radius in the integration set. In particular, by precisely the same argument as provided in the proof of Lemma 4.1 we obtain the existence of \(\varvec{\textit{v}}\in W^{1,p}(\mathcal {B}_1^m; T_{\varvec{\textit{a}}_0}\mathcal {N})\) such that \(\varvec{\textit{v}}_i\rightharpoonup \varvec{\textit{v}}\) in \(W^{1,p}(\mathcal {B}_1^m;\mathbb {R}^\ell )\). It then follows that the sequences \(\{\rho _i,\delta _i,\varvec{\textit{a}}_i,\varvec{\textit{z}}_i,\varvec{\textit{v}}_i\}_{i=1}^\infty \) and the coordinate chart \((\mathcal {V},\varvec{\varphi })\) satisfy all the hypotheses in Lemma 3.2. We therefore conclude that \(\varvec{\textit{v}}_i\) converges strongly to \(\varvec{\textit{v}}\) in \(W^{1,p}(\mathcal {B}_1^m;T_{\varvec{\textit{a}}_0}\mathcal {N})\).
We show, finally, that by the definition of \(\varvec{\textit{v}}_i\) together with the fact that \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) strongly in \(W^{1,p}\left( \mathcal {B}_1^m;T_{\varvec{\textit{a}}0}\mathcal {N}\right) \) a contradiction thus follows. To this end, let us first note that by the definition of \(\varvec{\textit{v}}_i\) we have on the one hand that, for some constant \( c_7 := c_7 (m)\),

where we have employed a change of variables, namely \(\widetilde{\varvec{\textit{x}}}\mapsto \varvec{\textit{x}}_i+R_i\varvec{\textit{x}}\). On the other hand, again employing the same change of variables as in (5.7) above, notice that, for each \(i\in \mathbb {N}\),

Thus, (5.8) implies that, for each \(i\in \mathbb {N}\),


Putting (5.7) and (5.9) together, we deduce that the contradiction hypothesis (5.6) may be rescaled to read

from which it follows that

Now recall that \(\varvec{\textit{v}}_i\rightarrow \varvec{\textit{v}}\) strongly in \(W^{1,p}\left( \mathcal {B}_1^m;T_{\varvec{\textit{a}}_0}\mathcal {N}\right) \) and, moreover, that \(\varvec{\textit{v}}\) is \((\varvec{\mathsf {B}},p)\)-harmonic. This fact implies that \(\varvec{\textit{v}}\) satisfies a reverse Hölder inequality, namely,

for some constant \(\widetilde{C}>0\). But, at the same time, the strong convergence combined with (5.10) implies that

In light of the fact that \(\varvec{\textit{v}}\) satisfies the above Caccioppoli inequality, by selecting the constant C such that it satisfies the inequality \(C>2 c_6 \widetilde{C}\), we obtain the desired contradiction at once. And this completes the proof. \(\square \)
5.2 Reverse Hölder inequality and an example
Finally, we provide the statement and proof of the reverse Hölder inequality for a minimizer of (1.1). We point out that this final result, Theorem 5.3, is really a statement about the higher integrability of the gradient of a minimizer of functional (1.1). In particular, the conclusion of this result asserts that such a minimizer with gradient a priori of class \(L^p\) has, in fact, gradient of class \(L^{p+\varepsilon }\) for some \(\varepsilon >0\).
Theorem 5.3
Let \(\varvec{\textit{u}}\) be a minimizer of (1.1). Then for each \(\mathcal {M}'\Subset \mathcal {M}_0\) and each \(\varvec{\textit{z}}_0\in \mathcal {M}'\), there exist numbers \(R_0>0\) and \(q>p\) and a constant \(C>0\) such that for each \(0<R<R_0\) and \(\varvec{\textit{z}}\in \mathcal {B}_{R_0}^{\mathcal {M}}\left( \varvec{\textit{z}}_0\right) \) it holds that

In particular,
Proof
Prior to proving the result, we establish a preliminary estimate, which will be used in the proof of inequality (5.11). Now, similar to the proof of Proposition 5.1, let \(M_{p,\frac{R}{4}}^{\mathcal {M}}\) be a minimizer of the map

We estimate by means of both the triangle inequality and Jensen’s inequality that

Then by utilizing the preceding inequality, invoking Proposition 5.1, switching back to the manifold \(\mathcal {M}\), and using the minimality of the map \(M_{p,\frac{R}{4}}\) we collectively arrive at the estimate

from which we obtain the estimate

This latter inequality then provides an upper bound dual to the lower bound established in Proposition 5.1.
With this preliminary estimate dispatched, we now essentially follow the well-known argument given in [38, §§6.3–6.4]. Since we only need the result to hold for a possibly small number \(R_0:=R_0\left( \rho _0,\varvec{\textit{z}}_0\right) >0\), there is, once again, no loss in assuming the existence of a single coordinate chart \((\mathcal {V},\varvec{\varphi })\) such that \(\mathcal {B}^{\mathcal {M}}_{4{\widetilde{R}_0}}\left( \varvec{\textit{z}}\right) \subseteq \mathcal {V}\) for each \(\widetilde{R_0}\in \left( 0,\frac{R_0}{4}\right) \). Moreover, estimates (4.1)–(4.2) are still applicable, and we shall use these repeatedly in the sequel.
So, on this coordinate chart, the partial Caccioppoli inequality of Theorem 5.2 assumes the form

where we have used the preliminary estimate (with a simple change of radii) from earlier in this proof. Applying the Sobolev–Poincaré inequality [38, Theorem 3.17, (3.34)] to (5.12) and absorbing the constant \( c_6 \) into the constant C we obtain the estimate

where we put \(\mu :=\frac{m}{m+p}<1\). From (5.13) we thus obtain

Finally, one may apply Gehring’s lemma—cf., [38, Lemma 6.2]—in order to deduce from (5.14) that

with \(q\in (p,p+\eta )\) for some \(\eta >0\). Pulling back to the manifold, we thus recover from (5.15) the estimate

which, as (5.16) is (5.11), completes the proof. \(\square \)
We conclude this section and this paper by providing a brief example to explicate the implications of the results derived in this work.
Example 5.4
Let \(p\ge 2\) and \(r<p\) be given and fixed. Consider the map \(G\ : \ \mathcal {M}\times \mathcal {N}\times \left( \mathbb {R}^{\ell }\otimes T^*\mathcal {M}\right) \rightarrow \mathbb {R}\) defined by
where \(\varvec{\mathsf {A}}\), \(\varvec{\mathsf {B}}\ : \ \mathcal {M}\times \mathcal {N}\rightarrow \left( \odot ^2\mathbb {R}^\ell \right) \otimes \left( \odot ^2 T^*\mathcal {M}\right) \). Suppose that \(\varvec{\mathsf {A}}\) satisfies conditions (A1)–(A2). We claim that if \(\varvec{\mathsf {B}}\) satisfies the Morrey regularity condition \(\left| \sup _{\varvec{\textit{u}}\in \mathcal {N}}\varvec{\mathsf {B}}(\cdot ,\varvec{\textit{u}})\right| \in L^{\frac{pr}{2(p-r)},\gamma }\left( \mathcal {M}\right) \), then conditions (A1)–(A4) are satisfied.
To see that this is true, notice first of all that Cauchy-Schwarz implies that
We conclude from the above inequality that \(\sigma _{\varepsilon }\) may be defined by
Since, by assumption, we must have \(\sigma _{\varepsilon }\in L^{p,\gamma }\left( \mathcal {M}_0\right) \), it follows that we need the condition
to hold. But since this condition is equivalent to
the claim holds. And this ensures that G is \((p,\gamma )\)-asymptotically related to the map \((\varvec{\textit{z}},\varvec{\textit{w}},\varvec{\xi })\mapsto \left\{ \varvec{\mathsf {A}}(\varvec{\textit{z}},\varvec{\textit{w}})(\otimes ^2\varvec{\xi })\right\} ^\frac{p}{2}\).
So, since G as defined above satisfies conditions (A1)–(A4), it follows that the associated integral functional
has the property that if \(\varvec{\textit{u}}\) is a minimizer of (5.17), then it holds that \(\varvec{\textit{u}}\in \mathscr {C}_{\mathrm {loc}}^{0,1-\frac{p+\beta -\alpha p}{p}}\left( \mathcal {M}_0\right) \) for each \(\beta \in (0,\min \{m-p,\alpha p\})\), as in the conclusion of Theorem 4.2. Furthermore, by means of Theorem 5.2 and Theorem 5.3, we conclude that if \(\varvec{\textit{u}}\) is a minimizer of (5.17), then \(\varvec{\textit{u}}\) satisfies a Caccioppoli inequality on the compact submanifold \(\mathcal {M}_0\) and, in addition, the map \(\varvec{\mathsf {d}}\varvec{\textit{u}}\) possesses higher integrability in the sense of Theorem 5.3.
Remark 5.5
We note that while the map \((\varvec{\textit{z}},\varvec{\textit{u}})\mapsto \varvec{\mathsf {B}}(\varvec{\textit{z}},\varvec{\textit{u}})\) must be uniformly bounded in \(\varvec{\textit{u}}\), it can experience blow-up in \(\varvec{\textit{z}}\) at a given \(\varvec{\textit{u}}\in \mathcal {N}\). Moreover, we see that even as \(|\varvec{\xi }|_{\mathbb {R}^{\ell }\otimes T_{\varvec{\textit{z}}}^{*}\mathcal {M}}\rightarrow +\infty \), the map \((\varvec{\textit{z}},\varvec{\textit{u}},\varvec{\xi })\mapsto G(\varvec{\textit{z}},\varvec{\textit{u}},\varvec{\xi })\) may, nonetheless, retain its dependence not only on the spatial variable \(\varvec{\textit{z}}\) but also \(\varvec{\textit{u}}\), which is unusual even in the Euclidean setting. And as mentioned in Sect. 1, this initiates a low-order regularity theory for asymptotically convex functionals in the Riemannian manifold setting.
References
Abatzoglou, T.J.: The minimum norm projection on \(C^{2}\)-manifolds in \(\mathbb{R}^n\). Trans. Am. Math. Soc. 243, 115–122 (1978)
Beck, L.: Boundary regularity for elliptic problems with continuous coefficients. J. Convex Anal. 16, 287–320 (2009)
Bögelein, V., Duzaar, F., Habermann, J., Scheven, C.: Partial Hölder continuity for discontinuous elliptic problems with VMO-coefficients. Proc. Lond. Math. Soc. (3) 103, 371–404 (2011)
Bögelein, V., Duzaar, F., Habermann, J., Scheven, C.: Stationary electro-rheological fluids: low order regularity for systems with discontinuous coefficients. Adv. Calc. Var. 5, 1–57 (2012)
Bögelein, V.: Partial regularity for minimizers of discontinuous quasi-convex integrals with degeneracy. J. Differ. Equ. 252, 1052–1100 (2012)
Chipot, M., Evans, L.C.: Linearisation at infinity and Lipschitz estimates for certain problems in the calculus of variations. Proc. R. Soc. Edinb. Sect. A 102, 291–303 (1986)
Danĕc̆ek, J., Viszus, E.: On Hölder regularity for vector-valued minimizers of quasilinear functionals. Math. Bohem. 135, 199–207 (2010)
De Giorgi, E.: Un esempio di estremali discontinue per un problema variazionale di tipo ellittico. Boll. Un. Mat. Ital. 1, 135–137 (1968)
Dolzmann, G., Kristensen, J., Zhang, K.: BMO and uniform estimates for multi-well problems. Manuscr. Math. 140, 83–114 (2013)
Duzaar, F., Fuchs, M.: Optimal regularity theorems for variational problems with obstacles. Manuscr. Math. 56, 209–234 (1986)
Duzaar, F., Fuchs, M.: Variational problems with nonconvex obstacles and an integral-constraint for vector-valued functions. Math. Z. 191, 585–591 (1986)
Duzaar, F., Mingione, G.: The \(p\)-harmonic approximation and the regularity of \(p\)-harmonic maps. Calc. Var. Partial Differ. Equ. 20, 235–256 (2004)
Duzaar, F., Mingione, G.: Regularity for degenerate elliptic problems via \(p\)-harmonic approximation. Ann. Inst. H. Poincaré Anal. Non Linéaire 21, 735–766 (2004)
Evans, L.C.: Partial regularity for stationary harmonic maps into spheres. Arch. Ration. Mech. Anal. 116, 101–113 (1991)
Evans, L.C., Gariepy, R.F.: Blowup, compactness and partial regularity in the calculus of variations. Indiana Univ. Math. J. 36, 361–371 (1987)
Fardoun, A., Regbaoui, R.: Regularity and uniqueness of \(p\)-harmonic maps with small range. Geom. Dedic. 164, 259–271 (2013)
Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93, 418–491 (1959)
Fey, K., Foss, M.: Morrey regularity results for asymptotically convex variational problems with \((p, q)\) growth. J. Differ. Equ. 246, 4519–4551 (2009)
Foss, M.: Global regularity for almost minimizers of nonconvex variational problems. Ann. Mat. Pura Appl. (4) 187, 263–321 (2008)
Foss, M., Goodrich, C.S.: Partial Hölder continuity of minimizers of functionals satisfying a general asymptotic relatedness condition. J. Convex Anal. 22, 219–246 (2015)
Foss, M., Mingione, G.: Partial continuity for elliptic problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 25, 471–503 (2008)
Foss, M., Passarelli di Napoli, A., Verde, A.: Global Morrey regularity results for asymptotically convex variational problems. Forum Math. 20, 921–953 (2008)
Foss, M., Passarelli di Napoli, A., Verde, A.: Global Lipschitz regularity for almost minimizers of asymptotically convex variational problems. Ann. Mat. Pura Appl. (4) 189, 127–162 (2010)
Fuchs, M.: \(p\)-harmonic obstacle problems. II. Extensions of maps and applications. Manuscr. Math. 63, 381–419 (1989)
Fuchs, M.: \(p\)-harmonic obstacle problems. I. Partial regularity theory. Ann. Mat. Pura Appl. (4) 156, 127–158 (1990)
Fuchs, M.: \(p\)-harmonic obstacle problems. III. Boundary regularity. Ann. Mat. Pura. Appl. (4) 156, 159–180 (1990)
Fuchs, M.: \(p\)-harmonic obstacle problems. IV. Unbounded side conditions. Analysis 13, 69–76 (1993)
Fuchs, M.: The blow-up of \(p\)-harmonic maps. Manuscr. Math. 81, 89–94 (1993)
Fusco, N., Hutchinson, J.: Partial regularity in problems motivated by nonlinear elasticity. SIAM J. Math. Anal. 22, 1516–1551 (1991)
Giaquinta, M.: Multiple Integrals in the Calculus of Variations and Nonlinear Elliptic Systems. Princeton University Press, Princeton (1983)
Giaquinta, M., Giusti, E.: On the regularity of the minima of variational integrals. Acta Math. 148, 31–46 (1982)
Giaquinta, M., Giusti, E.: Differentiability of minima of non-differentiable functionals. Invent. Math. 72, 285–298 (1983)
Giaquinta, M., Modica, G.: Regularity results for some classes of higher order nonlinear elliptic systems. J. Reine Angew. Math. 311(312), 145–169 (1979)
Giaquinta, M., Modica, G.: Almost-everywhere regularity results for solutions of nonlinear elliptic systems. Manuscri. Math. 28, 100–158 (1979)
Giaquinta, M., Modica, G.: Partial regularity of minimizers of quasiconvex integrals. Ann. Inst. H. Poincaré Anal. Non Linéaire 3, 185–208 (1986)
Giaquinta, M., Modica, G.: Remarks on the regularity of the minimizers of certain degenerate functionals. Manuscr. Math. 57, 55–99 (1986)
Geisler, M.: Morrey-Campanato spaces on manifolds. Comment. Math. Univ. Carol. 29, 309–318 (1988)
Giusti, E.: Direct Methods in the Calculus of Variations. World Scientific, River Edge (2003)
Goodrich, C.S.: Positive solutions to boundary value problems with nonlinear boundary conditions. Nonlinear Anal. 75, 417–432 (2012)
Goodrich, C.S.: On nonlocal BVPs with boundary conditions with asymptotically sublinear or superlinear growth. Math. Nachr. 285, 1404–1421 (2012)
Goodrich, C.S.: On nonlinear boundary conditions satisfying certain asymptotic behavior. Nonlinear Anal. 76, 58–67 (2013)
Goodrich, C.S.: On nonlinear boundary conditions involving decomposable linear functionals. Proc. Edinb. Math. Soc. (2) 58, 421–439 (2015)
Goodrich, C. S.: Partial Hölder continuity of minimizers of functionals satisfying a VMO condition. Adv. Calc. Var. (submitted)
Hamburger, C.: Regularity of differential forms minimizing degenerate elliptic functionals. J. Reine Angew. Math. 431, 7–64 (1992)
Jost, J.: Riemannian Geometry and Geometric Analysis. Springer, New York (2011)
Kristensen, J., Mingione, G.: The singular set of Lipschitzian minima of multiple integrals. Arch. Ration. Mech. Anal. 184, 341–369 (2007)
Lee, J.M.: Riemannian Manifolds: An Introduction to Curvature. Springer, New York (1997)
Leone, C., Misawa, M., Verde, A.: The regularity for nonlinear parabolic systems of \(p\)-Laplacian type with critical growth. J. Differ. Equ. 256, 2807–2845 (2014)
Luckhaus, S.: Partial Hölder continuity for minima of certain energies among maps into a Riemannian manifold. Indiana Univ. Math. J. 37, 349–367 (1988)
Mingione, G.: Regularity of minima: an invitation to the dark side of the calculus of variations. Appl. Math. 51, 355–426 (2006)
Mingione, G.: Singularities of minima: a walk on the wild side of the calculus of variations. J. Glob. Optim. 40, 209–223 (2008)
Passarelli di Napoli, A., Verde, A.: A regularity result for asymptotically convex problems with lower order terms. J. Convex Anal. 15, 131–148 (2008)
Ragusa, M., Tachikawa, A.: On continuity of minimizers for certain quadratic growth functionals. J. Math. Soc. Japan 57, 691–700 (2005)
Ragusa, M., Tachikawa, A.: Partial regularity of the minimizers of quadratic functionals with VMO coefficients. J. Lond. Math. Soc. (2) 72, 609–620 (2005)
Ragusa, M., Tachikawa, A.: Regularity of minimizers of some variational integrals with discontinuity. Z. Anal. Anwend. 27, 469–482 (2008)
Ragusa, M., Tachikawa, A.: Partal regularity of \(p(x)\)-harmonic maps. Trans. Am. Math. Soc. 365, 3329–3353 (2013)
Ragusa, M., Tachikawa, A.: On interior regularity of minimizers of \(p(x)\)-energy functionals. Nonlinear Anal. 93, 162–167 (2013)
Raymond, J.-P.: Lipschitz regularity of solutions of some asymptotically convex problems. Proc. R. Soc. Edinb. Sect. A 117, 59–73 (1991)
Rivière, T., Strzelecki, P.: A sharp nonlinear Gagliardo–Nirenberg-type estimate and application to the regularity of elliptic systems. Commun. Partial Differ. Equ. 30, 589–604 (2005)
Scheven, C., Schmidt, T.: Asymptotically regular problems. II. Partial Lipschitz continuity and a singular set of positive measure. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 8, 469–507 (2009)
Scheven, C., Schmidt, T.: Asymptotically regular problems. I. Higher integrability. J. Differ. Equ. 248, 745–791 (2010)
Schoen, R., Uhlenbeck, K.: A regularity theory for harmonic maps. J. Differ. Geom. 17, 307–335 (1982)
Schoen, R., Uhlenbeck, K.: Boundary regularity and the Dirichlet problem for harmonic maps. J. Differ. Geom. 18, 253–268 (1983)
Schoen, R., Uhlenbeck, K.: Regularity of minimizing harmonic maps into the sphere. Invent. Math. 78, 89–100 (1984)
Simon, L.: Theorems on Regularity and Singularity of Energy Minimizing Maps. Birkhäuser, Basel (1996)
Tachikawa, A.: A partial regularity result for harmonic maps into a Finsler manifold. Calc. Var. Partial Differ. Equ. 16, 217–224 (2003)
Tachikawa, A.: Partial regularity results up to the boundary for harmonic maps into a Finsler manifold. Ann. Inst. H. Poincaré Anal. Non Linéaire 26, 1953–1970 (2009)
Uhlenbeck, K.: Regularity for a class of non-linear elliptic systems. Acta. Math. 138, 219–240 (1977)
Acknowledgments
The second author (CSG) would like to thank the first author (MDF) for introducing him to this problem in the fall of 2011 and for the many encouraging and stimulating discussions that subsequently led to this paper. Furthermore, both authors would like to thank the anonymous referee both for his or her careful reading of the paper and for several helpful suggestions for its improvement.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Foss, M.D., Goodrich, C.S. On partial Hölder continuity and a Caccioppoli inequality for minimizers of asymptotically convex functionals between Riemannian manifolds. Annali di Matematica 195, 1405–1461 (2016). https://doi.org/10.1007/s10231-015-0521-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-015-0521-z