1 Introduction

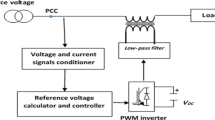
Now a days, there is unlimited significance to electrical energy as it is the most commonly used of all energies. Exclusive of the electric supply,life cannot be Imagined. At the same time, the quality and steadiness of the electric power supplied are also very important for the efficient operation of the end user’s equipment.Many of the commercial and industrial loads require high quality without interruptions and a constant quantity. Therefore, maintaining the power quality is one of the most important things in the world today.The nonlinear devices have a significant impact on the power supply’s quality and consistency. There may be power discontinuity, flicker, harmonics, voltage fluctuations, and other issues due to electronic power equipment. PQ issues include voltage sags and swells caused by network outages, lightning strikes, and switching capacitor banks.There are reactive and harmonic power disturbances in the power distribution system when non-linear loads (computers, lasers, printers, rectifiers) are used excessively.It is critical to address this type of issue, which has a potential to worsen in the future and have a detrimental impact. Passive filters have traditionally been employed for reactive power disturbances and harmonic production, but they have a number of drawbacks, including huge size, resonance issues, and the effect of the source impedance on performance.To increase energy quality, active power filters can be used. The system configuration can be used to classify active power filters.There are two types of active power filters: series active power filter and shunt active power filter.A device called UPQC is obtained by integrating both Series APF and shunt APF.Both Voltage and current distortions are eliminated by UPQC [1]. Harmonic current compensation, reactive power compensation, and power factor improvement are all obtained with a Shunt APF.A series APF compensates for voltage sag/swell on the load side, ensuring that the voltage is correctly controlled.Shunt APF is in shunt with the distribution System and Series APF is in series with the Distribution System. The UPQC is designed to mitigate various power quality problems of electrical power distribution system. Akagi et al. [2], Krishna et al. [3], Han et al. [4], Akagi and Fujita [5] it is a combination of series-APF and shunt-APF in [6]. In [7], it can be used to reduce current distortions by injecting a voltage proportionate to the source current and the injected series voltage at the PCC such that the design can act as a framework to remove voltage sag/swell [8]. Several approaches introduced like PI, PID, FLC, ANN, SMC, etc., are used. In [9] PI controller needs distinct linear numerical models, which is hard to receive, and hence fails to perform satisfactorily below highly sensitive load disruption.Recently some authors have proposed advanced control based on controllers such as state action controllers, self-calibration controllers,and MRC are used in [10, 11]. In this proposed work, a controller is designed UPQCbased on FOFL. As [12] proposed, these controllers also need numerical models and are consequently excitable to parameter change. The standard design of UPQC is a combination of a series APF and shunt APF and is adjoining to a mutual dc link [13]. A simple Configuration of a typical UPQC is shown in Fig. 1. Isolation of harmonics between sub transmission system and distribution system can be done by series active power filter proposed in [14]. This filter mitigates sag, swell and THD at PCC. The current harmonics are compensated by shunt APF [15]. The DC link is used to regulate DC voltage between two filters [14]. The UPQC circuit consists of two back-to-back IGBT-based voltage source bidirectional converters with a shared DC bus. One inverter is linked in series with the load, while the other is in shunt. The inverter works as a current source for injecting compensating current ish when it is connected in shunt with the load. The supply side inverter, which is coupled in series with the load, serves as a voltage source, supplying \(V_{sc}\) through an insertion transformer.In Conventional control technique, the hysteresis ”band” controller uses ”p-q theory” aimed at the shunt APF and the hysteresis band controller transforming the Park transformation or dq0 for the Series APF. In this paper P.Q of the system have been enhanced with the use of UPQC.

Fig. 1
figure 1

UPQC configuration

Full size image

1.1 Series APF

The Series APF adds a voltage that is in line with the supply, reducing voltage sags and swells at the load end. Under oscillation conditions, control activity is on the order of 2msec, guaranteeing a stable voltage supply.The assets of sensitive loads from voltage sags/swells arriving from the system are the most important aspect of an Series-APF.The Series-APF is set up to handle delicate loads.If a fault occurs on another line, the load is compensated to its pre-fault value by inserting series voltage.The short magnitudes of the three inserted phase Voltages are restricted in such a way to decimate any harmful effects of a bus fault to the load voltage.The series APF is designed based on the concept of single vector model (SVM) as projected in [13]. The SVM is elaborate from the distorted supply.The general configuration of Series APF shown in Fig. 2.

Fig. 2
figure 2

Series-APF configuration

Full size image

1.2 Shunt APF

The general configuration of shunt-APF is shown in Fig. 3, which filters equal but opposing harmonic compensatory current to compensate for load current harmonics.In essence, a shunt APF works as a current source filtering the load’s harmonic, but with a 180-degree phase shift. The APF is primarily used as a voltage regulator and a harmonic alienate between the nonlinear load and the consumer side source.The APF is controlled using the p-q hypothesis. These modeling equations are used to convert 3-\(\phi\) voltages and currents from abc to dq coordinates.

$$\begin{aligned}&\begin{bmatrix} v_{0} \\ v_{d} \\ v_{q}\\ \end{bmatrix} = \sqrt{3/2} \begin{bmatrix} {1/\sqrt{2}} &{1/\sqrt{2}} &{1/\sqrt{2}}\\ 1 &-1/2 &-1/2\\ 0 &{\sqrt{3}/2} &{\sqrt{3}/2}\\ \end{bmatrix} \begin{bmatrix} v_{s,a}\\ v_{s,b}\\ v_{s,c}\\ \end{bmatrix} \end{aligned}$$
(1)
$$\begin{aligned}&\quad \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q}\\ \end{bmatrix} = \sqrt{3/2} \begin{bmatrix} {1/\sqrt{2}} &{1/\sqrt{2}} &{1/\sqrt{2}}\\ 1 &-1/2 &-1/2\\ 0 &{\sqrt{3}/2} &{\sqrt{3}/2}\\ \end{bmatrix} \begin{bmatrix} i_{s,a}\\ i_{s,b}\\ i_{s,c}\\ \end{bmatrix} \end{aligned}$$
(2)

Real and reactive components are getting from the given in Eq. (3). Since Real and reactive components are a relation of \(I_{L}\) and \(V_{S}\).

$$\begin{aligned}&\begin{bmatrix} P \\ Q \\ \end{bmatrix} = \begin{bmatrix} v_{d} &v_{q}\\ -v_{q} &v_{d}\\ \end{bmatrix} \begin{bmatrix} i_{d}\\ i_{q}\\ \end{bmatrix} \end{aligned}$$
(3)
$$\begin{aligned}&\quad P_{0}=V_{0}*I_{0} \end{aligned}$$
(4)
$$\begin{aligned}&\quad P=\bar{P}+\tilde{P} \end{aligned}$$
(5)
$$\begin{aligned}&\quad \begin{bmatrix} I_{cd,r }\\ I_{cq,r} \\ \end{bmatrix} = 1/v^{2}_{\alpha }+v^{2}_{\beta } \begin{bmatrix} v_{\alpha } &v_{\beta }\\ -v_{\beta } &v_{\alpha }\\ \end{bmatrix} \begin{bmatrix} -\bar{P}+P_{0}+\bar{P_{Loss}}\\ -Q \end{bmatrix} \end{aligned}$$
(6)

\(I_{cd,r}\) and \(I_{cq,r}\) are mentioned currents of ”Shunt-APF” in d-q axis. These current are transformed to 3-\(\phi\) structure as shown in Eq. (7).

$$\begin{aligned} \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q}\\ \end{bmatrix} = \sqrt{3/2} \begin{bmatrix} 1 &0 \\ -1/2 &{\sqrt{3}/2}\\ -1/2 -&{\sqrt{3}/2}\\ \end{bmatrix} \begin{bmatrix} i_{cd,r}\\ i_{cq,r}\\ \end{bmatrix} \end{aligned}$$
(7)

The current reference in the 3-\(\phi\) scheme (\(I_{ca,r}\) , \(I_{cb,r}\) , \(I_{cc,r}\)) are deliberate in order to alter neutralized, harmonic and sensitive current in the load. HCC algorithm [16] is used to make a switch signal by examining the existent signal with mention point signal, depending on accelerate and quality of ”reference” point indicate the functioning of UPQC is reinforced.

Fig. 3
figure 3

Shunt-APF configuration

Full size image

2 Design of Fractional Order Controller

Sondhi and Hote [17] introduced the Reduced Ordered Controller in [17]. It is significant to realize the reduced order integral operator. The reduced order speculator was mathematically.

$$\begin{aligned} c(s) = kp + \frac{Ki}{s^{\lambda }} \end{aligned}$$
(8)

Where \(\lambda\) can accept some value in the range (0, 1). If \(\lambda\) \(\ge\) 2 is changed to a high-order construction which is different in equivalence to formal PI controller. The F.O described in equation (8) may be regarded as the common character of the formal PI controller [18].

2.1 Design of Filter Using Fractional Order Controller

The evolution of FOC (Fractional order Controller), there appeared various definitions of FOD’s and FOI’s presented in [1, 19]. Using filters is one of the most effective ways to solve the issues. Some consecutive filters are summarized in [3]. Assuming the awaited fitting range is \((\omega _{b};\omega _{h})\), the fractional order function \(\lambda\) can be approximated by ROF (Reduced Order Filter) can be written as

$$\begin{aligned} F(s)=\left[ \frac{1+\frac{as}{b\omega _{a}}}{1+\frac{bs}{b\omega _{h}}}\right] ^{\lambda } \end{aligned}$$
(9)

where 0\(\le\) \(\lambda\) \(\le\)1; s = j\(\omega\) ,a\(\ge\)0; b\(\ge\) 0 , and

$$\begin{aligned} F(s)=\left( \frac{as}{b\omega _{a}}\right) ^{\lambda }\left( 1+\frac{-bs+b}{bs^{2}+a\omega _{h}s}\right) ^{\lambda } \end{aligned}$$
(10)

In the frequency range ”\(\omega _{b}\) \(\ge\) \(\omega\) \(\ge\) \(\omega _{h}\)”,by using a ”Taylor- series” expansion, we obtain

$$\begin{aligned} F(s)=\left(\frac{as}{b\omega _{a}}\right)^{\lambda }\left(1+(s)+\frac{\lambda (\lambda -1)}{2}P^{2}(s).....\right) \end{aligned}$$
(11)

Where

$$\begin{aligned} F(s)=\left(1+\frac{-bs+b}{bs^{2}+a\omega _{h}s}\right) \end{aligned}$$
(12)

It is then found that

$$\begin{aligned} s^{\lambda }=\frac{\left(b\omega _{a}\right)^{\lambda }a^{\lambda }}{a^{\lambda }\left(1+(s)+\frac{\lambda (\lambda -1)}{2}P^{2}(s).....\right)}\left(\frac{1+as/b\omega _{a}}{1+bs/b\omega _{b}}\right)^{\lambda } \end{aligned}$$
(13)

from this the ”Taylor-series” to leads to

$$\begin{aligned} s^{\lambda }=\frac{(b\omega _{a})^{\lambda }a^{\lambda }}{a^{\lambda }(1+\lambda P(s))}\left(\frac{1+as/b\omega _{a}}{1+bs/b\omega _{b}}\right)^{\lambda } \end{aligned}$$
(14)

Thus, the FOD is characterized as

$$\begin{aligned} s^{\lambda }\approx \left(\frac{(b\omega _{a})}{b}\right)^{\lambda }\left(\frac{{\mathrm {d}}s^{2}+b\omega _{h}s}{{\mathrm {d}}(1-\lambda )s^{2}+b\omega _{h}s+{\mathrm {d}}\lambda }\right)\left(\frac{1+bs/{\mathrm {d}}\omega _{b}}{1+{\mathrm {d}}s/{\mathrm {d}}\omega _{h}}\right)^{\lambda } \end{aligned}$$
(15)

Equation (15) is balanced when all the poles are on LHS of the complex s-plane. The poles of the above equation are

  1. 1.

    one pole mut be located at -a\(\omega _{h}\) /b which is -Ve Real Pole since \(\omega _{h}\ge 0,a\ge 0,{\hbox {b}}\ge\) 0;

  2. 2.

    two other poles must be the roots of the equation

$$\begin{aligned} b(1-\lambda )s^{2}+a\omega _{h}s+b\lambda \end{aligned}$$
(16)

Thus, all the poles of Eq. (15) are stable within the range (\(\omega _{l}\),\(\omega _{h}\)). The irrational fractional-order part of expression in (14) can be approximated by the consecutive-time coherent model.

$$\begin{aligned} F(s)=\lim N\rightarrow \infty F_{N}(s)=\lim N\rightarrow \infty \prod _{F}^{N}=-N\frac{1+s/\omega _{k}^{'}}{1+s/\omega _{k}} \end{aligned}$$
(17)

according to the algorithmic distribution of real zeros and poles, the zero and pole of rank k can be written as

$$\begin{aligned} \omega _{k}^{'}=\left(\frac{b\omega _{a}}{a}\right)^{\frac{\lambda -2k}{2N+1}},\omega _{k}=\left(\frac{b\omega _{b}}{a}\right)^{\frac{\lambda +2k}{2N+1}} \end{aligned}$$
(18)

therefore, the model can be expressed as

$$\begin{aligned} s^{\lambda }\approx \left(\frac{(b\omega _{a})}{b}\right)^{\lambda }\left(\frac{{\mathrm {d}}s^{2}+b\omega _{h}s}{{\mathrm {d}}(1-\lambda )s^{2}+b\omega _{h}s+{\mathrm {d}}\lambda }\right)\prod _{F}^{N}=-N\frac{1+s/\omega _{k}^{'}}{1+s/\omega _{k}} \end{aligned}$$
(19)

This analysis similarity can prevail the good essence when a = 12 and b = 10. Through the estimation approach, the FOS may be accurate as the very eminent number-order system. A fractional Order Controller can obtain changing the sign of order (\(\lambda\)). Hence, the range of \(\lambda\) for integration is 0 \(\le\) \(\lambda\) \(\le\)1. The construction of FOPI-controller is shown in Fig. 4. For the design of a controller, the Kp element,\(\lambda\) are separately designed and arranged in the system as shown in Fig. 4.

Fig. 4
figure 4

Structure of FOPI controller

Full size image

2.2 Design of Fuzzy Logic Controller

The basic level of a Simple FLC is presented in Fig. 5. FLC consists of the fuzzification, Defuzzification modules and fuzzy inference rules, the input and the output variables. The block diagram of FLC shown in Fig. 5. The fuzzy sets are designed with seven membership functions for the E, CE and for the outputs shown in Fig. 6. The selection of the membership function that forms a fuzzy set is constructed [16, 20]. Figure 6 Shows the Fuzzy inference system with inputs Error is \(V_{dc;ref}\) and change in error is \(\Delta\) \(V_{dc;ref}\) . Figure 7 Shows membership functions of output i.e \(\Delta\) \(K_{P}\) and \(\Delta\) \(K_{I}\). For optimizing the inference [16]. The structure of FOFL controller is shown in Fig. 8. A control strategy with a new FOFL has been proposed, as shown in Fig. 9.

Fig. 5
figure 5

Structure of FL controller

Full size image
Fig. 6
figure 6

Membership functions of \(V_{dc;ref}\) and \(\Delta\) \(V_{dc; ref}\)

Full size image
Fig. 7
figure 7

Membership functions of tuned gain

Full size image
Fig. 8
figure 8

Structure of proposed FOFL controller

Full size image
Fig. 9
figure 9

Control diagram of proposed FOFL controller

Full size image

3 Learning Part

Fuzzy rule base set theory offers more adaptability in system design and expression observations in easy-to-follow knowledge base notation. FLC works best to optimize in closed loop control system [16, 21], in particular system with non-linearity between its i/p and o/p.The classic controllers including FOC work based on inputs errors with a gain value for Kp and Ki terms. So, the Controller action does not meet anticipated level for complex, non-linear systems [22, 23]. It can be incorporated the dynamic gain value for the Kp, full terms and Derivates alternatively of a fixed gain. Dynamic gain change in a FOPI control structure will improve controller execution and bring system output rapidly under stable conditions during variation and external disturbances [14]. Considering these aspects, a FLC combined with a FOC scheme is proposed here.The FOFL controller is a combination of FLC with FOF controller.In this Controller scheme the FLC is configured to use the system error and error derivative as inputs to obtain the proportional scale factor ‘E’ Full terms using these scale factors, the amount of controller gain will be updated in each sampling period.Framework of a typical FOFL control structure is shown in Fig. 8. In the proposed control structure, the FLC uses the error and the derivative of the error and calculates the scale factor for proportional and integral terms and therefore, these values are used to update the FOFL controller’s gain parameters.From these the \(K_{P}\) and \(K_{I}\) signal gain values for the FOFL controller are calculated from the following expressions

$$\begin{aligned} K_{P}= & k_{p} + \Delta K_{p} \end{aligned}$$
(20)
$$\begin{aligned} K_{I}= & k_{i} + \Delta K_{i} \end{aligned}$$
(21)

Where \(k_{p}\) and \(k_{i}\) are the Fixed gain values. The flowchart of the proposed system is shown in Fig. 10.

Fig. 10
figure 10

Flowchart for proposed system

Full size image

4 Simulation Results

4.1 Current Harmonics Compensation with FOPI and FOFL

In FOPI and FOFL controller ,the simulation results \(I_{s}\), \(I_{f}\) and \(I_{L}\) wave forms are shown in Fig. 11. It is observed that the FOFL controller regulates the dc-interface voltage faster than FOPI control, which shows that the proposed controller calculates the reference current more efficiently and quickly than FOPI controller.It is observed that source current and load current are well-balanced and reduce the distortion better compared to FOPI controller.

Fig. 11
figure 11

Compensation of current with FOPI and FOFLC

Full size image

4.2 Voltage Swell Compensation

As illustrated in Fig. 12, the simulation is run for a period of 0.2 seconds to 0.4 seconds. As illustrated in Fig. 12 , FOPI based UPQC successfully compensates for voltage swells. The power production is affected by the swell situation, as shown in Fig. 13.

Fig. 12
figure 12

Voltage swell mitigation with FOPI controller

Full size image

Swell is unaffected after using FOFL based UPQC. In the Fig. 13, the first waveform depicts grid voltage with Swell,the third waveform depicts affected and then injected voltage, and both added together, the corrected load voltage is depicted in the second waveform.

Fig. 13
figure 13

Voltage swell mitigation with FOFL controller

Full size image

4.3 Voltage Sag Compensation

As illustrated in Fig. 14, the simulation is run for duration of 0.5 to 0.7 seconds. As illustrated in Fig. 14,FOPI based UPQC successfully compensates for voltage sag .The power production is affected by the sag situation,as shown in Fig. 14. Sag is unaffected after using FOFL controller based UPQC which is shown in Fig. 15.

Fig. 14
figure 14

Voltage sag mitigation with FOPI controller

Full size image

In Fig. 15 using FOFL controller,the first wave form depicts grid voltage with Sag, the third wave form depicts affected and then injected voltage, and both combined, the adjusted load voltage is depicted in second waveform.In doing this, series filter demands active power which is drawn from the source through shunt APF via dc-link by drawing extra current component in order to maintain this DC link voltage at fixed level.

Fig. 15
figure 15

Voltage sag mitigation with FOFL

Full size image

Simulation results of Load Voltage and load current during Sag and swell are shown in Figs. 16 and 17 and DC-Link Voltage Regulation during sag and swell is shown in Fig. 18. THD for Load Current, Source Voltage , Load Voltage and Source Current with proposed Controllers is shown in Figs. 19, 20, 21, 22, 23, 24, 25, 26 respectively.The results show that the THD values of source Voltage is 0.48% and source Current THD is 2.17% and also THD values of Load Voltage is 0.65% and Load Current THD is 18.2% with FOFL controller.This controller is also able to effectively compensate all the parameter.Hence FOFL controller is most effective of the four controllers developed.Comparison of THD with all proposed controllers is shown in Tables 1 and 2 .

Fig. 16
figure 16

Simulation result of \(V_{L}\) and \(I_{L}\) with FOPI

Full size image
Fig. 17
figure 17

Simulation result of \(V_{L}\) and \(I_{L}\) with FOFL

Full size image
Fig. 18
figure 18

Simulation results of \(V_{DC-Link}\) regulation

Full size image
Fig. 19
figure 19

Comparision of THD for source current

Full size image
Fig. 20
figure 20

Comparision of THD for load current

Full size image
Fig. 21
figure 21

Comparision of THD for load voltage

Full size image
Fig. 22
figure 22

Comparision of THD for source voltage

Full size image
Fig. 23
figure 23

Comparison THD for \(I_{L}\)

Full size image
Fig. 24
figure 24

Comparison THD for \(V_{S}\)

Full size image
Fig. 25
figure 25

Comparison THD for \(I_{S}\)

Full size image
Fig. 26
figure 26

Comparison THD for \(V_{L}\)

Full size image
Table 1 Comparison THD for \(I_{s}\) and \(I_{L}\) using controllers
Full size table
Table 2 Comparison THD for \(V_{s}\) and \(V_{L}\) using controllers
Full size table

5 Conclusions

In this Paper FOFL Controller based UPQC is proposed to address the well-known power quality issues,Dynamic Performances and Regulation of \(V_{DC-Link}\). UPQC working is explained with 4 different controllers namely Fuzzy logic controller, Adaptive FLC ,FOPI and Fractional Order FLC.The model is developed in MATLAB Simulink and the results are analyzed. The THD values are calculated with each controller and compared. The Dynamic performance parameter is also noted. The results show that the THD values of source Voltage is 0.48% ,source Current THD is 2.17% with FOFL controller.This controller is also able to effectively compensate all the parameter.Hence FOFL controller is most effective of the four controllers develope.