1 Introduction

Due to the high cost of permanent magnet, induction motors (IMs) have attracted attention of modern industrial process designers. They have found their place in a wide range of industrial applications such as electric vehicles, transportation and aerospace industries. Induction motors offer several advantages compared to other motors such us ease of manufacturing, reliability, ruggedness, less maintenance and the most important its low price. However, IMs are highly coupled and multivariable systems. Consequently, parallel control of various variables is required to efficiently control the rotor speed and the torque. The reason why, it is essential to artificially obtain a decoupling between the flux and the torque using Field Oriented Control (FOC) for fast dynamic response and for better performances [29].

The use of a speed sensor in induction motor for precise signal measurement is required for closed loop speed drive. Therefore the presence of a speed sensor (encoder) can be an inconvenient. Instead of its extra cost, it leads to increase sensitivity to vibration and limits the application of induction motor in a relatively harsh environment. Thus, especially in the two last decades, and due to the recent advances in DSP, FPGA and ASICs technologies, sensorless control is becoming attractive to find solutions allowing to induction motor to operate at high performance without measurement of mechanical variables [26, 28].

In order to overcome these challenges, recently, various techniques for speed estimation that varies from open-loop to closed-loop estimator have been proposed and applied in medium and high speed regions. Among these techniques, Model Reference Adaptive System Observer (MRAS) [2, 32, 35, 36, 38] which is one of the popular observer due to its simplicity and ease of implementation in many forms (MRAS based rotor flux, Back EMF, reactive power…). However, at low speed region, inverter nonlinearity and uncertainties caused by parameters variation, especially the stator resistance, make the MRAS observer not able to provide required performances.

The Sliding Mode observer [8, 15, 25, 27] is one of the speed observer that gained a great attention in the last years because of its insensitivity against motor parameters variation and its robustness. However, this observer suffers from chattering phenomenon and requires an infinite switching rate. The Extended Kalman Filter [3, 11] and/or the Unscented Kalman Filter [33] as a speed observer, show high improvements in estimation for all region. But their main drawback is the use of a non-constant gain updated over time that increases computational complexity.

The high gain observer [12] which is also used for induction motor variables estimation, provides the advantage of using only one parameter for dynamic system adjustment. However, to find the optimal value of this parameter there is no clear analytical study that has been reported, only trial and error method that can be used for this issue.

Artificial neural networks have been also used for performance improvement of the induction motor parameters estimation [6, 7, 23]. Nevertheless, depending on the range of the operational speed and on the application, the number of neurons in hidden layer can be increased and then the computational complexity.

All these approaches differ with respect to accuracy, robustness, and sensitivity against model parameters variation especially stator and rotor resistances. Thus, the online identification of these parameters have attracted the research community in the field of robust sensorless drive. To overcome problems with machine model based techniques, methods with high-signal frequency injection were born [14, 24]. The advantages of these techniques are related to their insensitivity to parameters variation and their high precision at very low speed region. However, they require a special system for a real time implementation.

Out of various approaches, the Luenberger observer (LO) that was originally published by David G. Luenberger [21], received a lot of attention from other researchers [2, 9, 17,18,19, 22, 30]. Among the developed LO structures, we find the adaptive Luenberger observer which is one of the most popular adaptive observers used in sensorless motor control applications. It presents high performances and good stability, without forgetting its ease of implementation and low computational effort. Its structure is based on the IM model that estimates the state variables on the basis of different sets of input variables and an adaptive mechanism (AM).

In practice, considerable variations of stator resistance and rotor resistance/rotor time constant (RTC) take place when the motor temperature changes at varying load or speed or air temperature surrounding the motor, that’s why online adaptation of these quantities has improved the performance of the induction motor sensorless drive.

In literature, the majority of the proposed schemes, whether for speed estimation or for online parameters identification, utilize a simple PI type observer thanks to its accepted performance and simple structure. For example, in [9, 17] they have employed the PI adaptation mechanism for rotor speed, in [22] they have employed it for rotor speed and stator resistance, whereas in [19] they have employed it for rotor speed and rotor resistance. However, at very low speed region, the system noises get amplified because of the inverter nonlinearities and the use of fixed PI adaptation mechanism gains, and therefore the estimation degrades clearly and the obtained performance becomes limited [10].

In this paper, a promising solution is proposed in this case based on a fuzzy logic controller as adaptive mechanism to overcome PI controller’s limitations, and then developed experimentally with a dSPACE system based on DS1104 controller board to show its effectiveness compared to a PI Luenberger observer. Also, unlike the existing schemes and to improve the performance of sensorless Indirect FOC of the induction motor drive at very low speeds, this work aims at providing simultaneous estimation of rotor speed, stator resistance and RTC inverse using the adaptive fuzzy Luenberger observer (fuzzy logic based adaptive Luenberger observer) that has been proven stable according to the Lyapunov stability theorem.

2 Induction Motor Model and Indirect Field Oriented Control

From the state space representation of the induction motor model in the d-q reference frame, the electrical equations are written as follows [13, 20]:

$$\left\{ \begin{gathered} \frac{{dI_{sd} }}{dt} = - \lambda I_{sd} + \omega_{s} I_{sq} + \frac{{k_{s} }}{{T_{s} }}\varphi_{rd} + \omega k_{s} \varphi_{rq} + \frac{1}{{\sigma L_{s} }}V_{sd} \hfill \\ \frac{{dI_{sq} }}{dt} = - \omega_{s} I_{sd} - \lambda I_{sq} - \omega k_{s} \varphi_{rd} + \frac{{k_{s} }}{{T_{s} }}\varphi_{rq} + \frac{1}{{\sigma L_{s} }}V_{sq} \hfill \\ \end{gathered} \right.$$
(1)
$$\left\{ \begin{gathered} \frac{{d\varphi_{rd} }}{dt} = \frac{M}{{T_{r} }}I_{sd} - \frac{1}{{T_{r} }}\varphi_{rd} + \left( {\omega_{s} - \omega } \right)\varphi_{rq} \hfill \\ \frac{{d\varphi_{rq} }}{dt} = \frac{M}{{T_{r} }}I_{sq} - \left( {\omega_{s} - \omega } \right) \varphi_{rd} - \frac{1}{{T_{r} }}\varphi_{rq} \hfill \\ \end{gathered} \right.$$
(2)

where, (Isd, Isq) and (Vsd, Vsq) represent, respectively the d-q components stator currents and voltages. (φrd, φrq) denote the d-q rotor components fluxes. Tr = Lr/Rr and Ts = Ls/Rs denote the rotor and the stator time constants, respectively.

ωs, ω = pΩ and Ω represent respectively the synchronous, the rotor speed and the mechanical rotor speed. Lr and Ls are the rotor and the stator inductances, respectively. Rr and Rs are the rotor and the stator resistances, respectively. M represent the mutual inductance and p is the number of pole pairs.

And: \(\sigma = 1 - \frac{{M^{2} }}{{L_{s} L_{r} }}; k_{s} = \frac{M}{{\sigma L_{s} L_{r} }} = \frac{1 - \sigma }{{M\sigma }}; \lambda = \frac{1}{{T_{s} \sigma }} + \frac{1 - \sigma }{{T_{r} \sigma }}\) where \(\sigma\) is the blondel leakage coefficient.

The electromagnetic torque Ce and the mechanical equation in the d-q reference frame are given by:

$$C_{e} = p\frac{M}{{L_{r} }}(\varphi_{rd} I_{sq} - \varphi_{rq} \,I_{sd} )$$
(3)
$$\frac{d\Omega }{{dt}} = (C_{e} - C_{r} - f_{r} \,\Omega )/J\,$$
(4)

where, Cr is the load torque, J is the total inertia and fr is the friction coefficient.

The field oriented control principal consist of making the behavior of induction motor analogous to that of a DC motor in order to obtain a separation between the flux and torque by orienting the ‘d’ axis along the rotor flux axis as shown in Fig. 1. Under this condition we get [4, 16]:

$$\varphi_{rd} = \varphi_{r} ,\varphi_{rq} = 0$$
(5)

where \(\varphi_{r}\) is the total rotor flux.

Fig. 1
figure 1

Principle of the vector control

Full size image

By using Eq. (5) in Eq. (1), we get:

$$\left\{ \begin{gathered} V_{sd} = \sigma L_{s} \frac{{dI_{sd} }}{dt} + \lambda \sigma L_{s} I_{sd} - \sigma L_{s} \omega_{s} I_{sq} - \sigma L_{s} \frac{{k_{s} }}{{T_{s} }}\varphi_{r} \hfill \\ V_{sq} = \sigma L_{s} \frac{{dI_{sq} }}{dt} + \lambda \sigma L_{s} I_{sq} + \sigma L_{s} \omega_{s} I_{sd} + \sigma L_{s} \omega k_{s} \varphi_{r} \hfill \\ \end{gathered} \right.$$
(6)

From Eq. (6), it can be seen that both currents components (Isd, Isq) are controlled by voltages (Vsd, Vsq) and then acts on flux and torque. In this case, it is required to ensure a decoupling by introducing compensation terms Ed and Eq.

Where:

$$\left\{ {\begin{array}{*{20}c} {E_{d} = \sigma L_{s} \omega_{s} I_{sq} + \sigma L_{s} \frac{{k_{s} }}{{T_{s} }}\varphi_{r} \,\,\,\,\,} \\ {E_{q} = - \sigma L_{s} \omega_{s} I_{sd} - \sigma L_{s} \omega k_{s} \varphi_{r} } \\ \end{array} } \right.$$
(7)

Equation (6) becomes:

$$\left\{ \begin{gathered} V_{sd} = V_{sd}^{{\prime}} - E_{d} \hfill \\ V_{sq} = V_{sq}^{{\prime}} - E_{q} \hfill \\ \end{gathered} \right.$$
(8)

A new system of equations is obtained:

$$\left\{ {\begin{array}{*{20}c} {V_{sd}^{{\prime}} = \sigma L_{s} \frac{{dI_{sd} }}{dt} + \lambda \sigma L_{s} I_{sd} } \\ {V_{sq}^{{\prime}} = \sigma L_{s} \frac{{dI_{sq} }}{dt} + \lambda \sigma L_{s} I_{sq} } \\ \end{array} } \right.$$
(9)

Furthermore, the torque expression becomes:

$$C_{e} = p\frac{M}{{L_{r} }}\varphi_{r} I_{sq} \,$$
(10)

By using Eq. (5) in Eq. (2), we get:

$$\left\{ {\begin{array}{ll} {\varphi_{r} = MI_{sd} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(*)} \\ {\left( {\omega_{s} - \omega } \right) = \frac{{MI_{sq} }}{{T_{r} \varphi_{r} }} = \omega_{r} \,\,\,\,(**)} \\ \end{array} } \right.$$
(11)

where \(\omega_{r}\) is the slip speed.

Finally, by using the expression of φr (*) in (**) and integrating (**), we get:

$$\theta_{s} = \int {\left( {\frac{{I_{sq} }}{{T_{r} I_{sd} }} + \,\theta } \right)} \,dt$$
(12)

where, θs and θ are the position of the d-q reference frame and the rotor position, respectively. Later in this article, the following notations will be used:

$$a_{1} = - \lambda ;\,\,a_{2} = \frac{{k_{s} }}{{T_{r} }};\,\,a_{3} = k_{s} ;\,\,\,a_{4} = \frac{M}{{T_{r} }};\,\,a_{5} = - \frac{1}{{T_{r} }};\,\,a_{6} = \frac{1}{{\sigma L_{s} }};\,\,a_{7} = \frac{1 - \sigma }{\sigma };\,\,\beta_{r} = \frac{1}{{T_{r} }}$$

3 Sensorless Indirect FOC Using the Improved Luenberger Observer

The mathematical model of the induction motor in the stationary reference frame α-β using state space representation is described by the following equations [19]:

$$\begin{array}{*{20}c} {\dot{X} = A\left( {\omega ,R_{s} ,\beta_{r} } \right)X + BU} \\ {Y = CX \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, } \\ \end{array}$$
(13)

where,

$$\begin{gathered} A(\omega ,R_{s} ,\beta_{r} ) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - R_{s} a_{6} - \beta_{r} a_{7} } & 0 \\ 0 & { - R_{s} a_{6} - \beta_{r} a_{7} } \\ \end{array} } & {\begin{array}{*{20}c} {\beta_{r} a_{3} } & {\omega \,a_{3} } \\ { - \omega \,a_{3} } & {\beta_{r} a_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {M\beta_{r} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & 0 \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {M\beta_{r} } \\ \end{array} } & {\begin{array}{*{20}c} { - \beta_{r} } & { - \omega } \\ \omega & { - \beta_{r} } \\ \end{array} } \\ \end{array} } \right], \hfill \\ B = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 {\sigma L_{s} }}} \right. \kern-\nulldelimiterspace} {\sigma L_{s} }}} & 0 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 {\sigma L_{s} }}} \right. \kern-\nulldelimiterspace} {\sigma L_{s} }}} \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\,\,\,\,\,\,\,\,\,\,0} \\ 0 & {\,\,\,\,\,\,\,\,\,\,0} \\ \end{array} } \\ \end{array} } \right],C = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \\ \end{array} } \right],X = \left[ {\begin{array}{*{20}c} {I_{s\alpha } } \\ {I_{s\beta } } \\ {\varphi_{r\alpha } } \\ {\varphi_{r\beta } } \\ \end{array} } \right],\,\,U = \left[ {\begin{array}{*{20}c} {V_{s\alpha } } \\ {V_{s\beta } } \\ \end{array} } \right],\,\,Y = \left[ {\begin{array}{*{20}c} {I_{s\alpha } } \\ {I_{s\beta } } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(14)

And (Vsα, Vsβ) and (Isα, Isβ) represent the α-β stator voltages and currents components, respectively. (φrα, φrβ) are the α-β rotor fluxes components.

3.1 Luenberger Observer Structure

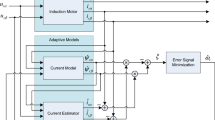
In this work, the adaptive Luenberger observer is a state observer estimating the induced fluxes, the stator currents and the other parameters (rotor speed, stator resistance and RTC inverse). These latter which constitute the output of the fuzzy adaptive mechanisms are estimated to be used for the tuning in the state matrix as shown in Fig. 2 and/or for feedback in the case of the estimated speed. The structure of the proposed observer is depicted in Fig. 2 whereas the overall block diagram of sensorless indirect FOC for induction motor drive using the adaptive fuzzy Luenberger observer is depicted in Fig. 3.

Fig. 2
figure 2

The adaptive Luenberger observer Structure

Full size image
Fig. 3
figure 3

Sensorless indirect FOC block diagram using the adaptive fuzzy Luenberger observer with online parameters identification

Full size image

The main components of this sensorless vector control are the adaptive fuzzy Luenberger observer, the speed control loop (an outer loop), the Isd and Isq currents control loops (inner loops), θs calculation block and the direct and inverse Park transformations. The input of the speed control loop is the reference speed Ω*. This latter is compared to the estimated speed \(\hat{\Omega }\) provided by the adaptive fuzzy Luenberger observer whose inputs are the measured stator currents and the reference stator voltages. The speed control error (\(\Omega^{*} - \hat{\Omega }\)) represents the input of the speed controller whose output is the reference torque given by \(C_{e}^{*}\) which provides the reference current \(I_{sq}^{*}\), obtained from Eq. (10). This latter, is compared to the measured current Isq given by the current sensor. The current control error (\(I_{sq}^{*} - I_{sq}\)) represents the input of the Q-axis current controller whose output is the reference voltage \(V_{sq}^{*}\). In parallel with this inner Isq control loop, we find another Isd control loop. The reference current \(I_{sd}^{*}\), obtained from equation Eq. (11) is compared to the measured current Isd given by the current sensor. The current control error (\(I_{sd}^{*} - I_{sd}\)) represents the input of the D-axis current controller whose output is the reference voltage \(V_{sd}^{*}\). Both reference voltages \(V_{sd}^{*}\) and \(V_{sq}^{*}\) are transformed to three-phase quantities (\(V_{sa}^{*}\),\(V_{sb}^{*}\),\(V_{sc}^{*}\)) using the position θs obtained from the estimated rotor speed and the slip speed given by Eq. (11). These reference voltages are considered as the input of the PWM (Pulse Width Modulation) blocks which drive the voltage source inverter.

The superscript ‘^’ represents estimated quantities and the superscript ‘*’ represents references of the quantities.

The Luenberger observer equations are given by [19]:

$$\begin{gathered} \hat{\dot{X}} = A\left( {\hat{\omega },\hat{R}_{s} ,\hat{\beta }_{r} } \right)\hat{X} + BU + L\left( {Y - \hat{Y}} \right) \hfill \\ \hat{Y} = C\hat{X} \hfill \\ \end{gathered}$$
(15)

where

$$\hat{X} = \left[ {\begin{array}{*{20}c} {\hat{I}_{s\alpha } } \\ {\hat{I}_{s\beta } } \\ {\hat{\varphi }_{r\alpha } } \\ {\hat{\varphi }_{r\beta } } \\ \end{array} } \right],\hat{Y} = \left[ {\begin{array}{*{20}c} {\hat{I}_{s\alpha } } \\ {\hat{I}_{s\beta } } \\ \end{array} } \right],A(\hat{\omega },\hat{R}_{s} ,\hat{\beta }_{r} ) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - \hat{R}_{s} a_{6} - \hat{\beta }_{r} a_{7} } & 0 \\ 0 & { - \hat{R}_{s} a_{6} - \hat{\beta }_{r} a_{7} } \\ \end{array} } & {\begin{array}{*{20}c} {\hat{\beta }_{r} a_{3} } & {\hat{\omega }\,a_{3} } \\ { - \hat{\omega }\,a_{3} } & {\hat{\beta }_{r} a_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {M\hat{\beta }_{r} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & 0 \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {M\hat{\beta }_{r} } \\ \end{array} } & {\begin{array}{*{20}c} { - \hat{\beta }_{r} } & { - \hat{\omega }} \\ {\hat{\omega }} & { - \hat{\beta }_{r} } \\ \end{array} } \\ \end{array} } \right]$$
(16)

We put:

$$A^{{\prime}} = A\left( {\hat{\omega },\hat{R}_{s} ,\hat{\beta }_{r} } \right) - LC$$
(17)

Equation (15) becomes:

$$\hat{\dot{X}} = A\left( {\hat{\omega },\hat{R}_{s} ,\hat{\beta }_{r} } \right)\hat{X} + BU + LY - LC\hat{X} = A^{{\prime}} \hat{X} + BU + LY$$
(18)

The stator current and the rotor flux estimation error is given by the following equation:

$$e = X - \hat{X} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {e_{{\mathop I\nolimits_{s\alpha } }} } \\ {e_{{\mathop I\nolimits_{s\beta } }} } \\ \end{array} } \\ {\begin{array}{*{20}c} {e_{{\mathop \varphi \nolimits_{r\alpha } }} } \\ {e_{{\mathop \varphi \nolimits_{r\beta } }} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {I_{s\alpha } - \hat{I}_{s\alpha } } \\ {I_{s\beta } - \hat{I}_{s\beta } } \\ \end{array} } \\ {\begin{array}{*{20}c} {\varphi_{r\alpha } - \hat{\varphi }_{r\alpha } } \\ {\varphi_{r\beta } - \hat{\varphi }_{r\beta } } \\ \end{array} } \\ \end{array} } \right]$$
(19)

By deriving Eq. (19), we obtain the following equation:

$$\dot{e} = \dot{X} - \hat{\dot{X}}$$
(20)

We then replace \(\dot{X}\) and \(\hat{\dot{X}}\) by their expressions from equations Eq. (13) and Eq. (15) and we add and subtract the quantity \(A^{{\prime}} X\) to get:

$$\dot{e} = \left( {A\left( {\omega ,R_{s} ,\beta_{r} } \right)X + BU} \right) - \left( {A^{{\prime}} \hat{X} + BU + LY} \right) = A\left( {\omega ,R_{s} ,\beta_{r} } \right)X - A^{{\prime}} \hat{X} - LY + A^{{\prime}} X - A^{{\prime}} X$$
(21)

By using Eq. (19) and by replacing A’ by its expressions (as expressed in Eq. (17)), we get:

$$\dot{e} = A\left( {\omega ,R_{s} ,\beta_{r} } \right)X - LY + A^{\prime}e - \left( {A\left( {\hat{\omega },\hat{R}_{s} ,\hat{\beta }_{r} } \right) - LC} \right)X$$
(22)

We finally obtain the expression of the error derivative:

$$\dot{e} = A^{{\prime}} e - \Delta A\hat{X}$$
(23)

where, \(\Delta A = A(\omega ,R_{s} ,\beta_{r} ) - A(\hat{\omega },\hat{R}_{s} ,\hat{\beta }_{r} ) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { -\Delta R_{s} a_{6} -\Delta \beta_{r} a_{9} } & 0 \\ 0 & { -\Delta R_{s} a_{6} -\Delta \beta_{r} a_{9} } \\ \end{array} } & {\begin{array}{*{20}c} {\Delta \beta_{r} a_{3} } & {\Delta \omega \,a_{3} } \\ { -\Delta \omega \,a_{3} } & {\Delta \beta_{r} a_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {M\Delta \beta_{r} } & { \,\,\,\,\,0} \\ {0\,\,\,\,} & { M\Delta \beta_{r} } \\ \end{array} } & {\begin{array}{*{20}c} { -\Delta \beta_{r} } & { -\Delta \omega } \\ {{ \Delta }\omega } & { -\Delta \beta_{r} } \\ \end{array} } \\ \end{array} } \right]\).

And \(\Delta \omega = \omega - \hat{\omega }\,;\,\,\Delta R_{s} = R_{s} - \hat{R}_{s} ;\,\,\Delta \beta_{r} = \beta_{r} - \hat{\beta }_{r}\).


For observer gain matrix L determination, conventional pole placement technique will be used:

In order to guarantee the system stability and to improve its transient response, the eigenvalues of the matrix \(A^{{\prime}}\) are placed in the left half of the complex plane. Thus, as presented in [17], the observer gain matrix L is calculated so that the observer poles are proportional to those of the induction motor (proportional constant k > 1).

This means that the eigenvalues of full order Luenberger observer (λLO) and the IM (λIM) must be satisfied using the following equation:

$$\lambda_{LO} = k\lambda_{IM}$$
(24)

The eigenvalues of the full order Luenberger observer can be calculated using the following equation:

$$\det \,\left( {\lambda_{LO} \,I_{4} - A\left( {\hat{\omega },\hat{R}_{s} ,\hat{\beta }_{r} } \right) + LC} \right) = 0$$
(25)

where, I4 is the (4 × 4) identity matrix.

Whereas the eigenvalues of the induction motor can be calculated using the following equation:

$$\det \,\left( {\lambda_{IM} I_{4} - A\left( {\omega ,R_{s} ,\beta_{r} } \right)} \right) = 0$$
(26)

The observer gain matrix can be considered as follows:

$$L = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {l_{1} } & {l_{2} } \\ { - l_{2} } & {l_{1} } \\ \end{array} } & {\begin{array}{*{20}c} {l_{3} } & {l_{4} } \\ { - l_{4} } & {l_{3} } \\ \end{array} } \\ \end{array} } \right]^{T} ,$$
(27)

The feedback gains are designed as follow:

$$\left\{ {\begin{array}{ll} {\begin{array}{*{20}c} {l_{1} = - \left( {k - 1} \right)\left( {a_{1} + a_{5} } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ {l_{2} = - \left( {k - 1} \right)\omega \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, } \\ \end{array} } \\ {\begin{array}{*{20}c} {l_{3} = \left( {k^{2} - 1} \right)\left( {\frac{{a_{1} }}{{a_{3} }} - a_{4} } \right) - \frac{1}{{a_{3} }}\left( {k - 1} \right)\left( {a_{1} + a_{5} } \right)\,} \\ {l_{4} = - \frac{1}{{a_{3} }}\left( {k - 1} \right)\omega } \\ \end{array} } \\ \end{array} } \right.$$
(28)

Figures 4a, b illustrate the motor and the observer poles trajectories (considering different values of the constant k) respectively. The speed ranges from − 140 to 140 rad/s. As shown in Fig. 4b, the constant k should not be very large in order not to destabilize the system.

Fig. 4
figure 4

a The IM poles trajectory for variable motor speeds; b the observer poles trajectory for variable motor speeds and for different values of ‘k’

Full size image

3.2 Rotor Speed, Stator Resistance and RTC Inverse Estimation Using the Adaptive fuzzy Luenberger Observer

The adaptive LO will be proved stable according to the Lyapunov method. In our case, the Lyapunov function candidate is defined as follow:

$$V = e^{T} e + \frac{{\Delta \omega^{2} }}{{\delta_{\omega } }} + \frac{{\Delta R_{s}^{2} }}{{\delta_{{R_{s} }} }} + \frac{{\Delta \beta_{r}^{2} }}{{\delta_{{\beta_{r} }} }}$$
(29)

where,\(\delta_{\omega }\),\(\delta_{{R_{s} }}\) and \(\delta_{{\beta_{r} }}\) are positive constants.

To satisfy the sufficient condition of the uniform asymptotic stability, the time derivative of the Lyapunov function should be negative definite [18]. \(\dot{V}\) is defined as:

$$\frac{dV}{{dt}} = \frac{{de^{T} }}{dt}e + e^{T} \frac{de}{{dt}} + \frac{1}{{\delta_{\omega } }}\frac{{d(\Delta \omega^{2} )}}{dt} + \frac{1}{{\delta_{{R_{s} }} }}\frac{{d(\Delta R_{s}^{2} )}}{dt} + \frac{1}{{\delta_{{\beta_{r} }} }}\frac{{d(\Delta \beta_{r}^{2} )}}{dt}$$
(30)

For the derivation of the adaptive mechanism, the parameters ω, Rs and βr are considered constant [17]. The expression of \(\dot{V}\) becomes:

$$\begin{gathered} \frac{dV}{{dt}} = + 2\Delta \omega \,a_{3} \left( {\hat{\varphi }_{r\beta } \,e_{{I_{s\alpha } }} - \hat{\varphi }_{r\alpha } \,e_{{ I_{s\beta } }} } \right) - 2\frac{1}{{\delta_{\omega } }}\Delta \omega \frac{{d\left( {\hat{\omega }} \right)}}{dt} + e^{T} \left[ {\left( {A^{{\prime}} } \right)^{T} + A^{{\prime}} } \right]e \hfill \\ +\, 2\Delta \beta_{r} \left( {a_{3} \hat{\varphi }_{r\alpha } \,e_{{I_{s\alpha } }} +\, a_{3} \hat{\varphi }_{r\beta } \,e_{{I_{s\beta } }} } \right.\left. { - a_{7} \hat{I}_{s\alpha } \,e_{{I_{s\alpha } }} - a_{7} \hat{I}_{s\beta } \,e_{{I_{s\beta } }} } \right) - 2\frac{1}{{\delta_{{\beta_{r} }} }}\Delta \beta_{r} \frac{{d\left( {\hat{\beta }_{r} } \right)}}{dt} \hfill \\ -\, 2a_{6}\Delta R_{s} \left( {\hat{I}_{s\alpha } \,e_{{I_{s\alpha } }} + \hat{I}_{s\beta } \,e_{{I_{s\beta } }} } \right) - 2\frac{1}{{\delta_{{R_{s} }} }}\Delta R_{s} \frac{{d\left( {\hat{R}_{s} } \right)}}{dt} +\, 2\Delta \omega \left( {\hat{\varphi }_{r\alpha } \,e_{{\varphi_{r\beta } }} - \hat{\varphi }_{r\beta } \,e_{{\varphi_{r\alpha } }} } \right) \hfill \\ + 2M\,\Delta \beta_{r} \left( {\hat{I}_{s\alpha } \,e_{{\varphi_{r\alpha } }} + \,\hat{I}_{s\beta } \,e_{{\varphi_{r\beta } }} } \right) - 2\Delta \,\beta_{r} \left( {\,\hat{\varphi }_{r\alpha } \,e_{{\varphi_{r\alpha } }} + \,\hat{\varphi }_{r\beta } \,e_{{\varphi_{r\alpha } }} } \right) \hfill \\ \end{gathered}$$
(31)

In order to satisfy the observer stability using Lyapunov criteria, the time derivative has to be negative. The term: eT([(A’)T+ (A’)])e is negative, because of the imposed eigenvalues of the observer whereas terms multiplied by the fluxes estimation errors \(e_{{\varphi_{r\alpha } }}\) and \(e_{{\varphi_{r\beta } }}\) are neglected if we suppose that in vector control these errors are very small.

The rest of the quantities can be set to values less than zero or equal to zero:

$$\begin{gathered} + 2\Delta \omega a_{3} e_{\omega } - 2\frac{1}{{\delta_{\omega } }}\Delta \omega \frac{{d\left( {\hat{\omega }} \right)}}{dt} = 0,\,\,\,\,\, - 2\Delta R_{s} a_{6} e_{{R_{s} }} - 2\frac{1}{{\delta_{{R_{s} }} }}\Delta R_{s} \frac{{d\left( {\hat{R}_{s} } \right)}}{dt} = 0 \hfill \\ + 2\Delta \beta_{r} e_{{\beta_{r} }} - 2\frac{1}{{\delta_{{\beta_{r} }} }}\Delta \beta_{r} \frac{{d\left( {\hat{\beta }_{r} } \right)}}{dt} = 0 \hfill \\ \end{gathered}$$
(32)

where,

$$\begin{gathered} e_{\omega } = \left( {\hat{\varphi }_{r\beta } \,e_{{I_{s\alpha } }} - \hat{\varphi }_{r\alpha } \,e_{{ I_{s\beta } }} } \right),\,\,\,\,\,\,e_{{R_{s} }} = \left( {\hat{I}_{s\alpha } \,e_{{I_{s\alpha } }} + \hat{I}_{s\beta } \,e_{{I_{s\beta } }} } \right), \hfill \\ e_{{\beta_{r} }} = \left( {a_{3} \hat{\varphi }_{r\alpha } \,e_{{I_{s\alpha } }} + a_{3} \hat{\varphi }_{r\beta } \,e_{{I_{s\beta } }} } \right.\left. { - a_{7} \hat{I}_{s\alpha } \,e_{{I_{s\alpha } }} - a_{7} \hat{I}_{s\beta } \,e_{{I_{s\beta } }} } \right) \hfill \\ \end{gathered}$$
(33)

Finally, we get:

$$\hat{\omega } = \delta_{\omega } a_{3} \int {e_{\omega } dt} ,\,\,\,\,\,\,\,\,\,\,\,\hat{R}_{s} = - \delta_{{R_{s} }} a_{6} \int {e_{{R_{s} }} dt} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\hat{\beta }_{r} = \delta_{{\beta_{r} }} \int {e_{{\beta_{r} }} dt}$$
(34)

Fuzzy logic that was originally developed by Lotfi Zadeh in 1965 [37], has been exploited successfully in several areas and utilized to solve many complex problems related to complex control of nonlinear and time varying parameters models. In the case of the IM, fuzzy logic techniques have been proposed for error minimization in different applications, such as,speed control, switching table of DTC and online tuning of the speed and/or the motor parameters [1, 5, 10, 20, 31, 34]. In this proposed Luenberger observer, fuzzy logic has been introduced as an adaptive mechanism to generate the speed and the other parameters from the errors (whose expressions are listed in Eq. (33)) and their derivatives.

As shown in Fig. 5, the fuzzy logic block is composed of three main blocks: Fuzzification, inference mechanism (rules base), and defuzzification. Figure 6 shows the input signals:\(er\) and its derivative \(\dot{e}r\) and the output signal:\(\hat{x}\) membership functions.

Fig. 5
figure 5

Internal structure of the fuzzy logic controller

Full size image
Fig. 6
figure 6

Inputs and output membership functions of the fuzzy logic controller

Full size image

The choice of the range (universe of discourse) of the membership functions variations is generally related to the nature of the input variables. In this article, we aim to improve the rotor speed and the parameters estimation using fuzzy logic based adaptive Luenberger observer (FL based ALO).

The input of the FL block is an error for which we have imposed this range [− 0.1, 0.1]. Thereafter, in order to have high performances of the observer, two adjustment gains K1 and K2 have been added in order to normalize the input quantities to always get the suitable weights of the membership functions.

Only three membership functions (triangular functions) that have been used for inputs and for output of the Fuzzy Logic block in order to simplify the practical implementation and in order to reduce execution time and algorithm complexity. In addition, through simulation tests, we noticed that the use of more than three membership function does not make a significant improvement to the system performances [20]. Therefore, the Fuzzy logic block has nine fuzzy IF–THEN rules as shown in Table 1. Where, N means Negative, Z means Zero and P means Positive. Defuzzification is done by centroid method based on the inference method Mamdani for more precision. All gains used in this sensorless drive are shown in Table 2.

Table 1 The fuzzy adaptation mechanism rules base
Full size table
Table 2 Gains of Controllers Used for Estimation
Full size table

4 Experimental Results and Discussions

The proposed sensorless IFOC of the induction motor drive using the Adaptive Fuzzy Luenberger Observer has been validated. The scheme shown in Fig. 3 has been used for experimental tests. The overview of the experimental setup shown in Fig. 7 consists of: (i) An Industrial IGBTs Voltage Source Inverter (VSI) from SEMIKRON connected to a DC voltage of 400 V, with a gate driver circuit SKHI20opA and two current sensors LEM 55-P. (ii) A dSPACE 1104 board with a 250 MHz 603-PowerPC processor and a slave-DSP based on 20 MHz TMS320F240 DSP from Texas Instrument used for PWM signals generation. In addition to DS1104_ADC converters with a resolution of 12 bits and a conversion time of 800 ns with a full-scale input voltage of ± 10 V. These latter were used for currents and speed acquisition. In fact, measurements obtained from currents sensors are converted to voltages ranging from 0 to ± 10 V before connection to the DS1104_ADC converters. Regarding the stator voltages, we used the reference stator voltages available in the algorithm to avoid the measurement of the high-frequency PWM stator voltages. (iii) A dSPACE panel serving as interface between the output sensor and the inputs of the dSPACE 1104 board (iv) A squirrel cage Induction Motor of 1 kW is used with parameters listed in Table 3. Load torque is adjusted by changing external resistances through a DC generator coupled to the induction motor. (v) A tachometer (20 V for 1000 rpm) is used to provide the real motor speed for comparison with its estimated value.

Fig. 7
figure 7

Block diagram of the experimental test bench

Full size image
Table 3 Motor Specifications and Parameters
Full size table

The tight integration of dSPACE software with MATLAB/Simulink®, which is a common engineering software, provides a powerful development environment. Indeed, according to Fig. 8, the six PWM TTL-signals are generated based on Simulink real-time blocks including the DS1104SL_DSP_PWM3 unit whose inputs are the reference voltages. To generate the real time C code, the Simulink file is built with the help of Real-Time Workshop (RTW) and Real Time Interface (RTI), and then downloaded on the 32 MB dSPACE memory. In order to ensure an optimal execution of the all parts of the sensorless drive, especially PWM generation and currents measurements, the PWM frequency was chosen equal to 6 kHz and the sampling time is equal to 100 µs.

Fig. 8
figure 8

Photograph of the experimental setup

Full size image

For real time monitoring, the dSPACE board is used with Control Desk software which makes easy data processing and visualization.

To show the validity and the effectiveness of the proposed IFOC sensorless drive, experimental tests were done in wide ranges of speed under load and no load especially at low and zero speed operations.

The experimental results are illustrated with relevant discussions in the following subsections.

The errors expressions are as follows:\(e_{FL} = \Omega - \hat{\Omega }_{FL}\) and \(e_{PI} = \Omega - \hat{\Omega }_{PI}\).Where,\(\hat{\Omega }_{FL}\) and \(\hat{\Omega }_{PI}\) are the estimated speed using the FL based ALO and PI based ALO, respectivly.

4.1 Open-Loop Comparison of the Estimated Speed Using PI and Fuzzy LO

The actual rotor speed and the estimated speeds obtained with PI and fuzzy adaptive scheme are presented in Fig. 9. For better comparison between the two adaptation mechanisms (FL and PI controllers respectively) speed estimation errors are observed in Fig. 10.

Fig. 9
figure 9

Actual and the estimated speeds responses with (PI Vs FL) Luenberger observer: a Step speed variations: from − 100 to 900 rpm; b Step speed variations: 100 → 0 → 100 rpm

Full size image
Fig. 10
figure 10

Speed estimation errors a speed: from − 100 to 900 rpm; b speed: 100 → 0 → 100 rpm

Full size image

In order to illustrate performance of the adaptive mechanism, an open loop test is mandatory when the IFOC control uses the actual speed as feedback signal. Also, in the comparative study of this paper, the main focus is on the operation of the speed estimators at low speeds due to poor operation of estimators in this region.

In the case of zero and low speed test as shown in Fig. 9(b), by comparing speed estimation errors in Fig. 10(b), it is completely clear that the PI controller has significant error especially at zero speed. From Figs. 9a and 10a, comparison between the operation of PI and fuzzy adaptive schemes from low to high speed tests confirm that fuzzy logic controller has better transient and steady-state behavior.

4.2 Rated Speed Response of the Drive

The performances of the sensorless drive (without stator resistance and RTC estimation) obtained with the PI based Adaptive Luenberger Observer and the proposed Fuzzy Logic based Adaptive Luenberger Observer are shown in Fig. 11. They show sensorless IM drive when different ranges of speed references are applied at no load with different speed reference profiles. Set of speed reference variations are applied from low to high speed (100 → 600 → 1100 → 1425) then a ramp speed command is applied from rated speed to low speed (100 rpm). In these tests, estimated speed is used as feedback in order to ensure a closed-loop control. Results show good tracking performance of the estimated speed at both transient and steady states. The speed estimation errors are given in Fig. 12 for comparison. We can observe that the speed estimation error with the PI based ALO is more important than the speed estimation error with FL based ALO especially in the case when the induction motor is running at high speed and not loaded.

Fig. 11
figure 11

Step speed responses from low to rated speed (off load) using: a FL based ALO, b PI based ALO

Full size image
Fig. 12
figure 12

Speed estimation errors: a FL based ALO, b PI based ALO

Full size image

4.3 Low and Zero Speed Performance of the Drive

Sensorless speed control experimental results are presented here at − 100 rpm (reverse direction) then zero speed then 100 rpm reference. Figures 13 and 14 present the reference, the real and the estimated speeds using the FL based ALO and the PI based ALO, whereas Figs. 15 and 16 represent the speed estimation errors. It can be noticed that around zero speed the actual speed and the estimated speed does not fit the speed reference because of the reference voltages (used as inputs of the adaptive Luenberger observer) that deviate substantially from the actual motor voltages. This problem which remains a challenge is caused by the inverter dead time effects and inverter nonlinearities. However, the estimated speed using FL based LO remains close to the reference speed and less undulated at very low speeds compared to the one obtained with the PI based ALO.

Fig. 13
figure 13

Ramp speed responses (off load) using: a FL based ALO, b PI based ALO

Full size image
Fig. 14
figure 14

Step speed responses at low speeds (off load) using: a FL based ALO, b PI based ALO

Full size image
Fig. 15
figure 15

Speed estimation errors: a FL based ALO, b PI based ALO

Full size image
Fig. 16
figure 16

Speed estimation errors: a FL based ALO, b PI based ALO

Full size image

4.4 Effect of Loading

The induction motor is running at 700 rpm with 2.75 N.m load when step reference of 300 rpm is introduced. The loading performances of the sensorless drives are observed in Figs. 17, 18 and 19. The induction motor is operated at 1000 rpm when a load torque of 1 N.m is introduced at 13.5 s/11.5 s to reach 3.75 N.m then withdrawn at 20.5 s. As one can see in Fig. 17, the estimated speeds follow the real speed in both transient and steady states, the undershoot and the overshoot appear in the real and estimated speed during load torque introduction and removal. However, Fig. 17a shows that the rotor speed estimated with FL based ALO is less undulated than the one obtained with the PI based ALO.

Fig. 17
figure 17

Effect of step load torque variation on speed responses using: a FL based ALO, b PI based ALO

Full size image
Fig. 18
figure 18

Speed estimation errors: a FL based ALO, b PI based ALO

Full size image
Fig. 19
figure 19

Electromagnetic torque responses using: a FL based ALO, b PI based ALO

Full size image

As shown in Fig. 18, the speed estimation error remains negligible using FL based ALO. The profiles of the electromagnetic torques are shown in Fig. 19, as shown it is obvious the increase of the torque ripples with the PI based ALO.

4.5 Responses of the Estimated RTC Inverse and Stator Resistance

In the rest of the tests, the rotor speed, the inverse of the RTC and the stator resistance are estimated simultaneously. In order to observe the stator resistance effect on the estimated and the real speeds, three rheostats in parallel with three phase circuit breaker have been put in series with the IM stator resistances as shown in Figs. 7 and 8. The stator resistances value is increased sharply at 4 s by 5.5 Ω to reach 12 Ω and decreased sharply by 5.5 Ω after some few seconds. It can be noticed that the estimated resistance follows the real one as shown in Fig. 21.

The estimated RTC inverse is used as input of the adaptive fuzzy Luenberger observer for both rotor speed and stator resistance estimation according to the adaptive model equations (the same for the stator resistance and the rotor speed). From Eq. (11) and as illustrated in Fig. 3, the RTC inverse is also used in slip speed expression. Figure 22 shows then a good convergence of βr.

On the other hand, as observed in Figs. 20a, 21a, 22a, the experimental results clearly highlight and demonstrate the efficiency of the proposed adaptive fuzzy Luenberger observer compared to the PI based ALO.

Fig. 20
figure 20

Speed responses in the presence of stator resistance and RTC inverse estimation (off load) using: a FL based ALO, b PI based ALO

Full size image
Fig. 21
figure 21

Responses of the estimated stator resistance (off load) using: a FL based ALO, b PI based ALO

Full size image
Fig. 22
figure 22

Responses of the estimated inverses of the RTC (off load) using: a FL based ALO, b PI based ALO

Full size image

We can observe that the FL based ALO has brought significant improvement to the PI based ALO by reducing clearly oscillations and ripples in all estimated quantities. This improvement is obtained even when the rotor speed and the other parameters are estimated simultaneously in the presence of stator resistance variation (when its value has increased by more than 25% from its nominal value).

4.6 Parameters Identification at Very Low Speeds

The motor speed is changed from 45 rpm to − 45 rpm then from − 45 rpm to 45 rpm as shown in Fig. 23. The test objective is to show performances of the proposed sensorless drive with parallel parameters identification at very low speeds in both directions of rotation.

Fig. 23
figure 23

Speed responses at very low speeds (off load) using: a FL based ALO, b PI based ALO

Full size image

In particular, Figs. 23 and 24 show very satisfying performances obtained at very low speeds with no-load torque since the effect of the inverter nonlinearities has been eliminated using FL based ALO.

Fig. 24
figure 24

Speed estimation errors: a FL based ALO, b PI based ALO

Full size image

Furthermore, the experimental results show that the estimated parameters obtained with FL based ALO are slightly affected by the speed variation compared to the ones obtained with the PI based ALO as shown in Figs. 25b, 26b, especially at zero crossing (at 2.5 s and 13 s).

Fig. 25
figure 25

Responses of the estimated stator resistance at very low speeds (off load) using: a FL based ALO, b PI based ALO

Full size image
Fig. 26
figure 26

Responses of the estimated inverses of the RTC at very low speeds (off load) using: a FL based ALO, b PI based ALO

Full size image

4.7 Parameters Identification in the Presence of Load Torque Variation

The motor speed is running at 300 rpm as shown in Fig. 27 and a load torque of 0,5 N.m is introduced at 12 s to achieve 1 N.m. The test objective is to show performances of the proposed sensorless drive with online parameters estimation in the presence of load torque and stator resistance variations. The stator resistance value is increased at 4 s by 5.5 Ω to reach 12 Ω and decreased by 5.5 Ω after some few seconds.

Fig. 27
figure 27

Speed responses in the presence of stator resistance and load torque variations using: a FL based ALO, b PI based ALO

Full size image

Figures 28, 29 and 30 show very satisfying performances using FL based ALO. Furthermore, the experimental results show that the estimated speed and stator resistance obtained with FL based ALO are slightly affected by the load torque variation compared to the ones obtained with the PI based ALO.

Fig. 28
figure 28

Speed estimation errors: a FL based ALO, b PI based ALO

Full size image
Fig. 29
figure 29

Electromagnetic torque responses using: a FL based ALO, b PI based ALO

Full size image
Fig. 30
figure 30

Responses of the estimated stator resistance in the presence of load torque variations using: a FL based ALO, b PI based ALO

Full size image

With regard to the electromagnetic torque, a comparison between the two developed electromagnetic torques in Fig. 29 shows a strong reduction of the torque ripples using the FL based ALO with respect to the PI based ALO.

Finally, the experimental results has shown high improvements achieved by this proposed observer. The consequent main advantage is obviously the reduction of ripples in the estimated speed and/or the electromagnetic torque and the preservation of all the advantages of the PI based ALO namely stability in all speed ranges and dynamic performances.

5 Conclusion

This paper proposes an improved speed estimation method for sensorless induction motor drive using an improved adaptive Luenberger observer with parameters identification using fuzzy logic techniques.

The stability of the proposed sensorless indirect field oriented control with stator resistance and rotor time constant tuning has been demonstrated by Lyapunov criterion and its validity has been proved by experimentation applied to an 1 kW squirrel-cage induction motor for a wide range of speed under load and no load.

The experimental results highlight clearly the effectiveness of the proposed system in terms of dynamic performance at high and very low speed regions during transient and steady states and its robustness against IM parameters uncertainties.

Further research work includes the implementation of the proposed technique in another powerful and less expensive DSP processor for industrial applications.