1 Introduction

A vibration signal of rotating machines contains background noise. Hence, fault signature of the rotating machines can disappear. These problems get severe when the fault signature is incipient. As a result, to reduce the noise from the faulty vibration is important. Many noise reduction techniques have been proposed such as wavelet de-noising [1], adaptive filter [2, 3], and Weiner filter. Since the vibration signals of rotating machines are not stationary due to its speed variation, it is important to remove the effect of speed variation. To remove the speed variation from faulty vibration signal of the rotating machine, order tracking is commonly used [4].

Fault signature is detected by analyzing the spectrum of the faulty vibration signal. Square envelope analysis and Hilbert transform are well-known methods for spectrum. Envelope analysis shows better performance over Hilbert transformation because its computational cost is lower and bandpass filtering is not required in envelope analysis. All magnitude of the fault signature is not dangerous for the breakdown of the machine, i.e., machine can sustain with some faulty condition. However, this faulty condition leads to the breakdown of rotating machines. Therefore, it is important to know the time when faults are getting dangerous for the breakdown. But, changes in fault magnitude are not linear. At the initial stage, magnitude of the fault changes slowly and later, it changes rapidly. Therefore, it is also important to know the rate of change of fault magnitude to determine the fault severity of rotating machines. The aim of this paper is to determine the fault signatures to identify the faulty condition of the rotating machines.

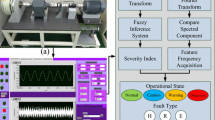
In this paper, fault detection and criticality classification (FDCC) method is proposed based on an adaptive filter, order tracking and fuzzy logic. The proposed FDCC method not only detects the faults of rotating machines but also classifies the faults severity. At first, the noises, as well as artificial artifacts, are reduced from the faulty vibration signal of the rotating machine using the adaptive filter. After that, computed order tracking is used to minimize the speed variation of the rotating machine. Then, fault signature is detected by envelope analysis. Finally, fuzzy logic is to classify the fault severity to determine the status of the machines.

2 Proposed fault detection and criticality classification method


Figure 1 represents the proposed fault detection and criticality classification (FDCC) method. At first, adaptive filter is used to minimize the noise since faulty signals can be severely affected by noise. After removing the noises from the faulty signal, order tracking is applied to remove the speed fluctuation. Then, the fault signature is determined by the envelop analysis. Finally, fault criticality classification is done by fuzzy logic to identify the status of the machine. The details procedures of FDCC are explained below:

Fig. 1
figure 1

Block diagram of the proposed FDCC approach

Full size image

Step 1: Noise reduction by adaptive filter


As the rotating machine’s fault signals are very weak and masked by the strong noise as well as signals from other rotating parts, de-noising and extracting the useful feature are crucial to fault detection. Therefore, the adaptive filter is used in this paper to reduce the noises from a faulty vibration signal.

An adaptive filter iteratively models the relationship between the input signals and output signals. Main feature of the adaptive filter is that it can adjust the filter coefficients by itself [3]. Generally adaptive filter is categorized into RMS and LMS. In this work, LMS filter is considered. The filter output is described as

$$y\left( n \right) = W_{n}^{\text{T}}$$
(1)

where LMS algorithm updates the weights in cooperates with error function during the nth iteration as follows:

$$W_{n + 1} = W_{n} + \delta e\left( n \right)X\left( n \right)$$
(2)

Here, e(n) is an error signal, X(n) denotes filter input vector, and δ is the step size of the filter that controls the convergence rate. The error signal can be represented as:

$$e\left( n \right) = d\left( n \right) - y\left( n \right)$$
(3)

X(n) includes the tap inputs \(x\left( n \right), x\left( {n - 1} \right), \ldots ,x\left( {n - M + 1} \right)\), wn is the weight vector \(w_{n} \left( 0 \right), w_{n} \left( 1 \right), \ldots , w_{n} \left( {M - 1} \right)\), and [*]T denotes transpose operation. The filter is a FIR filter of length M and the MSE function of the system, J(n) [3],

$$J\left( n \right) = E\left[ {d^{2} \left( n \right)} \right] - 2W_{n}^{\text{T}} r_{dx} + W_{n}^{\text{T}} R_{xx} \left( n \right)W_{n} ,$$
(4)

where \(R_{xx} \left( n \right) = E\left[ {X\left( n \right)X^{\text{T}} \left( n \right)} \right]\) and \(r_{dx} \left( n \right) = E\left[ {X\left( n \right)d\left( n \right)} \right]\).


The optimum filter coefficients, \(W_{{n_{\text{opt}} }}\), can be defined as

$$W_{{n_{\text{opt}} }} = R_{xx}^{ - 1} \left( n \right)r_{dx} \left( n \right).$$
(5)

Step 2: Order tracking


Since the rotating machine (even constant speed machine) has small speed variation, fault frequency has variation. To reduce this variation, order tracking is used. Order tracking considers order as frequency instead of absolute frequencies. Many effective order tracking methods have been proposed by researcher [4,5,6]. However, computed order tracking (COT) method is commonly used in rotating machine fault detection [5, 6]. COT can be described within three basic steps [6]. Both tacho pulses and vibration signal are sampled at constant increments of time, Δt in the first step. In the second step, determine the shaft angle corresponding to constant sample and the corresponding amplitudes of the faulty vibration signal are calculated in the third step. This step is explained as follow:

For three consecutive pulse signals, shaft angles,

$$\theta \left( t \right) = b_{o} + b_{1} t + b_{2} t^{2} .$$
(6)

If one keyphasor is considered on the shaft, then

$$\theta \left( {t_{1} } \right) = 0,\quad \theta \left( {t_{2} } \right) = 2\pi \quad {\text{and}}\quad \theta \left( {t_{3} } \right) = 4\pi .$$

Using these value, from Eq. 6,

$$\begin{array}{*{20}l} {0 = b_{o} + b_{1} t_{1} + b_{2} t_{1}^{2} } \hfill \\ {2\pi = b_{o} + b_{1} t_{2} + b_{2} t_{2}^{2} } \hfill \\ {4\pi = b_{o} + b_{1} t_{3} + b_{2} t_{3}^{2} } \hfill \\ \end{array} .$$
(7)

The b0, b1, and b1 can be determined from above equations. Now applying this value in Eq. (6),

$$t_{j} = \frac{{ - b_{1} + \sqrt {b_{1}^{2} - 4b_{2} \left( {\theta_{j} - b_{0} } \right)} }}{{2b_{2} }}$$
(8)

Using this resample times, amplitudes of the signal are determined in the third step.


Step 3: Envelope analysis


Envelope analysis is the most popular approach to recover modulating signal (i.e., fault signals) from modulated signal effectively. It has been successfully used for fault detection, specially bearing fault detection [7, 8]. Envelope analysis can justify the cyclostationary analysis of rolling element bearing properly. Moreover, it can be used to obtain the modulating signals (i.e., fault signals) from modulated signal with high accuracy for increasing the SNR of results [9].

To perform the envelope analysis, vibration signal of faulty machines is filtered using bandpass filter around the mechanical resonance, which serves as a carrier for the modulated signal. And then, this bandpass filtered signal is demodulated to separate the faulty signal from the modulated signal. Example of envelope analysis is shown in Fig. 2. The red line of Fig. 2 indicates the upper envelope (Eupp), and green line is lower envelope (Elow). Both modulating signal and carrier signal can be calculated (when modulation index is less than 1) using the following equations:

Fig. 2
figure 2

Example of envelope analysis [10]

Full size image

Modulating signal

$$m\left( t \right) = E_{\text{upp}} - E_{\text{low}}$$
(9)

And carrier signal

$$C\left( t \right) = E_{\text{upp}} + E_{\text{low}} ,$$
(10)

Envelope analysis shows the better performance over Hilbert transformation because its computational cost is lower and bandpass filtering is not required in envelope analysis. But, square envelope gives more advantages than the envelope itself.


Step 4: Fault detection


The spectrum of the faulty vibration signal often contains fault signatures. After square envelope analysis, the magnitude of the fault is determined. Initially, fault magnitudes are very small. This small magnitude may not dangerous for the rotating machines. However, small faults magnitude leads to the breakdown of the machines. Therefore, it is important to know the rate of change of fault magnitude to prevent the breakdown of the machines. In the next step, classification of fault is done using fuzzy logic.


Step 5: Criticality classification using fuzzy logic


All magnitude is not dangerous for the breakdown of the machine, i.e., machine can sustain at some degree of faults with certain magnitude. Therefore, it is important to know the time when faults are getting dangerous for the breakdown. But, changes in fault magnitude are not linear. Therefore, it is also important to know the rate of change of fault magnitude to determine the fault severity of rotating machines.

Fuzzy logic is used to determine the fault severity of rotating machines. Nowadays the fuzzy expert system is widely used for decision making in many applications [11, 12]. The fuzzy logic controller has four significant parts: fuzzification (crisp value to fuzzy), rule base (input–output relationship), inference engine (Mamdani or TS method) and defuzzification (fuzzy to crisp value). To design input and output membership function, Gaussian membership functions are applied in this method. A Gaussian membership function can be defined as follows:

$${\text{gaussian}}\left( {x; c,\sigma } \right) = e^{{\frac{1}{2}\left( {\frac{x - c}{\sigma }} \right)^{2} }}$$
(11)

Here c represents the center and σ indicates the width of the membership function. The Mamdani method is used as the inference system in the proposed method. For the defuzzification process, the centroid method is used.

To determine the severity of faults, two inputs and one output are considered in the fuzzy system. One input named “magnitude” represents the amplitude of fault, and another input named “change” indicates the rate of change of fault amplitude. The input magnitude has four membership functions: very low (VL), low (L), medium (M), and high (H), while input change also has four memberships function: very small (VS), small (S), medium (M), large (L). Figures 3 and 4 represent the input variables of magnitude and change, respectively. The output named “severity” provides information about the status of faults, i.e., breakdown information. Like the input variables, output variables severity consists of four membership functions: (NR), slightly flawed (SF), medium flawed (MF), seriously flawed (SEF) which are shown in Fig. 5.

Fig. 3
figure 3

Membership functions of input ‘Magnitude’

Full size image
Fig. 4
figure 4

Membership functions of input ‘Change’

Full size image
Fig. 5
figure 5

Membership functions of input ‘Severity’

Full size image

The severity of the faults not only depends on the fault magnitude but also the rate of change of faults magnitude. To determine the fault severity, the relationship between input and output is given in Table 1.

Table 1 Relationship between fuzzy inputs and output
Full size table

To determine the fault severity precisely, 16 rules are designed for the fuzzy system. The rules are given below:

  1. 1.

    If (Magnitude is VL) and (Change is VS), then (Severity is NR) (1)

  2. 2.

    If (Magnitude is VL) and (Change is S), then (Severity is NR) (1)

  3. 3.

    If (Magnitude is VL) and (Change is M), then (Severity is SF) (1)

  4. 4.

    If (Magnitude is L) and (Change is L), then (Severity is MF) (1)

  5. 5.

    If (Magnitude is L) and (Change is VS), then (Severity is NR) (1)

  6. 6.

    If (Magnitude is L) and (Change is S), then (Severity is SF) (1)

  7. 7.

    If (Magnitude is L) and (Change is M), then (Severity is MF) (1)

  8. 8.

    If (Magnitude is L) and (Change is L), then (Severity is MF) (1)

  9. 9.

    If (Magnitude is M) and (Change is VS), then (Severity is SF) (1)

  10. 10.

    If (Magnitude is M) and (Change is S), then (Severity is MF) (1)

  11. 11.

    If (Magnitude is M) and (Change is M), then (Severity is MF) (1)

  12. 12.

    If (Magnitude is M) and (Change is L), then (Severity is SEF) (1)

  13. 13.

    If (Magnitude is H) and (Change is VS), then (Severity is SF) (1)

  14. 14.

    If (Magnitude is H) and (Change is S), then (Severity is MF) (1)

  15. 15.

    If (Magnitude is H) and (Change is M), then (Severity is SEF) (1)

  16. 16.

    If (Magnitude is H) and (Change is L), then (Severity is SEF) (1)

3 Performance analysis of proposed FDCC

3.1 Simulation model

To evaluate proposed FDCC method, faulty rolling element bearing signals are considered in this paper. In the bearing, when a single point defect occurs, intense vibrations are generated accordingly. The fundamental frequency of these vibrations of the rotating machine is equivalent to the rate at which components move over the defect. As a result, unique frequency components will generate for bearing faults of the inner/outer raceway or rolling elements. These unique frequencies can be described as follows [1]:

Ball pass frequency of inner race (BPFI)

$${\text{BPFI}} = \frac{{N_{\text{b}} }}{2}\left( {\frac{{N_{\text{s}} }}{60}} \right)\left( {1 + \frac{{D_{\text{b}} \cos \theta }}{{D_{\text{p}} }}} \right)$$
(12)

Ball pass frequency of outer race (BPFO)

$${\text{BPFO}} = \frac{{N_{\text{b}} }}{2}\left( {\frac{{N_{\text{s}} }}{60}} \right)\left( {1 - \frac{{D_{\text{b}} \cos \theta }}{{D_{\text{p}} }}} \right)$$
(13)

Ball spin frequency (BSF)

$${\text{BSF}} = \frac{{N_{\text{b}} }}{2}\left( {\frac{{N_{\text{s}} }}{60}} \right)\left( {1 - \left( {\frac{{D_{\text{b}} \cos \theta }}{{D_{\text{p}} }}} \right)^{2} } \right)$$
(14)

where Nb is the total number of rolling elements, Ns is the rpm of the shaft, θ is the contact angle of the balls on the races, and Db and Dp are the ball diameter and the pitch diameter, respectively. Computer simulation is performed to validate the proposed methodology. In this paper, the fault signature is BPFO and bearing modulation model is considered as follow: [7]

$$s\left( t \right) = A\left( {1 + \mathop \sum \limits_{1}^{k} r_{1} \sin \left( {2\pi f_{1} t + \theta_{1} } \right)} \right)\sin \left( {2\pi f_{n} t + \varphi } \right) + n\left( t \right),$$
(15)

where f1 is the frequency of faulty signal (modulating signal) and fn is the natural frequency (Carrier frequency), respectively.

3.2 Fault detection

Figure 6 indicates the faulty signal for the rolling element bearing. Faults signature is not visible in this figure. The frequency spectrum of the faulty signal is presented in Fig. 7. This spectrum also does not provide the fault signature. After applying the proposed FDCC method, the fault signature is visible (circle) in Fig. 8. In this figure, bearing outer race fault signature is visible at 20 Hz and the magnitude of the fault signature is 1.2. This fault signature is not constant, and it will change with operating time that would lead to the breakdown of the machines.

Fig. 6
figure 6

Faulty signal of bearing

Full size image
Fig. 7
figure 7

Frequency spectrum of faulty signal

Full size image
Fig. 8
figure 8

Envelope analysis of faulty signal

Full size image

Figures 9, 10, 11 and 12 show the fault signatures with different fault magnitude 1.375, 1.638, 1.841 and 1.923, respectively. All of these fault signatures are not dangerous for the machines. To find the severity of the faults, fuzzy logic is used to classify the fault severity.

Fig. 9
figure 9

Envelope analysis of faulty signal (Magnitude = 1.375)

Full size image
Fig. 10
figure 10

Envelope analysis of faulty signal (Magnitude = 1.638)

Full size image
Fig. 11
figure 11

Envelope analysis of faulty signal (Magnitude = 1.814)

Full size image
Fig. 12
figure 12

Envelope analysis of faulty signal (Magnitude = 1.923)

Full size image

3.3 Severity classification

From the previous section, it is seen that fault magnitude is changed with operating time. Up to a certain value of fault magnitude and rate of change of fault magnitude, the machine can operate safely. Therefore, it is necessary to find the fault severity in order to prevent breakdown. Since this relation is not linear, fuzzy logic is used to determine the severity of the fault. Figure 13 represents the input–output relation of the proposed fuzzy logic. Fault severity based on fault magnitude and rate of change of fault magnitude can be found very easily from Fig. 14. According to fault severity, the operator easily can operate the machine without any breakdown. These could save not only reduce the production cost but also save the working time as well as human causality.

Fig. 13
figure 13

Input and output relationship

Full size image
Fig. 14
figure 14

Rule view of proposed fuzzy logic classifier

Full size image

4 Conclusion

To detect faults and classify the severity of the faults, the fuzzy-based FDCC approach is proposed in this paper. In this method, after reducing the noise from the faulty vibration signal using adaptive filter, envelope analysis is used to detect the faults. Order tracking is also used to remove the speed variation of the rotating machine. Classification of the fault severity is done by fuzzy logic. Based on the fault severity, the fault elements can be replaced using this FDCC method before breakdown. Therefore, proposed FDCC methods save rotating machinery from the breakdown. These could help not only reduce the industrial production cost but also save the working time as well as human causality. The effectiveness of the proposed FDCC method is measured by the simulation model. In this method, the fixed step size of the adaptive filter is used. The performance of the adaptive filter should be investigated by using real data with variable step size.