Introduction

Unlike ordinary machines, high-speed rotary machines work in harsh environments and under high stress, which results in cyclic fatigue, creep, and corrosion. All these physical phenomena lead to generation of fatigue cracks, which can severely damage machine components or even lead to catastrophic failure. In this regard, many studies have been made on rotator systems. In particular, many studies have been conducted in terms of the method of making a mathematical model of the Jeffcott rotor system and the vibration analysis method of the rotor system using the finite element method. Many advances have been made in the establishment of the mathematical model of the Jeffcott rotor system. Zalik [1] studied the properties of the solutions of the Jeffcott equations with deadband and the method making nonlinear rotordynamics equation. Joaquín Campos et al. [2] studied a simple model capable of allowing visualization of the parameters and problematic aspects associated with a Jeffecott rotor using bond graphs. Wagner et al. [3] examined how the natural frequencies and modal damping ratios of a shaft/rotor system are affected by changes in lubricant viscosity and bearing clearance. The analysis considers a uniform elastic shaft with a single rigid rotor mounted away from mid-span and supported by fully cavitated, T-film, short-length, plain journal bearings. Yao et al. [4] is introduced a concept of micro-relative displacement to describe the relative motion between each part of the planetary gear system, thus the positive semidefinite gear system is transformed into a positive definite system. By using the finite element method, the dynamic model of the whole ball bearing-rotor system is proposed by integrating the rigid body motion and the elastic vibration of the rotor [5]. A mathematical model of a lightweight flexible rotor disk bearing system with geometric eccentricity and mass imbalance was created. This mathematical model includes a bidirectional flexible shaft characterized by nonlinear curvature and gyroscopic effect, geometric eccentricity, a rigid disk crooked with unbalance mass, and nonlinear flexible bearings [6]. Lu et al. [7] formulated the kinematics equation of the system, taking into account the unbalance excitations of the two rotors, vertical constant forces acting on the rotor system and the gravities. A dynamic model of a rotor-blade system has established considering the effect of nonlinear supports at both ends, and in the proposed model, the shaft is modeled as a rotating beam where the gyroscopic effect is considered, while the shear deformation is ignored [8]. Yan et al. [9] formulated a novel fractional-order mathematical model of the rotor-bearing-seal system is established from the view of engineering applications by using the finite element method. Luo et al. [10] studied an improved transfer-matrix method (TMM) for investigating the steady-state response of complex rotor-bearing systems based on the mathematical model of the system. The method of constructing a dynamic model in a rotor system with cracks was described [11, 12]. The general contents of the nonlinear vibration, the method making the motion equation of the cracked rotor and the method of solving the nonlinear vibration were studied and analysed [13]. In the spring-mass-coupled system, the vibration analysis method and the calculation method of the critical speed were specifically mentioned [14]. In this paper, a model for the dynamics of fast rotating, elastic beams supported in hydrodynamic bearings is derived and its vibration behavior analyzed. The continuous rotor is modelled using Euler–Bernoulli beam theory under the inclusion of rotatory inertia and gyroscopic effects [15]. The natural frequency analysis and calculation method of the rotating machinery considering the gyroscopic effect, and the imbalance and balance were studied [16]. A rotordynamic analysis of a large turbocompressor that models both the casing and supports along with the rotor-bearing system was performed. A 3D finite element model of the casing captures the intricate details of the casing and support structure [17]. Bajpai et al. [18] studied of natural frequency characteristics of structural steel and alloy 6061 system composed of various material by using ANSYS program. Meshing method and modelling of a Simple 3D Cantilever Beam Using SOLID Elements is specifically mentioned [19]. In the rotary system considering the gyroscopic effect and whirl, the method of modelling and analyzing the system using the finite element method was mentioned [20]. Using ANSYS Workbench, the structure modelling, dynamic analysis, and vibration analysis method were analysed [21]. In the previous studies, the dynamic modelling and vibration analysis of the rotor system with cracks were widely discussed with many methods. In the dynamic modelling, however, no specific analysis has been made on the modelling methods of with and without cracks, and few have been made on the basis of this model to interpret the natural frequency problems of the rotor system in the two cases of cracks and without cracks. In this paper, therefore, the method of creating the dynamic equation of the rotor system with and without cracks by using the finite element method and the Lagrange equation, the method of calculating the critical speed, and How the natural frequency of the rotor system changes according to the position of the crack and the change of the non-dimensional crack depth and influence of eccentricity on the rotor system was analyzed in detail.

Mathematical Modelling of the Rotor-Disc-Bearing System

System Equation of Motion Without Crack

Motion Equation of Element

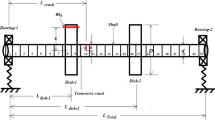
The rotor system is generally composed of a rigid disk, a rotor shaft, and a bearing. Their motion equations will be established respectively and further assembled to form the entire system equation (Fig. 1).

Motion Equation of Shaft Element

Figure 2 is an elastic axial segment whose local nodes are numbered as 1 and 2.

Fig.1
figure 1

Rotor-disc-bearing system

Full size image
Fig.2
figure 2

Elastic axial segment

Full size image

The generalized coordinate of this element is the displacement of the nodes at both ends, that is:

$$\left\{\begin{array}{l}\left\{{u}_{1z}\right\}={\left[{x}_{A},{\theta }_{yA},{x}_{B},{\theta }_{yB}\right]}^{T}\\ \left\{{u}_{2z}\right\}={\left[{y}_{A},{-\theta }_{xA},{y}_{B},{-\theta }_{xB}\right]}^{T}\end{array}\right.$$
(1)

In any section within the element, the displacement x,\({\theta }_{y}\), y,\({\theta }_{x}\) is a function of position s and time t. By using the displacement interpolation function and the displacement of the node of the element, the displacement x,\({\theta }_{y}\), y,\({\theta }_{x}\) can be expressed as:

$$\left\{\begin{array}{c}x\left(s,t\right)=\left[N\right]\left\{{u}_{1s}\right\}\\ y\left(s,t\right)=\left[N\right]\left\{{u}_{2s}\right\}\\ {\theta }_{y}=\left[{N}^{^{\prime}}\right]\left\{{u}_{1s}\right\}\\ -{\theta }_{x}=\left[{N}^{^{\prime}}\right]\left\{{u}_{2s}\right\}\end{array}\right.$$
(2)

where \(\left[N\right]\) is the undetermined displacement interpolation function matrix or shape function matrix.

$$\left[N\right]=\left[{N}_{1}\left(z\right),{N}_{2}\left(z\right),{N}_{3}\left(z\right),{N}_{4}\left(z\right)\right]$$
(3)

Substituting Eq. (3) into the first term and the second term of Eq. (2) is as follows:

$$\left\{\begin{array}{l}x\left(z,t\right)={N}_{1}\left(z\right){x}_{A}\left(t\right)+{N}_{2}\left(z\right){\theta }_{yA}\left(t\right)+{N}_{3}\left(z\right){x}_{B}\left(t\right)+{N}_{4}\left(z\right){\theta }_{yB}\left(t\right)\\ {\theta }_{y}\left(z,t\right)=\frac{\partial x}{\partial z}={N}_{1}^{^{\prime}}\left(z\right){x}_{A}\left(t\right)+{N}_{2}^{^{\prime}}\left(z\right){\theta }_{yA}\left(t\right)+{N}_{3}^{^{\prime}}\left(z\right){x}_{B}\left(t\right)+{N}_{4}^{^{\prime}}\left(z\right){\theta }_{yB}\left(t\right)\end{array}\right.$$
(4)

where \({N}_{i}^{^{\prime}}\)(\(i\)=1, 2, 3, 4) is the derivative of the function with respect to z.

The endpoint conditions of the axial segment element are as follows:

$$\left\{\begin{array}{c}x\left(0,t\right)={x}_{A}\left(t\right)\\ x\left(l,t\right)={x}_{B}\left(t\right)\\ {x}^{^{\prime}}\left(0,t\right)={\theta }_{yA}\left(t\right)\\ {x}^{^{\prime}}\left(l,t\right)={\theta }_{yB}\left(t\right)\end{array}\right.$$
(5)

From Eq. (4) and (5), each interpolation function should be as follows:

$$\left\{\begin{array}{c}{N}_{1}\left(0\right)=1;{N}_{1}^{\prime}(0)=0;{N}_{1}(l)=0;{N}_{1}^{\prime}(l)=0\\ {N}_{2}(0)=0;{N}_{2}^{\prime}(0)=1;{N}_{2}\left(l\right)=0;{N}_{2}^{\prime}\left(l\right)=0\\ {N}_{3}\left(0\right)=0;{N}_{3}^{\prime}\left(0\right)=0;{N}_{3}\left(l\right)=1;{N}_{3}^{\prime}\left(l\right)=0\\ {N}_{4}\left(0\right)=0;{N}_{4}^{\prime}\left(0\right)=0;{N}_{4}\left(l\right)=0;{N}_{4}^{\prime}\left(l\right)=1\end{array}\right.$$
(6)

Because each interpolation function has four endpoint conditions, it can be assumed to be a cubic polynomial of z.

$${N}_{1z}={a}_{0}+{a}_{1}z+{a}_{2}{z}^{2}+{a}_{3}{z}^{3}$$
(7)

Substituting Eq. (7) into Eq. (6), the constant \({a}_{i}\)(\(i\)=1, 2, 3, 4) can be determined below.

$${N}_{1}\left(\text{z}\right)=1-3{\left(\frac{z}{l}\right)}^{2}+2{\left(\frac{z}{l}\right)}^{3}$$
$${N}_{2}\left(\text{z}\right)=l\left[\frac{z}{l}-2{\left(\frac{z}{l}\right)}^{2}+{\left(\frac{z}{l}\right)}^{3}\right]$$
$${N}_{3}\left(\text{z}\right)=3{\left(\frac{z}{l}\right)}^{2}-2{\left(\frac{z}{l}\right)}^{3}$$
$${N}_{4}\left(\text{z}\right)=l\left[-{\left(\frac{z}{l}\right)}^{2}+{\left(\frac{z}{l}\right)}^{3}\right]$$

For shaft segment with axisymmetric cross-sections, similarly:

$$\text{y}\left(z,t\right)=\left[N\right]\left\{{u}_{2z}\right\}$$
(8)

Based on the above results:

$$\left\{\begin{array}{c}x=\left[N\right]\left\{{u}_{1z}\right\};{\theta }_{y}=\frac{\partial x}{\partial z}=\left[{N}^{\prime}\right]\left\{{u}_{1z}\right\}\\ y=\left[N\right]\left\{{u}_{2z}\right\};{-\theta }_{x}=\frac{\partial y}{\partial z}=\left[{N}^{{{\prime}}}\right]\left\{{u}_{2z}\right\}\end{array}\right.$$
(9)

The kinetic energy and flexural elastic potential energy of the element can also be expressed as the function of node displacement and node velocity.

$$\text{d}{T}_{z}=\frac{1}{2}{\left\{\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right\}}^{T}\left[\begin{array}{cc}\mu & 0\\ 0& \mu \end{array}\right]\left\{\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right\}dz+\frac{1}{2}\left\{\begin{array}{c}{\theta }_{y}\\ -{\theta }_{x}\end{array}\right\}\left[\begin{array}{cc}{j}_{d}& 0\\ 0& {j}_{d}\end{array}\right]\left\{\begin{array}{c}\dot{{\theta }_{y}}\\ \dot{{-\theta }_{x}}\end{array}\right\}+\Omega {\left\{\begin{array}{c}\dot{x}\\ {\dot{\theta }}_{y}\end{array}\right\}}^{T}\left[\begin{array}{cc}0& 0\\ 0& {j}_{p}\end{array}\right]\left\{\begin{array}{c}y\\ -{\theta }_{x}\end{array}\right\}dz+\frac{1}{2}{j}_{p}{\Omega }^{2}dz$$
(10)

Taking the derivative of Eq. (6) with respect to time and substituting it into for Eq. (10) is as follows:

$$\eqalign{& {d}{T_z} = \frac{1}{2}{\left\{ {{{\dot u}_{1z}}} \right\}^T}\left( {\mu {{\left[ N \right]}^T}\left[ N \right] + {j_d}{{\left[ {N'} \right]}^T}\left[ {N'} \right]} \right)\left\{ {{{\dot u}_{1z}}} \right\}dz + \frac{1}{2}{\left\{ {{{\dot u}_{2z}}} \right\}^T}\left( {\mu {{\left[ N \right]}^T}\left[ N \right] + {j_d}{{\left[ {N'} \right]}^T}\left[ {N'} \right]} \right)\left\{ {{{\dot u}_{2z}}} \right\}dz \\& + {j_p}{\Omega }{\left\{ {{{\dot u}_{1z}}} \right\}^T}{\left[ {N'} \right]^T}\left[ {N'} \right]\left\{ {{U_{2z}}} \right\}dz + \frac{1}{2}{j_p}{\Omega dz} \cr}$$
(11)

where z is the axial distance of nodal point A. The thickness of a microelement is dz, and u, \({j}_{d}\) and \({j}_{p}\) represent the mass, diameter, and pole moment of inertia per unit length of the axial segment, respectively. Ω is the rotational speed.

The elastic potential energy of the microelement is:

$${\text{dV}}_{z} = \frac{1}{2}EI\left\{ {_{{y^{\prime\prime}}}^{{x^{\prime\prime}}} } \right\}^{T} \left\{ {_{{y^{\prime\prime}}}^{{x^{\prime\prime}}} } \right\}^{T} dz\; = \;\frac{1}{2}\left( {\left\{ {u_{{1z}} } \right\}^{T} \left[ {N^{\prime\prime}} \right]^{T} \left[ {N^{\prime\prime}} \right]\left\{ {u_{{1z}} } \right\}\; + \;\left\{ {u_{{2z}} } \right\}^{T} \left[ {N^{\prime\prime}} \right]^{T} \left[ {N^{\prime\prime}} \right]\left\{ {u_{{2z}} } \right\}} \right)$$
(12)

For the circular section shaft with long \(l\) and radius r, the kinetic energy and potential energy of the element can be obtained by integrating the above two formulas along the full length of the element.

$${T}_{z}=\frac{1}{2}{\left\{{\dot{u}}_{1z}\right\}}^{T}\left(\left[{M}_{\text{zT}}\right]+\left[{M}_{\text{zR}}\right]\right)\left\{{\dot{u}}_{1z}\right\}+\frac{1}{2}{\left\{{\dot{u}}_{2z}\right\}}^{T}\left(\left[{M}_{\text{zT}}\right]+\left[{M}_{\text{zR}}\right]\right)\left\{{\dot{u}}_{2z}\right\}+\Omega {\left\{{\dot{u}}_{1z}\right\}}^{T}\left[{J}_{z}\right]\left\{{u}_{2z}\right\}+\frac{1}{2}{J}_{pz}{\Omega }^{2}$$
(13)
$${\text{V}}_{z}=\frac{1}{2}{\left\{{u}_{1z}\right\}}^{T}\left[{K}_{z}\right]\left\{{u}_{1z}\right\}+{\frac{1}{2}\left\{{u}_{2z}\right\}}^{T}\left[{K}_{z}\right]\left\{{u}_{2z}\right\}$$
(14)

where

$${J}_{\text{pz}}={j}_{\text{pz}}l$$
$$[{M_z}T] = \smallint_o^l\mu {[N]^T}[N]dz[{M_z}T]:element^{\prime}s\,moving\,inertia\,matrix$$
$$[{M_z}R] = \smallint_0^l{j_d}{[N^{\prime}]^T}[N^{\prime}]dz\quad [{M_z}R]:rotational\,inertia\,matrix$$
$$\left[ {{{\text{G}}_z}} \right] = {\Omega }\left[ {J_z} \right]: \, \left[ {{{\text{G}}_z}} \right]:rotation \, matrix,$$
$$\left[{J}_{z}\right]={\int }_{0}^{l}{j}_{p}{\left[N^{{\prime}}\right]}^{T}\left[N^{\prime}\right]\,{\rm d}z$$
$$[{K_z}] = \smallint_0^lEI{[N^{\prime\prime}]^T}[N^{\prime\prime}]dz[{K_z}]:stiffness\,matrix,$$

The motion equation of the axial segment element can be obtained from the Lagrange equation.

$$\left\{\begin{array}{c}\left[{\text{M}}_{\text{z}}\right]\left\{{\ddot{u}}_{1z}\right\}+\Omega \left[{J}_{\text{z}}\right]\left\{{\dot{u}}_{2z}\right\}+\left[{K}_{\text{z}}\right]\left\{{u}_{1z}\right\}=\left\{{Q}_{1z}\right\}\\ \left[{\text{M}}_{\text{z}}\right]\left\{{\ddot{u}}_{2z}\right\}-\Omega \left[{J}_{\text{z}}\right]\left\{{\dot{u}}_{1z}\right\}+\left[{K}_{\text{z}}\right]\left\{{u}_{2z}\right\}=\left\{{Q}_{2z}\right\}\end{array}\right.$$
(15)

where \({Q}_{1z}\),\({Q}_{2z}\) correspond to the generalized force.

\({\text{M}}_{\text{z}}\) is \(\text{sum of }\left[{M}_{zT}\right] \text{and }\left[{M}_{zR}\right]\)

The Equation of Motion of a Rigid Disk

Suppose the mass of the rigid disk, the axial area moment of inertia, and the polar moment of inertia are m, \({J}_{d}\), and \({J}_{p}\) respectively, and the generalized coordinate of the rigid disk is expressed by the displacement vectors of the axis node, which are \(\left\{{u}_{1d}\right\}={\left[x,{\theta }_{y}\right]}^{T}\) and \(\left\{{u}_{2d}\right\}={\left[y,{-\theta }_{x}\right]}^{T}\), respectively.

Assuming that the disk axis coincides with the center of gravity, its kinetic energy is expressed as Eq. 16:

$${T}_{d}=\frac{1}{2}{\left\{\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right\}}^{T}\left[\begin{array}{cc}m& 0\\ 0& m\end{array}\right]\left\{\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right\}+\frac{1}{2}{\left\{\begin{array}{c}{\omega }_{\xi }\\ {\omega }_{\eta }\\ {\omega }_{\zeta }\end{array}\right\}}^{T}\left[\begin{array}{ccc}{J}_{d}& 0& 0\\ 0& {J}_{d}& 0\\ 0& 0& {J}_{p}\end{array}\right]\left\{\begin{array}{c}{\omega }_{\xi }\\ {\omega }_{\eta }\\ {\omega }_{\zeta }\end{array}\right\}$$
(16)

where \({o}^{^{\prime}}\xi \eta \zeta\) takes the axis node as origin,\({o}^{^{\prime}}\xi\) is perpendicular to the disk plane, and the moving coordinate system fixed on the disk is shown in Fig. 3.

Fig.3
figure 3

Motion coordinate system fixed on the rigid disk

Full size image

For \({\theta }_{\xi }\text{ is}\) equal to \({\theta }_{x}\), so

$$\left\{\begin{array}{c}{\omega }_{\xi }\\ {\omega }_{\eta }\\ {\omega }_{\zeta }\end{array}\right\}=\left[{A}_{\varphi }\right]\left\{\begin{array}{c}{\omega }_{\xi 1}\\ {\omega }_{\eta 1}\\ {\omega }_{\zeta 1}\end{array}\right\}=\left\{-\begin{array}{c}{\omega }_{\xi 1}\text{cos}\varphi +{\omega }_{\eta 1}\text{sin}\varphi \\ {\omega }_{\xi 1}\text{sin}\varphi +{\omega }_{\eta 1}\text{cos}\varphi \\ {\omega }_{\zeta }\end{array}\right\}$$

where

$$\left\{\begin{array}{c}{\omega }_{\xi }\\ {\omega }_{\eta }\\ {\omega }_{\zeta }\end{array}\right\}=\left[\begin{array}{ccc}\text{cos}\varphi & \text{cos}{\theta }_{x}\text{sin}\varphi & 0\\ -\text{sin}\varphi & \text{cos}{\theta }_{x}\text{cos}\varphi & 0\\ 0& -\text{sin}{\theta }_{x}& 1\end{array}\right]\left\{\begin{array}{c}\dot{{\theta }_{x}}\\ \dot{{\theta }_{y}}\\ \varphi \end{array}\right\}$$
(17)

where \({\theta }_{x}\), \(\dot{{\theta }_{x}}\) and \(\dot{{\theta }_{y}}\) are all first-order microelement, and \({\varphi }\) is equal to \(\Omega\). Substitute Eq. (17) into Eq. (16), and omit microelement higher than the second order, and consequently, following equation comes out:

$${T}_{d}=\frac{1}{2}{\left\{{\dot{u}}_{1d}\right\}}^{T}\left[{M}_{d}\right]\left\{{\dot{u}}_{1d}\right\}+\frac{1}{2}{\left\{{\dot{u}}_{2d}\right\}}^{T}\left[{M}_{d}\right]\left\{{\dot{u}}_{2d}\right\}+\Omega {\left\{{\dot{u}}_{1d}\right\}}^{T}\left[J\right]\left\{{\dot{u}}_{2d}\right\}+\frac{1}{2}{J}_{p}{\Omega }^{2}$$
(18)

where

$$\left[ {M_d} \right] = \left[ {\begin{array}{*{20}{c}} m\quad0 \\ 0\quad{J_d} \end{array}} \right],\left[ J \right] = \left[ {\begin{array}{*{20}{c}} 0\quad0 \\ 0\quad{J_p} \end{array}} \right]$$

The motion equation of the disk element can be obtained from the Lagrange equation:

$$\left\{\begin{array}{c}\left[{\text{M}}_{\text{d}}\right]\left\{{\ddot{u}}_{1d}\right\}+\Omega \left[\text{J}\right]\left\{{\dot{u}}_{2d}\right\}=\left\{{Q}_{1d}\right\}\\ \left[{\text{M}}_{\text{d}}\right]\left\{{\ddot{u}}_{2d}\right\}-\Omega \left[\text{J}\right]\left\{{\dot{u}}_{1d}\right\}=\left\{{Q}_{2d}\right\}\end{array}\right.$$
(19)

where \(\left[{\text{M}}_{\text{d}}\right]\)is the mass matrix of the disk; \(\left[{\text{G}}_{\text{d}}\right]=\Omega \left[\text{J}\right]\) is the rotation matrix;\(\left\{{Q}_{1d}\right\}\)and \(\left\{{Q}_{2d}\right\}\) are the corresponding generalized forces.

The Equation of Motion of a Bearing

Takes a sliding bearing as bearing. For example, under the condition of good foundation rigidity, the bearing seat can be simplified into a mass-spring-damper model which is an anisotropic bearing model as shown in Fig. 4.

Fig.4
figure 4

Mass-spring-damper model

Full size image

The corresponding dynamic characteristic coefficient matrix is as below:

$$\left[ {C_b} \right] = \left[ {\begin{array}{*{20}{c}} {{c_{bxx}}}{{c_{bxy}}} \\ {{c_{byx}}}{{c_{byy}}} \end{array}} \right]\left[ {K_b} \right] = \left[ {\begin{array}{*{20}{c}} {{K_{bxx}}}{{K_{bxy}}} \\ {{K_{byx}}}{{K_{byy}}} \end{array}} \right]$$

The dynamic characteristic coefficient matrix comprehensively reflects the damping and stiffness characteristics of the bearing pedestal and foundation. The equivalent mass of bearing pedestal and foundation in x and y directions is expressed by M_bx and M_by respectively. On the supposition that the coordinate of the bearing center is x_b, y_b and the number of the corresponding journal center node is z(j) and the coordinate of the journal center is x_z(j) and y_z(j) , the motion equation of the bearing is shown below:

$$\left[\begin{array}{cc}{M}_{bx}& 0\\ 0& {M}_{by}\end{array}\right]\left\{\begin{array}{c}{\ddot{x}}_{b}\\ {\ddot{y}}_{b}\end{array}\right\}+\left[\begin{array}{cc}{c}_{xx}& {c}_{xy}\\ {c}_{yx}& {c}_{yy}\end{array}\right]\left\{\begin{array}{c}{\dot{x}}_{b}-{\dot{x}}_{z(j)}\\ {\dot{y}}_{b}-{\dot{y}}_{z(j)}\end{array}\right\}+\left[\begin{array}{cc}{k}_{xx}& {k}_{xy}\\ {k}_{yx}& {k}_{yy}\end{array}\right]\left\{\begin{array}{c}{x}_{b}-{x}_{z(j)}\\ {y}_{b}-{y}_{z(j)}\end{array}\right\}+\left[\begin{array}{cc}{c}_{bxx}& {c}_{bxy}\\ {c}_{byx}& {c}_{byy}\end{array}\right]\left\{\begin{array}{c}{\dot{x}}_{b}\\ {\dot{y}}_{b}\end{array}\right\}+\left[\begin{array}{cc}{K}_{bxx}& {K}_{bxy}\\ {K}_{byx}& {K}_{byy}\end{array}\right]\left\{\begin{array}{c}{x}_{b}\\ {y}_{b}\end{array}\right\}=\left\{0\right\}$$
(20)

If the foundation rigidity is good, that is, \({x}_{b} and {y}_{b}\text{ is }0\), then the generalized force of the oil film acting on the center of the journal is:

$$\left\{\begin{array}{c}{\text{Q}}_{1d}^{b}\\ {Q}_{2d}^{b}\end{array}\right\}=-\left[\begin{array}{cc}{c}_{xx}& {c}_{xy}\\ {c}_{yx}& {c}_{yy}\end{array}\right]\left\{\begin{array}{c}{\dot{x}}_{z\left(j\right)}\\ {\dot{y}}_{z\left(j\right)}\end{array}\right\}-\left[\begin{array}{cc}{k}_{xx}& {k}_{xy}\\ {k}_{yx}& {k}_{yy}\end{array}\right]\left\{\begin{array}{c}{x}_{z\left(j\right)}\\ {y}_{z\left(j\right)}\end{array}\right\}$$
(21)

If damping is excluded, and the coefficient can be simplified to an elastic bearing with equal stiffness where the rigidity coefficient is \({K}_{x}\) and \({k}_{y}\) respectively, then

$$\left\{\begin{array}{c}{\text{Q}}_{1d}^{b}\\ {Q}_{2d}^{b}\end{array}\right\}=-\left[\begin{array}{cc}{k}_{x}& 0\\ 0& {k}_{y}\end{array}\right]\left\{\begin{array}{c}{x}_{z\left(j\right)}\\ {y}_{z\left(j\right)}\end{array}\right\}$$
(22)

Equation of Motion of the Systems

For the rotor system connected by n nodes and n-1 axial segments, the displacement vector is:

$$\left\{\begin{array}{c}\left\{{U}_{1}\right\}=\left[{x}_{1},{\theta }_{y1},{x}_{2},{\theta }_{y2},\dots ,{x}_{n},{\theta }_{yn}\right]\\ \left\{{U}_{2}\right\}=\left[{y}_{1},-{\theta }_{x1},{y}_{2},-{\theta }_{x2},\dots ,{y}_{n},-{\theta }_{xn}\right]\end{array}\right.$$
(23)

By synthesizing the motion equations of the disc, shaft segment and bearing, the motion equation of the system can be obtained as follows:

$$\left\{\begin{array}{c}\left[{\text{M}}_{1}\right]\left\{{\ddot{U}}_{1}\right\}+\Omega \left[{\text{J}}_{1}\right]\left\{{\dot{U}}_{2}\right\}+\left[{k}_{1}\right]\left\{{U}_{1}\right\}=\left\{{Q}_{1}\right\}\\ \left[{\text{M}}_{1}\right]\left\{{\ddot{U}}_{2}\right\}-\Omega \left[{\text{J}}_{1}\right]\left\{{\dot{U}}_{1}\right\}+\left[{k}_{1}\right]\left\{{U}_{2}\right\}=\left\{{Q}_{2}\right\}\end{array}\right.$$
(24)

where \(\left[{M}_{1}\right]\) is the global mass matrix, Ω \(\left[{J}_{1}\right]\) is the rotation matrix, and \(\left[{K}_{1}\right]\) is the stiffness matrix.

System Equation of Motion Having Crack

When the rotor cracks, the opening and closing behavior caused by rotor rotation and shaft selection results in time-varying stiffness. This is called a breathing crack. The dynamic equation formulation of systems with cracks must be further examined in the stiffness when has the crack. The general dynamics equation is as follows:

$$M\ddot{U}+C\dot{U}+KU=Q$$
(25)

where M and K are the mass and stiffness matrices of the rotor without crack.

\(Q\) means the balance and gravitational forces.

The equations of the rotor with crack can be written as

$$M\ddot{U}+C\dot{U}+(K-{K}_{c}\left(t\right))U=Q$$
(26)

It may be noted that the global stiffness matrix of the rotor consists of a constant component K and a time-dependent component \({k}_{c}=f\left(t\right){k}_{crack}\).

\({k}_{crack}\) is the crack-related stiffness matrix. The \(f\left(t\right)\) function represents the breathing effect. The proportion of the crack face that is subject to tensile axial stresses will be a determining factor for the extent of crack opening. Based on assumption that the gravity force is much greater than the imbalance force, the breathing crack [3, 4] may be described as

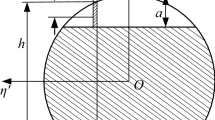
$$\text{f}\left(\text{t}\right)=\frac{1-\text{cos}\left(\Omega t\right)}{2}$$
(27)

where Ω is the rotational speed of the rotor. As shown in Fig. 5, for \(f\left(t\right)=0\), the crack is totally closed and the rotor with crack stiffness is equal to the rotor stiffness without crack. For \(f\left(t\right)=1\), the crack is full open. A transverse crack in a rotor shaft can be represented by the reduction of the second moment of area ΔI of the element at the location of the crack. By using Rayleigh's method, the change in ΔI can be represented as follows:

Fig.5
figure 5

Geometric relative positions of the shaft and transverse crack

Full size image
$$\frac{\Delta I/{I}_{0}}{1-\Delta I/{I}_{0}}=\frac{R}{l}\left(1-{\nu }^{2}\right)F\left(\mu \right)$$
(28)

where \({I}_{0}\), ν, μ, R, \(l\), and F(μ) represent the second moment of area, the Poisson's ratio, the non-dimensional crack depth, the shaft radius, the length of the section, and the compliance functions varied with the non-dimensional crack depth μ, respectively. The non-dimensional crack depth μ is given by μ = h/R, where h defines the crack depth of the shaft as shown in Fig. 5.

\({k}_{crack}\) is given by [3, 4].

$${K}_{\text{crack}}=\frac{E}{{l}^{3}}\left[\begin{array}{cccccccc}12{I}_{X}& 0& 0& 6l{I}_{X}& -12{I}_{X}& 0& 0& 6l{I}_{X}\\ & 12{I}_{Y}& -6l{I}_{Y}& 0& 0& -12{I}_{Y}& -6l{I}_{Y}& 0\\ & & 4{l}^{2}{I}_{Y}& 0& 0& 6l{I}_{Y}& 2{l}^{2}{I}_{Y}& 0\\ & & & 4{l}^{2}{I}_{X}& -6l{I}_{X}& 0& 0& 2{l}^{2}{I}_{X}\\ & & & & 12{I}_{X}& 0& 0& -6l{I}_{X}\\ & & & & & 12{I}_{Y}& 6l{I}_{Y}& 0\\ & & Sym& & & & 4{l}^{2}{I}_{Y}& 0\\ & & & & & & & 4{l}^{2}{I}_{X}\end{array}\right]$$
(29)

where

$${I}_{X}=\iint {Y}^{2}dA=\iint {Y}^{2}dXdY=\frac{{R}^{2}}{4}\left(\updelta \left(1-4\mu +2{\mu }^{2}\right)\gamma +\frac{\alpha }{2}\right)$$
$${I}_{Y}=\iint {X}^{2}dA-A{b}^{2}=\iint {X}^{2}dXdY-\left[{R}^{2}\left(\updelta \gamma +\frac{\alpha }{2}\right)\right]{\left(\frac{2}{3A}{R}^{3}{\gamma }^{3}\right)}^{2}==\frac{\pi {R}^{4}}{4}+{R}^{4}\left(\frac{2}{3}\updelta {\gamma }^{3}+\frac{1}{4}\updelta \left(1-4\mu +2{\mu }^{2}\right)\gamma +{sin}^{-1}\gamma \right)-\frac{4{R}^{4}{\gamma }^{6}}{9\left(\updelta \gamma +\frac{\alpha }{2}\right)}$$

where \(b\) and A are the centroid of the cross-section and the uncracked area of the cross-section, respectively, and the distance from the axis X to the centroid of the cross-section \(b\) are given by:

$$A={R}^{2}\left(\updelta \gamma +\frac{\alpha }{2}\right)$$
$$b=\frac{2}{3A}{R}^{3}{\gamma }^{3}$$
$$\alpha = 2co{s^{( - 1)}}\delta ;\quad \alpha :the \, crack \, angle$$
$$\upgamma ={\left(2\mu -{\mu }^{2}\right)}^{0.5}$$
$$\updelta =1-\mu$$

Nonlinear Analysis in a Rotor Disc-Bearing System by FEA

Geometric Modeling and Parameters

Geometric Modeling

Figure 6 shows the dynamic model of the rotor-disc-bearing system, which consists of a disc, a bearing and a rotating shaft. Figure 7 shows the geometric model of the rotor-disc-bearing system with crack and its geometric position relationship.

Fig. 6
figure 6

Dynamic model of the rotor-disc-bearing system

Full size image
Fig. 7
figure 7

Geometric model of the rotor-disc-bearing system

Full size image

Parameters of the Rotor System

The geometric dimension relations of rotor-disc-bearing-system and bearing are respectively shown in Table 1 and Table 2.

Table 1 Parameters of the rotor system
Full size table
Table 2 Geometric dimensions of the bearing
Full size table

Modelling by ANSYS

Modelling Methodology

The simulated flow chart of the rotor system using ANSYS is shown in Fig. 8.

Fig. 8
figure 8

Flow chart of ANSYS Simulation on Rotor System

Full size image

Modelling and Mesh using ANSYS

Rotor System Model and Meshing of Without Crack

The model and meshing of the rotor system without Crack using ANSYS are shown in Figs. 9 and 10.

Fig. 9
figure 9

Rotor System Model of without Crack

Full size image
Fig.10
figure 10

Rotor System Meshing of without Crack

Full size image
Rotor System Model and Meshing of with Crack

The model and meshing of the rotor system with Crack using ANSYS are shown in Figs. 11 and 12.

Fig.11
figure 11

Rotor System Model of with Crack

Full size image
Fig.12
figure 12

Rotor System Meshing of with Crack

Full size image

Simulation Results

Critical Speed Analysis of Shaft Without Crack and with Crack

A modal—analysis was investigated the critical speed of shaft with crack and without crack by exploitation Campbell diagram (Figs. 13, 14 and 15).

Fig.13
figure 13

Result of Campbell diagrams without Crack

Full size image
Fig.14
figure 14

Result of Campbell diagrams with Crack

Full size image
Fig.15
figure 15

Graph showing Critical Speed of Rotor System without Crack and with Crack (Present). *Δ is the difference between the two values with and without cracks

Full size image

The above table and graph shows the calculation results of the critical speed on the bearing-disc-rotor system with and without crack, and the result value is different from each other.

Considering identical material properties, disc specifications and geometrical parameters the obtained results are compared with those of Bajpai [18] as shown in Table 3. An excellent agreement could be observed in Table 3 with the results thus validating the critical speed analysis of the rotor system without crack and with crack.

Table 3 Critical speed of rotor system without crack and with crack critical speed
Full size table

Natural Frequencies Without Crack and with Crack

The above table and graph shows the calculation results of the natural frequency on the bearing-disc-rotor system with and without crack, and the result value is different from each other (Fig. 16).

Fig.16
figure 16

Graph showing the Natural frequencies of Rotor System without Crack and with Crack (Present). *Δ is the difference between the two values with and without cracks

Full size image

Considering identical material properties, disc specifications and geometrical parameters the obtained results are compared with those of Bajpai A [18] as shown in Table 4. An excellent agreement could be observed in Table 4 with the results thus validating the natural frequencies analysis of the rotor system without crack and with crack.

Table 4 Natural frequencies of rotor system without crack and with crack
Full size table

Influence of non-Dimensional Crack Depth and Position of the Crack on the Critical Speed

Influence of Position of the Crack on the Natural Frequencies

Table 5 and Fig. 17 show that the value of the natural frequency differs from each other according to the position of the crack as a result of the comparison of the natural frequency of the bearing-disc-rotor system that follows the position of the crack with the natural frequency value when there is no crack.

Table 5 Influence of position of the crack on the natural frequencies (the non-dimensional crack depth μ = 1)
Full size table
Fig.17
figure 17

Graph showing the influence of the position of the crack on the natural frequencies when the non-dimensional crack depth(μ) is 1

Full size image
Influence of Non-dimensional Crack Depth on the Natural Frequencies

Table 6 and Fig. 18 show that the contrast analysis result with the natural frequency value when there was no crack differed according to the non-dimensional crack depth with the length of the crack fixed, the change in the natural frequency of the bearing-disc-rotor system followed by the change in the non-dimensional crack depth.

Table 6 Influence of non-dimensional crack depth on the natural frequencies (\({L}_{crack}=0.35m\))
Full size table
Fig.18
figure 18

Graph showing the influence of non-dimensional crack depth on the natural frequencies when the Position of the crack is \({L}_{crack}=0.35m\)

Full size image

Influence Analysis of Eccentricity on the Rotor System

The important factors affecting the eccentricity of the rotor system are eccentric mass and eccentric distance. Using ANSYS program, the relation between eccentricity and nonlinearity was analyzed concretely by changing eccentricity distance and eccentricity mass when the rotation number was 10000 rpm. The simulation was performed with the eccentric distance changed from 0.05 m to 0.3 m and the eccentric mass from 0.001 kg to 0.0025 kg (Table 7).

Table 7 Disc center vibration amplitude under different eccentric masses (\({m}_{\text{e}}\)=0.001 kg)
Full size table

It can be seen from Tables 8, 9, 10 and Fig. 19 that the variation of the maximum amplitude when the eccentric mass is changed from 0.0025 kg to 0.001 kg is studied. The smaller the eccentric mass is, that is, the less than 0.001 kg, the effect of the eccentric mass on the rotor system is almost linear. Thus, in the eccentric rotor system, the eccentric distance and the eccentric mass are very important factors.

Fig.19
figure 19

Vibration amplitudes relationship of disk core under different eccentric distances and eccentric masses

Full size image

Discussion

As shown in the above results, the calculation results of the critical speed and natural frequency of the bearing-disc-rotor system differed with that of crack and no crack. At this time, the critical speed and natural frequency of the shaft for the crack were slightly smaller than that for no crack. Under fixation of the non-dimensional crack depth at μ = 1, the natural frequency of the rotor system was analyzed by varying the position of the crack as 0.25 m, 0.5 m, 0.75 m, and 0.95 m. The natural frequency gradually decreased at the crack near 0.5 m, and then increased slightly passing 0.5 m, however, all values were smaller than the natural frequency at no crack. In addition, when the position of the crack was fixed at \({L}_{crack}=0.35m\), natural frequency of the shaft was analyzed changing the non-dimensional crack depth as 0.25, 0.5, 0.75, and 1.0. As the non-dimensional crack depth increased, the natural frequency gradually decreased. It can be seen from Table 8,9,10 and Fig. 19 that the variation of the maximum amplitude when the eccentric mass is changed from 0.0025 kg to 0.001 kg is studied. The smaller the eccentric mass is, that is, the less than 0.001 kg, the effect of the eccentric mass on the rotor system is almost linear. Thus, in the eccentric rotor system, the eccentric distance and the eccentric mass are very important factors. If the eccentricity distance and the eccentricity mass are small, that is, under the condition of the eccentricity distance is less than 0.05 m and the eccentricity mass is 0.001 kg, the influence of the eccentricity force on the subsystem is approximately linear. And the value of the eccentricity factor is very large, that is, in the eccentricity distance is greater than 0.3 m, the mass of the eccentricity is greater than 0.0025 kg, we should consider the nonlinear effect of the eccentricity force.

Table 8 Disc center vibration amplitude under different eccentric masses (\({m}_{\text{e}}\)=0.0015 kg)
Full size table
Table 9 Disc center vibration amplitude under different eccentric masses (\({m}_{\text{e}}\)=0.002 kg)
Full size table
Table 10 Disc center vibration amplitude under different eccentric distances (\({m}_{\text{e}}\)=0.0025 kg)
Full size table

Conclusion

In this paper, how to write the dynamic equation of the rotor-disc-bearing system with and without crack was mentioned in detail combining the finite element analysis method with Lagrange method. In addition, the critical speed and natural frequency of the rotor system with and without crack were calculated using the ANSYS program. After that, how the non-dimensional crack depth and the position of the crack affect the change of the natural frequency of the rotor system was analyzed. In the analysis, the position of the crack and the non-dimensional crack depth were changed for studying the relationship between these factors and the natural frequency of the rotor system. The natural frequency of the rotor system involving two factors was smaller than that of the uncracked system. By using ANSYS software, the influence of eccentricity on the rotor system and the relationship between eccentricity and nonlinearity were obtained. The result showed that when the eccentric distance and the eccentric mass were relatively small, i.e. 0.05 m, 0.001 kg, the effect on the eccentric force is almost linear, but when the eccentric distance and the eccentric mass were relatively large, i.e. 0.1 m, 0.05 kg,the nonlinear effect of eccentric forces must be considered.