Free Vibration Analysis of Curved Stiffened Plates

Abstract

Background

Curved stiffened plates are most widely used in engineering struc- tures such as ships, aerospace vehicles, and bridges. These plates are frequently under the impact of dynamic loadings during their service life. Therefore, this paper’s main objective is to investigate the free vibration of the stiffened plates with curved bound- aries using the finite element method.

Purpose

The plates’ strength is improved by placement of the stiffeners either con- centrically or eccentrically, depending on the use. The stiffeners’ orientation, such as radial and circumferential, for the plates with curved boundaries such as annular sector, circular and elliptical plates is inevitable because of their contribution to the plate in that direction. The stiffeners’ size and shape play an important role in strengthening the plates, keeping the structure’s weight low. All these parameters contribute effectively to the vibration of the stiffened plates significantly. Hence, in this paper, an attempt has been made to present a parametric study for the free vibration characteristics of stiff- ened plates having various boundary conditions and considering the above parameters

Methods

An in-house finite element MATLAB code is developed for the study of bare plates and plates with stiffeners. An isoparametric quadratic plate bending ele- ment with shear deformation is considered to accomplish this. The plate and stiffener elements’ stiffness and mass matrices have been obtained separately and assembled to form the entire structure’s global matrices. Some of the example results have been verified with previously published results and the FEAST (Finite Element Analysis of STructures) software to show the method’s efficacy.

Results

Non-dimensional frequency results of plates with various types of stiffen- ers for different boundary conditions and diverse sector angles for bare and stiffened annular plates are reported. Parametric study of the vibration characteristics of stiff- ened plates of various shapes (annular sector, circular and elliptical) with different sizes, shapes, orientations (radial and circumferential), and dispositions (concentri- cally, eccentrically, and floating) of stiffeners have also been presented.

Conclusions

The non-dimensional frequencies are more significant for the I-beam eccentric stiffener than that of the R-beam and T-beam stiffener for the clamped condi- tions. The results are also higher with the increase of inner-to-outer radii ratios and the decrease of sector angles. The radially attached stiffeners show more pronounced non- dimensional frequencies than the circumferential ones for the circular and elliptical plate cases.

Introduction

A stiffened plate is the plate attached with ribs, which are often provided to improve its stiffness and enhance its load-carrying capacity. In many engineering structures, these are used for achieving higher strength with less amount of material, which elevates the strength-to-mass ratio and makes the structure economical. Mostly in engineering structures, such as floor systems, ship structures, aerospace, and highway bridges, stiffened plates are used more effectively. Further, these structures are frequently subjected to dynamic loading in their service life. Hence, the dynamic behavior of stiffened plates is of much interest to structural engineers. The resonance may occur due to undesirable vibrations leading the stiffened structure to a sudden failure. It is, therefore, crucial to assess the natural frequencies of these structures accurately. Hence, an in-depth study of these stiffened plates’ free vibration behavior is required to exploit their use.

In the literature, the free vibration analyses of rectangular or square plates with stiffeners have been reported where the investigators have used various methods, such as Rayleigh-Ritz, finite element method (FEM), or ANSYS software. Some of them can be found in Ahmad and Kapania[1], Leissa et al. [2], Holopainen [3], Nayak et al. [4], Panda and Barik [5], Sahoo and Barik [6, 7], Zeng and Bert [8] and Yadav et al. [9]. The free vibration of bare curved plates with various boundary conditions has been presented by Mukhopadhyay [10, 11] using the semi-analytical method. The dynamic analysis for free vibration of bare annular sector plates has been investigated with the influence of sector angle, radii ratio and different boundary conditions by Mirtalaie and Hajabasi [12], Shi et al. [13] and Kim and Dickinson [14] using differential quadrature method (DQM), analytical method and Rayleigh–Ritz method, respectively. Mukherjee and Mukhopadhyay [15] have presented natural frequencies of skew, curved and tapered plates using FEM. Finite element free vibration analysis for arbitrary plates has been carried out by Barik and Mukhopadhyay [16].

The free vibration of elliptical plates with free edges has been investigated by Narita [17] using the Ritz method. Yalcin et al. [18] have presented the free vibration of circular plates for different boundary conditions using the differential transformation method. Lam et al. [19] have investigated the free vibration analysis of circular and elliptical plates for free, clamped and simply supported boundary conditions using the Ritz method.

The frequency of bare and concentric stiffened annular sector plates has been presented using an analytical solution by Ramakrishnan and Kunukkasseril [20, 21]. Irie et al. [22] have analyzed the free vibration of the annular sector plate with curved radial edges using the Ritz method. Also, Irie et al. [23] have presented the free vibration of the annular plate with radially placed beams using spline function.

The free vibration of stiffened plate has been investigated by Mukherjee and Mukhopadhyay [24] using the finite element method. In this analysis, the effects on the vibration of various parameters, such as eccentricity, disposition and orientation of stiffeners and boundary conditions have been considered. Sheikh and Mukhopadhyay [25] have also explained the influence of same parameters as discussed above on the free vibration using spline finite strip method. Barik and Mukhopadhyay [26, 27] have investigated the free vibration analysis of arbitrary shaped stiffened plates using the finite element method.

The above review reveals that the works carried out on free vibration under the influence of parameters such as sector angles and radii ratio are only for bare curved plates. The literature on curved stiffened plates explains only the effects of the stiffeners’ disposition and orientation on vibration. Therefore in this paper, an attempt is made to present a parametric study on the free vibration characteristics of curved plates with concentric and eccentric stiffeners for various parameters such as sector angles, radii ratio, type of stiffeners, stiffener position, and different boundary conditions using the FEM. Also, the stiffeners are considered attached to the plate either in fixed or floating conditions. A quadratic stiffened plate bending element capable of accommodating curved boundaries is used for the analysis. The formulation considers shear deformation, torsional stiffness effect, and arbitrary stiffener placement, which need not follow the nodal lines. The results are compared with the previously published results and FEAST, which is an FEM-based software to solve structural engineering problems.

Theoretical Formulation

The plate and stiffener elements are formulated separately. A quadratic isoparametric plate element is considered for the formulation, which includes both in-plane and bending displacements.

Plate Element Matrices

Fig. 1

Isoparametric eight-noded plate element

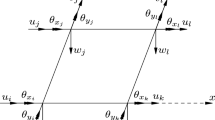
The displacements at a node ‘r’ of an eight node isoparametric plate element (Fig. 1) are $u_r$, $v_r$, $w_r$, $\theta _{x_r}$ and $\theta _{y_r}$. The notations u and v are the inplane displacements in x and y directions respectively; w is the tranverse diplacement in z direction; $\theta _{x}$ and $\theta _{y}$ are the rotations along x and y directions respectively. The geometry of the element in terms of nodal coordinates is defined as

$$\begin{aligned} \begin{Bmatrix} x\\ y \end{Bmatrix}=\sum _{r=1}^{8} \begin{bmatrix} N_r &{} 0 \\ 0 &{} N_r \end{bmatrix}\begin{Bmatrix} x_r\\ y_r \end{Bmatrix}=\sum _{r=1}^{8}N_r[I_2]\begin{Bmatrix} x_r\\ y_r \end{Bmatrix} \end{aligned}.$$

(1)

The displacements at any point in the element are defined as

$$\begin{aligned} \begin{Bmatrix} u\\ v\\ w\\ \theta _x\\ \theta _y \end{Bmatrix}=\sum _{r=1}^{8}N_r\;[I_5]\;\begin{Bmatrix} u_r\\ v_r\\ w_r\\ \theta _{x_r}\\ \theta _{y_r} \end{Bmatrix} \end{aligned},$$

(2)

where $I_2$ and $I_5$ are $(2\times 2)$ and $(5\times 5)$ indentity matrices respectively, and

$$\begin{aligned} N_r=\begin{Bmatrix} 0.25(\xi -1)(-\xi -\eta -1)(\eta -1)\\ 0.5(\xi ^2-1)(\eta -1)\\ 0.25(\xi +1)(-\xi +\eta +1)(\eta -1)\\ 0.5(\xi -1)(\eta ^2-1)\\ 0.5(\xi +1)(-\eta ^2+1)\\ 0.25(\xi -1)(\xi -\eta +1)(\eta +1)\\ 0.5(-\xi ^2+1)(\eta +1)\\ 0.25(\xi +1)(\xi +\eta -1)(\eta +1) \end{Bmatrix} \end{aligned}.$$

(3)

The displacement field is given by

$$\begin{aligned} \{f\}=\begin{Bmatrix} U\\ V\\ W \end{Bmatrix}=\begin{Bmatrix} u-z\theta _x\\ v-z\theta _y\\ w \end{Bmatrix} \end{aligned},$$

(4)

where z is the distance of a point from the plate mid plane.

Fig. 2

Deformation in the plate

Attributed to shear deformation, a specific distorting in the section occurs, as shown in Fig. 2. The $\theta _x$ and $\theta _y$ are considered average rotations, and a linear variation along the thickness of the plate is assumed. The average shear deformations are denoted as $\phi _x$ and $\phi _y$ in the x and y directions, respectively. Thus

$$\begin{aligned} \begin{Bmatrix} \theta _x\\ \theta _y \end{Bmatrix} =\begin{Bmatrix} \dfrac{\partial w}{\partial x}+\phi _x\\ \dfrac{\partial w}{\partial y}+\phi _y \end{Bmatrix} \end{aligned}.$$

(5)

The strain components can be shown with the help of Eqs. (4) and (5) as

$$\begin{aligned} \{\epsilon \}=\begin{Bmatrix} \dfrac{\partial U}{\partial x}\\ \dfrac{\partial V}{\partial y}\\ \left( \dfrac{\partial U}{\partial y}+\dfrac{\partial V}{\partial x}\right) \\ \left( \dfrac{\partial U}{\partial z}+\dfrac{\partial W}{\partial x}\right) \\ \left( \dfrac{\partial V}{\partial z}+\dfrac{\partial W}{\partial y}\right) \end{Bmatrix}=\begin{Bmatrix} \dfrac{\partial u}{\partial x}-z\dfrac{\partial \theta _x}{\partial x}\\ \dfrac{\partial v}{\partial y}-z\dfrac{\partial \theta _y}{\partial y}\\ \dfrac{\partial u}{\partial y}+\dfrac{\partial v}{\partial x}-z\left( \dfrac{\partial \theta _x}{\partial y}+\dfrac{\partial \theta _y}{\partial x}\right) \\ \left( \dfrac{\partial w}{\partial x}-\theta _x\right) \\ \left( \dfrac{\partial w}{\partial y}-\theta _y \right) \end{Bmatrix} \end{aligned}$$

(6)

$$\begin{aligned} \{\epsilon \}=[H]\{{\bar{\epsilon }}\}= \begin{bmatrix} 1 &{} 0 &{} 0 &{} z &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} z &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} z &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{bmatrix} \begin{Bmatrix} \dfrac{\partial u}{\partial x}\\ \dfrac{\partial v}{\partial y}\\ \left( \dfrac{\partial u}{\partial y}+\dfrac{\partial v}{\partial x} \right) \\ -\dfrac{\partial \theta _x}{\partial x}\\ -\dfrac{\partial \theta _y}{\partial y}\\ -\left( \dfrac{\partial \theta _x}{\partial y}+\dfrac{\partial \theta _y}{\partial x} \right) \\ \left( \dfrac{\partial w}{\partial x}-\theta _x \right) \\ \left( \dfrac{\partial w}{\partial y}-\theta _y \right) \end{Bmatrix} \end{aligned}.$$

(7)

Combining Eqs. (2) and (7), yields

$$\begin{aligned} \{{\bar{\epsilon }}\}=\sum _{r=1}^{8}\begin{bmatrix} \dfrac{\partial N_r}{\partial x} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \dfrac{\partial N_r}{\partial y} &{} 0 &{} 0 &{} 0\\ \dfrac{\partial N_r}{\partial y} &{} \dfrac{\partial N_r}{\partial x} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -\dfrac{\partial N_r}{\partial x} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{\partial N_r}{\partial y}\\ 0 &{} 0 &{} 0 &{} -\dfrac{\partial N_r}{\partial y} &{} -\dfrac{\partial N_r}{\partial x}\\ 0 &{} 0 &{} \dfrac{\partial N_r}{\partial x} &{} -N_r &{} 0\\ 0 &{} 0 &{} \dfrac{\partial N_r}{\partial y} &{} 0&{}-N_r \end{bmatrix} \begin{Bmatrix} u_r\\ v_r\\ w_r\\ \theta _{x_r}\\ \theta _{y_r} \end{Bmatrix} \end{aligned}$$

(8)

$$\begin{aligned} \{{\bar{\epsilon }}\} =\sum _{r=1}^{8}\;[B]_r\;\{\delta \}_r =[B]\;\{\delta \}. \end{aligned}$$

(9)

The quantities $\dfrac{\partial N_r}{\partial x}$ and $\dfrac{\partial N_r}{\partial y}$ are to be computed to evaluate the [B] matrix. The relationship between the derivatives of the shape function $N_r$ with respect to the natural coordinates to that in Cartesian coordinates is given by

$$\begin{aligned} \begin{Bmatrix} \dfrac{\partial N_r}{\partial x} \\ \dfrac{\partial N_r}{\partial y} \end{Bmatrix}=[J]^{-1}\begin{Bmatrix}\dfrac{\partial N_r}{\partial \xi } \\ \dfrac{\partial N_r}{\partial \eta } \end{Bmatrix}, \text {where } [J]=\begin{bmatrix} \dfrac{\partial x}{\partial \xi } &{} &{}\dfrac{\partial y}{\partial \xi }\\ \dfrac{\partial x}{\partial \eta } &{} &{}\dfrac{\partial y}{\partial \eta } \end{bmatrix}. \end{aligned}$$

(10)

The element stiffness matrix can be expressed as

$$\begin{aligned} {[}k]_e= & {} \int \int \;[B]^T \; [D_p]\; [B]\; {\text {d}}x\; {\text {d}}y\; \nonumber \\= & {} \int _{-1}^{1} \int _{-1}^{1} \;[B]^T \; [D_p]\; [B]\; |J|\; {\text {d}}\xi \; {\text {d}}\eta , \end{aligned}$$

(11)

where

$$\begin{aligned} {[}D_p]= \begin{bmatrix} D_{A} &{} D_{B} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ D_{B} &{} D_{A} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} D_{AB} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} D_{X} &{} D_{Y} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} D_{Y} &{} D_{X} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} D_{XY} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} S_A &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} S_A\\ \end{bmatrix}, \end{aligned}$$

(12)

where

$$\begin{aligned}&D_{A} = \dfrac{Eh^2}{(1-\nu ^2)}&\quad \qquad D_{B}=\nu D_{A}\\&D_{AB} = \dfrac{Eh}{2(1+\nu )}&\quad \qquad D_{X}= \dfrac{Eh^3}{12(1-\nu ^2)} \\&D_{Y} = \nu D_{X}&\quad \qquad D_{XY}=\dfrac{1-\nu }{2}D_{X} \\&S_A = \dfrac{Eh}{2\gamma (1+\nu )}, \end{aligned}$$

and E is the Young’s modulus, $\nu$ is the Poisson’s ratio, h is the plate thickness, $\gamma$ is the non-uniform shear strain distribution factor which is equal to 1.2 for isotropic rectangular section.

The element mass matrix can be expressed as

$$\begin{aligned} {[}m]_e= & {} \int \int [N]^T \;[m_p]\; [N]\; {\text {d}}x\;{\text {d}}y \nonumber \\= & {} \int _{-1}^{1} \int _{-1}^{1} [N]^T \;[m_p]\; [N]\;|J|\;{\text {d}}\xi \; {\text {d}}\eta , \end{aligned}$$

(13)

where

$$\begin{aligned}{}[N] = \sum _{r=1}^{8}\;N_r\;[I_5], \end{aligned}$$

(14)

$$\begin{aligned}{}[m_p]= \begin{bmatrix} \rho h &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \rho h &{} 0 &{} 0 &{} \\ 0 &{} 0 &{} \rho h &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \dfrac{\rho h^3}{12} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{\rho h^3}{12} \end{bmatrix}, \end{aligned}$$

(15)

where $\rho$ is the mass density of the material.

Stiffener Element Formulation

The stiffener element attached to the plate along the circumferential direction is considered, as shown in Fig. 3. The middle plane of the plate is taken as the reference axis for its formulation. The stiffener’s stiffness matrix is formulated in a general manner by expressing it in terms of the plate element’s displacement function. Because of this generality, the stiffener’s contribution to the plate element is reflected on all the plate elements’ nodes depending on its orientation.

Fig. 3

Plate Element with Stiffener

Element Stiffness Matrix

The displacement field is based on the assumption that the common normal to the plate and the stiffener system before bending remains straight after bending and is given by

$$\begin{aligned} \{f\}=\begin{Bmatrix} U\\ V\\ W \end{Bmatrix}=\begin{Bmatrix} u-z \;\theta _x(x)\\ -z \;\theta _y(x)\\ w+c\;\theta _y(x) \end{Bmatrix} \end{aligned}$$

(16)

where c is the distance of a point on the stiffener from the $x-z$ plane passing through the centroid of the stiffener cross-section.

The strain vector is given by

$$\begin{aligned} \{\epsilon _s\}= & {} \begin{Bmatrix} \dfrac{\partial u}{\partial x}-z\;\dfrac{\partial \theta _x}{\partial x}\\ -z \;\dfrac{\partial \theta _y}{\partial x}\\ \dfrac{\partial w}{\partial x}+c\;\dfrac{\partial \theta _y}{\partial x}-\theta _x \end{Bmatrix}= \begin{bmatrix} 1 &{} z &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} z\\ 0 &{} 0 &{} 1 &{} -c \end{bmatrix}\begin{Bmatrix} \dfrac{\partial u}{\partial x}\\ -\dfrac{\partial \theta _x}{\partial x}\\ \dfrac{\partial w}{\partial x}-\theta _x\\ -\dfrac{\partial \theta _y}{\partial x} \end{Bmatrix}\nonumber \\= & {} [H_s]\;\{{\bar{\epsilon }}_s\}. \end{aligned}$$

(17)

From Eq. 17, it may be noted that the stiffener’s strain vector is expressed in terms of the displacement components of the plate element. Hence, the plate element’s displacement function is used, which yields the stiffener’s stiffness matrix in terms of the plate element’s nodal parameters. In this, the compatibility between the stiffener and the plate element is maintained. The stiffener’s contribution to the plate element is now reflected on all its nodes.

Substituting the values of u, w, $\theta _x$ and $\theta _y$ from Eq. (2) into the Eq. (17), yields

$$\begin{aligned} \{{\bar{\epsilon }}_s\}=\sum _{r=1}^{8} [B_s]_r \; \{\delta \}_r=[B_s]\; \{\delta \}, \end{aligned}$$

(18)

where

$$\begin{aligned} {[}B_s]_r=\begin{bmatrix} \dfrac{\partial N_r}{\partial x} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -\dfrac{\partial N_r}{\partial x} &{} 0\\ 0 &{} 0 &{} \dfrac{\partial N_r}{\partial x} &{} -N_r &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{\partial N_r}{\partial x} \end{bmatrix}. \end{aligned}$$

(19)

Following steps similar to those for the plate, the element stiffness matrix can be expressed as

$$\begin{aligned} {[}k]_s=\int _{-1}^1 [B_s]^T \; [{\bar{D}}_s]\; [B_s]\; |J|\; {\text {d}}\xi , \end{aligned}$$

(20)

where

$$\begin{aligned} {[}{\bar{D}}_s]=\begin{bmatrix} E_sA_s &{} E_sS_{xs} &{} 0 &{} \\ E_sS_{xs} &{} E_sI_{xs} &{} 0 &{} 0\\ 0 &{} 0 &{} G_sS_{is} &{} 0\\ 0 &{} 0 &{} 0 &{} G_sJ_{s} \end{bmatrix}, \end{aligned}$$

(21)

where $A_{\text {s}}$ is the cross-sectional area of the stiffener. $S_{x{\text {s}}}$ is the first moment of the stiffener cross-section area about reference axis. $I_{x{\text {s}}}$ is the second moment of the stiffener cross-section area about reference axis. $S_{i{\text {s}}}$ is the shear area of the stiffener. $J_{\text {s}}$ is the polar moment of inertia of the stiffener cross sectional area.

Element Mass Matrix

At any point within the element the acceleration vector can be expressed as

$$\begin{aligned} \begin{Bmatrix} {\ddot{u}} \\ {\ddot{v}} \\ {\ddot{w}} \\ {\ddot{\theta }}_x \\ {\ddot{\theta }}_y \end{Bmatrix}=\sum _{r=1}^{8}\;N_r\;[I_5]\begin{Bmatrix} {\ddot{u}}_r\\ {\ddot{v}}_r\\ {\ddot{w}}_r\\ {\ddot{\theta }}_{xr}\\ {\ddot{\theta }}_{yr} \end{Bmatrix}. \end{aligned}$$

(22)

The acceleration field of the stiffener is given by

$$\begin{aligned} \{{\ddot{f}}\}=\begin{Bmatrix} {\ddot{U}}\\ {\ddot{V}}\\ {\ddot{W}} \end{Bmatrix}=\begin{Bmatrix} {\ddot{u}}-z{\ddot{\theta }}_x\\ -z{\ddot{\theta }}_y\\ {\ddot{w}}+c\;{\ddot{\theta }}_y \end{Bmatrix}. \end{aligned}$$

(23)

Combining Eqs. (22) and (23), the acceleration field may be expressed in terms of nodal accelerations,

$$\begin{aligned} \{{\ddot{f}}_s\}= \begin{bmatrix} 1 &{} 0 &{} 0 &{} -z &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -z \\ 0 &{} 0 &{} 1 &{} 0 &{} c \end{bmatrix}\;[N]\; \sum _{r=1}^{8} \begin{Bmatrix} {\ddot{u}}_r\\ {\ddot{v}}_r\\ {\ddot{w}}_r\\ {\ddot{\theta }}_{xr}\\ {\ddot{\theta }}_{yr} \end{Bmatrix}. \end{aligned}$$

(24)

Following the steps similar to those of plate element the element mass matrix can be expressed as

$$\begin{aligned} {[}m]_{\text {s}}= \int _{-1}^{1} [N]^T \;[m_{{\text {se}}}]\; [N]\;|J|\;{\text {d}}\xi , \end{aligned}$$

(25)

where

$$\begin{aligned} {[}m_{\text {se}}]=\rho _{\text {s}} \; \begin{bmatrix} A_{\text {s}} &{} 0 &{} 0 &{} -S_{x{\text {s}}} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} A_{\text {s}} &{} 0 &{} 0 \\ -S_{x{\text {s}}} &{} 0 &{} 0 &{} I_{x{\text {s}}} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} J_{\text {s}} \end{bmatrix}. \end{aligned}$$

(26)

Similarly, we can express the element matrices of a radial stiffener. In the fixed beam stiffener case, the stiffener is directly attached to the plate, whereas for the floating beam stiffener condition, the stiffener is attached to another stiffener, which is affixed to the plate. The formulation for the fixed and floating beam stiffeners are the same as expressed above; only their eccentricity values are different, as given below.

• 1. Eccentricity for fixed beam (Fig. 20) :

  $$\begin{aligned} c= \frac{h}{2}+\dfrac{d_1}{2} \end{aligned}$$

• 2. Eccentricity for floating beam (Fig. 21)

  $$\begin{aligned} c= \frac{h}{2}+d_1+\dfrac{d_2}{2} \end{aligned}$$

where $d_1$ is the depth of the stiffener 1. $d_2$ is the depth of the stiffener 2.

Boundary Condition Representation

edge1 and edge3 represent the radial edges whereas edge2 and edge4 are the circumferential edges as shown in Fig. 4. The nomenclature ’C’, ’S’ and ’F’ are used for clamped, simple and free supports respectively. The syntax of boundary condition is presented as ’edge1–edge2–edge3–edge4’.

Fig. 4

Plate element

The displacement conditions are,

• 1. Clamped support :

  $$\begin{aligned} u=v=w=\theta _x=\theta _y=0. \end{aligned}$$

• 2. Simple support : The simple supports are assumed to prevent the in-plane and the transverse displacements and offer no resistance to normal rotation [14].

  $$\begin{aligned} u=v=w=0. \end{aligned}$$

Solution Procedure

Free Vibration Analysis

The equation for free vibration of the system is

$$\begin{aligned}{}[M]\;\{{\ddot{u}}\}+[K]\;\{u\}=\{0\} \end{aligned}$$

(27)

where [M] and [K] are the global mass and stiffness matrices, $\{{\ddot{u}}\}$ and $\{u\}$ are the acceleration and displacement vectors. Since the free vibrations are periodic, by assuming

$$\begin{aligned} \{u\}=\{u_0\}\;e^{i \omega t} \end{aligned}$$

the time variable is separated from Eq. (27) and is obtained as

$$\begin{aligned}{}[K]\;\{u_0\}=\omega ^2\;[M]\;\{u_0\} \end{aligned}$$

(28)

where $\{u_0\}$ is the amplitude, $\omega$ is angular frequency and t is the time. Equation (28) is a standard form of the general eigenvalue problem.

Verification and Validation

The material properties shown in Table 1 of both plate and stiffener for all the free vibration verification examples of Sect. 4.1–4.5 in this paper.

Table 1 Material properties for both plate and stiffener

Bare Annular Sector Plate with Various Boundary Conditions

An annular sector plate of thickness (h) 0.005 m, as shown in Fig. 5 is considered for free vibration analysis. The mapping of the annular sector plate element for a 6$\times$6 mesh grid is shown in Fig. 6. The inner ($r_{\text {i}}$) and outer ($r_{\text {o}}$) radii of the plate are 0.5 m and 1 m respectively, and the sector angle ($\alpha$) is $45^{\circ }$. The convergence study of the non-dimensional frequency results is presented in Table 2 and compared with the differential quadrature method of Mirtalaie and Hajabasi [12] as well as with FEAST software. In addition, the non-dimensional frequency results for different boundary conditions are presented in Table 3 and compared with Mirtalaie and Hajabasi[12], and FEAST software.

The convergence study results of the S-F-S-F boundary condition for the non-dimensional frequencies shown in Table 2 are in excellent agreement with the published results of Mirtalaie and Hajabasi [12] and FEAST software. Also, the results obtained for the bare annular sector plates in Table  3 are in close agreement with those obtained by Mirtalaie and Hajabasi [12].

Fig. 5

Bare annular sector plate

Fig. 6

Mapping of plate element with 6 $\times$ 6 mesh grid

Table 2 Nondimensional frequencies for a bare annular sector plate with S-F-S-F boundary condition

Table 3 Non-dimensional frequencies for bare annular sector plate with S-S-S-S and S-C-S-C boundary conditions

Annular Sector Plate with Concentric Stiffeners

An annular sector plate of thickness (h) 0.005 m with two concentric circumferential stiffeners as shown in Fig. 7 is considered for the free vibration analysis. The sector angle ($\alpha$) is $45^\circ$ and the inner ($r_{\text {i}}$) and outer ($r_{\text {o}}$) radii are 0.25 m and 0.5 m respectively. The stiffener considered is rectangular in shape and dimensions are width (w) = 0.005 m and depth (d) = 0.02 m. The non-dimensional frequency results obtained are compared with that by finite strip method of Sheikh and Mukhopadhyay [25], and FEAST software in Table 4 which agree well.

Fig. 7

Plate with two circumferential stiffeners

Table 4 Non-dimensional frequencies of the plate with two concentric stiffeners

Annular Sector Plate with Eccentric Stiffeners

The annular sector plate of Sect. 4.2 is considered, but with two numbers of inverted T-shape eccentric stiffeners, as shown in Fig. 8. The non-dimensional frequency results are compared with the finite strip results of Sheikh and Mukhopadhyay [25] in Table 5 and found to be in good agreement.

Fig. 8

Inverted T beam stiffener

Table 5 Non-dimensional frequencies $\left( \omega r_{\text {i}}^2\sqrt{\displaystyle \frac{12 \rho (1-\nu ^2)}{Eh^2}}\right)$ of the plate with eccentric stiffeners

Bare Circular Plate

A bare circular plate of thickness 1 mm and radius ($r_{\text {i}}$) of 300 mm is considered for free vibration. The material properties of the plate are, Young’s modulus (E)=$6.87 \times 10^{7}$ ${\text {N}}/{\text {mm}}^2$, mass density ($\rho$)=$2.780 \times 10^{-6}$ kg/mm$^3$ and Poisson’s ratio ($\nu$)=0.34. The non-dimensional frequency results of bare plate with fully clamped and simply supported circumferential edges are presented in Table 6 and compared with the Rayleigh-Ritz results of Lam et al.[19], and the FEAST software.

Table 6 Non-dimensional frequencies of the bare circular plate with different boundary conditions

Bare Elliptical Plate

Elliptical plate of thickness 1 mm with major radius ($r_{\text {maj}}$) 600 mm and minor radius ($r_{\min }$) 300 mm is considered for the analysis. The material properties of the plate are the same as those given in Sect. 4.4. The non-dimensional frequency results of the bare elliptical plate with fully clamped and simply supported edges are presented in Table 7 and compared with the results of the Rayleigh–Ritz approach of Lam et al. [19], and the FEAST software.

Table 7 Non-dimensional frequencies of the bare elliptical plate with different boundary conditions

From Tables 6 and 7 , it may be noted that the vibration results for the bare circular and elliptical plates are showing excellent agreement with the published results of Lam et al. [19], and the FEAST software for both simply-supported and clamped conditions.

The results in Tables 2, 3, 4, 5, 6, 7, which are for verification and validation, show the accuracy of the present method.

Numerical Examples

The material properties shown in Table 1 of both plate and stiffener for all the free vibration verification examples of Sects. 5.1–5.6 in this paper.

Annular Sector Plate with Radial and Circumferential Stiffeners

The plate of thickness (h) 0.005 m with radial stiffeners shown in Fig. 9 and plate with circumferential stiffeners shown in Fig. 7 are considered for the analysis. The sector angle ($\alpha$) of the plate is $30^\circ$ and the inner ($r_{\text {i}}$) and outer ($r_{\text {o}}$) radii are 0.5 m and 1 m, respectively. The dimensions of the stiffener are shown in Fig. 10. The non-dimensional frequency results for a radially stiffened plate with circumferential edges clamped and circumferential stiffened plate with radial edges clamped are compared for both eccentric and concentric stiffeners in Table 8.

Fig. 9

Plate with radial stiffeners

Fig. 10

R-beam stiffener

Table 8 Non-dimensional frequencies of the plate with radial and circumferential stiffeners

While comparing the non-dimensional frequency results between the plates with circumferential and radial stiffeners, it is perceived from Table 8 that the circumferential attachment of stiffener with the plate increases the stiffness of the stiffened plate, as a consequence higher frequencies are achieved. In addition, the plate with eccentric stiffeners achieves higher non-dimensional frequencies in comparison to the concentric one.

Annular Sector Plate with Different Type of Stiffeners

An annular sector stiffened plate of thickness (h) 0.005 m shown in Fig. 11 with sector angle ($\alpha$) = $45^\circ$ and the inner ($r_{\text {i}}$) and outer ($r_{\text {o}}$) radii 0.4 m and 1 m, respectively is considered. Effect of different type of stiffeners (R-beam, I-beam and T-beam) shown in Figs. 10, 12 and 13 respectively are studied. The non-dimensional frequencies with different type of eccentric stiffeners for various boundary conditions are presented in Table 9. Also, the results for the plate with eccentric and concentric R-beam stiffeners are conferred in Table 10.

From the results presented in Table 9 with the consideration of the various combination of stiffeners, it is seen that the plate with I-beam eccentric stiffener is superior to that of the plate with R-beam and T-beam stiffeners. The non-dimensional frequencies of the I-beam stiffened plate achieve a higher value than that obtained with R-beam and T-beam stiffeners. Also, the non-dimensional frequency results for all edges clamped condition shows a higher value than obtained for other boundary conditions.

It is observed while considering the plate with R-beam stiffeners, from Table 10, that the non-dimensional frequencies are higher for the eccentrically attached stiffener than that of concentric ones. Also, the non-dimensional frequency values are higher for the clamped boundary condition than for other boundary conditions.

Fig. 11

Stiffened annular sector plate

Fig. 12

I-beam stiffener

Fig. 13

T-beam stiffener

Table 9 Non-dimensional frequencies of the plate with different type of stiffeners

Table 10 Non-dimensional frequencies of the plate with eccentric and concentric R-beam stiffener

Stiffened Annular Sector Plate for Different Inner-to-Outer Radii ($\frac{r_{\text {i}}}{r_{\text {o}}}$) Ratios and Different Sector Angles with Different Boundary Conditions

The free vibration analysis of the stiffened plate shown in Fig. 11 is investigated for varying sector angles ranging from $30^{\circ }$ to $150^{\circ }$). The dimensions of the stiffener are as shown in Fig. 10. The non-dimensional fundamental frequency results $\left( \omega r_{\text {i}}^2\sqrt{\displaystyle \frac{12 \rho (1-\nu ^2)}{Eh^2}}\right)$ with both eccentric and concentric stiffeners for different inner-to-outer radii ratios (0.2, 0.3, 0.4, 0.5, 0.6 and 0.7), and for different boundary conditions are presented in Figs. 14, 15, 16, 17, 18 and 19.

Fig. 14

Non-dimensional frequency of the C-C-C-C stiffened plate

Fig. 15

Non-dimensional frequency of the S-C-S-C stiffened plate

Fig. 16

Non-dimensional frequency of the C-S-C-S stiffened plate

Fig. 17

Non-dimensional frequency of the S-S-S-S stiffened plate

Fig. 18

Non-dimensional frequency of the C-F-C-F stiffened plate

Fig. 19

Non-dimensional frequency of the S-F-S-F stiffened plate

The influence of $(r_{\text {i}}/r_{\text {o}})$ ratios and sector angles on the stiffened plates’ non-dimensional frequencies can be observed in the detailed study presented in Figs. 14, 15, 16, 17, 18 and 19 for various boundary conditions. The non-dimensional fundamental frequency results give higher value with the increase of $(r_{\text {i}}/r_{\text {o}})$ ratios and decreased sector angles. It is noticed that the vibration results increases drastically for higher $(r_{\text {i}}/r_{\text {o}})$ ratios and lesser sector angles. A mild change is observed in the non-dimensional frequencies for the sector angles above $90^\circ$. It is also perceived that the eccentrically stiffened plates have higher non-dimensional frequency values than those of the concentric ones. The stiffened plate with C-C-C-C boundary condition shows higher non-dimensional fundamental frequency than those for other boundary conditions, which is obvious because of the increase in stiffness due to more fixity.

Stiffened Plates with Fixed and Floating Longitudinal Beams

A stiffened annular plate of thickness (0.005 m) with the longitudinal beams for both fixed and floating position shown in Figs. 20 and 21 are considered for the dynamic analysis. The sector angle ($\alpha$) of the plate is $30^\circ$ and the inner ($r_{\text {i}}$) and outer ($r_{\text {o}}$) radii are 0.5 m and 1 m, respectively. The dimensions of the transverse R-stiffener and longitudinal R-beam are shown in Fig. 10. The results for non dimensional frequency of stiffened plates with fixed and floating longitudinal beams for various boundary conditions are presented in Table 11.

Fig. 20

Annular sector plate with transverse beams with fixed longitudinal stiffeners (1-Plate, 2-transverse rectangular stiffeners, 3-longitudinal rectangular stiffeners )

Fig. 21

Annular sector plate with transverse beams with floating longitudinal stiffeners (1-Plate, 2-transverse rectangular stiffeners, 3-longitudinal rectangular stiffeners )

Table 11 Non-dimensional frequencies of the stiffened plate with fixed and floating longitudinal beams

It is observed from Table 11 that the non dimensional frequencies of the stiffened plate with floating beam stiffeners are greater than that of fixed ones. The higher eccentricity value makes the plate stiffer, which is the key factor for the higher frequency values of plate with floating beam stiffeners. It is also noticed that the difference between the frequency values of stiffened plate with floating and fixed beams are higher for C-F-C-F and S-F-S-F boundary conditions.

Stiffened Circular Plate

Circular plate with circumferential and radial stiffeners, shown in Figs. 22 and 23 respectively are considered for free vibration. The plate dimensions and material properties are the same as those given in Sect. 4.4. The stiffener’s material properties are the same as that of the plate, and the dimensions are width = 3 mm and depth = 20 mm. The non-dimensional frequency results of fully clamped plate with circumferential and radial (eccentric and concentric) stiffeners for varying $d_c$ and $d_r$ values are presented in Tables 12 and 13, respectively, where $d_c$ and $d_r$ are the distance of stiffener position from the centre of plate. The result for the eccentric stiffener at $d_r=0$ is compared with Barik and Mukhopdhyay [26] and presented in Table 13, which is in good agreement.

Fig. 22

Circular plate with circumferential stiffener

Fig. 23

Circular plate with radial stiffener

Table 12 Non-dimensional frequencies of the clamped circular plate with circumferential stiffener

Table 13 Non-dimensional frequencies of the clamped circular plate with radial stiffener

The non-dimensional frequencies of circular plates with radially attached stiffeners are more significant than that of circumferential ones, as shown in Tables 12 and 13 . The study of the circular stiffened plate leads to infer that the stiffener attached in circumferential direction closer to the edge (higher $d_c$ value) produces higher frequency values. As before, the eccentric stiffeners pronounce higher non-dimensional frequencies in comparison to the concentric ones.

Stiffened Elliptical Plate

Elliptical plates with circumferential and radial stiffeners, shown in Figs. 24 and 25, respectively, are considered for free vibration. The plate dimensions and material properties are the same as those given in Sect. 4.5. The same stiffener of Sect. 5.5 is used. The non-dimensional frequency results of fully clamped plate with circumferential eccentric and concentric stiffener for varying $d_{ca}$ and $d_{ci}$ values are presented in Table 14, where $d_{ca}$ and $d_{ci}$ are the distance of stiffener from the centre of plate in major and minor axis direction respectively. Similarly, Table 15 shows the non-dimensional frequency results of fully clamped plate with radial eccentric and concentric stiffeners for varying $d_r$ values.

Fig. 24

Elliptical plate with circumferential stiffener

Fig. 25

Elliptical plate with radial stiffener

Table 14 Non-dimensional frequencies of the clamped elliptical plate with circumferential stiffener

Table 15 Non-dimensional frequencies of the clamped elliptical plate with radial stiffener

It can be observed from Tables 14 and 15 that the elliptical plate depicts a similar behavior as the circular one.

Conclusions

The free vibration of unstiffened and stiffened curved plates is presented using the finite element method, where quadratic isoparametric elements are considered for the analysis. The formulation is accomplished separately for the plate and stiffener element and takes the shear deformation into account. The stiffeners are attached with the plate concentrically, eccentrically, and with floating disposition. The parametric study is carried out in detail for the dynamic response of the stiffened plates.

• Comparison of results has been reported for the stiffened plates and bare ones either with the published ones or with the FEAST results wherever possible, which shows the present method’s efficacy.

• The non-dimensional frequencies are higher for the stiffened plates with circumferential stiffeners than that of the radial ones.

• The non-dimensional frequencies are more significant for the I-beam eccentric stiffener than that of the R-beam and T-beam stiffeners.

• The non-dimensional frequencies are higher for the clamped conditions than for other boundary conditions.

• The non-dimensional fundamental frequency results achieve higher value with the increase of inner-to-outer radii ratios and decrease of sector angles, and also, the vibration results increase drastically for lesser sector angles and higher inner-to-outer radii ratios.

• The non-dimensional frequencies of the stiffened plate with floating beam stiffeners are higher than that of the fixed ones, which shows more significantly for C-F-C-F and S-F-S-F boundary conditions.

• The non-dimensional frequencies of circular and elliptical plates with radially attached stiffeners are more pronounced than that of the circumferential ones.