Introduction

The free vibration analysis of an engineering structure is highly significant in view of its proper design when it is subjected to any external dynamic force. For this analysis, various analytical and numerical methods have been proposed in the past. Even, engineering structures comprising of different materials have also been addressed in these analyses. Some of the recently published literature for dynamic analyses using various methods have been reported for plates as well as shells which can be found in the references [1,2,3,4]. These studies, however, limit themselves to the structures without any stiffener reinforcement. As the dynamic analysis of a stiffened plate structure is too much involved when attempted by an analytical approach, it is preferable to go for a numerical method such as finite element.

A stiffened plate is formed of a flat deck plate integrally attached with stiffeners in any direction. To make full use of the stiffness, stiffeners are often affixed to plates along with the main load-carrying directions. These are used in many engineering structures to acquire greater strength with a relatively small quantity of material use, which increases the strength–weight ratio and makes an economical structure.

The dynamic analyses of eccentrically stiffened plates have been reviewed by Srinivasan and Thiruvenkatachari [5] using the integral equation technique. Mukherjee and Mukhopadhyay [6] have investigated the free vibration characteristics of stiffened plates possessing symmetrical stiffeners by finite element method (FEM). Harik and Salamoun [7] have applied the analytical strip method to the analysis of rectangular stiffened plate where the plate and stiffeners have been modeled separately.

Palani et al. [8] have studied the vibration analysis of plates/shells with eccentric stiffeners by suggesting two isoparametric finite element models. The free vibration of rectangular stiffened plates has been analyzed by Koko and Olson [9] using a super element. Also, they have applied the plate beam idealization technique to finite element method where the stiffeners should have been placed on the nodal lines. A compound finite element model has been developed by Harik and Guo [10] to investigate the free vibration of eccentrically stiffened plates in free vibration where the plate elements and beam elements have been treated as integral parts of a compound section.

A finite element model has been proposed by Holopainen [11] for the free vibration analysis of eccentrically stiffened plates with an arbitrary number and orientation of stiffeners within a plate element. Zeng and Bert [12] have investigated the free vibration characteristics of an orthogonally stiffened skew plate using both the Rayleigh–Ritz method and finite element method. A four-noded stiffened plate element has been developed by Barik and Mukhopadhyay [13] for the free vibration analysis, which has accommodated any shape of the plate and arbitrary orientation of the stiffener. Sheikh and Mukhopadhyay [14] have studied the linear vibration analysis of stiffened plates using the spline finite strip method, where spline functions and finite element shape functions have been used as the displacement interpolation functions in one direction and the other directions, respectively.

The free vibration analysis of stiffened plates with unidirectional and orthogonal stiffeners has been carried out by Siddiqui and Shivhare [15, 16], respectively, using ANSYS parametric design language code. The free vibration analysis of integrally stiffened plates with plate-strip stiffeners has been explored by Ahmad and Kapania [17] using the Rayleigh–Ritz method and compared with ABAQUS software results. The free vibration characteristics of stiffened plates have been presented by Nayak et al. [18] for various parameters using finite element method.

It may be observed from above that the free vibration study on plates with non-orthogonal stiffener placement is scanty. The present endeavor is to perform a parametric study on the free vibration characteristics of plates with varying stiffener orientation using the finite element method and compare the results with those obtained by the FEAST software, and the APDL code.

The FEAST is the Indian Space Research Organisation’s structural analysis software based on Finite Element Method developed by structural engineering entity of Vikram Sarabhai Space Centre (VSSC) (http://www.vssc.gov.in). APDL code is an engineering structural solution software which is based on finite element analysis.

A continuous stiffened plated structure is assumed to be composed of a finite number of plate and stiffener elements interconnected at a limited number of nodes. The in-plane and transverse displacements within each element are uniquely defined with appropriate displacement functions. The effects of rotary inertia and torsional stiffness of the stiffeners are included in the formulation. The natural frequency results of stiffened plates are compared with the published ones. For the analysis of the stiffened plates, various types of stiffeners, both concentric as well as eccentric ones, have been used. The results for various parameters such as boundary conditions, aspect ratios, plate thickness–stiffener depth ratios, and stiffener width–depth ratios are analyzed. The effect of the orientation of the stiffeners placement on free vibration is also presented.

Theoretical Formulation

The stiffness and mass matrices are derived for the plate and the stiffener elements separately for the dynamic analysis of the stiffened plates.

Plate Element Matrices

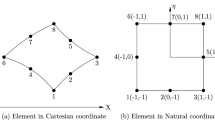
The nodal displacements considered for the plate element shown in Fig. 1 are \({u_i}\), \({v_i}\), \({ w_i}\), \(\theta _{xi}\) and \(\theta _{yi}\), where \(u_i\) and \(v_i\) are the in-plane displacements, \(w_i\) is the lateral displacement and \(\theta _{xi}\) and \(\theta _{yi}\) are the rotations in the y and x directions, respectively, for the node i. The distributed nodal forces that act along the boundaries of an element are replaced by statically equivalent concentrated forces at the nodes of the element. These nodal forces are \(f_{ui}\), \(f_{vi}\), \(f_{wi}\), \(m_{xi}\) and \(m_{yi}\), where \(f_{ui}\) and \(f_{vi}\) are the in-plane nodal forces, \(f_{wi}\) is the nodal lateral force and \(m_{xi}\) and \(m_{yi}\) are the nodal moments in the y and x directions, respectively, at node i.

Fig. 1
figure 1

Rectangular plate element

Full size image
$$\begin{aligned}&\text {The displacement field is expressed as}\;{\{u\}}_e\nonumber \\&\quad =\begin{Bmatrix} \ u \\ v\\ -- \\ w \end{Bmatrix}_e=\begin{bmatrix} N^m \\ -- \\ N^b \end{bmatrix}\{\delta \}_e, \end{aligned}$$
(1)

where [N] is the shape function, and m and b superscripts refer to the in-plane and bending effects, respectively, and expressed as

$$\begin{aligned} {[}N^m]= & {} \begin{bmatrix} (1-s)(1-t) &{} 0 &{} (1-s)t &{} 0 &{} s (1-t) &{} 0 &{} s t &{} 0\\ 0 &{} (1-s)(1-t) &{} 0 &{} (1-s)t &{} 0 &{} s (1-t) &{} 0 &{} s t \end{bmatrix}, \end{aligned}$$
(2)
$$\begin{aligned} {[}N^b]= & {} \begin{bmatrix} 1-st-(3-2s)s^2(1-t)-(1-s)(3-2t)t^2\\ -(1-s)t(1-t)^2b\\ (1-s)^2s(1-t)a\\ (3-2t)t^2(1-s)+s(1-s)(1-2s)t\\ (1-s)(1-t)t^2b\\ s(1-s)^2t a\\ (3-2s)s^2(1-t)+st (1-t)(1-2t)\\ -st(1-t)^2b\\ -(1-s)s^2(1-t)a\\ (3-2s)s^2t-st(1-t)(1-2t)\\ s(1-t)t^2b\\ -(1-s)s^2t a \end{bmatrix}^T, \end{aligned}$$
(3)

where \(s=\dfrac{x}{a}\) and \(t=\dfrac{y}{b}\); a and b are the plate dimensions in x- and y-directions, respectively.

The plate strains produced from the assumed displacements are:

$$\begin{aligned} \{ \epsilon \}_e=\begin{Bmatrix} \epsilon ^m \\ -- \\ \epsilon ^b \end{Bmatrix}=\begin{Bmatrix} \dfrac{\partial u}{\partial x}\\ \dfrac{\partial v}{\partial y}\\ \dfrac{\partial u}{\partial y}+\dfrac{\partial v}{\partial x}\\ ----\\ -\dfrac{\partial ^2w}{\partial x^2} \\ -\dfrac{\partial ^2w}{\partial y^2}\\ -2\dfrac{\partial ^2w}{\partial x\partial y} \end{Bmatrix}=\begin{bmatrix} B^m \\ -- \\ B^b \end{bmatrix}\{\delta \}_e. \end{aligned}$$
(4)

Plate stresses are expressed in terms of strains as:

$$\begin{aligned}&\{\sigma \}_e= [D]\;\{\epsilon \}_e, \end{aligned}$$
(5)
$$\begin{aligned}&{\mathrm{where}}\; \{ \sigma \}_e=\begin{Bmatrix} \sigma ^m \\ --\\ \sigma ^b \end{Bmatrix}=\begin{Bmatrix} N_{x}\\ N_{y}\\ N_{xy}\\ ---\\ M_{x}\\ M_{y}\\ M_{xy}, \end{Bmatrix} \end{aligned}$$
(6)
$$\begin{aligned}&{\mathrm{Elasticity matrix}} \;\; [D]=\begin{bmatrix} D^m\\ --\\ D^b \end{bmatrix}\nonumber \\&\quad = \begin{bmatrix} D_1 &{} \nu D_1 &{} 0 &{} 0 &{} 0 &{} 0\\ \nu D_1 &{} D_1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \dfrac{(1-\nu )D_1}{2} &{} 0 &{} 0 &{} 0\\ --&{} --&{}--&{}--&{}--&{}--\\ 0 &{} 0 &{} 0 &{} D_2 &{} \nu D_2 &{} 0\\ 0 &{} 0 &{} 0 &{} \nu D_2 &{} D_2 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{(1-\nu )D_2}{2}, \end{bmatrix} \end{aligned}$$
(7)

where \(D_1= \dfrac{Eh}{(1-\nu ^2)}\) and \(D_2= \dfrac{Eh^3}{12(1-\nu ^2)}.\)

Appropriate geometric transformation matrices are used to relate the displacements and forces from element coordinate system to the global coordinate system. Nodal displacements \(\{q\}_e\) from the global coordinate system can be transformed into those of the element coordinate system \(\{\delta \}_e\) by

$$\begin{aligned} \{\delta \}_e= [T]_e \; \{q\}_e, \end{aligned}$$
(8)

where \([T]_e\) is a transformation matrix for element e. The finite element mass, stiffness and load matrices in the element coordinate system are

$$\begin{aligned} {[}m]_e= & {} \int _{Ae}\rho \; h\;[N]^T\;[N]\;{\text {d}}A, \end{aligned}$$
(9)
$$\begin{aligned} {[}k]_e= & {} \int _{Ae} [B]^T\;[D]\;[B]\;{\text {d}}A, \end{aligned}$$
(10)
$$\begin{aligned} {[}f]_e= \; & {} \int _{Ae} [N]^T\;\{p\}_e\; {\text {d}}A, \end{aligned}$$
(11)

which can be expressed in global coordinate system as

$$\begin{aligned} {[}m]_{eg}= \; & {} [T]_e^T\;[m]_e\;[T]_e, \end{aligned}$$
(12)
$$\begin{aligned} {[}k]_{eg}= \; & {} [T]_e^T\;[k]_e\;[T]_e, \end{aligned}$$
(13)
$$\begin{aligned} {[}f]_{eg}= \; & {} [T]_e^T\;\{f\}_e, \end{aligned}$$
(14)

Stiffener Element Matrices

A stiffener element in the x-direction having an eccentricity \(e_{\text {c}}\) from the middle surface of the plate is shown in Fig. 2, where i and k are two ends of the stiffener. The torsional effect is considered after the evaluation of the in-plane and bending stiffness and mass matrices.

Fig. 2
figure 2

Eccentric stiffener element

Full size image

The nodal displacements and their corresponding nodal forces at node i, as shown in Fig. 2 are

$$\begin{aligned} \{\delta \}_{si}&=\begin{Bmatrix} u_{si}&w_{si}&\theta _{syi} \end{Bmatrix}, \end{aligned}$$
(15)
$$\begin{aligned} \{f\}_{si}&=\begin{Bmatrix} f_{sui}&f_{swi}&m_{syi} \end{Bmatrix}. \end{aligned}$$
(16)

The displacement functions of the centroidal line of the stiffener are,

$$\begin{aligned} \{u\}_s=\begin{Bmatrix} u_s \\ w_s \end{Bmatrix}=[N]_s \;\; \{\delta \}_{s}, \end{aligned}$$
(17)

where

$$\begin{aligned} {[}N]_s=\begin{bmatrix} (1-s) &{} 0 \\ \dfrac{6e_c}{a}(s-s^2) &{} (1-3s^2+2s^3)\\ 3e_c(s-s^2) &{} a(s-2s^2+s^3)\\ s &{} 0 \\ \dfrac{6e_c}{a}(-s+s^2) &{} (3s^2-2s^3)\\ 3e_c(s-s^2) &{} a(-s^2+s^3) \end{bmatrix}^T. \end{aligned}$$
(18)

and

$$\begin{aligned} \{\delta \}_{s}=\{ u_{si} \;\; w_{si}\;\; \theta _{syi}\;\; u_{sk}\;\; w_{sk}\;\; \theta _{syk} \}^T. \end{aligned}$$
(19)

This shape function is for stiffener in x-direction only. The strains for stiffener in terms of displacements are given by

$$\begin{aligned} \{ \epsilon \}_s=\begin{Bmatrix} \dfrac{\partial u_s}{\partial x}\\ -\dfrac{\partial ^2w_s}{\partial x^2} \end{Bmatrix}=[B]_s \;\{\delta \}_s. \end{aligned}$$
(20)

The elasticity matrix for the stiffener is expressed as

$$\begin{aligned}{}[D]_s=E_s\begin{bmatrix} A_x &{} 0\\ 0 &{} I_x, \end{bmatrix} \end{aligned}$$
(21)

where \(A_x\) is the cross-sectional area, \(I_x\) is the cross-sectional area moment of inertia and \(E_s\) is Young’s modulus of the stiffener material. The stiffness and mass matrices can be found in a similar manner as that of the plate element and can be expressed as

$$\begin{aligned} {[}k]_s= & {} \int _{Ae} [B]_s^T\;[D]_s\;[B]_s\;{\text {d}}A \end{aligned}$$
(22)
$$\begin{aligned} {[}m]_s= & {} \int _{Ae}\rho _s\; h\;[N]_s^T\;[N]_s\;{\text {d}}A. \end{aligned}$$
(23)

The torsional stiffness matrix is given by:

$$\begin{aligned} \begin{Bmatrix} m_{sxi} \\ m_{sxk} \end{Bmatrix}= \dfrac{G_{sx}J_x}{a}\begin{bmatrix} 1 &{} -1 \\ -1 &{} 1 \end{bmatrix}\begin{Bmatrix} \theta _{sxi} \\ \theta _{sxk}, \end{Bmatrix} \end{aligned}$$
(24)

where \({G_{sx}}\) is the modulus of rigidity of the stiffener, \(J_x\) is the torsional constant and \(\rho _s\) is the density of the stiffener. This torsional stiffness matrix and stiffness matrix for the in-plane and bending effects can be combined to obtain the stiffness matrix for the eccentric stiffener element as

$$\begin{aligned}&{[}k]_s=\begin{bmatrix} \dfrac{E_sA_x}{a} &{}&{}&{}&{}&{}&{}&{}&{}&{} \\ 0 &{} 0 &{}&{}&{}&{} &{}{\text {Sym}}.&{}&{}&{}\\ 0 &{} 0 &{} \dfrac{12E_sI_{ox}}{a^3} &{}&{}&{}&{}&{}&{}&{} \\ 0 &{} 0 &{} 0 &{}K3 &{}&{}&{}&{}&{}&{} \\ 0 &{} 0 &{} \dfrac{6E_sI_{ox}}{a^2} &{} 0 &{} K1 &{}&{}&{}&{}&{} \\ -\dfrac{E_sA_x}{a} &{} 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{E_sA_x}{a} &{}&{}&{}&{} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}&{}&{} \\ 0 &{} 0 &{} -\dfrac{12E_sI_{ox}}{a^3} &{} 0 &{} -\dfrac{6E_sI_{ox}}{a^2} &{} 0 &{} 0 &{} \dfrac{12E_sI_{ox}}{a^3} &{}&{} \\ 0 &{} 0 &{} 0 &{} -K3 &{} 0 &{} 0 &{} 0 &{} 0 &{} K3 &{} \\ 0 &{} 0 &{} \dfrac{6E_sI_{ox}}{a^2} &{} 0 &{} K2 &{} 0 &{} 0 &{} -\dfrac{6E_sI_{ox}}{a^2} &{} 0 &{} K1 \end{bmatrix}\nonumber \\&\begin{aligned} \text {where} \;\;\;&K1=\dfrac{4E_sI_{ox}}{a}-\dfrac{e_c^2 E_s A_x}{a}&K2=&\dfrac{2E_sI_{ox}}{a}+\dfrac{e_c^2 E_s A_x}{a} \\&K3=\dfrac{G_{sx}J_x}{a}&I_{ox}=&I_x+A_xe_c^2. \\ \end{aligned} \end{aligned}$$
(25)

The mass matrix for the stiffener can be obtained as

$$\begin{aligned}&{[}m]_s=\rho _s\;A_x\;a\begin{bmatrix} \dfrac{1}{J_x} &{} &{}&{}&{}&{}&{}&{}&{}&{} \\ 0 &{} 0 &{}&{}&{}&{} &{}&{}&{}&{} \\ \dfrac{e_c}{2a} &{} 0 &{} S1 &{}&{}&{}&{}&{}&{}{\text {Sym}}.&{}\\ 0 &{} 0 &{} 0 &{} \dfrac{J_x}{3A_x} &{}&{}&{}&{}&{}&{} \\ \dfrac{e_c}{4} &{} 0 &{} S2 &{} 0 &{} S3 &{}&{}&{}&{}&{} \\ \dfrac{1}{6} &{} 0 &{} \dfrac{e_c}{2a} &{} 0 &{} \dfrac{e_c}{4} &{} \dfrac{1}{J_x} &{}&{}&{}&{} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}&{}&{} \\ -\dfrac{e_c}{2a} &{} 0 &{} S5 &{} 0 &{} S4 &{} 0 &{} 0&{} S1 &{}&{} \\ 0 &{} 0 &{} 0 &{} \dfrac{J_x}{6A_x} &{} 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{J_x}{3A_x} &{} \\ \dfrac{e_c}{4} &{} 0 &{} -S4 &{} 0 &{} S6 &{} \dfrac{e_c}{4} &{} 0 &{} -S2 &{} 0 &{} S3 \end{bmatrix}\nonumber \\&\begin{aligned} \text {where}\;\;\;&S1 =\dfrac{13}{35}+\dfrac{6}{5}\dfrac{I_{ox}}{A_xa^2}&S2 =\dfrac{11a}{210}+\dfrac{I_{ox}}{10A_xa}+\dfrac{e_c^2}{2a} \\&S3 =\dfrac{a^2}{105}+\dfrac{2}{15}\dfrac{I_{ox}}{A_x}+\dfrac{e_c^2 }{6}&S4=\dfrac{13a}{420}-\dfrac{I_{ox}}{10A_xa}-\dfrac{e_c^2}{2a}\\&S5 =\dfrac{9}{70}-\dfrac{6}{5}\dfrac{I_{ox}}{A_xa^2}&S6=-\dfrac{a^2}{140}-\dfrac{I_{ox}}{30A_x}+\frac{e_c^2}{3}. \end{aligned} \end{aligned}$$
(26)

Similarly, the element matrices for the y-direction stiffener can be obtained.

Stiffener with Arbitrary Orientation

The plate stiffened with arbitrarily oriented stiffener are shown in Fig. 3, where the stiffener is along \(x'\)-axis and makes an angle \(\beta\) (anticlockwise) with the x-axis of the plate.

Fig. 3
figure 3

Plate with arbitrarily oriented stiffener

Full size image

Similar to Eq. (19), the displacement of the stiffener in \(x'- y'\) axis is given by

$$\begin{aligned} \{\delta '\}_{s\beta }=\{ u'_{si} \;\;v'_{si}\;\; w'_{si}\;\; \theta '_{sxi}\;\;\theta '_{syi}\;\; u'_{sk}\;\;v'_{sk}\;\; w'_{sk}\;\; \theta '_{sxk}\;\;\theta '_{syk} \}^T, \end{aligned}$$
(27)

which can be expressed in terms of the displacements in \(x-y\) axis as

$$\begin{aligned}&\{\delta '\}_{s\beta } =\begin{bmatrix} \cos \beta &{} \sin \beta &{} 0&{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{}0&{}0\\ -\sin \beta &{} \cos \beta &{}0&{}0 &{} 0 &{} 0 &{} 0 &{} 0&{}0&{}0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0&{} 0 &{} 0&{} \cos \beta &{} \sin \beta &{} 0 &{} 0 &{} 0&{}0&{}0\\ 0&{} 0 &{} 0&{} -\sin \beta &{} \cos \beta &{} 0 &{} 0 &{} 0&{}0&{}0\\ 0 &{} 0 &{} 0&{}0&{}0 &{} \cos \beta &{} \sin \beta &{} 0&{} 0 &{} 0\\ 0 &{} 0 &{} 0&{}0&{}0 &{} -\sin \beta &{} \cos \beta &{}0&{}0 &{} 0 \\ 0 &{} 0 &{} 0&{}0&{}0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0&{}0&{}0 &{} 0&{} 0 &{} 0&{} \cos \beta &{} \sin \beta \\ 0 &{} 0 &{} 0&{}0&{}0 &{} 0&{} 0 &{} 0&{} -\sin \beta &{} \cos \beta \end{bmatrix}\begin{Bmatrix} u_{si} \\ v_{si}\\ w_{si}\\ \theta _{sxi}\\ \theta _{syi}\\ u_{sk}\\ v_{sk}\\ w_{sk}\\ \theta _{sxk} \\ \theta _{syk}, \end{Bmatrix} \end{aligned}$$
(28)
$$\begin{aligned}&\{\delta '\}_{s\beta } =[T]_{s\beta }\; \{\delta \}_{s\beta }. \end{aligned}$$
(29)

Similar to Eq. (17), the displacement functions of the arbitrarily oriented stiffener are,

$$\begin{aligned} \{u\}_{s\beta }=[N]_{s\beta } \;\; \{\delta '\}_{s\beta }. \end{aligned}$$
(30)

Putting Eq. (29) in (30)

$$\begin{aligned} \{u\}_{s\beta }=[N]_{s\beta } \;\; [T]_{s\beta }\;\{\delta \}_{s\beta }. \end{aligned}$$
(31)

The strains for stiffener are given by

$$\begin{aligned} \{ \epsilon \}_{s\beta }=[B]_{s\beta } \;\{\delta '\}_{s\beta }. \end{aligned}$$
(32)

Putting Eq. (29) in (32)

$$\begin{aligned} \{ \epsilon \}_{s\beta }=[B]_{s\beta } \; [T]_{s\beta } \;\{\delta \}_{s\beta }. \end{aligned}$$
(33)

The stiffness and mass matrices for the stiffener are given by

$$\begin{aligned} {[}k]_{s\beta }= \; & {} \int _{Ae} [T]_{s\beta }^T \;[B]_{s\beta }^T\;[D]_s\;[B]_{s\beta } \;[T]_{s\beta }\;{\text {d}}A\nonumber \\=\, & {} [T]_{s\beta }^T \;[k]_s\;[T]_{s\beta }, \end{aligned}$$
(34)
$$\begin{aligned} {[}m]_{s\beta }= \; & {} \int _{Ae}\rho _s\; h\;[T]_{s\beta }^T\;[N]_{s\beta }^T\;[N]_s\;[T]_{s\beta }\;{\text {d}}A\nonumber \\= \, & {} [T]_{s\beta }^T \;[m]_s\;[T]_{s\beta }. \end{aligned}$$
(35)

Diagonal Stiffener

The plate with diagonal stiffener is where the stiffener is attached along the two diagonal corners of the plate element as shown in Fig. 4. The stiffness and mass matrices are same as Eqs. (34) and (35).

Fig. 4
figure 4

Plate with diagonal stiffener

Full size image

Boundary Conditions

The essential boundary conditions considered are

  1. (a)

    for a clamped support, the known displacement conditions are

    $$\begin{aligned} u=v=w=\theta _x=\theta _y=0 \end{aligned}$$
  2. (b)

    for a simply support (x = constant),

    $$\begin{aligned} v=w=\theta _x=0 \end{aligned}$$
  3. (c)

    for a simply support (y = constant),

    $$\begin{aligned} u=w=\theta _y=0. \end{aligned}$$

The nomenclatures C, S and F represent clamped, simply supported and free edges, respectively.

Solution Procedure

Free Vibration Analysis

The equation for free vibration of the system is

$$\begin{aligned} {[}M]\;\{\ddot{q}\}+[K]\;\{q\}=\{0\}, \end{aligned}$$
(36)

where [M] is the global mass matrix, [K] is the global stiffness matrix, \(\{\ddot{q}\}\) is the acceleration vector and \(\{q\}\) is the displacement vector. Since the free vibrations are periodic, by assuming

$$\begin{aligned} \{q\}=\{q_0\}\;e^{i \omega t} \end{aligned}$$

the time variable is separated from Eq. (36) and is obtained as

$$\begin{aligned} {[}K]\;\{q_0\}=\omega ^2\;[M]\;\{q_0\}, \end{aligned}$$
(37)

where \(\{q_0\}\) is amplitude of \(\{q\}\), \(\omega\) is angular frequency of vibrations, and t is the time. Eq. (36) is a standard form of the general eigenvalue problem. If the two square matrices [K] and [M] are of size (\(f\times f\)), then there will be, in general, f different values of the natural frequency \(\omega\).

Numerical Examples

Free Vibration Analysis of Square Plate Point Supported at Corners

A square plate shown in Fig. 5 of thickness 0.0016 m point-supported at corners is considered for free vibration analysis. The Young’s modulus E = 206 GPa, density \(\rho\) = 7929 kg/m\(^3\) and Poisson’s ratio \(\nu\) = 0.3. The results obtained by the present FEM, FEAST and APDL software for a grid size of (24 \(\times\) 24) are compared with finite difference results of Cox and Boxer [19] in Table 1. The results are in excellent agreement.

Fig. 5
figure 5

Square bare plate point supported at corners

Full size image
Table 1 Non-dimensional frequencies \(\left( \varOmega = \omega \sqrt{\dfrac{\rho _{\text {p}}ha^{4}}{D}}\right)\) for a square plate point-supported at corners
Full size table

Clamped Square Plate with a Central Concentric Stiffener

A square plate clamped in all edges (C–C–C–C), having a centrally placed stiffener as presented by Nair and Rao [20] in Fig. 6 using the package STIFPTI has been analyzed by the present method. The dimensions of the plate are 600 mm \(\times\) 600 mm \(\times\) 1.0 mm and the material properties are: Young’s modulus \(E = 6.87\times 10^7\) N/mm\(^2\), Poisson’s ratio \(\nu = 0.34\) and density \(\rho = 2.78 \times 10^{-6}\) kg/mm\(^3\). A stiffener of \(A_s = 67.0 \,{\text {mm}}^2\), \(I_s = 2290 \,{\text {mm}}^4\) and \(J_s = 22.33 \,{\text {mm}}^4\) is taken. The frequency results obtained from FEM, APDL and FEAST software are compared with Nair and Rao [20] and presented in Table 2 showing excellent agreement. Also, the result is compared with the diagonally stiffened plate as shown in Fig. 7 with eccentric stiffener in Table 2.

Fig. 6
figure 6

Clamped square plate with a central concentric stiffener

Full size image
Fig. 7
figure 7

Clamped square plate with a diagonal stiffener

Full size image
Table 2 Frequency (Hz) of a clamped square plate with a central concentric stiffener
Full size table

Clamped Square Plate with Eccentric Stiffener

A clamped square plate (C–C–C–C) results having a centrally placed eccentric stiffener shown in Fig. 8 is of dimension \(600\,{\text {mm}}\,\times \,600\,{\text {mm}} \,\times \,1.0\,{\text {mm}}\) has been compared with those of Sheikh and Mukhopadhyay [14]. The stiffener is of width \(w=3\, {\text {mm}}\) and depth \(d=20 \,{\text {mm}}\). The material properties for both the plate and stiffener are: Young’s modulus \(E = 6.87\times 10^7\, {\text {N/mm}}^2\), Poisson’s ratio \(\nu = 0.34\) and density \(\rho = 2.78 \times 10^{-6} \,{\text {kg/mm}}^3\). The natural frequencies are shown in Table 3 with results of spline finite strip method which compare well. Also, the result is compared with the diagonally stiffened plate as shown in Fig. 7 with eccentric stiffener in Table 3.

Fig. 8
figure 8

Clamped square plate with a central eccentric stiffener and the section A–A

Full size image
Table 3 Natural frequency (Hz) of square plate with an eccentric stiffener
Full size table

Plate with Diagonal Concentric Stiffener

A plate with diagonal concentric stiffeners shown in Fig. 9 is analyzed using FEM. The plate dimensions are: \(a=1\,{\text {m}},\,b=1\,{\text {m}}\) and thickness \(h= 0.005\,{\text {m}}\). The material properties of the plate are: Young’s modulus \(E = 20\,{\text {GPa}}\), Poisson’s ratio \(\nu = 0.2\) and unit weight \(\rho = 2400\, {\text {kg/m}}^3\). The rectangular beam (R-beam) stiffeners are attached diagonally for the free vibration analysis as shown in Fig. 10 and having the material properties, Young’s modulus \(E = 210\,{\text {GPa}}\), Poisson’s ratio \(\nu = 0.3\) and unit weight \(\rho = 7850 \,{\text {kg/m}}^3\). The results obtained for free vibration with different boundary conditions are compared with those by APDL software using SHELL181 element and presented in Table 4.

Fig. 9
figure 9

Plate with diagonal R-beam stiffeners

Full size image
Fig. 10
figure 10

Rectangular beam

Full size image
Table 4 Frequency (Hz) of square plate with diagonal concentric stiffeners
Full size table

It may be observed from Table 4 that the results from present formulation compare well with those obtained using APDL software package. For C–C–C–C boundary condition, the frequency is greater than that of other boundary conditions for the plate with concentric rectangular stiffeners.

Plate with Arbitrary Stiffener Orientation

Plates with arbitrary concentric stiffener orientation as shown in Fig. 11 are considered for free vibration analysis. The plate dimensions are: \(a=1000\,{\text {mm}}\), \(b=1000\,{\text {mm}}\) and thickness \(h= 5\,{\text {mm}}\). The material properties of the plate are: Young’s modulus \(E = 20\,{\text {GPa}}\), Poisson’s ratio \(\nu = 0.2\) and unit weight \(\rho = 2400\, {\text {kg/m}}^3\). The I-stiffeners are attached diagonally for the free vibration analysis shown in Fig. 12 and having the material properties, Young’s modulus \(E = 210\,{\text {GPa}}\), Poisson’s ratio \(\nu = 0.3\) and unit weight \(\rho = 7850 \,{\text {kg/m}}^3\). The frequency results for \(\beta\) values \(15^\circ\), \(30^\circ\) and \(45^\circ\) with all edges clamped are compared with APDL software package in Table 5, where the angle \(45^\circ\) is taken for the diagonal stiffener. It is observed that the frequency value increases with the increase of \(\beta\) values and the rate of increament is more in higher mode in comparison to the lower ones.

Fig. 11
figure 11

Plate with arbitrary stiffener

Full size image
Fig. 12
figure 12

I-beam

Full size image
Table 5 Natural frequency (Hz) of plate with arbitrary stiffeners
Full size table

Plate with Diagonal Stiffeners and Orthogonal Stiffeners

The plates with diagonal and orthogonal eccentric stiffeners as shown in Fig. 13 are considered for free vibration analysis separately. The plate dimensions are: \(a=1\,{\text {m}},\,b=1\,{\text {m}}\) and thickness \(h= 0.005\,{\text {m}}\). The material properties of the plate are: Young’s modulus \(E = 20\,{\text {GPa}}\), Poisson’s ratio \(\nu = 0.2\) and unit weight \(\rho = 2400\, {\text {kg/m}}^3\). The rectangular beam (R-beam) stiffeners are attached diagonally for the free vibration analysis shown in Fig. 10 and having the material properties, Young’s modulus \(E = 210\,{\text {GPa}}\), Poisson’s ratio \(\nu = 0.3\) and unit weight \(\rho = 7850 \,{\text {kg/m}}^3\). The non-dimensional frequency \(\left( \omega b^2\sqrt{{12 \rho (1-\nu ^2)}/{Eh^2}}\right)\) results for both plates with all edges clamped are compared in Table 6. The higher frequency results of diagonally stiffened plate shows that it becomes stiffer in comparison to the plate with orthogonal stiffeners.

Fig. 13
figure 13

Plate with diagonal and orthogonal eccentric stiffeners

Full size image
Table 6 Non-dimensional frequency \(\left( \omega b^2\sqrt{\displaystyle \frac{12 \rho (1-\nu ^2)}{Eh^2}}\right)\) for plate with diagonal and orthogonal stiffeners
Full size table

Plate with Diagonal Eccentric Stiffener

The free vibration response of a plate with diagonal eccentric stiffeners shown in Fig. 9 is analyzed. The plate dimensions and material properties are same as in section 4.4. Two types of stiffeners (I-beam and R-beam) are considered for the analysis which are shown in Figs. 10 and 12, respectively. The stiffeners are of Young’s modulus \(E = 210\,{\text {GPa}}\), Poisson’s ratio \(\nu = 0.3\) and unit weight \(\rho = 7850 \,{\text {kg/m}}^3\). The results for natural frequency with various boundary conditions are obtained for both the beams and presented in Table 7.

Table 7 Natural frequency(Hz) of square plate with diagonal eccentric stiffeners
Full size table

From Table 7, it is observed that the plate with I-eccentric stiffener’s natural frequencies are higher than that of plate with R-eccentric stiffener for all boundary conditions. All edges clamped stiffened plate’s frequencies are greater compared to those of the other boundary conditions because of the increased stiffness of clamped plates.

Stiffened Plate with Different Aspect Ratios

Stiffened plate with the same thickness and material properties as considered in section 4.7 is analyzed for both the I- and R-stiffeners. The non-dimensional fundamental frequency \(\left( \omega b^2\sqrt{{12 \rho (1-\nu ^2)}/{Eh^2}}\right)\) results for different aspect ratios \(\left( \dfrac{a}{b} \right)\) such as 0.2, 0.4, 0.6, 0.8 and 1.0 are investigated with different boundary conditions and presented in Figs. 14, 15, 16, 17 and 18.

Fig. 14
figure 14

Non-dimensional frequency of the C–C–C–C stiffened plate for different aspect ratios

Full size image
Fig. 15
figure 15

Non-dimensional frequency of the C–S–C–S stiffened plate for different aspect ratios

Full size image
Fig. 16
figure 16

Non-dimensional frequency of the S–S–S–S stiffened plate for different aspect ratios

Full size image
Fig. 17
figure 17

Non-dimensional frequency of the S–F–S–F stiffened plate for different aspect ratios

Full size image
Fig. 18
figure 18

Non-dimensional frequency of the C–F–F–F stiffened plate for different aspect ratios

Full size image

It is observed from Figs. 14, 15, 16, 17 and 18 that the non-dimensional fundamental frequency for I-eccentric stiffened plate is marginally higher than that of plate with eccentric R-stiffener. But for concentric stiffeners, R-beam stiffened plate has higher non-dimensional frequency than that of I-beam stiffened plate. It is also noted that the non-dimensional frequency is decreasing with the increase of aspect ratios for all type of stiffeners and for all boundary conditions. It is also observed that the non-dimensional frequency for all edges clamped stiffened plate is greater compared to that of other boundary conditions.

Stiffened Plate with Various Stiffener Depth-to-Thickness of Plate \(\left( \displaystyle \frac{d}{h}\right)\) Ratio

The plate investigated in section 4.7 is considered for free vibration analysis, but now with the I-stiffener shown in Fig 12. The non-dimensional frequency \(\left( \omega b^2\sqrt{{12 \rho (1-\nu ^2)}/{Eh^2}}\right)\) results for different stiffener depth–thickness of plate ratios are explored with various boundary conditions for both eccentric as well as concentric stiffeners and presented in Fig. 19 and 20.

Fig. 19
figure 19

Non-dimensional frequency of the eccentric stiffened plate for different \(\left( \displaystyle \frac{d}{h}\right)\) ratios

Full size image
Fig. 20
figure 20

Non-dimensional frequency of the concentric stiffened plate for different \(\left( \displaystyle \frac{d}{h}\right)\) ratios

Full size image

From Fig. 19 and 20, it is inferred that the non-dimensional frequency is increasing with the increase of \(\left( \displaystyle \frac{d}{h}\right)\) ratio and with the further increase of ratio, non-dimensional frequency values remain unchanged. It is also observed that the non-dimensional frequency value is higher for eccentric stiffeners than that of concentric stiffeners for the same boundary condition. The non-dimensional frequency is higher for C–C–C–C plate compared to other boundary conditions.

Stiffened plate with various stiffener width–depth \(\left( \displaystyle \frac{w}{d} \right)\) ratio

The plate with diagonal stiffeners considered in section 4.7 is investigated for the free vibration analysis to study the effect of various stiffener width–depth \(\left( \displaystyle \frac{w}{d} \right)\) ratios by keeping the area of rectangular beam stiffener constant. The non-dimensional frequency \(\left( \omega b^2\sqrt{\displaystyle \frac{12 \rho (1-\nu ^2)}{Eh^2}}\right)\) results for different boundary conditions of the plate with eccentric and concentric stiffeners are presented in Figs. 21 and 22.

Fig. 21
figure 21

Non-dimensional frequency \(\left( \omega b^2\sqrt{\displaystyle \frac{12 \rho (1-\nu ^2)}{Eh^2}}\right)\) of the stiffened plate for different \(\left( \displaystyle \frac{w}{d} \right)\) ratios

Full size image
Fig. 22
figure 22

Non-dimensional frequency \(\left( \omega b^2\sqrt{\displaystyle \frac{12 \rho (1-\nu ^2)}{Eh^2}}\right)\) of the stiffened plate for different \(\left( \displaystyle \frac{w}{d} \right)\) ratios

Full size image

Figures 21 and 22 shows that the non-dimensional frequency is decreasing with the increase of \(\left( \displaystyle \frac{w}{d}\right)\) ratio, and with the further increase of ratio, the change in frequency values is minimal. It is also observed that the eccentric stiffened plate achieves greater frequency values than that of concentric stiffened plate with the increase of \(\left( \displaystyle \frac{w}{d}\right)\) ratio.

Conclusions

A finite element method is presented for free vibration analysis of stiffened plates, where the plate and stiffener element matrices are derived separately. The stiffener disposition in the plate is considered for both the concentric as well as eccentric ones. The orientation of the stiffener position has been considered in a general manner by which its effect on the free vibration has been observed for different orientation. The difference in results between the orthogonally and diagonally stiffened plates has been discussed. A detailed parametric study is carried out for the dynamic response of the stiffened plates by varying the plate aspect ratio, stiffener depth–plate thickness ratio, stiffener width–depth ratio. Results have been compared either with the published ones or with the ANSYS/FEAST results wherever possible.