A Convex Programming Approach to Mid-course Trajectory Optimization for Air-to-Ground Missiles

Abstract

This paper addresses trajectory optimization in the mid-course phase of an air-to-ground missile, when the main objectives are (a) to ensure that the target is locked on in the center of the missile’s field-of-view at a specified flight path angle and (b) to attain maximum possible speed to allow for sufficient maneuverability in the terminal phase. The method presents as a second-order cone program (SOCP) formulation for this trajectory optimization, taking advantage of partial linearization and lossless convexification techniques that effectively handle underlying non-convex characteristics of the problem. A well-established SOCP solver can then be readily used to obtain the optimal solution to this convex program. The proposed approach is validated by (a) proving the losslessness of the convexification, and (b) numerically comparing the results with an existing pseudo-spectral method.

1 Introduction

The typical precision-guided tactical missiles are equipped with a seeker for target detection and/or recognition. Depending on whether the missile uses seeker information, the guidance algorithm is divided into two phases: one for mid-course guidance, the other for terminal guidance. The main objectives of the mid-course guidance are to ensure that the target is locked on in center of the missile’s FOV (field-of-view) at a specified flight path angle with sufficient maneuverability [1]. However, in the case of air-to-ground missiles, it is not trivial to design the optimal mid-course guidance considering wide regime of initial conditions and several constraints. Therefore, it is important to generate the optimal mid-course trajectory according to the initial condition in order to maximize the performance of the missile. In this paper, a convex programming approach to mid-course trajectory optimization for air-to-ground missiles is presented to find out the possibility of real-time trajectory optimization. The maximum allowable altitude constraint is additionally considered with impact angle and angle-of-attack constraints.

The way to generate the missile trajectory is largely divided into the analytic and numerical methods. The analytic method for impact angle control have been proposed based on the optimal control theory or proportional navigation guidance law using simplified linear model [2,3,4,5,6,7,8,9]. In recent years, although the practical constraints such as acceleration limit and seeker’s field-of-view have been considered for the derivation of guidance laws [6,7,8,9], they still depend on limited constraints and simplified models. In addition to the analytic method, various numerical methods have been also proposed to solve optimal control problems such as trajectory optimization [10,11,12]. The standard way to solve optimal control problems is to divide the whole interval of optimal control problems into specified subintervals, and to calculate the optimal values of states and controls at the ends of the specified subintervals using existing nonlinear programming methods [13]. However, nonlinear programming is very sensitive to initial conditions and cannot guarantee convergence, and also requires long computation time. As an alternative, convex programming approaches have been attempted in the aerospace field because it is robust to initial conditions and ensures convergence with the polynomial time [14, 15]. Particularly, in the case of the second-order cone programming, research papers in various areas including the real-time trajectory optimization technique have been published [16,17,18,19,20].

In order to use convex programming, it is necessary to convert general nonlinear optimal control problems into convex problems and the following three problems should be addressed. At first, an appropriate method for integration of objective function and dynamic model should be presented. While the pseudo-spectral methods define the specific differential and integral operator based on the representation, the convex programming approach needs to define the differentiation and integration method such as the trapezoidal rule [21, 22]. Second, nonlinear equations such as state constraints, control constraints and dynamic model should be convexified. There are two main ways to perform the convex transformation; one is linearization method and the other is relaxation method. Since linearization method sequentially calculates linear model for an equilibrium point, it is straightforward to implement [23,24,25,26]. However, the optimality and convergence of the solution cannot be generally guaranteed and the optimal solution can be obtained in the case where the nonlinear characteristics are not critical. On the other hand, relaxation method transforms a non-convex problem into a convex problem by relaxing the constraint. If the relaxation does not affect the solution of the original problem, it is called as lossless convexification and then we can easily obtain the optimal solution using convex programming [19, 27,28,29,30]. However, the proof for the lossless convexification should be performed based on the optimal control theory. Finally, a monotone-independent variable with a specific initial and final value should be defined. Although time is the typical independent variable for dynamics and objective function, there are a number of problems with free final time. If the final time is not specified, we need to sequentially predict the final time or find an independent variable in the state variables [19, 23].

In this paper, the convex approach to mid-course trajectory optimization problem of the air-to-ground missile with boost-glide phase is proposed. The objective is to maximize the final velocity satisfying the specific final impact angle with altitude and angle-of-attack constraints. Since the original problem is a nonlinear optimal control problem with free final time, it should be converted to convex optimization problem. The main contribution of this paper is as follows: (a) the losslessness of the convexification is proved based on the maximum principle of optimal control theory and (b) change of independent variable is proposed to tackle the free final time problem and (c) proposed approach is validated numerically comparing the results with an existing pseudo-spectral method.

The paper is organized as follows. Section 2 gives a summary of the mid-course trajectory optimization problem formulation with change of independent variable. In Sect. 3, details of partial linearization, discretization and lossless convexification are described for convex programming. And a sequential second-order cone programming algorithm is presented to obtain the convergent solution. Numerical simulations and conclusion are given in Sects. 4 and 5, respectively.

2 Problem Formulation

2.1 Mid-course Trajectory

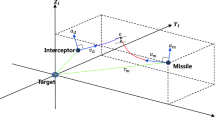
In this section, the mid-course trajectory optimization problem of an air-to-ground missile with boost-glide phases is described. Figure 1 shows the engagement scenario of the short-range air-to-ground missile with altitude constraint.

Fig. 1

Mid-course trajectory geometry. $x,y,V,\gamma$ represent the downrange, altitude, velocity and flight path angle, respectively. The subscripts $0,f,T$ denote the initial condition, final condition and target. And $y_{\hbox{max} } ,r_{\text{d}}$ represent the maximum allowable altitude and target detection range of seeker

The nonlinear equations of motion in a two-dimensional longitudinal plane are given in Eq. (1).

$$ \begin{aligned} \dot{x} & = V\cos \gamma , \\ \;\dot{y} & = V\sin \gamma , \\ \;\dot{V} & = \frac{1}{m}\left( {T\cos \alpha - D} \right) - g\sin \gamma , \\ \dot{\gamma } & = \frac{1}{mV}\left( {T\sin \alpha + L} \right) - \frac{1}{V}g\cos \gamma , \\ \end{aligned} $$

(1)

where $m = \left\{ {\begin{array}{*{20}c} {m_{0} - \frac{{\left( {m_{\text{f}} - m_{0} } \right)}}{{t_{\text{T}} }}t} & {t \le t_{\text{T}} } \\ {m_{\text{f}} } & {t > t_{\text{T}} } \\ \end{array} } \right., T = \left\{ {\begin{array}{*{20}c} {T_{0} } & {t \le t_{\text{T}} } \\ 0 & {t > t_{\text{T}} } \\ \end{array} } \right..$

Here, $m$ is the mass of missile, $g$ is the gravitational acceleration, and $T$ is the thrust magnitude with the burning time $t_{\text{T}}$. $L, D$ represent the aerodynamic lift and drag force and are assumed as the first order and second order function of angle-of-attack as follows:

$$ \begin{aligned} L = \left( {qS_{\text{ref}} } \right)\left( {C_{{{\text{L}}_{ 0} }} + C_{{{\text{L}}_{\alpha 1} }} \alpha } \right), \hfill \\ D = \left( {qS_{\text{ref}} } \right)\left( {C_{{{\text{D}}_{ 0} }} + C_{{{\text{D}}_{\alpha 2} }} \alpha^{2} } \right), \hfill \\ \end{aligned} $$

(2)

where $q = \frac{1}{2}\rho V^{2} ,\;S_{\text{ref}} ,q$ represent the reference area and dynamic pressure, respectively. $C_{{{\text{L}}_{0} }} ,C_{{{\text{L}}_{\alpha 1} }}$ and $C_{{{\text{D}}_{0} }} ,C_{{{\text{D}}_{\alpha 2} }}$ are the aerodynamic coefficients for lift and drag. Assuming the angle-of-attack is small enough for all $t \in \left[ {t_{0} ,t_{\text{f}} } \right]$, the trigonometric functions of angle-of-attack are approximated as follows:

$$ \cos \alpha \approx 1,\quad \sin \alpha \approx \alpha . $$

(3)

If we denote the state variables as $z = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} x & y \\ \end{array} } & {\begin{array}{*{20}c} V & \gamma \\ \end{array} } \\ \end{array} } \right]$ and the control variables as $u = \left[ {\begin{array}{*{20}c} \alpha & {\alpha^{2} } \\ \end{array} } \right]$, the dynamic equations (1) are described as follows:

$$ \begin{aligned} \dot{z} & = \frac{{{\text{d}}z}}{{{\text{d}}t}} = f_{\text{z}} \left( z \right) + B_{\text{z}} \left( z \right)u \\ & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {V\cos \gamma } \\ {V\sin \gamma } \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{T}{m} - \frac{{qS_{\text{ref}} }}{m}C_{{{\text{D}}_{ 0} }} - g\sin \gamma } \\ { - \frac{1}{V}g\cos \gamma + \frac{{qS_{\text{ref}} }}{mV}C_{{{\text{L}}_{0} }} } \\ \end{array} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ {\frac{1}{mV}\left( {T + qS_{\text{ref}} C_{{{\text{L}}_{\alpha 1} }} } \right)} \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} { - \frac{{qS_{\text{ref}} }}{m}C_{{{\text{D}}_{\alpha 2} }} } \\ 0 \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \alpha \\ {\alpha^{2} } \\ \end{array} } \right], \\ \end{aligned} $$

(4)

where $m = \left\{ {\begin{array}{*{20}c} {m_{0} - \frac{{\left( {m_{\text{f}} - m_{0} } \right)}}{{t_{\text{T}} }}t} & {t \le t_{\text{T}} } \\ {m_{\text{f}} } & {t > t_{\text{T}} } \\ \end{array} } \right., T = \left\{ {\begin{array}{*{20}c} {T_{0} } & {t \le t_{\text{T}} } \\ 0 & {t > t_{\text{T}} } \\ \end{array} } \right..$

The constraints on altitude and angle-of-attack are shown in Eq. (5):

$$ \begin{aligned} 0 & \le y \le y_{\rm{max} } , \\ - \alpha_{\rm{max} } & \le \alpha \le \alpha_{\rm{max} } . \\ \end{aligned} $$

(5)

Now we define problem P0 as nonlinear optimal control problem with dynamics, state constraint, control constraint, initial condition, and final condition.

$$ P0: \rm{min} - V\left( {t_{\text{f}} } \right) \;{\text{subject to:}} $$

Dynamics

$$ \dot{z} = f_{\text{z}} \left( z \right) + B_{\text{z}} \left( z \right)u . $$

State constraint

$$ 0 \le y \le y_{\rm{max} } . $$

Control constraint

$$ u_{1}^{2} = u_{2} ,\;0 \le u_{2} \le u_{2\rm{max} } = \alpha_{\rm{max} }^{2} . $$

Initial condition

$$ z\left( {t_{0} } \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x\left( {t_{0} } \right)} & {y\left( {t_{0} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} {V\left( {t_{0} } \right)} & {\gamma \left( {t_{0} } \right)} \\ \end{array} } \\ \end{array} } \right]. $$

Final condition

$$ \begin{aligned} x\left( {t_{\text{f}} } \right) & = x_{\text{f}} = x_{\text{T}} - r_{\text{d}} \cos \gamma_{\text{f}} , \\ y\left( {t_{\text{f}} } \right) & = y_{\text{f}} = y_{\text{T}} - r_{\text{d}} \sin \gamma_{\text{f}} , \\ \gamma \left( {t_{\text{f}} } \right) & = \gamma_{\text{f}} . \\ \end{aligned} $$

2.2 Transformation of Dynamic Equations

Since the problem P0 is a nonlinear optimal control problem, it is extremely difficult to find the solution analytically. Instead, the solution can be numerically obtained through nonlinear programming, convex programming, etc. In order to use numerical methods, there should be an independent variable that has boundary values and monotonic property. In this paper, since the final time is not specified, we set $x$ as an independent variable. As a result, the new state variable is defined as $q = \left[ {\begin{array}{*{20}c} y & {\begin{array}{*{20}c} V & \gamma \\ \end{array} } \\ \end{array} } \right]$ and the dynamic Eq. (4) is reconstructed as follows:

$$ \begin{aligned} q^{\prime} & = \frac{{{\text{d}}q}}{{{\text{d}}x}} = f_{\text{q}} \left( q \right) + B_{\text{q}} \left( q \right)u \\ & = \left[ {\begin{array}{*{20}c} {\tan \gamma } \\ {\frac{T}{mV\cos \gamma } - \frac{{qS_{\text{ref}} }}{mV\cos \gamma }C_{{{\text{D}}_{0} }} - \frac{g}{V}\tan \gamma } \\ { - \frac{1}{{V^{2} }}g + \frac{{qS_{\text{ref}} }}{{mV^{2} \cos \gamma }}C_{{{\text{L}}_{0} }} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{\left( {T + qS_{\text{ref}} C_{{{\text{L}}_{\alpha 1} }} } \right)}}{{mV^{2} \cos \gamma }}} \\ \end{array} \begin{array}{*{20}c} 0 \\ { - \frac{{qS_{\text{ref}} }}{mV\cos \gamma }C_{{{\text{D}}_{\alpha 2} }} } \\ 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \alpha \\ {\alpha^{2} } \\ \end{array} } \right], \\ \end{aligned} $$

(6)

where $m = \left\{ {\begin{array}{*{20}c} {m_{0} - \frac{{\left( {m_{\text{f}} - m_{0} } \right)}}{{t_{\text{T}} }}t} & {t \le t_{\text{T}} } \\ {m_{\text{f}} } & {t > t_{\text{T}} } \\ \end{array} } \right., T = \left\{ {\begin{array}{*{20}c} {T_{0} } & {t \le t_{\text{T}} } \\ 0 & {t > t_{\text{T}} } \\ \end{array} } \right..$

Then, the problem P1 is re-defined using new independent variable.

$$ P1: \hbox{min} - V\left( {x_{\text{f}} } \right) \;{\text{subject to:}} $$

Dynamics

$$ q^{\prime} = f_{\text{q}} \left( q \right) + B_{\text{q}} \left( q \right)u . $$

State constraint

$$ 0 \le y \le y_{\rm{max} } . $$

Control constraint

$$ u_{1}^{2} = u_{2} ,0 \le u_{2} \le u_{2\rm{max} } = \alpha_{\rm{max} }^{2} . $$

Initial condition

$$ q\left( {x_{0} } \right) = \left[ {\begin{array}{*{20}c} {y\left( {x_{0} } \right)} & {V\left( {x_{0} } \right)} & {\gamma \left( {x_{0} } \right)} \\ \end{array} } \right]. $$

Final condition

$$ \begin{aligned} y\left( {x_{\text{f}} } \right) & = y_{\text{f}} = y_{\text{T}} - r_{\text{d}} \sin \gamma_{\text{f}} , \\ \gamma \left( {x_{\text{f}} } \right) & = \gamma_{\text{f}} . \\ \end{aligned} $$

3 Formulation to Second-Order Cone Programming

The second-order cone programming, specific field of convex programming, is defined as follows [31]:

$$ \begin{aligned} \left( P \right): \hbox{min}\, c^{\text{T}} x \hfill \\ {\text{subject to}}\;Ax = b, x \in K, \hfill \\ \end{aligned} $$

(7)

where $x \in R^{n}$ is the optimization variables. $A \in R^{m \times n}$ with $m \le n$ and ${\text{rank}}\left( A \right) = n, c \in R^{n} , b \in R^{m}$ are all given. $K$ is convex set that is the Cartesian product of linear cones $K_{ + }$ and quadratic cones $K_{\text{q}}$ as follows:

$$ \begin{aligned} K_{ + } & = \left\{ {x \in R:x \ge 0} \right\}, \\ K_{\text{q}} & = \left\{ {x \in R^{n} :x_{n} \ge \sqrt {x_{1}^{2} + \cdots + x_{n - 1}^{2} } ,x_{n} \ge 0} \right\}. \\ \end{aligned} $$

(8)

Since the problem P1 still have nonlinear dynamics and non-convex control constraint, the proper convexification should be performed for the dynamic equation and control constraint. At first, in the case of nonlinear dynamics, linear equations are derived through partial linearization with trust region. And the discretization based on the trapezoidal rule is used to cope with the integration. Secondly, the non-convex control constraint is relaxed into the convex control constraint using the lossless convexification and the detailed proof is shown in “Appendix”.

3.1 Partial Linearization

Assume that $q^{k}$ is the $k$th optimal solution of the problem P1. The nonlinear equations (6) are converted to linear equations using the partial linearization:

$$ q^{\prime} = A\left( {q^{k} } \right)q + B_{q} \left( {q^{k} } \right)u + c\left( {q^{k} } \right), $$

(9)

where

$$ \begin{aligned} & A\left( {q^{k} } \right) = \frac{{\partial f_{q} \left( {q^{k} } \right)}}{\partial q}, \\ & c\left( {q^{k} } \right) = f_{\text{q}} \left( {q^{k} } \right) - A\left( {q^{k} } \right)q^{k} , \\ &a_{13} = \sec^{2} \gamma , \\ \end{aligned} $$

$$ \begin{aligned} a_{22} & = - \frac{T}{{mV^{2} \cos \gamma }} + \frac{g\tan \gamma }{{V^{2} }} - \frac{{\rho S_{\text{ref}} }}{2m\cos \gamma }C_{{{\text{D}}_{0} }} , \\ a_{23} & = \frac{T\tan \gamma }{mV\cos \gamma } - \frac{{g\sec^{2} \gamma }}{V} - \frac{{\rho VS_{\text{ref}} \tan \gamma }}{2m\cos \gamma }C_{{{\text{D}}_{0} }} , \\ \end{aligned} $$

$$ \begin{aligned} a_{32} & = \frac{2g}{{V^{3} }}, \\ a_{33} & = \frac{{\rho S_{\text{ref}} \tan \gamma }}{2m\cos \gamma }C_{{{\text{L}}_{ 0} }} , \\ a_{11} & = a_{12} = a_{21} = a_{31} = 0, \\ \end{aligned} $$

where $a_{ij}$ represents the element of the $i$th row and the $j$th column of the A matrix. Since the partial linearization technique does not require information about the control values for the linearization, it is known that it reduces the oscillation characteristics and also increases the convergence speed. In addition, the validity of the linearization is established by adding the following trust region:

$$ \left\| {q - q^{k} } \right\| \le \delta_{\text{q}} . $$

(10)

3.2 Discretization

For the numerical methods, the continuous optimal control problem such as problem P1 needs to be converted to nonlinear programming formulation through appropriate discretization process. The entire flight trajectory is divided into N equal sections according to the independent variable and the discrete points are denoted as follows:

$$ x_{i} = x_{0} + \left( {\frac{{x_{\text{f}} - x_{0} }}{N}} \right) \times i, i = 0,1, \ldots ,N - 1,N. $$

(11)

In this paper, the trapezoidal rule in Eq. (12) is used to deal with the dynamic equations. Through the discretization, the dynamic equations can be described as the algebraic form at all discrete points:

$$ q_{i}^{k} = q_{i - 1}^{k} + \frac{\Delta x}{2}\left[ {f_{\text{q}} \left( {q_{i - 1}^{k} } \right) + B\left( {q_{i - 1}^{k} } \right)u_{i - 1}^{k} + f_{\text{q}} \left( {q_{i}^{k} } \right) + B\left( {q_{i}^{k} } \right)u_{i}^{k} } \right], i = 1, \ldots ,N. $$

(12)

Since the air-to-ground missile with the solid propulsion system has the specific burning time, this should be considered for the dynamics formulation. At first, the $i_{\text{T}}$th section including the burning time $t_{\text{T}}$ is calculated in (13):

$$ t_{\text{Tsim}} \left( {i_{\text{T}} - 1} \right) \le t_{\text{T}} < t_{\text{Tsim}} \left( {i_{\text{T}} } \right), $$

(13)

where $t_{\text{Tsim}} \left( {i_{\text{T}} } \right) = \sum\nolimits_{i = 1}^{{i_{T} }} {\frac{2\Delta x}{{\left( {V_{i - 1} \cos \gamma_{i - 1} + V_{i} \cos \gamma_{i} } \right)}}} .$

Considering the mass dynamics of missiles in (1), the mass and thrust of missile is approximated as follows:

$$ m_{i}^{k} = \left\{ {\begin{array}{*{20}c} {m_{0} - \left( {m_{\text{f}} - m_{0} } \right)\left( {\frac{i - 1}{{i_{\text{T}} }}} \right)} & {i \le i_{\text{T}} } \\ {m_{\text{f}} } & {i > i_{\text{T}} } \\ \end{array} } \right., $$

(14)

$$ T_{i}^{k} = \left\{ {\begin{array}{*{20}c} {T_{0} } & {i \le i_{\text{T}} } \\ 0 & {i > i_{\text{T}} } \\ \end{array} } \right.. $$

(15)

3.3 Lossless Convexification

For the convex programming, the non-convex control constraint also needs to be represented as convex form. If the equality in the constraint can be replaced by the inequality yielding the same optimal solution, the problem P1 can be represented as convex problem. Such a convex relaxation is called as a lossless convexification [27,28,29,30]. In this section, we prove a lossless convexification related to the control constraint based on the maximum principle of optimal control theory [32].

3.3.1 Maximum Principle

From the optimal control theory, the Hamiltonian, the Lagrangian and the endpoint functions are defined as follows [30, 32]:

$$ H\left( t \right) = p_{0} l\left( t \right) + p^{\text{T}} \left( t \right)f\left( t \right), $$

(16)

$$ L\left( t \right) = H\left( t \right) + \lambda^{\text{T}} \left( t \right)g\left( t \right) + \nu^{\text{T}} \left( t \right)h\left( t \right), $$

(17)

$$ G\left( {t_{\text{f}} } \right) = p_{0} \varphi \left( {t_{\text{f}} } \right) + \xi^{\text{T}} \left( t \right)b\left( {t_{\text{f}} } \right) + \zeta^{\text{T}} \left( t \right)h\left( {t_{\text{f}} } \right), $$

(18)

where $l\left( t \right)$ and $\varphi \left( {t_{\text{f}} } \right)$ represent the Lagrange term for running cost and the Mayer term for terminal cost, respectively. And $p\left( t \right)$ is the costate variable, and $\lambda ,\nu ,\xi ,\zeta$ are multipliers. The following theorem represents the maximum principle with state constraints [30, 32].

Theorem 1

Let $\left\{ {x\left( \cdot \right),u\left( \cdot \right)} \right\}$ be an optimal pair on the interval $\left[ {t_{0} ,t_{\text{f}} } \right]$ such that $x\left( \cdot \right)$ has a finite number of junction times. Then there exists a constant $p_{0} \le 0$ , a piecewise absolutely continuous $p\left( \cdot \right)$ , piecewise continuous $\lambda \left( \cdot \right)$ and $\nu \left( \cdot \right)$ , a vector $\eta \left( {\tau_{i} } \right)$ for each point of discontinuity $\tau_{i}$ in $p\left( \cdot \right)$ , and constant $\xi$ and $\zeta$ such that the following conditions are satisfied:

• (i) the non-triviality condition

  $$ \left( {p_{0} ,p\left( t \right),\lambda \left( t \right),\nu \left( t \right),\xi ,\zeta ,\eta \left( {\tau_{1} } \right), \ldots } \right) \ne 0\;\;\forall t; $$

  (19)

• (ii) the pointwise maximum condition

  $$ u\left( t \right) = \arg \hbox{max} H\left( {t,x\left( t \right),\omega ,p\left( t \right),p_{0} } \right)\;\;{\text{a}} . {\text{e}} . {\text{t}}\;\omega \in \varOmega \left( t \right); $$

  (20)

• (iii) the differential equations

  $$ \dot{x}^{\text{T}} \left( t \right) = \partial_{p} L\left( t \right), $$

  (21)
  $$ - \dot{p}^{\text{T}} \left( t \right) = \partial_{x} L\left( t \right)\;\;{\text{a}} . {\text{e}} . {\text{t,}} $$

  (22)
  $$ \dot{H}\left( t \right) = \partial_{t} L\left( t \right); $$

  (23)

• (iv) the stationary condition

  $$ \partial_{u} L\left( t \right) = 0\;\;{\text{a}} . {\text{e}} . {\text{t;}} $$

  (24)

• (v) the complementary slackness conditions

  $$ g\left( t \right) \le 0,\;\lambda \left( t \right) \le 0,\;\lambda^{\text{T}} \left( t \right)g\left( t \right) = 0\;\;{\text{a}} . {\text{e}} . {\text{t,}} $$

  (25)
  $$ h\left( t \right) \le 0,\;\nu \left( t \right) \le 0,\;\;\nu^{\text{T}} \left( t \right)h\left( t \right) = 0\;\;{\text{a}} . {\text{e}} . {\text{t}}, $$

  (26)
  $$ h\left( {\tau_{i} } \right) \le 0,\;\eta \left( {\tau_{i} } \right) \le 0,\;\eta^{\text{T}} \left( {\tau_{i} } \right)h\left( {\tau_{i} } \right) = 0\;\;\forall \tau_{i} , $$

  (27)
  $$ h\left( {t_{\text{f}} } \right) \le 0,\;\zeta \le 0,\;\zeta^{\text{T}} h\left( {t_{\text{f}} } \right) = 0; $$

  (28)

• (vi) the jump conditions

  $$ p^{\text{T}} \left( {\tau_{i}^{ - } } \right) = p^{\text{T}} \left( {\tau_{i}^{ + } } \right) + \eta^{\text{T}} \left( {\tau_{i} } \right)\partial_{x} h\left( {\tau_{i} } \right)\;\quad \forall \tau_{i} , $$

  (29)
  $$ H\left( {\tau_{i}^{ - } } \right) = H\left( {\tau_{i}^{ + } } \right) - \eta^{\text{T}} \left( {\tau_{i} } \right)\partial_{t} h\left( {\tau_{i} } \right)\quad \;\forall \tau_{i} ; $$

  (30)

• (vii) the prescribed boundary conditions

  $$ x\left( {t_{0} } \right) = x_{0} ,\;b\left( {t_{\text{f}} } \right) = 0; $$

  (31)

• (viii) the transversality conditions

  $$ p^{\text{T}} \left( {t_{\text{f}} } \right) = \partial_{x} g\left( {t_{\text{f}} } \right), $$

  (32)
  $$ - H\left( {t_{\text{f}} } \right) = \partial_{t} g\left( {t_{\text{f}} } \right). $$

  (33)

3.3.2 Proof of Lossless Convexification

At first, the assumption for trust region is needed to facilitate the proof of lossless convexification. If the trust region is set to be large enough and system dynamics is not highly nonlinear, the following assumption is valid.

Assumption 1

The trust region (10) should be large enough to be inactive for all $x \in \left[ {x_{0} ,x_{\text{f}} } \right].$

For the problem P1 under the Assumption 1, the Hamiltonian, the Lagrangian and the endpoint functions are described as follows:

$$ H = p_{y} \left( {a_{13} \gamma + c_{y} } \right) + p_{V} \left( {a_{22} V + a_{23} \gamma + c_{V} + b_{22} u_{2} } \right) + p_{\gamma } \left( {a_{32} V + a_{33} \gamma + c_{\gamma } + b_{31} u_{1} } \right), $$

(34)

$$ L = H + \lambda_{0} \left( {u_{1}^{2} - u_{2} } \right) + \lambda_{1} \left( { - u_{2} } \right) + \lambda_{2} \left( {u_{2} - u_{2\rm{max} } } \right) + \nu_{y1} \left( { - y} \right) + \nu_{y2} \left( {y - y_{\rm{max} } } \right), $$

(35)

$$ G\left( {x_{\text{f}} } \right) = p_{0} \left( { - V\left( {x_{\text{f}} } \right)} \right) + \zeta_{y1} \left( { - y\left( {x_{\text{f}} } \right)} \right) + \zeta_{y2} \left( {y\left( {x_{\text{f}} } \right) - y_{\rm{max} } } \right). $$

(36)

The differential equations (22) for costate variables are described as follows:

$$ p_{y}^{'} = - \frac{\partial L}{\partial y} = \nu_{y1} - \nu_{y2} , $$

(37)

$$ p_{V}^{'} = - \frac{\partial L}{\partial V} = - \left( {p_{V} a_{22} + p_{\gamma } a_{32} } \right), $$

(38)

$$ p_{\gamma }^{'} = - \frac{\partial L}{\partial \gamma } = - \left( {p_{y} a_{13} + p_{V} a_{23} + p_{\gamma } a_{33} } \right). $$

(39)

The stationary equations (24) are represented as follows:

$$ \frac{\partial L}{{\partial u_{1} }} = p_{\gamma } b_{31} + 2\lambda_{0} u_{1} = 0, $$

(40)

$$ \frac{\partial L}{{\partial u_{2} }} = p_{V} b_{22} - \lambda_{0} - \lambda_{1} + \lambda_{2} = 0. $$

(41)

The complementary slackness conditions for the state and control variables are as follows:

$$ \lambda_{0} \le 0,\;\;\lambda_{0} \left( {u_{1}^{2} - u_{2} } \right) = 0, $$

(42)

$$ \lambda_{1} \le 0,\;\;\lambda_{1} \left( { - u_{2} } \right) = 0, $$

(43)

$$ \lambda_{2} \le 0,\;\;\lambda_{2} \left( {u_{2} - u_{2\rm{max} } } \right) = 0, $$

(44)

$$ \nu_{y1} \le 0,\;\;\nu_{y1} \left( { - y} \right) = 0, $$

(45)

$$ \nu_{y2} \le 0,\;\;\nu_{y2} \left( {y - y_{\rm{max} } } \right) = 0, $$

(46)

$$ \zeta_{y1} \le 0,\;\;\;\zeta_{y1} \left( { - y\left( {x_{\text{f}} } \right)} \right) = 0, $$

(47)

$$ \zeta_{y2} \le 0,\;\;\zeta_{y2} \left( {y\left( {x_{\text{f}} } \right) - y_{\hbox{max} } } \right) = 0. $$

(48)

The transversality conditions are as follows:

$$ p_{y} \left( {x_{\text{f}} } \right) = \frac{\partial G}{\partial y} = - \zeta_{y1} + \zeta_{y2} , $$

(49)

$$ p_{\text{V}} \left( {x_{\text{f}} } \right) = \frac{\partial G}{\partial V} = - p_{0} , $$

(50)

$$ p_{\gamma } \left( {x_{\text{f}} } \right) = \frac{\partial G}{\partial \gamma } = 0. $$

(51)

Since the handover point generally exists between the minimum and maximum altitude, the following assumption is valid for normal engagement scenarios.

Assumption 2

The final value of altitude exists between the minimum and maximum value.

Theorem 2 represents a lossless convexification for the control constraint. The detailed proof is given in “Appendix”.

Theorem 2

Under Assumptions 1 and 2, let $\left( {q^{*} ,u^{*} } \right)$ be an optimal solution of P2. Then, $u_{1}^{2} = u_{2}$ is satisfied almost everywhere on $\left[ {x_{0} ,x_{\text{f}} } \right].$

Based on Theorem 2, thus, the following problem P2 represents the final second-order cone problem based on discretization and relaxation.

$$ P2: \hbox{min} - V\left( {x_{\text{f}} } \right)\; {\text{subject to:}} $$

Dynamics

$$ H\bar{q} = F. $$

State constraint

$$ \begin{aligned} 0 \le y \le y_{\rm{max} } \hfill \\ \left\| {q - q^{k} } \right\| \le \delta_{\text{q}} . \hfill \\ \end{aligned} $$

Control constraint

$$ u_{1}^{2} \le u_{2} ,\;0 \le u_{2} \le u_{2\rm{max} } = \alpha_{\rm{max} }^{2} . $$

Initial condition

$$ q\left( {x_{0} } \right) = \left[ {\begin{array}{*{20}c} {y\left( {x_{0} } \right)} & {V\left( {x_{0} } \right)} & {\gamma \left( {x_{0} } \right)} \\ \end{array} } \right]. $$

Final condition

$$ \begin{aligned} y\left( {x_{\text{f}} } \right) & = y_{\text{f}} = y_{\text{T}} - r_{\text{d}} \sin \gamma_{\text{f}} , \\ \gamma \left( {x_{\text{f}} } \right) & = \gamma_{\text{f}} . \\ \end{aligned} $$

3.4 Sequential Second-Order Cone Programming

Sequential second-order cone programming is a local optimization method based on successive convex approximation. At first, we assume the initial state and control profile using initial and final values or any other approximation. From the second optimization, the information obtained at the previous optimization phase is used to convexify the dynamics and to approximate mass and thrust. The dynamics is sequentially convexified at the optimal point and mass and thrust profile is also estimated until we obtain the convergent solution.

4 Simulation Results

In this section, the mid-course trajectory optimization for air-to-ground missiles satisfying constraints is generated by applying the sequential SOCP. Table 1 shows the specification of the air-to-ground missiles used in numerical simulations.

Table 1 Specification of missile

The initial conditions is set to $q\left( {x_{0} } \right) = \left[ {\;\begin{array}{*{20}c} {1000\;{\text{m}}} & {100\;{\text{m/s}}} & {0\deg } \\ \end{array} } \right]^{\text{T}}$ and the discrete points are set to be 401 including the initial point. Trust region and convergence condition are set as follows:

$$ r_{\text{q}} = \left[ {\begin{array}{*{20}c} {500\;{\text{m}}} & {300\;{\text{m/s}}} & {30\deg } \\ \end{array} } \right], $$

(52)

$$ \varepsilon = \left[ {\begin{array}{*{20}c} {1\;{\text{m}}} & {0.5\;{\text{m/s}}} & {0.05\deg } \\ \end{array} } \right]. $$

(53)

As we mentioned in Assumption 1, trust region is set to be large enough considering the feasible range of each variable. And convergence condition is set to be small enough reflecting the computation time. To solve the SOCP, MOSEK, which is one of the state-of-the-art interior point methods, is applied.

4.1 SOCP Results for Mid-course Trajectory Optimization

The initial state and control profile is set as a line that linearly connects the initial condition and the final condition. Since the final velocity is not specified, it is set to Mach 1.0. Figure 2 shows the sequential convergence of missile trajectory as a result of 9 iterations by SOCP. It can be seen that the initial trajectory converges into the final trajectory even though it is set to be significantly different from the converged trajectory. After the second iteration, it can be seen that the trajectory is almost similar to the final trajectory satisfying constraints for the maximum altitude and final impact angle.

Fig. 2

Sequential convergence of missile trajectory

Figure 3 represents the natural logarithm of residual function $E$ measuring errors of trapezoidal approximation of original nonlinear dynamics in each iteration. The error seems to be decreased almost exponentially through the iteration except third iteration. The residual function is described as [19]:

$$ E\left( {q^{k} ,u^{k} } \right) = \mathop \sum \limits_{i = 1}^{N} \left\| {q_{i - 1}^{k} - q_{i}^{k} + \frac{\Delta x}{2}\left[ {f_{\text{q}} \left( {q_{i - 1}^{k} } \right) + B\left( {q_{i - 1}^{k} } \right)u_{i - 1}^{k} + f_{\text{q}} \left( {q_{i}^{k} } \right) + B\left( {q_{i}^{k} } \right)u_{i}^{k} } \right],} \right\|_{1} . $$

(54)

Fig. 3

Sequential values of residual function

Figure 4 represents the initial and final profile of velocity and flight path angle. Similar to the result of missile trajectory, it can be shown that the final convergent profile is quite different from the initial profile. Especially, the velocity profile is completely changed reflecting the burning time of thrust.

Fig. 4

Initial and final profile of velocity and flight path angle

Figure 5 shows the sequential estimation of burning time in (13). Although the initial estimation is completely different from the true value due to the initial very inaccurate profile of velocity, the burning time is stably estimated from the first optimization phase. The final estimation of burning time is 3.006 s which is 0.6% different from true value.

Fig. 5

Sequential estimation of burning time

Figure 6 gives the final profile of angle-of-attack generated within angle-of-attack limit. However, it can be seen that the initial command is largely generated in order to raise the altitude and the command slightly sharply changes at the end of burning. For the real application, some modification of the problem should be considered to reduce such phenomena.

Fig. 6

Final profile of angle-of-attack

Figure 7 represents the difference between square of $u_{1} \left( { = \alpha } \right)$ and $u_{2} \left( { = \alpha^{2} } \right)$. As we expected in Theorem 2, we can see that two values are almost identical in the entire trajectory.

Fig. 7

Validation of lossless convexification

4.2 Comparison with Nonlinear Programming

In this section, we compare the result of sequential SOCP and the results of GPOPS-II, which is a one of nonlinear programming software, to verify the proposed method. The solver and tolerance of GPOPS-II are set to IPOPT and $10^{ - 3}$, respectively. Figures 8, 9, 10 and 11 show the comparison of the trajectory, velocity, flight path angle, and angle-of-attack, then there is a slight difference between the two results. Since the initial angle-of-attack of SOCP is generated larger than that of GPOPS-II, the initial flight path angle increases up to about 27°.

Fig. 8

Comparison on missile trajectory

Fig. 9

Comparison on missile velocity

Fig. 10

Comparison on flight path angle

Fig. 11

Comparison on angle-of-attack

Because SOCP and GPOPS-II use the different transcription for numerical optimization, it is considered that the discrete change of the dynamics due to thrust affects the difference. While the collocation points of GPOPS-II based on pseudo-spectral methods are concentrated around the end of burning time, the discrete points of SOCP are uniformly distributed. Also, since the downrange is set to be as an independent variable in this paper, it is difficult to accurately estimate the burning time and reflect the phase transition effect in the model. Figure 12 represents the mesh point location result of GPOPS-II in each iteration. As the iteration goes on, more mesh points are created around the transition time unlike the uniform discrete points of SOCP.

Fig. 12

Mesh point location of GPOPS-II

In order to generate more accurate results, consideration for discrete change such as pseudo-spectral convex optimization [33, 34] should be given in the future research. Table 2 shows detailed values for both methods.

Table 2 Results for SOCP and GPOPS-II

5 Conclusion

This paper presents mid-course trajectory optimization of air-to-ground missile using SOCP, one of convex programming. Since the initial conditions and the engagement scenarios are so varied for air-to-ground missiles, it is necessary to quickly generate the mid-course trajectory according to the operational purpose. SOCP is applied to various aerospace problems due to the robustness of the initial conditions and computational efficiency. In this paper, the mid-course trajectory optimization problem with altitude constraint is reformulated as SOCP performing the proof of lossless convexification. And the sequential SOCP is proposed to cope with the nonlinear dynamics and it is verified through simulation. Finally, the results of SOCP are compared with results of nonlinear programming for validation.

Appendix: Proof of Lossless Convexification

The proof of lossless convexification is carried out using the proof by contradiction. Let us assume that there exists a certain interval $\left[ {x_{1} ,x_{2} } \right] \subset \left[ {x_{0} ,x_{\text{f}} } \right]$ that satisfies $u_{1}^{2} < u_{2}$. There should exist a constant $p_{0} \le 0$ for an optimal solution $\left( {q^{*} ,u^{*} } \right)$ satisfying the conditions in Eqs. (19)–(33) in Theorem 1.

• (a) In the interval $\left[ {x_{1} ,x_{2} } \right] \subset \left[ {x_{0} ,x_{\text{f}} } \right]$, the following relationship is obtained:

  $$ u_{1}^{2} < u_{2} ,\;u_{2} > 0. $$

  (55)

  The values of $\lambda_{1} ,\lambda_{2}$ can be determined from complementary slackness conditions (42) and (43):

  $$ \lambda_{0} = \lambda_{1} = 0. $$

  (56)

• (b) From the stationary condition (40), the following equation is derived:

  $$ \begin{aligned} \frac{\partial L}{{\partial u_{1} }} = p_{\gamma } b_{31} = p_{\gamma } \frac{{\left( {T + qS_{\text{ref}} C_{{{\text{L}}_{\alpha } }} } \right)}}{{mV^{2} \cos \gamma }} = 0, \hfill \\ \to p_{\gamma } = 0\;\quad \because T \ge 0,\;q > 0,\;S_{\text{ref}} > 0,\;C_{{{\text{L}}_{\alpha } }} > 0. \hfill \\ \end{aligned} $$

  (57)

• (c) From the stationary condition (41), the following equation is derived:

  $$ \begin{aligned} \frac{\partial L}{{\partial u_{2} }} = p_{V} b_{22} + \lambda_{2} = 0, \hfill \\ \to p_{V} b_{22} = - \lambda_{2} \ge 0. \hfill \\ \end{aligned} $$

  (58)

  Hamiltonian in Eq. (34) can be re-formulated as follows:

  $$ H = p_{y} \left( {a_{13} \gamma + c_{y} } \right) + p_{V} \left( {a_{22} V + a_{23} \gamma + c_{V} } \right) + p_{\gamma } \left( {a_{32} V + c_{\gamma } } \right) + p_{\gamma } b_{31} u_{1} + p_{V} b_{22} u_{2} . $$

  (59)

  Based on the pointwise maximum condition (20), $u_{2}$ is determined according to the switching function $p_{V} b_{22}$:

  $$ {\text{if}}\; p_{V} b_{22} = 0 \to u_{2} \in \left[ {0,u_{2\rm{max} } } \right], $$

  (60)
  $$ {\text{if }} p_{V} b_{22} > 0 \to u_{2} = 0. $$

  (61)

  Since $u_{2}$ should be positive as in Eq. (55), $p_{\text{V}}$ is determined as follows:

  $$ p_{V} = 0\quad \;\because b_{22} < 0. $$

  (62)

• (d) Since $p_{\gamma } = p_{V} = 0$ from (57) and (62), the differential equations (37)–(39) are described as follows:

  $$ p_{y}^{'} = - \frac{\partial L}{\partial y} = \nu_{y1} - \nu_{y2} , $$

  (63)
  $$ p_{V}^{'} = - \frac{\partial L}{\partial V} = - \left( {p_{V} a_{22} + p_{\gamma } a_{32} } \right) = 0, $$

  (64)
  $$ p_{\gamma }^{'} = - \frac{\partial L}{\partial \gamma } = - \left( {p_{y} a_{13} + p_{V} a_{23} } \right) = - p_{y} a_{13} = 0. $$

  (65)

  Since the downrange is monotonically increasing and $a_{13}$ cannot be 0, then

  $$ p_{y} = 0. $$

  (66)

  Therefore, we obtain $\nu_{y1} = \nu_{y2}$ from Eq. (63). If the altitude is larger than 0, then $\nu_{y1} = 0$ from Eq. (45) and if the altitude is less than $y_{\hbox{max} }$, then $\nu_{y2} = 0$ from Eq. (46). Thus, the multipliers $\nu_{y1}$ and $\nu_{y2}$ should be 0 regardless of the altitude condition:

  $$ \nu_{y1} = \nu_{y2} = 0. $$

  (67)

• (e) From Assumption 2, Eqs. (47), (48), (49) give

  $$ \zeta_{y1} = \zeta_{y2} = p_{y} \left( {x_{\text{f}} } \right) = 0. $$

  (68)

• (f) The altitude constraint is described as follows:

  $$ S\left( q \right) = y - y_{\rm{max} } \le 0. $$

  The constraint $S\left( q \right)$ is second-order constraint with respect to the control and then the derivatives of the constraint is calculated

  $$ \begin{aligned} \frac{S\left( q \right)}{\partial q} = \left( {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ \end{array} } \right), \;\frac{{S^{\prime}\left( q \right)}}{\partial q} = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ {\sec^{2} \gamma \left( {1 + 2\gamma \tan \gamma } \right)} \\ \end{array} } \right) , \hfill \\ {\text{where }}S^{\prime}\left( q \right) = y^{\prime} = \gamma \sec^{2} \gamma . \hfill \\ \end{aligned} $$

  (69)

  The jump condition (29) for the costate is

  $$ \left( {\begin{array}{*{20}c} {p_{y} \left( {\tau_{1}^{ - } } \right)} \\ {p_{V} \left( {\tau_{1}^{ - } } \right)} \\ {p_{\gamma } \left( {\tau_{1}^{ - } } \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {p_{y} \left( {\tau_{1}^{ + } } \right)} \\ {p_{V} \left( {\tau_{1}^{ + } } \right)} \\ {p_{\gamma } \left( {\tau_{1}^{ + } } \right)} \\ \end{array} } \right) + \eta_{1} \left( {\tau_{1} } \right)\left( {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ \end{array} } \right) + \eta_{2} \left( {\tau_{1} } \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ {\sec^{2} \gamma \left( {1 + 2\gamma \tan \gamma } \right)} \\ \end{array} } \right). $$

  (70)

  If the altitude constraint is active, the flight path angle should be 0. Therefore,

  $$ \left( {\begin{array}{*{20}c} {p_{y} \left( {\tau_{1}^{ - } } \right)} \\ {p_{V} \left( {\tau_{1}^{ - } } \right)} \\ {p_{\gamma } \left( {\tau_{1}^{ - } } \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {p_{y} \left( {\tau_{1}^{ + } } \right) + \eta_{1} \left( {\tau_{1} } \right)} \\ {p_{V} \left( {\tau_{1}^{ + } } \right)} \\ {p_{\gamma } \left( {\tau_{1}^{ + } } \right) + \eta_{2} \left( {\tau_{1} } \right)} \\ \end{array} } \right). $$

  (71)

  Since $p_{\gamma } ,p_{V} ,p_{y}$ are 0 from (57), (62), (66), then $\eta_{1} \left( {\tau_{1} } \right),\eta_{2} \left( {\tau_{1} } \right)$ should be 0:

  $$ \eta_{1} \left( {\tau_{1} } \right) = \eta_{2} \left( {\tau_{1} } \right) = 0. $$

  (72)

• (g) Because the Hamiltonian, endpoint, and state constraint functions are autonomous, then

  $$ H\left( t \right) = 0 \forall t. $$

  (73)

From Eqs. (51) and (68), $p_{\gamma } \left( {x_{\text{f}} } \right)$ and $p_{y} \left( {x_{\text{f}} } \right)$ are 0 and then:

$$ p_{V} \left( {x_{\text{f}} } \right) = - p_{0} = 0. $$

(74)

From the above results, we conclude

$$ \left( {p_{0} ,p\left( t \right),\lambda \left( t \right),\nu \left( t \right),\xi ,\zeta ,\eta_{1} ,\eta_{2} , \ldots } \right) = 0. $$

(75)

This contradicts the non-triviality condition (19). Therefore, the following equation holds:

$$ u_{1}^{2} \left( x \right) = u_{2} \left( x \right)\;{\text{a}} . {\text{e}} . x \in \left[ {x_{0} ,x_{\text{f}} } \right]. $$

(76)