1 Introduction

As autonomous driving technology advances, researchers are exploring more flexible and controllable vehicles. The four-wheel independent-driving electric vehicle (FWID-EV) has been studied extensively because of its fast response, high precision, flexibility, energy efficiency, and low emissions [1,2,3]. The FWID-EV has unique advantages in motor torque control, as it can adapt to different working conditions by directly and accurately controlling the motor output torque, improving the vehicle stability, especially at high speed.

Concurrently, control modes of autonomous vehicles are emerging, among which path-following control is one of the most basic ones considering only traditional working conditions. Zheng et al. [4] proposed a neural network proportional–integral–derivative (NNPID) method, using which the vehicle can follow the desired path with high stability. Hu et al. [5] proposed a robust controller, which considers the uncertainty of parameters and external interference and improves the path-following performance of the automated guided vehicle. A preview model was established in Ref. [6], and an optimal preview linear quadratic regulator (OPLQR) was developed on the basis of the sliding mode control (SMC) strategy. It can realize differential braking by distributing appropriate torque to four wheels during the path-following process. An MPC controller was designed in Ref. [7] to steady the longitudinal velocity and reduce the influence of the longitudinal velocity fluctuation during path following.

Under complex traffic scenarios, it is difficult to maintain vehicle stability with only path-following accuracy being considered, requiring more stability strategies. In Ref. [8], an SMC strategy was developed to ensure vehicle stability by tracking the target yaw rate. According to the path information, the control model predicts the steering angle of the vehicle when it moves laterally to achieve better following performance. A new robust MPC controller was developed in Ref. [9], which can surpass the limitations of the traditional robust MPC in the infinite time domain, thereby improving the path-following accuracy and handling stability of FWID-EV. In Ref. [10], a path re-planning controller and a rear wheel steering stability controller were designed. The zero sideslip angle is considered in the design of the cost function, which improves the trajectory tracking accuracy and maneuverability of the vehicle under some critical working conditions. A multi-agent system (MAS) architecture was developed in Ref. [11], and a Pareto-optimal theory was used to coordinate the direct yaw moment and the front wheel angle output by the controller, through which the vehicle controllability was improved.

A large number of driving motors of electric vehicles suffer from poor working conditions in real-world applications. Motor failure leads to unequal vehicle lateral driving force, resulting in vehicle yaw instability and threatening the safety of the vehicle. Hence, many algorithms have been proposed for fault-tolerant control (FTC) of vehicle drive motor failure. In Ref. [12], a new FTC strategy was designed based on back-stepping control theory, effectively improving the dynamic performance of the motor drive, decreasing torque ripple, and achieving high reliability. A highly reconfigurable architecture was proposed in Ref. [13]. The sliding vector distribution strategy was adopted to ensure the redistribution of torque when the four-wheel motor fails, which enables the tire to work in the linear region. An FTC method based on a cooperative game was designed in Ref. [14]. Four motors were modeled and interacted as four different players to ensure the stability of the FWID-EV when the motor fails. In Ref. [15], for vehicle parameter uncertainties, as well as some disturbances and actuator failure errors, an online update law and feedback law were designed through a triple-step method to improve vehicle stability.

Based on the above research and analysis, an automatic control system can be designed that follows the path, is fault-tolerant, and has strong real-time performance for an unmanned FWID-EV. When the vehicle follows the path, the front wheel angle must be as smooth as possible. More importantly, it must be able to adjust quickly to adapt to changes in trajectory. The MPC control algorithm can realize real-time rolling optimization of control variables and is capable of feedback correction, which can be used to control the vehicle to track the desired path. Moreover, to address vehicle instability due to motor failure and some parameter uncertainties, the SMC algorithm can be considered. The vehicle system is complex and changeable and often includes uncertainty. For example, external disturbances include road and lateral wind disturbances; internal disturbances include constant changes in tire lateral stiffness and other parameters. SMC can handle system disturbances well and has good robustness; therefore, it is often used in vehicle control [16,17,18]. When the traditional first-order SMC method is used to strengthen the response and anti-jamming capability of the vehicle system, a larger control gain is generally required, which leads to severe chattering, causing harm to the control system. Aiming to resolve the chattering problem caused by the traditional first-order SMC, the second-order SMC method was proposed, which was later proven to be feasible and perform better than the traditional SMC [19,20,21].

This paper develops an MPC and sliding mode fault-tolerant control integrated controller to solve the problem of vehicle instability when the motor fails. The main contributions of this paper are summarized as follows: (1) In contrast to most studies, which only consider the FTC of electric vehicles or vehicle path-following control, this paper considers both the path-following control and FTC of the vehicle to improve the vehicle stability while presenting effective path-following performance. (2) The second-order sliding mode fault-tolerant controller (SOSMFTC) is designed, and a disturbance observer is used to reduce the fluttering caused by the traditional first-order sliding mode fault-tolerant controller (FOSMFTC), thereby improving the control accuracy.

The remainder of this paper is organized as follows. First, the vehicle planar dynamics model is established in Sect. 2. Then, Sect. 3 describes the design process of the MPC controller and sliding mode FTC controller. A simulation is performed in Simulink/Carsim, and the results are analyzed in Sect. 4. Section 5 reports experimental verification through controller hardware-in-the-loop (CHIL) test. Finally, the conclusions are summarized in Sect. 6.

2 Description of Vehicle Control Model

2.1 Vehicle Dynamic Model

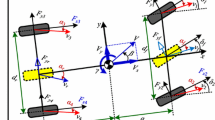
The vehicle planar dynamic model can accurately reflect vehicle states of lateral, longitudinal, and yaw motion, which makes it indispensable for designing vehicle control algorithms. The force analysis of the vehicle motion state is depicted in Fig. 1, through which the differential equations are determined as follows:

$$\begin{gathered} m(\dot{v}_{x} - v_{y} \dot{\theta }_{{\text{v}}} ) = (\overline{F}_{x,1} + \overline{F}_{x,2} )\cos \delta_{{\text{f}}} - (\overline{F}_{y,1} \; + \overline{F}_{y,2} ) \hfill \\ \quad \quad \quad \quad \quad \sin \delta_{{\text{f}}} + \overline{F}_{x,3} + \overline{F}_{x,4} \hfill \\ \end{gathered}$$
(1)
$$\begin{gathered} m(\dot{v}_{y} - v_{x} \dot{\theta }_{{\text{v}}} ) = (\overline{F}_{y,1} + \overline{F}_{y,2} )\cos \delta_{{\text{f}}} - (\overline{F}_{x,1} \; + \overline{F}_{x,2} ) \hfill \\ \quad \quad \quad \quad \quad \sin \delta_{{\text{f}}} + \overline{F}_{y,3} + \overline{F}_{y,4} \hfill \\ \end{gathered}$$
(2)
$$\begin{gathered} I_{{\text{z}}} \ddot{\theta }_{{\text{v}}} = a_{{\text{f}}} (\overline{F}_{y,1} + \overline{F}_{y,2} )\cos \delta_{{\text{f}}} + \frac{{d_{{\text{f}}} }}{2}(\overline{F}_{y,1} - \overline{F}_{y,2} ) \hfill \\ \quad \quad \sin \delta_{{\text{f}}} - b_{{\text{r}}} (\overline{F}_{y,1} + \overline{F}_{y,2} ) + \Delta M_{{\text{z}}} \hfill \\ \end{gathered}$$
(3)

where \(\Delta M_{{\text{z}}}\) can be expressed as

$$\begin{gathered} \Delta M_{{\text{z}}} = {{d_{{\text{f}}} } \mathord{\left/ {\vphantom {{d_{{\text{f}}} } 2}} \right. \kern-\nulldelimiterspace} 2}(\overline{F}_{x,1} - \overline{F}_{x,2} )\cos \overline{F}_{{\text{f}}} + a_{{\text{f}}} (\overline{F}_{x,1} + \overline{F}_{x,2} ) \hfill \\ \;\quad \quad \sin \delta_{{\text{f}}} + {{d_{{\text{r}}} } \mathord{\left/ {\vphantom {{d_{{\text{r}}} } 2}} \right. \kern-\nulldelimiterspace} 2}(\overline{F}_{x,4} - \overline{F}_{x,3} ) + \overline{d}(t) \hfill \\ \end{gathered}$$
(4)

where \(m\) is the mass of the vehicle; \(v_{x}\) denotes longitudinal speed; \(v_{y}\) denotes lateral speed; \(\dot{\theta }_{{\text{v}}}\) is the actual yaw rate, equal to \(\gamma\); \(\overline{F}_{x,i}\) and \(\overline{F}_{y,i}\) are the longitudinal forces and lateral forces of the tire, respectively (\(i\) = 1, 2, 3, 4, represents the left front wheel, right front wheel, left rear wheel, and right rear wheel, respectively); \(I_{{\text{z}}}\) denotes the rotation inertia of the vehicle; \(\delta_{{\text{f}}}\) denotes the front wheel angle of the vehicle; \(a_{{\text{f}}}\) is the distance from the vehicle centroid to the front axles, respectively; \(d_{{\text{f}}}\) and \(d_{{\text{r}}}\) are the track width of the front and rear wheels, respectively; \(\Delta M_{{\text{z}}}\) denotes the external yaw moment; \(\overline{d}(t)\) denotes the disturbance of vehicle internal uncertainty and external disturbances.

Fig. 1
figure 1

Vehicle model

Full size image

2.2 Vehicle Steady-State Analysis

The \(\gamma_{{\text{d}}}\) and \(\beta_{{\text{d}}}\) under steady-state conditions are usually used as expected values to evaluate vehicle stability. Let the actual yaw rate be \(\gamma\) and the actual sideslip angle be \(\beta\), the vehicle is considered stable when \(\gamma \approx \gamma_{\text{d}}\) and \(\beta \approx \beta_{{\text{d}}}\). From Ref. [22], it is known that \(\gamma_{{\text{d}}}\) and \(\beta_{{\text{d}}}\) can be described as

$$\gamma_{{\text{d}}} = \frac{{v_{x} }}{{(1 + \kappa v_{x}^{2} )(a_{{\text{f}}} + b_{{\text{r}}} )}}\delta_{{\text{f}}}$$
(5)
$$\beta_{{\text{d}}} = \frac{{b_{{\text{r}}} + ma_{{\text{f}}} v_{x}^{2} }}{{C_{{{\text{cr}}}} (1 + \kappa v_{x}^{2} )(a_{{\text{f}}} + b_{{\text{r}}} )^{2} }}\delta_{{\text{f}}}$$
(6)

where \(\kappa\) is the stability factor; \(b_{{\text{r}}}\) is the distance from the vehicle centroid to the rear axle; \(C_{{{\text{cr}}}}\) denotes the rear tire corning stiffness.

Moreover, since the maximum lateral acceleration \(a_{y,\max }\) is limited by the road adhesion coefficient, Eq. (7) must be satisfied [22]:

$$\left\{ \begin{gathered} \left| {\hat{\gamma }_{{{\text{d}},\max }} } \right| \le \frac{\mu g}{{v_{x} }} \hfill \\ \left| {\hat{\beta }_{{{\text{d}},\max }} } \right| \le \mu g\left( {\frac{{b_{{\text{r}}} }}{{v_{x}^{2} }} + \frac{{ma_{{\text{f}}} }}{{C_{{{\text{cr}}}} (a_{{\text{f}}} + b_{{\text{r}}} )}}} \right) \hfill \\ \end{gathered} \right.$$
(7)

where \(\mu\) is the road adhesion coefficient.

Thus, the combination of Eq. (6) and Eq. (7) can be rewritten as

$$\gamma_{{{\text{df}}}} = \min \left\{ {\left| {\gamma_{{\text{d}}} } \right|,\left| {\hat{\gamma }_{{{\text{d}},\max }} } \right|} \right\}{\text{sgn}} (\alpha_{\text{f}} )$$
(8)
$$ \beta_{{{\text{df}}}} = \min \left\{ {\left| {\beta_{{\text{d}}} } \right|,\left| {\hat{\beta }_{{{\text{d}},\max }} } \right|} \right\}{\text{sgn}} (\beta_{{\text{d}}} ) $$
(9)

3 Controller Design

The controllers in this section include the MPC controller, sliding mode FTC controller, and P controller that produces longitudinal torque through the speed difference to steady the vehicle’s longitudinal speed. Here compares the performance of the FOSMFTC and the SOSMFTC when the sliding mode FTC controller is considered. Figure 2 shows the algorithm framework.

Fig. 2
figure 2

Framework of the integrated controller

Full size image

3.1 MPC Controller Design

The MPC controller is a path-following controller that enables vehicles to travel along specified paths. The vehicle dynamic model in Sect. 2.1 is simplified based on the assumption of linear tire and wheel deflection at a small angle. The detailed equations are as follows:

$$\left\{ {\begin{array}{*{20}l} \begin{gathered} m\ddot{y}_{{\text{v}}} = - m\dot{x}_{{\text{v}}} \dot{\theta }_{{\text{v}}} + 2\left[ {C_{{{\text{cf}}}} (\delta_{{\text{f}}} - {{\dot{y}_{{\text{v}}} } \mathord{\left/ {\vphantom {{\dot{y}_{{\text{v}}} } {\dot{x}_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\dot{x}_{{\text{v}}} }}} \right. \hfill \\ \left. {\quad \quad - {{a_{{\text{f}}} \dot{\theta }_{{\text{v}}} } \mathord{\left/ {\vphantom {{a_{{\text{f}}} \dot{\theta }_{{\text{v}}} } {\dot{x}_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\dot{x}_{{\text{v}}} }}) + C_{{{\text{cr}}}} {{(b_{{\text{r}}} \dot{\theta }_{{\text{v}}} - \dot{y}_{{\text{v}}} )} \mathord{\left/ {\vphantom {{(b_{{\text{r}}} \dot{\theta }_{{\text{v}}} - \dot{y}_{{\text{v}}} )} {\dot{x}_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\dot{x}_{{\text{v}}} }}} \right] \hfill \\ \end{gathered} \hfill \\ \begin{gathered} m\ddot{x}_{{\text{v}}} = m\dot{y}_{{\text{v}}} \dot{\theta }_{{\text{v}}} + 2\left[ {C_{{{\text{lf}}}} s_{{\text{f}}} - C_{{{\text{cf}}}} (\delta_{{\text{f}}} - } \right. \hfill \\ \left. {\quad \quad {{(\dot{y}_{{\text{v}}} + a_{{\text{f}}} \dot{\theta }_{{\text{v}}} )} \mathord{\left/ {\vphantom {{(\dot{y}_{{\text{v}}} + a_{{\text{f}}} \dot{\theta }_{{\text{v}}} )} {\dot{x}_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\dot{x}_{{\text{v}}} }})\alpha_{{\text{f}}} + C_{{{\text{lr}}}} s_{{\text{r}}} } \right] \hfill \\ \end{gathered} \hfill \\ \begin{gathered} I_{{\text{z}}} \ddot{\theta }_{{\text{v}}} = 2a_{{\text{f}}} \left[ {a_{{\text{f}}} C_{{{\text{cf}}}} (\delta_{{\text{f}}} - {{\dot{y}_{{\text{v}}} } \mathord{\left/ {\vphantom {{\dot{y}_{{\text{v}}} } {\dot{x}_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\dot{x}_{{\text{v}}} }}} \right. \hfill \\ \left. {\quad \quad - {{a_{{\text{f}}} \dot{\theta }_{{\text{v}}} } \mathord{\left/ {\vphantom {{a_{{\text{f}}} \dot{\theta }_{{\text{v}}} } {\dot{x}_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\dot{x}_{{\text{v}}} }}) - b_{{\text{r}}} C_{{{\text{cr}}}} {{(b_{{\text{r}}} \dot{\theta }_{{\text{v}}} - \dot{y}_{{\text{v}}} )} \mathord{\left/ {\vphantom {{(b_{{\text{r}}} \dot{\theta }_{{\text{v}}} - \dot{y}_{{\text{v}}} )} {\dot{x}_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\dot{x}_{{\text{v}}} }}} \right] \hfill \\ \end{gathered} \hfill \\ {\dot{x}_{{\text{g}}} = \dot{x}_{{\text{v}}} \cos \theta_{{\text{v}}} - \dot{y}_{{\text{v}}} \sin \theta_{{\text{v}}} } \hfill \\ {\dot{y}_{{\text{g}}} = \dot{x}_{{\text{v}}} \sin \theta_{{\text{v}}} + \dot{y}_{{\text{v}}} \cos \theta_{{\text{v}}} } \hfill \\ \end{array} } \right.$$
(10)

where \(x_{{\text{v}}}\) and \(y_{{\text{v}}}\) are the longitudinal and lateral displacement of the vehicle, respectively; \(C_{{{\text{cf}}}}\) and \(C_{{{\text{lf}}}}\) are the front and rear tire longitudinal stiffness, respectively; \(s_{{\text{f}}}\) and \(s_{{\text{r}}}\) are the slip rate of the front and rear wheel; \(x_{{\text{g}}}\) and \(y_{{\text{g}}}\) are the vehicle longitudinal and lateral displacement in the inertial coordinate system, respectively.

Nonlinear control requires complex operation processing, making it hard to guarantee the high stability of the controller. Considering this, Eq. (10) is linearized. First, Eq. (10) is transformed into a state-space form, the state quantity is selected as \({{\mathbf{\varGamma}}} = [\dot{y}_{{\text{v}}} {\kern 1pt} {\kern 1pt} \dot{x}_{{\text{v}}} {\kern 1pt} {\kern 1pt} \theta_{{\text{v}}} {\kern 1pt} \;\dot{\theta }_{{\text{v}}} \;{\kern 1pt} \dot{y}_{{\text{g}}} \;{\kern 1pt} \dot{x}_{{\text{g}}} ]\), and the front wheel steering \(\mathbf{\varPhi} = \delta_{{\text{f}}}\) is set as the control input. Next, the nonlinear dynamic equation \({\dot{\mathbf{\varGamma }(t)}} = f({\Gamma} (t), \mathbf{\varPhi} (t))\) is established by Eq. (10). Nonlinear MPC can be designed through nonlinear equations, which could not guarantee high stability. Considering the advantages of linear time-varying MPC, such as simplicity of solutions and low computational costs [23, 24], the first-order Taylor expansion of Eq. (10) is performed at the current working point \((\Gamma (t_{0} ),\Phi (t_{0} ))\), and the linear time-varying equation can be obtained as follows:

$${\dot{\mathbf{\varGamma }}}(t) = {\varvec{R}}(t_{0} ){{\mathbf{\varGamma}}}(t_{0} ) - {\varvec{Z}}(t_{0} )\Phi (t_{0} ){ + }{\varvec{C}}(t_{0} )$$
(11)

where \({\varvec{R}}(t_{0} ) = \left[ {\begin{array}{*{20}c} {\frac{{\partial f_{{\dot{y}_{\text{v}} }} }}{{\partial \dot{y}_{\text{v}} }}} & {\frac{{\partial f_{{\dot{y}_{\text{v}} }} }}{{\partial \dot{x}_{\text{v}} }}} & 0 & {\frac{{\partial f_{{_{{\dot{y}_{\text{v}} {\kern 1pt} }} }} }}{{\partial \dot{\theta }_{\text{v}} }}} & 0 & 0 \\ {\frac{{\partial f_{{\dot{x}_{\text{v}} }} }}{{\partial \dot{y}_{\text{v}} }}} & {\frac{{\partial f_{{\dot{x}_{\text{v}} }} }}{{\partial \dot{x}_{\text{v}} }}} & 0 & {\frac{{\partial f_{{\dot{x}_{\text{v}} }} }}{{\partial \dot{\theta }_{\text{v}} }}} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ {\frac{{\partial f_{{\dot{\theta }_{\text{v}} }} }}{{\partial \dot{y}_{\text{v}} }}} & {\frac{{\partial f_{{\dot{\theta }_{\text{v}} }} }}{{\partial \dot{x}_{\text{v}} }}} & 0 & {\frac{{\partial f_{{\dot{\theta }_{\text{v}} }} }}{{\partial \dot{\theta }_{\text{v}} }}} & 0 & 0 \\ {\cos \theta_{\text{v}} } & {\sin \theta_{\text{v}} } & {\frac{{\partial f_{{\dot{x}_{\text{g}} }} }}{{\partial \theta_{\text{v}} }}} & 0 & 0 & 0 \\ { - \sin \theta_{\text{v}} } & {\cos \theta_{\text{v}} } & {\frac{{\partial f_{{\dot{y}_{\text{g}} }} }}{{\partial \theta_{\text{v}} }}} & 0 & 0 & 0 \\ \end{array} } \right]\), \({\varvec{Z}}(t_{0} ) = \left[ {\frac{{2C_{{{\text{cf}}}} }}{m},\frac{{ - 2C_{{{\text{cf}}}} }}{m}\left( {2\alpha_{{\text{f}}} - \frac{{\dot{y}_{{\text{v}}} {\kern 1pt} + a_{{\text{f}}} \dot{\theta }}}{{\dot{x}_{{\text{v}}} }}} \right),0,\frac{{2a_{{\text{f}}} C_{{{\text{cf}}}} }}{{I_{{\text{z}}} }},0,0} \right]\), \({\varvec{C}}(t_{0} ) = {{\mathbf{\varGamma}}}(t_{0} ) - {\varvec{R}}(t_{0} )({{\mathbf{\varGamma}}}) - {\varvec{Z}}(t_{0} )\Phi (t_{0} )\).

In order to solve Eq. (11) iteratively, it is discretized using the forward Euler method. Then, the following equation can be derived:

$$\left\{ \begin{gathered} {{\mathbf{\varGamma}}}_{{\text{k + 1,t}}} = {\varvec{R}}_{{\text{k,t}}} {{\mathbf{\varGamma}}}_{{\text{k,t}}} + {\varvec{Z}}_{{\text{k,t}}} {\mathbf\varPhi}_{{\text{k,t}}} + d_{{\text{k,t}}} \hfill \\ {\varvec{Y}}_{{\text{k,t}}} = {\varvec{Q}}_{{\text{k,t}}} {{\mathbf{\varGamma}}}_{{\text{k,t}}} + {\varvec{N}}_{{\text{k,t}}} {\mathbf\varPhi}_{{\text{k,t}}} + e_{{\text{k,t}}} \hfill \\ \end{gathered} \right.$$
(12)

where \({\varvec{R}}_{{\text{k,t}}} = {\varvec{I}} + T{\varvec{R}}(t_{0} )\) and \({\varvec{Z}}_{{\text{k,t}}} = T{\varvec{Z}}(t_{0} )\) (\({\varvec{I}}\) represents a unit matrix and \(T\) represents the sampling step).

In order to effectively constrain the increment of the control system, Eq. (12) is converted into an increment type:

$$\left\{ \begin{gathered} {\hat{\mathbf{\varGamma }}}_{{\text{k + 1,t}}} = {\hat{\varvec{R}}}_{{\text{k,t}}} {\hat{\mathbf{\varGamma }}}_{{\text{k,t}}} + {\hat{\varvec{Z}}}_{{\text{k,t}}} \Delta {\mathbf\varPhi}_{{\text{k,t}}} + {\hat{\varvec{C}}}_{{\text{k,t}}} \hfill \\ {\varvec{Y}}_{{\text{k,t}}} = {\hat{\varvec{Q}}}_{{\text{k,t}}} {\hat{\mathbf{\varGamma }}}_{{\text{k,t}}} + {\hat{\varvec{N}}}_{{\text{k,t}}} \Delta {\mathbf\varPhi}_{{\text{k,t}}} + {\varvec{E}}_{{\text{k,t}}} \hfill \\ \end{gathered} \right.$$
(13)

where \({\hat{\mathbf{\varGamma }}}_{{\text{k + 1,t}}} = \left[ {\begin{array}{*{20}c} {{{\mathbf{\varGamma}}}_{{\text{k,t}}} } \\ {{\mathbf\varPhi}_{{\text{k - 1,t}}} } \\ \end{array} } \right]\), \({\hat{\varvec{R}}}_{{\text{k,t}}} = \left[ {\begin{array}{*{20}c} {{\varvec{R}}_{{\text{k,t}}} } & {{\varvec{Z}}_{{\text{k,t}}} } \\ {{\varvec{0}}_{{{\text{m}} \times {\text{n}}}} } & {{\varvec{I}}_{{\text{m}}} } \\ \end{array} } \right]\), \({\hat{\varvec{Z}}}_{{\text{k,t}}} = \left[ {\begin{array}{*{20}c} {{\varvec{Z}}_{{\text{k,t}}} } \\ {{\varvec{I}}_{{\text{m}}} } \\ \end{array} } \right]\), \({\hat{\varvec{N}}}_{{\text{k,t}}} = {\varvec{N}}_{{\text{k,t}}}\),\({\hat{\varvec{C}}}_{{\text{k,t}}} = \left[ {\begin{array}{*{20}c} {{\varvec{C}}_{{\text{k,t}}} } \\ {{\varvec{0}}_{{\text{m}}} } \\ \end{array} } \right]\), \(\Delta {\mathbf\varPhi}_{{\text{k,t}}} = {\mathbf\varPhi}_{{\text{k,t}}} - {\mathbf\varPhi}_{{\text{k - 1,t}}}\), \({\hat{\varvec{Q}}}_{{\text{k,t}}} = [\begin{array}{*{20}c} {{\varvec{Q}}_{{\text{k,t}}} } & {{\varvec{N}}_{{\text{k,t}}} } \\ \end{array} ]\) (where \({\varvec{I}}_{{\text{m}}}\) denotes a matrix with \(m\) rows of 1, \({\varvec{0}}_{m}\) denotes a matrix with \(m\) columns of 0, and \({\varvec{0}}_{{{\text{m}} \times {\text{n}}}}\) denotes a matrix with \(m\) rows and \(n\) columns of 0).

There are two important measurement parameters when the vehicle follows the path: the heading angle and the lateral displacement. In addition, considering that control variables and control increments should be optimal, a cost function can be designed as follows:

$$\begin{gathered} J_{\min } \left( {\hat{\mathbf\varGamma }(t),{\mathbf{\varPhi}} (t - 1),\Delta \Xi (t),\omega } \right) \hfill \\ \quad \; = \sum\limits_{i = 1}^{Np} {\left\| {{\varvec{Y}}(t + i|t) - {\varvec{Y}}_{ref} (t + i|t)} \right\|}_{{Q_{1} }}^{2} \hfill \\ \quad \; + \sum\limits_{i = 0}^{Nc - 1} {\left\| {\Delta {\mathbf{\varPhi}} (t + i|t)} \right\|}_{{R_{1} }}^{2} \hfill \\ \quad + \;\sum\limits_{i = 0}^{Nc - 1} {\left\| {{\mathbf{\varPhi}} (t + i|t)} \right\|}_{S}^{2} + \rho \omega^{2} \hfill \\ \end{gathered}$$
(14)

where \(\Delta{\varvec{\varXi}}({\text{t}}) = [\Delta \varpi (t), \cdots ,\Delta \varpi (t + N_{c} - 1)]\),\({\varvec{Y}}_{{{\text{ref}}}} =\)

\([\theta_{{v{\text{ref}}}} ,y_{{g{\text{ref}}}} ]\), \(\omega\) is the relaxation factor, and \(\varepsilon \ge 0\); \(N_{{\text{p}}}\) represents the prediction step length; \(N_{c}\) represents the control step length; and \({\varvec{Q}}_{1}\), \({\varvec{R}}_{1}\), \({\varvec{S}}\), \(\rho\) represent the weight factors of the tracking error, control increment, control amount, and relaxation factor, respectively.

The physical meaning of Eq. (27) is explained below. The first item is used to ensure accurate tracking of the lateral displacement and heading angle in vehicle path following. The second item is used to produce an optimal front wheel angle increment to prevent severe shaking. The third item is used to generate a better front wheel angle. The last item is used to prevent the calculation from being unsolvable by adjusting the relaxation factor.

Combining Eq. (14) and the constraint conditions, the optimization problem of this dynamic model predictive controller can be described as follows:

$$\begin{gathered} \mathop {\min }\limits_{{\Delta {{\mathbf\varPhi}}(t),\varepsilon }} {\varvec{J}}_{\min } ({\hat{\mathbf{\varGamma }}}(t),{\mathbf\varPhi} (t - 1),\Delta {{\varvec{\Xi}}}(t),\omega ) \hfill \\ s.t \, \left\{ \begin{gathered} {\hat{\mathbf{\varGamma }}}_{{\text{k + 1,t}}} = {\hat{\varvec{R}}}_{{\text{k,t}}} {\hat{\mathbf{\varGamma }}}_{{\text{k,t}}} + {\hat{\varvec{Z}}}_{{\text{k,t}}} \Delta {\mathbf\varPhi}_{{\text{k,t}}} + {\hat{\varvec{C}}}_{{\text{k,t}}} ,k = t, \cdots ,t + N_{{\text{p}}} - 1 \hfill \\ {\varvec{Y}}_{{{\text{k}},{\text{t}}}} = {\hat{\varvec{Q}}}_{{\text{k,t}}} {\hat{\mathbf{\varGamma }}}_{{\text{k,t}}} + {\hat{\varvec{N}}}_{{\text{k,t}}} \Delta {\mathbf\varPhi}_{{\text{k,t}}} + {\varvec{E}}_{{\text{k,t}}} ,k = t, \cdots ,t + N_{{\text{p}}} - 1 \hfill \\ {\mathbf\varPhi}_{{{\text{k}},{\text{t}}}} = {\mathbf\varPhi}_{{{\text{k - }}1,{\text{t}}}} + \Delta {\mathbf\varPhi}_{{{\text{k}},{\text{t}}}} ,k = t, \cdots ,t + N_{{\text{c}}} - 1 \hfill \\ \Delta {\mathbf\varPhi}_{{{\text{k}},{\text{t}}}} = 0,k = t + N_{{\text{c}}} , \cdots ,t + N_{{\text{p}}} \hfill \\ {\mathbf\varPhi}_{\min } \le {\mathbf\varPhi}_{{{\text{k}},{\text{t}}}} \le {\mathbf\varPhi}_{\max } ,k = t + N_{{\text{c}}} , \cdots ,t + N_{{\text{p}}} \hfill \\ \Delta {\mathbf\varPhi}_{\min } \le \Delta {\mathbf\varPhi}_{{{\text{k}},{\text{t}}}} \le \Delta {\mathbf\varPhi}_{\max } ,k = t, \cdots ,t + N_{{\text{c}}} - 1 \hfill \\ \omega \ge 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(15)

Equation (15) can be converted into a standard quadratic programming form and solved in MATLAB.

3.2 Sliding Mode FTC Controller Design

An intelligent electric vehicle, when running on a wet road at a high speed, can easily sideslip if the motor fails. In this section, a sliding mode FTC controller is designed to improve the stability of the vehicle. The structure of the sliding mode FTC controller is as follows. The P controller produces longitudinal torque through the speed difference to maintain the vehicle’s longitudinal speed. The SMC layer produces additional yaw moment to improve vehicle stability. The FTC allocation layer appropriately distributes the longitudinal torque and additional yaw torque and outputs the torque to the four motors of the vehicle.

(1) Design of P controller. The longitudinal controller of the system is presented as follows:

$$T_{\text{p}} = (v_{{{\text{ref}}}} - v_{x} ) \cdot K_{\text{p}}$$
(16)

where \(T_{\text{p}}\) is the torque produced by the P controller, \(v_{{{\text{ref}}}}\) is the reference value of the speed, and \(K_{\text{p}}\) is gain constant.

(2) Design of FOSMFTC. Considering that the control goal is to ensure that the actual values of the yaw rate and the sideslip angle are close to their ideal values, the sliding surface is designed as follows:

$$s = \gamma - \gamma_{{{\text{df}}}} + k(\beta - \beta_{{{\text{df}}}} )$$
(17)

where \(k\) is a positive weight factor, which denotes the influence of the sideslip angle deviation in Eq. (17).

From the derivation of Eq. (17), the following can be obtained:

$$\dot{s} = \dot{\gamma } - \dot{\gamma }_{{{\text{df}}}} + k(\dot{\beta } - \dot{\beta }_{{{\text{df}}}} )$$
(18)

Combining Eq. (18) with Eq. (3), the following is obtained:

$$\begin{gathered} \dot{s} = \frac{1}{{I_{{\text{z}}} }}\left[ {a_{{\text{f}}} (\overline{F}_{y,1} + \overline{F}_{y,2} )\cos \delta_{{\text{f}}} + \frac{{d_{{\text{f}}} }}{2}} \right.\;(\overline{F}_{y,1} - \overline{F}_{y,2} ) \hfill \\ \left. {\;\;\;\;\sin \delta_{{\text{f}}} - b_{{\text{r}}} (\overline{F}_{y,3} + \overline{F}_{y,4} ) + \Delta M_{{\text{Z}}} + W_{1} (t)} \right] \hfill \\ \end{gathered}$$
(19)

where \(W_{1} (t) = I_{{\text{z}}} [k(\dot{\beta } - \dot{\beta }_{{{\text{df}}}} ) - \dot{\gamma }_{{{\text{df}}}} ]\). \(\dot{\beta }_{{{\text{df}}}}\) and \(\dot{\gamma }_{{{\text{df}}}}\) are bound, and there exists a constant \(\overline{W}_{1}\) satisfying \(\left| {W_{1} (t)} \right| \le \overline{W}_{1}\).

Based on Eq. (19), the direct yaw moment can be presented as

$$\begin{gathered} \Delta M_{{\text{Z}}} = - \varepsilon_{1} \cdot {\text{sign}}(s) - k_{1} s - a_{{\text{f}}} (\overline{F}_{y,1} + \overline{F}_{y,2} )\cos \delta_{{\text{f}}} + \hfill \\ \quad \quad \quad b_{{\text{r}}} (\overline{F}_{y,3} + \overline{F}_{y,4} ) - {{d_{{\text{f}}} (\overline{F}_{y,1} - \overline{F}_{y,2} )\sin \delta_{{\text{f}}} } \mathord{\left/ {\vphantom {{d_{{\text{f}}} (\overline{F}_{y,1} - \overline{F}_{y,2} )\sin \delta_{{\text{f}}} } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \end{gathered}$$
(20)

where \(\varepsilon_{1} > \overline{W}_{1}\), \(k_{1} > 0\).

Theorem 1

Suppose that Eq. (20) is satisfied, the sliding variable \(s\) will converge to 0 in finite time.

Proof

Substituting Eq. (20) into Eq. (19) yields

$$\dot{s} = \frac{{ - \varepsilon_{1} \cdot {\text{sign}}(s) - k_{1} s{ + }W_{1} (t)}}{{I_{{\text{z}}} }}$$
(21)

The Lyapunov function \(V_{1} (s) = s^{2} /2\) is defined; taking its derivative and substituting Eq. (21) into it yields

$$\begin{gathered} \dot{V}_{1} { = }s\dot{s} \hfill \\ \;\; = \frac{{ - \varepsilon_{1} \cdot {\text{sign}}(s) \cdot s - k_{1} s^{2} + W_{1} (t)s}}{{I_{{\text{z}}} }} \hfill \\ \;\; \le \frac{{ - \varepsilon_{1} \left| s \right| - k_{1} s^{2} + \left| {W_{1} (t)} \right|\left| s \right|}}{{I_{{\text{z}}} }} \hfill \\ \;\; \le \frac{{ - (\varepsilon_{1} - \overline{W}_{1} )}}{{I_{{\text{z}}} }}\left| s \right| \hfill \\ \end{gathered}$$
(22)

\(\varepsilon_{1} > \overline{W}_{1}\) and \(V(s) \le s^{2} /2\), \(\left| s \right| \ge \sqrt 2 V_{1}^{\frac{1}{2}}\) and \(\dot{V}_{1} \le {{ - \left( {\varepsilon_{1} } \right.\left. { - \overline{W}} \right)\sqrt 2 V_{1}^{\frac{1}{2}} } \mathord{\left/ {\vphantom {{ - \left( {\varepsilon_{1} } \right.\left. { - \overline{W}} \right)\sqrt 2 V_{1}^{\frac{1}{2}} } {I_{{\text{z}}} }}} \right. \kern-\nulldelimiterspace} {I_{{\text{z}}} }}\). The system, therefore, satisfies the finite-time Lyapunov stability theory [25], the sliding variable \(s\) will converge to 0 in finite time, and the convergence time \(T_{{\text{c}}}\) satisfies \(T_{{\text{c}}} \le {{\sqrt 2 I_{z} V_{1}^{\frac{1}{2}} (0)} \mathord{\left/ {\vphantom {{\sqrt 2 I_{z} V_{1}^{\frac{1}{2}} (0)} {(\overline{W} - \varepsilon_{1} )}}} \right. \kern-\nulldelimiterspace} {(\overline{W} - \varepsilon_{1} )}}\).

To ensure that the additional yaw moment can be reasonably distributed, the FTC allocation layer is designed. The ratio of the force currently experienced by the tire to the maximum torque it can provide is usually used to describe the tire utilization rate [26], which can be described by the following equation:

$$\lambda_{i} = \frac{{\;\;\sqrt {\overline{F}_{x,i}^{2} + \overline{F}_{y,i}^{2} } }}{{\mu_{i} \overline{F}_{{{\text{z}},i}} }}$$
(23)

where \(\lambda_{i}\) represents the tire utilization rate, and the value range is [0,1].

Expected longitudinal torque and additional yaw moment are controlled:

$${\varvec{v}} = (T_{{\text{p}}} ,\Delta M_{{\text{Z}}} )^{{\text{T}}}$$
(24)

The torque of the four wheels allocated by the FTC allocation is used as the control input, which must satisfy

$${\varvec{v}} = {\varvec{B}}{\mathbf\varPhi}_{1}$$
(25)

where \({{{\varPhi}}}_{1} = (T_{1} ,T_{2} ,T_{3} ,T_{4} )^{{\text{T}}}\),\({\varvec{B}} = \left( \begin{gathered} \,\;\;\;\sigma_{1} \;\;,\quad \;\sigma_{2} \;\;,\quad \;\sigma_{3} \;\;,\quad \;\sigma_{4} \hfill \\ - \frac{{d_{{\text{f}}} \sigma_{1} }}{2R}, - \frac{{d_{{\text{f}}} \sigma_{2} }}{2R}, - \frac{{d_{{\text{r}}} \sigma_{3} }}{2R}, - \frac{{d_{{\text{r}}} \sigma_{4} }}{2R} \hfill \\ \end{gathered} \right)\), \(\sigma_{i}\) is the motor fault factor, and the value range is [0,1].

The minimum objective function is established based on the sum of the squares of the four-tire utilization rates. Considering that the tire lateral force \(\overline{F}_{y,i}\) is uncontrollable, the lateral force is omitted. The optimization objective function \({\varvec{J}}_{1}\) is expressed by the following formula:

$${\varvec{J}}_{1} = \sum {\left( {\frac{{\;\;\sigma_{i} T_{i} }}{{\mu_{i} \overline{F}_{z,i} R}}} \right)}^{2}$$
(26)

where \(\mu_{i}\) represents the tire-road adhesion coefficient, which is considered to be equivalent to \(\mu\); \(\overline{F}_{z,i}\) is the vertical load of the tire.

Equation (25) needs to satisfy Eq. (24) and physical constraints, so the optimization problem is written as

$$\begin{gathered} \min {\varvec{J}}_{1} = {{\varvec{\Phi}}}_{{1}}^{{\text{T}}} {\varvec{H\Phi }}_{1} + ({\varvec{v}} - {\varvec{B\Phi }}_{1} )^{{\text{T}}} {\varvec{W}}({\varvec{v}} - {\varvec{B\Phi }}_{1} ) \hfill \\ s.t\quad \;\;{{\varvec{\Phi}}}_{1\min } \le {{\varvec{\Phi}}}_{1} \le {{\varvec{\Phi}}}_{1\max } \hfill \\ \end{gathered}$$
(27)

where \({\varvec{W}} = diag(W_{{{\text{Texp}}}} ,W_{{{\Delta M}}} )\), \({\varvec{H}} = diag({{\sigma_{{_{1} }}^{2} } \mathord{\left/ {\vphantom {{\sigma_{{_{1} }}^{2} } {(\mu }}} \right. \kern-\nulldelimiterspace} {(\mu }}\)

$$\overline{F}_{x,1} R),{{\sigma_{2}^{2} \;} \mathord{\left/ {\vphantom {{\sigma_{2}^{2} \;} {(\mu \overline{F}_{x,2} R)}}} \right. \kern-\nulldelimiterspace} {(\mu \overline{F}_{x,2} R)}},{{\sigma_{3}^{2} \;} \mathord{\left/ {\vphantom {{\sigma_{3}^{2} \;} {(\mu \overline{F}_{x,3} R)}}} \right. \kern-\nulldelimiterspace} {(\mu \overline{F}_{x,3} R)}},{{\sigma_{4}^{2} \;} \mathord{\left/ {\vphantom {{\sigma_{4}^{2} \;} {(\mu \overline{F}_{x,4} R)}}} \right. \kern-\nulldelimiterspace} {(\mu \overline{F}_{x,4} R)}}).$$

The physical meaning of Eq. (27) is explained below. The first formula is used to ensure the optimal total output torque. The second formula is used to adjust \(W_{{{\Delta M}}}\) to improve the vehicle stability and adjust \(W_{{{\text{Texp}}}}\) to steady the longitudinal speed.

(3) Design of SOSMFTC with a disturbance observer: In this design, the design of the FTC allocation layer is kept unchanged, but the sliding mode control layer is changed.

Equation (19) can be rewritten as follows:

$$\dot{s} = a_{1} + b_{1} u_{1}$$
(28)

where \(u_{1} = \Delta M_{{\text{z}}}\) is the control variable, \(b_{1} { = }{1 \mathord{\left/ {\vphantom {1 {I_{z} }}} \right. \kern-\nulldelimiterspace} {I_{z} }}\), and \(a_{1}\) is expressed as follows:

$$\begin{gathered} a_{1} = \frac{1}{{I_{{\text{z}}} }}\left[ {a_{{\text{f}}} (\dot{\overline{F}}_{y,1} + \dot{\overline{F}}_{y,2} )\cos \delta_{{\text{f}}} - a_{{\text{f}}} (\overline{F}_{y,1} + \overline{F}_{y,2} )\sin \delta_{{\text{f}}} \dot{\delta }_{{\text{f}}} } \right. \hfill \\ \;\;\;\;\; + {{d_{{\text{f}}} (\dot{\overline{F}}_{y,1} - \dot{\overline{F}}_{y,2} )\sin \delta_{{\text{f}}} } \mathord{\left/ {\vphantom {{d_{{\text{f}}} (\dot{\overline{F}}_{y,1} - \dot{\overline{F}}_{y,2} )\sin \delta_{{\text{f}}} } 2}} \right. \kern-\nulldelimiterspace} 2} + d_{{\text{f}}} (\overline{F}_{y,1} - \overline{F}_{y,2} ) \hfill \\ \left. {\quad \;{{\cos \delta_{{\text{f}}} \dot{\delta }_{{\text{f}}} } \mathord{\left/ {\vphantom {{\cos \delta_{{\text{f}}} \dot{\delta }_{{\text{f}}} } 2}} \right. \kern-\nulldelimiterspace} 2} - b_{{\text{r}}} (\dot{\overline{F}}_{y,3} + \dot{\overline{F}}_{y,4} ) + \dot{W}_{1} (t)} \right] \hfill \\ \end{gathered}$$
(29)

where \(a_{1}\) is at least locally bounded. Therefore, there exists a positive real number \(\overline{a}_{1}\) satisfying \(\left| {a_{1} } \right| \le \overline{a}_{1}\).

Then, \(u_{1}\) can be defined as follows:

$$u_{1} = {{\left[ { - \beta_{1} \left| s \right|^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\text{sign}}(s) - \beta_{2} \int\limits_{0}^{t} {{\text{sign}}(s)} {\text{d}}t} \right]} \mathord{\left/ {\vphantom {{\left[ { - \beta_{1} \left| s \right|^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\text{sign}}(s) - \beta_{2} \int\limits_{0}^{t} {{\text{sign}}(s)} {\text{d}}t} \right]} {b_{1} }}} \right. \kern-\nulldelimiterspace} {b_{1} }}$$
(30)

where \(\beta^{\prime}_{2} > \beta_{1}^{^{\prime}3} {{ + \overline{a}_{{_{1} }}^{2} \cdot (4\beta^{\prime}_{1} - 8)} \mathord{\left/ {\vphantom {{ + \overline{a}_{{_{1} }}^{2} \cdot (4\beta^{\prime}_{1} - 8)} {\left[ {\beta^{\prime}_{1} \cdot (4\beta^{\prime}_{1} - 8)} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\beta^{\prime}_{1} \cdot (4\beta^{\prime}_{1} - 8)} \right]}}\),\(\beta^{\prime}_{1} > 2\).

Let \(\beta^{\prime}_{2} { = }{{\beta_{2} } \mathord{\left/ {\vphantom {{\beta_{2} } {b_{1} }}} \right. \kern-\nulldelimiterspace} {b_{1} }}\), \(\beta^{\prime}_{1} { = }{{\beta^{\prime}_{1} } \mathord{\left/ {\vphantom {{\beta^{\prime}_{1} } {b_{1} }}} \right. \kern-\nulldelimiterspace} {b_{1} }}\).

Theorem 2

Supposing that Eq. (30) is satisfied, the sliding variable \(s\) will converge to 0 in finite time.

Proof

Combining Eq. (28) and Eq. (30), the following formulas can be obtained:

$$\left\{ \begin{gathered} \dot{s} = - \beta^{\prime}_{1} \left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} {\text{sign}}(s) + \omega_{1} \hfill \\ \hfill \\ \dot{\omega }_{1} = - \beta^{\prime}_{2} {\text{sign}}(s) + \dot{a}_{1} \hfill \\ \end{gathered} \right.$$
(31)

The positive definite matrix \({\varvec{Z}}\) is defined as

$${\varvec{Z}} = \frac{1}{2}\left[ \begin{gathered} 4\beta^{\prime}_{2} + \beta_{1}^{^{\prime}2} \hfill \\ \;\quad - \beta^{\prime}_{1} \hfill \\ \end{gathered} \right.\quad \left. \begin{gathered} - \beta^{\prime}_{1} \hfill \\ \;\;\;2 \hfill \\ \end{gathered} \right]$$
(32)

The quadratic Lyapunov function is selected as

$$V_{2} (s,\omega_{1} ){ = }{{\varvec{\upzeta}}}^{T} {\varvec{Z}} {{\varvec{\upzeta}}}$$
(33)

where \({{\varvec{\upzeta}}}^{{\text{T}}} { = }\left[ {\begin{array}{*{20}c} {\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} {\text{sign}}(s)} & {\omega_{1} } \\ \end{array} } \right]\).

Taking the derivative of \(\varvec{\upzeta}\) yields

$$\dot{\varvec{\upzeta}}{ = }\frac{1}{{\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}({\varvec{A}}_{1} {{\varvec{\upzeta}}} + {\varvec{B}}_{1} \tilde{\dot{a}}_{1} )$$
(34)

The derivative of Eq. (33) can be written as

$$\begin{gathered} \dot{V}_{2} (s,\omega_{1} ){ = 2}{\dot{\varvec{\upzeta}}}^{{\text{T}}} {\mathbf{{\varvec Z}\zeta }} \hfill \\ \;\; = \frac{1}{{\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}(2{{\varvec{\upzeta}}}^{{\text{T}}} {\varvec{A}}_{{_{1} }}^{{\text{T}}} + 2\tilde{\dot{a}}_{1} {\varvec{B}}_{{_{1} }}^{{\text{T}}} ){\mathbf{{\varvec Z}\zeta }} \hfill \\ \;\; \le \frac{1}{{\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}(2{{\varvec{\upzeta}}}^{{\text{T}}} {\varvec{A}}_{{_{1} }}^{{\text{T}}} {\mathbf{\varvec Z}}\zeta + 2\tilde{\dot{a}}_{1} {\varvec{B}}_{{_{1} }}^{{\text{T}}} {\mathbf{{\varvec Z}\zeta }} \hfill \\ \quad + \overline{a}_{1}^{2} \left| s \right| - \tilde{\dot{a}}_{1}^{2} ) \hfill \\ \;\; = \frac{1}{{\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}(2{{\varvec{\upzeta}}}^{{\text{T}}} {\varvec{A}}_{{_{1} }}^{{\text{T}}} {\mathbf{{\varvec Z}\zeta }} + 2\tilde{\dot{a}}_{1} {\varvec{B}}_{{_{{1}} }}^{{\text{T}}} {\mathbf{{\varvec Z}\zeta }} \hfill \\ \quad + \overline{a}_{1}^{2} {{\varvec{\upzeta}}}^{{\text{T}}} {\varvec{C}}_{{_{1} }}^{{\text{T}}} {\varvec{C}}_{1} {{\varvec{\upzeta}}} + {{\varvec{\upzeta}}}^{{\text{T}}} {\mathbf{{\varvec Z}}}{\varvec{B}}_{1} {\varvec{B}}_{{_{{1}} }}^{{\text{T}}} {\mathbf{{\varvec Z}\zeta }}) \hfill \\ \;\; \le \frac{1}{{\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}({{\varvec{\upzeta}}}^{{\text{T}}} {\varvec{A}}_{{_{1} }}^{{\text{T}}} {\mathbf{{\varvec Z}\zeta }} + {{\varvec{\upzeta}}}^{{\text{T}}} {\mathbf{{\varvec Z}A}}_{1} {{\varvec{\upzeta}}} + \hfill \\ \quad \overline{a}_{1}^{2} {{\varvec{\upzeta}}}^{{\text{T}}} {\varvec{C}}_{{_{1} }}^{{\text{T}}} {\varvec{C}}_{1} {{\varvec{\upzeta}}} + {{\varvec{\upzeta}}}^{{\text{T}}} {\mathbf{{\varvec Z}{\rm B}}}_{1} {\varvec{B}}_{{_{1} }}^{{\text{T}}} {\mathbf{{\varvec Z}\zeta }}) \hfill \\ \;\; = \frac{1}{{\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}{{\varvec{\upzeta}}}^{{\text{T}}} ({\varvec{A}}_{{_{1} }}^{{\text{T}}} {\mathbf{\varvec Z}} + {\mathbf{{\rm Z}}}{\varvec{A}}_{1} + \overline{a}_{1}^{2} {\varvec{C}}_{{_{1} }}^{{\text{T}}} {\varvec{C}}_{1} \hfill \\ \quad + {\mathbf{{\varvec Z}B}}_{1} {\varvec{B}}_{{_{1} }}^{{\text{T}}} {\mathbf{\varvec Z}}){{\varvec{\upzeta}}} \hfill \\ \end{gathered}$$
(35)

where \({\mathbf{\varvec A}}_{1} = \left[ \begin{gathered} - \frac{1}{2}\beta^{\prime}_{1} \hfill \\ \hfill \\ \; - \beta^{\prime}_{1} \hfill \\ \end{gathered} \right.\quad \left. \begin{gathered} \frac{1}{2} \hfill \\ \hfill \\ 0 \hfill \\ \end{gathered} \right]\), \({\varvec{B}}_{1} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]^{{\text{T}}}\), \({\varvec{C}}_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\), and \(\tilde{\dot{a}}_{1} = \left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \dot{a}_{1}\).

Let \({\varvec{Q}}_{2} = - ({\varvec{A}}_{{_{1} }}^{{\text{T}}} {\varvec{\rm Z}} + {\varvec{ZA}}_{1} + \overline{a}_{1}^{2} {\varvec{C}}_{{_{1} }}^{{\text{T}}} {\varvec{C}}_{1} + {\varvec{{\rm Z}B}}_{1} {\varvec{B}}_{{_{1} }}^{{\text{T}}} {\varvec{\rm Z}})\), then

$$\dot{V}_{2} (s,\omega_{1} ) \le - \frac{1}{{\left| s \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}{{\varvec{\upzeta}}}^{{\text{T}}} {\varvec{Q}}_{2} {{\varvec{\upzeta}}}$$
(36)

where \({\varvec{Q}}_{2} = \left[ {\begin{array}{*{20}c} {\beta^{\prime}_{1} \beta^{\prime}_{2} + \frac{{\beta_{1}^{^{\prime}3} }}{2} - \overline{a}_{1}^{2} - \frac{{\beta_{1}^{^{\prime}2} }}{4}} & {\frac{{\beta^{\prime}_{1} }}{2} - \frac{{\beta_{1}^{^{\prime}2} }}{2}} \\ {\frac{{\beta^{\prime}_{1} }}{2} - \frac{{\beta_{1}^{^{\prime}2} }}{2}} & {\frac{{\beta^{\prime}_{1} }}{2} - 1} \\ \end{array} } \right]\).

By the properties of the Schur complement [27], \({\varvec{Q}}_{2}\) is a positive definite matrix when \(\beta^{\prime}_{1} > 2\), \(\beta^{\prime}_{2} > \beta_{1}^{^{\prime}3} { + }{{\overline{a}_{{_{1} }}^{2} \cdot (4\beta^{\prime}_{1} - 8)} \mathord{\left/ {\vphantom {{\overline{a}_{{_{1} }}^{2} \cdot (4\beta^{\prime}_{1} - 8)} {\left[ {\beta^{\prime}_{1} \cdot (4\beta^{\prime}_{1} - 8)} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\beta^{\prime}_{1} \cdot (4\beta^{\prime}_{1} - 8)} \right]}}\), and \(\beta^{\prime}_{1} > 2\), then \(\dot{V}_{2} (s,\omega_{1} ) < 0\).

According to Lemma 2 in Ref. [28], the sliding variable \(s\) will converge to 0 in finite time and the convergence time \(T^{\prime}_{\text{c}}\) satisfies \(T^{\prime}_{{\text{c}}} \le \frac{{2\sqrt {\beta^{\prime}_{1\max } ({\mathbf{Z}})} }}{{\beta^{\prime}_{1\min } ({\mathbf{Q}}_{2} )}}V_{2}^{\frac{1}{2}} (s(0),\omega_{1} (0))\).

Let \(s = y_{1}\) and \(\dot{s} = y_{2}\), then Eq. (28) can be derived as

$$\left\{ \begin{gathered} \dot{y}_{1} = y_{2} \hfill \\ \dot{y}_{2} = \dot{a}_{1} + b_{1} \dot{u}_{1} \hfill \\ \end{gathered} \right.$$
(37)

Let \({\mathbf{y}} = \left[ {y_{1} ,y_{2} } \right]^{{\text{T}}}\), then Eq. (37) can be rewritten as

$${\dot{\varvec{y}}} = f({\varvec{y}}) + {\varvec{g}}_{1} \dot{u}_{1} + {\varvec{g}}_{2} \dot{a}_{1}$$
(38)

where \({\varvec{g}}_{1} = \left[ {0,b_{1} } \right]^{{\text{T}}}\), \({\varvec{g}}_{2} = \left[ {0,1} \right]^{{\text{T}}}\), \(f({\varvec{y}}) = \left[ {y_{2} ,0} \right]^{{\text{T}}}\).

The disturbance observer can be designed by Ref. [29] as follows:

$$\left\{ \begin{gathered} \dot{p} = - {\varvec{Kg}}_{2} p - {\varvec{K}}\left[ {{\varvec{g}}_{2} {\varvec{Ky}} + f({\varvec{y}}) + {\varvec{g}}_{1} \dot{u}_{1} } \right] \hfill \\ \dot{\hat{a}}_{1} = p + {varvec{Ky}} \hfill \\ \end{gathered} \right.$$
(39)

where \(\hat{a}_{1}\) is the estimate of \(a_{1}\), \({\varvec{K}} = \left[ {k_{1} ,k_{2} } \right]\).

The external yaw moment \(\Delta M_{Z}\) can be derived as

$$\Delta M_{Z} = {{\left[ { - \beta_{1} \left| s \right|^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\text{sign}}(s) - \beta_{2} \int\limits_{0}^{t} {({\text{sign}}(s)} ){\text{d}}t - \hat{a}_{1} } \right]} \mathord{\left/ {\vphantom {{\left[ { - \beta_{1} \left| s \right|^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\text{sign}}(s) - \beta_{2} \int\limits_{0}^{t} {({\text{sign}}(s)} ){\text{d}}t - \hat{a}_{1} } \right]} {b_{1} }}} \right. \kern-\nulldelimiterspace} {b_{1} }}$$
(40)

4 Simulation and Analysis

To analyze the performance of controllers, three simulations are performed in Simulink/Carsim. The vehicle parameters are listed in Table. 1.

Table 1 Vehicle parameters
Full size table

A standard double-lane change test on slippery pavement (where \(\mu { = }0.3\)) is designed in Carsim, where the initial longitudinal velocity \(v_{x}\) of the vehicle is set to 72 km/h. When analyzing simulation results, \(M_{1}\) represents the left front wheel motor, \(M_{2}\) is the right front wheel motor, \(M_{3}\) represents the left rear wheel motor, and \(M_{4}\) is the right rear wheel motor. The design concepts of these three simulations are described as follows:

  1. (1)

    Case 1: The results of the first simulation are compared with other simulation data, showing the control performance of the MPC-FOSMFTC and the MPC-SOSMFTC. The four motors of the vehicle are always normal (where \(\sigma_{1} { = }1\), \(\sigma_{2} { = }1\), \(\sigma_{3} { = }1\) and \(\sigma_{4} { = }1\)).

  2. (2)

    Case 2: The second simulation exhibits the robustness of the MPC-SOSMFTC in the case of a partial failure of the motor on the opposite side of the vehicle. At 3 s, \(M_{2}\) and \(M_{3}\) of the vehicle partially failed (where \(\sigma_{1}\) = 1, \(\sigma_{2}\) = 0.5, \(\sigma_{3}\) = 0.3, and \(\sigma_{4}\) = 1).

  3. (3)

    Case 3: The third simulation validates the robustness of the MPC-SOSMFTC in the case of partial faults of the motor on the same side of the vehicle. At 5 s, \(M_{1}\) and \(M_{3}\) of the vehicle partially failed (where \(\sigma_{1}\) = 0.6, \(\sigma_{2}\) = 1, \(\sigma_{3}\) = 0.3, and \(\sigma_{4}\) = 1).

First, the most intuitive control parameters are analyzed: vehicle trajectory \(x_{{\text{g}}} y_{{\text{g}}}\), \(\beta\), and \(\gamma\). In Fig. 3, the vehicle paths under different cases are plotted. When only the MPC controller is used, the vehicle cannot track the expected path at around 134 m. This is because the MPC algorithm is unable to find a feasible solution owing to the severe sideslip of the vehicle. However, the vehicle trajectory under the MPC-FOSMFTC and the proposed MPC-SOSMFTC can achieve path following. For vehicle trajectory in case 1, the maximum error of the proposed MPC-SOSMFTC is approximately 0.27 m, and that of the MPC-FOSMFTC is approximately 0.66 m. Compared with the latter, the former is reduced by 59%. For the proposed MPC-SOSMFTC, the maximum error of case 2 is approximately 0.37 m, and that of case 3 is approximately 0.53 m. It is worth noting that the results in case 2 and case 3 perform slightly worse than the MPC-SOSMFTC control results in case 1. This is because when the vehicle motor fails, the control performance of the controller will be slightly decreased; however, as the error in these results is negligible, high vehicle stability can still be achieved. Furthermore, MPC-SOSMFTC in case 3 and case 2 demonstrates better control performance than MPC-FOSMFTC in case 1.

Fig. 3
figure 3

Trajectory of the vehicle

Full size image

In Fig. 4(a), the comparison curves of \(\beta\) are plotted. The comparison curves of \(\gamma\) are plotted in Fig. 4(b). There is instability when only the MPC controller is used, as shown in Fig. 4(a) and (b). \(\beta\) and \(\gamma\) suddenly increase at a certain time, far beyond the stable range. However, \(\beta\) and \(\gamma\) are kept within a stable range under FOSMFTC and SOSMFTC. After calculation and analysis, some detailed data can be obtained. In case 1, comparing the results of SOSMFTC and FOSMFTC, the maximum value of \(\beta\) is reduced by approximately 17.1%. For the SOSMFTC, compared with the FOSMFTC results in case 1, the maximum value in case 2 is reduced by approximately 13.5% and that in case 3 is reduced by approximately 11.2%. In case 1, comparing the results of SOSMFTC and FOSMFTC, the maximum value of \(\gamma\) is reduced by approximately 39.8%. For the SOSMFTC, compared with the FOSMFTC results in case 1, the result in case 2 is reduced by about 28.6% and case 3 is reduced by approximately 14.6%. From the above analysis, it can be concluded that the proposed MPC-SOSMFTC presents better control performance than MPC-FOSMFTC. In addition, it should be noted that when the vehicle motor fails, the control accuracy of the proposed MPC-SOSMFTC has only a small error, which is within a reasonable range. Therefore, the above analysis shows that the proposed MPC-SOSMFTC shows better robustness during motor failure.

Fig. 4
figure 4

Sideslip angle and yaw rate

Full size image

Next, the control output direct yaw moment \(\Delta M_{{\text{Z}}}\), torque and vehicle speed \(v_{x}\) are analyzed. In case 1, the additional yaw moment \(\Delta M_{{\text{Z}}}\) obtained is recorded; as illustrated in Fig. 5, the FOSMFTC has a severe chattering problem, while the proposed controller can solve this problem. According to the calculation, the chattering value is reduced by approximately 94.6%. The torque under FOSMFTC and SOSMFTC is also recorded, as shown in Fig. 6(a) and (b), respectively. As illustrated in the figures, the torque under FOSMFTC also has a severe chattering problem, while the proposed controller effectively reduces the chattering of torque.

Fig. 5
figure 5

Direct yaw moment \(\Delta M_{{\text{Z}}}\) of case 1

Full size image
Fig. 6
figure 6

Torque under FOSMFTC and torque under SOSMFTC (case 1)

Full size image

The longitudinal torque under the P controller in case 2 is recorded; as shown in Fig. 7, the output torque of \(M_{2}\) and \(M_{3}\) of the vehicle decreases at 3 s, because of insufficient power invoked by the partial failure of the vehicle motor without FTC. The vehicle speed \(v_{x}\) in case 2 is plotted in Fig. 8. When FTC does not work, \(v_{x}\) cannot be maintained at 3 s, showing a downward trend. However, the proposed controller can still ensure a stable vehicle speed. The torque of the motor under the proposed controller in case 2 is shown in Fig. 9(a), and a torque comparison between motor failure and non-failure cases is plotted in Fig. 9(b). In Fig. 9(a), when the motor fails, the torques of the four motors increase to achieve high vehicle stability. According to Fig. 9(b), \(M_{2}\) and \(M_{3}\) fail at 3 s, and the output torque increases significantly.

Fig. 7
figure 7

Longitudinal torque in case 2

Full size image
Fig. 8
figure 8

Speed \(v_{x}\) of the vehicle in case 2

Full size image
Fig. 9
figure 9

Torque under SOSMFTC and torque comparison between motor failure and non-failure (case 2)

Full size image

The longitudinal torque under the P controller in case 3 is plotted in Fig. 10. At 5 s, the longitudinal torque decreases owing to the motor failure. The vehicle speed in case 3 is plotted in Fig. 11. The speed begins to decrease when the vehicle has no FTC, while the proposed controller can maintain a stable speed. The torque of the motor under the proposed controller in case 3 is shown in Fig. 12(a). The torque in motor failure and non-failure cases is compared, as illustrated in Fig. 12(b). Owing to the failure of \(M_{2}\) and \(M_{3}\), the calculated output torque increases at 5 s. From the above analysis, it is concluded that when the motor fails, the proposed control algorithm can reasonably adjust the size of the torque to maintain high vehicle stability.

Fig. 10
figure 10

Longitudinal torque in case 3

Full size image
Fig. 11
figure 11

Vehicle speed \(v_{x}\) in case 3

Full size image
Fig. 12
figure 12

Torque under SOSMFTC and torque comparison between motor failure and non-failure (case 3)

Full size image

5 Test Validation

5.1 Test Platform Design

To apply the algorithm in the real-world vehicle, a CHIL system is established. The CHIL test scheme is provided in Fig. 13(a) and the CHIL physical diagram in Fig. 13(b). As Fig. 13(b) shows, the main devices include mobile power, a laptop, a display, and a Raspberry Pi 4B as the core hardware. The main steps of the CHIL test are as follows. First, the control algorithm model is built in Simulink. Then, the algorithm model is converted into C code, which is compiled and run on the Raspberry Pi 4B. Finally, the ROS communication module is built in Simulink/Carsim, which is responsible for receiving the torque and angle information delivered by the Raspberry Pi 4B and sending vehicle status information to the Raspberry Pi 4B. As illustrated in Fig. 13(a), the Raspberry Pi 4B and MATLAB are in the same local network. Finally, the calculation results from the Raspberry Pi 4B are transmitted to Simulink through ROS communication.

Fig. 13
figure 13

CHIL test scheme and CHIL physical diagram

Full size image

5.2 CHIL Test Results

The standard double-lane change condition on slippery pavement (where \(\mu { = }0.3\)) is designed. In Carsim, the speed of the vehicle at the initial position is set to 72 km/h. At 4 s, \(M_{4}\) fails completely (where \(\sigma_{1}\) = 1, \(\sigma_{2}\) = 1, \(\sigma_{3}\) = 1, and \(\sigma_{4}\) = 0).

The trajectory of the vehicle under different controllers is plotted in Fig. 14. As illustrated in Fig. 14, when the MPC controller is used, the vehicle cannot track the expected path at approximately 134 m. The vehicle can eventually follow the required trajectory under the action of the MPC-FOSMFTC and the proposed MPC-SOSMFTC. When there is no motor failure, the maximum error of MPC is approximately 0.28 m. When the motor fails, the maximum error of the proposed MPC-SOSMFTC is approximately 0.36 m, and that of MPC-FOSMFTC is approximately 0.53 m. The conclusions obtained from the above data are essentially in agreement with that from the simulation results in Sect. 4. The proposed MPC-SOSMFTC can ensure the vehicle stability as much as possible while ensuring that the vehicle follows the path, and the control effect is better than that of MPC-FOSMFTC. The values of \(\beta\) are shown in Fig. 15(a), and those of \(\gamma\) are shown in Fig. 15(b). As demonstrated in the figures, when \(M_{4}\) fails completely, the proposed MPC-SOSMFTC can still ensure that \(\beta\) and \(\gamma\) are within a steady area. Compared with FOSMFTC, SOSMFTC reduces the error of \(\beta\) by approximately 17.6% under normal vehicle motor conditions. When the motor fails, the comparison error is reduced by 11.8%. For \(\gamma\), SOSMFTC and FOSMFTC reduce the maximum error by approximately 19.0% and 8.7%, respectively.

Fig. 14
figure 14

Trajectory of the vehicle

Full size image
Fig. 15
figure 15

Sideslip angle and yaw rate

Full size image

The torque of the motor under SOSMFTC is depicted in Fig. 16(a). The torque between motor failure and non-failure is compared in Fig. 16(b). According to Fig. 16(b), \(M_{4}\) fails completely at approximately 4.1 s because of network delay, but this does not significantly alter the effect of the proposed controller. At 6.5 s, the torque allocated by \(M_{2}\) increases to maintain vehicle stability. The experimental data indicate that the proposed MPC-SOSMFTC has high real-time capability and robustness.

Fig. 16
figure 16

Torque under SOSMFTC and torque comparison between motor failure and non-failure

Full size image

6 Conclusions

This paper develops an integrated controller of path-following control and FTC to improve the path-following performance and stability of the FWID-EV with failed motor. The main results include the following. First, an MPC controller is developed to achieve the accurate vehicle path following. Second, a SOSMFTC with a disturbance observer is designed, which can effectively reduce the severe chattering of the control quantity caused by the traditional FOSMFTC and enhance the stability of the faulted vehicle. Third, the optimal control allocation method can appropriately allocate the motor torque when the motor fails. Finally, the simulation and CHIL test results show that the proposed integrated controller has better robustness compared to MPC-FOSMFTC. The proposed integrated controller can track the expected path and improve stability when the motor fails, thus improving vehicle path-following performance and stability.

Although the proposed algorithm has been verified by the CHIL test, more conditions should be considered and tested using real vehicles. Future research will focus on how to introduce more hardware devices such as motors and steering wheels, and how to combine them with controllers to perform comprehensive hardware-in-the-loop experiments.