Model predictive control-based fault detection and reconstruction algorithm for longitudinal control of autonomous driving vehicle using multi-sliding mode observer

Abstract

This paper presents a model predictive control-based fault detection and reconstruction algorithm for longitudinal control of autonomous driving using a multi-sliding mode observer. In order to secure the safe longitudinal control of a vehicle, a numbers of factors must be ensured, such as the reliability of the longitudinal information, the data on the forward object from the environment sensor, and the acceleration of the ego vehicle. Thus, we propose a reasonable failure detection scheme for the acceleration signal of the host vehicle and the relative values of the front object of the radar. In order to identify the faults of the radar and the vehicle acceleration sensor related to the automated longitudinal control, the multiple sliding mode observer and prediction of model predictive control (MPC) algorithm are applied. The relative acceleration is reconstructed by applying a sliding mode observer (SMO) with clearance and relative speed measurements. The upper and lower limits of longitudinal acceleration were computed by analyzing human driving data under the preceding vehicle and reconstructed acceleration. A proper acceleration range can be defined precisely based on several reconstructed upper and lower bounds by using a multiple sliding mode observer with stored prediction data of relative values, making it possible to effectively identify the fault of the host vehicle’s acceleration sensor. By applying MPC for this study, optimal control input and prediction of relative states can be obtained that are more reasonable than those using the linear prediction model. The proposed fault detection algorithm can identify the abnormal state of the environment sensors by using the accumulated past sensor data. By comparing the stored prediction of relative states with the stored data on current states for a given period, the signal faults of the longitudinal target information can be detected from environment sensors. With these fault indices of states, the final fault diagnoses of sensors can be determined by assessing confidence through statistical analysis of 27 sets of normal driving data. In order to obtain a reasonable performance evaluation, this study uses actual driving data and a 3D full vehicle model constructed in the MATLAB/Simulink environment. The test results reveal that the proposed algorithm can successfully detect the fault of the radar and acceleration sensor of the automated driving vehicle.

1 Introduction

In recent years, major carmakers have begun to introduce vehicles with partially automated driving capabilities developed using Advanced Driver Assistance Systems. While the performance of the driving technology is also important, monitoring and responding to failures of sensors and algorithms is becoming essential in order to secure the safety of the automated driving system. In particular, a problem with the signal used for autonomous driving control could lead to very serious accidents on the road. Therefore, developing an algorithm to monitor and diagnose sensors and algorithm faults is crucial for the commercialization of such vehicles. Along with the development of algorithms to secure driving performance, a number of other algorithms—fault detection, isolation, diagnosis, and tolerant control—have been actively developed in various research institutes, companies, and universities.

The scheme of sensor fault detection and isolation using a particular sliding mode observer was proposed along with some validations and applications in (Tan and Edwards 2002; Edwards et al. 2000; Tan and Edwards 2003). Yan and Edwards (Yan and Edwards 2007) proposed an approach for robust fault estimation and reconstruction for a class of nonlinear systems using a sliding mode observer. Nah et al. (2010) designed a fault diagnosis algorithm for yaw-rate sensors, lateral acceleration sensors, steering wheel angle sensors, as well as the steer-by-wire, throttle-by-wire, and brake-by-wire processes of autonomous vehicles, and verified the performance of the algorithm through hardware-in-the-loop simulation (HiLs). Jeong (2015) proposed a fault detection methodology to monitor vehicle sensors and actuators, and verified it via data-based simulation and real-time vehicle test. In order to prevent misdiagnosis, the adaptive threshold was adopted with consideration of model and sensor uncertainty. Li et al. (2017) developed a new disturbance-decoupled fault reconstruction design for a continuous linear time-invariant system. The fault diagnosis techniques and their applications were reviewed from model- and signal-based perspectives by Gao et al. (2015). A functional reference structure for autonomous driving was described at the logical level regardless of any dependence on a specific implementation by Behere and Törngren (Behere and Törngren 2016). Garoudja et al. (2017) developed a statistical model-based fault detection and identification algorithm for photovoltaic systems based on a statistical approach. Jo et al. (2015) proposed a development methodology that facilitates the design and development of an automated vehicle by demonstrating the process of implementation. The application of a neural network-based fault detection to detect and track fault data injection attacks on the cooperative adaptive cruise control layer of a platoon of connected vehicles in real time was proposed in (Sargolzaei et al. 2016). Qin et al. (2017) developed a distributed fault diagnosis scheme for a formation system with velocity sensor faults, then verified its performance through simulations and real-time tests. In addition, in order to obtain the residuals of the sensor faults to diagnose, an extreme learning machine (ELM) prediction model was constructed to predict the output of the sensor of an underwater autonomous vehicle by Li (2017). Xiang et al. (2017) developed a two-layered fault treatment system consisting of a risk analysis subsystem and an intelligent decision subsystem.

Additionally, various optimization algorithms have been investigated to derive optimal solutions for automated driving control, and of these, a number of studies on model predictive control have been presented. Lee (2011) reviewed the major developments and achievements of research and industrial/commercial activities on model predictive control over the last three decades. Luo et al. (2010) proposed an adaptive cruise control algorithm with multi-objectives based on a model predictive control framework to meet the requirements of not only safety and car-following, but also driving comfort and fuel efficiency. A model predictive control approach for controlling the active front steering systems of autonomous vehicle systems was developed by Falcone et al. (2007). Suh et al. (2016) presented the design and evaluation of a model predictive control algorithm for automated driving on a motorway using a vehicle traffic simulator, and this algorithm was successfully implemented on a vehicle electronic control unit (ECU) evaluated on a real-time vehicle traffic simulator by comparing the vehicle behavior of manual driving.

In order to design fail-safe environment-aware sensors for ADAS and autonomous driving, a dual system for each module or sensor integration is required. However, not only is it uneconomical to have the same sensors fitted to all vehicles multiple times, but it is also inefficient from a structural point of view. In this study, a fault detection method that does not require additional duplicated sensors is proposed by using a vehicle sensor, environment sensor, MPC algorithm results, and road data analysis. From a practical perspective, this approach can be an effective and reasonable way to apply the fail-safe of ADAS and autonomous driving.

In this research, a fault detection and reconstruction algorithm using a multi-sliding mode observer for the acceleration sensor of the host vehicle and radar was presented in order to secure the safety of an autonomous vehicle’s longitudinal control. We focused on the current states of the ego vehicle and foregoing target measurements: acceleration, relative velocity, and clearance. In order to control an autonomous vehicle, MPC is applied based on radar and vehicle sensor information, and the desired control command over the predicted time horizon is computed and stored. The predicted cumulative data may be applied as failure detection reference values for environment sensors for longitudinal control, such as radars or cameras. The maximum and minimum acceleration bounds were derived by using a longitudinal kinematic model-based sliding mode observer. The acceleration bounds were defined using the probabilistic longitudinal acceleration distribution of a human driver under normal driving condition analyzed from actual data logs. By constructing a multiple sliding mode observer, we can obtain a number of allowable acceleration range that makes it possible to define reasonable acceleration bounds to enhance the performance of the acceleration fault detection. In addition, as opposed to single acceleration diagnosis using the Single sliding mode observer (SMO), rational fault diagnosis can be achieved by utilizing multiple acceleration normal ranges based on the construction of multiple SMO. Moreover, the prediction result of MPC is more rational than that of the linear prediction model. Using the prediction result from the model predictive control solution, the predictive fault diagnostic algorithm was developed to detect and diagnose fault signals in radar sensors.

The proposed algorithm was designed to monitor unusual signals for the fault of an offset situation. In the case of holding and turning off conditions, each sensor can automatically identify these abnormal signals. We conducted a performance evaluation via actual driving data-based offline simulation in the MATLAB/SIMULINK environment.

The rest of this paper is composed as follows. The second section shows the overall architecture and scheme of the algorithm for functional safety for autonomous driving. The third section explains the scheme of the model predictive control applied in this study. The fourth section describes the multi sliding mode observer-based relative acceleration reconstruction and fault detection algorithm of the acceleration sensor and radar. The fifth section presents the actual data-based performance evaluation for three fault injection cases by using two data sets in each case. Finally, a conclusion is provided in the sixth section.

2 Overall architecture and scheme of algorithm for functional safety for autonomous driving

The overall model schematic diagram of the fault detection and reconstruction algorithm based on a model predictive controller and 3D full vehicle model is depicted in Fig. 1. The model predictive controller computes the desired control input ($a_{des}$) by predicting the designated horizon by using the preceding target data ($c,\,\,v_{rel}$) and the host vehicle’s current acceleration ($a_{s}$). In a previous study, applying a linear prediction to fault detection was shown to lead to performance limitation (Oh and Yi 2017; Oh et al. 2018) Therefore, reasonable and accurate prediction results can improve the fail diagnosis performance of the proposed approach, so we used the prediction of clearance and relative velocity ($c_{pre}$, $v_{rel,pre}$) obtained from the MPC algorithm. In addition, by using the analysis of longitudinal acceleration standard deviation ($\sigma_{{a_{s} }}$) through driving data, the fault diagnosis of each sensor fail can be conducted.

Fig. 1

Overall model schematics of MPC, 3D full vehicle model, and fault detection and reconstruction algorithm

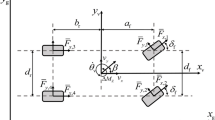
For the longitudinal control of autonomous vehicles, the system determines a proper speed by considering the in-lane front target in its heading direction. In this study, since we want to identify the fault of longitudinal control, a normal driving situation with the preceding vehicle is assumed. The driving condition considered in this case is shown in Fig. 2.

Fig. 2

Driving situation of a subject vehicle with an in-lane preceding vehicle

The proposed safety system architecture for autonomous driving vehicles in this study is composed of three major stages: (1) perception, (2) decision, and (3) control with regard to the functional perspective. First, in the perception stage, detection, isolation, and classification are conducted in order to determine the fault level. In the decision stage, the present fault level of the implemented system was determined by using the detected, isolated, and classified fault signals obtained in the previous stage. Finally, in the control stage, appropriate control action–ceding, emergency braking, and stop-were executed by using the determined fault level to avoid crash accidents. In this paper, we proposed the longitudinal fault detection algorithm as the first stage for autonomous vehicles.

Fig. 3

Model Predictive Control (MPC) scheme

3 Model predictive control formulation

Model predicted control (MPC) represents a type of control algorithm that uses the current dynamic state to predict the future response of the plant as well as to provide an optimized solution for future predictions in which the objective function is minimized. MPC is a well-known control scheme which can compute an optimized solution by using the prediction method as shown in Fig. 3, and it has been used in several studies (Lee 2011; Mayne et al. 2000; Falcone et al. 2008; Li et al. 2011; Oh et al. 2015).

In this study, the MPC is adopted to determine the optimized longitudinal control input and expected target values, such as clearance and relative velocity, for reasonable fault detection. In this study, the clearance ($c$) and relative velocity ($v_{rel}$) from the radar and the acceleration ($a_{s}$) from the vehicle acceleration sensor were used as the inputs, while the desired acceleration ($a_{des,command}$) for the control input and the prediction ($c_{pre}$,$v_{rel,pre}$) of the relative values of the target, such as relative displacement and velocity, were obtained from the MPC algorithm. Figure 4 shows a block diagram of the detailed MPC algorithm applied to proposed fault detection.

Fig. 4

Block diagram of Model Predictive Control

The MPC algorithm determines an optimized control sequence by minimizing a performance index on the valid area. Once the control sequence has been calculated, the first element of the control sequence can be applied to the actual vehicle model as a desired motion, and then the process is repeated. The vector formulation of the MPC problem is provided in the mathematical programming framework, which allows us to use the Quadratic Programming (QP) algorithm scheme. The following equivalent QP formulas and state space equation must be considered in the model in vector space.

In order to construct the MPC algorithm for longitudinal control and fault detection, the longitudinal position error ($e_{x}$) and relative velocity error ($e_{{\dot{x}}}$) are defined as follows:

$$ \begin{aligned} e_{x} &=& c - c_{d} \hfill \\ e_{{\dot{x}}} &=& v_{rel} = v_{p} - v_{s} \hfill \\ \end{aligned} $$

(1)

where,

$$ c_{d} = v_{x} \cdot t_{p} + c_{0} $$

In Eq. (1), $v_{p}$ and $v_{s}$ refer to the velocities of the preceding and subject vehicles, respectively. $c$ is the current clearance and $c_{d}$ is the desired clearance between the preceding and subject vehicles, respectively. Further, $v_{x}$ and $t_{p}$ respectively represent the relative velocity and preview time. $c_{0}$ represents the minimum clearance to avoid collision. Then, the state-space linear equation is defined as shown below.

$$ \left[ {\begin{array}{*{20}c} {\dot{e}_{x} (t)} \\ {\dot{e}_{{\dot{x}}} (t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {e_{x} (t)} \\ {e_{{\dot{x}}} (t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ { - 1} \\ \end{array} } \right]a_{s} + \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]a_{p} $$

(2)

where $a_{p}$ and $a_{s}$ are the longitudinal accelerations of the subject vehicle and preceding vehicle, respectively. In order to facilitate the state prediction of the MPC algorithm, the discretized state space equation is derived from Eq. (2) under the assumption that the mean of the preceding vehicle’s longitudinal acceleration is zero. The time gap ($\Delta t$) for discretization is defined as a value of 0.01 s in this study.

$$ \begin{aligned} &e(k + 1) = A_{d} e(k) + B_{d} u(k) \hfill \\ &y_{p} (k) = C_{w} e(k) \hfill \\ \end{aligned} $$

(3)

where,

$$ A_{d} = \left[ {\begin{array}{*{20}c} 1 & {\Delta t} \\ 0 & 1 \\ \end{array} } \right],\,\,B_{d} = \left[ {\begin{array}{*{20}c} 0 \\ { - \Delta t} \\ \end{array} } \right],\,\,C_{w} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] $$

The $y_{p}$ is the output of the discretized system, and the control input, $u(k)$, represents the desired acceleration of the current step k. The matrix $A_{d}$ represents the system matrix of the preview model while the matrix $B_{d}$ is the input. The $C_{w}$ matrix is the weighting matrix used to construct performance index $J$. In addition, the factors of the weighting of the prediction horizon are defined as a hyperbolic tangent equation.

Equation (4), shown below, is the performance index $J$ defined in this study to compute the optimal solution and predicted states.

$$ \mathop {\hbox{min} }\limits_{{\vec{u}}} J = \vec{y}_{p}^{ * } \vec{y}_{p} + R\vec{u}^{ * } D^{*} D\vec{u} $$

(4)

where,

$$ \begin{aligned} &\vec{y}_{p} = [y_{p} (k + 1)\,\, \cdots \,\,y_{p} (k + N)]^{ * } \hfill \\ &\vec{u} = [u(k)\,\, \cdots \,\,u(k + N)]^{ * } \hfill \\ &R = diag(\bar{R}(k + 1)\, \cdots \,\,\bar{R}(k + N)\,) \hfill \\ &D = \left[ {\begin{array}{*{20}c} 1 & { - 1} & 0 & 0 & 0 \\ 0 & 1 & { - 1} & 0 & 0 \\ 0 & 0 & 1 & \ddots & 0 \\ 0 & 0 & 0 & \ddots & { - 1} \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ \end{aligned} $$

The $N$ and $R$ represent the prediction step (the value of $N$ is 20) and weighting factor for input, respectively. And the $k$ is the step of present state. Then, the predictive model $\vec{y}_{p}$ is expressed as follows:

$$ \vec{y}_{p} = Me(k) + H\vec{u} + Fu(k) $$

(5)

where,

$$ \begin{aligned} M = \left[ {\begin{array}{*{20}c} {C_{w} A_{d} } & {C_{w} A_{d}^{2} } & \cdots & {C_{w} A_{d}^{N} } \\ \end{array} } \right]^{*} \hfill \\ H = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 \\ {C_{w} B_{d} } & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {C_{w} A_{d}^{N - 2} B_{d}^{{}} } & {C_{w} A_{d}^{N - 3} B_{d}^{{}} } & \cdots & 0 \\ \end{array} } \right] \hfill \\ F = \left[ {\begin{array}{*{20}c} {C_{w} B_{d} } & {C_{w} A_{d} B_{d} } & \cdots & {C_{w} A_{d}^{N - 1} B_{d} } \\ \end{array} } \right]^{*} \hfill \\ \end{aligned} $$

In Eq. (5), matrices $M$, $H$, and $F$ can be respectively constructed from the system, input, and disturbance matrices of the state space equation defined in Eq. (4). The $\vec{u}$ indicates the desired acceleration for the longitudinal control of N-step prediction horizon for autonomous driving. In addition, to drop the $\vec{y}_{p}$ terms in Eq. (4) by using Eq. (5), the cost function can be arranged as Eq. (6). With this cost function, the constraints of the control input as well as the desired acceleration can be derived by using $D$ and $L$ which, represent the upper and lower acceleration limits, respectively.

$$ \mathop {\hbox{min} }\limits_{{\vec{u}}} \frac{1}{2}\vec{u}^{ * } Pu + f^{ * } \vec{u}\,\,\,\,\,\,\,\,\,\,\,subject\,to\,D\vec{u} \le L\,\, $$

(6)

where,

$$ \begin{aligned} &D = [D_{upper} ,\,D_{lower} ]^{*} ,\,\,L = [L_{upper}^{*} ,\,L_{{_{lower} }}^{*} ]^{*} \hfill \\ &D_{upper} = I_{N \times N} ,\,\,D_{lower} = - I_{N \times N} \hfill \\ &L_{upper} = a_{upper,l\,im} \cdot \left[ {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \end{array} } \right]_{N \times 1} ,\,\,L_{lower} = a_{lower,l\,im} \cdot \left[ {\begin{array}{*{20}c} { - 1} \\ \vdots \\ { - 1} \\ \end{array} } \right]_{N \times 1} \hfill \\ \end{aligned} $$

$a_{upper,l\,im}$ and $a_{lower,l\,im}$ represent the maximum and minimum acceleration limit values. The $L_{upper}$ and $L_{lower}$ in the constraint of Eq. (6) are the array of length N (prediction step) with the respective limits of acceleration, $a_{upper,l\,im}$ and $a_{lower,l\,im}$. Further, the $P$ and $f$ matrices in Eq. (6) are defined as follows:

$$ P = RD^{*} D + H^{*} H $$

(7)

$$ f = H^{ * } (Me(k) + FU) $$

(8)

In order to test the convexity of Eq. (6) for the MPC, the positive definiteness of matrix $P$ has been evaluated. The quadratic function described in Eq. (6) is convex if and only if matrix $P$ is positive semi-definite. In addition, the function is strictly convex if and only if the matrix $P$ is positive definite. Various methods can be used to test the positive definiteness of the matrix, and the eigenvalue-based test has often been used to test whether or not the quadratic function is convex. Based on Eq. (7), matrix $P$ can be rewritten using matrices $C_{w}$, $A_{d}$, and $B_{d}$. In Eq. (7), the matrix terms, $D^{*} D$ and $H^{*} H$, are symmetric matrices with calculation results as follows.

$$ \begin{aligned} D^{*} D &= \left[ {\begin{array}{*{20}c} 1 & { - 1} & 0 & \cdots & 0 \\ { - 1} & 2 & { - 1} & \ddots & \vdots \\ 0 & { - 1} & 2 & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & { - 1} \\ 0 & \cdots & 0 & { - 1} & 2 \\ \end{array} } \right] \hfill \\ H^{*} H &= \left[ {\begin{array}{*{20}c} 0 & {C_{w} B_{d} } & \cdots & {C_{w} A_{d}^{N - 2} B_{d}^{{}} } \\ 0 & 0 & \cdots & {C_{w} A_{d}^{N - 3} B_{d}^{{}} } \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 \\ {C_{w} B_{d} } & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {C_{w} A_{d}^{N - 2} B_{d}^{{}} } & {C_{w} A_{d}^{N - 3} B_{d}^{{}} } & \cdots & 0 \\ \end{array} } \right] \hfill \\ \end{aligned} $$

(9)

According to Eq. (9), the resulting matrix $P$ in Eq. (7) is also real symmetric, and its eigenvalues and eigenvectors are real and orthogonal. Moreover, matrix $P$ is found to be diagonalizable by an orthogonal matrix. In order to make the quadratic function defined in Eq. (6) convex, weighting factor $R$ for input and weighting matrix $C_{w}$ for error state should be defined so that the eigenvalues of a real symmetric matrix $P$ are all positive. All of the eigenvalues of matrix $P$ were computed to be positive, as shown in Fig. 5.

Fig. 5

Eigenvalues of P matrix in complex plane

Therefore, the quadratic function defined in Eq. (6) is strictly convex, and the optimal inputs that make the equation minimize can be calculated based on quadratic programming. Then, the optimal control input ($\vec{u}_{opt}$) can be computed based on the Quadratic Programming solver provided by MATLAB. We can also use the following equation to obtain the prediction errors of the relative states.

$$ \vec{e}_{D,pre} = C_{p}^{ - 1} \left( {M\vec{e}_{D} (k) + H\vec{u}_{opt} + Fu(k)} \right) $$

(10)

where,

$$ C_{p} = \left[ {\begin{array}{*{20}c} {C_{w} } & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {C_{w} } \\ \end{array} } \right] $$

By using actual driving data such as preceding vehicle velocity and subject vehicle velocity, the optimal solution of the MPC algorithm can be calculated; specifically, the optimal longitudinal control input and the prediction of relative values. In Fig. 6a, the velocity profiles of the data-1 log are shown. The results from MPC, desired acceleration input, and prediction of relative values are presented in Fig. 6b and c.

Fig. 6

Characteristics of Data-1 and MPC solutions

Data-1:

The dashed lines in Fig. 6b and c represent the predicted states (clearance and relative velocity between the preceding vehicle and subject vehicle) by the MPC algorithm constructed in this study. Using the results of the MPC algorithms described in this section, the following section describes the fault detection and acceleration reconstruction based on a sliding mode observer.

4 Fault detection and reconstruction algorithm based on sliding mode observer

Previous studies have proposed fault detection based on a single sliding mode observer (Oh and Yi 2017; Oh et al. 2018). The single sliding mode observer was applied to reconstruct the relative acceleration between the preceding vehicle and the subject vehicle by using only the current state estimation result. Then, the upper and lower limits for reasonable acceleration were computed, which made it possible to diagnose the acceleration fault. In this study, in order to improve the performance of acceleration fault detection with this type of approach, a generation of multiple and proper reasonable acceleration range is required. By applying model predictive control with radar measurement ($x$), such as clearance ($c$) and relative velocity ($v_{rel}$), to the high level controller of autonomous driving, the predicted relative values ($x_{pre}$) for the designated time horizon are computed rationally with consideration of the optimized control solution. If accumulated data with prediction ($x_{pre,accum}$) are used to generate multiple reconstructed allowable acceleration boundaries ($a_{rel,re,pre[k]}$) consisting of upper ($\bar{a}_{rel,re,pre[k]}$) and lower bounds ($\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{rel,re,pre[k]}$), the performance of the acceleration fault detection will be rationally enhanced. Using reconstructed acceleration limits, we can determine signal information from the vehicle acceleration sensor ($a_{s}$) better than we could using the previous approach. Furthermore, with stored prediction of relative values, the fault detection index of the radar ($I_{R}$) is obtained by using the predictive fault detection algorithm. Thus, in this study, we propose multiple sliding mode observer-based acceleration fault detection by accumulating past state prediction and generating multiple allowable a_x ranges. The multi sliding mode observer-based fault detection scheme is described in the block diagram shown in Fig. 7.

Fig. 7

Fault detection architecture based on Multiple Sliding Mode Observer

As shown in Fig. 7a, the proposed algorithm largely consists of two parts: radar and acceleration fault detection. First, we compute the optimized control input for the predication horizon determined using MPC with the relative information of the front vehicle obtained through the radar, then perform fault diagnosis on the radar using the accumulated information. Secondly, the acceleration fault detection is performed by generating several allowable acceleration boundaries using multiple SMO, as shown in the block diagram in Fig. 7b. The multi-SMO selects values from the current point-in-time basis from accumulated historical prediction results, reconstructs the acceleration through individual SMOs, and calculates multiple allowable upper and lower acceleration bounds through statistical analysis of the acceleration results.

We applied the sliding mode observer to detect fault by reconstructing the relative acceleration using a longitudinal kinematic vehicle model as follows:

$$ \frac{d}{dt}\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]a_{p} + \left[ {\begin{array}{*{20}c} 0 \\ { - 1} \\ \end{array} } \right]a_{s} $$

(11)

where $x_{1}$ and $x_{2}$ are respectively the states of the clearance and relative speed acquired from the front radar; $a_{p}$ and $a_{s}$ are the mean accelerations of the foregoing and subject vehicle, respectively. In order to formulate the sliding mode observer, the output—$y$—is defined using observation matrix $C$ as follows:

$$ y = C\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right] $$

(12)

where,

$$ C = \left[ {\begin{array}{*{20}c} 1 & 1 \\ \end{array} } \right] $$

We defined the observer equation to reconstruct the relative acceleration as shown in Eq. (13). The reconstructed relative acceleration was used to derive the upper and lower limitations used in fault detection.

$$ \dot{\hat{x}} = A\hat{x} + Gv $$

(13)

where,

$$ A = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \right],\,\,G = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right] $$

The $\hat{x}$ and $v$ represent the estimated state and the discontinuous injection term, respectively. Coordinate transformation was necessary to guarantee the sliding mode observer’s convergence stability. We defined the transformation matrix with the observation matrix and its null space matrix in the sliding mode observer. The coordinate transformation is derived as follows:

$$ x_{c} = T_{c} x $$

(14)

$$ T_{c} = \left[ {\begin{array}{*{20}c} {null(C)} & C \\ \end{array} } \right]^{T} $$

(15)

where $C$ is the observation matrix and $x_{c}$ represents the transformed state.

Then, we can derive the transformed space state equation using the given transformation and partitioned error dynamics.

$$ \dot{x}_{c} = T_{c} AT_{c}^{ - 1} x_{c} + T_{c} B\left( {a_{p} - a_{s} } \right) $$

(16)

$$ \begin{aligned} \dot{e}_{1} = A_{c,11} e_{1} + A_{c,12} e_{y} + G_{c,1} v \hfill \\ \dot{e}_{y} = A_{c,21} e_{1} + A_{c,22} e_{y} + G_{c,2} v \hfill \\ \end{aligned} $$

(17)

By defining the term of discontinuous injection as shown in Eq. (18), the output error ($e_{y}$) can exist on the sliding surface: $S = \left\{ {e_{y} :e_{y} = 0} \right\}$.

$$ v = \rho sign(e_{y} ) $$

(18)

where $\rho$ refers to the magnitude of the injection term. According to the eta-reachability condition, the output error can converge along the sliding surface with proper $\rho$. Since the output error can converge to zero, the equivalent output injection term can be derived as shown below.

$$ v_{eq} = - G_{c,2}^{ - 1} A_{c,21} e_{1} $$

(19)

For the eigenvalue computation of the (1,1) element of the partitioned system matrix in Eq. (16), $T_{c} AT_{c}^{ - 1}$, is required to verify the stability of $e_{1}$, as follows:

$$ A_{c,11} - G_{c,1} G_{c,2} A_{c,21} = - 1 $$

(20)

Since the quantity of the (1,1) element of the system matrix, $T_{c} AT_{c}^{ - 1}$, always has a − 1 value, the error dynamics for estimating states are definitely stable. Using the sliding mode observer designed in this section, the performance evaluation for the acceleration reconstruction was conducted using actual driving logs. The relative acceleration reconstruction result obtained using real driving data log is shown in Fig. 8. In Fig. 8a, we can observe that the subject vehicle’s velocity is most likely to affect the speed of the preceding vehicle. The reconstructed relative acceleration result is presented in Fig. 8b. Figure 8c shows that the estimation errors for the state and output have converged to zero in a finite period.

Fig. 8

Evaluation results for relative acceleration reconstruction based on actual driving data

Based on the aforementioned state transformation and stability check, the derived equivalent injection term is found to be equal to relative acceleration by Eqs. (11) and (13). In addition, the reconstructed relative acceleration has been used to set the acceleration limits for fault detection.

$$ v_{eq} = a_{p} - a_{s} = a_{rel,r} $$

(21)

Assuming that the delay effect of the environment sensor is negligible, the final output of radar is used by the sliding mode observer. In the cases of other environment sensors, such as lidar and vision, since they may have a sensing delay that influences the operation performance, we need to devise an algorithm to cope with the delay problem. In order to obtain the upper and lower acceleration bounds to perform fault detection, the host vehicle’s acceleration for x-direction was calculated using the following equation:

$$ a_{s} = a_{p} - a_{rel,r} $$

(22)

where $a_{rel,r}$ is the reconstructed relative acceleration. If the host vehicle and preceding vehicle are connected with vehicle-to-vehicle (V2V) communication, accurate acceleration information of the preceding vehicle can be obtained. In this study, the algorithm was designed to obtain information of the foregoing vehicles collected by environment sensor-based recognition without a communication connection. Therefore, the acceleration of the preceding vehicle was estimated by using the relative distance and speed information obtained from the radar.

In addition, in order to identify and apply the characteristics of vehicle acceleration, the probabilistic distribution of longitudinal acceleration was derived from the actual driving data of the foregoing vehicle’s acceleration. In a previous paper, we conducted acceleration analysis using 16 sets of driving data under typical low speed driving conditions (0 ~ 25 m/s) to derive the characteristics of normal acceleration distribution. By analyzing the acceleration data obtained from that study, the average value of acceleration from all driving data is 0.0728 with a standard deviation of 0.6698 m/s² (Oh and Yi 2017). Based on this mean and standard deviation, we can estimate the upper and lower limits to define the allowable acceleration range.

$$ \begin{aligned} a_{s,upper} = a_{p, + 3\sigma } - a_{rel,r} \hfill \\ a_{s,lower} = a_{p, - 3\sigma } - a_{rel,r} \hfill \\ \end{aligned} $$

(23)

By applying three standard deviations (3$\sigma$) for the upper and lower acceleration limits, the range of 3-sigma bounds is guaranteed to cover 99.7% of the sample population. If the longitudinal acceleration measured by the in-vehicle sensors of autonomous vehicle lies within the upper and lower bounds, the algorithm determines that the acceleration sensor has not failed. However, if the measured a_x falls outside of the calculated limits, the proposed algorithm determines that the acceleration sensor is defective. The fault detection results obtained using a single sliding mode observer (SMO) are shown in Fig. 9a (Oh and Yi 2017)

Fig. 9

Acceleration limits: normal driving (with 3σ)

By using several sliding mode observers with stored prediction results of state estimation, we can reconstruct multiple relative acceleration to produce several upper and lower bounds of longitudinal acceleration for use in fault detection. Based on these multiple acceleration limits, it is possible to define a reasonable acceleration range for the current vehicle. Although more reconstructed accelerations can make various allowable ranges, in this study, five SMOs were designed and applied using data stored prior to three, six, nine, 12, and 15 steps for computation efficiency. Since the reliability of the stored data decreases over a longer period, the appropriate acceleration fault index was derived by applying a weighting array ($W$) of the data over time as follows:

$$ I_{A} = \sum\limits_{k = 1}^{{n_{p} }} {w_{i} \cdot f_{a,i} } \,\,\,\,\,\,(i = 3k - 2) $$

(24)

where

$$ W = \left[ {\begin{array}{*{20}c} {w_{1} } & {w_{2} } & \cdots & {w_{{n_{p} }} } \\ \end{array} } \right]\,\,\,\,\,\,\,\,\,\,\,\,\left( {\sum\limits_{i = 1}^{{n_{p} }} {w_{i} } = 1} \right) $$

The $f_{a,i}$ is a logical value if the current acceleration is out of the $a_{x}$ range defined in the ith previous step. The $n_{p}$ is the number of sliding mode observers designed, and we use the value of six in this study. The $w_{i}$ is the i-th component of the weighting array, and is defined as a high weight for values near the current. In this study, the weightings were set to be reduced by 5% per three predicted steps from current step k. Figure 9b describes the multi sliding mode observer-based $a_{x}$ fault detection.

Figure 9 Acceleration limits: normal driving (with $3\sigma$).

If there are no signal faults in the acceleration sensor, the measured information of acceleration should be within the range of the $3\sigma$ limits calculated in Eq. (22).

In order to detect environment sensor faults, we used the N-step prediction result of MPC described in the previous section. On the left side of Fig. 10, each column represents an MPC solution calculated at the time of the blue or gray painted box. The blue box at the bottom of the left column is the control input calculated at present, while the white box column directly above it represents the predicted control input of the N-step prediction horizon calculated through MPC. Likewise, the second column from the left shows the result of accumulating MPC solutions calculated from the previous k-1 step, and the longer the vertical rows further to the right are, the farther the solution will be from the past. In this study, we aim to diagnose faults by using control inputs computed based on a current point-in-time basis to determine whether they exist within the range of proper acceleration calculated through reconstructed accelerations. Thus, a horizontal line containing red colored boxes means refers to predicted control input of the current point-in-time basis among the predictions of accumulated past MPC solutions. For example, among the predictions made at the time of the past (k−1) step, the second value from the bottom of the column is the value of interest in the present time base. Similarly, among the prediction results at the past (k-N) step, the (N + 1)th value from the bottom is the value of interest. Therefore, the blue and red boxes enclosed by the dashed red line are used to determine whether they exist in the appropriate acceleration range.

Fig. 10

Fault detection concepts of relative values by using stored prediction states

For the fault detection of the relative values of $x_{1}$ and $x_{2}$, we calculated the limits of each state according to the analysis of the derived acceleration distribution. If the measured states are within the predicted upper and lower bounds, it is determined that there is no fault. Meanwhile, if at least one measured state is not located in the range of the predicted bounds, it is determined that unexpected fault signals exist. The concept of the fault detection of relative values with predicted limits is described on the right side of Fig. 10.

In this study, in order to identify the fault of the environment sensor such as a radar, we proposed an index that reflects the fault ratio. The fault ratio is a ratio in terms of the accumulated and predicted states. Therefore, the fault index ($I_{R}$) of relative values, relative distance, and relative velocity obtained from the front environment sensor can be derived as follows:

$$ I_{R} = \frac{{N_{f} }}{N} $$

(25)

where $N$ is the number of prediction steps and $N_{f}$ is the number of faults computed using Fig. 10.

The fault indices of the radar and acceleration sensor defined earlier have values between 0 and 1. In order to diagnose the sensor status using the derived indices ($I_{A}$, $I_{{R,x_{1} }}$, $I_{{R,x_{2} }}$), a suitable level of threshold indices is required. It is necessary to minimize the rate of false-positives of fault detection by properly setting the threshold values. In order to analyze the false-positive characteristics of the fault indices, the proposed algorithm was applied to 27 sets of normal driving data. The driving data were stored under relatively low traffic congestion and a smooth changing speed profile. As shown in Fig. 11, the simulation result based on normal driving data show that no fault index was produced for approximately 94% of the total simulated time, while false-positives occur for the remaining 6% of the total simulation period, as shown in Fig. 11. The simulation results that accounted for this 6% were analyzed to produce the statistical characteristics of false-positive indices. Figure 12 and Table 1 summarize the statistical analysis of false-positives based on driving data. In this study, we intend to introduce the scheme of effective fault diagnosis by introducing the concept of confidence level counting, and we use the average and standard deviation values obtained prior to determining the suitability of the fault index. In this study, the statistical characteristics of vehicle acceleration are used to limit the valid range of accelerations, which results in false-positive diagnosis in situations such as abrupt deceleration or acceleration. Therefore, in order to prevent such misdiagnosis, the concept of the confidence level of the fault index is introduced.

Fig. 11

Probability distribution of fault indices result for each state obtained from 27 normal driving data with no fault

Fig. 12

Histogram of fault indices for false-positive cases only

Table 1 Statistical analysis of fault indices (I_A, I _R,x1, I_R,x2) under normal driving conditions

$$ \begin{aligned} &if\,\,I_{j} \ge E(I_{j} )\,\, + \sigma (I_{j} ) \hfill \\ \quad \quad &Confid_{{I_{j} [k]}} = Confid_{{I_{j} [k - 1]}} + 1 \hfill \\ & else \hfill \\ \quad \quad &Confid_{{I_{j} [k]}} = Confid_{{I_{j} [k - 1]}} - 1 \hfill \\ end \hfill \\ \end{aligned} $$

(26)

where $j = A,\,R_{{x_{1} }} ,R_{{x_{2} }}$ and $k$ is the current step. The $E(I_{j} )\,\,$ and $\sigma (I_{j} )$ are the expectation and standard deviation of each fault index, respectively. With this fault confidence, we can determine the fault of each sensor by comparing the fault confidence with the designated threshold: ten for this study. Since the proposed algorithm operates on given systems with 100 Hz rates, it is possible to detect failures within a minimum of 100 ms due to the set threshold. If the behavior information of the foregoing vehicle is obtained using vehicle-to-vehicle communication, the evaluation criteria of confidence can be reduced, which will facilitate accurate and fast diagnosis. Furthermore, it is necessary to take into account the variation in the confidence level during the time period of acceleration and deceleration; the sampling time of the overall system and each sensor should be considered when implementing the threshold into the actual system.

By applying these proposed algorithms, the next section presents the performance evaluation via actual manual driving data with reasonable fault signals.

5 Simulation-based performance evaluation using actual driving data

In order to conduct a reasonable evaluation of the proposed algorithm, we used real driving logs. The actual data were obtained from a long-range radar installed in the front of the automated vehicle, along with an acceleration sensor. Additionally, appropriate fault signals, such as step, hold, and zero, were applied to the data for the performance evaluation. All of the simulations were conducted using actual driving data. The radar sensor used in this research for foregoing vehicle perception is the Delphi ESR model. It has a scanning rate of 20 Hz (50 ms), and the radar signal is received via the CAN network (100 Hz sampling rate) of the test vehicle system. The acceleration signal used in this study is obtained from the in-vehicle sensor through the CAN network. Figure 13 illustrates the model schematics for the performance evaluation. The specific values used in this proposed algorithm are listed in Table 2.

Fig. 13

Model schematics for performance evaluation based on 3D full vehicle model

Table 2 Parameters used in performance evaluation

According to the description so far, it has been shown that the sliding mode observer can successfully reconstruct the relative longitudinal acceleration, even in spite of the unexpected characteristics of signal faults for the acceleration. In addition, the injected offset signal of the acceleration and relative values can be detected using the proposed fault detection concept. In this simulation, the injection offsets for the three signals [x₁, x₂, a_x] were set as follows: x₁ offset magnitude, + 4; x₂ offset magnitude, − 10; and a_x offset magnitude, + 4. The offset fault signal was applied from 40s to 60s. Table 3 shows the classification of the four combination cases of fault injection for each of the two driving data. In particular, data with an abrupt deceleration of maximum -2.5 m/s² were used to verify the robustness of this algorithm in the case of a rapid deceleration situation of the preceding vehicle. The last column in Table 3 shows the figure number of each evaluation result.

Table 3 Simulation conditions of offset fault signal injection

According to this classification table, Figs. 14, 15, 16, 17, 18, 19, 20 and 21 depict the performance evaluation result based on actual driving data of normal condition. Figure 18 describes the driving data characteristics and signals obtained from MPC to adapt fault detection. The x₁ and x₂ indicate the state variables: the clearance and relative speed between the subject and the front target vehicle. The characteristics of the injected offset fault signals and the error calculation of state estimation are depicted in sub-figures (a) and (b). In sub-figure (c), the predictive fault detection results of the relative values of displacement and speed are represented by a contour plot. The acceleration diagnosis results are shown in sub-figure (d) and Fig. 25. The fault indices of each designated state of the above steps are described in sub-figure (e) as a fault index between 0 and 1. The final fault detection results are shown in sub-figure (f) as a logical value (0 or 1) for each sensor, as described in the previous section. Figure 23 describes the data characteristics of an abrupt deceleration of the preceding vehicle in the forms of velocity and acceleration profiles. Figure 24 shows the performance of the proposed fault detection and diagnosis algorithm under a sudden deceleration of the foregoing vehicle. The upper and lower limits of acceleration for each case are depicted in Fig. 25.

Data-1: Figs. 14, 15, 16, 17(Normal Driving)

Fig. 14

Fault diagnosis results with fault injection: data 1, Normal (No fault)

Fig. 15

Fault diagnosis results with fault injection: data 1, offset fault signals of relative values [x₁, x₂]

Fig. 16

Fault diagnosis results with fault injection: data 1, offset fault signal of acceleration [a_x]

Fig. 17

Fault diagnosis results with fault injection: data 1, offset fault signal of both relative values [x₁, x₂] and acceleration [a_x]

Data-2: Figs. 18, 19, 20, 21, 22(Normal Driving)

Fig. 18

Data characteristics (Data-2) and solutions obtained from MPC

Fig. 19

Fault diagnosis results with fault injection: data 1, Normal (no fault)

Fig. 20

Fault diagnosis results with fault injection: data 1, offset fault signals of relative values [x₁, x₂]

Fig. 21

Fault diagnosis results with fault injection: data 1, offset fault signal of acceleration [a_x]

Fig. 22

Fault diagnosis results with fault injection: data 2, offset fault signal of both relative values [x₁, x₂] and acceleration [a_x]

Fig. 23

Data characteristics of abrupt deceleration (data-3)

Data-3: Figs. 23, 24(Abrupt Deceleration)

Fig. 24

Fault diagnosis results with abrupt deceleration: data 3, normal (no fault)

Fig. 25

Reconstructed upper and lower limits of relative acceleration

The driving data-based simulation results of the proposed fault detection algorithm confirmed its enhanced performance in various driving situations. Two cases of manual driving data were applied to the simulation test. The offset fault signals are injected to the acceleration and relative values in terms of the front target during a few seconds with the three combinations shown above in Table 3.

The applied fault signals were detected using the predictive algorithm, then finally, the fault indices for each value were calculated to diagnose fault. In most cases, the logical decision of each sensor presented rational fault diagnosis results, as shown in sub-figure (f), with regard to fault indices (I_A, I_R,x1, I_R,x2), respectively. In sub-figure (e) in each of Figs. 15, 17, 20, and 22, for the fault detection performance of state x₂, the injected offset signal was not clearly detected. Since x₁ represents the integral of the state x₂, it was expressed that the state x₁ was relatively better detected than x₂. However, compared to the results of a previous study with regard to applying the linear prediction of states, it can be seen that the detection performance of x₂ is significantly improved. As the predicted relative states from MPC reflect the results of the optimal solution for longitudinal control, it is considered to be more reasonable than using simple linear prediction. Despite the low detection estimation performance of x₂, the radar sensor can be reasonably diagnosed, because the fault detection performance of x₁ is quite accurate. Moreover, the applied acceleration faults were successfully detected based on the multiple reconstructed upper and lower limits of the acceleration by applying a multi sliding mode observer. In Figs. 16, 17, 21, and 22, the acceleration fault is well detected and isolated, despite the fact that it was simultaneously applied with other fault signals. In addition, the acceleration can only be detected if the magnitude of the applied fault is larger than the magnitude of $3\sigma$ in sub-figure (c) in each of Figs. 16, 17, 21, and 22. As shown in Fig. 23, the data-3 produced an abrupt deceleration of the preceding vehicle around 20s, and this data was used to confirm the performance of the proposed algorithm in terms of avoiding false positives. Although no fault was injected, the fault indices were calculated due to the rapid behavior of the preceding vehicle as shown in Fig. 23. However, the introduction of confidence counting concept avoided misdiagnosis. As shown in Fig. 24e and f, the fault index error occurred because of a rapid deceleration at 20s, but no misdiagnosis occurred as there was no excess confidence threshold. This allows the proposed algorithm to achieve reliable fault detection performance even if the preceding vehicle is outside of the normal acceleration distribution.

Thus, the injected fault signals are considered to be detected properly using data accumulation of predicted states from MPC as well as several acceleration limits from the multiple sliding mode observer. The next section presents the conclusion summarized from this research, including suggested future work.

6 Conclusion

A model predictive control-based fault detection and reconstruction algorithm for the longitudinal control of autonomous driving using a multi-sliding mode observer has been presented in this paper. A reasonable failure detection scheme for the acceleration signal of the host vehicle and the relative values of the front object of the radar was proposed. The multi-sliding mode observer and prediction of the model predictive control (MPC) algorithm were applied in this research. The sliding mode observer was used to reconstruct the relative acceleration from the clearance and relative velocity as measured by radar. The upper and lower limits of longitudinal acceleration were calculated according to the probabilistic distribution of the vehicle acceleration data obtained from real-road driving data. By defining a proper acceleration range based on several reconstructed upper and lower limits by using a multiple sliding mode observer with stored prediction data of relative values, the proposed algorithm was able to effectively detect the acceleration sensor fault. By applying model predictive control, the relative values of the target could be predicted in consideration of the optimal control input, and the results were more reasonable than those using linear prediction. By comparing the stored predictions of relative states with the accumulated data of current states for a designated period, the signal faults of the longitudinal target information from the environment sensor—in this study, the radar—could be detected. Using the predictive diagnostic algorithm, the fault index that can quantitatively represent the ratio of fault was proposed for the evaluation of the system health diagnosis. It was difficult to cope with the extreme motion of the foregoing vehicle because only a statistical distribution of normal driving acceleration was used to determine the allowable range of relative states. Nevertheless, the confidence counting method enabled reasonable fault diagnosis without misdiagnosis in the event of rapid deceleration or acceleration of the front vehicle. In order to conduct a reasonable performance evaluation, three sets of actual driving data from a test vehicle and a 3D full vehicle model constructed in the MATLAB/Simulink environment were used. The simulation results revealed that the proposed algorithm can be used to rationally detect and isolate the applied fault. Moreover, the proposed algorithm was confirmed by simulation to prevent false-positives by using driving data including abrupt deceleration of the preceding vehicle. In this study, the scheme of confidence level counting was introduced to address the limitations of the data-based statistical approach for fault detection. If the acceleration of the preceding vehicle is obtained through V2V communication, it is expected to enhance reliability. Based on the obtained acceleration of the preceding vehicle, the acceleration of the subject vehicle can be reasonably reconstructed with communication noise and delay. Moreover, a proper threshold value considering communication noise and delay is necessary to achieve a reliable decision of fault confidence level. In addition, each environment recognition sensor has a different scan rate and time delay, so an appropriate approach considering those sensor characteristics is planned as future work. The topic of our future research is a fault detection algorithm for various environment cognitive sensors. Furthermore, by handling the fault detection results of each environment sensor, the enhanced fault diagnose algorithm can be designed to improve the reliability of the autonomous driving system.