Introduction

The inclusion of renewable energies in the main electricity grids is one of the objectives of the United Nations 2030 agenda to achieve sustainable development worldwide (U Nations 2015). In energy systems, this depends directly on the efficiency with which the technologies to be implemented are selected and on how their equipment and backup systems are dimensioned, as well as the operation of the system (Kakran and Chanana 2018). In the design of renewable energy systems (RES), the main obstacle that arises when using clean energies such as solar or wind is their intermittence and randomness (Fuentes-Cortés and Flores-Tlacuahuac 2018). If, in addition, the dynamic characteristics of electricity demand are considered, the analysis becomes even more difficult (García et al. 2019). A solution that is used to guarantee an adequate design of energy systems is to review extensive databases, which usually cover at least one year to visualize the behavior of variables in all seasons of the year (Kakran and Chanana 2018).

Traditionally, variations and uncertainties in input data for optimization models are addressed by two main strategies: stochastic programming and the use of forecasting models. Regarding stochastic programming, one of the most widely used methods is multi-scenario analysis (Yan et al. 2021). This can use the totality of available data, or generating scenarios based on a probabilistic approach of the phenomena, to address uncertainties and possible variations and find solutions under expected conditions or reduce impacts of scenarios with extreme conditions or minimize the chances of a worst-case scenario (Zakaria et al. 2020). Strategies such as chance-constrained (Odetayo et al. 2018), conditional value at risk (Cao et al. 2017) and Monte Carlo analysis (Meschede et al. 2017) have been used to achieve these objectives. In terms of forecasting models, there have been developed models for planning with stability analysis of operating conditions (Ahmad et al. 2020), data distribution analysis (Hernández-Romero et al. 2019; Wang et al. 2018) or models based on chaos theory (Cui et al. 2019). However, these types of strategies involve a high level of complexity in terms of modeling and a high computational cost, which increases when aspects such as the non-linearity of the phenomenon addressed are considered (Rudin et al. 2021).

Particularly, for systems based on renewable sources, addressing the variation in the availability of wind or solar radiation is a fundamental problem to define an optimal sizing of the system and an adequate operation policy of interconnection with local grids or the use of storage systems. Variations on availability of resources leads to instability and low quality of energy supply (Ciupageanu et al. 2020). In this sense, for distributed generation systems based on wind turbines, considering the variability of wind behavior, significant contributions have been made based on forecasting and scenario generation (Li et al. 2020). For photovoltaic systems, both approaches have been used for addressing variations and abnormal behavior associated with weather changes (Ahmed et al. 2020).

Derived from the trend of data-driven analysis and the availability of large data sets, a current issue has emerged in the design of RES: the handling of “a lot of information” (Calvillo et al. 2016). The difficulty that this presents, especially when calculating the optimal design (OD) of the RES, is that the computational capacity and resources required by optimization models (MO) to find a solution to the multivariate problem can be very demanding (Azuatalam et al. 2019). In general, to lighten the burden of handling so much information, one approach is to identify patterns of behavior of the variables of interest for different purposes as: the sizing of the RES, the forecast of the operation, and the generation of scenarios to perform sensitivity analysis of the system (Abdmouleh et al. 2017).

To identify the characteristics of the data sets there are different approaches, those that are simply statistical, probabilistic or those that use Statistical Learning. In Kettaneh et al. (2005) the importance of managing large data sets and how their size increases the difficulty and modifies the results of various problems of general interest is reviewed. Thus, due to the fact that large data sets continue to grow, it is concluded that their management and synthesis is a necessary subject of study (Kettaneh et al. 2005).

In the statistical branch, the principal component analysis (PCA) (Jolliffe 1986) leads to data reduction based on its dimensionality reduction (Shlens 2014). This technique allows comparing several variables or dimensions, then identifies statistical measures to form the matrix of principal components, in which the variance is recorded (Shlens 2014). The first principal component retains most of the variance and is then used as a model of the actual data set, which can be mapped to the initial data to return to the corresponding size or range (Shlens 2014). In Gordillo-Orquera et al. (2018), PCA was used to model a couple of large electrical load data sets in a first approach, by reducing the dimensionality of the original data, the authors were able to forecast electricity load consumption a year in advance. You can review other case studies where solar irradiance (α) (Azadeh et al. 2008), wind speed (υ) (Zhang et al. 2018), energy demand (WD) (Ribeiro et al. 2016) and other RES variables are reduced by methods involving PCA.

In the pattern recognition category, the k-means clustering method is used to group the initial data (Hamerly and Elkan 2004). This method consists of an optimization where random values are tested to identify centers or means of the cluster k, each cluster is formed by finding all the values close to the center of the cluster, until the distance of the closest data to each center is similar for each group (Hamerly and Elkan 2004). The classification of typical days (TD) of the solar irradiance (α) identifying its frequency and probability through a k-means-Markov chain coupled algorithm to construct a typical year is developed in Li et al. (2017), wind speed can be modeled using a k-means clustering approach if there are gaps in the data sets as demonstrated in Yesilbudak (2016) and electricity demand is modeled using k-means in Azad et al. (2014) to understand its usage behavior.

This article presents a comparison of three data reduction approaches. In the first approach, a random sample of actual days is evaluated with results indicating clear variability and dependence of the input data, then typical days are modeled using a PCA reduction (TDPCA) and a stochastic simulation based on a pattern recognition by k-means (TDkm). The optimization results are quantitatively compared using performance analysis (iterations required to achieve OD) and computation time (ToC) with data reduction using all three methods versus a no reduction approach as a benchmark.

Main contributions of the analysis performed are:

  • Developing a strategy based on statistical learning algorithms (PCA and k-means) for finding a balance between data reduction and keeping performance of OD.

  • Providing a strategy for implementing PCA and k-means, with a minimal loss of information over the original data, and obtaining suitable profiles of energy consumption and ambient conditions for the OD of RES.

  • A contrast and comparison is presented between the use of the total data and the patterns obtained through statistical learning strategies by analyzing deviations and gaps associated with data reduction.

  • The impacts of implementing statistical learning algorithms on the computational cost associated with solving a NLP model are considered.

This article is divided in seven sections: “Introduction”; “Problem Statement”, where the problem to be addressed is presented; “Model Definition”, where the optimization model is presented; “Data Reduction”, where the three approaches for data reduction are explained; “Case Study and Computational Issues”, where main features of data used are introduced; “Results and Discussion”; and, finally, “Conclusions”.

Problem Statement

The configuration of the addressed energy system is shown in Fig. 1. The set of wind turbines dynamically produces electrical energy, like the set of photovoltaic panels, the battery bank can be charged, or it can power the load while the electricity grid is used as a backup. In the inverter, depending on the battery charging conditions and the available energy, clean energies are directed to power the load or recharge the batteries, while the grid can only power the load.

Fig. 1
figure 1

RES with batteries and grid backup

Full size image

When the algorithm for calculating the optimal design is fed with large databases, the computation time and iterations for computing an optimal result increase in most cases. As can be seen in the “Results and Discussion” section, the system is also susceptible to the characteristics of the input parameters, it being possible that the number of iterations does not always increase as the input data increases, but sometimes fluctuates. This shows that removing unnecessary or outlier data, in addition to improving computational performance, can also ensure that the results are representative of the problem. Thus, data reduction becomes relevant and improves computational performance, achieving results that are similar to having large data sets involved in the calculation (see Fig. 2).

Fig. 2
figure 2

Data reduction implementation

Full size image

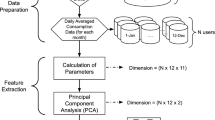
The process to have OD is shown in Fig. 3. The impact of performance of data reduction strategies can only be analyzed after the OD is obtained by the OM, however, some features can be revised to assure that the data inserted in the OM is representative of the original registers.

Fig. 3
figure 3

Data reduction flowchart

Full size image

The most important parameters of OM are solar irradiance α, T, WD and υ, as well as the efficiency parameter and other technical factors, as well as the energy selling price to main grid. As variables of the OM, the sizing of PV, WT and BS, many technical factors and considerations, also some of the balances that are described in the “Model Definition” section. The objective is solely the total annual cost.

In sum, the data reduction problem is addressed by considering the following points:

  • The aim is finding a balance between data reduction and keeping performance of OD. A first approach is to reduce data by sampling random real days (RRD) of a four-parameter-database, which represents no data handling nor pre-processing.

  • PCA is applied to four large data sets to identify the principal component (PC) characteristics that enable to reduce their dimensionality after each PCA, while retaining the most relevant values related to variance of the analyzed data set after reconstruct the PC over the sample.

  • TDkms of four variables are built based on the patterns identified by k-means clustering. First, each hour of the day is classified in a k-cluster, then the characteristic cluster (CC) of each hour of the day is selected, and then stochastic scenarios are constructed selecting values within standard deviation of CC.

  • A comparison among the three approaches of data reduction is presented, analyzing the gaps and differences on OD results.

Therefore, the optimization problem can be stated as follows: Given a large amount of raw data sets of energy demand, ambient temperature, wind speed and solar radiation, statistical learning techniques are applied to obtain different typical days which are used to feed an optimal design model of an energy supply system based on renewable energies: photovoltaic units, wind turbines and battery storage systems. The optimal design includes the computation of the system sizing to minimize the total annual cost of the system. The analysis to determine the effectiveness of the data reduction includes a comparison with the solution obtained using the total data sets.

Model Definition

The objective function for the NLP multi-scenario multi-period model is the total annual cost (TAC). The model inputs are: solar irradiance (α), wind speed (υ), temperature (T) and power demand (WD). Among these and some other characteristics of these energy sources, the power obtained by each equipment is calculated. In both cases, the catchment area is the common parameter and is proportional to the size of the installation for each of the two: photovoltaic panels (PV) and wind turbines (WT).

NLP Model

NLP modeling is defined by the sets \({\varsigma } = \left \{1,...,\mathtt {S}\right \}\) for all the scenarios and \(\tau = \left \{1,...,\mathtt {T}\right \}\) for all the operational periods. This approach allows considering different variations in ambient conditions and energy demand, as well as defining the optimal operational policy for each period and scenario.

PV System Modeling

The efficiency of PV system is defined by the ambient temperature conditions (Skoplaki and Palyvos 2009).

$$ \eta^{PV}_{t,s} = \eta^{PV}_{0} \left[ 1 - \beta_{Ref} \cdot \left( T^{amb}_{t,s} - T_{Ref} \right) \right], \forall t \in \tau, \forall s \in {\varsigma} $$
(1)

Where \(\eta ^{PV}_{t,s}\) is the efficiency at the period t and scenario s. \(\eta ^{PV}_{0}\) is the design efficiency, β is the temperature coefficient associated with the material of the PV panel. Tamb is the ambient temperature and TRef is the reference temperature associated with \(\eta ^{PV}_{0}\). A common value for TRef is 25 ∘C. As shown, efficiency is dependable on known data. As a consequence, it results in a known value.

Power generation (WPV) results from multiplying α, efficiency (ηPV) and the area of the PV system (APV).

$$ W^{PV}_{t,s} = \alpha_{t,s} \cdot \eta^{PV}_{t,s} \cdot A^{PV}, \forall t \in \tau, \forall s \in {\varsigma} $$
(2)

The power generation can be used for meeting the energy demand of the end user, in this case an apartment building (WPVB), sent to the battery system (WPVBS) or sold to the local utility grid (WPVG).

$$ W^{PV}_{t,s} = W^{PVB}_{t,s} + W^{PVBS}_{t,s} + W^{PVG}_{t,s}, \forall t \in \tau, \forall s \in {\varsigma} $$
(3)

As shown, APV is the area for collecting solar energy and defines the size of the PV system. It is constrained by the available area in the apartment building for installing the energy system, AB.

$$ A^{PV} \leq A^{B} $$
(4)

WT System Modeling

Power generation of WT system (WWT) is defined by υ presence and the limit that is known of the flow of air bring by Betz (β) coefficient. In addition, υ is classified into: cut-in υin, rated υr) and cut-out (υout). The υin is the speed at which power begins to be generated, around 4 meters per second. The υr is that at which the nominal power of the electric generator (\( W^{WT}_{nom}\)) is reached, around 12 meters per second. υout is at which the electric generator is at risk of being damaged and therefore disconnects from the wind turbine at around 30 meters per second (García et al. 2019). Thus, there are three values of υ that indicate how WWT performs:

$$ \begin{array}{@{}rcl@{}} W^{WT}_{t,s} = \begin{cases} 0& \text{if } \upsilon_{t,s} < \upsilon_{in}\\ \beta_{t,s} \cdot \rho^{air} \cdot A^{WT} \cdot \upsilon^{3}& \text{if } \upsilon_{in} \le \upsilon_{t,s} < {\upsilon_{r}} \\ W^{WT}_{nom}&\upsilon_{r} \le \upsilon_{t,s} < {\upsilon_{out}}\\ 0&\text{if } \upsilon_{t,s} \geq {\upsilon_{out}}\\ \end{cases} ,\\ \forall t \in \tau, \forall s \in {\varsigma} \end{array} $$
(5)

Similarly to PV system, energy generated by the WT is sent to the apartment building (WWTB), the battery system (WWTBS) and the local utility grid (WWTG).

$$ W^{WT}_{t,s} = W^{WTB}_{t,s} + W^{WTBS}_{t,s} + W^{WTG}_{t,s}, \forall t \in \tau, \forall s \in {\varsigma} $$
(6)

BS System Model

The energy stored (EBS) is defined by the inlets from the PV and WT systems (WBS), affected by the charge efficiency (ηBS), and the outlets, determined by the energy sent to the apartment building (WBSB), and the local utility grid (WBSG). ηBS is a function of the status of charge (0 ≤ SoC ≤ 1). SoC is a relationship between the energy stored at the operational period t and the size of the battery system (Eμ). As shown, the input and output efficiencies of the battery are defined by different functions dependable on the SoC. These functions are determined by coefficients a, b and c which are associated with the nature of the technology (Fuentes-Cortés and Flores-Tlacuahuac 2018; Ranaweera and Midtgård 2016; Yu et al. 2018).

$$ \begin{array}{@{}rcl@{}} E^{BS}_{t,s} - E^{BS}_{t-1,s} = \\ \eta^{BS_{input}}_{t,s} \cdot W^{BS}_{t,s} - \eta^{BS_{output}} \cdot \left( W^{BSB}_{t,s} - W^{BSG}_{t,s}\right), \\ \forall t \in \tau, \forall s \in {\varsigma} \end{array} $$
(7)
$$ W^{BS}_{t,s} = W^{WTBS}_{t,s} + W^{PVBS}_{t,s}, \forall t \in \tau, \forall s \in {\varsigma} $$
(8)
$$ SoC_{t,s} = \frac{E^{BS}_{t,s}}{E^{\mu}}, \forall t \in \tau, \forall s \in {\varsigma} $$
(9)
$$ \eta^{BS_{input}}_{t,s} = a_{1} \cdot SoC_{t,s}^{2} + b_{1} \cdot SoC_{t,s} + c_{1}, \forall t \in \tau, \forall s \in {\varsigma} $$
(10)
$$ \eta^{BS_{output}}_{t,s} = \frac{a_{2} \cdot SoC_{t,s}}{b_{2} \cdot SoC_{t,s} + c_{2}}, \forall t \in \tau, \forall s \in {\varsigma} $$
(11)
$$ E^{\mu} \geq E^{BS}_{t,s}, \forall t \in \tau, \forall s \in {\varsigma} $$
(12)

Power Supply

Energy demand (WD) is met using energy from the PV, WT, BS and the utility grid.

$$ W^{D}_{t,s} = W^{PVB}_{t,s} + W^{WTB}_{t,s} + W^{BSB}_{t,s} + W^{GB}_{t,s}, \forall t \in \tau, \forall s \in {\varsigma} $$
(13)

Total Annual Cost (TAC)

The TAC is the minimized objective function. It is determined by the Capital cost of equipment (CCost), operation and maintenance cost (OMCost) and the cost of energy from the utility grid (PCost). In addition, incomes from energy sales (PInc) are included as a negative term in the expression.

$$ TAC = CCost + OMCost + PCost -PInc $$
(14)

Capital cost (CCost) is defined by variable cost (ν) associated with the size of the equipment as well as the fixed cost of each of the technologies (ϕ) and the annualization factor ψ.

$$ CCost = \psi \cdot \left( \phi^{BS} + \phi^{PV} + \phi^{WT} + \nu^{PV} \cdot A^{PV} +\nu^{WT} \cdot A^{WT}+ \nu^{BS} \cdot E^{\mu} \right) $$
(15)

OMCost results from multiplying the unit O&M cost for each equipment by the total energy produced by the PV system and the total energy stored in the BS during all the operational periods (Θ) associated with the annual scenarios and operational periods.

$$ \begin{array}{@{}rcl@{}} OMCost &=& {\Theta} \cdot \sum\limits_{s=1}^{\mathtt{S}}\sum\limits_{t=1}^{\mathtt{T}} \left( {\Upsilon}^{OMPV} \cdot W^{PV}_{t,s} + {\Upsilon}^{OMWT} \cdot W^{WT}_{t,s} \right.\\ &&\left.+ {\Upsilon}^{OMBS} \cdot W^{BS}_{t,s}\right) \end{array} $$
(16)

Similarly, the cost of external energy from the utility grid (PCost) is computed using the unit cost of energy from the grid based on a scheduling tariff ΥG.

$$ PCost = {\Theta} \cdot \sum\limits_{s=1}^{\mathtt{S}}{\sum\limits_{t=1}^{\mathtt{T}}{{{\Upsilon}^{G}_{t}} \cdot W^{GB}_{t,s}}} $$
(17)

The incomes (PInc) are computed considering the unit price ϖP of energy sent to the end user and the local utility grid.

$$ PInc = {\Theta} \cdot \varpi^{P} \cdot \sum\limits_{s=1}^{\mathtt{S}}{\sum\limits_{t=1}^{\mathtt{T}}{\left( W^{GS}_{t,s} + W^{BSG}_{t,s}\right)}} $$
(18)

Data Reduction

Seeking to obtain an OD similar to that obtained when all the data is fed into the OM, three approaches to reduce the sample size were used. First, real days were randomly selected from the real sample, for which it was decided to select 60 days for two different seasons. Second, PCA was used to reduce the dimensionality of the sample that was arrayed in a certain way to be able to train, test and rebuild the principal components. Finally, k-means was used to find the general pattern of the behavior of each variable and typical days were generated from the characteristics of the clusters found. Each technique is described in detail below.

Selecting Random Real Days (RRD)

The first approach to reduce the input data and testing the performance and results obtained in the OD of RES was to randomly take r real days (RRD) as a sample from the database. All variables correspond to the same RRD. In a first selection, the RRD were taken from the total days of the year (365 days), later it was decided, based on the atmospheric conditions of different seasons of the year, to divide the population into two seasons: spring-summer and autumn-winter (see Fig. 4).

Fig. 4
figure 4

RRD selection process

Full size image

RRD were selected using a free selection and the number of permutations corresponds to the known formula:

$$_{n}P_{r} = \frac{n!}{(n-r)!} $$
(19)

where r is the number of days to be selected and n is the total data or days from which the selection is made. Five different selections were made to have a benchmark, it should be noted that in each RRD selection days that have been selected on other occasions may appear. So, there are r RRD for two seasons, where each selected day had the same probability of being selected as any other day within the season. With this, it is expected to observe a performance of the model such that the results will begin to stabilize as there is a greater number of input data.

In the “Results and Discussion” section, the comments about this topic will be expanded; however, it can be anticipated that the results are highly dependent on the RRD used and as they were selected by a simple random sample, days with atypical conditions may be included in the calculation, which can lead to a variable behavior of the OM, even when there is “enough” data.

Typical Days with PCA Data Reduction

The PCA process consists on identifying little relevant information in a database of n dimensions (Jolliffe 1986). Using the specific programming package in Julia called PCA, which belongs to MultivariateStats package (Statistics 2014), three functions that are found within PCA are used to correctly model the input data for the OD (see Fig. 5).

Fig. 5
figure 5

Flowchart of PCA reduction process, selecting TDPCA

Full size image

Previously to initiate PCA, the data of the four variables are standardize by \( X= \frac {(x_{i}-\bar {x})}{s} \) were \( \bar {x} \) is the mean of sample, s is the standard deviation and xi is the ith observation. This is a usual standardization use in statistical analysis (Forkman et al. 2019). Afterwards, the option to model and reconstruct approximately the original data is presented in Julia documentation as follows (Blaom et al. 2020): Given a PCA model M, one can use it to transform observations into principal components, as

$$ \mathbf{y}=\mathbf{P}^{\mathbf{T}}(\mathbf{x}-\mu) $$
(20)

or use it to reconstruct (approximately) the observations from principal components, as

$$ \tilde{x}=\mathbf{Py}+\mu $$
(21)

here, P is the projection matrix.

To complete the transform-reconstruction process, some functions of the PCA package must be used. First, a training step for the PCA model must be performed using part of the original data. When traversing this resulting matrix, each subsequent principal component has less representative of the original variance than the previous one, so that PC2 is much less relevant than PC1 and PC3 is much less relevant than PC2

The next step is to transform the results of the training step by a matrix operation with part of the original data to generate a matrix of n number of PCs, the first of these being the one that preserves the most information from the original data, this stage is called the testing stage.

Finally, in the reconstruction step the results obtained in the second process is projected to some original data reserved to perform test to the model to calculate an approximation in the same units and range (Statistics 2014).

Typical Days with k-means Pattern Recognition

When k-means is run on a database, each variable is treated as a vector, since this process examines each vector separately. The k-means technique is an optimization in which the data sample is separated into clusters according to some random values called cluster centers that change until approximately the same distance of data near to the center of cluster do not change (Hamerly and Elkan 2004).

The k-means technique is a classical method for clustering or vector quantization. It produces a fixed number of clusters, each associated with a center (also known as a prototype), and each data point is assigned to a cluster with the nearest center. From a mathematical standpoint, k-means is a coordinate descent algorithm that solves the following optimization problem (Statistics 2012):

$$ minimize \sum\limits_{i=1}^{n}{\left|{x}_{i}-\mu_{z_{i}}\right|}^{2} w.r.t.(\mu,z) $$
(22)

Here, μk is the center of the k th cluster, and zi is an index of the cluster for ith point xi.

Once the data has been separated into clusters each real datum is labeled with the cluster to which it belongs. After classifying the data, a probabilistic analysis is made to determine which is the most common cluster for each hour of the day, in this way it is assumed that the cluster with the highest frequency for a specific hour of the typical day (TDkm) is its characteristic cluster (CC).

In order to define the TDkm’s, it is assumed that the most common values for each hour of TDkm are those that are within the CC, therefore any value within the common values of the CC would be an acceptable value of a typical day. Thus, the TDkm indicators are the center or mean of the CC and its standard deviation. Therefore, to construct the typical days using this methodology, a scenario simulation can be performed within these parameters for each hour of a TDkm for any of the four variables, obtaining n TDkm with the most common characteristics of the analyzed data. Each TDkm is a probabilistic typical scenario within the parameters of corresponding CCs.

The scenario simulation consists in take a random value that is in the interval:

$$ (\mu_{k}- s_{k}) < v_{k} < (\mu_{k}+s_{k}) $$
(23)

For each variable, where μk and sk are features of the CC of that hour and vk is a typical value for an hour of the TDkm. This process can be observed in Fig. 6.

Fig. 6
figure 6

Flowchart of typical days process with k-means pattern recognition, obtaining TDkm

Full size image

Case Study and Computational Issues

In the case study presented, the electrical load of a residential building in the northwestern region of Mexico is analyzed (see Fig. 8), which location is between the coordinates: longitude 100∘ 26′ 31.20′′ W and 100∘ 10′ 01.20′′ W, latitude 25∘ 28′ 55.56′′ N and 25∘ 47′ 50.28′′ N.

The main environmental conditions in the site are that the available wind energy is relatively scarce, while solar radiation and temperature have a relatively consistent behavior throughout of the year. In this study, four variables are analyzed: temperature, solar radiation, wind speed and power demand. There are databases of the four parameters for a full year with measurements every 5 minutes, however, they have been condensed into hourly averages to feed the OM. In Fig. 7 these data are shown (See Fig. 8 for geographic allocation).

Fig. 7
figure 7

Real data, four variables

Full size image
Fig. 8
figure 8

Location of Monterrey, Nuevo León, México. Obtained from Inegi (2017)

Full size image

In Fig. 9 the average by hour of all variables is shown for two seasons of the year, spring-summer and autumn-winter. Where can be observed that for T, α and WD patterns are obvious and there is a clear gap or change between these two seasons, however, υ has a high randomness in both seasons and does not present a “smooth behavior”. In Table 1 the costs and parameters that are included in the calculation of OD are listed.

Fig. 9
figure 9

Real data average day for two seasons: spring-summer and autumn-winter

Full size image
Table 1 Values of cost variables
Full size table

ΥG does not change during the year (see Fig. 10). No other changes in time are considered for these variables.

Fig. 10
figure 10

Costs of energy from grid in USD/kW-h

Full size image

Since in the optimization problem the objective function to minimize is TAC, the results include the values of TAC, the size of photovoltaic panels (WPV), wind turbines (WWT) and battery system, as well as the time of computation (ToC) and the number of iterations (Iter) required in each optimization process.

The NLP model was implemented in the mathematical language Julia, using the optimization environment JuMP and the solver Ipopt (Dunning et al. 2017; Wächter and Biegler 2006) which is commonly used to solve nonlinear optimization problems using the interior point filter with a line-search algorithm (Breuer et al. 2018). As Ipopt is a local solver, for determining a suitable initial value for all the experiments, an algorithm for seeking feasibility, based on bootstrapping, was implemented (Chinneck 2008). In addition, the Multivariate Julia package was used to perform the principal component analysis (PCA) (Statistics 2014). Meanwhile, the package clustering was employed to carry out the CC classification (Statistics 2012). All OD were carried out in a core i5 2nd generation processor, with 4 GB of RAM, with Windows 10® operative system.

Results and Discussion

Results demonstrated that the OD for RES are highly dependent of the input data. Although the model can calculate solutions from as little information as 1 day of input data, it is advisable to include as much information as possible to achieve results that are closer to the actual operation. However, including all the available data produces long computation times, in addition to using infrequent data that could skew the results. Thus, three strategies to reduce input data were performed to original data and the OD resultant are presented below.

Random Real Days (RRD)

For the first approach (random selection of real days) 60 RRD for two seasons of the year are included in 5 different samples. With these sets, several optimizations are performed where the input RRD increases, and their results are recorded (see Fig. 11 where are plotted: (a) TAC, (b) PV, (c) WT, (d) BS, (e) ToC and (f) Iteratios).

Fig. 11
figure 11

OD results performance with 5 sets of RRD

Full size image

In Fig. 11 results for RRD indicate that in each RRD sample, as the number of days included in the optimization increases, this does not ensure that results of OD converge to a unique value, nor the (a) TAC, nor the (b) WPV, nor the (c) WWT nor the (d) WBS. It is noticed that the green and blue lines retain the WT reduce the size of PV and BS. In addition, (e) ToC has a peaking trend as increasing the number of RRD, however some fluctuations can be observed, meanwhile (f) Iter have a variant behavior with each change in RRD and not a clear trend is appreciated. However, the TAC increases and reaches values close to the benchmark (less than 0.5% of difference), WPV reaches 45 kW of main power, WWT oscillates around 1 kW until it is discarded in some cases, although in some optimizations it remains, WBS ranges between 130 and 140 A-hr, which is close to those of the benchmark’s. In Table 2 the results of 5 samples with 60 RRD per seasons are compared to all-data optimization.

Table 2 RRD comparison with benchmark (60 RRD per season)
Full size table

Typical Days with PCA Data Reduction (T D PCA)

The original information is presented in matrix form and then processed by the PCA, with two columns, in which the first represents half of the data and the second one is the remaining data. Previously, the data were separated into two seasons, spring-summer and autumn-winter. These two use 4608 data corresponding to 192 days, with an overlap between the end of the first and the beginning of the second season. This 192 actual days sample enhance the data reduction process due to it can be divided by two and the result is an integer for each new process. In this way, in the first iteration the matrix of the real data has two columns and 2304 rows, 50% of the data is used to train the PCA model obtaining a certain number of principal components (PC), in our case only PC1 and PC2 are computed. Then, the model is tested on the remaining data and, finally, function PC are re-size the to original range. At this point, as PC1 is solely considered, only half of initial number of data is conserved, now reconstructed, however, this data retains a high percentage of the variance of each variable data as found in the “PCA ratio” of PC1 (see Table 3). The results of this reduction are treated as a new sample and are arranged in a 2 × 1152 matrix, then, they are used as the new training set and are reduced once more in half on the next iteration and so on until a set of only three TDPCA of each variable is reached. To achieve this, six reductions were necessary. Please observe that υ retain 100% of the variance after the whole process in both seasons, as total PCA ratio (ratiototal) is calculated by multiplying PCA ratio of every reduction, while the lowest ratiototal is 97.52% for the WD in season 1. These values indicate that a high variance of the variables are preserved in the reduction process, even when only three TDPCA remain.

Table 3 PCA ratio for each reduction
Full size table

The results of the reduction have shown that when there is little data even, when they are significant, the OD results are not very reliable; thus, the more the number of TDPCA increases, a consistent performance is reached (ToC and Iter) and with a certain proximity to benchmark results.

In Fig. 12 the smallest TDPCA sets are presented, with 3, 6, 12 and 24 TDPCA. Given the characteristics of PCA, sometimes the reconstructed model can give results outside the physics of the problem, so a restriction to reconstructed α was included: there cannot be negative data.

Fig. 12
figure 12

Results of TDPCA reduction, four reduction sets

Full size image

Data reduction with PCA retain more than 97% of the variance of the original data sample for each reduction, according to the internal evaluation and the PCA ratio Fig. 3. However, if the most reduced model is used (3 TDPCA for each season), results of OD are highly variant, this can be observed in Fig. 12 with the red line, (a) TAC, (b) PV, (c) WT, (d) BS are “volatile”, as the Reduction is more conservative (blue line is the most conservative reduction), all values start to reach those of the benchmark’s see the 24 TDPCA reduction. The behavior of the model demonstrates some trends the more TDPCA it receives: more Iter and ToC are required to calculate OD; TAC reaches a benchmark-like value, as well as all the other variables, WPV approaches to 45 kW, WWT is finally discarded, and WBS lies around to 240 A-hr. These results are consistent to those of the benchmark, as presented in Table 4, where the reductions are labeled according to TDPCA.

Table 4 TDPCA comparison with benchmark (lowest number of TDs)
Full size table

Typical Days with Pattern Recognition by k-Means (T D km)

For the third approach, the number of clusters to be considered for each variable was empirically tested, and heuristically, α considers 8 clusters, while WD, T and υ only 5 clusters. The data was not treated previously to the clustering process. As describe in the “Typical Days with k-means Pattern Recognition” section, TDkm are constructed by using the center and the standard deviation of each CC, thus, sets of 60 TDkm were simulated for two seasons, in Fig. 13TDkm over total data can be observed, note that TDkm of T, α and WD are close to the area that actual data occupies, meanwhile, TDkm of υ are concentrated around the mean and do not show a recognizible pattern, actual υ appear to have a “white-noise-like” behavior.

Fig. 13
figure 13

Contrasting 10 TDkm over original data per hour

Full size image

In Fig. 14 the ODs obtained with this strategy are presented as well as their performance. Three sets of TDkm with 60 days are presented. Their behavior is consistent, notice that in all cases the WT remains, although it does not significantly changes the other results.

Fig. 14
figure 14

Results and performance of OD with TDkm

Full size image

In Fig. 14 (a), (b), (c) and (d) have some interesting features, additionally, for one of the sets, while the number of days increases, suddenly there is an unexpected peak of (e) ToC and (f) Iter with few TDkm, nevertheless, all the other OD have a rampant ToC as TDkm increase, and the results rapidly stabilize. This could be due to the stochastic simulation used to generate TDkm and the presence of the WT in every optimization.

While for a greater number of typical days the results of TAC, WPV, WWT and WBS stabilize quickly, as expected, it is striking that the number of iterations required and the ToC have a somewhat volatile behavior that is directly proportional between them. This fact is worth commenting because given the origin of the TDkm, it could be expected that the ToC and Iter would simply increase with each increment in the number of days, however, this may be due to the model obtained for the wind speed that does not seem to represent the real behavior of the wind and the randomness added by the stochastic simulation.

Some inconsistencies are found, when comparing these results to the benchmark, despite the results proximity, shown in Table 5. The criteria to select the CC to trace a general pattern has reduced significantly the variability in all cases of the modeled parameters, however, υ has a behavior more “uncertain” than the model. The TDskm of υ favor the WWT result that are close to 0.6 kW, which differs from all previous results, where WT is discarded.

Table 5 TDkm comparison with benchmark 60 TD per season
Full size table

The modeling of υ has the main obstacle of the CC frequency, due to the fact that the CC for each hour of TDkm has a frequency about 20%, which indicates that any hour may be classify in any cluster. It is evident that the pattern recognition of the υ needs to be enhanced, or to be modeled by another approach. However, TAC, WPV and WBS results are similar to the benchmark’s.

In addition, there is the fact that the optimized size of the wind turbine oscillates around 0.5 and 0.6 kW for all sets of TDkm. This fact is surely due to the modeling of the wind in which when determining the CC for different hours of the typical day, the production capacity of this variable has been overestimated on occasions (see Fig. 13 where the TDkm and the actual data are shown).

As shown in Tables 2, 4 and 5, it is possible to reach a solution near to the benchmark reducing TD without a significant variation on the results mitigating computational costs. However, it is important to consider the scale and limits of the case study used. In addition, using different statistical learning algorithms, in this case PCA and k-means have a different effect in the optimal design of the energy system. In addition, the use of limited computational resources leads to explore different strategies of data reduction for minimizing misinformation and design gaps.

Conclusions

The handling of large databases is a problem that produces a high computational cost and high calculation times for the optimal RES design. In this work, a comparison between three methods to reduce the input data in an optimization model is presented.

To perform the data reduction to feed the OM, the first approach is the simplest and consists of randomly sample real days from the database, this strategy allows reducing the amount of input data, at the same time that having enough data the RRD achieve results similar to those of the all-data optimization. This method turned out to be quite dependent on the selected RRD and presented rather random results. Mainly, the biggest difference with the result of the benchmark was that the sizing of the wind turbines remains around 1 kW, while in other cases WT is discarded. The second approach is to reduce information using the PCA, which proved to be quite reliable for modeling the four variables involved in the calculation, since a total PCA ratio above 97% for the four variables is obtained. Also, a quite stable behavior of the results is observed, although the maximum reduction reach three TDPCA, it may be necessary to be more conservative and reduce sample down to 24 TDPCA to assure a smooth behavior of the results as TD in the OD increase. If the smallest samples are used, some error in the calculation of the OD may occur, although when the fewest information was used (three TDPCA) similar results to the all-data optimization are achieved, while when using 24 TDPCA. The third approach is to use a k-means pattern recognition technique as a basis for obtaining typical days within the most usual values. The TDkm use the CCs for each hour, which are determined according to the frequency with which they appear, and then the means and standard deviation of those clusters are used to obtain the typical values for that hour of TDkm. The results showed limitations because, e.g., despite having a stable behavior, wind energy seems to be overestimated because the wind turbine always remains as part of the optimal solution with values ranging between 0.5 and 0.6 kw, differing from results of benchmark, surely, this is due to the selection of the CCs for υ. All CC of υ had low frequencies, approximately 20%, this indicates that the five clusters used appear throughout the year in a similar proportion, so although some of them are selected as the CC for a certain time on the TDkm pattern, about 78% of the remaining data is in the other clusters evenly distributed. For this reason, it is difficult to ensure that the behavior of wind in TDkm will represent accurately actual υ at the studied site.

From the three approaches used, the one that achieves the most adequate results is TDPCA since similar results to those of benchmark optimization are achieved and also presents a low variation of the results. Meanwhile, RRDs produce highly variant ODs, where WT is relevant in some solutions while in others does not appear, which affects other variables and objective function. Finally, TDkm has issues since it overestimates the availability of wind energy, this is because when simulating the TDkm for υ, the CCs are almost as frequent as the clusters that are discarded.

As future work, some enhancing action to this work are anticipated, as a better selection of the CC to trace a better pattern of υ in the TDkm approach, this may need a probabilistic selection among some CC to each hour. To do this, Markov Chains can be used. Another projects may concentrate to analyze the BS usage or operation to identify patterns of interest.