Abstract
Three different approaches to the treatment of quantum effects in plasmas are reviewed: quantum fluid theory (QFT), phase-space kinetic theory (PKT) and quantum plasmadynamics (QPD). The simplest form of QFT is analogous to a nonrelativistic fluid model for an unmagnetized plasma with a potential electric field, \(\phi \). The wave nature of the electron is included through the so-called Bohm term, as in the Madelung equations. The simplest form of PKT is based on the Wigner function and the kinetic equation that it satisfies in a quasi-classical \(\mathbf{p}\)–\(\mathbf{x}\) phase space. Further development of PKT involves including additional effects piecemeal. The electron spin is included through a classical model for a spin vector, \(\mathbf{s}\), with the phase space extended to include \(\mathbf{s}\). The inclusion of degeneracy is straightforward. Electromagnetic effects are described by including the vector potential, \(\mathbf{A}\), in Schrödinger’s equation. It is argued that further extensions, to a magnetized plasma and to include relativistic effects, raise conceptual difficulties concerning the phase-space approach. In a magnetic field, the electron (Landau) states are discrete, whereas the kinetic equation in PKT involves a derivative with respect to \(\mathbf{p}\). The relativistic case is based on Dirac’s equation, and to derive a Vlasov-like equation for electrons requires excluding the positron and virtual-pair contributions to the Dirac wavefunction, which cannot be achieved exactly. Moreover, specific spin states require a specific choice of spin operator in Dirac’s theory, whereas the Pauli matrices define the only (vectorial) spin operator in PKT. The Dirac wavefunctions for two spin operators are derived and shown to approximate the eigenstates of the Pauli theory only in the nonrelativistic limit. QPD is an exact theory, based on quantum electrodynamics, in which kinetic processes are described using Feynman diagrams. The presence of the plasma is taken into account through a statistical average of the electron propagator, analogous to the use of thermal Green functions. QPD is introduced for the unmagnetized case, and the generalization to include a background magnetic field is presented. It is shown how QPD is used to derive the linear response tensor for an electron gas in the relativistic quantum case for both unmagnetized and magnetized plasmas. A magnetized vacuum is shown to have response tensors analogous to a plasma, allowing processes (such as one-photon pair creation and photon splitting) that are forbidden in an unmagnetized vacuum. The various quantum effects that may be relevant to a plasma are summarized, and their possible application to laboratory and astrophysical plasmas are discussed briefly.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum plasma theory has a long history, includes several different approaches and involves a wide range of different applications: to solid-state plasmas, micro-electronics, compact stars and plasma-like processes in super-strong magnetic fields. Relevant quantum effects are quantum mechanical diffraction and tunneling, electron degeneracy, the quantization of electron states in a magnetic field, electron spin and quantum recoil. Renewed interest in quantum effects was triggered by the recognition that miniaturized semiconductor devices and nanoscale objects can have scales comparable with the de Broglie wavelength (Haas et al. 2000; Manfredi and Haas 2001), implying that quantum-mechanical tunneling and diffusion can be important. In this review, the various approaches used to describe such quantum effects are separated into three classes, called quantum fluid theory (QFT), phase-space kinetic theory (PKT) and quantum plasmadynamics (QPD), each of which is discussed separately. Each of these three approaches has been discussed in monographs: QFT by Haas (2011), PKT by Bonitz (2015), and QPD in the unmagnetized and magnetized cases by Melrose (2008, 2013).
In this review, these different approaches are compared and contrasted. Emphasis is given to the quantum counterparts of classical theories for collisionless plasmas, which are conventionally described by the Vlasov equation without any collisional term. In this sense, the present review complements a recent review in this journal (Manfredi et al. 2019) that concentrated on quantum effects in solid-state plasmas. More specifically, emphasis is placed here on relativistic quantum effects described by Dirac’s equation.
QFT is the simplest theory, analogous to the fluid theory of a classical plasma. As in the classical case the fluid equations may be simply written down or be derived by taking moments of an appropriate kinetic theory, which is the Vlasov theory in the classical case. The quantum effect in QFT is a quantum potential, which was first identified by Madelung (1926, 1927) and is now called the Bohm potential (Bohm 1952a, b). PKT is based on the Wigner function (Wigner 1932), which reduces to the classical distribution function in the non-quantum limit. Unlike its classical counterpart, the Wigner function is not positive definite, and cannot be interpreted as a probability density in phase space. The simplest versions of QFT and PKT are based on nonrelativistic quantum mechanics, described by Schrödinger’s equation (without spin) including a potential electric field that describes the perturbations in the plasma. The equation that describes the evolution of the Wigner function due to the potential electric field, which is treated as a perturbation, is a quantum counterpart of the Vlasov equation and is used as the basis for a quantum kinetic theory. Subsequent generalizations of PKT involved including the spin, electron degeneracy, an electromagnetic field rather than a potential electric field, relativistic effects and a background magnetic field. The generalization to include the spin, as in the Schrödinger–Pauli theory, involves introducing a generalized Wigner function that is a \(2\times 2\) matrix in spin space, calculated from the outer product of two spinor wave functions. The generalization to include relativistic effects involves replacing Schrödinger’s equation by Dirac’s equation, leading to a more general but more cumbersome version of PKT (e.g., Hurst et al. 2017; Ekman et al. 2019a). With this generalization, the Wigner function is a \(4\times 4\) matrix in Dirac spin space; this complication is avoided by making approximations, with different choices of approximation resulting in different versions of PKT.
It is straightforward to include degeneracy, which is relevant in relatively dense plasmas, notably solid-state plasmas. Exchange interactions also become significant in relatively dense plasmas, cf. Manfredi et al. (2019).
The response of the plasma is derived in PKT in an analogous way to that used in the classical Vlasov approach, that is, by using the kinetic equation to derive the response of the plasma through the weak-turbulence expansion. In this approach the Fourier transform of the induced current density, \({\mathbf{j}}(\omega ,\mathbf{k})\), is expanded in powers of the electric field, \({\mathbf{E}}(\omega ,\mathbf{k})\), in the plasma, defining linear, quadratic, etc., response tensors. The linear response is conventionally written in terms of the equivalent dielectric tensor, \(K_{ij}(\omega ,\mathbf{k})\).
QPD is a generalization of quantum electrodynamics (QED), which is the modern-day theory for the interaction of electrons and photons. QED is formally a quantum field theory that describes the interaction of the Dirac and electromagnetic fields. A conventional approach to QED involves describing interactions between electrons and photons, which are quanta of these two fields, respectively, in terms of Feynman diagrams. The theory contains divergence and needs to be renormalized, with the finite contributions of the divergent diagrams referred to as radiative corrections. In particular, the linear response of the vacuum is divergent, and the finite part gives the vacuum polarization tensor. Using a 4-tensor notation, the vacuum polarization is described by the linear term in the expansion of the 4-current, \(J^{\mu }(k)\), in powers of the 4-potential, \(A^{\mu }(k)\), with \(k^\mu \) denoting the 4-vector constructed from \(\omega ,\mathbf{k}\), giving \(J^{\mu }(k)=\varPi ^{\mu \nu }(k)A_\nu (k)\). A statistical average over a distribution of electrons allows one to generalize \(\varPi ^{\mu \nu }(k)\) to include the linear response of the plasma (e.g., Melrose 2008). This allows a generalization such that a “photon” in a Feynman diagram is re-interpreted as a quantum of a wave mode in the plasma. Similarly, the statistical average of the nonlinear terms in the weak-turbulence expansion defines a hierarchy of nonlinear response tensors, all of which may be calculated explicitly using QPD. The distributions of electrons (and positrons) and wave quanta are described in terms of their occupation numbers. The description of the distribution of particles, in terms of the Wigner function in PKT and in terms of occupation numbers in QPD, is discussed in Sect. 7.7.
A notable difference between PKT and QPD can be understood by considering classical counterparts. A classical version of PKT is the Vlasov theory, in which the wave fields are included as perturbations in the distribution function. A classical version of QPD is the forward-scattering method (e.g., Melrose 2008): scattering of a wave by a single particle leaves the particle unchanged in the forward-scattering case where the scattered wave is the same as the unscattered wave; one may then sum over forward scattering by all the particles to find the collective effect on the wave. In the forward-scattering case, the distribution function of the particles is fixed and the perturbation is to the motion of the scattering particle. The Vlasov and forward-scattering methods lead to different but equivalent expressions for the linear response tensor of the plasma, with the two forms being related by partially integrating over momentum to remove the derivatives of the distribution function that appear in the Vlasov approach but not in the forward-scattering approach. Both the Vlasov and forward-scattering approaches may be used to treat the nonlinear responses of the plasma. In the Vlasov approach, one expands the distribution function in powers of the perturbing field and uses the linear, quadratic and cubic terms to identify the linear, quadratic and cubic response tensors, respectively. In the forward-scattering approach, one calculates the scattering by a single particle of one wave into another wave, into two waves and into three waves, and integrates the forward-scattering amplitude over all the particles in the plasma to obtain the the linear, quadratic and cubic response tensors, respectively. The same procedures apply in the quantum case, with the PKT approach a generalization of the Vlasov method and the QPD approach a generalization of the forward-scattering method.
In QPD, as in QED, a distribution of particles is described by its occupation number, which is simply related to the classical distribution function in the non-quantum limit. Unlike the Vlavov and PKT methods where all the perturbations are included in the wavefunction and hence in the Wigner function, in the forward-scattering and QPD methods, the background distribution of particles is assumed independent of the wave fields, and all the perturbations are calculated directly for the given distribution of particles, defined by its occupation number. Similarly, the wave quanta (in a particular wave mode) are described by their occupation number, which is the wave action divided by \(\hbar \), with the classical wave action equal to the Fourier transform of the wave energy density divided by the wave frequency.
The inclusion of a strong background field, in either the Schrödinger–Pauli theory or the Dirac theory, is straightforward in principle but involves a considerable increase in mathematical complexity. In solving for the wavefunction, one needs to find the eigenvalues of a complete set of commuting operators, and this choice requires choosing a specific gauge to describe the magnetic field, with the wavefunctions depending on this choice. The generalizations of PKT to the magnetized case and to the relativistic case contain subtleties, relating to the discreteness of the energy levels in a magnetic field, and to the treatment of spin in Dirac’s theory, as discussed critically below. The generalization of QPD to apply to a plasma in a magnetic field, including strong-field effects, is straightforward in principle (e.g., Melrose 2013), albeit cumbersome in practice.
QFT is discussed in Sect. 2, PKT based on nonrelativistic quantum mechanics in Sect. 3, the extension of PKT to relativistic quantum mechanics in Sect. 4, QPD in Sect. 5, and various magnetic effects in Sect. 6. The various quantum effects are summarized and some possible applications are described briefly in Sect. 7.
2 Quantum fluid theory
In this section, the development of QFT is discussed, beginning with the simple form proposed in the multistream model of Haas et al. (2000). There was an earlier derivation of quantum fluid equations, by Takabayasi (1952, 1957), which is discussed briefly at the end of this section.
2.1 Schrödinger–Poisson system
The simplest quantum fluid theory is based on Schrödinger’s equation with a potential electric field, \(-e\phi \), where \(\phi \) is the electric potential, which is related to the charge density, \(\rho \), by Poisson’s equation.
Schrödinger equation Schrödinger’s equation is
where m is the electron mass and \(\psi \) is the wave function. The wavefunction may be written in the form
where A and S are real. All of \(\phi \), \(\psi \), A and S are implicit functions of time, t and position, \(\mathbf{x}\). A conventional interpretation is that \(A^2\) gives the probability density for the electron, and the gradient of S is its momentum, written here as \(m\mathbf{u}\):
Madelung equationsMadelung (1926, 1927) attempted to relate Schrödinger’s theory to classical Hamiltonian–Jocobi theory by writing the wave function in the form (3). The real and imaginary parts of Schrödinger’s equation (1) then imply the Madelung equations:
The final term in (5) is now referred to as the Bohm term, which may be regarded as describing the diffraction pattern of a single electron (Tsintsadze and Tsintsadze 2009).
In the Schrödinger–Poisson system, Eqs. (4) and (5) are supplemented by Poisson’s equation
where \(n_0\) is the number density of background ions.
Multistream model The multistream model follows from Eqs. (4) to (6) by adding a subscript i that labels each stream. In its original form, the multistream model was assumed one dimensional (Haas et al. 2000), corresponding to \(\nabla \rightarrow \partial /\partial x\). Haas et al. (2000) discussed both the one-stream and two-stream cases is some detail. They found that in the one-stream case, the equations possess two first integrals,
interpreted as charge and energy conservation. Writing \(J=n_0u_0\), and noting that the potential, \(\phi \), includes an arbitrary constant that may be chosen such that \({{\mathcal {E}}}=0\), Eqs. (4) and (5) may be reduced to a pair of equations that depend only on a single parameter,
where \(\omega _\mathrm{{p}}\) is the plasma frequency; H characterizes the importance of the quantum effects included in the model. Haas et al. (2000) showed that for \(H<1\) (weak quantum effects) the system can sustain periodic oscillations, whereas for \(H>1\) (strong quantum effects) the system is unstable. This one-stream model establishes the importance of the parameter H in characterizing quantum effects.
Small-amplitude oscillation Linearizing the Madelung equations to find small-amplitude oscillations in the absence in electric and magnetic fields gives the frequency of oscillations of a free electron (e.g., Tsintsadze and Tsintsadze 2009),
In the case of a one-stream model with streaming velocity \(u_0\), Haas et al. (2000) found that purely spatial oscillations (for \(\phi \ne 0\)) are possible for
In the classical case, \(H=0\), oscillations are at \(ku_0=\pm \omega _\mathrm{{p}}\), and for \(H<1\) oscillations are real. In the strong quantum case, \(H>1\), there are exponentially growing solutions, implying that quantum effects cause the system to become unstable.
In the case of two streams, with \(n_1=n_2=n_0/2\), \(u_1=-u_2=u_0\) and \(\phi =0\), the system is known to be unstable to the two-stream instability for \( |\mathbf{k}|^2u_0^2<\omega _\mathrm{{p}}^2\) in the classical limit \(H\rightarrow 0\). Haas et al. (2000) showed that for \(H<1\) the system is unstable for either \(0<H^2 |\mathbf{k}|^2u_0^2/\omega _\mathrm{{p}}^2<2-2\sqrt{1-H^2}\) or \(2+2\sqrt{1-H^2}<H^2 |\mathbf{k}|^2u_0^2/\omega _\mathrm{{p}}^2<4\). This two-stream case shows that for \(H<1\) quantum effects can have a destablizing effect, whereas for \(H>2\) they can have the opposite effect.
2.2 Generalizations of QFT
In the simplest version of QFT, the electrons are assumed to be nonrelativistic and spinless, so that they satisfy the Schrödinger equation, and the field in the plasma is assumed to be electrostatic. Specific generalizations are to include the spin, to replace the electrostatic field by an electromagnetic field, and to include relativistic effects. These generalizations are discussed below in connection with the corresponding generalizations in PKT. In relation to the derivation of fluid equations, several features of these generalizations are notable.
The generalization to include electron spin involves replacing the Schrödinger equation by the Schrödinger–Pauli equation, and then the Wigner function is derived from the outer product of two spinors, and hence is a \(2\times 2\) matrix. The four components of the Wigner function are replaced by their projection onto the unit \(2\times 2\) matrix and the three Pauli matrices. These projections define, respectively, a scalar and a vector quasi-distribution function, and moments of both are involved in the derivation of fluid equations. For example, the simplest moments give the electron density, the scalar n, and the spin density, the vector \(\mathbf{S}\). The derivation of the fluid equations that describe the evolution of these moments, and involve further moments, has been reviewed by Manfredi et al. (2019).
The generalization from electrostatic to electromagnetic fields can be confusing. As in classical Hamiltonian mechanics, this generalization involves a simple prescription called minimal coupling: the momentum \(\mathbf{p}\) is replaced by \(\mathbf{p}+q\mathbf{A}\), where \(\mathbf{A}\) is the vector potential and q (\(q=-e\) for electrons) is the charge on the particle. With this generalization \(\mathbf{p}\) is the canonical momentum, which is different from the kinetic momentum, \({\varvec{\pi }}\). In the unmagnetized case one has \({\varvec{\pi }}=\gamma m\mathbf{v}\) with \(\gamma =(1-v^2/c^2)^{-1/2}\), where \(\mathbf{v}\) is the velocity of the particle. The canonical momentum, the kinetic momentum and the variable \(\mathbf{p}\) introduced in defining the Wigner function are all different in general, and the difference between them needs to be recognized in deriving fluid equations.
The generalization to include all relativistic quantum effects involves replacing Schrödinger’s equation by Dirac’s equation, so that the Wigner becomes a \(4\times 4\) matrix in Dirac spin space. A difficulty that this introduces in the derivation of quantum fluid equations is that one then needs 16 distribution-like functions to describe the distribution of electrons, as was pointed out and discussed by Takabayasi (1957) in deriving an early version of relativistic quantum fluid-like equations. The first step in this approach is to project the Wigner function onto 16 basis matrices in Dirac spin space, e.g., the matrices \(1,\gamma ^5,\gamma ^\mu , \gamma ^5\gamma ^\mu ,S^{\mu \nu }\) (e.g., Takabayasi 1952; Vasak et al. 1987; Bialynicki-Birula et al. 1991, ) cf. also ( Melrose 2008, pp. 350–352), with the definitions (32) and (35). This results in the \(4\times 4\) Wigner function being replaced by a scalar, a pseudo-scalar, a 4-vector, a pseudo-4-vector and an anti-symmetric 4-tensor, respectively. This complication is by-passed in most discussions by making assumptions that simplify the Wigner function. Simplification occurs for an unpolarized electron gas (Hakim and Heyvaerts 1978); in this case, the pseudo-scalar and pseudo-4-vector components are zero. As discussed in Sect. 4, a favored approach is to make a transformation that separates the electron and positron contributions such that the electron contribution to the Wigner function is negligible except in a \(2\times 2\) subspace, which allows one to use a procedure similar to that used to include spin in nonrelativistic quantum theory. However, this procedure involves approximations. No exact version of QFT for the relativistic quantum case has been identified.
3 Phase-space representation of a quantum system
The subsequent development of the theory involved introducing additional effects piecemeal: starting with a derivation of the quantum fluid equations from the Wigner–Poisson equations, including the effect of spin, and generalizing from an electrostatic to an electromagnetic field. These development are described in this Section. The generalization to the relativistic case is discussed in Sect. 4.
3.1 Wigner–Poisson system
The Wigner function (Wigner 1932), cf. also Moyal (1949); Tatarskiĭ (1983), is defined in terms of the Schrödinger wave function, \(\psi (\mathbf{x},t)\):
The Wigner function is regarded as a pseudo-distribution function in \(\mathbf{p}\)–\(\mathbf{x}\) phase space. Note that \(\mathbf{p}\) is not introduced here as the physical momentum, but rather as the conjugate variable to a position vector in a Fourier transform. The \(\mathbf{p}\)–\(\mathbf{x}\) phase space is essentially a classical construction, and the Wigner function is an attempt at reformulation of quantum mechanics in classical phase-space language. There is no unique definition of a quasi-distribution; for example, Zamanian et al. (2010a) commented on two alternative definitions. Care is needed in ascribing any physical interpretation to the phase space. In particular, the physical quantum states in the magnetized case, cf. Sect. 6, have discrete values of the perpendicular momentum, implying that the physical states correspond to discrete surfaces in \(\mathbf{p}\)-space.
Kinetic equation for the Wigner function The Wigner function obeys a kinetic equation. In the one-dimensional (1D) case with a potential electric field, this equation is
with \(v=p/m\). Combining (12) with the 1D form of Poisson’s equation,
gives the 1D Wigner–Poisson system.
Derivation of QFT from the kinetic equationManfredi and Haas (2001) used the Wigner–Poisson equations to derive the fluid equations. The relevant moments are the number density, fluid velocity and pressure, given by, respectively,
where arguments x, t and p, x, t are omitted. Equations (12) and (13) then imply
The total pressure in (14) may be separated into a classical part and a quantum part. On substituting the form (2) for the wave function, the classical part arises from the derivative of the phase and the quantum part from the derivative of the amplitude. For a pure quantum state, the classical part gives zero; Manfredi and Haas (2001) introduced a statistical model to show how the standard form for the classical pressure can be reproduced for a mixture of states. The quantum part, \(P^Q\), with \(A=\sqrt{n}\) gives
The quantum pressure gradient, \(-\mathrm{{d}}P^Q/\mathrm{{d}}x\) divided by n, then reproduces the Bohm term in (5).
3.2 Inclusion of spin: Schrödinger–Pauli theory
The inclusion of spin in nonrelativistic quantum mechanics involves generalizing Schrödinger’s equation to the Schrödinger–Pauli equation. The wave function, \(\psi \), becomes a spinor, \(\psi ^\alpha \), where \(\alpha =1,2\) denoted components in the two-dimensional (Hilbert) spin space. The spin operator, \({\varvec{\sigma }}\), in this space is represented by the three Pauli matrices, \(\sigma _i^{\alpha \beta }\), with \(i=x,y,z\) the components in coordinate space. By replacing the product of wave functions by spinors, \(\psi ^*\psi \rightarrow \psi ^{*\alpha }\psi ^\beta \), in the definition (11) of the Wigner function, W, becomes the (spinor) matrix \(W^{\alpha \beta }\).
Spin vector The formal generalizations of the Wigner–Poisson equations to include the spin involves using a spinor formalism. This is avoided in PKT by introducing a classical model for the spin through a unit vector \(\mathbf{s}\). The probability of finding the electron with spin up in the \(\mathbf{s}\)-direction is included by generalizing the pseudo-distribution function to \(f(\mathbf{p},\mathbf{s},\mathbf{x},t)\), defined by
where \(\delta ^{\alpha \beta }\) is the unit \(2\times 2\) matrix. Cowley et al. (1986) introduced such a pseudo-distribution function for the spin, initially in connection with nuclear spins. As with the phase-space representation in the absence of spin, there is no unique definition of the phase-space representation; alternative representations were reviewed by Scully and Wódkiewicz (1994).
The spin \(\mathbf{s}\) is not a quantum-mechanical variable, in the sense that it is neither a quantum-mechanical operator nor the eigenvalue of a quantum-mechanical operator. As with the variable \(\mathbf{p}\) in the pseudo-distribution function in the absence of spin, it is introduced to allow the quantum mechanical (Wigner) function to be represented in a classical notation. In the presence of spin, the components of the \(2\times 2\) matrix Wigner function is projected onto basis vectors, \({\mathbf{1}}\) and \({\varvec{\sigma }}\), of the \(2\times 2\) spin space. Then \({\mathbf{s}}\) is interpreted as a classical variable (in the extended phase space) that describes the actual quantum mechanical spin. The use of the variable \(\mathbf{s}\) to describe the spin in the relativistic case is discussed in Sect. 7.7.
In a classical model for the spin, the vector \(\mathbf{s}\) evolves in the presence of a magnetic field. The equation of motion in the rest frame of the electron evolves according to
where \(g\approx 2\) is the gyromagnetic ratio.
Magnetization and polarization vectors The electron spin contributes to the magnetization and polarization, that is, the magnetic and electric dipole moment per unit volume, respectively. The model implies (e.g., Asenjo et al. 2012)
where the factor 3 arises from non-commutation of the spin components, where \(\mu _\mathrm{{B}}=e\hbar /2m\) is the Bohr magneton and where \(g=2.00232\) is the gyromagnetic ratio.
3.3 Inclusion of electromagnetic effects
The assumption of an electrostatic field, \(\phi \), needs to be generalized to include electromagnetic effects. This involves including the vector potential, \(\mathbf{A}\), with the electromagnetic field given by
The description of the fields in terms of potentials is not unique, with the fields being unchanged by an arbitrary gauge transformation.
Pauli equation The Hamiltonian for an electron with spin in an electromagnetic field may be written as
where \(\mathbf{p}\) is now the canonical momentum. The mechanical momentum is \({\varvec{\pi }}=\mathbf{p}+e\mathbf{A}\). The generalization of the Schrödinger equation (1) with the Hamiltonian in the form (21) is the Pauli equation
Gauge dependence The Hamiltonian (21) depends on the choice of gauge, and hence the specific form of the wavefunction is also gauge dependent. The definition of the Wigner function needs to be modified so that it is independent of the choice of gauge. The relevant generalization (Stratonovich 1957) involves the phase in the \(\mathbf{y}\)-integral:
The gauge dependence introduced by the generalization to the electromagnetic case not only increases the algebraic complexity, but also adds further complication to any physical interpretation of the \(\mathbf{p}\)–\(\mathbf{x}\) phase space.
3.4 Degenerate plasma
In a sufficiently dense plasma, the electrons become degenerate as the lowest energy states become filled. Inclusion of degeneracy in plasma kinetic theory has a long history (e.g., Lifshitz and Pitaevskii 1981), cf. Shukla and Eliasson (2011), Brodin et al. (2017) and Manfredi et al. (2019) for recent discussions relevant to the approach discussed here.
One example of the effect of degeneracy is in the derivation of the dispersion relation, \(\omega =\omega _\mathrm{{L}}(\mathbf{k})\), for Langmuir waves. A form that follows when the Bohm term is included is (e.g., Eliasson and Shukla 2008; Mushtaq and Melrose 2009)
with \(V_\mathrm{{e}}^2=T_\mathrm{{e}}/m\), where \(T_\mathrm{{e}}\) is the electron temperature, and with \(G=1\) for nondegenerate electrons and \(G=v_\mathrm{{F}}^2/5V_\mathrm{{e}}^2\) for completely degenerate electrons, where \(v_\mathrm{{F}}^2=T_\mathrm{{F}}/m\) is the Fermi speed and \(T_\mathrm{{F}}\) the Fermi temperature. The final term in (24) is determined by the Bohm potential in QFT.
Fermi–Dirac distribution Partially degenerate nonrelativistic thermal electrons have a Fermi–Dirac distribution
where \(\mu _\mathrm{{e}}\) is the chemical potential, with \(\mu _\mathrm{{e}}\) large and negative (\(\xi \ll 1\)) in the nondegenerate limit, and with \(\mu _\mathrm{{e}}\rightarrow T_\mathrm{{F}}\) in the completely degenerate limit.
Response of a partially degenerate electrons The dielectric tensor for a degenerate electron gas is derived in a similar way to that for a classical gas, with the distribution function given by (25). The definition of the classical plasma dispersion function is generalized to the form for the Fermi–Dirac distribution (Melrose and Mushtaq 2010a, b). Wave dispersion in such a plasma may then be treated in the standard way. For example, this leads to a determination of the factor G in the dispersion relation (24) that covers the range between nondegenerate and completely degenerate electrons.
Some care is needed in attempting to generalize models for degenerate plasmas. For example, it is inconsistent to assume two separate distributions of degenerate electrons with different temperatures, by analogy with the conventional treatment of electron acoustic waves in a nondegenerate plasma. The inconsistency is that the electron states below the lower of the two Fermi temperatures for the two distributions are assumed implicitly to be filled twice, which is not allowed. Similarly, assuming that both electrons and positrons are degenerate is inconsistent with the requirement of thermal equilibrium. In the relativistic case pair creation and annihilation are allowed, and this requires that in thermal equilibrium, the sum of the chemical potentials for electrons and positron be equal to that of photons, which is zero. Both chemical potentials cannot be positive, as would be implied if both electrons and positrons were degenerate.
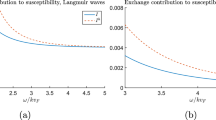
3.5 Exchange effects
Exchange effects become significant in relatively dense plasma. There is an extensive literature on this topic (e.g., Crouseilles et al. 2008; Andreev 2014; Trukhanova and Andreev 2015; Ekman et al. 2015). An example the exchange correction to the dispersion relation for Langmuir waves for \(V_\mathrm{{e}}\gg v_\mathrm{{F}}\), which gives (von Roos 1960; Zamanian et al. 2015)
The final term inside the parenthesis is the contribution from exchange effects. It is interesting to note that this is proportional to \(H^2\), that is, as the square of the parameter H, defined by (8), that describes when other quantum effects are important.
4 Phase-space kinetic theory: relativistic case
The inclusion of relativistic effects requires that the Schrödinger–Pauli equation for the wavefunction be replaced by the Dirac equation. This not only increases the complexity of PKT, but also raises questions about its validity, especially concerning the spin, whose treatment remains essentially nonrelativistic.
4.1 Dirac equation
The relativistic generalization of the nonrelativistic Hamiltonian, \(H=\mathbf{p}^2/2m\), may be written \(H=(m^2c^4 +\mathbf{p}^2c^2)^{1/2}\), which includes the rest energy \(mc^2\). The usual prescription for deriving a wave equation, by replacing H and \(\mathbf{p}\) by the operators \({{\hat{p}}}_0c={{\hat{H}}}=i\hbar \partial /\partial dt\) and \({\hat{\mathbf{p}}}=-i\hbar {{\varvec{\nabla }}}\), respectively, cannot be applied directly because it would involve the square root of an operator. This is avoided by first squaring and applying the prescription to \(H^2=m^2c^4 +\mathbf{p}^2c^2\). The resulting equation is the Klein–Gordon equation, which has positive and negative energy eigenvalues, \(\varepsilon =\pm (m^2c^4 +\mathbf{p}^2c^2)^{1/2}\). The conventional interpretation of the negative energy eigenvalues is that they describe anti-particles, with the anti-particle of the electron being the positron. Assuming spin-1/2, one may write the operator \({\hat{\mathbf{p}}}^2=({\varvec{\sigma }}\cdot {\hat{\mathbf{p}}})^2\) and assume separate spinor wavefunctions, \(\xi \) and \(\eta \) say, for the positive and negative energy solutions. The Klein–Gordon equation may then be factorized into two equations \(({{\hat{p}}}_0+{\varvec{\sigma }}\cdot {\hat{\mathbf{p}}})\eta =mc\xi \), \(({{\hat{p}}}_0-{\varvec{\sigma }}\cdot {\hat{\mathbf{p}}})\xi =mc\eta \) and combined into the \(4\times 4\) matrix equation
where the wavefunction has four components, with \({\mathbf{0}}\) the null \(2\times 2\) matrix. Equation (27) is one form of Dirac’s equation, in what is referred to as the spinor representation. For a particle at rest, the wavefunctions (1000), (0100), (0010), (0001) are identified as an electron with spin up and spin down and a positron with spin up and spin down, respectively.
There is no unique representation for the Dirac equation. In an arbitrary representation, the Dirac equation may be written in the form
where \({\varvec{\alpha }}\) and \(\beta \) are \(4\times 4\) matrices and the wavefunction \(\varPsi \) is a column matrix with four entries. The Dirac Hamiltonian is identified as
Different representations are connected by unitary transformations of the \(4\times 4\) matrices. In the standard representation one has, in terms of block matrices,
where each matrix component is itself a \(2\times 2\) matrix. One has
Another \(\gamma \)-matrix that appears is
which satisfies
where \(\dag \) denotes the Hermitian conjugate.
Covariant form of Dirac’s equation
For some formal purposes it is convenient to use a manifestly covariant form of Dirac’s equation, that is, one in terms of 4-tensor notation. In this notation, a Greek index denotes components, e.g., \(\mu =0,1,2,3\), with 0 denoting the time component, and is written as a superscript (subscript) corresponding to contravariant (covariant) component. It is also convenient to adopt natural units with \(\hbar =c=1\). The basic 4-vector is an event at time t and point \(\mathbf{x}\), written as \(x^\mu =(t,\mathbf{x})\) in units with \(c=1\). The metric tensor, \(g^{\mu \nu }\), is diagonal with components \(1,-1,-1,-1\), as is \(g_{\mu \nu }\). The covariant components of the event are \(x_\mu =g_{\mu \nu }x^\nu =(t,-\mathbf{x})\), where the sum over repeated indices is assumed. Other relevant 4-vectors are the 4-momentum \(p^\mu =(\varepsilon ,\mathbf{p})\), the 4-potential \(A^\mu =(\phi ,\mathbf{A})\) and the 4-derivative \(\partial _\mu =\partial /\partial x^\mu =(\partial /\partial t,{{\varvec{\nabla }}})\). The inner product of two 4-vectors is written, for example, \(kx=k^\mu x_\mu =\omega t-\mathbf{k}\cdot \mathbf{x}\) and \(k^2=k^\mu k_\mu =(\omega ^2-|\mathbf{k}|^2)\).
The covariant form of Dirac’s equation may be written
with \(/\!\!\partial =\gamma ^\mu \partial _\mu \), \(/\!\!A=\gamma ^\mu A_\mu \), and so on, \(\gamma ^\mu =(\gamma ^0,{\varvec{\gamma }})\), and where the relations with \({\varvec{\alpha }}\) and \(\beta \) follow by comparison with (29). The Dirac matrices are requires to satisfy \(\gamma ^\mu \gamma ^\nu +\gamma ^\nu \gamma ^\mu =2g^{\mu \nu }\). The spin 4-tensor is identified as
Dirac’s equation in an electromagnetic field On including an electromagnetic field, Dirac’s equations in the forms (28), in natural units, and (34) becomes
respectively. The covariant form may be rewritten by introducing \(D^\mu =\partial ^\mu -ieA^\mu \) and the ansatz
so that the equation becomes
where \(F^{\mu \nu }\) is the Maxwell 4-tensor. In terms of Cartesian components of \(\mathbf{E}\) and \(\mathbf{B}\), \(F^{\mu \nu }\) and \({{\mathcal {F}}}^{\mu \nu }=\textstyle {\frac{1}{2}}\epsilon ^{\mu \nu \alpha \beta }F_{\alpha \beta }\) have components
The term \(-e{\varvec{\sigma }}\cdot \mathbf{B}\) is interpreted as the magnetic energy due to the (anomalous) magnetic moment of the electron. (In ordinary units, the magnetic moment is \(\mu _\mathrm{{e}}=g\mu _\mathrm{{B}}\), with \(g=2\) and \(\mu _\mathrm{{B}}=e\hbar /2m\) the Bohr magneton.) The correct appearance of this term was a major success of the Dirac theory.
4.2 Foldy–Wouthuysen transformation
The Dirac equation describes a one-charge system, whereas a phase-space model is intended to describe a distribution of electrons. To isolate the electron part from the positron part and to ignore additional pairs, one needs, ideally, to choose a representation of the Dirac algebra in which the terms that connect the upper two and lower two components of \(\varPsi \) are removed. The Hamiltonian may be separated into even, \({{\mathcal {E}}}\), and odd, \({{\mathcal {O}}}\) parts, depending on whether they commute, \(\beta {{\mathcal {E}}}={{\mathcal {E}}}\beta \), or anticommute, \(\beta {{\mathcal {O}}}=-{{\mathcal {O}}}\beta \) with \(\beta \). This is achieved through a Foldy–Wouthuysen (FW) transformation (Foldy and Wouthuysen 1950). In the presence of a field, the FW transformation involves powers and derivatives of \(\phi \) and \(\mathbf{A}\). One can only minimize the odd terms by truncating the expansion after a finite number of terms.
For example, by applying the FW transformation four times, Asenjo et al. (2012) derived the Hamiltonian operator
which includes terms up to second order in \(\hbar \) and in relativistic corrections. The first four terms in (40) correspond to the Pauli Hamiltonian, the fifth is the Darwin term, the sixth and seventh give Thomas precession and spin–orbit coupling, and the eighth term is a higher order correction that also appears in the expansion of the Klein–Gordon hamiltonian \({{\hat{H}}}=[m^2c^4+({\hat{\mathbf{p}}}+e\mathbf{A})^2]^{1/2}-e\phi \).
Vlasov-type equations The (classical) Vlasov equation in the absence of collisions is
which is relativistically correct, with \(\mathbf{v}=\mathbf{p}c^2/\varepsilon \) with \(\varepsilon ^2=m^2c^4+p^2c^2\). The kinetic equations derived in PKT are of the same form as (41) with modifications to the velocity and the force terms and with a spin contribution included. Including the classical model for the spin in (41) involves including the explicit dependence of f on \(\mathbf{s}\) and adding a term
where (18) is used.
Various specific forms for the Vlasov-type equation in the quantum case have been derived (e.g., Cowley et al. 1986; Balescu and Zhang 1988; Zamanian et al. 2010a; Hurst et al. 2017; Ekman et al. 2017, 2019a). These forms differ due to differences in the truncation of the FW transformation, related to expansions in \(\hbar \) and 1/c. For example, Ekman et al. (2017) generalized an earlier form found by Zamanian et al. (2010a), to find a form to first order in \(\hbar \) on scales long compared with the localization scale of the electron. In this generalized form, the coefficients of the derivatives in (41) and (42) are replaced according to
with \(\varepsilon /m\) defined as the ratio of the electron energy to the rest energy. A further generalization was derived by Ekman et al. (2019a). Hurst et al. (2017), generalizing earlier work (Hurst et al. 2014), defined two different phase-space functions by integrating over \(\mathbf{s}\), and also included further terms in the kinetic equations for both distributions.
Response tensor and wave dispersion The linear response of a plasma to an electromagnetic disturbance is described by a response tensor, usually chosen to be the dielectric tensor, \(K_{ij}(\omega ,\mathbf{k})\). A conventional derivation of the response tensor from kinetic theory starts by assuming that the wave amplitude is small, expanding the Vlasov equation in powers of the wave amplitude, \(f=f_0+f_1+\ldots \), and solving for the first-order perturbation, \(f_1\), in terms of the background distribution, \(f_0\). In the absence of a background magnetic field, one writes \(\mathbf{E}\rightarrow \mathbf{E}_1\) and \(\mathbf{B}\rightarrow \mathbf{B}_1\) in the Vlasov equation, and in the presence of a background magnetic field, \(\mathbf{B}_0\), the latter is replaced by \(\mathbf{B}\rightarrow \mathbf{B}_0+\mathbf{B}_1\). The response of the plasma is described by the induced current, which is found in terms of \(f_1\). After Fourier transforming in time and space, the proportionality of the current to the electric field allows one to identify the conductivity tensor, which is simply related to \(K_{ij}(\omega ,\mathbf{k})\). The Fourier transform of Maxwell’s equations with this induced current included then leads to a wave equation, which is solved for the properties of the natural wave modes of the plasma. In the quantum case, the same procedure may be used to derive the response tensor, with f satisfying a generalized form of the Vlasov equation in the extended phase space.
The only current in the classical case is the free (F) current density,
In the quantum case, the spin introduces three further terms: \(\mathbf{j}_\mathrm{{F}}\) is modified by the replacement of \(\mathbf{v}\) in (44) by the spin-dependent term in the relation between velocity and momentum, cf. (43), approximated in the nonrelativistic case by \(\mathbf{v}=\mathbf{p}/m+(\mu _\mathrm{{B}}/2mc^2){\varvec{\sigma }}\times \mathbf{E}\). There are also the magnetization current, \(\mathbf{j}_\mathrm{{M}}={{\varvec{\nabla }}}\times \mathbf{M}\) and the polarization current, \(\mathbf{j}_\mathrm{{p}}={\partial \mathbf{P}}/{\partial t}\), with \(\mathbf{M}\) and \(\mathbf{P}\) given by (19). The total induced current is
Only a few special cases of wave dispersion including quantum effects have been treated using this theory. One example is for the effect of the Darwin term on the dispersion relation for Langmuir waves for a one-dimensional (1D) distribution with average momentum squared \(\langle p_z^2\rangle \): Asenjo et al. (2012) found the approximate dispersion relation
The term \(\hbar |\mathbf{k}|^2\). This term is similar in form to the contribution of the Bohm term to the oscillations of a free electron, cf. (9). The ratio of the two contributions is \(2 |\mathbf{k}|^2c^2/\omega _\mathrm{{p}}^2\), with the Zitterbewegung dominating when this term is large.
Another example (Zamanian et al. 2010b) is for waves propagating parallel to the magnetic field in a magnetized plasma, for which it was found that spin and dispersive effects modify the classical wave dispersion at short wavelengths.
5 Quantum plasmadynamics
The name quantum plasmadynamics (QPD) was coined to describe the theory that synthesizes quantum electrodynamics (QED) and the kinetic theory of plasmas (Melrose and Hardy 1996; Melrose 2008). QED is the quantum field theory for the interaction between electrons (including positrons), which are quanta of the Dirac field, and photons, which are quanta of the electromagnetic field. QPD involves, first, introducing a statistical average that allows one to use QED to calculate the response of the plasma and, second, including the response of the plasma in the electromagnetic field such that its quanta correspond to those of the natural wave modes of the plasma. The interaction between electrons and waves in plasmas is described in QPD by Feynman diagrams, as in QED.
5.1 Covariant form of response tensor
The response of a plasma may be described by the Fourier transform of the induced current in the plasma. The weak-turbulence expansion of this response in powers of the Fourier transform of the electromagnetic is, in 4-tensor notation,
The linear response tensor, \(\varPi ^{\mu \nu }(k)\), and the dielectric tensor, \(K_{ij}(\omega ,\mathbf{k})\), contain the same information, in the sense that the components of one may be written in terms of the components of the other.
A wave in a plasma may be described by its amplitude \(A^\mu (k)\), which satisfies the wave equation, derived from (the Fourier transform of) Maxwell’s with \(J^\mu (k)=\varPi ^{\mu \nu }(k)A_\nu (k)\),
where the right-hand side is an extraneous current that describes an arbitrary source term. The usual way of deriving the dispersion equation, whose solutions give the dispersion relations for the natural wave modes of the plasma, is to write the wave equation in matrix from and take the determinant of the matrix of coefficients. However, this determinant is identically zero in this 4-tensor notation, due to the identities \(k_\mu \varLambda ^{\mu \nu }(k)=0=\varLambda ^{\mu \nu }(k)k_\nu \) implying the \(k^\mu \) is an eigenfunction with zero eigenvalue. Formally, one may identify an invariant form of the dispersion equation by constructing the matrix of cofactors, \(\lambda ^{\mu \nu }(k)\), of \(\varLambda ^{\mu \nu }(k)\), noting that it satisfies \(\lambda ^{\mu \nu }(k)=\lambda (k)k^\mu k^\nu \), and setting this to zero, giving the invariant dispersion equation \(\lambda (k)=0\). Alternatively, one may write (48) in 3-tensor notation and set the determinant of the \(3\times 3\) tensor to zero, giving a dispersion equation equivalent to \(\lambda (k)=0\).
Photon propagator The photon propagator, \(D^{\mu \nu }(k)\), satisfies
A solution of (49) is found by first constructing the second-order matrix of cofactors, \(\lambda ^{\mu \alpha \nu \beta }(k)\), which satisfy
and noting that
is a solution. The solution (51) corresponds to a particular choice of gauge, \(k_\mu A^\mu (k)=0\). For an arbitrary choice of gauge condition of the form \(G_\mu A^\mu (k)=0\), \({k_\alpha k_\beta }/{k^4}\) is replaced by \(G_\alpha G_\beta /(Gk)^2\) in (51).
5.2 Quantum field theory
In quantum field theory, specifically QED, one solves the Dirac and Maxwell equations for the fields and re-interprets the fields as operators that create and annihilate quanta of these fields, called second quantization. The idea is to introduce the familiar raising and lowering operators, \({{\hat{a}}}^{\dag }\) and \({{\hat{a}}}\), respectively, for a simple harmonic oscillator (SHO) to describe creation and annihilation, respectively, of quanta. In the SHO case, these satisfy commutation relations, \([{{\hat{a}}},{{\hat{a}}}]=0\), \([{{\hat{a}}}^{\dag },{{\hat{a}}}^{\dag }]=0\), \([{{\hat{a}}},{{\hat{a}}}^{\dag }]=1\), and they determine the number operator, \({{\hat{n}}}={{\hat{a}}}^{\dag }{{\hat{a}}}\), for the excited state of the SHO. An important change for fermions is that the commutator, \([{{\hat{A}}},{{\hat{B}}}]={{\hat{A}}}{{\hat{B}}}-{{\hat{B}}}{{\hat{A}}}\), is replaced by the anti-commutator, \([{{\hat{A}}},{{\hat{B}}}]_+={{\hat{A}}}{{\hat{B}}}+{{\hat{B}}}{{\hat{A}}}\). In QED and QPD, the annihilation operators for electrons, positrons and wave quanta are denoted by, \({{\hat{a}}}\), \({{\hat{b}}}\) and \({{\hat{c}}}\), respectively, with \({{\hat{a}}}\) and \({{\hat{b}}}\) satisfying anti-commutation relations and \({{\hat{c}}}\) satisfying commutation relations. In describing the fields, additional labels and arguments are needed to specify the particular field. For example, if \(q,q'\) denote specific states, for electrons, the anti-commutation relations become \([{{\hat{a}}}_q,{{\hat{a}}}_{q'}]=0\), \([{{\hat{a}}}_q^{\dag },{{\hat{a}}}_{q'}^{\dag }]=0\), \([{{\hat{a}}}_q,{{\hat{a}}}_{q'}^{\dag }]=\delta _{qq'}\), and the number operator becomes \({{\hat{n}}}_q^+={{\hat{a}}}_q^{\dag }{{\hat{a}}}_q\), and for positrons, the anti-commutation relations become \([{{\hat{b}}}_q,{{\hat{b}}}_{q'}]=0\), \([{{\hat{b}}}_q^{\dag },{{\hat{b}}}_{q'}^{\dag }]=0\), \([{{\hat{b}}}_q,{{\hat{b}}}_{q'}^{\dag }]=\delta _{qq'}\), and the number operator becomes \({{\hat{n}}}_q^-={{\hat{b}}}_q^{\dag }{{\hat{b}}}_q\).
Dirac wavefunctions Let \(\psi _q(x)\) be a solution of Dirac’s equation with quantum numbers denoted collectively by q, with energy eigenvalues \(\varepsilon =\varepsilon _q\). The wavefunction may be written as a sum over q of two terms, \(\psi _q^+(\mathbf{x})\exp (-i\varepsilon _qt)\) and \(\psi _q^-(\mathbf{x})\exp (i\varepsilon _qt)\). The corresponding operator and its adjoint are
For a wave in an arbitrary wave mode M in a medium, the second quantized wave field is
where V is the volume of the system, \(a_\mathrm{{M}}(k)=(\mu _0R_\mathrm{{M}}/\omega _\mathrm{{M}} V)^{1/2}\) is the wave amplitude, \(R_\mathrm{{M}}\) is the ratio of electric to total energy, \(e_\mathrm{{M}}^\mu (k)=(0,\mathbf{e}_\mathrm{{M}}(\mathbf{k}))\) is the polarization 4-vector in term of the polarization 3-vector in the temporal gauge, and \(\omega =\omega _\mathrm{{M}}\) is the dispersion relation. For waves in vacuo, one has \(R_\mathrm{{M}}\rightarrow 1/2\), \(\omega _\mathrm{{M}}\rightarrow |\mathbf{k}|\).
Plane-wave solutions For free electrons and positrons, plane-wave solutions of Dirac’s equation are of the form
for a particle with spin s. Dirac’s equation requires
with \(p^0=\varepsilon \). Noting the identity \((\epsilon /\!\!p-m)(\epsilon /\!\!p+m)=0\), solutions of (55) may be found by constructing the matrix \(\epsilon /\!\!p+m\) and identifying any column of the matrix as a solution. Choosing the first two columns gives the conventional solution
with \(p_\pm =p_x\pm ip_y\) and where the normalization is to an energy \(\varepsilon \) in the volume V. These wavefunctions are often written in terms of \(u_{s}(\mathbf{p})\) and \(v_{s}(\mathbf{p})\), defined by writing
The spin s in (56) and (57) is the eigenvalue of an unidentified spin operator. Although the operator may be identified, it is not of any physical interest to do so. Two physically meaningful spin operators are the helicity \({\varvec{\sigma }}\cdot \mathbf{p}/|\mathbf{p}|\) and the magnetic moment operator, cf. (98).
Helicity eigensolutions Writing \(\mathbf{p}=(p_\perp \cos \phi ,p_\perp \sin \phi ,p_z)\) in cylindrical coordinates, the helicity eigenfunctions, for spin eigenvalues \(\sigma =\pm 1\), are
with \(\alpha _\pm =(\varepsilon \pm \epsilon m)^{1/2}\), \(\beta _\pm =(|\mathbf{p}|\pm \sigma \epsilon p_z)^{1/2}e^{\mp i\phi /2}\).
Magnetic-moment eigensolutions The magnetic moment eigenfunctions, for eigenvalues \(s\lambda \) with \(s=\pm 1\) and \(\lambda =(m^2+p_\perp ^2)^{1/2}\), are
with \(a_\pm =(\varepsilon -\epsilon s\lambda )^{1/2}\), \(b_\pm =(\lambda \pm sm)^{1/2}e^{\mp i\phi }\) and \({{\mathcal {P}}}=p_z/|p_z|\).
Nonrelativistic limit In the nonrelativistic limit, the eigenfunctions (58) for the helicity operator may be written
and the eigenfunctions (59) for the magnetic momentum operator may be written
It follows that, unlike the conventional wavefunctions (56), for a particle at rest, \(\mathbf{p}=0\), these wavefunctions reduce to (1000), (0100), (0010), (0001) for electron with spin up and down and positron with spin up and down, respectively. An interpretation is that both of these eigenfunctions effectively reduce to the Pauli theory for both electrons and positrons. This corresponds to the eigenvalues of the z-component of the spin operator \({{\varvec{\Sigma }}}\). Granted the classical description of the spin in terms of a vector \(\mathbf{s}\) as representing the Pauli theory, this would also apply approximately in the nonrelativistic limit for these choices of spin operators.
Relativistic limit In the ultra-relativistic limit, \(\varepsilon =|\mathbf{p}|\gg 1\), writing \(p_\perp =|\mathbf{p}|\sin \alpha \), \(p_z=|\mathbf{p}|\cos \alpha \), the helicity and magnetic moment eigenfunctions reduce to
respectively. These eigensolutions are obviously different from each other. Moreover, neither of them can be simply related to a classical vector \(\mathbf{s}\).
5.3 Electron propagator
The Dirac equation and Maxwell’s equations both need to be solved in two ways in QED and QPD. First, one needs to find the solutions for the wavefunctions of the electron and of the waves, respectively. Second, one needs to solve for the Green functions for the Dirac and electromagnetic fields. The Green function, referred to as a propagator in quantum field theory, describes the propagation of the field between two events, x and \(x'\). The electron propagator, \(G(x,x')\), is a \(4\times 4\) matrix, and the photon propagator, \(D^{\mu \nu }(x,x')\), is a 4-tensor. Provided that these propagators depend only on the space-time separation, \(x-x'\), of the two events, they can be represented by their Fourier transforms, G(P) and \(D^{\mu \nu }(k)\), respectively.
Electron propagator as a Green function The electron propagator is the Green function for the Dirac equation. It satisfies
with \(/\!\!\partial =\gamma ^\mu \partial _\mu \) and \(/\!\!P=\gamma ^\mu P_\mu \), and where the second form follows by Fourier transforming the first. Solution of the second form follows by premultiplying by \(/\!\!P+m\) and using \(/\!\!P/\!\!P=P^2\),
\(G(x,x')\) is found by inverting the Fourier transform and imposing appropriate boundary conditions. For the Feynman propagator, in which positrons are regarded as electrons propagating backward in time, the familiar causal condition is reversed for the negative energy states. With \(P^\mu =\epsilon p^\mu \), one has
with \(\varepsilon =(m^2+|\mathbf{p}|^2)^{1/2}\). The resonant part of the propagator is associated with the creation or annihilation of real particles.
Propagators as vacuum expectation values An alternative derivation of the propagators provides an insight that is important in understanding rules for drawing Feynman diagrams. In this alternative, the fields are regarded as operators, \({{\hat{\psi }}}(x)\) for the Dirac field, and \({{\hat{A}}}(x)\) for the electromagnetic field. One first defines the time-ordering operator, \({\hat{{\mathcal {T}}}}\), for a product of operators, as ordering in a causal sequence such that the operator at the earliest time operates first. Taking account of the anticommutation of operators for fermions, the vacuum expectation values give

where the operators joined by an underline are said to be contracted. Noting that the operator wavefunctions include creation and annihilation operators for both electrons and positrons, for \(t>t'\) say, \(G(x,x')\) corresponds to either an electron created at \(x'\), propagating to x, where it is annihilated, or a positron created at x, propagating (backwards in time) to \(x'\), where it is annihilated.
Statistically averaged electron propagator The generalization of QED to QPD involves taking the presence of real electrons in the plasma into account. The presence of electrons leads to modification of the resonant part of the electron propagator. (Physically, this is obvious when the electrons are degenerate because the creation of an electron below the Fermi level is then forbidden, and the resonant part must be zero due to the presence of degenerate electrons.) The statistically averaged electron propagator is, with \(P^\mu =\epsilon p^\mu \),
where \({{\mathcal {P}}}\) denotes the Cauchy principal value, and where \(n^\epsilon (\mathbf{p})\) is the occupation number of the electrons, \(\epsilon =+1\), or of the positrons, \(\epsilon =-1\). The statistically averaged propagator includes the special case of a thermal propagator, which is given by identifying the occupation number as that for a Fermi–Dirac distribution.
5.4 S-matrix
The S-matrix is determined by the operator \({{\hat{S}}}(t,t_0)\), defined such that it converts the initial state, \(|\,\mathrm{i}\,\rangle \), at \(t_0\), into the final state, \(|\,\mathrm{f}\,\rangle ={{\hat{S}}}(t,t_0)|\,\mathrm{i}\,\rangle \), at t, with \(t_0\rightarrow -\infty \), \(t\rightarrow \infty \). The S-matrix is the matrix element \(S_{\mathrm{fi}}=\langle \,\mathrm{f}\,|{{\hat{S}}}(\infty ,-\infty )|\,\mathrm{i}\,\rangle \), and \(p_{\mathrm{fi}}=|S_{\mathrm{fi}}|^2\) is the probability of a transition from the initial state to the final state.
The evolution of the state at time t in the interaction picture, due to an interaction Hamiltonian, \(H_{\mathrm{I}}(t)\), implies that \({{\hat{S}}}(t,t_0)\) satisfies the integral equation
where \({{\hat{1}}}\) is the unit operator and \({\hat{\mathcal {H}}}_{\mathrm{I}}(x)\) is the interaction Hamiltonian density operator. The interaction between the Dirac and electromagnetic fields is described by an interaction Hamiltonian density \({{\mathcal {H}}}_{\mathrm{I}}=J^\mu (x)A_\mu (x)\), with
where \({{\overline{\psi }}}(x)\) is the Dirac adjoint wavefunction. Converting this into an operator involves replacing the fields by the corresponding operators. However, while the order of the fields is irrelevant for non-operator functions, the order in which the operators are written needs to be specified when operators do not commute, specifically for fermion fields that anti-commute. The convention is that the operators are written in “normal order” corresponding to all annihilation operators to the right of all creation operators, taking the anti-commutation relations into account. With normal order denoted by colons, the interaction Hamiltonian density operator is identified as
Expansion of \({{\hat{S}}}\) One may solve (69) by a perturbation expansion, which gives
where \({\hat{{\mathcal {T}}}}\) is the time-ordering operator.
The term \({{\hat{S}}}^{(1)}\) describes first-order processes which involve a total of three quanta in the initial and final states, with the simplest example being an initial electron emitting a photon leaving the electron in its final state. There is a total of eight possible first-order diagrams: six with two lines in the initial or final state and one line in the other state, and two with all three lines in the initial of final states. All first-order processes are forbidden in vacuo, but they may be allowed in a medium. The terms \({{\hat{S}}}^{(n)}\) with \(n=2\) describe second-order processes, \(n=3\) describe third-order processes, and so on.
Wick’s theorem The terms with \(n\ge 2\) in (72) all involve time-ordered products of normal-ordered products, which are evaluated by appealing to Wick’s theorem. The theorem implies that the time-ordered normal product may be expressed as a sum over terms with no contraction, one contraction, etc.
Consider \(n=2\). The term with no contractions involves two independent first-order processes, at \(x_1\) and \(x_2\), and is of no particular interest. The terms with one contraction are conventional second-order processes, that include (Compton) scattering of a photon by an electron, when the contractions involve \({{\hat{\psi }}}(x_1)\) and \({\hat{{\overline{\psi }}}}(x_2)\) or \({\hat{{\overline{\psi }}}}(x_1)\) and \({{\hat{\psi }}}(x_2)\), and electron–electron (including electron–positron and positron–positron) scattering when the contraction involves the two photon operators. The terms involving two contractions described modifications to the propagators, specifically, to the photon propagator when the contractions involves \({{\hat{\psi }}}(x_1)\), \({\hat{{\overline{\psi }}}}(x_2)\) and \({\hat{{\overline{\psi }}}}(x_1)\), \({{\hat{\psi }}}(x_2)\), and to the electron propagator when one of the contractions involves the photon operators. These terms are discussed further below. The term with three contractions is ignored, as it has no external lines and so involves only an unobservable modification to the vacuum state.
Initial and final states The initial and final states may be constructed by operating on the vacuum with creation operators, and multiplying by the appropriate wavefunctions. For example, in the case of Compton scattering, the initial state involves an electron and a photon, and so is of the form \(|\,\mathrm{i}\,\rangle \propto {{\hat{a}}}^{\dag }{{\hat{c}}}^{\dag }|\,0\,\rangle \), where labels on the operators are omitted. The final state also involves an electron and a photon, and its adjoint is of the form \(\langle \,\mathrm{f}\,|\propto \langle \,0\,|{{\hat{a}}}{{\hat{c}}}\). The S-matrix, \(S_{\mathrm{fi}}=\langle \,\mathrm{f}\,|{{\hat{S}}}|\,\mathrm{i}\,\rangle \), then becomes a vacuum expectation value, which is nonzero only for those terms in \({{\hat{S}}}\) that include annihilation operators (\({{\hat{a}}}\), \({{\hat{c}}}\)) that match the creation operators in \(|\,\mathrm{i}\,\rangle \) and creation operators (\({{\hat{a}}}^{\dag }\), \({{\hat{c}}}^{\dag }\)) that match the adjoint operators in \(\langle \,{\mathrm{f}}\,|\). Other terms in the expansion of \({{\hat{S}}}\) that have unmatched creation or annihilation operators have a vacuum expectation value of zero, and hence do not contribute to this physical process. Higher order terms, \({{\hat{S}}}^{(n)}\) with \(n>2\), with an appropriate number of contractions contribute what are called radiative corrections to lower order processes, such as Compton scattering.
Conservation of 4-momentum In the unmagnetized case 4-momentum is conserved, in the sense that the final 4-momentum \(p_{\mathrm{f}}\), which is the sum over the 4-momenta of the final particles, is equal to the initial 4-momentum, \(p_{\mathrm{i}}\), which is the sum over the 4-momenta of the initial particles. It is convenient to write the S-matrix and the probability of a transition in the form
where V and T are the normalization volume and time, respectively. The probability of a transition per unit time is identified as \(w_{\mathrm{fi}}=p_{\mathrm{fi}}/T\).
5.5 Feynman diagrams
The terms in the expansion of the S-matrix are described by Feynman diagrams.
Rules for Feynman diagrams A Feynman diagram consists of lines that connect either two vertices or the initial or final state to a vertex. Here the initial state is chosen to be on the right and the final state on the left. There are three components in a Feynman diagram in QED: solid lines with arrows, dashed lines and vertices, where a solid line joins a dashed line. A solid line represents an electron or a positron, with the arrow pointing from right to left for an electron and left to right for a positron. The direction of the arrow is continuous along any given solid line. A vertex represents the operator \({{\mathcal {H}}}_{\mathrm{I}}\), and involves a photon line joining an electron line. (In QPD, there are also multiple-photon vertices that represent the nonlinear response of the plasma.) In general, there are external lines that begin or end in the initial or final state, and internal lines that connect two vertices, and represent propagators between the two vertices, with each propagator corresponding to a contraction in the expansion (72).
Each of the integrals in the expansion (72) is interpreted as an integral over the space-time point of a vertex, that is, \(x_i\) say is associated with the ith vertex, and it has a 4-tensor index, \(\mu _i\), and \(\gamma ^{\mu _i}\) associated with it.
Feynman diagram for Cerenkov emission by an electron, represented by the solid line with the arrow pointing from the initial state of the right to the final state on the left. The photon line (dashed) connects to the electron line at a vertex. 4-momentum is conserved, with the final 4-momentum of the electron given by \(p'=p-k\)
Momentum space representation In the unmagnetized case, 4-momentum is conserved at each vertex, and this allows one to perform all the space-time integrals over \(\delta \)-functions, allowing a momentum-space representation of the S-matrix. In this case, there are 4-momenta associated with each line in a Feynman diagram. A simple example of a Feynman diagram, that corresponds to Cerenkov emission by an electron, is shown in Fig. 1. In this case, there is an electron in the initial state and an electron and a photon in the final state. Conservation of 4-momentum in this case implies \(p'=p-k\), where p and \(p'\) are the 4-momenta of the initial and final electrons, respectively.
The eight first-order diagrams are related to that for Cerenkov emission by moving lines between the initial and final state. Conservation of 4-momentum in all cases is of the form \(\epsilon p-\epsilon 'p'\pm k=0\), with Cerenkov emission by an electron corresponding to \(\epsilon =\epsilon '=1\) and \(-k\). Moving the photon line from the final to the initial state, \(-k\rightarrow +k\), changes Cerenkov emission into the absorption of a photon, which may be referred to as Landau damping. Moving an electron line from the initial to final states, or vice versa, converts it into a positron line (the direction of the arrow is reversed). Cerenkov emission by a positron corresponds to \(\epsilon =\epsilon '=-1\) and \(+k\), in which case the primed state is the initial state and the unprimed state is the final state. Landau damping by a positron is described by \(+k\rightarrow -k\). One-photon pair creation and annihilation correspond to \(\epsilon =-\epsilon '\) so that both the electron and the positron are in either the initial or the final state, with the photon in the other state. All six of these processes are kinematically forbidden in vacuo: \(k^2=(\epsilon p-\epsilon 'p')^2=0\) and \(p^2=p'^2=m^2\) are incompatible.
a The Feynman diagram representing a contribution to Compton scattering in which an electron in a state q absorbs a photon \(k'\) at an index labeled \(\nu \) producing an electron in a virtual state \(q''\) which decays into the final electron \(q'\) and photon k at a vertex Labeled \(\mu \). b The Feynman diagram in which the sequence of absorption and emission in a is reversed. c An additional contribution to Compton scattering, referred to as nonlinear scattering, involving a three-photon vertex
Bubble diagram Of specific relevance when considering the response of a plasma are the second-order diagrams with one and two contractions over electron operators. The diagram with one contraction, shown in Fig. 2, describes Compton scattering by an electron; the contraction implies the electron propagator joining the two vertices. It is the forward-scattering case that is relevant to the plasma response. The two external electron lines then have the same 4-momentum, p, and they may be joined such that, in the forward-scattering case, Fig. 2 may be interpreted as a resonant part of the “bubble” diagram Fig. 3. The bubble diagram corresponds to two contractions giving two electron propagators between the two vertices, forming a closed loop connected to external photon lines. This diagram may be interpreted as a modification to the photon propagator that takes account of a photon decaying into a virtual electron–positron pair, which recombines to reproduce the photon. In QED, this diagram leads to a divergence, that is removed by renormalization. The renormalization procedure leaves a finite contribution, which implies the response tensor of the vacuum, called the vacuum polarization tensor. In the presence of a medium, the same procedure leads with the propagators in vacuo replaced by their statistical averages over the plasma, leads to the response tensor for the plasma.
5.6 Vertex function
An electron–photon interaction at x is described in the theory by a vertex function. Consider the first-order term in the expansion (72) with (71). The wavefunctions in the general case, where the states are labeled by quantum numbers \(\epsilon ,q\), \(\epsilon ',q'\) and the photon is in a mode M, the time dependence of the integrand is only in exponential functions, so that the integral over t is trivial, giving \(2\pi \delta (\epsilon \varepsilon _q-\epsilon '\varepsilon _{q'}+\omega _\mathrm{{M}})\). The \(\mathbf{x}\)-integral defines a vertex function
In the unmagnetized case, the \(\mathbf{x}\)-dependence also has only an exponential dependence; the integral over the \(\mathbf{x}\) gives \((2\pi )^3\delta ^3(\epsilon \mathbf{p}-\epsilon '\mathbf{p}'+\mathbf{k})\). Using (56), the vertex function then becomes
a The bubble diagram involving a single closed electron loop joined to two external photon lines. b, c The forward-scattering diagrams corresponding to the first two diagrams in Fig. 2 for Compton scattering
5.7 Response of a plasma in QPD
The response of a plasma in QPD may be derived by including the statistical average over the plasma electrons in the QED derivation of the vacuum polarization tensor. The first step in the derivation is to note that the electron propagator in vacuo is modified by the inclusion of the bubble diagram, Fig. 3: a photon spends part of its time as a virtual electron–positron pair, and this is described by including an infinite sequence of bubble diagrams in the propagator. Schematically, suppose one replaces (49) by a simpler equation, \(\varLambda D=1\), with \(\varLambda =\lambda _0+\varPi \) and with the photon propagator, \(D_0\), in the absence of bubble diagrams satisfying \(\varLambda _0D_0=1\). Including bubble diagrams, each with a contribution, w, one has \(D=D_0+D_0wD_0+D_0wD_0wD_0+\cdots =D_0/(1-wD_0)\), implying \(D^{-1}-D_0^{-1}=w\), and hence \(\varPi =w\). Thus, the response tensor is determined by the Feynman amplitude of the bubble diagram with the external (photon) lines omitted. The resulting expression for the linear response tensor of the vacuum is
where Tr denotes the trace over the \(\gamma \) matrices. The integral diverges, and a renormalization procedure is needed to find the finite result for the vacuum polarization tensor.
Linear response tensor The medium is included in the response tensor (76) by replacing the electron propagators by their statistical averages, given by (68). The statistical average is included separately in each propagator, resulting in two contributions. The resulting linear response tensor for a plasma reduces to
with \(u^\mu =p^\mu /m\) or \(ku=\gamma (\omega -\mathbf{k}\cdot \mathbf{v})=(\omega \varepsilon -\mathbf{k}\cdot \mathbf{p})/m\). The electrons and positrons contribute to the response in the same way, so that only the sum of their occupation numbers appears.
Quantum resonances In an unmagnetized, non-quantum plasma, the only resonance is at \(ku=0\), or \(\omega -\mathbf{k}\cdot \mathbf{v}=0\). In the quantum case, there are two resonances at \(ku\pm k^2/2m=0\) or, in ordinary units, \(\omega -\mathbf{k}\cdot \mathbf{v}\pm \hbar (\omega ^2-|\mathbf{k}|^2c^2)/2\gamma mc^2=0\). The response tensor may be written as a non-dispersive term plus two terms for the resonances at these two zeros.
Longitudinal and transverse parts One may write \(a^{\mu \nu }(k,u)=L^{\mu \nu }(k,u)+T^{\mu \nu }(k,u)\) with
In the case of an isotropic plasma, the components of the response tensor along \(L^{\mu \nu }\) and \(T^{\mu \nu }\) are the longitudinal and transverse parts of the response in the rest frame of the plasma. Provided the electrons are unpolarized, the wave modes of the plasma are either longitudinal or transverse, in the rest frame, with transverse waves having two degenerate states of polarization.
Response of a spin-dependent plasma Spin dependence is usually neglected in discussing the response of an unmagnetized plasma. It is of formal interest to include spin-dependence in the theory, and it is of some physical significance to consider possible implications. For example, electrons produced by decay of neutrons have a preferred spin helicity, and hence a preferred handedness, and a plasma in which the electrons have a preferred handedness is spin dependent.
Including the spin, in the general case Melrose and Weise (2003) found
Choosing the the spin operator to be the helicity, they showed that if the electrons have a net helicity this introduces a rotatory part to the response tensor in an isotropic plasma. Such a medium is said to be optically active, characterized by transverse wave modes that are circularly polarized. The rotatory part is determined by the difference between the occupation numbers of electrons with positive helicity, \(\sigma =+1\), and negative helicity, \(\sigma =-1\).
5.8 Nonlinear response tensors
The weak-turbulence expansion defines not only the linear response tensor, but also quadratic and cubic nonlinear response tensors. (Higher order response tensor are not usually considered.) These may be calculated in QPD in a similar way to the linear response tensor.
Quadratic response tensor The quadratic response tensor describes coupling between three electromagnetic fields, at \(k_0,k_1,k_2\) say, satisfying a matching condition of the form \(k_0\pm k_1 \pm k_2=0\). In QPD, the quadratic response tensor is related to the Feynman amplitude for the triangle diagram, with external photon lines omitted. The quadratic response tensor of the vacuum is identically zero. This follows from the fact that it depends on the sign of the charge, which is opposite for electrons and positrons. There are two triangle diagrams, Fig. 4, that contribute, and they differ only in the direction of the arrow around the triangle, corresponding to electron and positron contributions. In the presence of a plasma, there is a net contribution provided that the occupation numbers of electrons and positrons are different, with the net contribution depending on the difference between these two occupation numbers. The response tensor, \(\varPi ^{\nu _0\nu _1\nu _2}(k_0,k_1,k_2)\), may be symmetrized over permutations of \(\nu _i,k_i\), \(i=0,1,2\).
Cubic response tensor The cubic response tensor is derived, similarly to the quadratic response tensor, from the amplitude for the box (rather than the triangle) diagram with the external lines omitted. As with the linear response tensor, the contributions from electrons and positrons add. For a given box diagrams, there are four contributions, one from each of the statistically averaged propagators on the four sides of the box. As with the quadratic response tensor, the cubic response tensor may be symmetrized over permutations of the external lines and associated vertices.
5.9 Multiple-photon vertices
In QPD, as is classical plasma physics, the nonlinear response tensors imply that different wave fields may combine or split, described in the QPD case by coupling between wave quanta. Such coupling may be described by including additional terms in the interaction Hamiltonian: the quadratic response implies coupling between three wave fields, and the cubic response implies coupling between four wave fields. Additional components in Feynman diagrams are then implied, and it is convenient to describe these through m-photon vertices, with \(m=3\) for the quadratic response and \(m=4\) for the cubic response. An example of a Feynman diagram including a multiple-photon vertex is shown in Fig. 2c, corresponding to nonlinear scattering. A multiple-photon vertex arises from the statistical average over a closed electron loop, in the sense that each such loop in a Feynman diagram is replaced by the appropriate multiple-photon vertex. As in Fig. 2c, a multiple-photon vertex may be represented by shading the closed loop, indicating that it is replaced by its statistical average over the plasma.
6 Quantum magnetized plasmas
The inclusion of a background magnetic field, \(B\ne 0\), is straightforward in principle in QPD, but raises conceptual issues in PKT related to the discreteness of the eigenvalues and the interpretation of the spin. Before discussing magnetized plasmas, it is relevant to comment on the magnetized vacuum.
6.1 Response of a magnetized vacuum
The response of a magnetized vacuum has similar features to the response of a plasma, in that it includes a hierarchy of response tensors. The linear response implies that the magnetized vacuum is birefringent, with two linearly polarized wave modes. The quadratic nonlinear response is nonzero, allowing photon splitting (one photon splitting into two photons). These properties may be treated using a modification of QED to include the magnetic field in the propagators. This procedure leads to exact but cumbersome results for the magnetized vacuum. There is an older approach, that is simpler and more convenient for most purposes, based on the Heisenberg–Euler Lagrangian. This older approach gives the wave properties of the magnetized vacuum in the limit \(\omega \ll m\). The method may also be used to derive the quadratic (and higher order response tensors for the magnetized vacuum.
Heisenberg–Euler Lagrangian The response of the vacuum in the presence of a static electromagnetic field was derived by Heisenberg and Euler (1936). A more general derivation by Schwinger (1951) led to an expression for the Lagrangian density
with \(X^2=(\mathbf{B}+i\mathbf{E})^2=-2S+2iP\), where \(S=B^2-E^2\) and \(P=\mathbf{E}\cdot \mathbf{B}\) are Lorentz invariants describing the electromagnetic field. Expanding (80) in powers of the fields gives
Electromagnetic wrench For static electromagnetic field in vacuo, one is free to transform to a convenient inertial frame, with \(S=B^2-E^2\) and \(P=\mathbf{E}\cdot \mathbf{B}\) unchanged. In the special cases, (i) \(P=0\), \(S>0\) and (ii) \(P=0\), \(S<0\), one can transform to a frame in which (i) the electric field is zero and (ii) the magnetic field is zero, so that these correspond to (i) a magnetostatic field and (ii) an electrostatic field. For \(P\ne 0\), the field is referred to as an electromagnetic wrench.
Low-frequency response The Lagrangian (80) may be used to derive the hierarchy of response tensors for the vacuum for \(\omega ,|\mathbf{k}|\ll m\). The linear response tensor is given by
with
The tensors \(F^{\mu \nu }\) and \({{\mathcal {F}}}^{\mu \nu }\) are given explicitly by (39).
The quadratic nonlinear response tensor is
Susceptibility 3-tensors In 3-vector notation, the response may be described in terms of electric (e), magnetic (m) and magneto-electric (em, me) susceptibility tensors. The polarization, \(\mathbf{P}\), and magnetization, \(\mathbf{M}\), are related to \(\mathbf{E}\) and \(\mathbf{B}\) by
In the case \(E=0\) of a magnetization vacuum, the magneto-electric response tensors are zero, and the electric and magnetic susceptibility tensors are different perpendicular and parallel to \(\mathbf{B}\), with components, to lowest order in \(B^2\),
where \(\alpha _\mathrm{{c}}=e^2/4\pi \varepsilon _0\approx 1/137\) is the fine structure constant, and \(B_\mathrm{{c}}=m^2/e\approx 4.4.\times 10^9\,\)T is the critical magnetic field.
Wave modes The two natural wave modes of the magnetized vacuum have refractive indices and polarization vectors, in the approximation made in (86),
where \(\mathbf{B}\) is assumed along the 3-axis.
Spontaneous pair creation (Schwinger effect) An electrostatic field and an electromagnetic wrench are intrinsically unstable to spontaneous decay into pairs. The decay rate is extremely slow for electric fields much smaller than the critical electric field, \(E_\mathrm{{c}}=m^2c^3/e\hbar =1.3\times 10^{18}\mathrm \,V\,m^{-1}\), analogous to the critical magnetic field, \(B_\mathrm{{c}}=m^2c^2/e\hbar =4.4\times 10^{9}\,\)T, in that they depend only on fundamental constants.
The spontaneous decay rate in an electromagnetic wrench is determined by the imaginary part of the Lagrangian density (80). Writing \(X=a+ib\), there are poles at \(s=s_n=\pi n/eb\), and the imaginary parts are determined using the Landau prescription. The probability of spontaneous pair production (spe) per unit time and per unit volume is
where the latter expression, in ordinary units, applies in the limit \(B\rightarrow 0\), that is, to an electrostatic field.
6.2 Solutions of Dirac’s equation for \(B\ne 0\)
QPD may be generalized to include a background magnetic field exactly by assuming that the electron states are described by solutions of Dirac’s equation in the presence of a background magnetostatic field. Before discussing the solution of Dirac’s equation for \(B\ne 0\), it is helpful to consider the nonrelativistic case.
Landau quantum number A classical nonrelativistic electron spirals about a magnetic field line. The momentum, \(p_z\), parallel to the field line can have any value, and this translates into a continuous quantum number in the quantum case. However, the momentum, \(p_\perp \), perpendicular the field line has discrete values in a quantum treatment. Classically, the perpendicular motion is circular motion at the cyclotron frequency, \(\omega _\mathrm{{B}}=eB/m\), and circular motion is simple harmonic motion. Hence, the perpendicular energy is quantized as a simple harmonic oscillator, \(p_\perp ^2/2m=(l+\textstyle {\frac{1}{2}})\hbar \omega _\mathrm{{B}}\), with \(l=0,1,2,\ldots \) The spin contributes an additional energy \(\textstyle {\frac{1}{2}}s\hbar \omega _\mathrm{{B}}\), giving
where n is the Landau quantum number. The ground state, \(n=0,l=0,s=-1\) is nondegenerate, and each excited state, \(n=1,2,\ldots \), is doubly degenerate.
The quantization (89) also applies in the relativistic case. The energy eigenvalues found by solving Dirac’s equation are
As in the nonrelativistic case, the ground state, \(n=0\), is nondegenerate and all excited states are doubly degenerate.
Wavefunctions To solve Dirac’s equation, one needs to make a particular choice of gauge for the vector potential, \(\mathbf{A}\), for the background magnetic field. Choosing \(\mathbf{A}=(0,Bx,0)\) the Hamiltonian is independent of t, y, z, so that one may seek solutions of the form \(f(x)\exp (-iEt+iP_yy+iP_zz)\), where f(x) is a column matrix with component \(f_i(x)\), \(i=1,2,3,4\), and \(E,P_y,P_z\) are constants of the motion. One is free to write \(E=\epsilon \varepsilon \), \(P_y=\epsilon p_y\), \(P_z=\epsilon p_z\). Choosing the standard representation of the Dirac algebra, the \(f_i(x)\) satisfies
with x appearing only through
Normalizable solutions exist only for \(\varepsilon =\varepsilon _n(p_z)\), and involve simple harmonic oscillator wavefunctions
where \(H_n\) is a Hermite polynomial. The solutions of the two equations (91) are \(f_{1,3}\propto n_{n-1}(\xi )\), \(f_{2,4}\propto v_n(\xi )\). A general solution is
where the constants \(C_i\) are to be determined.
One choice of the coefficients \(C_i\), made by Johnson and Lippmann (1949), gives
where \(c_n\) is a normalization constant and with \(p_n=(2n\hbar eB)^{1/2}\). Although this is an acceptable solution, the eigenvalues \(s=\pm 1\) correspond to an unidentified spin operator, as discussed below.
For other choices of gauge, the solutions have different forms. For example, for the choice, \(\mathbf{A}=\textstyle {\frac{1}{2}}(-By,Bx,0)\), the solutions are found in terms of generalized Laguerre polynomials, rather than Hermite polynomials (e.g., Sokolov and Ternov 1968, 1986).
6.3 Spin operators
A point emphasized by Sokolov and Ternov (1968) is that the spin operator \(S^{\mu \nu }\), cf. (35), does not commute with the Dirac Hamiltonian, and hence its eigenvalues are not conserved. More generally, when seeking to find a wavefunction with eigenvalues that are constants of the motion, one needs to choose a complete set of commuting operators. Sokolov and Ternov (1968) identified several spin operators that commute with \({{\hat{H}}}={\varvec{\alpha }}\cdot {\hat{\mathbf{p}}}+\beta m\) by considering the components of the tensor
which commutes with \({{\hat{H}}}\) by construction. The components of the tensor (96),
are interpreted as components of the electric dipole moment operator, \({\hat{\mathbf{d}}}\), and magnetic dipole moment operator, \({{\hat{{\varvec{\mu }}}}}\), of the electron,
Another spin operator that commutes with \({\varvec{\alpha }}\cdot {\hat{\mathbf{p}}}+\beta m\) is the 4-vector operator
which is interpreted as the helicity (4-vector) operator.
Evolution of spin operators in an electromagnetic field When fields \(\mathbf{E}\ne 0\), \(\mathbf{B}\ne 0\) are included in the Hamiltonian, \(\mathbf{H}={\varvec{\alpha }}\cdot ({\hat{\mathbf{p}}}+e\mathbf{A})+\beta m-e\phi \), the operators \({{\tilde{S}}}^{\mu \nu }\) and \({{\hat{w}}}^\mu \) evolve, satisfying the equations
It follows that for \(\mathbf{E}=0\) and \(\mathbf{B}\) along the z-axis, the conserved components are \({{\hat{d}}}_z\), \({{\hat{\mu }}}_z\), \({{\hat{w}}}^0\) and \({{\hat{w}}}_z=0\). Any of these may be chosen as the spin operator. The helicity operator, \({{\varvec{\Sigma }}}\cdot {\hat{\mathbf{p}}}\), and the parallel component of the magnetic momentum operator, \({{\hat{\mu }}}_z\), are favored choices.
Helicity eigenstates For the helicity eigenstates, \(\sigma =\pm 1\), the coefficient \(C_i\) are given by
with \(h_n=(p_n^2+p_z^2)^{1/2}\).
Magnetic-momentum eigenstates For the magnetic-moment eigenstates, \(s=\pm 1\), the coefficient \(C_i\) are given by
with \(P_\pm =\textstyle {\frac{1}{2}}(1+P)\pm \textstyle {\frac{1}{2}}(1-P)\), \(P=p_z/|p_z|\), and where V is the normalization volume.
Sokolov and Ternov (1968) argued that when the radiative correction to the Hamiltonian is included, as discussed below, the only acceptable spin operator is \({{\hat{\mu }}}_z\). Herold (1979) gave a different argument that leads to the same conclusion, that \({{\hat{\mu }}}_z\) is the appropriate operator to choose when discussing gyromagnetic processes (Herold et al. 1982).
6.4 Radiative correction to Dirac Hamiltonian
The radiative correction to the Dirac Hamiltonian is actually to the anomalous gyromagnetic ratio \(g=2\); to lowest order in the fine-structure constant, \(\alpha _\mathrm{{c}}\), the correction is (Schwinger 1948) \(\textstyle {\frac{1}{2}}(g-2)=\alpha _\mathrm{{c}}/2\pi \).
Pauli (1941) wrote down a modified form of Dirac’s equation that takes the anomalous magnetic moment into account:
Sokolov and Ternov (1968) showed that only \({{\hat{\mu }}}_z\) satisfies this requirement that the spin operator commute with the Hamiltonian implied by (104) with final term included.
Mass operator for \(B\ne 0\) A derivation of the final term in (104) involves calculating the mass operator. Similar to the calculation of the polarization tensor in terms of the amplitude of the bubble diagram, the mass operator is calculation from the amplitude of the loop section of the Feynman diagram Fig. 5. The interpretation is that an electron, described by the solid line representing the electron propagator, emits and reabsorbs a virtual photon; summing over an infinite sequence of such emissions and absorptions leads to an additional term in the electron propagator, referred to as the mass operator. In the absence of a magnetic field, the amplitude of the diagram diverges implying an infinite correction to the mass, which is incorporated into the physical mass by a renormalization. In the presence of a magnetic field, additional finite terms that depend on B give the mass operator (e.g., Ritus 1972; Parle 1987). The final term in (104) is determined by the mass operator.
Splitting of degenerate excited states The radiative correction to the Hamiltonian leads to a splitting of the degenerate Landau states. The energy eigenvalues become (Sokolov and Ternov 1968; Parle 1987)
where \(s=\pm 1\) denote the spin states of the magnetic moment operator. Spontaneous emission from the state \(n, s=+1\) to the state \(n, s=-1\) is possible. Parle (1987) estimated the transition rate and found it to be very small. Such transitions are discussed briefly in Section 7.1.
6.5 Vertex function and electron propagator
Essential ingredients in QPD in the magnetized case are the form of the vertex function and the form of the propagator. Various different choices are possible.
Vertex function The vertex function is defined by (74), with the quantum numbers \(q'\) and q interpreted as \(n',s',p'_z\) and \(n,s,p_z\). The integral over \(\mathbf{x}\) in (74) is over a product of functions \(v_{n'}(\xi ')\), \(v_n(\xi )\), which can be evaluated in terms of a standard integral, giving an expression in terms of generalized Laguerre polynomials, \(L^\nu _n(x)\). It is helpful to write the quantum formulae in terms of the functions (e.g., Melrose and Parle 1983; Melrose 2013)
with, in ordinary units, \(x=\hbar k_\perp ^2/2eB\). An advantage of these functions is that they reduce to Bessel functions in the nonquantum limit, \(n\rightarrow \infty \)
An expression for the vertex function, for the choice of gauge \(\mathbf{A}=(0,Bx,0)\) and of \({{\hat{\mu }}}_z\) as spin operator, is
with \(P_\pm =\textstyle {\frac{1}{2}}(1+P)\pm \textstyle {\frac{1}{2}}(1-P)\), \(P=p_z/|p_z\).
The functions \(J^n_\nu (x)\), defined by (106), appear in the vertex function (107) and approximations to gyromagnetic emission involves approximation to \(J^n_\nu (x)\). The classical limit corresponds to \(\hbar \rightarrow 0\), \(n\rightarrow \infty \) with \(n\hbar \rightarrow p_\perp ^2/2eB\) and \(J^n_\nu (x)\rightarrow J_\nu (z)\) with \(z=k_\perp p_\perp /eB\). In the nonrelativistic case, both \(J^n_\nu (x)\) and \(J_\nu (z)\) are approximated by the leading terms in expansions in powers of x and z, respectively. In the highly relativistic (synchrotron) case, both functions are approximated by Airy functions.
Electron propagator for \(B\ne 0\) The statistical average of the electron propagator in a magnetized plasma with electron occupation number \(n^\epsilon _q\) is
with the wavefunction given by the general form (94) with (102) for the choice of \({{\hat{\mu }}}_z\) as the spin operator.
Propagator in a magnetized vacuum The unit term in the numerator in (108) gives the propagator in a magnetized vacuum. The sum over states may be performed explicitly in this case. The result gives a closed form for the electron propagator in a magnetized vacuum. This form, derived by Géhéniau and Demeur (1951) in a different way, is a product of a gauge-dependent term and a gauge-independent part.
6.6 Response tensor for a magnetized quantum electron gas
An expression for the linear response tensor for a magnetized quantum electron gas is derived using the same QPD procedure used to derive the response tensor for an unmagnetized electron gas, with the electron propagator replaced by the magnetized version. For unpolarized electrons with occupation number \(n^\epsilon _n(p_z)\) the response tensor summed over polarizations is (Melrose and Weise 2009)
with \(p_\parallel ^\mu =(\varepsilon _n,0,0,p_z)\), \(p'^\mu _\parallel =(\varepsilon '_{n'},0,0,p'_z)\), and with
The term proportional to \(\textstyle {\frac{1}{2}}(\epsilon '-\epsilon )\), after renormalization, gives the polarization tensor of the magnetized vacuum, and the remaining terms describe the response of the plasma.
Resonant values The resonant denominator in (109) may be rationalized to remove square roots by multiplying numerator and denominator by \(\omega +\epsilon \varepsilon _n-\epsilon '\varepsilon '_{n'}\) and rewriting the denominator using
with
and
The right-hand side of Eq. (111) is also equal to \(-(\epsilon ' p'_z-p'_{z+})(\epsilon ' p'_z-p'_{z-})\), with \(p'_{z\pm }=k_z(f_{nn'}-1)\pm \omega g_{nn'}\), \(\varepsilon '^\pm _{n'}=\omega ( f_{nn'}-1)\pm k_z g_{nn'}\).
The condition \(g_{nn'}=0\) corresponds to a threshold for a gyromagnetic process with given \(n,n'\).
Nongyrotropic and gyrotropic parts The sum over \(\epsilon '\) may be performed explicitly, with the result separating naturally into nongyrotropic (N) and gyrotropic (G) parts, that depend on the sum \({{\bar{n}}}\) of and difference \(n^d\) between the electron and positron occupation numbers \(n^\pm \):
The identity \((p_{z+}-p_{z-})/(\epsilon p_z-p_{z+})(\epsilon p_z-p_{z-}) =1/(\epsilon p_z-p_{z+})-1/(\epsilon p_z-p_{z-})\) allows one to write (114) as (a nondispersive part plus) a sum over contributions from the resonances at \(\epsilon p_\parallel ^\mu =p_\pm ^\mu =(\varepsilon '^\pm _{n'},0,0,p_{z\pm })\). Explicit expressions for \([N_{n'n}(p_\pm ,k)]^{\mu \nu }\) and \([G_{n'n}(p_\pm ,k)]^{\mu \nu }\) were given by Melrose and Weise (2009).
Relativistic plasma dispersion function The resonant integrals may be evaluated in terms of a relativistic plasma dispersion function (RPDF). Writing \(p_z/\varepsilon _n^0=2t/(1-t^2)\), \(\epsilon _n/\varepsilon _n^0=(1+t^2)/(1-t^2)\), with \(\varepsilon _n^0=(m^2+p_n^2)^{1/2}\), and similarly for \(p_z{\pm }\), \(\varepsilon ^\pm \) defining \(t_\pm \), the integrals may be reduced to the form
with n(t) any of \(n^\epsilon _n(p_z)\), \({{\bar{n}}}_n(p_z)\) or \(n^d_n(p_z)\). Melrose and Weise (2009) evaluated the RPDF (115) explicitly for a completely degenerate distribution and for a Jüttner distribution.
6.7 Gyromagnetic emission
Gyromagnetic emission is described by the same Feynman diagram as Cerenkov emission, Fig. 1, with electron states labeled by appropriate quantum numbers, \(q,q'\), rather than by 4-momenta. The inclusion of a magnetic field not only allows emission and absorption, but also allows one-photon pair creation and annihilation. Unlike the unmagnetized case in vacuo, six of the possible eight Feynman diagrams correspond to physically allowed processes. (The remaining two have an electron, a positron and a photon all in either the initial or the final state.) The classical theory of gyromagnetic emission and absorption is modified but not changed radically in the quantum case. An exception concerns the effect of the spin: the quantum theory includes spin-flip transitions that have no classical counterpart. The effect of the spin is emphasized in the following discussion. The spin operator is assumed to be \({{\hat{\mu }}}_z\): for all other choices of the spin operator, the eigenvalues of the spin evolve unrelated to emission and absorption.
Anharmonicity In nonrelativistic theory, the energy eigenvalues of an electron are equally spaced such that a transition between Landau levels n and \(n-1\) produces a photon at the cyclotron frequency \(\omega _\mathrm{{B}}\) for any n. This is not the case when relativistic effects are included, as illustrated in Fig. 6. The dependence of the transition frequency for \(n\rightarrow n-1\) on n is referred to as anharmonicity. Each such gyromagnetic transition occurs at a unique frequency. Also shown in Fig. 6 are the states for \(s=\pm 1\). It is convenient to refer to transitions in which the spin does not change as non-spin-flip (nsf), transitions in which \(s=+1\) changes to \(s=-1\) as spin-flip (sf), and transitions in which \(s=-1\) changes to \(s=+1\) as reverse-spin-flip (rsf).
Probability of gyromagnetic emission The probability per unit time that an electron emit a photon in the range \(d^3\mathbf{k}/(2\pi )^3\) at \(\mathbf{k}\), with frequency \(\omega \), due to a transition \(q=(n,s,p_z)\) to \(q'=n',s',p'_z\) is given by
with \(\epsilon 'p'_z=\epsilon p_z-k_z\), \(\varepsilon '_{n'}=(m^2+p'^2_z+2n'eB)^{1/2}\), and with \(\mathbf{\varGamma }^{\epsilon '\epsilon }_{q'q}(\mathbf{k})\) the space components of the vertex function (107). The relevant spin operator is \({{\hat{\mu }}}_z\). Gyromagnetic emission by an electron corresponds to \(\epsilon '=\epsilon =1\) with the transition \(q\rightarrow q'\); gyromagnetic emission by a positron corresponds to \(\epsilon '=\epsilon =-1\) with the transition \(q'\rightarrow q\). Pair creation and annihilation correspond to \(\epsilon '=-\epsilon \).
Gyromagnetic emission by a nonrelativistic electron
In the nonrelativistic limit, nsf transitions \(n\rightarrow n'=n-j\), \(s=s'\) correspond to \(2^j\)-electric-multipole transitions (dipole for \(j=1\), quadrupole for \(j=2\), and so on), sf transitions \(n\rightarrow n'=n-j\), \(s=+1\), \(s'=-1\), correspond to \(2^j\)-magnetic-multipole transitions, and rsf transitions \(n\rightarrow n'=n-j\), \(s=-1\), \(s'=+1\) correspond to higher order multipole radiation. The rate of a transition \(n\rightarrow n-j\) in vacuo may be found by summing the probability (116) over the two states of transverse polarization and integrating over \(d^3\mathbf{k}/(2\pi )^3\).
It is convenient write the transition rate for nsf transitions in terms of \(l=n-1\rightarrow l-j=n-1-j\) for \(s=+1\) and \(l=n\rightarrow l-j=n-j\) for \(s=-1\), giving (Melrose and Russell 2002)
with \(\omega =\varepsilon _n-\varepsilon _{n-j}\). To lowest order in \(B/B_\mathrm{{c}}\), one has \(\omega /m\approx jB/B_\mathrm{{c}}\); with this approximation the transition rate is proportional to \((B/B_\mathrm{{c}})^{j+1}\). The rate of sf transitions is
With \(\omega /m\approx jB/B_\mathrm{{c}}\), the sf transition rate is proportional to \((B/B_\mathrm{{c}})^{j+2}\), one power of \(B/B_\mathrm{{c}}\) higher than the nsf transition rate. The rsf transition rate is smaller than the sf rate by a further factor of \((B/B_\mathrm{{c}})^2\) (Melrose and Russell 2002) .
Relaxation to the ground state A nonrelativistic electron initially in a state \(n\gg 1\) relaxes to the ground state, \(n=0\) through spontaneous gyromagnetic emission. For \(B\ll B_\mathrm{{c}}\) the most probable transitions involve stepwise jumps from \(n\rightarrow n-1\) with no change in s. Electrons initially with \(s=+1\) tend to relax to \(n=1,l=0,s=+1\), before the slower final sf transition to \(n=0\). This effect plays an important role in determining the plasma properties in a pulsar magnetosphere, where \(B/B_\mathrm{{c}}\) can be of order 0.1. The transition rate to the ground state is determined primarily by the slowest transition, \(n=1\rightarrow n=0\), which occurs at a rate \((4\alpha _\mathrm{{c}}/3)(mc^2/\hbar )(B/B_\mathrm{{c}})^2\). This transition rate is very rapid, of order \(10^{21}(B/B_\mathrm{{c}})^2\mathrm \, s^{-1}\), leading to the conclusion that all electrons should be in their ground state, corresponding to a 1D plasma distribution that depends only on \(p_z\), with \(p_\perp =0\).
Gyromagnetic emission by a relativistic electron Gyromagnetic emission by a relativistic electron, referred to as synchrotron emission, is dominated by high harmonics \(j=n-n'\gg 1\). The relativistic quantum theory of synchrotron emission has been discussed in detail by Sokolov and Ternov (1968, 1986). The differences between the quantum and classical theories are relatively minor in comparison with the differences in the nonrelativistic case. Two notable differences that depend specifically on the spin are discussed here. The spin operator is \({{\hat{\mu }}}_z\) in this discussion.
Bump in synchrotron spectrum for spin-\(\textstyle {\frac{1}{2}}\) An interesting spin-dependent effect was discussed by Lieu and Axford (1993), who considered a peculiar bump in the synchrotron spectrum identified by Sokolov and Ternov (1968). Lieu and Axford (1993) showed that this bump is present for spin-\(\textstyle {\frac{1}{2}}\) particles, but not for spin-0 particles. No physical explanation for this bump seems to be available.
Sokolov–Ternov effect When high-energy electrons are allowed to relax to their ground state through gyromagnetic emission, sf transitions occur at a faster rate than rsf transitions. The fraction of electrons with \(s=-1\) to those with \(s=+1\) increases systematically. An initially unpolarized distribution of high-energy electrons develops a net polarization. Sokolov and Ternov (1968) showed that the degree of polarization approaches a limiting value \(8\sqrt{3}/15\approx 92.4\%\).
6.8 One-photon pair creation
One-photon pair creation is possible in the magnetized vacuum for a photon with perpendicular energy above twice the electron self-energy, that is, for \(\hbar k_\perp c>2mc^2\) in ordinary units. One may make a Lorentz transformation to the frame in which the photon is propagating across the magnetic field, and then conservation of parallel momentum implies that the parallel momenta of the electron and positron are equal and opposite. The resonance condition, in this frame, is \(\omega =\varepsilon _n+\varepsilon _{n'}\), with \(p_z=-p'_z\). The probability of decay of the photon into a pair is found by integrating the probability (116), with \(\epsilon =1,\epsilon '=-1\), over \({\text {d}}p_z/2\pi \). As with gyromagnetic emission, there is a nonrelativistic-like case in which the discreteness of the values of \(n,n'\) is important, and a relativistic, synchrotron-like, case in which \(n,n'\) are large and may be treated as continuous.
Synchrotron-like limit The synchrotron-like limit applies when the pair is highly relativistic, and \(n,n'\) are large such that the sums over them may be replaced by integrals. The probability per unit time that a photon (with frequency \(\omega \) propagating perpendicular to the magnetic field) decay into a pair is (e.g., Erber 1966; Tsai and Erber 1974)
where \(K_{1/3}\) is a Macdonald function that arises from the Airy-integral approximation, e.g., to \(J_\nu ^n(x)\). The rate (119) is a maximum for \(\chi \) of order unity, and cuts off exponentially as for \(\chi \gg 1\).
One-photon pair creation is an important ingredient in models for pulsar magnetospheres. Early models for the pair creation, following Sturrock (1971), were based on the synchrotron-like case (119). In early models, the high-energy photons were assumed to be emitted by “primary” particles (from the stellar surface) accelerated to very high energy by an electric field, \(E_\parallel \), parallel to the magnetic field. A very high energy particle emits into a small cone about its direction of motion, implying that the photons are initially directed nearly parallel to the magnetic field. A photon propagating in a straight line deviates away from the curved magnetic field line, such that \(k_\perp \) increases with distance from the point of emission. Pair creation becomes possible when \(k_\perp \) reaches the threshold \(2mc/\hbar \). The synchrotron-like approximation (119) applies only when this threshold is exceeded by a large factor.
Multiple singular thresholds As \(k_\perp \) increases, due to the increasing angle between the direction of the photon and the magnetic field, a photon with energy \(\hbar \omega \gg 2mc^2\) encounters multiple thresholds for creation of a pair with increasing values of \(n,n'\). The probability of producing a pair has a square-root singularity at the threshold for each \(n,n'\), as shown in Fig. 7. The square-root singularities are at \(g_{nn'}=0\), cf. (113), that is, in ordinary units in an arbitrary frame, at \(\hbar ^2(\omega ^2-k_z^2c^2)-(\varepsilon _0^n-\varepsilon ^0_{n'})^2=0\), with \(\varepsilon _0^n=(m^2c^4+2neB\hbar c^2)^{1/2}\) and where \((\omega ^2-k_z^2c^2)^{1/2}\) is equal to the wave frequency in the frame in which the photon is propagating across the magnetic field. Each square-root singularity is integrable, and one needs a specific model to determine whether or not a photon produces a pair at a given \(n,n'\). The probability of a pair being produced at the lowest threshold encountered, that is, at \(n=n'=0\) or \(n+n'=1\) depending on the polarization, is large for \(B/B_\mathrm{{c}}\gtrsim 0.2\), and it is only for weak fields, \(B/B_\mathrm{{c}}\ll 0.1\), that the synchrotron-like limit (119) applies.
The dependence of the logarithm of the emission coefficient on \(\omega /\omega _\mathrm{{B}}\) is shown for \(B/B_\mathrm{{c}}=0.5\) for the first three harmonics. The calculations were performed for \(\theta =\pi /2\) and radiation polarized a perpendicular to \(\mathbf{B}\), and b along \(\mathbf{B}\). The thresholds for the lowest transitions correspond to \(\omega /m=\sqrt{2}-1,\sqrt{3}-1,\sqrt{4}-1\) for \(n'-n=1,2,3\), respectively, with \(\omega _\mathrm{{B}}/m=B/B_\mathrm{{c}}\), (Melrose 2013)
Formation of positronium It was pointed out by Shabad and Usov (1986) that as the lowest threshold (\(n=n'=0\) or \(n+n'=1\) depending on the polarization) is approached, the initial photon can evolve into a bound pair, corresponding to a form of positronium. Due to the very strong magnetic field, the positronium state is different from the conventional picture of positronium, which corresponds to a hydrogen-like atom, in which the electron and positron are bound by the Coulomb force between them. To a first approximation, both the electron and positron are in 1D motion along the field line, with the Coulomb field binding them together, similar to a 1D model for the hydrogen atom (Loudon 1959).
Although it is of interest (notably when considering pulsed high-energy emission) to determine which of the various possibilities occurs, the net effect may be similar in all cases. Assuming the “primary” electron has a sufficiently high energy, a pair cascade develops, such that the initial energy is shared amongst a large number of secondary pairs. It is these secondary pairs that constitute the “pulsar plasma” from which the observed radiation is thought to originate.
7 Discussion
A variety of intrinsically quantum effects of direct or indirect relevance to plasmas are identified above. Familiar quantum effects, such as degeneracy, tunneling and diffusion, are relevant to solid-state plasmas, and have been reviewed recently by Manfredi et al. (2019). In the summary here, emphasis is on high-energy, high-field and relativistic quantum effects, and quantum treatments of linear and nonlinear response tensors.
7.1 Quantum effects in nonrelativistic, unmagnetized plasmas
Although applications to solid-state plasmas are not discussed in detail here, it is appropriate to summarize possibly relevant quantum plasma effects. Most of the quantum effects of interest in nonrelativistic thermal plasmas apply at high densities and low temperatures.
Degeneracy Degeneracy is perhaps the simplest example of an intrinsically quantum effect relevant to plasmas. The characteristic number density at which degeneracy becomes significant in an electron gas is when it exceeds the inverse cube of the de Broglie wavelength, \(\hbar /p\), with \(p\rightarrow mV_\mathrm{{e}}\) in a weakly degenerate plasma and \(p\rightarrow mv_\mathrm{{F}}\) as the completely degenerate limit is approached.
Bohm term The Bohm term describes intrinsically quantum effects associated with the wave-like nature of electrons: diffraction and tunneling, cf. (9). In QFT, the condition for the Bohm term to be important is characterized by the parameter H, given by (8). With the energy, \(mu_0^2\), of a particle in the fluid replaced by the thermal energy, \(T_\mathrm{{e}}=mV_\mathrm{{e}}^2\), this also requires high density and low temperature.
Exchange effects Two other effects that become increasingly significant as the electron density increases are exchange effects and electron–electron correlations. The exchange interaction (or force) is associated with the Pauli exclusion principle, which becomes relevant as degeneracy is approached. Electron–electron correlations also become increasingly important with increasing density. Properties of dense plasmas have been reviewed recently in this journal by Ichimaru (2017)
Electron spin The importance of spin is one quantum effect whose importance does not require high density or low temperature in a nonrelativistic plasma. In the Schrödinger–Pauli theory, spin is independent of the dynamics, and is described by components in a \(2\times 2\) spin space that is orthogonal to the Hilbert space used to describe the dynamics. The associated magnetic moments of individual electrons lead to a magnetization of the electron gas, which can play an important role in a solid-state plasma.
7.2 The semi-classical approach
The quantum recoil plays an important role in the semi-classical version of the kinetic theory of plasmas.
Quantum recoil and radiation reaction A weakness in classical electrodynamics is that energy and momentum are not conserved: on calculating the emission of radiation by an individual charged particle in a specified motion, the motion of the particle does not change as energy and momentum are carried away by the emitted radiation. The radiation reaction force is postulated as one way of overcoming this weakness in classical theory, but it is known to lead to other difficulties, such as pre-acceleration. Appeal to the quantum recoil (to the emission of a wave quantum) provides a simpler method of including the radiation reaction. One introduces quantum mechanical notation, and imposes energy and momentum conservation in the form \(\varepsilon '=\varepsilon -\hbar \omega \), \(\mathbf{p}'=\mathbf{p}-\hbar \mathbf{k}\), where a prime denoted the particle state after emission of a wave quantum. The requirement, e.g., in the relativistic case, \(\varepsilon '=(m^2c^4+\mathbf{p}'^2c^2)^{1/2}\), gives \(\varepsilon =(m^2c^4+\mathbf{p}^2c^2)^{1/2}\) to zeroth order in \(\hbar \), the classical (Cerenkov) resonance condition, \(\omega -\mathbf{k}\cdot \mathbf{v}=0\), to first order in \(\hbar \), and the quantum recoil to second order in \(\hbar \). The recoil term implies energy and momentum loss at the same rate as implied by the radiation reaction force in simple cases where the theories can be compared directly.
Detailed balance Detailed balance relates two processes that are the inverses of each other, specifically, emission and absorption in the present case. Let the probability of spontaneous emission between two states q and \(q'\) be \(w_{q,q'}(\mathbf{k})\), which can be calculated classically and rewritten in this notation. Assuming a distribution of particles with occupation number \(n_q\), the total rate of spontaneous emission is \(w_{q,q'}(\mathbf{k})n_q\) summed over q. The Einstein coefficients, which correspond to detailed balance in this case, imply that the total probability of emission is \(w_{q,q'}(\mathbf{k})n_q[1+N(\mathbf{k})]\), where \(N(\mathbf{k})\) is the occupation number for the wave quanta. The term proportional to \(N(\mathbf{k})\) is interpreted as stimulated emission. The probability of absorption \(q'\rightarrow q\) is \(w_{q,q'}(\mathbf{k})n_{q'}N(\mathbf{k})\).
Derivation of kinetic equations The major advantage of this semi-classical approach is that kinetic equations for the waves and the particles may be derived using a simple form of bookkeeping. Each transition \(q\rightarrow q'\) increases \(N(\mathbf{k})\) by unity and each transition \(q'\rightarrow q\) decreases \(N(\mathbf{k})\) by unity. The difference between the transition rates for emission and absorption summed over states q gives the semi-classical form of the kinetic equation for the waves. Each transition \(q\rightarrow q'\) decreases \(n_q\) by unity and increases \(n_{q'}\) by unity. The kinetic equation for the particles is found by considering, in addition, emission \(q''\rightarrow q\) and absorption \(q\rightarrow q''\), with \(q''\) interpreted at \(\mathbf{p}''=\mathbf{p}+\hbar \mathbf{k}\) for Cerenkov emission. The rate of change of \(n_q\) is found from the differences between gains due to emission \(q''\rightarrow q\) and absorption \(q'\rightarrow q\) and losses due to the inverse processes, integrated over \(\mathbf{k}\)-space. The classical forms of the kinetic equations are found by expanding in powers of \(\hbar \), with only the first-order terms included in deriving the kinetic equation for waves and second-order terms ruired in the derivation of the kinetic equation for the particles.
7.3 Relativistic quantum effects in gyromagnetic processes
Gyromagnetic emission by nonrelativistic electrons is cyclotron emission and gyromagnetic emission by highly relativistic electrons is synchrotron emission, both of which may be treated classically. Quantum effects in gyromagnetic emission include transitions between discrete Landau levels, spin-flip transitions and, in the relativistic quantum case, one-photon pair creation. Gyromagnetic transitions in the relativistic case are well-defined only if the spin is identified as the eigenvalue of the magnetic-moment operator (Sokolov and Ternov 1968). For other spin operators that do not commute with the Dirac Hamiltonian (including the radiation correction), the spin eigenvalue continuously evolves with time.
Gyromagnetic emission A particularly important quantum effect is the quantization of perpendicular momentum to discrete values, \(p_\perp =(2neB\hbar )^{1/2}\), where n is the Landau quantum number. First-order processes, which are forbidden in a vacuum with \(B=0\), are allowed: these are gyromagnetic emission and absorption of a photon by an electron or positron, and one-photon pair creation and annihilation, all of which depend on the quantum numbers \(n,n'\). For emission by an electron, n and \(n'\) are the quantum numbers before and after emission of the photon. Spontaneous emission leads to electrons losing their perpendicular energy very rapidly, even for modest values of \(B/B_\mathrm{{c}}\), such that all the electrons quickly relax to the ground Landau state, \(n=0\).
Spin-flip transitions Each Landau level, except \(n=0\), is doubly degenerate due to the spin. Transitions in which s changes sign are referred to as spin-flips for \(s=+1\rightarrow s=-1\) and reverse spin flips for \(s=-1\rightarrow s=+1\). In the nonrelativistic case for fields \(B\ll B_\mathrm{{c}}\), non-spin-flips, spin-flips and reverse spin-flips correspond to electric dipole, magnetic dipole and higher order magnetic multipole transitions, respectively, with transition rates proportional to increasing powers of \(B/B_\mathrm{{c}}\). In the relativistic case, difference between the spin-flip and reverse spin-flip rates leads to the Sokolov–Ternov effect in which electrons initially with high n become polarized, strongly favoring \(s=-1\), as they transition to lower n.
One-photon pair creation One-photon pair creation is important in populating a pulsar magnetosphere with pairs. The probability per unit time of a photon decaying into a pair has a square-root singularity at the threshold for a pair with given \(n,n'\). In the frame in which the photon is propagating across the magnetic field, the pair has \(p_z=-p'_z=0\) at threshold. Slightly above threshold the electron and positron are nonrelativistic, in the sense that one has \(p_z=-p'_z\) with \(|p_z|\ll mc\). This is qualitatively different from the synchrotron-like case discussed in earlier literature, where one has \(|p_z|\gg mc\) and \(n,n'\) are large and may be regarded as continuous, allowing the sums over them to be replaced by integrals.
Photon splitting The quadratic response tensor for the magnetized vacuum is nonzero, cf. (84), allowing three-wave coupling, and hence photon splitting in which one photon splits into two photons. Kinematic restrictions imply that photon splitting is allowed only when the refractive indices of the wave modes are taken into account. Photon splitting was first discussed in detail by Adler (1971).
7.4 Quantum effects in strong fields
There is a rich variety of quantum processes that occur in strong magnetic fields. Even in the absence of any plasma, the magnetized vacuum has plasma-like properties in the sense that it has a hierarchy of linear and nonlinear response tensors.
Birefringence of the magnetized vacuum It has been known since the 1930s that the magnetized vacuum is birefringent, with both wave modes having refractive indices slightly greater than unity, cf. (87). This is an intrinsically quantum effect, in the sense that the refractive indices depend on \((B/B_\mathrm{{c}})^2=(\hbar \omega _\mathrm{{B}}/mc^2)^2\). The wave modes are linearly polarized, so that the vacuum plasma has dispersive properties similar to a birefringent crystal.
Vacuum resonance Suppose that an electron gas is present in the strongly magnetized case. The combination of the response tensor of the magnetized vacuum and of the electron gas for the combined system leads to unusual properties of the wave dispersion (e.g., Gnedin et al. 1978). The plasma tends to dominate at low frequencies giving refractive indices less than unity and the magnetized vacuum tens to dominate at high frequencies giving refractive indices greater than unity. The frequency where the refractive index passes through unity is referred to as the vacuum resonance. As the resonance is approached (in frequency), the polarization of the natural modes changes from nearly linear to nearly circular. This change affects the absorption coefficient for X-rays propagating through the resonant region.
Schwinger effect An electrostatic field decays spontaneously into pairs. The rate of decay (88) is significant only if the \(E/E_\mathrm{{c}}\) is sufficiently large, with \(E_\mathrm{{c}}=1.3\times 10^{18}\mathrm \,V\,m^{-1}\). Electric fields strong enough for this effect to play a role appear in the surface layer of a bare quark star (e.g. Alcock et al. 1986; Usov 2004, ), which have been postulated as possible alternatives to neutron stars.
Splitting of degenerate Landau states The inclusion of the radiative correction to the Dirac Hamiltonian leads to splitting of the otherwise degenerate Landau levels, cf. (105). Spontaneous emission allows transitions between the split states with a given n: an electron in the state \(n,s=+1\) can jump to the state \(n,s=-1\) with emission of a photon with frequency (Parle 1987) \(\varDelta \omega _\mathrm{{B}}\approx (\alpha _\mathrm{{c}}/2\pi )\omega _\mathrm{{B}}\). The transition rate is very small, \(\approx (\alpha _\mathrm{{c}}^6/8(2\pi )^5)(B/B_\mathrm{{c}})^3m(p_n^2\varepsilon _n^2)\), which Parle (1987) estimated to be more than fifteen orders of magnitude smaller than the gyromagnetic transition rate from \(n=1,s=1\) to the ground state, \(n=0,s=-1\).
The frequency \(\varDelta \omega _\mathrm{{B}}\) of the transition between the split states appears in a recent discussion of linear waves in a quantum plasma (e.g., Ekman et al. 2019b), using the PKT approach discussed in Sect. 4. It is interesting to speculate whether waves associated with this splitting frequency might play a role, for example, in a pulsar magnetosphere. However, because the splitting only applies to excited states, \(n\ge 1\), whose lifetime is very short in a strong magnetic field, it seems unlikely that electrons could remain in an excited state for long enough for the effect to play a role.
7.5 Relativistic quantum calculations of linear and nonlinear response tensors
Of specific interest in plasma physics are specific forms for the linear and the nonlinear response tensors. Exact forms in the relativistic quantum case may be derived using QPD. These exact forms may be compared with the approximate forms derived using PKT, providing a check on the validity of the approximations made. The linear response tensor in QPD, \(\varPi ^{\mu \nu }(k)\), contains the same information as the dielectric tensor \(K_{ij}(\omega ,\mathbf{k})\), in the sense that given either one may construct the other.
Unpolarized electrons The linear response tensor in the both theunmagnetized and magnetized cases have relatively simple forms provided the electrons are unpolarized. These forms are given by (77) and (114), respectively. In both cases, the non-quantum resonance are modified by a quantum term: \(\omega -\mathbf{k}\cdot \mathbf{v}=0\rightarrow \omega -\mathbf{k}\cdot \mathbf{v}\pm \hbar (\omega ^2-|\mathbf{k}|^2c^2)/2mc^2\gamma \) in the unmagnetized case. In the magnetized case, the resonances are at \(\epsilon p_z-p_{z\pm }=0\), with \(p_{z\pm }\) given by (112) with (113). The dispersive part of the response in the magnetized case may be described by a single relativistic plasma dispersion function (RPDF) for a given electron distribution function. In the unmagnetized case, the response tensor may be evaluated in terms of a single RPDF provided the distribution is isotropic or 1D. No comparison of these QPD forms and the analogous forms derived using PKT has been made because the latter forms are not available.
Polarized electrons For polarized electrons examples of the linear response tensor derived using QPD are available for both the unmagnetized case (Melrose and Weise 2003) and the magnetized case (Melrose and Weise 2009). In both cases, specific spin operators that commute with the Dirac Hamiltonian are chosen. With existing forms of PKT based on FW transformations to separate the electron and positron contributions, no detailed comparison is possible because the distinction between the different spin operators in the Dirac theory is obscured by the FW transformation.
Nonlinear response tensors An advantage of the QPD method of calculation of nonlinear response tensors is that it builds in a natural symmetry. The quadratic response tensor, \(\varPi ^{\mu _0\mu _1\mu _2}(k_0,k_1,k_2)\) say, with signs chosen such that the 4-vectors satisfy \(k_0+k_1+k_2=0\), is calculated as a statistical average (over the electron gas) of the Feynman amplitude for two triangle diagrams that differ by interchange of two of the external lines. This response tensor is symmetric under permutations of the labels 0, 1, 2. In contrast, in the Vlasov approach, and analogously in PKT, the form of the quadratic response tensor is derived from the second-order terms in the expansion of the kinetic (e.g., Vlasov) equation, which involves derivatives of the form \(\mathbf{k}_1\cdot \partial /\partial \mathbf{p}\) and \(\mathbf{k}_2\cdot \partial /\partial \mathbf{p}\). The result is different depending on an arbitrary choice: the order in which the perturbations labeled 1 and 2 are included. No simplification occurs on symmetrizing over 1 and 2, which results in the sum of two different terms. Similarly, the symmetrized QPD form for the cubic nonlinear response tensor is simpler than the Vlasov form.
7.6 Quantum effects in plasma astrophysics
Quantum plasma effects are significant in astrophysical plasmas only under extreme conditions, such as superstrong fields and relativistic temperatures. For such effects to be of interest they need to have observational consequences for observed emission or play an important role in influencing how observed emission is generated. The following examples illustrate these points.
AGN Active galactic nuclei (AGN) emit high-energy radiation from hot plasma, in which pair creation can be important. Pairs in an unmagnetized plasma can be created by various processes with the most familiar being two-photon pair production, \(\gamma +\gamma \rightarrow e^++e^-\), which is related to Compton scattering by a crossing symmetry, and hence has a cross section that is simply related to the Thomson cross section, \(\sigma _T\). Assuming a spherical source of radius R, which can be estimated from the angular size of the source, this allows one to describe the importance of pair creation for a luminosity, L, through a compactness parameter, \(\ell =L\sigma _T/mc^3R\) (e.g., Done and Fabian 1989). For \(\ell \gg 1\), the plasma is dominated by pairs.
White dwarf stars It is sometimes suggested that various quantum plasma effects may be relevant to compact stars, including white dwarf stars. These stars are supported against their self-gravity by degenerate electrons pressure. However, although the interiors of these stars involve degenerate matter, the magnetospheres, from where nonthermal radiation can be emitted, are populated by non-degenerate plasma. Quantum plasma effects are relatively unimportant. A partial exception is a subclass of white dwarf stars, called cataclysmic variables (e.g., Mukai 2017), that are accreting from a companion, leading to X-ray cyclotron emission from accretion columns over the magnetic poles. The plasma in the source region is hot and strongly magnetized, and may be regarded as a quantum plasma. An interesting effect associated with CVs is that the columns can be optically thick to cyclotron emission, and the birefringence of the plasma implies that although the X mode is more strongly emitted than the O mode, it is also the more strongly absorbed, such that the escaping cyclotron radiation can be predominantly in the O mode.
Pair creation in pulsars One-photon pair creation plays a central role in the generation of the plasma that populates the source region for pulsar radio emission (Sturrock 1971). In the absence of screening by plasma, there is an extremely strong parallel electric field, \(E_\parallel \), due to the rapidly rotating magnetic field, and this \(E_\parallel \) accelerates charges to very high energy where they emit \(\gamma \)-rays due to curvature emission or Compton scattering of soft photons. One-photon pair creation by such \(\gamma \)-rays occurs provided that they exceed the threshold \(\hbar \omega \sin \theta >2mc^2\). On emission by an accelerated particle with Lorentz factor \(\gamma \), the \(\gamma \)-rays are confined to a cone \(\theta \lesssim 1/\gamma \). As a \(\gamma \)-ray propagates the angle \(\theta \) (between the ray path and the curved magnetic field line) increases systematically until the threshold is reached. It then triggers a pair cascade, which populates the magnetosphere with relativistic pairs. Although it was originally assumed that the pair creation operates in the synchrotron-like limit with \(n,n'\gg 1\) for both the electron and positron. However, as \(\theta \) increases and the threshold \(\hbar \omega \sin \theta =2mc^2\) is approached, two effects need to be considered: the square-root singularity at the threshold implies a significant probability that the electron and positron may be created in their ground states, \(n,n'=0\), or \(n+n'=1\), depending on the polarization of the photon. The other possibility is that the photon may evolve into a bound electron–positron pair, that is, into positronium. Which of these various possibilities occurs depends on \(B/B_\mathrm{{c}}\), with the latter two being likely for \(B/B_\mathrm{{c}}>0.1\)–0.2.
Pulsar plasma The plasma that results from the pair cascade, referred to as a “pulsar plasma”, consists of relativistic pairs propagating outward along the magnetic field lines. Due to the superstrong magnetic field, all particles quickly radiate away any perpendicular energy, so that all the particles in the pulsar plasma are in their ground Landau state, \(p_\perp =0\). Wave dispersion, at radio frequencies, in such a pulsar plasma is an exotic example of plasma dispersion theory (e.g., Rafat et al. 2019, ), but it may be treated classically. In this sense, pulsar plasma is not intrinsically quantum mechanical.
Photon splitting in pulsars Photon splitting (Adler 1971) is relevant to the propagation of \(\gamma \)-rays in a pulsar magnetosphere. Splitting of \(\gamma \)-rays with \(\hbar \omega >2mc^2\) may occur before they decay into a pair, thereby affecting the creation of the pair plasma (e.g., Baring and Harding 2001).
Magnetars Magnetars are pulsar-like objects with super-critical surface magnetic fields \(B\gtrsim B_\mathrm{{c}}\) (e.g., Duncan and Thompson 1992). Strong-field effects are expected to be important in magnetars, but definitive observational consequences are not obvious. One suggestion concerns the effect of the vacuum resonance, and its implications for the absorption coefficient for X-rays. The suggestion (e.g., Bulik and Miller 1997) was that the effect of this absorption may have observational consequences for soft gamma repeaters (SGRs) which are one subclass of magnetars.
It was also suggested that there should be no radio emission from magnetars due to the superstrong magnetic field (Baring and Harding 1998). However, subsequent discovery of radio emission from some magnetars required a reconsideration of this argument. Presumably, the source of the radio emission in these cases is at heights where the magnetic field has fallen to \(B\ll B_\mathrm{{c}}\).
Bare strange stars It is postulated that strange stars exist with the interior dominated by deconfined (i.e. free) strange quarks (Witten 1984; Alcock et al. 1986). The question arises as to what happens at the surface of “bare strange stars” that have no crust of ordinary nuclear matter. The electric field strength at the surface is estimated to be \(E\approx 5\times 10^{19}\mathrm \,,V\,m^{-1}\) (Alcock et al. 1986), which exceeds the Schwinger field \(E_\mathrm{{c}}=1.3\times 10^{18}\mathrm \,V\,m^{-1}\). The emission from bare strange stars is assumed to be dominated by pairs generated through the Schwinger effect. There is no observational confirmation of the existence of such bare strange stars.
7.7 Validity of the phase-space approach
The underlying idea in PKT is to represent the quantum mechanical system in a classical \(\mathbf{p},\mathbf{x}\) phase space. As already noted, no such representation is unique, and various alternative choices may be made. This implies an intrinsic uncertainty as to what is the most appropriate choice, and as to the implications of making different choices. There are three more serious concerns. The nonrelativistic version of PKT, discussed in Sect. 3, is founded on the Wigner function and the kinetic equation that it satisfies. The generalization to include the spin is less straight-forward, as discussed below, and the generalization to include relativistic effects introduces further difficulties, as discussed in Sect. 4. The relativistic case is based on Dirac’s equation, and in order to discuss an electron gas, the first step is to identify the electron contribution.
Neglect of positrons and pairs The FW transformation is applied to Dirac’s equation in an attempt to separate the electron component from the positron component, and to exclude virtual pairs. Neither objective can be achieved exactly. Approximations need to be made, including truncating an expansion in relativistic effects. The pseudo-distribution function \(f(\mathbf{p},\mathbf{x},t)\), for electrons, derived from the Wigner function in the case of Dirac’s theory, necessarily includes a contribution from virtual pairs. Qualitatively, this may be understood by considering a conventional interpretation of the Zitterbewegung: the instantaneous velocity of the electron is the speed of light, with the electron oscillating about a mean position that drifts with the classical velocity, and with the electron continuously emitting and absorbing virtual pairs. The pseudo-distribution function is an attempt to describe this is classical terms, and no such description can be exact. This adds uncertainty as to what the pseudo-distribution function actually describes.
In contrast, in quantum field theory, and in QPD, the occupation numbers of electrons and of positrons are well defined, and they must depend only on constants of the motion. The concept of a phase space is not relevant in this case: the occupation numbers do not include the influence of the wave fields on the particles. The wave-particle interactions are described by Feynman diagrams. This difference between PKT and QPD is analogous to the difference between two classical approaches used to derive the response of a plasma using kinetic theory: the Vlasov method and the forward-scattering method (cf. Melrose 2008, ).
Discrete energy levels in phase space The kinetic equation in PKT involves a derivative of the pseudo-distribution function with respect to \(\mathbf{p}\). This raises an obvious difficulty in the magnetized case, where \(p_\perp =(2neB\hbar )^{1/2}\) has only discrete values, corresponding to the Landau levels, \(n=0,1,\ldots \). The physically allowed states are cylinders in \(\mathbf{p}\)-space, centered on the \(p_z\)-axis and of radius \(p_\perp =(2neB\hbar )^{1/2}\). Allowed transitions involve jumps between these allowed states, and transition rates involve the difference between the occupation numbers in the two states. The derivative of the distribution function with respect to \(p_\perp \), e.g., in the linear response tensor, is replaced by differences between occupation numbers with different Landau quantum numbers. How the perpendicular component of \(\partial /\partial \mathbf{p}\) in the kinetic equation in PKT is to be interpreted is unclear. The momentum variable, \(\mathbf{p}\), in phase space is artificial, in the sense that it does not correspond to a physical momentum.
Quasi-classical spin space There are differences of opinion regarding the validity of the extension of phase space to include \(\mathbf{s}\), defined by (17). One view is that there is no loss of information, in the sense that that \(f(\mathbf{p},\mathbf{s},\mathbf{x},t)\) merely gives an alternative description of the quantum mechanical spin. This view is supported by showing that the same results may be derived using the Wigner function itself (e.g., Manfredi et al. 2019, ). A contrary view expressed by Zhang and Balescu (1988), Balescu and Zhang (1988): “the spin is a dynamical variable that has no classical analogue: it therefore cannot be described by a continuous variable, even in the quasi-classical limit.”
A more serious concern arises from the use of this formalism in the relativistic case. The extension of phase space to include dimensions defined by the spin vector \(\mathbf{s}\) is based on the Schrödinger–Pauli theory, where the inclusion of spin involves an extension of the Hilbert space by two dimensions, with the spin operator defined by the Pauli matrices in this additional 2D spin space. Thus the “spin operator” in the Schrödinger–Pauli theory is well defined, and there is no confusion as to what “spin operator” means. In contrast, in the Dirac theory, there is no unique spin operator, and any choice of spin operator must operate in the 4D Hilbert space defined by the Dirac matrices. None of the possible choices of spin operator reduces to the Schrödinger–Pauli theory, except in the nonrelativistic limit. The extension of phase space to include \(\mathbf{s}\) seems incompatible with Dirac’s theory, except in the nonrelativistic limit.
A critical comparison of PKT with exact theory is needed to explore the validity of including the spin through a classical model for the spin. This has not been done. Moreover, as emphasized above, there is no unique spin operator, and different choices of spin operator lead to different wavefunctions, especially in the relativistic case. The meaning of \(\mathbf{s}\) is then ill-defined. There is a favored spin operator (the parallel component of the magnetic moment operator) in the magnetized case, and any critical comparison needs to be made for this particular choice of spin operator.
In brief, despite the recent emphasis on the use of classical phase-space methods to treat quantum kinetic theory, there are unanswered questions relating to the validity of PKT, especially for magnetized plasma in general and in treating spin effects in particular.
References
S.L. Adler, Photon splitting and photon dispersion in a strong magnetic field. Ann. Phys. 67, 599–647 (1971). https://doi.org/10.1016/0003-4916(71)90154-0
C. Alcock, E. Farhi, A. Olinto, Strange stars. Astrophys. J. 310, 261 (1986). https://doi.org/10.1086/164679
P.A. Andreev, Exchange effects in Coulomb quantum plasmas: dispersion of waves in 2D and 3D quantum plasmas. Ann. Phys. 350, 198–210 (2014). https://doi.org/10.1016/j.aop.2014.07.019. arXiv:1403.6075
F.A. Asenjo, J. Zamanian, M. Marklund, G. Brodin, P. Johansson, Semi-relativistic effects in spin-1/2 quantum plasmas. New J. Phys. 14(7), 073042 (2012). https://doi.org/10.1088/1367-2630/14/7/073042. arXiv:1108.4781
R. Balescu, W.Y. Zhang, Kinetic equation, spin hydrodynamics and collisional depolarization rate in a spin-polarized plasma. J. Plasma Phys. 40(2), 215–234 (1988). https://doi.org/10.1017/S0022377800013234
M.G. Baring, A.K. Harding, Radio-quiet pulsars with ultrastrong magnetic fields. Astrophys. J. Lett. 507(1), L55–L58 (1998). https://doi.org/10.1086/311679. arXiv:astro-ph/9809115
M.G. Baring, A.K. Harding, Photon splitting and pair creation in highly magnetized pulsars. Astrophys. J. 547(2), 929–948 (2001). https://doi.org/10.1086/318390. arXiv:astro-ph/0010400
I. Bialynicki-Birula, P. Górnicki, J. Rafelski, Phase-space structure of the Dirac vacuum. Phys. Rev. D 44(6), 1825–1835 (1991). https://doi.org/10.1103/PhysRevD.44.1825
D. Bohm, A suggested interpretation of the quantum theory in terms of “Hidden” variables. I. Phys. Rev. 85(2), 166–179 (1952a). https://doi.org/10.1103/PhysRev.85.166
D. Bohm, A suggested interpretation of the quantum theory in terms of “Hidden” variables. II. Phys. Rev. 85(2), 180–193 (1952b). https://doi.org/10.1103/PhysRev.85.180
M. Bonitz, Quantum Kinetic Theory (Springer International Publishing, Berlin, 2015). https://doi.org/10.1007/978-3-319-24121-0
G. Brodin, R. Ekman, J. Zamanian, Quantum kinetic theories in degenerate plasmas. Plasma Phys. Control. Fusion 59(1), 014043 (2017). https://doi.org/10.1088/0741-3335/59/1/014043
T. Bulik, M.C. Miller, Spectral effects of the vacuum resonance in soft gamma-ray repeaters. Mon. Not. R. Astron. Soc. 288(3), 596–608 (1997). https://doi.org/10.1093/mnras/288.3.596. arXiv:astro-ph/9611021
S.C. Cowley, R.M. Kulsrud, E. Valeo, A kinetic equation for spin-polarized plasmas. Phys. Fluids 29(2), 430–441 (1986). https://doi.org/10.1063/1.865726
N. Crouseilles, P.A. Hervieux, G. Manfredi, Quantum hydrodynamic model for the nonlinear electron dynamics in thin metal films. Phys. Rev. B 78, 155412 (2008). 10.1103/PhysRevB.78.155412. https://link.aps.org/doi/10.1103/PhysRevB.78.155412
C. Done, A.C. Fabian, Pair Production in AGN. In: Osterbrock DE, Miller JS (eds) Active Galactic Nuclei, IAU Symposium, vol. 134 (Kluwer Academic Publishers, Dordrecht 1989), p. 194
R.C. Duncan, C. Thompson, Formation of very strongly magnetized neutron stars: implications for Gamma-Ray bursts. Astrophys. J. Lett. 392, L9 (1992). https://doi.org/10.1086/186413
R. Ekman, H. Al-Naseri, J. Zamanian, G. Brodin, Short-scale quantum kinetic theory including spin-orbit interactions (2019b) arXiv e-prints arXiv:1908.05131. arXiv:1908.05131
R. Ekman, J. Zamanian, G. Brodin, Exchange corrections in a low-temperature plasma. Phys. Rev. E 92(1), 013104 (2015). https://doi.org/10.1103/PhysRevE.92.013104. arXiv:1504.05339
R. Ekman, F.A. Asenjo, J. Zamanian, Relativistic kinetic equation for spin-1/2 particles in the long-scale-length approximation. Phys. Rev. E 96(2), 023207 (2017). https://doi.org/10.1103/PhysRevE.96.023207. arXiv:1702.00722
R. Ekman, H. Al-Naseri, J. Zamanian, G. Brodin, Relativistic kinetic theory for spin-1/2 particles: conservation laws, thermodynamics, and linear waves. Phys. Rev. E 100(2), 023201 (2019a). https://doi.org/10.1103/PhysRevE.100.023201
B. Eliasson, P.K. Shukla, Nonlinear quantum fluid equations for a finite temperature Fermi plasma. Phys. Scr. 78(2), 025503 (2008). https://doi.org/10.1088/0031-8949/78/02/025503
T. Erber, High-energy electromagnetic conversion processes in intense magnetic fields. Rev. Mod. Phys. 38, 626–659 (1966). https://doi.org/10.1103/RevModPhys.38.626
L.L. Foldy, S.A. Wouthuysen, On the dirac theory of spin 1/2 particles and its non-relativistic limit. Phys. Rev. 78(1), 29–36 (1950). https://doi.org/10.1103/PhysRev.78.29
J. Géhéniau, M. Demeur, Solutions singulières des équations de dirac, tenant compte d’un champ magnétique extérieur. Physica 17(1), 71–75 (1951). https://doi.org/10.1016/0031-8914(51)90038-9
Y.N. Gnedin, G.G. Pavlov, Y.A. Shibanov, Influence of polarization of vacuum in a magnetic field on the propagation of radiation in a plasma. Sov. J. Exp. Theor. Phys. Lett. 27, 305 (1978)
F. Haas, Quantum Plasmas: An Hydrodynamic Approach. Springer Series on Atomic, Optical, and Plasma Physics (Springer, New York, 2011)
F. Haas, G. Manfredi, M. Feix, Multistream model for quantum plasmas. Phys. Rev. E 62(2), 2763–2772 (2000). https://doi.org/10.1103/PhysRevE.62.2763
R. Hakim, J. Heyvaerts, Covariant Wigner function approach for relativistic quantum plasmas. Phys. Rev. A 18(3), 1250–1260 (1978). https://doi.org/10.1103/PhysRevA.18.1250
W. Heisenberg, H. Euler, Folgerungen aus der Diracschen Theorie des Positrons. Zeitschrift fur Physik 98(11–12), 714–732 (1936). https://doi.org/10.1007/BF01343663
H. Herold, Compton and Thomson scattering in strong magnetic fields. Phys. Rev. D 19(10), 2868–2875 (1979). https://doi.org/10.1103/PhysRevD.19.2868
H. Herold, H. Ruder, G. Wunner, Cyclotron emission in strongly magnetized plasmas. Astron. Astrophys. 115(1), 90–96 (1982)
J. Hurst, O. Morandi, G. Manfredi, P.A. Hervieux, Semiclassical vlasov and fluid models for an electron gas with spin effects. Eur. Phys. J. D 68(6), 176 (2014). https://doi.org/10.1140/epjd/e2014-50205-5
J. Hurst, P.A. Hervieux, G. Manfredi, Phase-space methods for the spin dynamics in condensed matter systems. Philos. Trans. R. Soc. Lond. Ser. A 375(2092), 20160199 (2017). https://doi.org/10.1098/rsta.2016.0199
S. Ichimaru, Phase transitions, interparticle correlations, and elementary processes in dense plasmas. Rev. Mod. Plasma Phys. 1(1), 6 (2017). https://doi.org/10.1007/s41614-017-0008-z
M.H. Johnson, B.A. Lippmann, Motion in a constant magnetic field. Phys. Rev. 76(6), 828–832 (1949). https://doi.org/10.1103/PhysRev.76.828
R. Lieu, W.I. Axford, Synchrotron radiation: an inverse Compton effect. Astrophys. J. 416, 700 (1993). https://doi.org/10.1086/173270
E. Lifshitz, L. Pitaevskii, Physical kinetics (Butterworth-Heinemann, Course of theoretical physics, 1981)
R. Loudon, One-dimensional hydrogen atom. Am. J. Phys. 27(9), 649–655 (1959). https://doi.org/10.1119/1.1934950
E. Madelung, Eine anschauliche Deutung der Gleichung von Schrödinger. Naturwissenschaften 14(45), 1004–1004 (1926). https://doi.org/10.1007/BF01504657
E. Madelung, Quantentheorie in hydrodynamischer Form. Zeitschrift fur Physik 40(3–4), 322–326 (1927). https://doi.org/10.1007/BF01400372
G. Manfredi, F. Haas, Self-consistent fluid model for a quantum electron gas. Phys. Rev. B 64(7), 075316 (2001). https://doi.org/10.1103/PhysRevB.64.075316. arXiv:cond-mat/0203394
G. Manfredi, P.A. Hervieux, J. Hurst, Phase-space modeling of solid-state plasmas. Rev. Mod. Plasma Phys. 3(1), 13 (2019). https://doi.org/10.1007/s41614-019-0034-0. arXiv:1906.08165
T.I. Mariya, P.A. Andreev, Exchange interaction effects on waves in magnetized quantum plasmas. Phys. Plasmas 22(2), 022128 (2015). https://doi.org/10.1063/1.4913435
D.B. Melrose, J.I. Weise, Optical activity in an isotropic gas of electrons with a preferred helicity. Phys. Rev. E 68, 046404 (2003). 10.1103/PhysRevE.68.046404. https://link.aps.org/doi/10.1103/PhysRevE.68.046404
D.B. Melrose, Quantum Plasmadynamics, Lecture Notes in Physics, vol 735 (Springer, Berlin, 2008). https://doi.org/10.1007/978-0-387-73903-8
D. Melrose, Quantum Plasmadynamics, Lecture Notes in Physics, vol 854 (Springer, Berlin, 2013). https://doi.org/10.1007/978-1-4614-4045-1
D.B. Melrose, S.J. Hardy, Quantum plasmadynamics: role of the electron self-energy and the vertex correction. J. Plasma Phys. 56(1), 95–105 (1996). https://doi.org/10.1017/S0022377800019127
D.B. Melrose, A. Mushtaq, Dispersion in a thermal plasma including arbitrary degeneracy and quantum recoil. Phys. Rev. E 82(5), 056402 (2010a). https://doi.org/10.1103/PhysRevE.82.056402
D.B. Melrose, A. Mushtaq, Plasma dispersion function for a Fermi–Dirac distribution. Phys. Plasmas 17(12), 122103 (2010b). https://doi.org/10.1063/1.3528272
D.B. Melrose, A.J. Parle, Quantum electrodynamics in strong magnetic fields III. Electron–photon interactions. Aust. J. Phys. 36, 799 (1983). https://doi.org/10.1071/PH830799
D.B. Melrose, K. Russell, Spin flips in cyclotron emission by an electron. J. Phys. A Math. Gen. 35(1), 135–150 (2002). https://doi.org/10.1088/0305-4470/35/1/311
D.B. Melrose, J.I. Weise, Response of a relativistic quantum magnetized electron gas. J. Phys. A Math. Gen. 42(34), 345502 (2009). https://doi.org/10.1088/1751-8113/42/34/345502
J.E. Moyal, Quantum mechanics as a statistical theory. Proc. Camb. Philos. Soc. 45(1), 99–124 (1949). https://doi.org/10.1017/S0305004100000487
K. Mukai, X-ray emissions from accreting white dwarfs: a review. Publ. Astron. Soc. Pac. 129(976), 062001 (2017). https://doi.org/10.1088/1538-3873/aa6736. arXiv:1703.06171
A. Mushtaq, D.B. Melrose, Quantum effects on the dispersion of ion acoustic waves. Phys. Plasmas 16(10), 102110 (2009). https://doi.org/10.1063/1.3253624
A.J. Parle, Quantum electrodynamics in strong magnetic fields. IV. Electron self-energy. Aust. J. Phys. (1987). https://doi.org/10.1071/PH870001
W. Pauli, Relativistic field theories of elementary particles. Rev. Mod. Phys. 13, 203–232 (1941). https://doi.org/10.1103/RevModPhys.13.203
M.Z. Rafat, D.B. Melrose, A. Mastrano, Wave dispersion in pulsar plasma. Part 1. Plasma rest frame. J. Plasma Phys. 85(3), 905850305 (2019). https://doi.org/10.1017/S0022377819000394. arXiv:1812.07121
V.I. Ritus, Radiative corrections in quantum electrodynamics with intense field and their analytical properties. Ann. Phys. 69(2), 555–582 (1972). https://doi.org/10.1016/0003-4916(72)90191-1
J. Schwinger, On quantum-electrodynamics and the magnetic moment of the electron. Phys. Rev. 73, 416–417 (1948). 10.1103/PhysRev.73.416. https://link.aps.org/doi/10.1103/PhysRev.73.416
J. Schwinger, On gauge invariance and vacuum polarization. Phys. Rev. 82(5), 664–679 (1951). https://doi.org/10.1103/PhysRev.82.664
M.O. Scully, K. Wódkiewicz, Spin quasi-distribution functions. Found. Phys. 24(1), 85–107 (1994). https://doi.org/10.1007/BF02053909
A.E. Shabad, V.V. Usov, Photon dispersion in a strong magnetic field with positronium formation-theory. Astrophys. Space Sci. 128(2), 377–409 (1986). https://doi.org/10.1007/BF00644586
P.K. Shukla, B. Eliasson, Colloquium: nonlinear collective interactions in quantum plasmas with degenerate electron fluids. Rev. Mod. Phys. 83(3), 885–906 (2011). https://doi.org/10.1103/RevModPhys.83.885
A.A. Sokolov, I.M. Ternov, Synchrotron Radiation (Pergamon Press, Oxford, 1968)
A.A Sokolov, I.M. Ternov, Radiation from Relativistic Electrons (AIP Press, Washington DC, 1986)
R.L. Stratonovich, On a method of calculating quantum distribution functions. Sov. Phys. Dokl 2, 416 (1957)
P.A. Sturrock, A model of pulsars. Astrophys. J. 164, 529 (1971). https://doi.org/10.1086/150865
T. Takabayasi, On the formulation of quantum mechanics associated with classical pictures. Prog. Theor. Phys. 8(2), 143–182 (1952). https://doi.org/10.1143/ptp/8.2.143
T. Takabayasi, Relativistic hydrodynamics of the Dirac matter—part I. General theory. Prog. Theor. Phys. Suppl. 4, 2–80 (1957). https://doi.org/10.1143/PTPS.4.2
V.I. Tatarskiĭ, Reviews of topical problems: the Wigner representation of quantum mechanics. Sov. Phys. Uspekhi 26(4), 311–327 (1983). https://doi.org/10.1070/PU1983v026n04ABEH004345
W.Y. Tsai, T. Erber, Photon pair creation in intense magnetic fields. Phys. Rev. D 10(2), 492–499 (1974). https://doi.org/10.1103/PhysRevD.10.492
N.L. Tsintsadze, L.N. Tsintsadze, Novel quantum kinetic equations of the fermi particles. EPL (Europhysics Letters) 88(3), 35001 (2009). https://doi.org/10.1209/0295-5075/88/35001
V.V. Usov, Electric fields at the quark surface of strange stars in the color-flavor locked phase. Phys. Rev. D 70(6), 067301 (2004). https://doi.org/10.1103/PhysRevD.70.067301. arXiv:astro-ph/0408217
D. Vasak, M. Gyulassy, H.T. Elze, Quantum transport theory for abelian plasmas. Ann. Phys. 173(2), 462–492 (1987). https://doi.org/10.1016/0003-4916(87)90169-2
O. von Roos, Boltzmann–Vlasov equation for a quantum plasma. Phys. Rev. 119(4), 1174–1179 (1960). https://doi.org/10.1103/PhysRev.119.1174
E. Wigner, On the quantum correction for thermodynamic equilibrium. Phys. Rev. 40(5), 749–759 (1932). https://doi.org/10.1103/PhysRev.40.749
E. Witten, Cosmic separation of phases. Phys. Rev. D 30(2), 272–285 (1984). https://doi.org/10.1103/PhysRevD.30.272
J. Zamanian, M. Marklund, G. Brodin, Scalar quantum kinetic theory for spin-1/2 particles: mean field theory. New J. Phys. 12(4), 043019 (2010a). https://doi.org/10.1088/1367-2630/12/4/043019. arXiv:0910.5165
J. Zamanian, M. Stefan, M. Marklund, G. Brodin, From extended phase space dynamics to fluid theory. Phys. Plasmas 17(10), 102109 (2010b). https://doi.org/10.1063/1.3496053. arXiv:1006.4317
J. Zamanian, M. Marklund, G. Brodin, On the contribution of exchange interactions to the Vlasov equation. Eur. Phys. J. D 69(1), 25 (2015). https://doi.org/10.1140/epjd/e2014-50158-7. arXiv:1402.7240
W.Y. Zhang, R. Balescu, Statistical mechanics of a spin-polarized plasma. J. Plasma Phys. 40(2), 199–213 (1988). https://doi.org/10.1017/S0022377800013222
Acknowledgements
I thank Victor Demcsak, Alpha Mastrano and Kai Yang for helpful comments on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is an extended version of a planned Invited Tutorial Review talk on this topic at the APPC-14 meeting at Kuching in November 2019. The author was unable to attend that meeting to present the talk.
Rights and permissions
About this article
Cite this article
Melrose, D.B. Quantum kinetic theory for unmagnetized and magnetized plasmas. Rev. Mod. Plasma Phys. 4, 8 (2020). https://doi.org/10.1007/s41614-020-00044-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41614-020-00044-8