1 Introduction

To understand the nature of neutron-rich nucleonic matter has been a major scientific goal in both nuclear physics and astrophysics. The density dependence of nuclear symmetry energy \(E_{{\text {sym}}}(\rho )\,\)has been a major uncertain part of the equation of state (EOS) of neutron-rich matter, especially at high densities, see, e.g., collections in Ref. [1]. Reliable knowledge about the \(E_{{\text {sym}}}(\rho )\,\)has significant ramifications in answering many interesting questions regarding the structure of rare isotopes and neutron stars, dynamics of heavy-ion collisions and supernova explosions as well as the frequency and strain amplitude of gravitational waves from deformed pulsars and/or cosmic collisions involving neutron stars. During the last two decades, significant efforts have been devoted to exploring the \(E_{{\text {sym}}}(\rho )\,\)using both terrestrial laboratory experiments [2,3,4,5,6,7,8,9,10,11,12] and astrophysical observations [13,14,15,16,17,18,19,20]. Extensive surveys of the extracted constraints on the \(E_{{\text {sym}}}(\rho )\,\)around the saturation density \(\rho _0\) indicate that the central values of the \(E_{{\text {sym}}}(\rho _0)\) and its slope \( L=\left[ 3 \rho (\partial E_{{\text {sym}}}/\partial \rho \right) ]_{\rho _0} \) scatter around 31.6 and 58.9 MeV, respectively [14, 21, 22]. At densities away from \(\rho _0\), however, the \(E_{{\text {sym}}}(\rho )\,\)remains rather unconstrained, especially at supra-saturation densities [12].

Interestingly, recent progresses in another seemingly different field may provide additional information about the density dependence of nuclear symmetry energy. Indeed, theoretical and experimental studies of cold atoms have made impressive progress in recent years, see, e.g., Refs. [23,24,25,26] for recent reviews, providing reliable information about the universal EOS (\(E_{{\text {UG}}}\)) of unitary gas (UG) interacting via pairwise s-waves with infinite scattering length but zero effective range. The universal \(E_{{\text {UG}}}\) constrains stringently the EOS of pure neutron matter (PNM) at sub-saturation densities, thus provides possibly additional constraints on the nuclear symmetry energy. In fact, it was recently conjectured that the \(E_{{\text {UG}}}\) provides the lower boundary of the EOS of PNM (\(E_{{\text {PNM}}}\)) [27, 28]. Moreover, using a set of known parameters of symmetric nuclear matter (SNM), and taking zero as an upper bound on the curvature \(K_{{\text {sym}}}=\left[ 9\rho ^2(\partial ^2E_{{\text {sym}}}(\rho )/\partial \rho ^2)\right] _{\rho _0}\) of \(E_{{\text {sym}}}(\rho )\,\)at \(\rho _0\), the authors of Refs. [27, 28] obtained a region of \(E_{{\text {sym}}}(\rho _0)\)-L space that is inconsistent with the unitary gas constraints, excluding many \(E_{{\text {sym}}}(\rho )\,\)functionals currently actively used in both nuclear physics and astrophysics.

Our original purposes were to examine several issues not clearly addressed in version-1 of Refs. [27, 28]. We notice that some of these issues are now discussed in more detail in its revised version. Nevertheless, it is still useful to provide our results and opinions on some of these issues. The derivation of the excluded region in \(E_{{\text {sym}}}(\rho _0)\)-L space by Refs. [27, 28] relies on several assumptions [29]: The most importance of which is the underlying conjecture that \(E_{{\text {PNM}}}(\rho )\ge E_{{\text {UG}}}(\rho )\) where \(E_{{\text {UG}}}(\rho )=\xi E_{\text{F}}(\rho )\) with \(\xi \) being the Bertsch parameter [23,24,25,26] and \(E_{\text{F}}\propto (\rho /\rho _0)^{2/3}\) is the energy of a noninteracting nonrelativistic degenerate Fermi gas of neutrons. This conjecture is not quite the same as stating that PNM has a greater energy than the UG at all densities, since the UG is experimentally accessible only at low densities. This conjecture merely employs an algebraic expression motivated by the result that apparently the low-density neutron gas has a higher energy than the UG, and by the inference that the repulsive nature of the three nucleon (NNN) interaction coupled with the finite values of the range and scattering length of the two-body (NN) s-wave interaction will ensure that the energy of PNM remains above this algebraic expression at higher densities. A further assumption is that possibly attractive higher-order NN interactions (p-wave, d-wave, etc.) are not important relative to the repulsive character of three- and higher-body interactions. Additionally, neutrons are assumed to remain non-relativistic in the density range considered. Given the important ramifications of the findings in Refs. [27, 28], we are motivated to critically examine them adopting the same assumptions. We include the third-order terms in density characterized by the skewness coefficients \(J_0=27\rho _0^3\partial ^3E_0(\rho )/\partial \rho ^3|_{\rho =\rho _0} \) and \(J_{{\text {sym}}}=27\rho _0^3\partial ^3E_{{\text {sym}}}(\rho )/\partial \rho ^3|_{\rho =\rho _0}\) in expanding the \(E_{{\text {0}}}(\rho )\) and \(E_{{\text {sym}}}(\rho )\), respectively. Particularly, we carefully examine the uncertainties of the curvature \(K_{{\text {sym}}}\) of the symmetry energy and the skewness coefficients \(J_0\) and \(J_{{\text {sym}}}\), taking into account energy density functionals that are consistent with the PNM EOS derived from microscopic calculations, and examine the effects of those uncertainties on the region of \(E_{{\text {sym}}}(\rho _0)\)-L space excluded by the unitary gas constraints.

While Skyrme models consistent with microscopic PNM calculations tend to give \(K_{{\text {sym}}}\) in the range \(-100\) to \(-\,200\) MeV [33, 38], relativistic mean field (RMF) models consistent with microscopic PNM calculations can give positive values of \(K_{{\text {sym}}}\) [32, 33], reflecting a difference in the form of these two classes of energy density functionals. Indeed, some reputable nonrelativistic and relativistic energy density functionals in the literature, see, e.g., reviews in Refs. [30,31,32, 34], predict positive \(K_{{\text {sym}}}\) values and meet all existing constraints including the EOS of PNM within their known uncertain ranges. For example, the TM2 RMF interaction has \(K_{{\text {sym}}}\) = 50 MeV and passes the PNM test of Ref. [32]. To our best knowledge, while the majority of existing models predict negative values for \(K_{{\text {sym}}}\), there is no fundamental physics principle excluding positive \(K_{{\text {sym}}}\) values. The current situation clearly calls for more studies on the \(K_{{\text {sym}}}\) especially its experimental constraints. Hopefully, ongoing experiments at several laboratories [35] to extract the isospin dependence of nuclear incompressibility and subsequently the \(K_{{\text {sym}}}\) from giant resonances of neutron-rich nuclei will help settle the issue in the near future. Interestingly, very recently by analyzing comprehensively the relative elliptical flows of neutrons and protons measured by the ASY-EOS and the FOPI-LAND collaborations at GSI using a quantum molecular dynamics (QMD) model [36], the extracted values for the slope and curvature parameters are \(L=59\pm 24\) MeV and \(K_{{\text {sym}}}=88\pm 372\) MeV at the \(1\sigma \) confidence level. After considering uncertainties of other model parameters including the incompressibility of SNM, neutron–proton effective mass splitting (related to the momentum dependence of the symmetry potential), Pauli blocking, and in-medium nucleon-nucleon cross sections, it was concluded that \(L = 59 \pm 24 ({\text {exp}}) \pm 16({\text {th}}) \pm 10 ({\text {sys}})\) MeV and \(K_{{\text {sym}}} = 0 \pm 370({\text {exp}}) \pm 220({\text {th}}) \pm 150({\text {sys}})\) MeV. To our best knowledge, the latter represents the latest and most accurate constraint on \(K_{{\text {sym}}}\).

2 The lower boundary of nuclear symmetry energy constrained by the universal EOS of unitary Fermi gas

Within the parabolic approximation for the EOS of isospin asymmetric nuclear matter (ANM) in terms of the energy per nucleon E, i.e., \( E(\rho ,\delta )=E_0(\rho )+E_{{\text {sym}}}(\rho )\delta ^{2} +{\mathcal {O}}(\delta ^4), \) the symmetry energy \(E_{{\text {sym}}}(\rho )= 2^{-1}[\partial ^{2}E(\rho ,\delta )/\partial \delta ^{2}]_{\delta =0}\) can be approximated by

$$ E_{{\text {sym}}}(\mu )\approx E_{{\text {PNM}}}(\mu )-E_{{\text {0}}}(\mu ), $$
(1)

where \(\mu =\rho /\rho _0\) is the reduced density and \(\delta =(\rho _{{\text{n}}}-\rho _{{\text{p}}})/\rho \) is the isospin asymmetry of ANM. Using the conjecture \(E_{{\text {PNM}}}(\rho )\ge E_{{\text {UG}}}(\rho )\) [27, 28] and the EOS of unitary gas

$$ E_{{\text {UG}}}(\mu )=\frac{3\hbar ^2k_{{\text {F}}}^2}{10m_{{{\text {n}}}}}\xi \equiv E^0_{{\text {UG}}}\mu ^{2/3}, $$
(2)

where \(k_{{\text {F}}}\) is the neutron Fermi momentum, the lower boundary of symmetry energy can be obtained from

$$ E_{{\text {sym}}}(\mu )\ge E_{{\text {UG}}}(\mu )-E_{{\text {0}}}(\mu )=E^0_{{\text {UG}}}\mu ^{2/3}-E_{{\text {0}}}(\mu ). $$
(3)

It is necessary to caution that the above lower boundary of \(E_{{\text {sym}}}(\mu )\) is estimated based on the conjecture \(E_{{\text {PNM}}}(\rho )\ge E_{{\text {UG}}}(\rho )\) and the assumption that \(\xi \) is a constant in the density range we study. As emphasized in Refs. [27, 28], the conjecture is empirical in nature. While there are strong supports for the conjecture by comparing the EOSs of PNM calculated from various microscopic many-body theories with the \(E_{{\text {UG}}}(\mu )\) using a constant \(\xi \approx 0.37\) (see Fig. 1 of Refs. [27, 28] and Fig. 2 of Ref. [37]) up to about \(\rho _0\), the rigorous condition for unitarity is expected to be reached in PNM only at very low densities. Although one cannot prove the validity of the conjecture at high densities, strong physical arguments were made to justify and use it up to about \(1.5\rho _0\) in Refs. [27, 28]. Thus, the results of our study should be understood with the caveat that they are obtained under the above reasonable but not rigorously proven conjecture and assumptions. Nevertheless, they are useful for comparing with the results of Refs. [27, 28] obtained using the same assumptions.

The EOS of SNM around \(\rho _0\) can be expanded to the third order in density as

$$ E_{{\text {0}}}(\mu )=E_0(\rho _0)+\frac{K_0}{18}(\mu -1)^2 +\frac{J_0}{162}(\mu -1)^3+{\mathcal {O}}[(\mu -1)^4] $$
(4)

in terms of the incompressibility \(K_0\) and skewness \(J_0\). At the saturation point of SNM, we adopt \(E_0(\rho _0) = -\,15.9\) MeV and \(\rho _0 = 0.164\) fm\(^{-3}\) [38]. The lower boundary of \(E_{{\text {sym}}}(\rho )\,\)thus depends on the values of \(K_0\), \(J_0\) and \(\xi \).

The incompressibility \(K_0\) of SNM has been extensively investigated [34, 39], and the most widely used values are \(K_0 = 240\pm 20\) MeV [40, 41] or \(230\pm 40\) MeV [42]. However, the skewness coefficient \(J_0\) is still poorly known [43,44,45,46,47,48]. In Fig. 1a, we show \(K_0\) and \(J_0\) from 274 parameterizations of the Skyrme and RMF models that pass the PNM tests of Dutra et al. [31, 32] and satisfy \(K_0 = 230\pm 40\) MeV. The spread in values for \(J_0\) is very large, covering the range \(\approx -800\,<\,J_0\,<\,400\) MeV.

Fig. 1
figure 1

(Color online) The skewness parameter \(J_0\) versus the incompressibility \(K_0\) for symmetric matter (a) and the total curvature parameter \(K_{\text {n}} = K_0 + K_{\text {sym}}\) versus the total skewness parameter \(J_{\text {n}} = J_0 + J_{\text {sym}}\) (b) for all 173 Skyrme and 101 RMF models examined by Dutra et al. [31, 32] which pass their pure neutron matter constraints and satisfy \(190\,<\,K_0\,<\,270\) MeV

Full size image

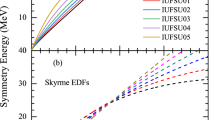
As reviewed recently in Refs. [26,27,28], currently the best estimate for the Bertsch parameter \(\xi \) from lattice Monte Carlo studies is \(\xi = 0.372(5)\) consistent with the most accurate experimental value of \(\xi = 0.376(4)\). While its values from various other models and experiments have scattered between 0.279 and 0.449(9) within the last decade, it appears that it now has converged to \(\xi = 0.37\pm 0.005\) which we adopt in this work. Shown in Fig. 2 with the red dashed lines is the variation of \(E_{{\text {sym}}}(\rho )\,\)with \(\xi = 0.37\pm 0.005\), \(J_0 = 0\), and \(K=230\) MeV. Effects of varying the \(\xi \) value are very small within the range considered.

Secondly, effects of the skewness parameter are shown by varying the value of \(J_0\) between \(-\,800\) and 400 MeV, the range covered by the models plotted in Fig. 1a. Although the range is very large, it translates into a range of uncertainty for \(E_{{\text {sym}}}(\rho )\,\)that is equivalent to the range of uncertainty in \(K_0\) (190 < K 0 < 270 MeV). This is easy to understand as the expansion of SNM’s EOS converges quickly around the normal density by design (the \(J_0\) contribution of \(J_0/162\) is a factor of 9 less than the \(K_0/18\) term).

Considering the uncertainties of all relevant parameters involved, the most conservative lower boundary of \(E_{{\text {sym}}}(\rho )\,\)shown as the shadowed region in Fig. 2 is obtained by using \( \xi =0.37\), \(\rho _0=0.157\) fm\(^{-3}\), \(E_0(\rho _0)=-\,15.5\) MeV, and \(K_0=270\) MeV; for \(\mu \le 1\), \(J_0=-800\) MeV and for \(\mu >1\), \(J_0=400\) MeV. Overall, our observations and results are consistent with the findings in Refs. [27, 28].

Fig. 2
figure 2

(Color online) The lower boundary of symmetry energy as a function of density for different skewness coefficients \(J_0 = 400\), 0, \(-\,400\), and \(-\,800\) MeV. The red dashed region represents the variation of \(E_{{\text {sym}}}(\mu )\) with \(K_0 = 230\) MeV and \(J_0 = 0\) MeV by adopting \(\xi = 0.37\pm 0.005\). The shadowed region shows the excluded region after considering the uncertainties of \(\xi \), K and \(J_0\)

Full size image

3 Constraining the \(\varvec{E}_{{\textbf{sym}}}({\boldsymbol{\rho}}_{\textbf{0}})\) versus L boundary

The symmetry energy \(E_{{\text {sym}}}(\mu )\) can be expanded around \(\rho _0\) to third order in density as

$$\begin{aligned} E_{{\text {sym}}}(\mu )=&\,E_{{\text {sym}}}(\rho _0)+\frac{L}{3}(\mu -1)+\frac{K_{{\text {sym}}}}{18}(\mu -1)^2 \\&+\frac{J_{{\text {sym}}}}{162}[(\mu -1)^3]+{\mathcal {O}}[(\mu -1)^4] \end{aligned}$$
(5)

in terms of its magnitude \(E_{{\text {sym}}}(\rho _0)\), slope L, curvature \(K_{{\text {sym}}}\), and skewness \(J_{{\text {sym}}}\) at \(\rho _0\). Inserting the above equation into Eq. (3), the lower boundary of \(E_{{\text {sym}}}(\rho _0)\) can be expressed as

$$\begin{aligned} E_{{\text {sym}}}(\rho _0)\ge&\, E_{{\text {UG}}}^0\mu ^{2/3} -E_0(\rho _0)-\frac{L}{3}(\mu -1)-\frac{K_{\text{n}}}{18}(\mu -1)^2 \\&-\frac{J_{\text{n}}}{162}(\mu -1)^3, \end{aligned}$$
(6)

where \(K_{\text{n}}=K_{{\text {sym}}}+K_0\) and \(J_{\text{n}}=J_{{\text {sym}}}+J_0\). Taking the derivative of the above equation with respect to density on both sides, one can readily get an expression for the lower boundary of L,

$$ L=\frac{2E_{{\text {UG}}}^0}{\mu ^{1/3}}-\frac{K_{\text{n}}}{3}(\mu -1)-\frac{J_{\text{n}}}{18}(\mu -1)^2. $$
(7)

Then, putting the above expression back to Eq. (6) the latter can be rewritten as

$$\begin{aligned} E_{{\text {sym}}}(\rho _0)\ge&\frac{E_{{\text {UG}}}^0}{3\mu ^{1/3}}(\mu +2)+\frac{K_{\text{n}}}{18}(\mu -1)^2 \\&+\frac{J_{\text{n}}}{81}(\mu -1)^3-E_0(\rho _0). \end{aligned}$$
(8)

These two equations reveal the correlation between the \(E_{{\text {sym}}}(\rho _0)\) and L along their lower boundaries through the arbitrary density \(\mu \). Setting \(J_{\text{n}}=0\), the Eqs. (7) and (8) reduce exactly to the parametric equations of \(E_{{\text {sym}}}(\rho _0)\) and L derived slightly differently in version-1 of Refs. [27, 28]. We note that the quantities that determine the boundary of allowed values of \(E_{\text {sym}}(\rho _0)\) and L are the total curvature parameter \(K_{\text{n}} \) and total skewness parameter \(J_{\text{n}}\) also emphasized in version-2 of Refs. [27, 28].

While having noted that \(K_{{\text {sym}}}\) is experimentally and theoretically poorly known, the \(E_{{\text {sym}}}(\rho _0)\) versus L correlation along their boundaries was obtained in Refs. [27, 28] by setting \(K_{{\text {sym}}}=0\) based on the prediction of a chiral effective field theory. It was found that the resulting correlation excludes many of the currently actively used models for \(E_{{\text {sym}}}(\rho )\,\). We reexamine this correlation by varying the \(\xi \), \(J_{\text{n}}\), and \(K_{{\text {sym}}}\) within their known uncertain ranges. Again, the value of \(\xi \) is now well settled around \(0.37\pm 0.005\). Taking \(K_{{\text {sym}}}=0\), \(J_{\text {n}}=0\) and \(K_0=230\) MeV, the two red dashed lines obtained with \(\xi = 0.37\pm 0.005\) in both (a) and (b) of Fig. 3 show the resulting lower boundaries of the \(E_{{\text {sym}}}(\rho _0)\) versus L correlation.

The skewness coefficients \(J_0\) and \(J_{{\text {sym}}}\) in \(J_{\text{n}}\) are both poorly known. We show in Fig. 1b values of \(J_{\text{n}}\) against \(K_{\text{n}}\) for the 275 Skyrme and RMF parametrizations. \(J_{\text{n}}\) varies approximately in the range \(-\,500\) MeV \(\le\, J_{\text{n}}\, \le\, 1000\) MeV. To our best knowledge, there is no experimental constraint available on this quantity. \(K_{\text{n}}\) varies approximately in the range \(-\,150\) MeV \(\le\, K_{\text{n}}\, \le 370\) MeV. Most of this comes from the big uncertainties in determining the value of \(K_{{\text {sym}}}\), which are discussed in detail in Ref. [12]. This is partially because the \(K_{{\text {sym}}}\) depends on not only L but also its derivative \(({\text {d}}L/ {\text {d}}\rho )_{\rho _0}\) by definition. Microscopically, it depends on not only the nucleon isoscalar effective mass \(m^*_0\) and neutron–proton effective mass splitting \(m_{\text{n}}^*-m_{\text{p}}^*\) but also their momentum and density dependences that are all essentially completely unknown [12]. The latest calculations within Skyrme Hartree–Fock and/or relativistic mean field models indicate that \(-\,400\, \le\, K_{{\text {sym}}}\,\le\, 100\) MeV [30,31,32, 34].

The results using \(K_{{\text {sym}}}=0\), \(K_0=230\) MeV (so \(K_{\text{n}} =\) 230 MeV), and \(\xi =0.37\) for different values for \(J_{\text{n}}\) are shown in Fig. 3a. It is seen that L becomes larger as \(J_0\) decreases and that the upper boundary of the allowed region will correspond to the lower limit of \(J_{\text{n}}\). At \(E_{{\text {sym}}}(\rho _0) = 40\) MeV, for example, the increase is only about \(20\%\).

By setting \(K_{{\text {sym}}}= -\,200, -\,100\), 0, and 100 MeV with \(K_0=230\) MeV (corresponding to \(K_{\text{n}}=30, 130, 230\), and 330 MeV), we can illustrate effects of the \(K_{{\text {sym}}}\) on the lower boundary of \(E_{{\text {sym}}}(\rho _0)\) versus L correlation in Fig. 3b. It is seen that the \(K_{{\text {sym}}}\) affects the results significantly; as \(K_{\text {sym}}\) (and hence \(K_{\text{n}}\)) increases, L increases, and the upper boundary of the allowed region will correspond to the largest value of \(K_{\text {sym}}\) (and hence \(K_{\text{n}}\)). The overall uncertainty in \(K_{\text{n}}\) leads to a variation of the upper boundary of the allowed region that is about twice caused by the uncertainty in \(J_{\text{n}}\). We note that many of the models allowed by \(K_{{\text {sym}}}= 0\) MeV would be excluded by using \(K_{{\text {sym}}}=-\,200\) MeV.

Fig. 3
figure 3

(Color online) The lower boundaries of symmetry energy parameters based on different parameter values. The effects of the uncertainty in \(J_{\text{n}}\) (a) and \(K_{{\text {sym}}}\) (b) are demonstrated by the blue lines, holding \(K_{\text{n}}=230\) MeV in a and \(J_{\text {n}}=0\) MeV in b. The red dashed region represents the deviation of \(E_{{\text {sym}}}\) with \(J_0 = 0\) MeV by adopting \(\xi = 0.37\pm 0.005\). The shadowed region shows the excluded region after considering all the uncertainties of \(\rho _0\), \(E_{0}(\rho _0)\), \(\xi \), \(K_0\), \(J_{\text{n}}\), and \(K_{{\text {sym}}}(\rho _0)\)

Full size image

Adopting the following values for the five parameters after taking into account the full range presented by the 275 Skyrme and RMF parametrizations, i.e.,

$$\begin{aligned} &\rho _0= 0.157\, {{\text {fm}}}^{-3}, \, E_{0}(\rho _0)=-\,15.5 \,{{\text {MeV}}}, \, \xi =0.37, \\ &K_{\text{n}}= 370\, {{\text {MeV}}},\,J_{\text{n}}=-\,500 \,{{\text {MeV}}}, \end{aligned}$$

a lower boundary excluding only the shadowed region in Fig. 3 is obtained. It is seen that only the TMA and NL\(\rho \delta \), NL3 and LS220 may be excluded, while the STOS, TM1, NL\(\rho \), LS220, and KVR, which have been surely excluded previously in Refs. [27, 28], may be allowed. This is mainly a result in extending the upper bound in the uncertainty region of \(K_{\text {sym}}\), since the additional uncertainty in \(J_{\text{n}}\) moves the excluded region to the right (because \(J_{\text{n}}\, \gtrsim \,0\)). As pointed out in the final analyses of Refs. [27, 28], we agree that strong empirical correlations among \(J_{\text {sym}}, K_{{\text {sym}}}\), and L exist. These correlations can be used to refine the \(E_{{\text {sym}}}(\rho _0)\)-L constraint shown in Fig. 3.

It is well known that the detailed density dependence of nuclear symmetry energy \(E_{{\text {sym}}}(\rho )\,\)contains many interesting and some unknown physics. It is probably not surprising that the estimation of the correlation between its zeroth-order and first-order density expansion coefficients \(E_{{\text {sym}}}(\rho _0)\) and L depends on what we assume about the immediate next high-order term characterized by the curvature \(K_{{\text {sym}}}\) at \(\rho _0\).

4 Concluding remarks

The universal EOS \(E_{{\text {UG}}}\) of the unitary Fermi gas was conjectured in Refs. [27, 28] to provide the lower boundary of the EOS \(E_{{\text {PNM}}}\) of PNM, and thus a constraint on nuclear symmetry energy. Although unproven, the conjecture has strong empirical supports, and its implications are important enough that they should be examined rigorously. We found that the \(E_{{\text {UG}}}\) does provide a useful lower boundary of nuclear symmetry energy. Moreover, this boundary is essentially not affected by the known uncertainty in the skewness coefficient \(J_0\) of SNM. However, it does not tightly constrain the correlation between the magnitude \(E_{0}(\rho _0)\) and slope L unless the curvature \(K_{{\text {sym}}}\) of the \(E_{{\text {sym}}}(\rho )\,\)at \(\rho _0\) and the skewness parameters \(J_0\) and \(J_{{\text {sym}}}\) are better known. Of these, \(K_{{\text {sym}}}\) is the more important quantity, its uncertainty affecting the lower boundary of \(E_{{\text {sym}}}(\rho )\,\)by up to twice as much as the uncertainty in \(J_{\text {n}}\). Most of the previously excluded \(E_{{\text {sym}}}(\rho )\,\)functionals by the universal EOS of unitary Fermi gas assuming \(K_{{\text {sym}}}=0\) may not be excluded considering the currently known big uncertainties of the \(K_{{\text {sym}}}(\rho _0)\).

For many purposes in both nuclear physics and astrophysics, it is necessary to map out precisely both the \(E_{{\text {sym}}}(\rho )\,\)and the EOS \(E_{0}(\rho )\) of SNM in a broad density range. Near the saturation density \(\rho _0\), this requires accurate knowledge of the \(K_{{\text {sym}}}\) and \(J_0\) besides the \(E_{0}(\rho _0)\), L, and \(K_0\). To this end, it is interesting to mention briefly quantities that are sensitive to the higher-order EOS parameters and current efforts to determine them. For example, the skewness coefficient \(J_0\) characterizes the high-density behavior of \(E_{0}(\rho )\), and it has been found to affect significantly the maximum mass of neutron stars [48]. Moreover, at the crust-core transition point where the incompressibility of neutron star matter at \(\beta \)-equilibrium vanishes, the value of \(J_0\) influences significantly the exact location of the transition point [49]. Thus, astrophysical observations of neutron stars can potentially constrain the \(J_0\) albeit probably not before other EOS parameters are well determined. On the other hand, in terrestrial laboratory experiments, there have been continued efforts to determine the \(K_{{\text {sym}}}\) [34]. One outstanding example is the measurement of the isospin dependence of nuclear incompressibility \(K(\delta )\approx K_0+K_{\tau }\delta ^2+{\mathcal {O}}(\delta ^4)\) where \(K_{\tau }=K_{{\text {sym}}}-6L-J_0L/K_0\) using giant resonances of neutron-rich nuclei [50, 51]. While the current estimate of \(K_{\tau }\approx -550\pm 100\) MeV [34] from analyzing many different kinds of terrestrial experiments is still too rough to constrain tightly the individual values of \(J_0\) and \(K_{{\text {sym}}} \), new experiments with more neutron-rich beams have the promise of improving significantly the accuracy of the measured \(K_{\tau }\) [35]. Thus, we are hopeful that not only the zeroth- and first-order parameters \(K_0\), \(E_{{\text {sym}}}(\rho _0)\), and L but also high-order coefficients \(J_0\) and \(K_{{\text {sym}}}\) can be pinned down in the near future by combining new analyses of upcoming astrophysical observations and terrestrial experiments.