1 Introduction

Predicting risks associated with drought requires information from a drought monitoring system that provides the onset, progress, severity, and spatial extent of drought. Such information, when available, could assist in drought contingency plans for mitigating potential impacts. Drought monitoring is usually performed using drought severity indices that are based on other meteorological variables such as temperature, evapotranspiration, and wind speed [1]. Owing to its complexity drought is one of the least understood natural hazards [2]. Drought and its impacts are variable at different spatial and temporal scale, therefore; it is difficult to have a standard definition of drought that fits for all circumstances.

Many indices for different categories of drought conditions have been developed in the past. Three primary indices that are most commonly in use include the Palmer Drought Severity Index (PDSI) [3], Standard Precipitation Index (SPI) [4], and Standard Precipitation Evaporation Index (SPEI) [5]. PDSI was the first drought indicator used for comprehensive assessment of drought and is widely used in the United States. PDSI generally reflects long-term drought, with the time span of 9–11 months [6] and has been extensively used when directing drought-relief funding and programs [7]. A long-term (at least 20–30 years) monthly precipitation values are required to compute SPI index [8]. The SPI can be calculated at a monthly to annual scale which is useful in short or long-term applications [4]. The SPEI is a recently developed multi-scalar drought index that is based on climatic water balance, which subtracts water demand (potential evapotranspiration: PET) from the water supply (total precipitation) in water balance equation.

The SPEI is robust and generally improved results over SPI [5, 9, 10]. The 6-month SPEI can characterize rainfall amounts during the preceding half-year that is useful in describing shallow soil moisture availability to crops and forage grasses. While 12-month and 24-month SPEI maps are mostly used for characterizing sufficiency of precipitation for recharge of reservoirs, some aquifers, and deep soil moisture [11]. Tree roots frequently penetrate lower soil horizons [12]. In this regard, soil moisture that is available to trees could be characterized by climate maps of 12-month SPEI.

Spatial interpolation techniques are widely used for rainfall [13], potential evapotranspiration [14], geophysical data [15], temperature [16], ozone [17], and drought indices: PDSI [18], SPI [19, 20] and SPEI [20]. Because SPEI is multi-scalar and is sensitive to both precipitation and atmospheric evaporative demand, it is a more useful measure of drought when the focus is on spatiotemporal patterns. Rhee et al. [18] evaluated drought index mapping using three deterministic and one geostatistical interpolation method in North and South Carolina, USA and found IDW as the best method. Ali et al. [1] evaluated the accuracy of drought index interpolation using IDW, OK, thin plate spline based on 27 climatic stations in the Boushehr province of Iran. They found that the IDW method was more appropriate for the spatial analysis of SPI index. Bae et al. [21] estimated SPEI index in South Korea using evapotranspiration based on Thornthwaite and Penman–Monteith equation and interpolated drought using the IDW method.

While several methods have been used to evaluate the accuracy of SPI and other drought indices, relatively fewer studies attempted using SPEI index in drought interpolation. Studies have reported that the SPEI correlates well with hydrological and ecological variable than other indices and can be computed at multiple time and scale to investigate the relationship between drought and ecological conditions. The choice of drought index may not affect the accuracy of interpolation, whereas the choice of interpolation techniques does [22]. Therefore, comparing several interpolation techniques yield valuable information about the suitability and effectiveness of these spatial interpolation methods in studying various drought conditions.

This study aimed to (1) assess the most effective interpolation techniques for drought conditions based on SPEI values, (2) understand and explain interpolation comparisons, with specific emphasis on sub-tropical humid areas that exhibit higher annual rainfall variability, and (3) validate the results obtained from interpolation through a pseudo-random validation dataset. To achieve this four interpolation techniques were evaluated: IDW, spline, ordinary kriging with Gaussian model (KG), and ordinary kriging with the spherical model (KS). The results of this study can be used as a for the cost-effective tool for local level drought mapping, agricultural planning, and water resources management.

2 Materials and methods

2.1 Study area

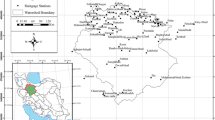
This study was conducted in East Texas, USA, where mean annual temperatures increase from north to south while annual precipitation generally increases from west to east [11] (Fig. 1). This study area includes two climatic divisions, East Texas and the Upper Coast. The wettest month of the year in this region is December followed by May, while the driest months are July, August, and September [23]. East Texas is far enough north of the tropics to experience continental wintertime disturbances, including periodic frost, and far enough east in the humid subtropics that there is generally ample moisture available when disturbances arrive.

Fig. 1
figure 1

Map of the study area. Red dots on the location map (right) represent weather stations used as test data, and green dots represent validation data. The upper part of the study area represents the East Texas climate division, and the bottom part represents the Upper Coast climate division. (Color figure online)

Full size image

Drought has historically been part of the natural climate pattern in Texas, and the state has experienced a procession of droughts and interspersed wet periods in recent years during the last 15–20 years. Statewide precipitation for the water year 2011 (October 2010 through September 2011) averaged 287 mm, a new record for the driest 12 consecutive months [24]. During the historic drought of 2011, Texas attained the lowest Palmer Drought Severity Index (PDSI) value in four distinct climate divisions: (1) High Plains, (2) Low Rolling Plains, (4) East Texas, and (5) Trans-Pecos.

2.2 Meteorological data and drought index calculation

Weather data in East Texas (N = 47 weather stations) were downloaded from the National Centers for Environmental Information (NCEI, formerly known as NCDC) hosted Climate Data Online (CDO). To understand average annual trends in temperature and precipitation, acquired monthly summary data were used.

This study used 34 years (1980–2013) of weather data from 47 weather stations in the study area (Fig. 1). However, for interpolation, the last 14 years (2000–2013) of SPEI values were used to calculate drought values for forest inventory plots in the study area during the years 2000–2013, which can help in extracting drought-affected plots for the same period [25]. Thirty-four years of monthly weather data were used because the calculation of the multi-scalar drought index required long-term data (20–30 years) [8, 26]. The study aimed to examine 12-month drought distribution patterns in East Texas forests to understand whether drought is responsible for increasing tree mortality. The forest inventory data for East Texas with multiple inventories of the same plots were available only after 1999. Therefore, the study only used last 14-years that coincide with forest inventory data for drought distribution analysis.

2.3 SPEI calculation

SPEI mimics the SPI calculation process, which is calculated using weekly or monthly precipitation as the input data. The SPEI utilizes precipitation and Potential Evapotranspiration (PET) and calculates the difference between precipitation and PET (\({\text{D}}_{\text{i}} = {\text{Precipitation}}_{\text{i}} - {\text{PET}}_{\text{i}}\)) which provides water surplus or deficit for the analyzed period (month). Calculated Di values can be aggregated at different time scales as in the calculation process of SPI. More detailed version of the calculation process is described in Vicente Serrano et al. [5].

2.3.1 PET calculation

PET was calculated using Thornthwaite’s [27] equation which requires only a few climatic variables.

$${\text{PET}} = 16{\text{K}} \times \left[ {\frac{{\left( {10 \times {\text{T}}_{\text{i}} } \right)}}{\text{I}}} \right]^{\upalpha}$$
(1)

where PET is measured in (mm), Ti is average temperature (°C) in month i, I is an annual heat index, which can be calculated using Eq. 2, α is an empirical derivative of Eq. 3, and K is a correction coefficient computed as a function of the latitude and month (Eq. 4) [5]

$${\text{I}} = \mathop \sum \limits_{{{\text{i}} = 1}}^{12} \left( {\frac{{{\text{T}}_{\text{i}} }}{5}} \right)^{1.514}$$
(2)
$$\upalpha = \left( {6.75 \times 10^{ - 7} {\text{I}}^{3} - 7.71 \times 10^{ - 5} {\text{I}}^{2} + 1.79 \times 10^{ - 2} {\text{I}} + 0.49} \right)$$
(3)
$${\text{K}} = \left( {\frac{\text{N}}{12}} \right)\left( {\frac{\text{NDM}}{30}} \right)$$
(4)

where N is the maximum number of sun hours, and NDM is the number of days in a month. N was calculated as,

$${\text{N}} = \frac{24}{\uppi}{\bar{\omega }}_{\text{s}}$$
(5)

where \({\bar{\omega }}_{\text{s}}\) is the hourly angle of the sun rising, which is calculated using Eq. 6

$${\bar{\omega }}_{\text{s}} = { \arccos }\left( { - \tan {\varphi } \tan\updelta} \right)$$
(6)

where φ is the latitude in radians and δ is the solar declination in radians as calculated using Eq. 7

$$\updelta = 0.4093{\text{sen}}\left( {\frac{{2\uppi{\text{J}}}}{365} - 1.405} \right)$$
(7)

where J is the average Julian day of the month.

2.3.2 Water surplus or deficit

After calculation of PET, water surplus or deficit for the ith month is calculated using Eq. 8

$${\text{D}}_{\text{i}} = {\text{Precipitation}}_{\text{i}} - {\text{PET}}_{\text{i}}$$
(8)

where Di is water surplus or deficit for the analyzed month. The Di values can be aggregated at different time scales.

2.3.3 Standardization of the variable (statistical distribution)

Modeling of D series was achieved using SPEI package in R [26], using three-parameter log-logistic distribution with the probability density function calculated using Eq. 9.

$${\text{f}}\left( {\text{x}} \right) = \frac{\upbeta}{\upalpha}\left( {\frac{{{\text{x}} -\upgamma}}{\upalpha}} \right)^{{\upbeta - 1}} \left( {1 + \left( {\frac{{{\text{x}} -\upgamma}}{\upalpha}} \right)^{\upbeta} } \right)^{ - 2}$$
(9)

where α, β are scale, shape and origin parameters, respectively, for the Di in the value range \(\left( {\gamma < D < \infty } \right)\).

Parameters of the Log-logistic model were obtained following the L-moment procedure and was calculated following Singh et al. [28]:

$$\begin{aligned} \beta & = \frac{{2W_{1} - W_{0} }}{{6W_{1} - W_{0} - 6W_{2} }}, \\ \alpha & = \frac{{\left( {W_{0} - 2W_{1} } \right) \beta }}{{\tau \left( {1 + \frac{1}{\beta }} \right)\tau \left( {1 - \frac{1}{\beta }} \right)}}, \\ \gamma & = W_{0} - \alpha \tau \left( {1 + \frac{1}{\beta }} \right)\tau \left( {1 - \frac{1}{\beta }} \right) \\ \end{aligned}$$

where \(\tau \left( \beta \right)\) is the gamma function of β

$$F\left( x \right) = \left[ {1 + \left( {\frac{\alpha }{x - \gamma }} \right)^{\beta } } \right]^{ - 1}$$

with F(x) the yields the standardized values for SPEI calculation. This study used the classical approximation of Abramowitz and Stegun [29] as used by Vicente-Serrano [5].

$${\text{SPEI}} = {\text{W}} - \frac{{{\text{C}}_{0} + {\text{C}}_{1} + {\text{C}}_{2} {\text{W}}^{2} }}{{1 + {\text{d}}_{1} {\text{W}} + {\text{d}}_{2} {\text{W}}^{2 + } {\text{d}}_{3} {\text{W}}^{3} }}$$

where \({\text{W}} = \sqrt { - 2\ln \left( {\text{P}} \right)}\) for P ≤ 0.5, P being the probability of exceeding a determined D value, P = 1 − F(x). If P > 0.5, P is replaced by 1 − P which reversed the SPEI sign. All other variables are constants: C0 = 2.515517, C1 = 0.802853, C2 = 0.010328, d1 = 1.432788, d2 = 0.189269, d3 = 0.001308. The SPEI is a standardized variable (mean = 0, standard deviation = 1), and it can therefore be compared across other spatiotemporal values of SPEI.

Table 1 depicts the SPEI classification based on the original classification by McKee [4] for SPI values. Refer to Vicente-Serrano et al. [5] for an in-depth understanding of the SPEI calculation process.

Table 1 Classification of SPEI values based on McKee et al. [4] and Vicente-Serrano et al. [5]
Full size table

2.4 Interpolation techniques

Interpolation techniques estimate surface values for unknown points using surface values of known points that surrounds unknown points. There are four types of spatial interpolation methods; they are local (Thiessen polygons, IDW, and spline), global (trend surfaces and regression models), geostatistical (kriging), and mixed methods. The mixed method combines the characteristic of the other three methods [19]. Methods above offer apparent circumstances of best application depending on the area of study and hence are all viable options for interpolation. However, after considering computational complexity, capabilities of the software, and size of East Texas; local (IDW, spline) and geostatistical (OK) methods of interpolation, which are often used by researchers elsewhere [1, 18, 19, 30], were chosen to compare the outputs. General interpolation techniques can be expressed as:

$$\hat{z}\left( {S_{i} } \right) = \mathop \sum \limits_{i = 1}^{n} f\left( {S_{j} } \right) + \varepsilon \left( {S_{i} } \right)$$
(10)

where \(\hat{z}\left( {S_{i} } \right)\) is the estimated value at location Si, f is a interpolation function and ε(Si) is the random errors.

2.4.1 Inverse distance weighting

IDW interpolation estimates values by averaging sample data point values in the neighborhood of each processing point. IDW assumes closer objects are more similar compared to objects in farther apart [31]. The closer objects are to the sample points the more influence they have in the computing process. The weight of a given object or point is inversely proportional to the square distance between the observed samples (Eq. 11).

$${\hat{\text{z}}}\left( {{\text{x}}_{0} } \right) = \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\rm n}} {\hbox{z}}\left( {{\text{x}}_{{\rm i}} } \right){\text{d}}_{{\rm ij}}^{{ - {\text{r}}}} }}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\rm n}} {\text{d}}_{{\rm ij}}^{{ - {\text{r}}}} }}$$
(11)

where x0 is the point to be estimated and xi are sample data points within a chosen neighborhood. The data points within (r) are related to distance by dij.

2.4.2 Spline

Spline tempers data through function minimization, which combines mean square residuals and signal surface, taking the model form of (zi, x1i, …., xdi), which measures z as the response variable and a set of d explanatory variables (x1, …, xd). The model, simply expressed as [1]:

$$C\left( h \right) = h^{k}$$
(12)

where C(h) is the covariance function, h the distance between the points, k = m − 1, and m is the order of relative derivation from observed points.

2.4.3 Ordinary kriging (OK)

In ordinary kriging z(xi) is assumed as a regionalized variable with a variogram γ(h). A variogram describes the spatial dependence of a stochastic process of z(xi). The experimental variogram has the value of half the average squared difference between the value at z(xi) and the value at z(xi + h) [32]:

$${\bar{\gamma }}\left( {\text{h}} \right) = \frac{1}{{2{\text{N}}\left( {\text{h}} \right)}}\mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{N}}\left( {\text{h}} \right)}} \left[ {{\text{z}}({\hbox{x}}_{\text{i}} ) - {\text{z}}({\hbox{x}}_{{\rm i}} + {\text{h}})} \right]^{2}$$
(13)

where N is the number of paired data points, z(xi) and z(xi + h) are the amounts of the variables z(xi), and z(xi + h) are the analysis of the experimental locations. The equation of the spherical (Eq. 14) and Gaussian (Eq. 15) model can be defined as:

$$\upgamma\left( {\text{h}} \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {h = 0} \hfill \\ {{\text{C}}_{0} + {\text{C}}\left( {\frac{{3{\text{h}}}}{{2{\text{a}}}} - \frac{{{\text{h}}^{3} }}{{2{\text{a}}^{3} }}} \right)} \hfill & {0 < h \le a} \hfill \\ {{\text{C}}_{0} + {\text{C}}} \hfill & {h > a} \hfill \\ \end{array} } \right.$$
(14)
$$\upgamma\left( {\text{h}} \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{h}} = 0} \hfill \\ {{\text{C}}_{0} + {\text{C}}\left( {1 - {\text{e}}^{{\frac{{{\text{r}}^{2} }}{{{\text{a}}^{2} }}}} } \right)} \hfill & {{\text{h}} > 0} \hfill \\ \end{array} } \right.$$
(15)

In both Eqs. 14 and 15, h measures the spatial lag between two locations, C0 is the nugget value, C0+ C is the partial still, and a is the range. For ordinary kriging, a semi variogram model, was used to select the best method (Supplementary material Fig. 1).

2.5 Model evaluation

To evaluate the accuracy of the SPEI interpolation three accuracy assessment metrics were employed. First, the formatted dataset (47 weather stations) was divided into two random datasets, i.e., a test dataset (70%, n = 33) and a validation dataset (30%, n = 14). The test dataset was used for interpolation while the validation dataset was used to check model accuracy by calculating mean absolute error (MAE), and root mean square error (RMSE), and relative mean error (RME) which were calculated as:

$${\text{MAE}} = \frac{1}{\text{n}}\mathop \sum \limits_{{{\text{i}} = 1}}^{\text{n}} \left| {{\hat{\text{y}}}_{\text{i}} - {\text{y}}_{\text{i}} } \right|$$
(16)
$${\text{RME}} = \frac{1}{\text{n}}\mathop \sum \limits_{{{\text{i}} = 1}}^{\text{n}} \frac{{\left| {{\hat{\text{y}}}_{\text{i}} - {\text{y}}_{\text{i}} } \right|}}{{{\text{y}}_{\text{i}} }}$$
(17)
$${\text{RMSE}} = \sqrt {\frac{1}{\text{n}}\sum \left( {{\hat{\text{y}}}_{\text{i}} - {\text{y}}_{\text{i}} } \right)^{2} }$$
(18)

where \(\hat{y}_{i }\) is the predicted index value at points i, yi is the observed SPEI value index at point i, and n is the total sample observations. These evaluation criteria have been used extensively in previous mapping of rainfall, soil organic carbon and drought condition research [1, 30, 33]. All data were analyzed in SPEI packages in R v 3.3.2 [26] and ArcGIS v 10.4.1.

3 Results

3.1 General trend in temperature and precipitation (2000–2013)

Average annual rainfall and temperature data from 2000 through 2013 in East Texas meteorological stations are represented in Fig. 2. Mean rainfall was lowest in 2011 (760 mm), followed by 2010 (760 mm) and 2005 (860 mm), respectively. Highest annual mean rainfall during the 14-year period occurred in 2001 (1702 mm). Fluctuating rainfall trends were witnessed in East Texas every 2–3 years.

Fig. 2
figure 2

Average annual rainfall and temperature in East Texas from 2000 to 2013. Vertical bars (primary Y-axis) indicate average annual precipitation (mm/year), while the line represents average annual temperature (secondary Y-axis)

Full size image

The year 2011 received consistently low monthly precipitation. However, the record low monthly precipitation was observed in October 2005. The lowest monthly average temperature was observed in December 2000 (6.32 °C). Average precipitation was highest in October 2009 (348 mm). Moreover, on average, the first 3 months of the year also received comparatively low precipitation. The range of average precipitation was highest during October (125 mm), followed by June (123 mm).

Average yearly temperature (2000–2013) was 19.9 °C with a minimum of 19.07 °C (2010), and a maximum of 20.22 °C (2012). Three peaks of temperature were observed: 2000, 2005–2006, and 2011–2012, corresponding to the three observed drought periods. Average monthly temperature (2000–2013) was 19.24 °C. Average minimum temperature (2000–2013) began dropping in August and reached a minimum in December (9.9 °C) and January (9.6 °C). Then temperatures slowly rose and to a maximum in August (28.8 °C).

3.2 Drought distribution (2000–2013)

Changes in 12-month SPEI distribution by month for the study period (2000–2013) in East Texas are presented in Fig. 3. In 2000, 2005–2006, and 2012 moderately dry conditions were seen throughout the region (− 1.5 < SPEI < − 1). East Texas experienced extremely dry conditions in 2010–2011 (− 2.5 < SPEI < − 2).

Fig. 3
figure 3

Twelve-month average SPEI values in East Texas for 2000 to 2013. The smaller SPEI (< − 0.5) values indicate drier conditions and larger SPEI (> 0.5) values indicate wetter conditions. SPEI values between − 0.5 and 0.5 represent normal conditions

Full size image

A 12-month representative example of drought distribution maps (Fig. 4) indicates partial north–south and west–east trends of drought without a clear trend except during significant drought periods. Characteristic dryness for 2011 is apparent as the entire region experienced a year-long drought (October 2010–October 2011).

Fig. 4
figure 4

SPEI distribution maps in sequential order, starting from 2000 (top left) to 2013 (bottom right) based on selected interpolation techniques used in the study (Table 2)

Full size image

The 2000 drought was a continuation of a 1999 drought, which reached its peak in East Texas in October 2000 (SPEI = − 1.23), whereas remaining regions in Texas experienced record-setting temperatures in early September 2000 [11]. The 2005–2006 drought, which mostly affected the East Texas climate division, reached its peak in September 2006 and slowly decreased (Fig. 4). Most of the study area remained near normal until September 2010 (Fig. 3). Interpolation of SPEI values for 2008–2010 (Fig. 4) suggested that the drought in East Texas had already started before the widespread record-breaking drought of 2010–2011.

3.3 Accuracy assessment

The accuracy of interpolation methods was assessed using MAE, RME, and RMSE. Interpolation techniques that yielded the least MAE, RME, RMSE, and the coefficient of determination (R2) close to unity are known to perform the best. Selected interpolation techniques for each year were subjected to test through the validation dataset to see variance explained by each technique (Fig. 5). Among the selected best models, the highest variation was explained by IDW in 2011 (R2 = 82%) and the least by KS in 2008 (R2 = 30%). Spline performed relatively poorly ranging from the smallest (0.234), and maximum (0.760) MAE values for 2003, and 2007, respectively. The spline method had a highest average error (0.47) followed by KS (0.322), KG (0.313) and IDW (0.293). Further, volatility of spline was substantially higher (0.022) than that of KG and KS (0.004). KG interpolation was the best fit for drought distribution for 2000, 2001, 2003, 2004, 2005, and 2013 while KS and spline performed best for 2008 and 2008, respectively. For the remaining 7 years, IDW outperformed all other methods (Table 2).

Table 2 Mean absolute error (MAE), relative mean error (RME) and root mean square error (RMSE) per interpolation method for 14 years (2000–2013)
Full size table
Fig. 5
figure 5

Differences between calculated and predicted values for SPEI in East Texas from various interpolation models in years arranged sequentially from 2000 (top left) to 2013 (bottom right)

Full size image

Around 90% of test stations and 88% of validation stations experienced droughts during the study period (Supplementary Table 1). At least six stations experienced moderate to extreme drought for 5 years, 20 stations for 3 years. The normal quantile plot (Supplementary Fig. 2) indicates that most of the data were approximately normally distributed for SPEI data. This indicates that the climatic input data (1980–2013) follows the gamma distribution. The normal probability plot (Supplementary Fig. 2) follows nearly a straight line, suggesting that the original dataset is close to normal distribution. A Kruskal–Wallis test for decadal analysis based on 12-month SPEI indicates that there was statistically significant variation among the three decades over the period of 1984–2013 at the five percent level (Supplementary Table 2).

4 Discussion

The best drought mapping techniques may change with changes of climatic variables mapped because climatic factors that determine spatial drought distribution may differ between variables used in the mapping process [19]. Twelve-month SPEI values were interpolated to examine the pattern of underground soil moisture available to plants, specifically deep-rooted species such as trees. Various interpolation techniques may result in different interpolation results impacted by the temporal scales examined as climate varies daily, monthly, and seasonally. High variation in rainfall within the same month may reflect low water percolation rates due to high-intensity, short duration events including flash floods, with remaining periods lacking significant precipitation.

Based on interpolation results, KG performed well in relatively dry (moderate to extreme) conditions (e.g., 2000, 2013 interspersion) and best described the variation of local precipitation within the study area. The Gaussian model performed better than the spherical model all the time when ordinary kriging outperformed deterministic techniques. Ly et al. [34], using 30 years of daily rainfall data from 70 rain gauges in two catchments in Belgium, also found improved in accuracy from ordinary kriging with Gaussian model compared to the spherical model. In general, KG and IDW were considered the best methods, because they yielded smallest MAE, RME, and RMSE values for most of the time. Generally, when KG performed the best, IDW also demonstrated competitive statistics marginally different from that of KG. The ordinary kriging values were close to observed values when precipitation values were low.

The spline method did not perform well when the variation of data was high, and data are more randomly spaced because spline known to produce a better result when applied to regularly spaced data with lower variability. Despite widespread use of the spline technique [15, 35], it produced the best results only in 2007. The minimum generalized cross-validation criterion of spline could have produced a different result, which this study did not use [35].

Studies suggest that deterministic techniques perform better when data points are densely populated as opposed to geostatistical methods, which perform better when input data points are sparsely distributed [18]. Dense networks of stations (at least 13 stations over 35 km2) are suggested by Dirks et al. [36] to expect a better result. This study had a relatively low density of stations (1 station per 75 km2), yet the geostatistical method (ordinary kriging) and the deterministic method (IDW) did not show a significant difference.

IDW is the most often used method for mapping of rainfall, temperature, and drought distribution [37, 38]. However, it can not be guaranteed that all the sites satisfy the positive spatial autocorrelation assumption of IDW. In such instances, the accuracy of the outputs cannot be warranted [13]. KG and IDW yielded equally competitive results both during dry and relatively wet conditions. Therefore, a comparison between geostatistical and deterministic models is necessary before choosing the best model.

5 Conclusions

This study examined the abilities of four different spatial interpolation techniques for accurate prediction of annual drought conditions in East Texas. Inverse distance weighting (IDW) and ordinary kriging with Gaussian model (KG) were considered the best and most robust methods since they offered lower mean absolute error, relative mean error and root mean square error. IDW and KG were the best methods for interpolation of SPEI indices during the period 2000–2013. Based on the overall power of the techniques, IDW was the best, followed by KG and KS and spline (IDW > KG > KS > spline). KG tended to perform well in relatively drier conditions while IDW showed mixed results, performing well both in dry and wet conditions.

Considering that the lower the error matrix value (MAE, RME, and RMSE) the better the model criteria and variance explained by validation dataset, IDW was well-suited for 6 years, KG for 6 years and KS and spline each for 1 year. It is recommended that before creating drought distribution maps at different spatiotemporal scales, the best models should be selected based on specific drought conditions of interest in a given region. Interpolation methods are context-specific calculations of different temporal scale drought indices; their comparison helps explain the most consistent methods of spatiotemporal interpolation.

The vulnerability of drought varies spatially and temporarily across the study area with drought frequency of about 2–3 years. Comparing different drought indices at different temporal scales would help identify and explain the method that is consistent and can be considered in future research. Use of ancillary topographical information could yield different results. With accurate drought distribution maps, drought affected forestry plots can be identified to model the rate of changes in tree mortality and drought triggered biomass loss. While the models presented here may not have captured local variation caused by the microclimatic condition, insight from this study can be improved for a wide array of environmental modeling.