Recurrent fuzzy time series functions approaches for forecasting

Abstract

The recurrent fuzzy time series function method can be obtained in two ways. First is using a similar model to the autoregressive moving average to obtain fuzzy functions and the second one is using recurrent connections in the combining equation. The recurrent structure provides less number of inputs and more accurate forecasts. The contribution of the paper is proposing a recurrent fuzzy time series function method and its bootstrapped version. The recurrent models are used to obtain fuzzy functions in the proposed method. The classical bootstrap method is applied and bootstrap samples are generated from learning samples. The bootstrap method provides lower forecast error variance for the proposed method. The performance of new methods is compared with some fuzzy function methods and classical approaches. First, Turkey electrical consumption data time series are analyzed. Second, the Australian beer consumption time series are analyzed. As a result of applications, new methods have good forecasting performance if compare to established benchmarks.

1 Introduction

Fuzzy sets have membership values for each member of a universal set like classical sets. A fuzzy set has a main difference from a classical set that membership values can be a real number in $[\mathrm{0,1}]$ closed interval. Membership values of fuzzy sets provide more information about universal set elements than classical sets. Let $U$ be universal set. A fuzzy set can be defined below.

$$A = \left\{ {\frac{x}{{\mu _{A} \left( x \right)}};x \in U} \right\},\quad 0 \le \mu _{A} \left( x \right) \le 1.$$

(1)

Observations of a time series are real numbers. Fuzzy sets can be defined on a universal set of observations. The universal set of observations have been defined as closed intervals which consist of all observations in the literature. Moreover, fuzzy clustering methods can be applied to time series observations for defining fuzzy sets for a time series. In the literature, fuzzy sets are defined for input–output matches for fuzzy function approaches. When fuzzy sets are defined, membership values are obtained and these values are the nonlinear combination of system inputs. Better modeling approaches can be obtained using membership values in time series models. One of these approaches is the fuzzy function approach and literature summary are summarized following section.

Fuzzy inference systems firstly proposed in Zadeh (1975) have been commonly used. It was first applied to a real-world problem in Mamdani and Assiliani (1981). The first fuzzy inference system was based on fuzzy rules and fuzzy rules have fuzzy sets on both left side and right side. Both sides of the fuzzy rules are constituted with fuzzy sets in Zadeh’s fuzzy inference system. Takagi and Sugeno (1985) proposed a new fuzzy inference system and their system used functions instead of fuzzy sets on the right side of the rules. Jang (1993) proposed an adaptive network fuzzy inference system (ANFIS) which used network structure. ANFIS is an optimized fuzzy inference system according to sample data of system input and targets. Chen and Hsu (2008), Chen and Wang (2010), Chen and Chen (2011), Chen and Jian (2017), Chen et al. (2019) and Zeng et al. (2019) studies proposed forecasting methods based on fuzzy sets. In these fuzzy inference systems, fuzzy rules have to be determined by experts or fuzzy clustering methods. Hataway and Bezdek (1993) proposed a fuzzy c-regression method (FCRM) based on the switching regression approach and fuzzy c-means clustering method. FCRM does not need to create a fuzzy rule base like other fuzzy inference systems. Fuzzy regression functions approach based on type 1 fuzzy sets was proposed in Turksen (2008). Fuzzy regression functions approaches are fuzzy inference systems but they do not use rule bases. In these approaches, fuzzy functions are created instead of constructing a fuzzy rule base. Fuzzy functions can be created using multiple linear regression method or other modeling techniques like artificial neural networks. Fuzzy functions are estimated for each fuzzy set using a modeling technique. Inputs of the multiple linear regression models are explanatory variables, lagged variables and membership values belong to the related fuzzy set. Turksen (2008) also suggested using some nonlinear transformations of membership values as inputs for the modeling techniques. Turksen (2008) stated that the more complicated input matrices produce better inference results. Çelikyilmaz and Turksen (2007) improved fuzzy function approach using support vector machines instead of the multiple regression method. Celikyilmaz and Turksen (2008a) proposed enhanced fuzzy function approach by merging optimization processes for clustering and creating fuzzy functions. Çelikyilmaz and Turksen (2008a) used multiple linear regression and a few types of support vector machines in their method. Çelikyilmaz and Turksen (2008b) used evolutionary algorithms to determine parameters of type 2 fuzzy functions approach. In these studies, fuzzy systems models applied to all kind of regression problems and forecasting is also considered. In Beyhan and Alci (2010), a linear ARX model was used instead of multiple linear regression and lagged variables were determined by trial and error method. Zarandi et al. (2013) proposed a hybrid fuzzy function approach. Aladag et al. (2016) used binary particle swarm optimization for determining lagged variables in the fuzzy regression function approach. Baser and Demirhan (2017) applied fuzzy functions with support vector machine to solar radiation data. Bas et al. (2019) used ridge regression technique in the fuzzy regression function approach. Tak et al. (2018) proposed recurrent fuzzy function approach. In this study, lagged error variables were employed in the models for each cluster. Error variables are the same for all fuzzy functions and they obtained from the forecasts of the system. Dalar and Egrioglu (2018) proposed bootstrap fuzzy regression functions approach based on subsampling bootstrap approach. Yolcu et al. (2019) proposed the intuitionistic fuzzy function approach based on multiple linear regression and intuitionistic fuzzy c-means algorithm. Yolcu et al. (2019) method use intuitionistic fuzzy sets instead of fuzzy sets. Kızılaslan et al. (2020) proposed an intuitionistic fuzzy function approach based on ridge regression, intuitionistic fuzzy c-means algorithm and particle swarm optimization. Tak (2020) proposed a recurrent intuitionistic fuzzy function approach based on gray wolf optimization technique. Bas et al. (2020) proposed picture fuzzy function approach based on ridge regression, particle swarm optimization and picture fuzzy clustering method. In this method, picture fuzzy sets were considered as a more general form of fuzzy sets. As a result of the literature review, many new type fuzzy functions approaches have been introduced to literature. Although fuzzy functions approaches can produce accurate inference results, initial conditions of optimization or clustering methods will be effective on forecasting performance. Especially, variations of the obtained results will be increased when the system employed recurrent connections or models contain lagged error variables. More stable results can be obtained using bootstrap techniques. Dalar and Egrioglu (2018) obtained fewer variations in the results of fuzzy regression functions approach using a subsampling bootstrap method when compared to Turksen (2008) fuzzy function method. Moreover, using subsampling bootstrap approach provided more accurate forecasts.

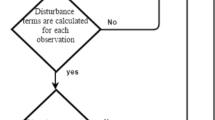
The motivation of this study is proposing a new type of recurrent fuzzy functions method using recurrent connections in each fuzzy function without considering recurrent connection in combination function. The contribution of the paper is proposing two forecasting methods. Tak et al. (2018) obtained error values from the system forecasts and lagged error variables have the same observations when obtaining each fuzzy functions. The proposed recurrent fuzzy time series function method obtains separate error variables for each fuzzy function, and this provides better fuzzy functions and more accurate forecasts. Moreover, it is considered improving recurrent fuzzy regression function approach using the bootstrap method. It is expected that this will provide less forecast error variance and more accurate forecasting results. In this study, recurrent fuzzy time series function and bootstrapped recurrent fuzzy time series function approaches are proposed using particle swarm optimization and the classical bootstrap approach applying on learning samples of the system.

In the second section, the proposed methods are explained by step-by-step algorithms and flow-charts. Experimental studies results are summarized in Sect. 3. Conclusions are given in section four.

2 Proposed method

Fuzzy regression functions methods are working as a combination of models. Models are constructed for each fuzzy sets. Fuzzy regression functions methods are used as powerful forecasting methods in the literature. The recurrent fuzzy regression functions method was first proposed in Tak et al. (2018). Using the same error values for each fuzzy functions is a problem in Tak et al. (2018) using the same error values for each fuzzy functions. In this study, a recurrent fuzzy time series function method is proposed. Each fuzzy function produces outputs for targets and forecast errors can be calculated for each fuzzy function. In the proposed method, error variables are obtained separately for each fuzzy functions apart from Tak et al. (2018). The algorithm of the proposed method is given below.

Algorithm 1. Recurrent Fuzzy Time Series Function (RFTSF) Method.

Step 1. The parameters of the proposed method are determined. Parameters are listed below:

${p}_{min}$: The minimum number of lagged variables for time series.

${p}_{max}$: The maximum number of lagged variables for time series.

${q}_{min}$: The minimum number of lagged variables for error terms.

${q}_{max}$: The maximum number of lagged variables for error terms.

$ntrain$: The length of training data.

$nval:$ The length of validation data.

$ntest:$ The length of test data.

$cmin:$ The minimum number of fuzzy sets.

$cmax:$ The maximum number of fuzzy sets.

The values ${p}_{min}, {p}_{max}, {q}_{min}, {q}_{max}$ of these parameters are determined according to time series components such as seasonality and trend. The values of $ntrain, nval, ntest$ are determined according to most preferred ratios in the literature. $cmin, cmax$ values are generally taken as $2$ and $10$, respectively.

Step 2. The input and target matrices for the system are constituted for $p\in [{p}_{min},{p}_{max}]$, and $c\in [cmin,cmax]$.

$$IM=\left[{X}_{t-1} {X}_{t-2}\dots {X}_{t-p}\right],$$

(2)

$$TM=\left[{X}_{t}\right],$$

(3)

${y}_{t}$ is original time series and ${X}_{t}$ is standardized time series by the following formula:

$${X}_{t}=\frac{{y}_{t}-\mathrm{mean}({y}_{t})}{\mathrm{std}({y}_{t})} ;t=\mathrm{1,2},\dots ,ntrain.$$

(4)

IM is a matrix with $ntrain-p$ rows and $p$ columns, TM is a vector with $ntrain-p$ rows.

Step 3. The input and target matrices for the fuzzy functions are constituted using IM and TM.

The fuzzy c-means clustering algorithm proposed by Bezdek (1981) is applied to the merged matrix which is given below:

$$MM=\left[IM\vdots TM\right].$$

(5)

The membership values and cluster centers are obtained from the fuzzy c-means algorithm.

$${u}_{i,j} ;i=\mathrm{1,2},\dots ,c ;j=\mathrm{1,2},\dots ,ntrain-p,$$

(6)

$$\mathrm{Centre}=\left[{c}_{ij}\right] ;i=\mathrm{1,2},\dots c;j=\mathrm{1,2},\dots ,p+1].$$

(7)

The cluster centers are reduced by excluding the last column or target centers. Then, the membership values are calculated with the reduced cluster centers.

$$\mathrm{Centre}(\mathrm{reduced})=\left[{c}_{ij}\right] ;i=\mathrm{1,2},\dots c;j=\mathrm{1,2},\dots ,p],$$

(8)

$${\mu }_{i,j} ;i=\mathrm{1,2},\dots ,c;j=\mathrm{1,2},\dots ,ntrain-p.$$

(9)

The small membership values are deleted and normalized membership values (${\gamma }_{ij})$ are obtained.

$$\mu _{{ij}} = \left\{ {\begin{array}{*{20}l} {\mu _{{ij}} ,} \hfill & {if\mu _{{ij}} \ge \alpha _{{{\text{cut}}}} } \hfill \\ {0,} \hfill & {Otherwise} \hfill \\ \end{array} } \right.,$$

(10)

$${\gamma }_{ij}=\frac{{\gamma }_{ij}}{\sum_{m=1}^{c}{\gamma }_{mj}} ;i=\mathrm{1,2},\dots ,c ;j=\mathrm{1,2},\dots ,ntrain-p,$$

(11)

$${IMF}_{i}=\left[{\gamma }_{i }{\gamma }_{i}^{2} {\gamma }_{i}^{3} \mathrm{exp}\left({\gamma }_{i}\right) {X}_{t-1} {X}_{t-2}\dots {X}_{t-p} {e}_{t-1}^{i} {e}_{t-2}^{i}\dots {e}_{t-q}^{i} \right] ;i=\mathrm{1,2},\dots ,c,$$

(12)

$${TMF}_{i}=TM;i=\mathrm{1,2},\dots ,c,$$

(13)

$${e}_{t}^{i}={TMF}_{i}-\widehat{{TMF}_{i}} , i=\mathrm{1,2},\dots ,c.$$

(14)

$Each\, {IMF}_{i}$ matrix has $ntrain-p$ rows and $p+q+4$ columns.

Step 4. The parameters of the following linear models are estimated by particle swarm optimization.

$${TMF}_{i}={IMF}_{i}{\beta }^{(i)}+\varepsilon ;i=\mathrm{1,2},\dots ,c,$$

(15)

${\beta }^{(i)}$ is a vector with $p+q+4$ rows. Elements of ${\beta }^{(i)}$ vectors are determined by particle swarm optimization. The number of positions for a particle is $c\times (p+q+4)$. The objective function of the particle swarm optimization is the root of mean square error (RMSE) value for training data in Eq. (18).

$$\widehat{{TMF}_{i}}={IMF}_{i}{\widehat{\beta }}^{(i)}, i=\mathrm{1,2},\dots ,c,$$

(16)

$${\widehat{X}}_{t}=\sum_{i=1}^{c}{\gamma }_{i}\widehat{{TMF}_{i}}; t=p+1,\dots ,ntrain,$$

(17)

$$RMSE=\sqrt{\frac{1}{ntrain-p}\sum_{t=p+1}^{ntarin}{\left({X}_{t}-{\widehat{X}}_{t}\right)}^{2}}.$$

(18)

Step 5. Membership values for validation set are calculated using reduced centers and they are eliminated and normalized using (11) and (12) formulas. Forecasts are calculated for the validation set in Eq. (19). ${IMVF}_{i}$ is the input matrix for validation data set and it is calculated like in Step 3

$${\widehat{X}}_{t}=\sum_{i=1}^{c}{\gamma }_{i}{IMVF}_{i}{\widehat{\beta }}^{(i)}; t=ntrain+1,\dots ,ntrain+nval.$$

(19)

Step 6. The RMSE for the validation set is calculating by the following formula

$$RMSE\left(val\right)=\sqrt{\frac{1}{nval}\sum_{t=ntarin+1}^{ntarin+nval}{\left({X}_{t}-{\widehat{X}}_{t}\right)}^{2}}.$$

(20)

Step 7. The calculations between Step 2 and Step 6 are repeated for all possible $p,q$ and c values. The $p,q$ and c values are selected as minimizing RMSE (val) values.

Step 8. The forecasts for the test set by applying Step 5. ${IMTF}_{i}$ is the input matrix for the test set and its elements are determined according to reduced cluster centers. Final forecasts are retransformed to ${\widehat{y}}_{t}$ using mean and standard deviation calculated in (3) equation.

$${\widehat{X}}_{t}=\sum_{i=1}^{c}{\gamma }_{i}{IMTF}_{i}{\widehat{\beta }}^{(i)}; t=ntrain+nval+1,ntrain+nval+2,\dots ,ntrain+nval+ntest.$$

(21)

After applying Algorithm 1, some error metrics can be calculated for the test set to compare the proposed method with alternatives. The flow-chart of the RFTSF method is given in Fig. 1.

Fig. 1

Flow-chart of the RFTSF method

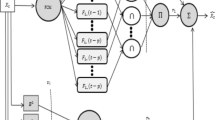
Recurrent fuzzy regression function approach has two sources of variations in its forecasting results. The first source is initial membership values in the fuzzy c-means clustering. The second source is the initial parameter estimations of autoregressive models. Because of these sources, forecasting results can be changed with different repetitions of the algorithm. Bootstrap methods can be used as a variance reduction technique in the fuzzy regression function approaches. In this study, the bootstrapped recurrent fuzzy time series functions method is proposed based on particle swarm optimization and classical bootstrap approach. It is expected that the proposed method can produce less forecast error variance and more unbiased results. The proposed method is given step- by-step in following algorithm below:

Algorithm 2. Bootstrapped Recurrent Fuzzy Time Series Function (B-RFTSF) Method.

Step 1. Algorithm 1 is applied and $p,q$ and c values are obtained.

Step 2. According to selected $p,q$ and c values, $IM{F}_{i};i=\mathrm{1,2},\dots ,c$ matrices and $TM{F}_{i};i=\mathrm{1,2},\dots ,c$ vectors are constituted by applying Step 2 and Step 3 in Algorithm 1. The $ntrain+nval$ number of observations of time series are used to obtain matrices and vectors. $IM{F}_{i}^{b};i=\mathrm{1,2},\dots ,c;b=\mathrm{1,2},\dots ,nbst$ matrices and $TM{F}_{i}^{b};i=\mathrm{1,2},\dots ,cb=\mathrm{1,2},\dots ,nbst$ vectors are obtained by generated random numbers and $nbst$ is the number of bootstrap repetitions. The rows of $IM{F}_{i}^{b}$ are randomly selected rows of $IM{F}_{i}$ and the elements of $TM{F}_{i}^{b}$ are selected according to the randomly selected row number of $IM{F}_{i}$.

Step 3. The parameters of the linear models are estimated using particle swarm optimization using the same procedure in Step 4 in Algorithm 1.

$${TMF}_{i}^{b}={IMT}_{i}^{b}{}^{b}{\beta }^{(i)}+\varepsilon ;i=\mathrm{1,2},\dots ,c;b=\mathrm{1,2},\dots ,nbst.$$

(22)

Step 4. The forecasts for all bootstrap repetitions are obtained for the test set by applying Step 5 in Algorithm 1. ${IMTF}_{i}$ is the input matrix for the test set and its elements are determined according to reduced cluster centers.

$${\widehat{X}}_{t}^{b}=\sum_{i=1}^{c}{\gamma }_{i}{IMTF}_{i}{\widehat{\beta }}^{(i)}; t=ntrain+nval+1,ntrain+nval+2,\dots ,ntrain+nval+ntest,$$

(23)

Step 5. Computing final forecast by aggregating bootstrap repetition forecasts with the median.

$${\widehat{X}}_{t}=\underset{b}{\mathrm{median}}\left\{{\widehat{X}}_{t}^{b};b=\mathrm{1,2},\dots ,nbst\right\}.$$

(24)

The flow-chart of the B-RFTSF method is given in Fig. 2. Flow-chart presents a more compact structure and to see the main algorithm without details.

Fig. 2

Flow-chart of the B-RFTSF method

Multistep forecasts can be calculated from the proposed methods. The forecasts are used instead of real observations to obtain multistep ahead forecasts. Membership values are always calculated from reduced cluster centers in Step 3 in Algorithm 1.

3 Experimental study

In the experimental analysis, the first time series is Turkey Electricity Consumption (TEC) data observed monthly between the first month of 2002 and last month of 2013. TEC data set was taken from Turkey Energy Ministry. TEC data were analyzed by multilayer perceptron artificial neural network (MLP-ANN) proposed by Rumelhart et al. (1986), seasonal autoregressive integrated moving average model (SARIMA) proposed by Box and Jenkins (1976), adaptive network fuzzy inference system (ANFIS) proposed by Jang (1993) and modified ANFIS (MANFIS) proposed by Egrioglu et al. (2014), type1 fuzzy function (T1FF) proposed by Turksen (2008) and type1 recurrent fuzzy function (T1RFF) proposed by Tak et al. (2018). TEC data are also solved using proposed RFTSF and B-RTTSF. The last twelve data points of TEC data are used as test data and other observations are constituted the training data. The analyzed results of TEC data are summarized in Table 1 using the following error metrics.

Table 1 Forecasting results for test set of TEC time series

The root of mean square error (RMSE), mean absolute percentage error (MAPE), symmetric mean absolute percentage error (SMAPE), mean absolute scaled error (MASE) and geometric mean relative absolute error (GMRAE) are calculated for evaluating forecasting results.

$$RMSE=\sqrt{\frac{1}{ntest}\sum_{t=1}^{ntest}{\left({x}_{t}-{\widehat{x}}_{t}\right)}^{2}},$$

(25)

$$MAPE=\frac{100}{ntest}\sum_{i=1}^{ntest}\left|\frac{{x}_{t}-{\widehat{x}}_{t}}{{x}_{t}}\right|,$$

(26)

$$SMAPE=200\times \frac{1}{ntest}\sum_{t=1}^{ntest}\frac{\left|{x}_{t}-{\widehat{x}}_{t}\right|}{\left|{x}_{t}\right|+\left|{\widehat{x}}_{t}\right|},$$

(27)

$$MASE=\frac{1}{ntest}\sum_{t=1}^{ntest}\left|\frac{{x}_{t}-{\widehat{x}}_{t}}{\frac{1}{n-1}\sum_{i=2}^{n}\left|{x}_{t}-{x}_{t-1}\right|}\right|,$$

(28)

$$DA = \frac{1}{{ntest}}\sum\limits_{{t = 1}}^{{ntest}} {a_{t} } ,a_{t} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\left( {x_{{t + 1}} - x_{t} } \right)\left( {\hat{x}_{{t + 1}} - y_{t} } \right) > 0} \hfill \\ {0,} \hfill & {otherwise} \hfill \\ \end{array} } \right..$$

(29)

According to Table 1, the proposed RFTSF method is better than all other methods and B-RFTSF in terms of all metrics. Moreover, B-RFTSF method is better than alternative forecasting methods in terms of RMSE, MAPE and DA. The graph of TEC time series test observations and forecasts for the RFTSF is given in Fig. 3.

Fig. 3

The graph of TEC time series test observations and forecasts of the proposed method

Second, Australian beer consumption (ABC) time series observed quarterly between the years 1956 and 1994 was analyzed. The time series was taken from Janacek (2001). ABC time series was used in many studies to compare the forecasting performance of alternative methods. Additionally, type 1 recurrent intuitionistic fuzzy function method by Tak (2020) is also used as an alternative forecasting method. Proposed methods RFTSF and B-RFTSF are applied to ABC time series and results are summarized with alternative results in Table 2. The graph of ABC time series test observations and forecasts for the RFTSF is given in Fig. 4.

Table 2 Forecasting results for test set of ABC time series

Fig. 4

The graph of ABC time series test observations and forecasts of the proposed method

According to Table 2, RFTSF is better than other methods in terms of all metrics. RFTSF is better than B-RFTSF in terms of all metrics.

4 Conclusions

In this study, recurrent fuzzy time series functions method and bootstrapped recurrent fuzzy time series functions are proposed. The contribution of the paper is proposing two new forecasting methods. In the proposed methods, each fuzzy function is created by its error values apart from the literature. The classical bootstrap approach is employed to reduce forecast variance and bias. The performance of the proposed method is investigated using well-known times series in the literature. According to many error metrics, proposed methods produce better forecasting results for ABC and TEC data sets. The proposed method RFTSF is better than Tak et al. (2018) and Tak (2020) recurrent fuzzy function methods as well as other fuzzy sets based methods. B-RFTSF can not produce better forecasting results than RFTSF method but B-RFTSF has smaller forecast error variance than RFTSF method and it is not too much affected from initial random points in the clustering method. In future studies, proposed methods can be improved using intuitionistic and picture fuzzy sets and different bootstrap methods.