1 Introduction

A time series is defined as a variable whose observations are determined over several time intervals. This time interval can be specified as hourly, daily, weekly, monthly, seasonally, yearly, or other lengths. To forecast time series datasets, numerous methods have recently been developed. These are called time series forecasting methods. Time series forecasting methods can be divided into two categories: probabilistic models and non-probabilistic models.

Probabilistic or stochastic methods, which are also called traditional methods, make some assumptions about the time series. Stationarity is an important assumption in probabilistic time series forecasting methods. This assumption states that the time series has a constant mean, variance, and covariance function. One of the most widely used models for probabilistic time series forecasting is the autoregressive integrated moving average (ARIMA) model, which was organized systematically to obtain the best ARIMA model parameters by Box-Jenkins [7].

However, ARIMA models assume a linear structure for the time series values. Hence, ARIMA models are not capable of dealing with a time series that has a nonlinear structure. Because most time series datasets do not satisfy the assumption of stationarity or linearity, many researchers have studied alternative methods. Of the alternative methods, artificial neural networks (ANNs) and fuzzy inference systems (FISs) are the most widely used ones. After fuzzy set theory was proposed by Zadeh [45], Zadeh introduced another paper on linguistic variables and fuzzy systems [46]. Later, several researchers combined fuzzy set theory with inference systems, called FISs. Well-known FISs include the FIS proposed by Mamdani and Assilian [34], the FIS proposed by Takagi and Sugeno [41], the adaptive neuro FIS, proposed by Jang [28], and the type-1 fuzzy function (T1FF) proposed by Turksen [42].

While the systems proposed by Mamdani and Assilian [34], and Takagi and Sugeno [41] are rule based, the system proposed by Turksen [42] is not rule based. The T1FF approach has an advantage over rule-based systems because the detection of rules is a difficult problem to tackle. Originally, FIS was not designed for time series forecasting problems but for classification problems.

Fuzzy time series forecasting methods were first proposed by Song and Chisom [37] in 1993. Song and Chisom [38, 39] defined a fuzzy time series forecasting process that consists of three stages: fuzzification, determination of the rules, and defuzzification. After Song and Chisom [38, 39] defined the fuzzy-time-series forecasting process, FIS-based time series forecasting methods were expanded by the following researchers. Chen [17] proposed a high-order fuzzy time series model for forecasting problems in 2002. ANN was used to forecast fuzzy time series by Huarng and Yu [25]. These two studies, among others, aimed to determine the fuzzy relations of fuzzy time series to improve forecasts.

Some of the studies using artificial intelligence techniques and the fuzzy set theory are listed below. Genetic algorithms were employed for time series forecasting problems by Kuo et al. [32], Chen and Chung [18], Kim and Kim [30], Egrioglu [20], and Bas et al. [4]. Multivariate fuzzy time series forecasting methods were studied by Egrioglu et al. [22], Chen and Tanuwijaya [19], Jilani et al. [29], and Huarng [24]. The particle swarm optimization (PSO) algorithm in fuzzy time series methods was employed by Chau [13], Park et al. [36], Kuo et al. [31], Aladag et al. [1], and Huang et al. [23].

On the one hand, probabilistic or linear models can deal with time series when the linear part of the time series dominates the non-linear part. On the other hand, when the non-linear part of the time series dominates the linear part, non-linear models produces acceptable outcomes. Thus, hybrid models have been developed to deal with both the linear and non-linear parts of the time series. The seasonal ARIA (SARIMA) model and multilayer perceptron ANN (MLP-ANN) were hybridized by Tseng et al. [43]. Various hybrid methods have been introduced by Bas et al. [3], Lee and Tong [33], Chen and Wang [16], Pai and Lin [35], Zhang [47], BuHamra et al. [8], Jain and Kumar [26], and Yolcu et al. [44].

Time series forecasting methods based on fuzzy inference systems have been studied by Catalao et al. [9], Chabaa et al. [11], Chang [12], Chen and Ma [14], Chen and Zhang [15], and Egrioglu et al. [21]. The fuzzy function approach was first used in time series forecasting by Beyhan and Alici [5]. Later, Aladag et al. [2] studied the T1FF approach for time series forecasting.

The methods that have been proposed so far, in terms of the T1FF approach, have not included disturbance terms as inputs. The objective of this paper is to propose a new method that takes into account the disturbance terms to obtain better forecasts. The proposed method combines an autoregressive (AR) model, moving average (MA) model, and T1FF approach into one algorithm. Disturbance terms are determined using the T1FF residuals. To minimize the sum of squared error (SSE), PSO is used. This paper is organized as follows. The algorithm and flowchart of the proposed method are given in Section 2. In Section 3, several applications are presented to evaluate the performance of the proposed method. Finally, the conclusions are discussed in Section 4.

2 Proposed method

The T1FF approach was designed as an FIS in 2008 by Celikyilmaz and Turksen [10]. Because the classic FISs are rule based, Turksen [42] proposed the T1FF approach to address the need for a non-rule based system. T1FF has an advantage over classic FIS because an expert opinion is needed for defining rules. Originally, T1FF was proposed for classification and regression problems. Therefore, it needed to be redesigned. The T1FF approach was first adapted to time series by Beyhan and Alici [5] and later, Aladag et al. [2] adapted T1FF to time series forecasting problems. Beyhan and Alici [5] used an auto-regressive with exogenous input (ARX) model structure that was not able to search for the best model. Therefore, Aladag et al. [2] proposed a fuzzy time series function method to search for the best model by adapting an AR model into their algorithm. Eventually, they obtained better forecasting results than Beyhan and Alici. AR and MA are the most important models in the probabilistic time series approaches. Aladag et al. [2] used an AR model in their approach. In the proposed method, the MA model is also taken into consideration. Thus, the proposed method combines the autoregressive moving average model (ARMA) with T1FF. The lagged values of the time series, lagged values of the disturbance terms, and degree of memberships obtained from the fuzzy c-means (FCM) clustering method are taken as inputs. Disturbance terms are obtained from residuals of the fuzzy functions. Because the objective function of the fuzzy functions is not derivative, the PSO algorithm is adopted.

The initial difference between a statistical approach and the proposed approach lies in the assumption of the models. A statistical approach assumes that the underlying structure of the disturbances are normally distributed and have constant covariance. However, there is no assumption about the disturbances in the proposed approach. Moreover, the most important contribution of the proposed method is that it takes the degree of membership into account.

2.1 Algorithm

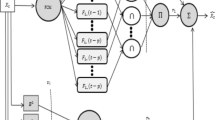
A flowchart of the proposed method is shown in Fig. 1, and its steps are detailed as follows.

  • Step 1. The dataset is partitioned into two datasets: a training dataset and a test dataset. To partition the dataset, a block partitioning structure is used because of the data dependency. Assume the size of the dataset is n. Then, the first k observations are chosen for the training dataset and the rest of the observations (n − k) are chosen for the test dataset.

  • Step 2. The model inputs are selected as lagged variables of the dataset and disturbances. Inputs are clustered using the FCM algorithm.

  • Step 3. Lagged variables, membership degrees, and the functions of the membership degrees are combined into the training dataset to obtain input matrix X. The dimension of the input matrix is n × p × c × k, where n is the number of observations, p is the number of parameters, c is the number of clusters, and k is the number of particles.

  • Step 4. Coefficients c 1 and c 2, the number of particles, and the number of iterations are specified for the PSO algorithm. The number of positions in each particle is (p + q + 4)c, where p is the lag for AR, q is the lag MA, and c is the number of clusters.

  • Step 5. Initial positions and corresponding velocities for each particle are generated randomly from a standard normal distribution. The initial personal best (pbest) values are assigned as initial positions. The initial global best (gbest) value is obtained using a fitness value.

  • Step 6. The values for the i th particle and the first observation e t−q are calculated as follows.

    $$ \widehat{Y}_{i}^{(j)(k)}= X_{(i)(.)}^{(j)(k)}{\beta^{T}}_{(i)(.)}^{(j)(k)} $$
    (1)
    $$ \widehat{Y^{*}}^{(j)(k)}= \widehat{Y}_{(i)}^{(j)(k)} {\mu^{T}}_{(i)(.)}^{(j)} $$
    (2)
    $$ {e_{k}^{i}}=Y_{i}-\widehat{Y^{*}}_{i}^{(k)} $$
    (3)
    $$ X_{(i+1)(p)}^{(.)(k)}={e_{k}^{i}} $$
    (4)

    Equation (1) is calculated for each cluster j and the values of \( \widehat {Y}_{i}^{(j)(k)} = \left [ ......... \right ] \) are obtained for the number of clusters c.

    In (2), \(\widehat {Y^{*}}_{i}^{(k)}\) is calculated, where \(\widehat {Y}_{(i)}^{(j)(k)}\) are the forecasts and \((\mu ^{T})_{(i)(.)}^{(j)}\) are the corresponding membership degrees.

    In (3), the \({e_{k}^{i}}\) values are obtained, where Y i is the actual value and \({e_{k}^{i}}\) is the same value for each cluster.

    In (4), \({e_{k}^{i}}\) value is assigned to input matrix X for each cluster.

  • Step 7. Because a disturbance term is calculated for the first observation and the i th particle in Step 6, (1)–(4) are repeated for each observation.

  • Step 8. Steps 6 and 7 are repeated for each particle.

  • Step 9. The pbest and gbest values are updated using the fitness value.

  • Step 10. The gbest value obtained for the training dataset is used to determine e t for the test dataset. The equations are given below.

    $$ \widehat{Y_{test_{i}}}^{(j)} = {X_{test}}_{i,.}^{(j)} {\beta_{test}^{T}}_{i,.}^{(j)} $$
    (5)
    $$ \widehat{Y_{test_{i}}}^{*} =\widehat{Y_{test_{i}}}^{(j)} {\mu_{test}^{T}}_{i,.}^{(j)} $$
    (6)
    $$ e_{test_{i}}=Y_{test_{i}}-\widehat{Y_{test_{i}}}^{*} $$
    (7)
    $$ X_{test_{(i+1)(p)}}^{(.)}=e_{test_{i}} $$
    (8)

    Equation (5) is repeated for each cluster, then (6)–(8) are calculated. These steps are repeated for each observation.

  • Step 11. The values for r 1 and r 2 are randomly generated from the standard normal distribution and new positions and velocities are updated as follows.

    $$ v_{id}^{k+1}=v_{id}^{k}+c_{1}{r_{1}^{k}}(pbest_{id}^{k}-p_{id}^{k}) + c_{2}{r_{2}^{k}}(gbest^{k}-p_{id}^{k}) $$
    (9)
    $$ p_{id}^{k+1}=p_{id}^{k} +v_{id}^{k+1} $$
    (10)

  • Step 12. Steps 6–11 are repeated for each iteration up to the maximum number of iterations.

  • Step 13. The final gbest value is used to forecast the future values of the time series using the equations below.

    $$ \widehat{Y_{test_{i}}}^{(j)} = {X_{test}}_{i,.}^{(j)} {\beta_{test}^{T}}_{i,.}^{(j)} $$
    (11)
    $$ \widehat{Y_{test_{i}}}^{*} =\widehat{Y_{test_{i}}}^{(j)} {\mu_{test}^{T}}_{i,.}^{(j)} $$
    (12)
Fig. 1
figure 1

Flowchart of the proposed method

Full size image

3 Evaluation

The proposed method’s performance was evaluated as follows. First, some initial possible solutions are generated from the standard normal distribution to determine the coefficients of the models. The disturbance terms are calculated recursively, observation by observation, for each model. Third, the models are evaluated in terms of SSE and the best solution (gbest) of the possible initial solutions is chosen. In short, the evaluation of the models in the proposed method is made sample by sample.

To evaluate the performance of the proposed method, 12 real world time series datasets were analyzed using R, a statistical programming language. The first dataset is the Australian Beer Consumption (ABC) dataset [27]. The observations of this dataset were observed for each quarter from 1956 to 1994. The next five datasets are from the Istanbul Stock Exchange (BIST100) datasets [6]. The data of the BIST100 datasets were observed daily for the first half of the years between 2009 and 2013. The data of the Taiwan Stock Exchange (TAIEX) dataset [40] were observed daily from 1999 to 2004. These datasets were chosen so that the performance of the proposed method could be compared with other methods that previously used the same datasets. The methods are evaluated using the root mean squared error (RMSE) and mean absolute percentage error (MAPE), calculated as follows.

$$ RMSE=\sqrt{\frac{1}{n}\sum\limits_{t=1}^{n}{(x_{t}-\widehat{x}_{t})^{2}}} $$
(13)
$$ MAPE=\frac{1}{n}\sum\limits_{t=1}^{n}\left| \frac{x_{t} - \widehat{x_{t}}}{x_{t}} \right| $$
(14)

The number of observations of the original datasets, number of observations of the test datasets, order of the AR model, order of the MA model, and number of clusters are listed in Table 1. ARMA -T1FF refers to the proposed method.

Table 1 Summary of the datasets and parameter selection criteria
Full size table

The complexity of the proposed method is difficult to compute. However, the calculation time for each dataset is given Tables 2 and 3. The calculations were computed on a PC equipped with an I7 CPU, 8 GB RAM, and 512 GB SSD HDD.

Table 2 Computation times of the BIST100 datasets
Full size table
Table 3 Computation times of the ABC and TAIEX datasets
Full size table

3.1 ABC dataset

In the first evaluation, the ABC dataset was used. This dataset consists of 148 observations that were observed quarterly from 1956 to 1994. To compare the results of the proposed method, the performances of the SARIMA model,

Winter’s Exponential Smoothing (WMES) method, MLP-ANN, adaptive neuro fuzzy inference system (ANFIS), and modified ANFIS (MANFIS) from the study of Egrioglu et al. [21] are used.

The length of the test dataset (ntest) is taken as 16. The algorithm searched for the best model when the number of clusters was varied from two to ten, the AR lag was varied one to ten, and the MA lag was varied from one to two. The number of particles and iterations were set to 35 and 100, respectively. Under these conditions, the minimum RMSE and MAPE values were obtained for five clusters, seven AR lags, and one MA lag. Looking at the RMSE and MAPE values in Table 4, it is obvious that the minimum RMSE and MAPE values are obtained by the proposed method. The forecasts obtained by the proposed method and the original observations are given in Fig. 2.

Table 4 Results obtained for the ABC test dataset when ntest = 16
Full size table
Fig. 2
figure 2

Forecasts and test data for the ABC dataset (ntest = 16)

Full size image

3.2 TAIEX dataset

To evaluate the performance of the proposed method for TAIEX dataset, the following methods were chosen: Chen (1996), Chen and Chang (2010), Chen and Chen (2011), and Chen et al. (2012). The results of the methods in Table 5 are taken from the paper of Bas et al. [3]. For the TAIEX datasets from 1999 to 2004, the results obtained by the proposed method are listed in Table 5.

Table 5 Results obtained for TAIEX
Full size table

The forecasting results from the proposed and other methods are compared in terms of the RMSE. For 1999 and 2001, the best forecasting results are obtained from the proposed method. For 2002 and 2003, MANFIS outperforms the other methods, and for 2004, Chen et al.’s method gives the best results. However, looking at the means of the years, it is obvious that the proposed method has better forecasting results than others. A comparison of the results of the proposed method with those of other methods by year is given in Fig. 3.

Fig. 3
figure 3

RMSE values of the proposed method and the other methods

Full size image

3.3 BIST100 dataset

For the BIST100 dataset, the outcomes of ARIMA, exponential smoothing (ES), MLP-ANN, T1FF, fuzzy time series network (FTS-N), and recurrent T1FF (ARMA-T1FF) are compared. The outcomes for ARIMA, ES, MLP-ANN, T1FF, and FTS-N are taken from Bas et al. [3].

The best results are obtained using the Box-Jenkins procedure for the ARIMA procedure. For the ES procedure, the best results are obtained from Holt and Winter’s method. For the MLP-ANN method, the hidden layer neurons and number of inputs were varied from 1 to 5 and the best model of these was chosen. While performing T1FF, the number of clusters and the model order was varied from 5 to 15 and from 1 to 5, respectively. The best outcomes were selected. For the results of FTS-N, the model order p was varied from 1 to 5 and the number of clusters from 5 to 15. To obtain the best results for the proposed method (ARMA-T1FF), the number of clusters was varied from 2 to 5, the AR lag was varied from 1 to 5, and the MA lag was varied from 1 to 2. In addition, the number of iterations was set to 100 and the number of particles was 25. The best forecasting results, year by year, were determined using the parameters given in Table 6. The results are listed in Tables 7, 8, 9 and 10.

Table 6 Parameter specifications for the best model
Full size table
Table 7 RMSE values for BIST100 when ntest=7
Full size table
Table 8 MAPE values for BIST100 when ntest=7
Full size table
Table 9 RMSE values for BIST100 when ntest=15
Full size table
Table 10 MAPE values for BIST100 when ntest=15
Full size table

When the length of the test dataset is seven, the best forecasting results of the proposed method for the applications of the BIST100 are listed in Tables 7 and 8 in terms of RMSE and MAPE values, respectively. The proposed method has better forecasting performance than the other methods. Figure 4 compares the RMSE values of the proposed method (ARMA-T1FF) with those obtained by the other methods.

Fig. 4
figure 4

RMSE values of the proposed and other methods when ntest=7

Full size image

Similarly, when the length of the test dataset is 15 for BIST100, the best forecasting results in terms of RMSE and MAPE values are given in Tables 9 and 10, respectively. Again, the proposed method outperforms the others. Figure 5 compares the RMSE values of the proposed method with those obtained by the other methods.

Fig. 5
figure 5

RMSE values of the proposed and other methods when ntest=15

Full size image

4 Conclusions

This study proposed a new method that uses T1FF as the AR and MA model terms. The proposed method is the first recurrent fuzzy function approach regarding times series forecasting. To estimate the coefficients of the model, the PSO method is preferred. The proposed approach has the following advantages and contributions.

  • Unlike most FISs, rules do not need to be defined in the proposed method.

  • The assumptions of classical time series forecasting methods are not needed for the proposed method. In other words, there is need for any assumptions on the time series for ARMA-T1FF.

  • Because the function that is to be optimized is not derivative, the PSO algorithm is preferred for estimating the coefficients of the model. The advantage of PSO is that it is less likely become stuck in a local optimum.

  • The ARMA-T1FF approach is the first method that uses a recurrent learning structure.

  • The number of inputs is fewer than for other methods because of the contribution of the MA model.

  • The proposed method obtains better forecasting results than many methods in the literature.

The results obtained for the datasets show that ARMA-T1FF obtains overall better forecasting results than other methods. The results of the ABC dataset clearly show that the proposed method outperforms the other methods in terms of RMSE and MAPE. For the BIST100 dataset from 2009 to 2013, the ARMA-T1FF approach has better forecasting results on average in terms of RMSE and MAPE. For the TAIEX dataset, the mean RMSE for all years is used as the performance metric of the models, and for this metric, the proposed method gives the best results. In summary, considering the ABC, BIST100, and TAIEX datasets, the ARMA-T1FF approach obtains better forecasting results.