1 Introduction

Granular computing is a framework for data and information processing that includes several methods of soft computing, machine learning, and artificial intelligence (Dubois and Prade 2016; Wang et al. 2017; Livi and Sadeghian 2016; Ciucci 2016). Granular computing is applied to various problems such as fuzzy systems (Apolloni et al. 2016; Liu and Zhang 2018), classification (Amezcua and Melin 2019; Liu and Cocea 2017; Aydav and Minz 2020; Antonelli et al. 2016; Liu and Cocea 2019), traffic scene recognition (Wu et al. 2019), situation awareness (Loia et al. 2016), and clustering (Chen et al. 2019b; Zhang et al. 2019a; Martino and Sessa 2020; Lingras et al. 2016; Peters and Weber 2016). Fuzzy clustering algorithms are designed to identify compact groups of data points within the data. In recent years, these algorithms have been applied to various research areas. For instance, color image can be segmented by fuzzy clustering (Ozdemir and Akarun 2011; Tolias and Panas 1998), where the objects are presented by clusters with different characteristics to preserve details of the image. It is shown that fuzzy clustering effectively determines spatial organization and compactness of pixel clusters (Beliakov et al. 2015). Type-II Fuzzy C-Means (FCM) algorithm is utilized to extract different features of scene images for a humanoid robot that shows the superior performance of this approach over other methods (Liu et al. 2014). A segmentation approach is presented based on fuzzy clustering and it is shown that the method is useable in object recognition, image retrieval, and human vision simulation (Makrogiannis et al. 2005). Fuzzy time series is employed for simulating behavior of imprecise data with a small number of samples and unclear trend (Li and Cheng 2010; Wong et al. 2010). Although some of the forecasting algorithms presented for such time series are based on intervals of the universe of discourse of the input variables (Chen and Jian 2017; Chen and Phuong 2017; Chen et al. 2012, 2013, 2019a; Chen and Chen 2015; Chen and Wang 2010), but it is shown that fuzzy clustering provides more accurate predictions for fuzzy time series (Zeng et al. 2019; Chen and Chang 2010; Chen and Tanuwijaya 2011a, b; Askari and Montazerin 2015; Cheng et al. 2008; Egrioglu et al. 2011; Aladag et al. 2012; Chen and Chen 2014; Duru and Bulut 2014; Askari et al. 2015a, b). It is shown that oil reservoir with noisy data is efficiently classified by fuzzy clustering algorithms (Askari 2017a). Because of high complexity, network type problems such as gas and water distribution networks and electrical grids require fast forecasting systems to predict their behavioral. (Askari et al. 2016a, b). It is shown that fuzzy systems based on fuzzy clustering are suitable choices for such problems (Askari et al. 2020). Fuzzy clustering is also used for system identification (Montazerin et al. 2015) and structure identification of fuzzy systems (Tung and Quek 2004; Zhang et al. 2002; Askari 2017b).

The FCM algorithm is the basic fuzzy clustering technique (Bezdek et al. 1984; Hathaway and Bezdek 2001) and its convergence proof is presented in (Groll and Jakel 2005). So far, many developments are made on the algorithm to overcome its deficiencies. The algorithm is developed to handle very large or big data that cannot be loaded in the working memory of a computer (Havens et al. 2012). A multiple-kernel FCM algorithm is proposed for image segmentation by linear combination of various kernels (Chen et al. 2011). The algorithm fuses different pixel information captured by different kernels in the image segmentation (Chen et al. 2011). Applying the algorithm to synthetic and medical images proves its advantages. Degree of fuzziness is typically set to 2.0 in fuzzy clustering algorithms, however, changing this parameter may seriously affect results of clustering. Large value of this parameter increases fuzziness and overlap of the clusters but when it tends to 1.0, the clusters become crisp. A generalized form of the FCM algorithm is proposed and its robustness and convergence are analyzed (Zhu et al. 2009). The algorithm shows some advantages over the FCM algorithm when applied to noisy images (Zhu et al. 2009). Fuzzy sets and rough sets are combined to utilize advantages of both concepts in fuzzy clustering (Maji and Pal 2007). Qualitative and quantitative examinations of this hybrid algorithm demonstrate its effectiveness when it is applied to real-life data.

The main objective of the present work is to formulate a fuzzy clustering algorithm to cancel impacts of noise and outliers on the cluster centers. To this purpose, the distance in the objective function of the FCM algorithm is replaced with an exponential function. As a result, an exponential function of distance appears in the update equation of the cluster centers. Since noise and outliers are mostly far away from the clusters centers, their impacts on the clustering results become negligible. Effectiveness of this idea is proved by several experiments carried out on the noisy data.

Rest of the paper is organized as follows. Research works closely related to the present study are briefly discussed in Sect. 2. Several algorithms are discussed in Sect. 3 along with the proposed algorithm. Performances of these algorithms on noisy data are compared in Sect. 4 and summary of the paper and its findings are provided in Sect. 5.

2 Related works

Sensitivity to noise and outliers is one of the main drawbacks of the FCM algorithm. The problem is addressed in many research works. The Credibilistic fuzzy C-means (CFCM) algorithm takes the credibility of data points to the whole data into account to reduce the sensitivity of the FCM algorithm to outliers (Chintalapudi and Kam 1998). Performance of this algorithm proves its superiority over the FCM algorithm. A noise-tolerant FCM algorithm is proposed for data stream regression (Song et al. 2019). It is shown that this algorithm provides more accurate regressions as compared to several well-known methods. The Density Oriented Fuzzy C-Means (DOFCM) algorithm is presented to identify outliers in the data (Kaur and Gosain 2010). Location of the cluster centers calculated by the DOFCM algorithm is not affected by noise and outliers. A robust fuzzy clustering algorithm is proposed based on membership linking and filtering for segmentation of noise images (Lei et al. 2018; Wang et al. 2020). These algorithms incorporate pixels labels into the clustering algorithm to apply to the supervised process of image segmentation. Performance of these algorithms is compared to that of several methods and it is shown that they are significantly more accurate than the other algorithms. Type-2 FCM algorithm is proposed to capture uncertainty and fuzziness of the data more efficiently (Gosain and Dahiya 2016). Since data points with higher membership grades determine the cluster centers calculated by this algorithm, it is supposed to be capable of removing noise and outliers impacts on the clustering results. The algorithm is further extended by replacing the distance in the objective function of the original algorithm with Gaussian kernels. This modification significantly improves performance of the algorithm when dealing with noise and outliers.

Possibilistic C-Means (PCM) algorithm is proposed to handle noise and outliers (Krishnapuram and Keller 1993, 1996; Koutroumbas et al. 2018; Anderson et al. 2010; Zhang et al. 2017a, b; Zhang and Leung 2004; Pal et al. 2005). Although it is applied to several problems such as boundary detection and surface approximation (Krisnapuram et al. 1995a, b), image segmentation (Kalist et al. 2015; Zhang et al. 2011; Xie et al. 2007), big data clustering (Zhang et al. 2019a, b), sensor big data (Zhang and Chen 2014), cloud computing (Srinivasan and Palanisamy 2015), system identification (Ahmed et al. 2015; Bouzbida et al. 2017), and outlier detection (Filippone et al. 2010), but the algorithm severely suffers from sensitivity to initialization and coincident clusters (Koutroumbas et al. 2018; Askari et al. 2017a, b.). To overcome these problems, the FCM and PCM algorithms are combined to make the hybrid Possibilistic Fuzzy C-Means (PFCM) algorithm to take advantages of both algorithms and avoid their deficiencies (Pal et al. 2005).

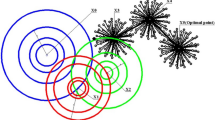
However, the PFCM algorithm does not provide the expected results and the cluster centers calculated by this algorithm are highly influenced by noise and outliers. For example, consider the data shown in Fig. 1 that are used in (Pal et al. 2005) (where the PFCM algorithm is introduced for the first time) to show the effectiveness of the PFCM algorithm in handling outliers. The data point \(\left[ {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right]^{\text{T}}\) is inlier and \(\left[ {\begin{array}{*{20}c} 0 & {10\,} \\ \end{array} } \right]^{\text{T}}\) is outlier. These data are clustered using the PCM, FCM, and PFCM algorithms and the cluster centers computed by these algorithms are indicated by ◊, +, and × , respectively. The PFCM algorithm obviously fails to find the accurate cluster centers because of these two points added to the original data that contains two diamond-shaped clusters. Similarly, the PCM and FCM algorithms calculate misplaced cluster centers. The cluster centers indicated by * are calculated by the noise-resistant FCM (nrFCM) algorithm presented in this paper that is discussed later. The nrFCM algorithm initializes by the FCM algorithm such that the initial cluster centers are calculated by the FCM algorithm and then the nrFCM algorithm updates these prototypes to find the final cluster centers.

Fig. 1
figure 1

Cluster centers of the data with two clusters calculated by the PCM, FCM, PFCM, and nrFCM algorithms

Full size image

3 Theoretical background

Three algorithms are discussed prior to nrFCM formulation including the FCM algorithm, Type-2 Fuzzy C-Means (T2FCM), and Kernelized Type-2 Fuzzy C-Means (KT2FCM)and. These algorithms are later used to evaluate the performance of the nrFCM algorithm.

3.1 Fuzzy C-means (FCM) algorithm

Objective function of the FCM algorithm is as follows (Pal et al. 2005) where \(c\) is the number of clusters, \(n\) is the number of data points, \(\vec{x}_{j}\) is the \(j{\text{th}}\) data point, and \(\vec{v}_{i}\) is the \(i{\text{th}}\) cluster center. Moreover, \(m\) is degree of fuzziness and \(u_{ij}\) is membership grade of \(\vec{x}_{j}\) in \(\vec{v}_{i}\).

$$J = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{c} {u_{ij}^{m} d_{ij}^{2} } } ,\sum\limits_{k = 1}^{c} {u_{kj} } = 1$$
(1)

where \(d_{ij}^{2} = \left( {\vec{x}_{j} - \vec{v}_{i} } \right)^{T} A\left( {\vec{x}_{j} - \vec{v}_{i} } \right)\) is distance of \(\vec{x}_{j}\) from \(\vec{v}_{i}\) and \(A_{r \times r}\) is a norm matrix where \(r\) is dimension of the data. Type of the norm matrix determines shape of the clusters. Identity norm matrix \(I_{r \times r}\) generates spherical clusters and the following covariance norm matrix provides elliptic clusters.

$$A = \left( {\frac{1}{n}\sum\limits_{j = 1}^{n} {\left( {\vec{x}_{j} - \bar{\vec{v}}} \right)} \left( {\vec{x}_{j} - \bar{\vec{v}}} \right)^{T} } \right)^{ - 1} ,\;\bar{\vec{v}} = \frac{1}{n}\sum\limits_{j = 1}^{n} {\vec{x}_{j} }$$
(2)

The membership grades and cluster centers are calculated by minimizing (1) that results in the following update equations for the FCM algorithm (Pal et al. 2005).

$$u_{ij} = \left[ {\sum\limits_{k = 1}^{c} {\left( {\frac{{d_{ij}^{2} }}{{d_{kj}^{2} }}} \right)^{{\frac{1}{m - 1}}} } } \right]^{ - 1} ,\vec{v}_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} \vec{x}_{j} } }}{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} } }}$$
(3)

3.2 Type-2 fuzzy C-means (T2FCM)

The T2FCM algorithm is based on Type-2 fuzzy sets. This algorithm calculates cluster centers differently as compared to the FCM algorithm such that data points with higher membership grades are more determinative of the final position of the cluster centers. Since membership grades of noise and outliers are less than those of actual data points, the T2FCM algorithm is supposed to show good performance on noisy data (Gosain and Dahiya 2016). Type-1 membership grades of this algorithm are calculated from (3) as follows.

$$u_{ij} = \left[ {\sum\limits_{k = 1}^{c} {\left( {\frac{{d_{ij}^{2} }}{{d_{kj}^{2} }}} \right)^{{\frac{1}{m - 1}}} } } \right]^{ - 1}$$
(4)

The Type-2 membership grades \(\mu_{ij}\) are then calculated from the Type-1 membership grades by the following equation (Gosain and Dahiya 2016).

$$\mu_{ij} = u_{ij} - \frac{{1 - u_{ij} }}{2}$$
(5)

Finally, cluster centers are calculated as follows (Gosain and Dahiya 2016).

$$\vec{v}_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {\mu_{ij}^{m} \vec{x}_{j} } }}{{\sum\nolimits_{j = 1}^{n} {\mu_{ij}^{m} } }}$$
(6)

3.3 Kernelized type-2 fuzzy C-means (KT2FCM)

The KT2FCM algorithm is proposed by further generalization of the T2FCM algorithm by replacing the distance in (1) with hyper tangent kernel, which leads to the following objective function (Gosain and Dahiya 2016).

$$J = 2\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{c} {\mu_{ij}^{m} \left( {1 - K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right)} \right)} } ,\;\sum\limits_{k = 1}^{c} {u_{kj} } = 1$$
(7)

where \(K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right)\) is the kernel, which is defined as follows (Gosain and Dahiya 2016).

$$K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right) = 1 - \tanh \left( { - \frac{{d_{ij}^{2} }}{{\omega^{2} }}} \right),\;d_{ij}^{2} = \left( {\vec{x}_{j} - \vec{v}_{i} } \right)^{\text{T}} A\left( {\vec{x}_{j} - \vec{v}_{i} } \right)$$
(8)

where \(\omega\) is the kernel width and is calculated by the following equations (Gosain and Dahiya 2016).

$$\begin{aligned} \vec{\bar{v}} & = \frac{1}{n}\sum\limits_{j = 1}^{n} {\vec{x}_{j} } \hfill \\ \bar{d} & = \frac{1}{n}\sum\limits_{j = 1}^{n} {\left\| {\vec{x}_{j} - \vec{\bar{v}}} \right\|_{A}^{2} } \hfill \\ \omega^{2} & = \frac{1}{n - 1}\sum\limits_{j = 1}^{n} {\left( {\left\| {\vec{x}_{j} - \vec{\bar{v}}} \right\|_{A}^{2} - \bar{d}} \right)^{2} } \hfill \\ \end{aligned}$$
(9)

It is shown that the following cluster centers and Type-2 membership functions minimize (7) (Gosain and Dahiya 2016).

$$\mu_{ij} = \left[ {\sum\limits_{k = 1}^{c} {\left( {\frac{{1 - K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right)}}{{1 - K\left( {\vec{x}_{j} ,\vec{v}_{k} } \right)}}} \right)^{{\frac{1}{m - 1}}} } } \right]^{ - 1} ,\;\vec{v}_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {\mu_{ij}^{m} K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right)\left( {2 - K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right)} \right)\vec{x}_{j} } }}{{\sum\nolimits_{j = 1}^{n} {\mu_{ij}^{m} K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right)\left( {2 - K\left( {\vec{x}_{j} ,\vec{v}_{i} } \right)} \right)} }}$$
(10)

3.4 Possibilistic C-means (PCM)

The possibilistic C-means (PCM) algorithm is proposed for data with noise and outliers. Objective function of this algorithm is as follows (Askari 2017b).

$$J = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{c} {t_{ij}^{\eta } d_{ij}^{2} } } + \sum\limits_{i = 1}^{c} {\gamma_{i} \sum\limits_{j = 1}^{n} {\left( {1 - t_{ij} } \right)^{\eta } } }$$
(11)

where \(t_{ij}\) is typicality of \(\vec{x}_{j}\) in the \(i{\text{th}}\) cluster and \(\eta\) is the possibilistic exponent. Update equations of the PCM algorithm are as follows (Askari 2017b).

$$\vec{v}_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {t_{ij}^{\eta } \vec{x}_{j} } }}{{\sum\nolimits_{j = 1}^{n} {t_{ij}^{\eta } } }},\;t_{ij} = \left( {1 + \left( {\frac{{d_{ij}^{2} }}{{\gamma_{i} }}} \right)^{{\frac{1}{\eta - 1}}} } \right)^{ - 1} ,\;\gamma_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} d_{ij}^{2} } }}{{\sum\nolimits_{j = 1}^{n} {d_{ij}^{2} } }}$$
(12)

where \(u_{ij}\) in \(\gamma_{i}\) are calculated from (3) by applying the FCM algorithm to the data.

3.5 Possibilistic fuzzy C-means (PFCM) algorithm

The PCM algorithm designed for noisy data suffers from two serious drawbacks including coincident clusters and sensitivity to initialization. The FCM and PCM algorithms are combined to provide the hybrid possibilistic fuzzy C-means (PFCM) algorithm to overcome these shortcomings (Askari 2017b). Objective function of this algorithm is as follows.

$$J = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{c} {\left( {u_{ij}^{m} + t_{ij}^{\eta } } \right)d_{ij}^{2} } } + \sum\limits_{i = 1}^{c} {\gamma_{i} \sum\limits_{j = 1}^{n} {\left( {1 - t_{ij} } \right)^{\eta } } } ,\;\sum\limits_{i = 1}^{c} {u_{ij} } = 1$$
(13)

It is shown that update equations of this algorithm are as follows.

$$\vec{v}_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {\left( {u_{ij}^{m} + t_{ij}^{\eta } } \right)\vec{x}_{j} } }}{{\sum\nolimits_{j = 1}^{n} {\left( {u_{ij}^{m} + t_{ij}^{\eta } } \right)} }},\;u_{ij} = \left[ {\sum\limits_{k = 1}^{c} {\left( {\frac{{d_{ij}^{2} }}{{d_{kj}^{2} }}} \right)^{{\frac{1}{m - 1}}} } } \right]^{ - 1} ,\;t_{ij} = \left( {1 + \left( {\frac{{d_{ij}^{2} }}{{\gamma_{i} }}} \right)^{{\frac{1}{\eta - 1}}} } \right)^{ - 1} ,\;\gamma_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} d_{ij}^{2} } }}{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} } }}$$
(14)

3.6 The noise-resistant FCM (nrFCM) algorithm

The present work proposes the noise-resistant FCM (nrFCM) algorithm by replacing the distance \(d_{ij}^{2}\) in (3) with \(f\left( {d_{ij}^{2} } \right)\) where \(f\) is a differentiable function whose derivative is uniform descending. This function reduces the impacts of noise and outliers on the cluster centers. Therefore, the following objective function is devised for the nrFCM algorithm.

$$J = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{c} {u_{ij}^{m} f\left( {d_{ij}^{2} } \right)} } ,\;\sum\limits_{k = 1}^{c} {u_{kj} } = 1$$
(15)

Incorporating the constraint \(\sum\nolimits_{k = 1}^{c} {u_{kj} } = 1\) in the objective function (15) using the Lagrange multipliers results in the following function.

$$J = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{c} {u_{ij}^{m} f\left( {d_{ij}^{2} } \right)} } + \sum\limits_{j = 1}^{n} {\lambda_{j} \left( {\sum\limits_{k = 1}^{c} {u_{kj} } - 1} \right)}$$

Zeroing derivative of this function with respect to cluster centers yields the update equation for \(\vec{v}_{i}\).

$$\frac{\partial J}{{\partial \vec{v}_{i} }} = \sum\limits_{j = 1}^{n} {u_{ij}^{m} f^{\prime}\left( {d_{ij}^{2} } \right)\frac{{\partial d_{ij}^{2} }}{{\partial \vec{v}_{i} }}} = \sum\limits_{j = 1}^{n} {u_{ij}^{m} f^{\prime}\left( {d_{ij}^{2} } \right)\left( {A + A^{T} } \right)\left( {\vec{x}_{j} - \vec{v}_{i} } \right)} = 0 \Rightarrow$$
$$\vec{v}_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} f^{\prime}\left( {d_{ij}^{2} } \right)\vec{x}_{j} } }}{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} f^{\prime}\left( {d_{ij}^{2} } \right)} }}$$
(16)

Similarly, zeroing derivative of this function with respect to \(u_{ij}\) results the update equation for the membership grades.

$$\frac{\partial J}{{\partial u_{ij} }} = mu_{ij}^{m - 1} f\left( {d_{ij}^{2} } \right) + \lambda_{j} = 0 \Rightarrow$$
$$u_{ij} = \left( {\frac{{ - \lambda_{j} }}{{mf\left( {d_{ij}^{2} } \right)}}} \right)^{{\frac{1}{m - 1}}} ,\;\sum\limits_{k = 1}^{c} {u_{kj} } = 1 \Rightarrow$$
$$u_{ij} = \left[ {\sum\limits_{k = 1}^{c} {\left( {\frac{{f\left( {d_{ij}^{2} } \right)}}{{f\left( {d_{kj}^{2} } \right)}}} \right)^{{\frac{1}{m - 1}}} } } \right]^{ - 1}$$
(17)

The nrFCM algorithm converts to the FCM algorithm by choosing \(f\left( x \right) = x\). Since the cluster centers calculated from (16) depend on \(f^{\prime}\), if the function \(f\) is chosen such that \(f^{\prime}\) be uniform descending, the effect of noise and outliers considerably reduces because these points are mostly far away from the cluster centers. Therefore, the following exponential function is used for this purpose.

$$f\left( {d_{ij}^{2} } \right) = 1 - \exp \left( { - \frac{{d_{ij}^{2} }}{{\sigma_{i}^{2} }}} \right),\;f^{\prime}\left( {d_{ij}^{2} } \right) = \frac{1}{{\sigma_{i}^{2} }}\exp \left( { - \frac{{d_{ij}^{2} }}{{\sigma_{i}^{2} }}} \right)$$
(18)
$$\sigma_{i}^{2} = \frac{{\lambda \sum\limits_{j = 1}^{n} {\mu_{ij}^{m} d_{ij}^{2} } }}{{\sum\limits_{j = 1}^{n} {\mu_{ij}^{m} } }},\;\mu_{ij} = \left[ {\sum\limits_{k = 1}^{c} {\left( {\frac{{d_{ij}^{2} }}{{d_{kj}^{2} }}} \right)^{{\frac{1}{m - 1}}} } } \right]^{ - 1}$$
(19)

where \(\sigma_{i}\) is width of the exponential function and \(\lambda\) is a constant (typically \(\lambda = {1 \mathord{\left/ {\vphantom {1 9}} \right. \kern-0pt} 9}\)).

Flowchart of the algorithm is shown in Fig. 2. Degree of fuzziness \(m\), adjusting parameter of clusters width \(\lambda\), convergence criterion \(\varepsilon\), number of clusters \(c\), and the data matrix \(X\) are inputs of the algorithm. Since the cluster centers change when the equations are updated, \(\sigma_{i}^{2}\) is updated in every iteration. When the data are inputted to the algorithm, \(c\) data points are randomly chosen from the data matrix \(X\) as the initial cluster centers to compute initial cluster centers matrix \(V^{\left( 1 \right)}\). Alternatively, a random partition matrix \(U = \left[ {u_{ij} } \right]^{{}}\) may be generated from which initial cluster centers are calculated using (3). The FCM algorithm starts with these cluster centers and converges when the criterion \(\left\| {V^{{\left( {t + 1} \right)}} - V^{\left( t \right)} } \right\| < \varepsilon\) is met that results in the matrix \(V\) by which the nrFCM algorithm initializes. Then, the nrFCM algorithm iterates until convergence that results the final cluster centers.

Fig. 2
figure 2

Flowchart of the nrFCM algorithm

Full size image

The algorithm is applied through the following step by step procedure.

  1. 1.

    User defined parameters including \(\lambda\), fuzzy exponent \(m\), termination threshold \(\varepsilon\), type of norm matrix \(A\), and number of clusters \(c\) are specified. A random partition matrix \(U_{c \times n}\) is used to initialize the algorithm where \(n\) is number of data points. For example, it can be generated by the command \(U = {\text{rand}}\left( {c,n} \right)\) in MATLAB.

  2. 2.

    The FCM algorithm is then applied to the data. For this purpose, with the initial partition matrix of step 2, initial cluster centers \(\vec{v}_{i}\) are calculated from (3). Membership grades \(u_{ij}\) and cluster centers \(\vec{v}_{i}\) are then repeatedly updated using (3) and at each iteration \(t\), the termination criterion \(\left\| {V^{{\left( {t + 1} \right)}} - V^{\left( t \right)} } \right\| < \varepsilon\) is examined. When the termination criterion is met, the FCM algorithm stops.

  3. 3.

    The cluster centers calculated by the FCM algorithm are used to initialize the nrFCM algorithm. At each iteration \(t\), \(\mu_{ij}\) and \(\sigma_{i}\) are calculated from (19) and then \(\vec{v}_{i}\) and \(u_{ij}\) are calculated from (16) and (17), respectively. These values are repeatedly updated until the termination criterion \(\left\| {V^{{\left( {t + 1} \right)}} - V^{\left( t \right)} } \right\| < \varepsilon\) is again met.

4 Performance analysis

The main objectives of the fuzzy clustering algorithm are identifying dense regions (clusters) in the data and finding centers of these clusters. Regarding these objectives, the performance of the nrFCM algorithms is compared with those of the FCM, PCM, PFCM, T2FCM, and KT2FCM algorithms in this section. Throughout the article, parameters of the nrFCM algorithm are considered as \(\lambda = {1 \mathord{\left/ {\vphantom {1 9}} \right. \kern-0pt} 9},\;m = 2,\;\varepsilon = 0.00001,\;A_{r \times r} = I_{r}\). For the rest of the algorithms the same values are used for \(m\), \(\varepsilon\), and \(A_{r \times r}\).

4.1 Calculating actual cluster centers

Actual cluster centers of real data are not known. Therefore, it is not possible to compare the clustering algorithms based on the accuracy of computed cluster centers of real data and instead synthetic data with known cluster centers are used. Three synthetic data sets are used to compare the performance of the FCM, PCM, PFCM, T2FCM, KT2FCM, and nrFCM algorithms. The first data set with three clusters is studied using these algorithms as shown in Fig. 3. The FCM algorithms cannot find actual cluster centers due to noise impacts on the clustering results. As discussed above, the PCM algorithm provides coincident cluster centers especially when the data are highly noisy, which is clearly apparent in Fig. 3.

Fig. 3
figure 3

Clustering the data with three clusters by different algorithms

Full size image

The FCM and PCM algorithms are combined to derive the hybrid PFCM algorithm for noisy data by utilizing the advantages of both algorithms and avoiding their drawbacks. Although this algorithm performs better than the FCM algorithm for data with few noise and outliers, however, its performance is inferior to that of the FCM algorithm for highly noisy data as shown in Fig. 3. Although cluster centers calculated by the T2FCM algorithm are more accurate than those of the PCM algorithm, but they are too close to each other and far away from the actual cluster centers. However, the KT2FCM algorithm that adds Gaussian kernels to the objective function of the T2FCM algorithm, outperforms the above algorithms. The nrFCM algorithm calculates the most accurate cluster centers by canceling noise impacts by the exponential function as shown in Fig. 3. The actual cluster centers and those calculated by these algorithms are as follows.

$$V_{\text{Actual}} = \left[ {\begin{array}{*{20}c} { - 1.0000} & {0.0000} & {1.0000} \\ {0.0000} & {1.0000} & {0.0000} \\ \end{array} } \right],$$
$$V_{\text{FCM}} = \left[ {\begin{array}{*{20}c} { - 0.9550} & { - 0.0004} & {0.9279} \\ {0.3203} & {0.9618} & {0.3104} \\ \end{array} } \right],$$
$$V_{\text{PCM}} = \left[ {\begin{array}{*{20}c} { 0. 0 5 0 9} & { 0. 0 5 5 9} & { 0. 0 5 2 5} \\ { 0. 6 0 0 7} & { 0. 6 0 8 5} & { 0. 6 0 3 2} \\ \end{array} } \right],$$
$$V_{\text{PFCM}} = \left[ {\begin{array}{*{20}c} { - 0.8781} & {0.0155} & {0.8575} \\ {0.3443} & {0.8875} & {0.3303} \\ \end{array} } \right],$$
$$V_{\text{T2FCM}} = \left[ {\begin{array}{*{20}c} { - 0.0348} & {0.0401} & {0.1341} \\ {0.6367} & {0.7789} & {0.6409} \\ \end{array} } \right],$$
$$V_{\text{KT2FCM}} = \left[ {\begin{array}{*{20}c} { - 0.9598} & {0.0105} & {0.9359} \\ {0.1124} & {0.9429} & {0.1270} \\ \end{array} } \right],$$
$$V_{\text{nrFCM}} = \left[ {\begin{array}{*{20}c} { - 1.0019} & { - 0.0005} & {0.9971} \\ {0.0029} & {1.0005} & {0.0056} \\ \end{array} } \right]$$

To measure the accuracy of different algorithms, the average deviation between the actual and computed cluster centers are calculated by the following equation (Askari et al. 2017b). This metric calculates the average distance between the actual and computed cluster centers.

$$E = \frac{1}{c}\sum\limits_{i = 1}^{c} {\sqrt {\left( {\vec{v}_{i}^{*} - \vec{v}_{i} } \right)^{T} A\left( {\vec{v}_{i}^{*} - \vec{v}_{i} } \right)} }$$
(20)

where \(\vec{v}_{i}^{*}\) and \(\vec{v}_{i}\) are the \(i{\text{th}}\) actual and computed cluster centers, respectively, and \(A\) is the norm matrix defined in (2). The following values are calculated for each of the above algorithms.

$$E_{\text{FCM}} = 0.2266,\;E_{\text{PCM}} = 0.9097,\;E_{\text{PFCM}} = 0.2795,\;E_{\text{T2FCM}} = 0.8194,\;E_{\text{KT2FCM}} = 0.1066,\;E_{\text{nrFCM}} = 0.0035$$

It is observed that the cluster centers calculated by the nrFCM algorithm are the most accurate ones with least deviation from the actual cluster centers.

The second data set with four clusters is studied by these algorithms as shown in Fig. 4. The PFCM algorithm outperforms the FCM algorithm but the PCM and T2FCM algorithms compute coincident clusters. The KT2FCM algorithm is more accurate than the PFCM algorithm. However, the nrFCM algorithm provides the most accurate cluster centers.

Fig. 4
figure 4

Clustering the data with four clusters by different algorithms

Full size image

The actual cluster centers and those calculated by the algorithms are as follows.

$$V_{\text{Actual}} = \left[ {\begin{array}{*{20}c} { - 3.0000} & {0.0000} & {0.0000} & {3.0000} \\ {0.0000} & {7.0000} & {3.0000} & {0.0000} \\ \end{array} } \right],$$
$$V_{\text{FCM}} = \left[ {\begin{array}{*{20}c} { - 2.6821} & { - 0.1260} & {0.0829} & {2.7489} \\ {0.7771} & {7.1040} & {3.5675} & {0.6646} \\ \end{array} } \right],$$
$$V_{\text{PCM}} = \left[ {\begin{array}{*{20}c} {0.0249} & { - 0.0468} & {0.0169} & {0.0198} \\ {3.1654} & {6.0873} & {3.1079} & {3.1260} \\ \end{array} } \right],$$
$$V_{\text{PFCM}} = \left[ {\begin{array}{*{20}c} { - 2.5035} & { - 0.0842} & {0.0502} & {2.6660} \\ {0.8423} & {6.8650} & {3.3904} & {0.6494} \\ \end{array} } \right],$$
$$V_{\text{T2FCM}} = \left[ {\begin{array}{*{20}c} { - 0.1242} & { - 0.1242} & {0.2067} & {0.2067} \\ {6.2008} & {6.2008} & {2.0681} & {2.0682} \\ \end{array} } \right]$$
$$V_{\text{KT2FCM}} = \left[ {\begin{array}{*{20}c} { - 2.6956} & { - 0.1185} & {0.0751} & {2.7619} \\ {0.7310} & {7.0838} & {3.5140} & {0.6286} \\ \end{array} } \right],$$
$$V_{\text{nrFCM}} = \left[ {\begin{array}{*{20}c} { - 2.9990} & { - 0.0134} & { - 0.0023} & {2.9992} \\ { - 0.0022} & {7.0117} & {3.0055} & {0.0053} \\ \end{array} } \right]$$

Average deviations of the cluster centers computed by different algorithms from the actual cluster centers are as follows that proves the superiority of the proposed algorithm over the others.

$$E_{\text{FCM}} = 0.5717,\;E_{\text{PCM}} = 2.4301,\;E_{\text{PFCM}} = 0.5652,\;E_{\text{T2FCM}} = 3.0185,\;E_{\text{KT2FCM}} = 0.5322,E_{\text{nrFCM}} = 0.0079$$

When sizes or densities of the clusters are different, cluster centers are misplaced even in noise-free data sets since larger or denser clusters pull cluster centers toward themselves. A noise-free data set of two clusters with different sizes is studied by the above algorithms as shown in Fig. 5. The FCM algorithm identifies center of the larger cluster accurately but center of the smaller one is displaced towards the large cluster. The PCM algorithm does not find the small cluster and computes coincident cluster centers. The PFCM algorithm places both cluster centers within the larger cluster due to the possibilistic term of the algorithm inherited from the PCM algorithm. The T2FCM algorithm performs better than PCM and PFCM algorithms but it is less accurate than FCM algorithm. The KT2FCM algorithm does not realize the presence of the small cluster and places both cluster centers within the large cluster. The nrFCM algorithm that is initialized by the cluster centers calculated by the FCM algorithm, cancels mutual interactions of the clusters by its exponential function and moves these cluster centers to their actual locations.

Fig. 5
figure 5

Clustering the data with different cluster sizes and densities by various algorithms

Full size image

4.2 Finding dense regions of data

Quality of clustering is indicated by density. High density shows that the cluster centers calculated by the algorithm are located in dense regions of the data. When there are many data points around each cluster center, a larger density \(\rho\) results from the following equation (Askari et al. 2017b).

$$\rho = \frac{{\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{i = 1}^{c} {u_{ij}^{m} d_{ij}^{2} } } }}{{\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{i = 1}^{c} {u_{ij}^{m} } } }}$$
(21)

Equation (3) shows that the FCM algorithm updates cluster centers by a linear equation. However, the nrFCM algorithm employs the nonlinear update Eq. (16) because of the exponential function used in the objective function (15). The nonlinear update equation takes more time per iteration and consequently the FCM algorithm is faster than the nrFCM algorithm. These algorithms are applied to 23 synthetic and real data sets and are compared in terms of density of clusters, runtime, and number of iterations as provided in Table 1. Data sets 1 to 4 are the four synthetic noisy data sets studied above and shown in Figs. 1, 3, 4, and 5. Data sets 5 to 17 are real data taken from the UCI Machine Learning Repository. The synthetic noise-free data sets 18 to 23 shown in Fig. 6 contain different numbers of clusters to study performance of the algorithms when there are large numbers of clusters in the data. Since the nrFCM algorithm initializes by the cluster centers calculated by the FCM algorithm and starts when the FCM algorithm converges, this algorithm demands higher number of iterations and runtime. For example, for DATA2 in Table 1, the FCM algorithm converges after 25 iterations with runtime of 7.835 s. Then the nrFCM algorithm starts and terminates after 20 iterations (45–25) and runtime of 15.23 s (23.065–7.835). On average, each iteration of the FCM algorithm takes 0.392 s (7.835/20) and each iteration of the nrFCM algorithm takes 0.761 s (15.23/20). For data sets 1 to 3 (shown in Figs. 1, 3, and 4) that contain noise and outliers, density of clustering results of the nrFCM algorithm is higher than that of the FCM algorithm because the nrFCM algorithm finds actual cluster centers where a large number of data points are concentrated. There is no noise or outliers in data set 4 (shown in Fig. 5) but the FCM algorithm cannot find actual cluster centers because of different sizes and densities of the clusters. Displacement of the cluster centers from their actual locations decreases density of clustering results. There are sporadic observations and probably outliers in the real data sets 5 to 17 and consequently the FCM algorithm cannot find dense regions of these data sets but the nrFCM algorithm identifies dense clusters with higher densities as compared to the FCM algorithm. There is no noise and outliers in data sets 18 to 23 and their clusters have the same sizes. Therefore, the FCM algorithm finds actual cluster centers of these data sets and has the same density as the nrFCM algorithm. Since the data sets are clean, the nrFCM algorithm iterates only two times to correct the insignificant displacements of the cluster centers calculated by the FCM algorithm due to the interactions between the clusters. For example, consider the cluster center \(\left[ {\begin{array}{*{20}c} 1 & { - 2} \\ \end{array} } \right]^{\text{T}}\) of DATA5 shown in Fig. 6. The FCM algorithm calculates this cluster center as \(\left[ {\begin{array}{*{20}c} {1.0030} & { - 2.0034} \\ \end{array} } \right]^{\text{T}}\) due to the interactions between this cluster and each of the other four clusters and then the nrFCM algorithm moves it to \(\left[ {\begin{array}{*{20}c} {1.0000} & { - 2.0000} \\ \end{array} } \right]^{\text{T}}\) by damping impacts of other clusters on this cluster by the exponential function.

Table 1 Number of iterations and runtime (seconds) of the FCM and nrFCM algorithms
Full size table
Fig. 6
figure 6

Six synthetic data sets with no noise and outliers

Full size image

In summary, according to Table 1, runtime and number of iterations of the nrFCM algorithm is higher than those of the FCM algorithm due to nonlinear update equation for cluster centers. Since the nrFCM algorithm finds dense regions of the data as fuzzy clusters, the density of the clusters calculated by this algorithm is higher than that of the FCM algorithm. Even if there are no noise and outliers in the data, the FCM algorithm cannot find exact cluster centers because of the interactions between the clusters. However, the nrFCM algorithm cancels these interactions by the exponential function introduced in the objective function (15) and finds precise locations of the cluster centers.

5 Conclusions

Presence of noise and outliers in data impairs the accuracy of clustering algorithms and results inaccurate cluster centers. Noise-resistant FCM (nrFCM) algorithm is presented in this article for the data with noise and outliers. The nrFCM algorithm reduces contributions of noise and outliers by introducing an exponential function in the objective function of the FCM algorithm. It is shown that when the data are noisy, the FCM algorithm fails to determine actual cluster centers but the nrFCM algorithm works satisfactorily. Moreover, the nrFCM algorithm finds dense regions of the data more precisely than the FCM algorithm, which is indicated by the density of the clustering results. It is also shown that even if the data are noise-free, the FCM algorithm cannot calculate actual cluster centers precisely because of different cluster sizes and the interactions between clusters.

In summary, the main contribution of the present work is to improve the performance of the well-known FCM algorithm by proposing the nrFCM algorithm with the following characteristics:

  1. 1.

    Finding accurate cluster centers in the presence of noise and outliers.

  2. 2.

    Placing the cluster centers in dense regions of the data so that they represent the actual structure of the data.

  3. 3.

    Finding accurate cluster centers when sizes of the clusters are considerably different.

Despite high accuracy, the nrFCM algorithm incurs higher runtime because of nonlinear update equation for the cluster centers. Therefore, the runtime of the algorithm mainly depends on the function \(f\) in Eq. (15) for which exponential function is used in the present work. It is possible to find a proper function capable of canceling noise impacts with less runtime. For example, stepwise linearization of the exponential function may be a proper choice. Moreover, although \(\lambda = 1/9\) works properly for the data sets studied in the article, but it is more appropriate to calculate this parameter according to the structure of the data (for example dispersion of the data in different dimensions). This makes the algorithm more robust and efficient.