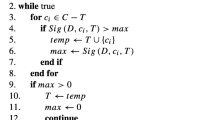Fast feature selection algorithm for neighborhood rough set model based on Bucket and Trie structures

Abstract

Feature selection is viewed as the problem of finding the minimal number of features from an original set with the minimum information loss. Due to its high importance in the fields of pattern recognition and data mining, it is necessary to investigate fast and effective search algorithms. In this paper, we introduce a novel fast feature selection algorithm for neighborhood rough set model based on Bucket and Trie structures. This proposed algorithm can guarantee to find the optimal minimal reduct by adopting a global search strategy. In addition, the dependence degree is subsequently used to evaluate the relevance of the attribute subset. Consequently, the proposed algorithm is tested on several standard data sets from UCI repository and compared with the most recent related approaches. The obtained theoretical and experimental results reveal that the present algorithm is very effective and convenient for the problem of feature selection, indicating that it could be useful for many pattern recognition and data mining systems.

1 Introduction

Currently, with the rapid development of modern technologies and the increasing rate of data generation, information sources like mobile phones, social media, imaging devices, and sensors automatically generate huge amount of information that needs to be stored and processed. As a result, the created data always contain some attributes that are redundant and irrelevant for the process of data analysis and pattern recognition (Cai et al. 2018). Feature Selection (FS) as a pivotal step of data preprocessing, it refers to the process of choosing a minimal subset of attributes from the original set of all attributes, by removing irrelevant and redundant features and maintaining only those which are most informative and significant, according to certain selection criterion (García et al. 2015). Feature selection has been widely studied in the fields of text mining (Wang et al. 2017), bioinformatics data analysis (Urbanowicz et al. 2018), image classification (Thangavel and Manavalan 2014), and information retrieval (Lai et al. 2018). In fact, there are many reasons for performing feature selection: removing irrelevant data, increasing predictive accuracy of the learning models, reducing the computation cost of analysis process, and improving the interpretability of the data (García et al. 2015). In general, Feature Selection that is also called Attribute Reduction can be based on statistical approach, spars learning approach, information theory, and rough set theory (Cai et al. 2018; Li et al. 2017).

Rough Set Theory (RST) was originally introduced by Pawlak (1982), as a mathematical tool to deal with imprecise, uncertain, and vague information. In fact, the Rough Set Theory is considered as a special form of Granular Computing, since the equivalence relation of RST can act as type of granularity, where the target concept is approximated by a single granular structure. In this context, a wide number of research have been established to study Rough Set models from the Granular Computing perspective. William-West and Singh (2018) studied information granulation for Rough Fuzzy Hypergraphs. Liang et al. (2018) proposed an optimal granulation selection method for multi-label data based on Multi-granulation Rough Sets. Mandal and Ranadive (2019) investigated interval-valued Fuzzy Probabilistic Rough Sets, based on multi-granulation approach. Skowron et al. (2016) emphasized the role of Rough Set-based methods in Interactive Granular Computing and discussed some of its important applications. In general, The RST involves two important concepts (Fan et al. 2018). The first concept is approximation, where any set of objects can be approximated by a pair of sets known as upper and lower approximations, based on an equivalence relation. The second concept is attribute reduction, which aims to reduce the number of attributes and preserve the same classification quality as the original full set of attributes (Fan et al. 2018). However, the classical RST is based on crisp equivalence relation that can only operate on discrete and categorical attributes. Therefore, processing continuous numerical features requires data discretization, resulting in a large amount of information loss. To overcome this problem, many generalization of the RST has been introduced; for instance, Fuzzy Rough Set (FRS) (Zhang et al. 2018b), Neighborhood Rough Set (NRS) (Hu et al. 2008; Yong et al. 2014), Dominance Rough Set (DRS) (Zhang and Yang 2017), and Variable Precision Rough Set (VPRS) (Shen and Wang 2011).

Basically, the main difference between all these RST generalizations is related with the exploitation of the equivalence relation and the definition of the subset operator. The NRS (Yong et al. 2014) employs a neighborhood relation to deal with numerical features directly without discretization. The DRS use a dominance relation instead of an equivalence relation. This allows DRSA to handle the inconsistencies that are typical of criteria and preference-ordered decision classes (Zhang and Yang 2017). The VPRS approach extends the classical RST, by relaxing the subset operator to deal with noisy data and uncertain information, allowing objects to be classified with an error smaller than a given predefined level or probability threshold (Shen and Wang 2011), while the FRS approach encapsulates the concepts of fuzziness and indiscernibility, which occurs as a result of uncertainty existing knowledge (Zhang et al. 2018b). The FRS combines fuzzy set theory and rough sets, so as to provide mathematical tools to reasoning with uncertainty for real-valued data. In fact, the Fuzzy Set Theory was introduced by Zadeh (1965) as an extension of the classical set theory, by employing a membership function in the real unit interval (Chen and Chang 2011; Chen and Chen 2015; Chen et al. 2012, 2013; Cheng et al. 2016). Finally, a detailed summary of some existing extensions of Rough Sets Theory and its relationships with other approaches, such as fuzzy set theory, granular computing, and multi-criteria decision analysis, can be found in Kacprzyk and Pedrycz (2015), and Pawlak and Skowron (2007) (Pedrycz and Chen 2011, 2014, 2015).

Neighborhood Rough Set (NRS) has been first proposed in Hu et al. (2008), to support numerical attributes using a neighborhood relation. This neighborhood relation can be used to produce a family neighborhood information granules, which are able to approximate the decision classes. In this regard, the notable point of the Neighborhood Rough Set models is their capability to control the granularity of data analysis by adjusting the neighborhood parameter $\theta$ (Chen et al. 2017). Figure 1 exemplifies the notion of upper and lower approximations of Rough Set and Neighborhood Rough Set Models. In general, NRS model is considered as an effective tool for feature selection, especially for numerical data. Consequently, much effort in the literature has been devoted to develop different measures for feature evaluation, where most existing evaluation criterion can be divided into three main approaches: Positive region (Qian et al. 2010), Combined region (Parthaláin et al. 2010), and Entropy (Sun et al. 2012). Indeed, the positive region is one of the most used evaluation metrics to distinguish between features, since it focuses on the consistent samples that can be correctly classified to the decision classes, simultaneously, ignoring noisy and irrelevant samples that belong to the overlapping boundaries of classes (Li et al. 2013; Qian et al. 2010).

Fig. 1

Schematic demonstration of the main components and the correspondence between a Rough Set Model and b Neighborhood Rough Set Model

Generally speaking, for a data set with m features, finding a minimal subset of features which simultaneously preserve suitable high accuracy in representing the original features, should evaluate $2^m$ candidate subsets using exhaustive search, and therefore, the problem of minimal reduct generation is unfortunately NP-hard (Swiniarski and Skowron 2003). In addition, since data set may have more than one reduct, most of solutions are aimed to find a reasonable short reduct, without exhaustively generating all possible subsets. In this connection, many approaches have been proposed to address this issue with respect to Rough Set Theory. The Quick Reduct (QR) algorithm, proposed by Chouchoulas and Shen (2001), is one of the classic methods, which is a greedy search algorithm using dependence of the positive region (Chouchoulas and Shen 2001). The QR algorithm provides good time performance for its fast heuristic search. However, it can be easily trapped in a local optimum (Jensen and Shen 2009), also the computational complexity of the QR algorithm grows exponentially with respect to the number of instance in the data set (Mannila and Räihä 1992). Qian et al. (2010) introduced a theoretic framework, called positive approximation, which is defined with respect to different granulation order. This approach was used to accelerate a heuristic process of attribute reduction. More recently, to enhance the computational time of QR algorithm, Yong et al. (2014) proposed a quick attribute reduct algorithm based on neighborhood rough set model. The key idea of this algorithm is to divide the data set into a set of buckets according to their Euclidean distances, and then iterate each record by the sequence of buckets to calculate the positive region of neighborhood rough set model. Yang and Yang (2008) introduced a condensing tree structure to reduce the storage requirement of the feature selection methods based on rough set model. This structure aims to provide a compact representation of the discernibility matrix, and, therefore, giving the possibility to obtain the heuristic information for feature reduction efficiently. For more relevant studies on Rough Set Theory, we refer the readers to Liu et al. (2018), Shi et al. (2018), Xu et al. (2017), and Zhang et al. (2018a).

On other research direction that deals with enhancing the search strategy of attribute reduction algorithm. Chen et al. (2011) presented a feature selection algorithm based on rough set model and the power set tree structure. In fact, the power set tree is an ordered tree representing the search space of all attribute subsets, where each possible reduct is mapped to a node of the tree. The authors used tree rotation and backtracking to enhance time required for finding minimal reduct set. Rezvan et al. (2015) proposed a new feature selection algorithm based on Rough Set Theory and Trie structure. The proposed algorithm is exact and can provide the optimal solution using a breadth-first traversal strategy of the Trie structure (Bodon and Rónyai 2003), where each node of the Trie is associated with a possible reduct. Recently, several meta-heuristic algorithms has been used to improve the search strategy of feature selection, such as genetic algorithms (Jing 2014), ant colony optimization (Chen et al. 2010), tabu search (Hedar et al. 2008), and particle swarm optimization (Wang et al. 2007). However, all these meta-heuristic algorithms are not exact and their convergence cannot be guaranteed due to their stochastic nature. Most of the existing researches considered the computation aspect of Rough Set model and only a few works focused on improving the computational time of Neighborhood Rough Set model. Therefore, lot of effort still needs to be done in this context. In addition, new algorithms can be presented to obtain better results when data sets become larger.

Motivated by the advantages of Trie structure, such as the efficient representation of the search space of feature selection problem, also inspired by the notion of Bucket structure, due to its ability to reduce the computation time of searching the neighbor samples (Yong et al. 2014). We aim, in this paper, to present a fast feature selection algorithm for Neighborhood Rough Set model based on Bucket and Trie structures. The Trie is used to store all the possible feature subsets in a particular order, so as to enhance the search and elimination for non-reduct subsets, while the Bucket structure is used to reduce the time required for evaluating the positive region. Consequently, several numerical experiment are carried out, in this study, to evaluate the performance of the proposed algorithm in comparison with different existing approaches for neighborhood rough set model. The proposed algorithm is experimented using different standard UCI data sets for testing the feature selection correctness and computational performance.

To summarize, the major contributions of the present paper include the following aspects: (1) The development of a new feature selection method based on Neighborhood Rough Set model. (2) Trie and Bucket structures are considered to design an efficient algorithm for searching the minimal feature reduct. (3) Extensive experiments on several data sets from UCI repository, verify the efficiency, and the effectiveness of the proposed feature selection method.

The remainder of this paper is organized as follows. In Sect. 2, we present the fundamental concept of Neighborhood Rough Set model. In Sect. 3, we introduce our proposed feature selection algorithm. Section 4 is devoted to present the experimental results and discussions. Finally, Sect. 5 concludes the paper and suggests directions for future works.

2 Fundamentals on neighborhood rough set

In this section, we briefly recall some basic concepts and definitions of the Neighborhood Rough Set Model with the Quick Reduct algorithm, which are needed for the following sections.

2.1 Neighborhood rough set model

As has been stated in the introduction, the classical rough set model introduced by Pawlak (1982) can only operate on data sets of nominal and categorical attributes. For real-valued features, we will present, in this subsection, the Neighborhood Rough Set model (Yong et al. 2014). One of the most important aspects of NRS is their capability to control the granularity of data analysis (Chen et al. 2017). First, we start by defining a metric function.

Definition 1

Given a nonempty set of records $U=\{x_1,x_2,\ldots ,x_n\}$, for any i and j a distance function $\varDelta (x_i,x_j):U\times U \mapsto [0,+\infty )$ satisfies the following properties:

• (1) $\varDelta (x_i,x_j)\ge 0$: Distances cannot be negative;

• (2) $\varDelta (x_i,x_j)=0$: If and only if $x_i=x_j$;

• (3) $\varDelta (x_i,x_j)=\varDelta (x_j,x_i)$: Distance is symmetric;

• (4) $\varDelta (x_i,x_k)+\varDelta (x_k,x_j)\ge \varDelta (x_i,x_j)$: Triangular inequality.

In fact, the p-norm is one of most widely used metric functions, where the Euclidean distance is special case of the p-norm for $p=2$. The p-norm is given by:

$$\begin{aligned} \varDelta _C(x_i,x_j)=\left( \sum _{a\in C}|f(x_i,a)-f(x_j,a)|^p \right) ^{1/p}, \end{aligned}$$

with $f(x_i,a)$ and $f(x_j,a)$ are, respectively, the values of the objects $x_i$ and $x_j$, corresponding to the attribute a with C is a set of attributes. Along this paper, we will use the Euclidean distance as metric function.

Definition 2

A neighborhood decision system is denoted by ${\mathrm{NDS}}=\langle U,C\cup D, \theta \rangle$, where $U=\{x_1,x_2,\ldots ,$$x_n\}$ is nonempty set of records, $C\cup D$ is a nonempty finite set of features, with $C\cap D=\emptyset$. $C=\{a_1,a_2,\ldots ,a_m\}$ is a nonempty set of conditional attributes, D is the set of decision attributes and $\theta$ is a neighborhood parameter $\theta \ge 0$. In addition, we can define a mapping function f for each $x\in U$ and $a\in C$, as $f(x,a)=V_a$, where $V_a$ is the value of the attribute a corresponding to the object x.

Table 1 presents an example of a decision system, which consists of four objects records $U=\{x_1,x_2,x_3,x_4 \}$ defined by four conditional features $C=\{a,b,c,d\}$ of numerical values, and one decision attribute $\{e\}$ that takes two class labels $\{1,2\}$. This table will be used to illustrate the basic operations and concepts of the Neighborhood Rough Set model.

Table 1 An example of a decision system

Definition 3

Let ${\mathrm{NDS}}=\langle U,C\cup D, \theta \rangle$, we note $\theta _B(x)$ as the neighborhood granule of $x_i$, and it can be defined as the hyper-sphere with center $x_i$ and radius $\theta$ by:

$$\begin{aligned} \theta _B(x)=\Big \{y: \forall y\in U, \varDelta _B(x,y)\le \theta \Big \}. \end{aligned}$$

More precisely, $\theta _B(x)$, also called information granule, it contains all the records that share the same characteristics as the object x.

Example 1

According to the previous definition, using $\theta =0.15$ and for $P=\{b\}$, we have: $\theta _P(x_1)=\{x_1,x_2,x_3\}$, $\theta _P(x_2)=\{x_1,x_2,x_3\}$, $\theta _P(x_3)=\{x_1,x_2,x_3\},$ and $\theta _P (x_4 )=\{x_4\}$.

Similar to the Pawlak’s rough set theory (Pawlak 1982), we can define the neighborhood lower and upper approximations of any subset of U.

Definition 4

Let ${\mathrm{NDS}}=\langle U,C\cup D, \theta \rangle$ a neighborhood decision system. For $B\subseteq C$ and $X\subseteq U$, the neighborhood lower and upper approximations of X, denoted, respectively, by $\underline{N_B}(X)$ and $\overline{N_B}(X)$, are defined as:

$$\begin{aligned} \underline{N_B}(X)= & {} \Big \{x \in U: \theta _B(x) \subseteq X\Big \},\\ \overline{N_B}(X)= & {} \Big \{x \in U: \theta _B(x) \cap X \ne \emptyset \Big \}. \end{aligned}$$

In the sense of Definition 4, the lower approximation $\underline{N_B}(X)$ is the set of all objects from U that can be correctly classified as elements from X with respect to the attributes B, while the upper approximation $\overline{N_B}(X)$ is the set that contains all objects from U that can be probably classified as elements from X with respect to the attributes B.

Based on the lower and upper approximations, we can note that the knowledge that can be retrieved from the universe U are about the elementary granules $\underline{N_B}(X)$ and $\overline{N_B}(X)$, instead of about the individual elements of X.

Definition 5

Let ${\mathrm{NDS}}=\langle U,C\cup D, \theta \rangle$, with $B\subseteq C$ and $X\subseteq U$. The universe U can be divided into three different regions: the positive region, the boundary region, and the negative region, with respect to X according to the set of attributes B. These regions are, respectively, defined by the following relations:

$$\begin{aligned} {\mathrm{NPOS}}_B(X) &= \underline{N_B}(X),\\ \mathrm{NBND}_B(X) &= \overline{N_B}(X)-\underline{N_B}(X),\\ \mathrm{NNEG}_B(X) &= U-\overline{N_B}(X). \end{aligned}$$

Let $U/D=\{D_1,D_2,\ldots ,D_r\}$ be a decision partition of the universe U, where $D_i$ is composed of all the objects associated with the class label i. For any subset $B\subseteq C$, we give the following definition.

Definition 6

The neighborhood positive region of the decision system, denoted by ${\mathrm{NPOS}}_B(D)$, which is a subset the records whose neighborhoods consistently belong to one of the decision classes $D_i$, is given by:

$$\begin{aligned} {\mathrm{NPOS}}_B(D)=\bigcup _{i=1}^{n}\underline{N_B}(D_i), \end{aligned}$$

where n is the total number of decision partitions.

Noting that the neighborhood positive region is defined as the union of all lower approximations of each decision partition.

Example 2

Based on decision attribute $\{e\}$ in Table 1, we can divide the set of records into two decision partitions $U/D=\{D_1,D_2 \}$, which are $D_1=\{x_1,x_2 \}$ and $D_2=\{x_3,x_4 \}$, assuming that $\theta =0.15$ and the set of features is $P=\{b\}$. First, we can calculate the lower approximations with respect to $D_1$ and $D_2$ as: $\underline{N_P}(D_1)=\{\emptyset \}$ and $\underline{N_P}(D_2)=\{x_4\}$. $\underline{N_P}(D_1)$ gives an empty set, since $x_1$, $x_2$, and $x_3$ belong to the same information granule, but with different decision labels (Example 1). Thus, ${\mathrm{NPOS}}_B(D)$ can be computed as: ${\mathrm{NPOS}}_B(D)=\underline{N_P}(D_1)\cup \underline{N_P}(D_2) =\{x_4\}$.

Definition 7

Let ${\mathrm{NDS}}=\langle U,C\cup D, \theta \rangle$ be a neighborhood decision system, with $B\subseteq C$. The dependence degree $\mu _B (D)$, also called the quality of classification, can be defined as:

$$\begin{aligned} \mu _B (D)=\frac{|{\mathrm{NPOS}}_B(D)|}{|U|}. \end{aligned}$$

It is worth mentioning that the greater the dependence degree $\mu _B (D)$, the stronger is the classification quality of the attribute subset B. If $\mu _B (D)=1$, then D depends totally on B. If $0<\mu _B (D)<1$, then D depends partially on B. While if $\mu _B (D)=0$ then D does not depends on B. In fact, the dependence degree can be used as relevance measure in greedy algorithm to compute the attribute reduct.

Example 3

Considering Table 1, let $\theta =0.15$ and $P_1=\{b\}$ and $P_2=\{c\}$. Based on (Example 2) and the definition of the dependence degree, it is easy to verify that: $\mu _{p_1} (D)=|{\mathrm{NPOS}}_{P_1}(D)|/|U|=0.25$. While, for $\mu _{P_2} (D)$, we can first compute ${\mathrm{NPOS}}_{P_1}(D)$ based on $\underline{N_{P_2}}(D_1)=\{x_1,x_2\}$ and $\underline{N_{P_2}}(D_2)=\{x_3,x_4\}$, and by simple calculations, we can demonstrate that $\mu _{P_2} (D)=1$. As a conclusion, we can confirm that the attribute $\{c\}$ is more relevant than $\{b\}$, and can preserve the same classification quality as the original full set of features.

Definition 8

Given the NDS $=\langle U,C\cup D, \theta \rangle$, with $R\subseteq C$. The set R is called a reduct if:

$$\begin{aligned} \mu _{R}(D)=\mu _{C}(D). \end{aligned}$$

In addition, R is called a minimal reduct if:

$$\begin{aligned}&\text {(i) }~~~ \mu _{R}(D)=\mu _{C}(D),\\&\text {(ii) }~~~ \forall a \in R ~~ \mu _{R-\{a\}}(D)<\mu _{C}(D). \end{aligned}$$

Indeed, this property shows that removing any attribute from the minimal reduct will lead to decreasing the significance of the present minimal reduct.

Proposition 1

Given a neighborhood decision system${\mathrm{NDS}}=\langle U,C\cup D, \theta \rangle$, with$B_1,B_2\subseteq C$and$B_1\subseteq B_2$, we have:

$$\begin{aligned} \mu _{B_1}(D)\le \mu _{B_2}(D). \end{aligned}$$

Proof

Given $B_1\subseteq B_2$, with $U/D=\{D_1,D_2,\ldots ,D_r\}$ is the decision partition of the universe U, we have $\underline{N_{B_1}}(D_1 )\subseteq \underline{N_{B_2}}(D_1 )$, $\underline{N_{B_1}}(D_2 )\subseteq \underline{N_{B_2}}(D_2 )$, $\ldots$ and $\underline{N_{B_1}} (D_r ) \subseteq \underline{N_{B_2}} (D_r )$. Using Definition 6, we can write ${\mathrm{NPOS}}_{B_1} (D)\subseteq {\mathrm{NPOS}}_{B_2} (D)$. Therefore, we have $\mu _{B_1} (D)\le \mu _{B_2} (D)$. The proof is completed. $\square$

This proposition is called the monotonicity property and it is very important for designing a forward feature selection algorithms, which guarantee that adding any new attribute into the existing subset does not lead to decrease in the classification quality of the new subset.

2.2 Feature selection based on quick reduct algorithm

The main objective of attribute reduction is to find a small subset of relevant attributes, which can provide the same quality of classification as the original set of attributes. In this respect, Quick Reduct algorithm, also called hill-climbing algorithm, usually employ rough set dependence degree as quality measure for selecting the attribute reduct.

In this subsection, we present the Quick Reduct algorithm given in Chen and Jensen (2004), which attempts to calculate a minimal reduct without exhaustively generating all possible subsets, by applying a forward selection and starting from an empty set of features. This algorithm tries to add in each iteration the most significant feature from the candidate set based on the dependence degree of its positive region. Accordingly, Algorithm 1 describes the steps involved in the generation of the neighborhood positive region according to a set of conditional attributes. Brief comments are provided after ”;” with italic text style.

In the following, the whole procedure for the feature selection based on quick reduct method is given in Algorithm 2. This algorithm will be named as Neighborhood Rough Set Feature Selection based on Quick Reduct, and denoted by NRSFSQR along this paper.

Although, the Quick Reduct algorithm have been extensively used due to its simplicity, the major limitation of QR algorithm, is it does not guarantee to find minimal reduct as long as it employs a greedy algorithm that can be easily stuck in a local optimum (Jensen and Shen 2009).

3 Proposed neighborhood rough set feature selection method

In this section, we first present the basic definitions, properties and operations of Bucket and Trie structure. Then, we introduce our proposed method for feature selection based on these two structures.

3.1 Bucket structure

The Bucket structure, also called bin structure, has been efficiently used in the distribution sort paradigm (Cormen et al. 2009). The concept of Bucket structure is very simple and its utility relies on distributing the elements of the universe into a finite number of regions, named buckets, according to a given criterion. Consequently, the content of each bucket can be processed individually. In this respect, the Bucket structure constitutes a basic component for the proposed attribute selection algorithm, since it can be used to reduce the time complexity of neighborhood positive region generation from $O(mN^2)$ to $O(mN^2/K )$ for the average case, where K, N, and m are, respectively, is the total number of used buckets, the number of conditional attributes, and the total number of records in U (Yong et al. 2014).

Definition 9

Let ${\mathrm{NDS}}=\langle U,C\cup D, \theta \rangle$ be a neighborhood decision system, with $S\subseteq C$. The set of records U can be divided into a finite number of buckets $B_0,B_1,\ldots$, $B_k$. These buckets are constructed as follows:

$$\begin{aligned} B_i = \left\{ x: x\in U \text { and } \left\lceil \frac{\varDelta _S (x,x_0)}{\theta }\right\rceil = i\right\} \end{aligned},$$

where $\lceil r\rceil$ is the largest integer lesser than or equal to r, and $x_0$ is a minimal record constructed from U as $\forall a\in S, f(x_0,a)=min_{x \in U} f(x,a)$

Remark 1

It is obvious that the neighborhood granule $\theta _S (x)$ of any record x is within the union of three adjacent buckets $B_{k-1}, B_k$ and $B_{k+1}$, where $k=\lceil \frac{\varDelta _S(x,x_0)}{\theta }\rceil$ with $S\subseteq C$. In fact, this remark is very important for time optimization of the proposed method, since it can reduce the time required for computing the neighborhood positive region ${\mathrm{NPOS}}_S (D)$. This remark is illustrated in Fig. 2.

Fig. 2

Illustration of the Bucket structure

According to the previous definition, the bucket generation is exemplified bellow.

Example 4

Considering the data set of Table 1, the corresponding Bucket structure, for the set of features $R=\{d\}$, $x_0=x_2$ and $\theta =0.1$, is given by: $B_0=\{x_2,x_4 \}$, $B_1=\{x_1 \},$ and $B_2=\{x_3 \}$. Therefore, based on the definition of Bucket, the neighborhood granule of the record $x_2$ is contained only in the union $B_0 \cup B_1$$(\theta _R(x_2)\subseteq B_0 \cup B_1$).

As mentioned above, the time complexity of positive region generation, using Algorithm 1, is $O(mN^2)$ for a decision table with N records and m conditional features. If the number m is fixed, Algorithm 1 for positive region generation becomes impracticable when the number N of sample is very large. Hence, based on the definition of Bucket structure, we present the fast algorithm for the evaluation of the neighborhood positive region as follows:

3.2 Trie structure

Trie structure has been first introduced by Fredkin (1960), and have been effectively used for dictionary representation and for storing associative arrays, where the keys are usually strings. The original idea behind using Trie structure is that they could be a good compromise between running time and memory (Bodon and Rónyai 2003). Moreover, a Trie has a number of advantages over binary search trees and other data structures (Bodon and Rónyai 2003), this is due to the fact that Trie structure stores data in particular fashion, so that the search and the insertion of a node are very fast, more precisely, in the worst case O(m) time, where m is the length of the key string.

Fig. 3

The result of the attributes Trie structure generation for $C=\{a,b,c,d\}$. In the left, the Trie with the binary codes of features set, while the Trie in the right corresponds to the names of features

In this paper, we will employ Trie structure for the representing the attribute searching domain. Accordingly, we propose a search strategy that exploits the important properties of Trie structure to enhance the computational cost of the selection algorithm and to significantly reduce the number of evaluated subsets.

Definition 10

Let $C=\{a_1,a_2,\ldots ,a_m\}$ a set of m conditional attributes. The Trie structure of attributes set C, denoted by T, is a search tree that is composed of $2^m$ nodes and m levels, where each node in a level i contains a unique set of $m-i$ attributes. The nodes in the Trie structure are represented by binary code of the attribute $bc=\{b_1,b_2,\ldots ,b_m\}$ and a list of children nodes $l=\{n_1,n_2,\ldots ,n_t\}$ with $b_i$ takes the values 1 or 0, meaning, respectively, the existence or the absence of the attribute $a_i$ in the set corresponding to the node.

The root node of the Trie represents the full set of attribute C, and therefore, bc is composed of m ones, where the child nodes order is defined in particular fashion that optimize the search and the elimination of given set of attributes.

According to the previous definition, Algorithm 4 gives the generation algorithm of the Trie structure.

Example 5

Considering a set of conditional attributes $C=\{a,b,c,d\}$. According to the generation procedure described in Algorithm 4, the Trie structure corresponding to set C is exemplified by Fig. 2. Indeed, the process for Trie generation can be simplified in two steps: First, the root node represents the full set of attributes and, therefore, its binary code is composed of 4 ones, $bc=\{1,1,1,1\}$. Then, we create the childes of root node, one by one, in the same order as in C, by deleting each time one attribute. This process is repeated iteratively for each of the child nodes, until we reach an empty set of attributes (i.e $bc=\{0,0,0,0\}$).

Remark 2

One can notice from Fig. 3 that the Trie is imbalanced and its left branches are larger than its right branches. Therefore, based on breadth-first traversal, the Trie structure allows us to eliminate a large number of possible candidate if a father node is not a reduct.

As previously mentioned, the Trie structure supports two basic operations, search and insert. Since the Trie structure is completely generated by Algorithm 4, we are not concerned by adding or searching for any new node and, therefore, the pseudocode for search and insert operations are not included in this paper.

3.3 Neighborhood rough set feature selection based on Bucket and Trie structure

In general, for constructing a feature selection algorithm, we should consider two main aspects: (1) attribute evaluation measures and (2) the search strategy. In this respect, our proposed fast attribute reduct algorithm adopts the dependence degree of the neighborhood positive region as an evaluation metric for attribute selection. In addition, we employ breadth-first search on the Trie structure as a search strategy.

As well known, the monotonicity property of the dependence degree (Proposition 1) is a suitable criterion to stop the search algorithm for attribute reduction, simultaneously, it guarantees that the minimal attribute subset has the same discrimination power as the original set of attributes. Therefore, it will be used in our proposed algorithm to greatly improve the computation speed.

Let ${\mathrm{NDS}}=\langle U,C\cup D,\theta \rangle$ be a neighborhood decision system and T be the Trie structure corresponding to C. For a given node n of T having an attributes set B ($B\subseteq C$), we can distinguish between two cases:

$\bullet$ Case 1: $\mu _B (D)= \mu _C (D)$, the dependence degree of D to B is equal to the dependence degree of D to the root node C. In this case, B is a reduct, and therefore, we should test all the children associated with the node n.

$\bullet$ Case 2: $\mu _B(D)< \mu _C(D)$, the dependence degree of D to B is lower than the dependence degree of D to the root node C. In this case, B is not a reduct, and using the monotonicity property, this guarantee that any subset of B is, consequently, not a reduct. Therefore, we can eliminate all the child nodes of the node n.

It is important to note that we will employ a breadth-first search, and thus, we are conducted to evaluate the nodes of the Trie, level by level, starting from the root node. Therefore, we will use a lookup table to store all the non-reduct set of features. In fact, this lookup table allows us to eliminate any node that is a subset of at least one of the elements of the lookup table.

Based on the above analysis, the whole procedure of the proposed feature selection algorithm is given in Algorithm 5. This algorithm will be denoted as NRSFSBT along this paper.

As a last remark of this subsection, if the number of features in the minimal reduct is very small compared to the total number of features, then the corresponding minimal solution is located at the low levels of the Trie structure. Thus, the algorithm may take more time to find the best reduct.

4 Experimental results and discussion

In this section, several numerical experiments are performed to validate the effectiveness of our proposed feature selection algorithm in comparison with different existing methods that are based on Rough Set Theory. Therefore, this section is divided into five subsections. In the first one, we provide a comparison in terms of feature selection exactitude between the newly introduced feature selection algorithms and the other existing ones. Then, we demonstrate the computational performance of our feature selection method, with regard to running time and the number of evaluated subsets in the second subsection. In the third one, we focus on the evaluation of the neighborhood parameter effects. And in the fourth one, we depict the influence of the number of samples in the data set on different algorithms. Finally, the classification performance induced by the selected feature of the newly introduced algorithm is evaluated using different learning methods. In what follows, to demonstrate the performance and the accuracy of the proposed algorithm NRSFSBT, we used three feature selection methods for comparison: the Neighborhood Rough Set Feature Selection based on the Quick Reduct algorithm (Yong et al. 2014), the Neighborhood Rough Set Feature Selection based on the Power Set Tree (Chen et al. 2011), and Neighborhood Rough Set Feature Selection based on the Trie structure (Rezvan et al. 2015). For convenience to the readers, the three feature selection algorithms are denoted as NRSFSQR, NRSFSPST, and NRSFST, respectively.

For the experiments, we selected nine data sets from the UCI Machine Learning Repository (Dheeru and Karra Taniskidou 2017). The information details of the selected data sets are summarized in Table 2. Since some data sets do not have the same scale of values for the attributes, we decided to normalize the values of each of attributes to be within the numerical range of [0, 1]. Finally, it is important to note that all the experimental simulations were conducted on a personal computer under Windows operating system, with Intel Core i7 3.4 GHz processor and 8 GB RAM, and all the algorithms were coded on Python 3.3.

Table 2 Description of data sets used in the experiments

4.1 Exactitude evaluation

In this experiment, the exactitude of the proposed feature selection algorithm is evaluated against the other three algorithms. For this, we will focus in this subsection on the correctness aspect of each algorithm and how they are able to identify the relevant features appropriately. In addition, we will employ a complete search algorithm as reference for the exact minimal reduct, since it can examine all the possible attributes subsets (Zhong et al. 2001). Consequently, Table 3 presents the selection results of each method for some values of the neighborhood parameter $\theta$, where the selected attribute sequence is given with respect to UCI data description for each data set.

Considering the results presented in Table 3, we can observe that the selected features by the proposed algorithm NRSFSBT are identical to the complete search minimal reducts for all the cases. In fact, this remark can be also generalized for the NRSFST. However, the results obtained by the existing algorithms, NRSFSQR and NRSFSPST, are slightly different from the minimal reduct of the complete search algorithm. More precisely, we can notice that NRSFSQR and NRSFSPST are not able to obtain the correct results for Cancer, Ecoli, Glass, Pima, and Australian data sets. This is caused by the local search behavior of NRSFSQR, which is a very greedy algorithm (Yong et al. 2014). While, for NRSFSPST, this issue is resulting from the rotation procedure on the Power Set Tree (Chen et al. 2011). Eventually, we can conclude that our proposed method NRSFSBT shows sufficient exactitude to be used for feature selection problems and it is able to exhibit very accurate results, as well as the complete search algorithm.

Table 3 Comparison of the selected minimal reduct for different values of the neighborhood parameter $\theta$ on each data set; the attribute sequence is given with respect to UCI data description

4.2 Computational performance

This subsection is devoted to demonstrate the computational efficiency of the introduced algorithm, with regard to the number of evaluated reduct candidates and the computational time.

In the first part of this subsection, we present a comparison between different algorithms, in terms of the number of tested candidates for minimal reduct; in other words, the number of generated neighborhood positive regions. The corresponding results of this experiment are summarized in Table 4, where columns from 4 to 8 present, respectively, the obtained results for the complete search algorithm, NRSFSQR, NRSFSPST, NRSFST, and the proposed NRSFSBT.

Table 4 Comparative results with respect to the number of evaluated attribute subsets for different values of the neighborhood parameter $\theta$ on each data set

It is evident from Table 4 that the number of tested attributes subsets is greatly reduced using NRSFSBT in comparison with the other algorithms for many data set. In fact, the used Trie structure and the proposed elimination process, which is based on a lookup table of the non-reduct subsets, lead to decreasing the number of evaluated subsets, and therefore, directly reducing the number of tested neighborhood positive regions for each data set.

In the second part of this subsection, we will compare the running time of five trials, for each algorithm with some values of the neighborhood parameter $\theta$. The results for this experiment are presented in Table 5. In addition, the value between brackets $(\cdot )$ denotes the rank of each method with respect to its running time. As can be observed from the results of Table 5, the computational cost of the NRSFSBT is significantly lower than the other algorithms for many cases. Furthermore, the average rank is the best among all the tested algorithms.

Table 5 Running time (s) on the used data set for various values of the neighborhood parameter $\theta$ using different attribute selection algorithms

Finally, a careful analysis of the results of Tables 4 and 5, we can observe that, even though the number of evaluated features subsets are quite close for the three algorithms NRSFSBT, NRSFSPST, and NRSFST, the computational time of the proposed algorithm is significantly lower than the other algorithms. This leads to an interesting remark, is that the Bucket structure plays significant role in reducing the computation cost required for calculating the positive region for each reduct candidate.

4.3 The influence of the neighborhood parameter

To further justify the efficiency and effectiveness of the proposed feature selection algorithm, we have performed a detailed experimental analysis using various parameters settings. In this respect, Fig. 4 shows the running time graphs of different algorithms, on the selected nine data sets, for an increasing value of the neighborhood parameter $\theta$ from 0.05 to 0.225 with interval 0.025. These graphs depict the influence of the neighborhood parameter on the computational performance of the tested algorithms.

According to the results of Fig. 4, the computational times of the proposed NRSFSBT algorithm are much lesser than the other tested algorithms for most of the values of the neighborhood parameter and under all the used data sets. In particular, the NRSFSBT performs considerably better than the other three algorithms in the data sets of Ecoli, Glass, Australian, Occupancy, Cmc, and Segment. Moreover, although some compared algorithms, NRSFSPST and NRSFST, have a very close number of evaluated attribute subsets to the proposed method (see Table 4), their computation costs are less stable, and the plots corresponding to NRSFSPST and NRSFST demonstrate large variation between two adjacent values of the neighborhood parameter.

Finally, from this experiment, we can conclude that the proposed algorithm presents a significant improvement in terms of computation time and can be very useful for feature selection. In addition, the value of the neighborhood parameter can be determined based on finding compromise between running time and dependence degree, which exhibits good feature subset in a reasonable time (Pacheco et al. 2017; Yong et al. 2014).

Fig. 4

Comparative analysis in terms of running time (second) between the proposed feature selection algorithm NRSFSBT and the existing NRSFSQR (Yong et al. 2014), NRSFSPST (Chen et al. 2011), and NRSFST (Rezvan et al. 2015), with a varying values the neighborhood parameter $\theta$ for different data sets

4.4 The influence of the number of samples

It is well known that many practical applications of data mining and pattern recognition include a large number of attributes as well as involve a variety of volumes of data. Therefore, it is important to understand the effect of number samples in data sets on the used feature selection algorithm. In this subsection, we carry out other comparative experiments that depict the influence of the number of records in each data set on the computational performance of the proposed NRSFSBT in comparison with the existing algorithm. Figures 5 and 6 show the running time graphs of different algorithms for two values of $\theta =0.1$ and $\theta =0.125$, respectively. Furthermore, we used a varying numbers of records starting from 10 to 100% with step of 10% of the original size of each data set, where the records are randomly selected.

Fig. 5

Comparative results with regards to running time (second) between the proposed feature selection algorithm NRSFSBT and the existing NRSFSQR (Yong et al. 2014), NRSFSPST (Chen et al. 2011), and NRSFST (Rezvan et al. 2015), for an increasing number of samples in each data set, where the neighborhood parameter $\theta =0.1$

Fig. 6

Comparative results with regards to running time (second) between the proposed feature selection algorithm NRSFSBT and the existing NRSFSQR (Yong et al. 2014), NRSFSPST (Chen et al. 2011), and NRSFST (Rezvan et al. 2015), for an increasing number of samples in each data set, where the neighborhood parameter $\theta =0.125$

From the results of Figs. 5 and 6, we can notice strong relationship between the running time and the number of records in each data set, as the number of samples increases the computation time increases. In addition, the computation cost of NRSFSBT performs competitively with the existing NRSFSQR for lower data set sizes, while, for the higher number of samples, it is very obvious that the proposed algorithm performs significantly better than all of the existing algorithms. On the contrary, the NRSFSPST and NRSFST present a large gap in the computation time and exhibit the highest running time for most of the testing cases, especially on Occupancy, Australian, Segment, and Wireless data sets.

Finally, we can conclude that the results obtained by NRSFSBT are more stable than those produced by the other algorithms. In addition, the proposed method runs rapidly and is applicable to data sets with different sizes, which ensures the usefulness of the proposed feature selection algorithm and validates the theoretical framework developed previously.

4.5 Classification performance

The purpose of this subsection is to evaluate the classification quality induced by the proposed feature selection algorithm NRSFSBT in comparison with the existing methods. As we know, all the tested feature selection algorithms exhibit almost the same attribute reducts when using large values of $\theta >0.15$. Therefore, we will consider, in this experiment, only the cases when $\theta \le 0.15$, more precisely $\theta =0.1$ and $\theta =0.125$, where these algorithms could obtain different attribute reductions.

In fact, the classification performance of different selection algorithms is measured through three learning algorithms, which are commonly used by the scientific community. The first algorithm is The k-Nearest Neighbor (k-NN) that is considered as one of the simplest machine learning algorithms, which belongs to the class of instance-based learning. The purpose of the k-NN is to classify any new object based on a plurality vote of its k nearest neighbors using a similarity measure. For the case of $k=1$, it simply assigns the object to the class of the single nearest neighbor. One of the most advantages of the k-NN is that it does not make any assumptions on the underlying data distribution (Cover and Hart 1967). The second one is Linear Support Vector Machine (LSVM). The goal of this type of algorithms is to find the hyperplane that better separate between two classes, where it can be generalized to handle case of multiclasses by applying one-vs-the rest scheme. One of the most important advantages of LSVM is associated with its suitability for the problems when the number of features and training samples is very large (Chang and Lin 2011). The last one is the Classification and Regression Tree (CART), which aims to builds a tree structure composed of decision nodes and leaf nodes, based on a recursive partitioning method. The CART model can be used for predicting categorical variables (classification) or predicting continuous variables (regression), where one can easily understand and interpret the resulted decision. In addition, the pruning mechanism allows to avoid the problem of overfitting and to better generalize the data in less complex tree (Breiman 2017).

Basically, this experiment is designed as follows: first, we use the fivefold cross validation approach to randomly split the data sets samples into ten approximately equal parts, where one of the ten parts is used as the test set, while the rest is used for the training. Then, three learning algorithms, k-NN (with $k = 1$), LSVM, and CART, were used to evaluate the classification performance of different reduction algorithms. All the parameters of the classifiers are set to default (Pedregosa et al. 2011). Finally, the recognition results for each of the classification algorithms, from the five-fold cross-validation experiment, are obtained and the means of the classification accuracies are summarized in Tables 6, 7, and 8. It is important to mention that the value $|\cdot |$ denotes the average cardinality of the feature subsets acquired by each feature selection algorithm. In addition, we have compared the obtained results with those of the original full set of attributes of each data set.

Table 6 Classification accuracies (%) of k-NN classifier, induced by different feature selection algorithms for $\theta =0.1$ and $\theta =0.125$

Table 7 Classification accuracies (%) of LSVM classifier, induced by different feature selection algorithms for $\theta =0.1$ and $\theta =0.125$

Table 8 Classification accuracies (%) of CART classifier, induced by different feature selection algorithms for $\theta =0.1$ and $\theta =0.125$

It can be clearly seen from Tables 6, 7, and 8, that, for many of the data sets, the proposed NRSFSBT outperforms the three existing feature selection algorithms in terms of both cardinality and accuracy of the feature subset. Moreover, the NRSFSBT algorithm exhibits the best overall performances simultaneously in terms of acquiring few features and achieving high accuracy, with respect to the three learning algorithms. More specifically, as presented in Table 8, the NRSFSBT achieves the smallest features subset cardinalities and maintained high accuracy for the three data sets, Ecoli, Occupancy, and Cmc.

In addition, it is noticeable from the three Tables 6, 7, and 8, that the results obtained by the proposed feature algorithm with the LSVM classifier with respect to the average classification are higher than those of the other two learning algorithms k-NN and CART. In addition, we can see that the NRSFSQR did not always perform better than the original full set of attributes.

As a last remark of this experiment, by taking the results obtained on Cancer data set from Table 7, as an illustration, we can observe that the proposed NRSFSBT achieves good average cardinality of the feature subsets (5.2) in comparison with the original data (9). Nevertheless, the classification result induced by the selected feature is lesser than which of the original data. In fact, this similar behavior also holds for Segment and Pima data sets from Tables 7 and 8, respectively. This observation shows that the proposed feature selection algorithm does not always guarantee improvement in classification accuracy, since the criterion of selection is based on dependence degree and some of the data sets have been already carefully selected by domain experts (Post et al. 2016). However, our feature selection approach could certainly provide significant improvement on raw data from production environments. The experimental results generally indicate that the proposed algorithm shows its effectiveness in selecting relevant attributes.

5 Conclusion

Feature selection with the NRS Model is an interesting topic in data mining and pattern recognition, and has shown to be very convenient for handling numerical data. The main contributions of this work are three-fold. First, we have presented a new fast feature selection algorithm for Neighborhood Rough Set Model. Second, we employ the Bucket and Trie structures to design the feature selection algorithm, which does not only reduce the computational complexity of the search process, but also guarantee to find a compact subset of relevant features. Third, numerous experiments on different standard data sets from UCI repository are carried out to verify the effectiveness of our algorithm in comparison with the related approaches. The experimental results showed that the proposed algorithm is very effective with respect to computational time and classification performance, and is able to select relevant attributes accurately. In future works, we will focus on multi-label feature selection based on our proposed algorithm. In addition, we aim to develop an approach for adjusting the neighborhood parameter, according to the properties of the data set. Finally, we plan to employ new data structure that could improve the results for heterogeneous and mixed data types' feature selection problems.