Concept lattice visualization of data with m-polar fuzzy attribute

Abstract

In the current, year’s most of the attention has been paid towards analysis of uncertainty and vagueness in fuzzy attributes. In this case, a major problem arises when the uncertainty exists in the attributes beyond the $\left\{ \in , \notin \right\}$ boundaries. The most of the time researchers faced problem in precise representation of given multi-polar or multi-decision attributes. To deal with this type of attributes, current paper introduces a method based on the properties of m-polar fuzzy set and its concept lattice diagram. The generation of line diagram is established using the vertices and nodes of a defined m-polar fuzzy graph and its properties. A method is also proposed to generate some of the pattern from the given m-polar fuzzy context at user required subset of attributes. In addition, the analysis derived from the proposed method is compared with Akram and Younas (J Appl Math Comput 53(1–2):365–382, 2017) as well as Mukherjee and Das (in: Proceedings of Third International Conference on Advanced Computing, Networking and Informatics, pp 21–28, 2016) based on various parameters.

1 Introduction

Knowledge discovery or extracting some of the meaningful pattern from a given data set is one of the major concern for the research communities. To deal with this problem, Wille (1982) introduced a mathematical model based on applied abstract algebra. This tool is well known as formal concept analysis (FCA). It starts the computation from a given binary matrix data set (X, Y, R) containing the set of objects (X), the set of attributes (Y), and the corresponding relationship ($R \subseteq X \times Y$) among them (Ganter and Wille 1999). The calculus of FCA provides formal concepts, concept lattice, and attribute implications from the given binary matrix to extract the meaningful information from the given data sets (Davey and Priestley 2002). In case, the attributes contain uncertainty and vagueness in the properties of fuzzy sets (Burusco and Fuentes-Gonzalez 1994) can be utilized in concept lattice theory (Bělohlávek et al. 2005). The orientation of concept lattice with fuzzy sets given a well-established tool to measure the partial ignorance in attributes more precisely using interval-valued (Burusco and Fuentes-Gonzales 2001; Singh et al. 2016a) and bipolar fuzzy sets (Singh and Kumar 2014a, b) based on their acceptation and rejection part. In case the attributes contains indeterminacy, then it can be measured via properties of three-way fuzzy concept lattice (Li et al. 2017; Singh 2017a) or complex-vague set (Singh 2017b, c, 2018). Some other approaches are introduced to process the linked fuzzy context (Singh 2016, 2018) beyond the unipolar space (Singh 2018) based on its various possible boundaries (Djouadi and Prade 2011) and their approximation using lower and upper boundaries (Yao 2004). Subsequently, the properties of granular computing (Pedrycz and Chen 2011, 2015a, b) are utilized to measure the randomness in fuzzy attributes using the calculus of entropy theory (Singh and Kumar 2017) and Huffman coding (Singh and Gani 2015) for precise analysis of hidden pattern in the data set based on user required information granules (Singh and Kumar 2017; Webb et al. 2016). All of these methods are well enough to process maximal fuzzy context in unipolar or bipolar fuzzy space. In case the data sets contains multi-polar information or multi-decision attributes (Singh 2018), these approaches lack in adequate mathematical representation of the data set and their graphical structure visualization (Voutsadakis 2002). There are many data sets which contain multi-polar context, as shown in.¹ In these type of multi-polar contexts, finding some of the interesting pattern is critical issues. It can be observed that less attention has been paid towards analysis of data with m-polar fuzzy attributes (Singh et al. 2016b, 2018; Voutsadakis 2002; Wang et al. 2017). To fill this backdrop, the current paper focuses on analysis of data with m-polar fuzzy attributes with step-by-step demonstration.

Table 1 Some inevitable conditions exists in a given formal fuzzy context

The multi-polar attributes and its examples can be found in each daily life. One of the suitable example is an employee who is in the office or not cannot be decided by binary value present and absent. Sometimes, the concern employee can be on sick leave, earned leave, on duty, medical leave, and maternity leave. Similarly, the feedback given by people is based on multi-criteria or multi-decision analysis. Representing this type of multi-polar information in the given context is a major challenge for the researchers of knowledge discovery and representation tasks. Due to that Table 1 provides some categorization exists in multi-polar information and its representation issues in formal context (Sebastian and Ramakrishnan 2010, 2011) as exists in several real-life examples:

• The relationship among India and USA (or other country) is based on multi-polar context.²

• The classification of algae based on their morphological behavior at given phase of time or place is based on m-polar fuzzy attributes (Pandey et al 2016).³

• Semantic web (Maio et al. 2016) vision of the World Wide Web (Rettinger et al. 2012) is data with m-polar attributes.

• Selection of a candidate for the advertised job is multi-criteria or m-polar decision based attributes as given in Akram and Younas (2017).

• Similarly, electing a leader for any democratic country is based on multi-attribute decision or m-polar attribute (Mesiarová-Zemanková and Ahmad 2014).

The above given examples show that there are several real-life examples which contains multi-polar or multi-decision attributes. Kroonenberg (2008) discussed other areas, where multi-attribute data sets exist (Mahmoudi1 et al. 2016). In this case, each of the m-polar side of the attribute coexists simultaneously as an integral part of the information (Zenzo 1988). This can be represented using the properties of m-polar fuzzy set. It can be defined for any given set (X) as a mapping $f:X\rightarrow [0,1]^{m}$, where (0, 0,..., 0) is least element and (1, 1,..., 1) is the greatest element. This set provides a way to represent each m-polar side of the information with its precise description and orientation. However, to discover, some of the interested pattern in the given data set with m-polar fuzzy attributes is another concern. For this purpose, some of the researchers have paid attention towards heterogeneous context (Antoni et al. 2014), vague context (Borzooei and Rashmanlou 2017; Singh 2017c), and m-polar fuzzy context (Chen et al. 2014; Ascar and Yener 2009; Singh 2018) to analyze them user required chosen subsets of attributes (Bělohlávek et al. 2005; Singh and Kumar 2017) using multi-adjoint concept lattice (Medina and Ojeda-Aciego 2012) or properties of m-polar fuzzy graph (Samanta et al. 2015; Selvachandrana et al. 2016a). Mesiarová-Zemanková and Ahmad (2014) introduced various t-conorms of m-polar fuzzy sets for precise analysis of multi-polar information. However, for knowledge processing tasks, the user or expert requires some of the meaningful information from the data set with m-polar fuzzy attributes (Singh 2018). Until now, none of the research method is introduced to discover the pattern in the given m-polar context (Singh et al. 2016b, 2018). The reason is simulating the multi-valued attributes (Sebastian and Ramakrishnan 2010, 2011) and its visualization is one of the major concern for the researchers (Aliev and Memmedova 2015). To achieve this goal, current paper introduces a method for generating the m-polar fuzzy concepts using the properties of applied abstract algebra in m-polar fuzzy space. The motivation is to provide a compressed graphical structure visualization of given m-polar context based on the vertices and edges of a defined m-polar fuzzy graph for precise analysis of hidden pattern rather than its mathematical representation. To understand the necessity of this paper some of the potential methods in FCA with unipolar, bipolar and three-polar or multi-polar fuzzy setting is analyzed in Table 2. It shows that a basis of method is need to introduced in FCA with m-polar fuzzy setting when compared to other approaches (as marked $*$ in Table 2). To fulfil this aim, current paper introduces a contextual way representation of multi-polar information using the properties of m-polar fuzzy matrix. Furthermore, method is proposed to discover some of the interesting m-polar fuzzy concepts based on user required subset of attributes for knowledge processing tasks. To validate the obtained results from the proposed method, the comparative study among them is shown with recently published method by Akram and Younas (2017) and Mukherjee and Das (2016) with an illustrative example. In addition, One suitable application of the proposed method is also shown to analyze the opinion of people in a democratic country.

Table 2 Important literature to understand the necessity of FCA with m-polar fuzzy setting

The remaining parts of this paper are constituted as follows: a brief background about FCA in the fuzzy setting and m-polar fuzzy graph is shown in Sect. 2. Section 3 contains the proposed method to discover all the m-polar fuzzy concepts with its illustration in Sect. 4. The comparative analysis of the proposed method with recently published methods is shown in Sect. 5. Section 6 demonstrates one suitable application of the proposed method followed by conclusions, acknowledgements, and references.

2 Background

2.1 Formal concept analysis in the fuzzy setting

The calculus of FCA with fuzzy setting provides a platform to process data with fuzzy attributes via scale of truth degrees L. The truth degree for the defined objects and attributes set is tabulated as formal fuzzy context F = (X, Y, $\tilde{R}$), where X is a set of objects, Y is a set of attributes and $\tilde{R}$ is an L-relation between X and Y, $\tilde{R}$: X $\times$ Y $\rightarrow \textit{L}$ (Bělohlávek et al. 2005). Each relation $\tilde{R}(\textit{x},\textit{y})\in L$ represents the membership value at which the object $x\in \textit{X}$ has the attribute $y\in \textit{Y}$ in L (2016). The set (L) of all truth degrees allow certain logical operators and connectives to process the data. The root of these logical operators and connectives is based on well defined mathematical structures and their expression (e.g., residuated lattice) to handle the various multi-polar or multi-valued logic. In this case, L set can be considered as a support set of some complete residuated lattice L.

A residuated lattice L = $(L,\wedge ,\vee ,\otimes ,\rightarrow ,0,1)$ is the basic structure of truth degrees, where 0 and 1 represent least and greatest elements, respectively. L is a complete residuated lattice iff (Pollandt 1998):

• (1) $(L,\wedge ,\vee ,0,1)$ is a bounded complete lattice with bound 0 and 1.

• (2) $(L,\otimes ,1)$ is commutative monoid.

• (3) $\otimes$ and $\rightarrow$ are adjoint operators (called multiplication and residuum, respectively), that is $a \otimes b \le c$ iff $a\le b\rightarrow c, \forall a,b,c\in \textit{L}$.

The operators $\otimes$ and $\rightarrow$ are defined, distinctly by Lukasiewicz, G$\ddot{o}$del, and Goguen t-norms and their residua as given below (Bělohlávek and Vychodil 2005; Bělohlávek et al. 2005):

Lukasiewicz:

• $a \otimes b$ = max (a+b–1, 0),

• $a \rightarrow b$ = min (1–a+b, 1).

G$\ddot{o}$del:

• $a \otimes b$ = min (a, b),

• $a \rightarrow b$ = 1 if $a \le b$, otherwise b.

Goguen:

• $a \otimes b$ = $a \cdot b$,

• $a \rightarrow b$ = 1 if $a \le b$, otherwise b/a.

Classical logic of FCA is an example of a complete residuated lattice which is represented as $(\left\{ 0, 1\right\} , \wedge , \vee , \otimes , \rightarrow , 0, 1)$.

For any L-set A $\in L^{{{X}}}$ of objects, an L-set A $^{\uparrow }\in L^{{{Y}}}$ of attributes can be defined using UP operator of Galois connection as follows:

A $^{\uparrow } (y) = \wedge _{x\in {\textit{X}}}( \textit{A}(x) \rightarrow \tilde{R}(\textit{x},\textit{y}))$.

Similarly, for any L-set of B $\in L^{{{Y}}}$ of attributes, an L-set B $^{\downarrow }\in L^{{{X}}}$ of objects set can be defined using down operator of Galois connection as given below:

B $^{\downarrow } (x) = \wedge _{y\in {\textit{Y}}}( \textit{B}(y) \rightarrow \tilde{R}(\textit{x},\textit{y}))$.

A $^{\uparrow } (y)$ is interpreted as the L-set of attribute y $\in \textit{Y}$ shared by all objects from A. Similarly, B $^{\downarrow } (x)$ is interpreted as the L-set of all objects x $\in \textit{X}$ having the same attributes from B in common. The formal fuzzy concept is a pair of (A, B) $\in L^{{{X}}}\times L^{{{Y}}}$ satisfying $\textit{A}^{\uparrow } = \textit{B}$ and $\textit{B}^{\downarrow } = \textit{A}$, where fuzzy set of objects A is called an extent and fuzzy set of attributes B is called an intent. The operators ($\uparrow , \downarrow$) are known as Galois connection and extensively used in fuzzy setting by Bělohlávek (2004) for crisply generated fuzzy concepts. It means that formal fuzzy concept is a maximal rectangle of a given context (F) while integrating the information from objects and attributes set. All the discovered formal fuzzy concepts follow the partial ordering principle, i.e., $(\textit{A}_{1},\textit{B}_{1})\le (\textit{A}_{2},\textit{B}_{2})\Longleftrightarrow \textit{A}_{1}\subseteq \textit{A}_{2}(\Longleftrightarrow \textit{B}_{2}\subseteq \textit{B}_{1})$. Including this ordering, there exists an infimum and a supremum for each formal concepts in the complete lattice as follows (Ganter and Wille 1999):

• $\wedge _{j\in J}(A_{j}, B_{j})$ = $(\bigcap _{j\in J} A_{j}, (\bigcup _{j\in J}B_{j})^{\downarrow \uparrow })$,

• $\vee _{j\in J} (A_{j}, B_{j})$ = $((\bigcup _{j \in J} A_{j})^{\uparrow \downarrow },\bigcap _{j\in J} B_{j})$.

The formal fuzzy concepts and their display in the concept lattice provide an adequate analysis for knowledge processing tasks in various ways as given in Bělohlávek and Vychodil (2005). To accelerate the knowledge processing tasks, the concept lattice theory is connected with graph theory (Berry and Sigayret 2004; fuzzy graph theory Ghosh et al. 2010) and its extension to unipolar (Singh and Kumar 2012) and bipolar fuzzy graph (Singh and Kumar 2014a). Recently, it is studied in three-polar (Singh 2017a) as well as m-polar fuzzy g raph by Singh (2018) for precise analysis of existing uncertainty in data sets. In this paper, a method is proposed for depth analysis of m-polar fuzzy context based on user required subset of attributes in the next section.

2.2 Some properties of m-polar set and its graphical visualization

To analyze the m-polar fuzzy context, some of the basic properties of m-polar fuzzy set, m-polar fuzzy graph, and its lattice theory are given to entrench the connection among them with an illustrative example:

Definition 1

(m-polar fuzzy set) (Chen et al. 2014): An m-polar (or a $[0,1]^{m}$) fuzzy set on X can be represented as a mapping $f:X\rightarrow [0,1]^{m}$, where (0, 0, ..., 0) is a least element and (1, 1, ..., 1) is a greatest element. The set of all m-polar fuzzy sets can be represented as m(X). It means m-polar set is an extension of fuzzy set which can be visualized using the extensive properties of fuzzy graph (Ghosh et al. 2010), interval-valued fuzzy graph (Singh et al. 2016a), bipolar fuzzy graph (Singh and Kumar 2014a, b), three-polar fuzzy graph (Singh 2017a) or m-polar fuzzy graph (Akram and Younas 2017).

Definition 2

(m-polar fuzzy relation) Akram and Younas (2017): An m-polar (or a $[0,1]^{m}$) fuzzy relation represents the relationship among objects and attributes more precisely through a defined multi-polar fuzzy space. It means the m-polar fuzzy relation ($\tilde{R}$) on the set X and Y can be represented as follows:

$\tilde{R} (x_{i},y_{j})$ = $\left\{ (x_{i},y_{j}) , \mu _{\tilde{R} } (x_{i},y_{j}) \right\}$, where $\mu _{\tilde{R} } (x_{i},y_{j})$ = ($\mu ^{1}_{\tilde{R}} (x_i, y_i),\ldots ,\mu ^{m}_{\tilde{R}} (x_i, y_i)$) and the relation is mapped in the interval [0, 1] as follows: $\mu ^{\tilde{R} }_{m} (x_i, y_j)$ $\rightarrow [0,1]$, where $x_{i} \in X, y_{j} \in Y$.

Definition 3

(m-polar fuzzy graph) (Samanta et al. 2015): An m-polar fuzzy graph with an underlying pair (V, E) (where $E\subseteq V \times V$ is symmetric, i.e., $(v_{1}, v_{2})\in E \Leftrightarrow (v_{2}, v_{1})\in E$ is defined to be a pair G = (I, J), where I: $V \rightarrow [0,1]^{m}$, i.e., it is an m-polar fuzzy set on V. Similarly, J: $E \rightarrow [0,1]^{m}$, i.e., m-polar fuzzy set on E. It follows $J (v_{1}v_{2})\le inf \left\{ I (v_{1}), I (v_{2})\right\}$ for each m-polar space. The given m-polar fuzzy graph is strong iff: $J (v_{1}v_{2}) = inf \left\{ I (v_{1}), I (v_{2})\right\}$, as shown in Example 1.

Example 1

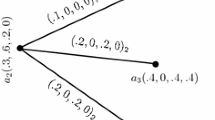
Let us suppose, a group of three friends $\left\{ v_{1}, v_{2}, v_{3} \right\}$ want to watch a movie based on their preferences. It can be observed that the preference is multi-decision attributes and based on rating of movie, songs of movies, story, or type of movie. This four polar attributes can be represented using the properties of m-polar fuzzy set, where 0 represents low, 1 represents high, and 0.5 represents an average movie. This multi-polar information given by three friends can be represented by 4-polar fuzzy set, as shown in Table 3. Table 4 represents the corresponding 4-polar relationship among them. Now, Tables 3 and 4 can be visualized using the vertices (V) and edges (E) of a graph defined in m-polar fuzzy space, as shown in Fig. 1.

Table 3 A m-polar fuzzy set representation of vertices (V) for Example 1

Table 4 A m-polar fuzzy set representation of edges E for Example 1

Definition 4

(Partial ordering of m-polar fuzzy set) (Mesiarová-Zemanková and Ahmad 2014): The m-polar fuzzy relation (or a $[0,1]^{m}$) defines partial ordering when it follows the pointwise reflexive, symmetric, and transitive ordering for among each of the given elements, i.e., m = $\left\{ n \in N| n \le m \right\}$ when $m>0$ then $x\le y \Leftrightarrow p_{i} (x) \le p_{i} (y)$ for each $i \in m$, $x, y, \in [0,1]^{m}$, and $p_{i}:[0,1]^{m}\rightarrow [0,1]$ is the projection mapping ($i \in m$). The partial ordering among m-polar fuzzy set provides a way to define the super- and sub-concept hierarchy among all the generated m-polar fuzzy concepts, as shown in Fig. 2.

Fig. 1

A 4-polar fuzzy graph for Example 1

Example 2

Let us suppose m = 2, i.e., $[0,1]^{2}$ to represent ordinary closed unit square in Euclidean space ($R^{2}$), as shown in Fig. 2. The upper point, i.e., y = (1,1) in this square, can be considered as greatest element of $[0,1]^{2}$, whereas lowest point, i.e., x = (0, 0) can be considered as lowest element of $[0,1]^{2}$. Now, suppose two elements u = (0.25,0.75) and v = (0.75,0.25) for defining the partial ordering among them, i.e., ($x \le u \le y)$ or $( x \le v \le y )$. The partial ordering among u and v can be defined in two ways $x \le u \le v \le y$ or $x \le v \le u \le y$, as shown in Fig. 2. The reason is both $u_{1}$ = 0.25 $\le$ 0.75 = $v_{1}$ and $u_{2}$ = 0.75 $\ge$ 0.25 = $v_{2}$.

Fig. 2

A partial ordering between m-polar elements

Figures 1 and 2 show that data with m-polar fuzzy attributes can be hierarchically visualized using the theory of concept lattice as fuzzy graph (Ghosh et al. 2010), interval-valued fuzzy graph (Singh et al. 2016a), bipolar fuzzy graph (Singh and Kumar 2014a, b; Singh 2017b, c), three-polar fuzzy graph (Singh 2017a) can be done. To accomplish this task, a method is proposed, in the next section for discovering all the m-polar fuzzy concepts and their display in the m-polar fuzzy concept lattice.

3 Proposed method for generating the m-polar fuzzy concepts

In this section, a method is proposed to generate the m-polar formal fuzzy concepts using the properties of m-polar fuzzy graph and componentwise G$\ddot{o}$del residuated lattice. Let us suppose, an m-polar formal fuzzy context F = (X, Y, $\tilde{R}$), where $|X| = n$, $|Y| = k$ and, $\tilde{R}$ represents corresponding m-polar fuzzy relation. Then, the m-polar formal fuzzy concepts can be generated as follows:

Definition 5

(m-polar formal fuzzy concepts): Let us suppose a set of attributes, i.e., (B) = $\left\{ y_{j}, (\mu _1 (y_{j}), \mu _2 (y_{j}), \ldots , \mu _m (y_{j})), y_{j} \in Y\right\}$, where $(\mu ^{Y}_{1} (y_{j}),\ldots , \mu ^{Y}_{m} (y_{j}))$ is m-polar representation of the attribute $y_j$. For the selected m-polar attribute set find their covering objects in the given context, i.e.,

(A) = $\left\{ x_{i}, (\mu _1 (x_{i}), \mu _2 (x_{i}), \ldots ,\mu _m (x_{i})), x_{i} \in X\right\}$, where $(\mu ^{X}_{1} (x_{i}),\ldots , \mu ^{X}_{m} (x_{i}))$ is m-polar representation of the object $x_i$.

The obtain pair (A, B) is called an m-polar formal fuzzy concept iff it is closed with componentwise Galois connection, i.e., $\textit{A}^{\uparrow }$ = $\textit{B}$ and $B^{\downarrow }$ = $\textit{A}$. This can be interpreted as m-polar fuzzy set of objects having maximal membership value while integrating the information from the common m-polar fuzzy set of attributes using $[0,1]^{m}$ componentwise Go$\ddot{}$del residuated lattice. If the obtain pair of objects and m-polar fuzzy set constituted by its covering attributes forms a formal concept, then none of the extra objects (attributes) can be found to make the constituted membership value larger. It means that an m-polar formal concept is a maximal rectangle covering objects and attributes set (A, B) in the given m-polar fuzzy context (F) while integrating the information from them. The obtained pair (A, B) of objects and attributes set can be visualized using the vertices and edges of a defined m-polar fuzzy graph, where $i \le n, j \le k$ to refine the knowledge more precisely when compared to its numerical representation. For this purpose, the proposed method considers maximal acceptance of m-polar fuzzy set for the given attributes, i.e., (1.0, 1.0,..., 1.0)$_{m}$ to generate the concepts as shown below:

Step 1: List out all the subsets $s_{2^{k}}$ of given m-polar fuzzy attributes to generate the concepts.

Step 2: User or expert can use any of the m-polar fuzzy set of attributes $s_{j}$ to discover the interesting pattern in the given data sets. The membership value for the chosen subset can be decided by user or expert to solve the particular problem. However, in this paper maximal acceptance of each component of the m-polar fuzzy attributes, i.e., (1.0, 1.0,..., 1.0)$_{m}$ is considered to generate the concepts.

Step 3: It can be written in precise way as follows: $B_{s_{j}}$ = $\mu _m^{B_{j}}(y_j)$ = 1 if $s_{j} \in S$ otherwise 0. Now, find the covering objects set which integrate the information from these objects set.

Step 4: To achieve this goal, the properties of Galois connection can be applied as follows:

$\left\{ y_{j}, (\mu _1 (y_{j}), \mu _2 (y_{j}), \ldots ,\mu _m (y_{j}))\right\} ^{\downarrow }$ = $\left\{ x_{i}, (\mu _1 (x_{i}), \mu _2 (x_{i}), \ldots ,\mu _m (x_{i}))\right\}$ for all $y_{j} \in Y, x_{j} \in X$.

Step 5: Now, compute the componentwise m-polar membership value of the obtained objects set as given below:

$min \left\{ x_{i}, (\mu _1 (x_{i}), \mu _2 (x_{i}),\ldots ,\mu _m (x_{i})) \right\}$.

Step 6: Now, apply the Galois connection on the constituted m-polar set of objects to find their covering attributes while integrating the information from them as follows:

$\left\{ x_{i}, min (\mu _1 (x_{i}), \mu _2 (x_{i}),\ldots ,\mu _m (x_{i})) \right\} ^{\uparrow }$ = $\left\{ y_{j}, (\mu _1 (y_{j}), \mu _2 (y_{j}), \ldots ,\mu _m (y_{j}))\right\}$ for all $x_{i} \in X, y_{j} \in Y$.

Step 7: Now, compute the componentwise m-polar membership value of the obtained attributes set as given below:

$min \left\{ y_{j}, (\mu _1 (y_{i}), \mu _2 (x_{i}),\ldots ,\mu _m (x_{i})) \right\}$

Step 8: The newly obtained attributes using the $\uparrow$ can be added iff it has maximal acceptance for each component of m-polar fuzzy set otherwise leave them.

Step 9: Similarly, generate all the m-polar fuzzy concepts using the remaining subset of attributes. The obtained pair of objects and attributes set ($A_{s_i}$, $B_{s_j}$) can be considered as m-polar formal fuzzy concepts.

Step 10: The line diagram can be drawn based on their subsets to derive the knowledge. Table 5 summarizes the proposed algorithm in form of a pseudo code.

Table 5 A proposed algorithm for generating the m-polar fuzzy concepts

Complexity It can be observed that Table 5 provides a method for investigating the pattern in given m-polar fuzzy context based on user required subset of attributes to solve the particular problem. To achieve this goal, the proposed method generates the subset of attributes which takes O$2^{k}$ time complexity. Now, the proposed method finds the maximal covering objects set for the chosen subset of attributes which may take maximal O($2^{k} *n$) computational time. At last, the proposed method computes the componentwise m-polar membership value for the obtained objects (or attributes) set which may take total O($2^{k} *n *m$) complexity. It can be observed that the proposed method takes exponential time, but it will work as basis of an algorithm for further improvement to deal with data of m-polar fuzzy attributes.

4 Illustrations

Analyzing pattern in data with multi-polar or multi-index attribute (Mahmoudi1 et al. 2016; Wang et al. 2017) is a major concern for researchers of semantic web (Maio et al. 2016), World Wide Web (Rettinger et al. 2012) or sentiments analysis (Xu et al. 2017) of people in a democratic country (Loia et al. 2016; Singh 2017a). Recently, Pandey et al (2016) addressed this issue in categorizing the Indian Algae based on their morphology.⁴ The issue is to find some of the interesting pattern in multi-polar context⁵ for knowledge processing tasks. To deal with this problem, recently, the calculus of fuzzy concept lattice is tried to characterize via acceptation, rejection, and indeterminacy regions by Li et al. (2017) and Singh (2017a) with two different techniques. Some other researchers represented the uncertainty and vagueness in attributes using the properties of m-polar fuzzy set (Chen et al. 2014; Mesiarová-Zemanková and Ahmad 2014), m-polar fuzzy graph (Akram and Younas 2017; Samanta et al. 2015) and its t-conorm (Mesiarová-Zemanková 2015) for analyzing multi-way data (Ascar and Yener 2009; Mukherjee and Das 2016). The current paper focuses on discovering all the hidden pattern in data with m-polar fuzzy attributes and their compact display in fuzzy concept lattice for refining the knowledge based on applied abstract algebra. To achieve the aforementioned goal, this paper proposes a method in Sect. 3 which is distinct from any of the available approaches in following aspects:

• The proposed method provides a compact way to represent the data with m-polar attributes in the formal context.

• The proposed method generates the formal concepts while considering maximal acceptance of given m-polar attributes for precise analysis of knowledge processing tasks within O($2^{k} *n *m$).

• The proposed method provides precise description of hidden pattern (i.e., m-polar fuzzy concepts) in data with m-polar fuzzy attributes and their visualization in the concept lattice. It is one of the major advantage of the proposed method to expedite the knowledge processing tasks when compared to any other available approaches.

In general the multi-polar information can be found in sentiments analysis, opinion mining or complex network. The most suitable place is social networking sites contains many multi-decision or multi-criteria attributes as discussed by Ascar and Yener (2009). The goal is to find some of the interested pattern among them to analyze its influence. This is a major concern for any company or organization while refining the knowledge. To explore this problem one of the example is given as below:

Example 3

Let us suppose a company wants to analyze suitability of given posts $\left\{ x_{1}, x_{2}, x_{3}, x_{4} \right\}$ for branding its manufacturing products. To achieve this goal the company advertise them on the social network sites and want to measure their importance. It is well known that the opinion of people on the social network sites can be measured using the “Like”, “Share” or “Comments”, i.e., $\left\{ y_{1}, y_{2}, y_{3}\right\}$. In this case, measuring the opinion of people become complex the reason is “Like”, “Share” and “Comments” on any given post is based on multi-criteria decisions, i.e., content of the post, available friends for the given id, the relationship building of people added in the given id as well as style of presenting the given post. These m-polar attributes can be analyzed using the fuzzy membership values. Suppose 50% people available in the friend list of given id “Likes $(y_{1})$” the given post then it can be represented using 0.5 membership values, as shown in Tables 6, 7, and 8, respectively. To understand the representation a entry of Table 6 can be considered as follows: $x_1$ = $\frac{0.2}{\mu _1 (y_1)}$+$\frac{0.2}{\mu _2 (y_1)}$+$\frac{0.2}{\mu _3 (y_1)}$+$\frac{0.2}{\mu _4 (y_1)}$. This entry represents that 20% people Likes post $x_1$ due to its contents (i.e., $\mu _1 (y_1)$), 60% people Likes post $x_1$ from their friend circle ($\mu _2 (y_1)$), 20% people Likes post $x_1$ for relationship building (i.e., $\mu _3 (y_1)$), whereas 40% people Like post $x_1$ based on its style of presentation (i.e., $\mu _3 (y_1)$). Similarly, other m-polar fuzzy relations shown in Tables 6, 7 and 8 can be interpreted. Table 9 represents the composed m-polar fuzzy membership values for each of the tables based on their m-polar attributes. Now, the company requires one of the best post for the global advertisement from the m-polar fuzzy context, as shown in Table 9. In this case, the goal is to discover some of the interesting pattern from the given context. To achieve this goal, the proposed method shown in Sect. 3 provides following m-polar fuzzy concepts:

Table 6 A 4-polar relation for posts-$x_{1},x_{2}, x_{3},x_{4}$ based on attribute “Like ($y_1$)”

Table 7 A 4-polar relation for posts-$x_{1},x_{2}, x_{3},x_{4}$ based on attribute “Share ($y_2$)”

Table 8 A 4-polar relation for posts-$x_{1},x_{2}, x_{3},x_{4}$ based on attribute “Comment($y_3$)”

Table 9 A 4-polar formal context representation of Tables 8, 9, and 10

The proposed algorithm shown in Table 5 generates following m-polar fuzzy concepts from the context, as shown in Table 9:

Step 1: In Step 1, the proposed method computes each of the subset of given attributes set shown in Table 9 with their maximal acceptance as follows:

• 1. $\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}\right\}$,

• 2. $\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}\right\}$,

• 3. $\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}\right\}$,

• 4. $\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}\right\}$,

• 5. $\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}\right\}$,

• 6. $\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}\right\}$,

• 7. $\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}\right\}$,

• 8. $\left\{ \frac{(0, 0, 0, 0)}{y_{1}}+ \frac{(0, 0,0, 0)}{y_{2}}+ \frac{(0, 0, 0, 0)}{y_{3}}\right\}$.

Step 2: Let us choose first subsets of attributes to generate the concepts, i.e.,

1.$\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}, \frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}, \frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}\right\}$.

Step 3: Investigate the maximal covering objects set for the chosen subset of attributes using the properties of Galois connection ($\downarrow$) as follows:

$\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}} +\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}\right\} ^\downarrow.$

Step 4: It provides following set of m-polar fuzzy set of objects using the properties of m-polar fuzzy sets as given below:

$\left\{ \frac{(0.2, 0.5, 0.2, 0.4)}{x_{1}}+\frac{(0.5, 0.6, 0.1, 0.3)}{x_{2}}+\frac{(0.2, 0.5, 0.4, 0.1)}{x_{3}}+\frac{(0.2, 0.1, 0.6, 0.1)}{x_{4}}\right\}$.

Step 5: Now, find the maximal covering attributes set for the above obtained objects set using the $\uparrow$ operator of Galois connection as follows:

$\left\{ \frac{(0.2, 0.5, 0.2, 0.4)}{x_{1}}+\frac{(0.5, 0.6, 0.1, 0.3)}{x_{2}} + \frac{(0.2, 0.5, 0.4, 0.1)}{x_{3}}+\frac{(0.2, 0.1, 0.6, 0.1)}{x_{4}}\right\} ^\uparrow.$

Step 6: It provides following set of attributes:

$\left\{ \frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}} +\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}\right\}$.

Step 7: In this process, none of the extra attributes is discovered which covers the constituted objects set. In this case, the obtain set of m-polar objects and attribute set can be considered as extent and intent of a m-polar fuzzy concepts.

Step 8: In this way, it provides following m-polar fuzzy concepts:

1. Extent = $\frac{(0.2, 0.5, 0.2, 0.4)}{x_{1}}+\frac{(0.5, 0.6, 0.1, 0.3)}{x_{2}} + \frac{(0.2, 0.5, 0.4, 0.1)}{x_{3}}+\frac{(0.2, 0.1, 0.6, 0.1)}{x_{4}}$.

Intent = $\frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}} +\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}$

Step 9: Similarly, other concepts can be generated using the remaining subsets shown in Step 1. In this case, it should the noted that any new attributes can be added iff it contains maximal acceptance:

2. Extent = $\frac{(0.2, 0.6, 0.2, 0.4 )}{x_{1}}+\frac{(0.5, 0.7, 0.1, 0.3)}{x_{2}} + \frac{(0.7, 0.5, 0.4, 0.2)}{x_{3}}+\frac{(0.9, 0.3, 0.8, 0.3)}{x_{4}}$

Intent = $\frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}$

3. Extent = $\frac{(0.5, 0.7, 0.6, 0.6)}{x_{1}}+\frac{(0.6, 0.8, 0.4, 0.3)}{x_{2}} + \frac{(0.4, 0.8, 0.6, 0.1)}{x_{3}}+\frac{(0.2, 0.1, 0.6, 0.1)}{x_{4}}$

Intent = $\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}$

4. Extent = $\frac{(0.6, 0.5, 0.2, 0.7)}{x_{1}}+\frac{(0.7, 0.6, 0.8, 0.5)}{x_{2}} + \frac{(0.2, 0.5, 0.6, 0.8)}{x_{3}}+\frac{(0.6, 0.4, 0.8, 0.7)}{x_{4}}$.

Intent = $\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}$.

5. Extent = $\frac{(0.2, 0.6, 0.2, 0.4 )}{x_{1}}+\frac{(0.5, 0.7, 0.1, 0.3)}{x_{2}} + \frac{(0.4, 0.5, 0.4, 0.1)}{x_{3}}+\frac{(0.2, 0.1, 0.6, 0.1)}{x_{4}}$.

Intent = $\frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}$

6. Extent = $\frac{(0.2, 0.5, 0.2, 0.4)}{x_{1}}+\frac{(0.5, 0.6, 0.1, 0.3)}{x_{2}} + \frac{(0.2, 0.5, 0.4, 0.2)}{x_{3}}+\frac{(0.6, 0.3, 0.8, 0.3)}{x_{4}}$

Intent = $\frac{(1.0, 1.0, 1.0, 1.0)}{y_{1}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}$

7. Extent = $\frac{(0.5, 0.5, 0.2, 0.6)}{x_{1}}+\frac{(0.6, 0.6, 0.4, 0.3)}{x_{2}} + \frac{(0.2, 0.5, 0.6, 0.1)}{x_{3}}+\frac{(0.2, 0.1, 0.6, 0.1)}{x_{4}}$

Intent = $\frac{(1.0, 1.0, 1.0, 1.0)}{y_{2}}+\frac{(1.0, 1.0, 1.0, 1.0)}{y_{3}}$

8. Extent = $\frac{(1, 1, 1, 1)}{x_{1}}+\frac{(1, 1, 1, 1)}{x_{2}} + \frac{(1, 1, 1, 1)}{x_{3}}+\frac{(1, 1, 1, 1)}{x_{4}}$

Intent = $\frac{(0, 0, 0, 0)}{y_{1}}+ \frac{(0, 0,0, 0)}{y_{2}}+ \frac{(0, 0, 0, 0)}{y_{3}}.$

Step 10: It can be observed that none of the new attributes are added in the chosen subset of attributes. The reason is that newly obtained attributes do not contain maximal acceptance of membership values (1.0, 1.0, 1.0, and 1.0). Hence, the proposed method provides crisply generated attribute (object) oriented m-polar concepts. The super- and sub-concept hierarchical format among generated concepts is shown via their subsets, as shown in Fig. 3.

Fig. 3

A 4-polar crisply generated fuzzy concept lattice from Table 9

The above generated m-polar fuzzy concepts provides following meaningful information from the context shown in Table 9 for knowledge processing tasks:

• Concept number-1 represents that post $\frac{(0.5, 0.6, 0.1, 0.3)}{x_{2}}$ contains maximal acceptance membership value for each of the m-polar attributes (i.e., Like, Share and Comments -$y_1$, $y_2$, $y_3$) when compared to other posts. In this case, the company will choose the post $x_2$ as first preference for the global advertisement.

• Concept number-2 represents that post $\frac{(0.9, 0.3, 0.8, 0.3)}{x_{4}}$ contains maximal membership value for the m-polar attribute “Like, i.e., ($y_1$)”. In this case, company will prefer post $x_{4}$ while considering the attribute “Like”.

• Concept number-3 represents that post $\frac{(0.6, 0.8, 0.4, 0.3)}{x_{2}}$ contains maximal membership value for the m-polar attribute “Share ($y_2$)”.

• Concept number-4 represents that post $\frac{(0.7, 0.6, 0.8, 0.5)}{x_{2}}$ contains maximal membership value for the m-polar attribute “Comments ($y_3$)”.

• Concept number-5 represents that post $\frac{(0.5, 0.7, 0.1, 0.3)}{x_{2}}$ contains maximal membership value for the m-polar attributes “Like and Share ($y_{1}, y_{2}$)” .

• Concept number-6 represents that post $\frac{(0.6, 0.3, 0.8, 0.3)}{x_{4}}$ contains maximal membership value while integrating the informal from m-polar attributes “Like and Comments ($y_{1}, y_{3}$)”. In this case, company will choose the post $x_{4}$ as first preference and $x_2$ as second preference while considering these two attributes.

• Concept number-7 represents that post $\frac{(0.6, 0.6, 0.4, 0.3)}{x_{2}}$ contains maximal membership value while integrating the information from the m-polar attributes “Share and Comments ($y_{2}, y_{3}$)”. In this case, company will choose the post $x_{2}$ as first preference when considering these two attributes.

• Concept number-8 represents that all posts cannot be chosen as best for the global advertisement.

The information extracted from the above-mentioned concepts shows that post $x_2$ will be given first preference for the global advertisement, whereas the post $x_4$ will be given second preference. Subsequently, other post can be analyzed using remaining pattern (i.e., formal concepts). It can be observed that a problem can be arisen when the size of m-polar concept lattice become larger. To deal with this problem author will try to focus on incorporating other metrics with m-polar fuzzy concept lattice. However, handling data with m-polar fuzzy attributes and its research is at infancy stage. In this case, the current research will be helpful for the researchers working on sentiments analysis (Xu et al. 2017), situation awareness (Loia et al. 2016), multi-decision (Wang et al. 2017) making process at multi-granulation (Liu and Cocea 2017) for precise analysis of knowledge processing tasks. To validate the obtained results from the proposed method is comparatively analyzed with other available approaches in the next section.

5 Comparative analysis

This paper introduced an alternative way to analyze the data with m-polar fuzzy attributes using the properties of concept lattice. Table 10 shows that m-polar fuzzy set is nothing but one of the generalized representation of fuzzy set for handling multi-polar information. This research needs depth analysis and new mathematical foundation to expedite the knowledge processing tasks. For this purpose a method is proposed in this paper to analyze the data with m-polar fuzzy attributes using the concept lattice theory. Recently, other researchers also depicted the similar problem related to data with m-polar fuzzy attributes (Akram and Younas 2017) and its analysis using an adaptive method (Mukherjee and Das 2016). Due to that these two recent methods are considered in this section to compare the analysis derived from the proposed method, as shown in Sects. 5.1 and 5.2, respectively.

Table 10 A study on different extension of fuzzy set based on their properties

5.1 Comparative analysis of the proposed method with Akram and Younas (2017)

To analyze the analysis derived from the proposed method with Akram and Younas (2017), the same example is adopted as shown below:

Example 4

Let us suppose, $\left\{ Mike, Helly, David, Bisma, Ali, Umair, Zahra\right\}$ are seven friends on a given social network website and their influence on each other. The attribute influence is multi-decision and multi-criteria attribute which can be based on logical persuading, exchanging, alliance building, legitimizing, and appealing. The corresponding relationship among these seven friends can be represented using m-polar fuzzy set, where 0.5 means average as shown below:

• (i). $\frac{(0.5, 0.4, 0.3, 0.2, 0.3)}{Mike}$.

• (ii). $\frac{(0.3,0.6, 0.5, 0.4, 0.2 )}{Helly}$.

• (iii). $\frac{(0.2, 0.4, 0.5, 0.3, 0.6 )}{David}$.

• (iv). $\frac{(0.5, 0.2, 0.6, 0.7, 0.4 )}{Bisma}$.

• (v). $\frac{(0.4, 0.2, 0.5, 0.6, 0.3 )}{Ali}$.

• (vi). $\frac{(0.7, 0.6, 0.8, 0.9, 0.5 )}{Umair}$.

• (vii). $\frac{(0. 6, 0.2, 0.1, 0.3, 0.2 )}{Zahra}$.

The goal is to measure the influence of $\left\{ Mike, Helly, David, Bisma, Ali, Umair, Zahra\right\}$ on each others using above collected data set. To deal with this problem a method is proposed method in Table 5 of this paper for finding all the hidden pattern in data with m-polar attributes. The proposed method provides following pattern based on above given data set (i.e., $2^{1} = 2$ subset for one attribute influence) as given below:

1. Extent = $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{Mike}$ + $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{Helly}$ + $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{David}$ + $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{Bisma}$+ $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{Ali}$ + $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{Umair}$ + $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{Zahra}$. Intent = $\frac{(0.2, 0.2, 0.1, 0.2, 0.2)}{Influence}$.

2. Extent = paper to find all the pattern among$\frac{(0.5, 0.4, 0.3, 0.2, 0.3)}{Mike}$ + $\frac{(0.3,0.6, 0.5, 0.4, 0.2 )}{Helly}$ + $\frac{(0.2, 0.4, 0.5, 0.3, 0.6 )}{David}$ + $\frac{(0.5, 0.2, 0.6, 0.7, 0.4 )}{Bisma}$ + $\frac{(0.4, 0.2, 0.5, 0.6, 0.3 )}{Ali}$ + $\frac{(0.7, 0.6, 0.8, 0.9, 0.5 )}{Umair}$ + $\frac{(0. 6, 0.2, 0.1, 0.3, 0.2 )}{Zahra}$. Intent = $\frac{(1.0, 1.0, 1.0, 1.0, 1.0)}{Influence}$.

$\bullet$ Concept number 1 represents that $\left\{ Mike, Helly, David, Bisma, Ali, Umair, Zahra\right\}$ influence each other equally except alliance building.

$\bullet$ Concept number 2 represents the following information:

• (i) Umair influence their friends maximally based on logical persuading with membership value 0.7, whereas Zahra with 0.6 membership value when compared to others.

• (ii) Umair and Helly equally influence their friends based on exchanging with 0.6 membership value.

• (iii) Umair influence their friends maximally based on alliance building with 0.8 membership value, whereas Bisma influence them with 0.6 membership value.

• (iv) Umair influence their friends maximally with 0.9 membership value based on legitimizing, whereas Bisma influence them with 0.7 membership value.

• (v) David influence their friends maximally based on appealing to values with 0.6 membership value, whereas Umair influence them with 0.5 membership value.

The above-mentioned analysis derived from the proposed method shows that Umair influence their friends maximally except the appealing to values, whereas Bisma influence them second. These derived conclusions from the proposed method is commensurate with Akram and Younas (2017). However, the proposed method provides an accurate analysis and precise description of pattern when compared to Akram and Younas (2017). Table 11 represents the comparison among these two methods based on various parameters. It shows that the proposed method will be more helpful for handling data with m-polar fuzzy attributes when compared to Akram and Younas (2017) in given time complexity.

Table 11 Comparison of proposed method with Akram and Younas (2017)

5.2 Comparative analysis of the proposed with Mukherjee and Das (2016)

To analyze the comparison of the proposed method with adjustable approach introduced in (Mukherjee and Das 2016). The same data set is considered as given below:

Example 5

Let us suppose, a set of houses ($U_1$) = $\left\{ h_1, h_2, h_3\right\}$, a set of cars $U_2$ = $\left\{ c_1, c_2, c_3\right\}$, and a set of hotels $U_3$ = $\left\{ v_1, v_2, v_3\right\}$ are represented based on some given parameters, as shown in Table 12. In this case, analyzing preference of customer to purchase the car, house or hotel is a major concern for any company related to this research field. For this purpose, a method is proposed in this paper to find all the pattern among given m-polar data set as demonstrated as below:

Extent = $\frac{(1.0, 1.0, 1.0, 1.0)}{a_1}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{a_2}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{a_3}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{a_4}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{a_5}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{a_6}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{a_7}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{a_8}.$ Intent = $\frac{(0.3, 0.4, 0.1, 0.0)}{U_1}$ + $\frac{(0.5, 0.3, 0.1)}{U_2}$ + $\frac{(0.5, 0.3, 0.4)}{U_3}.$

This concept represents following information:

$\bullet$ $\frac{(0.3, 0.4, 0.1, 0.0)}{U_1}$ represents that house $h_2$ will be purchased as first preference due to its highest membership value, i.e., 0.4, whereas $h_1$ as second preference.

$\bullet$ $\frac{(0.5, 0.3, 0.1)}{U_2}$ represents that car $c_1$ will be purchase as first preference due to its highest membership value, i.e., 0.5, whereas car $c_2$ as second preference.

$\bullet$ $\frac{(0.5, 0.3, 0.4)}{U_3}$ represents that hotel $v_1$ will be purchase as first preference due to its highest membership value, i.e., 0.5, whereas hotel $v_3$ as second preference.

The above analysis derived from the proposed method shows that house $h_2$, car $c_1$, hotel $v_1$ will be purchased as first preference, whereas house $h_1$, car $c_2$, hotel $v_3$ will be purchased as second preference. These conclusions from the proposed method approximately commensurate with the adjustable approach discussed by Mukherjee and Das (2016). Table 13 shows that the proposed method is better than adjustable approach in analyzing the data with m-polar fuzzy attribute.

Table 12 A 4-polar formal context for the car, houses and hotels based on given parameters

Table 13 Comparison of proposed method with adjustable approach given in Mukherjee and Das (2016)

6 One real life application of the proposed method

There are many real life data set which contains m-polar fuzzy attributes. One of the suitable examples is opinion of people in a democratic country is based on multi-polar or multi-decision attributes to vote the concern party. It is addressed by several Indian media in 2015 election of Bihar, as shown in.⁶ The problem with government agencies as well as private agencies become more complex to measure the pattern of people in different state. Subsequently, it was crucial for them to find those potential attributes for which the countrymen voted. This election was very crucial for ruling, opposition, other parties as well as political scientists of international media. To resolve this issue current paper introduced a method based on applied lattice theory and its generalization in the m-polar fuzzy space as given below:

Example 6

Let us suppose, three political parties $\left\{ x_1, x_2, x_3\right\}$ are participating in a election happens in any democratic country like India. The people from 29 states used to participate in the election. In this case, people used to vote on various parameters as follows: $y_1$ = Corruption; $y_2$ = Terrorism; $y_3$ = Un-employment; $y_4$ = Foreign policy; $y_5$ = Medical and health policy; $y_6$ = Education policy; $y_7$ = Economical policy; $y_8$ = Defense policy; $y_9$ = Speech of leader; $y_{10}$ = other issues. In this case, opinion of 29-states people can be considered as 29-polar dimension, political parties can be considered as objects, whereas the parameters as attributes. For better understanding the author select first three potential attributes and the 5-states for measuring the opinion of people and their pattern. To achieve this goal a 5-polar context is shown in Table 14.

Table 14 A 5-polar context to measure the opinion of people in a democratic country

The 5-polar relation $(x_1,y_1) = (0.5, 0.4, 0.6, 0.5, 0.4)$ represents that 50% people of state 1, 40% people of state 2, 60% people of state 3, 50% people of state 4, and 40% people of state 5 voted to political party $x_1$ based on their stand on corruption $y_1$. Similarly, other entries in given 5-polar fuzzy matrix can be interpreted. Now, the goal is to find some of the meaningful information from the given 5-polar matrix. This goal can be achieved using the proposed method shown in Sect. 3 of this paper. However to achieve this goal the government agencies do not require all m-polar concepts. They need specialized and generalized concepts for extracting a general information as given below:

1. Generalized concepts:

Extent = $\frac{(1.0, 1.0, 1.0, 1.0))}{x_1}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{x_2}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{x_3}$

Intent = $\frac{(0.5, 0.4, 0.5, 0.5, 0.4)}{y_1}$ + $\frac{(0.4, 0.5, 0.6, 0.6, 0.5)}{y_2}$ + $\frac{(0.5, 0.4, 0.4, 0.4, 0.5)}{y_3}.$

This shows that the 40 to 60% people of 5-states voted each of the parties based on the given parameters.

2. Specialized concepts:

Extent = $\frac{(0.4, 0.4, 0.4, 0.5, 0.4)}{x_1}$ + $\frac{(0.6, 0.6, 0.6, 0.6, 0.6)}{x_2}$ + $\frac{(0.5, 0.4, 0.5, 0.4, 0.5)}{x_3}$

Intent = $\frac{(1.0, 1.0, 1.0, 1.0))}{y_1}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{y_2}$ + $\frac{(1.0, 1.0, 1.0, 1.0)}{y_3}.$

This concept shows that the 40% people of four states and 50% people of one state people voted to political party $x_1$ based on the given parameters. More than 60% people voted to political party $x_2$ on the given parameters. Similarly, 50% people of three states and 40% people of two states voted to political party $x_3$ on the given parameters. In this case, the opinion shows that the political party $x_2$ may win the election as first preferences, whereas the political party $x_3$ as second place. The extracted information helps the political party to identify their weakness and strength for attracting the voters in a democratic country. It can be observed that the opinion of people used to fluctuate at each given phase of time. In this case, measuring the changes in multi-polar information is another concern. In the near future, the author research will focus on quantize the measurement of uncertainty and its fluctuation in data with m-polar attributes at given phase of time using the different metrics of granular computing (Djouadi and Prade 2016; Pedrycz and Chen 2011, 2015a, b; Skowron et al. 2016; Yao 2016) and complex fuzzy sets (Singh 2018; Selvachandrana et al. 2016a; Selvachandran et al. 2016b).

7 Conclusions and future work

This paper aimed at precise description of data with m-polar fuzzy attributes using the properties of concept lattice and its graphical analytics. To achieve this goal, a method is proposed to generate the m-polar fuzzy concepts based on user required subset of attributes within O($2^{k}*n *m$) time complexity. It is shown that the obtained results from the proposed method is concordant with recently available methods in Akram and Younas (2017) and Mukherjee and Das (2016). One of the significant advantages of the proposed method is that it provides a compact display of m-polar fuzzy context for extracting the meaningful information in data with m-polar fuzzy attributes. However, the proposed method takes exponential time which is one its major disadvantages. Same time it does not allow to measure the changes in multi-polar information (Singh 2018) at the given threshold. To deal with this problem, the author will focus on introducing other metrics of m-polar fuzzy sets in the near future to quantize the information.