Introduction and overview

For more than 3,500 years, stepped weir systems have been used to raise the energy dissipation rate on spillway chutes, thereby decreasing the size and expense of the stilling structure downstream [1,2,3]. A ‘stepped spillway’ is where the spillway's face has steps starting from the crest to the toe. Besides, this layout can help decrease the risk of cavitation—compared to smooth spillways—by expanding the length of the self-aerated flow zone [4,5,6]. The spillways can have different layouts depending on their use, such as downward inclined steps, non-uniform steps and pooled steps. Moreover, the stepped spillway system is well suited to modern construction techniques, e.g. roller compacted concrete (depending on step size), pre-cast concrete and hydraulic gabion structures [6].

The step configurations of stepped spillways can be either uniform where the step dimensions are consistent over the spillway chute or non-uniform, where the lengths and heights of the steps continuously change. Previous studies have revealed that the step configurations can significantly impact such spillways' design parameters, including energy dissipation, pressure distribution and the inception point location. To date, there have been minimal studies investigating the flow effects where non-uniform stepped spillways are used. One of the first attempts to study the effect of non-uniformity of the step heights was by Stephenson [7], who investigated the energy dissipation. The main finding was an increase of 10% in energy dissipation versus that from the uniform steps. Conversely, Felder and Chanson [8] examined the effect of non-uniformity of the spillway step heights experimentally and reported no significant difference between the two layouts. A more recent study by Li et al. [9] investigated experimentally and numerically the effect of the step height non-uniformity on the generated energy dissipation for curved spillways. The results revealed that the water flow between the concave bank to convex bank could raise the energy dissipation by around 66% compared to the smooth spillway. Ashoor and Riazi [10] explored the energy dissipation rate effect on different configurations such as convex, concave, random and semi-uniform step arrangements using a numerical solver InterFOAM, available in the OpenFOAM package. The results showed that the semi-uniform configuration produced the best performance in regard to energy dissipation. The disparity of findings between the previous studies is related to issues including differences in the adopted methodology, i.e. experimental or numerical, the examined flow rates, the scale of the models and finally, differences in the examined step configuration. This highlights the need for further investigation better to understand the flow effects for different spillway layouts.

One of the simplest and most cost-effective construction forms for stepped spillways is gabion-stepped spillways (GSS) (see Fig. 1). This system is formed by gathering several rectangular-shaped baskets (usually formed from a galvanized steel wire mesh) filled with different sized angular rocks and connected at the edges. Gabions are commonly used in low to medium-head stepped spillway applications and carry the advantages of being low cost and easier to construct than alternative forms such as in-situ concrete as well as having superior flexibility and noise abatement characteristics [1]. However, one of the shortcomings of the GSS system is that the maintenance cost after overtopping events can be high [11]. Therefore, it is critical to understand the effect on both the flow and energy dissipation patterns across gabion-stepped chutes. To date, a very limited number of studies have been performed to explore the flow characteristics and the construction parameters of GSS. For instance, the design of GSS, energy dissipation over the gabion steps and the seepage interactions with a free-surface flow are discussed and reviewed by Chanson [1]. Reeve et al. [12] explored GSS numerically with various step layouts (i.e. normal, inclined, overlapping and pooled steps). The step height of the impermeable steps in these layouts was constant. The main finding was that normal steps could dissipate more energy than the other layouts under the same flow rates.

Fig. 1
figure 1

2D schematic view of flow over gabion-stepped spillways

Full size image

Three types of flow regimes could be anticipated over GSS systems: nappe, transition and skimming flow [13]. Nappe flow is a series of small water jet-falls which can be achieved for low discharges. While skimming flow is when the water flows towards the toe of the spillway as a coherent free-stream gliding over the pseudo-bottom created by the steps' outer edges. The pseudo-bottom line starts from the outer edge of the first step to the outer edge of the last step. As skimming flow occurs when the water flow rate is high, the characteristic feature is represented by a high turbulence level [14,15,16]. Skimming flow is associated with the turbulence's recirculation in the step cavities, retained by the shear stress transmission from the free stream. Lastly, transition flow was initially presented by Ohtsu and Yasuda [17] and can occur when the water flow rates are in the intermediate range among the nappe flow and the skimming flow regimes [18,19].

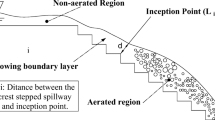
The turbulent boundary layer in the skimming flow will trap the natural air entrainment, which initiates a point between the aerated and non-aerated zone described as the 'inception point' (see Fig. 1). In the case of high discharges, aeration might not appear along a stepped chute, therefore the boundary layer might not get to the step surface. This is important in the case of small to medium dams running with high discharges [20]. Therefore, the lack of self-aeration would cause the spillway to be susceptible to cavitation damage [21]. The occurrence of cavitation damage is often observed in concrete stepped spillways over the non-aerated zone steps [21].

Problem definition

From the literature, both normal and gabion-stepped spillways have significant advantages in preventing cavitation damage and controlling the inception point location's length (i.e. non-aerated zone). Furthermore, the inception point has a substantial influence on the energy dissipation performance. Nevertheless, there are currently very limited studies investigating GSS with a non-uniform step layout. Finding the optimum GSS layout is essential to improve future designs. Consequently, this study investigates the impact of the step length non-uniformity on inception point locations. Different GSS layouts are explored, these being random length distribution of the steps, semi-uniform distribution of the step length, a convex configuration with longer steps at the beginning where the length of step decreases gradually towards the end of the spillway and a concave configuration having smaller steps in the start then gradually increasing the step length towards the end of the spillway. A numerical flume model was adopted to examine the GSS system performance. The results obtained in this study are used to estimate the inception point location. Finally, two novel equations are proposed to predict the non-aerated zone length for non-uniform GSS.

Numerical modelling approach

In this paper, a numerical flume (two-dimensional) model is used to examine flow behaviour over different non-uniform GSS. The numerical flume, NEWFLUME [22], is an open-source code based on the Reynolds-averaged Navier–Stokes approach (RANS) which adopts a volume-of-fluid capturing scheme. The adopted scheme allows accurate simulation of significant deformations of the water surface. NEWFLUME computes the water free surface and the turbulent flow by splitting the model's flow into two main components: the turbulent fluctuations and the mean flow. The equations describing the mean flow contribution to the fluctuating turbulent flow and the solution technique to understand the numerical code performance are described in the following section.

The formulae used for capturing water flow out of the porous media are;

$$\frac{{\partial \left\langle {u_{{\text{i}}} } \right\rangle }}{{\partial x_{{\text{i}}} }} = 0$$
(1)
$$\frac{{\partial \left\langle {u_{{\text{i}}} } \right\rangle }}{{\partial t}} + \left\langle {u_{{\text{j}}} } \right\rangle \frac{{\partial \left\langle {u_{{\text{i}}} } \right\rangle }}{{\partial x_{{\text{j}}} }} = - \frac{1}{\rho }\frac{{\partial {\text{p}}}}{{\partial x_{{\text{i}}} }} + g_{{\text{i}}} + \frac{1}{\rho }\frac{\partial }{{\partial x_{{\text{j}}} }}\left( {\mu \frac{{\partial \left\langle {u_{{\text{i}}} } \right\rangle }}{{\partial x_{{\text{j}}} }} - \rho \left\langle {u_{{\text{i}}}^{\prime } u_{{\text{j}}}^{\prime } } \right\rangle } \right)$$
(2)

where \(\left\langle {u_{{\text{i}}}^{\prime } } \right\rangle\) refers to the mean velocity in direction i in units of m.s−1; 〈p〉 is the mean pressure in units of kN.m−2; ρ is the density of the fluid in units of kg.m−3; \({{g}}_{\mathrm{i}}\) \({{g}}_{\mathrm{i}}\) is the acceleration in direction i in units of m.s−2; μ is the molecular viscosity in units of m2.s−1; and \(\left\langle {u_{{\text{i}}}^{\prime } u_{{\text{j}}}^{\prime } } \right\rangle \cdot \left\langle {u_{{\text{i}}}^{\prime } u_{{\text{j}}}^{\prime } } \right\rangle\) represents the Reynolds stress in units of kN.m−2.

The mean viscous stress calculation is defined as follows:

$$\langle \tau_{{{\text{ij}}}} \rangle = \mu \frac{{\partial \langle u_{{\text{i}}} \rangle }}{{\partial x_{{\text{j}}} }} + \mu \frac{{\partial \langle u_{{\text{j}}} \rangle }}{{\partial x_{{\text{i}}} }}.$$
(3)

Meanwhile, for the viscosity, a nonlinear eddy model was implemented to determine the Reynolds stress. That model has used turbulence kinematic energy (k), mean velocity and dissipation rate of turbulence (ɛ). The transport equation (k–ɛ) was applied to compute both k and ɛ, as described in Lin and Liu [22]. Thereby, the porous media mean flow is dominated by the following formula

$$\frac{{\partial \overline{u}_{{\text{i}}} }}{{\partial x_{{\text{i}}} }} = 0$$
(4)
$$\frac{{1 + C_{{\text{A}}} }}{n}{ }\frac{{\partial {\overline{\text{u}}}_{{\text{i}}} }}{\partial t} + \frac{{\overline{u}_{{\text{j}}} }}{{{\text{n}}^{2} }}\frac{{{ }\partial {\overline{\text{u}}}_{{\text{i}}} }}{{\partial {\text{x}}_{{\text{j}}} }} = - \frac{1}{{\uprho }}\frac{{{ }\partial {\overline{\text{p}}}}}{{\partial {\text{x}}_{{\text{i}}} }} + g_{{\text{i}}} + \frac{{\upnu }}{{\text{n}}}\frac{{\partial^{2} {\overline{\text{u}}}_{{\text{i}}} }}{{\partial {\text{x}}_{{\text{j}}} \partial {\text{x}}_{{\text{i}}} }} - ga_{{\text{p}}} {\overline{\text{u}}}_{{\text{i}}} - gb_{{\text{p}}} \sqrt {{\overline{\text{u}}}_{{\text{k}}} {\overline{\text{u}}}_{{\text{k}}} } {\overline{\text{u}}}_{{\text{i}}}$$
(5)

where \({\overline{{u}} }_{\mathrm{i}}\) can be defined as the i-th the mean velocity component; for porous medium, n is the porosity; \({{C}}_{\mathrm{A}}\), \({{a}}_{\mathrm{p}}\) and \({{b}}_{\mathrm{p}}\) are the coefficients; and the subscript K is the sum of velocities in two directions i and ii. The required coefficients are described by Lin and Liu [22] as

$${{C}}_{\mathrm{A}}={\upgamma }_{\mathrm{p}}\frac{1-{n}}{{n}}$$
$${{a}}_{\mathrm{p}}={\alpha }\frac{{(1-{n})}^{2}}{{{n}}^{3}}\frac{{v}}{{{gD}}_{50}^{2}}$$
$${{b}}_{\mathrm{p}}=\upbeta (1+\frac{7.5}{{KC}})\frac{1-{n}}{{{n}}^{3}}\frac{1}{{{gD}}_{50}}$$

\({{C}}_{\mathrm{A}}={\upgamma }_{\mathrm{p}}\frac{1-{n}}{{n}}\) where \({\upgamma }_{\mathrm{p}}=0.34,{\alpha }=200,\upbeta =1.1,\mathrm{ KC}=\frac{\sqrt{{\overline{{u}} }_{\mathrm{k}}{\overline{{u}} }_{\mathrm{k}}}{ T}}{{\mathrm{nD}}_{50}}\)

The volume-of-fluid technique (VOF) was applied as free-surface tracking was assumed. The approach was initially proposed by Hirt and Nichols [23] and was subsequently revised by Kothe et al. [24]. The VOF equation for an incompressible flow is:

$$\frac{{\partial {\text{F}}}}{{\partial {\text{t}}}} + \left\langle {{\text{u}}_{{\text{j}}} } \right\rangle \frac{{\partial {\text{F}}}}{{\partial {\text{x}}_{{\text{j}}} }} = 0$$
(6)

where F is the fluid function volume. This refers to the fraction fluid in the cell. For example, when F = 1, this reveals that the cell is full; however, the cell would be empty when F = 0. It is important to highlight that the fluid surface lies in the cell when F is between 1 and 0.

All partial differential equations were estimated using the finite-difference approach. The Navier–Stokes equation solver, RIPPLE established by Kothe et al. [24], has been applied to calculate the mean flow outside the porous medium. The momentum equations were resolved by applying a finite-difference technique that implemented a two-step projection. Thus, the discrete equation,

$$\frac{{{\text{u}}_{{\text{i}}}^{{{\text{n}} + 1}} - {\text{u}}_{{\text{i}}}^{{\text{n}}} }}{{\Delta {\text{t}}}} + {\text{u}}_{{\text{j}}}^{{\text{n}}} \frac{{\partial {\text{u}}_{{\text{j}}}^{{\text{n}}} }}{{\partial {\text{x}}_{{\text{j}}} }} = - \frac{1}{{{\uprho }^{{\text{n}}} }}\frac{{\partial {\text{p}}^{{{\text{n}} + 1}} }}{{\partial {\text{x}}_{{\text{i}}} }} + {\text{g}}_{{\text{i}}} + \frac{{\partial {\uptau }_{{{\text{ij}}}}^{{\text{n}}} }}{{\partial {\text{x}}_{{\text{j}}} }}$$
(7)

is split into two steps, i.e. step 1:

$$\frac{{{\tilde{\text{u}}}_{{\text{i}}}^{{{\text{n}} + 1}} - {\text{u}}_{{\text{i}}}^{{\text{n}}} }}{{\Delta {\text{t}}}} = - {\text{u}}_{{\text{j}}}^{{\text{n}}} \frac{{\partial {\text{u}}_{{\text{j}}}^{{\text{n}}} }}{{\partial {\text{x}}_{{\text{j}}} }} + {\text{g}}_{{\text{i}}} + \frac{{\partial {\uptau }_{{{\text{ij}}}}^{{\text{n}}} }}{{\partial {\text{x}}_{{\text{j}}} }}$$
(8)

and step 2,

$$\frac{{{\text{u}}_{{\text{i}}}^{{{\text{n}} + 1}} - {\tilde{\text{u}}}_{{\text{i}}}^{{{\text{n}} + 1}} }}{{\Delta {\text{t}}}} = - \frac{1}{{{\uprho }^{{\text{n}}} }}\frac{{\partial {\text{p}}^{{{\text{n}} + 1}} }}{{\partial {\text{x}}_{{\text{i}}} }}.$$
(9)

In this method, the velocity is estimated in the first step without the pressure gradient term; however, the velocity is altered in the second step using the updated pressure field:

$$\frac{\partial }{{\partial {\text{x}}_{{\text{i}}} }}\left( {\frac{1}{{{\text{p}}^{{\text{n}}} }}\frac{{\partial {\text{p}}^{{{\text{n}} + 1}} }}{{\partial {\text{x}}_{{\text{i}}} }}} \right) = \frac{1}{{\Delta {\text{t}}}}\frac{{\partial {\tilde{\text{u}}}_{{\text{i}}}^{{{\text{n}} + 1}} }}{{\partial {\text{x}}_{{\text{i}}} }}.$$
(10)

The equations that control the flow inside the porous media are similar to the RANS equations. Nevertheless, the linear and nonlinear friction terms have been applied to replace the Reynolds stresses. For the flow computation inside the porous media, two-step projection method was also applied. The pressure and velocity continuity was fulfilled over the interface of the porous media and the outside flow. The central difference method has been applied to discretize the stress gradient and pressure. The upwind scheme is merged with the central difference to discretize the k–ɛ transport equations and the advection terms. Lin and Xu [25] demonstrated the capability of NEWFLUME by performing a detailed analysis of different case studies involving several turbulent free-surface flows. The numerical model using NEWFLUME was validated against a set of experimental data for gabion-stepped spillways by Zuhaira et al. [26] and Reeve et al. [12]. According to Reeve et al. [12], the values of gravel porosity and gravel diameter size used in the experiments should be reflected in the numerical model to achieve a reasonable agreement with experimental data.

Due to the limited experimental data for gabion-stepped spillways, validation is conducted in the present work by simulating one of the normal stepped spillway cases tested experimentally by Felder [27]. Felder’s [27] experiment was performed in a facility equipped with a flat uniform step. The experiment consists of a stepped spillway model with a step height (10 cm) and a slope of 26.6°. The range of discharges examined were nappe, transition and skimming flows. Flow pattern discharges were recorded to be 0.004 ≤ q ≤ 0.262 m2/s per unit width and the Reynolds numbers were found to be between 1.6 × 104 ≤ Re ≤ 1.0 × 106. A broad crested weir section was tested with a length of 0.62 m and a height of 1.0 m with ten similar rigid steps with a length of 0.2 m and a height of 0.1 m, see Fig. 2.

Fig. 2
figure 2

The geometry set-up of Felder [27] with the grid distribution over the steps

Full size image

The same boundary conditions and geometry were created in the model domain, with a mesh size selected to be 0.012 m and 0.005 m in the x-direction and y-direction, respectively, to replicate the experiment. The mesh density was selected following previous work by Zuhaira [28], who conducted a wide range of numerical studies using NEWFLUME to investigate different geometries of normal stepped spillways and GSS. The present mesh density values were chosen due to the similarity of the flow regime to that investigated by Zuhaira [28] where it was found that the optimum number of cells in both directions should be around ~ 35 to capture the behaviour accurately and efficiently. The initial depth of water was taken as 1.6 m to get the necessary discharge. The discharge has been computed by establishing the critical section using the Froude number. In the models, the initial time step was selected as 0.0001 s to guarantee numerical stability and the total time for the simulation was taken as 20 s. All boundaries were assumed to be closed in the experimental works except the right boundary which was assumed to be open. The time required to achieve the skimming flow was 5.58 s. Seven different discharges were used for comparison. The discharge value was calculated by multiplying the water's depth by the critical section's velocity (assumed to be over the broad crested weir [29]). Moreover, a comparison of the flow rate results was conducted between the numerical model and the experimental results. The results indicated that there is a reasonable agreement with the experimental work with a relative error of 0.5556%, as tabulated in Table 1.

Table 1 Experimental and numerical discharge values
Full size table

According to Husain et al. [30], the inception point location may be estimated from the free-surface water and the location of a point intersection, that has a velocity about 99% of the maximum velocity over the pseudo-bottom. It can also be referred to as the point where the depth of the turbulent boundary layer equals the water depth. Therefore, the inception point represents the point where the turbulent velocity near the flow surface is high enough to eject water droplets into the air [31].

Chanson [32] demonstrated that the non-aerated zone length could be affected by three important factors: discharge, step height and chute slope. André [31] argued that one of the important benefits of using steps is to increase the spillway roughness, which would accelerate the turbulent boundary layer growth, allowing closer inception points to the upstream weir. Minimizing the non-aerated zone length is significantly important as that will reduce the probability to achieve cavitation damage which might be observed due to the absence of air entrainment. The experiments are summarized in Table 2, the numerical results reveal good agreement with the experimental work. For context, previous work by Zuhaira [28], which used NEWFLUME revealed an 8% relative error in the prediction of the inception point compared to the corresponding experimental work by Meireles and Matos [20].

Table 2 Comparison of experimental and corresponding numerical results for the inception point location
Full size table

Exploration of the effect of step configuration

The validated numerical model is now used to explore the impact of different geometries on skimming flow over GSS, particularly at the non-aerated zone where the air entrainment is absent. Step widths were set to different values to achieve non-uniform gabion steps [10]. All the models that have been numerically examined are described in Table 3. The average spillway slopes ranged from 22° to 27°. It is important to highlight that both porosity and the grain size (D50) of the gabion steps were fixed to 0.325 m and 0.017, respectively. These values have been selected in agreement with the range of the granular material that was used in the experimental studies of Wüthrich and Chanson [33], which focused on uniform step arrangements. The selection of these values provides a range of physical characteristics that replicate gabions in practice. A dam-break condition was adopted in all models to achieve the typical high flow discharge that might be expected during flood events (Fig. 3).

Table 3 Proposed configurations of the stepped spillways
Full size table
Fig. 3
figure 3

Geometric configurations of non-uniform GSS: a concave, b convex, c Random 1, d Random 2, e Random 3 and f Semi-uniform

Full size image

In the numerical model, gabion-stepped spillways with 0.1 m step height were located at 7.8 m and the weir was placed at 6.8 m. The length of the weir crest is 1.0 m (Fig. 4). Based on the recommendations which have been mentioned earlier regarding the critical depth over the weir crest, the crest length was set to 1.0 m. The initial water depth was 0.5 m above the weir crest, so the upstream tank's content was adequate to reach the expected discharge. The initial time step is selected to be 0.0001 s to fulfil the Courant stability criterion for all cases. The Courant number depends on the time step, cell-size and velocity. The Courant number value should be less than or equal to 0.3 for cells in the computational domain to achieve numerical stability. Thus, in this model, the mesh size was set to be 0.012 m and 0.005 m in the x- and y-directions, respectively. In this simulation, the total time was taken as 15 s. Closed boundaries were applied for the numerical model domain apart from the right-hand one that was set to be open mainly to allow the water flow to escape the numerical flume (Fig. 4).

Fig. 4
figure 4

Mesh distributions: a around the entire area of the GSS and b for the first two steps

Full size image

Determination of the onset of skimming flow

As mentioned earlier, all the experiments have been conducted under dam-break conditions, therefore different flow patterns can occur over the non-uniform gabion steps such as nappe flow, transition and skimming flow. It is essential to emphasize that identifying the onset of skimming flow is critical in these cases. Skimming flow conditions are more dangerous than the nappe and transition flow, especially at the non-aerated zone where issues can occur due to the absence of air.

Under dam-break conditions, jet forms could be noticed at the first stage due to the spillway steps' flow. The jet forms are dictated by the nature of the flow in turn governed by the total upstream head at the weir crest. The lower mainstream jet can impact the horizontal step face due to the water flows. This kind of flow can cause vortices over the horizontal steps and flow backwards against the step vertical face, i.e. the riser. However, the porous media can play a vital role here as the flow will try to seep inside the gabion between the particles and significantly reduce the vortices. When the porous media is almost completely saturated in water, these vortices may circulate within a triangular zone approximately one-third of the step length, whereas its height is almost equivalent to the step. The vortices will be ejected back into the main flow due to the direction of the main flow stream and the porous media flow. Coherent streamflow can be captured over the steps indicating skimming flow conditions over the GSS in line with the findings of Wüthrich and Chanson [33] who investigated a uniform GSS with a 26.6° slope.

It is important to highlight that skimming flow should be determined at the time when all the air pockets vanish inside and outside the gabion under the water free surface. However, in some cases, air pockets were observed during the whole simulation time due to the porous media's presence and the bottom chute slope's effect (Fig. 5). Water load is significantly important as it can control the amount of water that can seep inside the porous media and influence the air pockets' availability due to the applied forces. Consequently, it is vital to observe the flow during different stages of the onset of skimming flow conditions to understand the effect of the porous non-uniform steps and the slope of the spillways (Fig. 6). As shown in Figs. 6 and 7, the air pocket at the first step in the concave case always occurred, while that was not achieved in the convex case. The reason for that is due to the shape and the slope of the spillway, which had a significant effect on the skimming flow.

Fig. 5
figure 5

Skimming flow conditions over non-uniform GSS: a concave, b convex, c Random 1, d Random 2, e Random 3 and f Semi-uniform

Full size image
Fig. 6
figure 6

Visualization of flow over the concave configuration of GSS at different times

Full size image
Fig. 7
figure 7

Visualization of flow over the convex configuration of GSS at different times

Full size image

Inception point locations

As discussed earlier, the inception point position is significant for designers to determine the non-aerated zone where there is no air entrainment. In addition to the previously mentioned definitions, the inception point is also defined by Boes and Hager [5] to be the point when the air concentration reaches 1%. The inception point can be determined in experimental work by visual observation where the white water starts to appear due to air entrainment. However, determining the location of the inception point visually could have inherent inaccuracies. For numerical models, the definition of the inception point proposed by Chanson's [32] is more appropriate. Chanson's definition has represented the inception point as the point between the water free surface and the developed thickness of the turbulent boundary layer caused by the weir's upstream face (Fig. 8).

Fig. 8
figure 8

The non-aerated zone length and inception point location estimations for: a convex and b semi-uniform configurations

Full size image

The inception point definition proposed by Chanson’s was adopted in this study to establish the inception point location. The discharge is calculated in the same way as that conducted previously in the validation cases over the critical section located by testing the Froude Number. Therefore, when the Froude Number is equal to 1.0, the critical section's corresponding location can be anticipated to be over the broad crested weir. Meanwhile, the crest of the broad weirs' length must be sufficient to allow the crest's streamlines to exhibit parallel flow. Five different discharges have been selected to establish the inception point location. The selected discharges' values were picked to achieve various ranges of water flow, i.e. from high to low discharges (Fig. 9).

Fig. 9
figure 9

Free-surface profiles for various flow rates above a broad crested weir

Full size image

It is complicated to calculate Li, which represents the non-aerated zone length measured from the outer edge of the first step up to the inception point. This is due to the non-uniformity of the steps' geometry, which clearly affects the pseudo-bottom line as the line will not hit the outer edges of all steps as it does in the uniform steps' case. Therefore, to establish the pseudo-bottom over the non-uniform steps, the line starts from the outer edge of the first step and it terminates at the edge of the last step, neglecting all the steps in between (Fig. 10).

Fig. 10
figure 10

2D schematic illustrating the non-aerated zone length (Li) for different configurations

Full size image

The computational results for the non-uniform GSS with five different flow rates of 0.282, 0.227, 0.182, 0.139 and 0.1m2/s revealed that the gabion steps' geometry could impact the inception point location and non-aerated zone length significantly, as shown in Table 4.

Table 4 The non-aerated zone length (Li) at different flow rates for the non-uniform configurations
Full size table

From Table 4, the inception point location is anticipated to be near the weir crest's downstream side once the discharge is increased. It can be noticed that the non-aerated zone length raises with increasing the unit discharge as increasing the flow rates could lead to a rise in the flow depth and velocity values for the water. The increase in the flow depth might raise the boundary layer length required to develop an intersect surface with the free water profile. For a particular discharge case, the point location changes then shifts over the steps due to the steps' geometry non-uniformity. This could be related to the fact that the shape and the bottom chute slope of the stepped spillways can both have substantial impacts on the inception point location and the non-aerated zone length. The results showed that the semi-uniform and the random1 geometries produced the best performance in terms of the non-aerated zone length for different discharges (Fig. 11).

Fig. 11
figure 11

The non-aerated zone length (Li) at different flow rates for the non-uniform configurations

Full size image

Following the past studies and to justify the previous conclusions on the effect of geometry, Fig. 12 shows the computational results of Li/ks from the present work, calculated with different values of discharges against corresponding roughness Froude number values (F*). In this Figure, Li represents the non-aerated zone length measured from the first step's outer edge up to the inception point, ks is the roughness calculated from multiplying hs (the step height) by cosθ (θ is the average chute slope). Furthermore, the Froude number (the roughness) can be calculated from:

Fig. 12
figure 12

Computational results of the free-surface aeration location

Full size image
$${{F}}_{*}=\frac{{q}}{\sqrt{{g} \times \mathrm{sin }\theta \times {{{k}}_{s}}^{3}}}$$

where q is the discharge per unit width and g is the gravitational acceleration.

As can be seen from Fig. 12, some cases do not follow a clear trend due to the undulating free surface or the humps of water that can be observed over the gabion due to the seepage flow inside the porous media. The spillways' geometry could influence seepage flow, therefore that effect could accelerate the intersection between the free surface and the turbulent boundary layer or it could delay it depending on the circumstances.

Development of new correlations

Nonlinear multiple regression approach (NMR)

To estimate the non-aerated zone length and the inception point location, nonlinear multiple regression equations have been developed for uniform normal stepped spillways by several researchers, including Chanson [34]; Meireles and Matos [20] and Hunt and Kadavy [35], in addition to uniform GSS explored by Reeve et al. [12]. None of the previous studies have considered the effect of the step height non-uniformity for GSS on the performance, therefore the present study's computational results were used to derive a new empirical equation to determine the non-aerated zone length for non-uniform GSS. Accordingly, Li's values and the corresponding values of F* (obtained from the different non-uniform steps and discharges tested) were applied to attain Eq. 11. In developing Eq. 11 for non-uniform GSS, the equation proposed by Reeve et al. [12] (Eq. 12) for uniform GSS has been used as a basis.

The coefficients of Eq. 11 have been estimated by MATLAB code using the iterative least-squares estimation routine. The results obtained from numerical models for fitting purposes were divided into two parts. The first part included 80% of the data and obtained the equation coefficients (training data). The remaining 20% of the data was used as validation data to validate the equation proposed. It is worth noting that the data was randomly selected.

$$\frac{{{\text{L}}_{{\text{i}}} }}{{{\text{k}}_{s} }} = 5.965 \times ({\text{sin}}\theta )^{{ - 0.0019}} \times \left( {{\text{F}}_{*} } \right)^{{0.9747}} .$$
(11)

The value of the R2 factor was 0.9048 (Fig. 13). The value of R2 has been used to measure the correlation of the new equation where the regression line approximates the data. As shown in Fig. 13, the R2 value for Eq. 11 is relatively close to 1.0, indicating that the proposed formula gives a close estimation of the results. These relations represent the general trend for all the computational data. However, many individual points can be found in the database showing different performances due to several factors such as the skimming flow conditions, boundary layer development and geometry.

Fig. 13
figure 13

Comparison of Eq. 11 with the numerical data

Full size image

More in-depth comparison has been conducted against different empirical correlations which have been proposed by Chanson [34] Meireles and Matos [20], Hunt and Kadavy [35] and Reeve et al. [12] (Fig. 14). It is crucial to mention that Eq. 12 was proposed by Reeve et al. [12] for uniform GSS, while the other equations were developed for various cases of normal stepped spillways, i.e. non-porous steps. This is done to assess the empirical correlations' applicability to predict the inception point location for both gabion and normal stepped spillways.

Fig. 14
figure 14

Comparison of Eq. 11 with other existing equations

Full size image

The empirical formulae are:

$$\frac{{L_{i} }}{{k_{s} }} = 2.2281 \times ({\text{sin}}\theta )^{( - 0.3172)} \times (F_{*} )^{1.2486} \times (p)^{ - 0.2831} \times \left( {\frac{{D_{50} }}{{h_{s} }}} \right)^{0.1537} \quad {\text{Reeve et al}}.[12]$$
(12)
$$\frac{{L_{i} }}{{k_{s} }} = 6.1 \times (sin\theta )^{0.08} \times (F_{*} )^{0.86} \quad {\text{Huntand Kadavy}}\;[35]$$
(13)
$$\frac{{L_{i} }}{{k_{s} }} = 5.25(F_{*} )^{0.95} \quad {\text{Meireles and Matos}}\;[20]$$
(14)
$$\frac{{L_{i} }}{{k_{s} }}/ = 9.8 \times ({\text{sin}}\theta )^{0.08} \times (F_{*} )^{0.71} \quad {\text{Chanson}}\;[34].$$
(15)

The results show that Chanson's [34] correlation overestimated the inception point location when F* has a low value; however, the results are closer to the present study once the value of F* starts to increase to more than 4. Conversely, the Reeve et al. [12] equation returned the present study's closest result when the roughness Froude number is low. The Hunt and Kadavy [35] and Meireles and Matos [20] equations showed a consistent underestimation for all points, especially for the high flow rates. It is important to mention that although the Reeve et al. [12] equation was developed for various uniform GSS, the results have agreed with the present study only when F* is low. This is due to the non-uniformity of the gabion steps, which can significantly impact both the boundary layer growth and non-aerated zone length.

Since Eq. 11 is obtained by using a simple nonlinear regression following the past studies, another advanced method, evolutionary polynomial regression EPR, has been applied to find a new correlation to determine the length of the non-aerated zone over non-uniform GSS.

Evolutionary polynomial regression approach (EPR)

One of the intelligent regression analysis algorithms currently developed is the multi-objective genetic algorithm known as evolutionary polynomial regression (EPR). This uses automatic searches to find the best mathematical model and uses the mathematical model to characterize the relation between input and output variables. The best correlation's automatic searches can be accomplished by merging the genetic algorithm (GA) with the regression analysis [36,37]. The methodology of the EPR is based on creating several candidate relations between the input and output data to develop an evolutionary process guided by the GA. These relations depend on the proposed type of the dependency complexity for the data, the number of data used in the analysis, the proposed number of terms for the established new relation and the proposed range of exponents for the developed relationship [38].

In the current study, the data was randomly split into two parts: training and testing data. The training data consisted of 80% of the whole data, the remaining 20% of the data was used as testing data. The training data has been employed in the EPR to enable it to learn the correlation, while the testing data was employed to test the accuracy of the established correlation in computing the Li/ks using data that have not been employed in the correlation development. This process is common in soft computing techniques to ensure the developed correlation's robustness [39,40,41]. Significantly, considerable efforts have been paid in selecting the training and testing data to guarantee that the testing data is within the training data range. This approach has been deemed necessary to prevent correlation extrapolation as recommended by several previous studies [42,43]. The statistical indicators of the training and testing data are shown in Tables 5 and 6, respectively.

Table 5 Statistical indicators of the training data
Full size table
Table 6 Statistical indicators of the testing data
Full size table

Using the training and testing data, trials have been conducted employing the EPR to find the most suitable mathematical correlation that correlates the non-aerated zone length with chute slope and roughness Froude number. For each trial, the statistical performance indicators and the correlation's ability to predict the trend of the relationship between the independent and dependent variables have been carefully examined. Considering the criteria mentioned, the best correlation obtained from the EPR is shown in Eq. 16.

$$\frac{{L_{i} }}{{k_{s} }} = 89.2902 \times (F_{*} )^{0.5} - 29.3533({\text{sin}}\theta )^{0.5} \times (F_{*} )^{1} \times 94.848({\text{sin}}\theta )^{2} - 95.1706.$$
(16)

Figures 15 and 16 show the developed correlation's statistical performance indicators compared to the other correlations for both training and testing data. The developed EPR correlation, respectively, scored R2 (coefficient of determination) and MAE (Mean Absolute Error) values of 0.93 and 1.66 for the training data and 0.83 and 2.7 for testing data, indicating a marginal error of prediction. It is vital to highlight that comparing the statistical performance indicators of the developed correlation with the available correlations, including the one obtained in this study earlier (i.e. using nonlinear multiple regression) demonstrates the improved accuracy of the EPR correlation. This is because the EPR correlation scored a lower MAE and higher R2 for training and testing data.

Fig. 15
figure 15

Performance indicators of the developed hybrid intelligent correlation compared with the other correlations for training data

Full size image
Fig. 16
figure 16

Performance indicators of the developed hybrid intelligent correlation compared with the other correlations for testing data

Full size image

These empirical equations could help the designers anticipate the length of the non-aerated zone over GSS under skimming flow conditions with improved accuracy compared to the current approaches. It should be noted that both Eqs. 11 and 16 are valid for non-uniform step configurations of gabion-stepped spillways. Both equations have been developed from the computational results of a step height of 0.1 (1.002 ≤ Yc/hs ≤ 2.002). Furthermore, the proposed equations are only appropriate for porosity values close to 0.325 and D50 around 0.017 m. The maximum discharge applied was 0.282m2.s−1. However, the empirically derived formulae proposed in this study are limited to the cases explored in this work.

Conclusion

In this paper, the effect of step non-uniformity for gabion-stepped spillway systems on the inception point location was numerically explored. Then, the data was used to generate two novel empirical equations based on a nonlinear multiple and evolutionary polynomial regression analysis to predict the non-aerated zone length considering the impact of the step non-uniformity. The following conclusions can be drawn given the limitations of this work:

  • The novel numerical models developed using the NEWFLUME code and validated against the experimental data presented in the literature showed that the model could capture the behaviour with a relative error of 0.5556%.

  • The shape of the steps in GSS had a significant impact on the formation of air pockets within the aerated zone depending on the spillway slope.

  • The inception point location was affected directly by the discharge that correlates with the surface water flow rate. For instance, higher discharge resulted in moving the inception point location towards the weir crest's downstream side due to an increase in the flow depth and water velocity.

  • Both empirical equations developed in this study achieved better predictions of the non-aerated zone length in non-uniform GSS compared to the existing equations.

The results of this study can be used to help improve the design of GSS in the future. While the work has demonstrated the potential of the proposed approach, there are limitations in terms of the geometry and flow characteristics examined. The present work can be extended to explore other geometries and flow regimes found in practice.