A mixture model clustering approach for temporal passenger pattern characterization in public transport

Abstract

Smartcard data provide a great number of information that are increasingly used nowadays. In the field of transport, they offer the opportunity to study passenger behavior, leading to a better knowledge of public transit demand and thereby granting the transport operators the ability to adapt their transport offer and services accordingly, both in space and in time. In particular, an accurate characterization of mobility patterns using data mining approaches has a very strong interest for transport planning purposes. This paper aims to propose a two-level generative mixture model that partitions passengers according to their temporal profiles. Using the timestamps of the passengers’ transactions in the public transport network, the first level models the passengers partitioning into a reduced set of clusters, whereas the second level captures how the trips made by each cluster of passengers are distributed over time. The proposed approach is applied on real ticketing data collected from the urban transport network of Rennes Métropole (France). The obtained results show that different passenger profiles can be discovered, thus highlighting several patterns of transport demand. The crossing of the clustering results with smartcard fare types as well as city characteristics such as academic centralities is also conducted in order to identify the close link between urban mobility and the socioeconomic characteristics of the city.

1 Introduction

Nowadays, an ever increasing number of digital traces describing urban mobility is generated on a daily basis: check-ins and geo-tagged messages on social networks, trajectories collected from smartphones and GPS devices, etc. In the context of public transportation, passenger traces depicted by ticketing data collected through automated fare collection (AFC) systems can be leveraged not only to measure the quality of service but also to understand passenger behavior, characterize the travel demand, and adapt the transport offering accordingly. Compared to household travel surveys that are conducted on small samples of passengers and over a short duration, ticketing data provide a more comprehensive view of all trips made in the public transportation network over extended periods of time. However, due to privacy concerns, they are often stripped out of personal data regarding the passengers (e.g., age, income, etc.).

However, conducting an analysis on smartcard data raises a number of challenges. Among which we mention the following:

• How to manage the large amount of data that are generated continuously ($\approx$200.000 validations each day in Rennes)?

• How to conduct reliable analyses with some missing information? Origin stations are available but missing destination stations are missing.

• How to overcome the absence of socioeconomic passengers’ data due to privacy rules (use of an anonymized id)?

• How to take into account the time continuity of the data?

Understanding temporal passenger habits and travel patterns is of great interest to both public transportation operators and local authorities since it can help predict and manage inflow, measure the adequacy between the existing offer and the real usage, and take the appropriate measures to adapt to the observed demand. This goal can be achieved by using statistical learning techniques, in particular cluster analysis: By partitioning passengers into groups based on travel hours, it is possible to extract general patterns describing different types of usage (sporadic usage, typical home-work commute behavior, etc.). Different approaches to clustering passengers using ticketing logs have been presented in the literature [1, 5, 8, 11]. However, most propositions rely on a discrete representation of time in which trips are aggregated over pre-defined time slots (e.g., 1 h). This can lead to issues w.r.t. capturing travel regularity. For instance, frequent trips made on the boundary of two consecutive time slots (e.g., trips made between 8:55 a.m. and 9:05 a.m. when a 1 h binning is considered) will be strewn between both time slots, thus giving an impression of a diffuse usage instead of a regular one.

We address the aforementioned issues in the present paper. Namely, our contributions can be summarized as follows:

• We present a novel approach to passenger clustering based on travel hours. The proposed approach considers a continuous representation of time instead of the time binning used in most existing methods and relies on estimating a Gaussian mixture model from the temporal profiles of passengers.

• We also conduct an extensive experimental study on a real dataset and illustrate how our approach can help discover different types of passenger behaviors (irregular passengers, typical commuters, etc.).

• We cross our results with spatial information on the city and users cards’ type, in order to compensate the absence of socioeconomic information.

The remainder of this paper is organized as follows. Related work on ticketing data analysis and clustering is presented in Sect. 2. We describe the real dataset we use in our study along with preliminary statistics in Sect. 3. Our approach to clustering passengers based on temporal behavior is introduced in Sect. 4. Experimental results are presented and discussed in Sect. 5. Finally, concluding remarks and future work are presented in Sect. 6.

2 Related work

Using ticketing logs collected through AFC systems in order to analyze mobility in public transportation motivated a considerable amount of research in the past few years. The possible role of ticketing data for the analysis of travel practices and their potential to supplement or even replace more conventional approaches that rely on survey data were investigated as early as [2, 15].

One need identified in early studies is that of enriching ticketing logs by inferring missing data such as trip destinations and transfer information which are often omitted. A large amount of works have been dedicated to these problems, particularly [3, 4, 14, 16]. These enrichment can then lead to further studies on mobility data.

By applying data mining tools to smartcard data, different facets of mobility in public transportation can be studied such as the variability of travel behavior [11], the difference between perceived and actual travel behavior and the reaction to travel incentives [6], passenger loyalty [13], community well-being [7], etc. Lathia et al. in [8] apply hierarchical agglomerative clustering on passenger weekday profiles (trip counts over five time bins within the day) in order to uncover different travel behaviors (e.g., typical commutes, evening-only travel, etc.) and motivate the need for using smartcard data to build user-tailored transport information services.

One way to extract information about mobility patterns is by using clustering methods. Conducting cluster analysis on ticketing data was first introduced in [11]. The authors study individual travel regularity by aggregating transactions belonging to the same smartcard into daily profiles, each indicating the time slots (i.e., hours) when the cardholder made at least one boarding, and using k-means clustering in order to identify clusters of similar days w.r.t. boarding times. A similar analysis of weekly travel behavior is conducted in [1]: Bus trips are aggregated into profiles that summarize the weekday activity of passengers and hierarchical agglomerative clustering (HAC) and k-means are then applied in order to study group behavior. In [9], DBSCAN is applied to individual trip chains in order to retrieve recurrent travel patterns. Additionally, k-means++ is used to cluster passengers based on regularity.

All these works have in common their use of classical clustering approaches. However, some more advanced machine learning methods have also been developed in recent works. For instance, nonnegative matrix factorization (NMF) is used in [12] to discover a dictionary of behavioral atoms to describe passengers based on their subway journey transactions. The distribution of these atoms over the stations is then used to conduct multi-scale clustering and retrieve groups of stations with similar behavior. In the approach described in [5], individual trip chains are aggregated into weekly passenger profiles, each containing the number of trips a given passenger made over 1-h bins for each day of the week. Then, a mixture of unigrams model is estimated over the temporal profiles in order to retrieve clusters of passengers exhibiting similar temporal patterns.

The majority of the aforementioned approaches rely on a discretization of time (e.g., using a binning over 1-h over periods of interest such as the morning, midday, and evening peaks). One drawback of this representation is that it does not fully capture travel regularity. For example, if we consider a passenger who commutes to work everyday between 8:55 a.m. and 9:05 a.m. and a 1-h binning, the passenger’s trips will be scattered across two distinct time slots (8 a.m. and 9 a.m.), which can be misinterpreted as a diffuse usage (which is clearly not the case).

This issue is addressed by the approach we propose in this paper. The novelty of our approach resides in considering a mixture of Gaussians that accounts for the continuous nature of time.

3 Urban transportation network and data

In this work, we use real ticketing data collected during the month of April 2014 from the STAR (Service de Transport en Commun de l’Agglomération Rennaise) public transport network of Rennes Métropole (France). The network is composed of one metro line (ligne a) and around 135 bus lines. Forty-three municipalities containing more than 400,000 inhabitants are serviced by the STAR network.

In 2006, the city introduced a smartcard that passengers can use to make trips in the STAR network. Passengers are required to validate their card only when boarding a bus or entering a metro station (therefore, alighting locations are not collected). The AFC system keeps track of these validations. Each record of a validation contains a unique anonymized card ID, the boarding time (date and time up to the minute) and location, the boarded bus or metro line, and the smartcard’s fare type.

In this study, smartcards are categorized into seven fare types: (i) pay as you go, (ii) free travel (granted to some passengers based on social criteria such as income, employment), (iii) short-term subscribers (less than one week), (iv) young subscribers, (v) subscribers, (vi) elderly subscribers, and (vii) Keolis Rennes (KR) agents.

A pre-processing step is conducted on the raw data (using an approach similar to [3, 14]) in order to infer alighting locations, detect transfers, and reconstruct trip chains.

The distribution of the number of active days (i.e., days where at least one trip was made using a given smartcard) during the 30 days covered by the data is depicted in Fig. 1. We can see that this number is decreasing between 0 and 10 days. At ten days of active usage, a first inflection point can be observed followed by a steady increase of the number of passengers. A second inflection point occurs around 18 days as the number of passengers starts declining constantly. Additionally, we can inspect the average number of trips per day made by passengers. Figure 2 shows that most passengers only made one or two trips per day.

Fig. 1

Number of active days per passenger in the transport network during the month of April 2014

Fig. 2

Average number of day trip per user in the transport network during the month of April 2014

The number of trips per hour for each day of the week from April 7 to April 14 is shown in Fig. 3. A pattern is clearly visible during weekdays as three peaks can be observed in the morning, midday, and evening (this pattern is the same for the other weeks of the data). The morning peak is the more concentrated, which suggests that morning trips are more regular than evening trips. The midday peak is smaller than the others which is probably due to the fact that a large amount of passengers do not use the transport network during their lunch break. A different pattern is observable on Wednesday with an increase in midday validations. This high activity can be explained by the fact that schoolchildren and high school students in France often do not have courses to attend on Wednesday afternoon. The day with the most activity is Tuesday. Some days (Thursday, Friday, and Sunday), a night activity can also be observed with trips registered at the end and at the beginning of the service. Compared to weekday activity, the activity during the weekend is lower, especially on Sunday, and does not show the three peaks pattern. Instead, only one peak spread over the afternoon is observed.

Fig. 3

Number of validations in the STAR network during the week of April 7, 2014

Subsequently, we use the 10 days of activity mark as a threshold to distinguish between occasional and regular passengers and retain only the latter group for our study since our objective is to highlight frequent temporal passenger patterns. In the next section, the dataset we use contains the trips made by 10,000 passengers randomly sampled from those having more than 10 active days. This dataset contains 28 % of young subscribers, 25 % of pay as you go, 31 % of free travel, 12 % of subscribers, and the other fare types represent less than 15 %. Rennes is a student city which explains the high number of young subscribers. This dataset can be of great interest for studying passenger patterns, especially to identify different types of passengers using their temporal profiles.

In order to have a better understanding of the spatial variability in the data, we represent the number of trips for four distinct periods in Fig. 4. This figure is composed of 4 maps representing the number of trips per station on Tuesday 1st April between 8 a.m. and 9 a.m. (Fig. 4a), Tuesday 1st April between 5 p.m. and 6 p.m. (Fig. 4b), Saturday 5th April between 3 p.m. and 4 p.m. (Fig. 4c) and finally Sunday 6th April between 6 a.m. and 7 a.m. (Fig. 4d). We can observe different usages depending on the day and time. For instance, we notice a difference in the number of validations between Tuesday, which is a typical weekday, and Saturday and Sunday: There are more trips and active stations during the week than during the weekend. Moreover, we can observe some spatial differences between Tuesday morning and evening: While inactive during the first half of the day, stations located in industrial and commercial areas (highlighted in beige color) become active during the evening. Finally, Sunday station activity is mostly concentrated around the metro and the city center.

Fig. 4

Number of trips per station for different day and hours of the week. a 8–9 a.m. on Tuesday, April 1, 2014. b 5–6 p.m. on Tuesday, April 1, 2014. c 3–4 p.m. on Saturday, April 5, 2014. d 6–7 p.m. on Sunday, April 6, 2014

The aforementioned points illustrate the necessity of analyzing the temporal habits of passengers since their activity is constantly evolving with respect to both the number of trips and their spatial locality in time. Additionally, studying the mobility of Rennes residents sets out to gain a better understanding of how Rennes metropolis is taking shape. Regarding Fig. 4, for instance, the polycentric operation of the metropolitan area can be easily seen.

4 Methodology

Clustering passengers based on their temporal activities is an interesting topic in knowledge extraction from smartcard data. As a matter of fact, the presence of groups of similar passengers can reveal the most frequent travel patterns in a given public transport network which, in turn, can contribute to a better characterization of the demand.

Our approach to passenger clustering is detailed in this section. We present our generative model which integrates a continuous representation of time. The algorithm used to estimate the model’s parameters is also explained.

4.1 Model

Our clustering approach relies on estimating a two-level generative mixture model. The first level models the passengers’ partitioning into groups (passenger clusters), whereas the second level captures how the trips made by each group of passengers are distributed over time.

One common way that is often used by generative approaches (such as Latent Dirichlet Allocation and the mixture of unigrams model) in order to determine cluster memberships is to consider that they are given by a latent variable that follows a multinomial distribution. We adopt this approach in the first level of our mixture model and consider that each passenger’s membership to one of the K clusters (K being fixed a priori), denoted $Z^1$, follows a multinomial distribution.

In the same fashion, the distribution of the trip hours made by the passengers belonging to a given cluster can be represented by a mixture distribution. In this case, a mixture of Gaussians is a fit and natural choice to describe the temporal habits of the passenger when the continuous nature of timestamps needs to be preserved (i.e., when they are not to be discretized). With such a distribution, the different times of typical use as well as the variances around these peaks can be extracted.

More formally, this generative model can be written as:

$$\begin{aligned} Z_i^1\sim & {} \mathcal {M}(1,\mathbf {\pi }),\nonumber \\ Z_{ij}^2 | Z^1_{ik}D_{ijl}=1\sim & {} \mathcal {M}(1,\mathbf {\tau }_{khl}),\nonumber \\ X_{ij} | Z^1_{ik}Z^2_{ijh}D_{ijl}=1\sim & {} \mathcal {N}(\mu _{khl},\sigma _{khl}). \end{aligned}$$

$Z_i^1$ encodes the membership of the ith passenger ($i \in \lbrace 1,\ldots , M\rbrace$) to one of the K passenger clusters and is drawn using a multinomial distribution (denoted $\mathcal {M}$) with the cluster proportions $\pi = \{\pi _1, \pi _2, \ldots , \pi _K\}\cdot Z_{ij}^2$ encodes the membership of the jth trip ($j \in \lbrace 1,\ldots , N_i\rbrace$) made by this passenger to one of the H Gaussians describing the latter’s cluster and is drawn conditionally to the passenger’s cluster $Z^1_{ik}$ and the day of the week the trip was made $D_{ijl}$ using a multinomial distribution of parameter $\mathbf {\tau }_{khl}$ (describing the clusters of Gaussians’ proportions). The trip’s time $X_{ij}$ is then generated using the corresponding Gaussian $\mathcal {N}(\mu _{khl},\sigma _{khl})$. A graphical representation of the model is illustrated in Fig. 5.

The conditional density of $X_{ij}$ can then be written as:

$$\begin{aligned}&f(X_{ij} | \lbrace Z^1_{ik}Z^2_{ijh}D_{ijl}=1 \rbrace ) \nonumber \\&\quad = \> \sum _{h=1}^{H} \tau _{khd_{ij}}f(x;\mu _{khd_{ij}},\sigma _{khd_{ij}}), \end{aligned}$$

(1)

with $f(.;\mu ,\sigma ^2)$ the density of a Gaussian distribution of mean $\mu$ and variance $\sigma ^2$. The likelihood of this model is given by:

$$\begin{aligned} L(\theta ) = \prod _{i=1}^{M}\sum _{k=1}^K\pi _k \left( \prod _{j=1}^{N_i}\sum _{h=1}^{H} \tau _{khd_{ij}}f(x_{ij};\mu _{khd_{ij}},\sigma _{khd_{ij}})\right) ~ , \end{aligned}$$

with M the number of passengers, K the number of passenger clusters, $N_i$ the number of trips made by passenger i, and H the number of Gaussians.

All in all, $K + H\times K \times 7 \times 3$ parameters have to be estimated. But the parameters of this likelihood, $\varvec{\theta }=(\varvec{\pi },\varvec{\tau },\varvec{\mu },\varvec{\sigma })$, cannot be directly estimated, and we propose in the next section a conditional expectation maximization (CEM)-type algorithm to solve this problem.

Fig. 5

Graphical model representation of the two-level mixture of Gaussians model

4.2 CEM and EM algorithm

We want to maximize the complete likelihood of $Z^1$ and $Z^2$ using a simple CEM with an expectation (E) step to reconstruct $Z^2$. As mentioned before, the log-likelihood is too complex for parameter estimation and using the complete likelihood enables the use of estimation algorithms such as CEM and expectation maximization (EM), which are the most commonly used methods for mixture model estimation [10].

Since the aim of the model is to classify passengers rather than validation hours, only the complete log-likelihood in $Z^1$ is used as a maximization criterion (i.e., $Z^2$ is excluded from the classification process). The complete likelihood in $Z^1$ is expressed as:

$$\begin{aligned}&Lc (\varvec{\varTheta };\varvec{\mathbf {X}},\varvec{\mathbf {Z^1}})\nonumber \\&\quad = \prod _{i=1}^{M}\prod _{k=1}^{K}\left( \pi _k\prod _{j=1}^{N_i}\sum _{h=1}^{H} \tau _{khd_{ij}}f(x_{ij};\mu _{khd_{ij}},\sigma _{khd_{ij}})\right) ^{z^1_{ik}} ~ , \end{aligned}$$

Again, the rationale behind this is to work in a density estimation context for $Z^2$ and in a clustering context for $Z^1$. To this effect, we use a CEM algorithm since it has a classification step that assigns each observation to its most probable cluster (instead of yielding a vector of membership probabilities as in the classic EM).

During the E step (E1) of the CEM algorithm, the conditional expectation of (1) is calculated. This expectation will provide the lower bound of the log-likelihood that will be maximized during the maximization (M) step and is given by:

$$\begin{aligned} \mathcal {L}c(\varvec{\varTheta };\varvec{\mathbf {X}},\varvec{\mathbf {Z^1}})= & {} \sum _{i=1}^{M}\sum _{k=1}^{K}\hat{z}^1_{ik}\log (\pi _k)\nonumber \\&+ \sum _{i=1}^{M}\sum _{k=1}^K\sum _{j=1}^{N_i}\sum _{h=1}^{H}\hat{z}^1_{ik}t^2_{ijh} \nonumber \\&\times \log \left( \tau _{khd_{ij}}f(x_{ij};\mu _{khd_{ij}},\sigma _{khd_{ij}})\right) , \end{aligned}$$

(2)

where $z^1_{ik}$ and $t^2_{ijh}$ are the a posteriori probabilities of the passenger’s cluster and the Gaussian’s cluster, respectively, and $\hat{z}^1_{ik}$ is the estimation of $z^1_{ik}\cdot t^1_{ik}$ is then given by:

$$\begin{aligned} t_{ik}^{1} \propto \pi _k\prod \limits _{j=1}^{N_i} \sum \limits _{h=1}^{H} \tau _{khd_{ij}} \times f(x_{ij};\mu _{khd_{ij}},\sigma _{khd_{ij}}). \end{aligned}$$

$t_{ik}^{1}$ is calculated during the E1 step, whereas $\hat{z}_{ik}^1$ is calculated from $t_{ik}^{1}$ in the classification step C1.

$$\begin{aligned} \hat{z}_{ik}^1 = \left\{ \begin{array}{ll} 1&{} \quad \text{ if } k=\text {arg} \max \limits _k t_{ik}^{1},\\ 0&{} \quad \text {otherwise}.\\ \end{array} \right. \end{aligned}$$

We then maximize the bound during the M1 step to obtain the proportions $\pi$ of each passenger cluster.

$$\begin{aligned} \pi _{k}=\dfrac{M_k}{M}, \end{aligned}$$

with $M_k$ the number of passengers assigned to the $k^\mathrm{th}$ cluster. At the end of the CEM algorithm, we obtain a classification of the passengers.

However, as can be seen in (2), the likelihood is composed of two sums. That is why, we cannot only apply a CEM and we need to use an EM on the second sum to estimate the variables.

The second EM begins with an E2 step which calculates the a posteriori probability of $t^2_{ijh}$ conditionally to $Z^1$. The probability can then be written as:

$$\begin{aligned} t_{ijh}^{2}=\dfrac{ \tau _{khd_{ij}} \times f(x_{ij};\mu _{khd_{ij}},\sigma _{khd_{ij}})}{\sum \nolimits _{h=1}^H \tau _{khd_{ij}} \times f(x_{ij};\mu _{khd_{ij}},\sigma _{khd_{ij}})}. \end{aligned}$$

The M2 step gives us the final estimations of Gaussians proportions and parameters by maximizing the lower bound. The estimations are:

$$\begin{aligned} \tau _{kwh}= & {} \frac{\sum _{i=1}^{M}\sum _{j=1}^{N_i}z^1_{ik} d_{ijw} t_{ijh}^2}{\sum _{i=1}^{M}\sum _{j=1}^{N_i}z^1_{ik} d_{ijw}},\\ \mu _{kwh}= & {} \frac{\sum _{i=1}^{M}\sum _{j=1}^{N_i}z^1_{ik} d_{ijw} t_{ijh}^2 x_{ij}}{\sum _{i=1}^{M}\sum _{j=1}^{N_i}z^1_{ik} d_{ijw}t_{ijh}^2},\\ \sigma _{kwh}= & {} \frac{\sum _{i=1}^{M}\sum _{j=1}^{N_i}z^1_{ik} d_{ijw} t_{ijh}^2 (x_{ij}-\varvec{\mu }_k^{(q+1)})^2}{\sum _{i=1}^{M}\sum _{j=1}^{N_i}z^1_{ik} d_{ijw}t_{ijh}^2}. \end{aligned}$$

Pseudo-code of the algorithm is shown in Appendix 2.

4.3 Model calibration

We now present our model calibration choices. The number of Gaussians H needed to represent the temporal patterns of passengers will be discussed, and the choice of the number of passenger clusters K will be explained. For this model, two different initializations have been developed for the algorithm. These are described in Appendix 1.

Fig. 6

ICL criterion for passenger clusters $K=2, \ldots , 20$ and number of Gaussians $H=2, 3 \text { and } 4$

The algorithm is launched while varying the number of Gaussians H from 2 to 4 and the number of passenger clusters K from 2 to 20 and the estimated parameters of the Gaussians, cluster proportions, and complete log-likelihood obtained in each run are registered. The integrated classification likelihood (ICL) is then be calculated to choose the best model (cf. Fig. 6).

Fig. 7

The temporal activity profiles for each day of the week and card type of cluster 1 passengers. a Temporal profil. b Cards’ type

Fig. 8

The temporal activity profiles for each day of the week and card type of cluster 4 passengers. a Temporal profil. b Cards’ type

Fig. 9

The temporal activity profiles for each day of the week and card type of cluster 7 passengers. a Temporal profil. b Cards’ type

When the temporal profiles of passenger activities are represented with only two Gaussians, the ICL criterion’s values are higher than in the other models. Moreover, the plot of results shows that clusters from the models with $H=2$ lead to a precision loss. This translates the incapability of these models to capture three-peak patterns (morning, midday, and evening), thus resulting in the morning and evening peaks having a bigger variance and shifted means in order to compensate for the omission of the midday peak.

The results for the remaining two cases are very close since, for all values of K, the models with $H=4$ result in similar values of ICL to those with $H=3$. The study and visualization of results for $H=4$ (not depicted here) have shown that they do not produce a fourth peak contrary to what can be intuitively expected. Besides, a greater variability than in the three-Gaussian model appears from one day to another, and we noticed that some very thin peaks are appearing, which can be symptomatic of overfitting. This suggests that the simpler three-Gaussian models are sufficient to represent passenger travel in a single day and are preferable to work with since an additional Gaussian requires more parameters but does not contribute significant improvements to the clustering results.

Regarding the number of passenger clusters K, the ICL is not very helpful because it did not help us find an optimal number of clusters. It seems that the more clusters there are, the better the model representation is. For the experimental study presented in the following section, we chose to analyze the ten clusters model ($H = 3, K=10$) since it contains a variety of different and interesting passenger clusters. If we want to be more specific and to break clusters with a high percentage of passengers, we can choose more clusters.

5 Experimental results

Now that the numbers of Gaussians and passenger clusters are fixed, and it is interesting to interpret the results. We first present four passenger clusters that seem to be the most representative ones w.r.t. the trends they depict. The Tuesday activity curves of these clusters are then compared in order to highlight the key differences between their patterns. Finally, we focus on the spatial activity of young subscribers belonging to one specific cluster by locating the stations where they are most active and positioning them within the context of the city.

Fig. 10

The temporal activity profiles for each day of the week and card type of cluster 9 passengers. a Temporal profil. b Cards’ type

5.1 Clusters study

Cluster 1 (see Fig. 7) exhibits a two-peak pattern that occurs during weekdays. The study of these two peaks shows that the variance of the morning peak is very small as the peak is concentrate between 7 a.m. and 9 a.m., whereas the afternoon peak is more spread and goes from 3 p.m. to 8 p.m. Outside these peaks, there is very low to no activity at night and during the weekend. This suggests that passengers of this cluster are typical commuters that do not rely on public transportation outside of their regular home–work commute (e.g., during lunch breaks and for leisure activities). This observation is supported by the cluster’s composition w.r.t. fare types (see Fig. 7b), which shows that it contains a high percentage of subscribers (mostly active adults) and young subscribers (mostly students and schoolchildren) who have clear schedules around which their travel habits revolve.

A similar trend is observed in cluster 4 (see Fig. 8) and cluster 7 (see Fig. 9) in both of which the morning activity is also very regular with a steep peak. However, contrary to the first cluster, they present a three-peak pattern with the appearance of a third peak between 10 a.m. and 3 p.m. In cluster 4, midday and evening peaks are mingled and on Friday only two peaks are noticeable: The second and the third peaks are completely merged and form a bell-shape curve that spreads from 10 a.m. to midnight. Contrary to cluster 1, weekend and night present some noticeable activity. The cluster is composed of more than 50 % of young subscribers and more than 25 % of free travel which hints that it is majorly composed of students. In cluster 7, the three peaks are more distinguishable and there is less night activity on weekends than in cluster 4 (due to young subscribers being less present in the former).

Finally, cluster 9 (see Fig. 10) presents some interesting particularities. For instance, it has a more diffuse activity than in the other clusters. There is no thin morning peak but a mix of two peaks that spans across all the day. These mixed peaks have an inverted pattern: The second peak is the highest one, which implies that more activity occurs in the afternoon and the evening than during the morning. This can be explained by the high night activity present every day of the week: Passengers who are using public transportation later at night will also tend to use it later in the morning. As it can be seen in Fig. 10, pay as you go passengers (i.e., passengers using tickets) and those benefiting from free travel account for more than 50 % of the cluster’s composition. These card types are mostly owned by passengers that use public transport sporadically.

Fig. 11

The Tuesday temporal activity profiles for all ten clusters

Another interesting aspect is the comparison of different clusters based on temporal activity occurring on the same day of the week. To this effect, all the clusters’ curves for Tuesday are presented in Fig. 11. Indeed, the subtle differences between clusters become more apparent. For example, while presenting similar patterns, the morning peak hour of cluster 2 occurs earlier than the peak hour of cluster 7. Some clusters (such as cluster 6) also depict a very regular pattern which becomes more visible by comparing it to the others clusters.

Based on Fig. 11, it is possible to distinguish between three types of clusters. The first one is composed of clusters with two activity peaks, such as clusters 1, 2, 6, and 8. The difference between these clusters lies in the fact that cluster 8 has a bigger activity on midday even if a peak pattern does not appear. Cluster 2’s morning peak is a bit earlier than cluster 1’s morning peak, and cluster 6 has a greater variance than the other clusters. The second type is the three-peak pattern clusters, such as clusters 4, 5, and 7. They can be further distinguished using their peak hour and their shape (e.g., cluster 7 has more distinct peaks). Finally, we have the diffuse clusters, such as clusters 3, 9, and 10. The morning peak of cluster 10, while being spread on a large time interval, is still visible. In cluster 3, only one peak covering the whole the day is present, and cluster 9 presents an inverted pattern compared to all other clusters. Clusters of this last category regroup the majority of passengers (61.31 %). If required, the activity patterns they depict can be further refined by increasing the number of clusters (thus splitting them into smaller, more detailed clusters).

Compared to results obtained using a discretized-time approach, profile curves issued from our continuous time approach offer a better view of passenger activity: Instead of having discrete per hour activity probabilities, we now have a continuous time activity probability that does not suffer from potential bias resulting from aggregating observations into time bins. Additionally, mean and variance information for each activity peak is now available, which was not possible with aggregate time clustering. Finally, the graphical representation of the temporal activity profiles is still easy to understand and interpret.

5.2 Geographical location of student cluster

We now illustrate how the activities of a specific cluster of passengers can be positioned within the geographical context of the city. To this effect, we propose to study the specific case of student activity. The rationale behind choosing students is that their trip generators (i.e., academic institutions and related facilities) are more spatially confined than trip generators of other types of passengers (e.g., vast industrial and economical areas for working adults).

Inspecting the distribution of card types across clusters (see Fig. 12) reveals that most of young subscribers are present in clusters 4, 6, and 9. As mentioned before, cluster 9 corresponds to a more diffuse activity. In clusters 4 and 6, morning peaks are visible, and in clusters 4 and 9 an important night activity can be seen on weekend and on Thursday night, which corresponds to the most active night for French students.

Fig. 12

Distribution of each card type across passenger clusters

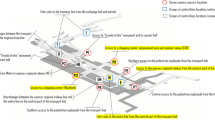
Consequently, we focus on young subscribers belonging to cluster 4 (with the assumption, based on the aforementioned observations, that most of them are students) and study how the spatial location of their trip generators impacts their activity in the transport network. To this purpose, a map of Rennes transport network is presented in Fig. 13. On this map, we present the socioeconomic specifications of the various neighborhoods of the city, the location of academic facilities, and the most active stations for young subscribers in clusters 4.

The most active stations are located in the northeast, south, and in the town center of Rennes. The activity in the south of Rennes is mainly observed along the subway line. As shown in Fig. 13, this part of the city corresponds to collective housing with low income which suggests that these stations are probably residential stations of the young subscribers. The highest activity, which is located in the town center, is not surprising because the town center regroups most of the city’s activities. Moreover, the STAR network is star-shape around the town center, which results in a lot of transfer activities occurring in this place. Finally, the northeast of Rennes is the area which regroups the most of academic facilities, which explains the high frequentation of stations located at this level (such as the Villejean Université metro station and its surrounding stations).

Fig. 13

Map of stations activity in Rennes for young subscribers of cluster 4

5.3 Spatial locality evolution during time

In the previous section, we have studied the spatial locality of a specific population by analyzing their station activity regardless of when this activity occured. Nevertheless, spatial activity can be analyzed in further detail by looking for example, at the evolution of the number of trips per station depending on the time of the day. Such analysis can potentially highlight more specific areas of interest and link them to particular usage trends. In previous work that relies on a pre-established time binning, each trip of a given passenger is deterministically assigned to a time bin regardless of whether or not the time binning is representative of the travel pattern it depicts. By relying on a mixture of Gaussians, our approach automatically captures the most relevant instants (and their variability) for each cluster. Moreover, this process is conducted separately for each day. Consequently, it is possible to probabilistically assign each trip of a passenger belonging to a given cluster to the most likely Gaussian of the day the trip was made. For a given day of interest, the trips made by the passengers belonging to a given cluster can be divided into three groups one for each Gaussian. Each group can then be studied separately in order to discover how usage evolves in time.

Fig. 14

Number of trips per station made by cluster 1 passengers on Tuesday 1st April 2014. a Trips assigned to first Gaussian of the day, with a mean at 8:07 a.m. and a standard deviation of 32 min. b Trips assigned to third Gaussian of the day, with a mean at 5:20 p.m. and a standard deviation of 80 mi

To illustrate this idea, we can study the activity occurring in cluster 1. As seen previously, the passenger activity in this cluster is mostly divided in two peaks of activity. The number of trips per station for the first Gaussian of the day (that corresponds to the morning activity) is depicted in Fig. 14a, whereas the third Gaussian of the day (that corresponds to late afternoon activity) is depicted in Fig. 14b. These two Gaussians capture most of the activity of the day, and they can reveal the differences of activity between the morning and the evening. It is then possible to locate the areas from which people are mostly departing in the morning (habitation locations) and from where they are traveling in the evening (work location).

The comparison of the two maps of Fig. 14 reveals, as expected, some differences of activity. The first observation that can be made is that activity occurring at the city center becomes more spread in the evening. As a matter of fact, during the morning, the center activity is mainly focused around two areas (République and Gares), while the evening activity is more spread. The second noteworthy observation is the appearance of activity in commercial and industrial areas (beige zones on the map). This suggests that a certain number of passengers work in these areas and validate their card at the end of the day, when they commute back home. Finally, we can notice some stations that are active at the end of the day and that were not in the morning and vice versa.

6 Conclusion

In this paper, we proposed a two-level Gaussian mixture model approach to clustering temporal passenger profiles in a public transport network. The first level consists of clustering the passengers based on their temporal activity which, in turn, is represented by a mixture of Gaussians inferred at the second level by clustering the ticketing logs based on their timestamp information. As shown in Sect. 5, a continuous weekly activity profile is obtained for each cluster. Cluster profiles can then be used to differentiate between passengers with regular travel hours and those with diffuse travel hours. The approach is also capable of detecting subtle trends such as the presence of nightlife activity. The results provided by our method could help the transport operators to have a better knowledge of their passengers’ behavior patterns and adapt their offer to suit the different demands they portray (e.g., specific card type for passengers with regular temporal pattern). Moreover, a more precise view of passenger activity peaks is also obtained with the proposed approach compared to classic aggregate time clustering.

By cross-comparing the clustering results with the geographical and socioeconomic data of the city, it is possible to assign passenger clusters to specific areas depending on their card types. For instance, we showed that young passengers of a cluster with a regular three-peak pattern during weekdays and with nightlife activity at the end of the week can be identified as students because of the high number of validations located near academic institutions. Pinpointing the stations where most of a given passenger group’s activity occurs gives the operator the opportunity to adapt its offer to the specificities of said group (e.g., reduce the number of buses serving stations that are solely used by students during school breaks and vacations).

Further investigation is needed w.r.t. choosing a suitable number of passenger clusters, which remains an open question. In this study, we limited this number to ten clusters merely for illustration purposes. However, our experiments suggest that increasing the number of clusters results in the “diffuse” clusters (i.e., in which no distinguishable pattern is visible) being split into finer clusters with more apparent patterns. Further work can also be conducted on passengers regularity. In fact, while this work goes further than most existing studies by using a continuous time instead of aggregated time (which allows the study of trip hour variability within groups of passengers), it would be very interesting to study travel variability on an individual level (e.g., passengers traveling every day with a variance of 5 min and passengers with a variance of 30 min). The data used in this study were treated on a calendar day basis (i.e., considering that the day starts at 0 a.m. and ends at 0 a.m. of the next day) which can lead to an artificial bias at midnight. Therefore, applying the algorithm on the data while considering “service days” (i.e., a delimitation using the start and end of service times) is needed in order to assess the existence and impact of such a bias. Finally, it would be interesting to inject the model with priors that model intuitive or existing knowledge about travel behavior (e.g., priors modeling typical commute patterns, leisure-centered usage, etc.) and study their impact on the clustering process and the produced results.

Appendices

Appendix 1: initialization method

Two initializations are possible for the clustering. The first one, named seeds, consists in a k-means initialization approach. First, small groups of passengers are sampled. A k-means is then applied on these groups to estimate model parameters. In the second method, named random, clusters are randomly initialized and parameters are estimated using these clusters. The aim here is to determine which one of these two methods is the most effective.

For both initializations, the algorithm is launched 50 times. The complete log-likelihood and the number of iterations before convergence are registered. The choice is made to compare these two initializations with a clustering on three Gaussians and fifteen clusters.

Fig. 15

Comparison of complete likelihood and number of iterations before convergence of the algorithm for methods seeds and random

In Fig. 15, boxplots of complete likelihood and of the number of iterations obtained are shown. Seeds method converges faster than random method with a mean equal to 260 iterations against 493. In addition, complete likelihood is on average equal to $-97{,}440$ for seeds method and to $-98{,}300$ for the other method. In this paper, seeds method is the only one used because of its convergence speed.

Appendix 2: EMCEM algorithm

The EM and CEM combined algorithm pseudo-code used for clustering is presented in Fig. 16.

Fig. 16

EMCEM algorithm