A Probabilistic Travel Time Modeling Approach Based on Spatiotemporal Speed Variations

Abstract

The rapid development and deployment of Intelligent Transportation Systems (ITSs) require the development of data driven algorithms. Travel time modeling is an integral component of travel and transportation management and travel demand management functions. Travel time has a massive impact on driver’s route choice behavior and the assessment of the transportation system performance. In this paper, a mixture of linear regression is proposed to model travel times. The mixture of linear regression models has three advantages. First, it provides better model fitting compared to simple linear regression. Second, the proposed model can capture the bi-modal nature of travel time distributions and link it to the uncongested and congested traffic regimes. Third, the means of the bi-modal distributions are modeled as functions of the input predictors. This last advantage allows for the quantitative evaluation of the probability of each travel time state as well as the uncertainty associated with each state at any time of the day given the values of the predictors at that time. The proposed model is applied to archived data along a 74.4-mile freeway stretch of I-66 eastbound to connect I-81 and Washington D.C. The experimental results show the ability of the model to capture the stochastic nature of the travel time and gives good travel time predictions.

1 Introduction

Minimizing drivers’ travel times from their origins to their destinations is a major Intelligent Transportation Systems (ITSs) objective. However, it is also extremely challenging due to the dynamic nature of traffic flow, which is, in most cases, highly unpredictable. One straightforward strategy involves directing vehicles or guiding drivers to follow routes that avoid congested paths. A critical step for this route planning or guidance to be effective is the ability to accurately predict travel times of different alternative routes from source to destination.

In addition, travel time represents an important performance measure for traffic system evaluation. It is easily understood by drivers and operators of traffic management systems, and can be viewed as a simple summary of a traffic system’s complex behavior. In order for an ITS to accurately predict the travel time, it must have the following capabilities, each of which comes with associated difficulties:

• 1. Sensing and acquiring the current state of the transportation network of interest where a number of data values need to be detected and collected, including traffic conditions and parameters at different parts of the network, whether some roads are currently congested, current weather conditions, time of day, whether there is an incident on any road in the network, etc. Gathering such data on every road and intersection with the quality that allows accurate forecasting of travel time between two points in the network may be fairly expensive.

• 2. Storing a long history of traffic parameters for the transportation network of interest to support future prediction of travel times. This historical dataset may be large and difficult to use and manage.

• 3. Feeding the current state of the network along with its traffic history to some type of model that predicts travel time if a trip will start from some point and end in another in the network at some specific time. Designing such a model is challenging, as is finding a set of current or historical parameters with real prediction power. The most useful model may be road dependent, and even for a single road, it has been shown that different models may describe the traffic behavior more accurately at different traffic conditions. For instance, one model may be more useful when the road is congested, while another model may be more accurate when vehicles are flowing freely, etc.

In short, accurate traffic time prediction is challenging due to the high cost of sensing and collecting enough useful current and historical traffic data. Even when such data is available, it is still difficult to determine which type of model best describes the traffic behavior, and which traffic parameters should be fed to the model for the best predictions. Moreover, the best course of action may be to use two or more models and switch between them depending on current traffic conditions. This option adds a new challenge, as it is necessary to decide which model from the set of models will be used for some specific input data, or whether different models will be used for prediction with some weight applied to each output prediction to reach a final travel time prediction.

In this paper, a new method for travel time prediction is proposed. This method uses a mixture of linear regressions motivated by the fact that travel time distribution is not unimodal, since two modes or regimes of traffic can exist—one at congestion state, and the other at free-flow state. We show how the proposed model is very flexible and gives slightly different accuracy when we model the travel time or the log of the travel time using two different set of predictors. The First set of predictors are the selected elements from the spatiotemporal speed matrix based on their estimated importance using random forest. Then these set of speeds will be the input predictors to the statistical model. The second set of predictors are the instantaneous travel time and the average of the historical travel time. The proposed model is built and tested using probe data provided by INRIX and supplemented with traditional road sensor data as well as mobile devices and other sources. The dataset was collected from a freeway stretch of I-66 eastbound connecting I-81 and Washington, D.C. The traffic on this stretch is often extremely heavy, which makes travel time prediction more challenging, but also makes the data more valuable and helps create a more realistic model.

2 Related Work

Various methods and algorithms have been proposed in the literature for travel time prediction. These methods can roughly be classified into two main categories: statistical-based data-driven methods and simulation-based methods. This section focuses on the statistical-based methods since the proposed solution in this paper falls under this class of methods, and because more research in the literature uses statistical methods.

Several researchers fit different regression models to predict travel time. A typical approach is to fit a multiple linear regression (MLR) model using explanatory variables representing instantaneous traffic state and historical traffic data, as, for example, [1, 2]. The model proposed in [1] was even able to use a single linear regression (SLR) to successfully provide acceptable travel time predictions. Some researchers developed hybrid methods where a regression model was used in conjunction with other advanced statistical methods. For example, [3] used regression with statistical tree methods. Another approach [4] proposed an SLR model using bus travel time to predict automobile travel time.

Regression models are generally powerful in predicting travel time for short-term prediction, whereas long-term predictions are less accurate. Regression models are also reported to be more suitable for use in free-flow rather than congested traffic, and fail to accurately predict when incidents have occurred [5].

The idea of using a mixture models for different traffic regimes has also previously been explored [6]. The model developed in this paper attempts to overcome the drawbacks of previous work that used mixture models of two or three components to model travel time reliability, which suffer from the following limitations:

• 1. The mean of each component is not modeled as a function of the available predictors.

• 2. The proportion variable is fixed at each time slot, which limits the model’s flexibility.

• 3. Information provided given the time slot of the day is the probability of each component (fixed) and the 90th percentile.

Another class of statistical-based methods in literature uses time series models for travel time prediction, using, for example, auto-regressive prediction models [7,8,9], multivariate time series models [10], and the auto-regressive integrated moving average (ARIMA) technique [11]. Similar to regression models, time series models are more suitable for free-flow traffic than for congested traffic, may fail with unusual incidents, and are more accurate for short-term predictions [5].

Another common technique used for travel time prediction is the use of artificial neural networks. A feed-forward neural network is used in [12] to predict journey time. Later, more advanced neural network techniques were used to model and predict travel time [13,14,15,16,17,18,19]. Accurate predictions were achieved for most proposed models; for example, in [20] the prediction error was only 4%.

3 Methods

The definitions of historical, instantaneous and ground truth travel times are introduced in this section. In addition, we present a brief introduction of the powerful modelling technique used in this paper. Expectation-maximization (EM) is used to fit the mixture of linear regression models to the historical data.

3.1 Travel Time Ground Truth Calculation

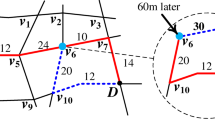
The calculation of the travel time ground truth is based on trajectory construction and the known speed through the trajectory’s cells. A simple example of travel time ground truth calculation based on trajectory construction is demonstrated in Fig. 1. In this example, the roadway is divided into four sections using segments of length $\Delta x$ and a time interval of $\Delta t$. We assumed that the speed is homogenous within each cell. The average speed of the red-dotted cell (i = 2, n = 3) in the figure is $u(x2,t3)$. Consequently, the trajectory slope represents the speed in each cell. Once the vehicle enters a new cell, the trajectory within this cell can be drawn as the straight blue line in Fig. 1 using the cell speed as the slope. Finally, the ground truth travel time can be calculated when the trip reaches the downstream boundary of the last freeway section. It should be noted that the ground truth travel times were computed using the same dataset and used as the response (y).

Fig. 1.

Illustration of travel time ground truth calculation.

3.2 Instantaneous Travel Time

The instantaneous method is very simple where it assumes the segment speed does not change during the entire trip time. The travel time using the instantaneous approach is shown in Eq. (1).

$$ {\text{instantaneous travel time}} = \mathop \sum \limits_{{{\text{i}} = 1}}^{\rm{h}} \frac{{{\text{L}}_{\rm{i}} }}{{\upupsilon_{\rm{i}}^{\rm{t0}} }} $$

(1)

Where

${\text{L}}_{\rm{i}}$ is the length of segment i

$\upsilon_{\rm{i}}^{{{\text{t}}0}}$ is the speed at segment i at the departure time t0

h is the total number of segments.

3.3 Historical Average Method

If the spatiotemporal speed matrices are known for several previous months, then the ground truth travel time at each time interval for each day can be calculated. The historical average at any time of day D is calculated using Eq. (2).

$$ {\text{average historical travel time}} = \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\rm{Z}}_{{{\text{D}}_{\rm{i}} }} }} \frac{{{\text{GTTT}}_{{{\rm{D}}_{\text{i}} }}^{{{\rm{t}}0}} }}{{{\text{Z}}_{{{\rm{D}}_{\text{i}} }} }} \forall {\rm{D}}_{\text{i}} = {\rm{Saturday}}, \ldots ,{\text{Friday}} $$

(2)

Where ${\text{GTTT}}_{{{\rm{D}}_{\text{i}} }}^{{{\rm{t}}0}}$ is the ground truth travel time at departure time $t0$ at historical day $D_{i}$ and ${\text{Z}}_{{{\rm{D}}_{\text{i}} }}$ is number of days included in the average.

3.4 Mixture of Linear Regressions

A mixture of linear regressions was studied carefully [21, 22]. It can be used to model travel time under different traffic regimes. The mixture of linear regression can be written as:

$$ {\rm{f}}\left( {\text{y|X}} \right) = \mathop \sum \limits_{{{\rm{j}} = 1}}^{\rm{m}} \frac{{\uplambda_{\text{j}} }}{{\upsigma_{\rm{j}} \sqrt {2\uppi} }}{\text{e}}^{{ - \frac{{\left( {{\text{y}} - {\rm{X}}^{\text{T}}\upbeta_{\text{j}} } \right)^{2} }}{{2\upsigma_{\text{j}}^{2} }}}} $$

(3)

where ${\text{y}}_{\rm{i}}$ is the response corresponding to a vector ${\text{p}}$ of predictors; ${\text{x}}_{\rm{i}}^{\rm{T}}$, $\upbeta_{\rm{j}}$ is the vector of regression coefficients for the ${\rm{j}}^{\rm{th}}$ component and $\uplambda_{\rm{j}}$ is mixing probability of the ${\rm{j}}^{\rm{th}}$ component.

The model parameters $\uppsi = {\{ \beta }_{1} ,\,\upbeta_{2} , \ldots ,\upbeta_{\rm{m}} \sigma_{1}^{2} ,\sigma_{2}^{2} , \ldots \sigma_{\rm{m}}^{2} ,\,\lambda_{1} ,\,\lambda_{2} , \ldots ,\,\lambda_{\rm{m}} \}$. can be estimated by maximizing the log-likelihood of Eq. (1) given a set of response predictor pairs $({\rm{y}}_{1} ,{\rm{x}}_{1} ),({\rm{y}}_{2} ,{\rm{x}}_{2} ), \ldots ,({\rm{y}}_{\text{n}} ,{\rm{x}}_{\text{n}} )$ using an EM algorithm. The EM algorithm iteratively finds the maximum likelihood estimates by alternating the E-step and M-step. Let $\uppsi^{{({\text{k}})}}$ be the parameters’ estimates after the ${\text{k}}^{\rm{th}}$ iteration. In the E-step, the posterior probability of the ${\text{i}}^{\rm{th}}$ observation from component ${\text{j}}$ is computed using Eq. (4).

$$ {\text{w}}_{\rm{ij}}^{{({\text{k}} + 1)}} = \frac{{\uplambda_{\rm{j}}^{{({\text{k}})}}\upphi_{\text{j}} \left( {{\rm{y}}_{\text{i}} | {\rm{x}}_{\text{i}} ,\uppsi^{{({\rm{k}})}} } \right)}}{{\mathop \sum \nolimits_{{{\text{j}} = 1}}^{\rm{m}}\uplambda_{\text{j}}^{{({\rm{k}})}}\upphi_{\text{j}} \left( {{\rm{y}}_{\text{i}} | {\rm{x}}_{\text{i}} ,\uppsi^{{({\rm{k}})}} } \right)}} $$

(4)

where $\upphi_{\rm{j}} \left( {{\rm{y}}_{\rm{i}} | {\rm{x}}_{\rm{i}} ,\uppsi^{{({\rm{k}})}} } \right)$ is the probability density function of the ${\rm{j}}^{\rm{th}}$ component.

In the M-step, the new parameters’ estimates $\uppsi^{{({\rm{k}} + 1)}}$ that maximize the log-likelihood function in Eq. (3) are calculated using Eqs. (5–7)

$$ \uplambda _{{\text{j}}}^{{({\text{k}} + 1)}} = \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{n}}} {\text{w}}_{{{\text{ij}}}}^{{({\text{k}} + 1)}} }}{{\text{n}}} $$

(5)

$$ \widehat{\upbeta}_{\rm{j}}^{{({\rm{k}} + 1)}} = ({\rm{X}}^{\rm{T}} {\rm{W}}_{\rm{j}} {\rm{X}})^{ - 1} {\rm{X}}^{\rm{T}} {\rm{W}}_{\rm{j}} $$

(6)

where X is the predictors’ matrix with ${\rm{n}}$ rows and $({\rm{p}} + 1)$ columns, Y is the corresponding n × 1 response vector, and W is an n × n diagonal matrix which has ${\rm{w}}_{\rm{ij}}^{{({\rm{k}} + 1)}}$ on its diagonal.

$$ {\hat{\sigma }}_{\rm{j}}^{{2({\rm{k}} + 1)}} = \frac{{\mathop \sum \nolimits_{{{\rm{i}} = 1}}^{\rm{n}} {\rm{w}}_{\rm{ij}}^{{({\rm{k}} + 1)}} ({\rm{y}}_{\rm{i}} - {\rm{x}}_{\rm{i}}^{\rm{T}} \widehat{\upbeta}_{\rm{j}}^{{({\rm{k}} + 1)}} )^{2} }}{{\mathop \sum \nolimits_{{{\rm{i}} = 1}}^{\rm{n}} {\rm{w}}_{\rm{ij}}^{{({\rm{k}} + 1)}} }} $$

(7)

The E-step and M-step are alternated repeatedly until the change in the incomplete log-likelihood is arbitrarily small as shown in Eq. (8).

$$ \left| {\prod\nolimits_{{{\rm{i}} = 1}}^{\rm{n}} {\sum\nolimits_{{{\rm{j}} = 1}}^{\rm{m}} {\uplambda_{\rm{j}}^{{({\text{k}} + 1)}}\upphi_{\rm{j}} \left( {{\text{y}}_{\rm{i}} | {\text{x}}_{\rm{i}} ,\uppsi^{{({\text{k}} + 1)}} } \right)} } - \prod\nolimits_{{{\rm{i}} = 1}}^{\text{n}} {\sum\nolimits_{{{\rm{j}} = 1}}^{\rm{m}} {\uplambda_{\rm{j}}^{{({\rm{k}})}}\upphi_{\rm{j}} \left( {{\rm{y}}_{\rm{i}} | {\rm{x}}_{\rm{i}} ,\uppsi^{{({\rm{k}})}} } \right)} } } \right| < \xi $$

(8)

where $\upxi$ is a small number.

4 The Predictors’ Sets

In this section, we describe the two approaches used to from the predictors’ sets. In the first approach, the random forest machine-learning algorithm (RF) is used to select a subset of important predictors for travel time modelling. Where the second approach incorporate information from the past by using the historical travel time and summarize the current speeds within a window starting right before the departure time ${\rm{t}}_{0}$ using the instantaneous travel time.

4.1 The First Set of Predictors

The I-66 stretch of the freeway section used for this research consists of 64 segments. The dataset comprises the spatiotemporal speed matrices for every day in 2013. The default approach for modelling and predicting travel time was to take all the speeds within a window starting right before the departure time ${\rm{t}}_{0}$ and covering L past time slots back to time ${\rm{t}}_{0} - {\rm{L}}$. Setting L = 30 min for example, the number of predictors will be 64 * 6 at 5 min time aggregation. In order to reduce the dimensions of the predictors’ vector, RF is used to select the most important predictors for the travel time model. Steps to select the most important predictors are as follows [23]:

• 1. For each month, build an RF consisting of 100 trees and find the out-of-bag samples that are not used in the training for each tree.

• 2. Find the mean square error ${\rm{MSE}}_{\text{out of bag}}$ of the RF using the out-of-bag samples.

• 3. Randomly permute the value for each predictor ${\rm{x}}_{\text{i}}$ among the out-of-bag samples and calculate the mean square error ${\rm{MSE}}_{\text{out of bag}}^{{{\text{permuted x}}_{\rm{i}} }}$ of the RF.

• 4. Finally, rank the predictors in descending order based on the $\frac{1}{12}\mathop \sum \limits_{{{\text{month}} = 1}}^{12} \left( {{\rm{MSE}}_{\text{out of bag}}^{{{\text{permuted x}}_{\rm{i}} }} - {\rm{MSE}}_{\text{out of bag}} } \right)$ and choose the top m ranked predictors.

The higher the predictor’s rank in step 4, the more important that predictor. The ranking result shows that, most of the important predictors are speeds of recent segments (${\text{t}}_{0} - 5$). In addition to speed predictors chosen by RF, the historical average travel time at ${\text{t}}_{0}$ given the day of the week is added as a predictor.

4.2 The Second Set of Predictors

The other set of predictors are the instantaneous travel time and the average of historical travel time. For example, if we are interested in the travel time reliability at $t0$ on day $D$, the predictor vector will be the instantaneous travel time at the times $\{ t0 - 45,t0 - 40, \ldots ,t0 - 5\}$ and the average of the historical travel times on days $D$ at times $\{ t0,t0 + 5, \ldots ,t0 + 45\}$. Figure 2 shows the average of the historical travel time for each day of the weak. There are two peaks of the travel time during morning and evening hours. The height of the peaks is different from one day to another especially between weekdays and weekends.

Fig. 2.

The average of historical travel time for each day of the week.

5 Data Description

The freeway stretch of I-66 eastbound connecting I-81 and Washington, D.C. was selected as the test site for this study. High traffic volumes are usually observed during morning and afternoon peak hours on I-66 heading towards Washington, D.C., making it an excellent environment to test travel time models.

The traffic data was provided by INRIX, which mainly collects probe data by GPS-equipped vehicles, supplemented with traditional road sensor data, along with mobile devices and other sources [24]. The probe data covers 64 freeway segments with a total length of 74.4 miles. The average segment length is 1.16 miles, and the length of each segment is unevenly divided in the raw data from 0.1 to 8.22 miles. Figure 3 shows the study site and deployment of roadway segments. The raw data provides average speed for each roadway segment and was collected at 1-m intervals.

Fig. 3.

(source: Google Maps) [25].

The study site on I-66 eastbound.

We sorted the raw data was the roadway direction according to each TMC station’s geographic information (e.g., towards eastbound of I-66). Data was examined to check any overlapping or inconsistent stations along the route. Afterward, speed data was aggregated by time intervals (5 min in this study) to reduce noise and smooth measurement errors. This way, the raw data was aggregated to the form of the daily data matrix along spatial and temporal intervals. Data was missing in the developed data matrix, so data input methods were conducted to estimate the missing data using values of neighboring cells. Finally, the daily spatiotemporal traffic state matrix was generated to model travel time.

6 Experimental Analysis

The experimental work is divided into two subsections. The first subsection is travel time modeling using a mixture of two linear regressions with fixed proportions $\left( {\uplambda_{1} ,\uplambda_{2} } \right)$. In this subsection, we will model the travel time and the log of the travel time using the first set and second set of predictors respectively. Consequently, we will show that log-normal model is better than the normal model. The second subsection describes the travel time reliability modelling approach, where we modified the proposed model to allow the proportions to vary as a function of the predictors. The modified model computes the probabilities of encountering free-flow and congested conditions together with the expected and 90-percentile travel times for each regime.

6.1 Modeling Travel Time Using a Mixture of Linear Regressions with Fixed Proportions

The purpose of this section is to experimentally compare the lognormal model and normal model. Each model used a different set of predictor. In other words, the log-normal model will explain the response vector $log(Y)$ using the corresponding predictors matrix $X_{2}$, where Y is the ground truth travel time and $X_{2}$ is the second set of predictors. Where the normal model will explain the response vector $Y$ using the corresponding predictors matrix $X_{1}$. For the sake of completeness, we also compare each model with the corresponding one component linear regression model, which assumes the travel time distribution is uni-modal distribution. To show that, the parameters of the proposed models are estimated using the EM algorithm. Then, two measures are used to compare the models. The Mean Absolute Percentage Error (MAPE) and the Mean Absolute Error (MAE) are used to quantify the errors of both models with respect to the ground truth. MAPE is the average absolute percentage change between the predicted $\widehat{{{\text{y}}_{ 1}^{\rm{j}} }}$ and the true values ${\text{y}}_{\rm{i}}^{\text{j}}$. MAE is the absolute difference between the predicted and the true values.

$$ {\text{MAPE}} = \frac{100}{{{\text{I}} \times {\text{J}}}}\mathop \sum \limits_{{{\text{j}} = 1}}^{\rm{J}} \mathop \sum \limits_{{{\text{i}} = 1}}^{\rm{I}} \frac{{\left| {{\text{y}}_{\rm{i}}^{\text{j}} - \widehat{{{\text{y}}_{ 1}^{\rm{j}} }}} \right|}}{{{\text{y}}_{\rm{i}}^{\text{j}} }} $$

(9)

$$ {\rm{MAE}} = \frac{1}{{{\text{I}} \times {\text{J}}}}\mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \mathop \sum \limits_{{{\text{i}} = 1}}^{\text{I}} \left| {{\text{y}}_{\rm{i}}^{\text{j}} - \widehat{{{\text{y}}_{ 1}^{\rm{j}} }}} \right| $$

(10)

Here, J is the total number of days in the testing dataset; I is the total number of time intervals in a single day; and y and ${\hat{\text{y}}}$ denote the ground truth and the predicted value, respectively, of the travel time for the time interval on the day. The lower the value of these error measures, the better the model.

Table 1 shows values for the MAE and MAPE for normal models using a different number of top-ranked predictors. As shown in Table 1, for all models that are built using a different number of predictors, the models built using the proposed mixture of regressions are better than the linear regression models with smaller MAE and MAPE.

Table 1. Comparison between one and two components normal models using the first set of predictors [25].

Table 2 shows values for the MAE and MAPE for lognormal models using the second set of predictors. Table 2 confirms that two component models are better than one-component models. Moreover, it shows that the lognormal models and the second set of predictors are better than the normal models and the first set of predictors (Table 3).

Table 2. Comparison between one and two components lognormal models using the second set of predictors.

Table 3. The EM parameters’ estimates for a mixture of linear regression assuming normal distribution [25]*.

Different number of predictors are shown in Tables 1 and 2. We tried different number of predictor in order to find the simplest and most accurate model. As shown in the above tables the improvement in the accuracy of the models in terms of MAE and MAPE is not significant. In real time running, we prefer simple models. So that, for the normal model and lognormal model the models which has 16 and 11 predictors respectively are chosen.

Based on the above experimental results we conclude that using the lognormal model is more accurate and simpler in terms of number of predictors than using normal model. So that we can choose the mixture of two linear regression with 11 predictors and use it for the next set of experiments.

6.2 Travel Time Reliability

Travel time reliability is the form of information that we can convey to traveler using the travel time model. Using the proposed model, we can provide the traveler what are the probabilities of congestion and free flow. Moreover, the expected and 90% percentile travel time for each regime can be provided. In order to get good estimates for the above quantities, the proportions should be a function of the predictor which means it varies depending on the values of the predictors. Revisiting the EM algorithm, it estimates the posterior probabilities $w_{ij}$ and the model parameters $\psi$ and returns only $\psi$ at convergence and does not use $w_{ij}$. As shown in Eq. (4), the returned $\lambda_{j}$ is an average of the posterior probabilities $w_{ij}$.In the two component models, if we modeled $w_{ij}$ using logistic regression at the convergence of the EM, this means that $\lambda_{j}$ becomes a function of the predictors as well as the components’ means. The final $w_{ij}$ obtained while fitting the model described in Table 4 are used to build a logistic regression. This logistic regression models the probability of predictor vector being drawn from component number two. Then using simple algebra manipulation, we got the coefficient of the logistic model for $\lambda_{2}$ which are shown in Table 5. Now, the new model is exactly the model in Table 4 but with variable $\lambda_{2}$ and $\lambda_{1}$.

Table 4. The EM parameters’ estimates for a mixture of linear regression assuming lognormal distribution.

Table 5. The estimated coefficient for the logistic model for $\varvec{\lambda}_{2}$.

We tested the proposed model by visually inspect the ground truth travel time for each day and the mean of each component as well as the $\lambda_{1}$, which is the probability of congestion in the fitted model. We visually check if the value of $\lambda_{1}$ is large at the time when the ground truth becomes large. As shown in Fig. 4 for weekday (top panel), there are two peaks at morning and evening and at the same time the values of $\lambda_{1}$ approach one which means the probability of congestion is high. The bottom panel shows a weekend where this no morning congestion but there is an evening congestion and $\lambda_{1}$ has only high values at the evening peak.

Fig. 4.

The ground truth travel time (red curve), the mean of each component of the proposed model (blue curves), and the $\lambda_{1}$ which is the congestion probability for two different days. The upper panel is weekday and the bottom panel is a weekend day (Color figure online).

In order to better test the proposed model, we calculate the mean, 90% percentile, and probabilities of congestion and free flow for each predictor vector in each day of May 2013. Then based on the curves in Fig. 2, we divided the day into four time interval and calculated the mean of the above quantities within each time interval given for each day of the weak. The result shown in Table 6 is consistent with the travel time pattern that we observe in Fig. 2 where at the congestion time of the day the probability of the congestion component becomes higher. Also, the model shows that the probability of the morning congestion during weekends is lower than its values at weekdays.

Table 6. Testing the model for travel time reliability using May 2013.

7 Conclusions

In this paper, we proposed a travel time model based on mixture of linear regressions. We compared two models using two different predictor sets. The first model assumes the distribution of each component in the mixture follows the normal distribution. The second model uses the log-normal distribution instead of the normal distribution. The experimental results show that the model that uses the log-normal distribution and the historical and instantaneous travel time predictors is better than the other model. The proposed model can capture the stochastic nature of the travel time. The two-component model assigns one component to the uncongested regime and the other component to the congested regime. The means of the components are a function of various input predictors. The proposed model can be used to provide travel time reliability information at any time-of-the-day for any day-of-the-week if the predictor vector is available. The experimental results show promising performance of the proposed algorithm.

The current model does not consider the weather condition, assumes no incidents, or work zones; however this model has the ability to easily integrate these factors if the historical data includes these variables. Our future work will focus on extending, the proposed model to include these factors and study their effect on the travel time distribution.