1 Introduction

Solar photovoltaics have received a lot of attention in the distribution network in recent years due to continuously expanding power demand and limited reserves of conventional energy sources. Aside from renewable energy sources, such as solar photovoltaic, other power sources, such as energy storage devices, are gaining appeal as a way to deliver power in areas where the grid is unstable (Verma et al. 2017). However, in this study, resources (power grid and renewable) are available, but smart scheduling is the major focus such that an uninterrupted power supply is provided with reduced losses, costs, and imbalance, further increasing system resilience (Karimyan et al. 2014).

In a rural village distribution system, the main problems are grid unavailability and unbalance (Kumar et al. 2019; Kandpal et al. 2019). Also, due to improper planning and uneven distribution of loads in three phases, power quality problems such as voltage unbalance are prevalent. Major challenges in the rural areas of India are excessive power cuts or grid supply being limited. Therefore, renewable energy-based distribution generation (DG), i.e., solar PV and energy storage systems, is located near the distribution loads and is the best option to fulfill the curtailed power demand. DGs are cost-effective and environmentally friendly ways to provide continuous power supply.

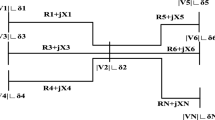
In this paper, an Indian village-based rural distribution eight-bus network is considered as shown in Fig. 1. In the network, each phase is loaded differently, so that each phase has different power requirements throughout the day. For such a practical case, one SPV and one BESS are allowed per phase, for a total of three SPVs and three BESS systems undertaken for the study. Because the battery can supply or receive power at any time between its rated power capacities, its use or scheduling can be done decisively at times when it becomes cost efficient. Their sizes in the different phases can be changed to reduce unbalance (Kandpal et al. 2019). The degradation cost of the battery is also considered in the presented paper. Solar PV should be sized in such a way that its entire input is used when it is available (Jannesara et al. 2018).

Fig. 1
figure 1

Eight bus network representation of a rural distribution system

Full size image

As a result, the author proposed optimal sizing, positioning, and timing of solar PV and batteries with a time-constrained grid to improve the distribution system's reliability (Ghanegaonkar and Pande 2017). To solve the problem with optimal solutions, the new advanced optimization technique, i.e., modified artificial bee colony (Akay and Karaboga 2012; GAO, W. F., Liu, S. Y. 2012), and resource management are used (Hosseina and Bathaee 2016). The demand response (DR) strategy (Chauhan and Saini 2017) is applied to manage the load/demand scheduling.

In the literature, several researchers have applied effective and analytical approaches to the scheduling, sitting, and sizing of DGs in distribution networks to minimize power losses (Acharya et al. 2006; Wang and Nehrir 2004; Gözel and Hocaoglu 2009; Kamel and Kermanshahi 2009). An efficient and an improved analytical method are investigated to achieve the optimal sizing and placement of multiple DGs in distribution networks where grid extension is challenging (Mahmoud et al. 2016; Hung and Mithulananthan 2013). Gampa and Das developed a multi objective technique to obtain optimal sitting and sizing of DGs and evaluate the economic and technical factors (Gampa and Das 2015) of the distribution system. A two-step optimization technique to investigate the effect of a battery system incorporating solar PV is presented in Chedid and Sawwas (2019).

Mehrjerdi and Hemmati deployed a battery energy storage system in a distribution network and investigated power losses and voltage magnitude with high accuracy (Mehrjerdi and Hemmati 2019). Saboori and Jadid presented movement scheduling of batteries in the distribution system and obtained optimal charging and discharging in different bus locations (Saboori and Jadid 2020). A model to increase the life span of the battery with uncertainties in the distribution system is presented in Mehmood et al. (2017). In order to lower operational and investment costs, Zhang et al. suggested a conservation voltage reduction methodology for implementing battery storage in an active distribution system (Zhang et al. 2017).

A hybrid modified shuffled frog leaping algorithm with fuzzy sets is applied to obtain optimal sizing and placement of DGs in the distribution network (Mojarrad et al. 2013). Tyagi and Verma presented a comparative study of two meta-heuristic techniques: bacterial foraging differential evolution and Improved Harmony Search for optimal DG placement (Tyagi and Verma 2016). Ganguly and Samajpati (Ganguly and Samajpati 2015) present an adaptive genetic algorithm with a fuzzy base for optimal DG placement and sizing. Maleki et al. and Ali et al. investigated optimal specifications for PV sizing and locations (Maleki et al. 2017; Ali et al. 2020).

Various researchers have also investigated the battery degradation cost in terms of charging and discharging, taking into account DGs and ESS with grid (Yoshida et al. 2016; Pelletier et al. 2017; Ziaa et al. 2019; Hossain et al. 2019; Aghdama et al. 2020; Nair et al. 2020). Several researchers have presented advanced optimization techniques for optimal placement, sizing, and scheduling of DGs in distribution networks, such as the Grey Wolf Optimization technique (Tyagi et al. 2019; Sobieh et al. 2017; Pradhan et al. 2016; Yahiaoui et al. 2017), Artificial Bee Colony (Karaboga and Basturk 2007, 2008; Abu-Mouti and El-Hawary 2011; Das et al. 2018), and Modified Artificial Bee Colony (Abu-Mouti and El-Hawary 2009; Das et al. 2017; Hussain and Roy 2012), in order to reduce the loss, improve voltage profile, and reduced costs.

In the literature, authors give numerous prominent solutions separately for the electrification of the distribution network. However, lots of information has been gathered about the optimal scheduling for rural electrification. Even so, there are only a few scenarios where the DGs, battery, and grid are scheduled in order of time constrained by the battery degradation cost. In the present scenario in India, almost all village-based rural/remote areas have grid supply connections. However, the power cuts or availability of grid supply in these areas is either at night only, or during the day only, or only for a few hours a day. Therefore, this paper overcomes the major challenge of power cuts and unbalanced load/generation in the present network system. Non-essential loads shifted toward the availability of irradiance are subjected to demand response and resource management (Kumar et al. 2019).

This may ensure a more realistic picture in most Indian villages where the grid is available, but only for the time being. Therefore, by using available local sources based on renewable energy and making intelligent decisions on DGs, BESS, and DR deployment, to reduce the cost of investment and losses. Such type of power supply can be useful and helpful for any developed or developing country. The MATLAB/Simulink is used for optimal solutions such that it ensures seven-day, 24-h electrical supply.

This paper is systematized into 6 sections; the contextual theory and introduction are presented in Sect. 1. Study areas and system modeling have been presented in Sect. 2. In Sect. 3, problem formulation and different objective functions subject to equality and inequality constraints are presented. Model formulation and optimization methodologies have been presented in Sect. 4. The most suitable optimal results and discussions are offered in Sect. 5. Section 6 presents the conclusion of the work.

2 System Modeling

The state of Uttar Pradesh lies in the northern region of India. It is located at 77.41° east longitude and 28.66° north latitude. The considered village Jalalabad has total geographical area of 5.81 km2 (Kumar et al. 2019). The average recorded minimum temperature of the village during winter is about 4–9 °C, whereas the average recorded maximum temperature is about 40–45 °C in summer. The locality of the study region is shown in Fig. 2.

Fig. 2
figure 2

Study area of rural distribution system

Full size image

2.1 Load Modeling

A 35-household rural village-based community has been chosen for this work. The load demand data of households has been assessed by a questionnaire and is based on a field survey. Total power has been projected on the basis of operative hours and the power rating of the apparatus used for a 24-h time period (Kumar et al. 2019).

2.2 Solar SPV Modeling

The scale factor for solar PV generation on a 24-h basis for all seasons is shown in Fig. 3. The solar SPV generation value 1 is presented as its maximum generation, which also varies with seasons and time (Kandpal et al. 2019). For analyzing the variation in losses for a radial unbalanced distribution network of an actual system, two cases are considered with varying maximum capacities of the available SPV. In this study, the maximum SPV capacity for each phase is taken to be 20 kWp, which will be placed on a certain bus in the distribution network. The cost of such an SPV installation is taken to be US $ 615 per kW as the capital cost and will include an additional 3% for operations and maintenance per year. The lifetime of the SPV system is taken to be 15 years.

Fig. 3
figure 3

SPV generation of different seasons on a 24-h basis

Full size image

The power generated by solar PV is proportional to the solar irradiance, and the area is given by (1).

$$ P_{n,t}^{PV} = \eta_{SPV} \times I \times A $$
(1)

where ηSPV = efficiency of the SPV system, I = solar irradiation in kW/m2 and A = area of the SPV system.

2.3 Energy Storage Modeling

Energy storage in the form of lithium-ion batteries is considered in this study and is scheduled according to the problem objective and the demand of the loads. For the optimization study, the batteries are allowed a maximum power rating of 20 kW and the energy rating of the batteries is calculated based on their calculated optimal schedule.

The charge and discharge of the battery is based on the simple coulomb counting method (Ng et al. 2009) as shown in the following equations.

$$ C\left( {t + 1} \right) = C\left( t \right) + \Delta t.P_{t} P_{t} > 0, \;{\text{if}} {\text{charging}};P_{t} < 0 \;{\text{if discharging}} $$
(2)

Additionally, initial and final limits on the battery storage energy are imposed such that their final SoC is set back to their initial SoC through charging/discharging at the end of the day.

$$ C\left( 0 \right) = C\left( T \right) = C_{s} $$
(3)

For the rated energy rated capacity of the storage system, the maximum amount of energy it receives while charging or gives while discharging is calculated for one typical day.

$$ E_{\min } = \max \sum\limits_{t}^{t + N} {\left| {P_{t} } \right|.\Delta t} \forall t \in \left[ {1, \ldots ,24} \right] $$
(4)

where N = window size, varies in the range from 1 to 24.

This will allow the battery to charge/discharge as will be required based on the optimal scheduling for the loads of the distribution system. The final minimum battery energy rating is taken as 20% extra capacity for considering the margin for losses.

$$ E_{\min }^{BESS} = 1.2 \times E_{\min } $$
(5)

The cost of a battery is determined by its energy rating. A higher energy-rated battery would linearly increase in cost. For this study, the cost of the battery is taken to be US $ 287.16 per kWh. The lifetime of the battery is taken to be 5 years.

3 Problem Statement

The following are the several objectives that have been considered in this paper:

(i) Reducing the total cost of installing and operating the system, including SPV, BESS, and grid power, with and without taking battery degradation into account.

(ii) Lowering total real-power losses in an eight-bus distribution network (Kandpal et al. 2019).

(iii) Excess power estimation using a fraction of non-essential load shifting (βNELS 0, 0.20, and 0.25 for each season).

The costs considered for the different elements are given in the previous sections. Based on these costs and grid costs per unit of electricity, analysis is done to optimally size, place, and schedule the resources in the system.

3.1 Cost-Based Objective Function

The first objective of this work is to minimize the total cost of capital and operation of the system, which comprises SPVs, BESS, and the cost of power from the grid.

The problem of cost minimization will be defined as:

$$ \min \left( {C_{o} } \right) = \min \sum\limits_{n \in BESS} {C_{n}^{BESS} } + \sum\limits_{n \in PV} {C_{n}^{PV} } \sum\limits_{t \in T} {C_{n}^{gr} } P_{n}^{gr} + \left( t \right).\Delta t $$
(6)
$$ C_{n}^{BESS} = S_{e} \times E_{min,n}^{BESS} { } + C_{n}^{BDC} $$
(7)
$$ C_{n}^{PV} = \left( {S_{p} \times P_{n}^{PV} } \right) + \sum\limits_{k = 1}^{T} {\frac{{O\& M_{k} }}{{(1 + r)^{k} }}} $$
(8)

The costs are divided into capital and operating/maintenance costs. For a photovoltaic system, 3% O & M costs are added per year on top of the initial investment. The present value of the O & M costs is calculated with a discount rate of 6%.

Subjected to the following constraints:

  • The sum of total losses and power demand should always be equal to the total generation.

    $$ \sum\limits_{n \in PV} {P_{n,t}^{PV} } + \sum\limits_{n \in BESS} {P_{n,t}^{BESS} } + P_{t}^{gr} = \sum\limits_{n \in H} {P_{n,t}^{dem} + P_{loss} \forall t} $$
    (9)

  • The voltage at each phase of the system should be within a considerable limit.

    $$ V_{\min }^{k,ph}\; \le V^{k,ph}\; \le V_{\max }^{k,ph} \forall k,\forall ph $$
    (10)

    where \({V}_{ph}^{k}\) is the phth phase voltage of kth bus, \({V}_{ph}^{k min}\) and \({V}_{ph}^{k max}\) are the minimum and maximum limits.

  • The generation of total active power from each SPV unit should not hit its maximum capacity.

    $$ P^{PV} \le P_{max}^{PV} $$
    (11)

    where \({P}_{PV}^{p}\) represents available power of pth SPV and \({P}_{PV}^{max}\) represents the maximum capacity of SPV.

  • SoC limits of the battery is also constrained to be equal to its initial value at the end of the day

    $$ \sum\limits_{t = 1}^{24} {P_{t}^{n} .{\Delta }t = 0; } \;\;\;\;\forall n \in BESS $$
    (12)

    This allows the battery to charge/discharge throughout the day as per the requirements of the grid while only constraining its final SoC level at the end of the day.

  • Power limits of the battery

    $$ P_{min}^{BESS} \le P^{BESS} \le P_{max}^{BESS} $$
    (13)

3.2 Losses-Based Objective Function

The second objective studied is minimizing the losses in the distribution network. To minimize the losses, the objective function will be

$$ {\text{min}}\left( {L_{o} } \right) = {\text{ min}}\sum\limits_{t \in T} {P_{loss}^{t,ph} }\; \forall ph \in \left[ {A,B,C} \right] $$
(14)

Constraints used for this objective are similar to the constraints for the cost-based optimization problem given in Eqs. (9–13).

4 Proposed Methodologies and Algorithm

4.1 Load Shifting through Demand Response

As discussed in Kumar et al. (2019), the non-essential loads are shifted throughout the day toward the times with higher solar irradiation through a demand response program.

The Optimization problem for the DR strategy considered can be expressed as:

$$ max \sum G\left( t \right)\Delta P_{{{\text{NE}}}} \left( t \right) $$
(15)
$$ {\text{subject to}}\mathop \sum \limits_{{t \in \Omega_{T} }} \Delta P_{{{\text{NE}}}} \left( t \right) = 0 $$
(16)
$$ - \left( {\beta_{{{\text{NELS}}}} } \right)P_{{{\text{NE}}}} \left( t \right) \le \Delta P_{{{\text{NE}}}} \left( t \right) \le \left( {\beta_{{{\text{NELS}}}} } \right)P_{{{\text{NE}}}} \left( t \right) $$
(17)

where the fraction of non-essential load shifting (\({\beta }_{NELS}\)) is assumed to be 25 percent or 0.25. ΩT is the set containing values of time from 19:00 pm to 07:00 am on hourly basis and PNE and ΔPNE is non-essential load and change in non-essential load.

4.2 Battery Degradation Cost

Energy storage such as lithium-ion batteries has a lifetime decided by the number of cycles of charge/discharge it can provide before its capacity reduces to below usable levels. As the battery degrades, its ability to store and release energy decreases. Several studies have given methods to theoretically convert battery degradation into monetary values. Most lithium-ion batteries are used in power systems due to their vigorous and efficient operation. The main essential parameters in battery degradation are rated energy, capacity, and lifetime (Ziaa et al. 2019). There are many other degradation factors that are not analyzed individually. Therefore, the state of charging/discharging time, depth of discharge, and life time of the battery are considered here (Hossain et al. 2019; Aghdama et al. 2020).

For this study battery degradation cost C(BDC) due to charging/discharging is taken from Ju et al. (2018).

$$ C_{{\left( {BDC} \right)}} = \frac{{\left\{ {C_{B} \cdot P_{B} \cdot {\Delta }t} \right\}}}{{\left\{ {2 \cdot L_{B} (d_{B} \left( {{\Delta }t} \right) \cdot E_{BA} \left( t \right).d_{B} \left( {{\Delta }t} \right) \cdot \eta_{BC} \cdot \eta_{BD} } \right\}}} $$
(18)

where Depth of Discharge: \({d}_{B}\left(\Delta t\right)=\frac{{P}_{B}\cdot\Delta t}{{E}_{BA}}\), Lifetime of Battery: \({L}_{B}\left({d}_{B}\right)=4980*{d}_{B}^{-1.98}*{e}^{-0.016*{d}_{B}}\), Battery Cost: \({C}_{B}\left(\Delta t\right)=287.16*[Battery Size (kWh)]\)

Using the above formulation for degradation cost C(BDC), the additional cost incurred over the initial battery cost can be calculated for the entire timeline of optimization.

4.3 Modified Artificial BEE Colony (MABC) Algorithm

The Artificial bee colony (ABC) is a new and popular metaheuristics algorithm (Karaboga 2005), primarily developed for unconstrained optimization. Due to its simplicity, it has gained interest among researchers for its application to various optimization problems. The ABC algorithm is found to be very effective in solving standard benchmark functions (Karaboga 2005). However, when applied to real-world constrained optimization problems, existing literature shows that ABC struggles to obtain satisfactory results (Karaboga and Akay 2011). Therefore, several modifications to the original ABC algorithm have been proposed by many researchers (Karaboga and Akay 2011) through (Karaboga and Gorkemli 2014). These modifications aim to improve the performance of ABC while retaining the structural simplicity of the original ABC algorithm. One of the recent changes to the ABC algorithm by the name of the modified ABC (MABC) algorithm has been proposed by the authors in Das et al. (2017). In this reference, the authors have proposed MABC to handle mixed-integer, nonlinear optimization problems, especially for transmission network expansion planning problems. It has also been shown to provide better results compared to existing methodologies for standard benchmark functions.

As optimal sitting, sizing, and scheduling of DGs is a mixed integer nonlinear optimization problem, therefore, MABC is used in this paper to obtain the optimal scheduling of the DGs. A brief description of MABC is provided here. The original ABC algorithm is based on the intelligent foraging behavior of honeybee swarms.

  • The Algorithmic Process of the Basic ABC Algorithm

The Algorithmic Process of the Basic ABC Algorithm is as follows (Das et al. 2017).

  • Initial food source sites: Initial food sources are formed randomly within the range of the boundaries of the parameters:

    $$ x_{e}^{d} = x_{e}^{d\min } + r\;{\text{and}}\left( {0, 1} \right)\left( {x_{e}^{d\max } - x_{e}^{d\min } } \right) $$
    (19)

where \(e=1,\dots \dots ,\frac{{CS}_{N}}{2}\),\(d=1,\dots \dots ,D\).\({CS}_{N}\) is the number of food sources and D being the number of problem dimensions. \(e\) denotes the \(e\)th EB.

  • Movement of the Employed bees: In ABC, the movement of an EB is defined by:

    $$ y_{e}^{d}\; =\; x_{e}^{d} + \emptyset_{0} \left( {x_{e}^{d} - x_{f}^{d} } \right) $$
    (20)

    where \({x}_{e}\) is the old food site, \({y}_{e}\) is the new site, \(d\) is the randomly selected problem dimension and \({x}_{f}\) is another employed bee and, \({\mathrm{\varnothing }}_{0}\) is a real random number between \(+1\) and \(-1\). The fitness value for each position is evaluated as:

    $$ fitness = \left\{ {\begin{array}{*{20}c} {\frac{1}{{\left( {1 + M} \right)}} \;if\; M_{e} \ge 0} \\ {1 + abs \left( M \right)\; if \; M_{e} < 0} \\ \end{array} } \right.{ } $$
    (21)

\(fitness\) is the fitness value associated with each food source and EB \(e\). \(M\) is the augmented objective function value at the eth location. The augmented objective function \(M\) is the summation of the original objective function and the penalties. Penalties are only added to the objective function when there is a violation of any constraint. If there is no violation of any constraints, the penalties become zero and \(M\) becomes equal to the actual objective function.

$$ M = \left( {C_{o}\; or\; L_{o} } \right) + Penalties $$
(22)

where \({C}_{o}\) is defined as in Eq. (6) and \({L}_{o}\) is defined as in Eq. (14). Penalties are defined as in Das et al. (2017) using Eqs. (9)–(13).

  • Selection of the EBs by OBs: Probability of selection of employed bees are as follows:

    $$ p_{e} = \frac{fitness}{{\mathop \sum \nolimits_{{{\text{e}} = 1}}^{{\frac{{CS_{N} }}{2}}} fitness}}{ } $$
    (23)

The initial locations of the OBs are the similar to those of the EBs selected.

MABC is based on the ABC algorithm, which is structurally similar to ABC. It is defined in Das et al. (2017) by incorporating the concepts of global attraction and universal gravitation (Tsai et al. 2009) into the original The most important modification introduced in MABC is that it changes each and every dimension of the problem in a run of the program. This removes the possibility of missing any problem dimension in the course of algorithm simulation.

The modifications introduced in the MABC algorithm for each dimension (\(d\)Das et al. 2017) are:

  1. 1.

    Employed bees’ phase: The new position for the EBs is defined by the equation:

    $$ \begin{aligned} y_{e}^{d}\; =\; & x_{e}^{d} + floor\left( {\emptyset_{0} {*}\left( {x_{e}^{d} - x_{f}^{d} } \right) + \omega_{g} {*}rand\left( {0,{ }1} \right){*}\left( {g_{o}^{d} - x_{e}^{d} } \right)} \right) \\ & \forall ,f \ne e,f \in \left\{ {1,2, \ldots \ldots .,\frac{{CS_{N} }}{2}} \right\}{ } \\ \end{aligned} $$
    (24)

    Here, \({g}_{0}\) is the position of the global optimum obtained till the instant of the algorithm run, and \({\omega }_{g}\) is the weightage that decides the effect of the global optimum on the movement of the EBs. The MATLAB function ‘\(floor\)’ is used only for integer variables. In other cases, where continuous variables are present, they are removed.

  2. 2.

    Onlooker’s bees’ phase: The OBs reach their new position as defined by the equation.

    $$ y_{e}^{d} = x_{e}^{d} + floor\left( {F_{{e,{ }\;f{ }norm}} } \right) $$
    (25)

    Here the function \(floor\) is used only when integer variables are to be considered. \({F}_{e, f norm}\) is the normalized force of attraction between two employed bees ‘\(e\)’ and ‘\(f\)’. This is calculated as per the procedure stated in Das et al. (2017).

  3. 3.

    Scout bees phase: According to Das et al. (2017), the scout bees provide better positions when it starts its search from the previously abandoned position of other EBs or OBs. Therefore, the equation governing the movement of the scout bees is as follows:

    $$ y_{e}^{d} = x_{e}^{d} + randi\left( {\left[ { - a,{ }b} \right],{ }1} \right) $$
    (26)

Here, \(a={x}_{e}^{d}-{x}_{e}^{dmin}\) and \(b={x}_{e}^{dmax}-{x}_{e}^{d}\).

Again, function ‘\(randi\)’ in MATLAB is used only for integer variables. For continuous variables, function ‘\(rand\)’ may be used in proper syntax.

The parameters of MABC are taken from Das et al. (2017), i.e., \(maxiteration\) = 30; \({w}_{g}\) = 1.5; \(lim= 6\) and \({CS}_{N}\) = 20. The algorithm flowchart of the MABC is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of MABC algorithm

Full size image

5 Results and Discussions

This work was performed in the village of Jalalabad in the district of Ghaziabad, Delhi-NCR, India. The data taken for the network is the same as that taken in Kumar et al. (2019); Kandpal et al. 2019).

A photovoltaic system with a maximum capacity of 30 kWp and a battery energy storage system with a maximum power rating of 100 kW in each phase is allowed. In addition, the grid is not available from 07:00 a.m. to 19:00 p.m. Consequently, the demand response programme as used in Kumar et al. (2019) shifts the non-essential loads (βNELS) to this period to coincide with the high SPV generation when the grid is not available. For the cost objective, a one-year timeline is considered, which will include the cost of installing the SPVs and BESS systems and consequently running them for this timeline with supplementary power from the grid.

As metaheuristics algorithms are used for obtaining the results, the results of only a single trial can’t be relied upon. At least 50 trials need to be run for an appropriate final schedule. The time provided in the next section corresponds to the time required for a single trial. The specification of the computing system is as follows: MATLAB R2018b; A desktop computer with 8 GB of RAM and an Intel (R) Core (TM) i7-3770 CPU processor running at 3.40 GHz.

5.1 Optimal Scheduling Based on Modified Artificial Bee Colony Algorithm

5.1.1 Case I: Cost-Based Objective without Including Degradation Cost of Batteries

For this objective, an optimization problem is run to reduce the total cost of the system, including the cost of power purchased from the grid over a one-year timeline. This cost includes the capital cost of purchasing the equipment, such as SPV panels of different power ratings and energy storage systems of different energy ratings, with the additional cost of maintaining them. Table 1 shows the results of optimal scheduling and the total cost of the system with a very low colony size of 20. It can be observed that with such a small colony size value, results are obtained extremely quickly. The location and size of SPV at phase B are different as compared to phases A and C, whereas the location and size of BESS are higher at phase C as compared with the other phases, A, and B. The total cost for colony size = 20 is $92,307.69, not including the degradation cost of the battery. The time taken per trial in this case is 2.06 h. However, the quality of the results suffers.

Table 1 Optimal scheduling and total cost of the system for Cost Minimization Objective
Full size table

5.1.2 Case II: Cost-Based Objective Including Degradation Cost of Batteries

In this case, to improve the power system performance, the degradation cost of the battery is considered under the cost-based objective. To show the effectiveness of using a large colony size, the results are computed with a value of 50. The results are provided in Table 1, with PV, grid, and battery. As phase-A, has the least load and phase-B, the highest, SPV, BESS, and grid systems are sized, located, and scheduled accordingly. The total cost obtained for colony size \({\mathrm{CS}}_{\mathrm{N}}\)=50 is $ 53,640, including the degradation cost of the battery. The degradation cost of the battery is $ 4,056.77 and the time taken per trial in this case is 5.15 h. Hence, the total cost obtained for the colony size \({\mathrm{CS}}_{\mathrm{N}}\) =50 is lower $ 53,640 as compared with colony size \({\mathrm{CS}}_{\mathrm{N}}\)=20 is $ 92,307.69.

The schedules of SPV, grid, and battery are provided in Figs. 5, 6, 7 for the 24-h time period, as per the loads in the respective phases to which they are connected. The SPV schedule for all the three phases for 24 h for cost minimization is shown in Fig. 5. The summer season is considered for SPV generation. Figure 6 shows the grid schedule which is available between 07:00 pm and 07:00 am. The grid is not available between the mornings of 7 am and evening of 7 pm. Therefore, the power consumed from the grid for all phases during this period is zero, as shown in Fig. 6. The battery schedule for all three phases for 24 h is shown in Fig. 7.

Fig. 5
figure 5

SPV Schedule for three phases for Cost Minimization Objective for 24 Hours

Full size image
Fig. 6
figure 6

Grid Schedule for three phases for Cost Minimization Objective for 24 Hours

Full size image
Fig. 7
figure 7

Battery Schedule for three phases for Cost Minimization Objective for 24 Hours

Full size image

Moreover, the demand response strategy management is implemented in such a way that non-essential loads have been shifted toward the available solar irradiance as mentioned in Kumar et al. (2019). By adding the strategy of demand response, it impacts on sizing, location, and gives better scheduling of SPV, BESS, and the grid. Also, the total cost and losses are reduced by implementing the DR strategy at \({\beta }_{NELS}\) at 25%.

5.1.3 Case III: Loss-Based Objectives

For this objective, the optimization programme reduces the total real power losses in the distribution system. The combined losses of all three phases are reduced with different scheduling and sizing of SPV, the grid, and batteries. The sizes and cost results of the system are provided in Table 2, with the colony sizes (with = 20), 20 and 50 (with = 50) for the 24-h time period. In the same spirit as in the previous case, to justify the selection of a higher colony size value in a metaheuristic algorithm, a higher value of 50 is also considered for obtaining the results. Table 2 provides the sizes of the SPV and BESS. The real power losses with a colony size of 20 are 9.5061 kW, whereas considering a higher colony size of 50, the losses decrease to 2.94 kW. Because Phase B has the highest load and Phase A has the lowest, SPV with colony size 20 has the largest size and location in Phase B and the smallest in Phase A. The size and location of the batteries are also greatest in phase B and lowest in phase C. By selecting the higher colony size of 50, the SPV size and location at Phase-B are the highest and least at Phase-A. The battery size and location are highest at Phase-B and lowest at Phase-A. The obtained results show a better reduction in losses for the higher colony size of 50.

Table 2 Optimal scheduling and total Losses of the system for Loss Minimization Objective
Full size table

The detailed scheduling results of SPV, BESS, and grid for the colony size 50 are provided in Figs. 8, 9, 10 for the 24-h time period. The grid scheduling is as per the grid availability between 7 pm and 7 am as shown in Fig. 8. Grid scheduling is not available between 07:00 am and 19:00 pm. SPV and battery scheduling are shown in Figs. 9 and 10, as per the connected load in all the three phases. The results are far better by incorporating the DR strategy into the non-essential load.

Fig. 8
figure 8

SPV Schedule for three phases for Loss Minimization Objective for 24 Hours

Full size image
Fig. 9
figure 9

Grid Schedule for three phases for Loss Minimization Objective for 24 Hours

Full size image
Fig. 10
figure 10

Battery Schedule for three phases for Loss Minimization Objective for 24 Hours

Full size image

5.1.4 Excess Power Analysis

The profile of excess electricity production depends upon the solar irradiation and the load profile of the considered study area (Kumar et al. 2019). Figure 11a–d shows the results of hourly data of annual excess electrical power production with and without non-essential load shifting, with βNELS 0%, 20% and 25%, respectively, for the different seasons. It can be observed from Fig. 11a–d that with the increase in the \({\beta }_{NELS}\), the excess electricity production in kW is reduced. The reason is that with the increase in \({\beta }_{NELS}\), the utilization of SPV or the combination of SPV and BESS increases, given the fact that more load is being shifted toward the availability of the SPV, thus resulting in the reduction in excess electricity production.

Fig. 11
figure 11

Hourly data of excess electrical production for a 15th January b 15th March c 15th July and d 15th October

Full size image

The excessive generation expressed in terms of percentage of the total energy demand or the total energy supplied has been calculated and is expressed in Table 3. With the increase in the \({\beta }_{NELS}\), from 0 to 25% the fraction of excessive energy generation decreases from 9.15 to 6.21%.

Table 3 Percentage of Excessive Energy generation in all the Load shift cases
Full size table

It can be observed from the results obtained by MABC that, for both the minimization objectives, better results with lower costs are obtained. However, the computational burden is very high in the MABC. The time consumed per trial of the solution process by MABC is even with a larger colony size of 50. Further, the time per trial required is lower by MABC with a small colony size of 20. As discussed earlier, at least 50 trials of the solution are required for a metaheuristic to provide a realistic final solution. Therefore, the computational burden required by MABC is only 256.5 h (\({\mathrm{CS}}_{\mathrm{N}}\) = 50).

It is also observed that for only scheduling, MABC provides fast results with reasonable optimization. It should be noted here that with CSN = 50, the results obtained by MABC validate the efficiency of MABC. Hence, in the planning stage, when the optimal size in a short time frame with scheduling and DR has to be evaluated, MABC should be used. MABC can be used for better efficiency.

The hybridization of MABC can be worked upon to make the algorithm more appropriate for online applications. The incorporation of the DR strategy and resource management on non-essential load shifting results in better SPV, BESS, and grid size, location, and scheduling.

The pattern of battery charging and discharging on a typical one day for all the four seasons with βNELS as 0 and 0.2 for the whole day is presented in Kumar et al. (2019).

The evaluation of excess power production gives the appropriate shifting of non-essential load with respect to the availability of solar irradiance. Moreover, the separate analysis of battery degradation cost shows its impact on the sizing and scheduling of DGs. The proposed method is based on an accurate representation of remote and rural distribution network systems. It can reduce unbalance and give optimal scheduling, sizing, and sitting of DGs, as well as battery and grid support.

6 Conclusions

The purpose of this article is to use scheduling to reduce the losses and costs of installing and maintaining SPVs and BESS in a rural distribution system. This analysis considers limitations such as restricted grid availability. Demand response is used to move non-essential loads to periods of increasing solar intensity during the day. SPV, BESS, and the grid are sized and scheduled optimally using this load data for the rural distribution system. For three different loaded phases of the grid, different sizes of SPV and battery storage systems were discovered. The research utilizes two different scheduling objectives: cost-based and loss-based system scheduling. For the cost-based goal, an optimization problem is addressed over a one-year period to reduce the system's capital and operational costs, as well as the cost of power received from the grid. A typical summer day's total losses are reduced over a 24-h period for the loss-based target. When the sizes of the SPV and BESS are proportional to the loading of the corresponding phase, losses are minimized.

The proposed method/algorithm/system is flexible enough to cover a wide range of circumstances and may be used to any other seasonal or network data. Because the hamlet under consideration is without grid power during the day, this research can assist decision-makers in determining the best location, size, and timing of alternative energy sources such as solar photovoltaics (SPVs) to match grid demand. As a result, unintended losses and expenses are avoided, which would otherwise result in a penalty for the distribution system operator and the municipality. The approach is also dependable, cost-effective, and environmentally friendly. Appropriate grid scheduling of DGs and BESS can be accomplished by considering a variety of factors, including the cost of total energy acquired by end users, the power system, and the cost of total energy acquired by end users.

Appropriate grid scheduling of DGs and BESS can be accomplished by considering a variety of factors, such as the overall cost of energy purchased by end users, power system losses, and so on. The optimal solutions are produced by combining DR approaches with a novel optimization technique called MABC to control the shiftable loads.

Once the distribution system operator (DSO) identifies the appropriate sizes and schedules for the DGs for the distribution network, the transmission system operator (TSO) can use this knowledge to improve unit commitment results. Only the summer season is addressed for SPV generation in this work, and the remaining seasons will be considered in future work with appropriate outcomes.