1 Introduction

Nowadays, fuzzy logic system is widely used in control and modeling applications. The learning ability of the fuzzy logic system is improved in fuzzy neural networks, due to the capability of fuzzy reasoning in the management of uncertain information and the ability of neural networks in learning from processes (Wai et al. 2015; Tang et al. 2017). Also, combining the wavelets with neural networks yields quick convergence, high precision and reduced network size. Hence, for optimizing the number of fuzzy rules and improving the approximation error and control precision, fuzzy wavelet neural network (FWNN) has been constructed. The first FWNN was proposed by Ho et al. (2001). It was based on multi-resolution analysis of wavelet transforms and was applied for approximation of nonlinear functions. Another FWNN structure has been presented in Abiyev and Kaynak (2008), which is based on the addition of wavelet functions in consequent parts of fuzzy rules. Then, it was used to control nonlinear dynamic plants. There have been many researches in recent years using FNN (FWNN and ANFIS) in various applications (Davanipour et al. 2012; Lin et al. 2014; Hung et al. 2015; Chen et al. 2015; Mai and Wang 2014; Engin et al. 2004; Kayacan and Kaynak 2006; Loussifi et al. 2016; Wang and Cao 2015; Tofighi et al. 2015). To control a six-phase permanent magnet synchronous motor for an electric power steering system, Lin et al. (2014) proposed an intelligent second-order sliding mode control using a FWNN with an asymmetric membership function estimator. For the same system, Hung et al. (2015) used FWNN based on asymmetric membership function with improved differential evolution algorithm. A recurrent FWNN has been adopted to control the rotor position of a thrust magnetic bearing in Chen et al. (2015). Control of manipulator robot (Mai and Wang 2014), liquid-level systems (Engin et al. 2004; Kayacan and Kaynak 2006), system identification (Loussifi et al. 2016), predicting power consumption (Wang and Cao 2015) and control of chaotic systems (Tofighi et al. 2015) are some of FWNN applications.

The PID-type controller is most widely used in many applications, primarily because of its simple structure, clear functionality and easy implementation (Kansha et al. 2008). However, it suffers from a main drawback. The precise knowledge of the plant should be available to tune the PID controller. This requirement is not easily removed in most industrial cases. In addition, even if there is a mathematical model of the system, environmental conditions may cause the obtained model to change, so it may be necessary to design another PID controller to fit the new changed model.

To overcome the mentioned limitations of the conventional PID controller, researchers have tried to apply self-tuning PID controller (Al Gizi et al. 2014; Li et al. 2005; Woo et al. 2000; Dhaouadi et al. 2008; Zheng et al. 2009; Nguyen et al. 2015). A self-tuning PID controller has the ability to tune its parameters according to the changes of the process. A radial basis function neural network has been used to enhance the PID parameters obtained from genetic algorithm in order to design Sugeno fuzzy PID controller (Al Gizi et al. 2014). A self-tuning PID controller based on wavelet neural networks was proposed in Li et al. (2005). In that work, two wavelet neural networks were used for identification and online tuning. The parameters of PID controller were the output of the second employed wavelet network. So, it was necessary to obtain suitable amounts of parameters as training data. In other words, it is not useful in practice when we have no previous information about the closed-loop system. In Woo et al. (2000), a PID-type fuzzy controller with self-tuning scaling factors has been proposed. They developed a method for online tuning of the scaling factors of PID controller. However, they have added four extra parameters which should be tuned. Determination of these extra parameters is another limitation, too. In Dhaouadi et al. (2008), a self-tuning adaptive PID controller was proposed using a dynamic wavelet network. The control scheme was tested with a second-order system with input saturation. The controller finally has tracked the desired signal; however, as it can be seen from the simulation results, it takes a long time. To improve the overall performance of servo-hydraulic press driven directly by switched reluctance motor, a fuzzy PID control method has been introduced in Zheng et al. (2009). The fuzzy rules have been established based on the error and change in error to adaptive adjustment of PID parameters. But, a lot of rules are needed for tuning of the PID coefficients. In Dhaouadi et al. (2008), an auto-tuning of the PID controller based on the radial basis function neural network and relay feedback approach has been introduced. As stated in Nguyen et al. (2015), ultimate gain and ultimate frequency of the control system have been recognized by the relay feedback approach for initial conditions of the neural network controller. But, this method increases the complexity of the control system.

In this paper to solve the mentioned problems concerned with PID controller, a self-tuning PID controller based on the FWNN has been proposed. By this way, there is no need to have an exact or approximation mathematical model of the plant. Besides, it enables us to benefit the advantages of FWNN. FWNN has some advantages over other intelligent networks. Since the consequent parts contain wavelet functions, it is able to approximate the details of system with higher precision.

However, as we know, one of the main difficulties with auto-tuning is having an efficient optimization method which could be suitable for online applications. One of the modern optimization algorithms is the chaos-based optimization (Jiaqiang et al. 2015; Farahani et al. 2012; Lv and Wu 2006; Ganjefar and Alizadeh 2012; Li and Jiang 1998; Yuan et al. 2012; Yuan et al. 2015). In Farahani et al. (2012), in order to solve the load frequency control problem, a PID optimized by Lozi map chaotic algorithm was proposed. In chaos optimization algorithm, the optimizing variables are transferred into chaotic variables according to the index function and the initial value. Then, by considering the condition of constraint, the optimal values are originated through the search of chaotic variables. Finally, to determine the ultimate optimal values of the system, a fine chaotic search is performed in the neighborhood of the optimal values (Jiaqiang et al. 2015). Chaos optimization algorithm finds the optimal values in higher speed than stochastic ergodic searches. Escape from local minima, independence from strict mathematical properties of optimization problem, easy implementation and short execution time are the main advantages of chaos optimization algorithm (Yuan et al. 2012; Yuan et al. 2015).

In this paper, tent map chaotic optimization has been applied to find the optimal values of the PID coefficients. Design of the controller is performed in two steps. In the first step, the system is modeled using FWNN. This network can identify the unknown model with appropriate accuracy using a few number of parameters. Then, in the second step, a self-tuning PID controller is designed based on the obtained model. The controller’s parameters are tuned using simple but powerful and robust tent map chaotic optimization algorithm. The tuning process can be begun without any trial and error unlike most of the researches in this area (Lin et al. 2014; Hung et al. 2015; Chen et al. 2015; Woo et al. 2000). Also, it does not include any additional parameters to be tuned or to be selected randomly. As the simulation results will show, the control performance is suitable, especially, in the steady-state error and in the speed of setpoint tracking.

This paper is organized as follows: Sect. 2 gives the structure of FWNN. Section 3 represents the proposed controller design. Simulation results are provided in Sect. 4. Section 5 includes the conclusion remarks.

2 Fuzzy Wavelet Neural Network

A fuzzy wavelet neural network integrates wavelet functions with Takagi–Sugeno–Kang fuzzy model. The structure of FWNN is given in Fig. 1. It is constructed by seven layers. The fourth layer is the consequent layer which includes wavelet neural network. In the figure, this subnet has denoted by WNN block. Each WNN corresponds to a three-layer structure, using wavelets as activation functions. The relation of (1) describes the FWNN structure (Abiyev and Kaynak 2008):

$$R_{i} :\quad {\text{If}} x_{1} is A_{1}^{i} , \quad {\text{and}}\quad x_{2} is A_{2}^{i} \ldots \quad {\text{and}}\quad x_{q} \quad is \quad A_{q}^{i} \quad {\text{Then}}\quad y_{i} = w_{i} \mathop \sum \limits_{j = 1}^{q} \psi_{ij} \left( {x_{j} } \right)$$
(1)

where \(x_{j} \left( {1 \le j \le q} \right)\) is the jth input and \(y_{i} \left( {1 \le i \le c} \right)\) is the output of the local model for rule Ri. \(A_{q}^{i}\) is a membership function for ith rule of the qth input defined as a Gaussian function. ψij is defined later in (3). The output signal of each WNN will be such as

$$y_{i} = w_{i} \mathop \sum \limits_{j = 1}^{q} \psi_{ij} \left( {x_{j} } \right)$$
(2)

in which wi shows the weight coefficient between the inputs and ith output. ψij indicates wavelet family defined in (3):

$$\psi_{ij} \left( {x_{j} } \right) = \psi \left( {\frac{{x_{j} - b_{ij} }}{{a_{ij} }}} \right),\quad a_{ij} \ne 0$$
(3)
Fig. 1
figure 1

Structure of FWNN (Davanipour et al. 2012)

Full size image

In the above relation, ψij is made of a mother wavelet function using dilations and translations parameters (a, b). The structure of WNN is given in Fig. 2. Each WNN corresponds to a three-layer structure, using wavelets as activation functions.

Fig. 2
figure 2

Structure of WNN (Davanipour et al. 2012)

Full size image

The defuzzification is made to calculate the output of the whole network in the sixth and the seventh layers. Consequently, the output of FWNN could be calculated as

$$\widehat{y} = \frac{{\mathop \sum \nolimits_{i = 1}^{c} \mu_{i} y_{i} }}{{\mathop \sum \nolimits_{i = 1}^{c} \mu_{i} }} \quad {\text{where}}\quad \mu_{i} \left( x \right) = \mathop \prod \limits_{j = 1}^{q} A_{j}^{i} \left( {x_{j} } \right)$$
(4)

Here, c is the number of fuzzy rules, q is used as an indicator for dimension of input vector, and yi are the output signals of the wavelet neural networks. In this paper, in order to describe the linguistic terms, the Gaussian membership functions are used. Gaussian membership function can approximate triangular and trapezoidal membership functions (Ho et al. 2001):

$$A_{j}^{i} \left( {x_{j} } \right) = \exp \left[ { - \frac{{\left( {x_{j} - c_{j}^{i} } \right)^{2} }}{{\left( {\sigma_{j}^{i} } \right)^{2} }} } \right]$$
(5)

in which \(\sigma_{j}^{i}\) and \(c_{j}^{i}\) indicate the center and the half-width of membership function, respectively. Also, Mexican Hat wavelet function which is commonly applied in FWNN is used here (Ho et al. 2001; Abiyev and Kaynak 2008; Davanipour et al. 2012):

$$\psi \left( x \right) = \frac{1}{{\sqrt {\left| a \right|} }}\left( {1 - 2x^{2} } \right)\exp \left( { - \frac{{x^{2} }}{2}} \right)$$
(6)

It is a mother wavelet function, the dilated and translated versions of which will be used in consequent parts of each fuzzy rule. The use of wavelets with different dilation and translation values allows us to capture different behaviors and essential features of the nonlinear model under fuzzy rules.

3 Proposed Controller

In the previous section, the FWNN model was described. It is used for modeling of the unknown plant. In this section, the proposed controller will be designed. At first, the structure of the self-tuning controller is designed, and then, the optimization procedure is explained.

3.1 Auto-Tuning Controller Design

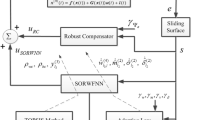
The structure of closed-loop system constructed with identifier network and auto-tuning PID controller is shown in Fig. 3. In that figure, eid is the identification error which is the difference between the actual output and the output of the model. The unknown plant is identified with FWNN. Then, the PID controller is designed based on this model. FWNN has some advantages over other intelligent networks. Since the consequent parts contain wavelet functions, it is able to approximate the details of system with higher precision.

Fig. 3
figure 3

Structure of the proposed controller

Full size image

The adjustment of control parameters (P, I, D) to reach optimum values is the duty of the control loop tuning. The auto-tuner calculates the optimum control parameters by minimizing the following cost function:

$$E = \frac{1}{2}\mathop \sum \limits_{k = 1}^{T} \left( {y_{d} \left( k \right) - \hat{y}\left( k \right)} \right)^{2}$$
(7)

where yd(k) is the desired output and y(k) is the actual output of the system in sample time k. T is integrating horizon. Here, it is equal to 20. The structure of PID controller is as follows:

$$\begin{aligned} u\left( k \right) & = u\left( {k - 1} \right) + P\left[ {e\left( k \right) - e\left( {k - 1} \right)} \right] + I e\left( k \right) \\ & \quad + D\left[ {e\left( k \right) - 2e\left( {k - 1} \right) + e\left( {k - 2} \right)} \right] \\ \end{aligned}$$
(8)

where e(k) is the difference between the desired output and the actual output. According to (7) and (8), the cost function contains P, I and D called control parameters. So, by finding the optimum values of these parameters the cost function in (7) will be minimized. The next section is allocated to finding these optimum parameters.

3.2 Optimization Procedure

After designing the structure of model-based controller, it is necessary to apply an efficient optimization algorithm to tune the controller parameters. By comparison with the next section, one can conclude that the gradient method described at Appendix needs more computations and handling with formula and derivation calculations. To reduce the computations, increase the robustness in noisy conditions and get faster and confident tracking, it is appropriate to apply chaos-based optimization.

As it was discussed in the Introduction section, chaos-based optimization can escape from local minima. The full description of this group of algorithms can be found in Li and Jiang (1998). In this context, tent map chaos optimization has been used. The equation of tent map to generate chaotic time series is:

$$x_{i + 1} = \left\{ {\begin{array}{*{20}l} {2x_{i} } \hfill & {x_{i} \in \left[ {0, 0.5} \right]} \hfill \\ {2\left( {1 - x_{i} } \right) } \hfill & {x_{i} \in \left[ {0.5, 1} \right]} \hfill \\ \end{array} } \right.$$
(9)

where xi is the chaotic variable.

Here, the main problem is finding the parameters \(\left[ {P, I, D} \right]\) via tent map chaos optimization. Since three parameters are needed to be optimized, three initial chaotic variables \(0 \le x_{1,0} , x_{2,0} , x_{3,0} \le 1\) are selected randomly. Then, for each variable the lower bound and upper bound are defined and indicated by lbd and ubd. After that, the initial value for \(\left[ {P, I, D} \right]\) and E (cost function) should be selected and denoted as \(\left[ {P^{*} , I^{*} , D^{*} } \right]\) and E*. Here, zero and infinite have been considered, respectively. The major steps of the FWNN-PID-based tent map chaos optimization are described as follows:

  • Step 1. At first sample time, compute the cost function and determine \(E\left( {\left[ {P, I, D} \right]} \right)\).

  • Step 2. Apply the tent map chaos optimization to find new parameters which minimize the cost function:

    • Substitute \(x_{1,k} , x_{2,k} , x_{3,k}\) in (9) to generate three new chaotic variables via tent map in sample time k.

    • Using the following formula, namely first carrier wave, compute the (k + 1)th parameters:

      $$\left[ {\begin{array}{*{20}c} {P_{k + 1} } \\ {I_{k + 1} } \\ {D_{k + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {l_{{{\text{bd}} - P}} } \\ {l_{{{\text{bd}} - I}} } \\ {l_{{{\text{bd}} - D}} } \\ \end{array} } \right] + \left( {\left[ {\begin{array}{*{20}c} {u_{{{\text{ub}} - P}} } \\ {u_{{{\text{ub}} - I}} } \\ {u_{{{\text{ub}} - D}} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {l_{{{\text{ld}} - P}} } \\ {l_{{{\text{ld}} - I}} } \\ {l_{{{\text{ld}} - D}} } \\ \end{array} } \right]} \right).\left[ {\begin{array}{*{20}c} {x_{1,k + 1} } \\ {x_{2,k + 1} } \\ {x_{3,k + 1} } \\ \end{array} } \right].$$
      (10)

    • Compute the cost function in (7) and assign the new optima as follows: If \(E_{k + 1} \le E^{ *}\), then \(E^{ *} = E_{k + 1} , \left[ {P^{ *} ,I^{ *} , D^{ *} } \right] = \left[ {P_{k + 1} , I_{k + 1} , D_{k + 1} } \right]\); otherwise, do nothing. Repeat the above steps until there is no improvement for cost function during certain steps. Then, go to the next step as follows:

    • Again, use the tent map equation in (9) to generate new chaotic variables. Then, start to search utilizing the second carrier wave.

      $$\left[ {\begin{array}{*{20}c} {P_{k + 1} } \\ {I_{k + 1} } \\ {D_{k + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {P^{*} } \\ {I^{*} } \\ {D^{*} } \\ \end{array} } \right] + \beta \left[ {\begin{array}{*{20}c} {x_{1,k + 1} } \\ {x_{2,k + 1} } \\ {x_{3,k + 1} } \\ \end{array} } \right]$$
      (11)

      in which β is a chaos variable with small ergodic interval. It is normally chosen as a small positive constant, here, β = 0.001.

    • Again, compute the cost function in (7), and assign the new optima such as follows:

      If \(E_{k + 1} \le E^{ *}\), then \(E^{ *} = E_{k + 1} , \left[ {P^{ *} ,I^{ *} , D^{ *} } \right] = \left[ {P_{k + 1} , I_{k + 1} , D_{k + 1} } \right]\); otherwise, do nothing.

      Repeat the above steps until there is no improvement for cost function during certain steps.

  • Step 3. Fit the obtained optimum parameters to the controller and send the controller output to the process.

  • Step 4. For the next sample time, go to the step 1.

4 Simulation Results

In this section, two examples have been considered to investigate the proposed controller. The first example is a nonlinear dynamic system, and the second example is a nonlinear liquid-level system.

Example 1

Consider the nonlinear dynamic plant as below:

$$y\left( k \right) = f\left( {y\left( {k - 1} \right), y\left( {k - 2} \right), y\left( {k - 3} \right), u\left( k \right), u\left( {k - 1} \right)} \right)$$
(12)

in which

$$f\left( {x_{1} , x_{2} , x_{3} , x_{4} , x_{5} } \right) = \frac{{x_{1} x_{2} x_{3} x_{5} \left( {x_{3} - 1} \right) + x_{4} }}{{1 + x_{2}^{2} + x_{3}^{2} }}$$
(13)

The identification process of the above system is done using the FWNN described in Sect. 2. Here, FWNN is constructed with only two rules. Then, it is trained using the algorithm proposed in Davanipour et al. (2012). Details of the separate parts of this algorithm such as clustering, recursive least square and back propagation algorithms can be found in many reports (Shi et al. 2010; Nells 2001; Jang et al. 1997). After training, an input such as what is shown below has been applied to the FWNN as the test input.

$$u\left( k \right) = \left\{ {\begin{array}{*{20}l} {\sin \left( {\frac{\pi k}{25}} \right)} \hfill & {k < 250} \hfill \\ {1.0} \hfill & {250 \le k < 500} \hfill \\ { - 1.0} \hfill & {500 \le k < 750} \hfill \\ {0.3\sin \left( {\frac{\pi k}{25}} \right) + 0.1\sin \left( {\frac{\pi k}{32}} \right) + 0.6\sin \left( {\frac{\pi k}{10}} \right)} \hfill & {750 \le k < 1000} \hfill \\ \end{array} } \right.$$
(14)

The result of system identification is shown in Fig. 4. The capability of FWNN in nonlinear dynamic system identification can be seen in that figure. After the identification stage, the proposed controller has been applied to the plant and its performance has been verified in both normal and noisy conditions. The reference signal is unit step, and the final values of the PID parameters are \(P = 1.4, I = 2, D = 1.2\). Figure 5 shows the performance of the controller when there is no noise in the measurement. Tracking error and the control input are illustrated in Figs. 6 and 7, respectively. The performance of the controller has been also tested when the output is contaminated with a 3 db white noise. Figure 8 illustrates that the chaos-based FWNN-PID controller can be robust in this condition. In order to have a comparison, the gradient-based controller is also tested in noisy condition and Fig. 9 shows that the output has become unstable. Therefore, it cannot track the desired output. Table 1 represents a brief summary of this example in normal condition and compares the proposed controller with the other approaches reported in the literature. In Table 1, MAE points to mean absolute of the tracking error. As can be seen, no overshoot, less settling time and less MAE value in chaos-based FWNN-PID controller have been achieved, despite the considerably smaller number of parameters and rules.

Fig. 4
figure 4

The comparison between the actual output and the output of FWNN in the identification of system (Example 1)

Full size image
Fig. 5
figure 5

Performance of the proposed controller (Example 1)

Full size image
Fig. 6
figure 6

Tracking error (Example 1)

Full size image
Fig. 7
figure 7

Control Input

Full size image
Fig. 8
figure 8

Performance of the proposed controller in noisy condition (Example 1)

Full size image
Fig. 9
figure 9

Performance of the gradient-based controller in noisy condition (Example 1)

Full size image
Table 1 The results of Example 1
Full size table

Example 2

The plant considered in this example is a nonlinear model of a liquid-level system because it is difficult to be controlled optimally using only a conventional PID controller as the parameters of the plant are changing continuously. The plant has a relation as shown below:

$$h\left( t \right) = h\left( 0 \right) + \frac{1}{A}\mathop \int \nolimits_{0}^{t} \left( {q_{\text{in}} \left( \tau \right) - q_{\text{out}} \left( \tau \right)} \right) {\text{d}}\tau$$
(15)

in which

$$\begin{aligned} & q_{\text{in}} = Q_{\text{in}} \sin \left( {\theta \left( t \right)} \right),\quad \theta \left( t \right) \in \left[ {0,\frac{\pi }{2}} \right] \hfill \\ & q_{\text{out}} = a_{\text{out}} \sqrt {2gh\left( t \right)} \hfill \\ \end{aligned}$$
(16)

In the above relation, h is the output variable in m which is the level of the liquid, \(a_{out} = 0.01\,\hbox{m}^{2}\) is the surface area of the outlet, A is the surface of the tank (1 m2), θ is the control valve’s flap angle in rad, and \(g = 9.81\,{\text{m}}/{\text{s}}^{2}\). The details of this example can be found in Engin et al. (2004).

As the previous example, here, the plant is also first identified by a FWNN constructed with two rules; then, the proposed controller has been applied. Here, the reference signal is unit step and the final values of the PID parameters are \(P = 0.95,\; I = 0.15,\; D = 0.03\). The results are shown in Figs. 10, 11, 12 and 13.

Fig. 10
figure 10

The comparison between the actual output and the output of FWNN in the identification of system (Example 2)

Full size image
Fig. 11
figure 11

Performance of the proposed controller (Example 2)

Full size image
Fig. 12
figure 12

Tracking error (Example 2)

Full size image
Fig. 13
figure 13

Control input (Example 2)

Full size image

In order to consider some practical points of PID controllers, in this example disturbance attenuation, control signal amplitude limitations and windup problem have also been included. It is assumed that there is a constraint on the control input such that the input cannot be larger than 1.4, in amplitude. So, the control input is saturated, even though the output has not tracked the desired output correctly. The result of this situation is shown in Fig. 14. As the figure shows, the response is still satisfactory, although there is a larger overshoot and settling time in comparison with the previous status. In Fig. 15, the output tracking has been depicted when there is a 30 percent step signal as an input disturbance. As the figure shows, the disturbance is attenuated after a short time.

Fig. 14
figure 14

Performance of the proposed controller with input saturation (Example 2)

Full size image
Fig. 15
figure 15

Performance of the proposed controller in front of disturbance (Example 2)

Full size image

In Table 2, a brief comparison of the proposed method with gradient-based FWNN-PID, ANFIS-based PID and ANFIS-based fuzzy (Engin et al. 2004) is presented. Improvements in settling time, overshoot and MAE are clear, in spite of the smaller number of parameters and rules, based on the results of Table 2.

Table 2 The results of Example 2
Full size table

5 Conclusion

Using the capability of FWNN in modeling of nonlinear dynamic systems, an auto-tuning controller was designed. Tent map chaotic optimization algorithm made the controller powerful in finding the optimal amounts of parameters. The proposed controller obviated the famous drawback of PID controller which is still an open problem, especially when the system has an unknown structure. The simulation part demonstrated the good performance of the controller in both transient and steady-state response.