Vibration Analysis of a Micropolar Membrane in Contact with Fluid

Abstract

In this paper, vibrations of micropolar membranes in contact with fluid are investigated. The fluid is assumed to be incompressible and contained in a cube and the only non-rigid lateral face is made of a flexible micropolar membrane and interacts with the fluid. The Chebyshev–Ritz polynomials are adopted to attain the dry and wet frequencies of the membranes. The microrotational frequencies evaluated in the present study are also compared with those from the analytical solutions. This comparison shows that the differences between the calculated frequencies and analytical ones are negligible.

1 Introduction

The micropolar theory constitutes extension of the classical field theories where every particle of the material can make both microrotation and volumetric microelongation in addition to the bulk deformation. Since this theory includes the influence of microstructure on the overall behavior of the medium, it reflects physical realities significantly better than the classical theory for the engineering materials.

In the micropolar theory, the material points are considered to possess orientations. A material point carrying three rigid directors introduces one extra degree of freedom over the classical theory, since in micropolar continuum a point is endowed with three rigid directors only. A material point is then equipped with the degrees of freedom for rigid rotations, in addition to the classical translational degrees of freedom. In fact, the micropolar covers the results of the classical continuum mechanics. The micropolar theory recently gained attention in fluid mechanics and, consequently, mathematicians and engineers are implementing this theory in various theoretical (Eringen 1999, 2001, 1976; Kumar and Partap 2007; Altenbach and Eremeyev 2014) and practical applications (Genç 2013; Rojratsirikul et al. 2011).

Moreover, the vibration analysis of the membranes modeled by micropolar theory has been carried out. This analysis shows the appearance of some additional frequencies among the values of the frequencies obtained from the classical theory of elasticity, due to the micropolarity of the membrane. These new frequencies are called microrotational waves. Also, these additional frequencies disappear when the micropolar material constants vanish and only the classical frequencies remain. More importantly, these additional frequencies are more sensitive to the change of the microelastic constants than the classical frequencies. In the sequel, the mode shapes are attained for the micropolar structure, micropolar structure in contact with a fluid and finally the classical ones are attained for comparison. Comparing the analytical results of classical membrane with numerical ones documents their small differences, which confirms our proposed method. The microrotational wave frequencies and mode shapes are developed. The results of natural frequencies and mode shapes for the transverse vibrations of the membrane confirm the classical ones.

In the classical theory of continuum mechanics, materials are assumed to be homogeneous. Nevertheless, some modern engineering structures have a number of defects with different sizes and forms which violate the assumption of continuity at microscale. Such structures are made of materials possessing an internal structure. Polycrystalline materials, materials with fibrous or coarse grain structure come in this category (Dos Reis and Ganghoffer 2012). The analysis of such materials requires incorporating the theory of oriented media.

Micropolar theory has been developed by Eringen (1999, 2001, 1976) for elastic solids and fluid and further for nonlocal polar fields. Micropolar theory constitutes extension of the classical field theories concerned with the rotations, in microscopic scale and short time scales. Mathematically, material particles are assumed to be geometrical points that possess physical and mathematical properties, e.g., mass, charge and rigid directors. The field equations constructed with this model are expected then to represent many new and wider classes of physical phenomena that fall outside the classical field.

In the micropolar theory, the material is endowed with microstructure, like atoms and molecules at microscopic scale. Homogenization of a basically heterogeneous material depends on scale of interest. When stress fluctuation is small enough compared to microstructure of the material, homogenization can be made without considering the detailed microstructure of the material. However, if it is not the case, the microstructure of material must be considered properly in a homogenized formulation (Eringen 2001; Dos Reis and Ganghoffer 2012).

At each particle of a micropolar continuum, it is assumed that a microstructure rotates independently from the surrounding medium (Ramezani et al. 2009). Accordingly, every particle contains six degrees of freedom, three translational motions which are assigned to the macro-element and three rotational ones which are referred to the microstructure.

Due to theoretical and practical importance, many problems of waves and vibration of micropolar elasticity have been investigated by different researchers. A micropolar elasticity behavior analysis has been carried out for macroscopically heterogeneous materials (Eringen 1999, 2001; Beveridge et al. 2013).

Recently, a linear theory for the analysis of beams based on the micropolar continuum mechanics has been developed by Ramezani et al. (2009). Power series expansions for the axial displacement and microrotation fields were assumed in the mentioned work. The governing equations were derived by integrating the momentum and moment of momentum equations in the micropolar continuum theory.

On the other hand, the fluid–structure problems have also been extensively contemplated by many researchers (Amabili et al. 1998; Amabili 2001). In such studies, the fluid is considered to be ideal and incompressible (compressible) with the Laplace (wave) as its governing equation, where the structure has a variety of shapes and assumptions. For fluid–structure systems, the vibration of the structure in contact with a fluid has been thoroughly analyzed by many authors (Amabili 2003; Amabili et al. 2000; Morand and Ohayon 1995). Such problems appear frequently in practice, for example when studying the veins, pulmonary passages and urinary systems which can be modeled as shells conveying fluid, aero-elastic instabilities around flexible aircraft, container conveying the fluids and dams (Amabili 2003; Amabili et al. 2000; Morand and Ohayon 1995; Amabili and Paıdoussis 2003).

In the present work, fluid–structure interaction problems having microstructure are modeled by the microstretch theory. Then, an analytical formulation for vibration analysis of a micropolar membrane in contact with fluid and based on the micropolar continuum mechanics is developed. We follow Eringen’s method for constructing the micropolar membrane theory (Beveridge et al. 2013).

Next, we study the coupled problem to obtain natural frequencies of the fluid–structure problem. The Chebyshev polynomials are employed in this paper to simplify computations, in addition to the high accuracy and numerical reliability (Dong 2008; İnan and KiriŞ 2008).

Finally, an analytical approach is utilized to investigate the vibration characteristics of the aforementioned fluid–structure problem. The fluid is considered to be non-viscous and incompressible. Duplicate Chebyshev series, multiplied by boundary functions are used as admissible functions and the frequency equations of the micropolar membrane are obtained by the use of Chebyshev–Ritz method.

2 Mathematical Model

As stated in the previous section, there are instances in which the assumption of material homogeneity is inadequate: either the size of the loaded structure is very small and comparable to the length scale of its constituent material microstructure or the length scale of the heterogeneity with the material structure is significantly larger than microscopic. Many nano-devices fall into the first category, whereas materials such as ceramics, cement, rock, soil, bone and short fiber and particulate-reinforced composites may be referred to as the second category (Eringen 1999, 2001, 1976). Micropolar theory is an alternative theory describing the behavior of heterogeneous materials. The mathematical foundation of micropolar continuum mechanics theory has been developed through the works of Eringen and his coworkers (Eringen 2001). In this section, we present some basic relations of the micropolar elasticity needed for our derivation in the next sections.

2.1 Structure Domain

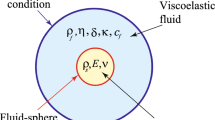
The vibration analysis of a micropolar membrane in contact with a fluid is considered. The fluid is contained in a cube with all faces except one of the lateral faces being rigid. The only non-rigid lateral face is made of a flexible micropolar membrane. Therefore, it interacts with the fluid. The problem is shown in Fig. 1.

Fig. 1

Schematic view of micropolar membrane in contact with a fluid

As mentioned earlier, the micropolar elasticity defines more degrees of freedom. We consider the linear isotropic membrane of lowest order. The governing equations of the three-dimensional micropolar elasticity are as follows (Eringen 1999, 2001, 1976):

$$\left( {\mu + \kappa } \right)\nabla^{2} u + \left( {\lambda + \mu } \right)\frac{\partial }{\partial x}\left( {u,_{x} + v,_{y} + w,_{z} } \right) - \kappa \left( {\zeta_{y} ,_{z} - \zeta_{z} ,_{y} } \right) = \rho u,_{tt}$$

(1)

$$\left( {\mu + \kappa } \right)\nabla^{2} v + \left( {\lambda + \mu } \right)\frac{\partial }{\partial y}\left( {u,_{x} + v,_{y} + w,_{z} } \right) - \kappa \left( {\zeta_{z} ,_{x} - \zeta_{x} ,_{z} } \right) = \rho v,_{tt}$$

(2)

$$\left( {\mu + \kappa } \right)\nabla^{2} w + \left( {\lambda + \mu } \right)\frac{\partial }{\partial z}\left( {u,_{x} + v,_{y} + w,_{z} } \right) - \kappa \left( {\zeta_{x} ,_{y} - \zeta_{y} ,_{x} } \right) = \rho w,_{tt}$$

(3)

$$\nabla^{2} \zeta_{x} - 2\kappa \zeta_{x} + \left( {\alpha + \beta } \right)\frac{\partial }{\partial x}\left( {\zeta_{x} ,_{x} + \zeta_{y} ,_{y} + \zeta_{z} ,_{z} } \right) - \kappa \left( {v,_{z} - w,_{y} } \right) = \rho j\zeta_{x} ,_{tt}$$

(4)

$$\gamma \nabla^{2} \zeta_{y} - 2\kappa \zeta_{y} + \left( {\alpha + \beta } \right)\frac{\partial }{\partial y}\left( {\zeta_{x} ,_{x} + \zeta_{y} ,_{y} + \zeta_{z} ,_{z} } \right) - \kappa \left( {w,_{x} - u,_{z} } \right) = \rho j\zeta_{y} ,_{tt}$$

(5)

$$\gamma \nabla^{2} \zeta_{z} - 2\kappa \zeta_{z} + \left( {\alpha + \beta } \right)\frac{\partial }{\partial z}\left( {\zeta_{x} ,_{x} + \zeta_{y} ,_{y} + \zeta_{z} ,_{z} } \right) - \kappa \left( {u,_{y} - v,_{x} } \right) = \rho j\zeta_{z} ,_{tt}$$

(6)

where ρ is the mass density, j is the microinertia, $\lambda , \mu , \kappa , \alpha , \beta$ and γ are material constants. Also, u, v, w and $\zeta_{x} , \zeta_{y} , \zeta_{z}$ are displacement and microrotation components, respectively.

$$\left\{ \begin{array}{l} k = \mu + \kappa \hfill \\ k_{1} = \lambda + 2\mu + \kappa \hfill \\ k_{2} = \alpha + \beta + \gamma \hfill \\ k_{3} = \alpha + \beta \hfill \\ k_{4} = \lambda + \mu \hfill \\ \end{array} \right.$$

(7)

For attaining the governing equations of the micropolar membrane from three-dimensional micropolar elasticity, various methods have been used (Eringen 1999). Some authors have used the perturbation method, while some others have used the asymptotic analysis (Aganović et al. 2006). Based on the method used in Eringen (1999), the governing equations of the lowest-order micropolar membrane are obtained by some integration in the thickness direction of the micropolar media. The result is as follows:

$$\left( {G + \frac{\kappa }{2}} \right)\nabla^{2} w + \kappa \varepsilon_{kl3} \psi_{l} ,_{k} + \rho_{s} \left( {F_{ } - \ddot{w}} \right) = 0$$

(8)

$$\left( {\alpha + \beta } \right)\psi_{k} ,_{lk} + \gamma \psi_{l} ,_{kk} - \kappa \varepsilon_{kl3} w,_{k} - 2\kappa \psi_{l} + \rho_{s} \left( {L_{l} - j\ddot{\psi }_{l} } \right) = 0$$

(9)

where w and ψ_l are displacement and microrotation component, respectively.

We consider the simply supported problem in which the boundary conditions are as follows:

$$w = 0, \psi_{1} = \psi_{2} = 0 \,\text{on}\, x = - 1,1$$

(10)

$$w = 0, \psi_{1} = \psi_{2} = 0\,\text{on}\,y = - 1,1$$

(11)

2.2 Fluid Domain

For the fluid domain, we have the following equations (Amabili et al. 1998; Amabili 2001):

$$\nabla^{2}\Phi = 0$$

(12)

where $\Phi$ is the deformation potential (Amabili et al. 1998; Amabili 2001). The related boundary conditions are as follows (Fig. 1):

$$\frac{\partial \varPhi }{\partial n} = 0\varvec{ }\quad {\text{on}}\quad x = 0,a$$

(13)

$$\frac{\partial \varPhi }{\partial n} = 0\quad {\text{on}}\quad \varvec{ }y = 0,b$$

(14)

$$\frac{\partial \varPhi }{\partial n} = 0\varvec{ }\quad {\text{on}}\quad z = - c$$

(15)

$$\frac{\partial \varPhi }{\partial n} = w(x,y,0,t)\quad {\text{on}}\quad z = 0$$

(16)

Using separations of variable in fluid domains yields the following results (Greenberg 1988):

$$\varphi = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } E_{mn} \cos \left( {m\pi x} \right)\cos \left( {n\pi y} \right)\cosh \left( {\varLambda_{mn} \left( {z + c} \right)} \right)$$

(17)

where

$$\begin{aligned} \varLambda_{mn} & = \left[ {\left( {m\pi } \right)^{2} + \left( {n\pi } \right)^{2} } \right]^{1/2} \\ \varPhi & = \varphi \left( {x,y,z} \right)e^{{i\left( {\omega t + \theta } \right)}} \\ \end{aligned}$$

(18)

And E_mn’s are duplicate Fourier series coefficients.

3 Natural Frequencies and Mode Shapes of the Free Vibration of the Structure

For the natural frequencies and mode shapes of the free vibration of the structure (Rao 2007), we have

$$\left( {\varvec{G} + \frac{\varvec{\kappa}}{2}} \right)\nabla^{2} \varvec{w} + \varvec{\kappa \varepsilon }_{{\varvec{kl}3}} \phi_{\varvec{l}} ,_{\varvec{k}} =\varvec{\rho}_{\varvec{s}} \ddot{w}$$

(19)

$$\left( {\alpha + \beta } \right)\psi_{k} ,_{lk} + \gamma \psi_{l} ,_{kk} - \kappa \varepsilon_{kl3} w,_{k} - 2\kappa \psi_{l} = \rho_{s} j\ddot{\psi }_{l}$$

(20)

As shown in Fig. 2, the boundary conditions are ( 10 ) and ( 11 ).

Fig. 2

Micropolar membrane shape

For the natural frequencies and mode shapes of the free vibrating micropolar membrane, the following results can be obtained after performing some mathematical operations,

$$\left\{ {\begin{array}{*{20}c} w \\ {\psi_{1} } \\ {\psi_{2} } \\ \end{array} } \right\} = \left( {1 - x^{2} } \right)\left( {1 - y^{2} } \right)\mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } \left\{ {\begin{array}{*{20}c} {w_{mn} } \\ {\psi_{1mn} } \\ {\psi_{2mn} } \\ \end{array} } \right\}e^{{i\left( {\omega t + \theta } \right)}}$$

(21)

where

$$w_{mn} = A_{mn} P_{m} \left( x \right)P_{n} \left( y \right)$$

(22)

$$\psi_{1mn} = B_{mn} P_{m} \left( x \right)P_{n} \left( y \right)$$

(23)

$$\psi_{2mn} = C_{mn} P_{m} \left( x \right)P_{n} \left( y \right)$$

(24)

P_m(x) is the mth Chebyshev polynomial and is defined as P_m(x) = cos((m − 1)Arccos(x)).

Also, the terms (1 − x²) and (1 − y²) are the boundary functions to meet the necessary condition for admissibility of the functions.

The corresponding potential energy and kinetic energy functionals of the structure are obtained as [for more details see (Eringen 1999)]

$$V_{s} = \frac{1}{2}\mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} \left[h\left( {\alpha \psi_{k} ,_{k} \psi_{l} ,_{l} + \beta \psi_{k} ,_{l} \psi_{l} ,_{k} + \gamma \psi_{k} ,_{l} \psi_{k} ,_{l} } \right) + Ghw,_{k} w,_{k} + 2\kappa h\left( {r_{k} - \psi_{k} } \right)\left( {r_{k} - \psi_{k} } \right)\right]{\text{d}}x{\text{d}}y$$

(25)

$$T_{s} = \frac{h}{2}\mathop \int\limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} [\rho_{s} j\dot{\psi }_{k} \dot{\psi }_{k} + \rho_{s} \dot{w}^{2} \left] {{\text{d}}x{\text{d}}y = \frac{h}{2}\omega^{2} \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} [\rho_{s} j\psi_{k} \psi_{k} + \rho_{s} w^{2} } \right]{\text{d}}x{\text{d}}y$$

(26)

Based on the above relations, one can have the reference kinetic energy of the structure as

$$\varvec{T}_{\varvec{s}}^{\varvec{*}} = \frac{\varvec{h}}{2}\mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} [\varvec{\rho}_{\varvec{s}} \varvec{j\psi }_{\varvec{k}}\varvec{\psi}_{\varvec{k}} +\varvec{\rho}_{\varvec{s}} \varvec{w}^{2} ]{\mathbf{d}}\varvec{x}{\mathbf{d}}\varvec{y}$$

(27)

The maximum reference potential energy of the structure can also be written as

$$\varvec{V}_{\varvec{s}} = \frac{1}{2}\mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} \left[\varvec{h}\left( {\varvec{\alpha \psi }_{\varvec{k}} ,_{\varvec{k}}\varvec{\psi}_{\varvec{l}} ,_{\varvec{l}} + \varvec{\beta \psi }_{\varvec{k}} ,_{\varvec{l}}\varvec{\psi}_{\varvec{l}} ,_{\varvec{k}} + \varvec{\gamma \psi }_{\varvec{k}} ,_{\varvec{l}}\varvec{\psi}_{\varvec{k}} ,_{\varvec{l}} } \right) + \varvec{Ghw},_{\varvec{k}} \varvec{w},_{\varvec{k}} + 2\varvec{\kappa h}\left( {\varvec{r}_{\varvec{k}} -\varvec{\psi}_{\varvec{k}} } \right)\left( {\varvec{r}_{\varvec{k}} -\varvec{\psi}_{\varvec{k}} } \right)\right]{\mathbf{d}}\varvec{x}{\mathbf{d}}\varvec{y}$$

(28)

Since we need to attain the natural frequencies and mode shapes of the free vibration of the structure, we define the following functional:

$$\varPi = V_{s} - T_{s} = V_{s} - \omega^{2} T_{s}^{*}$$

(29)

By minimizing this functional with respect to $A_{mn} , B_{mn} , C_{mn}$, one can obtain the natural frequencies and natural modes of the free vibrations.

3.1 Numerical Results

In this paper, we use the Chebyshev polynomials because of their simplicity for computations and coding and also their high accuracy and numerical reliability. The first six terms of the Chebyshev polynomials are

$$\begin{aligned} T_{0} & = 1; \\ T_{1} & = x; \\ T_{2} & = 2x^{2} - 1; \\ T_{3} & = 4x^{3} - 3x; \\ T_{4} & = 8x^{4} - 8x^{2} + 1; \\ T_{5} & = 16x^{5} - 20x^{3} + 5x; \\ \end{aligned}$$

These functions are mutually orthogonal in the interval [− 1, 1] with the weighting function $\left( {1 - x^{2} } \right)^{ - 1/2}$.

The six polynomial graphs are shown in Fig. 3.

Fig. 3

Chebyshev polynomials

Using Chebyshev–Ritz method, and approximating the number of series (we use 48 terms for all three variables), the problems turn to

$$\det \left( {\left[ {\begin{array}{*{20}c} {K_{ww} } & {K_{{w\psi_{1} }} } & {K_{{w\psi_{2} }} } \\ {K_{{\psi_{1} w}} } & {K_{{\psi_{1} \psi_{1} }} } & {K_{{\psi_{1} \psi_{2} }} } \\ {K_{{\psi_{2} w}} } & {K_{{\psi_{2} \psi_{1} }} } & {K_{{\psi_{2} \psi_{2} }} } \\ \end{array} } \right]_{48 \times 48} - \omega^{2} \left[ {\begin{array}{*{20}c} {M_{ww} } & 0 & 0 \\ 0 & {M_{{\psi_{1} \psi_{1} }} } & 0 \\ 0 & 0 & {M_{{\psi_{2} \psi_{2} }} } \\ \end{array} } \right]_{48 \times 48} } \right) = 0$$

(30)

where

$$K_{ww} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial (A_{mn} )^{2} }}} \right]_{16 \times 16}$$

(31)

$$K_{{w\varvec{\psi}_{1} }} = K_{{\varvec{\psi}_{1} w}} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial A_{mn} \partial B_{mn} }}} \right]_{16 \times 16}$$

(32)

$$K_{{w\varvec{\psi}_{2} }} = K_{{\varvec{\psi}_{2} w}} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial A_{mn} \partial C_{mn} }}} \right]_{16 \times 16}$$

(33)

$$K_{{\varvec{\psi}_{1}\varvec{\psi}_{1} }} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial (B_{mn} )^{2} }}} \right]_{16 \times 16}$$

(34)

$$K_{{\varvec{\psi}_{2}\varvec{\psi}_{2} }} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial (C_{mn} )^{2} }}} \right]_{16 \times 16}$$

(35)

$$M_{ww} = \left[ {\frac{{\partial^{2} \varvec{T}_{\varvec{s}}^{\varvec{*}} }}{{\partial (A_{mn} )^{2} }}} \right]_{16 \times 16}$$

(36)

$$M_{{\varvec{\psi}_{1}\varvec{\psi}_{1} }} = \left[ {\frac{{\partial^{2} \varvec{T}_{\varvec{s}}^{\varvec{*}} }}{{\partial (B_{mn} )^{2} }}} \right]_{16 \times 16}$$

(37)

$$M_{{\varvec{\psi}_{2}\varvec{\psi}_{2} }} = \left[ {\frac{{\partial^{2} \varvec{T}_{\varvec{s}}^{\varvec{*}} }}{{\partial (C_{mn} )^{2} }}} \right]_{16 \times 16}$$

(38)

The numerical results from the present study for dry structure are compared with those obtained from analytical solution (Rao 2007) in Table 1.

Table 1 Natural frequencies of vibration for dry structure obtained from classical theory, ω (${\text{s}}^{ - 1} )$

The numerical results for frequencies of transverse vibration of dry structure obtained by using the micropolar theory are given in Table 2 and are compared with the results of analytical method. The different parameters for the micropolar theory are also presented in Table 3.

Table 2 Natural frequencies of transverse vibration for dry structure obtained from micropolar theory, ω (${\text{s}}^{ - 1} )$

Table 3 Microrotaional wave natural frequencies for dry structure, $\omega$(${\text{s}}^{ - 1} )$

As can be seen, even though in our computations the micropolar frequencies are a bit less than the classical frequencies, the micropolar frequencies are very close to the classical one (with two decimal digit accuracy). The main reason is that the micropolar theory admits the rigid body rotation for microelements. It should also be noted that some additional frequencies are observed due to microstructure of the membrane among the values of the frequencies obtained from classical theory of the elasticity. The results for the microrotational wave frequencies are presented in Table 3. It should be noted that these additional frequencies disappear when all micropolar parameters are considered to be zero.

As mentioned previously, the microrotational wave which arises from the micromotion assumptions in micropolar theory enables us to explain more phenomena than the classical theory; also their accuracy is more than the classical theory. Therefore, the most important part of this theory is that it presents micromotion and microrotation waves.

The shapes for the first three mode shapes of the transverse displacement of the micropolar structure are shown in Figs. 4, 5, 6 and 7.

Fig. 4

First mode shape of the micropolar structure for w as the transverse displacement (all parameters are in centimeters)

Fig. 5

Second mode shape of the micropolar structure for w as the transverse displacement

Fig. 6

Third mode shape of the micropolar structure for w as the transverse displacement

Fig. 7

First mode shape of the micropolar fluid–structure for w (all parameters are in centimeters)

4 Fluid–Structure Interaction

The coupling between the fluid and structure occurs in a boundary condition at $z = 0$ (16) and fluid domain is (17). Also, (8) and (9) are the structure’s equations with the boundary conditions of (10), (11) and (16).

where P is the hydrodynamic pressure due to interaction between fluid and structure. At this step, we use the Chebyshev polynomials to write the membrane parameters.

$$\left( {1 - x^{2} } \right)\left( {1 - y^{2} } \right)\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} P_{m} \left( x \right)P_{n} \left( y \right) = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty }\Lambda _{mn} E_{mn} \cos \left( {m\pi x} \right)\cos \left( {n\pi y} \right)\sinh \left[ {\Lambda _{mn} c} \right]$$

(39)

By some straightforward algebraic operations, one can obtain

$$E_{pq} = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } csch\left( {\varLambda_{pq} c} \right)A_{mn} \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} \left( {1 - x^{2} } \right)\left( {1 - y^{2} } \right){\text{cos }}\left( {m\pi x} \right){ \cos }\left( {n\pi y} \right)P_{m} \left( x \right)P_{n} \left( y \right){\text{d}}x{\text{d}}y$$

(40)

Because of the orthonormality nature of the Chebyshev polynomials in [− 1, 1], the above relations can easily be computed.

4.1 Chebyshev–Ritz Method

At this step, we are ready to find natural frequencies of the coupled problem by using Chebyshev–Ritz method. It is necessary to construct the Rayleigh quotient. To find the Rayleigh quotient, the related reference energies should be determined (Rao 2007).

4.2 Fluid Reference Kinetic Energy

The reference kinetic energy of the fluid is due to the fluid–structure interaction (Amabili et al. 1998; Amabili 2001).

$$\varvec{T}_{\varvec{L}}^{\varvec{*}} = \frac{1}{2}\varvec{\rho}_{\varvec{L}} \mathop {\iint }\limits_{\varvec{S}}^{\varvec{ }} \varvec{\varphi }\frac{{\partial \varvec{\varphi }}}{{\partial \varvec{n}}}{\mathbf{d}}\varvec{S}$$

(41)

which yields the following relation for the fluid reference kinetic energy

$$T_{L}^{*} = \frac{1}{4}\rho_{L} \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } E_{mn}^{2} \varLambda_{mn} sinh\left( {2\varLambda_{mn} c} \right)$$

(42)

4.3 Energy of the Structure

The reference kinetic energy of the structure is (27) and the maximum potential energy of the structure is (28). Hence, we are ready to find the natural frequencies of the coupled problem. Utilizing Rayleigh quotient,

$${\varvec{\Omega}}^{2} = \frac{{\varvec{V}_{\varvec{s}} }}{{\varvec{T}_{\varvec{L}}^{\varvec{*}} + \varvec{T}_{\varvec{s}}^{\varvec{*}} }}$$

(43)

And minimizing the following functional

$$\varPi = V_{s} - \varOmega^{2} \left( {T_{L}^{*} + T_{S}^{*} } \right)$$

(44)

With respect to $A_{mn}^{ } ,$$B_{mn}^{ }$ and $C_{mn}^{ }$ as

$$\frac{\partial \varPi }{{\partial A_{pq}^{ } }} = 0$$

(45)

$$\frac{\partial \varPi }{{\partial B_{pq}^{ } }} = 0$$

(46)

$$\frac{\partial \varPi }{{\partial C_{pq}^{ } }} = 0$$

(47)

yields the desired result. Noting that $E_{mn}^{ '} {\text{s}}$ are functions of $A_{mn}^{ } , B_{mn}^{ } , C_{mn}^{ }$, therefore we can compute the mode shapes and natural frequencies of the coupled problem.

4.3.1 Numerical Results

Using again Chebyshev–Ritz method, and approximating the number of series (we use 16 terms for fluid domain), the problem turns to

$${ \det }\left( {\left[ {\begin{array}{*{20}c} {K_{ww} } & {K_{{w\psi_{1} }} } & {K_{{w\psi_{2} }} } \\ {K_{{\psi_{1} \psi_{1} }} } & {K_{{\psi_{1} \psi_{1} }} } & {K_{{\psi_{1} \psi_{2} }} } \\ {K_{{\psi_{2} w}} } & {K_{{\psi_{2} \psi_{1} }} } & {K_{{\psi_{2} \psi_{2} }} } \\ \end{array} } \right]_{48 \times 48} - \varOmega^{2} \left[ {\begin{array}{*{20}c} {M_{ww} } & 0 & 0 \\ 0 & {M_{{\psi_{1} \psi_{1} }} } & 0 \\ 0 & 0 & {M_{{\psi_{2} \psi_{2} }} } \\ \end{array} } \right]_{48 \times 48} } \right) = 0$$

(48)

where

$$K_{ww} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial (A_{mn} )^{2} }}} \right]_{16 \times 16}$$

(49)

$$K_{{w\varvec{\psi}_{1} }} = K_{{\varvec{\psi}_{1} w}} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial A_{mn} \partial B_{mn} }}} \right]_{16 \times 16}$$

(50)

$$K_{{w\varvec{\psi}_{2} }} = K_{{\varvec{\psi}_{2} w}} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial A_{mn} \partial C_{mn} }}} \right]_{16 \times 16}$$

(51)

$$K_{{\varvec{\psi}_{1}\varvec{\psi}_{1} }} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial (B_{mn} )^{2} }}} \right]_{16 \times 16}$$

(52)

$$K_{{\varvec{\psi}_{2}\varvec{\psi}_{2} }} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial (C_{mn} )^{2} }}} \right]_{16 \times 16}$$

(53)

$$K_{{\varvec{\psi}_{2}\varvec{\psi}_{2} }} = \left[ {\frac{{\partial^{2} \varvec{V}_{\varvec{s}} }}{{\partial (C_{mn} )^{2} }}} \right]_{16 \times 16}$$

(54)

$$M_{ww} = \left[ {\frac{{\partial^{2} \left( {\varvec{T}_{\varvec{L}}^{\varvec{*}} + \varvec{T}_{\varvec{s}}^{\varvec{*}} } \right)}}{{\partial (A_{mn} )^{2} }}} \right]_{16 \times 16}$$

(55)

$$M_{{\varvec{\psi}_{1}\varvec{\psi}_{1} }} = \left[ {\frac{{\partial^{2} \left( {\varvec{T}_{\varvec{L}}^{\varvec{*}} + \varvec{T}_{\varvec{s}}^{\varvec{*}} } \right)}}{{\partial (B_{mn} )^{2} }}} \right]_{16 \times 16}$$

(56)

$$M_{{\varvec{\psi}_{2}\varvec{\psi}_{2} }} = \left[ {\frac{{\partial^{2} \left( {\varvec{T}_{\varvec{L}}^{\varvec{*}} + \varvec{T}_{\varvec{s}}^{\varvec{*}} } \right)}}{{\partial (C_{mn} )^{2} }}} \right]_{16 \times 16}$$

(57)

The numerical results from the present study for wet-micropolar structure are given in Table 4 and are compared with those obtained for the dry micropolar structure.

Table 4 Results for FSI natural frequencies ($\varOmega^{ }$) in (${\text{s}}^{ - 1} )$

In Table 5, we compare the results from the classical theory and micropolar theory in FSI problem. As one can see, they are same as each other.

Table 5 Results for FSI natural frequencies of micropolar and classical structures ($\varOmega^{ }$) in (${\text{s}}^{ - 1} )$

Figures 7, 8 and 9 represent the shapes for the first three mode shapes of the transverse displacement of the micropolar fluid–structure in FSI problem.

Fig. 8

Second mode shape of the micropolar fluid–structure for w

Fig. 9

Third mode shape of the micropolar fluid–structure for w

The results for microrotations ψ_1,2 are obtained similarly and therefore we omit them.

5 Conclusion

In this paper, the coupled vibration of the lowest-order micropolar membrane in contact with the ideal incompressible fluid has been investigated. The micropolar membrane shows the more accurate response in comparison with classic membranes. The method for finding the natural frequencies of the coupled vibration relies on the Chebyshev–Ritz method.

It is known that using the Chebyshev polynomials, more eigenfrequencies than using other polynomial functions can be obtained because of the excellent mathematical properties of Chebyshev polynomial series in approximation. The Chebyshev polynomials have an additional advantage in that they can be expressed in terms of cosine functions, which facilitate the analysis and programming.

The nature of waves in the micropolar membrane has been investigated. This theory predicts the existence of microrotational waves which are not present in any of the known membrane theories based on the classical continuum mechanics. We see the excellent agreements between micropolar elasticity and classical elasticity in finding natural frequencies for free vibration of the membrane. Also, for fluid–structure frequencies, we see that the natural frequencies in coupling are less than natural frequencies in free vibrations of the micropolar membrane which is expected. Moreover, if the micropolar constants are considered to be zero, the classical elasticity results for the frequencies will be obtained. Results for classical problem have been compared to analytical ones; we saw that their differences are so small and therefore negligible, which verifies our results and method.