1 Introduction

Stepped spillway is a spillway where steps are installed on the surface. Installing steps starts close to the crest and continues to the toe of dams (Chen 2015). Stepped spillways have two main features: high efficiency for energy dissipation and dramatic decrease in the probability of cavitation occurrence (Chanson 2002; Frizell et al. 2013; Pfister and Hager 2011). In terms of energy dissipation, the feature causes a significant decrease in the size of energy dissipator structure at the toe of dam (Felder and Chanson 2011). This characteristic considerably reduces the cost of construction, since energy dissipators are among the most costly parts of dam construction projects (Sorensen 1985). Due to the high efficiency of stepped spillways in terms of energy dissipation and removing cavitation, several investigations including experimental and numerical methods have been conducted on hydraulic behavior of flow over them (Dehdar-Behbahani and Parsaie 2016; Husain et al. 2014; Morovati et al. 2016; Nikseresht et al. 2013; Parsaie et al. 2015; Zhan et al. 2016). In experimental studies, flow pattern on stepped spillways and the effect of geometry of steps on energy dissipation have been evaluated (Mohammad Rezapour Tabari and Tavakoli 2016). By observing the pattern of flow over stepped spillways, investigators have proposed three classes for flow regime on these structures. They proposed that flow regimes can be divided into three classes as napped flow, transition flow and skimming flow. Napped flow occurs at low discharge values. In this condition, flow leaves the upper step and falls down onto the lower step (Fen et al. 2016; Tabbara et al. 2005). Energy dissipation in this condition is due to the collision of the jet of flow with steps and hydraulic jump that may occur completely or incompletely. Skimming flow occurs in large discharge value, and in this status a pseudo-bottom is created between steps and passing flow. Transition regime is a condition between napped and skimming flow. For more information on flow regime over stepped spillways, refer to Boes et al. 2000; Tatewar and Ingle 1996. Nowadays, by advances in computer facilities and due to the high cost of experiments, investigators have encouraged the use of numerical method for simulation of hydraulic phenomena. In this regard, computational fluid dynamic (CFD) methods for simulation of flow over steeped spillways have been conducted (Chatila and Jurdi 2004; Parsaie and Haghiabi 2015a, b; Zare and Doering 2012). Using CFD techniques is required to solve Navier–Stokes equations along turbulence models. Fortunately, powerful open source codes such as Open Foam and commercial packages such as Flow3D and Fluent have been proposed (Attarian et al. 2014; Cheng et al. 2006). Recently, by developing soft computing techniques in most areas of engineering, investigators have tried to use them for accurate presentation of results of experiments (Noori et al. 2015; Samadi et al. 2015; Zahiri and Azamathulla 2014). Some of the soft computing techniques such as artificial neural networks (ANNs) (Noori et al. 2010b), adaptive neuro-fuzzy inference system (ANFIS) (Noori et al. 2010a) and support vector machine (SVM) (Azamathulla and Wu 2011; Noori et al. 2009) developed a network for modeling and predicting desired phenomena. Other types of soft computing techniques also have been proposed. In the last few decades, in addition to developing a network, smart functions have also been presented. In this regard, genetic programming (GP) (Azamathulla and Ghani 2011), gene expression programming (GEP) (Azamathulla 2013; Azamathulla and Mohd. Yusoff 2013; Emamgholizadeh et al. 2016; Emamgolizadeh et al. 2015; Guven and Kişi 2011; Sattar and Gharabaghi 2015), group method of data handling (GMDH), and multivariate adaptive regression splines (MARS) technique can be mentioned. In these methods, during development process, more weight is attributed to inputs that have more influence on the output. Using multilayer perceptron neural network (MLP), ANFIS (Salmasi and Özger 2014) and GEP (Roushangar et al. 2014) have been reported for modeling energy dissipation of flow over stepped spillways. In this paper, mathematical expression of the relation between parameters involved in energy dissipation of flow over stepped spillways using the GMDH, MARS, and GP is considered. To developed mentioned techniques, results of a series of experiments that were conducted by authors on the hydraulic laboratory of soil conservation and watershed management research institute (Tehran, Iran) are used. To increase the reliability of modeling the results of similar experiments were collected and used, as well.

2 Materials and Methods

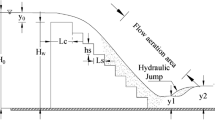
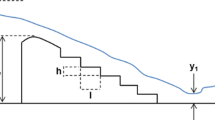
To define the effect of geometrical parameters involved in efficiency of stepped spillways, several investigations have been conducted. Figure 1 shows a sketch of stepped spillways. In this figure, height and length of steps are shown by h and l, respectively. Depth of flow over stepped spillways is shown by y 0; upstream specific energy is defined with E 0. Depth of flow at the toe of the dam is shown by y 1, and y 2 is the conjugate depth of flow at hydraulic jump. To calculate energy dissipation of flow over stepped spillways, Bernoulli equation is applied between the upstream and downstream of stepped spillway. Equations (1, 2) are used for calculation of upstream and downstream specific energies of flow.

$$E_{0} = H_{w} + y_{0} + \frac{{V_{0}^{2} }}{2g} = H_{w} + y_{0} + \frac{{q^{2} }}{{2g\left( {H_{w} + y_{0} } \right)}}$$
(1)
$$E_{0} = y_{1} + \frac{{V_{1}^{2} }}{2g} = y_{1} + \frac{{q^{2} }}{{2gy_{1}^{2} }}$$
(2)
Fig. 1
figure 1

Main parameters involved in energy dissipation in skimming flow over stepped spillways

Full size image

In these equations, q is the discharge per weir length, V 0 is the velocity of approached flow, and g is the acceleration gravity. Energy dissipation ratio (EDR) is calculated using Eq. (3).

$$\frac{\Delta E}{{E_{0} }} = \frac{{E_{0} - E_{1} }}{{E_{0} }} = 1 - \frac{{E_{1} }}{{E_{0} }}$$
(3)

Geometrical and hydraulic parameters involved in energy dissipation are arranged in Eq. (4) to determine those that affect EDR.

$$\frac{\Delta E}{{E_{0} }} = f\left( {q,l,h,H_{w} ,g,N} \right)$$
(4)

where H w is the height of dam and N is the number of steps. Salmasi and Özger (2014) used the Buckingham Π theory as the most famous dimensional analysis technique and derived dimensionless parameters effective on EDR as Eq. (5).

$$\frac{\Delta E}{{E_{0} }} = f\left( {\frac{{q^{2} }}{{gH_{w}^{3} }},\frac{h}{l},N,\frac{{y_{c} }}{h},Fr_{1} } \right)$$
(5)

In Eq. (5), q 2/gH 3 w is named drop number and shown by DN and h/l is declared as the slope of stepped spillway, and therefore, it is shown by S. Equation (5) can be rewritten as:

$$\frac{\Delta E}{{E_{0} }} = f\left( {{\rm DN},S,N,\frac{{y_{c} }}{h},Fr_{1} } \right)$$
(6)

Equation (6) is the foundation for developing soft computing methods. To develop soft computing methods including ANN, SVM, GMDH, MARS, and GP, in addition to obtained results of experiments conducted by authors, related datasets were collected from Salmasi and Özger (2014). The histogram of collected dataset is shown in Fig. 2.

Fig. 2
figure 2

Histogram of collected datasets related to energy dissipation

Full size image

Physical laboratory models of stepped spillways were constructed from the galvanized iron sheets. The main channel was 12 m long whose cross section was rectangular with 0.90 m depth and 0.60 width. The side walls of the channel were made of Plexiglas and its bed was made from well-pointed steel sheet. In order to control the formation of hydraulic jump, a sluice gate was set at downstream. The longitudinal slope of main channel was equal to 0.001. The depths of flow at upstream and downstream of the structure were measured by point gage with ±0.1 mm sensitivity. Discharge of flow was measured with a V notch weir that was installed at downstream for this purpose. Figure 1 shows a laboratory model. The properties of models are given in Table 1.

Table 1 Summary of models of stepped spillways and flow rates
Full size table

2.1 Review on ANN

Artificial neural network is a common type of soft computing technique composed of a number of neurons arranged in input, hidden, and output layers. Each neuron is an independent unit in the network where each input is multiplied by a specific weight and then introduced to it. Inputs for the first layer are the original dataset, and inputs for the second and next layers are the output of each neuron in previous layer. As stated earlier, inputs are multiplied by the weights and passed through transfer function that is given on each neuron. The most common types of transfer functions are Gaussian, sigmoidal and tansing. The output of each neuron is summed by a constant value called bias. The most famous types of ANNs are multilayer perceptron neural networks (MLP) that have been widely used in most areas of engineering, especially in hydraulic engineering. MLP usually includes three layers: the input layer used for introducing dataset, hidden layer(s) where main network computation is conducted, and output layer where the results of computation in hidden layer(s) are accumulated and presented. As stated, each input is multiplied by a weight for being introduced to a neuron, and then, results of acting transfer function on them are summed by a bias; the values of weights and biases for all neurons available in networks are validated using training algorithm. Training means adjusting the variables (weights and biases) to achieve the lowest difference between model output and observed data. Training MLP model can be performed using conventional methods such as Levenberg–Marquardt method. This subject can also be assumed as an optimization problem where modern optimization techniques can be applied to solve it. In this study, an MLP model was developed; the structure of which is shown in Fig. 3. In this model, tangent sigmoid and pure line functions were chosen as governing functions on neurons of hidden and output layers, respectively (Emamgholizadeh et al. 2014a, b), Emamgholizadeh et al. 2016.

Fig. 3
figure 3

Structure of multilayer perceptron neural network

Full size image

2.2 Review on SVM

Support vector machine is a Kernel-based technique that represents a major advance in machine learning algorithm. Support vector machine (SVM) is based on machine learning concept to maximize predictive accuracy; that is,

$$\begin{aligned} {\text{Minimize:}}\quad R_{\text{svm}} \left( {\omega ,\xi^{*} } \right) = \frac{1}{2}\left\| \omega \right\|^{2} + C\sum\limits_{i = 1}^{n} {\left( {\xi_{i} + \xi_{i}^{*} } \right)} \hfill \\ {\text{Subject}} \hfill \\ d_{i} - \omega \varphi \left( {x_{i} } \right) + b_{i} \le \varepsilon + \xi_{i} \hfill \\ \omega \varphi \left( {x_{i} } \right) + b_{i} - d_{i} \le \varepsilon + \xi_{i} \hfill \\ \xi_{i} ,\xi_{i}^{*} \ge 0,\quad i = 1, \ldots ,l, \hfill \\ \end{aligned}$$
(7)

where w is a normal vector, (1/2)‖ω‖2 is the regularization term, C is the error penalty factor, b is a bias, ε is the loss function, xi is the input vector, di is the target value, l is the number of elements in the training dataset, φ(xi) is a feature space, and ξ i and ξ * i are upper and lower excess deviations. The architecture of SVM is shown in Fig. 4. Famous kernel functions are denoted as follows.

Fig. 4
figure 4

Network architecture of SVM

Full size image
  1. 1.

    Linear kernel: K(x i , x j ) = x T i x j

  2. 2.

    Polynomial kernel: \(K\left( {x_{i} ,x_{j} } \right) = \left( {x_{i}^{\text{T}} x_{j} + \gamma } \right)^{d} ,\quad \gamma > 0\)

  3. 3.

    RBF kernel: \(K\left( {x_{i} ,x_{j} } \right) = \exp \left( { - \gamma \left\| {x_{i} - x_{j} } \right\|} \right)^{2} ,\quad \gamma > 0\)

  4. 4.

    Sigmoid kernel: \(k\left( {x_{i} ,x_{j} } \right) = \tanh \left( {\gamma x_{i}^{\text{T}} x_{j} + r} \right),\quad \gamma > 0\)

where variables xi and xj are vectors in the input space, and γ is the regularization parameter. Lagrange multipliers are presented as αi = αi − αi ∗. The accuracy of prediction is based on selection of three parameters, i.e., γ, ε, and C: the values of which are determined using firefly algorithm (Parsaie et al. 2016; Azamathulla and Wu 2011).

2.3 Review on GP

Genetic programming (GP) technique is a machine learning approach used for modeling input–output complex nonlinear systems that are based on dataset. Developing GP is based on the concept of genetic algorithm (GA). It means that the concepts used in genetic algorithm (GA) are repeated in GP such as genes, multigene, mutation. GP is also used to build a semiempirical formula from the input–output dataset; therefore, it often known as symbolic regression. GP creates the formula that consists of inputs variables and several mathematical operators, namely (+, −, /, and *) and functions, namely (ex, x, sin, cos, tan, lg, sqrt, ln, power). GP performs this process by randomly generating a population of computer programs (represented by tree structures) and then mutating and crossing over the best performing trees to create a new population. This process is continued until the formula is achieved with a suitable accuracy. Unlike classical regression analysis where the designer defined the structure of the empirical formula, GP automatically generates both the structure and the parameters of empirical formula. An individual multigene is comprised of one or more genes and is called GP tree. To improve the performance of fitness (e.g., to reduce a model’s sum of squared errors on a dataset), the genes are obtained incrementally. The final formula may be a weighted linear or nonlinear combination of each gene. The optimal weights for the genes are automatically obtained using ordinary least squares to regress genes against the output data (Azamathulla et al. 2010; Azamathulla et al. 2008).

2.4 Review on MARS

MARS, proposed by Friedman (1991), is a pliable method to amp the relationship between independent and dependent variables in a desired system. MARS method is used to recognize the hidden pattern in dataset in complex systems. Recognition of pattern is defined via proposing a number of coefficients and basic functions. These coefficients and basic functions are justified during regression operation on the used dataset. The main advantage of MARS includes its high ability for mapping input parameters and desired outputs, developing a simple but robust model and its being rational in terms of computational cost. MARS technique is based on simple basis functions defined as follows:

$$\left| {x - t} \right|_{ + } = \hbox{max} \left( {0,x - t} \right) = \left\{ {\begin{array}{*{20}c} {x - t} & {x > t} \\ 0 & {x \le t} \\ \end{array} } \right.$$
(8a)
$$\left| {t - x} \right|_{ + } = \hbox{max} \left( {0,t - x} \right) = \left\{ {\begin{array}{*{20}c} {t - x} & {x < t} \\ 0 & {x \ge t} \\ \end{array} } \right.$$
(8b)

where t denotes the knot. Basic functions are sometimes called mirrored pair functions. These functions are defined for each input variable such as Xj at observed dataset related to them. Sets of basic functions are defined as

$$C = \left\{ {\left( {x_{j} - t} \right)_{ + } ,\left( {t - x_{j} } \right)_{ + } } \right\};\left\{ {x_{1j} ,x_{2j} , \ldots ,x_{nj} } \right\},\quad j = 1, \ldots ,p$$
(9)

The general form of function derived from MARS model is written as an adaptive function as

$$y = \beta_{0} + \sum\limits_{i = 1}^{M} {\beta_{i} } {\text{BF}}_{i} \left( X \right)$$
(10)

where β 0 is constant, BF i (X) is known as basic function, and β i is the coefficient of basic functions. The constant and coefficient of derived function in MARS model are justified using least square error technique. M is the number of basic functions derived from the final stage of model development. Developing MARS model includes two stages. The first one is forward stage. In this stage, the number of basic functions increases to decrease the difference between the results of model and observed data. In the next step of model development, to avoid over-parameterization and over-fitting, pruning some of the basic functions is considered. In this stage, regarding cross-validation (GCV) criteria given below, basic functions are pruned.

$${\text{GCV}} = \frac{\text{SSE}}{{n\left( {1 - \left( {\frac{C\left( B \right)}{n}} \right)} \right)^{2} }}$$
(11.a)
$$C\left( B \right) = \left( {B + 1} \right) + dB$$
(11.b)

where SSE is the sum of square of residuals, n denotes the number of records, and C(B) defines difficulty criteria, which increases by the number of basic functions. For more information, see (Parsaie et al. 2016; Emamgolizadeh et al. 2015; Haghiabi 2016)

2.5 Review on GMDH

GMDH is a soft computing approach categorized in self-organizing methods developed by Ivakhnenko (1971). In this model, complex networks are gradually developed with regard to the performance of a combination of pairs of inputs and desired output. Each pair of inputs is introduced to a neuron in GMDH network. In the first hidden layer, all combinations of input pairs are evaluated. The number of neurons in the first hidden layer is calculated as shown below.

$$\frac{{N_{\text{inp}} \left( {N_{\text{inp}} - 1} \right)}}{2}$$
(12)

As stated, in the first hidden layer, each pair of inputs is introduced to a neuron in the governing equation on which is a quadratic polynomial function. In other words, each pair of inputs is passed through a quadratic polynomial function as

$$\overline{y} = G\left( {x_{i} ,x_{j} } \right) = w_{0} + w_{1} x_{i} + w_{2} x_{j} + w_{3} x_{i}^{2} + w_{4} x_{j}^{2} + w_{5} x_{i} x_{j}$$
(13)

where \(\bar{y}\) is the output of each neuron; x i and x j are the inputs; w 1,…,5 are the weights (coefficients); and w 0 is a bias (constant). G(x i , x j ) means that the governing function on neurons is only a proportional pair of inputs. Values of weights and biases are justified in training stage. Training means minimizing the difference between output of each neuron with observed data by adapting coefficients and constant of governing equation. To this end, conventional algorithms such as least square (LM) method can be applied. Training can be assumed as an optimization problem, and advanced modern optimization algorithms such as genetic algorithm (GA), particle swarm optimization (PSO) can be used to this end. The idea of using the quadratic polynomial function as transfer function governing neurons was taken from the Volterra functional series, which states a complete system can be estimated via infinite series of polynomial of inputs. This series is also known as Kolmogorov–Gabor polynomial; the general form of which is given below.

$$y = w_{0} + \sum\limits_{i = 1}^{n} {w_{i} } x_{i} + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {w_{ij} } } x_{i} x_{j} + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\sum\limits_{k = 1}^{k} {w_{ij} } } x_{i} x_{j} } x_{k} + \cdots$$
(14)

In development of GMDH, some concepts of GA algorithm, namely seeding, rearing, crossbreeding, selection, and rejection, have been used. In other words, only for developing the first hidden layer do all inputs participate. For developing the second hidden layer in GMDH network, inputs are selected based on their performance. This means that neurons with more accurate answer are selected. Figure 5 shows a sketch of GMDH model. As shown here, for developing the second and next hidden layer(s), neuron(s) with suitable performance in the previous layer are selected (Karbasi and Azamathulla 2016; Najafzadeh 2016; Najafzadeh and Azamathulla 2015; Najafzadeh and Barani 2011; Najafzadeh and Bonakdari 2016; Najafzadeh et al. 2016; Najafzadeh and Sattar 2015; Najafzadeh and Tafarojnoruz 2016; Najafzadeh and Zahiri 2015).

Fig. 5
figure 5

Schematic of GMDH model development

Full size image

3 Results and Discussion

Development of soft computing techniques is based on dataset. This means that the basic stage of modeling is data preparation. In this stage, dataset should be divided into two groups as training and testing. Assigning dataset to each group is performed with regard to random approach. It is notable that it is better to choose a range of groups near each other. The range of training and testing dataset is given in Table 2. Training encompasses 80% of dataset, and the rest (20%) is considered as testing dataset. Training and testing datasets are used for developing models given in materials and methods section. The next step of preparation of some models such as ANNs is designing the structure of model. Designing the structure includes choosing the number of hidden layer(s), the number of neuron(s) in each hidden layer, types of transfer functions on neuron, and learning algorithm. Learning means justifying the weights and biases in order to minimize the difference between the model outputs and observed desired data.

Table 2 Range of dataset assigned to stages of preparing soft computing models
Full size table

Developing ANN model is based on designer’s experiment. However, recommendations of a researcher who conducted similar studies are also very useful. In this study, preparing the multilayer perceptron neural network as a common type of ANN was developed based on recommendations of Azamathulla et al. (2016). They stated that to develop MLP model, after data preparation, designing the structure should be considered step by step. Based on these recommendations, initially one hidden layer is considered and then a number of neurons are chosen. There are different types of transfer functions. In this study, different types of transfer functions created in MATLAB software were tested. In the next step and after finding the proper transfer function, the number of neurons in the same hidden layer may increase in order to improve the performance of developed model. Another way to increase the performance of MLP is to increase the number of hidden layers. A summary of the development process is presented in Table 3. As given in this table, the tansig as transfer function has the best and most suitable performance compared to other tested functions. Models shown in row number four are chosen for predicting energy dissipation of flow over stepped spillways. As shown in this table, increasing the number of hidden layers does not have a significant effect on increasing the model accuracy. It is notable that the proposed MLP model was trained using LM method. Results of MLP model in training and testing stages are shown in Figs. 6 and 7. In these figures, the outcome of MLP model is shown versus the observed data.

Table 3 Summary of performance of MLP model during development stage
Full size table
Fig. 6
figure 6

Results of proposed applied models in training stage

Full size image
Fig. 7
figure 7

Results of proposed applied models in testing stage

Full size image

Development of SVM is similar to MLP model. This means that to prepare SVM, the first step is data preparation. In this study, the same dataset used for developing MLP was used for preparation of SVM. The next step of preparing SVM is designing the structure. One subroutine of designing is choosing transfer function. In this study, the structure of SVM developed for prediction of energy dissipation is given in Fig. 4. Four kernel functions are given in the review on SVM section were tested. Training SVM can be used as optimization problem. To perform this task, quadratic optimization method is used. A summary of testing kernel functions is given in Table 4. As illustrated in this table, RBF has the best performance among tested transfer functions. The value of parameters of kernel function including Gamma value = 33,391.97 and C = 47.61 was obtained in preparation stages. Results of SVM in training and testing stages are given in Figs. 6 and 7.

Table 4 Summary of performance of kernel functions
Full size table

As stated in the review on GP section, GP is a smart function fitting method. The main point in smart function fitting is related to assigning more weight to inputs that are more effective on output. To develop GP model for mathematical expression of involved parameters on energy dissipation ratio, input parameters regarding Eq. (6) (i.e., inputs: DN, S, N, y c /h, Fr and output: ΔE/E 0) were used. It is notable that in this study, training dataset used for development of ANN and SVM was used for developing GP and testing dataset is used for evaluating the derived model. To develop GP, mathematical operations including [summation (+), mines (−), multiply (×), and division (÷)] and a number of mathematical functions such as (times, minus, plus, square, tanh, exp) were applied. To derive a suitable model, several generations were performed. To derive a suitable model based on GP, the same approach considered for developing ANN was considered for using GP. The number of genes increased one by one and mathematical functions were added one by one. Results of values of justified parameters in GP are given in Table 5.

Table 5 Justified parameters of GP model
Full size table

General form of derived model from GP is \(\Delta E /E_{0} = w + \sum\nolimits_{i = 1}^{n} {\alpha_{i} {\text{gene}}_{i} }\). In this equation, w is the bias and α i is the weight of each gene. Results of derived model are expressed as Eq. (15). The structure derived from GP is given in Fig. 8. As shown in this figure, there are five genes available in derived model. Results of derived model from GP in training and testing stages are given in Figs. 6 and 7. As stated in GP model description, GP is a smart fitting function method. Reviewing the structure of derived model genes shows that the ratio of critical depth to step height, drop number, and the number of steps and drop number appear in most genes. Comparing the performance of MLP and SVM shows that GP has accuracy close to MLP; however, the performance of SVM is slightly better than GP.

$$\begin{aligned} \frac{\Delta E}{{E_{0} }} = & 87.75 + 3.095\frac{{y_{c} }}{h} + 3.095N - 0.02761\,{\text{square}}\,\left( {N + 9.532} \right) \ldots \\ - 49.14\tanh\,\left( {\frac{{y_{c} }}{h}} \right) + 3.095{\rm DN} \times S - 8.666Fr_{1} {\text{DN}} \times {\text{square}}\,\left( {Fr_{1} } \right) \ldots \\ - 1.963Fr_{1} \frac{{y_{c} }}{h}\tanh \left( {Fr_{1} \, } \right) \\ \end{aligned}$$
(15)
Fig. 8
figure 8

Structure of derived model from GP

Full size image

Developing GMDH as smart fitting function similar to other types of soft computing techniques such as MLP, SVM, and GP is based on dataset. The same dataset used for preparation of MLP, SVM, and GP was used to develop GMDH. As stated in the review on GMDH section, the number of neurons in the first layer is equal to 10. However, some of them do not deserve to attend the next layer. Each neuron is trained using training dataset and then assessed using testing dataset. Being selected to attend in the next layer is according to performance of neurons in the previous layer. Results of selected neuron in each layer are shown in Fig. 9. Values of justified coefficients and biases of equation of selected neurons are presented in Table 6. As shown in Fig. 9, proposed model includes three hidden layers. Reviewing the structure of developed model indicated that the most effective parameters for modeling energy dissipation of flow over stepped spillways are Fr 1, DN, and y c /h. Results of developed GMDH model in training and testing stages are presented in Figs. 6 and 7. Comparing the performance of developed GMDH model with MLP, SVM, and GP shows that the accuracy of GMDH is slightly better than MLP and GP; SVM is more accurate compared to GMDH.

Fig. 9
figure 9

Structure of developed GMDH model

Full size image
Table 6 Results of adjusting parameters of transfer function of GMDH model
Full size table

Preparation of MARS model similar to MLP, SVM, GP, and GMDH is based on dataset. The same dataset used for developing applied models was used to prepare MARS model. Developing MARS model, as stated in the section of review on MARS, includes two stages of growing and pruning. In growing stage, 30 basic functions were considered and in the next stage (pruning stage) 17 basic functions were pruned. At the end, optimal MARS model with 13 basic functions was derived. The inclusive form of obtained MARS model is given in Eq. (16). Extended form of MARS model is given in Table 7. The pruning criteria introduced with GVC parameter in development of MARS model were derived equal to 0.0021. As mentioned in the review on MARS model, each basic function has a coefficient and a constant which is adjusted in MARS model development process and derived using least square method.

$${\text{EPR}} = - 2321.246 + \sum\limits_{M = 1}^{13} {\beta_{m} } h_{m} \left( x \right)$$
(16)
Table 7 Basic functions and related coefficients of MARS model
Full size table

Input parameters were considered regarding Eq. (5). This implies that DN, S, N, y c /h, and Fr 1 were considered as inputs and ΔE/E 0 as output. Results of MARS model during model development (preparation and testing) are shown in Figs. 6 and 7. As seen in these figures, MARS model has a high ability for modeling energy dissipation over stepped spillways. Comparing the results of MARS with MLP, SVM, GP, and GMDH shows that MARS is more accurate. Reviewing Table 7 shows that Fr 1 and DN are the most important parameters for modeling and predicting energy waste of flow over stepped spillways. This obtained point also upheld the results of GP.

Fig. 10
figure 10

Histogram of errors of applied models in training stage

Full size image
Fig. 11
figure 11

Histogram of errors of applied models in testing stage

Full size image
Fig. 12
figure 12

Results of DDR index of applied models in training stages

Full size image
Fig. 13
figure 13

Results of DDR index of applied models in testing stages

Full size image

Evaluation of performance of applied models regarding standard error indices provided an average value of errors of models. To provide more information about the distribution of errors through the dataset two famous approaches including histogram of errors and calculating the developed discrepancy ratio (DDR) index have been proposed. In this study, the histogram of errors of each model in development and evaluation stages of preparation are proposed, as shown in Figs 10 and 11. Histogram of errors of MLPNN shows that most errors are accumulated in the range of -20 to 20 percent in training and -15 to 25 percent for testing stage. Results of histogram of errors of SVM show that most errors are accumulated in the range of -20 to 20 percent for training and -10 to 10 percent for testing. Histogram of errors of GMDH shows that errors are accumulated in the range of -20 to 20 percent in training and -12 to 10 percent in testing stage. Our assessment of histogram of errors of applied models shows that the minimum range of error is related to MARS model. To provide an introductory view about the reliability of applied models, it is better to calculate the DDR index. The DDR index is defined as the ratio of outcome of models to the observed data. Ranges of DDR index for applied models in training and testing are given in Figs 12 and 13. As shown, the lowest DDR index is for the MARS model. This indicates that the results of MARS model are more reliable compared with others.

4 Conclusion

In this paper, energy dissipation of flow over stepped spillways was modeled and predicted using powerful soft computing techniques including multilayer perceptron neural network, support vector machine (SVM), genetic programming (GP), group method of data handling (GMDH), and multivariate adaptive regression splines (MARS). MARS, GP, and GMDH were categorized as smart function fitting techniques which, in addition to developing a network, also propose a smart function. Properties of MARS, GP, and GMDH in terms of smart fitting function cause more weight to be assigned to inputs that are more affective on output. Results of all developed models indicated that those with suitable performance predict the ratio of energy dissipation. However, MARS model is more accurate compared to others. Reviewing the structure of obtained models from GP, GMDH, and MARS techniques revealed that drop number, number of steps, and ratio of the critical depth to the height of steps are the most effective parameters on energy dissipation ratio.