Application of Probabilistic Particle Swarm in Optimal Design of Large-Span Prestressed Concrete Slabs

Abstract

In this paper, a new modified particle swarm optimization (PSO) algorithm is utilized in optimal design of large-span prestressed concrete slabs. The modification is performed by adding some probabilistic coefficients to the velocity of particles, and it is called probabilistic particle swarm optimization (PPSO). These coefficients provide simultaneous exploration and exploitation for the algorithm, and decrease dependency of PSO on its constants. To examine the robustness of the enhanced algorithm, the model of a large-span prestressed concrete slab is generated using SAP2000 and is linked to the considered metaheuristic code to provide an optimal design. Results of PPSO are compared to those of the PSO and harmony search. A better performance of the PPSO is shown compared to the metaheuristics considered. PPSO is shown to converge faster and results in lower weight. Furthermore, a parametric study shows that the PPSO is less sensitive to the inertia weight.

1 Introduction

Prestressed concrete slabs are efficient systems for covering the long spans where placing columns interrupts the serviceability of the structure. For instance, audiences, parking lots, hotels, airports, etc., are examples of such structures in which columns may cause problems for the users. Prestressed concrete slabs provide floor scheme with smaller thickness which not only reduces the cost of the structure, but also decreases the mass of the structure; as a result, the earthquake effects can be decreased.

In recent decades, metaheuristic algorithms have been applied to many structural problems, and floor systems are no exception. Kaveh and Shakouri Mahmud Abadi (2010) utilized IHS for optimal design of composite floor systems; in the case of optimal design of prestressed concrete floor systems, the work of Rozvany and Hampson (1963) is one of the pioneering attempts. MacRae and Cohn (1987) used a nonlinear programming and conjugate direction method as optimization algorithm along with equivalent load method as the analysis method to achieve this goal. Kuyucular’s (1991) attempt was to minimize the weight of prestressing cables by considering several predefined cable profiles for each section. He also used a combined finite element method and equivalent load method for structural analysis. Lounis and Cohn (1993) considered two objective functions to be minimized consisting of the cost and initial camber. One of these functions was used as the objective function, and the other was treated as a constraint for ε-constraint approach. In sum, they employed a projected Lagrangian algorithm for optimization and a sectional stress analysis and force-in-tendon method for analysis of floor slabs. Based on the work of Semelawy et al. (2012), a concrete slab was modeled using a consistent triangular shell element that was originally developed by Koziey and Mirza (1997). Steel tendons are modeled as a discrete integral part of the shell element. Direct search heuristic optimization techniques, such as genetic algorithms, and multiobjective optimization techniques are utilized. Sharafi et al. (2012) considered a heuristic approach for optimum cost and layout design of 3D reinforced concrete frames. Sharafi et al. (2013) worked on the cost optimization of column layout design of reinforced concrete buildings. Kaveh et al. (2014) used PSO and recently developed PSOHS algorithms for performance-based optimal design of RC shear walls. Based on the work of Sharafi et al. (2014), a continuous reinforced concrete beam by considering geometric design optimization for its dynamic response was modeled.

Metaheuristic optimization algorithms, due to fewer limitations of application, have attracted many researchers (Kaveh 2014). One of the robust metaheuristic algorithms is particle swarm optimization, PSO, proposed by Eberhart and Kennedy (1995). The capability of searching in a continuous feasibility space, easy implementation, and not being trapped in a local minimum are the main characteristics of this algorithm. Other applications of PSO can be found in Kaveh and Malakouti Rad (2010) and Kaveh and Laknejadi (2011). However, the lack of balanced exploration and exploitation and shortcoming in dealing with the violated particles from feasibility boundaries reduce its robustness significantly. To remove these problems, a linearly varying inertia weight was introduced by Shi and Eberhart (1998) that provided a balanced exploration and exploitation, and a harmony search (Geem et al. 2001)-based algorithm for violation handling was proposed by Kaveh and Talatahari (2009). Some other applications of HS can be found in Kaveh and Shakouri (2010) and Kaveh and Ahanghran (2012).

The capability of searching in a continuous feasibility space, easy implementation, and not being trapped in local minima are the main characteristics of this algorithm. However, the velocity updating scheme utilized in the classical PSO has a steady form and hence does not provide exploration and exploitation which are necessary to most of the optimization processes. To remove this problem, Kaveh and Nasrollahi (2014) and Kaveh and Nasrollahi 2014) proposed a probabilistic PSO algorithm, called PPSO. The PPSO performs global or local search with a predefined probability and thus provides two phases of search for the algorithm simultaneously in all the iterations.

The main objective of the present study is to apply PPSO to the design of large-span prestressed concrete slabs. The commercial SAP2000 analysis package is employed to facilitate the analysis procedure. Furthermore, to examine the efficiency of the improvements, results of the PPSO are compared with those of PSO and HS algorithms.

2 A Probabilistic Particle Swarm Optimization Algorithm

2.1 Background

Great effort has been put into creating and improving various metaheuristic optimization algorithms, and this has led to various powerful tools in this field. Many biological and social interactions between natural systems and many physical laws are utilized in optimization algorithms (Kaveh 2014). On the other hand, many special concepts such as how to deal with violated variables from feasible search space, balancing global and local searches, and how to handle the constraints are developed to enhance the quality of the obtained solution. Each algorithm has its own characteristics, and none of them is perfect. Utilizing these useful tools in one algorithm can lead to a better optimization algorithm. Elements of an optimization problem are: (a) cost function, (b) design variable (solution), (c) constraints, and (d) search space. The relations between the above-mentioned elements are as follows:

$$ {\text{Minimize:}}\, \, f(x) $$

(1a)

$$ X = \left\{ {x_{1} , x_{2} , \ldots ,x_{p} } \right\} $$

(1b)

$$ {\text{Subjected}}\,{\text{to:}}\,\left\{ {\begin{array}{*{20}l} {g_{1} (X) \le 0} \hfill \\ {g_{2} (X) \le 0} \hfill \\ \ldots \hfill \\ {g_{m} (X) \le 0} \hfill \\ \end{array} } \right.,\quad {\text{Subjected}}\,{\text{to}}\,\left\{ {\begin{array}{*{20}l} {h_{1} (X) \le 0} \hfill \\ {h_{2} (X) \le 0} \hfill \\ \ldots \hfill \\ {h_{n} (X) \le 0} \hfill \\ \end{array} } \right. $$

(1c)

$$ {\text{In}}\,{\text{which:}}\,X_{\hbox{min} } \le X \le X_{\hbox{max} } $$

(1d)

where f(X) is the cost function; X is the design vector (solution) consisting of p independent variables $x_{1}$, $x_{2}$, …, and $x_{p}$; $g_{1} (X)$, $g_{2} (X)$, …, and $g_{m} (X)$ are $m$ unequal constraints; $h_{1} (X)$, $h_{2} (X)$, …, and $h_{n} (X)$ are $n$ equal constraints; and $X_{\hbox{min} }$ and $X_{\hbox{max} }$ are minimum and maximum feasible design vectors; therefore, Eq. (1d) denotes the feasible search space of the problem. Note that there is no relation between $p$, $n$, and $m$.

Steps of most of the metaheuristic algorithms are as follows:

• 1. Initialization Most of the metaheuristic algorithms need a population of initial solutions. Usually, these initial solutions are produced randomly in the search space.

• 2. Searching for a better solution in the feasible search space Having random initial solutions, the existing solutions should be updated using a logical manner. This process is called searching. In this step, solutions are updated iteratively using a search engine which is inspired from nature or physics.

To reach a good solution, search engine of each algorithm should provide two main phases which are (a) exploration (diversification or global search) and (b) exploitation (intensification or local search). At initial iterations, the algorithm should perform a global search and cover the whole search space. In this stage, some points that are expected to be near the global minimum of the cost function are found. Then at the latest iterations, the algorithm should perform a local search using the solution vectors found so far to increase the precision of the solution. In every metaheuristic algorithm, there should be a balance between exploration and exploitation. Further exploration diversifies the optimization process and brings down the precision of the solution. On the contrary, further exploitation intensifies the optimization process and the risk of finding a local optimum instead of a global optimum increases.

• 3. Stopping criteria There are some criteria to finish the iterative process. Some of these are:

  • Maximum number of iterations: The optimization process is terminated after a fixed number of iterations, for example 1000 iterations.

  • Number of iterations without improvement: The optimization process is terminated after some fixed number of iterations without any improvement.

  • Minimum objective function error: The difference between the values of the best objective function and the global optimum is less than a prefixed anticipated threshold.

  • Difference between the best and the worst solutions: The optimization process is stopped if the difference between the objective values of the best and the worst solutions becomes less than a specified accuracy (Geem et al. 2001).

2.2 Standard PSO

Particle swarm optimization (PSO) is a multiagent metaheuristic algorithm. It uses a velocity vector to update the current position of each particle in the swarm. The velocity vector is updated using a memory in which the best position of each particle and the best position among all particles are stored, and it can be considered as an autobiographical memory. Therefore, the position of each particle in the swarm adapts to its environment via flying in the direction of the previous velocity vector, the best position of whole particles, and the best position of particle itself. This mechanism provides the search of the PSO. The position of the ith particle at iteration k + 1 can be calculated as:

$$ x_{k + 1}^{i} = x_{k}^{i} + v_{k + 1}^{i} \cdot\Delta t $$

(2)

where $x_{k + 1}^{i}$ is the new position; $x_{k}^{i}$ stands for the ith particle’s position at iteration k; $v_{k + 1}^{i}$ represents the updated velocity vector of the ith particle; and $\Delta t$ is the time step which is considered as unity. The velocity vector of each particle is determined as:

$$ v_{k + 1}^{i} = w \cdot v_{k}^{i} + c_{1} \cdot r_{1} \cdot \frac{{\left( {p_{k}^{i} - x_{k}^{i} } \right)}}{{\Delta t}} + c_{2} \cdot r_{2} \cdot \frac{{\left( {p_{k}^{g} - x_{k}^{i} } \right)}}{{\Delta t}} $$

(3)

where $v_{k}^{i}$ is the velocity vector at iteration k; $r_{1}$ and $r_{2}$ are two random numbers between 0 and 1; $p_{k}^{i}$ represents the best ever position of ith particle, local best; $p_{k}^{g}$ is the global best position in the swarm up to iteration k; $c_{1}$ is the cognitive parameter; $c_{2}$ is the social parameter; and $w$ is a constant named inertia weight.

With the above description of PSO, the algorithm can be summarized as follows:

• 1. Initialization

Initial position, $x_{0}^{i}$, and velocities, $v_{0}^{i}$, of particles are distributed randomly in feasible search space using Eqs. (4) and (5).

$$ x_{0}^{i} = x_{\hbox{min} } + r \cdot \left( {x_{\hbox{max} } - x_{\hbox{min} } } \right) $$

(4)

$$ v_{0}^{i} = \frac{{x_{\hbox{min} } + r \cdot \left( {x_{\hbox{max} } - x_{\hbox{min} } } \right)}}{{\Delta t}} $$

(5)

where r is a random number uniformly distributed between 0 and 1; $x_{\hbox{min} }$ and $x_{\hbox{max} }$ are minimum and maximum possible variables for the ith particle, respectively.

• 2. Solution evaluation

Evaluate the objective function value for each particle, $f(x_{k}^{i} )$, using the design variables correspond to iteration $k$.

• 3. Updating memory

Update the local best of each particle, $p_{k}^{i}$, and the global best, $p_{k}^{g}$, at iteration $k$.

• 4. Updating positions

Update the position of each particle utilizing its previous position and updated velocity vector as specified in Eqs. (2) and (3).

• 5. Stopping criteria

Repeat steps 2–4 until the stopping criteria are met.

2.3 Probabilistic Particle Swarm Optimization Algorithm

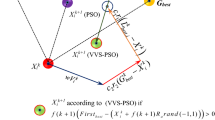
This section presents a recently developed variant of the PSO algorithm including probabilistic global and local search mechanisms. For this purpose, some probabilistic functions are added into the standard PSO formulation. Doing this, three various searches are performed in all iterations: (1) global search; (2) local search toward the global best; and (3) local search toward the combination of global and local bests. The new optimization algorithm utilized in this research is termed probabilistic particle swarm optimization (PPSO). In PPSO, the velocities of particles are updated as follows:

$$ v_{k + 1}^{i} = \alpha \cdot w \cdot v_{k}^{i} + \beta \cdot c_{1} \cdot r_{1} \cdot \frac{{\left( {p_{k}^{i} - x_{k}^{i} } \right)}}{{\Delta t}} + \gamma \cdot c_{2} \cdot r_{2} \cdot \frac{{\left( {p_{k}^{g} - x_{k}^{i} } \right)}}{{\Delta t}} $$

(6)

where $\alpha$, $\beta$, and $\gamma$ are probabilistic functions and are defined as:

$$ \left\{ {\begin{array}{*{20}l} {\alpha = r\;{\text{and}}\; \beta = 1 , \gamma = 1.} \hfill & {{\text{if}}\; p < p_{1} } \hfill \\ {\alpha = 0, \,\beta = 1,\, \gamma = 0. } \hfill & {{\text{if}}\;p_{1} \le p \le p_{2} } \hfill \\ {\alpha = 0 ,\,\beta = 0,\,\gamma = 1.} \hfill & {{\text{if}}\;p > p_{2} } \hfill \\ \end{array} } \right. $$

(7)

where p is a random number in the interval [0, 1]; $p_{1}$ and $p_{2}$ are predefined levels of probabilities set by the user, and they can be determined using a trial-and-error or parametric study; $\beta$ and $\gamma$ are parameters for selection of the type of search. $\beta = 1$ provides local search toward local best, and $\gamma = 1$ provides local search toward global best. Thus, the values of $\beta$ and $\gamma$ are selected to be 0 or 1. On the other hand, $\alpha$ controls the amount of global search and it should be chosen randomly from a range of real numbers rather than 0 or 1.

PPSO can simultaneously perform global and local searches. This approach is a step further toward the common belief that metaheuristic algorithms should perform only global search in the initial iterations and only local search in the final iterations. However, if a particle is close to the global optimum in the early stages of the optimization process, global search may force that particle to fly away from such a good position. As a result, the optimization algorithm becomes less robust. By setting $\alpha$ as a random number, exploration and exploitation can simultaneously be performed in all iterations: Global search will be performed for some particles, while other particles will perform local search. Therefore, if a better location is found, it is saved as the local or global best, and in the subsequent iterations that particle may commit in a global search, while it has a better local best; as a result, the overall performance of the algorithm will be improved using this search strategy. Furthermore, $\beta$ and $\gamma$ provide two different local searches toward local best and global best, respectively. This variety in exploitation may lead to finding better points when near optimum is being searched.

3 Formulation for Optimal Design of Prestressed Concrete Slabs

In general, cost function, constraints and feasible search space are three main components of an optimization problem. In optimal design of prestressed concrete slabs, it is desirable to minimize the cost of materials and construction which in this paper consists of the costs of concrete and tendon. Therefore, the cost function is defined as:

$$ F(X) = C_{\text{c}} \cdot V_{\text{c}} + \mathop \sum \limits_{i = 1}^{n} C_{\text{s}} \cdot L_{\text{s}} $$

(8)

where $F(X)$ is the cost function; $C_{\text{c}}$ stands for the cost of concrete per volume including the cost of material and forming; $V_{\text{c}}$ represents the total volume of the concrete; n is the number of tendons in two directions; $C_{\text{s}}$ is the cost of steel per unit meter including the cost of material and forming; and $L_{\text{s}}$ is the total length of tendons.

In Eq. (8), $X$ is the design variable vector and consists of: (1) thickness of slab (t), (2) number of tendons in x-direction (N _x ), (3) number of tendons in y-direction (N _y ), (4) diameter of tendons in the x-direction (d _x ), (5) diameter of tendons in y-direction (d _y ), (6) tendon eccentricity at one end of the slab (e ₁), (7) tendon eccentricity at the other end of the slab (e ₂), (8) tendon eccentricity at middle of the slab (e ₃), (9) allowable tensile stress of tendons ($S_{\text{tendon}}$). These variables are delineated in Figs. 1 and 2.

Fig. 1

Eccentricity of tendons in the considered problem

Fig. 2

Cross section: tendons located between A and B, and the considered cover dc

In order to meet Canadian Standard Association (CSA) requirements, constraints are based on those provided in Table 1. A penalty function approach is employed to meet the constraints.

Table 1 Constraints of prestressed concrete design based on CSA

4 Numerical Example

A large-span prestressed concrete slab example is considered to be designed using the PPSO and the above-mentioned formulation. This problem is solved using PSO, PPSO, and HS algorithms to examine the PPSO both in terms of performance of the PPSO compared to some other algorithms and formulation proposed for prestressed concrete slab. The considered problem is optimal design of a 10 m × 10 m prestressed concrete slab with an edge beam of 100 cm depth and 80 cm width. The slab is supported by columns at four corners with dimensions of 80 cm × 80 cm. Moreover, the concrete cover on tendons is considered to be equal or more than 40 mm. The geometry of the slab is schematically shown in Fig. 3, and the positions of the tendons are also illustrated in Fig. 4. The applied loads are determined based on a typical residential structure as: slab and other elements self-weight made of reinforced concrete with specific weight of 24 kN/m³, and dead and live surplus loads of 2.40 kN/m² imposed on the slab. The concrete compressive strength, $f_{\text{c}}^{{\prime }}$, is 40 MPa, and tensile yielding stress of tendons, $f_{y}$, is 186 MPa. The cost of concrete and tendons are included in Table 2; moreover, the feasible range of each variable is presented in Table 3.

Fig. 3

Schematic view of slab and edge beams

Fig. 4

Positions of tendons in the considered problem

Table 2 Cost of materials

Table 3 Upper and lower limits for variables

Since all metaheuristic algorithms are sensitive to the constant parameters and random initialization, in order to reach the best result, several values are considered for inertia weight, $w$, which are 0.5, 1.0, 1.5, and 2. Also, all algorithms are run 20 times for each value to compensate the effect of random initialization. Both $c_{1}$ (cognitive parameter) and $c_{2}$ (social parameter) are set to one in both PSO and PPSO algorithms.

The best result obtained by PPSO is compared with those of PSO and HS in Table 4. It is observed from the table that the best result associated with PPSO is $3787.6, while the best result of PSO and HS is 3998.8 and 4678.51, respectively. Moreover, the convergence history of the PSO, HS, and PPSO shows that although PSO and HS need fewer analyses to achieve the optimum design, these do not provide designs as good as PPSO. This fact is due to a lack of exploitation in PSO and HS. Based on Fig. 5, PSO and HS stop searching when the number of analyses is less than 200, while PPSO continues searching in more than 400 analyses in the form of local search which can be seen through Figs. 5 and 6; as a result, it provides better results. Small variations of the results in the middle and the end of convergence history graph denote local search, which is observed only in PPSO’s diagram. Moreover, as we can see in Figs. 7 and 8, the results of the PPSO are less parameter dependent than those of the PSO and this can be the reason of the existing difference between the final penalized cost value for the best result of PSO and for the average of 20 of the best results of PSO which is clearly visible from Fig. 7.

Table 4 The best results for HS, PSO, and PPSO

Fig. 5

Convergence history of the best runs of the PPSO, PSO, and HS

Fig. 6

Logarithmic convergence history of the best runs of the PPSO, PSO, and HS

Fig. 7

Average of 20 of the best independent runs of the PSO and the best run of the PSO

Fig. 8

Average of 20 of the best independent runs of the PPSO and the best run of the PPSO

Considering Table 4, the obtained penalized cost using PSO is $3998.80. In the case of PPSO, the penalized cost is $3787.60 for all values of w, which is 5.28 % less than the best result of PSO. Among the considered algorithms, HS has the worst result which is $4678.51. Also, the active constraint is the stress in concrete.

The ratios of penalized cost function to the best obtained cost function of each algorithm are presented in Table 5 for different values of w. According to this table and Fig. 9, it can be concluded that the dependency of PPSO on w is far less than that of the PSO; as a result, PSO necessitates examining the algorithm with different values for w to ensure an optimum result, while all values of w secure a desirable design scheme when PPSO is utilized as the optimization algorithm.

Table 5 The ratio of PSO/PSO_best and PPSO/PPSO_best for different values of w

Fig. 9

Comparison between the best results of the PSO and PPSO

To examine the impact of P ₁ and P ₂ on the results, a parametric study is performed using w = 1.0 and different values of P ₁ and P ₂, and the results are presented in Table 6. It can be observed from this table that P ₁ in the range of 0.2–0.4 and P ₂ in the range of 0.7–0.8 provide the best results.

Table 6 Best results for PPSO considering different values of P ₁ and P ₂

5 Conclusion

In this study, optimal design of prestressed concrete slabs is performed using PSO and its recently modified version, PPSO. The results obtained by PSO depend significantly on the constant value of inertia weight (w), which controls the diversity (global search) of the algorithm, and there is no unified approach to determine w. On the other hand, PPSO uses a variety of w in each iteration via probabilistic function $\alpha$; therefore, it is not necessary to determine w to achieve the best results. Moreover, probabilistic functions $\beta$ and $\gamma$ provide various local searches; as a result, both global and local searches are improved using these functions. To examine the efficiency of the PPSO in design procedure of long-span prestressed concrete slabs, a large-scale slab is considered for optimal design based on the CSA. Results indicate that the PPSO is less susceptible to the value of w, and a desirable design scheme is achieved regardless of the value of w being employed. In addition, when probabilistic functions are added, local search of the PSO is improved significantly. A parametric study is also conducted to examine various ranges of P ₁ and P ₂ and find the best range for design of large-span prestressed concrete slab problems.