Mathematical design and preliminary mechanical analysis of the new lattice structure: “GE-SEZ*” structure processed by ABS polymer and FDM technology

Abstract

In this study, the authors propose a new design of a novel class of lattice structures. The new design is based on two main geometrical properties, the “volume” and the “surface to volume ratio”. It takes advantage of the strongest column designed against buckling proposed by Keller (Arch Ration Mech Anal 5:275–285, 1960) and Seiranyan (J Appl Math Mech 51(2):272–275, 1987). The Schoen minimal gyroid is used as a reference to establish the necessary lightweight property of the proposed design. This is to say, the surface to volume ratio and the volume of the new class of structures and their gyroid equivalent are equal. Models are built using CAD software and printed with UP mini 2.0 using acrylonitrile butadiene styrene (ABS) copolymer. Moreover, compression tests are conducted, using “MTS Criterion—Model 45”. The results show that after the phases of elasticity, relaxation and plasticity, the structure (three samples) is stable in the sense that it did not buckle nor collapse. Furthermore, reaching 7.35 mm of platen displacement (14.7% of strain) and 7.5 kN of resistance (3 MPa of equivalent stress), an additional progressive hardening is observed due to material densification and friction phenomena. A normalized comparison between the proposed structure and several lattice structures is conducted, showing a higher competitive behavior of the new design. The results of this study could possibly be a major contribution in the fields of biomechanics, aeronautic, and mechanical parts design.

1 Introduction

To cut costs, certainly engineers tend to develop lightweight structures [1] with precise physico-chemical and mechanical characteristics for specific uses. Reverse engineering, retro-engineering, and well thought-out designing have been the main contributors to multi-criteria optimization strategies. Such strategies include technical constraints related to mass production and quality of products vis-à-vis the production rate [2], and the reliability of the production tools [3, 4]. These criteria are important parameters in the global product-process design [2, 5,6,7]. Likewise, the final use and products recycling are equally important criteria [2].

At the outset of the twentieth century, Taylor set out to develop his own industrial approach where he transformed all the labor aspects in terms of time and cost indicators [8]. Every manufacturing process was then analyzed from the “added value” prospective. Nowadays, different industrial engineering tools have been designed to evaluate and optimize the added value of a given process [9]. Additive manufacturing technologies have been seeking optimal solutions for unit costs versus production volume [10]. Additionally, 3D printing technologies have been offering substantial flexibility to production methods [11]. Therefore, producers can efficiently adopt more complex functional design and geometries, while minimizing processing complications, assembling time, and at the same time mitigating various technical constraints [12,13,14].

In actuality, in the last years, the topology optimization (TO) and generative design (GD) have more often been used in both multi-objective and multi-criteria contexts, enforcing an increase of the part design complexity [15,16,17,18]. It must be noted that additive manufacturing leads to find the compromise between part complexities and manufacturing flexibility for series or unit production.

General speaking, the GD attempts to reach a minimum of matter with a maximum of rigidity [19, 20]. The optimization procedures make use of specific objective functions to perform some minimization tasks, such as the mass of the parts or the potential energy of the deformed volume [19] while others use the surface of the analyzed body [21]. Results of the TO procedures are given in terms of matter density distribution from 0 (voids) to 100% (solid material). Hereafter, the designed parts are seen as complex and irregular lattice structures [16, 20] where other structures are necessarily optimized in terms of minimum thickness or fiber orientation of each element depending on the sector of application of the designed parts [19]. Thus, lattice structures are seen to present a very interesting compromise between mechanical functionalities and lightness properties. Important amount of research is produced in the past few years to characterize these types of structures to link the mechanical behavior to materials and geometry aspects.

In this context, the present study proposes a new lattice structure design that will be mechanically tested. The corresponding parts were produced by the fused deposit modeling (FDM) that are considered as 3D printing extrusion technique according to ISO 52900 standard. The main objective of the proposed design is to obtain a family of high compressive lightweight (HCLW) structures.

The rest of the paper will be organized as follows: the next section will discuss related works; the third section will be devoted to the methodology; the fourth section is dedicated to the mathematical modeling of the proposed family of structures; the fifth section will discuss the results of the experiments; and the last section will present the conclusion.

2 Related works in topology optimization

Cellular materials have been used for centuries in a wide variety of applications and are common in natural materials, such as wood, bone, sponge and coral [22]. These structures are composed of a huge number of planar or linear elements that are organized in stochastic or non-stochastic (regular) ways [23]. Gibson and Ashby [24] grouped several examples and engineering case studies regarding cellular materials and the ways to exploit them in engineering design [24]; the processing of such structures is also detailed in the book. Furthermore, the functional design and processing of the cellular and lattice structures have been studied for multiple uses and in industrial areas. Depending on the required precision in each industry, material development is seen from nanometric, mesoscopic, and macroscopic standpoints. A case in point is the design and processing of the membranes as lattice and porous structures for the process industry (filtration, depollution, chemical industries, and so forth) are studied on nanometric and mesoscopic scales [25,26,27]. In automotive, aeronautics and other mechanical fields, the majority of lattice structures are presented as macroscale trusses (bars assembly) or plans networks that are generated by TO using some specialized software and numerical procedures [15, 19, 23].

In the classical design, the shape or the architecture of the parts are more or less fixed depending on the level of design and calculation adopted by engineers. Classically, the improvement of structures is based upon specific hand modifications applied on the parts to ensure technical constraints determined in the functional analysis phase of design or in the optimization loop. In fact, in hand improvement, the structure architecture is modified step by step to determine the limit states defined in the preliminary design’s steps. Currently, the possibility of automation of the TO leads researchers to test several constrained optimization criteria, and hence choose the best. TO can be observed as a finite loop optimization method. Both architecture of the system and matter distribution are considered as variable input of the optimization procedures. This leads to higher degrees of freedom for the designer and customized solutions for each technical problem encountered.

From practical and regulatory standpoints, the structural design is grounded upon the limit state approach [28]. This standardized approach is based on a semi-probabilistic analysis of mechanical parts and construction elements [29]. As a recall limit, state analysis is a set of procedures which use the analytical formulations of mechanical engineering and the material properties as stochastic variables. Security coefficients and loading factors determination are premised upon a statistical analysis of the loads and material resistance [30]. The criteria’s acceptation of a limit state utilizes the empirical models and data coming from the material degradation experimentations or industrial databases [28,29,30]. Even if structural engineering is the origin of the philosophy of the limit states based design, the entire mechanical design is implicitly based on it. This should be the same for lattice design. These criteria are utilized as constraints functions in the TO problem formulations.

On Abaqus FEM software, Saadlaoui et al. [16] used three different TO techniques for the compression testing of simple cubes. The industrial codes adopted by these authors were as follows [16]:

• The stress-constrained optimization problem (SCO);

• The continuous compliance optimization problem (CCO);

• The discrete compliance optimization problem (DCO);

In each optimization problem adopted by Saadlaoui et al. [16]:

• First, for (SCO) problem, the objective function corresponds to the volume of the cube to minimize (mass equivalence) whereas (CCO) and (DCO) problems used the potential energy as objective function to minimize;

• Second, the limit states criteria are ensured by fixing the adequate constraint functions. For instance, in the (SCO) problem, the limit state corresponds to the exceed of the elastic constraints in each matter point; this corresponds to a mechanical criterion. While for the (CCO) and (DCO) problems, the constraints functions force the system to pinpoint a target level of stiffness.

A very interesting way to exploit TO approach is proposed by Jankovics et al. [31] where the authors used the compliance minimization approach to minimize the usage of the handling supports of surfaces that are angled less than a critical angle [31]. A topology optimizer was developed by the authors in ANSYS^® using ANSYS Parametric Design Language (APDL). The authors treated the cantilever and the MBB beams. The results showed the complexity of the optimized structures produced by the TO procedures when trying to reach producible parts without handling supports.

Other operational TO and GD solutions are found in industrial use, such as TOSCA module, developed by Dassault systems, that can be interfaced with Abaqus, ANSYS or NASTRAN [32]. In addition, Autodesk developed Fusion 360 software specialized in GD to design parts dedicated to AM processes. Given the above, the software presents simplified environments to include the major functions for the TO according to the simplest properties of the optimized parts as part volumes, optimized surfaces and perimeters choice, etc. Moreover, for more complex needs, the designer is enforced to code into the dedicated modules of those software.

In the TO, the geometry and matter distribution belongs to the list of the most important variables of the problem. Hence, their optimum values depend on the objective and constraints functions formulation and the resolution approach. In consequence, the initial distribution of matter is varied in each step of the optimization procedure until reaching the convergence of the algorithms. This step is obtained when all the constraints are ensured and the minimization of matter or potential energy is reached [17, 20].

Moreover, evolutionary algorithms are used to resolve TO that are analytically formulated for some problems. For instance, Brackett et al. utilized the Bidirectional Evolutionary Structural Optimization (BESO) algorithm so as to minimize the weight and the matter distribution of a 2D plate considered as a cantilever beam [20]. The computed geometry corresponded to a kind of truss beam with irregular elements. (BESO) algorithm was adopted by Brackett et al. because its inherent solid-void representation means that it is possible to identify the boundaries with a variable density method [20].

It is to notice that TO causes more complexity in the parts design because of the relatively non-controlled distribution of matter. This is why AM is required to build such complex parts. Nevertheless, the transition from the optimized structure to the CAD model is not obvious and it is very hard to achieve [20], whereas several researchers do not mention this issue and consider only, with an optimistic standpoint, the advantages of AM in complex parts processing neglecting the post-processing TO step [15,16,17,18].

In the case of lattice structures, Panesar et al. demonstrated that a closer interplay between lattice design approaches and TO is the next step in realizing optimal designs for AM [22]. To derive a solid-void structure from the initial part studied, the authors presented several families of TriPeriodic Minimal Structures (TPMS) as candidate features for the mesoscopic scale of the materials developed. Hence, the authors did not adopt the part architecture as TO process input, but they fixed the D-P (double variant of Schwarz’s Primitive) lattice and the BCC (body-centered cubic) cells as reference geometries for lattice generation. In this particular case study, the scaling of the cell units and the variation of the matter’s density are the major input variables of the topological optimization strategies tested by the authors [22].

The TO principals permit also to integrate a different level of structures optimization. Xu et al. proposed a multiscale TO using feature-driven method that adopts flexible bars to build truss-lattice; the orientation and the number of bars are considered as input variables of the calculation procedures [19]. The orientation of the microstructural features is also one of the process inputs of the TO problem. The approach of Xu et al. is highly significant because it permits to generate various lattice structures. For the same part with different loadings and graded materials, the methodology can propose optimal lattices in terms of orientation and geometrical properties of the trusses bars adopted from both macroscopic and mesoscopic scales. To prove the efficiency of their approach, the authors treated four case studies: a Cantilever beam, a MBB beam, a bridge structure, and a two-holes structure with a complicated outer boundary. The conclusion of the authors is that both macroscale and microscale of all these structures are optimized, but compared to the solid-material design, no obvious improvement of structural stiffness was obtained through the multiscale design.

More generally in civil engineering, the TO takes another form; this new domain is called GD [33]. This new engineering area GD could be seen from two main angles: either as a broad umbrella, encompassing topology optimization or as a wholly distinct technology [34]. This new concept gathers the principals of the classical TO, high-performance optimization algorithms [35, 36] and the integrated technologies of Building Information Modeling (BIM) platforms [34, 37]. In addition to the classical mechanical constraints and objectives, GD includes energetic criteria like building sites and orientations, solar radiation, area management of the construction, organization and room’s dimensions, offices and compartments [37].

Therefore, in this context, the impetus of this paper is to propose a new design of a family of lattice structures based upon coupling the advantages of two reference structures:

• The high compressive resistance of the KT structure;

• The lightweight property of Sheon minimal gyroid.

The main objective is to exploit this new lattice family in the topological optimization of mechanical parts that are subject to compression solicitation, or at least in the part areas subject to the compressive solicitation.

From the mathematical standpoint, the modeled problem will be considered as an isoperimetric problem instead of the min/max optimization problems.

3 Methodology

The design of the proposed structures family is based on the following steps:

• Proposition of a new parametrization of the KT 2D profile;

• The Gyroid Equivalent SEZ structure (GE-SEZ*¹) is built according to the equality of the “Surface To Volume Ratio” (SVR) of the assembly of SEZ structures and the SVR of the Schoen minimal Gyroid. This equality permitted to find the first characteristic equation where variables correspond to the parameters of the previous step;

• The second characteristic equation is obtained according to the volumes equality of the adopted structures. This allows to compute the thickness of the GE-SEZ family;

• For a given tuple of GE-SEZ geometrical parameters, testing specimens are processed, using the FDM and ABS copolymer;

• The mechanical characterization of the GE-SEZ adopted, using compression tests;

Figure 1 presents the workflow proposed in the modeling and experimental approach of this study.

Fig. 1

Workflow of the study

3.1 Mathematical design

3.1.1 Reference geometry: the KT column

3.1.1.1 Historical background

The longitudinal profile of the best compressive structure that resists against buckling was calculated by Clausen (1849) for circular transversal section [38] in the case of pinned–pinned boundary condition. Subsequently, it was re-determined [39], using the internal energy minimization at the limit buckling state, according to the elasticity theory. However, the boundary conditions used in the work of Keller corresponds to a column pinned at its ends [39]. Later on, Keller and Tadjbakhsh studied and discussed the pinned-hinged and pinned-free boundary conditions [38]. In addition to the analyzed mechanical aspects, the problem was modeled as an isoperimetric problem, leading to a larger analytic formulation that was adopted in the 1990s by Cox and Overtone [40, 41].

As a matter of fact, the latter generalized the problem for more boundary conditions and corrected the findings of Keller and Tadjbakhsh in terms of maximal buckling load and the necessary optimality conditions. The analysis of the optimality conditions according to the eigenvalues optimization policies was based on the works of Masur [42], Bratus and Seipanian [43] and Seiranyan [44]. However, the profiles presented by Keller–Tadjbakhsh, even after the modifications brought by Cox and Overtone, remained correct.

Cox and Overtone stated, in their conclusion, that deeper correction of the models must be based on a parameter that introduces the material asymmetry and imperfections that exist in the real mechanical structures. Finally, Cox and Overtone approached the problem numerically, which led to the analytical verification of the profiles proposed by Keller and Tadjbakhsh [41].

The KT structures are still of great interest since several researchers further analyzed and characterized them. Olhoff and Seyranian studied the post-buckling behavior on two of the KT structures, the pinned–pinned and the pinned-simply supported boundary conditions. The authors proposed the geometry handling of the KT structures by affecting non-dimensional parameters, which are concerned with the geometry (longitudinal and cross-section profiles) and the materials (Young modulus).

The results of Olhoff and Seyranian study led to the simulation of the bi-modal buckling profiles [45].

Adopting the same mathematical formulation of the KT profiles, different elastic boundary conditions, proper weight of the structures, a set of axial loads and Hencky bar chain model (HBM) were included by Ruocco et al. to compute the distribution of the diameters of the KT structures along with the principal axis of revolution by the mean of Genetic algorithms [46].

3.1.1.2 Formalism

Based on the formulation of the longitudinal profile of the pinned–pinned KT structure chosen in this paper, the system of Eq. (1) generates the curve $C_{0}$ as presented in Fig. 2:

$$f\left( x \right) = \left\{ {\begin{array}{*{20}l} {f_{1} \left( x \right) = \frac{3}{2}\left( {1 - 16x^{2} } \right) ;\,x \in \left[ {0,\frac{1}{4}} \right] } \hfill \\ {f_{2} \left( x \right) = \frac{3}{2}\left( { - 3 + 16 x - 16x^{2} } \right) ;\,x \in \left[ {\frac{1}{4};\,\frac{3}{4} } \right]} \hfill \\ {f_{3} \left( x \right) = \frac{3}{2}\left( { - 15 + 32x - 16x^{2} } \right) ;\,x \in \left[ {\frac{1}{4};\,1 } \right]} \hfill \\ \end{array} } \right..$$

(1)

Fig. 2

$C_{0} { }$ curve in $\left( {\vec{x},\vec{y}} \right)$ plan

The structure that results from the rotation of the curve $C_{0}$ around the $\left( {D:{\text{"}}y = 0{\text{"}}} \right)$ axis is presented on Fig. 3a, b.

Fig. 3

3D shape generated by the rotation of $C_{0}$ around $\vec{x}$ axis a isometric view, b projection on (z, x) plan

We have to mention that the previous studies tried to modify the geometry, the shape or other dimensions of the KT structures [40, 41, 46]. In consequence, these changes will cause a shift from the optimal shapes that were developed by the original authors and researchers (Keller and Tadjbakhsh, Cox and Overtone). This can also be applicable for the present work.

Some characteristics of the adopted pinned–pinned KT profile are defined below.

3.1.1.3 Property of symmetry of pinned–pinned KT profile

The property of symmetry represented by the functions y_i that constitute the profile of the pinned–pinned KT structure is very important. It will serve to simplify the calculation of the surface and volume of revolution of the SEZ structures designed in this paper.

Thus we define:

• (a) Symmetry between $\left( {x,y_{1} \left( x \right)} \right)$ and $\left( {x,f_{2} \left( x \right)} \right)$ according to the $\left({\Delta_{1}:x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}} \right)$ axis;

• (b) Symmetry of $\left( {x,f_{2} \left( x \right)} \right)$ itself around the $\left( {\Delta_{2}\!\!:x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)$ axis;

• (c) Symmetry between $\left( {x,f_{1} \left( x \right)} \right)$ and $\left( {x,f_{3} \left( x \right)} \right)$ according to the $\left( {\Delta_{2}\!\! :x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)$ axis;

Since the symmetries have been proven (see Appendix A1), only the first function y₁ (x) will be handled to calculate the surface to volume ratio, as well as the volume of the proposed structures.

3.1.2 Schoen minimal gyroïd

As presented in the introduction, the aim of the paper is to propose HCLW structures family that couples the resistance against buckling (KT structures) with a minimum weight. Therefore, the Schoen minimal gyroid is adopted as lightness reference to modify the dimensions of the KT structure proposed to obtain a HCLW structure. More details of the gyroid structures are presented by Scherer [47].

In general, the gyroid structures belong to the TPMS that presents a minimum area with zero mean curvature [47, 48]. The Schoen minimal gyroid is chosen in this study. The mean curvature of this latter value is zero. This could be represented by the implicit Eq. (2) [48]:

$$\begin{gathered} \cos \left( x \right)\sin \left( y \right) + \cos \left( y \right)\sin \left( z \right) + \cos \left( z \right)\sin \left( x \right) = t \hfill \\ x,y,z \in \left[ { - a,a} \right]; \hfill \\ \end{gathered}$$

(2)

$a$ is the length of the container cube of the gyroïd; In this case we use, ${\text{"}} t = 0{\text{"}}.$

Since the Eq. (2) is implicit and very difficult to simplify to an explicit one, the surface and surface to volume ratio are computed, using Enneper–Weierstrass representation [48, 49].

It should be noted that the developed structures will be used as mechanical parts, so the gyroïd as a surface has no utility for a mechanical use. Thus, for the exploitation of the gyroïd characteristics as a mechanical part, it is mandatory to add a thickness of the surface described by the Eq. (2). The thickness value chosen in this study is 4 mm.

The volume $\left( {V_{{\text{G}}} } \right)$ and the SVR of the gyroïd are estimated as:

$$\left\{ {\begin{array}{*{20}l} {V_{{\text{G}}} = 125237.49874 \, {\text{mm}}^{3} } \hfill \\ {\left( {{\raise0.7ex\hbox{$S$} \!\mathord{\left/ {\vphantom {S V}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$V$}}} \right)_{{\text{G}}} = 0.544} \hfill \\ \end{array} .} \right.$$

(3)

Figure 4 shows the design of the adopted Schoen minimal gyroïd on solidworks, having a thickness of 4 mm. The length of the cube is 102 mm.

Fig. 4

Faces and 3D visualization of the Schoen minimal gyroïd with 4 mm of thickness

3.1.3 Handling the profile of the SEZ structure: KT profile parametrization

The idea of the parametrization of the KT structure comes from the fact that the volume and surface of this geometry structure are null on some specific points, such as ${\varvec{x}} = {\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {\mathbf{4}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathbf{4}}$}}$ and ${\varvec{x}} = {\raise0.7ex\hbox{${\mathbf{3}}$} \!\mathord{\left/ {\vphantom {{\mathbf{3}} {\mathbf{4}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathbf{4}}$}}$ as shown on the Figs. 2 and 3b. Shifting these specific points, real geometry could be exploited mechanically. This transformation is ensured by an additional positive term “b”, as reported in the equation or mapping (4) presented in the next paragraph.

Second, since the objective of the study is to fill the volume of a given geometry of mechanical part (under compression) with linear repetitions of SEZ structures, the confinement of a set of SEZ unities has to be also analyzed mathematically to ensure the genericity of the proposed design. Moreover, multiple multipliers that affect the two initial variables x and y (see the mapping (2) below) are introduced: the parametrization on x variable will affect the length of the SEZ unities and the parametrization on y (x) variable will affect the local diameters of the SEZ unities.

3.1.3.1 Mapping

The mapping (4) permits to confine a specific assembly of SEZ unities into a cubic volume L³. It should be noted that the mapping $\theta$ is a C¹ diffeomorphism [50].

According to the symmetries defined in the Sect. 2.1, the mapping (4) is limited to the [0, 1/4] interval:

$$\begin{gathered} \theta :\left[ {0,\frac{1}{4}} \right] \times \left[ {0,\frac{3}{2} } \right] \to \left[ {0,\frac{L}{4m}} \right] \times \left[ {0,\frac{L}{2n} } \right] \hfill \\ \left( {x,f\left( x \right)} \right) \to \left( {\tilde{x}, \tilde{y}} \right) \hfill \\ {\text{s}}.{\text{t}}. \quad \theta \left( {x,f\left( x \right)} \right) = \left( {\begin{array}{*{20}l} {\tilde{x} = d \cdot x} \hfill \\ {\tilde{y} = c\left( {\frac{2}{3}a f\left( {\tilde{x}} \right) + b} \right)} \hfill \\ \end{array} } \right), \hfill \\ \end{gathered}$$

(4)

where:

• m: the number of SEZ unities confined along the $\vec{x}$ axis of the SEZ;

• n: the number of SEZ unities confined on the diametrical direction;

• n: the number of SEZ unities confined on the diametrical direction;

• $\left( {\frac{2}{3} a} \right)$: parameter that permits to scale the amplitude of the initial KT profile (along the diameter axis);

• $b$ (> 0): parameter that permits to enforce a non-null radius to the structure;

• c: parameter that scale the total diameter of the SEZ profile; d: parameter that scales the length of the SEZ unities. This permits the stretching or the compression of its length.

3.1.3.2 Geometrical compatibilities and parameters expressions

Since the control volume adopted for the geometrical equivalence of the SEZ and the gyroïd structure is cubic, it should be expressed as L³ (L length if the cube edge).

Thus, the equations of geometrical compatibility are given as:

• length of one unique SEZ:

  $$L_{{{\text{SEZ}}}} = {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}$$

  (5)

• the greater diameter of one confined SEZ:

  $$\emptyset_{0} = {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L n}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$n$}} = 2\tilde{y}\left( 0 \right)$$

  (6)

  Injecting the Eqs. (5) and (6) in the mapping (4), we find:

  $$c = {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L {2n\left( {a + b} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2n\left( {a + b} \right)}$}}$$

  (7)
  $$d = {\raise0.7ex\hbox{$m$} \!\mathord{\left/ {\vphantom {m L}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$L$}}.$$

  (8)

Since the c and d parameters are expressed by other parameters, the handling of the SEZ structure has to be guaranteed by the parameters $\left( {a,b,m,n} \right)$. So, the profile of the SEZ is given by the expression (9):

$$\tilde{y} = \frac{L}{{2n\left( {a + b} \right)}}\left( {a\left( {1 - 16\left( {\frac{m}{L}x} \right)^{2} } \right) + b} \right).$$

(9)

Figure 5 plots the curve $C_{{{\text{ext}}}} \left( {x,\tilde{y}\left( x \right)} \right)$ in the $\left( {\vec{x},\overrightarrow {{\tilde{y}}} } \right)$ plan. This curve corresponds to the external profile of the SEZ structure.

Fig. 5

$C_{1}$ curve in $\left( {\vec{x},\overrightarrow {{\tilde{y}}} } \right)$ plan

The greater external diameter of the SEZ is given by the expression (10):

$$\emptyset_{{{\text{ext}}}} = 2\tilde{y}\left( 0 \right) = {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L n}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$n$}}.$$

(10)

3.1.3.3 Thickness of the SEZ, external and internal shapes

To create a mechanical part, it is mandatory to add thickness to the proposed design. Thus, the resulting volume of the SEZ is composed by the subtraction of an interior volume described by the rotation of the curve $C_{{\text{int}}} \left( {x,\tilde{y}_{{\text{int}}} \left( x \right)} \right)$ around $\left( {D:{\text{"}}\tilde{y} = 0{\text{"}}} \right)$ from an exterior volume described by the rotation of the curve $C_{{{\text{ext}}}} \left( {x,\tilde{y}_{{{\text{ext}}}} \left( x \right)} \right)$ around $\left( {D:{\text{"}}\tilde{y} = 0{\text{"}}} \right)$.

On the interval $\left[ {0, {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L {4m}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${4m}$}}} \right],$ the profiles of the exterior and interior shapes are given by the system (11):

$$\left\{ {\begin{array}{*{20}l} {\tilde{y}_{{{\text{ext}}}} \left( x \right) = \tilde{y}\left( x \right) = \frac{L}{{2n\left( {a + b} \right)}}\left( {a\left( {1 - 16\left( {\frac{m}{L}x} \right)^{2} } \right) + b} \right)\quad (11.1) } \hfill \\ {\tilde{y}_{{\text{int}}} \left( x \right) = \tilde{y}_{{{\text{ext}}}} \left( x \right) - e = \frac{L}{{2n\left( {a + b} \right)}}\left( {a\left( {1 - 16\left( {\frac{m}{L}x} \right)^{2} } \right) + b} \right) - e;\quad e > 0} \quad (11.2) \hfill \\ \end{array} } \right.$$

(11)

To minimize the number of decision variables, the thickness noted e is represented as a fraction of the external diameter as described in Eq. (12):

$$e = k \emptyset_{{{\text{ext}}}} = k\left( 2 \right) = k {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L n}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$n$}}.$$

(12)

Further, the volume generated on the interval $\left[ {\frac{1}{4} {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}, {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \right]$ is constructed by the symmetries presented in the Sect. 3.1.1.

3.1.3.4 Surface and volume generation

The volume of the one SEZ is described by an external shape, having a profile $C_{{{\text{ext}}}} \left( {x,\tilde{y}_{{{\text{ext}}}} \left( x \right)} \right)$, and an internal shape with a profile described by the curve $C_{{\text{int}}} \left( {x,\tilde{y}_{{\text{int}}} } \right)$ (see system (11) above).

For a given point $M\left( {x,y\left( {r,\theta } \right),z\left( {r,\theta } \right)} \right)$ of the SEZ surface (exterior or interior), the coordinates of the point $M$ are described by the cylindrical parametrization (13):

$$\left\{ {\begin{array}{*{20}l} {r\left( x \right) = \tilde{y}\left( x \right)} \hfill \\ {y\left( x \right) = r\left( x \right) \cdot \cos \left( \theta \right)} \hfill \\ {z\left( x \right) = r\left( x \right) \cdot \sin \left( \theta \right)} \hfill \\ {\tilde{y}\left( x \right) = \left\{ {\begin{array}{*{20}c} {\tilde{y}_{{{\text{ext}}}} \left( x \right)\, {\text{for}}\,{\text{the}}\,{\text{external}}\,{\text{profile}}} \\ {\tilde{y}_{{\text{int}}} \left( x \right)\, {\text{for}}\,{\text{the}}\,{\text{internal}}\,{\text{profile}}} \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(13)

where: $r\left( x \right)$: is the external or internal radius of the surface; $\theta$: is the angle $\left( {O\left( x \right),\widehat{{\vec{y}\left( x \right),\overrightarrow {{e_{r} }} \left( x \right)}}} \right)$, $\theta \in \left[ {0,2\pi } \right]$. $O\left( x \right)$: is the center of the circle described by the rotation of a given point of the external or interior surface. In the cylindrical basis $O\left( {0,0,x} \right)$; $\overrightarrow {{e_{r} }} \left( x \right)$: is the polar axis corresponding to the x position.

Denoting the volume external generated volume V_ext and the internal generated volume V_int.

3.1.4 Expression of the SVR and volume of the GE-SEZ structures

To construct the surface to volume equivalence between the GE-SEZ structure and the gyroïd adopted, it is mandatory to use the same SVR. But firstly, we should define the (GE-SEZ)_n²_×m.

We define the (GE-SEZ)_n²_×m as the linear repetitions of assembly of units of several SEZ unities:

• n repetition of the SEZs is the $\vec{X}$ direction.

• n repetition of the SEZs is the $\vec{Y}$ direction.

• m repetition of the SEZs is the $\vec{Z}$ direction.

Figure 6 presents an isometric view of a $\left( {\text{GE } - \text{ SEZ}} \right)_{n \times n \times m}$ confined into a cubic volume of $L^{3}$, for ${\text{"}} \left( {n,m} \right) = \left( {20,5} \right){\text{"}}$.

Fig. 6

$\left( {\text{GE } - \text{ SEZ}} \right)_{{n^{2} \times m}}$ definition with the parameters $n = 20$ and $m = 5$

In consequence, the SVR of the GE-SEZ is calculated by dividing the sum of the SEZ unities lateral surfaces by the cubic volume L³.

3.1.5 Characteristic system of the equation of $\left( {\text{GE } - \text{ SEZ}} \right)_{n \times n \times m}$ structures

To summarize, the dimensions of the $\left( {\text{GE } - \text{ SEZ}} \right)_{n \times n \times m}$ are obtained according to:

• The equality of the SVR ratios of the structures;

• The expression of the thickness “e” of the SEZ unities;

So the characteristic system of equations of the $\left( {\text{GE } - \text{ SEZ}} \right)_{n \times n \times m}$ structures is obtained by resolving the systems (14). This system is composed by the Eqs. (29) and (39) that are developed in the “Appendix A2”:

$$\left\{ {\begin{array}{*{20}l} {P_{n,m} \left( {a,b} \right) = 0} \hfill & {(14.1)} \hfill \\ {e\left( {a,b} \right) = e^{ + } \, {\text{or}} \, e^{ - } } \hfill & {(14.2)} \hfill \\ \end{array} } \right.$$

(14)

where:

$$\begin{array}{c} \begin{array}{c} P_{n,m}\left(a,b\right)=\frac{8\ \pi \ \left(A\times B-C\times D\right)}{E}-\gamma \\ \left\{ \begin{array}{c} \ \\ A=A_{n,m}\left(a,b\right)=256a\left(a+b\right)d^2c^2+1 \\ B=B_{n,m}\left(a,b\right)={\mathrm{log} \left(\sqrt{32a*c*d^2+1}+32acd^2x_1\right)\ } \\ C=C_{n,m}\left(a,b\right)=32acd^2x_1\sqrt{{\left(32acd^2x_1\right)}^2+1} \\ D=D_{n,m}\left(a,b\right)=256ac^2d^2\left(a\left(8d^2x^2_1-1\right)-b\right)+1 \\ E_{n,m}\left(a,b\right)=16{\left(32acd^2\right)}^2 \end{array} \right. \end{array} \\ s.t\ \left\{ \begin{array}{c} c=\frac{L}{2n\left(a+b\right)} \\ d=\frac{m}{L} \\ x_1=\frac{L}{4m} \\ \gamma ={\left({S}/{V_{Gy}}\right)}_{Gyroid} \\ V_{Gy}:the\ effective\ volume\ of\ the\ Gyroid \end{array} \right. \\ e\left(a,b\right)=\left\{ \begin{array}{c} e^+=\frac{-B_{a,b}+\sqrt{\Delta }}{2A_{a,b}} \\ e^-=\frac{-B_{a,b}-\sqrt{\Delta }}{2A_{a,b}} \end{array} \ \right. \end{array}$$

(15)

The resolution of the system (14) will be detailed in the result and discussion section in Sect. 4.1.1.

3.2 Materials and methods

3.2.1 Material

The material adopted for processing is the acrylonitrile butadiene styrene (ABS). The material is furnished as a bobbin having 1.75 mm of filament diameter [51].

The mechanical properties of the ABS formulations generally depend on [52,53,54,55,56]:

• Elastomer rate.

• Nodules dimensions and dispersion in the rubbery phase.

• Reticulation density of the rubbery phase.

• Graft level of the acrylonitrile styrene on the nodules.

Table 1 presents the mechanical properties of the ABS material processed by FDM according to Stratasys, Inc [51]. under tension solicitation.

Table 1 Mechanical properties of the ABS produced by FDM technology [51]

In comparison with the ABS material processed by the injection processes, the ABS processed presents low properties (for more details on the mechanical behavior, please refer to [52]).

For the GE-SEZ samples, the core of the SEZ unities are built layer by layer according to a polar movement of the injection nozzle because the SEZ unities are axisymmetric (revolution) parts.

3.2.2 Samples

3.2.2.1 New design samples

To proceed with mechanical testing of the new design, three samples of the ${\mathbf{GE - SEZ}}_{{{\mathbf{20}} \times {\mathbf{20}} \times {\mathbf{6}}}}$ were fabricated by additive manufacturing, using FDM technology. The paragraph Sect. 4.1.2 presents the structure parameters. These parameters are the solutions of the characteristic system (30, 31).

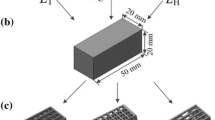
Figure 7a presents the ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ of the structure that is highlighted with blue color. Figure 7b shows the dimensions of the samples after scaling. It corresponds to the structure tested by compression solicitation.

Fig. 7

a Highlighted isometric view of the ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ of the structure, (b) 2D draw of the ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ of the structure with the corresponding transformed dimensions

Due to technical constraints, concerning the resolution of the printer (nozzle minimal diameter of 0.4 mm) and the maximal dimensions of the printer building chamber, some transformations were absolutely necessary to manufacture the testing parts:

• Scaling the GE-SEZ_20×20×6 by multiplying all the dimensions by 2;

• Producing the ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ of the structure according to the building platform volume which is restricted to 120 × 120 ×120  mm as presented in the Table 2.

3.2.2.2 Cylindrical samples

In addition to the GE-SEZ processing, three cylindrical samples were fabricated to characterize the ABS material under compression load. The tensile properties, according to the ASTM D638 standards, of the material are presented in Table 1. The dimensions of the testing cylinders are:

• Initial diameter of 25 mm.

• Initial length of 30 mm.

3.2.3 Printer and process parameters

The FDM device used for processing the new design samples is the UP Mini-2 ES [51]. The process parameters are exhibited in Table 2.

Table 2 Specifications for the ABS printing [51]

In this paper, the authors are interested in general compressive behavior of the GE-SEZ structures, specifically the buckling state instability. For this reason, they utilized the “Tiertime-UP Mini 2 ES” that is very easy to use, independently to the material analysis, with relatively fixed parameters to command.

3.2.4 Testing parameters

The machine used in the compression test is the “MTS Criterion—Model 45”.

The following parameters were adopted:

• Command by platen displacement;

• Speed of displacement: 0.02 mm s⁻¹;

• Temperature test: ambient temperature that is regulated at 20 °C;

• Friction between platens of the test machine and the parts tested: no lubrication is applied between the loading platens and the specimens (see next paragraph for the effect of the friction coefficient);

• Stop criteria:

  • manual command: reaching plasticity with a high rate of strain without breaking;

  • regulated command: at the breaking of the specimen.

3.3 Comparison of the GE-SEZ with other structures: a benchmark study

The final step to validate the new design is to compare it to several structures studied in the bibliography. Thus, it is necessary to explain the comparison base of the benchmark analysis.

Firstly, scientific works were selected and treated, especially the lattice structures fabricated by FDM/ABS and characterized by compression tests [57,58,59]. Secondly, since the mechanical properties are highly affected (increased) by the relative density (RD) and displacement rate of the compression test platen, the mechanical properties are compared based on two major indicators:

• The normalized Young modulus (formulated in Sect. 4.3.1): in a first step, it corresponds to the Young modulus (E), estimated experimentally for each structure, divided by the corresponding RD; and in a second step, it corresponds to the Young modulus divided by the previous denominator and also by the displacement rate of the test denoted v;

• The normalized yield strengths (formulated in Sect. 4.3.2): in a first step, it corresponds to the yield strength (σ_y), estimated experimentally for each structure, divided by the corresponding RD; and in a second step, it corresponds to the yield strength divided by the previous denominator and also by the speed rate of the test denoted.

These two indicators will permit to take into account both the mechanical properties (E and σ_y) and the lightness of the structures expressed by the related density, along with the effect of displacement rate of different tests.

The results of the benchmark are detailed in Sect. 4.3.

4 Results and discussion

This section chiefly presents the resolution of the characteristic system (14) and the compression test results of both cylindrical and $\left( {{\mathbf{GE - SEZ}}} \right)_{{{\mathbf{20}} \times {\mathbf{20}} \times {\mathbf{6}}}}$ samples.

4.1 Characteristics equations resolution

4.1.1 General strategy for resolution

The resolution of the system (14) is performed in two steps.

For a given couple of the parameters (n, m), in this case (20, 6):

• The numerical resolution of the Eq. (29) (Eq. 15) permits to detect the set of feasible solutions denoted (a*, b*). All the solutions are equivalent to SVR and volume equivalences standpoint. The numerical resolution is performed by the Newton–Raphson algorithm;

• For a given couple of feasible solution (a*, b*), the calculation of the thickness “e” is direct using Eq. (39) (Eq. 16).

4.1.2 Application

As mentioned above, we choose arbitrary the following parameters:

$$\begin{gathered} \left\{ {\begin{array}{*{20}l} {{\varvec{n}} = {\mathbf{20}}} \hfill \\ {{\varvec{m}} = {\mathbf{6}}} \hfill \\ \end{array} } \right. \hfill \\ {\text{s}}.{\text{t}}.\quad {\varvec{L}} = {\mathbf{102}}\,{\mathbf{mm}} \hfill \\ \end{gathered}$$

According to the system (14), the definition of the $\left( {{\mathbf{GE - SEZ}}} \right)_{{{\mathbf{20}} \times {\mathbf{20}} \times {\mathbf{6}}}}$ is equivalent to the system (16):

$$\left\{ {\begin{array}{*{20}l} {{\varvec{P}}_{{\left( {{\mathbf{20}},{\mathbf{6}}} \right)}} \left( {{\varvec{a}},{\varvec{b}}} \right) = {\mathbf{0}}\quad \left( {{\mathbf{16}}.{\mathbf{1}}} \right)} \hfill \\ {{\varvec{e}}^{*} = {\varvec{e}}\left( {{\varvec{a}}^{*} ,{\varvec{b}}^{*} } \right)\quad \left( {{\mathbf{16}}.{\mathbf{2}}} \right)} \hfill \\ {\left( {{\varvec{a}}^{*} ,{\varvec{b}}^{*} } \right) = {\mathbf{arg}}\left( {\text{"}}{\varvec{P}}_{{\left( {{\mathbf{20}},{\mathbf{6}}} \right)}} \left( {{\varvec{a}},{\varvec{b}}} \right) = {\mathbf{0}}{\text{"}} \right)} \hfill \\ \end{array} } \right.$$

(16)

Figure 8 displays the graphical representation of the solution of the Eq. (16.1) before numerical resolution. This solution corresponds to the intersection of the surface ${\varvec{P}}_{{\left( {{\mathbf{20}},{\mathbf{6}}} \right)}} \left( {{\varvec{a}},{\varvec{b}}} \right)$ and the plan ${\varvec{P}}_{{\varvec{Z}}} \left( {{\varvec{a}},{\varvec{b}}} \right) = {\mathbf{0}}$.

Fig. 8

a 3D-graphical visualization of the surface ${\varvec{P}}_{{\left( {{\mathbf{20}},{\mathbf{6}}} \right)}} \left( {{\varvec{a}},{\varvec{b}}} \right)$ and the surface $P_{Z} \left( {a,b} \right)$. b 2D visualization of the intersection of the two surfaces ${\varvec{P}}_{{\left( {{\mathbf{20}},{\mathbf{6}}} \right)}} \left( {{\varvec{a}},{\varvec{b}}} \right)$ and ${\text{"}} P\left( {a,b} \right) = 0{\text{"}}$ defining the solution of the Eq. (16.2)

Figure 9 portrays the detected solutions of the Eq. (16.1) with the proposed linear fit. The linear fit of the solutions can be expressed by the Eq. (17):

$$\left\{ {\begin{array}{*{20}l} {{\varvec{b}}^{*} \left( {{\varvec{a}}^{*} } \right) = {\mathbf{0}}{\mathbf{.7727}} {\varvec{a}}^{*} + {\mathbf{0}}{\mathbf{.0007}}} \hfill \\ {{\varvec{R}}^{{\mathbf{2}}} = {\mathbf{0}}{\mathbf{.9988}}} \hfill \\ \end{array} } \right..$$

(17)

Fig. 9

Plots of the solution of Eq. (16.1) and the linear fit adopted

Now, the thickness “${\varvec{e}}^{*}$” corresponding to each solution $\left( {{\varvec{a}}^{*} ,{\varvec{b}}^{*} } \right)$ is calculated, using the Eq. (16.2). Figure 10 presents the 3D plot of the feasible solutions expressed by the triplet $\left( {{\varvec{a}}^{*} ,{\varvec{b}}^{*} ,{\varvec{e}}^{*} } \right)$.

Fig. 10

3D Plot of the solution of feasible solution (a*, b*, e*) according to the Eq. (16.2)

According to the values of the parameters n and m adopted in this simulation, the positive root that has physical signification corresponds to e⁺ (Eq. 39 of the appendix).

To proceed to the mechanical testing of a given $\left( {{\mathbf{GE}}{ - }{\mathbf{SEZ}}} \right)_{{{\mathbf{20 \times 20 \times 6}}}}$, the authors arbitrary choose a triple of the command parameters (a^*, b^*, e^*) such that:

$$\left\{ {\begin{array}{*{20}l} {{\varvec{a}}^{*} = {\mathbf{0}}.{\mathbf{8}}} \hfill \\ {{\varvec{b}}^{*} = {\mathbf{0}}.{\mathbf{618}}} \hfill \\ {{\varvec{e}}^{*} = {\mathbf{0}}.{\mathbf{3137}}} \hfill \\ \end{array} } \right..$$

4.2 Compression tests results

4.2.1 Manufacturing validation of the GE-SEZ and cylindrical specimens

The manufactured GE-SEZ parts were measured at some specific points to estimate the fabrication precision. More precisely, the measurements concerned the biggest diameter, the smallest diameter corresponding to the structure necks (Fig. 5), the width and height of the structure. Ten measurements per dimension were conducted.

Table 8 of Appendix 3 groups the corresponding statistics. The variation coefficients (VC) for all dimensions are less than 2%, while the absolute value of the 1st order errors are less than 1% for all dimensions of the GE-SEZ.

Table 9 groups the statistics of the dimensions of the cylindrical samples. VC and absolute value of the 1st order errors do not exceed 0.5%, meaning that the manufacturing is good.

4.2.2 Compression test on the cylindrical samples and general compression behavior

Figure 11 presents the plot of the compression test results of one of the cylindrical samples. Two cycles of load-unload reaching the plasticity of the material have been tested. The cycle 3 corresponds to loading until reaching 35% of real strain where the yielding increases. The test is then stopped at this value of the strain.

Fig. 11

Strain/stress compression curve of cylindrical specimen no. 1

At the first loading, the yield stress was not reached, so no yielding has been detected for the second cycle of loading. But for the third loading, an increase of yielding stress around 16% is observed. The loading continued until 35% of true strain.

It should be noted that the shape of the deformed cylinders perfectly corresponds to the shape of cylinder of compression test with a friction coefficient around 0.1 and 0.2 between the cylinder basis and the compression platens [60].

As a result, the mechanical properties estimated by these tests are listed in the Table 3 (elastic modulus E and apparent yield strength Re).

Table 3 Average values of the E and apparent Re of the cylindrical specimens

From the compression test curves, the behavior of the cylinders corresponds absolutely to the polymers behavior, described by the four principal phases as detailed in [61]:

• Phase I: Visco-elastic domain;

• Phase II: The maximum resistance is attained at the local maxima and a softening occurs, that could be caused by the relaxation of the material at some areas that are in traction;

• Phases III and IV: increase of the resistance with different tendency, corresponding to the J₂-plasticity model.

At the development of the plastic phases III and IV, localized bends are created, hence expressing the shear stress evolution at these areas [61, 62]. These bends are visible on the compression cylinders as shown in Fig. 12b. The figure also shows the whitening phenomenon at the external lateral surfaces. This whitening is caused by the development of the cavitation into the material. More details about these phenomena are detailed in the next paragraph.

Fig. 12

Compressed cylindrical specimen no. 1 a global view, b shear bends

So according to the cylinders compression tests, the yield strength of the ABS under compression (Table 4) corresponds approximately to those reported in Table 1. But the elastic modulus of the cylindrical specimens is very weak compared to the value of Table 1. This low value could be caused by the asymmetry between the tensile test (Table 1) and compression test (in the case of this study), but also to the displacement rate of test and manufacturing parameters.

Table 4 Values of the equivalent stiffness and Young modulus of the samples with the related statistics

It is important to recall that the objective of these additional tests applied on cylindrical specimens, is to compare the behavior, not the strength values, of the GE-SEZ, under compression load, to solid ABS material under the same solicitation. Deeper analysis and structural comparison of GE-SEZ with other lattice structures are discussed in the Sect. 4.3 of the paper.

4.2.3 Compression tests on the (GE-SEZ)_20×20×6 samples

As stated previously, the aim of this paper is not oriented to a detailed material or mechanical characterization of the parts. The main objective is to present newly developed lattice structures. However, it is essential to present a first mechanical characterization to quantify the most important mechanical properties listed below:

• The existence of the elastic domain;

• The existence of the plasticity domain that permits to delay the collapse of the structure (ductile behavior);

• The stability of each SEZ column composing the assembly of the GE-SEZ assembly at the compression regarding the buckling phenomenon.

Figure 13 presents the results of the compression tests applied to three similar specimens. The curves approximately present similar behaviors for all samples.

Fig. 13

Compression curve of ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ SEZ-GE_20×20×6 samples

4.2.3.1 Elastic analysis

• Equivalent stiffness and Young modulus

  The elastic domain is apparent and it is similar for the three ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ SEZ-GE_20×20×6 samples. The estimated equivalent stiffness and Young modulus of are reported in Table 4 with the related determination coefficient R². The table shows the average, the standard deviation, and the variation coefficient VC.

  According to the values of the determination coefficient R², it is clear that the precision of the modeling of the elastic domain is very high, reaching at least 98%. This is why the mean value of the stiffness and the Young modulus are to adopt as a references of the “${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ SEZ-GE_20×20×6” since the variation coefficient VC is very small (approximately 1%).

  So, for this ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ GE-SEZ_20×20×6 model, the equivalent stiffness is taken equal to:

  $$\begin{gathered} {\varvec{k}}_{{\varvec{a}}} = \mu_{{\varvec{k}}} = {\mathbf{4}}.{\mathbf{28}}\, {\raise0.7ex\hbox{${{\mathbf{kN}}}$} \!\mathord{\left/ {\vphantom {{{\mathbf{kN}}} {{\mathbf{mm}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{mm}}}$}} \hfill \\ {\mathbf{with}} \left\{ {\begin{array}{*{20}l} {{\varvec{s}}_{{\varvec{k}}} = {\mathbf{0}}.{\mathbf{0818}}\,\,{\raise0.7ex\hbox{${{\mathbf{kN}}}$} \!\mathord{\left/ {\vphantom {{{\mathbf{kN}}} {{\mathbf{mm}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{mm}}}$}} } \hfill \\ {{\mathbf{VC}}_{{\varvec{k}}} = {\mathbf{1}}.{\mathbf{191}}\% } \hfill \\ \end{array} } \right.. \hfill \\ \end{gathered}$$

  (18)

  Since the compression tests were applied on the ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ GE-SEZ_20×20×6, the equivalent stiffness of the whole GE-SEZ_20×20×6 could be deduced, using the spring models. Figure 14 presents the spring model of the whole GE-SEZ_20×20×6 deduced from the stiffness of ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ SEZ-GE_20×20×6 unity.

  Fig. 14

  

  Spring model of the whole GE-SEZ_20×20×6 starting from the spring model of the ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ GE-SEZ_20×20×6

  The equivalent model of the GE-SEZ is composed by ${\mathbf{4}}^{{\mathbf{3}}}$ springs that express ${\mathbf{4}}^{{\mathbf{3}}}$ of SEZ unities: 4 levels in series of 4² springs in parallel.

  The expression of the equivalent stiffness is formulated by the simplified spring model [63] as follows:

  • Stiffness of each horizontal level:

    $${\varvec{k}}_{{{\mathbf{level}}_{{\varvec{i}}} }} = {\mathbf{4}}^{{\mathbf{2}}} {\varvec{k}}_{{\varvec{a}}} = {\mathbf{16}}{\varvec{k}}_{{\varvec{a}}} .$$

    The stiffness of the four levels ${\varvec{k}}_{{{\mathbf{level}}}}$ in parallel expresses the global equivalent stiffness ${\varvec{k}}_{{{\mathbf{eq}}}}$:

    $$\begin{gathered} \frac{{\mathbf{1}}}{{{\varvec{k}}_{{{\mathbf{eq}}}} }} = \mathop \sum \limits_{{{\varvec{i}} = {\mathbf{1}}}}^{{\mathbf{4}}} \frac{{\mathbf{1}}}{{{\varvec{k}}_{{{\mathbf{level}}_{{\varvec{i}}} }} }} = {\mathbf{4}}\frac{{\mathbf{1}}}{{{\varvec{k}}_{{{\mathbf{level}}_{{\varvec{i}}} }} }} = \frac{{\mathbf{1}}}{{{\mathbf{4}} {\varvec{k}}_{{\varvec{a}}} }} \hfill \\ {\varvec{k}}_{{{\mathbf{eq}}}} = {\mathbf{4}} {\varvec{k}}_{{\varvec{a}}} = {\mathbf{17}}.{\mathbf{12}}\, {\raise0.7ex\hbox{${{\mathbf{kN}}}$} \!\mathord{\left/ {\vphantom {{{\mathbf{kN}}} {{\mathbf{mm}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{mm}}}$}} \hfill \\ \end{gathered}$$

    (19)

It is now possible to assemble any given number of GE-SEZ_20×20×6 and calculate the equivalent stiffness according to the spring model in the elastic domain [63].

• Apparent yield strength ${\varvec{F}}_{{\mathbf{e}}}$ and yield stress ${\varvec{\sigma}}_{{\varvec{y}}}$.

Table 5 groups the values of the yield strength F_e and the equivalent yield stress of the GE-SEZ samples.

Table 5 Values of the yield strength

Since the value of the VC is very low, the average of the apparent yield strength (7.34 kN) and yield stress (2.70 MPa) could be considered as characteristic values of the yield strength and stress of the ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ portion of the GE-SEZ_20×20×6 structure.

4.2.3.2 Post-elastic analysis: plasticity and damage

With regard to all samples of Fig. 13, it could be noticed that when the yield strength is reached, the plastic phase starts, with a stabilization of the resistance between 8 and 12% of strain. This behavior is quasi-similar to the J₂-plasticity model with isotropic hardening which might be the most used type of plasticity theory [61, 64]. The model is widely used in numerical simulation according to its simplicity from the numerical implementation regarding the physical considerations [65,66,67,68]. For uniaxial loads (traction and compression), the J₂-plasticity model is a mathematical model that decomposes the hardening in the plastic domain as a succession of segments [60, 64].

Hence, for this work linear models are proposed to fit the compression curves for the phase III and IV of deformation. The resulting models are presented in Fig. 15a–c.

Fig. 15

J₂ model for plastic domain a sample no. 1, b sample no. 2, c sample no. 3

More specifically, the post-elastic domain is composed of three major phases:

• Post-elastic relaxation: this domain corresponds to a small increase of the resistance until the yielding local maxima, and then decrease and stabilization of the resistance can be observed. The interpretation of this phenomenon is related to the viscous behavior of the material that can be essentially caused by the slop/displacement of the nodules into the rubbery phase of the ABS material [55, 69]. In this stage, the resistance is stabilized as the deformation continues. It essentially corresponds to a stress relaxation at a constant strain rate [61, 62]. Indeed, the programmed strain rate at the test parameters is constant (Sect. 3.2.2). Carrega (2000) mentioned that in the case of tension solicitation, the ABS can creep when attaining the yields stress [54]. This remark is very important since specific areas of the characterized structures are solicited in tension and are subsequently creeping, locally, generating the macroscale creep, which causes the stress relaxation observed in Figs. 13 and 15.

  To visualize the tensile zones on the SEZ units, a simple compression test simulation for a unique SEZ unit was performed. Figure 16 presents the results of the simulation for a SEZ unit in terms of normal stress to quantify the stretched areas (stress positive values) and the compressed areas (stress negative values). According to the results of the simulation, the only areas that are compressed are located around the necks of the SEZ unity; this corresponds to the neighborhood of the minimal diameter of the structure, while all the other parties of the structure operate in traction. Therefore, this simple simulation allows to show the areas where the creeps and the relaxation are concentrated located in the tensile areas.

  Fig. 16

  

  Normal stress distribution of one compressed SEZ unit

  At the end of this stage, the whitening of the necks neighborhood of the SEZs unities began to be more apparent as presented in Fig. 17. The compressed areas perfectly correspond to the compressed zones of Fig. 16. In fact, according to Makke (2011), under hydrostatic load (compression), the failure of the amorphous polymers is caused by the cavitation phenomena, followed by crazing [69]. The same phenomenon was observed for the benchmark structure that we analyzed in the next section [57,58,59].

  Fig. 17

  

  The deformed ${\raise0.7ex\hbox{${\mathbf{1}}$} \!\mathord{\left/ {\vphantom {{\mathbf{1}} {{\mathbf{4}}^{{\mathbf{3}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\mathbf{4}}^{{\mathbf{3}}} }$}}$ GE-SEZ_20×20×6

• Hardening phase: After the relaxation phenomenon and the starting of the cavitation of the necks of the SEZ units, the hardening of the GE-SEZ structures began. In this phase, three principal sources of the observed hardening could be considered:

  • The plasticity/hardening related to the non-linear behavior of the rubber phase of the ABS material as given in the phases III and IV [54, 61, 62];

  • The increase of the resistance related to the friction between the SEZ-unites, because the SEZ unites are tangent in some positions (at the greatest diameters) and the pressure of contact increases on these positions (see left arrows of the Fig. 17).

• Densification and damage phase: at this stage, SEZ necks are broken and the fitting of the blocs of the SEZ units, one into another, started causing the hardening increase. This corresponds to the densification stage of compression. This is in total concordance with the densification of lattice structures under compression that are manufactured by AM technologies [23, 57,58,59].

4.2.3.3 General model

According to the J₂ plasticity model, the deformation is linear with hardening; so the rheological equivalent model of the global mechanical behavior could be modeled as presented in Fig. 18.

Fig. 18

Rheological model proposed [70, 71]

Where: E is the equivalent Young modulus; K is the slope of the plastic linear domain (estimated at the Fig. 20a–c according to the J₂-plastcity model); σ_e: corresponds to the elastic stress presented in Table 5 and denoted σ_y; ε_e and ε_p: resp. equivalent to the elastic and plastic strains at a given plastic solicitation of the strain–stress curve.

4.3 Benchmark study

To compare the new design with the works already existing in the bibliography, a benchmark was conducted. This latter compares the normalized mechanical properties (Young modulus and yield strength) of the three sample of the new design with 17 other structures. Table 6 groups the reference structures, their designation, the mechanical properties before normalization, the relative density and the compression platen displacement speed for each reference.

Table 6 Mechanical properties and compression platen speed of the benchmark structures and GE-SEZ

Furthermore, the failures modes analysis (Sect. 4.3.3) will permit to discuss the global and local stability behaviors and compare them in the benchmark analysis.

For a good reading of Table 6, below some related remarks guided by the exponents presented in the table.

• Note (d): Khan et al. studied an experiments plan composed by 12 different gyroid structures that differ one another by the unit cell size and the volume fraction. The three more resistant gyroids were chosen for the benchmark, named in this work Gyr 1, Gyr 2 and Gyr 3. Since Khan et al. did not present the numerical results tables of the compression tests, the corresponding Young modulus and yield stresses were extracted graphically from Fig. 9 of Khan et al. [57].

• Note (e): Gautam and Idapalapati studied three Struts Reinforced Kagome (SRK) structures that are composed by three struts by cell differentiated by the diameter and the length [58].

• Note (f): Maconachie et al. adopted a design of experiments (DOE) related to 20 different gyroid structures. Its DOE consists of varying the cell count per layer and the wall thickness. Eleven of these gyroids are analyzed in this paper where they correspond to the most resistant ones; the resistance and/or the Young modulus are superior to the GE-SEZ designed. Maconachie et al. did not calculate the RD, but they formulated empirical expressions of it. According to their work, the RD depends on the cell count per layer and the wall thickness. In Table 6, the RD are calculated from Eq. (8) of Maconachie et al. [59].

4.3.1 Step 1 of comparison: Mechanical properties related to relative density

As stated in the previous paragraph, step 1 of the comparison compares the structures from the following point of views:

• First normalized Young modulus

  $$Er_{1} = {\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E {{\text{RD}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RD}}}$}}\quad \left[ {{\text{MPa}}} \right].$$

  (20)

• First normalized yield stress

  $$\sigma_{y} r_{1} = {\raise0.7ex\hbox{${\sigma_{y} }$} \!\mathord{\left/ {\vphantom {{\sigma_{y} } {{\text{RD}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RD}}}$}} \quad \left[ {{\text{MPa}}} \right].$$

  (21)

Figure 19a, b present, respectively, the classification of the structures according to the ${\varvec{Er}}$ and ${\varvec{\sigma}}_{{{\varvec{yr}}}}$.

Fig. 19

Structures classification a according to Er₁, b according to σ_yr₁ (MPa)

From Fig. 19a, b:

• According to the normalized modulus Er₁, the GE-SEZ structures are classified in the top 8 of the total of 20 structures;

• According to the normalized yield stress σ_yr₁, the GE-SEZ structures are classified in the 7th, 8th and 9th positions of the 20 structures;

4.3.2 Step 2 of comparison: Mechanical properties related to relative density and compression displacement speed

In this step, the idea is to start from the fact that the mechanical properties (E and σ_y) are highly enhanced (increasing) according to the speed rate of the solicitation. While consulting the benchmark used in this paper [57,58,59], it was clear that each article used a given speed of compression platen displacement. This is why the authors propose in this paragraph to normalize the mechanical properties using the second set of indicators:

• Second normalized Young modulus:

  $$Er_{2} = {\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E {\left( {{\text{RD}} \times v} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {{\text{RD}} \times v} \right)}$}}\quad \left[ {{\text{MPa}}/\left( {{\text{mm}}\,{\text{s}}^{ - 1} } \right) } \right]$$

  (22)

• Second normalized yield stress

  $$\sigma_{y} r_{2} = {\raise0.7ex\hbox{${\sigma_{y} }$} \!\mathord{\left/ {\vphantom {{\sigma_{y} } {\left( {{\text{RD}} \times v} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {{\text{RD}} \times v} \right)}$}} \quad \left[ {{\text{MPa}}/\left( {{\text{mm}}\,{\text{s}}^{ - 1} } \right) } \right].$$

  (23)

Figure 20a, b show that the new GE-SEZ design is competitive while the three samples belong to the top 5 of structures at the time of classification

Fig. 20

Structures classification a according to Er₂, b according to σ_yr₂ (MPa)

It is to notice that for the first three lattices SRK 1 to SRK 3, the corresponding values can be considered as outliers. It is essentially due to the very low value of the RD of these structures. But the ultimate conclusion from Fig. 20 plots is that the GE-SEZ design surpasses the other structures from the second normalization stand-point, where all the surpassed structures correspond to a gyroid geometry.

4.3.3 Failure modes assessment

The failure modes assessment is important to be considered to compare the new design and to position it within the large spectrum of existing structures, especially those corresponding to this benchmark [57,58,59].

Table 7 groups the failure and collapse modes of the benchmark structures, and also the instabilities denoted on them.

Table 7 Failure/collapse modes and stability analysis

After analyzing the list of failure modes and stability discussion of Table 7, it is possible to draw up the advantages of the designed GE-SEZ structure as follows:

• Local and global stabilities are ensured because no sudden behavior has appeared;

• Stability of the strain–stress curve leading a rigorous modeling of the mechanical properties and permitting a reliable behavior’s expectation of the GE-SEZ structure;

• No filament fracture is observed, so no local weakness could happen;

• Even when the structure collapses, the nesting of the SEZ unities one into another allows to increase the resistance by densification with a global stable behavior.

5 Conclusions

The study presented in this paper began by a preliminary intuition to couple the resistance of the KT column against buckling with the lightness given by the Schoen minimal gyroïd structure. The objective was to produce a new family of high compressive light weight structures that resists against buckling at compression solicitation with clumped-clumped limit conditions. The mathematical formulation of the problem was presented according to the “surface to volume ratio” and the “volume” equivalences between the KT and gyroïd structures. For a given couple of occurrence parameters $\left( {{\varvec{n}} = {\mathbf{6}}, {\varvec{m}} = {\mathbf{20}}} \right)$, the geometric and dimensional solutions of the problem were numerically calculated and the thickness of the (GE-SEZ)_20×20×6 structure was determined.

The main objective of the GE-SEZ samples processing is to characterize their stability against buckling, and simultaneously to model the mechanical behavior. In addition, to classify the new design within the different families of lattice structures, a benchmark study was carried out. Several conclusions can be drawn up from the observed behavior and benchmark analysis:

• The elasticity of the structures is quasi-perfect, since the precision of the equivalent stiffness, estimated at $4.2833\, {\raise0.7ex\hbox{${{\text{kN}}}$} \!\mathord{\left/ {\vphantom {{{\text{kN}}} {{\text{mm}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{mm}}}$}}$ is higher than 98%. The corresponding equivalent Young modulus is estimated at $85.67$ MPa.

• After reaching an equivalent yield stress around at 2.70 MPa, the relaxation phenomenon is observed. This phenomenon is typical to the rubbery copolymers lie ABS material.

• After relaxation, the quasi-linear plasticity mode appears: The phase III and IV of the deformation continues until the end of the test. The J₂-plasticity model was adopted to describe the behavior of these zones.

• The whitening of the necks of the GE-SEZ unities started when the deformation reached the limit of phase III. Hence, the structure damage began: the necks were broken and the densification of the mater started until reaching the end of the test at 12 mm of the displacement.

Finally, the stability of the GE-SEZ unities is ensured since no buckling is observed on the (GE-SEZ)_{20 × 20 ×  6} unities.

Compared to more than 30 printed structures made by the same process and material, gyroid and SRK structures, the benchmark study permitted to test the performance of the new design from a mechanical properties and lightweight stand-points. The authors do attest that the structure is very competitive according to the results of Sect. 4.3 and the related discussion related to stability assessment of the structures.

5.1 Further works

Future research will focus on four major points:

• The mathematical analysis of the optimality of the KT structures according to the mapping (4);

• The mechanical study of other KT structures;

• GE-SEZ building using complex machines as the 3DP 1000 [72] or the X400 Printers [73] and mechanical testing, using robust design of experiment;

• Varying geometries and materials of the GE-SEZ structures for a larger benchmark analysis.

Appendices

Appendix A1: Symmetry proof of the pinned–pinned KT column

Symmetries definition:

• (a) Symmetry between $\left( {x,y_{1} \left( x \right)} \right)$ and $\left( {x,f_{2} \left( x \right)} \right)$ according to the $\left( {\Delta_{1} :x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}} \right)$ axis;

• (b) Symmetry of $\left( {x,f_{2} \left( x \right)} \right)$ itself around the $\left( {\Delta_{2} :x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)$ axis;

• (c) Symmetry between $\left( {x,f_{1} \left( x \right)} \right)$ and $\left( {x,f_{3} \left( x \right)} \right)$ according to the $\left( {\Delta_{2} :x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)$ axis;

Proof

Symmetry (a)

To prove the symmetry between $\left( {x,f_{1} \left( x \right)} \right)$ and $\left( {x,f_{2} \left( x \right)} \right)$ relatively to the axis $\left( {\Delta_{1} :x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}} \right)$, we prove that:

$$f_{1} \left( x \right) = f_{2} \left( {x + 2\alpha } \right)\quad {\text{where}} \,\alpha = \frac{1}{4} - x \forall x \in \left[ {0,\frac{1}{4} } \right].$$

(24)

We calculate the right member of the Eq. (24):

$$f_{2} \left( {x + 2\alpha } \right) = f_{2} \left( {x + 2\left( {\frac{1}{4} - x} \right)} \right) = f_{2} \left( { - x + \frac{1}{2}} \right)$$

$$f_{2} \left( {x + 2\alpha } \right) = f_{2} \left( { - x + \frac{1}{2}} \right) = \frac{3}{2}\left( { - 3 + 16\left( { - x + \frac{1}{2}} \right) - 16\left( { - x + \frac{1}{2}} \right)^{2} } \right).$$

Thus $y_{2} \left( {x + 2\alpha } \right) = \frac{3}{2}\left( {1 - 16x^{2} } \right) = y_{1} \left( x \right)$

$$\forall x \in \left[ {0,\frac{1}{4} } \right].$$

Symmetry (b)

To prove the symmetry between $\left( {x,f_{2} \left( x \right)} \right)$ to itself around the axis $\left( {\Delta_{1} :x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)$, we prove that:

$$f_{2} \left( x \right) = f_{2} \left( {x + 2\alpha } \right)\quad {\text{where}}\,\alpha = \frac{1}{2} - x\quad \forall x \in \left[ {\frac{1}{4},\frac{1}{2} } \right]$$

(24a)

We calculate the right member of the Eq. (24a):

$$f_{2} \left( {x + 2\alpha } \right) = f_{2} \left( {x + 2\left( {\frac{1}{2} - x} \right)} \right) = f_{2} \left( { - x + 1} \right)$$

$$f_{2} \left( {x + 2\alpha } \right) = f_{2} \left( { - x + 1} \right) = \frac{3}{2}\left( { - 3 - 16x^{2} + 16x} \right)$$

Thus $f_{2} \left( {x + 2\alpha } \right) = f_{2} \left( x \right)\quad \forall x \in \left[ {0,\frac{1}{2} } \right].$

Symmetry (c)

To prove the symmetry between $\left( {x,f_{1} \left( x \right)} \right)$ and $\left( {x,f_{2} \left( x \right)} \right)$ relatively to the axis $\left( {\Delta_{1} :x = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}} \right)$, we prove that:

$$f_{1} \left( x \right) = f_{3} \left( {x + 2\alpha } \right)\quad {\text{where}}\,\alpha = \frac{1}{2} - x\quad \forall x \in \left[ {0,\frac{1}{4} } \right]$$

(24b)

We calculate the right member of the Eq. (24b):

$$f_{3} \left( {x + 2\alpha } \right) = f_{3} \left( {x + 2\left( {\frac{1}{2} - x} \right)} \right) = f_{3} \left( { - x + 1} \right)$$

$$f_{3} \left( {x + 2\alpha } \right) = f_{3} \left( { - x + 1} \right) = \frac{3}{2}\left( { - 15 - 16\left( { - x + 1} \right)^{2} + 32\left( { - x + 1} \right)} \right)$$

$$f_{3} \left( {x + 2\alpha } \right) = \frac{3}{2}\left( {1 - 16x^{2} } \right)$$

Thus $f_{3} \left( {x + 2\alpha } \right) = f_{1} \left( x \right)\quad \forall x \in \left[ {0,\frac{1}{2} } \right].$

Appendix A2: SVR and volume of the GE-SEZ structure calculation

The external and internal lateral surfaces of the SEZ structure, are calculated using the Gauss formula (25):

$$S_{{{\text{lateral}}}} = 2\pi \mathop \int \limits_{a}^{b} g\left( x \right)\sqrt {1 + \left( {g^{\prime}\left( x \right)} \right)^{2} } {\text{d}}x$$

(25)

We apply Eq. (15) on the curve $C_{{{\text{ext}}}} \left( {x,\tilde{y}_{{{\text{ext}}}} } \right)$ presented in the Eq. (12.2):

$$S_{{{\text{lateral}} \left[ {0,\frac{L}{4m}} \right]}} = 2\pi \mathop \int \limits_{0}^{\frac{L}{4m}} \tilde{y}_{{{\text{ext}}}} \left( x \right)\sqrt {1 + \left( {\tilde{y}_{{{\text{ext}}}}^{\prime } \left( x \right)} \right)^{2} } {\text{d}}x.$$

(26)

This equation describes a quart of the surface of a SEZ. In other words, since the authors consider the different symmetries of the SEZ structure, as proved in the Sect. 3.1.1, the lateral revolution surface of the SEZ will be equal to four times the surface calculated by the Eq. (26). Thus, the total external surface is given by Eq. (17):

$$S_{{{\text{SEZ}} \left[ {0,\frac{L}{m}} \right]}} = 4 \times \left( {2\pi \mathop \int \limits_{0}^{\frac{L}{4m}} \tilde{y}_{{{\text{ext}}}} (x)\sqrt {1 + \left( {\tilde{y}_{{{\text{ext}}}}^{\prime } \left( x \right)} \right)^{2} } {\text{d}}x} \right).$$

(27)

It should be noted that in the Eq. (15), the index of $S_{{{\text{lateral}} \left[ {0,\frac{L}{4m}} \right]}}$ specifies that the calculation is made on the interval $\left[ {0,\frac{L}{4m}} \right]$. The index of $S_{{{\text{SEZ}} \left[ {0,\frac{L}{m}} \right]}}$ mentions that the calculation of this surface is performed on the whole length of the SEZ in the corresponding interval of $\left[ {0,\frac{L}{m}} \right]$ (see Fig. 5). An equivalent calculus could be performed by Pappus theorems [52], using the orthogonal distance between the barycenter of the function that will be spinning.

From the mapping (4), we recall that:

$$\tilde{y}_{{{\text{ext}}}} \left( x \right) = c\left( {a\left( {1 - 16\left( {d x} \right)^{2} } \right) + b} \right).$$

The derivative of $\tilde{y}_{{{\text{ext}}}} \left( x \right)$ is equal to:

$$\tilde{y}_{{{\text{ext}}}}^{\prime } \left( x \right) = \frac{{d\left( {\tilde{y}_{{{\text{ext}}}} \left( x \right)} \right)}}{{{\text{d}}x}} = 32acd^{2} x.$$

(28)

The Eq. (27) becomes:

$${\text{SEZ}}_{{ \left[ {0,\frac{L}{m}} \right]}} = 8\pi \mathop \int \limits_{0}^{\frac{L}{4m}} c\left( {a\left( {1 - 16\left( {{\text{d}}x} \right)^{2} } \right) + b} \right)\sqrt {1 + \left( {32acd^{2} x} \right)^{2} } {\text{d}}x,$$

which leads to the expression (29):

$$\begin{array}{c} \begin{array}{c} P_{n,m}\left(a,b\right)=\frac{8\ \pi \ \left(A\times B-C\times D\right)}{E}-\gamma \\ \left\{ \begin{array}{c} \ \\ A=A_{n,m}\left(a,b\right)=256a\left(a+b\right)d^2c^2+1 \\ B=B_{n,m}\left(a,b\right)={\mathrm{log} \left(\sqrt{32a*c*d^2+1}+32acd^2x_1\right)\ } \\ C=C_{n,m}\left(a,b\right)=32acd^2x_1\sqrt{{\left(32acd^2x_1\right)}^2+1} \\ D=D_{n,m}\left(a,b\right)=256ac^2d^2\left(a\left(8d^2x^2_1-1\right)-b\right)+1 \\ E_{n,m}\left(a,b\right)=16{\left(32acd^2\right)}^2 \end{array} \right. \end{array} \\ s.t\ \left\{ \begin{array}{c} c=\frac{L}{2n\left(a+b\right)} \\ d=\frac{m}{L} \\ x_1=\frac{L}{4m} \\ \gamma ={\left({S}/{V_{Gy}}\right)}_{Gyroid} \\ V_{Gy}:the\ effective\ volume\ of\ the\ Gyroid \end{array} \right. \end{array}$$

(29)

Since the cubic volume, for $n^{2} \times m$ SEZ structures confined into the is equation to L³, the ${\text{SVR}}_{{\left( {\text{GE } - \text{ SEZ}} \right)_{{n^{2} \times m}} }}$ is obtained by the following equation:

$${\text{SVR}}_{{\left( {\text{GE } - \text{ SEZ}} \right)_{{n^{2} \times m}} }} = \frac{{n^{2} {\text{mS}}_{{{\text{SEZ}} \left[ {0,\frac{L}{m}} \right]}} }}{{L^{3} }}.$$

(30)

We calculate the volume of the GE-SEZ assembly as a sum of SEZs volumes Eq. (31).

The volume of a SEZ unit if given by the Gauss formula presented in the Eq. (32):

$$V_{{\text{GE } - \text{ SEZ}}} = n^{2} \times m V_{{{\text{SEZ}}}}$$

(31)

$$V_{{{\text{SEZ}}}} = \pi \mathop \int \limits_{0}^{\frac{L}{m}} \left( {y_{{{\text{ext}}}}^{2} - y_{{\text{int}}}^{2} } \right){\text{d}}x$$

(32)

Since the authors consider the symmetries introduced in the Sect. 3.1.1 (see “Appendix A1”), the volume of the SEZ can be calculated by:

$$V_{{{\text{SEZ}}}} = \pi 4 \times \left( {\mathop \int \limits_{0}^{\frac{L}{4m}} \left( {y_{{{\text{ext}}}}^{2} - y_{{\text{int}}}^{2} } \right){\text{d}}x} \right).$$

(33)

where

$$y_{{{\text{ext}}}}^{2} - y_{{\text{int}}}^{2} = \left( {y_{{{\text{ext}}}} - y_{{\text{int}}} } \right)\left( {y_{{{\text{ext}}}} + y_{{\text{int}}} } \right)$$

according to the Eq. (11.2):

$$y_{{{\text{ext}}}} - y_{{\text{int}}} = e.$$

And according to the expression of the functions $y_{{{\text{ext}}}}$ and $y_{{\text{int}}}$:

$$V_{{{\text{SEZ}}}} = \frac{4\pi e}{{nm}}\left[ {Ln + enm - \frac{{aL^{2} }}{{12\left( {a + b} \right)}}} \right].$$

(34)

Hence, the volume of the ${\text{GE } - \text{ SEZ}}_{n \times n \times m}$ assembly is equal to:

$$V_{{\text{GE } - \text{ SEZ}}} = n^{2} m V_{{{\text{SEZ}}}} = 4\pi en\left[ {Ln + enm - \frac{{aL^{2} }}{{12\left( {a + b} \right)}}} \right].$$

(35)

The volume equivalence is ensured by the equality between the GE-SEZ volume and the volume of the Gyroïd as shown below:

$$\frac{{V_{{\text{GE } - \text{ SEZ}}} }}{{V_{{\text{G}}} }} = 1.$$

(36)

Reporting the expression (35) in (38), the second characteristic equation corresponds to the Eq. (37):

$$4\pi en\left[ {Ln + enm - \frac{{aL^{2} }}{{12\left( {a + b} \right)}}} \right] - V_{{\text{G}}} = 0$$

(37)

$$\begin{gathered} A_{a,b} e^{2} + B_{a,b} e + C_{a,b} = 0 \hfill \\ \left\{ {\begin{array}{*{20}l} {A_{a,b} = \frac{{4\pi n^{2} m}}{{V_{{\text{g}}} }}} \hfill \\ {B_{a,b} = \frac{4\pi n}{{V_{{\text{g}}} }}\left( {Ln - \frac{{aL^{2} }}{{12\left( {a + b} \right)}}} \right)} \hfill \\ {C = - 1} \hfill \\ \end{array} } \right.. \hfill \\ \end{gathered}$$

(38)

The characteristic Eq. (37) permits to calculate the thickness e, that permits to ensure the second characteristic equation, that is to say, the equality of the volumes of the GE-SEZ and the gyroid.

The discriminant of the equation is given by:

$$\Delta = B_{a,b}^{2} - 4 A_{a,b} C_{a,b} .$$

Hence

$$\Delta = \left( {\frac{4\pi n}{{V_{{\text{g}}} }}\left( {Ln - \frac{{aL^{2} }}{{12\left( {a + b} \right)}}} \right)} \right)^{2} + 4\left( {\frac{{4\pi n^{2} m}}{{V_{{\text{g}}} }}} \right).$$

Since the parameters n, m and V_g are strictly positive, the discriminant is also strictly positive.

So the roots of the Eq. (37) are defined as:

$$e = \left\{ {\begin{array}{*{20}c} {e^{ + } = \frac{{ - B_{a,b} + \sqrt \Delta }}{{2A_{a,b} }}} \\ {e^{ - } = \frac{{ - B_{a,b} - \sqrt \Delta }}{{2A_{a,b} }}} \\ \end{array} } \right..$$

(39)

Appendix A3: Statistics on dimensions measurement of the $\left( {{\text{GE-SEZ}}} \right)_{{20 \times 20 \times 6}}$ and the cylindrical specimens

Table 8 groups the statistics of the dimension measurement related to the biggest diameter, neck diameter (smallest diameter), the width and height of the $\left( {{\mathbf{GE}}{\text{-}}{\mathbf{SEZ}}} \right)_{{{\mathbf{20}} \times {\mathbf{20}} \times {\mathbf{6}}}}$ manufactured.

Table 8 Statistics related to $\left( {\text{GE-} \text{ SEZ}} \right)_{20 \times 20 \times 6}$ samples dimensions

Table 9 groups the statistics of the dimension measurement related to the diameter and height of the cylindrical specimens manufactured.

Table 9 Statistics of dimensions of the cylindrical specimens