Adhesive connections in glass structures—part II: material parameter identification on thin structural silicone

Abstract

The present paper proposes two methodologies of identifying hyperelastic material parameters of thin structural silicones based on so-called direct and inverse methods. Based on part I of this paper, analytical investigations were performed to conduct homogeneous experiments with structural silicones. To obtain more insight wether or not an experiment provides a homogeneous stress state, the so-called triaxiality was introduced, which allows one to illustrate differences between homogeneous and inhomogeneous experiments. With the help of this scalar, it was possible to design experimental test setups, which ensure a homogeneous stress and strain distribution within the tested rubber-like material. Furthermore an engineering approach to determine the testing speed of arbitrary experiments dependent on one reference testing speed and experiment was presented. This approach ensured equivalent strain energies between arbitrary and reference test specimens during testing, by which expensive strain rate controlled experiments can be relinquished. Based on these analytical studies, experimental data could be provided for the material parameter identification, which exhibits firstly a nearly homogeneous stress state in accordance to the desired stress and strain field of the applied mathematical model and secondly providing nearly equivalent strain energies within different experimental test set-ups and geometries of test specimens. Returning to the present paper, the first methodology identifies simultaneously hyperelastic material parameters based on a set of conventional and homogeneous experimental tests, like uniaxial tension and uniaxial compression, biaxial tension as well as shear-pancake tests. The second methodology determines inversely hyperelastic material parameters utilizing the inverse Finite Element Method based on one single unconventional and inhomogeneous experimental test, here a microindentation test. The main idea is to obtain reliable hyperelastic material parameters based on a single, inhomogeneous experiment to avoid many, time-consuming homogeneous experiments. To validate the inversely determined hyperelastic material parameters, simultaneous multi-experiment data fits are performed to relate the obtained material parameters to those of the microindentation tests. Considering the set of homogeneous experiments, two classical hyperelastic constitutive equations (Neo-Hooke and Mooney–Rivlin) were utilized to determine constitutive parameters. Due to the simplicity of the classical material laws, a more sophisticated, novel phenomenological hyperelastic material law will be proposed and compared with the results of the classical models respectively the results obtained by a modern hyperelastic material model after Kaliske & Heinrich, which generally delivers outstanding results for the material parameter identification.

1 Introduction

In general, structural silicones belong to the group of hyperelastic materials, which are characterized by strain energy density functions respectively Helmholtz free energy functions. In literature, there exist three ways of classifying Helmholtz free energy functions: (i) molecular-statistical hyperelastic material models accounting for the molecular structure and the motion of the macromolecules (Treloar 1975; Arruda and Boyce 1993; Yeoh and Fleming 1997; Kaliske and Heinrich 1999; Miehe et al. 2004). (ii) phenomenological Helmholtz free energy functions, which are characterized by treating hyperelasticity only under a mathematical framework without referencing to molecular concepts (Mooney 1940; Rivlin 1948; Ogden 1972). Since for both models material parameters have to be determined, within the last classification (iii) tabulated formulations of hyperelasticity were developed, where the experimental data is used directly as input data to characterize the material behavior (Marlow 2003; Kolling et al. 2007). Hence, no material parameters have to be determined within this class of constitutive models.

Since the focus of the present paper lies in the determination of hyperelastic material parameters, for the following studies phenomenological and molecular-statistical material models will be utilized, where material parameters will be determined based on experimental tests presented in part I (Drass et al. 2017). In general, there exist two methods for obtaining hyperelastic material parameters. The conventional procedure is characterized by fitting hyperelastic material parameters based on experimental data of homogeneous experiments, which can be understood as direct method. Therefore, expressions for the stress strain behavior dependent on the deformation state can be analytically derived from hyperelastic constitutive equations to determine material parameters by regression analyses (Ogden et al. 2004; Berselli et al. 2011; Khajehsaeid et al. 2013; Gorash et al. 2015). Here, in addition, one can choose between incompressible and slightly compressible hyperelastic material models, however, in the present work incompressibility will assumed for the sake of mathematical convenience.

An unconventional method of material parameter identification (MPI) is based on inhomogeneous experiments, where arbitrary stress and strain fields are inherent in the specimen. From this, the inverse Finite Element Method (iFEM) based on Mainçon (2004a), Mainçon (2004b), Tessler and Spangler (2004), Hauser et al. (2008), Pacheco et al. (2016) can be utilized, where material parameters are inversely determined. Another established expression for iFEM is Finite Element Model Updating (FEMU) technique. FEMU describes a method, where, for instance, numerical calculations with randomly chosen initial material parameters are conducted iteratively and compared with experimental data as long as the residuum between experiment and simulation is smaller than a fixed tolerance (Farhat and Hemez 1993; Cottin et al. 1984; Avril et al. 2008; Pagnacco et al. 2005). Additionally, a gradient-based optimization algorithm can be coupled with the FEMU results to improve the constitutive parameters (Drass and Schneider 2016b).

In part I (Drass et al. 2017), homogeneous and inhomogeneous experiments were presented, which are the basis for the MPI. Based on homogeneous experiments (Uniaxial Tension—UT, Uniaxial Compression—UC, Biaxial Tension—BT, Shear-Pancake—SPC) on TSSA, in the present paper a simultaneous multi-experiment data fit will be presented and compared with inversely determined material parameters based on an inhomogeneous experiment, here a microindentation test (MI). For this purpose, the iFEM coupled with an optimization algorithm will be utilized to simulate the MI test under optimizing material parameters.

Generally, regarding the analyzed transparent silicone, TSSA, which belong to the group of rubber-like materials, a broad application form are laminated connections (Santarsiero et al. 2016). The laminated connection is achieved by directly bonding glass to metal using adhesives like TSSA, SentryGlas or PVB (see Fig. 1). To reduce the application effort, which is obviously with regard on classical connection systems, like articulated and undercut point fixing courtesies (Overend 2005), in laminated connections the same production process as for laminated glass components is utilized, which was analyzed by Santarsiero et al. (2016). Furthermore, by utilizing laminated connections, thermal bridges and local stresses within the glasses can be reduced. As local bonding materials, transparent structural silicones have prevailed because of their transparent appearance and mechanical properties (Sitte et al. 2011).

Fig. 1

Point fixing connected to a glass pane with TSSA—Permission of Dow Corning Europe SA (2017)

2 Basics on continuum mechanics

Deforming a body ${\mathcal {B}_0}$ to ${\mathcal {B}}$, the material points ${{P}_0}$ of the reference configuration are mapped to the current configuration. The position vectors $\mathbf {X}$ and $\mathbf {x}$ of the reference and current configuration describe the movement of ${{P}_0}$ by a second order tensor, which is called deformation gradient $\mathbf F = \mathrm{{Grad}}\,\mathbf {x}$.

Considering incompressible materials, the determinant of $\mathbf F$ must satisfy $\det \mathbf F = J = 1$. The assumption of incompressibility enables one to directly solve the stress strain relationship for hyperelastic materials, which is a common assumption for the sake of mathematical convenience. In contrast, regarding compressible hyperelasticity, a relation between the principle stretches $\lambda _i$ and the relative volume J exists, hence it can only be solved with respect to J using Newton’s method.

With the help of the polar decomposition, the deformation gradient can be written as $\mathbf F = RU = VR$, where the left and right Cauchy-Green stretch tensors can be derived by $\mathbf b = \mathbf{V ^2} = \mathbf F \mathbf{F ^\mathrm{T}}$ and $\mathbf C = \mathbf{U ^2} = \mathbf{F ^\mathrm{T}}{} \mathbf F$.

In the area of hyperelasticity, there exists a so-called Helmholtz free energy $\varPsi \left( \mathbf C \right)$ or $\varPsi \left( \mathbf b \right)$ defined per unit volume, which is symmetrically dependent on the principal stretches $\lambda _i$ with $i \in \left[ {1,2,3} \right]$. The principal stretches can be calculated by ${\lambda _i} = 1 + \varepsilon _i^{\mathrm{{eng}}}$, where $\varepsilon _i^{\mathrm{{eng}}}$ represents the engineering strain. Generally, hyperelastic constitutive equations can be formulated based on strain invariants of b, which leads to the strain invariants

$$\begin{aligned} {I_{\mathbf{{ b}}}}= & {} {b_{ii}} = \lambda _\mathrm{{1}}^2 + \lambda _2^2 + \lambda _3^2, \end{aligned}$$

(1)

$$\begin{aligned} {II_{\mathbf{{ b}}}}= & {} {1 \over 2}\left( {{b_{ii}}{b_{jj}} - {b_{ji}}{b_{ij}}} \right) \nonumber \\= & {} \lambda _\mathrm{{1}}^2\lambda _2^2 + \lambda _2^2\lambda _3^2 + \lambda _\mathrm{{1}}^2\lambda _3^2, \end{aligned}$$

(2)

$$\begin{aligned} {III_{\mathbf{{ b}}}}= & {} \det {b_{ii}}= \lambda _\mathrm{{1}}^2\lambda _2^2\lambda _3^2. \end{aligned}$$

(3)

Regarding compressible hyperelasticity, the isochoric part of b can be reformulated into ${\bar{\mathbf{b}}} = {J^{ - {2 \over 3}}}{} \mathbf{{b}}$, whereas ${\bar{\mathbf{b}}} = \mathbf{{b}}$ for incompressible materials. The principal engineering stresses ${t_i}$ for incompressible materials can be derived by

$$\begin{aligned} {t_i} = {{\partial \varPsi } \over {\partial {\lambda _i}}} - p\lambda _i^{ - 1} \equiv {\sigma _i}\lambda _i^{ - 1}\;\;\;\mathrm{{with}}\;\;\;i \in \left[ {1,2,3} \right] , \end{aligned}$$

(4)

where p is a Lagrange multiplier, which can be obtained by boundary constraints and $\sigma _i$ describes the principal Cauchy stress in the current configuration. To get more insight into nonlinear solid mechanics with the focus on rubber-like materials respectively hyperelasticity, the reader is referred to the classical monographes of Holzapfel (2000) and Chaves (2013).

3 Isochoric, hyperelastic Helmholtz free energy functions

Considering a Helmholtz free energy $\varPsi (\mathbf F )$, there exist two approaches to built up this functional under exclusion of tabulated formulations like Kolling et al. (2007); Marlow (2003). The first approach is based on molecular-statistics, which analyzes the deformation behavior of rubber-like materials on a micro-scale level deriving the stress strain interaction from idealized, macromolecular models (cf. Sect. 3.1). The second approach treats the mechanical behavior of rubber-like materials on a phenomenological level regarding hyperelasticity from a mathematical viewpoint, while disregarding the molecular concept (cf. Sects. 3.2 and 3.3).

3.1 Molecular-statistical constitutive laws

The elementary statistical theory was found by the work of Kuhn (1934, 1936a, b), Kuhn and Grün (1942) and James and Guth (1943), where rubber-like materials are treated as materials exhibiting long, flexible chain molecules, weak intermolecular forces and partial cross linkings between molecules, which are forming networks. During the deformation process the entropy decreases in accordance to statistical thermodynamics, hence it can be postulated that the change in entropy is directly dependent on the work done by temperature. The macroscopic Neo-Hookean free energy attributed with a micro-mechanical background reads

$$\begin{aligned} \varPsi = {\mu \over 2}{I_{{\bar{\mathbf{b}}}}}\;\;\;\mathrm{{with}}\;\;\;\mu \equiv nkT, \end{aligned}$$

(5)

where n represents the number of network chains per unit volume, k is the Boltzmann’s constant and T is the absolute temperature. Since no free energy should be available in the undeformed state, which is conterminous when the first isochoric invariant is ${I_{\bar{\mathbf{b}}}} = 3$, the originally proposed form of the micro-mechanically motivated Neo-Hookean (NH) constitutive law (Treloar 1975) is given by

$$\begin{aligned} {{\varPsi _{\mathrm{{iso,NH}}}} = {\mu \over 2}\left( {{I_{\bar{\mathbf{b}}}}- 3} \right) , } \end{aligned}$$

(6)

which will be considered in the following, since only one material parameter has to be determined.

Due to well-known reasons the affine deformation assumption stays in contrast to experimental results (Miehe and Schänzel 2013), consequently a non-affine deformation was introduced by the micro-sphere model, which was developed by Miehe et al. (2004). Since the proposed micro-mechanically motivated models do not account for topological constraint effects because the idealized polymer networks are free in motion and only considering a single polymer chain, the constrained segment theories and constrained junction theories have been developed. In this work, the constrained segment theory, which was seized by Deam and Edwards (1976), Edwards and Vilgis (1988), Heinrich and Straube (1983), Kaliske and Heinrich (1999), plays an important role, so it will be presented more in detail, i.e. the extended tube model (ExtTube) of Kaliske and Heinrich (1999).

The extended tube model accounts for the above-mentioned topological constraints as well as the limited chain extensibility of network chains. It is described by four material parameters with physical meaning. The Helmholtz free energy of this model is presented by

$$\begin{aligned} {\varPsi _{\mathrm{{iso,ExtTube}}}}= & {} {{{G_c}} \over 2}\left[ {{{\left( {1 - {\delta ^2}} \right) \left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) } \over {1 - {\delta ^2}\left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) }}} \right] \nonumber \\&+ \,{{{G_c}} \over 2}\left[ {\ln \left( {1 - {\delta ^2}\left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) } \right) } \right] \nonumber \\&+ \,{{2{G_e}} \over {{\beta ^2}}}\sum \limits _{A = 1}^3 {\left( {\lambda _A^{ - \beta } - 1} \right) } . \end{aligned}$$

(7)

In this hyperelastic material law the parameter $G_c$ describes cross-link distribution of the shear modulus, whereas $G_e$ represents the constraint distribution of the shear modulus. The total shear modulus is the sum of both parts. The parameter $\beta$ describes the rearrangement of cross-links upon deformations and $\delta$ stands for the maximal extensibility of a polymer chain.

3.2 Phenomenological constitutive law

An important phenomenological model was developed by Mooney (1940), where an incompressible, homogeneous and isotropic material obeys Hooke’s law in simple shear considering two material parameters. This model was generalized by Rivlin (1948) expressing the Helmholtz free energy as an infinite power series, which yields

$$\begin{aligned} \varPsi \left( {{\bar{\mathbf{b}}}} \right) = \sum \limits _{i = 0}^\infty {\sum \limits _{j = 0}^\infty {{C_{ij}}} {{\left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) }^i}{{\left( {I{I_{{\bar{\mathbf{b}}}}} - 3} \right) }^j}} . \end{aligned}$$

(8)

Considering the originally proposed form with two parameters, the Mooney-Rivlin (MR2) material law is given by

$$\begin{aligned} {\varPsi _{\mathrm{{iso,MR2}}}} = {C_{10}}\left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) + {C_{01}}\left( {I{I_{{\bar{\mathbf{b}}}}} - 3} \right) , \end{aligned}$$

(9)

which will be utilized for all following studies.

3.3 Internal development of a constitutive law

Additionally to the above-mentioned constitutive models, an internal development of a novel Helmholtz free energy $\varPsi$ will be proposed, which is based on an inverse polynomial function, which was originally developed by Nelder (1966) to describe processes in agriculture. The initial proposal of Nelder (1966) is formulated by

$$\begin{aligned} {x \over y} = {\beta _0} + {\beta _1}x + {\beta _2}{x^2}. \end{aligned}$$

(10)

The Nelder function has the advantages over usual quadratic polynomial functions, that it has no built-in symmetry and its two extremes are described by two separately parameters. By reformulating the original function of Nelder (1966) and setting $\beta _2=0$, the function yields to

$$\begin{aligned} y = {x \over {{\beta _0} + {\beta _1}x}}. \end{aligned}$$

(11)

Considering that Eq. (11) can be formulated in the context of hyperelasticity, it can be presented as a Helmholtz free energy respectively as a strain energy density function only accounting for isochoric deformation modes by

$$\begin{aligned} \varPsi \left( {\overline{\mathbf{b}}} \right) = {{\left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) } \over {\alpha + \beta \left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) }}. \end{aligned}$$

(12)

In this context the first isochoric, principal invariant is assembled by ${I_{{\bar{\mathbf{b}}}}} = \mathrm{{tr}}\left( {{\bar{\mathbf{b}}}} \right)$, whereas the second isochoric principal invariant, which is presented in Eq. (2) and Eq. (13), can be described by the first isochoric, principal invariant and the trace of the isochoric left Cauchy-Green tensor with $I{I_{{\bar{\mathbf{b}}}}} = {1 \over 2}\left[ {I_{{\bar{\mathbf{b}}}}^2 - \mathrm{{tr}}\left( {{{{\bar{\mathbf{b}}}}^2}} \right) } \right]$. Since the second isochoric, principal invariant $I{I_{{\bar{\mathbf{b}}}}}$ plays an important role to describe biaxial deformation loading conditions (Wineman 2005; Horgan and Smayda 2012), in the following the Nelder function will be extended towards the second invariant in the same manner as the first invariant was incorporated. Hence, Eq. (11) is reformulated by

$$\begin{aligned} \boxed { {\varPsi _{\mathrm{{iso,MD}}}} = {{\left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) } \over {\alpha + \beta \left( {{I_{{\bar{\mathbf{b}}}}} - 3} \right) }} + {{\left( {I{I_{{\bar{\mathbf{b}}}}} - 3} \right) } \over {\chi + \delta \left( {I{I_{{\bar{\mathbf{b}}}}} - 3} \right) }},} \end{aligned}$$

(13)

which only accounts for isochoric deformation modes. In contrast to an isochoric formulation of a Helmholtz free energy, in Drass and Schneider (2016a), the Nelder function was successfully reformulated to describe the volumetric behavior of rubber-like materials in terms of a Helmholtz free energy function accounting for isotropic cavitation (void growth) at finite strains.

An advantage of the novel hyperelastic material model is, that it can be easily transfered to classical material models, like the NH model by setting $\beta = 0$ and disregarding the second isochoric, principal invariant $I{I_{{\bar{\mathbf{b}}}}}$, hence a reconciliation between molecular-statistical and phenomenological theory is given. Setting $\beta = \delta =0$, one obtains the MR2 material model.

Since the proposed isochoric hyperelastic strain energy density function is from its derivation purely phenomenological, the analysis of a physical background will be addressed in further investigations by proving the Baker–Ericksen inequality, the Truesdell–Noll condition or Hill’s inequality and/or the analysis of quasi-convexity, polyconvexity and ellipticity in accordance to Hartmann (2001).

4 Material parameter identification

4.1 Conventional material parameter identification

For the classical procedure of MPI, test data of different homogeneous experimental test set-ups can be utilized to determine material parameters, which are on an average adequately suitable to describe numerically different strain and stress states. Therefore, it is essential to conduct a simultaneous multi-experiment data fit to obtain optimized material parameters for a large number of deformation modes (Ogden et al. 2004). Since the formulation of an objective function for a single-experiment data fit is easily determinable after Ogden et al. (2004), the objective function for more than one experiment has to be modified to account for the whole experimental data basis. Hence, a modified objective function $\mathcal {S}$ has been formulated coupled with so-called trigger functions $\varPhi _{{k}}$ to extend the L2-norm towards a multi-experiment data fit, which yields into

$$\begin{aligned} \mathcal {S} = \sum \limits _{k = 1}^m {{\varPhi _k}} \left\| { t_{i;k}^{\mathrm{{sim}}}\left( {{{ \lambda }_{i;k}}, p_j} \right) - t_{i;k}^{\exp }} \right\| _2^2. \end{aligned}$$

(14)

Fig. 2

Plot of stress strain relationship for four experiments dependent on trigger functions (black lines)/plot of fitted surface (colored surface)

In this context, the index (subscript) k takes integer values from ${k} = 1,\ldots ,{{m}}$, which corresponds to the number of experiments k. Furthermore, it is important to note that ; k defines a sub-subscript, ${\left( \bullet \right) _{i;k}} \buildrel \wedge \over = {\left( \bullet \right) _{{i_k}}}$, of the corresponding vectors.

The trigger function $\varPhi _{{k}}$ with $k \in \left[ {1,2,3,4} \right]$ and $y =k-1$ are defined with

$$\begin{aligned} {\varPhi _1}= & {} {{\left( {3+y} \right) \left( {{y^2} - 3y + 2} \right) } \over 6} = \left\{ \begin{array}{l} {1\,\mathrm{{for}}\,y \in \left[ 0 \right] }\\ {0\,\mathrm{{for}}\,y \in \left[ {1,2,3} \right] } \end{array} \right. , \nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned} {\varPhi _2}= & {} {1 \over 2}\left( {y - 3} \right) \left( {y - 2} \right) y\;\;\;\;\;=\left\{ \begin{array}{l} {1\,\mathrm{{for}}\,y \in \left[ 1 \right] }\\ {0\,\mathrm{{for}}\,y \in \left[ {0,2,3} \right] } \end{array} \right. , \nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned} {\varPhi _3}= & {} - {1 \over 2}\left( {y - 3} \right) \left( {y - 1} \right) y\;\;= \left\{ \begin{array}{l} {1\,\mathrm{{for}}\,y \in \left[ 2 \right] }\\ {0\,\mathrm{{for}}\,y \in \left[ {0,1,3} \right] } \end{array} \right. , \nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned} {\varPhi _4}= & {} {1 \over 6}\left( {y - 2} \right) \left( {y - 1} \right) y\;\;\;\;\;= \left\{ \begin{array}{l} {1\,\mathrm{{for}}\,y \in \left[ 3 \right] }\\ {0\,\mathrm{{for}}\,y \in \left[ {0,1,2} \right] } \end{array} \right. .\nonumber \\ \end{aligned}$$

(18)

Based on the defined four trigger functions, a maximum of four experiments can be utilized for the present material parameter fitting routine. To understand the behavior of the trigger functions by trying to fit four experiments simultaneously, Fig. 2 can be adduced, where the fitting results are illustrated. Since the present four trigger functions are either 1 or 0, depending on the applied experiment, the fitting routine is able to choose the right stress strain relation dependent on the applied constitutive model and deformation field. To obtain the stress strain relationship of a hyperelastic constitutive model accounting for the deformation field, which is inherent during experimental testing, Eq. 4 has to be utilized. Here, the deformation gradient in accordance of the governed experiment, see part I (Drass et al. 2017) has to be inserted into Eq. 4 and differentiated with respect to the principal stretches $\lambda _i$. Afterwards the obtained expressions have to be inserted into the objective function $\mathcal {S}$.

Returning to the modified objective function $\mathcal {S}$, the function ${\mathbf {t}^{\mathrm{{sim}}}} \Rightarrow { t_{i;k}^{\mathrm{{sim}}}\left( {{{ \lambda }_{i;k}},p_j} \right) }$ is the derivative of the strain energy density function in accordance to the activated experiment k. The principal stretch vector is defined by $\mathbf {\lambda }\Rightarrow {{{\lambda }_{i;k}}} = {\left[ {{\lambda _{1;k}},{\lambda _{2;k}},\ldots ,{\lambda _{n;k}}} \right] ^\mathrm{{T}}}$ corresponding to the length of data points of the experiment. The unknown material parameters $\mathbf {p} \Rightarrow {{p_j}} = {\left[ {{p_1},{p_2},\ldots ,{p_\mathrm{{o}}}} \right] ^\mathrm{{T}}}$ can be determined by formulating the minimization problem with

$$\begin{aligned} \min \mathcal {S} \equiv \mathop {\min }\limits _{\mathbf {p}} \mathcal {S}\left( {\mathbf {p}} \right) . \end{aligned}$$

(19)

To solve the minimization problem under utilizing different sets of start values and constraining the lower and upper bounds to physically plausible values, adequate numerical algorithms must be chosen. Since the curve fitting toolbox of MatLab was utilized, one can choose between the Trust-Region-Method or the Levenberg–Marquard-Algorithm to obtain optimized material parameters for different constitutive equations. Regarding the goodness of the results, better results were achieved utilizing the Trust Region Method (TRM) coupled with Least Absolute Residuals method (LAR), which calculates a curve that minimizes the absolute difference of the residuals, rather than the squared differences. Therefore, extreme values have a minor impact on the fitting results. To initialize the experimental data, each experiment was manipulated in a way that it is described by 1000 data points. Furthermore, it is to note that a non-weighted optimization was conducted to determine the unknown material parameters, however, a weighted optimization can also be easily conducted.

Finally, to compare the analytical with the experimental results, an error estimator, respectively relative error for every data point dependent on the applied stretch will be utilized, which has the form

$$\begin{aligned} \mathrm{{error}} = \left| {{{t_{i;k}^{\mathrm{{sim}}}\left( {\lambda _{i;k}^{\exp },{p_j}} \right) } \over {t_{i;k}^{\exp }\left( {\lambda _{i;k}^{\exp }} \right) }} - 1} \right| , \end{aligned}$$

(20)

which is slightly different to the approach after Ogden et al. (2004). In Ogden et al. (2004), a scalar was put in the denominator to avoid divisions by small values of ${t_{i;k}^{\exp }}$, what would lead to large errors for the relative error. Hence, with the present relative error large errors at small strains are presumably due to divisions by small values of ${t_{i;k}^{\exp }}$. To summarize the direct identification of hyperelastic material parameters, the flow chart presented in Fig. 3 can be adduced. The optimization ends, if $\mathcal {S}\le \,\mathrm{{Tol}}$, where the tolerance was set to ${\text {Tol = 1.0e-8}}$ and the maximal iteration was set to ${\text {MaxIter = 10.000}}$. Additionally, the maximum number of function evaluations within MatLab toolbox equals ${\text {MaxFunEvals = 10.000}}$.

Fig. 3

Flow chart to optimize hyperelastic material parameters with curve fitting toolbox of MatLab

4.2 Inverse material parameter identification

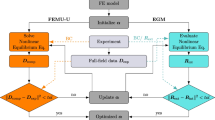
The inverse MPI can be conducted via FEMU approach (Avril et al. 2008), which is a numerical method based on the Finite Element Method to solve inverse problems, which can be understood as ill-posed and ill-conditioned after Hadamard (1902), Shkarayev. et al. (2001). Within this class of problems, the existence, uniqueness and stability of the solution is not per se given. The FEMU approach describes a technique, where numerical calculations with randomly chosen initial parameters are conducted iteratively and compared with experimental data as long as a pre-defined residuum is smaller than the fixed tolerance. This is similar to the formulation of an objective function, where the numerical response, here the global force displacement response of a numerical simulation of a complete experimental model, is compared with the experimental response under minimizing the L2-norm by adjusting the material parameters of the chosen constitutive material law. Clearly speaking, the force displacement response of the MI tests are compared with the results of the numerical simulation of the MI tests under optimizing the initially assumed material parameters. Hence, the objective function is formulated for an initial set of material parameters ${p_j^{\mathrm{{init}}}}$ by

$$\begin{aligned} \mathcal {S} = \sqrt{{1 \over n}\sum \limits _{i = 1}^n { {{{\left[ {{{ t_{i;k}^{\mathrm{{sim}}}\left( {{{ \lambda }_{i;k}},{{p_j^{\mathrm{{init}}}}}_{\mathrm{{}}}} \right) - t_{i;k}^{\exp }} \over { t_{i;k}^{\exp }}}} \right] }^2}} } } . \end{aligned}$$

(21)

If $\mathrm{{Tol< }}\,\mathcal {S}$, the optimization procedure proceeds with a perturbation of the initially chosen material parameter ${p_j^{\mathrm{{init}}}}$ by $p_j^{\mathrm{{init}}} + \varDelta {p_j}$ resulting in

$$\begin{aligned} \mathcal {S }= \sqrt{{1 \over n}\sum \limits _{i = 1}^n { {{{\left[ {{{t_{i;k}^{\mathrm{{sim}}}\left( {{\lambda _{i;k}},p_j^{\mathrm{{init}}} + \varDelta {p_j}} \right) - t_{i;k}^{\exp }} \over {t_{i;k}^{\exp }}}} \right] }^2}} } } , \end{aligned}$$

(22)

until a defined tolerance is deceeded with $\mathcal {S}\le \,\mathrm{{Tol}}$. Within the sensitivity analysis of material parameters, the input parameters are deliberately varied within a minimum number of trials in an optimal manner based on a stochastic sampling algorithm, here the Advanced Latin Hypercube Sampling method (Iman and Conover 1982; Iman 2008), where unwanted correlations between parameters are strongly minimized by optimization. Thereby the impact of the single input parameters of the pre-defined objective function can be determined. Here, every parameter set has to be numerically simulated to build up a so-called Meta Model of Optimal Prognosis (MOP). This MOP is based on the results of the sensitivity analysis and is generated by non-linear regression analysis of the single data points (see Fig. 9). Utilizing the response surface of the MOP, optimization algorithms like a gradient-based algorithm can be adopted to find the global minimum in the sense of the response surface. Here, no additional numerical simulations of the full model are necessary since the optimization algorithm only works on the response function. In a final step, the optimized material parameters have to be validated by solving the inverse problem for a last time. To obtain more insight into the presented procedure of inverse material parameter identification, in Schwarz et al. (2015) a detailed description is presented.

5 Results of material parameter identification

5.1 Conventional multi-experiment data fit

Here, the results of the MPI are illustrated, which are based on the experimental evaluation of UT, UC, BT and SPC utilizing Eq. (14). As isochoric strain energy density functions four different constitutive equations are applied to prove the accuracy of them. Hereby, the material models NH with one parameter, MR2 with two parameters and the ExtTube model with four parameters will be analyzed and set into comparison with a newly developed, phenomenological material model (MD model).

Fig. 4

Illustration of the fitting results concerning the stress strain relationships respectively the relative error of UT, UC, BT and SPC dependent on four hyperelastic material laws

In Fig. 4, the fitting results of the experimental data are illustrated qualitatively. Furthermore, the relative errors are also presented to show the accuracy of the fitting procedure. As it can be seen from Fig. 4, even the simple NH constitutive equation produces acceptable results regarding the accuracy of MPI for UT and SPC, whereas the results for UC and BT show relative errors between 10 and 20%. From the fitting procedure an initial shear modulus of $\mu =2 C_{10} = 2.530\;\left[ {\mathrm{{MPa}}} \right]$ was obtained, which can be understood as a reference point for the following inversely determined material parameters on the basis of MI tests. It is interesting to note that the relative errors for UT and SPC lie beneath 5% for moderate deformations, however, regarding the results for UC and BT, the relative error is a multiple of the relative error of UT and SPC. Hence, it can be stated that with a NH constitutive model the structural behavior for simple deformations can be adequately represented, however, regarding BT the present material model with only one material parameter, incorporating only the first principal strain invariant is not able to represent complex deformations, which can be explained by the missing second principal strain invariant. Finally, regarding small deformations the relative error is extremely large since the simulated engineering stress ${t_{i;k}^\mathrm{{sim} }}$ is divided by small values of ${t_{i;k}^{\exp }}$, which is logical since a classical formulation for the relative error was chosen in contrast to the approach after Ogden et al. (2004).

Regarding the results of MR2 model, the relative errors are improved to those of the NH model. Additionally, the results for BT could be improved dominantly, which can be explained since for MR2 model, the second isochoric strain invariant is incorporated. Thus, it can be stated that (i) the second isochoric strain invariant must be incorporated in hyperelastic material models to improve the fitting results for biaxial deformations, (ii) a linear relation between material parameters and strain invariants is not sufficient to account for strong nonlinearity and (iii) two material parameters are not sufficient to represent the structural responses of four different experiments at the same time.

As proposed by Ogden et al. (2004), an upper bound for the relative error of 5% was stated for fitting only one experiment. Furthermore, following Ogden et al. (2004), a more widened relative error of 20% produces valuable results, if two experiments are fitted at the same time. A relative error of 20% might be questionable at first glance, however, if one considers that each experiment, which has to be fitted, exhibits uncertainties due to experimental handling, variance of material properties as well as post-processing of experimental data, the stated bound is acceptable. Thus, the results for NH and MR2 produces valuable results after the comprehension of Ogden et al. (2004).

However, for all following considerations the upper bound of 20% after Ogden et al. (2004) will be reduced to 7.5%. This bound seems to be a severe bound when trying to fit four experiments at the same time, however, the accuracy and efficiency of the following two material models as well as the algorithm for MPI must be proved.

Regarding the results for the ExtTube model, this bound is only exceeded by BT under finite strains, however, the ExtTube model is acutely adequate to represent the structural response of TSSA under four different deformation modes. Since Marckmann and Verron (2006) state that the ExtTube model is the best hyperelastic material model, which captivates by its molecular-statistical motivation and goodness for MPI, it is straight-forward to compare the results of the ExtTube model with those of the novel hyperelastic material model (MD model), which is presented in Eq. 13.

Hence, regarding the results of the MD model, all relative errors lie beneath the upper bound of 7.5%, which is conterminous with a considerable fitting results, keeping in mind that four different experiments were fitted at the same time. Furthermore, the large relative error at small strains, which occurs due to mathematical circumstances, decreases rapidly for all four experiments. This could also be verified by the ExtTube model. Regarding the results for BT, the MD model shows a strongly improved result in comparison to the ExtTube model. Regarding the results between the MR2 model and the MD model, the MD model shows improved results, especially regarding the approximation of UC. Finally, it can be stated the MD model is excellently suitable to describe the complex structural behavior of TSSA under different deformation modes, which is proved because all results lie beneath a severe bound for the relative error. When trying to fit less than four experiments at the same time, the fitting results can be more improved, which expresses itself with relative error below 5% for the whole deformation regime. However, it is questionable that the obtained material parameters, especially the material parameters for sophisticated material models like the ExtTube model and MD model, were able to represent arbitrary deformation fields, which may even lead unphysical results. For the sake of completeness, an overview of all experiments is given in “Appendix A” and all directly optimized material parameters are listed in Table 1 and “Appendix B”.

Table 1 Material parameters of MPI considering four different constitutive laws

Fig. 5

Illustration of the mesh of the numerical model for the simulation of MI

5.2 Inverse MPI—microindentation test

Here, the numerical simulation of the MI and the results of the MPI for the MI tests are presented. As constitutive material model, only the results for MR2 are presented as an example, however, the proposed methodology and results for all the other Helmholtz free energy functions are represented in “Appendix C”. Due to the fact that MR2 has only two material parameters, the results for the relative error dependent on both material parameters can be vividly illustrated. Furthermore, since only two material parameters have to be determined, it is not likely to find local minima during the optimization process, which is beneficial since if more sophisticated material models, like the ExtTube model and the MD model, are applied, the global minimum of the objective function cannot per se be found. Additionally, by increasing the number of material parameters, the calculation time is also increased dominantly, so that all following calculations will be performed utilizing the two parametric MR2 model. For the numerical simulation of the MI, which was performed using ANSYS FE Code, a 2D numerical model was built up, where symmetry of the experimental test set-up is considered. A mesh study showed that no great influence of a finer mesh with respect to the numerical results, which can be explained by the applied contact algorithm, where no element penetration is allowed. Therefore, the numerical model was meshed with the mesh shown in Fig. 5. However, considering the contact surfaces respectively the edges of the numerical model, a slight mesh refinement was conducted to avoid numerical instabilities within the contact finding procedure. The numerical model, which is shown in Fig. 5, uses 958 2D plane stress elements. For the contact modeling, the normal Lagrangian detection method was used. The normal Lagrangian defines a surface to surface contact, in which the status of the contact can only be open or closed. The normal Lagrangian formulation will close any gaps and eliminate the penetration between the contact and target surface. During the experiment, the test specimen was clamped by under-inflation, hence in the numerical model the bottom side of TSSA is fixed supported. By studying the effects of friction, it was observable that the coefficient of friction has no impact on the force displacement behavior, since no large deformations occur during MI tests. Hence, the applied contact algorithm was equipped with a frictionless conditions.

Fig. 6

Flow chart to optimize hyperelastic material parameters with ANSYS FE Code and OptiSlang

Fig. 7

Results of the MPI for restricted and non-restricted optimization problem considering MI tests

In the following, the results of the inversely determined hyperelastic material parameters, here ${C}_{10}$ and ${C}_{01}$ of the second order constitutive law after Mooney-Rivlin, based on the inhomogeneous MI test are illustrated. Regarding the bounds for the material parameters two different approaches have been applied during FEMU approach. The first analysis was accomplished by an unrestricted analysis, which is conterminous with the fact that both material parameters can have values from $\pm \;\infty$. Since the Drucker stability cannot be ensured with negative material parameters, the second approach uses only positive values for ${C}_{10}$ and ${C}_{01}$. A flow chart for the inverse MPI utilizing ANSYS FE Code coupled with OptiSlang is presented in Fig. 6. On the basis of these assumptions, the results for the force displacement behavior in comparison to the experimental results as well as the relative error in every data point are illustrated in Fig. 7. From this, it can be immediately observed that, the results of the inversely determined material parameters considering the non-restricted optimization problem show a good approximation of the experimental results. This can be proved with regard on the relative error in every single data point, which approximates an error smaller than 10% for moderate displacements. The obtained material parameters are ${C}_{10}=12.0368\;\left[ {\mathrm{{MPa}}} \right]$ and ${C}_{01}=-10.0476\;\left[ {\mathrm{{MPa}}} \right]$. In contrast, the results considering the restricted MPI delivers worse results, especially regarding large displacements. Here, the optimized material parameters are ${C}_{10}=0.997792\;\left[ {\mathrm{{MPa}}} \right]$ and ${C}_{01}=0.631406\;\left[ {\mathrm{{MPa}}} \right]$.

5.3 Comparison of MPI-approaches

To provide a vivid comparison, all obtained material parameters are set in relation with each other. Therefore, on the one hand the obtained material parameters from the MI analyses, which have been determined by inverse methods, are utilized to simulate the conventional experiments. On the other hand, the material parameters from the conventional or direct method, here conventional experiments like UT, UC, BT and SPC, are applied in the numerical model to simulate the MI test.

Fig. 8

Comparison of different MPI approaches concerning conventional and unconventional experimental tests

Therefore, in Fig. 8a–b the results for MPI of the non-restricted inverse method are utilized to represent the structural responses of UT, UC, BT and SPC to show whether the inversely determined parameters are able to represent the structural responses of the homogeneous experimental tests. As it can be seen from Fig. 8a–b unphysical results can be observed, which can be explained through the violation of inequality requirements, like Druckers’s postulate of

$$\begin{aligned} d\varvec{\sigma } :d{\varvec{\varepsilon }} \ge 0, \end{aligned}$$

(23)

which states that, the incremental internal energy always has to increase. In Eq. (23), the variable $d\varvec{\sigma }$ represents the incremental stress, whereas as the incremental strain is represented by $d\varvec{\varepsilon }$. The internal energy can therefore be calculated by the double scalar product of both incremental tensors. In contrast, the solutions represented in Fig. 8c–d show an improvement of the results, especially while regarding the trend of the solutions. Here, the inversely determined material parameters based on a restricted MPI are utilized to represent the structural responses of homogeneous experiments (UT, UC, BT and SPC). From Fig. 8c–d, it is obvious that the results now got a physical character, which is trivial, since considering positive material parameters for ${C}_{10}$ and ${C}_{01}$, Drucker’s postulate is always fulfilled.

Considering the obtained material parameters from the conventional or direct method of MPI, for instance, four different stress and strain states and fitting afterwards hyperelastic material parameters, the simulation of the MI test shows adequate results, but it has to be admitted that the relative error between the simulation and experiment is still high.

From the obtained results, it has to be admitted that it is improbable to identify a unique solution for hyperelastic material parameters, which is able to represent conventional test set-ups, like UT, UC, BT and SPC, only on the bases of inversely determined material parameters by one inhomogeneous experiment, here the MI test. The reasons for this fact can be explained by firstly, trying to solve inverse problems generally and secondly, the experimental analysis of filled rubber-like materials.

Regarding inverse mathematical problems in general, these problems are ill-posed and ill-conditioned with a non-unique solution (Hadamard 1902). In this context, an ill-conditioned problem means that, the small errors in the experimental data can result in large errors in the answers, here the determined material parameters. After Shutov and Kreißig (2010), MPI is in general an ill-conditioned problem, since the solution does not depend continuously on the input data. If a strong correlation exists among the parameters, numerical difficulties arise. Generally speaking, ill-conditioned means in the field of numerical analysis, that the condition number of a function with respect to an argument measures how much the output value of the function can change for a small change in the input argument. This means for the MPI that small changes of the calculated material parameters have a major influence on the output, here on the stress strain behavior under four different experiments.

Fig. 9

3D-Plot of different material parameter combinations for the MR2-model dependent on the RMSE under simulation of the MI-tests

To improve the bad character of inverse problems, regularization strategies, like the Tikhonov regularization, can be applied to mitigate the applied assumptions of the solution. This means, one can perform a restricted optimization routine by setting e.g bounds for the material parameters. For example, to guarantee physical behavior, all material parameters with respect to elasticity constants must satisfy ${p_j} \ge 0$. Furthermore, if the material parameters are getting more complex e.g. regarding the ExtTube model, the parameter $\beta$ must satisfy $0 \le \beta \le 1$ (Kaliske and Heinrich 1999). To illustrate the non-uniques of solution, in Fig. 9 the MOP is illustrated. In this graph, different material parameter combinations dependent on the resulting obtained value of the objective function $\mathcal {S}$ (see Eq. 21), which is also called as the root mean squared error (RMSE), are illustrated as data points. By fitting the obtained data points by a surface fitting routine, a valley of adequate solutions is obvious. The data points are generated based on sensitivity analysis, where each data point correspond to one numerical calculation, where for all simulations, the RMSE was calculated. The plotted surface is a 3D surface fit by a cosine function, which is illustrated for the purpose of clearness. Here, the valley represents the non-uniqueness since many material parameter combinations were able to minimize the RMSE. The second possible explanation of the poor correlation between the fitted material parameters from the inverse method can be described by the tested material, which can be understood as a nano-silica filled rubber (Drass and Schneider 2016b). Following Marco et al. (2011), who also tested silica filled rubbers, the obtained results showed large discrepancies between the inversely determined material parameters and the conventionally obtained material parameters, too. Therefore, Marco et al. (2011) stated that, for filled-rubbers a scale-transition of material parameters is not possible, which is attributed by the content of fillers, their viscous behavior and stiffness-differences between filler and matrix. However, by testing natural rubbers without any fillers the proposed methodology was confirmed by various authors, where the fitted material parameters on the micro-scale represents the macro-scale nearly perfect and vice versa (Saux et al. 2011; Marco et al. 2011; Chen et al. 2013).

6 Conclusion

The present paper introduced two methodologies to determine hyperelastic material parameters based on homogeneous and inhomogeneous experimental test set-ups, which were presented in part I of this paper, utilizing the so-called direct and inverse method. Since hyperelastic materials, here i.e. thin structural silicone adhesives, have a broad application in glass structures e.g. laminated connections, it is of major interest to adequately characterize the material behavior in an experimental, analytical and numerical sense. The objective was to replace a set of time-consuming and expensive homogeneous experiments by one inhomogeneous MI test to determine material parameters. Therefore, uniaxial tension and compression, biaxial tension as well as shear-pancake tests were conducted and on this basis hyperelastic material parameters were determined by regression analyses considering four different constitutive equations, which is the conventional or direct methodology. To do this, three standard hyperelastic constitutive equations were utilized and compared with a new developed, phenomenological hyperelastic material law. Following the results of the conventional MPI, for NH material model and the MR2 material model adequate results could be obtained based on the identification of material parameters, where four experiments were fitted simultaneously. These results could be further improved regarding a more sophisticated material model after Kaliske and Heinrich (1999). As an indicator for the goodness of the results, an upper bound of 7.5% for the relative error was utilized, which is a severe bound since Ogden et al. (2004) proposed an upper bound of 20%, when two experiments are fitted simultaneously. However, even with the severe bound of 7.5% for the relative error, the ExtTube model provides considerable results. Considering the novel constitutive model for hyperelastic materials, the MD model, the results could be further improved in comparison to the ExtTube model. Hence, the MD model is excellently suitable to represent the structural behavior of TSSA under arbitrary and isochoric deformations. Regarding the unconventional methodology of determining hyperelastic material parameters, the inverse Finite Element Method was applied to simulate the microindentation test with initially chosen material parameters. Both procedures (direct and inverse method) of identifying hyperelastic parameters were compared to each other utilizing the second order Mooney-Rivlin material model. The results of the inverse method showed minor correlation between the obtained material parameters trying to represent the macroscopic structural behavior of experiments like UT, UC, BT and SPC. On the one hand, this can be explained by trying to solve an inverse problem, where the existence, uniqueness and stability of the solution is not given per se. On the other hand, the experimental tests were conducted on nano-silica filled rubbers, where, due to the content of fillers, viscous effects and stiffness-differences between filler and matrix occur, whereby the scale-transition of determined material parameters on the micro-scale towards material parameters on the macro-scale for finite strains is improbable. This fact was proven by various authors, but it was also shown that the proposed methodology is straightforward considering unfilled rubbers, where nearly perfect correlation between the material of the micro- and macro-scale was observed. Therefore, further investigations will focus on regularization strategies to constrain the material parameter space as well as accounting for more sophisticated hyperelastic material laws accounting for compressibility.

Appendices

Appendix-A

A data package of the presented experimental raw data including the engineering stress strain responses for UT, UC, BT, SPC experiments based on mean values can be granted upon e-mail request to the authors. Table 2 gives an overview of the testing data and the utilized fitting algorithm.

Table 2 Summary of experiments (see part I)

Appendix-B

In this appendix, the determined constitutive material parameters for thin structural silicone will be provided based on the applied two methodologies - direct/inverse method. The constitutive parameters are listed with respect to the applied constitutive model (Table 3).

Table 3 Material parameters of MPI utilizing the direct and inverse method

Fig. 10

Illustration of the fitting and simulation results for the direct and inverse method utilizing different constitutive models: a–d NH model; e–h ExtTube model and i–l MD model

Appendix-C

For the sake of completeness, in the following graphs the comparison for the conventional and unconventional MPI will be illustrated for the material models NH, ExtTube and MD (see Fig. 10) in accordance to Fig. 8.