Abstract
We call a group G very Jordan if it contains a normal abelian subgroup \(G_0\) such that the orders of finite subgroups of the quotient \(G/G_0\) are bounded by a constant depending on G only. Let Y be a complex torus of algebraic dimension 0. We prove that if X is a non-trivial holomorphic \({\mathbb {P}}^{1}\)-bundle over Y then the group \(\mathrm{Bim}(X)\) of its bimeromorphic automorphisms is very Jordan (contrary to the case when Y has positive algebraic dimension). This assertion remains true if Y is any connected compact complex Kähler manifold of algebraic dimension 0 without rational curves or analytic subsets of codimension 1.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let X be a compact complex connected manifold. We denote by  and
and  the groups of automorphisms and bimeromorphic selfmaps of X, respectively. If X is projective,
the groups of automorphisms and bimeromorphic selfmaps of X, respectively. If X is projective,  denotes the group of birational automorphisms of X. As usual, \({\mathbb {P}}^n\) stands for the n-dimensional complex projective space; a(X) stands for the algebraic dimension of X. All manifolds in this paper are assumed to be complex compact and connected unless otherwise stated.
denotes the group of birational automorphisms of X. As usual, \({\mathbb {P}}^n\) stands for the n-dimensional complex projective space; a(X) stands for the algebraic dimension of X. All manifolds in this paper are assumed to be complex compact and connected unless otherwise stated.
Vladimir L. Popov in [24] defined the Jordan property of a group and raised the following question: When the groups  and
and  are Jordan?
are Jordan?
Definition 1.1
-
A group G is called bounded if the orders of its finite subgroups are bounded by a universal constant that depends only on G [24, Definition 2.9].
-
A group G is called Jordan if there is a positive integer J such that every finite subgroup B of G contains an abelian subgroup A that is normal in B and such that the index
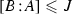 [24, Definition 2.1].
[24, Definition 2.1].
In this paper we are interested in the following property of groups.
Definition 1.2
We call a group G very Jordan if there exist a commutative normal subgroup \(G_0\) of G and a bounded group F that sit in a short exact sequence
Remark 1.3
-
1.
Every finite group is bounded, Jordan, and very Jordan.
-
2.
Every commutative group is Jordan and very Jordan.
-
3.
Every finitely generated commutative group is bounded.
-
4.
A subgroup of a very Jordan group is very Jordan.
-
5.
“Bounded” implies “very Jordan”, “very Jordan” implies “Jordan”.
The first goal of the paper is to find complex manifolds with very Jordan group  or
or  . To this end we prove the following generalization of [19, Lemma 2.5] and [16, Lemma 3.1].
. To this end we prove the following generalization of [19, Lemma 2.5] and [16, Lemma 3.1].
Proposition 2.1
Let X be a connected compact complex Kähler manifold and  , where
, where  is the connected identity component of
is the connected identity component of  . Then Fis bounded.
. Then Fis bounded.
It follows that if the group is commutative, then  is very Jordan.
is very Jordan.
Example 1.4
If X is a compact complex Kähler manifold of non-negative Kodaira dimension, then  is very Jordan ([13, Proposition 5.11] and Corollary 2.3 below).
is very Jordan ([13, Proposition 5.11] and Corollary 2.3 below).
We also study another wide and interesting class of complex manifolds with very Jordan group of automorphisms, namely, compact uniruled manifolds that are equidimensional rational fibrations (i.e., all components of all the fibers are one-dimensional and the general fiber is \({\mathbb {P}}^{1}\)) over complex tori of algebraic dimension zero.
In order to demonstrate the role of such manifolds, we shall survey Jordan properties of  and
and  for various types of compact complex manifolds X.
for various types of compact complex manifolds X.
The group  of any connected complex compact manifold X carries a natural structure of a complex (not necessarily connected) Lie group such that the action map
of any connected complex compact manifold X carries a natural structure of a complex (not necessarily connected) Lie group such that the action map  is holomorphic (a theorem of Bochner–Montgomery [6]). It is known, for example, to be Jordan if
is holomorphic (a theorem of Bochner–Montgomery [6]). It is known, for example, to be Jordan if
Moreover, the connected identity component  of
of  is Jordan for every compact complex space X [25, Theorems 5 and 7].
is Jordan for every compact complex space X [25, Theorems 5 and 7].
Groups  and
and  of birational and bimeromorphic transformations, respectively, are more complicated.
of birational and bimeromorphic transformations, respectively, are more complicated.
Example 1.5
In the case of projective varieties X, it was proven by Popov [24] that  is Jordan if
is Jordan if  and X is not birational to a product of an elliptic curve and \({\mathbb {P}}^{1}\!\). (The case of \(X={\mathbb {P}}^2\) was done earlier by Serre [32].)
and X is not birational to a product of an elliptic curve and \({\mathbb {P}}^{1}\!\). (The case of \(X={\mathbb {P}}^2\) was done earlier by Serre [32].)
Consider the following LIST of manifolds:
-
E an elliptic curve;
-
\(A_n\) an abelian variety of dimension n;
-
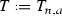 a complex torus with dimension
a complex torus with dimension 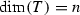 and algebraic dimension \(a(T)=a\);
and algebraic dimension \(a(T)=a\); -
\(S_b\) a bielliptic surface;
-
\(S_{K1}\) a surface of Kodaira dimension 1;
-
\(S_{K}\) a Kodaira surface (it is not a Kähler surface).
Example 1.6
1. If S is a projective surface with non-negative Kodaira dimension then \(\mathrm{Bir}(S)\) is bounded unless it appears on the LIST [28, Theorem1.1].
2. If X is a non-uniruled projective variety with irregularity \(q(X)=0\), then \(\mathrm{Bir}(X)\) is bounded [26, Theorem1.8].
Example 1.7
1. \(\mathrm{Bir}(X)\) is Jordan for a projective variety X if either X is not uniruled or \(X ={\mathbb {P}}^N\) (proven in [26] modulo the Borisov–Alekseev–Borisov conjecture that was later established by Birkar [4]).
2. If X is a uniruled smooth projective variety that is a non-trivial conic bundle over a non-uniruled smooth projective variety Y then \(\mathrm{Bir}(X)\) is Jordan [1].
3. If X is a projective threefold then \(\mathrm{Bir}(X)\) is Jordan unless X is birational to a direct product \(E{\times }{\mathbb {P}}^2\) or \(S{\times }{\mathbb {P}}^1\), where a surface S appears on the LIST [27].
4. If X is a non-algebraic compact uniruled complex Kähler threefold then \(\mathrm{Bim}(X) \) is Jordan unless X is either the projectivization of a rank 2 vector bundle over \(T_{2,1}\) (and \(a(X)=1\)) or X is bimeromorphic to \({\mathbb {P}}^1{\times }T_{2,1}\) (and \(a(X)=2\)) [8, 29].
Example 1.8
1. If X is a projective variety, birational to \({\mathbb {P}}^m{\times }A_n\), \(n,m>0\), then \(\mathrm{Bir}(X)\) is not Jordan [36].
2. The group \(\mathrm{Bim}(X) \) is not Jordan for a certain class of \({\mathbb {P}}^1\)-bundles (including the trivial ones) over complex tori of positive algebraic dimension [37].
These examples show that the worst case scenario for Jordan properties of  or
or  occurs when X is a uniruled variety (Kähler manifold) that is fibered over a torus of positive algebraic dimension.
occurs when X is a uniruled variety (Kähler manifold) that is fibered over a torus of positive algebraic dimension.
The second goal of this paper is to check what happens in a similar situation when a compact complex manifold is uniruled and fibered over a torus of algebraic dimension 0. It appears that the Jordan properties are drastically different from the situation when the torus has positive algebraic dimension.
Let X, Y be compact connected complex manifolds endowed with a holomorphic map \(p:X\rightarrow Y\). Assume that
-
Dimension of the fiber
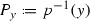 is 1 for every point \(y\in Y\);
is 1 for every point \(y\in Y\); -
There is an analytic subset \(Z\varsubsetneq Y\) such that for every point \(y\not \in Z\) the fiber \(p^*(y)\) is reduced and isomorphic to \({\mathbb {P}}^{1}\!\).
In this situation we call \(P_y\), \(y\not \in Z\), a general fiber and X (or a triple (X, p, Y) ) an equidimensional rational bundle over Y. (Such bundles appear naturally in the classification of non-projective smooth compact Kähler uniruled threefolds [8].) If X is a holomorphically locally trivial fiber bundle over Y with fiber \({\mathbb {P}}^{1}\) we call it a \({\mathbb {P}}^{1}\)-bundle. If X is a projectivization \({\mathbb {P}}(E)\) of a rank 2 holomorphic vector bundle E over Y, we will say that X is a linear \({\mathbb {P}}^{1}\)-bundle over Y. We consider manifolds Y with \(a(Y)=0\) meeting certain additional conditions.
Definition 1.9
We say that a compact connected complex manifold Y of positive dimension is poor if it enjoys the following properties:
-
The algebraic dimension a(Y) of Y is 0.
-
Y does not contain analytic subspaces of codimension 1.
-
Y does not contain rational curves, i.e., it is meromorphically hyperbolic in the sense of Fujiki [14].
A complex torus T with  and \(a(T)=0\) is a poor Kähler manifold. Indeed, a complex torus T is a Kähler manifold that does not contain rational curves. If \(a(T)=0, \) it contains no analytic subsets of codimension 1 [5, Chapter 2, Corollary 6.4]. An explicit example of such a torus is given in [5, Example 7.4]. Another example of a poor manifold is provided by a non-algebraic K3 surface S with
and \(a(T)=0\) is a poor Kähler manifold. Indeed, a complex torus T is a Kähler manifold that does not contain rational curves. If \(a(T)=0, \) it contains no analytic subsets of codimension 1 [5, Chapter 2, Corollary 6.4]. An explicit example of such a torus is given in [5, Example 7.4]. Another example of a poor manifold is provided by a non-algebraic K3 surface S with  (see [3, Chapter VIII, Proposition 3.6]).
(see [3, Chapter VIII, Proposition 3.6]).
Remark 1.10
1. Clearly, the complex dimension of a poor manifold is at least 2.
2. A generic complex torus of given dimension \(\geqslant 2\) has algebraic dimension 0 and therefore is poor.
Let (X, p, Y) be an equidimensional rational bundle over a poor manifold Y. Since Y contains no rational curves, there are no non-constant holomorphic maps \({\mathbb {P}}^{1}\!\rightarrow Y\). It follows that every map  is p-fiberwise, i.e., there exists a group homomorphism
is p-fiberwise, i.e., there exists a group homomorphism  (see Lemma 3.3) such that for all
(see Lemma 3.3) such that for all 

We denote by  (
( ) the kernel of \(\tau \), i.e., the subgroup of all those
) the kernel of \(\tau \), i.e., the subgroup of all those  (respectively,
(respectively,  ) that leave every fiber
) that leave every fiber  , \(y\in Y\), fixed. We prove the following
, \(y\in Y\), fixed. We prove the following
Theorem 1.11
Let (X, p, Y) be an equidimensional rational bundle over a poor manifold Y. Then:
-
(X, p, Y) is a \({\mathbb {P}}^{1}\)-bundle (see Proposition 3.6).
-
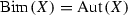 (see Corollary 4.1).
(see Corollary 4.1). -
The restriction homomorphism
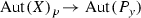 , \( f\rightarrow f |_{P_y}\) is a group embedding. Here \(P_y=p^{-1}(y)\) for any point \(y\in Y\) (Lemmas 4.3, 4.4, and Case C(h) of Sect. 4).
, \( f\rightarrow f |_{P_y}\) is a group embedding. Here \(P_y=p^{-1}(y)\) for any point \(y\in Y\) (Lemmas 4.3, 4.4, and Case C(h) of Sect. 4).
Assume additionally that Y is Kähler and X is not bimeromorphic to the direct product  . Then:
. Then:
-
The connected identity component
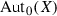 of the complex Lie group
of the complex Lie group 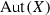 is commutative (Theorem 5.4).
is commutative (Theorem 5.4). -
The group
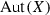 is very Jordan. Namely, there is a short exact sequence
is very Jordan. Namely, there is a short exact sequence 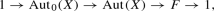
where F is a bounded group (Theorem 5.4).
-
The commutative group
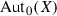 sits in a short exact sequence of complex Lie groups
sits in a short exact sequence of complex Lie groups 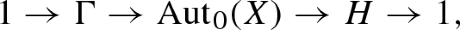
where H is a complex torus and one of the following conditions holds (Proposition 4.8 and (15)):
-
\(\Gamma =\{\mathrm{id}\}\), the trivial group;
-
\(\Gamma \cong {\mathbb {C}}^{+}\!\), the additive group of complex numbers;
-
\(\Gamma \cong {\mathbb {C}}^{*}\!\), the multiplicative group of complex numbers.
-
The paper is organized as follows. Section 2 contains preliminary results about automorphisms of equidimensional rational bundles and meromorphic groups in a sense of Fujiki. In Sect. 3, we deal with equidimensional rational bundles over poor manifolds and prove that every such equidimensional rational bundle is a \({\mathbb {P}}^{1}\)-bundle. In Sect. 4, we study \({\mathbb {P}}^{1}\)-bundles X over a poor manifold T and classify their non-trivial fiberwise automorphisms in terms of the corresponding fixed points sets. In particular, we prove that  . In Sect. 5, assuming that our poor manifold T is Kähler we prove that the connected identity component
. In Sect. 5, assuming that our poor manifold T is Kähler we prove that the connected identity component  of
of  is commutative. In Sect. 6, we provide a class of examples of \({\mathbb {P}}^{1}\)-bundles X over complex tori T of algebraic dimension 0 that do not admit a section but admit a bisection that coincides with the set of fixed points of a certain equivariant automorphism.
is commutative. In Sect. 6, we provide a class of examples of \({\mathbb {P}}^{1}\)-bundles X over complex tori T of algebraic dimension 0 that do not admit a section but admit a bisection that coincides with the set of fixed points of a certain equivariant automorphism.
2 Preliminaries and notation
We assume that all complex manifolds under consideration are connected and compact. We use the following notation and assumptions.
Notation and Assumptions 1
-
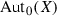 stands for the connected identity component of (as a complex Lie group).
stands for the connected identity component of (as a complex Lie group). -
If \(p:X\rightarrow Y\) is a morphism of complex manifolds, then
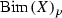 (respectively,
(respectively, 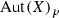 ) is the subgroup of all
) is the subgroup of all 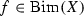 (respectively,
(respectively, 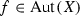 ) such that
) such that 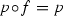 .
. -
\(\cong \) stands for “isomorphic groups” (or isomorphic complex Lie groups if the groups involved are the ones), and \(\sim \) for biholomorphically isomorphic complex manifolds.
-
id stands for the identity automorphism.
-
\({\mathbb {P}}^n_{(x_0:\dots :x_n)}\) stands for a complex projective space \({\mathbb {P}}^n\) with homogeneous coordinates
 .
. -
\({\mathbb {C}}_z\) (respectively, \(\overline{{\mathbb {C}}}_z\sim {\mathbb {P}}^{1}\)) is the complex line (extended complex line, respectively) with coordinate z.
-
For an element
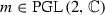 we define
we define 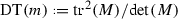 where
where 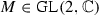 is any matrix representing m,
is any matrix representing m, 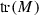 and
and 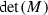 are the trace and the determinant of M, respectively.
are the trace and the determinant of M, respectively. 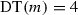 if and only if m is proportional either to the identity matrix or to a unipotent matrix.
if and only if m is proportional either to the identity matrix or to a unipotent matrix. -
\({\mathbb {C}}^+\) and \({\mathbb {C}}^*\) stand for the complex Lie groups \({\mathbb {C}}\) and \({\mathbb {C}}^*\) with additive and multiplicative group structure, respectively.
-
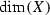 , a(X) are the complex and algebraic dimensions of a compact complex manifold X, respectively.
, a(X) are the complex and algebraic dimensions of a compact complex manifold X, respectively. -
Let X, Y be two compact connected irreducible reduced analytic complex spaces. A meromorphic map \(f:X\rightarrow Y\) relates to every point \(x\in X\) a subset \(f(x)\subset Y\) (the image of x) such that the following conditions are met:
-
The graph
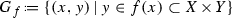 is a connected irreducible complex analytic subspace of
is a connected irreducible complex analytic subspace of 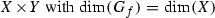 .
. -
There exists an open dense subset \(X_0\subset X\) such that f(x) consists of one point for every \(x\in X_0\).
-
-
We say that a compact complex manifold Y contains no rational curves if there are no non-constant holomorphic maps \({\mathbb {P}}^{1} \!\rightarrow Y\).
-
Following Fujiki, we call a compact complex manifold meromorphically hyperbolic if it contains no rational curves [14].
-
According to Fujiki [13, Definition 2.1], a meromorphic structure on a complex Lie group G is a compactification \(G^*\) of G such that the group multiplication
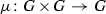 extends to a meromorphic map
extends to a meromorphic map 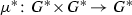 and \(\mu ^*\) is holomorphic on
and \(\mu ^*\) is holomorphic on 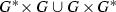 .
. -
Following Fujiki, we say that a complex Lie group G acts meromorphically on a complex manifold Z if
-
G acts biholomorphically on Z;
-
there is a meromorphic structure \( G^*\) on G such that the G-action
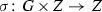 extends to a meromorphic map
extends to a meromorphic map  (see [13, Definition 2.1] for details).
(see [13, Definition 2.1] for details).
-
It was proven in [14] that if a manifold Y is meromorphically hyperbolic then
-
Every meromorphic map \(f:X\rightarrow Y\) is holomorphic for any complex manifold X.
-
If, in addition, Y is Kähler then
-
Every connected component of the set H(Y, Y) of all holomorphic maps \(Y\rightarrow Y\) (regarded as a certain subspace of the Douady complex analytic space \(D_{Y\times Y}\)) is compact.
-
In particular,
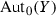 is a compact complex Lie group, that is isomorphic to a certain complex torus
is a compact complex Lie group, that is isomorphic to a certain complex torus 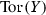 (see also [13, Corollary 3.7]).
(see also [13, Corollary 3.7]). -
Actually,
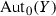 is isomorphic to a complex torus for any compact complex Kähler manifold X of non-negative Kodaira dimension [13, Proposition 5.11].
is isomorphic to a complex torus for any compact complex Kähler manifold X of non-negative Kodaira dimension [13, Proposition 5.11].
-
In general, let Z be a compact complex connected Kähler manifold. The group  acts meromorphically on Z, and the analogue of the Chevalley decomposition for algebraic groups is valid for the complex Lie group
acts meromorphically on Z, and the analogue of the Chevalley decomposition for algebraic groups is valid for the complex Lie group  :
:

where L(Z) is bimeromorphically isomorphic to a linear group, and  is a complex torus ([13, Theorem 5.5], [18, Theorem 3.12], [7, Theorem 3.28]).
is a complex torus ([13, Theorem 5.5], [18, Theorem 3.12], [7, Theorem 3.28]).
If L(Z) in (1) is not trivial, Z contains a rational curve. Moreover, according to [13, Corollary 5.10], Z is bimeromorphic to a fiber space whose general fiber is \({\mathbb {P}}^{1}\!\).
The next proposition is similar to [16, Lemma 3.1].
Proposition 2.1
Let X be a connected complex compact Kähler manifold and  . Then the group F is bounded.
. Then the group F is bounded.
Proof
By functoriality, there is a natural group homomorphism

The connected Lie group  is arcwise connected. Hence, \(f^*\) is the identity map for all
is arcwise connected. Hence, \(f^*\) is the identity map for all  . The image
. The image  is bounded, since it is a subgroup of a bounded (thanks to Minkowski’s theorem [33, Section 9.1]) group
is bounded, since it is a subgroup of a bounded (thanks to Minkowski’s theorem [33, Section 9.1]) group  . (Here \(b_2(X)=\dim _{{\mathbb {Q}}}H^{2}(X,{\mathbb {Q}})\) is the second Betti number of X.) On the other hand, if
. (Here \(b_2(X)=\dim _{{\mathbb {Q}}}H^{2}(X,{\mathbb {Q}})\) is the second Betti number of X.) On the other hand, if  then its action on
then its action on  is trivial as well. Thus, if \(\omega \) is a Kähler form on X, and \(\overline{\omega } \) is its cohomology class in \(H^{2}(X,{\mathbb {R}})\), and if
is trivial as well. Thus, if \(\omega \) is a Kähler form on X, and \(\overline{\omega } \) is its cohomology class in \(H^{2}(X,{\mathbb {R}})\), and if  , then
, then
Let  be the subgroup of all automorphisms meeting condition (2). We have
be the subgroup of all automorphisms meeting condition (2). We have  . Since the quotient group
. Since the quotient group  is finite ([13, Theorem 4.8], [18, Proposition 2.2]), the quotient
is finite ([13, Theorem 4.8], [18, Proposition 2.2]), the quotient  is a finite group. Thus, we have a short exact sequence of groups
is a finite group. Thus, we have a short exact sequence of groups

The group  is finite, the group
is finite, the group  is bounded, thus the quotient group
is bounded, thus the quotient group  is also bounded. \(\square \)
is also bounded. \(\square \)
Remark 2.2
Our proof was inspired by the proofs of [16, Lemma 3.1] and [19, Lemma 2.5]. Namely, [16, Lemma 3.1] states the following. Let X be a normal compact Kähler variety. Then there exists a positive integer l, depending only on X, such that for any finite subgroup G of  acting biholomorphically and meromorphically on X we have
acting biholomorphically and meromorphically on X we have  . We cannot use straightforwardly this lemma since a finite subgroup of
. We cannot use straightforwardly this lemma since a finite subgroup of  may not be isomorphic to a quotient
may not be isomorphic to a quotient  where G is a finite subgroup of
where G is a finite subgroup of  .
.
Corollary 2.3
Let X be a compact complex Kähler manifold of Kodaira dimension \(\varkappa (X)\geqslant 0\). Then  is very Jordan.
is very Jordan.
Proof
In view of Proposition 2.1 it is sufficient to prove that  is commutative. But this follows from [13, Proposition 5.11] that asserts that
is commutative. But this follows from [13, Proposition 5.11] that asserts that  in this case is a complex torus. \(\square \)
in this case is a complex torus. \(\square \)
3 Equidimensional rational bundles over poor manifolds
We will use the following property of poor manifolds.
Lemma 3.1
Let X, Y be connected compact manifolds and let \(f:X\rightarrow Y\) be a unramified finite holomorphic covering. Then
-
(i)
If Y is Kähler, so is X.
-
(ii)
If Y contains no rational curves, so does X.
-
(iii)
If Y contains no analytic subsets of codimension 1, so does X.
-
(iv)
If Y is poor, so is X.
Proof
Indeed, (i) If \(\omega \) is a Kähler form on Y, then its pullback \(f^*\omega \) is a Kähler form on X, thus X is a Kähler manifold. (ii) If X contained a rational curve C then f(C) would be a rational curve in Y. (iii) If X contained an analytic subset Z of codimension 1, then f(Z) would be a codimension-1 analytic subset in Y. Thus if Y is poor, according (i) and (ii), X contains neither rational curves nor analytic subsets of codimension 1. In particular, \(a(X)=0\). Thus, X is poor. \(\square \)
An equidimensional rational bundle (X, p, Y) defines the holomorphically locally trivial fiber bundle with fiber \({\mathbb {P}}^{1}\) over a certain open dense subset \(U\subset Y \). Indeed, by definition, there is an open dense subset \(U\subset Y\) of points \(y\in Y\) such that for all \(y\in U\) the fiber \(P_y=p^{-1}(y)\sim {\mathbb {P}}^{1}\!\). By a theorem of Fischer and Grauert [12], the triple \( (p^{-1}(U),p,U)\) is a holomorphically locally trivial fiber bundle. Actually, we may (and will) assume that U is a complement of an analytic subset of Y, since the image of the set of points where p is singular is an analytic subset (see, for example, [23, Theorem 1.22]).
Definition 3.2
(cf. [2]) Let X, Y, Z be three complex manifolds, \(f:X\rightarrow Y\), \(g:Z\rightarrow Y\) be holomorphic maps, and \( h:X\rightarrow Z\) be a meromorphic map. We say that h is f, g-fiberwise if there exists a holomorphic map \(\tau (h):Y\rightarrow Y\) that may be included into the following commutative diagram:

If \(X=Z\) and \(f=g\) we say that h is f-fiberwise (or equivariant). If \(\tau (h)=\mathrm{id}\) we say that h is fiberwise.
Lemma 3.3
(cf. [1, Lemma 3.4] for the algebraic case) Assume that Y is a connected compact complex meromorphically hyperbolic manifold, and let \((X,p_X,Y)\) and \((Z,p_Z,Y)\) be two equidimensional rational bundles over Y. Then any surjective meromorphic map \(f:X\dashrightarrow Z\) is \(p_X,p_Z\)-fiberwise.
Proof
Consider the meromorphic map  . It is holomorphic [14, Proposition 1] since Y has no rational curves. Let \(U\subset Y \) be a dense Zariski open subset of Y such that \( (p_X^{-1}(U),p_X,U)\) is a holomorphically locally trivial fiber bundle. Take a fiber \(P_u=p_X^{-1}(u)\), \(u\in U\). Since \(g_f\) is holomorphic, the image \(g_f(P_u)\) may be either a point or a rational curve. Since Y contains no rational curves, the restriction map
. It is holomorphic [14, Proposition 1] since Y has no rational curves. Let \(U\subset Y \) be a dense Zariski open subset of Y such that \( (p_X^{-1}(U),p_X,U)\) is a holomorphically locally trivial fiber bundle. Take a fiber \(P_u=p_X^{-1}(u)\), \(u\in U\). Since \(g_f\) is holomorphic, the image \(g_f(P_u)\) may be either a point or a rational curve. Since Y contains no rational curves, the restriction map
Since U is dense and the set of points \(y\in Y\) such that \(g_f |_{P_y}\) is a constant, is closed, we get that \(g_f |_{P_y}\) is constant for any \(y\in Y\). Put  .
.
For a fiber \(P_u\) with \(u\in U\), there exists an open neighborhood W of u in U such that \(V=p_X^{-1}(W)\) is \(p_X, p_1\)-fiberwise isomorphic to  , where \(p_1\) stands for the natural projection to the second factor. Then for \(w\in W\) we have
, where \(p_1\) stands for the natural projection to the second factor. Then for \(w\in W\) we have  , hence is a holomorphic function on w. Thus, \(\tau (f)\) is holomorphic on U, defined and continuous on Y. Let
, hence is a holomorphic function on w. Thus, \(\tau (f)\) is holomorphic on U, defined and continuous on Y. Let  and \(z=\tau (f)(y)\). Let us choose open neighbourhoods \(W_y, W_z\subset Y\) of y, z, respectively, such that
and \(z=\tau (f)(y)\). Let us choose open neighbourhoods \(W_y, W_z\subset Y\) of y, z, respectively, such that
-
both \(W_y\) and \( W_z\) are biholomorphic to an open ball in \({\mathbb {C}}^n\) with induced coordinates \(y_1,\dots ,y_n\) and \(z_1,\dots ,z_n\), respectively;
-
\(\tau (f)(W_y)\subset W_z\).
Then the induced functions \(\tau (f)^*(z_i)\) are holomorphic in \(W_y\cap U\), defined and locally bounded in \(W_y\), thus, by the first Riemann continuation theorem ([15, Chapter 1, C, 3], [11, Section 2.23]) are holomorphic in \(W_y\). Hence, \(\tau (f)\) is a holomorphic map. \(\square \)
Corollary 3.4
For an equidimensional rational bundle (X, p, Y) over a meromorphically hyperbolic (complex connected compact) manifold Y there is a group homomorphism  such that
such that

for every  . Thus every
. Thus every  is p-fiberwise.
is p-fiberwise.
Remark 3.5
If, in addition, Y is Kähler, then  has a natural meromorphic structure and the group homomorphism
has a natural meromorphic structure and the group homomorphism

is a meromorphic map, in particular, \(\tau \) is a holomorphic homomorphism of complex Lie groups and  is a complex Lie subgroup of
is a complex Lie subgroup of  [13, Lemma 2.4, (3)].
[13, Lemma 2.4, (3)].
Proposition 3.6
Let (X, p, Y) be an equidimensional rational bundle. Assume that Y contains no analytic subsets of codimension 1. Then (X, p, Y) is a \({\mathbb {P}}^{1}\)-bundle.
Proof
Let  , and
, and

be the set of all points in X where the differential dp of p does not have the maximal rank. Then S and \({\widetilde{S}}=p(S)\) are analytic subsets of X and Y, respectively (see, for instance, [20, Chapter VII, Theorem 2], [23, Theorem 1.22], [31]). Moreover, [30]. Since Y contains no analytic subsets of codimension 1, we obtain: \({\widetilde{S}}=\varnothing \). Thus the holomorphic map p has no singular fibers. \(\square \)
Remark 3.7
We used the following theorem of Ramanujam [30]. Let X and Y be connected complex manifolds, \(f:X\rightarrow Y\) a proper flat holomorphic map such that the general fiber is Riemann sphere, D the set of points in X such that df is not of maximal rank, and \(E=f(D)\). Then E is pure of codimension 1 in Y. In the algebraic case this result was proven by Dolgachev [10].
Consider now a \( {\mathbb {P}}^{1}\)-bundle over a compact complex connected manifold Y, i.e., a triple (X, p, Y) such that X is a holomorphically locally trivial fiber bundle over Y with fiber \({\mathbb {P}}^{1}\) and with the corresponding projection \(p:X\rightarrow Y\). Let us fix some notation.
Notation and Assumptions 2
-
\(P_y\) stands for the fiber \(p^{-1}(y)\).
-
We call the covering \(Y=\bigcup U_i\) by open subsets of Y fine if for every i there exist an isomorphism \( \phi _i\) of \( V_i=\pi ^{-1}(U_i)\) to direct product of \( U_i\) and \({\mathbb {P}}^{1}_{(x_i:y_i)}\) that is compatible with the natural projection \(\mathrm {pr}\) on the second factor (i.e., \(p,\mathrm {pr}\)-fiberwise). In other words \( V_i\subset X\) stands for \(p^{-1}(U_i)\): we have an induced isomorphism
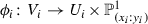 and
and 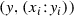 are coordinates in \(V_i\).
are coordinates in \(V_i\).In
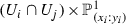 defined is a holomorphic map \(\Phi _{i,j}=(\mathrm{id}, A_{i,j}(y))\):
defined is a holomorphic map \(\Phi _{i,j}=(\mathrm{id}, A_{i,j}(y))\): 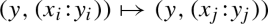
such that
-
\(\star \)
 with representative
with representative 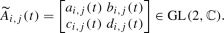
-
\(\star \)
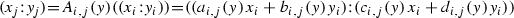 .
. -
\(\star \) \(A_{i,j}(y)= A_{j,i}(y)^{-1}\!\).
-
\(\star \) The following diagram commutes:
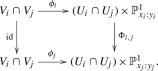
-
\(\star \) \(A_{i,j}(y) \) depend holomorphically on y in
 .
. -
\(\star \) \(A_{i,j}(y) A_{j,k}(y) = A_{i,k}(y)\).
-
Lemma 3.8
Let \(Z\subset Y\) be an analytic subset of Y with  and
and  . Let
. Let  be p-fiberwise. If f is defined at every point
be p-fiberwise. If f is defined at every point  then
then  .
.
Proof
Let \( \{U_i\}\) be a fine covering of Y. Since  is p-fiberwise as well,
is p-fiberwise as well,  is a biholomorphic map. Let \(z \in {\widetilde{Z}}\) and \(W\subset U_i\) be an open neighborhood of p(z) such that
is a biholomorphic map. Let \(z \in {\widetilde{Z}}\) and \(W\subset U_i\) be an open neighborhood of p(z) such that  for some j. Let
for some j. Let  ,
,  . For every \(t\in A \) the restriction \(f |_{P_t}\) is an isomorphism of \(P_t\) with
. For every \(t\in A \) the restriction \(f |_{P_t}\) is an isomorphism of \(P_t\) with  defined in corresponding coordinates by an element of
defined in corresponding coordinates by an element of  . Thus, we have a holomorphic map
. Thus, we have a holomorphic map

such that

Since  is an affine variety, and
is an affine variety, and  , by Levi’s continuation theorem ([17], see also [20, Chapter VII, Theorem 4] or [11, Section 4.8]) there exists a holomorphic extension
, by Levi’s continuation theorem ([17], see also [20, Chapter VII, Theorem 4] or [11, Section 4.8]) there exists a holomorphic extension  . We define
. We define

Thus we can extend f holomorphically at any point \(z\in \widetilde{Z}\). Since outside \({\widetilde{Z}}\) all the extensions coincide, this global extension is uniquely defined. \(\square \)
Definition 3.9
An n-section S of p is a codimension 1 analytic subset \(D\subset X\) such that the intersection \(X\cap P_y\) is finite for every \(y\in Y\) and consists of n distinct points for the general \(y\in Y\). A bisection is a 2-section. A section S of p is a 1-section.
Remark 3.10
For a section S of p there is a holomorphic map \(\sigma :Y\rightarrow X\) such that the section \(S=\sigma (Y)\) and  on Y. In every \(U_i\) the map \(\sigma \) is defined by a function \(\sigma _i:U_i\rightarrow V_i\) such that
on Y. In every \(U_i\) the map \(\sigma \) is defined by a function \(\sigma _i:U_i\rightarrow V_i\) such that

Lemma 3.11
If Y contains no analytic subsets of codimension 1, then
-
(i)
any two distinct sections of p in X are disjoint;
-
(ii)
an n-section has no ramification points (i.e., the intersection \(X\cap P_y\) consists of n distinct points for every \(y\in Y\)).
Proof
(i) If a section \(S=\sigma (Y)\) meets a section \(R=\rho (Y)\) then the intersection \(S\cap R\) is either empty or has codimension 2 in X. Since none of sections contains a fiber, \(p(S\cap R)\) is either empty or has codimension 1 in Y. Since Y carries no analytic subsets of codimension 1, \(p(S\cap R)=\varnothing \).
(ii) Let R be an n-section of p, let A be the set of all points \(x\in R\) where the restriction \(p |_R:R\rightarrow Y\) of p onto R is not locally biholomorphic. Then the image p(A) is either empty or has pure codimension 1 in Y([9, Sections 1, 9], [22, Theorem 1.6], [31]). Since Y carries no analytic subsets of codimension 1, \(p(A) =\varnothing \). Hence, \(A=\varnothing \). \(\square \)
4 \(\pmb {{\mathbb {P}}^{1}}\)-bundles over poor manifolds
We now fix a poor complex manifold T and consider a \( {\mathbb {P}}^{1}\)-bundle over T, i.e., a triple (X, p, T) such that
-
X and T are connected compact complex manifolds;
-
T contains neither a rational curve nor an analytic subspace of codimension 1, and algebraic dimension \(a(T)=0\);
-
X is a holomorphically locally trivial fiber-bundle over T with fiber \({\mathbb {P}}^{1}\) and with the corresponding projection map \(p:X\rightarrow T\).
Corollary 4.1
 .
.
Proof
Since T contains no rational curves, by Lemma 3.3, every  is p-fiberwise. For
is p-fiberwise. For  let \(\widetilde{S}_f\) be the indeterminancy locus of f that is an analytic subspace of X of codimension at least 2 [31, p. 369]. Let \(S_f={p({\widetilde{S}}_f)}\), which is an analytic subset of Y ([31, 20, Chapter VII, Theorem 2]). Since T contains no analytic subsets of codimension 1,
let \(\widetilde{S}_f\) be the indeterminancy locus of f that is an analytic subspace of X of codimension at least 2 [31, p. 369]. Let \(S_f={p({\widetilde{S}}_f)}\), which is an analytic subset of Y ([31, 20, Chapter VII, Theorem 2]). Since T contains no analytic subsets of codimension 1,  . Moreover, f is defined at all points of
. Moreover, f is defined at all points of  . By Lemma 3.8, both
. By Lemma 3.8, both  and, similarly,
and, similarly,  may be holomorphically extended to X, hence we get
may be holomorphically extended to X, hence we get  . \(\square \)
. \(\square \)
Recall that by  we denote the kernel of the group homomorphism
we denote the kernel of the group homomorphism  , i.e., the subgroup of automorphisms of X that leave every fiber of p invariant.
, i.e., the subgroup of automorphisms of X that leave every fiber of p invariant.
Let  , \(f\ne \mathrm{id}\). By Lemma 3.1 of [34] we know that the set of fixed points of f is a divisor in X. The following consideration shows that this divisor is either a smooth section of p, or a union of two disjoint sections of p, or a smooth 2-section.
, \(f\ne \mathrm{id}\). By Lemma 3.1 of [34] we know that the set of fixed points of f is a divisor in X. The following consideration shows that this divisor is either a smooth section of p, or a union of two disjoint sections of p, or a smooth 2-section.
Proposition 4.2
Assume that  . Let
. Let  , \(f\ne \mathrm{id}\), and let S be the set of all fixed points of f. Then one of three following cases holds:
, \(f\ne \mathrm{id}\), and let S be the set of all fixed points of f. Then one of three following cases holds:
- A.:
-
\(S=S_1\cup S_2 \) is a union of two disjoint sections \(S_1\) and \(S_2\) of p.
- B.:
-
S is a section of p.
- C.:
-
S is a 2-section of p (meeting every fiber at two distinct points).
Proof
Let \(\{U_i\}\) be a fine covering of T. Let  be defined (see Notation and Assumptions 2) in \(V_i\) with coordinates
be defined (see Notation and Assumptions 2) in \(V_i\) with coordinates  by
by  , where
, where
-
1.
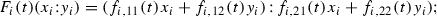
-
2.
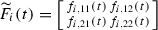 represents
represents 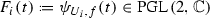 (see the proof of Lemma 3.8);
(see the proof of Lemma 3.8); -
3.
the set of fixed points of
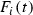 is the analytic subset of X defined by the equation
is the analytic subset of X defined by the equation 
that is
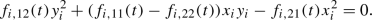 (3)
(3)
It is obviously an analytic subset of X. In every \(U_i\) the function

is defined and holomorphic. Since  represent the globally defined map
represent the globally defined map  , we get (see Notation and Assumptions 2)
, we get (see Notation and Assumptions 2)

which means that

where  are some complex functions in
are some complex functions in  . From (4) we have
. From (4) we have
-
(i)
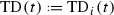 for \(t\in U_i, \) is holomorphic and globally defined on T, hence constant, we denote this number by
for \(t\in U_i, \) is holomorphic and globally defined on T, hence constant, we denote this number by 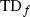 .
. -
(ii)
If
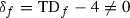 , then fix a square root
, then fix a square root 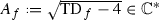 and define \(\lambda _f=\frac{T_f+A_f}{T_f-A_f}\) as the ratio of the eigenvalues of
and define \(\lambda _f=\frac{T_f+A_f}{T_f-A_f}\) as the ratio of the eigenvalues of 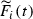 (it does not depend on i). Then for every i one can define coordinates
(it does not depend on i). Then for every i one can define coordinates 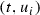 , \( u_i\in \overline{{\mathbb {C}}}\), in \(V_i=p^{-1}(U_i)\) in such a way that
, \( u_i\in \overline{{\mathbb {C}}}\), in \(V_i=p^{-1}(U_i)\) in such a way that 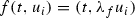 . The set \(S\cap V_i\) of fixed points of f in \(V_i\) is \(\{u_i=0\}\cup \{u_i=\infty \}\). Thus S is an unramified double cover of T: it may be either a union of two disjoint sections or one bisection (see Cases A, C below for details).
. The set \(S\cap V_i\) of fixed points of f in \(V_i\) is \(\{u_i=0\}\cup \{u_i=\infty \}\). Thus S is an unramified double cover of T: it may be either a union of two disjoint sections or one bisection (see Cases A, C below for details). -
(iii)
If
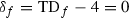 then
then 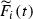 is proportional to a unipotent matrix and for every i one can define in \(V_i=p^{-1}(U_i)\) coordinates
is proportional to a unipotent matrix and for every i one can define in \(V_i=p^{-1}(U_i)\) coordinates 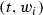 , \(w_i\in \overline{{\mathbb {C}}}\), in such a way that
, \(w_i\in \overline{{\mathbb {C}}}\), in such a way that 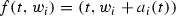 where
where 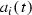 are holomorphic functions in \(U_i\). The set S of fixed points in \(V_i\) is thus the union of the section \(\{w_i=\infty \}\) and \(p^{-1}(R_f)\), where
are holomorphic functions in \(U_i\). The set S of fixed points in \(V_i\) is thus the union of the section \(\{w_i=\infty \}\) and \(p^{-1}(R_f)\), where 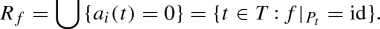
Since it has codimension 1, it has to be empty (see Case B below for details).
In other words, for every \(t\in T\) the selfmap  of \(P_t\) is either the identity map, or has two fixed points, or has one fixed point. If
of \(P_t\) is either the identity map, or has two fixed points, or has one fixed point. If  then (3) defines a smooth analytic subset S of X and \(S\) contains precisely two distinct points for any \(t\in T\). Therefore, S is either an unramified smooth double cover of T or a union of two smooth disjoint sections of p. If
then (3) defines a smooth analytic subset S of X and \(S\) contains precisely two distinct points for any \(t\in T\). Therefore, S is either an unramified smooth double cover of T or a union of two smooth disjoint sections of p. If  then (3) defines a smooth section of p over the complement to an analytic subset \(R_f\) of T (that has to be empty) or holds identically on X. \(\square \)
then (3) defines a smooth section of p over the complement to an analytic subset \(R_f\) of T (that has to be empty) or holds identically on X. \(\square \)
Thus we have the following three cases.
Case A. The set of all fixed points of a non-identity map  is the union of two disjoint sections \(S_1\) and \(S_2\) of p. We will say that f has type A with Data \( (S_1,S_2)\) (an ordered pair). Changing Data \( (S_1,S_2)\) to Data \( (S_2,S_1)\) would lead to changing \(\lambda _f\) to \({1}/{\lambda _f}\).
is the union of two disjoint sections \(S_1\) and \(S_2\) of p. We will say that f has type A with Data \( (S_1,S_2)\) (an ordered pair). Changing Data \( (S_1,S_2)\) to Data \( (S_2,S_1)\) would lead to changing \(\lambda _f\) to \({1}/{\lambda _f}\).
Lemma 4.3
Assume that  , \(f\ne \mathrm{id}\), has type A with Data \( (S_1,S_2)\) and
, \(f\ne \mathrm{id}\), has type A with Data \( (S_1,S_2)\) and  . Then
. Then
-
 is the total body of a holomorphic line bundle \({\mathscr {L}}_f\) with zero section \(S_1\);
is the total body of a holomorphic line bundle \({\mathscr {L}}_f\) with zero section \(S_1\); -
\({\mathscr {L}}_f\) has no other sections;
-
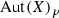 contains a subgroup \(\Gamma _A\cong {\mathbb {C}}^*\) of all \( g\in \) with the same Data \( (S_1,S_2)\);
contains a subgroup \(\Gamma _A\cong {\mathbb {C}}^*\) of all \( g\in \) with the same Data \( (S_1,S_2)\); -
any automorphism
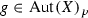 of type A belongs to \(\Gamma _A\);
of type A belongs to \(\Gamma _A\); -
an automorphism \(g\in \Gamma _A\) is uniquely determined by its restriction to any fiber \(P_t\) with \(t\in T\) (cf. [34, Lemma 4.3]).
Proof
Similarly to the proof of Proposition 4.2, let \(\{U_i\}\) be a fine covering of T. Let be defined in \(V_i=p^{-1}(U_i)\) with coordinates  by
by  . Let \(z_i= {y_i}/{x_i}\in \overline{{\mathbb {C}}}\) and
. Let \(z_i= {y_i}/{x_i}\in \overline{{\mathbb {C}}}\) and

Since  depend on t holomorphically,
depend on t holomorphically,  and
and  are meromorphic functions in \(U_i\). Since \(S_1\cap S_2=\varnothing \),
are meromorphic functions in \(U_i\). Since \(S_1\cap S_2=\varnothing \),  for all \(t\in U_i \) and all i. The holomorphic coordinate change in \(V_i\) introduced in item (ii) of the proof of Proposition 4.2 is
for all \(t\in U_i \) and all i. The holomorphic coordinate change in \(V_i\) introduced in item (ii) of the proof of Proposition 4.2 is

In these coordinates \(S_1\cap V_i=\{u_i=0\}\), and \(S_2\cap V_i=\{u_i=\infty \} \). Since both sections are globally defined and f-invariant, there are holomorphic functions  , \(\mu _{i,j}\ne 0\), such that
, \(\mu _{i,j}\ne 0\), such that

Since  in
in  , we have \(\mu _{i,k}=\mu _{j,k}\mu _{i,j}\), that is we have a cocycle. It defines a holomorphic line bundle \({\mathscr {L}}_f\) on T with transition functions \( \mu _{i,j}\) such that
, we have \(\mu _{i,k}=\mu _{j,k}\mu _{i,j}\), that is we have a cocycle. It defines a holomorphic line bundle \({\mathscr {L}}_f\) on T with transition functions \( \mu _{i,j}\) such that  is the total body of \({\mathscr {L}}_f\) and \(S_1\) is the zero section of \({\mathscr {L}}_f\). Moreover (see item (ii) of the proof of Proposition 4.2),
is the total body of \({\mathscr {L}}_f\) and \(S_1\) is the zero section of \({\mathscr {L}}_f\). Moreover (see item (ii) of the proof of Proposition 4.2),

If \({\mathscr {L}}_f\) had another section, then the \({\mathbb {P}}^{1}\)-bundle X would have three disjoint sections, thus would be isomorphic to  (the excluded case). Since every
(the excluded case). Since every  of type A has sections as the set of fixed points, it has to have the same Data \((S_1,S_2) \).
of type A has sections as the set of fixed points, it has to have the same Data \((S_1,S_2) \).
The maps having the same Data differ only by the coefficient \(\lambda _f\in {\mathbb {C}}^*\!\). It follows that an automorphism of type A is uniquely defined by its restriction to any fiber \(P_t\), \(t\in T\) (cf. [34, Lemma 4.3]). On the other hand, for every \(\lambda \in {\mathbb {C}}^*\) one can define an automorphism  of type A on X by the formula
of type A on X by the formula

Thus all automorphisms of type A on X form a subgroup \(\Gamma _A\cong {\mathbb {C}}^*\) of  . \(\square \)
. \(\square \)
Case B. If the set of all fixed points of a non-identity  is a section S of (X, p, T) we will say that f has type B with Data S.
is a section S of (X, p, T) we will say that f has type B with Data S.
Lemma 4.4
Assume that  , \(f\ne \mathrm{id}\), has type B with Data S and
, \(f\ne \mathrm{id}\), has type B with Data S and  . Then
. Then
-
(i)
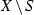 is an \({\mathbb {A}}^{1}\)-bundle \({\mathscr {A}}_{f}\) over T;
is an \({\mathbb {A}}^{1}\)-bundle \({\mathscr {A}}_{f}\) over T; -
(ii)
\({\mathscr {A}}_{f}\) has no sections;
-
(iii)
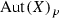 contains a subgroup \(\Gamma _B\cong {\mathbb {C}}\) of all
contains a subgroup \(\Gamma _B\cong {\mathbb {C}}\) of all 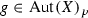 with the same Data S;
with the same Data S; -
(iv)
any automorphism
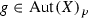 of type B belongs to \(\Gamma _B\);
of type B belongs to \(\Gamma _B\); -
(v)
an automorphism \(g\in \Gamma _B\) is uniquely determined by its restriction to any fiber \(P_t\) with \(t\in T\);
-
(vi)
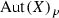 contains no automorphisms of type A.
contains no automorphisms of type A.
Proof
In notation of Proposition 4.2 in this case \(\delta _f=TD_f-4=0\). Thus (3) has the set of solutions  of fixed points of f. Consider the set \(R_f\subset T\) defined locally by the conditions
of fixed points of f. Consider the set \(R_f\subset T\) defined locally by the conditions

Since \(f\ne \mathrm{id}\), \(R_f\) is an analytic subset of T, and  . Note that \(p^{-1}(R_f)\subset S\). Consider the function
. Note that \(p^{-1}(R_f)\subset S\). Consider the function

(the equality follows from \(\delta _f=0\)). The function \(g_i\) is meromorphic in  . Since
. Since  , by Levi’s theorem ([17, 20, Chapter VII, Theorem 4], [11, Section 4.8]) \(g_i\) may be extended to a meromorphic function to \(U_i\). Define
, by Levi’s theorem ([17, 20, Chapter VII, Theorem 4], [11, Section 4.8]) \(g_i\) may be extended to a meromorphic function to \(U_i\). Define  . The direct computation shows that
. The direct computation shows that  , where
, where  . Since \(\delta _f=0\), the denominator never vanishes, thus
. Since \(\delta _f=0\), the denominator never vanishes, thus  is a holomorphic function in \(U_i\). The set
is a holomorphic function in \(U_i\). The set  has codimension 1 in \(U_i\), which is impossible if \(R_f\ne \varnothing \). It follows that \(R_f=\varnothing \). Thus, \(f |_{P_{t}}\ne \mathrm{id}\) for any \(t\in T\) and
has codimension 1 in \(U_i\), which is impossible if \(R_f\ne \varnothing \). It follows that \(R_f=\varnothing \). Thus, \(f |_{P_{t}}\ne \mathrm{id}\) for any \(t\in T\) and  does not vanish in \( U_i\).
does not vanish in \( U_i\).
Since  is globally defined, we have
is globally defined, we have  , where \(\nu _{i,j}\) and \(\tau _{i,j}\) are holomorphic functions in
, where \(\nu _{i,j}\) and \(\tau _{i,j}\) are holomorphic functions in  . Since f is globally defined
. Since f is globally defined

we have
-
\(\{\nu _{i,j}\}\) do not vanish in
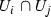 and form a cocycle, thus define a holomorphic line bundle \(\mathscr {M}_f\) on T;
and form a cocycle, thus define a holomorphic line bundle \(\mathscr {M}_f\) on T; -
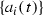 is a section of \({\mathscr {M}}_f\).
is a section of \({\mathscr {M}}_f\).
Since a non-trivial holomorphic line bundle on T has no nonzero sections, either  and \(f=\mathrm{id}\) (the excluded case), or \({\mathscr {M}}_f\) is trivial and we have a global holomorphic, hence constant function
and \(f=\mathrm{id}\) (the excluded case), or \({\mathscr {M}}_f\) is trivial and we have a global holomorphic, hence constant function

Thus,
-
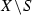 is an \({\mathbb {A}}^{1}\)-bundle \({\mathscr {A}}_f\) with transition holomorphic functions \(\tau _{ij} \) in
is an \({\mathbb {A}}^{1}\)-bundle \({\mathscr {A}}_f\) with transition holomorphic functions \(\tau _{ij} \) in 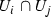 ;
; -
for every \(b\in {\mathbb {C}}\) there is
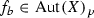 defined in each \(V_i\) by
defined in each \(V_i\) by 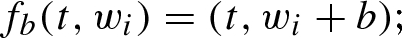
-
the subgroup \(\Gamma _B\) of all \(f_b\), \(b\in {\mathbb {C}}\), is isomorphic to \({\mathbb {C}}^+\!\).
Let us show that \({\mathscr {A}}_f\) has no sections. If it had a section \(S_1\), then \(S, S_1, f(S_1)\) would be three disjoint sections of X. Since  , this is impossible. It follows that
, this is impossible. It follows that  contains neither an automorphism of type A nor an automorphism of type B with Data different from S. The maps having the same Data S differ only by the summand \(a_f\in {\mathbb {C}}\). It follows that an automorphism of type B is uniquely defined by its restriction to a fiber \(P_t\) for every \(t\in T\). \(\square \)
contains neither an automorphism of type A nor an automorphism of type B with Data different from S. The maps having the same Data S differ only by the summand \(a_f\in {\mathbb {C}}\). It follows that an automorphism of type B is uniquely defined by its restriction to a fiber \(P_t\) for every \(t\in T\). \(\square \)
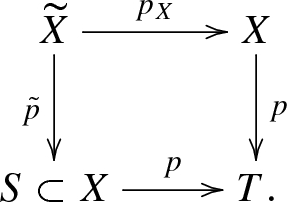
Case C. Assume that  and the set \(S\subset X\) of all fixed points of a non-identity map is a smooth unramified double cover of T. We will call such an f an automorphism of type C defined by Data S. Consider
and the set \(S\subset X\) of all fixed points of a non-identity map is a smooth unramified double cover of T. We will call such an f an automorphism of type C defined by Data S. Consider

We denote the restriction of p to S by the same letter p, while \(p_X\) and \({\tilde{p}}\) stand for the restrictions to \(\widetilde{X}\) of natural projections  and
and  , respectively. We write \({{\,\mathrm{inv}\,}}:S\rightarrow S\) for an involution (the only non-trivial deck transformation for \( p |_S\)). We have
, respectively. We write \({{\,\mathrm{inv}\,}}:S\rightarrow S\) for an involution (the only non-trivial deck transformation for \( p |_S\)). We have
-
(a)
The following diagram commutes:
 (5)
(5) -
(b)
\(p_X:{\widetilde{X}}\rightarrow X \) is an unramified double cover of X.
-
(c)
Every fiber \({\widetilde{p}}^{-1}(s)\), \(s\in S\), is isomorphic to
$$\begin{aligned} P_{p(s)}=p^{-1}(p(s))\sim {\mathbb {P}}^{1}\!. \end{aligned}$$ -
(d)
The \({\mathbb {P}}^{1}\)-bundle \({\widetilde{X}}\) over S has two sections
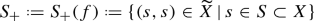
and
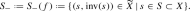
They are mapped onto S isomorphically by \(p_X\).
-
(e)
Every section
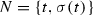 of p in X induces the section
of p in X induces the section 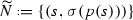 of \({\tilde{p}} \) in \({\widetilde{X}}\). We have \(p_X({\widetilde{N}})=N\) is a section of p, thus \({\widetilde{N}}\) cannot coincide with \( S_+\) or \( S_-\).
of \({\tilde{p}} \) in \({\widetilde{X}}\). We have \(p_X({\widetilde{N}})=N\) is a section of p, thus \({\widetilde{N}}\) cannot coincide with \( S_+\) or \( S_-\). -
(f)
Every
 induces an automorphism
induces an automorphism 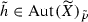 defined by $$\begin{aligned} {\tilde{h}}(s,x)=(s,h(x)). \end{aligned}$$
defined by $$\begin{aligned} {\tilde{h}}(s,x)=(s,h(x)). \end{aligned}$$ -
(g)
In particular, for the lift \({\tilde{f}}\) of f all the points of \(S_+\) and \(S_-\) are fixed, hence \({\tilde{f}}\) is of type A with Data \(( S_+, S_-)\).
-
(h)
The map \({\tilde{f}}\) is uniquely determined by its restriction to any fiber \({\widetilde{P}}_s={\tilde{p}}^{-1}(s)\) (see Case A), hence f is uniquely determined by its restriction on the fiber
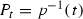 . Indeed, if \(f |_{P_t}=\mathrm{id}\), then
. Indeed, if \(f |_{P_t}=\mathrm{id}\), then-
\({\tilde{f}} |_{P_s}=\mathrm{id}\), \(t=p(s)\), hence
-
\({\tilde{f}}=\mathrm{id}\), hence
-
\({\tilde{f}} |_{P_{s_1}}=\mathrm{id}\) for every \(s_1\in S\), hence
-
\(f |_{P_{t_1}}=\mathrm{id}\) for \(t_1=p(s_1)\in T\).
-
-
(i)
It follows that \(h\mapsto {\tilde{h}}\) is a group embedding of
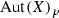 to
to 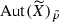 .
. -
(j)
The involution \(s\rightarrow {{\,\mathrm{inv}\,}}(s)\) may be extended from S to a holomorphic involution \({\widetilde{X}}\) by
$$\begin{aligned} {{\,\mathrm{inv}\,}}(s,x)= ({{\,\mathrm{inv}\,}}(s),x). \end{aligned}$$ -
(k)
S is a poor manifold by Lemma 3.1.
Clearly, the maps having the same Data differ only by the coefficient \(\lambda _{{\tilde{f}}}\in {\mathbb {C}}^*\!\).
Corollary 4.5
If X admits a non-identity automorphism of type C and  then the \({\mathbb {P}}^{1}\)-bundle \(p:X\rightarrow T\) does not have a section. In particular, it does not admit automorphisms of type A or B.
then the \({\mathbb {P}}^{1}\)-bundle \(p:X\rightarrow T\) does not have a section. In particular, it does not admit automorphisms of type A or B.
Proof
Indeed, if X admitted an automorphism of type A or B then, by Proposition 4.2, there would be a section \(\Sigma \) of p in X. The preimage \(p_X^{-1}(\Sigma )\subset {\widetilde{X}}\) would be a section \({\widetilde{S}}\) of \({\tilde{p}}\) in \({\widetilde{X}}_f\). Thus \({\widetilde{X}}_f\) would admit three disjoint sections: \(S_-, S_+\), and \({\widetilde{S}} \). In this case \({\widetilde{X}}_f\) would be the direct product  . \(\square \)
. \(\square \)
Lemma 4.6
Assume that  , \(f\ne \mathrm{id}\), has type A with Data \( (S_1,S_2)\) and
, \(f\ne \mathrm{id}\), has type A with Data \( (S_1,S_2)\) and  . Let \({\mathscr {L}}_f\) be defined by f (see Case A for the definition) holomorphic line bundle on T with transition functions \(\mu _{ij}\) and such that \(S_1 \) is its zero section. Then one of the following holds:
. Let \({\mathscr {L}}_f\) be defined by f (see Case A for the definition) holomorphic line bundle on T with transition functions \(\mu _{ij}\) and such that \(S_1 \) is its zero section. Then one of the following holds:
-
(i)
 and X admits only automorphisms of type A except \(\mathrm{id}\);
and X admits only automorphisms of type A except \(\mathrm{id}\); -
(ii)
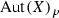 contains an automorphism h of type C with Data S. In this case \({\mathscr {L}}_f^{\otimes 2}\) is a trivial holomorphic line bundle and the corresponding to h double cover
contains an automorphism h of type C with Data S. In this case \({\mathscr {L}}_f^{\otimes 2}\) is a trivial holomorphic line bundle and the corresponding to h double cover 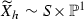 .
.
Proof
(i) By Lemma 4.4, we know that \(\mathrm{Aut}(X)_p\) contains no automorphisms of type B. If there is no automorphism of type C then all \(f\in \mathrm{Aut}(X)_p\) are of type A except \(\mathrm{id}\). By Lemma 4.3, in this case \(\mathrm{Aut}(X_p)=\Gamma _A\cong {\mathbb {C}}^*\).
(ii) Let \(h\in \mathrm{Aut}(X)_p\) be of type C with Data S. Let a point \(t\in U_i\subset T\), where \(U_i\) is a fine covering of T, and let \((u, t_i)\), \( u\in U_i\), \( t_i\in \overline{{\mathbb {C}}}\), be coordinates in \(V_i=p^{-1}(U_i)\subset X\). Since \(S_1\cup S_2\) are the only sections of \(p:X\rightarrow T\) and points of \(S_1\cup S_2\) are not fixed by h, we have
where \(\nu _i\) are holomorphic in \(U_i\) functions. Since h is defined globally, we have

Thus  . Since a non-trivial line bundle over T has only zero section, it follows that \({\mathscr {L}}_f^{\otimes 2}\) is a trivial bundle and \(\nu _i(u)=\nu \) is a constant function. The bisection S is defined locally by the equation \(t_i^2=\nu \). By Corollary 4.5,
. Since a non-trivial line bundle over T has only zero section, it follows that \({\mathscr {L}}_f^{\otimes 2}\) is a trivial bundle and \(\nu _i(u)=\nu \) is a constant function. The bisection S is defined locally by the equation \(t_i^2=\nu \). By Corollary 4.5,  . \(\square \)
. \(\square \)
Assume that  , \( f\ne \mathrm{id}\), and f is of type C defined by Data (bisection) S. Let
, \( f\ne \mathrm{id}\), and f is of type C defined by Data (bisection) S. Let  be the corresponding double cover (see Case C in Sect. 4 and diagram (5)). Recall that S is poor and \({\tilde{p}}:{\widetilde{X}}\rightarrow S\) has two sections.
be the corresponding double cover (see Case C in Sect. 4 and diagram (5)). Recall that S is poor and \({\tilde{p}}:{\widetilde{X}}\rightarrow S\) has two sections.
Lemma 4.7
Assume that  , \( f\ne \mathrm{id}\), and f is of type C defined by Data (bisection) S.
, \( f\ne \mathrm{id}\), and f is of type C defined by Data (bisection) S.
-
(i)
If the corresponding double cover (see Case C)
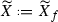 is not isomorphic to
is not isomorphic to 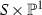 then
then 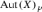 has exponent 2 and consists of two or four elements.
has exponent 2 and consists of two or four elements. -
(ii)
If
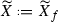 is isomorphic to
is isomorphic to 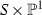 then there are two sections \(S_1,S_2\subset X\) of p. Moreover,
then there are two sections \(S_1,S_2\subset X\) of p. Moreover, 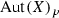 is a disjoint union of its abelian complex Lie subgroup \(\Gamma \cong {\mathbb {C}}^*\) of index 2 and its coset \(\Gamma ^{\prime }\!\). The subgroup \(\Gamma \) consists of those
is a disjoint union of its abelian complex Lie subgroup \(\Gamma \cong {\mathbb {C}}^*\) of index 2 and its coset \(\Gamma ^{\prime }\!\). The subgroup \(\Gamma \) consists of those 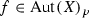 that fix \(S_1\) and \(S_2\). The coset \(\Gamma ^{\prime }\) consists of those
that fix \(S_1\) and \(S_2\). The coset \(\Gamma ^{\prime }\) consists of those 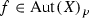 that interchange \(S_1\) and \(S_2\).
that interchange \(S_1\) and \(S_2\).
Proof
Choose a point \(a\in S\). Let \(b=p(a)\in T\). It means that a is one of two points in \(S\cap P_b\). The lift \({\tilde{f}}\) of f onto \({\widetilde{X}} \) has type A, and for the corresponding line bundle \({\widetilde{{\mathscr {L}}}}_{{\tilde{f}}}\) we may assume that \(S_+\) is a zero section. Let
-
\({\widetilde{U}}_i\) be the fine covering of S;
-
\(\mu _{ij}\) be transition functions of \({\widetilde{{\mathscr {L}}}}_{\tilde{f}}\) in
 ;
; -
\({\widetilde{V}}_i={\tilde{p}}^{-1}({\widetilde{U}}_i)\subset {\widetilde{X}} \);
-
\((u, z_i)\) be the local coordinates in \({\widetilde{V}}_i\) such that
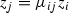 in
in 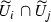 ;
; -
\(a\in {\widetilde{U}}_i\), \( {{\,\mathrm{inv}\,}}(a)\in {\widetilde{U}}_k\) and \({\widetilde{U}}_k\cap {\widetilde{U}}_i=\varnothing \);
-
\(b=p(a)=p({{\,\mathrm{inv}\,}}(a))\in T\).
Since \(S_+\) is the zero section, \(z_i=0\) on \(S_+\cap {\widetilde{V}}_i, \) \(z_i=\infty \) on \(S_-\cap {\widetilde{V}}_i \), while \(z_k=0\) on \(S_+\cap {\widetilde{V}}_k, \) and \(z_k=\infty \) on \(S_-\cap \widetilde{V}_k\). We have
It may be demonstrated by the following diagram:

Here the isomorphism \(\alpha :\overline{{\mathbb {C}}}_{z_i}\rightarrow \overline{{\mathbb {C}}}_{z_k}\) is defined in such a way that the diagram is commutative.
We get from (7) that \(\alpha (0)=\infty \), \(\alpha (\infty )=0\). Hence
for some \(\nu \ne 0\). By construction,
Consider an automorphism  . Let \({\tilde{h}}\) be its pullback to
. Let \({\tilde{h}}\) be its pullback to  defined by \(\tilde{h}(s,x)=(s,h(x))\). Let \(n_1(z_i)={\tilde{h}} |_{{\tilde{P}}_a}, \) which means that \(h(a,z_i)=(a,n_1(z_i))\). Let \(n_2(z_k)={\tilde{h}} |_{\tilde{P}_ {{{\,\mathrm{inv}\,}}(a)}}, \) which means that \(h( {{\,\mathrm{inv}\,}}(a),z_k)=(a,n_2(z_k))\). Choose in \(P_b\) the coordinate z such that \(z_i=p_X^*(z)\), i.e., \( p_X(a,z_i)=(b, z_i)\) for a point \((a,z_i)\in {\widetilde{P}}_a \). By construction, \( z(a)=0\), \(z({{\,\mathrm{inv}\,}}(a))=\infty \). We have the following commutative diagram:
defined by \(\tilde{h}(s,x)=(s,h(x))\). Let \(n_1(z_i)={\tilde{h}} |_{{\tilde{P}}_a}, \) which means that \(h(a,z_i)=(a,n_1(z_i))\). Let \(n_2(z_k)={\tilde{h}} |_{\tilde{P}_ {{{\,\mathrm{inv}\,}}(a)}}, \) which means that \(h( {{\,\mathrm{inv}\,}}(a),z_k)=(a,n_2(z_k))\). Choose in \(P_b\) the coordinate z such that \(z_i=p_X^*(z)\), i.e., \( p_X(a,z_i)=(b, z_i)\) for a point \((a,z_i)\in {\widetilde{P}}_a \). By construction, \( z(a)=0\), \(z({{\,\mathrm{inv}\,}}(a))=\infty \). We have the following commutative diagram:

Hence
(i) Assume that  . It follows from (6) and the proof of Lemma 4.6 (applied to \({\widetilde{X}}\)) that for every
. It follows from (6) and the proof of Lemma 4.6 (applied to \({\widetilde{X}}\)) that for every  in every
in every  of our fine covering either
of our fine covering either  or
or  for some \(\lambda \in {\mathbb {C}}^*\!\), and \(\lambda \) does not depend on s or j. Thus, one of following two conditions holds:
for some \(\lambda \in {\mathbb {C}}^*\!\), and \(\lambda \) does not depend on s or j. Thus, one of following two conditions holds:
-
\(n_1(z_i)=\lambda z_i\), \( n_2(z_k)=\lambda z_k\), \(z_k={\nu }/{z_i}\) and from (8)
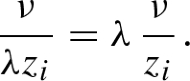
-
\(n_1(z_i)={\lambda }/{ z_i}\), \(n_2(z_k)={\lambda }/{ z_k}\), \(z_k={\nu }/{z_i}\) and from (8)
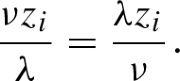
In the former case \(\lambda =\pm 1 \), in the latter \(\lambda =\pm \nu \). Hence, at most four maps are possible. Clearly, the squares of all these maps are the identity map.
(ii) Assume that  . Let
. Let  be the natural projection. Since \(S_+\!=\{(s,s) \,{|}\, s\in S\}\) and \(S_-\!=\{(s,{{\,\mathrm{inv}\,}}(s))\,{|}\, s\in S\}\) have algebraic dimension 0, the rational function z is constant along these sections. We may assume that \(z=0\) on \( S_+\!=\{(s,s)\}\), \(z=\infty \) on \(S_-\!=\{(s,\hbox {inv}(s))\}\), and all
be the natural projection. Since \(S_+\!=\{(s,s) \,{|}\, s\in S\}\) and \(S_-\!=\{(s,{{\,\mathrm{inv}\,}}(s))\,{|}\, s\in S\}\) have algebraic dimension 0, the rational function z is constant along these sections. We may assume that \(z=0\) on \( S_+\!=\{(s,s)\}\), \(z=\infty \) on \(S_-\!=\{(s,\hbox {inv}(s))\}\), and all  . Moreover, in this case
. Moreover, in this case  and
and

On the other hand, it follows from (8) that the map \(\tilde{h}(s,z)\) defined by (9) may be pushed down to X if and only if
In the expression \(\alpha (z)={\nu }/{z}\), we may assume that \(\nu =1\). (Indeed, choose a \(\sqrt{ \nu }\) and divide z by it). The map \({\tilde{h}}(s,z)\) defined by (9) may be pushed down to X if and only if

For every  , \(a^2-b^2\ne 0 \), two types of \({\tilde{h}}\) with property (10) are possible:
, \(a^2-b^2\ne 0 \), two types of \({\tilde{h}}\) with property (10) are possible:
Note that the only non-trivial automorphism of \({\widetilde{X}}\) leaving \(z=0\), \(z=\infty \) invariant is \(-{\tilde{h}}_{a,0}\), which is the lift \({\tilde{f}}\) of f. All the transformations \( h_{a,b}\) form an abelian group \({\widetilde{\Gamma }}\) with
The transformations \( -h_{a,b}\) form a coset  . All the transformations from \({\widetilde{\Gamma }}\cup \widetilde{\Gamma }'\) may be pushed down to X. We have:
. All the transformations from \({\widetilde{\Gamma }}\cup \widetilde{\Gamma }'\) may be pushed down to X. We have:  is embedded into \(\mathrm{Aut}({\widetilde{X}})_{{\tilde{p}}} \) and its image is \(\widetilde{\Gamma }\cup {\widetilde{\Gamma }}'\!\). Thus,
is embedded into \(\mathrm{Aut}({\widetilde{X}})_{{\tilde{p}}} \) and its image is \(\widetilde{\Gamma }\cup {\widetilde{\Gamma }}'\!\). Thus,  is the disjoint union of a subgroup \(\Gamma \) and its coset \(\Gamma '\) corresponding to \({\widetilde{\Gamma }}\) and \({\widetilde{\Gamma }}'\!\), respectively. The index of \(\Gamma \) in
is the disjoint union of a subgroup \(\Gamma \) and its coset \(\Gamma '\) corresponding to \({\widetilde{\Gamma }}\) and \({\widetilde{\Gamma }}'\!\), respectively. The index of \(\Gamma \) in  is 2.
is 2.
Note that the sets \(\{z=1\}\) and \(\{z=-1\}\) consist of fixed points of all the maps \({\tilde{h}}_{a,b}\) if \(b\ne 0\). Moreover, they are invariant under the deck transformation \((s,z)\mapsto ({{\,\mathrm{inv}\,}}(s), {1}/{z})\). Their images provide two sections \(S_1, S_2\) of the \({\mathbb {P}}^{1}\)-bundle \(p:X\rightarrow T\). Hence, in this case \(X={\mathbb {P}}(E)\) for some decomposable rank 2 vector bundle E over T. If we change coordinates \(w=({z+1})/({z-1})\) then  and \( {\tilde{h}}_{a,b}({\tilde{h}}_{\alpha ,\beta }w)\) corresponds to \(\mu _{a,b}\mu _{\alpha ,\beta }\). The condition \(a^2-b^2\ne 0\) means that \(\mu \ne 0,\infty \). Thus, \(\Gamma \cong {\mathbb {C}}^*\) as a complex Lie group. In coordinates w we have \({}-\tilde{h}_{a,b}(w)={1}/({w\mu _{a,b}})\), thus \(\Gamma '\) consists of maps interchanging the sections. \(\square \)
and \( {\tilde{h}}_{a,b}({\tilde{h}}_{\alpha ,\beta }w)\) corresponds to \(\mu _{a,b}\mu _{\alpha ,\beta }\). The condition \(a^2-b^2\ne 0\) means that \(\mu \ne 0,\infty \). Thus, \(\Gamma \cong {\mathbb {C}}^*\) as a complex Lie group. In coordinates w we have \({}-\tilde{h}_{a,b}(w)={1}/({w\mu _{a,b}})\), thus \(\Gamma '\) consists of maps interchanging the sections. \(\square \)
Proposition 4.8
Let (X, p, T) be a \({\mathbb {P}}^{1}\)-bundle over a poor manifold T. Then one of the following holds:
- (i):
-
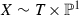 ;
; - (ii):
-
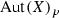 has exponent at most 2 and consists of one, two or four elements;
has exponent at most 2 and consists of one, two or four elements; - (iii):
-
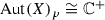 ;
; - (iv):
-
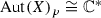 ;
; - (v):
-
 where \(\Gamma \cong {\mathbb {C}}^*\) is a complex Lie subgroup of
where \(\Gamma \cong {\mathbb {C}}^*\) is a complex Lie subgroup of 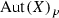 and \(\Gamma ^{\prime }\) is its coset in
and \(\Gamma ^{\prime }\) is its coset in 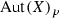 .
.
Proof
We use the following: assume that  and
and  , \(f\ne \mathrm{id}\). Then
, \(f\ne \mathrm{id}\). Then
-
f being of type A implies the existence of exactly two sections of p (see Case A);
-
f being of type B implies the existence of exactly one section of p (see Case B);
-
f being of type C implies the existence of either no or exactly two sections of p (see Case C and Lemma 4.7).
Consider the cases.
(ii) If X contains no sections of p then either  or there is
or there is  of type C. Let S be a bisection of p that is the fixed points set of f. The corresponding to f double cover \({\widetilde{X}}_f\) of X cannot be isomorphic to
of type C. Let S be a bisection of p that is the fixed points set of f. The corresponding to f double cover \({\widetilde{X}}_f\) of X cannot be isomorphic to  by Lemma 4.7(ii), since there are no sections of p. Thus, by Lemma 4.7(i),
by Lemma 4.7(ii), since there are no sections of p. Thus, by Lemma 4.7(i),  has exponent at most 2 and consists of two or four elements.
has exponent at most 2 and consists of two or four elements.
(iii) Assume that X contains exactly one section S of p. Then  or there is non-identity
or there is non-identity  of type B only. Then
of type B only. Then  by combination of Lemma 4.4, Corollary 4.5, and Lemma 4.7.
by combination of Lemma 4.4, Corollary 4.5, and Lemma 4.7.
(iv) Assume that X contains exactly two sections \(S_1\) and \(S_2\) of p. Then there are two options:
-
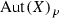 consists of automorphisms of type A only (except id) and
consists of automorphisms of type A only (except id) and 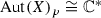 according to Lemma 4.3;
according to Lemma 4.3; -
 contains automorphisms of type A and C. By Lemma 4.7,
contains automorphisms of type A and C. By Lemma 4.7,  where \(\Gamma \cong {\mathbb {C}}^*\) is a complex Lie subgroup of
where \(\Gamma \cong {\mathbb {C}}^*\) is a complex Lie subgroup of 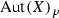 consisting of those maps that fix \(S_1\) and \(S_2 \), and \(\Gamma '\) is its coset in
consisting of those maps that fix \(S_1\) and \(S_2 \), and \(\Gamma '\) is its coset in 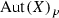 that consists of maps that interchange the sections. \(\square \)
that consists of maps that interchange the sections. \(\square \)
Remark 4.9
Let us formulate a byproduct of the proof of Proposition 4.2. Assume that (V, p, U) is a \({\mathbb {P}}^{1}\)-bundle over a connected complex (not necessarily compact) manifold U, and let  , \( f \ne \mathrm{id}\). Then
, \( f \ne \mathrm{id}\). Then
-
The function
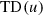 is globally defined.
is globally defined. -
If
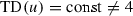 on U then the set of fixed points of f is an unramified (may be reducible) double cover of U.
on U then the set of fixed points of f is an unramified (may be reducible) double cover of U. -
If
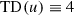 on U and U contains no analytic subset of codimension 1, then the set of fixed points of f is a section of p.
on U and U contains no analytic subset of codimension 1, then the set of fixed points of f is a section of p.
5 \(\pmb {{\mathbb {P}}^{1}}\)-bundles over poor Kähler manifolds
In this section we continue to consider a triple (X, p, T) that is a \({\mathbb {P}}^{1}\)-bundle over a poor manifold T. Further on we assume that T is a Kähler manifold. Recall that this means that
-
X and T are connected complex compact manifolds;
-
T contains no rational curves and no analytic subspaces of codimension 1 (in particular, \(a(T)=0\));
-
T is Kähler;
-
\(p:X\rightarrow T\) is a surjective holomorphic map;
-
X is a holomorphically locally trivial fiber bundle over T with fiber \({\mathbb {P}}^{1}\) and projection p.
Lemma 5.1
If T is a poor Kähler manifold and  then X is a Kähler manifold.
then X is a Kähler manifold.
Proof
Let  , \(f\ne \mathrm{id}\). Then either X or its étale double cover \({\widetilde{X}}\) is \({\mathbb {P}}(E)\) where E is a holomorphic rank 2 vector bundle over a Kähler manifold T or its double cover, respectively (that is also Kähler, see Lemma 3.1). In both cases X is Kähler according to [35, Proposition 3.18]. \(\square \)
, \(f\ne \mathrm{id}\). Then either X or its étale double cover \({\widetilde{X}}\) is \({\mathbb {P}}(E)\) where E is a holomorphic rank 2 vector bundle over a Kähler manifold T or its double cover, respectively (that is also Kähler, see Lemma 3.1). In both cases X is Kähler according to [35, Proposition 3.18]. \(\square \)
Corollary 5.2
 is Jordan.
is Jordan.
Proof
The statement follows from the result of [16]. \(\square \)
Lemma 5.3
Consider a short exact sequence of connected complex Lie groups:
Here i is a closed holomorphic embedding and j is surjective holomorphic. Assume that D is a complex torus and A is isomorphic as a Lie group either to \( {\mathbb {C}}^+\) or to \({\mathbb {C}}^*\!\). Then B is commutative.
Proof
Step 1. First, let us prove that A is a central subgroup in B. Take any element \(b\in B\). Define a holomorphic map \(\phi _ b:A\rightarrow A\), \( \phi _b(a)= bab^{-1}\!\in A\) for an element \(a\in A\). Since it depends holomorphically on b, we have a holomorphic map  , \( b \rightarrow \phi _b\).
, \( b \rightarrow \phi _b\).
Since A is commutative, for every \(a\in A\) we have \(\phi _{a b}=\phi _b\). Thus there is a well-defined map \(\psi \) fitting into the following commutative diagram:

The map  is defined at every point of D. It is holomorphic (see, for example, [21, Section 3]). Since D is a complex torus, we have \(\psi (D)\) is \(\{\mathrm{id}\}\). It follows that A is a central subgroup of B.
is defined at every point of D. It is holomorphic (see, for example, [21, Section 3]). Since D is a complex torus, we have \(\psi (D)\) is \(\{\mathrm{id}\}\). It follows that A is a central subgroup of B.
Step 2. Let us prove that B is commutative. Consider a holomorphic map  defined by
defined by  . Since A is a central subgroup of B, similarly to Step 1 we get a holomorphic map
. Since A is a central subgroup of B, similarly to Step 1 we get a holomorphic map  . It has to be constant, since D is a complex torus and A is either \({\mathbb {C}}^+\) or \({\mathbb {C}}^*\!\). \(\square \)
. It has to be constant, since D is a complex torus and A is either \({\mathbb {C}}^+\) or \({\mathbb {C}}^*\!\). \(\square \)
Theorem 5.4
Let X be a \({\mathbb {P}}^{1}\)-bundle over a Kähler poor manifold T and  . Then the connected identity component
. Then the connected identity component  of
of  is commutative and the quotient
is commutative and the quotient  is a bounded group.
is a bounded group.
Proof
From equation (1), applied to X and T, combined with Lemma 3.4 and Remark 3.5, we get the following commutative diagram of complex Lie groups and their holomorphic homomorphisms:

Let us identify a complex torus with the group of its translations and put  . Then H is the image of a complex torus
. Then H is the image of a complex torus  under a holomorphic homomorphism, thus is a complex subtorus of
under a holomorphic homomorphism, thus is a complex subtorus of  . Let G be the preimage of H in
. Let G be the preimage of H in  with respect to
with respect to  . By definition, G is a a complex Lie group that contains
. By definition, G is a a complex Lie group that contains  as a closed complex Lie subgroup. Since
as a closed complex Lie subgroup. Since  , the identity connected component of G coincides with
, the identity connected component of G coincides with  . One has the following short exact sequences of complex Lie groups:
. One has the following short exact sequences of complex Lie groups:


According to Proposition 4.8 only the following cases may occur.
Case 1.  is finite. Then
is finite. Then  is finite as well, hence
is finite as well, hence  is a surjective holomorphic homomorphism of connected complex Lie groups with finite kernel, thus an unramified finite covering [21, Section 4.3]. It follows that
is a surjective holomorphic homomorphism of connected complex Lie groups with finite kernel, thus an unramified finite covering [21, Section 4.3]. It follows that  is a complex torus, hence commutative.
is a complex torus, hence commutative.
Case 2.  or
or  . In this case in the short exact sequence (11) both H and
. In this case in the short exact sequence (11) both H and  are connected. This implies that G is connected, hence
are connected. This implies that G is connected, hence  . According to Lemma 5.3,
. According to Lemma 5.3,  is commutative.
is commutative.
Case 3.  has a closed subgroup \(\Gamma \cong {\mathbb {C}}^*\) of index 2. According to Lemma 4.7 and Proposition 4.8, it happens when X admits precisely two sections \(S_1, S_2\) of p, and these sections are disjoint. In addition, all automorphisms \( f \in \Gamma \) leave invariant these sections as subsets of X. As for automorphisms from coset
has a closed subgroup \(\Gamma \cong {\mathbb {C}}^*\) of index 2. According to Lemma 4.7 and Proposition 4.8, it happens when X admits precisely two sections \(S_1, S_2\) of p, and these sections are disjoint. In addition, all automorphisms \( f \in \Gamma \) leave invariant these sections as subsets of X. As for automorphisms from coset  of \(\Gamma \), they interchange \(S_1\) and \(S_2\).
of \(\Gamma \), they interchange \(S_1\) and \(S_2\).
Let us show that in this case
(a) Every automorphism \(f\in \mathrm{Aut}(X)\) moves a section S of p to a section of p. Indeed, since f is p-fiberwise, for every \(t\in T\) we have
Thus, since S meets every fiber at one point, the same is valid for f(S). Since there are only two sections of p,
(b) The action  , \( (f,x)\mapsto f(x)\), on X is holomorphic, hence continuous. Thus the image S of a connected set
, \( (f,x)\mapsto f(x)\), on X is holomorphic, hence continuous. Thus the image S of a connected set  in X is connected. Since sections \(S_1, S_2\) are disjoint, from (14) it follows that \(S=S_1\) or \(S=S_2\). On the other hand, \(\mathrm{id}\in \mathrm{Aut}_0(X)\). It follows that \(f(S_1)=S_1\), \( f(S_2)=S_2\) for every \(f\in \mathrm{Aut}_0(X)\), and
in X is connected. Since sections \(S_1, S_2\) are disjoint, from (14) it follows that \(S=S_1\) or \(S=S_2\). On the other hand, \(\mathrm{id}\in \mathrm{Aut}_0(X)\). It follows that \(f(S_1)=S_1\), \( f(S_2)=S_2\) for every \(f\in \mathrm{Aut}_0(X)\), and  . This proves (13).
. This proves (13).
Now, (12) maybe rewritten as a short exact sequence of holomorphic maps of complex Lie groups

Lemma 5.3 implies that  is commutative.
is commutative.
Cases 1–3 give us that  is commutative. The group
is commutative. The group  is bounded according to Proposition 2.1. \(\square \)
is bounded according to Proposition 2.1. \(\square \)
Now Theorem 1.11 follows from combination of Proposition 3.6, Corollary 4.1, Proposition 4.2, Theorem 5.4, equations (11), (15), and Proposition 4.8.
6 Examples of \(\pmb {{\mathbb {P}}^{1}}\)-bundles without sections
If S is a complex manifold then we write \({\mathbf {1}}_S\) for the trivial line bundle  over S. In this section we construct a \({\mathbb {P}}^{1}\)-bundle (X, p, T) such that
over S. In this section we construct a \({\mathbb {P}}^{1}\)-bundle (X, p, T) such that
-
T is a complex torus with
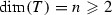 , \( a(T)=0\);
, \( a(T)=0\); -
the projection \(p:X\rightarrow T\) has no section, i.e., there is no divisor \( \Delta \subset X\) that meets every fiber \(P_t\) at a single point;
-
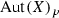 contains no automorphisms of type A or B;
contains no automorphisms of type A or B; -
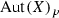 contains an automorphism of type C;
contains an automorphism of type C; -
there exists a bisection of p that intersects every fiber \(P_t\) at two distinct points.
We use the fact that distinct sections of a \({\mathbb {P}}^{1}\)-bundle over a torus T with \(a(T)=0\) do not intersect, thus our example is impossible with  .
.
Let S be a torus with

Let \({\mathscr {L}}\) be a non-trivial holomorphic line bundle over S such that
-
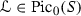 ;
; -
\({\mathscr {L}}^{\otimes 2}={\mathbf {1}}_S\).
Let Y be the total body of \({\mathscr {L}}\) and \(q:Y\rightarrow S\) the corresponding surjective holomorphic map. Consider the rank 2 vector bundle  on S, let \(\overline{Y} ={\mathbb {P}}(E)\) be the projectivization of E, and let \(\overline{q}:\overline{Y} \rightarrow S\) be the holomorphic extension of q to \(\overline{Y} \). The holomorphic map \(\overline{q}\) has precisely two sections, namely, \(D_0\) that is the zero section of \({\mathscr {L}}\) and
on S, let \(\overline{Y} ={\mathbb {P}}(E)\) be the projectivization of E, and let \(\overline{q}:\overline{Y} \rightarrow S\) be the holomorphic extension of q to \(\overline{Y} \). The holomorphic map \(\overline{q}\) has precisely two sections, namely, \(D_0\) that is the zero section of \({\mathscr {L}}\) and  . Since \({\mathscr {L}}\) is a non-trivial line bundle and \(a(S)=0\), there are no other sections of \(\overline{q}\). We may describe Y in the following way (see [5, Chapter 1, Section 2]). Let \(S=V/\Gamma \), where \(V={\mathbb {C}}^n\) is the n-dimensional complex vector space,
. Since \({\mathscr {L}}\) is a non-trivial line bundle and \(a(S)=0\), there are no other sections of \(\overline{q}\). We may describe Y in the following way (see [5, Chapter 1, Section 2]). Let \(S=V/\Gamma \), where \(V={\mathbb {C}}^n\) is the n-dimensional complex vector space,  and \(\Gamma \) is a discrete lattice of rank 2n. Then there exists a non-trivial group homomorphism
and \(\Gamma \) is a discrete lattice of rank 2n. Then there exists a non-trivial group homomorphism
such that Y is the quotient  with respect to the action of group \(\Gamma \) on
with respect to the action of group \(\Gamma \) on  by automorphisms
by automorphisms

We may extend the action of \(\Gamma \) to  by the same formula (16) and get
by the same formula (16) and get  .
.
Let us consider the following three holomorphic automorphisms of \(\overline{Y}\).
(i) The line bundles \({\mathscr {L}}\) and \({\mathscr {L}}^{-1}\) are isomorphic. Hence, there is a holomorphic involution map \(I_L:\overline{Y}\rightarrow \overline{Y}\) such that \(I_L(D_0)=D_\infty \) and  . The automorphism \(I_L\) may be included into the commutative diagram
. The automorphism \(I_L\) may be included into the commutative diagram

In order to define \(I_L\) explicitly, let us consider a holomorphic involution

We have for all \(\gamma \in \Gamma \),

since \(\xi (\gamma )^2=1\). In other words, \( \widetilde{I}_L\) commutes with the action of \(\Gamma \) and therefore descends to the holomorphic involution of  and this involution is our \(I_L\).
and this involution is our \(I_L\).
(ii) Let us choose \(\gamma _0\in \Gamma \) such that
(Such a \(\gamma _0\) does exist, since the rank of \(\Gamma \) is greater than 1.) Let us put

and consider an order 2 point  . Then the translation map
. Then the translation map
is a holomorphic involution on \(S:{\mathbf {T}}_P^2=\mathrm{id}\). Since  , the translation \({\mathbf {T}}_P\) induces a holomorphic involution \(I_P:\overline{Y}\rightarrow \overline{Y}\) [37] that “lifts” \({\mathbf {T}}_P\) and leaves \(D_0\) and \(D_\infty \) invariant. The automorphism \(I_P\) may be included in the commutative diagram
, the translation \({\mathbf {T}}_P\) induces a holomorphic involution \(I_P:\overline{Y}\rightarrow \overline{Y}\) [37] that “lifts” \({\mathbf {T}}_P\) and leaves \(D_0\) and \(D_\infty \) invariant. The automorphism \(I_P\) may be included in the commutative diagram

In order to describe \(I_P\) explicitly, let us consider a holomorphic automorphism

Clearly, \( \widetilde{I}_P^{\,2}=g_{\gamma _0}\) (recall that \(\xi (\gamma _0)=1\)). For all \(\gamma \in \Gamma \)

i.e., \( \widetilde{I}_P\) and \(g_{\gamma }\) do commute. This implies that \(\widetilde{I}_P\) descends to the holomorphic involution of  , and this involution is our \(I_P\).
, and this involution is our \(I_P\).
(iii) Let  be the holomorphic involution that acts as multiplication by \(-1\) in every fiber of \({\mathscr {L}}\). (In notation of [37],
be the holomorphic involution that acts as multiplication by \(-1\) in every fiber of \({\mathscr {L}}\). (In notation of [37],  ) In
) In  the map \(\overline{h} \) is induced by the holomorphic involution
the map \(\overline{h} \) is induced by the holomorphic involution

which commutes with all \(g_{\gamma }\). Indeed, for all \(\gamma \in \Gamma \),

Let us show that \(I_L,I_Y\), and \(\overline{h}\) commute. It suffices to check that \(\widetilde{I}_L,\widetilde{I}_Y\) and \({\widetilde{h}}\) commute, which is an immediate corollary of the following direct computations:

Let us put now

Then:
-
(a)
\(\mathrm{inv}^2=\mathrm{id}\);
-
(b)
;
-
(c)
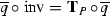 ;
; -
(d)
\({\mathbf {T}}_P\) has no fixed points, thus \({{\,\mathrm{inv}\,}}\) has no fixed points;
-
(e)
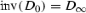 ;
; -
(f)
if \(d_1,d_2\in D_0\) then
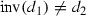 .
.
Let X be the quotient of \(\overline{Y}\) by the action of the order 2 group \(\{\mathrm{id}, {{\,\mathrm{inv}\,}}\}, \) and \(\pi _Y:\overline{Y} \rightarrow X\) be the corresponding quotient map. Let T be the quotient of S by the action of the order 2 group \(\{\mathrm{id}, {\mathbf {T}}_P\}\), and \(\pi _S:S \rightarrow T\) be the corresponding quotient map. Then X and T enjoy the following properties:
-
For any \(x\in X\) there are precisely two points \(y, {{\,\mathrm{inv}\,}}(y)\) in \(\pi _Y^{-1}(x)\).
-
For any \(t\in T\) there are precisely two points \(s, {\mathbf {T}}_P(s)\) in
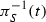 .
. -
Both \(\pi _Y:\overline{Y}\rightarrow X\) and \(\pi _S:S\rightarrow T\) are double unramified coverings.
-
X is a smooth complex manifold (by (d)).
-
T is a complex torus with \(a(T)=0\),
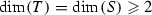 .
. -
It follows from (c) that there is a holomorphic map \(p:X\rightarrow T\) such that the following diagram commutes:
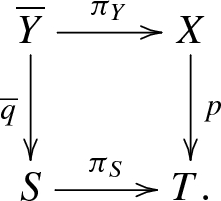
-
If \(\pi _S(s)=t\in T\) then
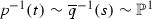 .
. -
It follows from (b) that there is a holomorphic map (pushdown) \(h:X\rightarrow X\) such that the following diagram commutes:
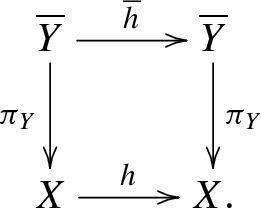
-
Thanks to (e), we have
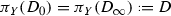 .
. -
Thanks to (f), the restriction \(p |_D:D\rightarrow T\) is a double covering.
It follows that X is a \({\mathbb {P}}^{1}\)-bundle over T, D is a bisection of p, and h is a non-trivial automorphism in  of order 2, whose set of fixed points coincides with D.
of order 2, whose set of fixed points coincides with D.
Lemma 6.1
There is no section of p.
Proof
Assume that p has a section \(\sigma :T\rightarrow X\). Let  and
and  . As we have already seen, both maps \(\pi _S\) and \(\pi _Y\) are double unramified covers. For every point \(t\in T\) there are precisely two distinct points s and \({{\,\mathrm{inv}\,}}(s)\) in
. As we have already seen, both maps \(\pi _S\) and \(\pi _Y\) are double unramified covers. For every point \(t\in T\) there are precisely two distinct points s and \({{\,\mathrm{inv}\,}}(s)\) in  , and there are precisely two distinct points in
, and there are precisely two distinct points in  , say, \(y_t\) and \({{\,\mathrm{inv}\,}}(y_t)\). One of them is mapped by \(\overline{q}\) to s, another to \({{\,\mathrm{inv}\,}}(s)\). It follows that for every \(s\in S\) there is precisely one point in \(\Delta \cap \overline{q}{}^{-1}(s)\). Hence, \(\Delta \) is a section of \(\overline{q}\). By construction, \(\overline{q}\) has no sections except \(D_0\) and \(D_{\infty }\). But \(\Delta \) cannot coincide with \(D_0\) or \(D_{\infty }\) since \(\pi _Y(\Delta )=\Sigma \) is a section of p and D is not. The contradiction shows that section \(\sigma :T\rightarrow X\) does not exist. \(\square \)
, say, \(y_t\) and \({{\,\mathrm{inv}\,}}(y_t)\). One of them is mapped by \(\overline{q}\) to s, another to \({{\,\mathrm{inv}\,}}(s)\). It follows that for every \(s\in S\) there is precisely one point in \(\Delta \cap \overline{q}{}^{-1}(s)\). Hence, \(\Delta \) is a section of \(\overline{q}\). By construction, \(\overline{q}\) has no sections except \(D_0\) and \(D_{\infty }\). But \(\Delta \) cannot coincide with \(D_0\) or \(D_{\infty }\) since \(\pi _Y(\Delta )=\Sigma \) is a section of p and D is not. The contradiction shows that section \(\sigma :T\rightarrow X\) does not exist. \(\square \)
Hence, p has no sections and, therefore, there are no automorphisms of type A and B in  .
.
References
Bandman, T., Zarhin, Yu.G.: Jordan groups, conic bundles and abelian varieties. Algebr. Geom. 4(2), 229–246 (2017)
Bandman, T., Zarhin, Yu.G.: Jordan properties of automorphism groups of certain open algebraic varieties. Transform. Groups 24(3), 721–739 (2019)
Barth, W.P., Hulek, K., Peters, C.A.M., Van de Ven, A.: Compact Complex Surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 4. Springer, Berlin (2004)
Birkar, C.: Singularities of linear systems and boundedness of Fano varieties (2016). arXiv:1609.05543
Birkenhake, C., Lange, H.: Complex Tori. Progress in Mathematics, vol. 177. Birkhäuser, Boston (1999)
Bochner, S., Montgomery, D.: Groups on analytic manifolds. Ann. Math. 48, 659–669 (1947)
Campana, F., Peternell, T.: Cycle spaces. In: § 8 of: Grauert, H., et al. (eds.) Several Complex Variables VII. Encyclopaedia of Mathematical Sciences, vol. 74, pp. 319–349. Springer, Berlin (1994)
Campana, F., Peternell, T.: Complex threefolds with non-trivial holomorphic \(2\)-forms. J. Algebraic Geom. 9(2), 223–264 (2000)
Dethloff, G., Grauert, H.: Seminormal complex spaces. In: § 4 of: Grauert, H., et al. (eds.) Several Complex Variables VII. Encyclopaedia of Mathematical Sciences, vol. 74, pp. 183–220. Springer, Berlin (1994)
Dolgačev, I.V.: On the purity of the degeneration loci of families of curves. Invent. Math. 8, 34–54 (1969)
Fischer, G.: Complex Analytic Geometry. Lecture Notes in Mathematics, vol. 538. Springer, Berlin (1976)
Fischer, W., Grauert, H.: Lokal-triviale Familien kompakter komplexer Mannigfaltigkeiten. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II 1965, 89–94 (1965)
Fujiki, A.: On automorphism groups of compact Kähler manifolds. Invent. Math. 44(3), 225–258 (1978)
Fujiki, A.: On the minimal models of complex manifolds. Math. Ann. 253(2), 111–128 (1980)
Gunning, R.C., Rossi, H.: Analytic Functions of Several Complex Variables. Prentice-Hall, Englewood Cliffs (1965)
Kim, J.H.: Jordan property and automorphism groups of normal compact Kähler varieties. Commun. Contemp. Math. 20(3), # 1750024 (2018)
Levi, E.E.: Studii sui punti singolari essenziali delle funzioni analitiche di due o più variabili complesse. Annali di Matematica Pura ed Applicata 17, 61–87 (1910)
Lieberman, D.I.: Compactness of the Chow scheme: applications to automorphisms and deformations of Kähler manifolds. In: Norguet, F. (ed.) Fonctions de Plusieurs Variables Complexes, vol. 3. Lecture Notes in Mathematics, vol. 670, pp. 140–186. Springer, Berlin (1978)
Meng, Sh., Zhang, D.-Q.: Jordan property for non-linear algebraic groups and projective varieties. Am. J. Math. 140(4), 1133–1145 (2018)
Narasimhan, R.: Introduction to the Theory of Analytic Spaces. Lecture Notes in Mathematics, vol. 25. Springer, Berlin (1966)
Onishchik, A.L., Vinberg, E.B.: Foundations of Lie theory. § 1 of: Lie Groups and Lie Algebras I. Encyclopaedia of Mathematical Sciences, vol. 20, pp. 1–94. Springer, Berlin (1993)
Peternell, T.: Modifications. § 7 of: Grauert, H., et al. (eds.) Several Complex Variables VII. Encyclopaedia of Mathematical Sciences, vol. 74, pp. 285–319. Springer, Berlin (1994)
Peternell, T., Remmert, R.: Differential calculus, holomorphic maps and linear structures on complex spaces. § 2 of: Grauert, H., et al. (eds.) Several Complex Variables VII. Encyclopaedia of Mathematical Sciences, vol. 74, pp. 97–144. Springer, Berlin (1994)
Popov, V.L.: On the Makar–Limanov, Derksen invariants, and finite automorphism groups of algebraic varieties. In: Daigle, D., Ganong, R., Koras, M. (eds.) Affine Algebraic Geometry, CRM Proceedings and Lecture Notes, vol. 54, pp. 289–311. American Mathematical Society, Providence (2011)
Popov, V.L.: The Jordan property for Lie groups and automorphism groups of complex spaces. Math. Notes 103(5–6), 811–819 (2018)
Prokhorov, Yu., Shramov, C.: Jordan property for groups of birational selfmaps. Compositio Math. 150(12), 2054–2072 (2014)
Prokhorov, Yu., Shramov, C.: Finite groups of birational selfmaps of threefolds. Math. Res. Lett. 25(3), 957–972 (2018)
Prokhorov, Yu., Shramov, C.: Bounded automorphism groups of complex compact surfaces (2019). arXiv:1909.12013
Prokhorov, Yu., Shramov, C.: Finite groups of bimeromorphic selfmaps of uniruled Kähler threefolds (2019). arXiv:1910.12334
Ramanujam, C.P.: On a certain purity theorem. J. Indian Math. Soc. (N.S.) 34, 1–9 (1970)
Remmert, R.: Holomorphe und meromorphe Abbildungen komplexer Räume. Math. Ann. 133, 328–370 (1957)
Serre, J.-P.: A Minkowski-style bound for the orders of the finite subgroups of the Cremona group of rank \(2\) over an arbitrary field. Moscow Math. J. 9(1), 193–208 (2009)
Serre, J.-P.: Finite Groups. Surveys of Modern Mathematics, vol. 10. International Press, Somerville (2016)
Shramov, C.: Fiberwise bimeromorphic maps of conic bundles. Internat. J. Math. 30(11), # 1950059 (2019)
Voisin, C.: Hodge Theory and Complex Algebraic Geometry I. Cambridge Studies in Advanced Mathematics, vol. 76. Cambridge University Press, Cambridge (2002)
Zarhin, Yu.G.: Theta groups and products of abelian and rational varieties. Proc. Edinbourg Math. Soc. 57(1), 299–304 (2014)
Zarhin, Yu.G.: Complex tori, theta groups and their Jordan properties. Proc. Steklov Inst. Math. 307, 22–50 (2019)
Acknowledgements
We are grateful to Frédéric Campana, Vladimir L. Popov, and Constantin Shramov for useful, stimulating discussions and very helpful comments. We thank Igor Dolgachev for help with references. We are deeply grateful to the referees: their valuable comments led us to substantial revision of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The second named author (Yu.Z.) was partially supported by Simons Foundation Collaboration Grant # 585711.
Rights and permissions
About this article
Cite this article
Bandman, T., Zarhin, Y.G. Bimeromorphic automorphism groups of certain \(\pmb {{\mathbb {P}}^{1}}\)-bundles. European Journal of Mathematics 7, 641–670 (2021). https://doi.org/10.1007/s40879-020-00419-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-020-00419-8
Keywords
- Automorphism groups of compact complex manifolds
- Algebraic dimension 0
- Complex tori
- Conic bundles
- Jordan properties of groups



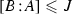 [
[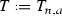 a complex torus with dimension
a complex torus with dimension 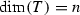 and algebraic dimension
and algebraic dimension 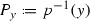 is 1 for every point
is 1 for every point 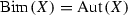 (see Corollary
(see Corollary 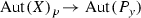 ,
, 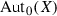 of the complex Lie group
of the complex Lie group 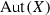 is commutative (Theorem
is commutative (Theorem 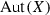 is very Jordan. Namely, there is a short exact sequence
is very Jordan. Namely, there is a short exact sequence 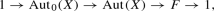
 sits in a short exact sequence of complex Lie groups
sits in a short exact sequence of complex Lie groups 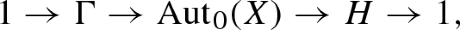
 stands for the connected identity component of (as a complex Lie group).
stands for the connected identity component of (as a complex Lie group).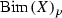 (respectively,
(respectively, 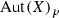 ) is the subgroup of all
) is the subgroup of all 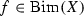 (respectively,
(respectively, 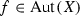 ) such that
) such that 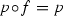 .
. .
.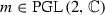 we define
we define 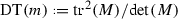 where
where 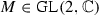 is any matrix representing m,
is any matrix representing m, 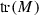 and
and 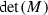 are the trace and the determinant of M, respectively.
are the trace and the determinant of M, respectively. 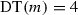 if and only if m is proportional either to the identity matrix or to a unipotent matrix.
if and only if m is proportional either to the identity matrix or to a unipotent matrix.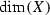 , a(X) are the complex and algebraic dimensions of a compact complex manifold X, respectively.
, a(X) are the complex and algebraic dimensions of a compact complex manifold X, respectively.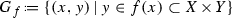 is a connected irreducible complex analytic subspace of
is a connected irreducible complex analytic subspace of  .
.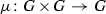 extends to a meromorphic map
extends to a meromorphic map 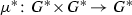 and
and 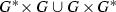 .
.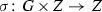 extends to a meromorphic map
extends to a meromorphic map  (see [
(see [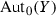 is a compact complex Lie group, that is isomorphic to a certain complex torus
is a compact complex Lie group, that is isomorphic to a certain complex torus 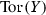 (see also [
(see also [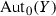 is isomorphic to a complex torus for any compact complex Kähler manifold X of non-negative Kodaira dimension [
is isomorphic to a complex torus for any compact complex Kähler manifold X of non-negative Kodaira dimension [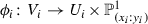 and
and 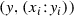 are coordinates in
are coordinates in 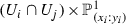 defined is a holomorphic map
defined is a holomorphic map 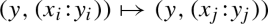
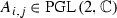 with representative
with representative 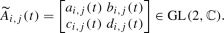
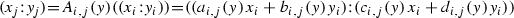 .
.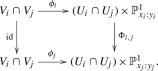
 .
.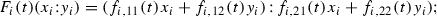
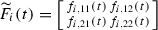 represents
represents 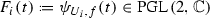 (see the proof of Lemma
(see the proof of Lemma  is the analytic subset of X defined by the equation
is the analytic subset of X defined by the equation 
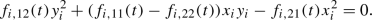
 for
for 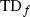 .
.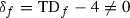 , then fix a square root
, then fix a square root 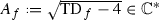 and define
and define  (it does not depend on i). Then for every i one can define coordinates
(it does not depend on i). Then for every i one can define coordinates 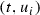 ,
, 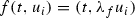 . The set
. The set 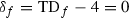 then
then  is proportional to a unipotent matrix and for every i one can define in
is proportional to a unipotent matrix and for every i one can define in 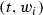 ,
, 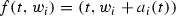 where
where 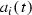 are holomorphic functions in
are holomorphic functions in 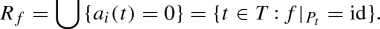
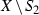 is the total body of a holomorphic line bundle
is the total body of a holomorphic line bundle 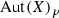 contains a subgroup
contains a subgroup 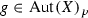 of type A belongs to
of type A belongs to 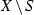 is an
is an 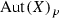 contains a subgroup
contains a subgroup 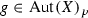 with the same Data S;
with the same Data S;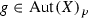 of type B belongs to
of type B belongs to 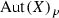 contains no automorphisms of type A.
contains no automorphisms of type A.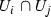 and form a cocycle, thus define a holomorphic line bundle
and form a cocycle, thus define a holomorphic line bundle 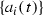 is a section of
is a section of 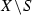 is an
is an 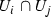 ;
;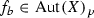 defined in each
defined in each 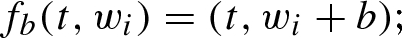

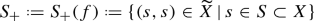
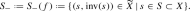
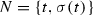 of p in X induces the section
of p in X induces the section 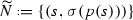 of
of  induces an automorphism
induces an automorphism 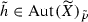 defined by
defined by 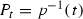 . Indeed, if
. Indeed, if 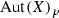 to
to 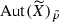 .
. and X admits only automorphisms of type A except
and X admits only automorphisms of type A except 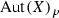 contains an automorphism h of type C with Data S. In this case
contains an automorphism h of type C with Data S. In this case 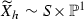 .
.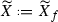 is not isomorphic to
is not isomorphic to 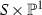 then
then  has exponent 2 and consists of two or four elements.
has exponent 2 and consists of two or four elements.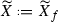 is isomorphic to
is isomorphic to 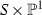 then there are two sections
then there are two sections 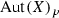 is a disjoint union of its abelian complex Lie subgroup
is a disjoint union of its abelian complex Lie subgroup 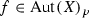 that fix
that fix 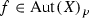 that interchange
that interchange 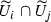 ;
;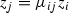 in
in 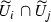 ;
;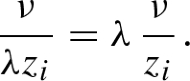
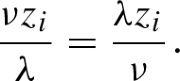
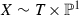 ;
;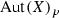 has exponent at most 2 and consists of one, two or four elements;
has exponent at most 2 and consists of one, two or four elements;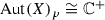 ;
;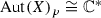 ;
; where
where 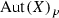 and
and 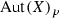 .
.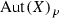 consists of automorphisms of type A only (except id) and
consists of automorphisms of type A only (except id) and 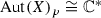 according to Lemma
according to Lemma 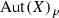 contains automorphisms of type A and C. By Lemma
contains automorphisms of type A and C. By Lemma  where
where 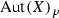 consisting of those maps that fix
consisting of those maps that fix 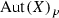 that consists of maps that interchange the sections.
that consists of maps that interchange the sections. 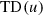 is globally defined.
is globally defined.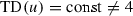 on U then the set of fixed points of f is an unramified (may be reducible) double cover of U.
on U then the set of fixed points of f is an unramified (may be reducible) double cover of U.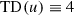 on U and U contains no analytic subset of codimension 1, then the set of fixed points of f is a section of p.
on U and U contains no analytic subset of codimension 1, then the set of fixed points of f is a section of p.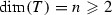 ,
, 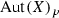 contains no automorphisms of type A or B;
contains no automorphisms of type A or B;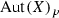 contains an automorphism of type C;
contains an automorphism of type C;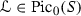 ;
;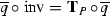 ;
;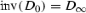 ;
;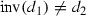 .
.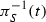 .
.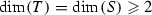 .
.
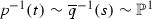 .
.
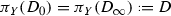 .
.