Abstract
We study abelian varieties over finitely generated fields K of characteristic zero, whose \(\ell \)-adic Tate modules are isomorphic as Galois modules for all primes \(\ell \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let K be a field, \(\overline{K}\) its separable algebraic closure,  the absolute Galois group of K. If A is an abelian variety over K then we write
the absolute Galois group of K. If A is an abelian variety over K then we write  for its ring of all K-endomorphisms and \(\mathrm{End}^0(A)\) for the corresponding (finite-dimensional semisimple) \({\mathbb {Q}}\)-algebra
for its ring of all K-endomorphisms and \(\mathrm{End}^0(A)\) for the corresponding (finite-dimensional semisimple) \({\mathbb {Q}}\)-algebra  .
.
If \(\ell \) is a prime different from  then we write \(T_{\ell }(A)\) for the \({\mathbb {Z}}_{\ell }\)-Tate module of A [7, 9] which is a free \({\mathbb {Z}}_{\ell }\)-module of rank
then we write \(T_{\ell }(A)\) for the \({\mathbb {Z}}_{\ell }\)-Tate module of A [7, 9] which is a free \({\mathbb {Z}}_{\ell }\)-module of rank  provided with the natural continuous group homomorphism
provided with the natural continuous group homomorphism
and the \({\mathbb {Z}}_{\ell }\)-ring embedding

The image of  commutes with \(\rho _{\ell ,A}(G_K)\). Tensoring by \({\mathbb {Q}}_{\ell }\) (over \({\mathbb {Z}}_{\ell }\)), we obtain the \({\mathbb {Q}}_{\ell }\)-Tate module of A
commutes with \(\rho _{\ell ,A}(G_K)\). Tensoring by \({\mathbb {Q}}_{\ell }\) (over \({\mathbb {Z}}_{\ell }\)), we obtain the \({\mathbb {Q}}_{\ell }\)-Tate module of A

which is a  -dimensional \({\mathbb {Q}}_{\ell }\)-vector space containing
-dimensional \({\mathbb {Q}}_{\ell }\)-vector space containing  as a \({\mathbb {Z}}_{\ell }\)-lattice of maximal rank. We may view \(\rho _{\ell ,A}\) as an \(\ell \)-adic representation [11]
as a \({\mathbb {Z}}_{\ell }\)-lattice of maximal rank. We may view \(\rho _{\ell ,A}\) as an \(\ell \)-adic representation [11]
and extend \(e_{\ell }\) by \({\mathbb {Q}}_{\ell }\)-linearity to the embedding of \({\mathbb {Q}}_{\ell }\)-algebras

which we still denote by \(e_{\ell }\). Further we will identify  with its image in \(\mathrm{End}_{{\mathbb {Q}}_{\ell }}(V_{\ell }(A))\). This provides \(V_{\ell }(A)\) with the natural structure of \(G_K\)-module; in addition,
with its image in \(\mathrm{End}_{{\mathbb {Q}}_{\ell }}(V_{\ell }(A))\). This provides \(V_{\ell }(A)\) with the natural structure of \(G_K\)-module; in addition,  is a \({\mathbb {Q}}_{\ell }\)-(sub)algebra of endomorphisms of the Galois module \(V_{\ell }(A)\). In other words,
is a \({\mathbb {Q}}_{\ell }\)-(sub)algebra of endomorphisms of the Galois module \(V_{\ell }(A)\). In other words,

Let K be a field of characteristic zero that is finitely generated over \({\mathbb {Q}}\). Suppose we are given an abelian variety A of positive dimension over K. Let B be an abelian variety over K such that the \({\mathbb {Z}}_{\ell }\)-Tate modules of A and B are isomorphic as Galois modules for all \(\ell \) (we call such A and B
almost isomorphic). In this paper we discuss the structure of the corresponding right  -module
-module  . Using a theorem of Faltings [4, 5] (conjectured by Tate [12]), we prove that
. Using a theorem of Faltings [4, 5] (conjectured by Tate [12]), we prove that  is a locally free module of rank 1. In addition, using a special case of Serre’s tensor construction ([3, Section 7], [2, Section 1.7.4]), we prove that there is a natural bijection between isomorphism classes of locally free modules of rank 1 over
is a locally free module of rank 1. In addition, using a special case of Serre’s tensor construction ([3, Section 7], [2, Section 1.7.4]), we prove that there is a natural bijection between isomorphism classes of locally free modules of rank 1 over  and isomorphism classes of abelian varieties B over K, whose Tate modules are isomorphic to ones of A.
and isomorphism classes of abelian varieties B over K, whose Tate modules are isomorphic to ones of A.
The paper is organized as follows. Section 2 deals with isogenies of abelian varieties and corresponding homomorphisms of their Tate modules. In Sect. 3 we discuss locally free modules of rank 1 over orders in semisimple \({\mathbb {Q}}\)-algebras. In Sect. 4 we apply results of Sect. 3 to a construction of almost isomorphic abelian varieties.
2 Isogenies
If \(\ell \) is a prime then we write \({\mathbb {Z}}_{(\ell )}\) for the subring in \({\mathbb {Q}}\) that consists of all the rational numbers, whose denominators are prime to \(\ell \). We have
(Here the intersection is taken in \({\mathbb {Q}}_{\ell }\).) In addition, if m is a positive integer that is prime to \(\ell \) then

The intersection of all \({\mathbb {Z}}_{(\ell )}\) (in \({\mathbb {Q}}\)) coincides with \({\mathbb {Z}}\).
Let K be an arbitrary field. If  and X is an abelian variety over K then we write
and X is an abelian variety over K then we write  for the kernel of multiplication by \(\ell \) in \(X(\overline{K})\). It is well known that
for the kernel of multiplication by \(\ell \) in \(X(\overline{K})\). It is well known that  is a finite \(G_K\)-submodule in \(X(\overline{K})\) of order
is a finite \(G_K\)-submodule in \(X(\overline{K})\) of order  and there is a natural isomomorphism of \(G_K\)-modules
and there is a natural isomomorphism of \(G_K\)-modules  .
.
Lemma 2.1
Let A and B be abelian varieties of positive dimension over K.
-
(a)
If A and B are isogenous over K then the right
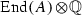 -module
-module 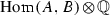 is free of rank 1. In addition, one may choose as a generator of
is free of rank 1. In addition, one may choose as a generator of 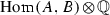 any isogeny \(\phi {:} A \rightarrow B\).
any isogeny \(\phi {:} A \rightarrow B\). -
(b)
The following conditions are equivalent:
-
(i)
The right
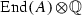 -module
-module 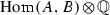 is free of rank 1.
is free of rank 1. -
(ii)
 and there exists a
and there exists a 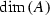 -dimensional abelian K-subvariety \(B_0\subset B\) such that A and \(B_0\) are isogenous over K and
-dimensional abelian K-subvariety \(B_0\subset B\) such that A and \(B_0\) are isogenous over K and 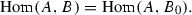
In particular, the image of every K-homomorphism of abelian varieties \(A \rightarrow B\) lies in \(B_0\).
-
(i)
-
(c)
If the equivalent conditions (i) and (ii) hold and
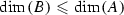 then
then 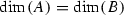 , \(B=B_0\), and A and B are isogenous over K.
, \(B=B_0\), and A and B are isogenous over K.
Proof
(a) is obvious.
Suppose (bii) is true. Let us pick an isogeny
\(\phi {:} A \rightarrow B_0\). It follows that 
 is a free right
is a free right  -module of rank 1 generated by \(\phi \). Now (bi) follows from the equality
-module of rank 1 generated by \(\phi \). Now (bi) follows from the equality

Suppose that (bi) is true. We may choose a homomorphism of abelian varieties \(\phi {:} A \rightarrow B\) as a generator (basis) of the free right  -module
-module  . In other words, for every homomorphism of abelian varieties \(\psi {:} A \rightarrow B\) there are
. In other words, for every homomorphism of abelian varieties \(\psi {:} A \rightarrow B\) there are  and a nonzero integer n such that \(n\psi =\phi u\). In addition, for each nonzero
and a nonzero integer n such that \(n\psi =\phi u\). In addition, for each nonzero
 the composition \(\phi u\) is a nonzero element of
the composition \(\phi u\) is a nonzero element of  . Clearly, \(B_0=\phi (A)\subset B\) is an abelian K-subvariety of B with
. Clearly, \(B_0=\phi (A)\subset B\) is an abelian K-subvariety of B with  . We have
. We have
It follows that the identity component of \(\psi (A)\) lies in \(B_0\). Since \(\psi (A)\) is a (connected) abelian K-subvariety of B, we have \(\psi (A)\subset B_0\). This proves that  . On the other hand, if
. On the other hand, if  then \(\phi {:} A \rightarrow B_0\) is an isogeny and we get (bii) under our additional assumption. If
then \(\phi {:} A \rightarrow B_0\) is an isogeny and we get (bii) under our additional assumption. If  then
then  has positive dimension that is strictly less than
has positive dimension that is strictly less than  . By the Poincaré complete reducibility theorem [7], there is an endomorphism
. By the Poincaré complete reducibility theorem [7], there is an endomorphism  such that the image \(u_0(A)\) coincides with the identity component of
such that the image \(u_0(A)\) coincides with the identity component of  ; in particular, \(u_0 \ne 0\),
; in particular, \(u_0 \ne 0\),  . This implies that \(\phi u_0=0 \) in
. This implies that \(\phi u_0=0 \) in  and we get a contradiction, which proves (bii).
and we get a contradiction, which proves (bii).
(c) follows readily from (bii).\(\square \)
Lemma 2.2
Suppose that A, B, C are abelian varieties over K of positive dimension that are mutually isogenous over K. We view  and
and  as right
as right  -modules. Then the natural map
-modules. Then the natural map

that associates to \(\tau {:} B \rightarrow C\) a homomorphism of right  -modules
-modules

is a group isomorphism.
Proof
Clearly, \(m_{B,C}\) is injective. In order to check the surjectiveness, notice that the statement is clearly invariant by isogeny, so we can assume that \(B=A\) and \(C=A\), in which case it is obvious.\(\square \)
Now till the end of this paper we assume that K is a field of characteristic zero that is finitely generated over \({\mathbb {Q}}\), and A and B are abelian varieties of positive dimension over K. By a theorem of Faltings [4, 5],

Lemma 2.3
Let \(\ell \) be a prime. Then the following conditions are equivalent:
-
(i)
There is an isogeny \(\phi _{\ell }{:} A \rightarrow B\), whose degree is prime to \(\ell \).
-
(ii)
The Tate modules \(T_{\ell }(A)\) and \(T_{\ell }(B)\) are isomorphic as
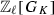 -modules.
-modules.
If the equivalent conditions (i) and (ii) hold then the right  -module
-module  is free of rank 1 and the right
is free of rank 1 and the right  -module
-module  is free of rank 1.
is free of rank 1.
Proof
(i) implies (ii). Indeed, let \(\phi _{\ell }{:} A \rightarrow B\) be an isogeny such that its degree  is prime to \(\ell \). Then there exists an isogeny \(\varphi _{\ell }{:} B \rightarrow A\) such that
is prime to \(\ell \). Then there exists an isogeny \(\varphi _{\ell }{:} B \rightarrow A\) such that  is multiplication by d in B and
is multiplication by d in B and  is multiplication by d in A. This implies that \(\phi _{\ell }\) induces a \(G_K\)-equivariant isomorphism of the \({\mathbb {Z}}_{\ell }\)-Tate modules of A and B.
is multiplication by d in A. This implies that \(\phi _{\ell }\) induces a \(G_K\)-equivariant isomorphism of the \({\mathbb {Z}}_{\ell }\)-Tate modules of A and B.
Suppose that (ii) holds. Since the rank of the free \({\mathbb {Z}}_{\ell }\)-module \(T_{\ell }(A)\) (resp. \(T_{\ell }(B)\)) is  (resp.
(resp.  ), we conclude that
), we conclude that  , i.e.,
, i.e.,  . By the theorem of Faltings (\(\star \)), there is an isomorphism of the \({\mathbb {Z}}_{\ell }\)-Tate modules of A and B that lies in
. By the theorem of Faltings (\(\star \)), there is an isomorphism of the \({\mathbb {Z}}_{\ell }\)-Tate modules of A and B that lies in  . Since
. Since  is dense in
is dense in  in the \(\ell \)-adic topology, and the set of isomorphisms \(T_{\ell }(A)\cong T_{\ell }(B)\) is open in
in the \(\ell \)-adic topology, and the set of isomorphisms \(T_{\ell }(A)\cong T_{\ell }(B)\) is open in  , there is \(\phi _{\ell }\in \mathrm{Hom}(A,B)\) that induces an isomorphism \(T_{\ell }(A)\cong T_{\ell }(B)\). Clearly,
, there is \(\phi _{\ell }\in \mathrm{Hom}(A,B)\) that induces an isomorphism \(T_{\ell }(A)\cong T_{\ell }(B)\). Clearly,  does not contain points of order \(\ell \) and therefore is finite. This implies that \(\phi _{\ell }\) is an isogeny, whose degree is prime to \(\ell \). This proves (i).
does not contain points of order \(\ell \) and therefore is finite. This implies that \(\phi _{\ell }\) is an isogeny, whose degree is prime to \(\ell \). This proves (i).
In order to prove the last assertion of Lemma 2.3, one has only to observe that  is a generator of the (obviously) free right \({\mathbb {Z}}_{(\ell )}\)-module
is a generator of the (obviously) free right \({\mathbb {Z}}_{(\ell )}\)-module  and of the free right \({\mathbb {Z}}_{\ell }\)-module
and of the free right \({\mathbb {Z}}_{\ell }\)-module  . \(\square \)
. \(\square \)
We say that A and B are almost isomorphic if for all primes \(\ell \) the equivalent conditions (i) and (ii) of Lemma 2.3 hold. Clearly, if A and B are isomorphic over K then they are almost isomorphic. It is also clear that if A and B are almost isomorphic then they are isogenous over K. Obviously, the property of being almost isomorphic is an equivalence relation on the set of (nonzero) abelian varieties over K.
Corollary 2.4
Suppose that A and B are almost isomorphic. Then A and B are isomorphic over K if and only if  is a free
is a free  -modules of rank 1. In particular, if
-modules of rank 1. In particular, if  is a principal ideal domain (for example,
is a principal ideal domain (for example,  \()\) then every abelian variety over K, which is almost isomorphic to A, is actually isomorphic to A.
\()\) then every abelian variety over K, which is almost isomorphic to A, is actually isomorphic to A.
Proof
Suppose  is a free
is a free  -module, i.e., there is a homomorphism of abelian varieties \(\phi {{:}} A \rightarrow B\) such that
-module, i.e., there is a homomorphism of abelian varieties \(\phi {{:}} A \rightarrow B\) such that  . We know that for any prime \(\ell \) there is an isogeny \(\phi _{\ell }{{:}} A \rightarrow B\) of degree prime to \(\ell \). (In particular,
. We know that for any prime \(\ell \) there is an isogeny \(\phi _{\ell }{{:}} A \rightarrow B\) of degree prime to \(\ell \). (In particular,  .) Therefore there is
.) Therefore there is  with \(\phi _{\ell }=\phi u_{\ell }\). In particular, \(\phi _{\ell }(A)\subset \phi (A)\) and
with \(\phi _{\ell }=\phi u_{\ell }\). In particular, \(\phi _{\ell }(A)\subset \phi (A)\) and  is divisible by
is divisible by  . Since \(\phi _{\ell }(A)=B\) and
. Since \(\phi _{\ell }(A)=B\) and  is prime to \(\ell \), we conclude that \(\phi (A)=B\) (i.e., \(\phi \) is an isogeny) and \(\deg (\phi )\) is prime to \(\ell \). Since the latter is true for all primes \(\ell \), we conclude that
is prime to \(\ell \), we conclude that \(\phi (A)=B\) (i.e., \(\phi \) is an isogeny) and \(\deg (\phi )\) is prime to \(\ell \). Since the latter is true for all primes \(\ell \), we conclude that  , i.e., \(\phi \) is an isomorphism.
, i.e., \(\phi \) is an isomorphism.
Conversely, if \(A\cong B\) then  is obviously a free
is obviously a free  -module generated by an isomorphism between A and B.
-module generated by an isomorphism between A and B.
The last assertion of corollary follows from the well-known fact that every finitely generated module without torsion over a principal ideal domain is free.\(\square \)
Remark 2.5
The special case of Corollary 2.4 when  was actually done in [10, second paragraph of p. 1205].
was actually done in [10, second paragraph of p. 1205].
The next statement is a generalization of Corollary 2.4.
Corollary 2.6
Suppose that A, B, C are abelian varieties of positive dimension over K that are almost isomorphic to each other. Then B and C are isomorphic over K if and only if the right  -modules
-modules  and
and  are isomorphic.
are isomorphic.
Proof
We know that all A, B, C are mutually isogenous over K. Let us choose an isogeny \(\phi {{:}} B \rightarrow C\). We are given an isomorphism  of right
of right  -modules that obviously extends by \({\mathbb {Q}}\)-linearity to the isomorphism
-modules that obviously extends by \({\mathbb {Q}}\)-linearity to the isomorphism  of right
of right  -modules, which we continue to denote by \(\delta \). By Lemma 2.2, there exists
-modules, which we continue to denote by \(\delta \). By Lemma 2.2, there exists  such that \(\delta =m_{B,C}(\tau _0)\), i.e.,
such that \(\delta =m_{B,C}(\tau _0)\), i.e.,

There exists a positive integer n such that  and \(\tau \) is not divisible in
and \(\tau \) is not divisible in  . This implies that
. This implies that

Since B and C are almost isomorphic, for each \(\ell \) there is an isogeny \(\phi _{\ell }{:} B \rightarrow C\) of degree prime to \(\ell \). Since  , we conclude that \(\tau \) is an isogeny and
, we conclude that \(\tau \) is an isogeny and  is prime to \(\ell \) if \(\ell \) does not divide n. We need to prove that \(\tau \) is an isomorphism. Suppose it is not, then there is a prime \(\ell \) that divides
is prime to \(\ell \) if \(\ell \) does not divide n. We need to prove that \(\tau \) is an isomorphism. Suppose it is not, then there is a prime \(\ell \) that divides  and therefore divides n. We need to arrive to a contradiction. Since A and B are almost isomorphic, there is an isogeny \(\psi _{\ell }{:} A \rightarrow B\) of degree prime to \(\ell \). We have
and therefore divides n. We need to arrive to a contradiction. Since A and B are almost isomorphic, there is an isogeny \(\psi _{\ell }{:} A \rightarrow B\) of degree prime to \(\ell \). We have  . This implies that \(\tau \) kills all points of order \(\ell \) on B and therefore is divisible by \(\ell \) in
. This implies that \(\tau \) kills all points of order \(\ell \) on B and therefore is divisible by \(\ell \) in  , which is not the case. This gives us the desired contradiction.\(\square \)
, which is not the case. This gives us the desired contradiction.\(\square \)
Remark 2.7
Let \({\mathcal {Z}}(A)\)
\((\hbox {resp.}\;{\mathcal {Z}}(B))\) be the center of  (resp.
(resp.  ). Then
). Then  (resp.
(resp.  ) is the center of
) is the center of  (resp.
(resp.  ) and for all primes \(\ell \) the \({\mathbb {Z}}_{(\ell )}\)-subalgebra
) and for all primes \(\ell \) the \({\mathbb {Z}}_{(\ell )}\)-subalgebra

(resp. the \({\mathbb {Z}}_{(\ell )}\)-subalgebra  ) is the center of
) is the center of  (resp. of
(resp. of  ). Every K-isogeny \(\phi {:} A \rightarrow B\) gives rise to an isomorphism of \({\mathbb {Q}}\)-algebras
). Every K-isogeny \(\phi {:} A \rightarrow B\) gives rise to an isomorphism of \({\mathbb {Q}}\)-algebras

such that \(i_{\phi }({\mathcal {Z}}(A)_{{\mathbb {Q}}})={\mathcal {Z}}(B)_{{\mathbb {Q}}}\) and the restriction \(i_{\mathcal {Z}}{:} {\mathcal {Z}}(A)_{{\mathbb {Q}}} \cong {\mathcal {Z}}(B)_{{\mathbb {Q}}}\) of \(i_{\phi }\) to the center(s) does not depend on a choice of \(\phi \) [14]. If \(\phi _{\ell }{:} A \rightarrow B\) is a K-isogeny of degree prime to \(\ell \) then  and therefore \(i_{\mathcal {Z}}({\mathcal {Z}}(A)_{(\ell )}) = {\mathcal {Z}}(B)_{(\ell )}\). This implies that if A and B are almost isomorphic then \(i_{\mathcal {Z}}({\mathcal {Z}}(A))\) coincides with \({\mathcal {Z}}(B)\) and therefore \(i_{\mathcal {Z}}\) defines a canonical isomorphism of commutative rings \({\mathcal {Z}}(A)\cong {\mathcal {Z}}(B)\). In particular, if
and therefore \(i_{\mathcal {Z}}({\mathcal {Z}}(A)_{(\ell )}) = {\mathcal {Z}}(B)_{(\ell )}\). This implies that if A and B are almost isomorphic then \(i_{\mathcal {Z}}({\mathcal {Z}}(A))\) coincides with \({\mathcal {Z}}(B)\) and therefore \(i_{\mathcal {Z}}\) defines a canonical isomorphism of commutative rings \({\mathcal {Z}}(A)\cong {\mathcal {Z}}(B)\). In particular, if  is commutative then
is commutative then  is also commutative (because
is also commutative (because  and
and  are isomorphic) and there is a canonical ring isomorphism
are isomorphic) and there is a canonical ring isomorphism  .
.
3 Locally free modules of rank 1
Throughout this section, \({\Lambda }\) is a ring with 1 that, viewed as an additive group, is a free \({\mathbb {Z}}\)-module of finite positive rank. In addition, we assume that the finite-dimensional \({\mathbb {Q}}\)-algebra  is semisimple. We write \({\Lambda }_{\ell }\) (resp. \({\Lambda }_{(\ell )}\)) for the \({\mathbb {Z}}_{\ell }\)-algebra
is semisimple. We write \({\Lambda }_{\ell }\) (resp. \({\Lambda }_{(\ell )}\)) for the \({\mathbb {Z}}_{\ell }\)-algebra  (resp. for the \({\mathbb {Z}}_{(\ell )}\)-algebra
(resp. for the \({\mathbb {Z}}_{(\ell )}\)-algebra  ). We have
). We have

In addition, the intersection of \({\Lambda }_{\ell }\) and \({\Lambda }_{{\mathbb {Q}}}\) (in  ) coincides with \({\Lambda }_{(\ell )}\).
) coincides with \({\Lambda }_{(\ell )}\).
Let M be an arbitrary free commutative group of finite positive rank that is provided with the structure of a right \({\Lambda }\)-module. We write \(M_{{\mathbb {Q}}}\) for the right \({\Lambda }_{{\mathbb {Q}}}\)-module  , \(M_{\ell }\) for the right \({\Lambda }_{\ell }\)-module
, \(M_{\ell }\) for the right \({\Lambda }_{\ell }\)-module  and \(M_{(\ell )}\) for the right \({\Lambda }_{(\ell )}\)-module
and \(M_{(\ell )}\) for the right \({\Lambda }_{(\ell )}\)-module  . We have
. We have

In addition, the intersection of \(M_{\ell }\) and \(M_{{\mathbb {Q}}}\) (in  ) coincides with \(M_{(\ell )}\).
) coincides with \(M_{(\ell )}\).
Definition 3.1
We say that M is a locally free right \({\Lambda }\)-module of rank 1 if for all primes \(\ell \) the right \({\Lambda }_{\ell }\)-module \(M_{\ell }\) is free of rank 1, see [6].
Theorem 3.2
Let M be a locally free right \({\Lambda }\)-module of rank 1. Then it enjoys the following properties:
-
(i)
M is a projective \({\Lambda }\)-module. More precisely, M is isomorphic to a direct summand of a free right \({\Lambda }\)-module of rank 2.
-
(ii)
The right \({\Lambda }_{\mathbb {Q}}\)-module \(M_{{\mathbb {Q}}}\) is free of rank 1.
-
(iiii)
The right \({\Lambda }_{(\ell )}\)-module \(M_{(\ell )}\) is free of rank 1 for all primes \(\ell \).
Proof
Let \(J({\Lambda }_{{\mathbb {Q}}})\) be the (multiplicative) idele group of \({\Lambda }_{{\mathbb {Q}}}\), i.e., the group of invertible elements of the adele ring of \({\Lambda }_{{\mathbb {Q}}}\) [6, p. 114] (in the notation of [6, Section 2], \(\mathfrak {o}={\mathbb {Z}}\), \( K={\mathbb {Q}}\), \(A={\Lambda }_{{\mathbb {Q}}}\), \(\mathfrak {U}={\Lambda }\)). To each \(\alpha \in J({\Lambda }_{{\mathbb {Q}}})\) corresponds a certain right \({\Lambda }\)-submodule \(\alpha {\Lambda }\subset {\Lambda }_{{\mathbb {Q}}}\) that is a locally free \({\Lambda }\)-module of rank 1 and a \({\mathbb {Z}}\)-lattice of maximal rank in the \({\mathbb {Q}}\)-vector space \({\Lambda }_{{\mathbb {Q}}}\), i.e., the natural homomorphism of \({\mathbb {Q}}\)-vector spaces  is an isomorphism [6, p. 114]. This implies that \((\alpha {\Lambda })_{{\mathbb {Q}}}\) is a free \({\Lambda }_{{\mathbb {Q}}}\)-module of rank 1. In addition, the direct sum
is an isomorphism [6, p. 114]. This implies that \((\alpha {\Lambda })_{{\mathbb {Q}}}\) is a free \({\Lambda }_{{\mathbb {Q}}}\)-module of rank 1. In addition, the direct sum  is a free right \({\Lambda }\)-module of rank 2 [6, Theorem 1, pp. 114–115]. This implies that \(\alpha {\Lambda }\) is isomorphic to a direct summand of a rank 2 free module; in particular, it is projective. By the same [6, Theorem 1], every right locally free \({\Lambda }\)-module M of rank 1 is isomorphic to \(\alpha {\Lambda }\) for a suitable \(\alpha \). This proves (i) and (ii).
is a free right \({\Lambda }\)-module of rank 2 [6, Theorem 1, pp. 114–115]. This implies that \(\alpha {\Lambda }\) is isomorphic to a direct summand of a rank 2 free module; in particular, it is projective. By the same [6, Theorem 1], every right locally free \({\Lambda }\)-module M of rank 1 is isomorphic to \(\alpha {\Lambda }\) for a suitable \(\alpha \). This proves (i) and (ii).
Let \(f_0\) be a generator of the free \({\Lambda }_{\mathbb {Q}}\)-module \(M_{{\mathbb {Q}}}\) of rank 1. Multiplying \(f_0\) by a sufficiently divisible positive integer, we may and will assume that  . Clearly, the right
. Clearly, the right  -module
-module

is free of rank 1 for all primes \(\ell \) and \(f_0\) is also a generator of  . It is also clear that every generator \(f_{\ell }\) of the \({\Lambda }_{\ell }\)-module \(M_{\ell }\) is a generator of the
. It is also clear that every generator \(f_{\ell }\) of the \({\Lambda }_{\ell }\)-module \(M_{\ell }\) is a generator of the  -module
-module  . We claim that there is a generator \(f_{\ell }\) that lies in M. Indeed, with respect to the \(\ell \)-adic topology, the subset
. We claim that there is a generator \(f_{\ell }\) that lies in M. Indeed, with respect to the \(\ell \)-adic topology, the subset

is dense in \(M_{\ell }\) while the set of generators of the free \({\Lambda }_{\ell }\)-module \(M_{\ell }\) is open, because the group of units \(({\Lambda }_{\ell })^{*}\) is open in \({\Lambda }_{\ell }\). This implies that there exists a (nonzero) generator \(f_{\ell } \in M\subset M_{\ell }\) of the \({\Lambda }_{\ell }\)-module \(M_{\ell }\). Recall that \(f_{\ell }\) is also a generator of the free  -module
-module  . This implies that there exists
. This implies that there exists  such that
such that  . On the other hand, since \(f_{\ell }\) lies in the free rank 1 \({\Lambda }_{{\mathbb {Q}}}\)-module \(M_{{\mathbb {Q}}}=f_0{\Lambda }_{{\mathbb {Q}}}\), we have \(\mu _0\in {\Lambda }_{{\mathbb {Q}}}\). This implies that \(\mu _{0}\) is not a zero divisor in the finite-dimensional \({\mathbb {Q}}\)-algebra \({\Lambda }_{{\mathbb {Q}}}\) (because it is invertible in
. On the other hand, since \(f_{\ell }\) lies in the free rank 1 \({\Lambda }_{{\mathbb {Q}}}\)-module \(M_{{\mathbb {Q}}}=f_0{\Lambda }_{{\mathbb {Q}}}\), we have \(\mu _0\in {\Lambda }_{{\mathbb {Q}}}\). This implies that \(\mu _{0}\) is not a zero divisor in the finite-dimensional \({\mathbb {Q}}\)-algebra \({\Lambda }_{{\mathbb {Q}}}\) (because it is invertible in  ) and therefore lies in \({\Lambda }_{{\mathbb {Q}}}^{*}\). It follows that \(f_{\ell }\) is also a generator of the free \({\Lambda }_{{\mathbb {Q}}}\)-module \(M_{{\mathbb {Q}}}\) of rank 1.
) and therefore lies in \({\Lambda }_{{\mathbb {Q}}}^{*}\). It follows that \(f_{\ell }\) is also a generator of the free \({\Lambda }_{{\mathbb {Q}}}\)-module \(M_{{\mathbb {Q}}}\) of rank 1.
We want to prove that  (this would prove that \(M_{(\ell )}\) is a free right \({\Lambda }_{(\ell )}\)-module of rank 1 with the generator \(f_{\ell }\)). For each \(x \in M_{(\ell )}\) there exists a unique \(\lambda \in {\Lambda }_{\ell }\) with \(x= f\lambda \). We need to prove that \(\lambda \in {\Lambda }_{(\ell )}\). Notice that \(x \in M_{(\ell )}\subset M_{{\mathbb {Q}}}\). Since \(f_{\ell }\) is a generator of the free \({\Lambda }_{{\mathbb {Q}}}\)-module \(M_{{\mathbb {Q}}}\), there exists exactly one \(\mu _0 \in {\Lambda }_{{\mathbb {Q}}}\) such that \(x=f \mu _0\). We get the equalities \(f \mu _0=x=f \mu \) in
(this would prove that \(M_{(\ell )}\) is a free right \({\Lambda }_{(\ell )}\)-module of rank 1 with the generator \(f_{\ell }\)). For each \(x \in M_{(\ell )}\) there exists a unique \(\lambda \in {\Lambda }_{\ell }\) with \(x= f\lambda \). We need to prove that \(\lambda \in {\Lambda }_{(\ell )}\). Notice that \(x \in M_{(\ell )}\subset M_{{\mathbb {Q}}}\). Since \(f_{\ell }\) is a generator of the free \({\Lambda }_{{\mathbb {Q}}}\)-module \(M_{{\mathbb {Q}}}\), there exists exactly one \(\mu _0 \in {\Lambda }_{{\mathbb {Q}}}\) such that \(x=f \mu _0\). We get the equalities \(f \mu _0=x=f \mu \) in  .
.
Since \(f_{\ell }\) is a generator of the free  -module
-module  , we get \(\mu =\mu _0\). Since \({\Lambda }_{(\ell )}\) coincides with intersection of \({\Lambda }_{\ell }\) and \({\Lambda }_{{\mathbb {Q}}}\) in
, we get \(\mu =\mu _0\). Since \({\Lambda }_{(\ell )}\) coincides with intersection of \({\Lambda }_{\ell }\) and \({\Lambda }_{{\mathbb {Q}}}\) in  , we conclude that \(\mu =\mu _0 \in {\Lambda }_{(\ell )}\) and therefore
, we conclude that \(\mu =\mu _0 \in {\Lambda }_{(\ell )}\) and therefore  . This implies that \(M_{(\ell )}\) is a free right \({\Lambda }_{(\ell )}\)-module of rank 1, which proves (iii).\(\square \)
. This implies that \(M_{(\ell )}\) is a free right \({\Lambda }_{(\ell )}\)-module of rank 1, which proves (iii).\(\square \)
Corollary 3.3
Let M be a free commutative group of finite positive rank that is provided with a structure of a right \({\Lambda }\)-module. Then M is a locally free \({\Lambda }\)-module of rank 1 if and only if the right \({\Lambda }_{(\ell )}\)-module \(M_{(\ell )}\) is free of rank 1 for all primes \(\ell \).
Proof
Clearly, if \(M_{(\ell )}\) is a free right \({\Lambda }_{(\ell )}\)-module of rank 1 then the right \({\Lambda }_{\ell }\)-module \(M_{\ell }\) is free of rank 1. The converse follows from Theorem 3.2 (iii).\(\square \)
Remark 3.4
Suppose that \({\Lambda }\) is an order in a number field E, i.e., \({\Lambda }\) is a finitely generated over \({\mathbb {Z}}\) a subring (with 1) of E such that \({\Lambda }_{{\mathbb {Q}}}=E\). Let M be a finitely generated \({\Lambda }\)-submodule in E, i.e., a free commutative additive (sub)group of finite rank in E such that  . In particular, \(M_{{\mathbb {Q}}}=E\) is a free \(E={\Lambda }_{{\mathbb {Q}}}\)-module of rank 1.
. In particular, \(M_{{\mathbb {Q}}}=E\) is a free \(E={\Lambda }_{{\mathbb {Q}}}\)-module of rank 1.
-
(i)
If \({\Lambda }\) is the ring of all integers in E then it is a Dedekind ring and each of its localizations \({\Lambda }_{(\ell )}\) is a Dedekind ring with finitely many maximal ideals and therefore is a principal ideal domain [8, Chapter III, Proposition 2.12, p. 93]. This implies that \(M_{(\ell )}\) is a free \({\Lambda }_{(\ell )}\)-module, whose rank is obviously 1. By Corollary 3.3, M is locally free of rank 1.
-
(ii)
Suppose that E is a quadratic field. We do not impose any restrictions on \({\Lambda }\) but instead assume that
 . Then it is known [1, Lemma 2, p. 55] that for each prime \(\ell \) there is a nonzero ideal \(\mathfrak {J}\subset {\Lambda }\) such that the order of the finite quotient \({\Lambda }/\mathfrak {J}\) is prime to \(\ell \) and the \({\Lambda }\)-modules M and \(\mathfrak {J}\) are isomorphic. This implies that the \({\Lambda }_{(\ell )}\)-module \(J_{(\ell )}={\Lambda }_{(\ell )}\) is free and therefore the \({\Lambda }_{(\ell )}\)-module \(M_{(\ell )}\) is also free and its rank is obviously 1. By Corollary 3.3, M is locally free of rank 1.
. Then it is known [1, Lemma 2, p. 55] that for each prime \(\ell \) there is a nonzero ideal \(\mathfrak {J}\subset {\Lambda }\) such that the order of the finite quotient \({\Lambda }/\mathfrak {J}\) is prime to \(\ell \) and the \({\Lambda }\)-modules M and \(\mathfrak {J}\) are isomorphic. This implies that the \({\Lambda }_{(\ell )}\)-module \(J_{(\ell )}={\Lambda }_{(\ell )}\) is free and therefore the \({\Lambda }_{(\ell )}\)-module \(M_{(\ell )}\) is also free and its rank is obviously 1. By Corollary 3.3, M is locally free of rank 1.
4 Tensor products
Now we are going to use Theorem 3.2, in order to construct abelian varieties  over K that are almost isomorphic to a given A. Notice that our
over K that are almost isomorphic to a given A. Notice that our  are a rather special naive case of powerful Serre’s tensor construction [3, Section 7], [2, Section 1.7.4].
are a rather special naive case of powerful Serre’s tensor construction [3, Section 7], [2, Section 1.7.4].
Suppose we are given a free commutative group M of finite (positive) rank that is provided with the structure of a right locally free  -module of rank 1. Let \(F_2\) be a free right \({\Lambda }\)-module of rank 2. It follows from Theorem 3.2 (i) that there is an endomorphism \(\gamma {:} F_2 \rightarrow F_2\) of the right \({\Lambda }\)-module \(F_2\) such that \(\gamma ^2=\gamma \) and whose image
-module of rank 1. Let \(F_2\) be a free right \({\Lambda }\)-module of rank 2. It follows from Theorem 3.2 (i) that there is an endomorphism \(\gamma {:} F_2 \rightarrow F_2\) of the right \({\Lambda }\)-module \(F_2\) such that \(\gamma ^2=\gamma \) and whose image  is isomorphic to M. Notice that
is isomorphic to M. Notice that  is the matrix algebra \({\mathbb {M}}_2({\Lambda })\) of size 2 over \({\Lambda }\). So, the idempotent
is the matrix algebra \({\mathbb {M}}_2({\Lambda })\) of size 2 over \({\Lambda }\). So, the idempotent

where  . Let us define the K-abelian (sub)variety
. Let us define the K-abelian (sub)variety

Clearly, B is a direct factor of \(A^2\). More precisely, if we consider the K-abelian (sub)variety  then the natural homomorphism
then the natural homomorphism  , \((x,y) \mapsto x+y\) of abelian varieties over K is an isomorphism, i.e.,
, \((x,y) \mapsto x+y\) of abelian varieties over K is an isomorphism, i.e.,  . This implies that the right
. This implies that the right  -module
-module  coincides with
coincides with

and therefore the right  -module
-module  is canonically isomorphic to \(\gamma (F_2)=M' \cong M\). It also follows that for every prime \(\ell \)
is canonically isomorphic to \(\gamma (F_2)=M' \cong M\). It also follows that for every prime \(\ell \)

Theorem 4.1
Let M be a free commutative group of finite rank which is a right locally free \(\mathrm{End}(A)\)-module of rank 1. Let us consider the abelian variety  over K. Then:
over K. Then:
-
(i)
A and B are isogenous over K.
-
(ii)
The right
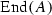 -module
-module 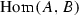 is isomorphic to M.
is isomorphic to M. -
(ii)
A and B are almost isomorphic.
Proof
We have already seen that  , which proves (ii). Since the right
, which proves (ii). Since the right  -module
-module  is free of rank 1, the same is true for the right
is free of rank 1, the same is true for the right  -module
-module  . By Lemma 2.1,
. By Lemma 2.1,  and there exists a
and there exists a  -dimensional abelian K-subvariety \(B_0\subset B\) such that A and \(B_0\) are isogenous over K and
-dimensional abelian K-subvariety \(B_0\subset B\) such that A and \(B_0\) are isogenous over K and

We claim that \(B=B_0\). Indeed, if \(B_0 \ne B\) then, by the Poincaré Complete Reducibility theorem [7, Theorem 6, p. 28], there is an “almost complimentary” abelian K-subvariety \(B_1\subset B\) of positive dimension  such that the intersection \(B_0\cap B_1\) is finite and \(B_0+B_1=B\). It follows from (\(\star \star \star \)) that
such that the intersection \(B_0\cap B_1\) is finite and \(B_0+B_1=B\). It follows from (\(\star \star \star \)) that  . However, \(B_1\subset B \subset A^2\) is an abelian K-subvariety of \(A^2\) and therefore there is a surjective homomorphism
. However, \(B_1\subset B \subset A^2\) is an abelian K-subvariety of \(A^2\) and therefore there is a surjective homomorphism  and therefore there exists a nonzero homomorphism \(A\rightarrow B_1\). This is a contradiction, which proves that \(B=B_0\), the right
and therefore there exists a nonzero homomorphism \(A\rightarrow B_1\). This is a contradiction, which proves that \(B=B_0\), the right  -module
-module  is isomorphic to M, and A and B are isogenous over K. In particular,
is isomorphic to M, and A and B are isogenous over K. In particular,  . This proves (i).
. This proves (i).
Let \(\ell \) be a prime. Since  is a free right
is a free right  -module of rank 1,
-module of rank 1,  is a free right
is a free right  -module of rank 1. Let us choose a generator
-module of rank 1. Let us choose a generator  of the module
of the module  . Thesurjection
. Thesurjection
 is defined by a certain pair of homomorphisms \(\phi _1, \phi _2{:} A\rightarrow B\), i.e.,
is defined by a certain pair of homomorphisms \(\phi _1, \phi _2{:} A\rightarrow B\), i.e.,
Since \(\phi \) is a generator, there are  such that
such that
in  . It follows that
. It follows that

By (\(\star \star \)),  . This implies that \(\phi \) induces a surjective homomorphism
. This implies that \(\phi \) induces a surjective homomorphism  . Since finite groups
. Since finite groups  and
and  have the same order, \(\phi \) induces an isomorphism
have the same order, \(\phi \) induces an isomorphism  . This implies that
. This implies that  does not contain points of order \(\ell \) and therefore is an isogeny of degree prime to \(\ell \). This proves (iii).\(\square \)
does not contain points of order \(\ell \) and therefore is an isogeny of degree prime to \(\ell \). This proves (iii).\(\square \)
Corollary 4.2
Suppose that for each \(i=1,2\) we are given a commutative free group \(M_i\) of finite positive rank provided with the structure of a right locally free  -module of rank 1. Then abelian varieties
-module of rank 1. Then abelian varieties  and
and  are isomorphic over K if and only if the
are isomorphic over K if and only if the  -modules \(M_1\) and \(M_2\) are isomorphic.
-modules \(M_1\) and \(M_2\) are isomorphic.
Proof
By Theorem 4.1 (ii), the right  -module
-module  is isomorphic to \(M_i\). Now the result follows from Theorem 4.1 (iii) combined with Corollary 2.6.\(\square \)
is isomorphic to \(M_i\). Now the result follows from Theorem 4.1 (iii) combined with Corollary 2.6.\(\square \)
Corollary 4.3
Let A and B be abelian varieties over K of positive dimension. Suppose that the Galois modules \(T_{\ell }(A)\) and \(T_{\ell }(B)\) are isomorphic for all primes \(\ell \). Then abelian varieties B and  are isomorphic over K.
are isomorphic over K.
Proof
By Theorem 4.1 (ii), the right  -module
-module  is isomorphic to
is isomorphic to  . Now the result follows from Theorem 4.1 (iii) combined with Corollary 2.6.\(\square \)
. Now the result follows from Theorem 4.1 (iii) combined with Corollary 2.6.\(\square \)
Remark 4.4
Let \(g \geqslant 2\) be an integer and a g-dimensional abelian variety A is a product  where \(A_1\) and \(A_2\) are abelian varieties of positive dimension over K with
where \(A_1\) and \(A_2\) are abelian varieties of positive dimension over K with  . Then
. Then  . Suppose that for each \(i=1,2\) we are given a commutative free group \(M_i\) of finite positive rank provided with the structure of a right locally free
. Suppose that for each \(i=1,2\) we are given a commutative free group \(M_i\) of finite positive rank provided with the structure of a right locally free  -module of rank 1.
-module of rank 1.
Then the direct sum  becomes a right locally free module of rank 1 over the ring
becomes a right locally free module of rank 1 over the ring  .
.
There is an obvious canonical isomorphism between abelian varieties  and
and  over K.
over K.
For example, we may take as \(A_2\) (for a suitable number field K) an elliptic curve such that  is the ring of integers in an imaginary quadratic field with class number \(>1\) while \(A_1\) is a
is the ring of integers in an imaginary quadratic field with class number \(>1\) while \(A_1\) is a  -dimensional principally polarized abelian variety with
-dimensional principally polarized abelian variety with

(If \(g>2\) then one may take as \(A_1\) the \((g-1)\)-dimensional jacobian of the hyperelliptic curve  , see [13].) Clearly, all \(\overline{K}\)-endomorphisms of A are defined over K; in particular, \(A_1\) is absolutely simple. Let us take \(M_1={\mathbb {Z}}\). Clearly,
, see [13].) Clearly, all \(\overline{K}\)-endomorphisms of A are defined over K; in particular, \(A_1\) is absolutely simple. Let us take \(M_1={\mathbb {Z}}\). Clearly,  . Actually, every \(\overline{K}\)-homomorphism between \(A_1\) and \(A_2\) is 0. Let \(M_2\) be a non-principal ideal in
. Actually, every \(\overline{K}\)-homomorphism between \(A_1\) and \(A_2\) is 0. Let \(M_2\) be a non-principal ideal in  . Then the elliptic curves \(A_2\) and
. Then the elliptic curves \(A_2\) and  are almost isomorphic but are not isomorphic over K and even over \(\overline{K}\). This implies that
are almost isomorphic but are not isomorphic over K and even over \(\overline{K}\). This implies that  is almost isomorphic over K but is not isomorphic to
is almost isomorphic over K but is not isomorphic to  over \(\overline{K}\). Notice that both A and
over \(\overline{K}\). Notice that both A and  are principally polarized, since \(A_1\) is principally polarized while both \(A_2\) and
are principally polarized, since \(A_1\) is principally polarized while both \(A_2\) and  are elliptic curves.
are elliptic curves.
Remark 4.5
See last section of [15] for examples of almost isomorphic but not isomorphic elliptic curves over finite fields.
References
Borevich, Z.I., Faddeev, D.K.: Integral representations of quadratic rings. Vestnik Leningrad. Univ. 15(19), 52–64 (1960) (in Russian). MR0153707 (27 #3668)
Chai, C.-L., Conrad, B., Oort, F.: Complex Multiplication and Lifting Problems. Mathematical Surveys and Monographs, vol. 195. American Mathematical Society, Providence (2014)
Conrad, B.: Gross-Zagier revisited. With an appendix by W.R. Mann. In: Darmon, H., Zhang, S. (eds.) Heegner Points and Rankin L-Series. Mathematical Sciences Research Institute Publications, vol. 49, pp. 67–163. Cambridge University Press, Cambridge (2004)
Faltings, G.: Endlichkeitssätze für abelsche Varietäten über Zahlkörpern. Invent. Math. 73(3), 349–366 (1983)
Faltings, G.: Complements to Mordell. In: Faltings, G., Wüstholz, G., et al. (eds.) Rational Points. Aspects of Mathematics, vol. E6, pp. 203–227. Vieweg, Braunschweig (1986)
Fröhlich, A.: Locally free modules over arithmetic orders. J. Reine Angew. Math. 274/275, 112–124 (1975)
Lang, S.: Abelian Varieties, 2nd edn. Springer, New York (1983)
Lorenzini, D.: An Invitation to Arithmetic Geometry. Graduate Studies in Mathematics, vol. 9. American Mathematical Society, Providence (1996)
Mumford, D.: Abelian Varieties. Tata Institute of Fundamental Research Studies in Mathematics, vol. 5. 2nd edn. Oxford University Press, London (1974)
Patrikis, S., Voloch, F., Zarhin, Yu.G.: Anabelian geometry and descent obstructions on moduli spaces. Algebra Number Theory 10(6), 1191–1219 (2016)
Serre, J.-P.: Abelian \(\ell \)-Adic Representations and Elliptic Curves. Advanced Book Classics, 2nd edn. Addison-Wesley, Redwood City (1989)
Tate, J.: Endomorphisms of abelian varieties over finite fields. Invent. Math. 2, 134–144 (1966)
Zarhin, Yu.G: Hyperelliptic Jacobians without complex multiplication. Math. Res. Lett. 7(1), 123–132 (2000)
Zarhin, Yu.G.: Homomorphisms of abelian varieties. In: Aubry, Y., Lachaud, G. (eds.) Arithmetic, Geometry and Coding Theory. Séminaires & Congres, vol. 11, pp. 189–215. Société Mathématique de France, Paris (2005)
Zarhin, Yu.G.: Homomorphisms of abelian varieties over finite fields. In: Kaledin, D., Tschinkel, Yu. (eds.) Higher-Dimensional Geometry over Finite Fields. NATO Science for Peace and Security Series D, vol. 16, pp. 315–343. IOS, Amsterdam (2008)
Acknowledgements
Part of this work was done in May–June 2015 when the author was visiting Department of Mathematics of the Weizmann Institute of Science (Rehovot, Israel) and in May–June 2016 when the author was a visitor at the Max-Planck-Institut für Mathematik (Bonn, Germany). The hospitality and support of both Institutes are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
In memoriam of Bill Waterhouse (1941–2016)
The author is grateful to Jiangwei Xue for useful discussions, to Stefan Patrikis and Felipe Voloch for their interest in this paper and to the Simons Foundation for financial and moral support (via Grant # 246625 to Yuri Zarkhin).
Rights and permissions
About this article
Cite this article
Zarhin, Y.G. Almost isomorphic abelian varieties. European Journal of Mathematics 3, 22–33 (2017). https://doi.org/10.1007/s40879-016-0122-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-016-0122-4



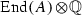 -module
-module 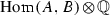 is free of rank 1. In addition, one may choose as a generator of
is free of rank 1. In addition, one may choose as a generator of 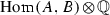 any isogeny
any isogeny 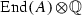 -module
-module 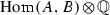 is free of rank 1.
is free of rank 1. and there exists a
and there exists a 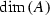 -dimensional abelian K-subvariety
-dimensional abelian K-subvariety 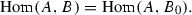
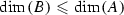 then
then 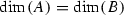 ,
, 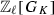 -modules.
-modules. . Then it is known [
. Then it is known [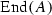 -module
-module 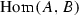 is isomorphic to M.
is isomorphic to M.