1 Introduction

The research on fractional calculus and its related problems has been conducted extensively in the community of engineering and mathematics. These fields include mechanical engineering, viscoelasticity, Lévy motion , electron transport , dissipation, heat conduction and high-frequency financial data [1,2,3,4,5,6,7,8]. It is very interesting to us that fractional differential equations can be used to model some anomalous diffusion phenomena in engineering, physics, chemistry and other fields of science [9,10,11,12]. Many experiments show that, in the process of modeling real physical phenomena, fractional calculus sometimes provides more accurate simulation than traditional calculus with classical derivatives. The forward problem of fractional differential equation is well investigated in recent years.

However, sometimes the inverse problem of fractional differential equation is inevitable in the field of engineering. It is well known that many kinds of inverse problems are ill-posed in the sense that a small error in the input data may cause an enormous perturbation in the solution. Therefore, some regularization methods are needed, i.e., find a stable approximation solution to the exact solution. In this paper, we focus on a fractional inverse heat conduction problem (IHCP) in two-dimensional space, which is severely ill-posed. For one-dimensional classical IHCP, in [13, 14], Berntsson and Eldén proposed a Fourier method. For one-dimensional fractional-order IHCP, many authors have used different methods to study the related problems. Cheng [15] proved the uniqueness of an inverse problem for one-dimensional fractional diffusion equation by the Gelfand–Levitan theory. In [16], Zheng and Wei proved an error estimate by a regularization method for a Cauchy problem of the time-fractional advection–dispersion equation. Bondarenko, Ivaschenko [17] and Murio [18] investigated some numerical methods. In [19], Qian gave an optimal regularization method with the time-fractional-order \(\alpha =\frac{1}{2}\). In [20], Cheng and Fu used an iterative-type regularization method to solve a time-fractional inverse diffusion problem. However, two-dimensional fractional inverse heat conduction problem is more difficult than one-dimensional case.

To the authors’ knowledge, the study on the inverse heat conduction problem in two-dimensional space is very few. In [21], Xiong devised a regularization solution to the two-dimensional fractional inverse heat conduction problem by using static and dynamic Fourier methods and proved the corresponding error estimate. In this paper, we will use a new fractional Tikhonov method [22] to approximate the problem. This fractional Tikhonov method was proposed by Li and Xiong when they considered a heat conduction problem backward in time. We extend this method to deal with the current problem.

Generally, the solution of classical Tikhonov method over-smooths and cannot recover the characteristics (e.g., the jump of the solution) of exact solutions well. Therefore, some fractional Tikhonov methods are introduced. The fractional Tikhonov methods have been well studied for the ill-posed operator equation with a compact forward operator [23,24,25]. Some weighted and iterative versions are also studied by Gerth [26] and Bianchi [27], respectively. Recently, Qian applied a fractional Tikhonov method to solving a Cauchy problem of the Helmholtz equation [28].

However, the theoretical results on the fractional Tikhonov methods in the literature only gave the error estimates under the a priori regularization parameter choice rules. In this study, we will prove the corresponding error estimates under both of the choice rules of priori and posteriori regularization parameters.

This paper is organized as follows: In Sect. 2, we give an analysis on the ill-posedness of the 2-D FIHCP. The regularized solution by fractional Tikhonov method, moreover, an order-optimal error estimate, is proved for the a priori parameter choice rule. The a posteriori parameter choice rule is investigated in Sect. 4, which also leads to a Hölder-type error estimate. The numerical verification is demonstrated in Sect. 5 in which an example is presented for testing the validity of the proposed fractional Tikhonov regularization method.

2 Mathematical Formulation

In some engineering problems, it is often necessary to estimate the surface temperature or heat flux in a body from a measured temperature history at a fixed location inside a body, which is called inverse heat conduction problem. In this paper, we consider an inverse heat conduction problem for a fractional-order diffusion equation in the two-dimensional (2-D) case [21]

$$\begin{aligned} \left\{ \begin{array}{ll} _0D_t^{\alpha }u(x,y,t)-u_{xx}(x,y,t)-u_{yy}(x,y,t)=0,\, &{} 0<x<1, y>0, t>0, 0<\alpha \le 1,\\ u(1,y,t)=g(y,t),\, &{} y\ge 0, t\ge 0,\\ u(x,y,0)=0,\, &{} x>0,y\ge 0,\\ u(x,0,t)=0,\, &{} x>0,t\ge 0,\\ u_{y}(x,0,t)=0,\, &{} x>0,t\ge 0,\\ u(x,y,t)|_{x\rightarrow \infty }\, \mathrm {bounded}, &{} y>0, t>0, \end{array} \right. \end{aligned}$$
(2.1)

where the time-fractional derivative \(_0D_t^{\alpha }u(x,y,t)\) is the Caputo fractional derivative of order \(\alpha (0<\alpha \le 1)\) defined by [29].

$$\begin{aligned}&\displaystyle {_{0}}D_t^{\alpha }u(x,y,t)=\frac{1}{\Gamma (1-\alpha )} \int _{0}^{t}\frac{\partial u{(x,y,s)}}{\partial s} \frac{\mathrm{d}s}{(t-s)^\alpha },0<\alpha <1,&\end{aligned}$$
(2.2)
$$\begin{aligned}&\displaystyle {_{0}}D_t^{\alpha }u(x,y,t)=\frac{\partial u{(x,y,t)}}{\partial t},\alpha =1.&\end{aligned}$$
(2.3)

Since the order \(\alpha \) of the derivative with respect to time in the heat equation can be of arbitrary real order, the heat equation is called the fractional diffusion equation. For \(\alpha =1\), the equation becomes the classical diffusion equation. For \(0<\alpha <1\), it is called the ultraslow diffusion model [30].

In this paper, we extend all the functions to the whole plane \(-\infty<t<\infty , -\infty<y<\infty \) by setting the functions to be zero for \(t<0\) and \(y<0\). Let

$$\begin{aligned} {\hat{f}}(\xi ,\eta )=\frac{1}{2\pi }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(y,t)e^{-i(\xi y+\eta t)}\mathrm{d}y\mathrm{d}t,\,\,\,i=\sqrt{-1} \end{aligned}$$
(2.4)

be the Fourier transform of the function \(f(y,t)\in L^2({\mathbb {R}}^{2})\), the corresponding inverse Fourier transform of the function \({\hat{f}}(\xi ,\eta )\) is given by

$$\begin{aligned} f(y,t)=\frac{1}{2\pi }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty } {\hat{f}}(\xi ,\eta )e^{i(\xi y+\eta t)}\mathrm{d}\xi \mathrm{d}\eta . \end{aligned}$$
(2.5)

We apply the Fourier transform technique to problem (2.1) with respect to the variable y, t and yield the following problem in frequency domain space:

$$\begin{aligned} \left\{ \begin{array}{ll} (i\eta )^{\alpha }{\hat{u}}(x,\xi ,\eta )-{\hat{u}}_{xx}(x,\xi ,\eta ) +\xi ^2{\hat{u}}(x,\xi ,\eta )=0,\, &{} x>0, \xi \in {\mathbb {R}}, \eta \in {\mathbb {R}},\\ {\hat{u}}(1,\xi ,\eta )=g(\xi ,\eta ),\, &{} \xi \in {\mathbb {R}}, \eta \in {\mathbb {R}},\\ {\hat{u}}(x,\xi ,\eta )|_{x\rightarrow \infty }\, \text{ bounded }, &{} \xi \in {\mathbb {R}}, \eta \in {\mathbb {R}}. \end{array} \right. \end{aligned}$$
(2.6)

We can easily get the solution of problem (2.6)

$$\begin{aligned} {\hat{u}}(x,\xi ,\eta )=e^{(1-x)\sqrt{(i\eta )^{\alpha }+\xi ^{2}}} {\hat{g}}(\xi ,\eta ), \end{aligned}$$
(2.7)

where

$$\begin{aligned} (i\eta )^{\alpha }={|\eta |}^{\alpha }\Big (\cos \Big (\frac{\alpha \pi }{2}\Big )+i\, \mathrm {sign}(\eta )\sin \Big (\frac{\alpha \pi }{2}\Big )\Big ). \end{aligned}$$
(2.8)

Let

$$\begin{aligned} \omega :=\sqrt{(i\eta )^{\alpha }+\xi ^{2}}. \end{aligned}$$
(2.9)

Throughout this paper, we denote the real part and imaginary part of \(\omega \) as follows:

$$\begin{aligned} a:=\mathfrak {Re}(\omega );\,\,\,\,b:=\mathfrak {Im}(\omega ). \end{aligned}$$

\(\omega \) can be written in complex number, i.e.,

$$\begin{aligned} \omega =a+bi, \end{aligned}$$
(2.10)

where

$$\begin{aligned} a&=\sqrt{\frac{\sqrt{{|\eta |}^{2\alpha }\sin ^{2} \Big (\frac{\alpha \pi }{2}\Big )+\Big (\xi ^{2}+{|\eta |}^{2\alpha }\cos \Big (\frac{\alpha \pi }{2}\Big )\Big )^{2}}+\Big (\xi ^{2}+{|\eta |}^{2\alpha } \cos \Big (\frac{\alpha \pi }{2}\Big )\Big )}{2}},\\ b&=i\, \mathrm {sign}\Big (\mathrm {sign}(\eta )\sin \Big (\frac{\alpha \pi }{2}\Big )\Big ) \\&\quad \times \sqrt{\frac{\sqrt{{|\eta |}^{2\alpha }\sin ^{2} \Big (\frac{\alpha \pi }{2}\Big )+\Big (\xi ^{2}+{|\eta |}^{2\alpha } \cos \Big (\frac{\alpha \pi }{2}\Big )\Big )^{2}}-\Big (\xi ^{2} +{|\eta |}^{2\alpha }\cos \Big (\frac{\alpha \pi }{2}\Big )\Big )}{2}}. \end{aligned}$$

The inverse Fourier transform on (2.7) yields

$$\begin{aligned} u(x,y,t)=\frac{1}{2\pi }\int _{{\mathbb {R}}^{2}}{\hat{g}} (\xi ,\eta )e^{(1-x)\sqrt{(i\eta )^{\alpha }+\xi ^{2}}}e^{i(\xi y +\eta t)}\mathrm{d}\xi \mathrm{d}\eta . \end{aligned}$$
(2.11)

We want to seek the solution u(x, y, t) from the given data g(y, t). Physically, g(y, t) can only be measured, there should be measurement errors, and we would actually have the noisy data function \(g^\delta (y,t)\in L^2({\mathbb {R}}^{2})\) which satisfies

$$\begin{aligned} \Vert g^{\delta }(\cdot ,\cdot )-g(\cdot ,\cdot )\Vert \le \delta , \end{aligned}$$
(2.12)

where the constant \(\delta >0\) represents the noise level, \(\Vert \cdot \Vert \) denotes the \(L^{2}\)-norm. In order to obtain the error estimate, we impose the a priori bound on the exact solution at \(x=0\), i.e.,

$$\begin{aligned} \Vert u(0,\cdot ,\cdot )\Vert \le E, \end{aligned}$$
(2.13)

where \(E>0\) is a constant.

From (2.7) and the Parseval equality, we note that for a fixed \(0<x<1\), when \(\mathfrak {Re}(\omega )\rightarrow \infty \), \(|e^{(1-x)\omega }|\) is unbounded. Therefore, problem (2.1) is severely ill-posed and the ill-posedness is caused by the high-frequency components of \(e^{(1-x)\omega }\). In the following, we will solve problem (2.1) with the fractional Tikhonov regularization method.

3 Fractional Tikhonov Method and Error Estimate

We consider fractional Tikhonov regularization method to solve the ill-posed problem (2.1). From (2.7), we know

$$\begin{aligned} {\hat{u}}(x,\xi ,\eta )=e^{(1-x)\sqrt{(i\eta )^{\alpha }+\xi ^{2}}} {\hat{g}}(\xi ,\eta ). \end{aligned}$$

We denote

$$\begin{aligned} A(x,\xi ,\eta )= & {} e^{(1-x)\sqrt{(i\eta )^{\alpha }+\xi ^{2}}}, \end{aligned}$$
(3.1)
$$\begin{aligned} A(0,\xi ,\eta )= & {} e^{\sqrt{(i\eta )^{\alpha }+\xi ^{2}}}. \end{aligned}$$
(3.2)

We rewrite \({\hat{u}}(x,\xi ,\eta )\) as

$$\begin{aligned} {\hat{u}}(x,\xi ,\eta )=A(x,\xi ,\eta ){\hat{g}}(\xi ,\eta ). \end{aligned}$$
(3.3)

Then, we construct the fractional Tikhonov regularization solution in the frequency domain as

$$\begin{aligned} {\hat{u}}_\mu ^{\delta }(x,\xi ,\eta )=\frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}(\xi , \eta ), \,\,\,\,\,\frac{1}{2}\le \gamma \le 1, \end{aligned}$$
(3.4)

\(\mu >0\) plays the role of regularization parameter. We call \(\gamma \) the fractional parameter. When \(\gamma =1\), it is the classical Tikhonov method. When \(\gamma =\frac{1}{2}\), it is the quasi-boundary regularization method. When \(\frac{1}{2}<\gamma <1\), we interpret the method (3.4) as an ‘interpolation’ between the classical Tikhonov method and quasi-boundary method. It can prevent the effect of over-smoothing for the Tikhonov method [31].

In the following, we need an auxiliary lemma [32].

Lemma 3.1

Let \(0<m\le n\), \(\mu >0\), then

$$\begin{aligned} \sup _{s>0}\frac{e^{sm}}{1+\mu e^{sn}}\le \mu ^{-\frac{m}{n}}. \end{aligned}$$
(3.5)

Theorem 3.2

Assume the a priori bound (2.13) and noise assumption (2.12) hold, if we select

$$\begin{aligned} \mu ={\Big (\frac{\delta }{E}\Big )}^{2\gamma },\,\,\, \frac{1}{2}\le \gamma \le 1, \end{aligned}$$
(3.6)

then we have the following error estimate for \(0<x<1\),

$$\begin{aligned} \Vert u_\mu ^{\delta }(x,\cdot ,\cdot )-u(x,\cdot ,\cdot )\Vert \le 2\delta ^xE^{1-x}. \end{aligned}$$
(3.7)

Proof

By the triangle inequality and Parseval’s equality, we know

$$\begin{aligned} \begin{aligned} \Vert u_\mu ^{\delta }(x,\cdot ,\cdot )-u(x,\cdot ,\cdot )\Vert&=\Vert {\hat{u}}_\mu ^{\delta }(x,\cdot ,\cdot )-{\hat{u}}(x,\cdot ,\cdot )\Vert \\&=\Vert {\hat{u}}_\mu ^{\delta }(x,\cdot ,\cdot )-{\hat{u}}_\mu (x,\cdot ,\cdot )+{\hat{u}}_\mu (x,\cdot ,\cdot )-{\hat{u}}(x,\cdot ,\cdot )\Vert \\&\le \Vert {\hat{u}}_\mu ^{\delta }(x,\cdot ,\cdot )-{\hat{u}}_\mu (x,\cdot ,\cdot )\Vert +\Vert {\hat{u}}_\mu (x,\cdot ,\cdot )-{\hat{u}}(x,\cdot ,\cdot )\Vert \\&=I_1+I_2. \end{aligned} \end{aligned}$$
(3.8)

Denote \(I_1=\Vert {\hat{u}}_\mu ^{\delta }(x,\cdot ,\cdot )-{\hat{u}}_\mu (x,\cdot , \cdot )\Vert ,\,\, I_2=\Vert {\hat{u}}_\mu (x,\cdot ,\cdot )-{\hat{u}}(x,\cdot ,\cdot )\Vert \). Firstly, we need to estimate of \(I_1\) , with Lemma 3.1 we have

$$\begin{aligned} I_1&=\Big \Vert \frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}} {\hat{g}}^\delta (\xi , \eta )-\frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}(\xi , \eta )\Big \Vert \\&=\Big \Vert \frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}} \big ({\hat{g}}^\delta (\xi , \eta )-{\hat{g}}(\xi , \eta )\big )\Big \Vert \\&\le \delta \sup \Big |\frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi , \eta )|^{2\gamma }}}\Big |. \end{aligned}$$

From (3.1) and (3.2), it yields

$$\begin{aligned} |A(x,\xi ,\eta )|= & {} e^{(1-x)a}, \end{aligned}$$
(3.9)
$$\begin{aligned} |A(0,\xi ,\eta )|= & {} e^{a}. \end{aligned}$$
(3.10)

So

$$\begin{aligned} I_1&\le \delta \sup \Big |\frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}\Big |\\&=\delta \sup \Big |\frac{e^{(1-x)(a+bi)}}{1+\mu e^{2a\gamma }}\Big |\\&\le \delta \sup \frac{e^{a(1-x)}}{1+\mu e^{2a\gamma }}. \end{aligned}$$

According to Lemma 3.1, we get

$$\begin{aligned} I_1\le \mu ^{-\frac{1-x}{2\gamma }}\delta . \end{aligned}$$
(3.11)

Now we estimate \(I_2\) and use a priori bound (2.13); we obtain

$$\begin{aligned} I_2&=\Big \Vert \frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi , \eta )|^{2\gamma }}}{\hat{g}}(\xi , \eta )-A(x,\xi , \eta ){\hat{g}}(\xi ,\eta )\Big \Vert \\&=\Big \Vert A(x,\xi ,\eta ){\hat{g}}(\xi ,\eta )\frac{ \mu {|A(0,\xi ,\eta )|^{2\gamma }}}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}\Big \Vert \\&\le \mu \cdot E \sup \Big |\frac{{A(x,\xi ,\eta )|A(0,\xi , \eta )|^{2\gamma -1}}}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}\Big |. \end{aligned}$$

By (3.9), (3.10), we have

$$\begin{aligned} I_2\le \mu \cdot E\sup \Big |\frac{e^{(2\gamma -x)a}}{1+\mu e^{2\gamma a}}\Big | \end{aligned}$$

Noting \(2\gamma -x>0\) and using Lemma 3.1, we have

$$\begin{aligned} I_2\le E\mu ^{\frac{x}{2\gamma }}. \end{aligned}$$
(3.12)

Combining (3.6), (3.11) and (3.12), we obtain

$$\begin{aligned} \Vert u_\mu ^{\delta }(x,\cdot ,\cdot )-u(x,\cdot ,\cdot )\Vert \le 2\delta ^xE^{1-x}. \end{aligned}$$

\(\square \)

4 The Discrepancy Principle and Error Estimate

In this section, we investigate the a posterior regularization parameter choice rule, i.e., Morozov’s discrepancy principle, to choose the regularization parameter \(\mu \). The most general a posteriori rule is the Morozov’s discrepancy principle [33]. Morozov’s discrepancy principle for our case is to find \(\mu \) such that the following equation holds:

$$\begin{aligned} \bigg \Vert \frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}^\delta (\xi , \eta )-{\hat{g}}^\delta (\xi , \eta )\bigg \Vert =\tau \delta . \end{aligned}$$
(4.1)

where \(\frac{1}{2}\le \gamma \le 1, \tau >1\) is a constant, \(\mu >0\) is regularization parameter. According to the following lemma, we know there exists a unique solution for Eq. (4.1) if \(0<\tau \delta <\Vert {\hat{g}}^\delta \Vert \).

Lemma 4.1

Let \(\rho (\mu )=\Big \Vert \frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}} {\hat{g}}^\delta (\xi , \eta )-{\hat{g}}^\delta (\xi , \eta )\Big \Vert \), if \(0<\delta <\Vert {\hat{g}}^\delta \Vert \) then the following hold:

  1. (a)

    \(\rho (\mu )\) is a continuous function;

  2. (b)

    \(\lim _{\mu \rightarrow 0}\rho (\mu )=0\);

  3. (c)

    \(\lim _{\mu \rightarrow \infty }\rho (\mu )=\Vert {\hat{g}}^\delta \Vert _{L^{2} ({\mathbb {R}})}\);

  4. (d)

    \(\rho (\mu )\) is a strictly increasing function over \((0, \infty )\).

Proof

The proofs are straightforward by virtue of

$$\begin{aligned} \rho (\mu )=\bigg \Vert \frac{\mu |{e^{\sqrt{(i\eta )^{\alpha }+\xi ^{2}}}|^{2\gamma }}}{1+\mu {|e^{\sqrt{(i\eta )^{\alpha }+\xi ^{2}}}|^{2\gamma }}}{\hat{g}}^\delta (\xi , \eta )\bigg \Vert . \end{aligned}$$

\(\square \)

Lemma 4.2

If \(\mu \) is the solution of Eq. (4.1), then we obtain the following inequality

$$\begin{aligned} \Big \Vert \frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}^\delta (\xi , \eta )-{\hat{g}}(\xi , \eta )\Big \Vert \le (\tau +1)\delta . \end{aligned}$$
(4.2)

Proof

Using the triangle inequality and Eq. (4.1), we get

$$\begin{aligned}&\Big \Vert \frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}} {\hat{g}}^\delta (\xi ,\eta )-{\hat{g}}(\xi ,\eta )\Big \Vert \\&=\Big \Vert \frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}} {\hat{g}}^\delta (\xi ,\eta )-{\hat{g}}^\delta (\xi ,\eta ) +{\hat{g}}^\delta (\xi ,\eta )-{\hat{g}}(\xi ,\eta )\Big \Vert \\&\le \Big \Vert \frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}} {\hat{g}}^\delta (\xi ,\eta )-{\hat{g}}^\delta (\xi ,\eta )\Big \Vert +\big \Vert {\hat{g}}^\delta (\xi ,\eta )-{\hat{g}}(\xi ,\eta )\big \Vert&\le (\tau +1)\delta . \end{aligned}$$

\(\square \)

Lemma 4.3

If \(\mu \) is the solution of Eq. (4.1), we have the following inequality:

$$\begin{aligned} \mu ^{-\frac{1}{2\gamma }}\le \frac{E}{(\tau -1)\delta }. \end{aligned}$$
(4.3)

Proof

Due to (3.9), (3.10) and (4.1), we obtain

$$\begin{aligned} \begin{aligned} \tau \delta&=\Big \Vert \frac{\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}^\delta (\xi , \eta )\Big \Vert \\&\le \Big \Vert \frac{\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}({\hat{g}}^\delta (\xi ,\eta ) -{\hat{g}}(\xi ,\eta ))\Big \Vert +\Big \Vert \frac{\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}(\xi ,\eta )\Big \Vert \\&\le \delta +\Big \Vert \frac{\mu {|A(0,\xi ,\eta )|^{2\gamma -1}}}{1 +\mu {|A(0,\xi ,\eta )|^{2\gamma }}}|A(0,\xi ,\eta )|{\hat{g}}(\xi ,\eta )\Big \Vert \\&\le \delta +\sup _{a\ge 0}\Big |\frac{e^{(2\gamma -1)a}}{1+\mu e^{2\gamma a}}\Big |\cdot \mu \cdot E. \end{aligned} \end{aligned}$$

According to Lemma 3.1, we have

$$\begin{aligned} \tau \delta \le \delta +\mu ^\frac{1}{2\gamma }E. \end{aligned}$$
(4.4)

So

$$\begin{aligned} \mu ^{-\frac{1}{2\gamma }}\le \frac{E}{(\tau -1)\delta }. \end{aligned}$$

\(\square \)

Theorem 4.4

Suppose the a priori condition (2.13) and the noise assumption (2.12) hold. The regularization parameter \(\mu \) is chosen by Morozov’s discrepancy principle (4.1); then we have the following error estimate:

$$\begin{aligned} \Vert u_\mu ^{\delta }(x,\cdot ,\cdot )-u(x,\cdot ,\cdot )\Vert \le c E^{1-x}\delta ^{x}, \end{aligned}$$
(4.5)

where \(c=(\frac{\tau }{\tau -1})^{1-x}(\tau +1)^{x}\).

Proof

Denote

$$\begin{aligned} I=\Vert u(x,\cdot ,\cdot )-u_\mu ^{\delta }(x,\cdot ,\cdot )\Vert \end{aligned}$$
(4.6)

Using Parseval’s equality and Lemmas 4.2, 4.3, we know

$$\begin{aligned} \begin{aligned} I^{2}&=\Vert u(x,\cdot ,\cdot )-u_\mu ^{\delta }(x,\cdot ,\cdot )\Vert ^{2} =\Vert {\hat{u}}(x,\cdot ,\cdot )-{\hat{u}}_\mu ^{\delta }(x,\cdot ,\cdot )\Vert ^{2}\\&=\Big \Vert A(x,\xi ,\eta ){\hat{g}}(\xi ,\eta )-\frac{A(x,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}^\delta (\xi , \eta )\Big \Vert ^{2}\\&=\Big \Vert A(x,\xi ,\eta )\Big ({\hat{g}}(\xi , \eta )-\frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{\hat{g}}^\delta (\xi , \eta )\Big )\Big \Vert ^{2}\\&=\int _{{\mathbb {R}}^{2}}\Big |A(x,\xi ,\eta )\Big ({\hat{g}} (\xi , \eta )-\frac{1}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}} {\hat{g}}^\delta (\xi , \eta )\Big )\Big |^{2}\mathrm{d}\xi \mathrm{d}\eta \end{aligned} \end{aligned}$$

By the Hölder inequality and (3.9), (3.10), we have

$$\begin{aligned} I^{2}\le & {} \int _{{\mathbb {R}}^{2}}e^{2(1-x)a} \Big |{\hat{g}}(\xi , \eta )-\frac{1}{1+\mu e^{2\gamma a}} {\hat{g}}^\delta (\xi , \eta )\Big |^{2}\mathrm{d}\xi \mathrm{d}\eta \nonumber \\= & {} \int _{{\mathbb {R}}^{2}}e^{2(1-x)a}\Big |{\hat{g}}(\xi , \eta ) -\frac{1}{1+\mu e^{2\gamma a}}{\hat{g}}^\delta (\xi ,\eta )\Big |^{2(1-x)}\nonumber \\&\quad \cdot \Big |{\hat{g}}(\xi ,\eta )-\frac{1}{1+\mu e^{2\gamma a} }{\hat{g}}^\delta (\xi ,\eta )\Big |^{2x}\mathrm{d}\xi \mathrm{d}\eta \nonumber \\\le & {} \bigg (\int _{{\mathbb {R}}^{2}}\Big (e^{(1-x)a}\Big |{\hat{g}}(\xi , \eta )-\frac{1}{1+\mu e^{2\gamma a}}{\hat{g}}^\delta (\xi ,\eta ) \Big |^{2(1-x)}\Big )^{\frac{1}{1-x}}\mathrm{d}\xi \mathrm{d}\eta \bigg )^{(1-x)}\nonumber \\&\quad \times \bigg (\int _{{\mathbb {R}}^{2}}\Big (\Big | {\hat{g}}(\xi ,\eta )-\frac{1}{1+\mu e^{2\gamma a}}{\hat{g}}^\delta (\xi ,\eta )\Big |^{2x}\Big )^{\frac{1}{x}}\mathrm{d}\xi \mathrm{d}\eta \bigg )^{x}\nonumber \\\le & {} \bigg (\int _{{\mathbb {R}}^{2}}e^{2a}\Big |{\hat{g}}(\xi ,\eta ) -\frac{1}{1+\mu e^{2\gamma a}}{\hat{g}}^\delta (\xi ,\eta )\Big |^{2} \mathrm{d}\xi \mathrm{d}\eta \bigg )^{(1-x)}\nonumber \\&\quad \times \bigg (\int _{{\mathbb {R}}^{2}}\Big |{\hat{g}}(\xi , \eta )-\frac{1}{1+\mu e^{2\gamma a}}{\hat{g}}^\delta (\xi ,\eta )\Big |^{2} \mathrm{d}\xi \mathrm{d}\eta \bigg )^{x}\nonumber \\= & {} \Big \Vert A(0,\xi ,\eta )\Big ({\hat{g}}(\xi ,\eta )-\frac{1}{1+\mu {|A(0,\xi , \eta )|^{2\gamma }}}{\hat{g}}^\delta (\xi ,\eta )\Big )\Big \Vert ^{2(1-x)}\nonumber \\&\quad \times \Big \Vert {\hat{g}}(\xi , \eta )-\frac{1}{1+\mu {|A(0,\xi , \eta )|^{2\gamma }}}{\hat{g}}^\delta (\xi ,\eta )\Big \Vert ^{2x}\nonumber \\\le & {} \bigg (\Big \Vert A(0,\xi ,\eta ){\hat{g}}(\xi ,\eta )\Big (1-\frac{1}{1 +\mu {|A(0,\xi ,\eta )|^{2\gamma }}}\Big )\Big \Vert \nonumber \\&\quad +\Big \Vert \frac{A(0,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2 \gamma }}}\big ({\hat{g}}(\xi ,\eta )-{\hat{g}}^\delta (\xi ,\eta )\big ) \Big \Vert \bigg )^{2(1-x)}\cdot \big ((\tau +1)\delta \big )^{2x}\nonumber \\\le & {} \bigg (E\cdot |\frac{\mu {|A(0,\xi ,\eta )|^{2\gamma }}}{1 +\mu {|A(0,\xi ,\eta )|^{2\gamma }}}|+\sup \Big |\frac{A(0,\xi ,\eta )}{1+\mu {|A(0,\xi ,\eta )|^{2\gamma }}}\Big |\cdot \delta \bigg )^{2(1-x)} \cdot \big ((\tau +1)\delta \big )^{2x}\nonumber \\\le & {} \bigg (E+\delta \sup \frac{e^{a}}{1+\mu e^{2\gamma a}} \bigg )^{2(1-x)}\cdot \big ((\tau +1)\delta \big )^{2x}. \end{aligned}$$
(4.7)

According to Lemma 3.1, we have

$$\begin{aligned} \sup \frac{e^{a}}{1+\mu e^{2\gamma a}}\le \mu ^{-\frac{1}{2\gamma }}. \end{aligned}$$
(4.8)

Combining (4.6), (4.7), (4.8) and Lemma 4.3, we have

$$\begin{aligned} I^{2}&\le \Big (E+\delta \cdot \frac{E}{(\tau -1)\delta } \Big )^{2(1-x)}\big ((\tau +1)\delta \big )^{2x}\\&=\Big (\frac{\tau }{\tau -1}\Big )^{2(1-x)}(\tau +1)^{2x} E^{2(1-x)}\delta ^{2x}. \end{aligned}$$

So

$$\begin{aligned} \Vert u_\mu ^{\delta }(x,\cdot ,\cdot )-u(x,\cdot ,\cdot )\Vert \le \Big (\frac{\tau }{\tau -1}\Big )^{1-x}(\tau +1)^{x}E^{1-x}\delta ^{x}. \end{aligned}$$

Denote \(c=(\frac{\tau }{\tau -1})^{1-x}(\tau +1)^{x}\), we have

$$\begin{aligned} \Vert u_\mu ^{\delta }(x,\cdot ,\cdot )-u(x,\cdot ,\cdot )\Vert \le c E^{1-x}\delta ^{x}. \end{aligned}$$

This completes the proof of Theorem 4.4. \(\square \)

Remark 4.5

It is easy to see that the error estimates (3.7), (4.5) are not convergent for the location at \(x=0\). If we add the following a priori condition

$$\begin{aligned} \Vert u(0,\cdot ,\cdot )\Vert _p\le E, \end{aligned}$$

where \(p>0, E>0\), \(\Vert \cdot \Vert _p\) denotes the norm of the Sobolev space \(H^p({\mathbb {R}}^{2})\), then the convergence rate is logarithmic. Please refer to [34, 35].

5 A Numerical Example

In this section, we show some numerical results reconstructed by the fractional Tikhonov regularization method and compare it with the classical Tikhonov method.

Let us consider the direct problem with the exact input data f(y, t):

$$\begin{aligned} \begin{array}{ll} \frac{\partial ^\alpha u }{\partial t^\alpha }-u_{xx} -u_{yy}=0,&{} 0<x<1, y>0, t>0,\\ u(x,y,0) = 0,&{} x>0, y>0,\\ u(x,0,t) = 0,&{} x>0, t>0 ,\\ u_y(x,0,t) = 0,&{} x>0, t>0 ,\\ u(0,y,t) = f(y,t),&{} y>0,t>0,\\ u(x,y,t)|_{x \rightarrow \infty } \,\, \mathrm {bounded},&{} y>0,t>0. \end{array} \end{aligned}$$
(5.1)

This problem is well-posed, and its solution at \(x=1\) can be given by

$$\begin{aligned} g(y,t):=u(1,y,t)=\frac{1}{2\pi }\int _{-\infty }^{\infty } \int _{-\infty }^{\infty }f(\xi ,\eta )e^{-\sqrt{(i\eta )^{\alpha } +\xi ^2}}e^{-i(\xi y+\eta t)}\mathrm{d}\xi \mathrm{d}\eta . \end{aligned}$$
(5.2)

In numerical tests, we give the data f(y, t) and sample at an equidistant grid \([0,1]\times [0,1]\) with \(100 \times 100\) grid points and then perform 2-dimensional discrete Fourier transformation. We can get the data g(y, t) via 2-dimensional inverse discrete Fourier transformation according to (5.2) and then generate the noisy data \(g_\delta \) according to the following equation

$$\begin{aligned} g_\delta =g+g_{\max }*\delta \cdot \text{ rand } \text{(size(g)) }, \end{aligned}$$
(5.3)

where \(\delta \) represents the error level of g, \(g_{\max }\) is the maximum value of sampled data g. Let RMS(g) denote the root-mean-square for a sampled function \(g(\cdot ,\cdot )\):

$$\begin{aligned} {\text {RMS}}(g)=\sqrt{\frac{1}{(n+1)^2}\sum \nolimits _{j=1}^{n+1} \sum \nolimits _{k=1}^{n+1}(g(y_j,t_k))^2}, \end{aligned}$$
(5.4)

where \(n+1\) is the total number of test points. Similarly, the root- mean-square error (RMSE) can be defined for the computed data and exact data. The symbol \(rand(size(\cdot ))\) is a random number between [0, 1].

The regularized solutions were computed by the 2D discrete fast Fourier transform (2D FFT) and 2D inverse discrete fast Fourier transform (2D IFFT) according to formulas in Sect. 3. The regularization parameter \(\mu \) is chosen by (3.6) where E is computed by (5.4) for the sampled f(y, t) at the grids.

An Example. Let \(\Omega =\{(y,t)\big | 0.1 \le y \le 0.3,\, 0.1 \le t \le 0.3\}\bigcup \{(y,t)\big | 0.4 \le y \le 0.6,\,0.4 \le t \le 0.6 \}\bigcup \{(y,t)\big | 0.7 \le y \le 0.9,\,0.7 \le t \le 0.9 \}\). Let the following non-smooth function

$$\begin{aligned} f(y,t) = \left\{ \begin{array}{lll} 1, &{} \text{ if } &{} (y,t)\in \Omega \\ 0, &{} \text{ if }&{} \text{ else }, \end{array}\right. \end{aligned}$$

be the exact solution at \(x=0\).

In this example, we fix the parameters \(\delta =1\%\) and \(x=0.2\).

Figure 1 shows the noisy data \(g_\delta (y,t)\) with \(\delta =1\%\).

Fig. 1
figure 1

Noisy input data \(g_\delta (y,t)\) with \(\alpha =0.4\)

Full size image

Figure 2 shows the result by Fourier method and Method 1 with \(\delta =1\%\), \(\alpha =0.4\).

Fig. 2
figure 2

Exact solution u(x, y, t) with \(\alpha =0.4,x=0.2\)

Full size image

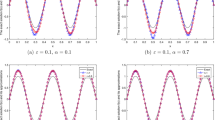
Figure 3 shows the comparison between the fractional and classical Tikhonov regularization methods. The result shows that the fractional Tikhonov method outperforms the classical one. For different \(\alpha \)-s and x-s, we find the same result.

Fig. 3
figure 3

a The classical Tikhonov method (\(\gamma =1\)) with \(\mu =1.36*10^{-5}\); b the fractional Tikhonov method (\(\gamma =1/2\)) with \(\mu =3.66*10^{-3}\)

Full size image