Domination-Related Parameters in Rooted Product Graphs

Abstract

A set S of vertices of a graph G is a dominating set in G if every vertex outside of S is adjacent to at least one vertex belonging to S. A domination parameter of G is related to those sets of vertices of a graph satisfying some domination property together with other conditions on the vertices of G. Here, we investigate several domination-related parameters in rooted product graphs.

1 Introduction

Domination in graphs constitutes a very important area in graph theory [9]. An enormous quantity of researches on domination in graphs have been developed in the recent years, especially in the last 2 years, for instance: [6, 18, 23, 24] are some of the most recent ones. Nevertheless, there are still several open problems and incoming researches on that. One interesting question in this area is related to the study of domination-related parameters in product graphs. For instance, the Vizing’s Conjecture [20, 21] is one of the most popular open problems about domination in product graphs. The Vizing’s Conjecture states that the domination number of Cartesian product graphs is greater than or equal to the product of the domination numbers of the factor graphs. Moreover, several kinds of domination-related parameters have been studied in the last years. Some of the most remarkable examples are the following ones. The domination number of direct product graphs was studied in [3, 11, 15]. The total domination number of direct product graphs was studied in [5]. The upper domination number of Cartesian product graphs was studied in [2]. The independence domination number of Kronecker product graphs was studied in [10]. Some relationships between some domination parameters of composite graphs were presented in [6]. Several domination-related parameters of corona product graphs and the conjunction of two graphs were studied in [23] and [25], respectively. The Roman domination number of lexicographic product graphs was studied in [18], and the Roman domination numbers of Cartesian product graph and strong product graph have been studied recently in [22]. According to the major quantity of works devoted to the study of domination-related parameters in product graphs, it is noted that not only Vizing’s Conjecture is an interesting topic related to domination in product graphs. In this paper, we make some contributions to the study of some domination-related parameters for the case of rooted product graphs.

We begin establishing the principal terminology and notation which we will use throughout the article. Hereafter, $G=(V,E)$ represents an undirected finite graph without loops and multiple edges with set of vertices V and set of edges E. The order of G is $|V|=n(G)$ and the size $|E|=m(G)$ (if there is no ambiguity, we will use only n and m). We denote two adjacent vertices $u,v\in V$ by $u\sim v$ and in this case, we say that uv is an edge of G or $uv\in E$. For a nonempty set $X\subseteq V$ and a vertex $v\in V$, $N_X(v)$ denotes the set of neighbors that v has in X: $N_X(v):=\{u\in X: u\sim v\}$, and the degree of v in X is denoted by $\delta _{X}(v)=|N_{X}(v)|.$ In the case $X=V$, we will use only N(v), which is also called the open neighborhood of a vertex $v\in V$, and $\delta (v)$ to denote the degree of v in G. The close neighborhood of a vertex $v\in V$ is $N[v]=N(v)\cup \{v\}$. The minimum and maximum degrees of G are denoted by $\delta$ and $\Delta$, respectively. The subgraph induced by $S\subset V$ is denoted by $\langle S\rangle$, and the complement of the set S in V is denoted by $\overline{S}$. The distance between two vertices $u,v\in V$ of G is denoted by $d_G(u,v)$ (or d(u, v) if there is no ambiguity). Given a vertex v of G, $G-v$ denotes the subgraph of G obtained by removing the vertex v and all the edges incident with v.

The set of vertices $D\subset V$ is a dominating set of G if for every vertex $v\in \overline{D}$ it is satisfied that $N_D(v)\ne \emptyset$. The minimum cardinality of any dominating set of G is the domination number of G, and it is denoted by $\gamma (G)$. A set D is a $\gamma (G)$-set if it is a dominating set and $|D|=\gamma (G)$. Throughout the article, we follow the terminology and notation of [9].

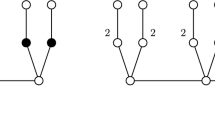
Given a graph G of order n and a graph H with root vertex v, the rooted product graph $G\circ H$ is defined as the graph obtained from G and H by taking one copy of G and n copies of H and identifying the vertex $u_i$ of G with the vertex v in the ith copy of H for every $1\le i\le n$ [8]. If G or H is the singleton graph, then $G\circ H$ is equal to H or G, respectively. In this sense, to obtain the rooted product $G\circ H$, we will only consider graphs G and H of orders greater than or equal to two. Figure 1 shows the case of the rooted product graph $P_4\circ C_3$. Hereafter, we will denote by $V=\{u_1,u_2,\ldots ,u_n\}$ the set of vertices of G and by $H_i=(V_i,E_i)$ the ith copy of H in $G\circ H$.

Fig. 1

The rooted product graph $P_4\circ C_3$

It is clear that the value of every parameter of the rooted product graph depends on the root of the graph H. In the present article, we give some results related to some domination parameters in rooted product graphs.

2 Domination Number

We begin with the following remark which will be useful into proving next results.

Lemma 1

Let G be a graph of order $n\ge 2$ and let H be any graph with root v and at least two vertices. If v does not belong to any $\gamma (H)$-set or v belongs to every $\gamma (H)$-set, then

$$\begin{aligned} \gamma (G\circ H)=n\gamma (H). \end{aligned}$$

Proof

If $A_i$ is a dominating set of minimum cardinality in $H_i=(V_i,E_i)$, $i\in \{1,\ldots ,n\}$, then it is clear that $\bigcup _{i=1}^nA_i$ is a dominating set in $G\circ H$. Thus, $\gamma (G\circ H)\le n\gamma (H)$. Suppose v does not belong to any $\gamma (H)$-set. Let S be a $\gamma (G\circ H)$-set, and let $S_i=S\cap V_i$ for every $i\in \{1,\ldots ,n\}$. Notice that the set $S_i$ dominates all the vertices of $H_i$ except maybe the root $v_i$ which could be dominated by other vertex not in $H_i$.

If $v_j\notin S_j$ for some $j\in \{1,\ldots ,n\}$, then $S_j$ is a dominating set in $H_j-v_j$. So $\gamma (H_j-v_j)\le |S_j|$. Moreover, since $v_j$ does not belong to any $\gamma (H_j)$-set, it is satisfied that $\gamma (H_j-v_j)=\gamma (H_j)$. If $|S_j|<\gamma (H)$, then we have that $\gamma (H_j-v_j)\le |S_j|<\gamma (H_j)=\gamma (H_j-v_j)$, a contradiction. On the other side, if $v_l\in S_l$ for some $l\in \{1,\ldots ,n\}$, then $S_l$ is a dominating set in $H_l$. So $\gamma (H_l)\le |S_l|$. Therefore, $|S_i|\ge \gamma (H)$ for every $i\in \{1,\ldots ,n\}$, and we obtain that $\gamma (G\circ H)=n\gamma (H)$.

On the other hand, let us suppose v belongs to every $\gamma (H)$-set. Thus, v dominates at least one vertex in H which is not dominated by any other vertex in every $\gamma (H)$-set and, as a consequence, $\gamma (H-v)\ge \gamma (H)$. As noted above, S denotes a $\gamma (G\circ H)$-set, and $S_i=S\cap V_i$ for every $i\in \{1,\ldots ,n\}$. If $v_j\notin S_j$ for some $j\in \{1,\ldots ,n\}$, then either $S_j$ is not a dominating set in $H_j$ or $|S_j|$ is not a dominating set of minimum cardinality in $H_j$. Hence, by exchanging in S, the set $S_j$ with a $\gamma (H_j)$-set (which contains $v_j$), we obtain a dominating set $S^{\prime }$ of $G\circ H$ with cardinality less than cardinality of S, a contradiction. Hence, $v_j\in S_j$ and $S_j$ is a dominating set in $H_j$, which leads to that $|S_j|\ge \gamma (H_j)$. Therefore, we have that $|S|=\sum _{i=1}^n|S_i|\ge \sum _{i=1}^n\gamma (H_i)=n\gamma (H)$ and the proof is complete. $\square$

Theorem 2

Let G be a graph of order $n\ge 2$. Then for any graph H with root v and at least two vertices,

$$\begin{aligned} \gamma (G\circ H)\in \{n\gamma (H),n(\gamma (H)-1)+\gamma (G)\}. \end{aligned}$$

Proof

It is clear that $\gamma (G\circ H)\le n\gamma (H)$ and also, from Lemma 1, there are rooted product graphs $G\circ H$ such that $\gamma (G\circ H)=n\gamma (H)$. Now, let us suppose that $\gamma (G\circ H)<n\gamma (H)$. Let V be the set of vertices of G and let $V_i$, $i\in \{1,\ldots ,n\}$, be the set of vertices of the copy $H_i$ of H in $G\circ H$. If S is a $\gamma (G\circ H)$-set, then there exists $j\in \{1,\ldots ,n\}$ such that $|S\cap V_j|<\gamma (H)$. Notice that the set $S\cap V_j$ dominates all the vertices in $V_j$ excluding $v_j$. If $|S\cap V_j|<\gamma (H)-1$, then the set $(S\cap V_j)\cup \{v_j\}$ is a dominating set in $H_j$ and $|(S\cap V_j)\cup \{v_j\}|\le |(S\cap V_j)|+1<\gamma (H)$, which is a contradiction. Hence, $|S\cap V_i|\ge \gamma (H)-1$ for every $i\in \{1,\ldots ,n\}$.

Let x be the number of copies $H_{j_1},H_{j_2},\ldots ,H_{j_x}$ of H in which the vertex $v_{j_i}$ of G is not dominated by $S\cap V_{j_i}$ (i.e., $v_{j_i}$ is dominated by a vertex of G belonging to other copy $H_l$, with $l\notin \{j_1,\ldots ,j_x\}$). On the contrary, let $y=n-x$ be the number of copies $H_{k_1},H_{k_2},\ldots ,H_{k_y}$ of H in which the vertex $v_{k_i}$ of G is dominated by $S\cap V_{k_i}$ or $v_{k_i}\in S$. Note that the y vertices $v_{k_i}$ of G satisfying the above property form a dominating set in G and, as a consequence, $\gamma (G)\le y$. Since $n=x+y$, we have that $x\le n-\gamma (G)$. Also, notice that if the vertex $v_{k_i}$ of G is dominated by $S\cap V_{k_i}$ or $v_{k_i}\in S$, then $S\cap V_{k_i}$ is a dominating set in $H_{k_i}$. Hence, $\gamma (H)\le |S\cap V_{k_i}|$ for every copy $H_{k_i}$ in which the vertex $v_{k_i}$ of G is dominated by $S\cap V_{k_i}$ or $v_{k_i}\in S$. Thus, we have the following:

$$\begin{aligned} \gamma (G\circ H)=|S|&=\left| \bigcup _{i=1}^{x}(S\cap V_{j_i})\cup \bigcup _{i=1}^{y}(S\cap V_{k_i})\right| \\&=\sum _{i=1}^{x}|S\cap V_{j_i}|+\sum _{i=1}^{y}|S\cap V_{k_i}|\\&\ge x(\gamma (H)-1)+y\gamma (H)\\&=n\gamma (H)-x\\&\ge n\gamma (H)-n+\gamma (G)\\&=n(\gamma (H)-1)+\gamma (G). \end{aligned}$$

On the other side, let A be a $\gamma (G\circ H)$-set. Since $\gamma (G\circ H)<n\gamma (H)$, there exists at least one copy $H_k$ of H such that $|A\cap V_k|<\gamma (H)$, which implies $|A\cap V_k|\le \gamma (H)-1$. Since $A\cap V_k$ dominates all the vertices of $H_k$ except maybe the root $v_k$, we have that if $v_k\in A\cap V_k$, then $A\cap V_k$ is a dominating set in H, which is a contradiction. Hence, $v_k\notin A\cap V_k$. Now, as $|A\cap V_i|\ge \gamma (H)-1$ for every $i\in \{1,\ldots ,n\}$, we obtain that $|A\cap V_k|=\gamma (H)-1$. Hence, $A^{\prime }=(A\cap V_k)\cup \{v_k\}$ is a $\gamma (H)$-set. Let us denote by $A^{\prime }_i$, $i\in \{1,\ldots ,n\}$, the set of vertices of $A^{\prime }-\{v_i\}$ in each copy $H_i$ of $G\circ H$.

Let B be a $\gamma (G)$-set and let $D=\left( \bigcup _{i=1}^nA^{\prime }_i\right) \cup B$. Since $A^{\prime }_i$ dominates the vertices of $H_i-\{v_i\}$ for every $i\in \{1,\ldots ,n\}$ and B dominates the vertices of G, we obtain that D is a dominating set in $G\circ H$. Thus,

$$\begin{aligned} |D|=\sum _{i=1}^n|A^{\prime }_i|+|B|=n(|A^{\prime }|-1)+|B|=n(\gamma (H)-1)+\gamma (G). \end{aligned}$$

Therefore, we obtain that $\gamma (G\circ H)\le n(\gamma (H)-1)+\gamma (G)$ and the result follows.

$\square$

3 Roman Domination Number

Roman domination number was defined by Stewart in [17] and studied further by some researchers, for instance in [4]. Given a graph $G=(V,E)$, a map $f : V \rightarrow \{0, 1, 2\}$ is a Roman dominating function for G if for every vertex v with $f(v) = 0$, there exists a vertex $u\in N(v)$ such that $f(u) = 2$. The weight of a Roman dominating function is given by $f(V) =\sum _{u\in V}f(u)$. The minimum weight of a Roman dominating function on G is called the Roman domination number of G and it is denoted by $\gamma _R(G)$. A function f is a $\gamma _R(G)$-function in a graph $G=(V,E)$ if it is a Roman dominating function and $f(V)=\gamma _R(G)$.

Let f be a Roman dominating function on G and let $B_0$, $B_1$ and $B_2$ be the sets of vertices of G induced by f, where $B_i = \{v\in V\;:\; f(v) = i\}$. Frequently, a Roman dominating function f is represented by the sets $B_0$, $B_1$ and $B_2$, and it is common to denote $f=(B_0,B_1, B_2)$. It is clear that for any Roman dominating function f on the graph $G=(V,E)$ of order n, we have that $f(V)=\sum _{u\in V}f(u)=2|B_2|+|B_1|$ and $|B_2|+|B_1|+|B_0|=n$. The following lemmas will be useful into proving other results in this section.

Lemma 3

[4] For any graph G, $\gamma (G)\le \gamma _R(G)\le 2\gamma (G)$.

Lemma 4

Let $G=(V,E)$ be a graph and let $f=(B_0,B_1,B_2)$ be a $\gamma _R(G)$-function. Then for every $v\in V$,

• (i) if $v\in B_0$, then $\gamma _R(G)-1\le \gamma _R(G-v)\le \gamma _R(G)$,

• (ii) if $v\in B_1$, then $\gamma _R(G-v)=\gamma _R(G)-1$,

• (iii) if $v\in B_2$, then $\gamma _R(G)-1\le \gamma _R(G-v)\le \gamma _R(G)+\delta (v)-2$.

Proof

Let $f^{\prime }=(A_0,A_1,A_2)$ be a $\gamma _R(G-v)$-function. By making $f^{\prime }(v)=1$, we have that $f^{\prime }$ is a Roman dominating function in G. Thus,

$$\begin{aligned} \gamma _R(G)\le \gamma _R(G-v)+1. \end{aligned}$$

(1)

Now, if $v\in B_0$, then it is clear that $\gamma _R(G-v)\le \gamma _R(G)$ and (i) is proved.

Moreover, if $v\in B_1$, then $(B_0,B_1-\{v\},B_2)$ is a Roman dominating function in $G-v$. Thus, $\gamma _R(G-v)\le \gamma _R(G)-1$. Therefore, by (1), we obtain (ii).

On the other hand, if $v\in B_2$, then $(B_0,B_1\cup (N(v)-B_2),B_2-\{v\})$ is a Roman dominating function in $G-v$. Thus,

$$\begin{aligned} \gamma _R(G-v)&\le 2|B_2-\{v\}|+|B_1\cup (N(v)-B_2)|\\&=2|B_2|-2+|B_1|+|N(v)-B_2|\\&\le \gamma _R(G)+\delta (v)-2. \end{aligned}$$

Therefore, (iii) is proved. $\square$

Lemma 5

Let $G=(V,E)$ be a graph. If for every $\gamma _R(G)$-function $f=(B_0,B_1,B_2)$ is satisfied that $v\in B_0$, then

$$\begin{aligned} \gamma _R(G-v)=\gamma _R(G). \end{aligned}$$

Proof

From Lemma 4 (i), we have that $\gamma _R(G-v)\le \gamma _R(G)$. If $\gamma _R(G-v)<\gamma _R(G)$, then there exists a $\gamma _R(G-v)$-function $h=(A_0,A_1,A_2)$ such that $h(V-\{v\})=\gamma _R(G-v)<\gamma _R(G)$, which leads to $h(V-\{v\})\le \gamma _R(G)-1$. If $h^{\prime }$ is a function in G such that for every $u\in V$, $u\ne v$, we have that $h^{\prime }(u)=h(u)$ and $h^{\prime }(v)=1$, then $h^{\prime }$ is a Roman dominating function in G. Thus, $\gamma _R(G)\le h^{\prime }(V)=h(V-\{v\})+1\le \gamma _R(G)$. Hence, $\gamma _R(G)=h^{\prime }(V)=h(V-\{v\})+1=\gamma _R(G)$ and, we have that $h^{\prime }$ is a $\gamma _R(G)$-function such that $h^{\prime }(v)=1$, which is a contradiction. Therefore, $\gamma _R(G-v)=\gamma _R(G)$.

$\square$

The Roman domination number of rooted product graphs is studied at next.

Theorem 6

Let G be a graph of order $n\ge 2$. Then for any graph H with root v and at least two vertices,

$$\begin{aligned} n(\gamma _R(H)-1)+\gamma (G)\le \gamma _R(G\circ H)\le n\gamma _R(H). \end{aligned}$$

Proof

It is clear that $\gamma _R(G\circ H)\le n\gamma _R(H)$. Let $V_i$ be the set of vertices of $H_i$ for every $i\in \{1,\ldots ,n\}$ and let $f=(B_0,B_1,B_2)$ be a $\gamma _R(G\circ H)$-function. Now, for every $i\in \{1,\ldots ,n\}$ and every $k\in \{0,1,2\}$, let $B^{(i)}_k=B_k\cap V_i$. Let $j\in \{1,\ldots ,n\}$. We consider the following cases.

Case 1: $v_j\in B^{(j)}_0$. If $N_{H_j}(v_j)\cap B^{(j)}_2\ne \emptyset$, then $f_j=(B^{(j)}_0-\{v_j\},B^{(j)}_1,B^{(j)}_2)$ is a Roman dominating function in $H_j-v_j$. On the contrary, if $N_{H_j}(v_j)\cap B^{(j)}_2=\emptyset$, then $v_j$ is adjacent to some vertex $v_k\in B^{(k)}_2$, with $k\ne j$ and, again $f_j=(B^{(j)}_0-\{v_j\},B^{(j)}_1,B^{(j)}_2)$ is a Roman dominating function in $H_j-v_j$. Hence, $\gamma _R(H_j-v_j)\le 2 \left| B^{(j)}_2\right| +\left| B^{(j)}_1 \right|$. By Lemma 4 (i), we have that $\gamma _R(H_j-v_j)\ge \gamma _R(H)-Hence,$. Thus, $2\left| B^{(j)}_2 \right| +\left| B^{(j)}_1\right| \ge \gamma _R(H)-1$.

Case 2: $v_j\in B^{(j)}_1$. Hence, it is clear that $f_j=(B^{(j)}_0,B^{(j)}_1-\{v_j\},B^{(j)}_2)$ is a Roman dominating function in $H_j-v_j$. Hence, $\gamma _R(H_j-v_j)\le 2\left| B^{(j)}_2\right| +\left| B^{(j)}_1\right| -1$. By Lemma 4 (ii), we have that $\gamma _R(H_j-v_j)=\gamma _R(H)-1$. Thus, $2\left| B^{(j)}_2\right| +\left| B^{(j)}_1\right| \ge \gamma _R(H)$.

Case 3: $v_j\in B^{(j)}_2$. Thus, $f_j=(B^{(j)}_0,B^{(j)}_1,B^{(j)}_2)$ is a Roman dominating function in $H_j$. Hence, $2\left| B^{(j)}_2\right| +\left| B^{(j)}_1\right| \ge \gamma _R(H)$.

Now, let V be the set of vertices of G and let $A\subseteq V\cap B_0$ be the set of vertices of G such that for every vertex $v_l\in A$ is satisfied that $N_{H_l}(v_l)\cap B^{(l)}_2=\emptyset$. Hence, every vertex $v_l\in A$ is dominated by some vertex in $(V-A)\cap B^{(k)}_2$, with $k\ne l$. As a consequence, $V-A$ is a dominating set and $\gamma (G)\le n-|A|$. Since $A\subseteq V\cap B_0$, it is satisfied that |A| equals at most the numbers of copies $H_j$ of H such that $2\left| B^{(j)}_2\right| +\left| B^{(j)}_1\right| \ge \gamma _R(H)-1$ (those copies satisfying Case 1). Thus, we have the following,

$$\begin{aligned} \gamma _R(G\circ H)&=2|B_2|+|B_1|\\&=\sum _{i=1}^n\left( 2\left| B^{(i)}_2\right| +\left| B^{(i)}_1\right| \right) \\&=\sum _{i=1}^{n-|A|}\left( 2\left| B^{(i)}_2\right| +\left| B^{(i)}_1\right| \right) +\sum _{i=1}^{|A|}\left( 2\left| B^{(i)}_2\right| +\left| B^{(i)}_1\right| \right) \\&\ge (n-|A|)\gamma _R(H)+|A|(\gamma _R(H)-1)\\&=n\gamma _R(H)-|A|\\&\ge n(\gamma _R(H)-1)+\gamma (G). \end{aligned}$$

Therefore the lower bound is proved. $\square$

As the following proposition shows, the above bounds are tight.

Theorem 7

Let G be a graph of order $n\ge 2$ and let H be a graph with root v and at least two vertices. Then,

• (i) if for every $\gamma _R(H)$-function $f=(B_0,B_1,B_2)$ is satisfied that $f(v)=0$, then

  $$\begin{aligned} \gamma _R(G\circ H)=n\gamma _R(H), \end{aligned}$$

• (ii) if there exist two $\gamma _R(H)$-functions $h=(B_0,B_1,B_2)$ and $h^{\prime }=(B^{\prime }_0,B^{\prime }_1,B^{\prime }_2)$ such that $h(v)=1$ and $h^{\prime }(v)=2$, then

  $$\begin{aligned} \gamma _R(G\circ H)=n(\gamma _R(H)-1)+\gamma (G). \end{aligned}$$

Proof

Let $f^{\prime }=(B^{\prime }_0,B^{\prime }_1,B^{\prime }_2)$ be a $\gamma _R(G\circ H)$-function and let $V_i$ be the set of vertices of $H_i$, $i\in \{1,\ldots ,n\}$. Now, for every $i\in \{1,\ldots ,n\}$, let $f_i=(B^{(i)}_0=B^{\prime }_0\cap V_i,\,B^{(i)}_1=B^{\prime }_1\cap V_i,\,B^{(i)}_2=B^{\prime }_2\cap V_i)$. From Theorem 6, we have that $\gamma _R(G\circ H)\le n\gamma _R(H)$. If $\gamma _R(G\circ H)<n\gamma _R(H)$, then there exists $j\in \{1,\ldots ,n\}$ such that $f_j(V_j)=2\left| B^{(j)}_2\right| +\left| B^{(j)}_1\right| <\gamma _R(H)$. So $f_j=(B^{(j)}_0,B^{(j)}_1,B^{(j)}_2)$ is not a Roman dominating function in $H_j$. If $f^{\prime }(v_j)=1$ or $f^{\prime }(v_j)=2$, then every vertex in $B^{(j)}_0$ is adjacent to a vertex in $B^{(j)}_2$ and, as a consequence, $(B^{(j)}_0,B^{(j)}_1,B^{(j)}_2)$ is a Roman dominating function in $H_j$, which is a contradiction. So $f^{\prime }(v_j)=0$ and $f_j=(B^{(j)}_0-\{v_j\},B^{(j)}_1,B^{(j)}_2)$ is a $\gamma _R(H_j-v_j)$-function. Since $f(v)=0$ for every $\gamma _R(H)$-function, by Lemma 5, we have that $2\left| B^{(j)}_2\right| +\left| B^{(j)}_1\right| =\gamma _R(H-v)=\gamma _R(H)$ and this is a contradiction. Therefore, $\gamma _R(G\circ H)=n\gamma _R(H)$ and (i) is proved.

To prove (ii), for every $i\in \{1,\ldots ,n\}$, we consider two $\gamma _R(H_i)$-functions $h_i=(A^{(i)}_0,A^{(i)}_1,A^{(i)}_2)$ and $h^{\prime }_i=(B^{(i)}_0,B^{(i)}_1,B^{(i)}_2)$ such that $h_i(v)=1$ and $h^{\prime }_i(v)=2$, and let S be a $\gamma (G)$-set. Now, we define a function g in $G\circ H$ in the following way.

• For every vertex x belonging to a copy $H_j$ of H such that the root $v_j\in S$, we make $g(x)=h^{\prime }(x)$ (notice that $g(v_j)=2$).

• For every vertex y, except the corresponding root, belonging to a copy $H_l$ of H such that the root $v_l\notin S$, we make $g(x)=h(x)$.

• For every root of every copy $H_l$ satisfying the conditions of the above item, we make $g(x)=0$ (note that these vertices are adjacent to a vertex w of G for which $g(w)=2$).

Since every vertex $u\in V_j$ not in G, with $g(u)=0$, is adjacent to a vertex $u^{\prime }$ such that $g(u^{\prime })=2$ and also, every vertex $v_l$ of G, with $g(v_l)=0$, is adjacent to a vertex $v_k\in S$ with $g(v_k)=2$, we obtain that g is a Roman dominating function in $G\circ H$. Thus,

$$\begin{aligned} \gamma _R(G\circ H)&\le \sum _{i=1}^{|S|}\left( 2\left| B^{(i)}_2\right| +\left| B^{(i)}_1\right| \right) +\sum _{i=1}^{n-|S|}\left( 2\left| A^{(i)}_2\right| +\left| A^{(i)}_1\right| -1\right) \\&=|S|\gamma _R(H)+(n-|S|)(\gamma _R(H)-1)\\&=n(\gamma _R(H)-1)+|S|\\&=\gamma (G)+n(\gamma _R(H)-1). \end{aligned}$$

Therefore, (ii) follows by Theorem 6. $\square$

On the other hand, we can see that there are rooted product graphs for which the bounds of Theorem 6 are not achieved.

Theorem 8

Let G be a graph of order $n\ge 2$, and let H be a graph with root v and at least two vertices. If for every $\gamma _R(H)$-function f is satisfied that $f(v)=1$, then

$$\begin{aligned} \gamma _R(G\circ H)=n(\gamma _R(H)-1)+\gamma _R(G). \end{aligned}$$

Proof

Let $f=(B_0,B_1,B_2)$ be a $\gamma _R(H)$-function and let $f^{\prime }=(B^{\prime }_0,B^{\prime }_1,B^{\prime }_2)$ be a $\gamma _R(G)$-function. Now, let us define a function h in $G\circ H$ such that if $u\ne v$, then $h(u)=f(u).$ Otherwise, $h(u)=f^{\prime }(u)$. Since $f(v)=1$ for every $\gamma _R(H)$-function, it is satisfied that every vertex x of $G\circ H$ with $h(x)=0$ is adjacent to a vertex y in $G\circ H$ with $h(y)=2$. Thus, h is a Roman dominating function in $G\circ H$, and we have that

$$\begin{aligned} \gamma _R(G\circ H)&\le (2|B^{\prime }_2|+|B^{\prime }_1|)+\sum _{i=1}^n (2|B_2|+|B_1|-1)\\&=n(\gamma _R(H)-1)+\gamma _R(G). \end{aligned}$$

On the other hand, let $V_i$, $i\in \{1,\ldots ,n\}$, be the set of vertices of the copy $H_i$ of H in $G\circ H$ and let V be the set of vertices of G. Now, let $g=(A_0,A_1,A_2)$ be a $\gamma _R(G\circ H)$-function and for every $i\in \{1,\ldots ,n\}$ let $g_i=(A^{(i)}_0=A_0\cap V_i,\,A^{(i)}_1=A_1\cap V_i,\,A^{(i)}_2=A_2\cap V_i)$. Since the root $v_i$ of $H_i$ satisfies that $f(v_i)=1$ for every $\gamma _R(H_i)$-function f, we have the following cases.

Case 1: If there exists $l\in \{1,\ldots ,n\}$ such that $g(v_l)=2$, then $g_l$ is a Roman dominating function in $H_l$, but it is not a $\gamma _R(H)$-function. Thus, $\gamma _R(H_l)<2|A^{(l)}_2|+|A^{(l)}_1|$, which leads to

$$\begin{aligned} \gamma _R(H_l)\le 2|A^{(l)}_2|+|A^{(l)}_1|-1=2|A^{(l)}_2-\{v_l\}|+|A^{(l)}_1|+1. \end{aligned}$$

Case 2: If there exists $j\in \{1,\ldots ,n\}$ such that $g(v_j)=1$, then $g_j$ is a Roman dominating function in $H_j$ and $g^{\prime }_j=(A^{(j)}_0,A^{(j)}_1-\{v_j\},A^{(j)}_2)$ is a Roman dominating function in $H_j-v_j$. Thus, by Lemma 4 (ii), it is satisfied that

$$\begin{aligned} \gamma _R(H_j)=\gamma _R(H_j-v_j)+1\le 2|A^{(j)}_2|+|A^{(j)}_1-\{v_j\}|+1. \end{aligned}$$

Case 3: If there exists $i\in \{1,\ldots ,n\}$ such that $g_i(v_i)=0$, then we have one of the following possibilities:

• $g_i$ is not a Roman dominating function in $H_i$. Hence, $v_i$ should be adjacent to a vertex $v_j$, $j\ne i$, of G such that $g_j(v_j)=2$. Moreover, $g^{\prime }_i=(A^{(i)}_0-\{v_i\},A^{(i)}_1,A^{(i)}_2)$ is a Roman dominating function in $H_i-v_i$ and by Lemma 4 (ii) it is satisfied that $\gamma _R(H_i)=\gamma _R(H_i-v_i)+1\le 2|A^{(i)}_2|+|A^{(i)}_1|+1$.

• $g_i$ is a Roman dominating function in $H_i$. Since $f(v_i)=1$ for every $\gamma _R(H_i)$-function f, we have that $g_i(V_i)>\gamma _R(H_i)$. Let $f_i$ be a $\gamma _R(H_i)$-function. Now, by taking a function $g^{\prime }$ on $G\circ H$, such that if $u\in V_i$, then $g^{\prime }(u)=f^{\prime }(u)$ and, if $u\notin V_i$, then $g^{\prime }(u)=g(u)$, we obtain that $g^{\prime }$ is a Roman dominating function for $G\circ H$ and the weight of $g^{\prime }$ is given by

  $$\begin{aligned} g^{\prime }\left( \bigcup _{j=1}^{n}V_j\right)&=g\left( \bigcup _{j=1,j\ne i}^{n}V_j\right) +f_i(V_i)\\&=g\left( \bigcup _{j=1,j\ne i}^{n}V_j\right) +\gamma _R(H_i)\\&<g\left( \bigcup _{j=1,j\ne i}^{n}V_j\right) +g_i(V_i)\\&=g\left( \bigcup _{j=1}^{n}V_j\right) \\&=\gamma _R(G\circ H). \end{aligned}$$

  and this is a contradiction.

As a consequence, we obtain that if $g_i(v_i)=0$, then $g_i$ is not a Roman dominating function in $H_i$. Hence, every vertex $v_l$ of G for which $g(v_l)=0$ is adjacent to a vertex $v_k$, $k\ne l$, of G such that $g(v_k)=2$ and it is satisfied that the function $g^{\prime }=(X_0=A_0\cap V,\,X_1=A_1\cap V,\,X_2=A_2\cap V)$ is a Roman dominating function in G and $\gamma _R(G)\le 2|X_2|+|X_1|$. Thus, we have the following:

$$\begin{aligned} \gamma _R(G\circ H)&=2|A_2|+|A_1|\\&=\sum _{v_i\in X_0}\left( 2 \left| A^{(i)}_2 \right| +\left| A^{(i)}_1\right| \right) +\sum _{v_i\in X_1}\left( 2\left| A^{(i)}_2\right| +\left| A^{(i)}_1\right| \right) \\&\quad +\sum _{v_i\in X_2}\left( 2\left| A^{(i)}_2\right| +\left| A^{(i)}_1\right| \right) \\&=\sum _{v_i\in X_0}\left( 2\left| A^{(i)}_2\right| +\left| A^{(i)}_1\right| \right) +\sum _{v_i\in X_1}\left( 2\left| A^{(i)}_2\right| +\left| A^{(i)}_1-\{v_i\}\right| \right) +\\&\quad +\sum _{v_i\in X_2}\left( 2\left| A^{(i)}_2-\{v_i\}\right| +\left| A^{(i)}_1\right| \right) +|X_1|+2|X_2|\\&\ge \sum _{v_i\in X_0}(\gamma _R(H_i)-1)\\&\quad +\sum _{v_i\in X_1}(\gamma _R(H_i)-1)+\sum _{v_i\in X_2}(\gamma _R(H_i)-1)+2|X_2|+|X_1|\\&\ge \sum _{i=1}^n(\gamma _R(H_i)-1)+\gamma _R(G)\\&=n(\gamma _R(H)-1)+\gamma _R(G). \end{aligned}$$

Therefore the result follows. $\square$

4 Independent Domination Number

A set of vertices S of a graph G is independent if the subgraph induced by S has no edges. The maximum cardinality of an independent set in G is called the independence number of G and it is denoted by $\alpha (G)$. A set S is a $\alpha (G)$-set if it is independent and $|S|=\alpha (G)$. A set of vertices D of a graph G is an independent dominating set in G if D is a dominating set and the subgraph $\langle D\rangle$ induced by D is independent in G [1]. The minimum cardinality of any independent dominating set in G is called the independent domination number of G and it is denoted by i(G). A set D is a i(G)-set if it is an independent dominating set and $|D|=i(G)$. Then, we study the independent domination number of rooted product graphs, and we begin by studying the independence number.

Lemma 9

Let v be any vertex of a graph G. If v belongs to every $\alpha (G)$-set, then $\alpha (G)\ge \alpha (G-v)+1$.

Proof

Let S be a $\alpha (G-v)$-set. Since S is still independent in G, we have $\alpha (G)\ge |S|$. If $\alpha (G)=|S|$, then S is a $\alpha (G)$-set and $v\notin S$, a contradiction. Hence, $\alpha (G)\ge \alpha (G-v)+1$. $\square$

Theorem 10

For any graph G of order $n\ge 2$ and any graph H with root v and at least two vertices,

• (i) if there is a $\alpha (H)$-set not containing the root v, then $\alpha (G\circ H)=n\alpha (H)$,

• (ii) if the root v belongs to every $\alpha (H)$-set, then $\alpha (G\circ H)=n(\alpha (H)-1)+\alpha (G)$.

Proof

Let $S_i$, $i\in \{1,\ldots ,n\}$, be a $\alpha (H_i)$-set not containing the root $v_i$. Hence, $\bigcup _{i=1}^nS_i$ is independent in $G\circ H$. Thus, $\alpha (G\circ H)\ge n\alpha (H)$. If $\alpha (G\circ H)>n\alpha (H)$, then there exists $j\in \{1,\ldots ,n\}$ such that $|S_j|>\alpha (H)$ and $S_j$ is independent, a contradiction. Therefore, $\alpha (G\circ H)=n\alpha (H)$.

On the other hand, suppose the root v belongs to every $\alpha (H)$-set. Let $A_i$ be a $\alpha (H_i)$-set and let B be a $\alpha (G)$-set. Since $v_i\in A_i$ for every $i\in \{1,\ldots ,n\}$, by taking $A=B\cup \left( \bigcup _{i=1}^n A_i-\{v_i\}\right)$, we have that A is independent in $G\circ H$. Thus,

$$\begin{aligned} \alpha (G\circ H)\ge |A|=|B|+\sum _{i=1}^n|A_i-\{v_i\}|=n(\alpha (H)-1)+\alpha (G). \end{aligned}$$

Now, let $V_i$, $i\in \{1,\ldots ,n\}$, be the set of vertices of the copy $H_i$ of H in $G\circ H$ and let V be the set of vertices of G. Let X be a $\alpha (G\circ H)$-set and let $X_i=X\cap (V_i-\{v_i\})$ for every $i\in \{1,\ldots ,n\}$ and let $Y=V\cap X$. Notice that Y and $X_i$ are independent sets. Hence, $\alpha (H_i-v_i)\ge |X_i|$ and $\alpha (G)\ge |Y|$ and by Lemma 9, we have that $|X_i|\le \alpha (H_i)-1$. Thus,

$$\begin{aligned} \alpha (G\circ H)=|Y|+\sum _{i=1}^n|X_i|\le \alpha (G)+\sum _{i=1}^n(\alpha (H_i)-1)=\alpha (G)+n(\alpha (H)-1). \end{aligned}$$

Therefore, the proof is complete. $\square$

Lemma 11

Let $G=(V,E)$ be a graph. Then for every set of vertices $A\subset V$,

$$\begin{aligned} i(G-A)\ge i(G)-|A|. \end{aligned}$$

Proof

Let us suppose $i(G-A)<i(G)-|A|$. Hence, there exists an independent dominating set $S\subset V-A$ in $G-A$ such that $|S|<i(G)-|A|$. Let $v\in A$. If $N_S(v)\ne \emptyset$, then v is independently dominated by the set S in G. On the contrary, if $N_S(v)=\emptyset$, then the set $S\cup \{v\}$ is still independent. Hence, by adding those vertices which maintain the independence in the set S, we obtain a set $S^{\prime }$ which is independent and dominating in G, and we have that $i(G)\le |S^{\prime }|\le |S|+|A|<i(G)-|A|+|A|=i(G)$, which is a contradiction. Therefore, $i(G-A)\ge i(G)-|A|$. $\square$

Lemma 12

If v does not belong to any i(G)-set, then

$$\begin{aligned} i(G-v) = i(G). \end{aligned}$$

Proof

Let S be an i(G)-set. Since $v\notin S$, S is still independent and dominating in $G-v$. Hence, $i(G-v)\le i(G)$. On the other hand, let A be an $i(G-v)$-set. Let us suppose that $|A| < i(G)$. Hence, $|A|\le i(G)-1$. If $N_{A}(v) = \emptyset$ in G, then $A\cup \{v\}$ is independent and dominating in G. Hence, $i(G)\le |A\cup \{v\}|=|A|+1\le i(G)$. Thus, $|A+\{v\}|=i(G)$ and this is a contradiction because v does not belong to any i(G)-set. On the contrary, if $N_{A}(v) \ne \emptyset$, then A is independent and dominating in G, which is a contradiction ($|A|<i(G)$). Hence, $|A|\ge i(G)$. Therefore, $i(G-v) = |A| \ge i(G)$ and the result follows. $\square$

Theorem 13

Let $G=(V,E)$ be a graph of order $n\ge 2$ and let H be a graph with root v and at least two vertices. Then

$$\begin{aligned} n(i(H)-1)+i(G)\le i(G\circ H)\le i(H)\alpha (G) + i(H-v)(n - \alpha (G)). \end{aligned}$$

Proof

Let S be an $i(G\circ H)$-set and let $S_i=S\cap V_i$, $i\in \{1,\ldots ,n\}$. If $v\in S_j$ for some $j\in \{1,\ldots ,n\}$, then $S_j$ is an independent dominating set in $H_j$. Hence, $|S_j|\ge i(H)$. On the contrary, if $v\notin S_k$ for some $k\in \{1,\ldots ,n\}$, then $S_k$ independently dominates all vertices of $H_k-v$. Hence, $S_k$ is an independent dominating set in $H_k-v$ and by Lemma 11, we have that $|S_k|\ge i(H_k-v)\ge i(H)-1$. If $|S_j|=i(H_j)-1$ for some $j\in \{1,\ldots ,n\}$, then v is not independently dominated by $S_j$. Also, if v is independently dominated by $S_l$ for some $l\in \{1,\ldots ,n\}$, then $|S_l|\ge i(H_l)$. Let $A=S\cap V$ and let $B\subset V$ be the set of vertices of G such that every vertex $u_i\in B$ is independently dominated by a vertex not in G. Notice that A is an independent dominating set in $G-B$. Hence, by Lemma 11 we have that $|A|\ge i(G-B)\ge i(G)-|B|$ and so, $|B|\ge i(G)-|A|$. Also, for every vertex $u_i\in B$, we have that $|S_i|\ge i(H_i)$, and we have the following:

$$\begin{aligned} |S|&=\sum _{i=1}^n|S_i|\\&=\sum _{i=1}^{|A|}|S_i| + \sum _{i=1}^{|B|}|S_i|+\sum _{i=1}^{n-|A|-|B|}|S_i|\\&\ge \sum _{i=1}^{|A|}i(H)+\sum _{i=1}^{|B|}i(H)+\sum _{i=1}^{n-|A|-|B|}(i(H)-1)\\&=|A|i(H)+|B|i(H)+(n-|A|-|B|)(i(H)-1)\\&=n(i(H)-1)+|A|+|B|\\&\ge n(i(H)-1)+i(G). \end{aligned}$$

Therefore, the lower bound follows.

To obtain the upper bound, let A be an independent set of maximum cardinality in G. Now, for every vertex $u_i\in A$ let $A_i$ be an independent dominating set in $H_i$. Also, for every $u_j\notin A$ let $B_j$ be an independent dominating set in $H_j-v$. Then, it is clear that $\left( \bigcup _{i=1}^{|A|}A_i\right) \cup \left( \bigcup _{j=1}^{n-|A|}B_j\right)$ is an independent dominating set in $G\circ H$. Therefore the upper bound follows. $\square$

Notice that the above bounds are tight. For instance, if G is the path graph $P_n$ and H is the star graph $S_{1,m}$, $m\ge 2$, with root v in the central vertex, (notice that $G\circ H$ is a caterpillar), then by the above theorem,

$$\begin{aligned} i(G\circ H)&\le i(S_{1,m})\alpha (P_n) + i(\overline{K_m})(n - \alpha (P_n))\\&=\left\lceil \frac{n}{2}\right\rceil +m\left( n-\left\lceil \frac{n}{2}\right\rceil \right) \\ {}&=mn-\left\lceil \frac{n}{2}\right\rceil (m-1). \end{aligned}$$

On the contrary, let S be an independent dominating set in $G\circ H$, let A be the set of vertices of $P_n$ belonging to S and let $B_i$, $i\in \{1,\ldots ,n\}$, be the set of vertices of $H_i-v$ belonging to S. If there is a copy $H_j$ of H in $G\circ H$ such that the root v of $H_j$ belongs to S, then neither any vertex of $H_j-v$ nor any neighbor of v in G belongs to S. Moreover, if for some copy $H_l$ of H in $G\circ H$ is satisfied that the root v of $H_l$ does not belong to S, then every vertex of $H_l-v$ belongs to S. Thus,

$$\begin{aligned} |S|&=|A|+ \sum _{i=1}^{n-|A|}|B_{j_i}|\\ {}&=|A|+m(n-|A|)\\ {}&=mn-|A|(m-1)\\ {}&\ge mn-\alpha (G)(m-1)\\ {}&=mn-\left\lceil \frac{n}{2}\right\rceil (m-1). \end{aligned}$$

Hence, $i(G\circ H)=mn-\left\lceil n/2\right\rceil (m-1)$ and the upper bound is tight. To see the sharpness of the lower bound, consider G as a path graph $P_n$ and the graph H obtained from the star graph $S_{1,m}$, $m\ge 2$, by subdividing an edge. Let v be the vertex of H having distance two from the central vertex of the star. If v is the root of H, then Theorem 13 leads to

$$\begin{aligned} i(G\circ H)\ge n(i(H)-1)+i(G)=n(2-1)+\left\lceil \frac{n}{3}\right\rceil =\left\lceil \frac{n}{3}\right\rceil +n. \end{aligned}$$

On the other side, let A be the set of all central vertices of all copies of the star $S_{1,m}$, used to obtain $G\circ H$. Since $i(H)=2$, we have that $|A|=n(i(H)-1)$. Let B be an independent dominating set in the path $P_n$. It is clear that $A\cup B$ is an independent dominating set in $G\circ H$. Hence, $i(G\circ H)\le n(i(H)-1)+i(G)=n+\left\lceil n/3\right\rceil$. As a consequence $i(G\circ H)= n+\left\lceil n/3\right\rceil$ and the lower bound of Theorem 13 is achieved.

Moreover, notice that there are graphs which are not attained any one of the above bounds. The next theorem is an example of that. In order to present such a result, we need to introduce some notation. Let D be a subset of vertices of a graph G, and let $v\in D$. We say that a vertex x is a private neighbor of v with respect to D if $N[x]\cap D = \{v\}$. The private neighbor set of v with respect to D is $pn[v,D] = N[v] - N[D - \{v\}]$.

Theorem 14

Let $G=(V,E)$ be a graph of order $n\ge 2$ and let H be a graph with at least two vertices and root v. Then,

• (i) if v does not belong to any i(H)-set, then $i(G\circ H)=ni(H)$,

• (ii) if v belongs to every i(H)-set S, then

  $$\begin{aligned} i(G\circ H)\le \alpha (G)i(H) + (n - \alpha (G))(|pn[v,S]| + i(H) - 1). \end{aligned}$$

Proof

(i) Let us suppose v does not belong to any i(H)-set. From Lemma 12, we have that $i(H-v)=i(H)$. Hence, Theorem 13 leads to $i(G\circ H)\le ni(H)$. Let $S^{\prime }$ be a $i(G\circ H)$-set such that $|S^{\prime }| < ni(H)$. Hence, there exists at least one copy $H_j$ of H such that $S_j = V_j\cap S^{\prime }$ and $|S_j| < i(H)$. Since $S_i$ independently dominates $V_i-v$ for every $i\in \{1,\ldots ,n\}$, we have that v is not dominated by $S_j$ in $H_j$. Thus, $S_j$ is an independent dominating set in $H_j-v$ and $i(H_j-v)\le |S_j|<i(H)$, which is a contradiction, since $i(H-v) = i(H)$. Therefore, $i(G\circ H)\ge ni(H)$, and the result follows.

(ii) Let $B_i$ be an $i(H_i)$-set, $i\in \{1,\ldots ,n\}$ and let C be an independent set of maximum cardinality in G. Let $S = \bigcup _{i = 1}^{\alpha (G)} B_i\cup \bigcup _{j=1}^{n - \alpha (G)} (pn[v,B_j] \cup B_j -\{v\})$. We will show that S is an independent dominating set of $G\circ H$.

Let $B = \bigcup _{i=1}^{n}B_i$. Notice that B is a dominating set in $G\circ H$. If $G = \overline{K_n}$, then B is also independent set in $G\circ H$. In this case, $\alpha (G) = n$, and the upper bound follows. Now let us suppose that $G\ncong \overline{K_n}$. Since the root of every copy of H belongs to B, there exists at least two roots $v_i$ and $v_j$, $i\ne j$, which are adjacent in $G\circ H$. Thus, B is not independent in $G\circ H$.

Hence, $B^{\prime } = \left( \bigcup _{i=1}^{\alpha (G)}B_i\right) \cup \left( \bigcup _{\alpha (G) + 1}^{n}(B_i - \{v\})\right)$ is independent set in $G\circ H$ and dominates every vertex in $H_i$, except $pn[v, B_i]$. Notice that $B_i-\{v\}$ is still independent in $H_i$, and also, it dominates every vertex in $H_i$, except $pn[v, B_i]$.

Therefore, we have that $i(G\circ H)\le \alpha (G)i(H) + (n - \alpha (G))(|pn[v,S]| + i(H) - 1)$ and the upper bound follows. $\square$

5 Connected Domination Number and Convex Domination Number

A set of vertices D of a graph G is a connected [16] (or convex [13]) dominating set in G if D is a dominating set and the subgraph induced by D, (or the set D) is connected (or convex) in G. The minimum cardinality of any connected (or convex) dominating set in G is called the connected (or convex) domination number of G and it is denoted by $\gamma _c(G)$ (or $\gamma _{con}(G)$). A set D is a $\gamma _c(G)$-set (or a $\gamma _{con}(G)$-set) if it is a connected (or a convex) dominating set and $|D|=\gamma _c(G)$ (or $|D|=\gamma _{con}(G)$). Then, we study the connected (or convex) domination number of rooted product graphs. We begin with connected domination. This parameter was defined by Sampathkumar and Wallikar in [16].

Theorem 15

Let G be a graph of order $n\ge 2$. Then for any graph H with at least two vertices and root v,

$$\begin{aligned} \gamma _c(G\circ H)\in \{n\gamma _c(H),n(\gamma _c(H)+1)\}. \end{aligned}$$

Proof

Since the vertex v of H is a cut vertex of $G\circ H$, the vertex v of each copy $H_i$ of H belongs to every connected dominating set of $G\circ H$. Also, the intersection of every connected dominating set of $G\circ H$ and the set of vertices of every copy of H contains a connected dominating set of H. Hence, $\gamma (G\circ H)\ge \sum _{i=1}^n\gamma _c(H)=n\gamma _c(H)$.

Hence, if v belongs to a $\gamma _c(H_i)$-set $S_i$, then by taking $S=\bigcup _{i=1}^n S_i$ we have that S is a connected dominating set. Hence, $\gamma _c(G\circ H)\le \sum _{i=1}^n|S_i|=n\gamma _c(H)$. Therefore, $\gamma _c(G\circ H)=n\gamma _c(H)$.

Now, let us suppose that $\gamma _c(G\circ H)\ne n\gamma _c(H)$. Hence, v does not belong to any $\gamma _c(H_i)$-set $S_i$. Let S be a $\gamma _c(G\circ H)$-set. If $|S|< n\gamma _c(H)$, then there exists a copy $H_l$ of H in $G\circ H$ in which $|S\cap V_l|<\gamma _c(H)$ and $S\cap V_l$ is a connected dominating set in H, which is a contradiction. Hence, $|S|>n\gamma _c(H)$ and there exists a copy $H_j$ of H such that $|S\cap V_j|>\gamma _c(H)$. Since the root v of H does not belong to any $\gamma _c(H)$-set, and also v belongs to every $\gamma _c(G\circ H)$-set, we obtain that

$$\begin{aligned} |S|=\sum _{i=1}^n|S\cap V_i|+|V|\ge n\gamma _c(H)+n=n(\gamma _c(H)+1). \end{aligned}$$

On the other hand, let $S_i$ be a $\gamma _c(H_i)$-set, $i\in \{1,\ldots ,n\}$. Since v does not belong to any $\gamma _c(H)$-set, it is satisfied that $v\notin S_i$ for every $i\in \{1,\ldots ,n\}$. Thus, by taking the set $S=V\cup \left( \bigcup _{i=1}^{n}S_i\right)$, we have that S is a connected dominating set and, as a consequence,

$$\begin{aligned} \gamma _c(G\circ H)\le |S|=\sum _{i=1}^n|S_i|+|V|=n\gamma _c(H)+n=n(\gamma _c(H)+1). \end{aligned}$$

Therefore, the result follows. $\square$

Next, we study the connected domination number of some particular cases of rooted product graphs. We denote by $n_1(G)$ the number of end vertices (vertices of degree one) in G and by $\Omega (G)$ the set of end vertices in G;  $|\Omega (G)|=n_1(G).$

Lemma 16

[16] If T is a tree of order at least three, then $\gamma _c(T)=n(T)-n_1(T).$

Lemma 17

If G is a connected graph, H is a tree of order at least three, and the root v is not an end vertex of H,  then $\gamma _c(G\circ H)=n\gamma _c(H).$

Proof

Since the root of the graph H is a cut vertex in the graph $G\circ H,$ we have that root of each copy $H_i$ of H belongs to every connected dominating set of $G\circ H$. Also, the intersection of every connected dominating set of $G\circ H$ and the set of vertices of every copy of H contains a connected dominating set of H. Hence, $\gamma _c(G\circ H)\ge \sum _{i=1}^n\gamma _c(H)=n\gamma _c(H)$. Let D be a connected dominating set of $G\circ H.$ Since H is a tree, from Lemma 16, not any end vertex belongs to any minimum connected dominating set of H and $\gamma _c(H)=n(H)-n_1(H).$ Also, for every $H_i,$ $\gamma _c(H_i)=n(H_i)-n_1(H_i).$ Since v is not an end vertex of H,  we have that $|D|=|V\cup \sum _{i=1}^n(V_i-\Omega _i)|.$ Thus, $\gamma _c(G\circ H)\le |D|=n \gamma (H)$ and we are done. $\square$

Lemma 18

If $T_1, T_2$ are trees of order at least three, then $T_1 \circ T_2$ is also a tree of order $n(T_1\circ T_2)=n(T_1)n(T_2)$. Moreover, $n_1(T_1\circ T_2)\in \{n(T_1)n_1(T_2), n(T_1)(n_1(T_2)-1)\}.$

Proof

For a graph $T_1\circ T_2$ is $n(T_1\circ T_2)=n(T_1)+ n(T_1)(n(T_2)-1)=n(T_1)n(T_2).$ If a root vertex v is an end vertex of $T_2,$ then $n_1(T_1\circ T_2)= n(T_1)(n_1(T_2)-1).$ On the contrary, if v is not an end vertex of $T_2,$ then $n_1(T_1\circ T_2)= n(T_1)n_1(T_2).$ $\square$

Theorem 19

Let $T_1, T_2$ be trees of order at least three. Then $\gamma _c(T_1\circ T_2)=n(T_1) \gamma _{c}(T_2)$ if and only if the rooted vertex v of $T_2$ is not an end vertex of $T_2$.

Proof

From Lemma 16, we have $\gamma _c(T_1 \circ T_2)=n(T_1\circ T_2)-n_1(T_1\circ T_2).$ Also, from Lemma 18, we have $n(T_1\circ T_2)=n(T_1)n(T_2).$ Let v be a non end vertex of $T_2$. Hence, $n_1(T_1\circ T_2)=n(T_1)n_1(T_2).$ Thus, $\gamma _c(T_1 \circ T_2)=n(T_1)n(T_2)-n_1(T_2)n(T_1)$ $=n(T_1)(n(T_2)-n_1(T_2))=n(T_1)\gamma _c(T_2).$

Assume now $\gamma _c(T_1\circ T_2)=n(T_1) \gamma _{c}(T_2)$ and suppose v is an end vertex of $T_2.$ Hence, we have $n_1(T_1 \circ T_2)=(n_1(T_2)-1)n(T_1)=n_1(T_2)n(T_1)-n(T_1).$ Since $n(T_1\circ T_2)=n(T_1)n(T_2),$ we have $\gamma _c(T_1\circ T_2)=n(T_1)n(T_2)-(n_1(T_2)n(T_1)-n(T_1))$ $=n(T_1)(n(T_2)-n_1(T_2)+1)=n(T_1)(\gamma _c(T_2)+1),$ what gives a contradiction. $\square$

From Theorems 15 and 19, we can conclude the following:

Corollary 20

$\gamma _c(T_1\circ T_2)=n(T_1)(\gamma _c(T_2)+1)$ if and only if the root v of $T_2$ is an end vertex of $T_2$.

Convex domination was defined by Topp in [19] and it was first characterized in [13]. Notice that for the case of the convex domination number of $G\circ H$, the result is similar to Theorem 15 about connected domination. The proofs of the following results are omitted due to the analogy with the above ones.

Theorem 21

Let G be a graph of order $n\ge 2$. Then for any graph H with root v and at least two vertices,

$$\begin{aligned} \gamma _{con}(G\circ H)\in \{n\gamma _{con}(H),n(\gamma _{con}(H)+1)\}. \end{aligned}$$

Theorem 22

If $T_1, T_2$ are trees, then $\gamma _{con}(T_1\circ T_2)=n(T_1) \gamma _{con}(T_2)$ if and only if the root v of $T_2$ is not an end vertex of $T_2$.

Corollary 23

$\gamma _{con}(T_1\circ T_2)=n(T_1)(\gamma _{con}(T_2)+1)$ if and only if the root of $T_2$ is an end vertex.

5.1 Weakly Connected Domination Number

Now, we consider the weakly connected domination number of rooted product graphs. A dominating set $D\subset V(G)$ is a weakly connected dominating set in G if the subgraph $G[D]_{w}=(N_{G}[D],E_{w})$ (also called subgraph weakly induced by D) is connected, where $E_{w}$ is the set of all edges having at least one vertex in D. Dunbar et al. [7] defined the weakly connected domination number $\gamma _{w}(G)$ of a graph G to be the minimum cardinality among all weakly connected dominating sets in G.

Theorem 24

Let G be a graph of order $n\ge 2$. Then for any graph H with at least two vertices and root v,

$$\begin{aligned} \gamma _w(G\circ H)\in \{n\gamma _w(H), n\gamma _w(H)+\gamma _w(G)\}. \end{aligned}$$

Proof

Let $D_H$ be a minimum weakly connected dominating set of H and $D_{H_i}$ be the copy of $D_H$ in the ith copy $H_i$ of $H, 1\le i\le n.$ Let D be a minimum weakly connected dominating set of $G\circ H.$ We consider two cases.

• 1. $v \in D_H.$ Then, the identified vertices belong to a minimum weakly connected dominating set of $G\circ H$ and $\gamma _w(G\circ H)=n \gamma _w(H).$

• 2. $v\notin D_H.$ Then $\bigcup _{i=1}^n D_{H_i}\subset D$ and the identified vertices are dominated by $\bigcup _{i=1}^n D_{H_i}.$ But the set $\bigcup _{i=1}^n D_{H_i}$ is not weakly connected. To make this set weakly connected, we need to add to this set $\gamma _w(G)$ vertices. Hence, $\gamma _w(G\circ H)=|D|=|\bigcup _{i=1}^n D_{H_i}|+\gamma _w(G)=n\gamma _w(H)+\gamma _w(G)$. $\square$

The following lemma presented in [14] will be useful into obtaining some interesting results.

Lemma 25

[14] For any tree T of order $n\ge 3$,

$$\begin{aligned} \frac{1}{2}(n-n_1(T)+1)\le \gamma _w(T)\le n-n_1(T). \end{aligned}$$

Theorem 26

If $T_1,T_2$ are trees and v is not an end vertex of $T_2$, then

$$\begin{aligned} \frac{1}{2}(n_1(T_1)\gamma _w(T_2)+1)\le \gamma _w(T_1\circ T_2)\le n_1(T_1)(2 \gamma _w(T_2)-1). \end{aligned}$$

Proof

From Lemma 25, $(1/2)(n(T_1\circ T_2)-n_1(T_1\circ T_2)+1)\le \gamma _w(T_1\circ T_2)\le n(T_1\circ T_2)-n_1(T_1\circ T_2).$ Thus, from Lemma 18, we have $(1/2)(n(T_1)n(T_2)-n(T_1)n_1(T_2)+1)\le \gamma _w(T_1\circ T_2)\le n_1(T_1)(n(T_2)-n_1(T_2)).$ We have $\gamma _w(T_1\circ T_2)\le n_1(T_1)(n(T_2)-n_1(T_2))=n_1(T_1)2 (1/2)(n(T_2)-n_1(T_2))=$ $n_1(T_1) 2 (1/2)(n(T_2)-n_1(T_2)+1-1)\le n_1(T_1) 2 \gamma _w(T_2)-n_1(T_1)=n_1(T_1)(2 \gamma _w(T_2)-1).$ From the other side, we have $\gamma _w(T_1\circ T_2)\ge (1/2)(n_1(T_1)(n(T_2)-n_1(T_2))+1)\ge (1/2)(n_1(T_1)\gamma _w(T_2)+1)$, and finally we obtain the desired result. $\square$

By using similar methods, we obtain the following result:

Theorem 27

Let $T_1$ be a tree of order $n(T_1)$. If v is a non-end vertex of a tree $T_2$, then

$$\begin{aligned} \frac{1}{2}(\gamma _w(T_2)n(T_1)+1)\le \gamma _w(T_1\circ T_2)\le 2 n(T_1)\gamma _w(T_2). \end{aligned}$$

5.2 Super Domination Number

We continue with the super domination number of the rooted product graph. This parameter was defined in [12]. A subset D of V is called a super dominating set if for every $v\in V-D$ there exists $u\in N_G(v)\cap D$ such that $N_G(u)\subseteq D\cup \{v\}.$ The minimum cardinality of a super dominating set is called the super domination number of G, and it is denoted by $\gamma _{sp}(G)$. In [12], a paper has proven the following result:

Lemma 28

[12] For any tree of order $n\ge 3$, $n/2\le \gamma _{sp}(T)\le n-s(T),$ where s(T) is the number of support vertices in T.

Theorem 29

Let G be a graph of order $n\ge 2$. Then for any graph H with root v and at least two vertices,

$$\begin{aligned} \gamma _{sp}(G\circ H)= n\gamma _{sp}(H). \end{aligned}$$

Proof

Let $D_H$ be a minimum super dominating set of H and $D_{H_i}$ be the copy of $D_H$ in the $i^{th}$ copy $H_i$ of $H, 1\le i\le n.$ Let D be a minimum super dominating set of $G\circ H.$ We consider two cases as follows:

• 1. $v\in D_H.$ Then identified vertices belong to a minimum super dominating set of $G\circ H$ and $\gamma _{sp}(G\circ H)=n \gamma _{sp}(H).$

• 2. $v\notin D_H.$ Then $\bigcup _{i=1}^n D_{H_i}\subset D$ and identified vertices are dominated by $\bigcup _{i=1}^n D_{H_i}.$ Also, every vertex belonging to $\bigcup _{i=1}^n V_i - \bigcup _{i=1}^nD_{H_i} - U,$ where U is the set of identified vertices is super dominated by $\bigcup _{i=1}^n D_{H_i}.$ Suppose there exists a vertex $u\in U$ which is not super dominated by $\bigcup _{i=1}^n D_{H_i}.$ Then for a vertex u, there does not exist any $v\in \bigcup _{i=1}^n D_{H_i}$ such that $N_{G\circ H}(v)\subseteq \bigcup _{i=1}^n D_{H_i}.$ Hence, there is $1\le i \le n$ such that in $H_i$, there exists a vertex which is not super dominated, a contradiction. Thus, $\bigcup _{i=1}^n D_{H_i}$ is a minimum super dominating set of $G\circ H$ and $\gamma _{sp}(G\circ H)=|\bigcup _{i=1}^n D_{H_i}|=n\gamma _{sp}(H).$ $\square$

Now, by using Lemma 28 result, we can prove the following:

Theorem 30

If $T_1, T_2$ are trees of order $n(T_1)\ge 3$ and $n(T_2)\ge 3$, respectively, then

$$\begin{aligned} n(T_1)s(T_2)\le \gamma _{sp}(T_1\circ T_2)\le n(T_1)(n(T_2)-s(T_2)). \end{aligned}$$

Proof

If a root v is a support vertex of $T_2,$ then $s(T_1\circ T_2)=n(T_1)+(s(T_2)-1)n(T_1)=n(T_1)s(T_2).$ If v is not a support vertex, then also $s(T_1\circ T_2)=n(T_1)s(T_2).$ The upper bound follows directly from Lemma 28. For the lower bound, we have $\gamma _{sp}(T_1\circ T_2)\le 2 \gamma _{sp}(T_1\circ T_2)-n(T_1)s(T_2)$, which leads to the result. $\square$