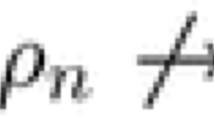Normal Families and Shared Values of Meromorphic Functions

Abstract

Let a and b be two given meromorphic functions on a domain D. We study normality of the family $\mathcal {F}$ of meromorphic functions that satisfy $f(z)f ^{(k)}(z) = a(z) \Leftrightarrow f^{(k)}(z) = b(z)$ for every $f\in \mathcal {F}$ on D. Examples are also given to show the necessity of the conditions in our results.

1 Introduction and Main Result

Let $\mathcal {F}$ be a family of meromorphic functions on a domain $D\subset {\mathbb {C}}$. Then $\mathcal {F}$ is said to be normal on D in the sense of Montel, if each sequence of $\mathcal {F}$ contains a subsequence which converges spherically uniformly on each compact subset of D to a meromorphic function which may be $\infty$ identically. See [1–3].

For two functions f and g meromorphic on D, and two complex numbers or meromorphic functions a and b, we write $f(z)=a(z)\Rightarrow {g(z)=b(z)}$ if $g(z)=b(z)$ whenever $f(z)=a(z)$, and write $f(z)=a(z)\Leftrightarrow {g(z)=b(z)}$ if $f(z)=a(z)$ if and only if $g(z)=b(z)$. When a is a complex value and $f(z)=a\Leftrightarrow {g(z)=a}$, we also say that f and g share the value a or a is a shared value of f and g. For families of meromorphic functions, the connection between normality and shared values has been studied frequently following Schwick’s initial paper [4]. Some recent results in this area appear in [5–9].

The starting point of this paper is the following result.

Theorem A

[10, Theorem 2] Let $\mathcal {F}$ be a family of meromorphic functions on a domain D, k be a positive integer, and let $a\ne 0$ and b be two finite values. If, for every $f\in \mathcal {F}$, all zeros of f have multiplicity at least k and $f(z)f ^{(k)}(z) = a \Leftrightarrow f^{(k)}(z) = b$, then the family $\mathcal {F}$ is normal on D.

In this paper, we prove the following result.

Theorem 1.1

Let k be a positive integer, and let $a(z)(\not \equiv 0)$ and b(z) be two functions meromorphic on D such that

• (i) all zeros of a have multiplicity at most $k-1$ and all poles of a have multiplicity at most k;

• (ii) each pole of b that is not a zero of a has multiplicity at most $\lceil \frac{k}{2}\rceil -1$; and each pole of b that is a zero of a with multiplicity m has multiplicity at most $\lceil \frac{k-m}{2}\rceil -1$.

Then the family $\mathcal {F}$ of meromorphic functions on a domain D, all of whose zeros have multiplicity at least k, such that $f(z)f ^{(k)}(z) = a(z) \Leftrightarrow f^{(k)}(z) = b(z)$ for every $f\in \mathcal {F}$, is normal on D.

Here, $\lceil x \rceil$ denotes the smallest integer that is not less than x. For example, $\lceil 2.1 \rceil =3$ and $\lceil 2 \rceil =2$.

Example 1.1

Let $D=\{z:|z|<1\}$ and $\mathcal {F}=\{f_n\}$, where

$$\begin{aligned} f_n(z)=e^{nz}-\frac{1}{n}. \end{aligned}$$

Then $f_n'(z)=ne^{nz}$, and $f_n(z)f_n'(z)=n\left( e^{nz}-\frac{1}{n}\right) e^{nz}$. It follows that $f_n(z)f_n'(z)=0\Leftrightarrow f_n'(z)=1$, but $\mathcal {F}$ is not normal at 0. This shows that the condition $a(z)\not \equiv 0$ is necessary in Theorem 1.1.

Example 1.2

Let $D=\{z:|z|<1\}$ and $\mathcal {F}=\{f_n\}$, where

$$\begin{aligned} f_n(z)=z+\frac{1}{nz}, \end{aligned}$$

and let $a(z)=z$ and $b=1$. We see that $f_n'(z)=1-\frac{1}{nz^2}\ne 1$ and $f_n(z)f_n'(z)=z\left( 1-\frac{1}{n^2z^4}\right) \ne z$. So for every $f_n\in \{f_n\}$ satisfies that $f_n(z)f_n'(z) = a(z) \Leftrightarrow f_n'(z) = b(z)$. But $\mathcal {F}$ is not normal at 0. This shows that the condition that every zero of a has multiplicity at most $k-1$ (at least for $k=1$) is sharp in Theorem 1.1.

Example 1.3

Let $D=\{z:|z|<1\}$ and $\mathcal {F}=\{f_n\}$, where $f_n(z)=nz^{k+1}$, and let $a(z)=z^{k+2}$ and $b(z)=z$. We see that $f_n^{(k)}(z)=n(k+1)!z$ and $f_n(z)f_n^{(k)}(z)=n^2(k+1)!z^{k+2}$. So for every $f_n\in \{f_n\}$ satisfies that $f_n(z)f_n^{(k)}(z) = a(z) \Leftrightarrow f_n^{(k)}(z) = b(z)$. But $\mathcal {F}$ is not normal at 0. This shows that the condition that every zero of a has multiplicity at most $k-1$ is necessary in Theorem 1.1.

Example 1.4

Let $D=\{z:|z|<1\}$ and $\mathcal {F}=\{f_n\}$, where $f_n(z)=1/nz$, and let $a(z)=1/z^{k+2}$ and $b=1/z^{k+1}$. We see that $f_n^{(k)}(z)=(-1)^kk!/nz^{k+1}$ and $f_n(z)f_n'(z)=(-1)^kk!/n^2z^{k+2}$. So for every $f_n\in \{f_n\}$ satisfies that $f_n(z)f_n'(z) = a(z) \Leftrightarrow f_n'(z) = b(z)$. But $\mathcal {F}$ is not normal at 0. This shows that the condition that every pole of a has multiplicity at most k is necessary in Theorem  1.1.

2 Some Lemmas

In order to prove our theorem, we require the following results. We assume the standard notations of value distribution theory, as presented and used in [2]. In particular, we write on D to denote that the sequence $\{f_n\}$ converges spherically locally uniformly to f on D and denote $f_n\rightarrow f$ on D if the convergence is in Euclidean metric.

Lemma 2.1

([11, Theorem 2]; [12, Lemma 2]) Let $\mathcal {F}$ be a family of functions meromorphic on D, all of whose zeros have multiplicity at least k. Then if $\mathcal {F}$ is not normal at some point $z_0$ in D, there exist, for each $0\le \alpha <k$, points $z_n$ in D with $z_n\rightarrow z_0$, positive numbers $\rho _n\rightarrow 0$ and functions $f_n\in \mathcal {F}$ such that on $\mathbb {C}$, where g is a nonconstant meromorphic function on $\mathbb {C}$, all of whose zeros have multiplicity at least k, such that $g^{\sharp }(\zeta )\le {g^{\sharp }(0)}=1$. In particular, g has order at most two.

Here, as usual, $g^\sharp (\zeta )= |g'(\zeta )|/(1 + |g(\zeta )|^2)$ is the spherical derivative.

Lemma 2.2

[10, Lemmas 9 and 10] Let g be a nonconstant meromorphic function in $\mathbb {C}$, and a be a nonzero constant. If all zeros of g have multiplicity at least k and $g^{(k)}\ne 0$, then the equation $gg^{(k)}=a$ has solutions on $\mathbb {C}$, where k is a positive integer.

Lemma 2.3

[13, Lemma 8] Let f be a nonpolynomial rational function such that $f'(z)\not =1$ for $z\in \mathbb {C}$. Then

$$\begin{aligned}f(z)=z+c+\frac{a}{(z+b)^m},\end{aligned}$$

where $a\not =0,b,c$ are constants and m is a positive integer.

Lemma 2.4

[14, Theorem 1.1] Let g be a transcendental meromorphic function on $\mathbb {C}$, and $R\not \equiv 0$ be a rational function. If all zeros and poles of g are multiple except possibly finitely many, then $g'-R$ has infinitely many zeros on $\mathbb {C}$.

Lemma 2.5

Let $k\ge 2$ and m be two integers, and let g be a meromorphic function on $\mathbb {C}$, all of whose zeros have multiplicity at least k. If $g(\zeta )g^{(k)}(\zeta )\ne \gamma \zeta ^m$ on $\mathbb {C}\setminus \{0\}$ and $g^{(k)}(\zeta )\ne 0$ on $\mathbb {C}\setminus \{0\}$, where $\gamma$ is a given nonzero constant, then $m\ge k$ or $m\le -(k+2)$, and g must be a rational function of the form $g(\zeta )=C\zeta ^{\frac{m+k}{2}}$ for some nonzero constant C.

Proof

Without loss of generality, we may assume that $\gamma =1$. If not, we can use $G(\zeta )=\gamma ^{-\frac{1}{2}}g$ to replace g. The conditions guarantee that all zeros of g, possibly except $\zeta =0$, have multiplicity k exactly.

Suppose first that g is transcendental. Then by Nevanlinna’s second fundamental theorem, we have

$$\begin{aligned} T\left( r,\frac{gg^{(k)}}{\zeta ^m}\right)&\le \overline{N}\left( r,\frac{gg^{(k)}}{\zeta ^m}\right) + \overline{N}\left( r,\frac{1}{\frac{gg^{(k)}}{\zeta ^m}}\right) + \overline{N}\left( r,\frac{1}{\frac{gg^{(k)}}{\zeta ^m}-1}\right) +S(r,g)\nonumber \\&= \overline{N}(r,g)+\overline{N}\left( r,\frac{1}{g}\right) +S(r,g). \end{aligned}$$

(2.1)

where $S(r,g) = o(T(r, g))$ as $r\rightarrow \infty$, possibly outside a set of finite measure. On the other hand, we have by Nevanlinna’s first fundamental theorem

$$\begin{aligned} T\left( r,\frac{gg^{(k)}}{\zeta ^m}\right)&\ge {N}\left( r,\frac{gg^{(k)}}{\zeta ^m}\right) \ge N(r,g)+N(r,g^{(k)})+S(r,g)\nonumber \\&= 2N(r,g)+k\overline{N}(r,g)+S(r,g)\nonumber \\&\ge (k+2)\overline{N}(r,g)+S(r,g) \end{aligned}$$

(2.2)

and

$$\begin{aligned} T\left( r,\frac{gg^{(k)}}{\zeta ^m}\right)&\ge {N}\left( r,\frac{\zeta ^m}{gg^{(k)}}\right) \ge N\left( r,\frac{1}{g}\right) +N\left( r,\frac{1}{g^{(k)}}\right) +S(r,g)\nonumber \\&=k\overline{N}\left( r,\frac{1}{g}\right) +S(r,g). \end{aligned}$$

(2.3)

Then by (2.1)–(2.3), we have

$$\begin{aligned} T\left( r,\frac{gg^{(k)}}{\zeta ^m}\right) \le \left( \frac{1}{k+2}+\frac{1}{k}\right) T\left( r,\frac{gg^{(k)}}{\zeta ^m}\right) +S(r,g). \end{aligned}$$

(2.4)

Since $k\ge 2$, we see from (2.4) that

$$\begin{aligned} T\left( r,\frac{gg^{(k)}}{\zeta ^m}\right) =S(r,g). \end{aligned}$$

(2.5)

Then by (2.2) and (2.3), we have

$$\begin{aligned} N(r,g)=S(r,g),\ N\left( r,\frac{1}{g}\right) =S(r,g). \end{aligned}$$

Thus

$$\begin{aligned} T\left( r,\frac{g}{g^{(k)}}\right) =T\left( r,\frac{g^{(k)}}{g}\right) +O(1)= N\left( r,\frac{g^{(k)}}{g}\right) +S(r,g)=S(r,g), \end{aligned}$$

(2.6)

and hence by (2.5) and (2.6),

$$\begin{aligned} 2T(r,g)=T\left( r,\zeta ^m\cdot \frac{gg^{(k)}}{\zeta ^m}\cdot \frac{g}{g^{(k)}}\right) =S(r,g). \end{aligned}$$

This is a contradiction. Hence there is no transcendental function that satisfies the conditions of the lemma. $\square$

Now we consider the case that g is a rational function.

Case 1. g has at least one nonzero pole. We denote by $\zeta _i(i=1,2,\ldots ,n)$ all distinct poles of g on $\mathbb {C}\setminus \{0\}$, and $p_i(i=1,2,\ldots ,n)$ their corresponding multiplicities. Since $g^{(k)}(\zeta )\ne 0$ on $\mathbb {C}\setminus \{0\}$, $g^{(Ak)}$ has the form

$$\begin{aligned} g^{(k)}(\zeta )=\frac{{\uplambda }\zeta ^s}{\prod _{i=1}^n(\zeta -\zeta _i)^{p_i+k}}, \end{aligned}$$

(2.7)

where $s\in \mathbb {Z}$ is an integer and ${\uplambda }$ is a nonzero constant. And since $g(\zeta )g^{(k)}(\zeta )\ne \zeta ^m$ on $\mathbb {C}\setminus \{0\}$, we have

$$\begin{aligned} g(\zeta )g^{(k)}(\zeta )=\zeta ^m+\frac{\mu \zeta ^l}{\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}} =\frac{\zeta ^m\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}+\mu \zeta ^l}{\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}} \end{aligned}$$

(2.8)

for some integer $l\in \mathbb {Z}$ and nonzero constant $\mu$. So, by (2.7) and (2.8),

$$\begin{aligned} g(\zeta )=\frac{\zeta ^m\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}+\mu \zeta ^l}{{\uplambda }\zeta ^s\prod _{i=1}^n(\zeta -\zeta _i)^{p_i}}. \end{aligned}$$

(2.9)

Next, we consider three cases according to $m>l$, $m=l$ and $m<l$.

Case 1.1. Suppose that $m>l$. Then as all zeros of g, possibly except $\zeta =0$, have multiplicity k exactly, we see from (2.9) that all zeros of the polynomial

$$\begin{aligned} P_1(\zeta )=\zeta ^{m-l}\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}+\mu \end{aligned}$$

on $\mathbb {C}\setminus \{0\}$, and hence on $\mathbb {C}$ since $P_1(0)=\mu \ne 0$, have exact multiplicity $k\ge 2$. This shows that $P_1$ has

$$\begin{aligned} \tau _1=\frac{\deg P_1}{k}=\frac{m-l+\sum _{i=1}^n(2p_i+k)}{k}>n \end{aligned}$$

distinct zeros, and each zero of $P_1$ is a zero of $P_1'$ with multiplicity $k-1$. By computation, we have

$$\begin{aligned} P_1'(\zeta )&=\zeta ^{m-l-1}\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k-1}\Bigg [(m-l)\prod _{i=1}^{n}(\zeta -\zeta _i) +\zeta \sum _{i=1}^n(2p_i+k)\\&\quad \; \times \prod _{j\ne i}(\zeta -\zeta _j)\Bigg ]. \end{aligned}$$

Since $P_1(\zeta _i)\ne 0$ and $P_1(0)\not =0$, it follows that the polynomial

$$\begin{aligned} Q_1(\zeta )=(m-l)\prod _{i=1}^{n}(\zeta -\zeta _i) +\zeta \sum _{i=1}^n(2p_i+k)\prod _{j\ne i}(\zeta -\zeta _j) \end{aligned}$$

has at least $\tau _1$ distinct zeros with multiplicity $k-1$. Thus,

$$\begin{aligned} n=\deg Q_1\ge (k-1)\tau _1>(k-1)n. \end{aligned}$$

This is impossible, since $k\ge 2$.

Case 1.2. Suppose that $m=l$. Then as showed in Case 1.1, all zeros of the polynomial

$$\begin{aligned} P_2(\zeta )=\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}+\mu \end{aligned}$$

on $\mathbb {C}\setminus \{0\}$ have exact multiplicity $k\ge 2$. Denote by $\alpha$ the multiplicity if 0 is a zero of $P_2$, and say $\alpha =0$ if $P_2(0)\not =0$. This shows that $P_2$ has

$$\begin{aligned} \tau _2=\frac{\deg P_2-\alpha }{k}=\frac{\sum _{i=1}^n(2p_i+k)-\alpha }{k} \end{aligned}$$

distinct zeros on $\mathbb {C}\setminus \{0\}$, and each zero of $P_2$ on $\mathbb {C}\setminus \{0\}$ is a zero of $P_2'$ with multiplicity $k-1$. By computation, we have

$$\begin{aligned} P_2'(\zeta )=\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k-1}Q_2(\zeta ),\ \text{ where }\ Q_2(\zeta )=\sum _{i=1}^n(2p_i+k)\prod _{j\ne i}(\zeta -\zeta _j). \end{aligned}$$

Since $P_2(\zeta _i)\ne 0$, the polynomial $Q_2$ has at least $\tau _2$ distinct zeros on $\mathbb {C}\setminus \{0\}$ with multiplicity $k-1$. Further, if $\alpha \ge 2$, then 0 is a zero of $Q_2$ with multiplicity $\alpha -1$. Let $\beta =\alpha -1$ if $\alpha \ge 2$, and $\beta =0$ if $\alpha =0$ or $\alpha =1$. Thus, we see that

$$\begin{aligned} n-1= & {} \deg Q_2\ge (k-1)\tau _2+\beta = \frac{k-1}{k}\sum _{i=1}^n(2p_i+k)+\beta -\frac{k-1}{k}\alpha \\\ge & {} \frac{(k-1)(k+2)n}{k}+\beta -\alpha . \end{aligned}$$

Then we have

$$\begin{aligned} \alpha -1\ge \frac{k^2-2}{k}n+\beta >\beta , \end{aligned}$$

which is a contradiction.

Case 1.3. Suppose that $m<l$. Then as showed in Case 1.1, all zeros of the polynomial

$$\begin{aligned} P_3(\zeta )=\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}+\mu \zeta ^{l-m} \end{aligned}$$

on $\mathbb {C}\setminus \{0\}$ have exact multiplicity $k\ge 2$. Note that $P_3(0)\ne 0$. This shows that $P_3$ has

$$\begin{aligned} \tau _3=\frac{\deg P_3}{k} \end{aligned}$$

distinct zeros on $\mathbb {C}\setminus \{0\}$, and each zero of $P_3$ is a zero of $P_3'$ with multiplicity $k-1$. By computation, we have

$$\begin{aligned} \left( \zeta ^{m-l}P_3(\zeta )\right) '=\zeta ^{m-l-1}\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k-1}Q_3(\zeta ), \end{aligned}$$

where

$$\begin{aligned} Q_3(\zeta )=(m-l)\prod _{i=1}^{n}(\zeta -\zeta _i) +\zeta \sum _{i=1}^n(2p_i+k)\prod _{j\ne i}(\zeta -\zeta _j). \end{aligned}$$

Since $P_3(\zeta _i)\ne 0$ and $P_3(0)\not =0$, it follows that the polynomial $Q_3$ has at least $\tau _3$ distinct zeros with multiplicity $k-1$. Thus,

$$\begin{aligned} \deg Q_3\ge (k-1)\tau _3. \end{aligned}$$

(2.10)

If $\deg P_3\ge \sum _{i=1}^n(2p_i+k)$, then $\tau _3\ge \sum _{i=1}^n(2p_i+k)/k\ge (k+2)n/k$. This, together with (2.10) and the fact $\deg Q_3\le n$, leads to a contradiction.

Thus $\deg P_3<\sum _{i=1}^n(2p_i+k)$. Since $\deg P_3=\max \{\sum _{i=1}^n(2p_i+k),\ l-m\}$ if $\sum _{i=1}^n(2p_i+k)\not =l-m$, we see that

$$\begin{aligned} \sum _{i=1}^n(2p_i+k)=l-m \end{aligned}$$

(2.11)

and $\mu =-1$. Hence $\deg Q_3\le n-1$, so that by (2.10)

$$\begin{aligned} \tau _3\le \frac{n-1}{k-1}. \end{aligned}$$

(2.12)

Now since $P_3$ has $\tau _3$ distinct zeros with exact multiplicity k, we can obtain that

$$\begin{aligned} \prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+k}-\zeta ^{l-m}=c\left[ \prod _{i=1}^{\tau _3}(\zeta -w_i)\right] ^{k} \end{aligned}$$

(2.13)

for some nonzero constant c and $\tau _3$ distinct nonzero points $w_i$. It follows from (2.13) with the transformation $\zeta \rightarrow 1/z$ that

$$\begin{aligned} R(z):=\prod _{i=1}^n(1-\zeta _iz)^{2p_i+k}-1 =cz^{l-m-\tau _3k}\left[ \prod _{i=1}^{\tau _3}(1-w_iz)\right] ^{k}. \end{aligned}$$

Thus 0 is a zero of R with multiplicity $l-m-\tau _3k$. Since

$$\begin{aligned} R'(z)=\prod _{i=1}^n(1-\zeta _iz)^{2p_i+k-1}\left[ \sum _{i=1}^n(2p_i+k)(-\zeta _i) \prod _{j\ne i}(1-\zeta _jz)\right] , \end{aligned}$$

we see that 0 is a zero of $R'$ with multiplicity at most $n-1$. Hence

$$\begin{aligned} l-m-\tau _3k\le n. \end{aligned}$$

This with (2.11) and (2.12) shows that

$$\begin{aligned} (k+2)n\le \sum _{i=1}^n(2p_i+k)=l-m\le \tau _3k+n\le \frac{k(n-1)}{k-1}+n, \end{aligned}$$

which is impossible.

Case 2. g has no nonzero poles. Then as $g^{(k)}(\zeta )\ne 0$ on $\mathbb {C}\setminus \{0\}$, we have $g^{(k)}(\zeta )=c\zeta ^s$ for some constant $c\ne 0$ and integer $s\in \mathbb {Z}$.

If $s\ge 0$, then g is a polynomial with $\deg g=s+k$. And since $g(\zeta )g^{(k)}(\zeta )\ne \zeta ^m$ on $\mathbb {C}\setminus \{0\}$, we also have $g(\zeta )g^{(k)}(\zeta )=\zeta ^m+{\uplambda }\zeta ^t$ for some constant ${\uplambda }\ne 0$ and integer t. Thus

$$\begin{aligned} g(\zeta )=\frac{1}{c}\zeta ^{m-s}+\frac{{\uplambda }}{c}\zeta ^{t-s}. \end{aligned}$$

If $m\not =t$, then it can be seen that g has at least one simple zero on $\mathbb {C}\setminus \{0\}$, which contradicts that all zeros of g on $\mathbb {C}\setminus \{0\}$ have multiplicity $k\ge 2$. Thus $m=t$, then ${\uplambda }+1\not =0$ and $g(\zeta )=({\uplambda }+1)\zeta ^{m-s}/c$. Thus $m-s=\deg g=s+k$, and hence $m-s=(m+k)/2$, so that $g(\zeta )=C\zeta ^{\frac{m+k}{2}}$ for some nonzero constant C and $m\ge k$.

If $s<0$, then 0 is the pole of g with multiplicity $-s-k>0$. And since $g(\zeta )g^{(k)}(\zeta )\ne \zeta ^m$ on $\mathbb {C}\setminus \{0\}$, we also have $g(\zeta )g^{(k)}(\zeta )=\zeta ^m+{\uplambda }\zeta ^t$ for some constant ${\uplambda }\ne 0$ and integer t. Thus

$$\begin{aligned} g(\zeta )=\frac{1}{c}\zeta ^{m-s}+\frac{{\uplambda }}{c}\zeta ^{t-s}. \end{aligned}$$

If $m\not =t$, then it can be seen that g has at least one simple zero on $\mathbb {C}\setminus \{0\}$, which contradicts that all zeros of g on $\mathbb {C}\setminus \{0\}$ have multiplicity $k\ge 2$. Thus $m=t$, then ${\uplambda }+1\not =0$ and $g(\zeta )=({\uplambda }+1)\zeta ^{m-s}/c$. Thus $-m+s=-s-k$, and hence $m-s=(m+k)/2<0$, so that $g(\zeta )=C\zeta ^{\frac{m+k}{2}}$ for some nonzero constant C. Note, $m=2s+k\le -2(k+1)+k\le -(k+2)$.

The lemma is proved.$\square$

Lemma 2.6

Let g be a meromorphic function on $\mathbb {C}$. If $g'(\zeta )\ne 0$ on $\mathbb {C}\setminus \{0\}$, then the equation $g(\zeta )g'(\zeta )= \gamma \zeta ^{-1}$ has solutions on $\mathbb {C}\setminus \{0\}$, where $\gamma$ is a given nonzero constant.

Proof

Without loss of generality, we may assume that $\gamma =1$.

Suppose first that g is transcendental. Then by Lemma 2.4, $\frac{1}{2}(g^2)'-\zeta ^{-1}$ has infinitely many zeros on $\mathbb {C}$, hence $g(\zeta )g'(\zeta )= \zeta ^{-1}$ has infinitely many zeros on $\mathbb {C}\setminus \{0\}$.

Next we suppose that g is a polynomial. Since $g'(\zeta )\ne 0$ on $\mathbb {C}\setminus \{0\}$, we have $g(\zeta )=a\zeta ^n+b$, where $a\ne 0$. Then $g(\zeta )g'(\zeta )-\zeta ^{-1}=n\zeta ^{-1}(a\zeta ^{2n}+b\zeta ^{n}+1)$ must have zero on $\mathbb {C}\setminus \{0\}$. $\square$

Finally, we suppose that g is non-polynomial rational function.

Case 1. If $g'(\zeta )\ne 0$ on $\mathbb {C}$, then by Lemma 2.3, $g(\zeta )=B+A/(z+a)^n$, where $A\ne 0,B$ are two constants. Then

$$\begin{aligned} g(\zeta )g'(\zeta )-\zeta ^{-1}=\frac{-An[A+B(\zeta +a)^n]\zeta -(\zeta +a)^{2n+1}}{\zeta (\zeta +a)^{2n+1}}. \end{aligned}$$

If $a\ne 0$, we see that $g(\zeta )g'(\zeta )-\zeta ^{-1}$ must have zeros on $\mathbb {C}\setminus \{0\}$. If $a=0$, then

$$\begin{aligned} g(\zeta )g'(\zeta )-\zeta ^{-1}=\frac{-An(A+B\zeta ^n)-\zeta ^{2n}}{\zeta ^{2n+1}} \end{aligned}$$

also has zeros on $\mathbb {C}\setminus \{0\}$.

Case 2. If $g'(\zeta )\ne 0$ on $\mathbb {C}\setminus \{0\}$ and $g'(0)=0$, then we can suppose that

$$\begin{aligned} g'(\zeta )=\frac{\mu \zeta ^l}{\prod _{i=1}^n(\zeta -\zeta _i)^{p_i+1}}, \end{aligned}$$

(2.14)

where $\zeta _i\ne 0(i=1,2,\ldots ,n)$ are all distinct poles of g, $\mu$ is a nonzero constant and $l\in \mathbb {Z}$ is a positive integer. If $g(\zeta )g'(\zeta )\ne \zeta ^{-1}$ on $\mathbb {C}\setminus \{0\}$, then we can suppose that

$$\begin{aligned} g(\zeta )g'(\zeta )=\zeta ^{-1}+\frac{{\uplambda }\zeta ^s}{\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+1}}, \end{aligned}$$

where ${\uplambda }$ is a nonzero constant. We see that $s=-1$, otherwise $\zeta =0$ would be a pole of $gg'$, hence of g, which contradicts that $g'(0)=0$. Then we have

$$\begin{aligned} g(\zeta )g'(\zeta )= \frac{\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+1}+{\uplambda }}{\zeta \prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+1}}, \end{aligned}$$

hence

$$\begin{aligned} g(\zeta )=\frac{Q(\zeta )}{\mu \zeta ^{l+1}\prod _{i=1}^n(\zeta -\zeta _i)^{p_i}},\ \text {where}\ Q(\zeta )=\prod _{i=1}^n(\zeta -\zeta _i)^{2p_i+1}+{\uplambda }. \end{aligned}$$

Case 2.1. If $g(0)=0$, then $\zeta =0$ is a zero of $Q(\zeta )$ with multiplicity $2(l+1)$ and

$$\begin{aligned} g(\zeta )=\frac{\zeta ^{l+1}P(\zeta )}{\mu \prod _{i=1}^n(\zeta -\zeta _i)^{p_i}}, \end{aligned}$$

where $P(\zeta )$ is a monic polynomial and

$$\begin{aligned} \deg P=\deg Q-2(l+1)=\sum _{i=1}^n(2p_i+1)-2(l+1)\ge 0. \end{aligned}$$

Then we have

$$\begin{aligned} g'(\zeta )=\frac{\zeta ^l P_1(\zeta )}{\mu \prod _{i=1}^n(\zeta -\zeta _i)^{p_i+1},} \end{aligned}$$

(2.15)

where $P_1(\zeta )=[(l+1)P(\zeta )+\zeta P'(\zeta )]\prod _{i=1}^n(\zeta -\zeta _i)-\zeta P(\zeta )\sum _{i=1}^n{p_i}\prod _{j\ne i}(\zeta -\zeta _j)$. We see that the polynomial $P_1(\zeta )$ is not a constant, since the first coefficient of $P_1(\zeta )$ is

$$\begin{aligned} l+1+\deg P-\sum _{i=1}^np_i=\sum _{i=1}^n(p_i+1)-(l+1)\ge \frac{n}{2}>0. \end{aligned}$$

Hence comparing with (2.15) and (2.14), it is a contradiction.

Case 2.2. If $g(0)\ne 0$, then $\zeta =0$ is a zero of $Q(\zeta )$ with multiplicity $l+1$ and

$$\begin{aligned} g(\zeta )=\frac{P(\zeta )}{\mu \prod _{i=1}^n(\zeta -\zeta _i)^{p_i}}, \end{aligned}$$

where $P(\zeta )$ is a monic polynomial and

$$\begin{aligned} \deg P=\deg Q-(l+1)=\sum _{i=1}^n(2p_i+1)-(l+1)\ge 0. \end{aligned}$$

Then we have

$$\begin{aligned} g'(\zeta )=\frac{P_2(\zeta )}{\mu \prod _{i=1}^n(\zeta -\zeta _i)^{p_i+1}}, \end{aligned}$$

(2.16)

where $P_2(\zeta )=P'(\zeta )\prod _{i=1}^n(\zeta -\zeta _i)-P(\zeta )\sum _{i=1}^n{p_i}\prod _{j\ne i}(\zeta -\zeta _j)$. We see that the leading term of $P_2(\zeta )$ is

$$\begin{aligned} \left( \deg P-\sum _{i=1}^np_i\right) \zeta ^{\deg P+n-1}=\left[ \sum _{i=1}^n(p_i+1)-(l+1)\right] \zeta ^{\sum _{i=1}^n(2p_i+2)-(l+2)}. \end{aligned}$$

If $\sum _{i=1}^n(p_i+1)-(l+1)\ne 0$, then $\sum _{i=1}^n(2p_i+2)-(l+2)\ne l$. Hence comparing with (2.16) and (2.14), it is a contradiction.

If $\sum _{i=1}^n(p_i+1)-(l+1)=0$, then $\sum _{i=1}^n(2p_i+2)-(l+2)=l$. Hence comparing with (2.16) and (2.14), it is also a contradiction.

The lemma is proved.

3 Proof of Theorem 1.1

In this section, we first prove the following theorem.

Theorem 3.1

Let $\{f_n\}$ be a sequence of meromorphic functions on D whose zeros have multiplicity at least k, where k is a positive integer. Let $\{a_n\}$ and $\{h_n\}$ be two sequences of meromorphic functions on D such that and on D, where $a(z)\ne 0,\infty ,h(z)\ne 0,\infty$ on D, and let $l\in \mathbb {Z}$ be an integer such that $2l<k$. Then the family $\{f_n\}$ is normal on D provided that $f_n(z)f_n ^{(k)}(z) = a_n(z) \Leftrightarrow f_n^{(k)}(z) = z^{-l}h_n(z)$ for every $f_n\in \{f_n\}$.

Proof

Suppose that $\{f_n\}$ is not normal at some point $z_0\in D$. Then by Lemma 2.1, there exist points $z_n\rightarrow z_0$, a subsequence of $\{f_n\}$ (we still denote $\{f_n\}$) and positive numbers $\rho _n\rightarrow 0$, such that

on D, where g a nonconstant meromorphic function with bounded spherical derivative (and hence of order at most two), all of whose zeros are of multiplicity at least k. We denote $a_0=a(z_0)(\not =0,\infty )$. $\square$

Case 1. $l\le 0$, or $l>0$ with $z_0\not =0$.

We claim that (i) $gg^{(k)} \not \equiv a_0$, and (ii) $g^{(k)} \not \equiv 0$.

In fact, if $gg^{(k)}\equiv a_0$, then g is a nonconstant entire function (and hence of exponential type) and $g\ne 0$. Hence $g(\zeta ) = \mathrm{{e}}^{c\zeta +d}$, where $c(\ne 0), d \in \mathbb {C}$. But then $g(\zeta )g^{(k)}(\zeta )=c^k\mathrm{{e}}^{2c\zeta +2d}\not \equiv a_0$ , a contradiction. Similarly, if $g^{(k)}\equiv 0$, then g is a nonconstant polynomial of degree less than k. This contradicts that all zeros of g have multiplicity at least k.

We further claim that (iii) $gg^{(k)} \ne a_0$, and (iv) $g^{(k)} \ne 0$.

To prove (iii), suppose that $g(\zeta _0)g^{(k)}(\zeta _0)= a_0$ for some $\zeta _0\in \mathbb C$. Then g is holomorphic on some close neighborhood U of $\zeta _0$, and hence $g_n(\zeta )g_n^{(k)}(\zeta )-a_n(z_n+\rho _n\zeta )\rightarrow g(\zeta )g^{(k)}(\zeta )- a_0$ on U uniformly. Since $gg^{(k)}\not \equiv a_0$, by Hurwitz’s theorem, there exist points $\zeta _n\rightarrow \zeta _0$ such that (for n sufficiently large)

$$\begin{aligned} a_n(z_n+\rho _n\zeta _n) = g_n(\zeta _n)g^{(k)}(\zeta _n)=f_n(z_n+\rho _n\zeta _n)f_n^{(k)}(z_n+\rho _n\zeta _n). \end{aligned}$$

Hence by the condition, $f_n^{(k)}(z_n+\rho _n\zeta _n)=(z_n+\rho _n\zeta _n)^{-l}h_n(z_n+\rho _n\zeta _n)$, so that $g_n^{(k)}(\zeta _n)=\rho _n^{\frac{k}{2}}f_n^{(k)}(z_n+\rho _n\zeta _n) =\rho _n^{\frac{k}{2}}(z_n+\rho _n\zeta _n)^{-l}h_n(z_n+\rho _n\zeta _n).$ Thus $g^{(k)}(\zeta _0)=\lim _{n\rightarrow \infty }g^{(k)}(\zeta _n)=0$, which contradicts that $g(\zeta _0)g^{(k)}(\zeta _0)= a_0\ne 0$. This proves (iii).

Next we prove (iv). Suppose that $g^{(k)}(\zeta _0)= 0$ for some $\zeta _0\in \mathbb C$. Then g is holomorphic on some close neighborhood U of $\zeta _0$, and hence $g_n^{(k)}(\zeta )-\rho _n^{\frac{k}{2}}(z_n+\rho _n\zeta _n)^{-l}h_n(z_n+\rho _n\zeta )\rightarrow g^{(k)}(\zeta )$ on U uniformly. Since $g^{(k)}(\zeta )\not \equiv 0$, by Hurwitz’s theorem, there exist points $\zeta _n\rightarrow \zeta _0$ such that (for n sufficiently large)

$$\begin{aligned} g_n^{(k)}(\zeta _n)-\rho _n^{\frac{k}{2}}(z_n+\rho _n\zeta _n)^{-l}h_n(z_n+\rho _n\zeta _n)=0. \end{aligned}$$

It follows that $f_n^{(k)}(z_n+\rho _n\zeta _n)=(z_n+\rho _n\zeta _n)^{-l}h_n(z_n+\rho _n\zeta _n)$, and hence by the condition, we have

$$\begin{aligned} a_n(z_n+\rho _n\zeta _n)=f_n(z_n+\rho _n\zeta _n)f_n^{(k)}(z_n+\rho _n\zeta _n)=g_n(\zeta _n)g_n^{(k)}(\zeta _n). \end{aligned}$$

This leads to a contradiction that

$$\begin{aligned} a_0=a(z_0)=\lim _{n\rightarrow \infty }g_n(\zeta _n)g_n^{(k)}(\zeta _n)=g(\zeta _0)g^{(k)}(\zeta _0)=0. \end{aligned}$$

(iv) is also proved.

However, by Lemma 2.2, there is no nonconstant meromorphic function g on $\mathbb {C}$ with the properties (iii) and (iv) such that all zeros have multiplicity at least k.

Case 2. $l\ge 1$ and $z_0=0$. Then we have $k>2$ for the condition $2l<k$. In this part, we consider two cases.

Case 2.1. Suppose that $\frac{z_n}{\rho _n}\rightarrow \infty$. Let

$$\begin{aligned} G_n(\zeta )=z_n^{-\frac{k}{2}}f_n(z_n+z_n\zeta ). \end{aligned}$$

Then we see that

$$\begin{aligned} G_n(\zeta )G_n^{(k)}(\zeta )=a_n(z_n+z_n\zeta )\Longleftrightarrow G_n^{(k)}(\zeta )=z_n^{\frac{k}{2}-l}(1+\zeta )^{-l}h_n(z_n+z_n\zeta ). \end{aligned}$$

By Case 1, we see that $\{G_n\}$ is normal on $\Delta (0,1)$. Say on $\Delta (0,1)$. We claim that $G(0)=0$ and hence $G\not \equiv \infty$. Suppose $G(0)\not =0$, then by $\frac{z_n}{\rho _n}\rightarrow \infty$, we have

on $\mathbb {C}$. This is a contradiction. Hence $G(0)=0$, so that $G_n^{(k)}\rightarrow G^{(k)}$ in some neighborhood of 0. It follows that

on $\mathbb {C}$. Thus $g^{(k)}\equiv 0$, which contradicts that all zeros of g have multiplicity at least k and g is nonconstant.

Case 2.2. So we may assume that $\frac{z_n}{\rho _n}\rightarrow c$, a finite complex number. Then we have

on $\mathbb {C}$, and all zeros of $H(\zeta )$ have multiplicity at least k. And since g is nonconstant, we see that H is also nonconstant. We see from the condition that

$$\begin{aligned} H_n(\zeta )H_n^{(k)}(\zeta )=a_n(\rho _n\zeta )\Longleftrightarrow H_n^{(k)}(\zeta )=\rho _n^{\frac{k}{2}-l}\zeta ^{-l}h_n(\rho _n\zeta ). \end{aligned}$$

(3.1)

We claim that (i) $HH^{(k)}\not \equiv a_0$ and (ii) $H^{(k)}\not \equiv 0$.

If $HH^{(k)}\equiv a_0$, then H is a zero-free entire function of finite order and H is not a polynomial. Thus $H(\zeta )=\mathrm{{e}}^{Q(\zeta )}$, where Q is a nonconstant polynomial, then $H^{(k)}(\zeta )=P(\zeta )\mathrm{{e}}^{Q(\zeta )}$, where P is a polynomial. It follows that $H(\zeta )H^{(k)}(\zeta )=P(\zeta )\mathrm{{e}}^{2Q(\zeta )}\not \equiv a_0$, which is a contradiction. So $HH^{(k)}\not \equiv a(0)$. If $H^{(k)}\equiv 0$, H would be a polynomial of degree less than k. Since H is nonconstant, H has at least one zero. The multiplicity of the zero cannot be larger than the degree of the polynomial H. This contradicts that all zeros of H have multiplicity at least k.

We further claim that (iii) $HH^{(k)} \ne a_0$ on $\mathbb C\setminus \{0\}$, and (iv) $H^{(k)} \ne 0$ on $\mathbb C\setminus \{0\}$.

Suppose that $H(\zeta _0)H^{(k)}(\zeta _0)= a_0$ at some point $\zeta _0\ne 0$. Then $H(\zeta _0)\ne \infty$, and hence H is holomorphic on some close neighborhood U of $\zeta _0$. Thus

$$\begin{aligned} H_n(\zeta )H_n^{(k)}(\zeta )-a_n(\rho _n\zeta )\rightarrow H(\zeta )H^{(k)}(\zeta )-a_0 \end{aligned}$$

on U uniformly. Since $H(\zeta )H^{(k)}(\zeta )\not \equiv a_0$, by Hurwitz’s theorem, there exist points $\zeta _n,\zeta _n\rightarrow \zeta _0$, such that (for n sufficiently large)

$$\begin{aligned} H_n(\zeta _n)H_n^{(k)}(\zeta _n)-a_n(\rho _n\zeta _n)=0. \end{aligned}$$

By (3.1), we have $H_n^{(k)}(\zeta _n)=\rho _n^{\frac{k}{2}-l}\zeta _n^{-l}h_n(\rho _n\zeta _n)$ and hence

$$\begin{aligned} H^{(k)}(\zeta _0)=\lim _{n\rightarrow \infty }H_n^{(k)}(\zeta _n) =\lim _{n\rightarrow \infty }\rho _n^{\frac{k}{2}-l}\zeta _n^{-l}h_n(\rho _n\zeta _n) =0, \end{aligned}$$

which contradicts that $H(\zeta _0)H^{(k)}(\zeta _0)= a_0\ne 0$. The claim (iii) is proved.

Next we suppose that $H^{(k)}(\zeta _0)= 0$ at some point $\zeta _0\ne 0$. Then $H(\zeta _0)\ne \infty$, so that H is holomorphic on some close neighborhood U of $\zeta _0$, and hence

$$\begin{aligned} H_n^{(k)}(\zeta )-\rho _n^{\frac{k}{2}-l}\zeta ^{-l}h_n(\rho _n\zeta )\rightarrow H^{(k)}(\zeta ) \end{aligned}$$

on U uniformly. Since $H^{(k)}(\zeta )\not \equiv 0$, by Hurwitz’s theorem, there exist points $\zeta _n,\zeta _n\rightarrow \zeta _0$, such that (for n sufficiently large)

$$\begin{aligned} H^{(k)}(\zeta _n) -\rho _n^{\frac{k}{2}-l}\zeta _n^{-l}h_n(\rho _n\zeta _n)=0.\end{aligned}$$

Then by (3.1), we have $H_n(\zeta _n)H_n^{(k)}(\zeta _n)=a_n(\rho _n\zeta _n)$, and hence

$$\begin{aligned} H(\zeta _0)H^{(k)}(\zeta _0) =\lim _{n\rightarrow \infty }H_n(\zeta _n)H_n^{(k)}(\zeta _n)=\lim _{n\rightarrow \infty }a_n(\rho _n\zeta _n)=a_0. \end{aligned}$$

This contradicts the claim (iii). The claim (iv) is also proved.

Thus, by Lemma 2.5 with $m=0$, $H(\zeta )=C\zeta ^{\frac{k}{2}}$. This contradicts that all zeros of H have multiplicity at least k.

Hence $\mathcal {F}$ is normal on D. The proof is completed. $\square$

Proof of Theorem 1.1

By the proof of Theorem 3.1, we have showed that $\mathcal {F}$ is normal on $D\setminus a^{-1}(0)\bigcup a^{-1}(\infty )$, where $a^{-1}(0)$ stands for the set of zeros of a and $a^{-1}(\infty )$ stands for the set of poles of a. Next, we prove that $\mathcal {F}$ is also normal at every zero or pole of a in D.

Suppose that $\mathcal {F}$ is not normal at $z_0\in D$, where $z_0$ is a zero or a pole of a. Without loss of generality, we may say $z_0=0$ and assume that $a(z)=z^mh(z)$ and $b(z)=z^{-l}b_1(z)$, where $m,l\in \mathbb {Z}$, h(z), and $b_1(z)$ are holomorphic and zero free on $\Delta (0,\delta )\subset D$. We assume that $h(0)=1$. We note by the condition that $-k\le m \le k-1,m\ne 0$ and $l<\frac{k-m}{2}$ if $l>0$. In particular, $0\le \frac{m+k}{2}<k$.

Then by Lemma 2.1, there exist points $z_n\rightarrow 0$, functions $f_n\in \mathcal F$, and positive numbers $\rho _n\rightarrow 0$ such that

on $\mathbb C$, where g is a nonconstant meromorphic function of finite order, and all zeros of g have multiplicity at least k.

Case 1. Suppose that $\frac{z_n}{\rho _n}\rightarrow \infty$. Let

$$\begin{aligned} G_n(\zeta )=z_n^{-\frac{m+k}{2}}f_n(z_n+z_n\zeta ). \end{aligned}$$

Then by the condition $f(z)f ^{(k)}(z) = a(z) \Leftrightarrow f^{(k)}(z) = b(z)$, we have

$$\begin{aligned} G_n(\zeta )G_n^{(k)}(\zeta )=(1+\zeta )^mh(z_n+z_n\zeta )\Longleftrightarrow G_n^{(k)}(\zeta )=z_n^{\frac{k-m}{2}-l}(1+\zeta )^{-l}b_1(z_n+z_n\zeta ). \end{aligned}$$

Since $z_n\rightarrow 0$ and $h(0),\ b_1(0)\not =0,\infty$, by Theorem 3.1, we see that $\{G_n\}$ is normal on $\Delta (0,1)$. Say on $\Delta (0,1)$. We claim that $G(0)=0$ and hence $G\not \equiv \infty$. Suppose $G(0)\not =0$, then by $\frac{z_n}{\rho _n}\rightarrow \infty$, we have

on $\mathbb {C}$. This is a contradiction. Hence $G(0)=0$, so that $G_n^{(k)}\rightarrow G^{(k)}$ in some neighborhood of 0. It follows that

on $\mathbb {C}$. Thus $g^{(k)}\equiv 0$, which contradicts that all zeros of g have multiplicity at least k and g is nonconstant.

Case 2. So we may assume that $\frac{z_n}{\rho _n}\rightarrow c$, a finite complex number. Then we have

on $\mathbb {C}$, and all zeros of $H(\zeta )$ have multiplicity at least k. And since g is nonconstant, we see that H is also nonconstant. We see from the condition that

$$\begin{aligned} H_n(\zeta )H_n^{(k)}(\zeta )=\zeta ^mh(\rho _n\zeta )\Longleftrightarrow H_n^{(k)}(\zeta )=\rho _n^{\frac{k-m}{2}-l}\zeta ^{-l}b_1(\rho _n\zeta ). \end{aligned}$$

(3.2)

We claim that (i) $H(\zeta )H^{(k)}(\zeta )\not \equiv \zeta ^m$ and (ii) $H^{(k)}(\zeta )\not \equiv 0$.

In fact, if $H(\zeta )H^{(k)}(\zeta )\equiv \zeta ^m$, then $\zeta =0$ is the only possible zero or pole of H. If H is a transcendental function, then $H(\zeta )=\zeta ^{\alpha }\mathrm{{e}}^{Q(\zeta )}$ for some $\alpha \in \mathbb {Z}$ and polynomial Q. Thus $H^{(k)}(\zeta )=P(\zeta )\mathrm{{e}}^{Q(\zeta )}$, where $P(\zeta )(\not \equiv 0)$ is a rational function. It follows that $HH^{(k)}$ is also a transcendental function, which is a contradiction. If H is a rational function and $\zeta =0$ is a pole of H, then $\zeta =0$ is the pole of $HH^{(k)}$ with multiplicity at least $k+2$, which contradicts $H(\zeta )H^{(k)}(\zeta )\equiv \zeta ^m, -k\le m\le k-1$. If H is a rational function and $\zeta =0$ is not a pole of H, then H is a polynomial. If $\deg H\ge k$, then $\deg (HH^{(k)})\ge k$. Otherwise, $HH^{(k)}\equiv 0$. Both cases contradict that $H(\zeta )H^{(k)}(\zeta )\equiv \zeta ^m$. So $H(\zeta )H^{(k)}(\zeta )\not \equiv \zeta ^m$.

If $H^{(k)}\equiv 0$, H would be a polynomial of degree less than k. Since H is nonconstant, H has at least one zero. The multiplicity of the zero cannot be larger than the degree of the polynomial H. This contradicts that all zeros of H have multiplicity at least k.

We further claim that (iii) $H(\zeta )H^{(k)}(\zeta ) \ne \zeta ^m$ on $\mathbb C\setminus \{0\}$, and (iv) $H^{(k)}(\zeta ) \ne 0$ on $\mathbb C\setminus \{0\}$.

Suppose that $H(\zeta _0)H^{(k)}(\zeta _0)= \zeta _0^m,\zeta _0\ne 0$. Then $H(\zeta _0)\ne \infty$. H is holomorphic on some close neighborhood U of $\zeta _0$, and hence

$$\begin{aligned} H_n(\zeta )H_n^{(k)}(\zeta )-\zeta ^m h(\rho _n\zeta )\rightarrow H(\zeta )H^{(k)}(\zeta )-\zeta ^m \end{aligned}$$

on U uniformly. Since $H(\zeta )H^{(k)}(\zeta ) \not \equiv \zeta ^m$, by Hurwitz’s theorem, there exist points $\zeta _n,\zeta _n\rightarrow \zeta _0$, such that (for n sufficiently large)

$$\begin{aligned} H_n(\zeta _n)H_n^{(k)}(\zeta _n)-\zeta _n^m h(\rho _n\zeta _n)=0. \end{aligned}$$

By (3.2), we have

$$\begin{aligned} H_n^{(k)}(\rho _n\zeta _n) =\rho _n^{\frac{k-m}{2}-l}\zeta _n^{-l}b_1(\rho _n\zeta _n). \end{aligned}$$

By the condition $\frac{k-m}{2}-l>0$ and $\zeta _n\rightarrow \zeta _0\ne 0$, we have

$$\begin{aligned} H^{(k)}(\zeta _0)=\lim _{n\rightarrow \infty }H_n^{(k)}(\zeta _n) =\lim _{n\rightarrow \infty }\rho _n^{\frac{k-m}{2}-l}\zeta _n^{-l}b_1(\rho _n\zeta _n) =0,\end{aligned}$$

which contradicts that $H(\zeta _0)H^{(k)}(\zeta _0)= \zeta _0^m\ne 0$. Then (iii) is proved.

Next we suppose that $H^{(k)}(\zeta _0)= 0,\zeta _0\ne 0$. Thus $H(\zeta _0)\ne \infty$. H is holomorphic on some close neighborhood U of $\zeta _0$, and hence

$$\begin{aligned} H_n^{(k)}(\zeta )-\rho _n^{\frac{k-m}{2}-l}\zeta ^{-l}b_1(\rho \zeta )\rightarrow H^{(k)}(\zeta ) \end{aligned}$$

on U uniformly. Since $H^{(k)}(\zeta ) \not \equiv 0$, by Hurwitz’s theorem, there exist points $\zeta _n,\zeta _n\rightarrow \zeta _0$, such that (for n sufficiently large )

$$\begin{aligned} H^{(k)}(\zeta _n) -\rho _n^{\frac{k-m}{2}-l}\zeta _n^{-l}b_1(\rho \zeta _n)=0. \end{aligned}$$

Then by (3.2) we have $H_n(\zeta _n)H_n^{(k)}(\zeta _n)=\zeta _n^mh(\rho _n\zeta _n)$, thus

$$\begin{aligned} H(\zeta _0)H^{(k)}(\zeta _0) =\lim _{n\rightarrow \infty }H_n(\zeta _n)H_n^{(k)}(\zeta _n) =\lim _{n\rightarrow \infty }\zeta _n^mh(\rho _n\zeta _n)=\zeta _0^m. \end{aligned}$$

This contradicts to claim (iii). So (iv) is proved.

If $k\ge 2$, then by Lemma 2.5 and claims (iii) and (iv), we get $m\ge k$ or $m\le -(k+2)$, which are ruled out by the assumption.

If $k=1$, then $m=-1$. By Lemma 2.6, there is no meromorphic function satisfying claims (iii) and (iv).

The proof of Theorem 1.1 is completed. $\square$